Nonlinear surface SH waves in a half-space covered by an irregular layer

Abstract

Research on the shear horizontal (SH) waves propagating in a nonlinear elastic half-space coated with a nonlinear elastic layer having slow variation in the boundary surfaces is presented. It is assumed that both the free surface and interface change as a function of the distance in the direction of propagation of the waves. By employing a perturbation method, nonlinear self-modulation of the surface SH waves for a general geometry is characterized by a generalized nonlinear Schrödinger (GNLS) equation with variable coefficients depending on functions representing the irregularities of boundary surfaces in addition to linear and nonlinear material parameters of the medium. The solitary wavelike solutions of this GNLS equation are obtained for certain special cases of the irregular boundary surfaces. It has been demonstrated by graphs that the propagation characteristics of SH waves are significantly affected by slowly varying layer and nonlinear properties of the media.

1 Introduction

The existence of horizontally polarized surface shear waves in linear elastic layered half-space bounded by regular boundary surfaces is discovered by Love [35]. Love waves become dispersive due to repeated reflections which take place between the top and bottom surface of the layer. It is well known that crustal part of the Earth is not always uniform such as continental margins and mountain roots. The propagation of SH waves in layers with irregular boundaries has received much attention in geophysics, seismology, especially in earthquake engineering due to importance of the seismic wave propagation inside the earth with varying crustal thickness. Many researchers have studied the effect of variations in the crustal thickness on the propagation characteristics of linear surface SH waves. As the analysis of problem in a layered crustal structure with an arbitrary surface shape is very complicated, investigators have been considering the wave propagation for particular types of irregular boundary surfaces. Noyer [1] has derived frequency equation of Love waves in a semi-infinite media underlying an irregular crust whose interface varies sinusoidally. Sato [2] has searched for the transmitted and reflected SH waves in a layered structure whose thickness has a discontinuous jump. Mal [3] has investigated the effect of the abruptly increasing layer thickness on the phase velocity of Love waves. Takahashi [4] has studied the transmission of Love waves in a layer overlying a semi-infinite media when the thickness of surface layer varies hyperbolically. Wolf [5, 6] has determined the reflected field when a Love wave is incident on a layer having irregular free surface by using a perturbation method. Woodhouse [7] has applied a perturbation procedure to surface waves in a laterally varying layer resting on semi-infinite elastic medium. Gjevic [8] has formulated a variational principle for the modulation of Love waves in a layer that slowly varies at the boundary surfaces with an underlying half-space for a general geometry. Markenscoff and Lekoudis [9] have obtained a uniformly valid asymptotic solution for the amplitude function of Love waves by considering the similar model as Gjevic. Hador and Buchen [10] have derived a perturbation formula from a first-order perturbation theory introduced by Whitham [11] for the propagation of Love and Rayleigh waves in multilayered structures with lateral variations in the layer thickness. Moreover, Ahmad et. al. have derived an explicit asymptotic model for transient Love waves propagating in a half-space with a thin coating [12]. Acharya and Roy [13] have investigated the effect of rectangular and parabolic irregularities of the interface, surface stress and magnetic field on the propagation of SH waves in a magneto elastic crust resting on an isotropic elastic half-space. Singh [14] has performed numerical computation of phase velocity and group velocity of Love waves which propagate in a corrugated layer overlying a semi-infinite media for the special types of boundary surfaces. Considering the plane problem in linear elasticity for a coated half-space with a clamped surface, Kaplunov et al. have numerically analysed the dispersion relation of Rayleigh-type waves by utilizing their similarity with Love-type waves [15]. Then Kaplunov et al. have studied on the integral and differential formulations for antiplane shear surface waves in a nonlocally elastic half-space [16].

Over the past few years, the effect of nonlinear constituent materials on the Love wave propagation has also been studied by many researchers for reasons similar to those mentioned above. Teymur [17] has studied the nonlinear modulation of Love waves propagating in a finite layer of uniform thickness based on an elastic half-space. Maugin and Hadouaj [18] have considered the similar problem in which the nonlinear substrate is coated with a very thin linear film. Teymur et al. [19] have taken into account the case that nonlinear half-space is covered by a thin but nonlinear layer and have derived a nonlinear Schrödinger (NLS) equation characterizing the nonlinear modulation of Love waves. Moreover, in [19], the comparisons of the approximations for nonlinear thin layer with the linear thin layer and with the finite nonlinear layer were performed. Then, Deliktas and Teymur [20] have expanded the propagation of nonlinear SH waves to a double-layered half-space and investigated the influence of the nonlinear characteristics of a second layer on the wave propagation.

In this article, the effect of nonlinear material properties as well as irregular boundary surfaces on the propagation characteristics of surface SH waves in a half-space underlying a layer of nonuniform thickness is studied for a general geometry. It is assumed that the irregularities of boundary surfaces are the functions of the distance in the direction of propagation of the waves; moreover, variations of the boundary surfaces are regarded as small compared to the layer’s average thickness. In the linear case, the problem reduces to propagation of Love wave searched by Markenscoff and Lekoudis [9]. When the scale of small variation is of order $\epsilon$, the analysis required to derive nonlinear evolution equation is dauntingly complex. Hence, we suppose that the boundary surfaces are the slowly varying functions of the scale $\epsilon ^2$ as in the study of water waves moving over variable depth [21], where $\epsilon$ is a small parameter. To reveal the effect of slow variation and construct the evolution equation, we use the multiple scales perturbation method. For a general geometry, nonlinear modulation of SH waves is characterized by a GNLS equation with variable coefficients depending on linear and nonlinear constitutional properties of the media and also slowly varying boundary surfaces. When the amplitudes of the functions representing the irregularities of the boundary surfaces are zero, the geometry of the problem reduces to the one studied by Teymur [17], and also, GNLS equation with variable coefficients reduces to the NLS equation produced for the case of plane boundary surfaces. While the governing NLS equation with constant coefficients is always integrable, GNLS equation with variable coefficients may no longer be integrable because of the coefficients depending on the irregularities of boundary surfaces. We reveal that the GNLS equation preserves integrability while the functions representing the irregularities of free surface and interface are equal to each other. In this case, the layer thickness remains constant, whereas the boundary surfaces change. We have obtained the exact soliton-like solutions of the GNLS equation, assuming that the change in the boundary surfaces is periodic. For the case of slowly varying thickness which does not allow the integrability of the GNLS equation, because of the difficulties for the analytical solutions, the numerical solutions to the GNLS equation are sought by means of the pseudo-spectral method. The effects of periodic boundary surfaces and nonlinear material parameters of the media on the propagation characteristics of solitary waves have been presented graphically.

2 Equations of motion and boundary conditions

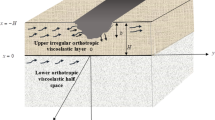
Let $(x_1,x_2,x_3)$ and $(X_1,X_2,X_3)$ denote, respectively, the spatial and material coordinates of a point referred to the same rectangular Cartesian system of axes. An elastic half-space underlying a layer having irregular boundary surfaces is considered. In the reference frame $(X_1,X_2,X_3)$, the layer $(P_1)$ and the half-space $(P_2)$ occupying the respective regions $f_2(X_1)< X_{2} < h+ f_1( X_{1})$ and $-\infty< X_{2} < f_2(X_1)$ are illustrated in Fig. 1 where h represents the layer’s average thickness. Irregularities of the free surface and interface are represented by the functions ${f_1(X_1), f_2(X_1)}\in C^{1}$.

Fig. 1

Layer with nonuniform thickness over a half-space

An SH wave which propagates along the $X_1$-axis is defined by

$$\begin{aligned} x_1=X_1,\quad x_2=X_2, \quad x_3= X_3 +u^{(r)}(X_1,X_2,t), \quad r=1,2 \end{aligned}$$

(2.1)

where the superscript r indicates the region $P_{r}$ and t represents the time. The particle displacement in the $X_3$ direction in $P_{r}$ is denoted by $u^{(r)}$. $det x_{k,K}=1$ yields that the deformation field (2.1) is isochoric; hence, the densities $\rho ^{(1)}$ and $\rho ^{(2)}$ remain unchanged.

In the reference state, the equations of motion without the body forces are [22]

$$\begin{aligned} T_{K\beta ,K}^{(r)}= 0, \quad \quad T_{K3,K}^{(r)}=\rho ^{(r)}\ddot{u}^{(r)},\quad r=1,2. \end{aligned}$$

(2.2)

Here, $T_{Kl}^{(r)}$ represents the first Piola–Kirchoff stress tensor, the ranges for Latin and Greek indices are (1, 2, 3) and (1, 2), respectively, subscripts preceded by a comma imply partial differentiation with respect to the material coordinates, and also, a dot over ${u}^{(r)}$ indicates the partial differentiation with respect to t. The summation convention on repeated indices is implied in (2.2) and in the sequel.

The assumption that tractions on the irregular free surface $X_2=h+f_1(X_1)$ vanish gives

$$\begin{aligned} N_{k}^{(1)}T_{kl}^{(1)}=0 \quad \hbox {on} \quad X_2=h+f_1(X_1). \end{aligned}$$

(2.3)

The displacements and stresses at the interface $X_2=f_2(X_1)$ are continuous if

$$\begin{aligned} u^{(1)}=u^{(2)} \quad \hbox {and} \quad N_{k}^{(2)}T_{kl}^{(1)}=N_{k}^{(2)}T_{kl}^{(2)}, \quad \hbox {on} \quad X_2=f_2(X_1), \end{aligned}$$

(2.4)

the radiation condition implies

$$\begin{aligned} u^{(2)} \rightarrow 0, \quad \hbox {as} \quad X_{2} \rightarrow - \infty \end{aligned}$$

(2.5)

where $N^{(1)}_{k}$ and $N^{(2)}_{k}$ denote the components of the vectors normal to the irregular boundary surfaces.

The considered materials are assumed to be nonlinear, homogeneous, isotropic and made of different generalized neo-Hooken materials; hence, their strain energy functions depend only on the first invariant of the Finger deformation tensor ${{\textbf {c}}}^{(-1)}=[x_{k,K} x_{l,K}]$, i.e. $\Sigma ^{(r)}=\Sigma ^{(r)}(I^{(r)})$, $r=1,2$ [23]. For the deformation field (2.1), the first invariants $I^{(r)}=tr {{\textbf {c}}}^{-1}$, $r=1,2$, can be evaluated as

$$\begin{aligned} I^{(r)}=3+\left( \frac{\partial u^{(r)} }{\partial X_1}\right) ^2+\left( \frac{\partial u^{(r)}}{\partial X_2}\right) ^2 \quad r=1,2. \end{aligned}$$

(2.6)

The stress constitutive equations for such a material are represented by (see, for example, [20])

$$\begin{aligned} t _{kl}^{(r)}=2\frac{\mathrm{d} \Sigma ^{(r)}}{\mathrm{d} I^{(r)}} \left( -{\delta }_{kl}+c_{kl}^{-1}\right) , \quad r=1,2 \end{aligned}$$

(2.7)

where $t_{kl}$ is the Cauchy stress tensor.

Since $T _{Kl}=j X_{K,k}t _{kl}$, where $j= det(x_{k,K})=1$, the Piola–Kirchoff stress tensor’s components are found to be

$$\begin{aligned} T_{\alpha \beta }^{(r)}=T_{33}^{(r)}=0~, \quad T_{\alpha 3}^{(r)}=T_{3 \alpha }^{(r)}=2\frac{\mathrm{d} \Sigma ^{(r)}}{\mathrm{d} I^{(r)}}u_{,\alpha }^{(r)}. \end{aligned}$$

(2.8)

Therefore, the first two equations in (2.2) are satisfied identically and the existence of antiplane wave motion (2.1) emerges in the absence of body forces.

Let $X=X_1$, $Y=X_2$, $Z=X_3$, then the third equation in (2.2) is expressed by

$$\begin{aligned} \frac{\partial }{\partial X}\left( 2\frac{\mathrm{d} \Sigma ^{(r)}}{\mathrm{d} I^{(r)}}\frac{\partial u^{(r)}}{\partial X}\right) +\frac{\partial }{\partial Y}\left( 2\frac{\mathrm{d} \Sigma ^{(r)}}{\mathrm{d} I^{(r)}}\frac{\partial u^{(r)}}{\partial Y}\right) =\rho ^{(r)} \frac{\partial ^{2}u^{(r)}}{\partial t^{2}}, \quad r=1,2. \end{aligned}$$

(2.9)

3 Nonlinear self-modulation of SH waves

In this article, nonlinear self-interaction of small but finite amplitude surface SH waves propagating in a half-space underlying a layer having slowly varying boundaries is studied. The amplitudes of irregularities in the boundary surfaces are assumed to be small compared to the layer’s average thickness. To make explicit distinction between slow and fast variables and to facilitate the derivation of the nonlinear evolution equation, multiple scales method is used and the following new variables are introduced [21, 24]:

$$\begin{aligned} \xi = \epsilon ^2 X, \quad \tau =\epsilon \left( \frac{1}{\epsilon ^2}\int \limits ^\xi \frac{1}{V_g(X')}\mathrm{d}X'-t\right) , \quad y=Y \quad \end{aligned}$$

(3.1)

where $(\xi , \tau )$ are the slow variables representing the slow variations, $\epsilon >0$ is a small parameter measuring the strength of nonlinearity and irregularities on the boundary surfaces and $V_g$ is the group velocity. As an extension of the multiple scale method, the phase function is introduced

$$\begin{aligned} \frac{\partial \theta }{\partial X}= k, \quad \frac{\partial \theta }{\partial t}= -\omega , \end{aligned}$$

(3.2)

where k and $\omega$ represent the wave number and frequency, respectively. Conservation of waves, $(\theta _{t})_{X}=(\theta _{X})_{t}$, implies that the frequency remains unchanged, whereas the wave number varies with X due to the spatial inhomogeneities on the boundary surfaces [24,25,26].

When the scale of irregularities of the boundary surfaces is $\epsilon$, the required analysis to derive nonlinear evolution equation is so complex that we suppose the boundary surfaces change on the scale of $\epsilon ^{2}$. Hence, the functions $f_1$ and $f_2$ representing the irregularities of free surface and interface in the direction of wave propagation, respectively, are the functions of $\xi$, with the assumption $\mathrm{d}f_1/\mathrm{d}\xi , \mathrm{d}f_2/\mathrm{d}\xi \sim O(1)$. In conformity with the slow variation in the boundary surfaces, the wave number $k = k(\xi )$ and the group velocity $V_g= V_g(\xi )$ characterizing the wave change with $\xi$.

Then $u^{(r)}$, $r=1,2$ as functions of (3.1) and $\theta$ are expanded in the following asymptotic series of $\epsilon$:

$$\begin{aligned} u^{(r)}=\sum _{n=1}^{\infty }\epsilon ^{n}u_{n}^{(r)}(\theta ,\xi ,\tau ,y). \end{aligned}$$

(3.3)

Employing the new stretched variables (3.1) in the governing equations (2.9) and boundary conditions (2.3)–(2.5) and then equating the coefficients of same powers of $\epsilon$ yield a hierarchy of problems. Hence, $u_{n}^{(r)}$ can be determined successively. First three problems are given by: $O(\epsilon )$:

$$\begin{aligned}&L(u_{1}^{(r)})\triangleq \omega ^2\frac{\partial ^{2}u_{1}^{(r)}}{\partial \theta ^{2}}-c_{r}^{2}\left( k^2\frac{\partial ^{2}u_{1}^{(r)}}{\partial \theta ^{2}}+\frac{\partial ^{2}u_{1}^{(r)}}{\partial y^{2}}\right) =0 \quad r=1,2. \end{aligned}$$

(3.4)

$$\begin{aligned}&\hbox {On} \quad y=h+f_1(\xi ),\quad \frac{\partial u_{1}^{(1)}}{\partial y}=0. \end{aligned}$$

(3.5)

$$\begin{aligned}&\hbox {On}\quad y=f_2(\xi ),\quad u_{1}^{(1)}=u_{1}^{(2)}\quad \text{ and }\quad \frac{\partial u_{1}^{(1)}}{\partial y}-\gamma \frac{\partial u_{1}^{(2)}}{\partial y}=0. \end{aligned}$$

(3.6)

$$\begin{aligned}&\hbox {As} \quad y\rightarrow -\infty ,\quad u_{1}^{(2)}\rightarrow 0 . \end{aligned}$$

(3.7)

$O(\epsilon ^{2})$:

$$\begin{aligned}&L(u_{2}^{(r)})=2\left( c_{r}^{2}\frac{k}{V_g}-\omega \right) \frac{\partial ^{2}u_{1}^{(r)}}{\partial \theta \partial \tau } \quad r=1,2. \end{aligned}$$

(3.8)

$$\begin{aligned}&\hbox {On} \quad y=h+f_1(\xi ), \quad \frac{\partial u_{2}^{(1)}}{\partial y}=0. \end{aligned}$$

(3.9)

$$\begin{aligned}&\hbox {On} \quad y=f_2(\xi ), \quad u_{2}^{(1)}=u_{2}^{(2)}\quad \hbox {and} \quad \frac{\partial u_{2}^{(1)}}{\partial y}-\gamma \frac{\partial u_{2}^{(2)}}{\partial y}=0. \end{aligned}$$

(3.10)

$$\begin{aligned}&\hbox {As} \quad y\rightarrow -\infty , \quad u_{2}^{(2)}\rightarrow 0. \end{aligned}$$

(3.11)

$O(\epsilon ^{3})$:

$$\begin{aligned} L(u_{3}^{(r)})= & {} 2\left( c_{r}^{2}\frac{k}{V_g}-\omega \right) \frac{\partial ^{2}u_{2}^{(r)}}{\partial \theta \partial \tau }+c_{r}^{2}\left( \frac{1}{V_g^2}\frac{\partial ^{2}u_{1}^{(r)}}{\partial \tau ^{2}}+2k\frac{\partial ^{2}u_{1}^{(r)}}{\partial \theta \partial \xi }+\frac{\partial k}{\partial \xi }\frac{\partial u_1^{(r)}}{\partial \theta }\right) -\frac{\partial ^{2}u_{1}^{(r)}}{\partial \tau ^{2}} \nonumber \\&\quad +\,n_{r}\left( k \frac{\partial }{\partial \theta }\left( k \frac{\partial u_{1}^{(r)}}{\partial \theta }{\mathcal {K}}(u_{1}^{(r)})\right) +\frac{\partial }{\partial y}\left( \frac{\partial u_{1}^{(r)}}{\partial y}{\mathcal {K}}(u_{1}^{(r)})\right) \right) \quad r=1,2, \end{aligned}$$

(3.12)

$$\begin{aligned}&\hbox {On} \quad y=h+f_1(\xi ), \quad \frac{\partial u_{3}^{(1)}}{\partial y}-\frac{\partial f_{1}}{\partial \xi }k\frac{\partial u_{1}^{(1)}}{\partial \theta }=0. \end{aligned}$$

(3.13)

$$\begin{aligned}&\hbox {On}\quad y=f_2(\xi ), \quad u_{3}^{(1)}=u_{3}^{(2)}\quad \hbox {and} \nonumber \\&\frac{\partial u_{3}^{(1)}}{\partial y}-\gamma \frac{\partial u_{3}^{(2)}}{\partial y}-\frac{\partial f_{2}}{\partial \xi }k\left( \frac{\partial u_{1}^{(1)}}{\partial \theta }-\gamma \frac{\partial u_{1}^{(2)}}{\partial \theta }\right) = \gamma \beta _{2}{\mathcal {K}}(u_{1}^{(2)})\frac{\partial u_{1}^{(2)}}{\partial y}-\beta _{1}{\mathcal {K}}(u_{1}^{(1)})\frac{\partial u_{1}^{(1)}}{\partial y},\end{aligned}$$

(3.14)

$$\begin{aligned}&\hbox {as} \quad y\rightarrow -\infty , \quad u_{3}^{(2)}\rightarrow 0\quad . \end{aligned}$$

(3.15)

where

$$\begin{aligned} {\mathcal {K}}(\psi )=\left( k \frac{\partial \psi }{\partial \theta }\right) ^{2}+\left( \frac{\partial \psi }{\partial y}\right) ^{2}. \end{aligned}$$

(3.16)

Linear shear velocities of the layer and half-space are denoted by $c_{1}$ and $c_{2}$, respectively, such that $c_{r}^{2}=\mu ^{(r)}/\rho ^{(r)}$ and linear shear modulus $\mu ^{(r)}=2 \mathrm{d}\Sigma ^{(r)}(3)/\mathrm{d}I^{(r)}$. Nonlinear material constants $n_r=(2/\rho ^{(r)})\mathrm{d}^2 \Sigma ^{(r)}(3)/\mathrm{d}I^{2}$ correspond to the hardening relevant medium if positive and softening if negative. The constants $\gamma$ and $\beta _r$ are defined by $\gamma =\mu ^{(2)}/\mu ^{(1)}$, $\beta _{r}=n_{r}/c_{r}^2$.

It should be noted that order problems given above are linear and the first-order problem is the problem of propagation of linear Love waves in slowly varying layered half-space which was previously investigated in [9]. Employing the method of separation of variables, one can be found the solutions of the equations (3.4) as

$$\begin{aligned} u_{1}^{(1)}= & {} \sum _{l=1}^{\infty }\left\{ A_{1}^{(l)}(\xi , \tau )e^{ilkpy} +B_{1}^{(l)}(\xi , \tau )e^{-ilkpy}\right\} e^{il\theta }+c.c., \end{aligned}$$

(3.17)

$$\begin{aligned} u_{1}^{(2)}= & {} \sum _{l=1}^{\infty } C_{1}^{(l)}(\xi , \tau )e^{lkvy}e^{il\theta }+c.c.. \end{aligned}$$

(3.18)

Here

$$\begin{aligned} p^2=\left( \frac{c^{2}}{c_{1}^{2}}-1\right)>0, \quad v^2=\left( 1-\frac{c^{2}}{c_{2}^{2}}\right) >0, \quad c_1<c<c_2, \end{aligned}$$

and $~c=\omega /k~$ is the phase velocity; “c.c.” stands for the complex conjugate of the preceding terms, and also, $A_1^{(l)},~B_1^{(l)}$ and $C_1^{(l)}$ are the first-order amplitude functions of slow variables. Substituting the solutions (3.17)-(3.18) into the boundary conditions (3.5)-(3.6) gives

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_1^{(l)}=\mathbf{0}, \quad l=1,2,..., \end{aligned}$$

(3.19)

where $\mathbf{U}_1^{(l)}=(A_1^{(l)},B_1^{(l)},C_1^{(l)} )^T$ and the dispersion matrix $~\mathbf{W}_l~$ is

$$\begin{aligned} {{\textbf {W}}}_{l}=\left( \begin{array}{ccc} ilkpe^{ilkp(h+f_{1})} &{} -ilkpe^{-ilkp(h+f_{1})} &{} 0 \\ ilkpe^{ilkpf_{2}} &{} -ilkpe^{-ilkpf_{2}} &{} -\gamma lkve^{lkvf_{2}} \\ e^{ilkpf_{2}} &{} e^{-ilkpf_{2}} &{} -e^{klvf_{2}} \\ \end{array} \right) \end{aligned}$$

(3.20)

$~\det \mathbf{W}_1=0~$ leads to the dispersion relation

$$\begin{aligned} \frac{v\gamma }{p}=\tan [(f_{1}-f_{2}+h)kp]. \end{aligned}$$

(3.21)

When the functions representing the irregularities of boundary surfaces are chosen as $f_1=f_2=0$, geometry of the problem corresponds to the geometry of the half-space covered by a layer of uniform thickness and the dispersion equation (3.21) becomes the following well-known classical equation for Love wave propagation in a homogeneous half-space coated with a uniform layer [27].

$$\begin{aligned} \frac{v\gamma }{p}=\tan (hkp). \end{aligned}$$

(3.22)

Since only nonlinear self-modulation will be considered, the harmonic resonance phenomena are not included. Hence,

$$\begin{aligned} \det \mathbf{W}_l\ne 0~~ \hbox {hence} \quad \mathbf{U}_1^{(l)}\equiv \mathbf{0} \quad \hbox {for} \quad l\ge 2. \end{aligned}$$

(3.23)

Under these conditions, solution of the system (3.19) for $l=1$ can be given by

$$\begin{aligned} \mathbf{U}_1^{(1)}=\textit{A}_{1}(\xi ,\tau ){{\textbf {R}}}. \end{aligned}$$

(3.24)

Here, $~\textit{A}_{1}~$ is the first-order slowly varying complex amplitude of the self-modulation and the column vector $~\mathbf{R}~$ satisfies

$$\begin{aligned} ~\mathbf{W}_1\mathbf{R}=\mathbf{0}. \end{aligned}$$

(3.25)

The components of $~\mathbf{R}~$ are found to be

$$\begin{aligned} R_{1}=\frac{1}{2}{\mathrm{{e}}^{ - \mathrm{{i}}\left( {f_1 + h} \right) kp + f_2kv}}\sec \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ,\quad R_{2}=\frac{1}{2}{\mathrm{{e}}^{\mathrm{{i}}\left( {f_1 + h} \right) kp + f_2kv}}\sec \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ,\quad R_{3}=1.\nonumber \\ \end{aligned}$$

(3.26)

Then the first-order solutions (3.17)-(3.18) can be expressed by

$$\begin{aligned} u_{1}^{(1)}= & {} \textit{A}_{1}(R_{1}e^{ikpy}+R_{2}e^{-ikpy})e^{i\theta }+c.c.\end{aligned}$$

(3.27)

$$\begin{aligned} u_{1}^{(2)}= & {} \textit{A}_{1}R_{3}e^{kvy}e^{i\theta }+c.c. \end{aligned}$$

(3.28)

In an effort to determine the first-order solution explicitly, $\textit{A}_{1}$ must be found . Therefore, second-order problem should be examined. Using the first-order solutions in (3.8) yields

$$\begin{aligned} {\mathcal {L}}(u_{2}^{(1)})= & {} 2i\left( -\omega +\frac{kc_{1}^{2}}{V_g}\right) \frac{\partial \textit{A}_{1} }{\partial \tau }(R_{1}e^{ikpy}+ R_{2}e^{-ikpy})e^{i\theta }+c.c.,\end{aligned}$$

(3.29)

$$\begin{aligned} {\mathcal {L}}(u_{2}^{(2)})= & {} 2i\left( -\omega +\frac{kc_{2}^{2}}{V_g}\right) \frac{\partial \textit{A}_{1} }{\partial \tau }R_{3}e^{kvy}e^{i\theta }+c.c. \end{aligned}$$

(3.30)

Now, we decompose the second-order solutions $u_{2}^{(r)}$ as

$$\begin{aligned} u_{2}^{(r)}={\bar{u}}_{2}^{(r)}+{\hat{u}}_{2}^{(r)} \quad r=1,2, \end{aligned}$$

(3.31)

where $~{{\overline{u}}}_2^{(r)}$ are the particular solutions which can be found via the method of undetermined coefficients while $~{\hat{u}}_2 ^{(r)}$ represent the solutions of the corresponding homogeneous equations that can be written similarly to first-order solutions

$$\begin{aligned} {\hat{u}}_{2}^{(1)}= & {} \sum _{l=1}^{\infty }\left\{ A_{2}^{(l)}(\xi ,\tau )e^{ilkpy} +B_{2}^{(l)}(\xi ,\tau )e^{-ilkpy}\right\} e^{il\theta }+c.c., \end{aligned}$$

(3.32)

$$\begin{aligned} {\hat{u}}_{2}^{(2)}= & {} \sum _{l=1}^{\infty } C_{2}^{(l)}(\xi ,\tau )e^{lkvy}e^{il\theta }+c.c. \end{aligned}$$

(3.33)

Using the decomposition (3.31) in the boundary conditions (3.9)-(3.10), one can obtain following algebraic system for the second-order amplitudes $A_2^{(l)},B_2^{(l)},C_2^{(l)}$

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_2^{(l)}=\mathbf{b}_2^{(l)}, \end{aligned}$$

(3.34)

where $\mathbf{U}_2^{(l)}=(A_2^{(l)},B_2^{(l)},C_2^{(l)})^T$. $\mathbf{b}_2^{(l)}$ are expressed as

$$\begin{aligned} {{\textbf {b}}}_{2}^{(1)}=i\left( \frac{\partial {{\textbf {W}}}_{1}}{\partial \omega }+\frac{1}{V_g}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}\right) \frac{\partial \textit{A}_{1}}{\partial \tau }{{\textbf {R}}} ~~~\text{ and }~~~\mathbf{b}_2^{(l)}\equiv \mathbf{0}~~~\text{ for } \text{ all }~~~l\ge 2 .~~ \end{aligned}$$

(3.35)

For $l\ge 2$, since $~\det \mathbf{W}_l$ is assumed to be nonzero, $\mathbf{U}_2^{(l)}\equiv \mathbf{0}$, whereas $~\det \mathbf{W}_1=0~$ and $~\mathbf{b}_2^{(1)}\ne \mathbf{0}~$, the compatibility condition

$$\begin{aligned} \mathbf{L}.\mathbf{b}_2^{(1)}=0. \end{aligned}$$

(3.36)

must hold for the equation (3.34) to be algebraically solvable for $~\mathbf{U}_2^{(1)}$. The components of $\mathbf {L}$ satisfying $~\mathbf {L}\mathbf {W}_1=\mathbf{{0}}~$ are

$$\begin{aligned} L_{1}={\mathrm{{e}}^{ - \mathrm{{i}}\left( {f_1 - f_2 + h} \right) kp}}\left( { - \mathrm{{i}}p + v\gamma } \right) , \quad L_{2}= \mathrm {i} p,\quad L_{3}= - \mathrm{{i}}kpv\gamma . \end{aligned}$$

(3.37)

Differentiating (3.25) with respect to k yields

$$\begin{aligned} \left( \frac{1}{V_{g}}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}+ \frac{\partial {{\textbf {W}}}_{1}}{\partial \omega }\right) {{\textbf {R}}}+{{\textbf {W}}}_{1}\left( \frac{1}{V_{g}}\frac{\partial {{\textbf {R}}}}{\partial k}+ \frac{\partial {{\textbf {R}}}}{\partial \omega }\right) ={{\textbf {0}}} \end{aligned}$$

(3.38)

If (3.38) is multiplied by $~\mathbf {L}$ from the left and $~\mathbf {L}\mathbf {W}_1=\mathbf{{0}}~$ is used , then one finds

$$\begin{aligned} V_{g}=-\left( {{\textbf {L}}} \frac{\partial {{\textbf {W}}}_{1}}{\partial k}{{\textbf {R}}}\right) /\left( {{\textbf {L}}} \frac{\partial {{\textbf {W}}}_{1}}{\partial \omega }{{\textbf {R}}}\right) . \end{aligned}$$

(3.39)

Hence, by using this result, the compatibility condition (3.36) is confirmed. Then $~\mathbf{U}_2^{(1)}~$ is found to be

$$\begin{aligned} {{\textbf {U}}}_{2}^{(1)}=\textit{A}_{2}(\xi ,\tau ){{\textbf {R}}}-i \frac{\partial \textit{A}_{1}}{\partial \tau }\left( \frac{1}{V_{g}}\frac{\partial {{\textbf {R}}}}{\partial k}+ \frac{\partial {{\textbf {R}}}}{\partial \omega }\right) , \end{aligned}$$

(3.40)

where $~\textit{A}_{2}=\textit{A}_{2}(\xi ,\tau )~$ denotes the second-order slowly varying complex amplitude of the wave. Since the focus of this work is on weakly nonlinear waves, calculation of $~\textit{A}_{2}$ is not necessary. The uniformly valid first-order solution will be found. Finding the first-order solution requires the determination of $~\textit{A}_1~$ by the third-order perturbation problems. Plugging the obtained solutions ${u}_{1}^{(r)}$ and ${u}_{2}^{(r)}$ into the equations (3.12) gives

$$\begin{aligned} {\mathcal {L}}(u_{3}^{(1)})= & {} ({\mathcal {D}}_{1}e^{ikpy}+{\mathcal {D}}_{2}ye^{ikpy}+{\mathcal {D}}_{3}e^{-ikpy}+{\mathcal {D}}_{4}ye^{-ikpy}+{\mathcal {D}}_{5}e^{3ikpy} \nonumber \\&+\,{\mathcal {D}}_{6}e^{-3ikpy})e^{i\theta }+ \hbox {terms in} \, ({e^{\pm 3i\theta }})+ c.c., \end{aligned}$$

(3.41)

$$\begin{aligned} {\mathcal {L}}(u_{3}^{(2)})= & {} ({\mathcal {D}}_{7}e^{kvy}+{\mathcal {D}}_{8}ye^{kvy}+{\mathcal {D}}_{9}e^{3kvy})e^{i\theta } + \hbox {terms in} \,({e^{\pm 3i\theta }})+ c.c. \end{aligned}$$

(3.42)

The coefficients ${\mathcal {D}}_{i}$, $i=1,2,...,9$ are given in Appendices by (A.1). ${u}_{3}^{(r)}$ are decomposed like in the solution of second-order problem

$$\begin{aligned} u_{3}^{(r)}={\bar{u}}_{3}^{(r)}+{\hat{u}}_{3}^{(r)},\quad r=1,2 \end{aligned}$$

(3.43)

where $~{{\overline{u}}}_3^{(r)}$ are the particular solutions which can be found via the method of undetermined coefficients while $~{\hat{u}}_3 ^{(r)}$ represent the solutions of the corresponding homogeneous equations which can be written similarly to second-order solutions replacing $~\mathbf{U}_2^{(l)}~$ by third-order amplitude functions $~\mathbf{U}_3^{(l)}=(A_3^{(l)},B_3^{(l)},C_3^{(l)})^T~$ in the equations (3.32)-(3.33). Substituting the solutions $~{u}_3^{(r)}$ and $~{u}_1^{(r)}$ in (3.13)-(3.143.15) gives the following algebraic system:

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_3^{(l)}=\mathbf{b}_3^{(l)}~~ \end{aligned}$$

(3.44)

where $\mathbf{b}_3^{(1)}\ne \mathbf{0},$ $\mathbf{b}_3^{(3)}\ne \mathbf{0}$ and $\mathbf{b}_3^{(l)}\equiv \mathbf{0}$ for $l\ne 1,3$, and $\mathbf{b}_3^{(1)}$ can be expressed as follows

$$\begin{aligned} {{\textbf {b}}}_{3}^{(1)}= & {} \Bigg [i\left( \frac{\partial {{\textbf {W}}}_{1}}{\partial \omega }+\frac{1}{V_g}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}\right) \frac{\partial \textit{A}_{2}}{\partial \tau }+i\frac{\partial {{\textbf {W}}}_{1}}{\partial k}\frac{\partial \textit{A}_{1}}{\partial \xi }+\frac{1}{2}\left( \frac{\partial ^{2}{{\textbf {W}}}_{1}}{\partial \omega ^{2}}+\frac{2}{V_g}\frac{\partial ^{2}{{\textbf {W}}}_{1}}{\partial k\partial \omega }+\frac{1}{V_g^2}\frac{\partial ^{2}{{\textbf {W}}}_{1}}{\partial k^{2}}\right) \frac{\partial ^{2}{} \textit{A}_{1}}{\partial \tau ^{2}}\Bigg ]{{\textbf {R}}}\nonumber \\&+\,\left( \frac{1}{V_g}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}+\frac{\partial {{\textbf {W}}}_{1}}{\partial \omega }\right) \left( \frac{1}{V_g}\frac{\partial {{\textbf {R}}}}{\partial k}+\frac{\partial {{\textbf {R}}}}{\partial \omega }\right) \frac{\partial ^{2}{} \textit{A}_{1}}{\partial \tau ^{2}}+{{\textbf {F}}}|\textit{A}_{1}|^{2}{} \textit{A}_{1}+i{{\textbf {G}}}{} \textit{A}_{1}. \end{aligned}$$

(3.45)

Here, ${{\textbf {G}}}$ depends only on linear material parameters while $~{{\textbf {F}}}$ also depends on nonlinear material parameters. Components of these vectors are given by A.2 and A.3 in Appendices. The vector $~\mathbf{b}_3^{(3)}~$ is not used for self-modulation solution, so it is not given explicitly. Since $~\det \mathbf{W}_1~$ vanishes, such that (3.44) is solvable for $~\mathbf{U}_3^{(1)}~$, one obtains the following compatibility condition

$$\begin{aligned} \mathbf{L}.\mathbf{b}_3^{(1)}=0. \end{aligned}$$

(3.46)

Defining the following nondimensional variables

$$\begin{aligned} \textit{A}=\textit{A}_{1}/h, \quad {\widetilde{\xi }}= \xi /h, \quad {\widetilde{\tau }}= \tau \omega \end{aligned}$$

(3.47)

and using the compatibility condition (3.46), one gets the following GNLS equation with variable coefficients

$$\begin{aligned} i\frac{\partial \textit{A}}{\partial \xi }+{\Gamma }\frac{\partial ^{2}{} \textit{A}}{\partial \tau ^{2}}+{\Delta }|\textit{A}|^{2}{} \textit{A}=i {\Lambda } \textit{A} \end{aligned}$$

(3.48)

where tildes on ${\widetilde{\xi }}$ and ${\widetilde{\tau }}$ are omitted. $\Gamma$, $\Delta$ and $\Lambda$ in dimensionless units are defined by

$$\begin{aligned} {\Gamma }(\xi )= & {} \omega ^2 h\frac{1}{2V_g^3}\frac{\mathrm{d}V_{g}}{\mathrm{d}k}=\omega ^2 h\frac{1}{2V_g^3}\frac{\mathrm{d}^{2}\omega }{\mathrm{d}k^{2}},\end{aligned}$$

(3.49)

$$\begin{aligned} {\Delta }(\xi )= & {} h^3{{\textbf {L}}}.{{\textbf {F}}}/\left( {{\textbf {L}}}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}{{\textbf {R}}} \right) ,\end{aligned}$$

(3.50)

$$\begin{aligned} {\Lambda }(\xi )= & {} -h{{\textbf {L}}}.{{\textbf {G}}}/\left( {{\textbf {L}}}\frac{\partial {{\textbf {W}}}_{1}}{\partial k}{{\textbf {R}}} \right) . \end{aligned}$$

(3.51)

The coefficients ${\Lambda }(\xi )$ and ${\Gamma }(\xi )$ depend on the linear material constants and the slowly varying functions $f_1(\xi )$, $f_2(\xi )$ representing the irregularities of boundary surfaces, whereas ${\Delta }(\xi )$ also depends on nonlinear material parameters. For reasons of simplicity, their explicit expressions are excluded.

Once a solution of GNLS equation (3.48) is obtained for an initial data $~\textit{A}(\tau ,0)=\textit{A}(\tau )$, then $~u_1^{(1)}$ and $~u_1^{(2)}$ can be found from (3.27)-(3.28).

4 Soliton-like solutions of the GNLS equation

Now, we seek for soliton-like solutions of the GNLS equation (3.48) via the following ansatz

$$\begin{aligned} \textit{A}(\xi ,\tau )= B(\xi ,\tau ) \mathrm {e}^{i g(\xi )} \end{aligned}$$

(4.1)

where g and also B are chosen as the functions of $\xi$ due to the coefficients of GNLS equation depending on $\xi$. To construct nonzero bright soliton-like solutions, we set

$$\begin{aligned} B(\xi ,\tau )= B_1(\xi )sech(\tau ). \end{aligned}$$

(4.2)

Substituting the ansatz (4.1) together with (4.2) in the GNLS equation (3.48), one obtains that

$$\begin{aligned} B_1(\xi )=\sqrt{\frac{2\Gamma }{\Delta }} , \quad g(\xi )=\int \limits ^\xi \Gamma (x') \mathrm{d}x' \end{aligned}$$

(4.3)

and

$$\begin{aligned} {\Lambda }=\frac{\Delta \Gamma _{\xi }-\Gamma \Delta _{\xi }}{2\Gamma \Delta } \end{aligned}$$

(4.4)

which is the integrability condition of the GNLS equation with variable coefficients derived in [28,29,30]. Thus, the bright soliton-like solution of the form

$$\begin{aligned} \textit{A}(\xi ,\tau )= \sqrt{ \frac{2\Gamma }{\Delta }} sech(\tau ) \mathrm {e}^{i \int \limits ^\xi \Gamma (x') \mathrm{d}x'} \end{aligned}$$

(4.5)

is obtained by means of ansatz (4.1) for the GNLS equation under the integrability condition (4.4). The solution (4.5) coincides with the solution which is derived by using the Darboux transformation in [31]. Note that the solution (4.5) is just valid for ${\Gamma }{\Delta }>0$.

For ${\Gamma }{\Delta }<0$, to obtain the dark soliton-like solutions for the GNLS equation, ansatz (4.1) is used with

$$\begin{aligned} B(\xi ,\tau )= B_1(\xi ) \tanh (\tau ). \end{aligned}$$

(4.6)

By inserting (4.1) along with (4.6) into the GNLS equation, it is obtained that

$$\begin{aligned} B_1(\xi )=\sqrt{ \frac{-2\Gamma }{\Delta }}, \quad g(\xi )=\int \limits ^\xi -2 \Gamma (x') \mathrm{d}x' \end{aligned}$$

(4.7)

with the integrability condition (4.4) of the GNLS equation .

Thus, for ${\Gamma }{\Delta }<0$, the following dark soliton-like solution is obtained

$$\begin{aligned} \textit{A}(\xi ,\tau )= \sqrt{ \frac{-2\Gamma }{\Delta }}\tanh (\tau ) \mathrm {e}^{-2 i \int \limits ^\xi \Gamma (x') \mathrm{d}x'} \end{aligned}$$

(4.8)

which coincides with the solution first obtained by Serkin and Belyaeva [29].

Note that the soliton-like solutions (4.5) and (4.8) exist under the integrability condition (4.4). Yet, the governing equation may not be integrable due to the coefficients depending on the irregularities of boundary surfaces. In the next section, some special types of irregular surfaces which allow integrability are investigated. Assuming that the change in the boundary surfaces is periodic, we have examined the effects of the irregularities and nonlinear constitutional properties on the propagation characteristic of the exact soliton-like solutions obtained above. For other special cases which do not allow the integrability condition (4.4), we use the pseudo-spectral method to obtain numerical solutions of the GNLS equation (3.48). For that purpose, we use the discrete Fourier transform for approximation of the $\tau$ derivatives, and apply the fourth-order Runge–Kutta scheme for the $\xi$ derivative [32, 33]. Then, we have examined the effect of the irregularities in the boundary surfaces on the nonlinear evolution of the numerically obtained solitons and the effects of the amplitudes of periodic surfaces on the wave amplitude during the evolution.

5 Special cases for boundary surfaces and numerical evaluations

Numerical calculations are performed for four different cases of irregular boundary surfaces. Assuming that the change in the boundary surfaces is periodic, the effect of irregular surfaces and the effect of nonlinear material parameters on the propagation of SH waves characterized by the GNLS equation are graphically observed.

In the numerical calculations, the linear material constants and dimensionless phase velocity of the waves $C=c/c_1$ are fixed as

$$\begin{aligned} c_2/c_1= 1.297 , \quad \gamma = 2.159, \quad C=1.19. \end{aligned}$$

(5.1)

Case 1 Nonuniform boundary surfaces of the layer with constant thickness

Fig. 2

When layered half-space consists of hardening material for $\beta _1=\beta _2=1.5$ and for case 1. a Nonlinear evolution of the bright soliton-like solution. b View from top. c Maximum amplitude as a function of the propagation distance $\xi$. d Variation of the wave profile with $\tau$ for $\xi =2$ and $\xi =100$

Fig. 3

When layered half-space consists of softening material for $\beta _1=\beta _2=-1.5$ and for case 1. a Nonlinear evolution of the dark soliton-like solution. b View from top. c Maximum amplitude as a function of the propagation distance $\xi$. d Variation of the wave profile with $\tau$ for $\xi =2$ and $\xi =100$

Solving equation (4.4) for the functions $f_1$ and $f_2$ representing the irregularities on the boundary surfaces shows that the coefficients of GNLS equation satisfy the condition of integrability (4.4) only when these functions are equal, i.e. when $f_1=f_2$. In this case, assuming that the boundary surfaces take the shape of a cosine curve, their effects on the wave propagation are investigated. Hence, the functions $f_1(\xi )$ and $f_2(\xi )$ are chosen as $u \cos (k_1\xi )$ where u, $k_1$ and $\xi$ are, respectively, amplitudes, wave number and position parameter of the periodic boundary surfaces. Note that, while the boundary surfaces change as a cosine function, thickness of the layer remains constant for the case of $f_1=f_2$. We have examined the effect of corrugated layer of constant thickness bounded by the periodic free surface $y=h+u \cos (k_1\xi )$ and periodic interface $y=u \cos (k_1\xi )$ as well as the influence of nonlinear material constants on the wave propagation characterized by the GNLS equation via exact soliton-like solutions (4.5) and (4.8) obtained above and the results are illustrated by Figs. 2 and 3. In the evaluations of solutions, the dimensionless flatness parameter $U=u/h$ and corrugation parameter $s=k_1h$ associated with the oscillation of the boundary surfaces are chosen as $U=0.05$ and $s=1.4$. It is observed that when $\beta _1=1.5$, $\beta _2=1.5$, i.e. layered half-space exhibits hardening characteristic, $\Gamma \Delta >0$ and bright soliton-like waves (4.5) propagate. When layered half-space exhibits softening characteristic for $\beta _1=-1.5$ and $\beta _2=-1.5$, $\Gamma \Delta <0$ and propagation of dark soliton-like waves (4.8) exists in this media having same slowly varying fluctuation in boundary surfaces. Moreover, in Figs. 2 and 3, one can clearly notice the influence of slowly varying irregularities of the boundary surfaces on the evolution characteristic of soliton-like SH waves. Although the layer has constant thickness, small oscillations of the boundary surfaces give rise to periodic and small fluctuation attached on the bright soliton-like waves propagating in the hardening half-space coated with the hardening layer. It is also observed that the dark soliton-like solution given by (4.8) exists on a periodically modulated background as a result of the periodic oscillation on the boundary surfaces of the softening half-space covered by softening layer. As shown in these figures, obtained solutions have soliton-like features. Periodic boundary surfaces cause a change in wave amplitude without causing distortion in the wave profile. It is also seen that the maximum amplitudes of the bright and dark soliton-like waves oscillate with relatively small amplitude.

Fig. 4

Variation of $|\textit{A}|^2$ with $\tau$ for different values of flatness parameter U a for bright soliton-like solutions, b for dark soliton-like solutions with fixed $\xi =7$, $s=1.4$

In Fig. 4 , the variation in the wave amplitude have been observed with the flatness parameter U of the boundary surfaces. We have selected the corrugation parameter as $s=1.4$, and evaluate the soliton-like solutions (4.5), (4.8) for the values of the flatness parameter $U=(0, 0.01, 0.1, 0.2, 0.5)$. Figure 4 clearly shows that amplitudes of both bright and dark solitary-like solutions increase with increasing value of the parameter U.

Case 2 Nonuniform boundary surfaces of the layer with variable thickness

For this case, the functions $f_1(\xi )$ and $f_2(\xi )$ representing the irregularities of free surface and interface, respectively, are chosen as $u \cos (k_1\xi )$ and $v \cos (k_1\xi )$ where u and v are amplitudes, $k_1$ is wave number and $\xi$ is position parameter of the periodic boundary surfaces. When $f_1\ne f_2$, variable coefficients of GNLS equation (3.48) do not satisfy the integrability condition (4.4). Hence, the GNLS equation is solved numerically for this case by means of the pseudo-spectral method. In order to reveal the difference between effects of the oscillating interface and the oscillating free surface on the propagation characteristics of surface SH waves, the following two cases where the oscillation occurs only at the free surface and only at the interface are examined separately.

Case 3 Periodic free surface and plane interface

Fig. 5

When layered half-space consists of hardening material for $\beta _1=\beta _2=1.5$. and for case 3 a Nonlinear evolution of the bright soliton-like solution. b View from top. c Maximum amplitude as a function of the propagation distance $\xi$. d Variation of the wave profile with $\tau$ for $\xi =1$ and $\xi =100$

If periodic free surface $y=h+u \cos (k_1\xi )$ and plane interface $y=0$, i.e. $f_2=0$, are bounds the corrugated layer of nonuniform thickness, it is observed the effect of irregular free surface on the nonlinear evolution of the solitons in Fig. 5. In the evaluations of solutions, the dimensionless flatness parameter U and corrugation parameter s associated with the free surface are chosen as $U=0.05$ and $s=1.4$. When layered half-space exhibits hardening characteristics for $\beta _1=1.5$ and $\beta _2=1.5$, bright soliton-like wave evolution has been investigated. As shown in Fig. 5, the small oscillations on the free surface of the layered half-space cause small undulations attached to the bright soliton-like waves without causing distortion in the wave profile. It is also seen that the maximum amplitude of the bright soliton-like wave has relatively small undulations due to the oscillation on the free surface during wave evolution.

Case 4 Plane free surface and periodic interface

Fig. 6

When layered half-space consists of hardening material for $\beta _1=\beta _2=1.5$ and for case 4. a Nonlinear evolution of the bright soliton-like solution. b View from top. c Maximum amplitude as a function of the propagation distance $\xi$. d Variation of the wave profile with $\tau$ for $\xi =1$ and $\xi =100$

Considering the layer having free surface $y=h$ (planar) without corrugation, i.e. $f_1=0$, and periodic interface $y=v\cos (k_1\xi )$, we have examined the effect of the corrugated interface on the wave profile. In the evaluations of solutions, the dimensionless flatness parameter $V=v/h$ and corrugation parameter s associated with the interface are chosen as $V=0.05$ and $s=1.4$. As shown in Fig. 6, the small undulations at the interface of the layered media give rise to the small fluctuations attached on the bright soliton-like waves. Periodic interface leads to relatively small undulations in the maximum amplitude of bright soliton-like wave without causing distortion in the wave profile during wave evolution.

Fig. 7

Variation of $|\textit{A}|^2$ with $\tau$ for different values of flatness parameter of the free surface U a when interface is planar, i.e. V=0 (case 3), b when interface has corrugation with $V=0.05$ (case 2); for fixed $s=1.4$, $\beta _1=1.5$, $\beta _2=1.5$, $\xi =7$

Fig. 8

Variation of $|\textit{A}|^2$ with $\tau$ for different values of flatness parameter of the interface V a when free surface is planar, i.e. U=0 (case 4), b when free surface has corrugation with $U=0.05$ (case 2); for fixed $s=1.4$, $\beta _1=1.5$, $\beta _2=1.5$, $\xi =7$

The effects of dimensionless flatness parameters $U=u/h$ and $V=v/h$ related to the corrugated free surface and interface of the layer, respectively, on the amplitude of bright soliton-like waves are examined in Figs. 7 and 8. Figure 7a, b shows the effect of the variation in the flatness parameter U associated with the oscillating free surface on the amplitude of bright soliton-like waves when the interface is considered to be planar and corrugated, respectively. The curves in Fig. 7a representing case 3 in which corrugation of the interface is neglected and the curves in Fig. 7b corresponding to case 2 where layer is bounded by oscillating free surface and oscillating interface are plotted for different values of $U=(0,0.05,0.1,0.2)$. It is seen from these figures that wave amplitude increases with increasing flatness parameter U. In Fig. 7a curve 5 and in Fig. 7b curve 4 correspond to cases which allow the integrability condition. For these cases, it is seen that the exact bright soliton-like solutions (4.5) obtained via ansatz coincide with the numerical solutions obtained by means of pseudo-spectral method under the initial condition $\textit{A}(0,\tau )=0.22 sech(\tau )$ for fixed linear material parameters (5.1) and nonlinear ones $\beta _1=1.5$ and $\beta _2=1.5$. This gives an idea about the precision of the numerical calculation we performed.

In Fig. 8a, b, we have observed that the variation of amplitude of the bright soliton-like waves with the flatness parameter V associated with the interface for the cases 2 and 4 in which free surface is corrugated and planar, respectively. From these figures, plotted for the different values of $V=(0,0.05,0.1,0.2)$, the wave amplitude of SH waves is observed to increases as the flatness parameter V increases.

5.1 Energy analysis

The effect of irregular boundary surfaces on the soliton energy during the wave evolution is investigated. The soliton energy is defined as [34]

$$\begin{aligned} E=\int \limits ^{\infty }_{-\infty } |\textit{A}(\xi , \tau )|^2 \mathrm{d} \tau . \end{aligned}$$

(5.2)

For the soliton-like solution (4.5), the energy is explicitly obtained as

$$\begin{aligned} E=\frac{2\Gamma }{\Delta }\int \limits ^{\infty }_{-\infty } |sech(\tau )|^2 \mathrm{d} \tau =4 \frac{\Gamma }{\Delta }. \end{aligned}$$

(5.3)

Fig. 9

Variation of the soliton energy during the wave evolution for the case 1 ($f_1=f_2\ne 0$), case 3 ($f_2=0, f_1= u cos(k_1 \xi )$) and case 4 ($f_1=0, f_2= v \cos (k_1 \xi )$)

Depending on the variation of ${\Gamma }$ and ${\Delta }$ with $\xi$, wave energy changes during its evolution. In order to make better comparison of the effects of corrugation of the boundary surfaces on the soliton energy during wave evolution, the energy graphs for three different cases described above (cases 1–3–4) are given in Fig. 9. It is seen that wave energy also has relatively small undulations with the effect of slowly varying boundary surfaces.

6 Concluding remarks

In this article, the effect of nonlinear materials besides irregular boundary surfaces on the propagation characteristics of surface SH waves in a layered semi-space with slowly varying boundary surfaces is investigated. For arbitrary shape of layer’s boundary surfaces, the modulation of nonlinear surface SH waves is described by the GNLS equation whose coefficients depending on the functions representing the irregular boundary surfaces in addition to linear and nonlinear material constants of the media. When the functions representing the irregularities of boundary surfaces are zero, this GNLS equation reduces to the NLS equation characterized the nonlinear propagation of Love waves in a layered half-space having plane boundary surfaces. While the governing NLS equation with constant coefficients is always integrable, the GNLS equation with variable coefficients may not be integrable due to the coefficients depending on the irregularities of boundary surfaces. By means of ansatz, we have derived integrability condition and soliton-like solutions for the GNLS equation. Then, we have investigated some special types of irregular boundary surfaces which allow integrability of the GNLS equation. Assuming that the change in the boundary surfaces is periodic, we have examined the effects of irregular surfaces and nonlinear material properties on the propagation characteristics of the exact soliton-like waves. For other spacial types of undulated boundary surfaces which do not allow integrability, the numerical solutions to the derived GNLS equation are sought by means of the pseudo-spectral method and the results are depicted graphically. The graphs reveal that as a result of small oscillations in the boundary surfaces, the background of dark-like solitary waves and the top of bright-like solitary waves undergo periodic and small fluctuation. It is also seen that obtained solutions have soliton-like features. Periodic boundary surfaces cause a small change in wave amplitude without causing distortion in the wave profile during the evolution. It is also shown that the amplitudes of soliton-like solutions increase with the increasing amplitude of the undulation in the boundary surfaces of the crustal layer. It is also observed that wave energy of soliton-like waves oscillates with relatively small amplitude due to the effect of oscillations of the boundary surfaces.

Appendices

Appendices

A.1

$$\begin{aligned} {\mathcal {D}}_{1}= & {} 2iR_{1} {\mathcal {M}}_{2}^{(1)}+2 \Lambda _{1}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+R_{1}{\mathcal {N}}^{(1)}+2iR_{1}c_1^2 k \frac{\partial \textit{A}_1}{\partial \xi } -{\mathcal {P}}_{1}+2i\mathcal {\zeta }_{1}^{(1)}{} \textit{A}_1, \\ {\mathcal {D}}_{2}= & {} (-2iR_{1}/pkc_{1}^{2})\left( -\omega + \frac{kc_{1}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+2c_1^2\frac{k}{p} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_{1}, \\ {\mathcal {D}}_{3}= & {} 2iR_{2} {\mathcal {M}}_{2}^{(1)}+2 \Lambda _{2}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+R_{2}{\mathcal {N}}^{(1)}+2iR_{2}c_1^2 k \frac{\partial \textit{A}_1}{\partial \xi }-{\mathcal {P}}_{2}+2i\mathcal {\zeta }_{2}^{(1)}{} \textit{A}_1,\\ {\mathcal {D}}_{4}= & {} (2iR_{2}/pkc_{1}^{2})\left( -\omega +\frac{kc_{1}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}-2c_1^2\frac{k}{p} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_2, \\ {\mathcal {D}}_{5}= & {} {\mathcal {Q}}_{1},\quad {\mathcal {D}}_{6}={\mathcal {Q}}_{2} \\ {\mathcal {D}}_{7}= & {} 2iR_{3} {\mathcal {M}}_{2}^{(2)}+2 \Lambda _{3}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(2)}+R_{3}{\mathcal {N}}^{(2)}+2iR_{3}c_2^2 k \frac{\partial \textit{A}_1}{\partial \xi }+2i\mathcal {\zeta }_{3}^{(2)}{} \textit{A}_1, \\ {\mathcal {D}}_{8}= & {} (2R_{3}/vkc_{2}^{2})\left( -\omega +\frac{kc_{2}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(2)}+2ic_2^2\frac{k}{v} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_3,\\ {\mathcal {D}}_{9}= & {} n_{2}k^{4}(-3+2v^{2}+9v^{4})|R_{3}|^{2}R_{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1} , \end{aligned}$$

with

$$\begin{aligned} {\mathcal {M}}_{\beta }^{(\alpha )}=\left( -\omega +\frac{kc_{\alpha }^{2}}{V_g}\right) \frac{\partial \textit{A}_{\beta } }{\partial \tau }, \quad {\mathcal {N}}^{(\alpha )}=\left( \frac{c_{\alpha }^{2}}{V_g^2}-1\right) \frac{\partial ^{2}{} \textit{A}_{1} }{\partial \tau ^{2}}, \quad \Lambda _{\alpha }=\left( \frac{1}{V_g}\frac{\partial R_{\alpha }}{\partial k}+\frac{\partial R_{\alpha }}{\partial \omega }\right) \end{aligned}$$

$$\begin{aligned} {\mathcal {P}}_{1}= & {} n_{1}k^{4}\left( |R_{1}|^{2}R_{1}(9+2p^{2}+9p^{4})\right) |\textit{A}_{1}|^{2}{} \textit{A}_{1}, \quad {\mathcal {P}}_{2}=n_{1}k^{4}\left( |R_{2}|^{2}R_{2}(9+2p^{2}+9p^{4})\right) |\textit{A}_{1}|^{2}{} \textit{A}_{1}, \\ \mathcal {\zeta }_{\beta }^{(\alpha )}= & {} k c_{\alpha }^{2} \frac{\partial R_{\beta }}{\partial \xi }+\frac{R_{\beta }}{2}c_{\alpha }^{2} \frac{\partial k}{\partial \xi }, \\ {\mathcal {Q}}_{1}= & {} n_{1}k^{4}|\textit{A}_{1}|^{2}{} \textit{A}_{1}R_{1}^{3}(-3-2p^{2}+9p^{4}),\quad {\mathcal {Q}}_{2}=n_{1}k^{4}|\textit{A}_{1}|^{2}{} \textit{A}_{1}R_{2}^{3}(-3-2p^{2}+9p^{4}), \end{aligned}$$

A.2

$$\begin{aligned} F_{1}= & {} - \frac{1}{8}{\mathrm{{e}}^{3f_2kv}}\left( {f_1 + h} \right) {k^4}\left( {9 + 2{p^2} + 9{p^4}} \right) \beta _1 \sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^3}, \\ F_{2}= & {} \frac{1}{32pv}{\mathrm{{e}}^{3f_2kv}}{k^3}\{4p\left( {9 + 2{v^2} - 3{v^4}} \right) \beta _2\gamma - 4f_2 kp\left( {9 + 2{p^2} + 9{p^4}} \right) v\beta _1\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\\&-\, 4\left( { - 9 + 2{p^2} + 3{p^4}} \right) v\beta _1\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \\&+\, \left( {27 + 2{p^2} - 33{p^4}} \right) v\beta _1\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2} \tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \},\\ F_{3}= & {} -\frac{{\mathrm{{e}}^{3f_2kv}}{k^2}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^3}}{32 p^2 v^2}\{ 3{p^2}\beta _2\left( { - 3 + 2{v^2} + 9{v^4}} \right) \cos \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \\&+\, \left( { - 3{v^2}\beta _1 + {p^2}\left( { - 3\beta _2 + 9{v^4}\beta _2 + {v^2}\left( { - 2\beta _1 + 9{p^2}\beta _1 + 2\beta _2} \right) } \right) } \right) \cos \left[ {3\left( {f_1 - f_2 + h} \right) kp} \right] \\&-\,4f_2kp {v^2}\beta _1\left( {9 + 2{p^2} + 9{p^4}} \right) \sin \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \}. \end{aligned}$$

A.3

$$\begin{aligned} G_{1}= & {} \frac{{}{\mathrm{{e}}^{f_2kv}}\left( {f_1 + h} \right) \sec \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] }{2p^2v}\{2{k^2}{p^2}v\left( {p\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \left( {f{_1^\prime } - f{_2^\prime }} \right) + vf{_2^\prime }} \right) \\&+\, \left( {v + p\left( {2f_2kp + v\left( {p - 2\left( {f_1 - f_2 + h} \right) k\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] } \right) } \right) } \right) k'\}, \\ G_{2}= & {} \frac{1}{{2k{p^3}{v^3}}}{}{\mathrm{{e}}^{f_2kv}}\{2{k^2}{p^2}{v^3}(- f_2k{p^2}\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] f{_2^\prime } - v\tan \left[ {\left( {f1 - f_2 + h} \right) kp} \right] f{_2^\prime } \\&+\,2{k^2}{p^3}{v^3}\left( {\left( {f_2kv - \gamma } \right) f{_2^\prime } + \sec {{\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] }^2}\left( { - f{_1^\prime } + f{_2^\prime }} \right) } \right) ) \\&+\,p\left( {f_2k{v^3} + {p^2}\left( {\gamma + v\left( { - f{_2^2}{k^2}v\left( { - 2 + \gamma } \right) - v\gamma - f_2k\left( {{v^2}\left( { - 1 + \gamma } \right) + \gamma } \right) } \right) } \right) } \right) k' \\&+\, 2\left( {f_1 - f_2 + h} \right) kp{v^3}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\\&+ {v^2}\left( { - v + {p^2}\left( { - v + f_2k\left( { - 2 + f_2kv} \right) } \right) } \right) \tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] k' \}, \\ G_{3}= & {} -\frac{{}{\mathrm{{e}}^{f_2kv}}f_2}{2kp^3v^3}\{ 2{k^2}{p^3}{v^3}f{_2^\prime } + p\left( { - f_2k{v^3} + {p^2}\left( { - 1 + f_2kv + {v^2}} \right) } \right) k' \\&+\,2kp{v^3}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\left( {k{p^2}\left( {f{_1^\prime } - f{_2^\prime }} \right) - \left( {f_1 - f_2 + h} \right) k'} \right) \\&+\,{v^2}\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \left( {2{k^2}{p^2}{v^2}f{_2^\prime } + \left( {v + {p^2}\left( {2f_2k + v} \right) } \right) k'} \right) \}. \end{aligned}$$