Probabilistic Characterization of Rock Mass from Limited Laboratory Tests and Field Data: Associated Reliability Analysis and Its Interpretation

Abstract

Probabilistic methods are the most efficient methods to account for different types of uncertainties encountered in the estimated rock properties required for the stability analysis of rock slopes and tunnels. These methods require estimation of various parameters of probability distributions like mean, standard deviation (SD) and distributions types of rock properties, which requires large amount of data from laboratory and field investigations. However, in rock mechanics, the data available on rock properties for a project are often limited since the extents of projects are usually large and the test data are minimal due to cost constraints. Due to the unavailability of adequate test data, parameters (mean and SD) of probability distributions of rock properties themselves contain uncertainties. Since traditional reliability analysis uses these uncertain parameters (mean and SD) of probability distributions of rock properties, they may give incorrect estimation of the reliability of rock slope stability. This paper presents a method to overcome this limitation of traditional reliability analysis and outlines a new approach of rock mass characterization for the cases with limited data. This approach uses Sobol’s global sensitivity analysis and bootstrap method coupled with augmented radial basis function based response surface. This method is capable of handling the uncertainties in the parameters (mean and SD) of probability distributions of rock properties and can include their effect in the stability estimates of rock slopes. The proposed method is more practical and efficient, since it considers uncertainty in the statistical parameters of most commonly and easily available rock properties, i.e. uniaxial compressive strength and Geological Strength Index. Further, computational effort involved in the reliability analysis of rock slopes of large dimensions is comparatively smaller in this method. Present study also demonstrates this method through reliability analysis of a large rock slope of an open pit gold mine in Karnataka region of India. Results are compared with the results from traditional reliability analysis to highlight the advantages of the proposed method. It is observed that uncertainties in probability distribution type and its parameters (mean and SD) of rock properties have considerable effect on the estimated reliability index of the rock slope and hence traditional reliability methods based on the parameters of probability distributions estimated using limited data can make incorrect estimation of rock slope stability. Further, stability of the rock slope determined from proposed approach based on bootstrap method is represented by confidence interval of reliability index instead of a fixed value of reliability index as in traditional methods, providing more realistic estimates of rock slope stability.

1 Introduction

Rock mass characterization is a challenging task due to high uncertainties involved in its various geological and mechanical properties. These uncertainties in rock properties can be inherent, statistical or systematic based on their characterization (Duzgun et al. 2002). Uncertainties in rock properties make the stability estimation of rock slopes difficult due to unavailability of a single deterministic value of a rock property that can be used in stability analysis. In practice, average of the sample properties is generally used in the stability analysis in deterministic analysis (Pain et al. 2014; Tiwari and Latha 2016), resulting in overestimation of the stability of rock slopes. Probabilistic approaches provide a better alternative as compared to deterministic approaches for the stability analysis of rock structures since they can include the effect of uncertainties in rock properties (Duzgun et al. 1995; Mauldon and Ureta 1996; Duzgun and Bhasin 2009; Li et al. 2015a; Tiwari and Latha 2017). Different probabilistic methods like first-order reliability method (FORM), second-order reliability method (SORM), Monte Carlo (MC) simulation have been developed by researchers over the years. In these approaches, stability of rock structures is defined in terms of reliability index or probability of failure, which requires accurate values of the statistical parameters, i.e. mean, SD and type of distributions of different rock properties, which are random variables. To estimate these parameters of rock properties, generally rock samples are collected from a few locations of the site for laboratory testing or some in situ tests are carried out in excavated drifts. Samples collected for laboratory testing are often limited because of high costs involved in samples extraction and testing. Limited number of in situ tests are generally carried out inside the excavated drift due to high costs and practical difficulties (Ramamurthy 2013). Considering the variable nature of rock masses, it is impossible to represent the properties of entire rock mass in its spatial extents through properties determined from these limited number of tests. Reliability of rock slope stability estimated using these uncertain statistical parameters and distribution of various rock properties from limited test data becomes questionable and the design of slopes based on these estimates may lead to errors.

The type of epistemic uncertainty associated with the limited availability of samples is called estimation uncertainty (Rocquingny 2012). It includes limited size of samples, observation errors, discrepancies in expert opinion, etc. The impact of this type of epistemic uncertainty leads to uncertainty in plausible values of statistical parameters of input variables and the selection of appropriate model type (probabilistic distribution). It is important to incorporate estimation uncertainty along with the inherent variability in the analysis, when the number of samples available to characterize input parameters is small.

To include the above-mentioned uncertainties associated with limited number of samples, resampling techniques such as bootstrap (Efron 1979; Luo et al. 2013; Most and Knabe 2010; Li et al. 2015b) can provide an efficient alternative. Resampling techniques provide complimentary cumulative distribution function (CCDF) representation of aleatory and epistemic uncertainty combination (Helton 1993). These resampling techniques could be more useful in the field of rock mechanics, since the projects are large in scale and data are often limited. Limited studies have been carried out in the past to estimate the effect of uncertainty in the statistical parameters and distributions of input soil properties in reliability estimation of small-scale soil slopes (Most and Knabe 2010; Luo et al. 2013). However, no studies are so far available in the literature which have tried to provide a method to overcome the difficulty regarding limited available data on rock properties in the stability analysis of rock slopes and which can be used for slopes of large dimensions with small computational effort.

In this study, a practical probabilistic rock mass characterization approach is proposed, which considers the effect of uncertainties in the probability distributions, i.e. statistical parameters and distributions of different rock properties in the reliability estimation of rock slopes. This method is based on resampling technique coupled with Sobol’s global sensitivity analysis and response surface analysis. The method uses numerical tools like finite element method (FEM)/finite difference method (FDM) for calculation and hence can be used for rock slopes of any shape and rock masses exhibiting different constitutive behaviour. This method considers uncertainty in the statistical parameters and distribution types of most commonly available rock properties, i.e. uniaxial compressive strength (UCS) and Geological Strength Index (GSI) as they contribute the most towards the variability of factor of safety (FOS) of slope among all the input parameters, as determined by sensitivity analysis. The proposed method is demonstrated through an example of rock slope of large dimensions. The reliability index of rock slope is estimated using the traditional approach for two cases, first by characterizing the rock mass strength parameters using fewer available data and second by accounting for the estimation uncertainty along with inherent variability associated with fewer samples using bootstrap method. Further, a comparison is made between both the cases and importance of the proposed method is outlined.

2 Details of the Proposed Method

The proposed method is based on four components—construction of response surface, global sensitivity analysis, applying resampling techniques (bootstrap method) and estimation of reliability index of rock structure with uncertain distributions and statistical parameters of input random variables. This section provides brief details regarding these components of the proposed method.

2.1 Details of the Response Surface

In the reliability analysis, most important step is to find out the performance function in terms of input random variables. In case of slope stability problems, performance function is usually the FOS of slope and rock properties are input random variables. In the sampling-based reliability methods, random realization of input random variables (rock properties) is generated and then using appropriate calculation methods like FEM/FDM, output (performance function) is evaluated for each realization. This process is repeated number of times which requires evaluation of numerical model many times, involving huge computational effort. To overcome this limitation of huge computational effort, a simple surrogate relation called response surface between input variables and output is constructed by solving the numerical model using limited realizations of input variables. Once the response surface is constructed, MC simulations can be carried out on this response surface by generating a large number of random realizations of input variables to obtain the output for each realization, which is then used to estimate the distribution of output and thus avoiding repeated evaluation of numerical models using FEM/FDM.

For the current study, we have adopted augmented RBF-based response surface (Krishnamurthy 2003; Pandit and Babu 2017), owing to its high accuracy as compared to global polynomial-based response surface (Krishnamurthy 2003; Fang and Horstemeyer 2006). Construction of response surface is executed in two steps. First step involves careful selection of samples from input space and evaluation of numerical model on those samples. Second step involves computation of unknown coefficients in RBF equation, so that an appropriate correlation between input and output can be made. Several space-filling designs such as Latin hypercube (LH) sampling, uniform design, etc., are employed to generate samples which are distributed throughout the input space. Also, several RBFs can be adopted to construct the response surface (Krishnamurthy 2003). Augmented RBF response surface can be mathematically represented as:

$$g({\varvec{X}}) \approx \mathop \sum \limits_{{i=1}}^{n} {\lambda _i}\phi \left( {\parallel {\varvec{X}} - {{\varvec{X}}_{\varvec{i}}}\parallel } \right)+\mathop \sum \limits_{{j=1}}^{m} {P_j}({\varvec{X}}){b_j},$$

(1)

where $g({\varvec{X}})$ is a function representing the numerical model with inputs as vector ${\varvec{X}},{P_i}({\varvec{X}})$ are monomial terms of polynomial P (x), b_j are unknown coefficients, X_i is the input vector at ith sampling point, ϕ is the RBF, $\parallel {\varvec{X}} - {{\varvec{X}}_{\varvec{i}}}\parallel$ is the Euclidean norm (distance) of vector X from X_i and λ_i are constants associated with ith RBF. In this study, LH sampling was adopted and compactly supported RBF type-II developed by Wu (1995) was used in the response surface. It is represented as:

$$\begin{aligned} \phi (r) & ={(1 - t)^6}\,(6+36t+82{t^2}+72{t^3}+30{t^4}+5{t^5})\quad 0 \leqslant r \leqslant {r_0} \\ & =~0\quad r>{r_0}, \\ \end{aligned}$$

(2)

where t = r/r₀, where r is Euclidean distance and r₀ is the radius of compact support.

RBF approximation can be visualized as a weighted contribution from the sampling points in the input space. As the point moves away from the sampling point, its contribution also reduces. The constant r₀ is a free parameter and decides the region of influence of a sampling point. r₀ can be different for different sampling points, but for simplicity it is assumed equal for all sampling points. Value of r₀ is chosen by minimizing the leave one out cross validation error (LOOCV). LOOCV involves constructing the response surface with n − 1 points and checking approximation error at the left-out point. This procedure of leaving out one data is repeated for all n points, and squares of error are added cumulatively. Thus, the value of r₀ for which LOOCV is minimum is adopted for RBF response surface:

$${\text{LOOCV}}=~\mathop \sum \limits_{{i=1}}^{n} {\left( {g({{\varvec{X}}_{\varvec{i}}}) - {y_i}} \right)^2},$$

(3)

where ${g_i}({{\varvec{X}}_{\varvec{i}}})$ is approximated output of left-out point from the response surface constructed from n − 1 points and y_i is the actual output obtained from the numerical model at left-out point. Now, MC simulation can be performed by realizing random vectors from input space and substituting it in the response surface and subsequently reliability index of the structure can be estimated.

2.2 Global Sensitivity Analysis

Global sensitivity analysis (GSA) is conducted to identify the input parameters (rock properties) that significantly contribute towards the variability in the output (FOS). This generally fulfil two objectives: (1) efficiently allocate the resources towards the estimation of distribution type and its parameters of the input variables; (2) reduce the computational burden by reducing the number of input variables if they do not influence the output. Global sensitivity analysis is advantageous because it considers whole variation in the range of a parameter in the input space, keeping other parameters constant, in contrast to the local sensitivity analysis which deals with the impact of small perturbations of input parameters on the output, around a nominal point. In this study, GSA was used to identify the input parameters for which bootstrap resampling must be conducted. Other input variables which do not influence the FOS of slope by significant amount were assumed random variables whose distribution and parameters were derived from limited data available/literature and no bootstrap resampling was conducted. GSA was conducted via Sobol/Saltelli method (Saltelli et al. 2008), which involves the computation of variance-based sensitivity indices that quantify the relative contribution of each input parameter on the output variability. Sobol variance decomposition procedure involves the representation of performance function in high-dimensional model representation (HDMR), from which first order, interaction effects and total effects of the input parameters are determined. A detailed explanation of this method is mentioned in Satlelli et al. (2008). However, only first order and total effects of the parameters are determined in this study.

The first-order index gives the main contribution of each input parameter, excluding any contribution of that parameter from the interaction terms. For the ith input parameter, it is computed using the following equation:

$${S_i}=\frac{{V\left[ {E\left( {Y\left| {{X_i}} \right.} \right)} \right]}}{{V(Y)}},$$

(4)

where V is variance, E is expectation, Y is output, $Y=g({\varvec{X}})$ is a function of input vector X and X_i is the ith component of X. Total effects of the input parameter include the main contribution (first order) as well as contribution from all the higher order interaction effects. It is computed using equation:

$${S_{{T_i}}}=1 - \frac{{V[E(Y|{{\varvec{X}}_{\sim i}})}}{{V(Y)}},$$

(5)

where ${{\varvec{X}}_{\sim i}}$ is a vector having all components except the ith component of X.

Saltelli (2002) provides an MC-based numerical procedure to compute the first and total order Sobol indices. The number of quasi-random samples must be gradually increased until the computed Sobol indices become almost constant. This procedure is described in more detail in the “Appendix”.

2.3 Bootstrap Method for Characterizing Uncertainty in Distribution Type and Its Parameters

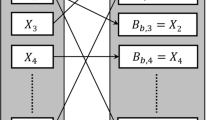
Traditional reliability analyses are often carried out in the stability analysis of different types of rock structures to counter the variability in rock mass properties (Wang et al. 2016; Dadashzadeh et al. 2017). These methods treat input parameters as random variables, define a performance function to obtain output from the input variables and aim at identifying failure region in input domain. Evaluation of probability of failure of rock structures by traditional reliability analysis is accurate only if the input parameters of distributions are accurately characterized. Characterization of distributions of input variables requires testing of large number of samples, which is often not possible in rock engineering cases due to budget constraints, effort and time involved. Therefore, sample statistics and distribution type are determined using limited observations and hence, these parameters themselves contain estimation uncertainties. Resampling technique such as bootstrap (Efron 1979; Luo et al. 2013; Most and Knabe 2010; Li et al. 2015b) can provide an alternate way to estimate the reliability of rock structures having limited data of rock properties. Basic principle of bootstrap method is to obtain the bootstrap samples by resampling from the original data (estimated rock properties) with replacement, i.e. sampling is performed directly from the empirical distribution. Consider an input random variable (rock property) X having N observations ${X_1},~{X_2},~{X_3}, \ldots ,{X_N}$ with mean ${\bar {X}_N}$ and SD S_N. The bootstrap sample set ${{\varvec{B}}_{\varvec{i}}}=\left\{ {{B_{i,1}},{B_{i,2}}, \ldots ,{B_{i,N}}} \right\}$ is obtained by random sampling with replacement from original data set ${X_1},~{X_2},~{X_3}, \ldots ,{X_N}$. For each bootstrap sample, statistical parameters (mean, SD and distribution type) of a random variable can be estimated. This is called non-parametric bootstrap which brings distribution free hypotheses for estimation uncertainty (Rocquingny 2012). The above procedure is repeated N_s times to obtain N_s bootstrap sample sets which will give N_s values of statistical parameters of random variable and from these values, variability in statistical parameters (mean, SD and distribution type) of random variables, i.e. rock properties can be estimated. The uncertainty in the parameters of random variables is present in both the distribution type and statistical parameters (mean and SD) and it is important to characterize uncertainties in both as explained below.

2.3.1 Characterizing Probabilistic Distribution Type of Input Variables

Defining a single best-fit probability distribution to a random variable with small sample size is not possible. Akaike Information Criterion (AIC), developed by Akaike (1973), is generally used to rank different probability distributions as to suggest which distribution is more suited for a data set. To characterize this uncertainty in distribution type, large bootstrap sample sets are generated, these bootstrap samples are evaluated for their AIC values to identify the best-fit distribution among different candidate distributions. AIC of a dataset associated with a probability distribution D denoted as AIC_D is defined as:

$${\text{AI}}{{\text{C}}_D}= - 2\left( {\log ({L_D})} \right)+2{K_D},$$

(6)

where L_D is maximum likelihood estimator of the data set associated with the distribution D and K_D is the number of parameters required to fully characterize the distribution D. Among all the distributions, the best distribution is the one having the least value of AIC_D. Moreover, after obtaining the N_s values of AIC_D from bootstrap sampling, AIC value of original data set can be evaluated statistically (Li et al. 2015b), with mean AIC $({\mu _{{\text{AI}}{{\text{C}}_D}}})$ and SD of AIC $({\sigma _{{\text{AI}}{{\text{C}}_D}}})$ calculated as follows:

$${\mu _{{\text{AI}}{{\text{C}}_D}}}=\frac{1}{{{N_{\text{s}}}}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {\text{AI}}{{\text{C}}_{{i_D}}},$$

(7)

$${\sigma _{{\text{AI}}{{\text{C}}_D}}}=\sqrt {\frac{1}{{{N_{\text{s}}} - 1}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {{\left( {{\text{AI}}{{\text{C}}_{{i_D}}} - {\mu _{{\text{AI}}{{\text{C}}_D}}}} \right)}^2}} ,$$

(8)

where ${\text{AI}}{{\text{C}}_{{i_D}}}$ is the AIC value of ith bootstrap sample associated with the distribution D.

2.3.2 Characterizing Uncertainty in Parameters (Mean and SD) of Input Variables

To calculate the distribution parameters, bootstrap sample statistics are evaluated for each bootstrap sample. Statistics of the bootstrap sample—mean (${\bar {B}_i}$) and SD (${S_i}$) are calculated using the equations:

$${\bar {B}_i}=\frac{1}{N}\mathop \sum \limits_{{j=1}}^{N} {B_{i,j}},$$

(9)

$${S_i}=\sqrt {\frac{1}{{N - 1}}\mathop \sum \limits_{{j=1}}^{N} {{\left( {{B_{i,j}} - {{\bar {B}}_i}} \right)}^2}} .$$

(10)

Through bootstrap samples, statistical measures of original data set can be evaluated statistically, i.e. each statistic (mean, SD) investigated for original data set can be evaluated in terms of its mean and SD (Most and Knabe 2010; Luo et al. 2013; Li et al. 2015b). Thus, the bootstrap mean and SD of original data set mean value are estimated as:

$${\left[ {{{\bar {X}}_{{N_{\text{s}}}}}} \right]_{{\text{mean}}}} \approx \frac{1}{{{N_{\text{s}}}}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {\bar {B}_i},$$

(11)

$${\sigma _{{{\bar {X}}_{{N_{\text{s}}}}}}} \approx \sqrt {\frac{1}{{{N_{\text{s}}} - 1}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {{\left( {{{\bar {B}}_i} - {{\left[ {{{\bar {X}}_{{N_{\text{s}}}}}} \right]}_{{\text{mean}}}}} \right)}^2}} .$$

(12)

Similarly, bootstrap mean and SD of original data set SD are estimated as:

$${\left[ {{S_{{N_{\text{s}}}}}} \right]_{{\text{mean}}}} \approx \frac{1}{{{N_{\text{s}}}}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {S_i},$$

(13)

$${\sigma _{{S_{{N_{\text{s}}}}}}} \approx \sqrt {\frac{1}{{{N_{\text{s}}} - 1}}\mathop \sum \limits_{{i=1}}^{{{N_{\text{s}}}}} {{\left( {{S_i} - {{\left[ {{S_{{N_{\text{s}}}}}} \right]}_{{\text{mean}}}}} \right)}^2}} .$$

(14)

A large value of N_s (Most and Knabe 2010) leads to converged values of bootstrap mean and SD of sample mean and SD.

2.4 Proposed Methodology to Estimate Reliability of Rock Structure with Uncertain Input Parameters Distributions

Present section describes the methodology adopted to estimate the reliability index of rock slopes from limited available data. Basic principle of the proposed methodology involves the estimation of the range of reliability index using bootstrap method coupled with response surface analysis. Figure 1 provides a flowchart for the proposed methodology. The following section outlines the steps to be followed in the proposed methodology.

Fig. 1

Flowchart of the proposed bootstrap methodology

Step 1: construct a numerical model which would take input as rock mass properties and outputs the system response. Define a failure condition of the rock structure based on exceedance of a certain threshold value of output. Further, using some sample vectors from the input space, evaluate the numerical model and construct the response surface as mentioned in Sect. 2.1. To increase the accuracy of the response surface, increase the number of sample vectors and construct the response surface again till acceptable accuracy is reached. It should be noted that any type of response surface can be used whose accuracy is sufficient throughout the input space. In this paper augmented RBF based response surface is adopted because it is accurate for both linear and highly nonlinear performance functions.

Step 2: conduct a global sensitivity analysis to identify those parameters which highly influence the variability of the output. Computation of first order and total effects Sobol indices quantifies the relative contribution of each input parameter towards variability in output. The methodology of sensitivity analysis is given in Sect. 2.2. A set of candidate probability distributions are also defined for each sensitive parameter, as given in the literature.

Step 3: determine the number of bootstrap sampling to be conducted for each sensitive parameter. The number of bootstrap samples N_s must be sufficiently large so that for each parameter X, the bootstrap mean and SD of original data set mean $\left( {{{\left[ {{{\bar {X}}_{{N_{\text{s}}}}}} \right]}_{{\text{mean}}}},{\sigma _{{{\bar {X}}_{{N_{\text{s}}}}}}}} \right)$ and bootstrap mean and SD of original data set SD $\left( {{{\left[ {{S_{{N_{\text{s}}}}}} \right]}_{{\text{mean}}}},{\sigma _{{S_{{N_{\text{s}}}}}}}} \right)$ becomes nearly constant.

Step 4: once bootstrap sample is obtained and its mean and SD values are determined. For each candidate probability distribution, AIC_D values are evaluated. Further, the best distribution is selected among the candidate distribution, and its parameters are computed based on bootstrap mean and SD. Now, MC simulation is conducted on the response surface with this best distribution and its parameters and reliability index are evaluated. This is repeated for N_s number of bootstrap samples. Thus, N_s reliability indices corresponding to each bootstrap sample are obtained and further interpretation is done.

3 Case Study

3.1 General Details

Slope selected for the case study is a part of an important mining project known as the Ganajur Gold Mining Project in Karnataka region of India. To extract gold deposits at the site, open pit mining was implemented which requires stability analysis of open pit gold mine slopes. One of these large slopes is selected for the current study to demonstrate the current methodology. The slope is situated near the Ganajur village, 14°49′54.08″–14°50′16.84″N latitude; 75°24′16.57″–75°24′48.39″E longitude. Figure 2 shows the location map of the site.

Fig. 2

Location map of the Ganajur Main prospect

The major rock type present at the site is greywacke and inter-bedded banded auriferous ferruginous chert (the banded iron formation), which are the part of the greenstone Shimoga belt. Figure 3 shows the site photograph. Geological features of the rock joints and rock mass were varying with the locations as observed during exploratory drilling carried out at the site. Random joint sets were observed along with four major joint sets. Joints parameters were characterized using ISRM-suggested methods (ISRM 1981). Undulating joints were more often found with smooth to rough texture. Water condition along the joints varied from wet to dry along different locations at the site. Joint spacing varied from extremely close to wide at greater depth. Rock mass was classified according to various well-accepted rock mass classification systems. A range of these ratings along with their average values is provided due to the varying quality of rock mass at the site. Table 1 shows the average value and range of the values of the rock mass classification ratings for the rock mass present at the site. For more details on the geology of this site, refer to Pandit et al. (2018).

Fig. 3

Photographs of typical landscape in the Ganajur Main project area (Srk 2012): a typical landscape looking north; b on the southwest border of the tenement; c on the old workings of Karajgi Block 3; d on the exposure of auriferous banded sulphidic chert

Table 1 Summary of rock mass classification ratings for slope

Samples of intact rock were collected during drilling to determine various intact rock properties. Statistical description of different intact rock properties, i.e. UCS, Young’s modulus (${E_i}$), Poisson’s ratio (ν), tensile strength (σ_t) and unit weight (γ) estimated from laboratory testing methods suggested by ISRM (1981) are given in Table 2.

Table 2 Statistical moments of the intact rock properties present at the site

3.2 Stability Analysis of the Slope by Characterizing the Rock Mass Strength Parameters Using Fewer Data

Traditional reliability analysis was carried out using MC simulation performed on response surface, with distribution type and its parameters of input random variables determined using limited samples. For the construction of response surface, FOS of slope is evaluated at n vectors of input parameters, i.e. UCS, Hoek–Brown constant for intact rock (m_i), E_i and GSI which were obtained from LH sampling (Montgomery 2001) from input parameter space. Since, the FOS of the slope is governed by rock mass parameters, these n vectors are converted into rock mass properties using relations provided by Hoek et al. (2002) and Hoek and Diederichs (2006) and serve as input to numerical model.

Numerical calculation has been carried out using finite difference program FLAC2D (Itasca 2011) in plane strain mode. Figure 4 shows the numerical model prepared in FLAC2D for the calculation. Height of the benches in the slope is 10 m and inclination is 68°. Bottom boundary of the model is fixed with no displacement allowed in any direction. Along the lateral boundaries, displacement is allowed in vertical direction and restrained in horizontal direction. Slope face boundary and upper boundary were kept free with allowance of displacement in both directions. For the estimation of factor of safety, strength reduction factor technique was adopted. 12,349 zones were used to discretize the slope. Convergence technique as suggested by Pain et al. (2014) was used to decide the number of zones. For this method, no of zones were increased for the numerical model until factor of safety becomes constant or results becomes independent of the number of the zones. Hoek–Brown model was considered as the yield criterion to estimate the yielded zone in slope. Statistical parameters of input intact rock properties are shown in Table 2.

Fig. 4

Finite difference grid used for slope stability analysis

75 samples from input parameter space are utilized to construct the response surface. This response surface takes input values of UCS, m_i, E_i and GSI to give FOS of slope as output. LOOCV optimization procedure is carried out in Matlab (2016). Estimation of the accuracy of the response surface is checked using three quantitative indices namely Nash–Sutcliffe efficiency (NSE), percent bias (PBIAS) and the ratio of root-mean-square error to SD of observed data (RSR) (Moriasi et al. 2007; Pandit and Babu 2017) by generating 25 off sample points via LH sampling. Response surface performance was found to be very good for all three indices and it produces highly accurate approximation of FOS of slope.

After construction of response surface, 10⁶ MC simulations are performed with input parameter characterized using the original dataset of input rock properties and mean and SD of FOS of slope is computed. Failure of slope is defined as FOS value being less than 1 during MC realization. Lognormal distribution was observed to be the best fit to the FOS data obtained by MC simulations as shown in Fig. 5. Reliability index (R) is calculated as:

$$R=\frac{{\ln \left( {\frac{{{\mu _{{\text{FOS}}}}}}{{\sqrt {1+V_{{{\text{FOS}}}}^{2}} }}} \right)}}{{\sqrt {\ln \left( {1+V_{{{\text{FOS}}}}^{2}} \right)} }},$$

(15)

where μ_FOS is mean FOS and V_FOS is coefficient of variation of FOS. Results of the reliability analysis are given in Table 3 which include mean and SD of FOS, reliability index, probability of failure and expected performance level. Expected performance level of slope determined using reliability index falls under Above Average category even for high mean FOS according to the classification given by U.S. Army Corps of Engineers (1999) due to large variation in rock properties which led to high coefficient of variation of FOS.

Fig. 5

Simulated data and best-fit probability distribution for factor of safety in traditional probability method

Table 3 Summary of the results obtained from traditional probabilistic method analysis

4 Stability Analysis of the Slope Using Proposed Method

As mentioned in the previous sections, stability analysis of the slope from the proposed methodology involves four major steps. The first step, which is the construction of response surface is already explained in Sect. 3.2. In following sections, steps two to four are described in detail for the case study to show the applicability and efficiency of the proposed method.

4.1 Global Sensitivity Analysis

In this section, global sensitivity analysis (GSA) is conducted to identify input parameters (rock mass properties) which significantly contributes towards the variability in the output (FOS) as suggested in step 2 of Fig. 1. The sensitivity indices of the four input parameters of rock mass namely, UCS, m_i, E_i and GSI are computed as suggested in Sect. 2.2 (Table 4). Number of quasi-random samples k in this study was taken as 10⁵. It can be observed that UCS and GSI contribute almost equally towards the variability of FOS, in both first order and total effect analysis. Therefore, only UCS and GSI are sensitive parameters and are considered for bootstrap analysis.

Table 4 First order and total effects Sobol indices of rock mass parameters

4.2 Estimation of Uncertainty in Distributions and Statistical Parameters of Rock Mass Properties

After identifying the most sensitive rock mass properties (UCS, GSI), estimation of uncertainty in the distribution and statistical parameters of these properties is carried out in this section (step 3 in Fig. 1). To estimate the probabilistic distribution of GSI, the relation between RQD and joint condition factor of RMR (Bieniawski 1989) (JCond₈₉) was used as given in equation below. This equation was provided by Hoek et al. (2013):

$${\text{GSI}}=1.5JCon{d_{89}}+\frac{{{\text{RQD}}}}{2}.$$

(16)

Original data set of the UCS, RQD and JCond₈₉ obtained from laboratory and field investigation is mentioned in Table 5. All the three parameters were assumed independent. Since UCS and GSI (RQD and JCond₈₉) are most sensitive parameters which govern the stability of rock slope, bootstrap analysis is performed only on these two parameters. The bootstrap mean, SD and AIC values corresponding to three well-accepted distributions for each bootstrap sample of UCS is computed. Similarly, for bootstrap RQD and JCond₈₉ samples, bootstrap mean, SD and AIC values associated with their candidate distributions are evaluated. Furthermore, the estimates of mean, SD and COV of sample mean, SD and AIC values of original data set are computed. Empirical distribution of bootstrap mean and SD estimates are best fitted using kernel density smoothing (Bowman and Azzalini 1997) and are plotted. A value of N_s = 1000 was deemed sufficient for the analysis in this paper as demonstrated in Fig. 6.

Table 5 Data set of UCS of intact rock and GSI of rockmass

Fig. 6

Statistics for UCS of intact rock with increasing bootstrap samples a mean, b standard deviation

The candidate distributions of RQD were normal and lognormal distributions (Basarir et al. 2016; Madani et al. 2018) while JCond₈₉ was assumed to be normally distributed (Basarir et al. 2016). First, bootstrap mean, SD and AIC values were computed for RQD and JCond₈₉. Subsequently, bootstrap mean, SD and AIC values of GSI was estimated by conducting 10⁵ MC simulation in Eq. (16), for each bootstrap of RQD and JCond₈₉ after assigning them best-fit distribution and its parameters. The MC samples thus obtained for GSI were evaluated for mean, SD and AIC values associated with the candidate distributions of GSI.

For UCS, candidate distributions comprise normal, lognormal and Weibull distributions, truncated at 0 MPa and 152 MPa. For GSI, normal and lognormal distributions were considered, with truncation limits of 0 and 70. These distributions were commonly observed and adopted for UCS and GSI in previous studies (Jiang et al. 2016; Morelli 2015). Figure 7 shows PDF after kernel density smoothing of AIC values associated with respective distributions. Bootstrap mean and SD estimates of AIC are provided in Table 6. It can be observed that SD of AIC is high, which indicates large variation from the AIC estimated from fewer sample size (original data set). For UCS parameter, SD of AIC associated with normal and Weibull distributions are almost comparable, however, it is slightly higher for lognormal distribution. For GSI parameter, the AIC mean value is higher for normal distribution as compared to lognormal distribution, however the SD of AIC for former is lower than the latter. These variations in AIC values indicate the existence of uncertainty associated with type of best-fit PDF of a certain input parameter.

Fig. 7

PDFs of AIC values for candidate distributions for a UCS and b GSI

Table 6 Sampling statistics of mean, standard deviation and AIC values for UCS and GSI

Figure 8 shows the probability density function (PDF) of bootstrap mean and SD of UCS and their statistical estimates are provided in Table 6. As evident from Tables 2 and 6, bootstrap sampling provides variation in statistics of estimate of mean and SD of original UCS data. The mean values of bootstrap samples match the statistics that have been estimated from original data set (small sample). However, the SD of statistics is quite high. Similar observations can be derived from Fig. 9 which gives PDF of mean and SD estimates of GSI data. These variations demonstrate existing uncertainty in mean and SD of original data sets and subsequently uncertainty in probability distribution parameters assigned to them.

Fig. 8

PDF of a mean of UCS, b standard deviation of UCS

Fig. 9

PDF of a mean of GSI, b standard deviation of GSI

The best-fit distribution among the candidate distributions can be identified by choosing the PDF having the highest probability of low AIC value associated with that PDF. 1000 bootstrap samples thus obtained are associated with 1000 best-fit distributions, choosing one among the candidate PDFs. It is not possible to have a single best-fit PDF for small sample size of parameters; hence different candidate PDFs were found to be best fits with different probabilities. The number of times a candidate PDF was chosen as best fit for UCS and GSI variables is given in Table 7. For UCS, lognormal and Weibull PDFs are found to be best fits with a probability of 67% and 33%, respectively. Lognormal has high probability of being the best-fit PDF of GSI with a probability of 96%. AIC values associated with normal and lognormal for UCS parameters are very close, leading to inaccurate judgment regarding the best-fit PDF among them.

Table 7 Number of times a candidate distribution selected as best-fit PDF in 1000 bootstrap samples

4.3 Step 4: Estimation of Reliability Index of the Rock Slope

In this section, estimation of the variability in the reliability index of the slope is carried out using the estimated uncertainty in the statistical parameters and distribution of the sensitive rock mass properties (step 4 in Fig. 1). It includes the effect of considering the uncertainty in statistics of input parameters and type of its best-fit PDF on reliability index of rock slope. The augmented RBF-based response surface is utilized for conducting MC simulation corresponding to statistics obtained from each bootstrap sample.

As mentioned in Sect. 4.1, only GSI and UCS are considered as input parameters, owing to their high sensitivity towards the FOS of the rock slope. The best-fit distribution is chosen among the candidate distributions of UCS and GSI for every bootstrap sample. Their best-fit distribution parameters corresponding to each bootstrap sample are also computed. The distributions of UCS and GSI along with other input parameter PDFs are input in augmented RBF based response surface. 10⁶ MC simulations are conducted and output, i.e. FOS of the slope is obtained and its statistics are determined. Thus for 1000 bootstrap samples, 1000 statistics of FOS are obtained (Fig. 10). Finally, 1000 reliability indices of the slope are evaluated. They are plotted in Fig. 11 after kernel density smoothing of empirical distribution of reliability index. 1000 reliability indices are also found to best fit by lognormal distribution.

Fig. 10

PDFs of statistical moments of FOS of slope obtained in bootstrap simulation a mean and b standard deviation

Fig. 11

PDF of reliability index of rock slope

Results indicated that reliability index of slope varies from 3.12 to 5.26, which corresponds to 10⁵ order of magnitude when viewed in terms of probability of failure. The mean and SD of reliability index are 3.83 and 0.29, respectively. The mean of bootstrap estimates of reliability index matches well with the value found from traditional reliability method. Thus, inclusion of uncertainties associated with distribution parameters and type of GSI and UCS, allows interpretation of reliability index in terms of confidence intervals, instead of a fixed value. Table 8 shows three different reliability index intervals for 90%, 95% and 99% confidence intervals. Expected performance level also ranges between “Above average–High” according to the classification given by U.S. Army Corps of Engineers (1999).

Table 8 Reliability index interval corresponding to different confidence intervals

5 Discussion

Stability of a large rock slope is analysed for both the approaches, using the traditional reliability method and results are compared. Although both approaches are showing that slope is stable, the stability or performance is evaluated in different terms and hence implication of the results obtained from these approaches is different. Mean FOS evaluated using both these methods is close to 3.5. However, as we express the stability or performance level of slope in terms of reliability index computed using first approach which characterizes the rock mass strength parameters using fewer available data, expected performance level of slope is “Above average”, which shows the effect of considering uncertainty in rock properties while analysing the stability of slope. Although mean FOS is very high, performance level is above average due to high SD in the estimated FOS. When we analyse the slope stability using proposed methodology which accounts for the estimation uncertainty along with inherent variability associated with fewer samples using the bootstrap method, it was observed that expected performance level of slope is ranging between “Above Average–High”. It can be observed that by the proposed approach, a better estimate of performance of the slope is made which can help in the more accurate determination of stabilization measures if required for the slope. It is more important to implement this technique specifically for the stability analysis of rock slopes due to their large scale and hence engineers remain more uncertain regarding rock properties data obtained from limited laboratory or in situ investigations. Although for this case study slope seems to be stable for both the methods, there could be a possibility that while the slope is stable according to one method and unstable according to other method.

From the practical point of view, it is well known in the field of rock mechanics that even to determine a single property of rock mass in the field, different types of tests are required to be conducted at the site and results of one type of test cannot be relied upon. One such example is the determination of deformation modulus of rock mass in the field which needs to be estimated using different types of field tests, i.e. plate load test, dilatometer test, radial jack test, etc., to get a better idea regarding rock mass deformability. Hence, conducting different types of tests at the site and that too in large number is almost impossible due to high costs involved. Further, most of the times, these tests are conducted inside the drifts which may give variability in rock mass properties inside a small area as compared to large slope dimensions. These practical issues make the reliable estimate of the rock mass properties at the site difficult and this difficulty increases for small projects where budget constraints are high. Estimation of statistical parameters (mean, SD) of rock properties from these limited tests and that too inside a small area of drift will not give reliable estimates of the distribution type and parameters of rock mass properties which may finally lead to incorrect estimation of reliability of rock slope. To overcome these problems, the method proposed here uses two most easily and commonly available parameters of rock mass, i.e. UCS and GSI and gives much more reliable estimate of slope stability which considers estimation uncertainty along with inherent variability in the parameters of rock mass properties distributions, is computationally efficient and practical too.

Proposed methodology in the current article is mostly applicable to the rock slopes which are expected to show a circular failure. Circular failure is expected in the rock slopes which are heavily jointed or weathered and possibility of structurally controlled failures, i.e. planar, wedge or toppling failures do not exist. However, this study can be extended to the rock slopes having the possibility of structurally controlled failures by carrying out bootstrap on the strength and orientation parameters of discontinuities in a similar manner. Moreover, the method successfully accounts for inherent variability and some types of the epistemic uncertainty such as estimation uncertainty and propagation uncertainty arising due to limited number of MC simulations. Epistemic uncertainty arising due to numerical errors involved in deterministic method of solving (FEM/FDM methods) is not considered in the proposed method and can be taken up in further studies.

6 Summary and Conclusion

Due to natural formation of the rocks, variability exists in their properties making determination of the precise values of rock properties impossible. This problem becomes worse when the available data of rock properties are not sufficient enough to use traditional deterministic or probabilistic stability analysis methods as observed mostly in small projects due to budget constraints or in the initial stages of large projects. This paper presents an approach for the evaluation of the stability of rock slopes of large dimensions efficiently by addressing three major issues: (a) variability in the rock properties; (b) availability of limited data of rock properties as explained in the previous section; (c) computational effort required in stability analysis of large slopes. This approach is based on four important steps: (a) response surface construction; (b) global sensitivity analysis; (c) bootstrap technique; (d) estimation of reliability index of rock structure. Major advantage of this is that approach requires estimation of GSI along with UCS which is now widely used to derive engineering design parameters such as the Hoek–Brown strength parameters and deformation moduli of jointed rock masses. This approach is demonstrated for a real rock slope of large dimensions required to be excavated at a gold mine site. It is evident from the analysis that uncertainty in defining input parameter distribution type and its parameters can have significant influence on the reliability index and hence must be included in the analysis. It was observed from the analysis that expected performance level of slope was varying from above average–high with the reliability index varying in the range of 3.19–4.87 for the confidence interval of 0.5–99.5%. Minimum value of reliability index is 3.19 which come in the range of above–average performance level of slope; however, this can be improved by using some stabilization techniques like bench flattening commonly used for mining slopes. Various other stabilization measures like rock bolting can also be used for the rock slopes which come under civil engineering practices. However, for now it seems that the possibility of slope failure is very small, and this small uncertainty can be dealt with using the observational construction method.

Appendix

Monte Carlo method to determine first order and total effect Sobol indices (Saltelli 2002).

• 1. A quasi-random number was generated in form of matrix of size (k, 2d), where k is called base sample and d is the dimension of the input vector. k in this study was taken as 10⁵. Quasi-random numbers were generated in the Matlab 2016. Further, two matrices A and B are defined having half of the sample.

  $$A=\left[ {\begin{array}{*{20}{l}} {X_{1}^{{(1)}}}&{X_{2}^{{(1)}}}& \cdots &{X_{i}^{{(1)}}}& \cdots &{X_{d}^{{(1)}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {X_{1}^{{(k)}}}&{X_{2}^{{(k)}}}& \cdots &{X_{i}^{{(k)}}}& \cdots &{X_{d}^{{(k)}}} \end{array}} \right]$$

  (17)
  $$B=\left[ {\begin{array}{*{20}{l}} {X_{{d+1}}^{{(1)}}}&{X_{{d+2}}^{{(1)}}}& \cdots &{X_{{d+i}}^{{(1)}}}& \cdots &{X_{{2d}}^{{(1)}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {X_{{d+1}}^{{(k)}}}&{X_{{d+2}}^{{(k)}}}& \cdots &{X_{{d+i}}^{{(k)}}}& \cdots &{X_{{2d}}^{{(k)}}} \end{array}} \right].$$

  (18)

• 2. Another matrix C_i is defined which contains all elements of B, except the ith column, which is taken from A.

  $${C_i}=\left[ {\begin{array}{*{20}{c}} {X_{{d+1}}^{{(1)}}}&{X_{{d+2}}^{{(1)}}}& \cdots &{X_{i}^{{(1)}}}& \cdots &{X_{{2d}}^{{(1)}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {X_{{d+1}}^{{(k)}}}&{X_{{d+2}}^{{(k)}}}& \cdots &{X_{i}^{{(k)}}}& \cdots &{X_{{2d}}^{{(k)}}} \end{array}} \right].$$

  (19)

• 3. Compute the output from of A, B and C_i matrices to obtain column matrix of outputs Y_A, Y_B and ${Y_{{C_i}}}$.

• 4. Now, the first-order sensitivity index S_i and total effects ${S_{{T_i}}}$ are calculated via Eqs. (20) and (21):

  $${S_i}=\frac{{\left( {\frac{1}{k}} \right)\mathop \sum \nolimits_{{j=1}}^{k} y_{A}^{{(j)}}y_{{{C_i}}}^{{(j)}} - f_{0}^{2}}}{{\left( {\frac{1}{k}} \right)\mathop \sum \nolimits_{{j=1}}^{k} {{\left( {y_{A}^{{(j)}}} \right)}^2} - f_{0}^{2}}},$$

  (20)
  $${S_{{T_i}}}=1 - \frac{{\left( {\frac{1}{k}} \right)\mathop \sum \nolimits_{{j=1}}^{k} y_{B}^{{(j)}}y_{{{C_i}}}^{{(j)}} - f_{0}^{2}}}{{\left( {\frac{1}{k}} \right)\mathop \sum \nolimits_{{j=1}}^{k} {{\left( {y_{A}^{{(j)}}} \right)}^2} - f_{0}^{2}}},$$

  (21)

  where $y_{A}^{{(j)}}$, $y_{B}^{{(j)}}$ and $y_{{{C_i}}}^{{(j)}}$ are the jth element of column vectors Y_A, Y_B and ${Y_{{C_i}}}$, and

  $$f_{0}^{2}=~{\left( {\frac{1}{k}\mathop \sum \limits_{{j=1}}^{k} y_{A}^{{(i)}}} \right)^2}.$$

  (22)