Stability Analysis of a Large Gold Mine Open-Pit Slope Using Advanced Probabilistic Method

Abstract

A large gold reserve was recently discovered at Haveri district of Karnataka state of India where open-pit mining was planned to extract these deposits. Stability analysis for open-pit mine slope at this site is presented in the article. Extensive geological investigations and laboratory testing suggested high variability in geological features of discontinuities, rock mass quality and intact rock properties. Hence, it was decided to perform stability analysis of the rock slope using probabilistic approach along with deterministic approach. Deterministic analysis was carried out with average properties of rock, and reliability analysis of the rock slope was carried out using both traditional and advanced probabilistic methods. In traditional probabilistic method, rock mass strength properties were treated as random variables without considering spatial variation of rock properties and reliability index was evaluated by Monte Carlo (MC) simulation on augmented radial basis function-based response surface. In advanced probabilistic analysis, spatial variability of rock mass strength properties was considered by generating anisotropic random field using Fourier series method with spatial averaging over finite difference zones. Reliability index was then estimated by performing MC simulation using random finite difference method. A comparison was provided between the results of stability analysis of slope from all these approaches. Rock slope was found to be stable in both deterministic and probabilistic approaches; however, the degree of stability predicted was different for both methods. Deterministic approach was found to be inappropriate to analyse the stability of slope having rock mass with variable properties. Further, reliability index and expected performance level of slope were highly underestimated by traditional probabilistic method as compared to advanced probabilistic method.

1 Introduction

A large gold reserve was recently discovered at Ganajur village, which is located in Haveri district in Karnataka state of India. A drilling programme was carried out at the site, which suggested an inferred resource of 1.53 million tones gold grading 3.79 g/t (approximately 122,000 oz of contained gold). Most of the drill holes intersected significant gold mineralisation over a considerable width. A mineralised zone of 600 m along the strike direction and 120 m along the depth was discovered. Open-pit mining is planned at the site to extract gold deposits. One of the biggest challenges of the project is the stability analysis of open-pit slope because of large variability in geological features and rock properties at the site.

Rock slope stability is a very complex problem because of various types of uncertainties present in the rock mass properties. The uncertainties in rock mass are generally classified into three types, i.e., inherent uncertainty, statistical uncertainty and systematic uncertainty (Duzgun et al. 2002). These uncertainties are accounted for in deterministic analyses by a certain factor of safety (FOS). This might ensure safe design for the structure, but a clear understanding of relative importance of input variables and failure mechanism of structure is not possible (Phoon and Kulhawy 1999). Studies are available in the literature regarding stability analysis of rock slopes using deterministic approach (Bhasin and Kaynia 2004; Pal et al. 2012; Tiwari and Latha 2016). Thus, it becomes necessary to include these uncertainties in the assessment of stability of rock slopes. Probabilistic methods provide an efficient method to consider these uncertainties in the stability analysis of rock slopes by assessing the performance of slope in terms of probability of failure (P_f) and reliability index. However, the application of probabilistic methods in the field of rock mechanics especially for the stability of rock slopes is not very common and limited research is available in this field.

Different types of probabilistic methods have been developed over the years to analyse the stability of various geotechnical structures. These methods can broadly be divided into two types, one which ignores and other, which includes the spatial variation of rock mass properties. Reliability index for first method can be obtained via MC sampling after generating a response surface for response of system (FOS for slopes), but the spatial variability is ignored, whereas advanced probabilistic methods aim to capture the heterogeneity of the rock mass properties. This is incorporated in the slope by modelling rock mass properties as random field and assuming a suitable correlation function and scale of fluctuation (SOF). The magnitude of SOF determines the extent to which the random variables are significantly correlated (Vanmarcke 1983). Estimation of SOF is difficult since it requires large amount of test data and its value varies from site to site. Since it is difficult to perform testing for rock due to high cost involved and difficulties in interpretation of results, probabilistic analysis of real rock slopes is generally carried out by ignoring spatial variability of rock mass properties (Park et al. 2005; Duzgun and Bhasin 2009; Li et al. 2011). However, the studies conducted on soils slopes (Griffiths and Fenton 2000, 2004; Griffiths et al. 2009; Suchomel and Mašín 2010) and some rock slopes (Hsu and Nelson 2006; Srivastava 2012) indicate that ignoring spatial variability in rock mass properties may significantly affect the reliability index of the slopes. It can be concluded from literature review that limited studies are available regarding slope stability analysis for real rock slopes using probabilistic methods and most of the studies have applied traditional probabilistic approaches by ignoring spatial variability in rock mass strength.

The objective of this paper is to evaluate stability of a large rock slope using deterministic and different probabilistic approaches and to describe the merits and demerits of each of these methods. Extensive laboratory tests have been carried out to estimate various rock properties using samples obtained from boreholes at different locations. Statistical parameters like mean, standard deviation, SOF are estimated using the test results. Deterministic analysis is carried out by adopting average values of rock mass properties. In the first probabilistic approach namely traditional probabilistic approach, augmented radial basis functions (RBF) are generated for the analysis and reliability index and $P_{\rm f}$ is estimated by MC simulation. In the second probabilistic approach, i.e., advanced probabilistic approach, reliability index and $P_{f}$ are estimated using random finite difference method (RFDM) implemented via Fourier series method. Results of different approaches are compared and insights gained are discussed.

2 Details of the Case Study

2.1 General Description

The area under the study known as Ganajur Main prospect is located in the Haveri district in north-western part of Karnataka state of India. The area surrounding the Ganajur Main prospect is known for ancient gold mining. Particularly evidences of old workings existed for the adjacent Karajgi block; however, the Ganajur Main prospect is the latest discovery made. A drilling programme was carried out at the site, which suggested an inferred resource of 1.53 million tones gold grading 3.79 g/t (approximately 122,000 oz of contained gold). Most of the drill holes intersected significant gold mineralisation over a considerable width. A mineralised zone of 600 m along the strike direction and 120 m along the depth is discovered. The area is generally a gently undulating plain with few north–west–south–east trending small ridges. The average elevation difference is in the order of 50–60 m, and the landmass of the area is situated between the elevations of 515–570 m above mean sea level (msl). The area enjoys a subtropical climate with temperatures ranging between 18 and 40 °C. The rainfall in the region varies from over 903 mm in west to less than 592 mm in east. Figure 1 shows the photograph of the site. Figure 2 shows the location map of the site.

Fig. 1

Photographs of typical landscape in the Ganajur Main project area (SRK 2012). a Typical landscape looking north, b on the south-west border of the tenement, c on the old workings of Karajgi Block 3, d on the exposure of auriferous banded sulphidic chert

Fig. 2

Location map of the Ganajur Main prospect (SRK 2012)

2.2 General Geology

The Ganajur Main Deposit is located within the late Archaean western Dharwar Craton of Southern India and occurs as a part of the Ranibennur Group and in the Dharwar–Shimoga (or the Shimoga) greenstone belt. The Shimoga greenstone belt contains numerous banded cherty iron formations within a vast mass of greywacke. The eastern part of the iron formation is of sulphide facies containing mainly pyrite and arsenopyrite. The sulphide facies iron formation is auriferous, and the Shimoga greenstone belt has been known for ancient artisanal gold mining, notably at Chinmulgund and Karajgi.

The mineralisation at Ganajur Main Deposit is hosted largely by greywacke and inter-bedded banded auriferous ferruginous chert (the banded iron formation), which are the part of the greenstone Shimoga belt. The ferruginous chert is characteristic of sulphide facies, as pyrite, arsenopyrite and chalcopyrite occur as significant component. Gold mineralisation, occurring as disseminations and fine veinlets, demonstrates close association with the strong sulfidation. The mineralisation is mainly strata bound, dominantly confined to the sulphide facies banded iron formation and is characterised by strong sulphide mineralisation, silica breccia and minor quartz veining developed within a sulfidic chert unit. The gold mineralisation is epigenetic in nature but strata bound because it is confined to the cherty iron formation. The main gold zones form a moderately to steeply dipping tabular body trending north-west to north–north-west and dipping north-east. Fractures are filled with remobilised silica or quartz carbonate veinlets. The amount of gold is directly proportional to the amount of sulphides. The mineralisation dominantly occurs as disseminations with a small amount in fine veinlets. Figure 3 shows the geological map of the Ganajur main prospect.

Fig. 3

Geological map of Ganajur Main prospect (SRK 2012)

Field observations, discontinuity surveying, core drilling and laboratory tests are carried out for this study. Four exploratory boreholes were drilled using diamond core drilling rig with 63.5 mm core diameter to investigate the joint conditions. The boreholes were drilled up to a depth ranging from 84.0 to 90.0 m from the existing ground level. Field core logging was done with description of layers, depth of ground water level, core recovery and rock quality designation (RQD). A total of 190 joints were measured, and major joint sets were identified using DIPS based on equal-area stereographic projection (Fig. 4). It was observed that there are four major joint sets (J1, J2, J3, and J4) at the site along with some random joint sets. The mean orientations (dip/dip directions) of joints are J1—32°/038°, J2—40°/090°, J3—80°/180° and J4—80°/200°. Joint parameters such as the spacing, persistence, roughness, filling and aperture were determined in the field in accordance with ISRM-suggested methods (ISRM 1981). It was observed that joint parameters were highly varying at the site with high variations in joint spacing, roughness and alteration parameters. Most of the joints were found to be undulating with smooth to rough texture. Joints were found to be wet to damp in the upper part of rock mass, while joints were dry at higher depths. Joint spacing was varying from extremely close to wide at some locations. Unaltered fresh to slightly altered joints with infill were prevalent.

Fig. 4

Stereographic projections of major joint sets—J1, J2, J3 and J4 at the site with mean orientations

Rock mass at the site is classified according to well-accepted classification systems like RQD, Rock Mass Rating (RMR) and Geological Strength Index (GSI). Because of the variations in the intact rock properties, joint conditions and joint set spacing at the site, it was not appropriate to specify a single value of rock mass classification rating and hence a range of rock mass classification ratings was estimated. Average value and range of the values of the rock mass classification ratings for the rock mass are summarised in Table 1.

Table 1 Summary of rock mass classification ratings for slope

2.3 Laboratory Tests

Physical and mechanical properties of intact rock were determined through laboratory testing of samples collected from boreholes. As mentioned earlier, for the geotechnical investigation on the intact rock, four exploratory boreholes were drilled using diamond core drilling rig with 63.5 mm core diameter. The boreholes were drilled up to a depth ranging from 84.0 to 90.0 m from the existing ground level. A total of 237 core samples were collected from the boreholes, and various laboratory tests were conducted. Uniaxial compressive strength (UCS), Young’s modulus (E_i), Poisson’s ratio (ν), tensile strength (σ_t) and unit weight (γ) were determined through the tests conducted according to the suggested methods (ISRM 1981). Variability in the rock properties was observed, and hence ranges of the properties estimated in the laboratory testing are given in Table 2. Figure 5 shows the pictures of rock samples before testing and after testing for UCS test.

Table 2 Statistical moments of the intact rock properties present at the site

Fig. 5

Photographs of the samples used for UCS testing of rock a before testing and b after testing

3 Slope Stability Analysis Using Deterministic Method

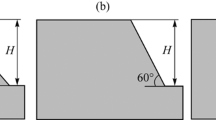
For the stability analysis of rock slope, it is important to analyse the possibility of any structurally controlled failures. Hence for the current study, a kinematic analysis has been carried out using mean joint set orientations of major joint sets to analyse the stability of slope and benches against various structurally controlled failures, i.e., planar, wedge and toppling failures. Figure 6 shows the possibility of kinematic failures for the typical steepest bench, i.e., with maximum bench angle of 68° against different types of structurally controlled failures, i.e., planar (Fig. 6a), wedge (Fig. 6b) and toppling (Fig. 6c) failures. It is observed that the possibility of any structurally controlled failures along the slope and benches is nil.

Fig. 6

Kinematic analysis using mean orientation of joint sets a planar failure, b wedge failure, c toppling failure

Since, for this slope, possibility of structurally controlled failures does not exist and further the slope dimensions are large as compared to joint spacing, stability analysis of the slope has been carried out using equivalent continuum approach. Rock slope stability analysis is performed in two-dimensional explicit finite difference software FLAC (Fast Lagrangian Analysis and Continua) in plane strain mode. The rock slope is discretised into total of 12,349 square finite difference zones some of which reduces to triangular zones at the slope face boundary as shown in Fig. 7. The bottom boundary of slope is fixed in both horizontal and vertical directions, while the side boundaries of slope are fixed only in horizontal direction and vertical movement is allowed. Rock mass yielding was defined using Hoek–Brown strength criterion. The rock mass strength properties are derived from intact rock strength parameters and GSI using the relations provided by Hoek et al. (2002). Summary of rock mass properties used in the stability analysis is given in Table 3. The FOS of slope is estimated by shear strength reduction (SSR) technique.

Fig. 7

Finite difference grid used for slope stability analysis

Table 3 Rock mass properties used for deterministic analysis

FOS obtained from deterministic analysis is 3.84. The slip surface can be seen by plotting maximum shear strain increment contours as shown in Fig. 8. This plot shows the toe of slope having high concentration of shear strain rate having a magnitude of 2.5E−06, and thus failure would initiate at this point and will propagate upwards. It is observed that FOS is higher than the target FOS, i.e., 1.5 and hence slope seems to be highly stable using deterministic analysis.

Fig. 8

Shear strain contour for the slope in deterministic approach

4 Slope Stability Analysis Using Probabilistic Methods

While the variability in rock mass properties cannot be taken into account in deterministic analysis, probabilistic methods are generally aimed at statistical characterisation of output (FOS for this case) for a given input statistics, i.e., rock mass properties. The stability of slope is defined in terms of P_f/reliability index instead of a FOS which is necessary owing to the uncertainties in rock mass properties. In this section, assessment of stability of the slope using two different types of probabilistic methods is carried out, i.e., by ignoring spatial variability and by considering spatial variability of rock mass properties.

4.1 Traditional Probabilistic Methods

In this method, reliability index of slope is estimated by treating input parameters as random variables and spatial variability in rock mass properties is ignored. There are two commonly adopted approaches in traditional probabilistic methods: the most probable point-based approaches and the sampling-based approaches. Most probable point approach involves searching a design point in input space with an objective depending on method adopted (FORM/SORM) (Ang and Tang 1975). This approach divides the input space into safe region and unsafe region. A performance function, i.e., $Y = g\left( \varvec{Z} \right)$ where $\varvec{Z}$ is vector of input variables required to obtain the FOS. The input space for which input values yield FOS less than 1 is called failure region. It involves calculation of derivatives of performance function and hence generally adopted where an explicit expression of the performance function can easily be obtained such as slopes with simple geometry. Stability analysis of slopes with complex geometries and constitutive behaviour is generally carried out using numerical programs, and this approach cannot be used for such cases.

The sampling-based approaches use MC sampling/Latin hypercube sampling (LHS). It involves generating random input vectors ($\varvec{Z}_{1} ,\varvec{Z}_{2} , \ldots \varvec{ },\varvec{ Z}_{\varvec{k}} )$ from input variable space (rock properties for this case) and repeated calculation of the FOS is carried out. This is easy to be implemented in numerical programs but is computationally expensive and time consuming as it requires large number of runs. One of the methods to reduce this computational effort is response surface method—a simpler explicit function is developed which acts as surrogate to actual input(rock properties)–output (FOS) relationship. This is also known as meta-modelling technique. Augmented RBF-based response surface is adopted in this study since its accuracy is higher for both linear and nonlinear responses.

As mentioned earlier, rock mass strength is defined using Hoek–Brown criterion for the current study and hence estimation of FOS for the slope requires different rock mass properties, i.e., Hoek–Brown constants ($m_{\rm b} , s_{\rm b}$), deformation modulus (E_m) and intact rock UCS. All of these important rock mass properties, i.e., $m_{\rm b} , s_{\rm b} , E_{\rm m}$ required to estimate FOS are related to rock mass classification rating GSI and intact rock properties, i.e., $m_{\rm i} , E_{\rm i}$ by well-accepted relations (Hoek et al. 2002; Hoek and Diederichs 2006). Hence, the rock mass classification rating GSI and intact rock properties, i.e., $m_{i} , E_{i}$ and UCS considered to be random variables in the present study. Since the rock mass properties can be obtained with intact rock properties and GSI, a single realisation of $m_{\rm i} , E_{\rm i}$, GSI and intact rock UCS can be understood as an indirect single realisation of rock mass properties, i.e., $m_{\rm b} , s_{\rm b}$, E_m and intact rock UCS required to estimate FOS of the slope. Statistical parameters of GSI and intact rock parameters (input random variables) are given in Tables 1 and 2, and distributions of these random variables were assumed to be lognormal as suggested in the literature (Ching et al. 2011). Figure 9 shows the histogram of UCS data for intact rock and lognormal curve fitting over these data. Rest all input parameters are treated as deterministic at their mean values. Space filling design, LHS, is adopted to obtain k vectors from input parameter distributions (Montgomery 2001). These Latin hypercube samples of intact rock properties and GSI are converted into rock mass properties and input in deterministic FLAC-2D model as shown in Fig. 7, and FOS is calculated for each of them. Seventy-five input vectors were utilised for response surface construction, and its methodology is outlined in appendix. A compactly supported RBF type II (Wu 1995) augmented with linear polynomial is adopted for the response surface. The response surface can then be constructed by either considering rock mass properties or intact rock properties as input; however, to reduce computational effort during estimation of probability of failure, the response surface is constructed which requires intact rock parameters and GSI as input and gives FOS as output directly. Hence, the requirement of determining rock mass properties for each random realisation of intact rock properties is removed during probability of failure estimation. It is to be noted that relations provided between intact rock and rock mass properties by Hoek et al. (2002) and Hoek and Diederichs (2006) are implicitly embedded in the response surface.

Fig. 9

Best-fit probability distribution for uniaxial compressive strength of intact rock

The response surface’s accuracy is determined before calculating the P_f as it is a surrogate model. Since errors at the sample points (input vectors) are zero for RBF meta-models (Krishnamurthy 2003), 25 off sampling points are generated and FOS is calculated for them. FOS obtained from this is denoted as observed value (FOS^obs). These 25 off sample points are then also substituted in response surface, and FOS is calculated and is denoted as simulated values (FOS^sim). The accuracy of the response surface is then determined on the basis of three quantitative indices, i.e., Nash–Sutcliffe efficiency (NSE), percent bias (PBIAS) and the ratio of root-mean-square error to standard deviation of observed data (RSR) as recommended by Moriasi et al. (2007). These indices are defined as

$${\text{NSE}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} - {\text{FOS}}_{i}^{\text{sim}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} - {\text{FOS}}_{i}^{\text{mean}} } \right)^{2} }}} \right]$$

(1)

$${\text{PBIAS}} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} - {\text{FOS}}_{i}^{\text{sim}} } \right)*100}}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} } \right)}}} \right]$$

(2)

$${\text{RSR}} = \frac{{\left[ {\sqrt {\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} - {\text{FOS}}_{i}^{\text{sim}} } \right)^{2} } } \right]}}{{\left[ {\sqrt {\mathop \sum \nolimits_{i = 1}^{k} \left( {{\text{FOS}}_{i}^{\text{obs}} - {\text{FOS}}_{i}^{\text{mean}} } \right)^{2} } } \right]}}$$

(3)

The performance indices for the response surface constructed for this slopes are mentioned in Table 4. It can be observed that the performance of response surface developed is Very Good according to all the indices and hence reliability index of the slope is estimated using this response function.

Table 4 Performance of RBF-based response function based on different criteria

It is required to estimate the reliability index estimation of probability density function (PDF) and statistical parameters of FOS. Now MC simulation is conducted directly on the evaluated response function by substituting randomly realised values of input parameters, i.e., UCS, m_i, E_i and GSI. A total of 10⁶ MC simulations were carried out for this slope, and number of simulations which results in value of FOS less than one (failure criterion) divided by total number of simulations is defined as P_f. Figure 10 shows the MC simulation and best-fit lognormal curve for the FOS in this method. Reliability index (R) is then calculated as

$$R = \frac{{{ \ln }\left( {\frac{{\mu_{\text{FOS}} }}{{\sqrt {1 + V_{\text{FOS}}^{2} } }}} \right)}}{{\sqrt {{ \ln }(1 + V_{\text{FOS}}^{2} )} }}$$

(4)

where μ_FOS is mean FOS and V_FOS is CV of FOS. Table 5 gives detailed results of statistical parameters of FOS, reliability index, $P_{\text{f}}$ and expected performance level for the slope estimated using this method. It can be observed that mean FOS is close to the FOS value estimated from deterministic analysis. Although the FOS is much higher than the target FOS still the expected performance level of the slope is Above Average. This is due to high coefficient of variation (CV) of the FOS for the slope due to high variability in rock properties. This shows that it is important to consider variability in rock properties and to evaluate stability of slopes in terms of reliability index and $P_{\text{f}}$ along with FOS instead of FOS alone.

Fig. 10

Simulated data and best-fit probability distribution for FOS in traditional probability method

Table 5 Summary of the results obtained from traditional probabilistic method analysis

4.2 Advanced Probabilistic Methods

As mentioned earlier, neglecting spatial variability of strength parameters of rock mass may lead to significant underestimation/overestimation of $P_{\text{f}}$ and reliability index, depending on amount of variability in rock mass properties. Random fields are usually adopted to model spatial variability in rock properties of the slope. One of the important components of random field characterisation is autocorrelation function which provides the measure of correlation between same rock properties at two different spatial locations as function of distance. In 2D isotropic random field, correlation between two points only depends on absolute distance between them and not on the orientation relative to each other. This is not the usual case with many geotechnical problems since correlation between strength properties is generally different in horizontal and vertical direction. Thus, anisotropic 2D stationary random field is adopted for the present study in which correlation between two locations is defined as

$$\rho_{w} \left( {\Delta x,\Delta {\text{z}}} \right) = \frac{{{\text{COV}}\left[ {w\left( {x,z} \right),w\left( {x + \Delta x,z + \Delta z} \right)} \right]}}{{{\text{VAR}}\left[ {w\left( {x,z} \right)} \right]}}$$

(5)

where $\rho_{w} \left( {\Delta x,\Delta {\text{z}}} \right)$ is autocorrelation function, $w\,(x, z)$ is the random field—a function of horizontal and vertical coordinates (x, z), $\Delta x,\Delta z$ are horizontal and vertical distances from (x, z), COV is covariance and VAR is variance. Two widely used correlation functions are single exponential and squared exponential. For simplicity, single exponential 2D autocorrelation model is adopted and can be written as

$$\rho_{w} \left( {\Delta x,\Delta {\text{z}}} \right) = { \exp }\left( { - \frac{{2\left| {\Delta x} \right|}}{{\delta_{x} }} - \frac{{2\left| {\Delta z} \right|}}{{\delta_{z} }}} \right)$$

(6)

where δ _x and δ _z are horizontal and vertical SOFs, respectively. It is a measure of distance within which properties are significantly correlated (Vanmarcke 1983). The autocorrelation model is a function of the lag $\left( {\tau_{x} = \left| {\Delta x} \right|;\,\tau_{z} = \left| {\Delta z} \right|} \right)$. Equation 6 is also known as separable Markov correlation model. Small values of δ _x and δ _z lead to domain being correlated only till shorter distances resulting in rougher random fields, and for increasing values of SOFs, the spatial distribution of rock property becomes smoother, i.e., less spatial variability. Directional influence on extent of correlation has also been accounted. There are number of methods to generate realisations from a random field (Fenton and Griffiths 2008). In this paper, we have discretised random field through Fourier series method (Jha and Ching 2013). This method is suitable for large domain random fields with short correlation lengths.

4.2.1 Estimating Scale of Fluctuations

SOFs (δ _x , δ _z ) are site dependent and are difficult to estimate if the data points collected are not closely spaced. SOFs also vary for different rock types at a particular site because of the different formation process of various rock types, and thus different spatial correlation is expected. Ching et al. (2011) postulated SOFs of strength of sedimentary rock being equal to those for the forming soils. Two procedures are reported in the literature for the estimation of SOF from the available data. First is maximum likelihood method which involves assuming different sets of numerical values of parameters of proposed autocorrelation function (ACF) model, and the set of parameter values which maximises the maximum likelihood function are considered optimal. The second method is curve fitting method proposed by Vanmarcke (1983), who suggested that the parameters of ACF must be adjusted so as to best fit the actual sample correlation coefficients obtained from the measured data, i.e., fitting theoretical correlation model to the experimental correlation. It is required that data point must be equally spaced which acts as a disadvantage for curve fitting method in this case. Since test data points are unequally spaced in the slope domain, maximum likelihood method is adopted to estimate ACF parameters. The data point values along with their spatial locations are listed in Table 6.

Table 6 Variation in uniaxial compressive strength of intact rock with sample extraction location

Figure 11 shows the contour of likelihood function evaluated for probable ranges of $\delta_{x}\,{\text{and}}\,\delta_{z}$ in log scale. It is maximised for values of δ _x  = 1.67 and δ _z  = 64. These values of SOFs of UCS are valid only for this site, and it matches well with the ranges specified in Ching et al. (2011) for sedimentary rocks. These values of SOFs will be used by random field simulation of UCS as well as those of m_i and E_i. Reason for this is similar to as explained by Fenton et al. (2005) for soil properties, i.e., the spatial correlation structure for various soil parameters is similar because they are governed by same set of factors like stress history, geologic conditions and source materials. Furthermore, it is also assumed that SOFs of intact rock property (i.e., $\delta_{x}\,{\text{and}}\,\delta_{z}$ calculated above) and those of rock mass are same (Ching et al. 2011).

Fig. 11

Contour of likelihood function evaluated for probable ranges of $\delta_{x}\, {\text{and}}\, \delta_{z}$ with δ _x in log scale

4.2.2 Local Averaging of Random Field

In continuum softwares such as in finite difference software, it is required to assign one single value to each zone. Hence, an average value of the field over the element needs to be evaluated. It can be obtained by integration over the rectangular zone as

$$w_{\text{D}} \left( {x,z} \right) = \frac{1}{{D_{x} D_{z} }}\mathop \int \limits_{{x - D_{x} /2}}^{{x + D_{x} /2}} \mathop \int \limits_{{z - D_{z} /2}}^{{z + D_{z} /2}} w\left( {x,z} \right){\text{d}}z{\text{d}}x$$

(7)

where w_D(x, z) is spatial average of the Gaussian field w(x, z) over the rectangular zone of size D _x and D _z . w_D(x, z) has the same expected value as that of w(x, z) as shown in Eq. 8a. But the variance gets reduced by certain factor γ(D _x , D _z ) called variance reduction factor as shown in Eq. 8b.

$$E\left[ {w_{\text{D}} \left( {x,z} \right)} \right] = E\left[ {w\left( {x,z} \right)} \right]$$

(8a)

$${\text{Var}}\left[ {w_{\text{D}} \left( {x,z} \right)} \right] = \sigma_{w}^{2} \gamma \left( {D_{x} ,D_{z} } \right)$$

(8b)

where E and Var denote expected value and variance, respectively, σ ² _w is the variance of w(x, z). For the autocorrelation function that is separable and symmetric in all the quadrants, like the function adopted in Eq. 6, γ(D _x , D _z ) is given by

$$\gamma \left( {D_{x} ,D_{z} } \right) = \frac{4}{{D_{x}^{2} D_{z}^{2} }}\mathop \int \limits_{0}^{{D_{x} }} \mathop \int \limits_{0}^{{D_{z} }} \left( {\left| {D_{x} } \right| - \tau_{x} } \right)\left( {\left| {D_{z} } \right| - \tau_{z} } \right)\rho \left( {\tau_{x} ,\tau_{z} } \right){\text{d}}\tau_{x} {\text{d}}\tau_{z}$$

(9)

Since strength of geo-materials is dominated by its low strength domains, Fenton and Griffiths (2008) recommended geometric mean for estimating overall strength as geometric mean weighs more for low values as compared to high values. Geometric mean Y_GM is obtained by taking pth root of product of p non-negative random variables ($\varvec{Y}$). For discrete random variables, it is defined as

$$Y_{\text{GM}} = \left( {Y_{1},Y_{2},Y_{3}, \ldots, Y_{p} } \right)^{1/p}$$

(10)

For 1D random field $X$, geometric average X_GM over an element of length D is expressed as

$$X_{\text{GM}} = { \exp }\left( {\frac{1}{D}\mathop \int \limits_{0}^{D} { \ln }\left( {X\left( \xi \right)} \right){\text{d}}\xi } \right)$$

(11)

where ξ is spatial coordinate.

For a lognormal random field X, its logarithm will be normally distributed. This implies that geometric mean in original space gets transformed into arithmetic mean in logarithmic space expressed as (similar to Eq. 10).

$${ \ln }(X_{\text{GM}} ) = \frac{1}{D}\mathop \int \limits_{0}^{D} { \ln }\left( {X\left( \xi \right)} \right){\text{d}}\xi$$

(12)

After evaluating arithmetic average in logarithmic space, it is transformed back into original space by taking exponential.

Fenton and Vanmarcke (1990) developed a procedure called Local Average Subdivision (LAS) which is an efficient algorithm for generating spatially averaged random fields. One limitation of LAS is that it can be used only for equally spaced rectangular cells. Spatial averaging can also be performed in Fourier discretisation scheme with the flexibility of dealing with non-rectangular cells (Jha and Ching 2013). For the current study, spatial averaging with Fourier discretisation was used.

4.2.3 Random Field Modelling

For the present study, the random field is assumed as stationary which implies that mean $\left( {\mu_{\rm w} } \right)$ and standard deviation (σ_w) of rock property in consideration do not change within distance (i.e., remains same throughout the slope) and there are no irregular fluctuations. This assumption greatly facilitates in modelling the random field. The numerical analysis is performed in FLAC2D software with slope geometry as given in Fig. 7.

Zero mean stationary Gaussian random field is simulated first, and it is then converted to Gaussian field with mean of rock property. Further exponential of this stationary Gaussian field is taken to obtain lognormal random field. Procedure to simulate zero mean stationary Gaussian random field is given below.

w_D(x _e , z _e ) is the averaged rock property over the rectangular zone defined by $[ {x_{\rm e} - \frac{\Delta x}{2},x_{\rm e} + \frac{\Delta x}{2}} ]$ and $[ {z_{\rm e} - \frac{\Delta z}{2}, z_{\rm e} + \frac{\Delta z}{2}} ]$ where $x_{\rm e}$ and z_e denote the centroid of the zone. Ching et al. (2011) derived an expression for obtaining w_D(x _e , z _e )

$$\begin{aligned} w_{D} \left( {x_{{\text{e}}} ,z_{{\text{e}}} } \right) & = \frac{{ - L_{x} L_{z} }}{{\Delta x\Delta z\pi ^{2} }}Re\left\{ \sum\limits_{{m = - \infty }}^{\infty } {\sum\limits_{{n = - \infty }}^{\infty } {\left( {\frac{{a_{{mn}} + ib_{{mn}} }}{{mn}}} \right)} } \right.\\ & \left.\quad \times \exp \left( {\frac{{i2m\pi x_{{\text{e}}} }}{{L_{x} }} + \frac{{i2n\pi z_{{\text{e}}} }}{{L_{z} }}} \right)\sin \left( {\frac{{m\pi \Delta x}}{{L_{x} }}} \right)\sin \left( {\frac{{n\pi \Delta z}}{{L_{z} }}} \right)\right\} \\ \end{aligned}$$

(13)

where L _x and L _z are length and width of rectangular region in which random field is generated, Re is the real part of the complex number and a _mn and b _mn are zero mean independent Gaussian random variables with variance σ ² _mn obtained through Fourier series expansion with summation indices $m, n$ and it depends on variance of random field σ ² _w as

$$\sigma_{mn}^{2} = \frac{{\sigma_{\rm w}^{2} }}{{L_{x} L_{z} }}\left[ {\frac{{\delta_{x} - \exp \left( { - \frac{{L_{x} }}{{\delta_{x} }}} \right)\delta_{x} \left( { - 1} \right)^{m} }}{{1 + m^{2} \pi^{2} \delta_{x}^{2} /L_{x}^{2} }}} \right]\left[ {\frac{{\delta_{z} - \exp \left( { - \frac{{L_{z} }}{{\delta_{z} }}} \right)\delta_{z} \left( { - 1} \right)^{n} }}{{1 + n^{2} \pi^{2} \delta_{z}^{2} /L_{z}^{2} }}} \right]$$

(14)

For a lognormal field q(x, z) having mean value μ _q and CV v _q , the mean and standard deviation in logarithmic space would be

$$\mu_{\rm w} = \log \left( {\frac{{\mu_{q} }}{{\sqrt {1 + v_{q}^{2} } }}} \right) \quad \sigma_{\rm w} = \sqrt {{ \log }\left( {1 + v_{q}^{2} } \right)}$$

(15)

Now the random field log (q(x, z)) − μ_w will be a zero mean stationary Gaussian random field with standard deviation as σ_w. These locally averaged value of rock property for each zone is calculated using Eq. 13, and it is converted back to original space by performing the operation exp[μ_w + w _D (x _e , z _e )]. From Eq. 11, it can be seen that this value would be geometric mean of lognormal random field.

4.2.4 MC Simulation and Evaluation of Reliability Index

In this section, the results of full nonlinear RFDM are evaluated. First step in RFDM is to generate locally averaged values of rock mass properties and assigning them in respective zones in slope geometry. This analysis is repeated number of times as a part of MC simulations. Each realisation of MC simulation involves same mean, standard deviation and correlation length of input parameters, i.e., rock mass properties, but the spatial distribution of the properties will vary for different realisation as shown in Fig. 12. Numerical calculation has been carried out using FLAC2D for each MC simulation. The statistical characterisation of FOS is done after a sufficient number of MC simulations have been conducted. P_f can be computed after counting number of realisations leading to FOS less than one and dividing it by total number of realisations.

Fig. 12

Variation of spatial distribution of the rock mass properties for different Monte Carlo simulation realisation

Since the slope geometry in this paper is large, it would not be computationally feasible to run these many MC simulations realisations. Therefore, MC simulations are performed till the mean and standard deviation of FOS become approximately constant. As shown in Fig. 13a, b, the values of mean and standard deviation almost converged at 420 realisations. A probabilistic distribution is fitted to the FOS data, and then the fitted distribution is used to predict failure probability (Fenton and Griffiths 2008). In this method, we assume that the fitted distribution continues to represent response of the system at the tails. Lognormal distribution is best fit to FOS data as shown in Fig. 14, and thus the reliability index is computed according to Eq. 4.

Fig. 13

Convergence of different statistical parameters of FOS in advanced probabilistic method a mean FOS and b standard deviation of FOS

Fig. 14

Simulated data and best-fit probability distribution for FOS in advanced probability method

Results are mentioned in Table 7. It was observed that mean FOS was much above the target FOS of 1.5. CV of FOS was as high as 21% but it is much smaller than traditional probabilistic method. Expected performance level was found to be High which shows that slope is stable, and even though the bench angles are high still the slope seems to be highly stable and no slope flattening is required.

Table 7 Summary of the results obtained from advanced probabilistic method analysis

5 Comparisons of Results

It can be observed from the analysis that the level of computational complexity encountered increases as we move from deterministic to advanced probabilistic method. It must be noted that among all the methods used in the analysis, advanced probabilistic method represents the most realistic analysis of slope stability (Griffiths et al. 2007) and hence conservative/unconservative terms will be referred with respect to RFDM results.

It was observed that mean factors of safety obtained from all the analysis were more or less found to be the same. Slight difference was observed for factors of safety with maximum value observed for deterministic approach and minimum value for advanced probabilistic method. The percentage differences in mean FOS for traditional and advanced probabilistic method were 2.5 and 8%, respectively, when compared to deterministic approach. However, the expected stability level or performance level of the slopes were different for different methods. The stability of slope for deterministic approach is determined on the basis of the comparison of estimated FOS with the target FOS, and it was observed that the slope is “highly stable” since the estimated FOS, i.e., 3.84, is much higher (more than double) than the target FOS, i.e., 1.5. However, predicting the stability of slope on the basis of mean FOS could be inappropriate if the rock mass properties variability is high in the slope. As the variability of rock mass was incorporated in the analysis using traditional probabilistic method, the expected performance level was found to be “Above Average”. The reason is the consideration of CV of FOS in the estimation of reliability index which is a criterion to estimate stability level of slope in probabilistic method instead of mean FOS in deterministic approach. This shows the difference in the expected level of stability of slope by ignoring and considering uncertainties in rock mass properties.

Another important factor is regarding the consideration of spatial variability of rock mass strength in the slope. Figure 15 shows a comparison between PDFs of FOS for both traditional and advanced probabilistic methods. It was observed that for the traditional probabilistic method, the mean FOS was very slight, i.e., 5% overestimated while the CV of FOS was highly overestimated, i.e., approximately 37% as compared to advanced probabilistic method. This can be seen in Fig. 15 that both methods are showing almost same mean FOS while the spread in PDF was much higher for traditional method. This difference in the CV of FOS leads to the considerable underestimation of reliability index, i.e., approximately 34% by traditional probabilistic method. This can be attributed to the fact that variance reduction takes place during local averaging in Gaussian fields. Adoption of lognormal random field reduces both mean and standard deviation during spatial averaging (Huang and Griffiths 2015) leading to decrease in P_f. It can be observed that PDF of random field analysis results is less spread out as compared to random variable analysis, which are in accordance with the results of rock foundation analysis of Al-Bittar and Soubra (2016), which states that as correlation length increases, CV of the output of system tends to a maximum constant value. This can be explained as each realisation of random variable is perfectly correlated (same value at all spatial locations of rock mass), it represents homogenous rock mass whose strength values vary from low to high according its PDF giving rise to highly variable output, i.e., FOS. For random field analysis, spatial correlation is introduced, which results in different strength values of rock mass at different spatial locations. A single realisation of random field generates weak and strong zones of rock mass whose position changes from one realisation to other. The extent of these weak and strong zones depends on correlation structure of the random field. This can be interpreted as different realisations of heterogeneous rock mass (zones of strong and weak rock mass distributed throughout the slope). Analysis of such a slope reduces the FOS variability as compared to FOS variability resulting from traditional probabilistic analysis (realisations of weak and strong homogenous rock mass). The failure surface/slip surface seeks out the path of least resistance through heterogeneous rock mass as shown in Fig. 16 for different realisations of random field analysis of slope. As the correlation length further decreases, rock property will vary rapidly in nearby locations making the failure path become more and more tortuous and larger in length giving approximately similar values of FOS for each realisation which reduces the CV of the FOS (Griffiths et al. 2007; Al-Bittar and Soubra 2016).

Fig. 15

Probability density functions of factors of safety for the slope using both traditional probabilistic method and advanced probabilistic method

Fig. 16

Different slip circles seeking the path of least resistance in random field analysis

6 Conclusions

Stability analysis of a large rock slope was performed using three methods—deterministic, traditional probabilistic and advanced probabilistic methods. Slope was found to be stable in all the approaches according to their defined criteria; however, the degree of stability predicted by all the methods was different. It was observed that it is better to evaluate the stability of slope in terms of reliability index and $P_{\text{f}}$ along with FOS instead of FOS alone. While the mean FOS for the slope was more or less the same for all the approaches, expected stability level or performance level of slope was different for probabilistic approach as compared to deterministic approach due to ignorance of uncertainty in rock mass strength properties in deterministic approach. It was observed that probabilistic method ignoring spatial variability in rock mass strength properties underestimated the reliability index and expected performance level of slope. Hence, it was concluded that although extensive geological and laboratory investigation is required and method is computationally complex, advanced probabilistic method should be used as it is able to model actual failure mechanism, i.e., slip surface seeking path of weakest link. It was also concluded that slope was stable despite its steep bench angles and no further flattening or external reinforcement is required.

7 Suggestions for Future Work

For the current study, the stability analysis of slope is carried out using continuum approach which is valid when the rock mass is more moderately to heavily jointed and the rock mass strength is approximately isotropic. However, the approach described in the current study should not be used where the discontinuity spacing is large as compared to the dimensions of rock slope or stability is more governed by the shear strength of individual discontinuities. In this case, spatial variability of shear strength of discontinuity should be evaluated as performed by Sow et al. (2017). It is further suggested to generate a more realistic 3D random field by obtaining correlation length in all three directions for analysis in 3D software in future research.

In this study, intact rock properties and GSI are treated as uncertain parameters. Rock mass parameters are derived from intact rock properties and GSI through empirical relationship provided by Hoek et al. (2002) and Hoek and Diederichs (2006). The transformation uncertainties associated with these empirical relationships are not considered in this study. Thus variability in rock mass parameters are underestimated by unknown amount and this issue can be taken up in future studies.

Appendix

1.1 Augmented Radial Basis Function

In conventional RBF-based models, the numerical (FEM/FDM) model output $g\left( \varvec{X} \right)$ is approximated by linear combination of radial functions.

$$g\left( \varvec{Z} \right) \approx g\left( \varvec{Z} \right) = \mathop \sum \limits_{i = 1}^{k} \lambda_{i} \psi \left( {\parallel \varvec{Z} - \varvec{Z}_{\varvec{i}} \parallel } \right)$$

(16)

where k is the no. of sampling points obtained using design of experiment (DOE) method, $\varvec{Z}_{\varvec{i}}$ is the input vector at ith sampling point, ψ is the radial basis function, $\parallel \varvec{Z} - \varvec{Z}_{\varvec{i}} \parallel$ is the Euclidean norm (distance) of vector $\varvec{Z}$ from $\varvec{Z}_{\varvec{i}}$ and λ_i are coefficients for the ith basis function. RBFs have been explained in more detail in Krishnamurthy (2003).

For evaluating unknown constants λ_i, k vectors of input sample is evaluated to obtain k outputs and finally solving the matrix Equation.

$$\varvec{g}_{{\varvec{k} \times 1}} = \varvec{A}_{{\varvec{k} \times \varvec{k }}}\varvec{\lambda}_{{\varvec{k} \times 1}}$$

(17)

where $\varvec{g}$ output vector is obtained by solving numerical model at k input samples, $\varvec{A}_{{\varvec{i},\varvec{j}}} = \varvec{ }\psi \left( {\parallel \varvec{Z}_{\varvec{j}} - \varvec{Z}_{\varvec{i}} \parallel } \right)$ i, j = 1, 2, 3,…,k and $\varvec{\lambda}$ is vector of coefficient to be determined. This RBF meta-model provides good accuracy if the performance function is highly nonlinear. A linear or quadratic polynomial is further added to this meta-model to enhance its performance in approximating both linear and non-linear response (Krishnamurthy 2003). This is known as augmented RBF model expressed as

$$g\left( \varvec{Z} \right) \approx \mathop \sum \limits_{i = 1}^{k} \lambda_{i} \psi \left( {\parallel \varvec{Z} - \varvec{Z}_{\varvec{i}} \parallel } \right) + \mathop \sum \limits_{j = 1}^{l} P_{j} \left( \varvec{Z} \right)b_{j}$$

(18)

where $P_{j} \left( \varvec{Z} \right)$ are monomial terms of polynomial $P\left( \varvec{Z} \right)$ and b_j are l constants introduced. For a linear polynomial l = d + 1 where d is the dimension of input vector. In Eq. 18, total numbers of unknowns are k + l which are more than the number of FDM model evaluations. To avoid additional sampling, orthogonality condition is imposed (Eq. 19)

$$\mathop \sum \limits_{i = 1}^{k} \lambda_{i} P_{j} \left( {Z_{i} } \right) = 0 \quad {\text{for}}\quad j = 1,2, \ldots l$$

(19)

From Eqs. (18) and (19) we get all the unknown coefficients $\varvec{\lambda}$ and $\varvec{b}$ by solving

$$\left[ {\begin{array}{*{20}c} {\varvec{A}_{{\varvec{k} \times \varvec{k}}} } & {\varvec{B}_{{\varvec{k} \times \varvec{l}}} } \\ {\varvec{B}_{{\varvec{k} \times \varvec{l}}} } & {0_{{\varvec{l} \times \varvec{l}}} } \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\varvec{\lambda}_{{\varvec{k} \times 1}} } \\ {\varvec{b}_{{\varvec{l} \times 1}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varvec{g}_{{\varvec{k} \times 1}} } \\ {0_{{\varvec{l} \times 1}} } \\ \end{array} } \right\}$$

(20)

where $\varvec{A}$ and $\varvec{g}$ are same vectors as in Eq. 17, $0_{{\varvec{m} \times \varvec{m}}}$ is zero matrix. While $B_{ij} = P_{j} \left( {Z_{i} } \right) j = 1,2, \ldots , l$ and $i = 1,2, \ldots ,k$ where Z_i is ith component of vector $\varvec{Z}$ and P_j is jth term of the polynomial. There are many types of radial basis functions, most widely used are linear, cubic, Gaussian, thin plate spline, multiquadratic, and compactly supported functions (see Table 8). The compactly supported RBF used in this article were developed by Wu (1995). This generates very efficient response surfaces as $\varvec{A}$ is sparse and positive definite. Compact support type II is used here

$$\psi \left( r \right) = \left( {1 - t} \right)^{6} \left( {6 + 36t + 82t^{2} + 72t^{3} + 30t^{4} + 5t^{5} } \right)\, 0 \le r \le r_{0} = 0\;r > r_{0}$$

(21)

where t = r/r₀ and r₀ is the radius of domain of compact support and r is $\parallel \varvec{Z} - \varvec{Z}_{\varvec{i}} \parallel$.

Table 8 Commonly used radial basis functions (Krishnamurthy 2003)