An efficient Bayesian multi-model framework to analyze reliability of rock structures with limited investigation data

Abstract

Availability of insufficient data is a frequent issue resulting in the inaccurate probabilistic characterization of properties and, finally the inaccurate reliability estimates of rock structures. This study presents a Bayesian multi-model inference methodology which couples multi-model inference with traditional Bayesian approach to characterize uncertainties in both—(1) probability models, and (2) model parameters of rock properties arising due to insufficient data, and to estimate the reliability of rock slopes and tunnels considering their effect. Further, this methodology was coupled with Sobol’s sensitivity, metropolis–hastings Markov chain Monte Carlo sampling and moving least square-response surface method to improve the computational efficiency and applicability for problems with implicit performance functions (PFs). Methodology is demonstrated for a Himalayan rock slope (implicit PF) prone to stress-controlled failure in India. Analysis is also performed using recently developed limited data reliability methods, i.e., traditional Bayesian (considers uncertainty in model parameters only) and bootstrap-based re-sampling reliability methods (considers uncertainties in model types and parameters). Proposed methodology is concluded to be superior to other methods due to its capability of considering uncertainties in both model types and parameters, and to include the prior information in the analysis.

1 Introduction

Stability analysis of rock structures is a complex problem majorly due to uncertainties in rock properties emanating due to inherent and knowledge-based reasons. Reliability methods provide a suitable alternative to analyze the stability of these structures in the presence of these uncertainties. Several reliability methods like Monte-Carlo simulations (MCSs) [50], first/second-order reliability methods (F/SORMs) [19, 20] and point estimate methods (PEMs) [1] etc., have been developed over the years and are currently used for different in situ problems [2, 42, 52, 54, 60]. Although the mathematical and operational framework of different reliability methods vary, their inputs are the parameters representing the uncertainties in properties, i.e., (1) statistical parameters [i.e., mean and standard deviation (SD)], and (2) best fit probability model. Accurate estimation of these best fit distribution model and model parameters is seldom possible for the rock projects due to availability of insufficient data. This is due to the high costs and significant practical difficulties in lab and in situ testing of rock masses [21, 44, 62]. Frequentist reliability approaches like MCSs, F/SORMs, PEMs, etc., assumes that the model type and distribution parameters estimated from the site-specific test data are deterministic and accurate quantities which is not true in the presence of limited data [31,32,33, 38, 43]. This in turn raises the question on the accuracy of the analysis based on frequentist reliability approaches.

Traditional Bayesian approaches provide an improvement in the frequentist approaches by considering the model parameters as random variables to consider their uncertainties. This is performed by incorporating the existing or prior available information from various sources with limited site-specific information [7]. Statistical inference is employed to determine a single “best” probability model and identified sole model is used to make inference from the data. These methods, however, suffer a major limitation of ignoring the uncertainty associated with probability model selection. It is difficult to identify a unique best probability model in the presence of a limited data set, rather than a large data set. In rock mechanics, most of the studies employing these approaches are restricted to explicitly model the uncertainties in intact rock properties and empirical models only [3,4,5, 8, 9, 12, 17, 57, 58]. Very limited studies are available in literature employing these approaches for analyzing the stability of practical rock slopes and tunnels as shown in Table 1. Further, the available studies neglect the uncertainty related to the probability model and consider the uncertainties in the parameters of the unique “best” model. Therefore, a methodology is required which can quantify both the model type and model parameters uncertainties in rock properties and propagate it to the reliability estimates of rock structures.

Table 1 A summary of the studies on the application of Bayesian approach for the reliability analysis of rock structures

In this spirit, a Bayesian multi-model inference (BMMI) approach is developed to consider the effect of uncertainties related to probability model type and model parameters in input properties on the reliability estimates of rock slopes and tunnels in the presence of limited test data. To attain the objective, the multi-model inference approach [13], wherein a set of possible probability models for a rock property can be identified to incorporate the uncertainty associated with model type, is coupled with the traditional Bayesian approach. In addition, this methodology employs Sobol’s global sensitivity and the moving least square-response surface method (MLS-RSM) to enhance its computational efficiency and applicability for analyzing the problems with both explicit/implicit performance functions (PFs). The developed approach was demonstrated for a Himalayan rock slope prone to stress-controlled failure (single implicit PF) in India. A comparative assessment is also made with the results of the other methods currently in use for estimating engineering reliability in the presence of limited data—(1) traditional Bayesian approach (considers only model parameter uncertainty), and (2) recently developed resampling reliability method coupling bootstrap re-sampling with frequentist approaches (considers both model type and parameters uncertainties) [31, 32, 43].

2 Details of the components of methodology

This section explains the components involved in the present methodology.

2.1 Bayesian inference

The Bayesian inference is used to quantify the uncertainty associated with the parameters of the probability model (M). Bayesian inference treats model parameters (${\varvec{\theta}}$) probabilistically (as a random variable) by combining prior knowledge in the formulation via prior distribution ($p\left( {{\varvec{\theta}};M} \right)$) and site-specific observation data (${\varvec{d}}$) expressed in terms of the likelihood function ($p({\varvec{d}}|{\varvec{\theta}},M)$. The posterior distribution $p\left( {{\varvec{\theta}}{|}{\varvec{d}},M} \right)$, i.e., the updated probability density function of parameters ${\varvec{\theta}}$ according to the Baye’s rule can be written as given below [7].

$$p\left( {{\varvec{\theta}}{|}{\varvec{d}},M} \right) = \frac{{p({\varvec{d}}|{\varvec{\theta}},M)p\left( {{\varvec{\theta}};M} \right)}}{{p\left( {{\varvec{d}};M} \right)}} \propto p\left( {{\varvec{d}}{|}{\varvec{\theta}},M} \right)p\left( {{\varvec{\theta}};M} \right)$$

(1)

where $p\left( {{\varvec{d}};M} \right)$ is known as the normalizing factor or evidence used to make the cumulative distribution function (CDF) of posterior distribution equals to one and can be estimated as given below.

$$p\left( {{\varvec{d}};M} \right) = \int p({\varvec{d}}|{\varvec{\theta}},M)p\left( {{\varvec{\theta}};M} \right)$$

(2)

The likelihood function $p({\varvec{d}}|{\varvec{\theta}},M)$ for a property with observation data ${\varvec{d}} = \left\{ {d_{1} .d_{2} , \ldots ,d_{N} } \right\}$ which is being modeled using probability distribution model M having parameters ${\varvec{\theta}}$ can be formulated as below [7].

$$p\left( {{\varvec{d}}{|}{\varvec{\theta}},M} \right) = f\left( {d_{1} {|}{\varvec{\theta}}} \right) \times f\left( {d_{2} {|}{\varvec{\theta}}} \right) \times \cdots \times f\left( {d_{n} {|}{\varvec{\theta}}} \right) = \mathop \prod \limits_{i = 1}^{n} f\left( {d_{i} {|}{\varvec{\theta}}} \right)$$

(3)

where $f\left( {d_{i} |{\varvec{\theta}},M} \right)$ is the PDF value corresponding to model probability distribution M evaluated at the i-th data point $d_{i}$, and ${\varvec{\theta}}$ represents the parameters of the M.

Estimation of posterior distribution $p\left( {{\varvec{\theta}}{|}{\varvec{d}},M} \right)$ involves multi-dimensional integration and analytical solutions are computationally complex and in-efficient, except for the conjugate prior distributions. To overcome this issue, a numerical process known as Markov chain Monte Carlo (MCMC) simulation can be employed to generate a sequence of random samples from the posterior distribution [6]. Details of MCMC sampling are presented in Sect. 2.3.

2.2 Multimodal selection and model uncertainty

This methodology employs the multi-model inference approach [13, 63] to incorporate the uncertainty associated with the model identification of properties. Kullback–Leibler (K–L) information theory-based akaike information criterion (AIC) was used for the model selection in this study. The probability model with minimum AIC value is considered as a best fit model to represent the data. For small datasets, an updated AIC, i.e., AIC_c has been developed as given below [26].

$${\text{AIC}}_{{\text{c}}} = - 2\log \left( {p\left( {{\varvec{d}}{|}\hat{\user2{\theta }},M} \right)} \right) + 2K + \frac{{2K\left( {K + 1} \right)}}{N - K - 1}$$

(4)

where $p({\varvec{d}}|\hat{\user2{\theta }},M)$ is the likelihood function given the maximum likelihood estimate of the parameters $\hat{\user2{\theta }}$, K is the number of parameters of the candidate model M, and N is the sample size of the data set. AIC_c should be used when $\frac{N}{K} < \sim 40$ and AIC_c converges to AIC with the increasing value of N [13, 63]. Given the small datasets, AIC_c is utilized for multi-model selection in this study. Once the AIC_c value is known for each model in the candidate set, the AIC differences values (${{\varvec{\Delta}}}_{{\text{A}}}$) can be calculated to interpret a ranking of candidate models as given below [13].

$$\Delta_{{\text{A}}}^{\left( i \right)} = {\text{AIC}}_{{\text{c}}}^{\left( i \right)} - {\text{AIC}}_{{\text{c}}}^{\min }$$

(5)

where ${\text{AIC}}_{{\text{c}}}^{\min }$ is the minimum of the ${\text{AIC}}_{{\text{c}}}^{\left( i \right)}$ values, $i = 1,2,3, \ldots ,N_{d}$ and $N_{d}$ is the total number of candidate models in the set. This transformation forces the best model to have ${\Delta }_{{\text{A}}}^{\left( i \right)} = 0$ and all the other models to have positive values. Further, the likelihood of the model $M_{i}$ can be expressed as $\exp \left( { - \frac{1}{2}{\Delta }_{{\text{A}}}^{\left( i \right)} } \right)$ and by normalizing these likelihoods the AIC_c based model probabilities ${\mathfrak{p}}_{i}$ can be estimated as given below.

$${\mathfrak{p}}_{i} = p\left( {M_{i} |d} \right) = \frac{{\exp \left( { - \frac{1}{2}{\Delta }_{{\text{A}}}^{\left( i \right)} } \right)}}{{\mathop \sum \nolimits_{m = 1}^{{N_{d} }} \exp \left( { - \frac{1}{2}{\Delta }_{{\text{A}}}^{\left( m \right)} } \right)}}$$

(6)

Larger the ${\mathfrak{p}}_{i}$ or lesser the ${\Delta }_{{\text{A}}}^{\left( i \right)}$, the more plausible is model being the best fit for the given dataset among the candidate models. Therefore, ${\mathfrak{p}}_{i}$ and ${\Delta }_{{\text{A}}}^{\left( i \right)}$ can be utilized to rank the models among the candidate sets.

2.3 Metropolis–hastings (MH) MCMC sampling

MCMC sampling was used in this study due to its feasibility to generate samples from an arbitrary distribution particularly when the density function is difficult to express analytically [11, 45]. Samples are obtained by exploring the entire domain of uncertain parameters based on their prior distributions. The MCMC was coupled with the Bayesian inference to allow any general prior distribution selection where the posterior distribution becomes complex and difficult to express analytically. Among the available options, the metropolis–hastings (MH) algorithm was employed in this study due its simplicity and efficiency to implement the MCMC sampling for the posterior of parameter ${\varvec{\theta}}$ [25, 39]. The procedure of the MH algorithm can be summarized as given below.

(i) At stage $t = 1$, assume an initial value of parameter ${\varvec{\theta}} = {\varvec{\theta}}_{1}$, which can be chosen randomly from the prior distribution or may simply be assigned the mean value.

(ii) At any subsequent stage t ($t = 2,3, \ldots )$, generate a new proposal value ${\varvec{\theta}}^{*}$ from a proposal distribution $T({\varvec{\theta}}^{*} |{\varvec{\theta}}_{t - 1} )$, which is considered to be multivariate Gaussian distribution for simplicity with mean value ${\varvec{\theta}}_{t - 1}$ and standard deviation ${\varvec{s}}$ [6, 56, 59]. Parameter ${\varvec{s}}$ is also known as tunning parameter or width/scaling of proposal distribution.

(iii) Calculate the ratio of the posterior density for the candidate (${\varvec{\theta}}^{*}$) and current (${\varvec{\theta}}_{t - 1}$) values as shown below.

$${\varvec{r}} = \min \left( {\frac{{p\left( {{\varvec{\theta}}^{*} {|}{\varvec{d}},M} \right) T\left( {{\varvec{\theta}}^{*} ,{\varvec{\theta}}_{t - 1} } \right)}}{{p\left( {{\varvec{\theta}}_{t - 1} {|}{\varvec{d}},M} \right) T\left( {{\varvec{\theta}}_{t - 1} ,{\varvec{\theta}}^{*} } \right)}},1} \right)$$

(7)

For the symmetric proposal distributions, i.e., $T\left( {{\varvec{\theta}}^{*} ,{\varvec{\theta}}_{t - 1} } \right) = T\left( {{\varvec{\theta}}_{t - 1} ,{\varvec{\theta}}^{*} } \right)$, the ratio ${\varvec{r}}$ is reduced to the expression as shown below.

$${\varvec{r}} = \min \left( {\frac{{p\left( {{\varvec{\theta}}^{*} {|}{\varvec{d}},M} \right)}}{{p\left( {{\varvec{\theta}}_{t - 1} {|}{\varvec{d}},M} \right)}},1} \right)$$

(8)

(iv) Draw a random number ${\varvec{u}}$ from the uniform distribution ${\varvec{U}}\left( {0,1} \right)$, i.e., ${\varvec{u}}\sim {\varvec{U}}\left( {0,1} \right)$.

(v) Accept the candidate state ${\varvec{\theta}}_{t} = {\varvec{\theta}}^{*}$, if ${\varvec{r}} \ge {\varvec{u}}$. Otherwise, the current value is taken as the next value ${\varvec{\theta}}_{t} = {\varvec{\theta}}_{t - 1}$.

(vi) Repeat step (ii)–(v) till the target number of samples (i.e., ${\varvec{\theta}}_{2} ,{\varvec{\theta}}_{3} , {\varvec{\theta}}_{4} , \ldots$) are obtained.

The choice of initial value and proposal distribution have strong influence on the convergence of the Markov chain toward stationary condition. The initial samples may be discarded as burn-in samples, as they might not be completely valid depending upon the assumption of initial value. The optimal selection (neither too high nor too low) of tunning parameter or scaling of proposal distribution can be made graphically through the trace plot (i.e., Markov chain sample versus sample number) and autocorrelation plot (i.e., autocorrelation function (ACF) against increasing lag values) of the simulated Markov chain samples. For a stationary Markov chain, trace plot should look like a hairy caterpillar (not show apparent anomalies) and autocorrelation plot should show a quick, exponential decrease between the correlation of sample. Beside visual inspection, the performance of chain can be assessed numerically through acceptance rate (i.e., percentage of accepted samples). An acceptance rate in between 20 and 40% is considered sufficiently efficient [24]. A MATLAB code was written to generate random samples from the posteriors.

2.4 Bootstrap re-sampling reliability approach

Bootstrap re-sampling approach is usually employed to quantify the effect of statistical uncertainties associated with both model type and parameters arising due to small size of sample and to estimate its effect on the response of structures by coupling this approach with frequentist reliability approach, i.e., MCSs [31, 32, 43]. In this method, a large number of re-constituted samples from the original data sample are generated which are assumed to be in close resemblance to the original sample. These surrogate samples are generated through random sampling with replacement from the original sample. Figure 1 shows an example of a bootstrap re-constituted sample for the variable ${\varvec{X}} = \left\{ {X_{1} , X_{2} , \ldots , X_{N} } \right\}$ with N sample data points. For each re-constituted sample every data point in the original sample has an equal probability of being chosen. Size of re-constituted samples is kept same as that of original sample that avoids any biasness resulting into sample statistics [29]. From these re-constituted samples, the bootstrap statistics [i.e., bootstrap mean $\mu_{{{\text{B}}_{\alpha } }}$ and bootstrap standard deviation (SD) $\sigma_{{{\text{B}}_{\alpha } }}$] for a sample statistical parameter $\alpha$ (i.e., sample mean and sample SD) quantifying the statistical uncertainty can be obtained as following.

$$\mu_{{{\text{B}}_{\alpha } }} = \frac{1}{B}\mathop \sum \limits_{b = 1}^{{N_{{\text{B}}} }} \alpha_{b} ; \sigma_{{B_{\alpha } }} = \sqrt {\frac{1}{{N_{{\text{B}}} - 1}}\mathop \sum \limits_{b = 1}^{{N_{{\text{B}}} }} \left( {\alpha_{b} - \mu_{{{\text{B}}_{\alpha } }} } \right)^{2} }$$

(9)

where $\alpha_{b}$ is the sample statistical parameter estimated for the bth bootstrap re-constituted sample and $N_{{\text{B}}}$ is the total number of re-constituted samples. For each re-constituted sample, traditional reliability analysis was performed via MCSs, and statistical parameters of P_f were estimated using standard statistical methods.

Fig. 1

Procedure to generate re-constituted samples using bootstrap approach from the original sample

2.5 Sensitivity analysis

Sensitive properties were identified with significant effect on the PF using sensitivity analysis. This aided the improvement in the computational efficiency of the methodology by considering the uncertainties in sensitive properties only. Sobol’s global sensitivity analysis (GSA) [48] was employed in this study due to its efficiency to explore the whole space of input variables. This is not possible in the local sensitivity analysis. Total order/effects ($S_{{T_{i} }}$) quantifying the relative contributions of input properties on the output variability can be estimated as given below.

$$S_{{T_{i} }} = 1 - \frac{{V[E(Y|{\varvec{X}}_{\sim i} )}}{V\left( Y \right)}$$

(10)

where E and V are the expectation and variance; $X_{i}$ is the ith input parameter; ${\varvec{X}}_{\sim i}$ represents the components of input vector ${\varvec{X}}$ except $X_{i}$. Saltelli’s MCSs based numerical method was employed to estimate $S_{{T_{i} }}$ in which quasi-random samples for ${\varvec{X}}$ were generated and arranged in the matrices ${\varvec{A}}$ and ${\varvec{B}}$ as shown below.

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} {x_{1}^{\left( 1 \right)} } & {x_{2}^{\left( 1 \right)} } & \cdots & {x_{i}^{\left( 1 \right)} } & \cdots & {x_{n}^{\left( 1 \right)} } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {x_{1}^{\left( k \right)} } & {x_{2}^{\left( k \right)} } & \cdots & {x_{i}^{\left( k \right)} } & \cdots & {x_{n}^{\left( k \right)} } \\ \end{array} } \right]$$

(11)

$${\varvec{B}} = \left[ {\begin{array}{*{20}c} {x_{n + 1}^{\left( 1 \right)} } & {x_{n + 2}^{\left( 1 \right)} } & \cdots & {x_{n + i}^{\left( 1 \right)} } & \cdots & {x_{2n}^{\left( 1 \right)} } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {x_{n + 1}^{\left( k \right)} } & {x_{n + 2}^{\left( k \right)} } & \cdots & {x_{n + i}^{\left( k \right)} } & \cdots & {x_{2n}^{\left( k \right)} } \\ \end{array} } \right]$$

(12)

where k is the base sample and n is the input vector dimension. ${\varvec{C}}_{{\varvec{i}}}$ is the matrix containing elements of ${\varvec{B}}$ except the ith column, which is taken from ${\varvec{A}}$.

$${\varvec{C}}_{{\varvec{i}}} = \left[ {\begin{array}{*{20}c} {x_{n + 1}^{\left( 1 \right)} } & {x_{n + 2}^{\left( 1 \right)} } & \cdots & {x_{i}^{\left( 1 \right)} } & \cdots & {x_{2n}^{\left( 1 \right)} } \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {x_{n + 1}^{\left( k \right)} } & {x_{n + 2}^{\left( k \right)} } & \cdots & {x_{i}^{\left( k \right)} } & \cdots & {x_{2n}^{\left( k \right)} } \\ \end{array} } \right]$$

(13)

The output column vectors ${\varvec{Y}}_{{\varvec{A}}} , {\varvec{Y}}_{{\varvec{B}}}$ and ${\varvec{Y}}_{{{\varvec{C}}_{{\varvec{i}}} }}$ are constructed by evaluating the PF, i.e., ${\varvec{Y}} = G\left( {\varvec{X}} \right)$, for the realizations of ${\varvec{A}}$, ${\varvec{B}}$ and ${\varvec{C}}_{{\varvec{i}}}$, respectively. $S_{{T_{i} }}$ for the input $X_{i}$ then can be calculated by employing Janon estimators [28] as given below.

$$S_{{T_{i} }} = 1 - \frac{{\left( \frac{1}{k} \right)\mathop \sum \nolimits_{j = 1}^{k} y_{B}^{\left( j \right)} y_{{C_{i} }}^{\left( j \right)} - \left( {\left( \frac{1}{k} \right)\mathop \sum \nolimits_{j = 1}^{k} \left[ {\frac{{y_{B}^{\left( j \right)} + y_{{C_{i} }}^{\left( j \right)} }}{2}} \right]} \right)^{2} }}{{\left( \frac{1}{k} \right)\mathop \sum \nolimits_{j = 1}^{k} \left[ {\frac{{\left( {y_{B}^{\left( j \right)} } \right)^{2} + \left( {y_{{C_{i} }}^{\left( j \right)} } \right)^{2} }}{2}} \right] - \left( {\left( \frac{1}{k} \right)\mathop \sum \nolimits_{j = 1}^{k} \left[ {\frac{{y_{B}^{\left( j \right)} + y_{{C_{i} }}^{\left( j \right)} }}{2}} \right]} \right)^{2} }}$$

(14)

where $y_{A}^{\left( j \right)} , y_{B}^{\left( j \right)}$ and $y_{{C_{i} }}^{\left( j \right)}$ are the jth element of column vectors $Y_{A} , Y_{B}$ and $Y_{{C_{i} }}$, respectively.

2.6 Moving least square-response surface method (MLS-RSM)

MLS-RSM was used to obtain an explicit surrogate relationship between input–output for the problems lacking explicit PFs, thus eliminating the requirement of repeated numerical simulations. This issue will be shown in the later sections. MLS-RSM can be mathematically expressed as given below [37].

$$\hat{G}\left( {\varvec{X}} \right) = {\varvec{p}}\left( {\varvec{X}} \right){\varvec{a}}\left( {\varvec{X}} \right)$$

(15)

where ${\varvec{p}}\left( {\varvec{X}} \right) = \left[ {1 x_{1} x_{2} ... x_{d} x_{1}^{2} x_{2}^{2} ... x_{d}^{2} } \right]_{1 \times m}$ is a quadratic polynomial basis of function ($m = 2d + 1$). ${\varvec{a}}\left( {\varvec{X}} \right)$ is a set of unknown coefficients, which is dependent on the ${\varvec{X}}$ and can be determined, as given below.

$${\varvec{a}}\left( {\varvec{X}} \right) = {\varvec{A}}_{m \times m}^{{{-}1}} {\varvec{B}}_{m \times h} {\varvec{Y}}_{h \times 1}$$

(16)

where ${\varvec{Y}} = \left[ {G\left( {{\varvec{X}}_{1} } \right) G\left( {{\varvec{X}}_{2} } \right)...\user2{ }G\left( {{\varvec{X}}_{h} } \right)} \right]^{{\mathbf{T}}}$ is the matrix of known PF values obtained from the opted solution technique. Matrices ${\varvec{A}}$ and ${\varvec{B}}$ can be written as given below.

$${\varvec{A}}\left( {\varvec{X}} \right) = {\varvec{P}}_{m \times h}^{{T{\text{T}}}} {\varvec{W}}_{h \times h} {\varvec{P}}_{h \times m} ; {\varvec{B}}\left( {\varvec{X}} \right) = {\varvec{P}}_{m \times h}^{{\text{T}}} {\varvec{W}}_{h \times h}$$

(17)

where

$${\varvec{P}} = \left[ {\begin{array}{*{20}c} {{\varvec{p}}\left( {{\varvec{X}}_{1} } \right)} \\ {{\varvec{p}}\left( {{\varvec{X}}_{2} } \right)} \\ {\begin{array}{*{20}c} {...} \\ {{\varvec{p}}\left( {{\varvec{X}}_{h} } \right)} \\ \end{array} } \\ \end{array} } \right]_{h \times m} ; {\varvec{W}} = \left[ {\begin{array}{*{20}c} {w_{1} \left( {\varvec{X}} \right)} & 0 & 0 \\ 0 & {...} & 0 \\ 0 & 0 & {w_{h} \left( {\varvec{X}} \right)} \\ \end{array} } \right]_{h \times h}$$

(18)

where $w_{i} \left( {\varvec{X}} \right)$ is the spline weighting function (C¹ continuous) with compact support as shown below.

$$w_{i} \left( {\varvec{X}} \right) = \left\{ {\begin{array}{*{20}l} {1{-}6r_{i}^{2} + 8r_{i}^{3} {-}3r_{i}^{4} ;} \hfill & {\quad r \le 1} \hfill \\ {0;} \hfill & {\quad r > 1} \hfill \\ \end{array} } \right.$$

(19)

where $r = {{{\varvec{X}}{-}{\varvec{X}}_{i2} } \mathord{\left/ {\vphantom {{{\varvec{X}}{-}{\varvec{X}}_{i2} } {l_{i} }}} \right. \kern-0pt} {l_{i} }}$, $l_{i}$ is the influence domain size chosen as twice the distance between $\left( {1 + 2d} \right)$th sample point and design point ${\varvec{X}}$, d is the number of random variables and h is the number of sampling points. Latin Hypercube Sampling (LHS) based design of experiments technique was used for generating sampling points (random input vectors realizations) from input parameter distributions [40]. Nash–Sutcliffe efficiency (NSE) index was adopted to assess the accuracy of the RSM [41]. NSE was evaluated by estimating the PF values using original solving technique and RSM, i.e., $G_{i}^{{{\text{original}}}} \left( {\varvec{X}} \right)$ and $\hat{G}_{i}^{{{\text{RSM}}}} \left( {\varvec{X}} \right)$ at p random off-sample points of input properties generated via the LHS, as given below.

$${\text{NSE}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{p} \left( {G_{i}^{{{\text{original}}}} \left( {\varvec{X}} \right) - \hat{G}_{i}^{{{\text{RSM}}}} \left( {\varvec{X}} \right)} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{p} \left( {G_{i}^{{{\text{original}}}} \left( {\varvec{X}} \right) - G_{i}^{{{\text{mean}}}} \left( {\varvec{X}} \right)} \right)^{2} }}} \right]$$

(20)

where $G_{i}^{{{\text{mean}}}} \left( {\varvec{X}} \right)$ is the mean value of $G_{i}^{{{\text{original}}}} \left( {\varvec{X}} \right)$. The RSM is rated very good for NSE value 0.75–1.0.

3 Methodology

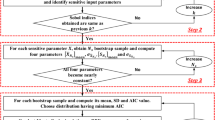
This section explains the steps involved in the proposed BMMI methodology. As mentioned earlier, the main idea of the BMMI methodology is to couple the multi-model inference with traditional Bayesian and probabilistic tools. Figure 2 shows the flowchart explaining the implementation steps for the methodology.

Fig. 2

Flowchart to implement the proposed Bayesian multi-model inference (BMMI) approach along with the traditional Bayesian and bootstrap re-sampling reliability approach

As mentioned earlier, analysis performed by the proposed methodology was also compared with the recently developed methodologies employed for the reliability analysis in the presence of limited data. Two such methodologies, i.e., traditional Bayesian methodology and bootstrap re-sampling reliability were used for the analysis in the next section. Hence, the steps involved in these methodologies are also briefly summarized in Fig. 2. A MATLAB code was written to implement all the above steps sequentially in analyzing the stability of rock slopes.

4 Application example

Application example used in this study is a rock slope supporting the piers of world’s highest Chenab railway bridge in the Jammu and Kashmir, India. The major reason to select the case study for this study is the well-studied geological and geotechnical properties of the rock mass at the site. Slope under consideration is a large slope with dimensions 293 × 196 m. Rock mass at the site was heavily jointed dolomite (unit weight = 25 kN/m³) intersected by three major joint sets along with some random joint sets. Slope was adjudged to be prone to stress-controlled failure due to very close joint spacing and large dimensions. More details on the geology, location and geotechnical of the slope can be found in the literature [52]. Analysis was performed using different methodologies via the steps shown in flowchart in Fig. 2.

4.1 Analysis using Bayesian multi-model inference (BMMI) methodology

4.1.1 Step 1: estimation of rock properties

Intact rock and rock joint properties were estimated for this site using the standard tests conducted as per ISRM suggested guidelines [27]. Table 2 shows the statistics of the properties relevant to this study [52]. The original sample of rock properties contains 22 data points only, which are statistically small and insufficient.

Table 2 Statistical parameters and best fit probability distribution (PD) model of rock properties from the original sample

4.1.2 Step 2: derivation of performance function (PF)

PF for the slope stability is usually expressed in terms of factor of safety (FOS). Slope under consideration is prone to stress-controlled failure and hence, the analytical formulation of PF was not possible. Hence, an explicit surrogate relationship between input rock properties and output response parameter (i.e., FOS) was derived using MLS-RSM. A total of $h = 200$ sampling points of input properties were generated using LHS based on their statistics (Table 2). FOSs were estimated for these realizations using Shear Strength Reduction (SSR) [18] in Phase² [46] by assuming rock as elastic perfectly plastic Hoek–Brown material. A typical finite element model of the slope prepared in Phase² is shown in Fig. 3. Vectors ${\varvec{X}}$ and ${\varvec{Y}}$ were determined using the realizations of input properties and corresponding FOSs (Sect. 2.6). NSE of the constructed MLS-RSM was 0.9748 for p = 50 off-sample points and hence, the performance of the RSM was rated to be as very good.

Fig. 3

Typical numerical model prepared in Phase² for the stability analysis of rock slope

It is important to note that the authors have used the moving least square-response surface method (MLS-RSM) to construct an explicit expression between the input rock properties and FOS. MLS-RSM uses a locally weighted regression approach to fit a surface to the input–output data. In this method, the coefficients of the monomials change for every observation, which makes it difficult to write an explicit expression unlike the polynomial RSMs where the coefficients of the monomials remain constant for every observation [30, 37].

4.1.3 Step 3: identification of sensitive properties

Sensitive properties were identified using Sobol’s GSA and only the identified sensitive properties were considered for BMMI. Sobol’s analysis was performed using the PF derived in the previous step. A total of $k = 10^{5}$ quasi-random samples were used for the Sobol’s analysis (Sect. 2.5). Results are summarized in Fig. 4. $S_{{T_{i} }}$ of UCS and GSI were estimated to be 30–64% more than those of $E_{i}$ and $m_{i}$ indicating their high sensitivities. Hence, the Bayesian analysis was performed by considering statistical uncertainties in UCS and GSI only while considering $E_{i}$ and $m_{i}$ as random variables.

Fig. 4

Sobol’s indices indicating the sensitivities of rock properties toward the FOS of the rock slope

4.1.4 Step 4: identification of plausible models

Initially, the candidate probability models for UCS and GSI were decided with the requirement that their values (i.e., ${\varvec{x}}$) are always non-negative and real (i.e., ${\varvec{x}}$ ∈ [0, $\infty$)) (Table 3). This is due to non-negative nature of rock properties under consideration. Table 3 shows the estimated AIC_c and probability ${\mathfrak{p}}_{i}$ values for these models using Eqs. (4)–(6). Figure 5 also shows the histogram of data for UCS and GSI along with the candidate models pdfs. For UCS, the candidate probability models have approximately similar AIC_c or probability ${\mathfrak{p}}_{{\varvec{i}}}$ values, except exponential model. Further, the values of ${\Delta }_{{\text{A}}}^{\left( i \right)}$ were estimated to be minimal for these models indicating that any of these models can be considered to fit the data satisfactorily. Similar observations were made for GSI regarding AIC_c, ${\mathfrak{p}}_{{\varvec{i}}}$ and ${\Delta }_{{\text{A}}}^{\left( i \right)}$ values of candidate models, except Rayleigh and exponential models. This reinforces the argument that the identification of a best fit model is impractical from the small sized sample. The models with ${\Delta }_{{\text{A}}}^{\left( i \right)} < 10$ [13] have much higher probabilities to be considered as the best fit model to represent the data satisfactorily. Due to this reason, all the models mentioned above (Table 3) except exponential model for UCS, and Rayleigh and exponential models for GSI were considered as plausible models for further analyses.

Table 3 Candidate probability distribution models and their corresponding AIC_c, AIC_c difference $\Delta_{{\text{A}}}^{\left( i \right)}$ and AIC_c based probability ${\mathfrak{p}}_{i}$ values for the UCS and GSI

Fig. 5

Histogram plot of the original sample along with the candidate probability models for the a GSI and b UCS

Further, an analysis has been performed to emphasize the effect of sample size on the determination of best fit model. For this analysis, ${\mathfrak{p}}_{i}$ values for candidate models were determined for the samples of sizes ($N_{{\text{s}}}$) varying between 22 (size of original data) to 10⁶ for GSI. Samples of different sizes were obtained by generating random realizations from the model having least AIC_c for original dataset (best fit for original data). Best fit model form original data of GSI was found to be inverse Gaussian (Table 2). Figure 6 shows the analysis results. It can be observed that the ${\mathfrak{p}}_{i}$ values for candidate models were of approximately similar magnitudes for small sized samples ($N_{{\text{s}}} \le 300$ approximately). As the sample size increases, lognormal and inverse Gaussian were found to have approximately similar ${\mathfrak{p}}_{i}$ values for $N_{{\text{s}}} \le 8 \times 10^{4}$. This coincidence of ${\mathfrak{p}}_{i}$ values for these distributions up to a large $N_{{\text{s}}}$ value could be due to approximately similar AIC_c values from original sample. As $N_{{\text{s}}}$ increases beyond this, ${\mathfrak{p}}_{i}$ values for inverse Gaussian and lognormal distributions monotonically increased and decreased, respectively. The ${\mathfrak{p}}_{i}$ value for inverse Gaussian distribution became unity for $N_{{\text{s}}} = 10^{6}$. It can be concluded that $N_{{\text{s}}}$ should be significantly higher ($N_{{\text{s}}} \ge 8 \times 10^{4}$ for this case) to assess the best fit model with acceptable certainty and much higher with complete certainty ($N_{{\text{s}}} = 10^{6}$) which is practically impossible.

Fig. 6

Variation of ${\text{AIC}}_{{\text{c}}}$ based probability ${\mathfrak{p}}_{{\text{i}}}$ with the size of data sample of the plausible models for GSI

4.1.5 Step 5: estimation of posterior model parameters

Once the plausible models were known, the posterior model parameters for these models (i.e., $p\left( {{\varvec{\theta}}{|}{\varvec{d}},M} \right)$) were estimated through Bayesian inference utilizing MH-MCMC sampling (Sect. 2.3). The prior distribution was taken as the uniform distribution, i.e., $p\left( {{\varvec{\theta}};M} \right)$ [6, 57, 58]. The bounds of mean and standard deviation (SD) for UCS and GSI were adopted from the literature [5]. Aladejare and Wang [5] summarized the typical ranges of mean and SD of properties for sedimentary rocks based on extensive literature review (~ 135 research articles). Table 4 summarizes the prior values for mean and SD of UCS and GSI. To perform MCMC analysis, the range of model parameters corresponding to each plausible model, i.e., ${\varvec{\theta}}$, were estimated from the bounds of mean and SD using standard relations [7]. Table 5 summarizes the estimated prior range of model parameters. MCMC analysis was then performed by generating a total of 5 × 10⁴ random samples. Initial 5 × 10⁴ samples were discarded by considering them as burn-in samples identified via visual inspection of trace plots. The convergence of simulated chains was assessed through the trace and autocorrelation plots. Trace plots did not show any anomalies and autocorrelation plot showed an exponential decrease between the sample correlation. Further, the acceptance rate of all Markov chains simulated was within 20–40% for each model parameter. Figure 7 shows the typical trace and autocorrelation plots of the Markov chain samples of lognormal distribution parameters for the GSI. It was observed that the simulated Markov chains are stationary for GSI. Similar observations were made for all the plausible models of other properties.

Table 4 Prior information/knowledge for the sedimentary rock properties [5]

Table 5 Range of plausible model parameters to define the uniform prior distribution for the UCS and GSI

Fig. 7

Convergence analysis of the Markov chains a trace plot for parameter 1 ‘a’ b autocorrelation plot for parameter 1 ‘a’ c trace plot for parameter 2 ‘b’ and d autocorrelation plot for parameter 2 ‘b’ of the lognormal probability model for GSI

Figure 8 also shows the joint probability density functions (jpdf) and the marginal pdfs of model parameters for plausible models of GSI quantifying the uncertainties in the parameters. The red points along the jpdf show the parameter values estimated from the original data. It can be concluded that significant uncertainties exist in the model parameters in the presence of limited data and should be considered in the analysis.

Fig. 8

Marginal and joint pdf of the posterior model parameters for the plausible models a Lognormal b Weibull c Gamma d Inverse Gaussian e Nakagami and f Loglogistic of GSI

4.1.6 Step 6: establishment of a MCSs model set

In this step, the MCSs model set of UCS and GSI were constructed based on the ${\mathfrak{p}}_{i}$ values of candidate models. The ${\mathfrak{p}}_{i}$ values were considered as the weighting factor which is the ratio of the number of times a candidate model pdf was generated to the total generated pdfs (M). For this study, a total (M) of 10⁴ models for the UCS and GSI were generated. For example, a value of ${\mathfrak{p}}_{i}$ = 0.172 for a model (for e.g., Rayleigh model for UCS) implies that this model was generated for 1720 (${\mathfrak{p}}_{i} \times M = 0.172 \times 10^{4} = 1720$) times out of 10⁴ models. Associated model parameters for the model were chosen at random from the posterior distribution of model parameters (Fig. 8 for GSI) evaluated in the previous step. Figure 9 shows the results of total generated models (i.e., MCSs model set) of the plausible models for UCS and GSI. These MCSs model sets were used to quantify the uncertainties in the statistics of properties (i.e., mean and SD) and response parameter (probability of failure, P_f) of the slope from small sample size in the next steps.

Fig. 9

MCSs model sets with a total of 10⁴ models established for the a GSI and b UCS for the BMMI approach

4.1.7 Step 7: quantification of statistical uncertainties

Sample statistics, i.e., mean and SD, of the property were estimated for total generated models in the previous step via standard relations between model parameters of pdfs and moments. This results in a total of 10⁴ sample statistics values from which their mean and SD were evaluated. Table 6 and Fig. 10 summarize the analysis results. It can be observed that the means of the sample statistics were coinciding with the sample statistics estimated for the original sample (Table 2). Further, the SDs of the sample statistics indicate the statistical uncertainties in them due to small size of samples.

Table 6 Statistics of the sample statistics for UCS and GSI estimated via different reliability methodologies

Fig. 10

Empirical CDFs of a mean of GSI and b SD of GSI estimated via different reliability methodologies

4.1.8 Step 8: estimation of statistics of response parameter

In this step, a model from the MCSs set constructed in the previous step was selected and traditional reliability analysis was performed resulting the values of P_f corresponding to the model in the MCSs set. This step is repeated for all models sequentially in the MCSs sets ($M = 10^{4}$) resulting into a total of 10⁴ P_f values from which the statistics P_f were estimated. Traditional reliability analysis for the model in set was performed by carrying out MCSs on the PF (prepared in step 2). MCSs was performed by generating 5 × 10⁴ random samples based on the statistics of selected model from the MCSs set of UCS and GSI and the best fit models of $m_{i}$ and $E_{i}$ (Table 2). P_f was considered as the area under the pdf of FOS with value less than 1. Figure 11 and Table 7 show the analysis results including empirical CDFs P_f, respectively. The SD signifies the effect of statistical uncertainties on the P_f due to small size samples. The expected performance level of the slope in accordance with probability descriptions provided by the USACE [55] was mapped in the range of good to unsatisfactory.

Fig. 11

Empirical CDF of the probability of failure P_f (%) for the rock slope via different reliability methodologies

Table 7 Statistics of probability of failure (P_f) for the rock slope estimated via various reliability methodologies

An important point is that the uncertainties in the sample statistics and P_f could be affected by the ${\Delta }_{{\text{A}}}^{\left( i \right)}$ values of plausible models of a property. Data of a property with multiple plausible probability models having very small ${\Delta }_{{\text{A}}}^{\left( i \right)}$ (close to zero) values may have higher effect of model type uncertainty on the sample statistics and P_f. Reason is the significant mixing of plausible models (approximately equal contribution from multiple plausible models) in the established MCSs model set which may eventually lead to higher uncertainties in the sample statistics and P_f.

4.2 Analysis using traditional Bayesian methodology

Initial three steps involved in the traditional Bayesian methodology are same as that of the BMMI methodology. The candidate probability models for UCS and GSI were first chosen similar to BMMI. AIC_c values were estimated for these models [Eq. (4)] corresponding to the original sample. Best fit models for GSI and UCS (with least AIC_c values) were estimated to be inverse Gaussian and loglogistic, respectively (Table 3).

Posterior model parameters of the best fit models for the UCS and GSI were estimated through Bayesian inference utilizing MH-MCMC sampling by generating 5 × 10⁴ random samples. The major difference, compared to the BMMI, is that the analysis was performed only for best fit models instead of all plausible models. Analysis details are similar as explained in BMMI (step 5). Figure 8d shows the jpdf and marginal pdfs of inverse Gaussian model parameters (best fit for GSI) estimated from the MH-MCMC sampling quantifying the uncertainties associated with them. Further, the MCSs model sets having $M = 10^{4}$ models based on the best fit models were constructed for the UCS and GSI. The major difference is that all models in the MCSs set were corresponding to best fit models instead of the mixing of plausible models. Figure 12 shows the constructed MCSs model sets corresponding to best fit models for UCS and GSI.

Fig. 12

MCSs model sets with a total of 10⁴ models established for the a GSI and b UCS for the traditional Bayesian reliability methodology

Statistical uncertainties in the UCS and GSI were quantified by estimating the sample statistical parameters corresponding to each model in the MCSs set via standard relations between model parameters of pdfs and moments. Table 6 and Fig. 10 provide the results obtained from the traditional Bayesian approach. It can be observed that the means of the sample statistics were coinciding with sample statistics estimated from the original sample (Table 2). Statistical uncertainties due to the small size of sample is indicated by the SDs of sample statistics. Finally, the traditional reliability analysis was performed corresponding to each model ($M = 10^{4}$) in the MCSs model sets for UCS and GSI constructed in the previous step. Analysis details are similar as explained for the BMMI (step 8). Figure 11 and Table 7 show the analysis results including empirical CDF of P_f. The effect of statistical uncertainties due to small size samples is indicated by the SD of P_f. From this approach, the expected performance level of the slope was mapped in the range of good to poor.

4.3 Analysis using bootstrap re-sampling reliability methodology

Initial procedures in the bootstrap reliability methodology are same to that of BMMI methodology. In this step, a total of $N_{{\text{B}}} = 10^{4}$ number of bootstrap re-constituted samples were generated for sensitive properties (i.e., UCS and GSI). Re-constituted samples were generated from their original samples as explained in Sect. 2.4.

Quantification of statistical uncertainties in the statistics of sensitive properties was done by estimating their bootstrap statistics. Sample statistics were estimated for individual re-constituted sample of GSI and UCS. From these values, the bootstrap statistics (mean and SD) of the sample statistics were evaluated using Eq. (9). Table 6 and Fig. 10 summarize the results. It was observed that bootstrap means of the sample statistics were coinciding with the ones estimated for the original sample (Table 2). Further, significant bootstrap SDs were observed for sample statistics of both properties signifying the statistical uncertainties in sensitive properties invoked by the small size of samples. Finally, the traditional reliability analysis was performed for each re-constituted sample of the UCS and GSI generated resulting in a value of P_f corresponding to individual re-constituted sample. Firstly, the best fit model with least AIC_c value was selected. Then, the traditional reliability analysis was performed ($N_{{\text{B}}} = 10^{4}$ times) via MCSs on the PF by generating 5 × 10⁴ random samples. Random samples were generated based on the statistics of re-constituted samples of UCS and GSI and the best fit models of $m_{i}$ and $E_{i}$. Figure 11 and Table 7 show the analysis results. The SD signifies the effect of statistical uncertainties on P_f due to small size samples. From this approach the expected performance level of the slope was mapped in the range of good to unsatisfactory.

5 Discussions

It is well-known that the rock projects often suffer with the availability of insufficient data of rock properties. Limited data restricts the capability of rock designers to accurately perform the probabilistic characterization of input properties. It is very difficult to state a precise threshold number of data points to classify the terminology “minimum number” precisely. Ruffolo and Shakoor [47] observed that for a 95% confidence interval and a maximum of 20% acceptable strength deviation from the mean of UCS of rocks, 10 UCS samples are needed to be tested. Some studies state this threshold number to be 30 [38, 61]. These guidelines are very crude as they lack statistical proof and are based on limited data. Tang et al. [51], based on their detailed statistical study, concluded that this “minimum number” could be 54–458 for COV ranging from 0.3 to 0.1 for the marginals and 25–2577 for correlation coefficient varying from − 0.9 to − 0.1 for the copula of geotechnical properties, respectively.

An analysis was performed for the present case study to determine the quantity of data required to obtain the best fit model and convergence of model parameters for input properties precisely. Figures 6 and 13 show the analysis results. The observable differences between AIC values of candidate models could initially be observed for a sample size of ~ 500 and the clear identification of the best-fit model could be made for ~ 100,000 samples. Amount of data required to obtain the convergence for model parameters was significantly lower (~ 10³) than that to determine the best fit model accurately (10⁶). Overall, it is highly impractical to perform this quantity of lab/in situ tests to obtain the precise statistics of geotechnical properties invoking statistical uncertainties which are required to be considered in the analysis as suggested in the proposed methodology which could be used for very limited data of inputs. However, it is still practically impossible to perform this amount of lab and in situ testing required to determine even the parameters of the model (~ 10³) accurately. This is due to practical difficulties (such as sample collection, sample disturbance, site preparation and data interpretation), high costs, time consumption, etc., involved in the rock testing. Hence, it is inaccurate to assume that the best fit model and its parameters estimated from the limited site-specific test data are “true estimates” of the statistics of rock mass properties under consideration. This is even true for the high budget rock projects where the quantity of in situ and laboratory testing is often limited. For example, the number of in situ plate load tests conducted for Chenab Bridge in India and Kazunogawa hydro power cavern in Japan to determine the rock mass deformability were approximately 20–30 [14, 53]. Condition is worser for small budget rock projects, where a very limited amount is spent on rock investigation. Under these conditions, analysis performed by the traditional reliability methods are highly inaccurate which assumes that the best fit model and its parameters estimated from the limited test data are “true estimates” of the population parameters. Previous section demonstrated the proposed BMMI methodology for the reliability analysis of a rock slope with limited data of input properties.

Fig. 13

Variation of the a mean of GSI and b SD of GSI with the size of data sample

5.1 Comparative analyses

BMMI methodology differs from the traditional Bayesian approach as it can consider the uncertainties in both model type and associated parameters. It was observed that the uncertainty associated with model type has significant effect on the total uncertainty of input properties along with that of response parameter (i.e., P_f) for the rock slope. While the mean values of sample statistics were matching well with each other (0.21–16.42% difference) for the case study, the major difference was observed in the SDs of the statistics of properties (2.88–51.61% difference) as shown in Table 6. SD was significantly lower for the traditional Bayesian approach compared to BMMI signifying the underestimation of uncertainties in the statistics of properties majorly due to ignorance of model type uncertainty in traditional Bayesian approach. These underestimated uncertainties propagated during the estimation of statistics of P_f also. Statistics of P_f were estimated to be approximately 50% lower (Table 7) for traditional Bayesian as compared to BMMI methodology emphasizing the importance of considering the uncertainty in model type along with uncertainties of model parameters.

In contrast, bootstrap-based methodology can consider the uncertainties in both model types and parameters like BMMI methodology. For this criterion (considering uncertainties in both model and parameters), both bootstrap-based method and BMMI are superior to traditional Bayesian method. While the mean values of sample statistics were matching with each other (0.05–3.02% difference) for the case study, the major difference was observed in the SDs of the statistics of properties (9.87–47.05% difference) as shown in Table 6. SDs were significantly lower for the bootstrap-based methodology as compared to BMMI. The reason could be the difference in the analysis procedure adopted in these methodologies. Bootstrap method estimates the sampling distributions of properties by resampling (with replacement) from the original sample (data at hand) and creating many bootstrap samples [49]. There is no provision of inclusion of prior information in this method and standard deviation may only fluctuate in a range defined by the data of original sample only. In contrast to this, BMMI includes the prior information in the estimation of statistics of input properties. This prior information is usually collected from literature. Prior information can have wide range (hence significant SD) in it since data are collected from the wide variety of sites around the world as observed for this case study. This may contribute to the higher SD in the estimated statistics of input properties. These uncertainties propagated during the estimation of statistics of P_f also. Statistics of P_f were underestimated by 6.35–17.68% by bootstrap reliability methodology as compared to the BMMI (Table 7) for the considered case study. Effect of prior knowledge on the statistics of input properties and P_f are discussed in next section in detail.

A comparison was also made with the recently proposed Bayesian Model Averaging (BMA) methodology. Details of the methodology can be seen in the literature [35, 64]. The BMA starts from identifying the plausible probability models for all the inputs. Then, a set of models comprising all possible combinations from plausible probability model are constructed and their corresponding fitting probabilities are estimated. Then, for each combination the Bayesian inference is performed and samples from the posterior distribution of model parameters are generated via MCMC sampling. Next, corresponding to each of these samples, the probability of failure (P_f) is estimated using MCSs by generating random realizations of inputs. Thus, for each combination in the set a probability distribution function (PDF) of P_f is estimated, which are then averaged as per their fitting probabilities. The averaged PDF of P_f considered to have the impact of both the model selection and model parameters uncertainties. An analysis was also performed using the BMA and its results were compared with those from the proposed methodology. While the mean and SD of P_f from both approaches matched well (~ 5%), the BMMI required 99.52% less computational efforts as compared to the BMA.

It could be observed that the proposed methodology is relatively complex and mathematical compared to the traditional deterministic and reliability methods. Further, the final decision-making in the proposed methodology is more difficult as the outputs are the intervals of the probability of failure (i.e., P_f) in the proposed methodology as compared to the precise values of performance functions (deterministic) and P_f (traditional reliability method). However, the traditional methods often include the originally unavailable information in the analysis, like assigning a precise value to the inputs (generally mean), neglecting all other data (in deterministic analysis) and/or assigning a precise PDF using limited data (in traditional reliability). In contrast, the proposed methodology accepts and considers (with no subjective judgements) the lack of available input data and propagates this imprecision to the outputs by estimating the intervals of P_f. As per Dubois [10], “It is better for engineers to know that you do not know than make a wrong decision because you delusively think you know. It allows one to postpone such a wrong decision in order to start a new measurement campaign, for instance.”

5.2 Impact of prior knowledge on the statistics of properties and response parameter

Informativeness and confidence of prior knowledge is regarded as a key factor in the uncertainty characterization via Bayesian approach [15, 56]. To assess the importance of prior information in BMMI methodology, an analysis was performed to evaluate the effect of prior information on the statistics of response parameter. Effect of prior information was estimated for (1) range of statistics, and (2) prior-distribution of properties. To evaluate the effect of prior range of statistics of properties, ranges were narrowed down by approximately 60%, 90% and 95%, respectively, for prior knowledge II (PK-II), prior knowledge III (PK-III) and prior knowledge IV (PK-IV) cases as compared to original ranges represented by prior knowledge I case (PK-I). Reducing range implies the higher (or more accurate) information. Based on the information levels, these cases could be arranged as: PK-IV > PK-III > PK-II > PK-I. Prior distributions of statistics of properties were assumed to be same (i.e., uniform) for all the cases. Figure 14a shows the corresponding prior distribution for the mean of GSI. Results are summarized in Tables 8 and 9; and Fig. 14b. With the increasing level of information, the uncertainty in the sample statistical parameters was continuously reducing as indicated by decrease in SDs of sample statistical parameters (0.51–53.25%). The uncertainty in P_f was also continuously reducing as indicated by the reducing length of confidence intervals. Minor change was observed in the confidence interval length for PK-II case (0.46%), however, significant changes were observed for PK-III and PK-IV cases (11.02–17.24%) as compared to PK-I case. In the case of rock mechanics, the level of prior information could be higher for a site if the data are available from the nearby sites. In this scenario, the uncertainty in the estimated P_f would be lower as compared to the case, where the statistics of properties are directly adapted from the literature which is based on the world-wide collected data. Hence, it would be better if the prior information could be collected from the nearby sites to reduce the uncertainties in the prior information and hence, the resulting uncertainties in the response estimates for rock structures.

Fig. 14

a Prior knowledge–I (PK–I), PK–II, PK–III and PK–IV with uniform distribution for Mean of GSI b probability of failure P_f (%) corresponding to PK–I, PK–II, PK–III and PK–IV with uniform distribution from BMMI c PK–III with three prior distribution, Uniform (U), Normal (N) and Weibull (W) [i.e., PK–III(U), PK–III(N) and PK–III(W)] for Mean of GSI and d Probability of failure P_f (%) corresponding to PK–III(U), PK–III(N) and PK–III(W) from BMMI

Table 8 Statistics of the sample statistics of UCS and GSI for four different prior knowledge ranges estimated through BMMI

Table 9 Statistics of probability of failure (P_f) for four different prior knowledge ranges estimated through BMMI

It should be noticed in the previous sections that the analysis was performed by considering the prior distribution of properties to be uniform. To assess the effect of prior distribution, an analysis was performed by changing the prior distributions of statistics of properties with constant ranges. PK-III case explained in the previous section was considered for the analysis with three types of distributions [i.e., Uniform (U), Normal (N) and Weibull (W)]. In other words, the analysis was considered for three different prior cases, i.e., PK-III (U), PK-III (N) and PK-III (W). Figure 14c shows the distributions for mean of GSI. Tables 10 and 11; and Fig. 14d summaries the analysis results. It was observed that the uncertainty in the sample statistical parameters was lower for Weibull and normal distributions compared to uniform distribution as indicated by decrease in SDs of sample statistical parameters (9.39–39.05%). Similar trend was also observed for the uncertainty in the P_f indicated by the reduced length of confidence interval of P_f for Weibull and normal distributions (7.28–8.75%) as compared to uniform distribution. This could be due to less informative nature of uniform distribution (also known as non-informative prior) as compared to the normal and Weibull distributions [36]. In other words, more confidence is shown by the normal and Weibull distributions to central values as compared to the uniform distribution.

Table 10 Statistics of the sample statistics of UCS and GSI for three types of prior distributions estimated through BMMI

Table 11 Statistics of probability of failure (P_f), for three types of prior distributions estimated through BMMI

6 Conclusion

This study presented a novel Bayesian multi-model inference (BMMI) approach to characterize the uncertainties associated with both the probability model type and parameters arising due to limited data of properties and to assess their effect on the reliability estimates of rock structures. For this methodology, model type uncertainty was first quantified by employing the multi-model inference approach and then the uncertainties in the model parameters were estimated via traditional Bayesian framework. The proposed framework uses the MCMC method with the MH algorithm to simulate the posterior distributions of model parameters. Response surface methodology and global sensitivity analysis were coupled with this methodology to enhance its robustness and to reduce computational efforts. The proposed methodology was demonstrated for a Himalayan rock slope prone to stress-controlled failure in detail. Further, analyses were also performed using methods, i.e., traditional Bayesian and bootstrap reliability, frequently employed to perform reliability analysis with limited data. The proposed methodology was found to be superior to other methods as it can consider the uncertainties in both model types and parameters and can include the prior information in the analysis. Traditional Bayesian and bootstrap methods underestimated the uncertainties in the statistics of input properties (0.21–51.61% and 0.05–47.05%, respectively) as compared to BMMI due to their inherent issue of neglecting uncertainties in model type and prior information in the analysis respectively. This leads to the underestimation of uncertainty in P_f (49.42–53.06% and 6.35–17.68%, respectively) by these methods as compared to BMMI. Overall, this method overcomes the limitations of traditional methods and can be used for a wide variety of problems with explicit/implicit and single/multiple PFs.