Global synchronization of memristive hybrid neural networks via nonlinear coupling

Abstract

This paper probes into the synchronization for memristor-based hybrid neural networks via nonlinear coupling. At first, a new condition is established to judge whether quadratic functions are negative or not on a closed interval regardless of their concavity or convexity. Then, by utilizing Legendre orthogonal polynomials, a recent extended integral inequality with free matrices is popularized to get tighter lower bound of some integral terms. Next, based on a novel Lyapunov functional, by applying our new integral inequality with free matrices, linear convex combination method and the new criterion, a new delay-dependent condition is gained to reach the global synchronization for the considered neural networks. At last, an example is presented to account for the validity of our results.

1 Introduction

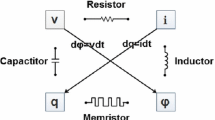
For the sake of retaining symmetry with capacitor, resistor, and inductor in logicality, Chua [5] conceived there must exist a fourth elementary circuit component that connects flux and charge with a curvilinear relation. Chua entitled it memristor, as a condensation of memory and resistor (cf Fig. 1). In 2008, Chua’s conjecture was corroborated by the Hewlett–Packard Labs [34]. This scientific research team produced the model of memristor. Since the memristor’s resistance relies on the charge that had previously passed through the device, the memristor is thought as a auspicious successor to simulate biological synapses in circuit implementation of neural networks. Replacing resistors with memristors as the connection weights of neural networks in the circuit realization, it will produce neural networks called as MNNs. MNNs have a lot of applications in image processing, brain emulation, and pattern recognition, therefore get widespread attention from scientific researchers (see [1, 3, 7, 16, 28, 38, 40, 43, 44, 51]).

Fig. 1

Relationship between the four fundamental circuit components [8]

As we know, since the potential paper [27] was revealed to the world, many researchers have strenuously committed to exploring various synchronization issues of chaos. So far, a great variety of synchronization results have been presented due to their potential applications in cryptography, biological system, secure communication, information processing, chemical reactions [15, 19, 39, 49, 50]. By introducing linear diffusive term and sign function term, Guo et al. [7] derived several global exponential synchronization criteria for coupled MNNs (CMNNs) which are based on some suitable Lyapunov–Krasovskii functionals (LKFs). By the Lyapunov stability theory, Yang et al. [43] proposed a set of global robust synchronization conditions and a pinning adaptive coupling issue for a class of CMNNs with nonidentical uncertain parameters a discontinuous diffusive term. By using Halanay inequality and the matrix measure method, Rakkiyappan et al. [28] established a sufficient condition that ensures the exponential synchronism of coupled inertial MNNs based on a state feedback controller. Based on Lyapunov functional and matrix inequality method, Zhang et al. [51] designed periodically intermittent controller to ensure exponential synchronism of CMNNs with time-varying delays. By means of simple feedback controllers and adaptive feedback controllers, the authors [3, 44] put forward sufficient conditions to assure exponential synchronism of CMNNs with impulsive and stochastic turbulence. Based on Lyapunov functions, matrix inequalities, and Halanay inequality, Bao et al. [1] obtained sufficient conditions of exponential synchronism of stochastic CMNNs with probabilistic delay coupling and impulsive delay. By utilizing differential inclusion and Halanay inequality, Li et al. [16] proposed some new sufficient conditions to achieve synchronization of inertial CMNNs with linear coupling. In order to provide deep applications, it is important to investigate synchronization problem of MNNs with less conservativeness.

Over the past years, Jensen integral inequality [6] has been extensively utilized in time-delay systems because of its high efficiency in acquiring easy-to-verify stability criteria expressed as linear matrix inequality. To get less conservative result, the authors [13, 22, 30] presented Wirtinger-based integral inequalities of single, double and multiple integral forms which include the Jensen ones and obtain greater lower bounds of integral term; by means of auxiliary functions, Park et al. [26] presented some integral ones which include those in [6, 13, 22, 30]. To further abate conservativeness, Chen et al. [4] established two general integral inequalities which include those [6, 13, 22, 26, 30] and are greater than all existing ones. In fact, there still exists some space to advance with respect to integral inequality.

Stimulated by mentioned before, in this paper we discuss the global synchronization of a class of CMNNs with linear diffusive and discontinuous sign terms. The main devotion of this paper can be epitomized as follows:

• (1) A new condition (see Lemma 5) is established to ascertain whether quadratic functions are negative or not on a general closed interval regardless of their concavity or convexity, which includes Lemma 2 [12] and Lemma 4 [45] as its special cases and raises another different confirming criterion with (i), (ii), (iii)$'$.

• (2) On the basis of Lemma 2 [24], a further developed integral inequality with free matrices is established in Lemma 4 by utilizing Legendre polynomials, which encompasses Lemma 2 [24] and Lemma 5 [4] as its special cases. In fact, Lemma 5 [4] can be acquired by fixing some slack matrices of Lemma 4.

• (3) Enlightened by [31] and [14], a new Lyapunov functional is constructed based on the sector condition of the activation function. Due to this new functional, less conservative delay-dependent synchronism criteria can be obtained from linear matrix inequality technology.

• (4) Proper integration of Chen et al.’s integral inequality (cf Lemma 3) with Lemmas 4, 5 can result in less conservative synchronization conditions than existing ones. It is proved [4] that Lemma 3 includes the Jensen inequality, Wirtinger-based one and auxiliary function-based ones as its peculiar cases, and is greater than all existing ones.

The developed results thus provide insight into hybrid neural networks via nonlinear coupling with memristors, which may help appreciate biological evolution and neural learning.

Notation Throughout this paper, solution of a system is in Filippov’s sense. $Q^{-1},Q^T$ mean the inverse and the transpose of a matrix separately. $Q<0(>0)$ means a definite negative (positive) symmetric matrix, $0_{n},\ I_{n}$ mean the zero matrix and the identity matrix of $n-$dimension separately, $0_{m\times n}$ means an $m\times n$ zero matrix, symbols $\alpha Q(*)^T,$ $\alpha ^T Q(*)$ mean $\alpha Q\alpha ^T$ and $\alpha ^T Q\alpha$, respectively. The expression ${\mathrm{col}}\{Q_1,Q_2,\ldots ,Q_k\}$ means a column matrix with the matrices $Q_1,Q_2,\ldots ,Q_k.$ sym(Z) means $Z+Z^T,$ ${\mathrm{diag}}\{\cdot \}$ means a diagonal or block-diagonal matrix. For $\chi >0, {\mathcal {C}}\big ([-\chi ,0];{\mathbb {R}}^n\big )$ means the set of all continuous functions $\phi$ from $[-\chi ,0]$ to ${\mathbb {R}}^n$ with norm $||\phi ||=\sup _{-\chi \le s\le 0}|\phi (s)|.$ If not declared in advance, matrices are required to have proper dimensions. $\bigg [\begin{array}{cc} A&{} B\\ *&{}C\end{array}\bigg ]$ means $\bigg [\begin{array}{cc} A&{} B\\ B^T &{}C\end{array}\bigg ].$

2 Problem description

As shown in [39], a single memristor-based recurrent network can be expressed as the following simple form:

$$\begin{aligned} \dot{y}(t)&=-Ay(t)+B(y)k(y(t))\nonumber \\&\quad +\, C(y)k(y(t-\omega (t)))+v(t), \end{aligned}$$

(1)

where $y(t)=(y_{1}(t),y_{2}(t),\ldots ,y_{n}(t))^T\in {\mathbb {R}}^n$ denotes the state vector of the networks at time $t,\ n$ indicates the number of neurons, A is a diagonal positive matrix indicating neuron self-inhibitions, $B(y)=(b_{jq}(y(t)))_{n\times n},C(y)=(c_{jq}(y(t)))_{n\times n}$ are the feedback connection matrix and the delayed feedback connection matrix, respectively. $k(y(\cdot ))=\big (k_1(y_{1}(\cdot )),k_2(y_{2}(\cdot )),\ldots ,k_n(y_{n}(\cdot ))\big )^T\in {\mathbb {R}}^n$ is the neural activation function. The bounded function $\omega (t)$ is unknown time-varying delay with $0\le \omega (t)\le {\bar{\omega }}, \omega _1\le \dot{\omega }(t)\le \omega _2,$ where ${\bar{\omega }}>0,\omega _1$ and $\omega _2$ are scalars. v(t) is an external input vector. On the basis of the feature of memristor and the current-voltage characteristics, we define

$$\begin{aligned} b_{jq}(y(t))&=\left\{ \begin{array}{ll} b'_{jq},&{} {\mathrm{sign}}\frac{\mathrm{d}}{\mathrm{d}t}[k_q(y_q(t))-y_j(t)]\le 0,\\ b''_{jq},&{} {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}[k_q(y_q(t))-y_j(t)]>0,\end{array}\right. \end{aligned}$$

and

$$\begin{aligned} c_{jq}(y(t))=&\left\{ \begin{array}{ll} c'_{jq},&{} {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}[k_q(y_q(t-\omega (t)))-y_j(t)]\\ &{}\le 0,\\ c''_{jq},&{} {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}[k_q(y_q(t-\omega (t)))-y_j(t)]\\ &{}>0,\end{array}\right. \end{aligned}$$

for $j,q\in {\mathcal {N}}=\{1,2,\ldots ,n\},$ where $b'_{jq},b''_{jq},c'_{jq},c''_{jq}$ being known constants. Throughout this paper, we denote ${\bar{B}}=({\bar{b}}_{jq})_{n\times n},{\bar{C}}=({\bar{c}}_{jq})_{n\times n}$ with ${\bar{b}}_{jq}=\max \{b'_{jq},b''_{jq}\},{\bar{c}}_{jq}=\max \{c'_{jq},c''_{jq}\},$ and ${\hat{b}}_{jq}=|b'_{jq}-b''_{jq}|,{\hat{c}}_{jq}=|c'_{jq}-c''_{jq}|.$

As well known, because of disturbances from environment noises or modeling errors, the network parameters often embody uncertainties. Therefore, (1) can be revised as a more practical one

$$\begin{aligned} \dot{y}(t)&=-Ay(t)+[B(y)+\varDelta B(t)]k(y(t))\nonumber \\&\quad +\, [C(y)+\varDelta C(t)]k(y(t-\omega (t)))\nonumber \\&\quad +\, v(t), \end{aligned}$$

(2)

where matrices $\varDelta B(t)$ and $\varDelta C(t)$ indicate the parameter uncertainties.

Now, we discuss a system containing m identical MNNs with nonlinear coupling

$$\begin{aligned} \dot{y}_p(t)&=-Ay_p(t)+[B(y_p)+\varDelta B_p(t)]k(y_p(t))\nonumber \\&\quad +\,[C(y_p)+\varDelta C_p(t)]k(y_p(t-\omega (t)))\nonumber \\&\quad +\, \sum _{\jmath =1}^{m}d^1_{p\jmath }\varLambda _1y_\jmath (t)+\sum _{\jmath =1}^{m}d^2_{p\jmath }\varLambda _2y_\jmath (t-\omega (t))\nonumber \\&\quad +\, \sum _{\jmath =1}^{m}\varsigma _{p\jmath }\varTheta \mathrm{sgn}(\dot{y}_\jmath (t)-\dot{y}_p(t))\nonumber \\&\quad +\, v(t),\ \ p\in {\mathcal {M}}=\{1,2,\ldots ,m\}, \end{aligned}$$

(3)

where $y_p(t)=(y_{p1}(t),y_{p2}(t),\ldots ,y_{pn}(t))^T\in {\mathbb {R}}^n$ denotes the state vector of the pth MNN. $D_\imath =(d^\imath _{p\jmath })_{m\times m},\imath =1,2$ and $\varXi =(\varsigma _{p\jmath })_{m\times m}$ indicate outer coupling matrices satisfying conditions: $d^\imath _{p\jmath }\ge 0,\varsigma _{p\jmath }>0(p\ne \jmath ),\ d^\imath _{pp}=-\sum ^m_{\jmath =1,\jmath \ne p}d^\imath _{p\jmath },\varsigma _{pp}=0,\ p,\jmath \in {\mathcal {M}}.$ Matrices $\varLambda _1,\varLambda _2$ and $\varTheta ={\mathrm{diag}}\{\theta _1,\theta _2,\ldots ,$ $\theta _n\}>0$ indicate inner coupling interests between two states. $\mathrm{sgn}(x)=({\mathrm{sign}}(x_1),{\mathrm{sign}}(x_2),\ldots ,{\mathrm{sign}}(x_n))^T$ for $x=(x_1,x_2,\ldots ,x_n)^T\in {\mathbb {R}}^n$ with

$$\begin{aligned}&{\mathrm{sign}}(z)=\left\{ \begin{array}{ll} 1,&{}\quad z>0,\\ 0,&{}\quad z=0,\\ -1,&{}\quad z<0.\end{array}\right. \end{aligned}$$

Remark 1

Many existing results suppose the coupling matrices being symmetric, see for instance [17, 20, 21, 32, 36, 39, 48]. In this paper, this requirement is deleted. Thus our conditions are more efficacious than those results.

Similar to [43], the uncertain matrices $\varDelta B_p(t)$ and $\varDelta C_p(t)$ are supposed as follows:

$$\begin{aligned}&\varDelta B_p(t)=EN_{1p}(t)L_1,\nonumber \\&\varDelta C_p(t)=EN_{2p}(t)L_2,\ p\in {\mathcal {M}} \end{aligned}$$

(4)

where E and $L_1,L_2$ are known real matrices, and $N_{ip}(t)$ is unknown matrix with

$$\begin{aligned} ||N_{\imath p}(t)||_1\le 1,\ \imath =1,2;p\in {\mathcal {M}} \end{aligned}$$

(5)

and $||\cdot ||_1$ is the 1-norm of a matrix.

The initial conditions of (3) are $y_p(s)=\varphi _p(s)\in {\mathcal {C}}\big ([-{\bar{\omega }},0];{\mathbb {R}}\big ),p\in {\mathcal {M}}.$

With different initial conditions, MNN (1) or (2) will have different dynamical trajectories in general. But in the coupled system (3), all MNNs’ states may be synchronized finally although with different initial conditions.

The following suppositions are needed for our result.

Assumption 1

The activation functions are bounded, i.e., there is constant ${\bar{k}}_j>0$ such that $\big |{k}_j(\cdot )\big |\le {\bar{k}}_j,\ j\in {\mathcal {N}}$. Furthermore, there exist real constants $k_j^-,k_j^+$ such that

$$\begin{aligned} k_j^-\le&\frac{k_j(u)-k_j(v)}{u-v}\le k_j^+,\nonumber \\&\forall \ u,v\in {\mathbb {R}},\ u\ne v. \end{aligned}$$

(6)

Denote ${K _1} = {\mathrm{diag}}\left\{ {k_1^-k_1^+, k_2^-k_2^+, \cdots ,k_n^-k_n^+} \right\} ,$ ${K _2} =\frac{1}{2} {\mathrm{diag}}\left\{ k_1^-+k_1^ + , k_2^-\right.$ $\left. +k_2^ + , \cdots ,k_n^-+k_n^ + \right\} ,$ ${K} = {\mathrm{diag}}\left\{ {k_1^2,\ k_2^2,\ \cdots ,k_n^2} \right\}$ with $k_j=\max \{|k_j^-|,$ $|k_j^+|\},\ j\in {\mathcal {N}}$ and ${\bar{k}}=\sum _{j=1}^{n}{\bar{k}}_j.$

Remark 2

In Assumption 1, $k_j^-,k_j^+(j\in {\mathcal {N}})$ can be negative, zero or positive. Such a description was raised in [18] at first, which includes monotonic nondecreasing or the Lipschitz condition as particular cases. Thus, the activation functions satisfying Assumption 1 can be more common than the usual sigmoid functions. Further, when utilizing the Lyapunov theory to discuss the stability, this assumption is particularly appropriate since it quantifies the activation functions that supply the feasibility of reducing the conservativeness.

The following definition and lemmas are required.

Definition 1

The coupled networks (4) are said to be globally robustly synchronized if $\lim _{ t\rightarrow \infty }$ $\{||y_p(t)-y_l(t)||_1\} = 0, \ \forall p, l\in {\mathcal {M}}$ holds for any initial values and any parameter uncertainties $\varDelta B_p(t)$ and $\varDelta C_p(t)$ with (4) and (5).

Definition 2

(Wu et al [42]). Given a ring ${\hat{R}},$ denote ${\mathcal {T}}({\hat{R}},\epsilon )$ the set of matrices with entries in ${\hat{R}}$ satisfying that the sum of the entries in each row equals $\epsilon$ for some $\epsilon \in {\hat{R}}.$

Lemma 1

(Horn et al [9]). Let $\otimes$ indicate the Kronecker product, X, Y, Z and W are matrices with proper dimensions. The following properties hold:

• (1) $(cX)\otimes Y = X\otimes (cY),$ where c is a constant;

• (2) $(X+Y)\otimes Z = X\otimes Z+Y\otimes Z;$

• (3) $(X\otimes Y)(Z\otimes W) = (XZ)\otimes (YW).$

Lemma 2

(Wu et al [42]). Let G be an $m\times m$ matrix in the set ${\mathcal {T}}({\hat{R}},\epsilon )$. Then the $(m-1)\times (m-1)$matrix Q defined by $Q= JGP$ satisfies $JG=QJ$, where

$$\begin{aligned}&J=\left[ \begin{array}{cccccc} {\mathbf {1}}&{}-{\mathbf {1}}&{}0&{}0&{}\ldots &{}0\\ 0&{}{\mathbf {1}}&{}-{\mathbf {1}}&{}0&{}\ldots &{}0\\ 0&{}0&{}{\mathbf {1}}&{}-{\mathbf {1}}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}\ldots &{}{\mathbf {1}}&{}-{\mathbf {1}}\end{array}\right] _{(m-1)\times m},\\&P=\left[ \begin{array}{ccccc} {\mathbf {1}}&{}{\mathbf {1}}&{}{\mathbf {1}}&{}\ldots &{}{\mathbf {1}}\\ 0&{}{\mathbf {1}}&{}{\mathbf {1}}&{}\ldots &{}{\mathbf {1}}\\ 0&{}0&{}{\mathbf {1}}&{}\ldots &{}{\mathbf {1}}\\ \vdots &{}\vdots &{}\ddots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}0&{}{\mathbf {1}}\\ 0&{}0&{}\ldots &{}0&{}0 \end{array}\right] _{m\times (m-1)}, \end{aligned}$$

where ${\mathbf {1}}$ is the multiplicative identity of ${\hat{R}}$.

Lemma 3

(Chen et al [4]). Assume that matrix $Q>0$ and function $\mu :[\alpha ,\beta ]\rightarrow {\mathbb {R}}$ $^n$ is continuous, the following inequalities are correct:

• (i)
  $$\begin{aligned}&(\beta -\alpha )\int ^\beta _\alpha \mu (\upsilon )^TQ\mu (\upsilon ){\mathrm{d}}\upsilon \ge \\&\quad \pi _1^TQ\pi _1+3(*)^TQ(\pi _1-\pi _2)+5{\bar{\pi }}_1^TQ{\bar{\pi }}_1+7{\bar{\pi }}_2^TQ{\bar{\pi }}_2,\\ \end{aligned}$$
• (ii)
  $$\begin{aligned}&2\int ^{\beta }_{\alpha }(\upsilon -\alpha )\mu (\upsilon )^TQ\mu (\upsilon ){\mathrm{d}}\upsilon \ge \\&\quad \pi _2^TQ\pi _2+8(*)^TQ(\pi _2-\pi _3) +3{\bar{\pi }}_3^TQ{\bar{\pi }}_3,\\ \end{aligned}$$
• (iii)
  $$\begin{aligned}&\frac{1}{\beta -\alpha }\int ^{\beta }_{\alpha }(\upsilon -\alpha )^2\mu (\upsilon )^TQ\mu (\upsilon ){\mathrm{d}}\upsilon \\&\quad \ge \frac{1}{3}\pi _3^TQ\pi _3+5(*)^TQ(\pi _3-\pi _4), \end{aligned}$$

where $\pi _1=\int ^\beta _\alpha {\mu }(\upsilon ){\mathrm{d}}\upsilon ,\ \pi _2=\frac{2}{\beta -\alpha }\int _\alpha ^\beta (\upsilon -\alpha ){\mu }(\upsilon ){\mathrm{d}}\upsilon ,$ ${\bar{\pi }}_1=\pi _1-3\pi _2+2\pi _3,\ {\bar{\pi }}_2=\pi _1-6\pi _2+10\pi _3-5\pi _4,\ {\bar{\pi }}_3=3\pi _2-8\pi _3+5\pi _4$ with $\pi _3=\frac{3}{(\beta -\alpha )^2}\int ^\beta _\alpha (\upsilon -\alpha )^2{\mu }(\upsilon ){\mathrm{d}}\upsilon ,\ \pi _4=\frac{4}{(\beta -\alpha )^3}\int ^\beta _\alpha (\upsilon -\alpha )^3{\mu }(\upsilon ){\mathrm{d}}\upsilon .$

Inspired by [24], we establish the following lemma.

Lemma 4

(The proof is put in "Appendix 1"). Assume that matrix $U>0$ and function $\mu :[\alpha ,\beta ]\rightarrow {\mathbb {R}}$ $^n$ is continuous, vector $\chi$ and matrices $T_\zeta (\zeta =1,2,3,4)$ are with proper dimensions, the following inequality is correct:

$$\begin{aligned}&-\int ^\beta _\alpha \mu (\upsilon )^TU\mu (\upsilon ){\mathrm{d}}\upsilon \\&\quad \le (\beta -\alpha )\sum _{\zeta =1}^{4}\frac{1}{2\zeta -1}\chi ^T\left( T_\zeta U^{-1}T_\zeta ^T\right) \chi \\&\quad \quad +\, {\mathrm{sym}}\left\{ \chi ^T\left[ T_1\pi _1+T_2(\pi _2-\pi _1)+T_3{\bar{\pi }}_1-T_4{\bar{\pi }}_2 \right] \right\} , \end{aligned}$$

where $\pi _1,\pi _2,{\bar{\pi }}_1,{\bar{\pi }}_2$ are defined in Lemma 3.

Remark 3

Letting $\chi ^TT_1=-\frac{1}{\beta -\alpha }\pi _1^TU,\chi ^TT_2=-\frac{3}{\beta -\alpha }(\pi _2-\pi _1)^TU,\chi ^TT_3=-\frac{5}{\beta -\alpha }{\bar{\pi }}_1^TU$ and $\chi ^TT_4=\frac{7}{\beta -\alpha }{\bar{\pi }}_2^TU$ yields

$$\begin{aligned}&-(\beta -\alpha )\bigg [(\beta -\alpha )\sum _{\jmath =1}^{4}\frac{1}{2\jmath -1}\chi ^T\left( T_\jmath U^{-1}T_\jmath ^T\right) \chi \\&\qquad +\, {\mathrm{sym}}\left\{ \chi ^T\left[ T_1\pi _1+T_2(\pi _2-\pi _1)+T_3{\bar{\pi }}_1-T_4{\bar{\pi }}_2 \right] \right\} \bigg ] \\&\quad =-\left[ \pi _1^TU\pi _1+5{\bar{\pi }}_1^TU{\bar{\pi }}_1\right. \\&\qquad \left. +\, 3(*)^TU(\pi _1-\pi _2)+7{\bar{\pi }}_2^TU{\bar{\pi }}_2\right] . \end{aligned}$$

Then Lemma 4 reduces to Lemma 3 (i). Thus, Lemma 4 encompasses Lemma 3 (i). That is, Lemma 3 (i) is a particular case of Lemma 4 and can be acquired by fixing some slack matrices. Thus, Lemma 4 is less conservative due to additional freedom from the slack matrices.

Lemma 5

(The proof is put in "Appendix 2"). Define a quadratic function $f(x) =a_2x^2 +a_1x+a_0,$ where $a_0, a_1,a_2\in {\mathbb {R}}.$ if

${\mathrm{(i)}}\ f(\alpha )<0,\ \mathrm{(ii)} \ f(\beta )<0$, $\ \mathrm{(iii)} \ -(\beta -\alpha )^2a_2+f(\alpha )<0,$ or $\ \mathrm{(iii)}' \ -(\beta -\alpha )^2a_2+f(\beta )<0,$ then $f(x)<0, \forall x\in [\alpha ,\beta ]$.

Remark 4

Lemma 5 presents a condition to ascertain whether quadratic functions are negative or not on a closed interval $[\alpha ,\beta ]$ taking no account of their concavity or convexity, which includes Lemma 2 [12] and Lemma 4 [45] as its special cases. This lemma will play important role in establishing our main result.

3 Main result

For a clear presentation, we define

$$\begin{aligned} {\mathbf {y}}(t)&={\mathrm{col}}\{y_1(t),y_2(t),\ldots ,y_m(t)\},\\ {\mathbf {v}}(t)&={\mathrm{col}}\{v(t),v(t),\ldots ,v(t)\},\\ {\mathbf {k}}({\mathbf {y}}(t))&={\mathrm{col}}\{k(y_1(t)),k(y_2(t)),\ldots ,k(y_m(t))\},\\ {\widetilde{B}}(y_p)&={B}(y_p)+\varDelta {B}_p(t),\\ {\widetilde{\mathbf {B}}}({\mathbf {y}})&={\mathrm{diag}}\big \{{\widetilde{B}}(y_1),{\widetilde{B}}(y_2),\ldots ,{\widetilde{B}}(y_m)\big \}, \\ {\widetilde{C}}(y_p)&={C}(y_p)+\varDelta {C}_p(t),\\ {\widetilde{\mathbf {C}}}({\mathbf {y}})&={\mathrm{diag}}\big \{\widetilde{C}(y_1),{\widetilde{C}}(y_2),\ldots ,{\widetilde{C}}(y_m)\big \}. \end{aligned}$$

By means of the Kronecker product, the coupled neural networks (3) can be changed into a compact form:

$$\begin{aligned} \dot{{\mathbf {y}}}(t)&= -{\mathbf {A}}{\mathbf {y}}(t)+{\widetilde{\mathbf {B}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}(t))\nonumber \\&\quad +\,{\widetilde{\mathbf {C}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}(t-\omega (t)))\nonumber \\&\quad +\,{\mathbf {D}}_1{\mathbf {y}}(t)+{\mathbf {D}}_2{\mathbf {y}}(t-\omega (t))\nonumber \\&\quad +\, {\mathbf {v}}(t)+{\mathbf {e}}, \end{aligned}$$

(7)

where ${\mathbf {A}}=I_m\otimes A,\ {\mathbf {D}}_\imath =D_\imath \otimes \varLambda _\imath ,\imath =1,2,$ and

$$\begin{aligned} {\mathbf {e}}=\left[ \begin{array}{c} \sum _{j=1}^{m}\varsigma _{1j}\varTheta \mathrm{sgn}(y_j(t)-y_1(t))\\ \sum _{j=1}^{m}\varsigma _{2j}\varTheta \mathrm{sgn}(y_j(t)-y_2(t))\\ \vdots \\ \sum _{j=1}^{m}\varsigma _{mj}\varTheta \mathrm{sgn}(y_j(t)-y_m(t))\end{array}\right] \in {\mathbb {R}}^{nm}. \end{aligned}$$

For simplicity, denote ${\mathbf {J}} = J\otimes I_n,{\mathbf {y}}_{t}={\mathbf {y}}(t),{\mathbf {y}}_{\omega }={\mathbf {y}}(t-\omega (t)),{\mathbf {y}}_{\bar{\omega }}={\mathbf {y}}(t-{\bar{\omega }}),\dot{{\mathbf {y}}}_t=\dot{{\mathbf {y}}}(t),\dot{{\mathbf {y}}}_\omega =\dot{{\mathbf {y}}}(t-\omega (t)),\dot{{\mathbf {y}}}_{{\bar{\omega }}}=\dot{{\mathbf {y}}}(t-{\bar{\omega }}),$ where J is defined in Lemma 2 with ${\hat{R}}={\mathbb {R}}.$ Define

$$\begin{aligned} \xi _t & = {\mathrm{col}}\bigg \{{\mathbf {J}}{\mathbf {y}}_{t},{\mathbf {J}}{\mathbf {y}}_{{\omega }},{\mathbf {J}}{\mathbf {y}}_{\bar{{\omega }}},{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_{t}),{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_{{\omega }}),\\ &\quad {\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_{\bar{{\omega }}}),{\mathbf {J}}\dot{{\mathbf {y}}}_t,{\mathbf {J}}\dot{{\mathbf {y}}}_\omega ,{\mathbf {J}}\dot{{\mathbf {y}}}_{\bar{\omega }},\tau _1,\tau _2,\tau _3,\tau _4,\tau _5,\tau _6,\\&\quad \left. \int _{t-{\bar{{\omega }}}}^t(2\upsilon -2t+\bar{{\omega }}){\mathbf {J}}{{{\mathbf {y}}}}_\upsilon {\mathrm{d}}\upsilon \right\} , \end{aligned}$$

where

$$\begin{aligned} \tau _1=&\frac{1}{{\omega }(t)}\int _{t-{\omega }(t)}^{t} {\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u,\\ \tau _2=&\frac{1}{{\bar{{\omega }}}-{\omega }(t)}\int _{t-{\bar{{\omega }}}}^{t-{\omega }(t)} {\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u,\\ \tau _3=&\frac{2}{{\omega }^2(t)}\int _{t-{\omega }(t)}^{t}[u-t+{\omega }(t)] {\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u,\\ \tau _4=&\frac{2}{[{\bar{{\omega }}}-{\omega }(t)]^2}\int _{t-{\bar{{\omega }}}}^{t-{\omega }(t)}(u-t+{\bar{{\omega }}}){\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u,\\ \tau _5=&\frac{3}{{\omega }^3(t)}\int _{t-{\omega }(t)}^{t}[u-t+{\omega }(t)]^2 {\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u,\\ \tau _6=&\frac{3}{[{\bar{{\omega }}}-{\omega }(t)]^3}\int _{t-{\bar{{\omega }}}}^{t-{\omega }(t)}(u-t+{\bar{{\omega }}})^2{\mathbf {J}}{{\mathbf {y}}}_u {\mathrm{d}}u. \end{aligned}$$

From the integral mean-value theorem, we have that

$$\begin{aligned}&\lim _{{\omega }(t)\rightarrow 0^{^+}}\tau _{2g-1}={\mathbf {J}}{{\mathbf {y}}}_{t},\ \lim _{{\omega }(t)\rightarrow {\bar{{\omega }}}^-}\tau _{2g}={\mathbf {J}}{{\mathbf {y}}}_{\bar{{\omega }}}. \end{aligned}$$

Therefore $\tau _1,\ldots ,\tau _{6}$ are well defined if we set

$$\begin{aligned} \tau _{2g-1}|_{{\omega }(t)=0}={\mathbf {J}}{{\mathbf {y}}}_{t},\ \tau _{2g}|_{{\omega }(t)={\bar{{\omega }}}}={\mathbf {J}}{{\mathbf {y}}}_{\bar{{\omega }}},\ g=1,2,3. \end{aligned}$$

Denote $n'=(m-1)n$ and

$$\begin{aligned}&e_q^T=\left[0_{n'\times (q-1)n'},\ I_{n'}, 0_{n'\times (16-q)n'}\right ],\\&\ q=1,2,\ldots ,16, \\&{\mathbf{H}}=I_{m-1}{\otimes} H,\ {\mathbf{A}}'=I_{m-1}{\otimes} A,\ {\mathbf{K}}=I_{m-1}{\otimes} K,\\&{\mathbf{D}}'_{\imath} =(J{D_{\imath} }P){\otimes} {\varLambda _{\imath} },\ {\mathbf{K}}_{\imath} =I_{m-1}{\otimes} {K}_{\imath},\\ &{\mathcal{Y}}_1=[\ Y_1,Y_2,Y_3,Y_4\ ],\ {\mathcal{Y}}_2=[\ Y_5,Y_6,Y_7,Y_8\ ],\\ &{\varrho} _p=\sum _{l=1}^{n}2{\bar{k}}_l{\hat{b}}_{pl},\ {\vartheta} _p=\sum _{l=1}^{n}2{\bar{k}}_l{\hat{c}}_{pl},\ p\in {\mathcal{N}},\\ &{\mu}_{\iota }={\varsigma} _{{\iota },{\iota }+1}+{\varsigma} _{{\iota }+1,{\iota }}-{\sum} _{s=1,s\ne {\iota },{\iota }+1}^{m}({\varsigma} _{{\iota }s}+{\varsigma} _{{\iota }+1,s}),\\ &\quad \quad \ \iota =1,2,\ldots ,m-1,\\&{\mathcal{Q}}_1={\mathrm{diag}}\{Q_1,3Q_1,0_{n'},0_{n'}\},\ \\ &{\mathcal{Q}}=\left[\begin{array}{cc} Q_1 &{} {\mathcal{Q}}_3\\ *&{} {\mathcal{Q}}_4\end{array}\right],\ {\mathcal{Q}}_3=[\ Q_2,\ Q_3\ ],\ {\mathcal {Q}}_4=\left [\begin{array}{cc}Q_4 &{} Q_5\\ *&{} Q_6\end{array}\right ],\\&{\mathcal{Q}}_l={\mathrm{diag}}\{{Q}_l,\ 3{Q}_l,\ 5{Q}_l,\ 7{Q}_l\},\ l=7,8,9,10,\\ &{\mathcal{U}}_{\imath} =\left[\begin{array}{cc}W_{\imath }{\mathbf{K}}-U_{\imath}{\mathbf{K}}_1 &{}U_{\imath }{\mathbf{K}}_2\\ *&{} -U_{\imath}-W_{\imath}\end{array}\right],\imath =1,2,\\&{\mathcal {F}}_{\imath \jmath }=\bigg [\begin{array}{cc}{R}_{\imath \jmath }{\mathbf {K}}-{F}_{\imath \jmath }{\mathbf {K}}_1 &{}{F}_{\imath \jmath }{\mathbf {K}}_2\\ *&{} -{F}_{\imath \jmath }-{R}_{\imath \jmath }\end{array}\bigg ],\ \jmath =1,2,3;\\&\varUpsilon _1=\left[ \ e_1,\ e_2,\ e_{10}\ \right] ,\ \varUpsilon _2=\left[ \ 0_{(16n')\times (2n')},\ e_1-e_2\ \right] ,\\&\varUpsilon _3=\left[ \ e_2,\ e_3,\ e_{11}\ \right] ,\ \varUpsilon _4=\left[ \ {\bar{\omega }}e_{8},\ {\bar{\omega }}e_{9},\ e_2-e_3\ \right] ,\\&\varUpsilon _5=\left[ \ e_7,\ e_8,\ 0_{(16n')\times n'}\ \right] ,\\&\varUpsilon _6=\left[ \ e_{8},\ e_{9},\ 0_{(16n')\times n'}\ \right] ,\\&\varUpsilon _7=\left[ \ 0_{(16n')\times (2n')},\ e_2-e_{10}\ \right] ,\\&\varUpsilon _8=\left[ \ -{\bar{\omega }}e_{8},\ 0_{(16n')\times n'},\ e_{11}-e_{2}\ \right] ,\\&\varUpsilon _9=\left[ \ 0_{(16n')\times n'},\ e_8,\ 0_{(16n')\times n'}\ \right] ,\\&\varUpsilon _{10}=\left[ \ e_8,\ 0_{(16n')\times (2n')}\ \right] ,\\&\varUpsilon _{11}=\left[ \ e_7,\ e_1,\ 0_{(16n')\times n'}\ \right] ,\\&\varUpsilon _{12}=\left[ \ e_{1},\ e_4\ \right] ,\ \varUpsilon _{13}=\left[ \ e_3,\ e_6\ \right] ,\\&\varUpsilon _{14}=\left[ \ e_{2},\ e_5\ \right] ,\ \varUpsilon _{15}=\left[ \ e_{1},\ 0_{(16n')\times n'}\ \right] ,\\&\varUpsilon _{16}=\left[ \ e_2,\ e_1-e_{2}\ \right] ,\ \varUpsilon _{17}=\left[ \ e_{3},\ e_{1}-e_{3}\ \right] ,\\&\varUpsilon _{18}=\big [\ e_1-e_{2},\ e_1+e_{2}-2e_{10}, \ e_1-e_{2}+6e_{10} \\&\quad \quad \quad -\, 6e_{12},\ e_1+e_{2}-12e_{10}+30e_{12}-20e_{14}\big ],\\&\varUpsilon _{19}=\left[ \ e_{10},\ e_1-e_{10}\ \right] ,\ \varUpsilon _{21}=\left[ \ e_{11},\ e_{1}-e_{11}\ \right] ,\\&\varUpsilon _{20}=\big [\ e_2-e_{3},\ e_2+e_{3}-2e_{11},\ e_2-e_{3}+6e_{11} \\&\quad \quad \quad -\, 6e_{13}, e_2+e_{3}-12e_{11}+30e_{13}-20e_{15}\big ],\\&\varPi _1={\bar{\omega }}e_7\Big \{Q_7+{\bar{\omega }}Q_8+\frac{1}{2} {\bar{\omega }}^2Q_9+\frac{1}{3} {\bar{\omega }}^3Q_{10}\Big \}e_7^T,\\&\varPi _2=-{\mathrm{sym}}\Big \{(e_1-e_2)\big [({\bar{\omega }}Q_2+G_1) e_{10}^T\\&\quad \quad \quad +\, ({\bar{\omega }}Q_3-G_1)(e_1-e_{10})^T\big ]+3(e_1+e_2\\&\quad \quad \quad -\, 2e_{10})({\bar{\omega }}Q_2-{\bar{\omega }}Q_3+2G_1)(e_{10}-e_{12})^T\Big \}, \\&\varPi _3=-3{\bar{\omega }}(e_{10}-e_{12})(Q_4-2Q_5+Q_6)(*)^T, \end{aligned}$$

$$\begin{aligned}&\varPi _4=-{\mathrm{sym}}\Big \{(e_2-e_3)\big [({\bar{\omega }}Q_2+G_2) e_{11}^T\\&\quad \quad \quad +\, ({\bar{\omega }}Q_3-G_2)(e_1-e_{11})^T\big ]+3(e_2+e_3\\&\quad \quad \quad -\, 2e_{11})({\bar{\omega }}Q_2-{\bar{\omega }}Q_3+2G_2)(e_{11}-e_{13})^T\Big \}, \\&\varPi _5=-3{\bar{\omega }}(e_{11}-e_{13})(Q_4-2Q_5+Q_6)(*)^T,\\&\varPi _6=-2(e_1-e_{10})Q_9(*)^T\\&\quad \quad \quad -\, 4(e_1+2e_{10}-3e_{12})Q_9(*)^T\\&\quad \quad \quad -\, 6(e_1-3e_{10}+12e_{12}-10e_{14})Q_9(*)^T,\\&\varPi _7=-2(e_2-e_{11})Q_9(*)^T\\&\quad \quad \quad -\, 4(e_2+2e_{11}-3e_{13})Q_9 (*)^T \\&\quad \quad \quad -\, 6(e_2-3e_{11}+12e_{13}-10e_{15})Q_9(*)^T,\\&\varPi _8=-3(e_1-e_{12})Q_{10}(*)^T\\&\quad \quad \quad -\, 5(e_1+3e_{12}-4e_{14})Q_{10}(*)^T,\\&\varPi _9=-4(e_1-e_{10})Q_{10}(*)^T\\&\quad \quad \quad -\, 8(e_1+2e_{10}-3e_{12})Q_{10} (*)^T \\&\quad \quad \quad -\, 12(e_1-3e_{10}+12e_{12}-10e_{14})Q_{10}(*)^T,\\&\varPi _{10}=-3(e_2-e_{13})Q_{10}(*)^T\\&\quad \quad \quad -\, 5(e_2+3e_{13}-4e_{15})Q_{10}(*)^T,\\&\varPi _{11}={\mathrm{sym}}\big \{e_7\big [{\mathbf {H}}{\mathbf {D}}_2'e_2^T-{\mathbf {H}}e_7^T-{\mathbf {H}}({\mathbf {A}}'-{\mathbf {D}}_1')e_1^T \\&\quad \quad \quad +\, (I_{m-1}\otimes H\bar{B})e_4^T+(I_{m-1}\otimes H{\bar{C}})e_5^T\big ]\big \},\\&\varPi _{12}=-2(e_{10}-e_{11})\left( X_{23}+X^T_{23} \right) (e_{10}-e_{11})^T\\&\quad \quad \quad +\,{\mathrm{sym}}\big \{(-2e_{10}+e_{12}+e_{13})Me_{16}^T\big \},\\&\mathcal {X}_1=(X_{ij})_{3\times 3},\\&\varDelta _1(r)=\big [\ e_1,\ re_{10}+({{\bar{\omega }}}-r)e_{11},\ e_{16}\big ],\\&\varDelta _2(r)=\big [e_7,\ e_1-e_3,\\&\quad {{\bar{\omega }}}(e_1+e_3)-2re_{10}-2({{\bar{\omega }}}-r)e_{11}\big ],\\&\varDelta _3(r)=r({{\bar{\omega }}}-2r)e_{10}+r^2e_{12}\\&\quad \quad \quad +\,({{\bar{\omega }}}-r)^2e_{13}-{{\bar{\omega }}}({{\bar{\omega }}}-r)e_{11}-e_{16},\\&\varXi (r,s)={\mathrm{sym}}\left\{ \varDelta _1(r)\mathcal {X}_1\varDelta _2(r)^T+\varDelta _3(r)Me_{16}^T\right\} \\&\quad \quad \quad +\, r\Big (-{\bar{\omega }}\varPi _3+{\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _5^T-\varUpsilon _3\mathcal {X}_3\varUpsilon _6^T\right\} \\&\quad \quad \quad -\, {\bar{\omega }}\varUpsilon _{19}{\mathcal {Q}}_4\varUpsilon _{19}^T+\varUpsilon _{12}{\mathcal {F}}_{11}\varUpsilon _{12}^T+\varUpsilon _{14}{\mathcal {F}}_{12}\varUpsilon _{14}^T\\&\quad \quad \quad +\, \varPi _8+\varUpsilon _{13}{\mathcal {F}}_{13}\varUpsilon _{13}^T\Big )+({{\bar{\omega }}}-r)\Big (-{\bar{\omega }}\varPi _5\\&\quad \quad \quad -\, {\bar{\omega }} \varUpsilon _{21}{\mathcal {Q}}_4\varUpsilon _{21}^T +\varUpsilon _{18}{\mathcal {Q}}_{10}\varUpsilon _{18}^T+\varUpsilon _{12}{\mathcal {F}}_{21}\varUpsilon _{12}^T\\&\quad \quad \quad +\, \varPi _9+\varPi _{10}+ \varUpsilon _{14}{\mathcal {F}}_{22}\varUpsilon _{14}^T+\varUpsilon _{13}{\mathcal {F}}_{23}\varUpsilon _{13}^T\Big )\\&\quad \quad \quad +\, rs\big [{\mathrm{sym}}\left\{ -\varUpsilon _1\mathcal {X}_2\varUpsilon _9^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _{10}^T\right\} \big ]\\&\quad \quad \quad +\, s\big [ \varUpsilon _1\mathcal {X}_2\varUpsilon _1^T+{\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _7^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _8^T\right\} \\&\quad \quad \quad -\, \varUpsilon _3\mathcal {X}_3\varUpsilon _3^T\big ]-(1-s)\varUpsilon _{14}(\mathcal {U}_1-\mathcal {U}_2)\varUpsilon _{14}^T\\&\quad \quad \quad +\, {\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _2^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _4^T\right\} +\varPi _1+\varPi _2\\&\quad \quad \quad +\, {\bar{\omega }}^2\varUpsilon _{11}{\mathcal {Q}}\varUpsilon _{11}^T+\varPi _4+\varPi _6+\varPi _7+\varPi _{11}\\&\quad \quad \quad +\, \varUpsilon _{12}\mathcal {U}_1\varUpsilon _{12}^T-\varUpsilon _{13}\mathcal {U}_2\varUpsilon _{13}^T+\varUpsilon _{15}G_1\varUpsilon _{15}^T \end{aligned}$$

$$\begin{aligned}&\quad \quad \quad -\, \varUpsilon _{16}G_1\varUpsilon _{16}^T+\varUpsilon _{16}G_2\varUpsilon _{16}^T -\varUpsilon _{17}G_2\varUpsilon _{17}^T\\&\quad \quad \quad +\, \varUpsilon ^T_{18}\big (\mathcal {Y}_1+\mathcal {Y}_1^T\big )\varUpsilon _{18}+\varUpsilon ^T_{20}\big (\mathcal {Y}_2+\mathcal {Y}_2^T\big )\varUpsilon _{20} \\&\quad \quad \quad -\, \big [\varUpsilon _{18}, \varUpsilon _{20}\big ] \bigg [\begin{array}{ll}{\mathcal {Q}}_{1}+{\mathcal {Q}}_{8} &{} {\mathcal {Q}}_{2}\\ *&{} {\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}\end{array}\bigg ]\bigg [\begin{array}{c}\varUpsilon _{18}^T \\ \varUpsilon _{20}^T\end{array}\bigg ]. \end{aligned}$$

Next we derive the following synchronism result for system (7).

Theorem 1

(The proof is put in "Appendix 3"). Under Assumption 1 is satisfied. Given scalars ${\bar{\omega }}>0,\omega _1,\omega _2,$ the system (7) is globally robustly synchronized for $0\le \omega (t)\le {\bar{\omega }},$ $\omega _1\le \dot{\omega }(t)\le \omega _2,$ if there exist positive definite matrices $\mathcal {X}_\jmath ,{\mathcal {Q}},Q_l(l=7,8,9,10),$ positive diagonal matrices $U_\imath ,W_\imath ,F_{\imath \jmath },R_{\imath \jmath }$ $(\jmath =1,2,3),H={\mathrm{diag}}\{h_1,h_2,\ldots ,h_n\},$ symmetric matrices $G_\imath (\imath =1,2),$ real matrices ${\mathcal {Q}}_2,M,Y_p(p=1,2,\ldots ,8)$ of appropriate dimensions such that

$$\begin{aligned}&\bigg [\begin{array}{cc}{\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}+{\mathcal {Q}}_{9}+\bar{\omega }{\mathcal {Q}}_{10} &{} {\mathcal {Q}}_{2}\\ *&{} {\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}\end{array}\bigg ]\ge 0, \end{aligned}$$

(8)

$$\begin{aligned}&\sigma _{ij}=\varrho _j+\vartheta _j-\theta _j\mu _{i}+2{\bar{k}}||E||_1\left( ||L_1||_1+ ||L_2||_1\right) \nonumber \\&\ \ \ \ \le 0,\ \ i=1,2,\ldots ,m-1;j\in {\mathcal {N}}, \end{aligned}$$

(9)

and one of the following two groups of inequalities holds:

• (1) ${\widetilde{\varXi }}_{\rho \imath }<0, \rho =1,2,3; \imath =1,2;$

• (2) ${\widetilde{\varXi }}_{\rho \imath }<0, \rho =1,2,4; \imath =1,2;$

where

$$\begin{aligned}&{\widetilde{\varXi }}_{\rho \imath }=\left[ \begin{array}{cccc} {\varXi }_{\rho \imath } &{} \varUpsilon ^T_{20}\mathcal {Y}_2\\ *&{} -{\mathcal {Q}}_7\end{array}\right] ,\ \rho =1,3;\imath =1,2; \end{aligned}$$

and

$$\begin{aligned}&{\widetilde{\varXi }}_{\rho \imath }=\left[ \begin{array}{cccc} {\varXi }_{\rho \imath } &{} \varUpsilon ^T_{18}\mathcal {Y}_1\\ *&{} -{\mathcal {Q}}_7\end{array}\right] ,\ \rho =2,4;\imath =1,2; \end{aligned}$$

with $\varXi _{1\imath }={\varXi }(0,\omega _\imath ),$ $\varXi _{2\imath }={\varXi }({\bar{\omega }},\omega _\imath ),$ $\varXi _{3\imath }=\varXi _{1\imath }$ $-{\bar{\omega }}^2\varPi _{12},$ $\varXi _{4\imath }=-{\bar{\omega }}^2\varPi _{12}+\varXi _{2\imath }.$

Remark 5

For continuous networks, there are a lots of skills to get less conservative result, for instance delay partitioning technique, triple integrals term, quadruple integrals term, and multiple integrals terms. All these skills can also be applied for delayed memristive neural networks to cut down conservatism. To present a concise result, we utilize a simple Lyapunov–Krasovskii functional in this paper.

Remark 6

Noting that stochastic disturbances, impulsive perturbations, bounded and unbounded distributed delays can be embedded into MNNs. To emphasize our new analysis technique, this paper considers networks (3) such that the obtained results are not too intricate.

4 Illustrative example

This section proposes an example to reveal the effectiveness of Theorem 1.

Example 1

Consider system (3) with following parameters:

$$\begin{aligned} \omega (t)&=0.4+0.4\cos (2t),\ A=8I_2,\ v(t)=0,\\ k_q(s)&=(|s+1|-|s-1|)/2,\ q=1,2,\\ b_{11}(y_1(t))&=\Bigg \{\begin{array}{ll} 0.38,&{}\quad {\mathrm{sign}}\dot{k}_{11}(t)\le 0,\\ 0.77,&{}\quad {\mathrm{sign}}\dot{k}_{11}(t)>0,\end{array}\\ b_{12}(y_2(t))&=\Bigg \{\begin{array}{ll} 0.98,&{}\quad {\mathrm{sign}}\dot{k}_{12}(t)\le 0,\\ 1.45,&{}\quad {\mathrm{sign}}\dot{k}_{12}(t)>0,\end{array}\\ b_{21}(y_1(t))&=\Bigg \{\begin{array}{ll} 2.05,&{}\quad {\mathrm{sign}}\dot{k}_{21}(t)\le 0,\\ 1.62,&{}\quad {\mathrm{sign}}\dot{k}_{21}(t)>0,\end{array}\\ b_{22}(y_2(t))&=\Bigg \{\begin{array}{ll} 3.53,&{}\quad {\mathrm{sign}}\dot{k}_{22}(t)\le 0,\\ 4.07,&{}\quad {\mathrm{sign}}\dot{k}_{22}(t)>0,\end{array}\\ c_{11}(y_1(s))&=\Bigg \{\begin{array}{ll} -0.29,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{11}(t-\omega (t))\le 0,\\ -0.55,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{11}(t-\omega (t))>0,\end{array}\\ c_{12}(y_2(s))&=\Bigg \{\begin{array}{ll} -3.07,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{12}(t-\omega (t))\le 0,\\ -3.76,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{12}(t-\omega (t))>0,\end{array}\\ c_{21}(y_1(s))&=\Bigg \{\begin{array}{ll} 2.31,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{21}(t-\omega (t))\le 0,\\ 1.78,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{21}(t-\omega (t))>0,\end{array}\\ c_{22}(y_2(s))&=\Bigg \{\begin{array}{ll} -1.79,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{22}(t-\omega (t))\le 0,\\ -2.04,&{}\quad {\mathrm{sign}}\frac{\mathrm{d}}{{\mathrm{d}}t}k_{22}(t-\omega (t))>0,\end{array} \end{aligned}$$

where $k_{jq}(t)=k_q(y_q(t))-y_j(t),k_{jq}(t-\omega (t))=k_q(y_q(t-\omega (t)))-y_j(t),\ j,q=1,2.$ The parameter uncertainties are supposed as $\varDelta B_p(t)=0.1\sin (t)I_2,$ $\varDelta C_p(t)=0.1\cos (t)I_2,p=1,2,\ldots ,9.$ Set $E=I_2,L_\imath =0.1I_2,N_{1p}=\sin (t),N_{2p}=\cos (t),$ then $\varDelta B_p(t),$ $\varDelta C_p(t)$ can be expressed as (4). Therefore, we have $||E||_1=1,||L_\imath ||_1= 0.1$, and $||N_{\imath p}||_1\le 1,\imath =1,2;p=1,2,\ldots ,9.$ Then condition (5) is satisfied. The inner coupling gains are given by $\varLambda _\imath =I_2,\imath =1,2;\varTheta =9I_2.$

Calculation yields that ${\bar{\omega }}=0.8,\omega _1=-0.8,\omega _2=0.8,\varrho _1=1.72,\varrho _2=1.94,\vartheta _1=1.9,\vartheta _2=1.56,$

$$\begin{aligned} {\bar{B}}=\left[ \begin{array}{ll} 0.77&{}\quad 1.45 \\ 2.05 &{}\quad 4.07 \end{array}\right] , \ {\bar{C}}=\left[ \begin{array}{ll} -0.29 &{}\quad -3.07\\ 2.31&{} -1.79 \end{array}\right] , \end{aligned}$$

and Assumption 1 is satisfied with $k^-_\imath =0,k^+_\imath =1,{\bar{k}}_\imath =1,\imath =1,2.$ Thus, $K_1=0,K_2=0.5I_2,K=I_2,{\bar{k}}=2.$

Furthermore, outer coupling matrices are taken as

$$\begin{aligned} D_\imath&=\left[ \begin{array}{ccccccccc} -2 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1&{}\quad -3 &{}\quad 1 &{}\quad 1 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 1 &{}\quad -4 &{}\quad 1 &{}\quad 1 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 1 &{}\quad -5 &{}\quad 1 &{}\quad 1 &{}\quad 1&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad -5 &{}\quad 1 &{}\quad 1&{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad -5 &{}\quad 1 &{}\quad 1&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad -4 &{}\quad 1 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad -3 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad -2\end{array}\right] ,\imath =1,2,\\ \varXi&=\left[ \begin{array}{ccccccccc} 0 &{}\quad 13.7 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0 &{}\quad 12 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0 &{}\quad 10.3 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0 &{}\quad 8.6 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0 &{}\quad 6.9 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0.1 &{}\quad 0.1&{}\quad 0 &{}\quad 5.2 &{}\quad 0.1 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0.1 &{}\quad 0.1&{}\quad 0 &{}\quad 3.5 &{}\quad 0.1 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0 &{}\quad 1.8 \\ 0.1 &{}\quad 0.1 &{}\quad 0.1 &{}\quad 0.1&{}\quad 0.1 &{}\quad 0.1&{}\quad 0.1 &{}\quad 0.1&{}\quad 0 \end{array}\right] . \end{aligned}$$

Computation gives that $\mu _i=0.5,\sigma _{i1}=-0.08,$ $\sigma _{i2}=-0.20, i=1,2,\ldots ,8.$ Therefore, condition (9) holds. Seeking the solutions of the inequalities in Theorem 1 by utilizing the Matlab LMI Toolbox, we can get a feasible solution. Portion of the decision matrices are made a list as follows:

$$\begin{aligned}&H={\mathrm{diag}}\left\{ 0.3712,0.1254\right\} ,\\&U_1={\mathrm{diag}} \left\{ 0.2702,1.2704,0.4493,0.2419,\right. \\&\quad 1.5288,1.5583,1.3358,4.3973,5.2856,5.1382, \\&\quad \left. 4.3175,4.1147,3.1181,0.3483,0.5947,0.3250\right\} ,\\&U_2={\mathrm{diag}} \left\{ 2.8234,0.7107,1.4356,2.8723,\right. \\&\quad 1.3831,1.7874,0.3616,0.2420,1.1100,1.9953, \\&\quad \left. 0.7582,1.3567,0.5577,0.5509,0.4005,0.3457\right\} ,\\&W_1={\mathrm{diag}} \left\{ 0.3053 ,0.3431,0.2927,2.7834,\right. \\&\quad 1.2356,2.8723,9.9873,5.7513,5.0724,6.0720, \\&\quad \left. 4.5918,6.2468,8.8097,1.8041,2.0695,5.0804\right\} ,\\&W_2={\mathrm{diag}} \left\{ 0.4695,10.0951,0.5100,0.3440,\right. \\&\quad 0.4195,0.4248,0.5998,0.5539,0.3463,0.2232, \\&\quad \left. 1.2769,0.3351,1.6033,0.1860,0.9534,0.9816\right\} ,\\&F_{11}={\mathrm{diag}} \left\{ 0.6231,0.2336,0.3824,0.5015,\right. \\&\quad 0.1137,0.9230,0.5988,0.5785,0.8674,1.8495, \\&\quad \left. 0.4480,1.2405,0.9220,0.2360,2.0413,0.7994\right\} ,\\&F_{21}={\mathrm{diag}}\left\{ 0.4373,0.3224,0.1311,2.6117,\right. \\&\quad 0.8428,0.4852,1.2352,0.3253,0.2474,1.1734, \\&\quad \left. 0.3394,0.5325,0.9164,0.3788,0.5179,0.2775\right\} . \end{aligned}$$

To simulate numerically, we select nine values at random in $(-0.2,0.2)^T$ and $(-0.5,0.2)^T$, respectively, as the initial states. The state curves y(t) are drawn in Fig. 2 and the synchronism error $\varepsilon _1(t),\varepsilon _2(t)$ are drawn in Figs. 3 and 4, respectively, where $\varepsilon _j(t)=(y_{pj}(t)-y_{1j}(t)),\ p=2,\ldots ,9,\ j=1,2$.

Fig. 2

The state curves $t-y(t).$

Fig. 3

The synchronism error of $t-\varepsilon _1(t).$

Fig. 4

The synchronism error of $t-\varepsilon _2(t).$

It has been verified that none of the conditions in [1, 3, 7, 43, 51] can testify whether system (3) is synchronized or not for this example.

However, the conditions of [2, 10, 11, 33, 35, 37, 39,40,41, 46, 47] were all established under the following representative hypotheses:

$$\begin{aligned}&[{\underline{B}},\bar{B}]k(x(t))-[{\underline{B}},\bar{B}]k(y(t))\\&\quad \subseteq [{\underline{B}},\bar{B}](k(x(t))-k(y(t))),\\&\quad [{\underline{C}},{\bar{C}}]k(x(t))-[{\underline{C}},{\bar{C}}]k(y(t))\\&\quad \subseteq [{\underline{C}},{\bar{C}}](k(x(t))-k(y(t))). \end{aligned}$$

It is easy to verify that the above hypotheses are not satisfied by this model. That is, none of these conditions can be applied to justify the synchronism of this example.

Therefore we may say that the result of this paper is less conservative than the conditions in [1,2,3, 7, 10, 11, 33, 35, 37, 39,40,41, 43, 46, 47, 51].

5 Conclusion

This paper inquires into the synchronism of a class of CMNNs with linear diffusive and discontinuous sign terms. The proposed conditions are expressed in terms of linear matrix inequalities (LMIs) which can be checked numerically very efficiently by using the interior-point algorithms, such as the Matlab LMI Control Toolbox. In the future, there are some issues that deserve further investigation, such as (1) the adaptive synchronization control of MNNs because adaptive control can avoid high control gains effectively, (2) synchronization of the MNNs with mismatch features since nonidentical characteristics often exist between the drive and response systems, (3) investigations other control schemes, such as pinning control, event-triggered control, sample-data control, intermittent control, quantized control and event-based control.

6 Appendix 1: Proof of Lemma 4

Take the first four Legendre orthogonal polynomials on $[\alpha ,\beta ]$ ( [29]): $l_0(\upsilon )=1,l_1(\upsilon )=\frac{1}{\beta -\alpha }(2\upsilon -\alpha -\beta ),l_2(\upsilon )=\frac{1}{(\beta -\alpha )^2}[6\upsilon ^2-6(\alpha +\beta )\upsilon +(\alpha ^2+4\alpha \beta +\beta ^2)],l_3(\upsilon )=\frac{1}{(\beta -\alpha )^3}[20\upsilon ^3-30(\alpha +\beta )\upsilon ^2+12(\alpha ^2+3\alpha \beta +\beta ^2)\upsilon -(\alpha ^3+9\alpha ^2\beta +9\alpha \beta ^2+\beta ^3)].$ Simple calculation derives

$$\begin{aligned}&\int ^{\beta }_{\alpha }l_i(\upsilon )l_j(\upsilon ){\mathrm{d}}\upsilon =\bigg \{\begin{array}{cc} 0,&{} i\ne j,\\ \frac{\beta -\alpha }{2i+1},&{} i=j,\end{array}\ \ i,j=0,1,2,\ldots . \end{aligned}$$

For continuous function $x(\upsilon )$ and continuous differentiable function $f(\upsilon ),$ calculation on the basis of integration by parts gives

$$\begin{aligned}&\int ^{\beta }_{\alpha }f(\upsilon )x(\upsilon ){\mathrm{d}}\upsilon \\&\quad =f(\alpha )\int ^{\beta }_{\alpha }x(\upsilon ){\mathrm{d}}\upsilon +\int ^{\beta }_{\alpha }\dot{f}(\upsilon )\int ^{\beta }_{\upsilon }x(s){\mathrm{d}}s{\mathrm{d}}\upsilon ,\\&\int ^{\beta }_{\alpha }f(\upsilon )\int ^{\beta }_{\upsilon }x(s){\mathrm{d}}s{\mathrm{d}}\upsilon \\&\quad =f(\alpha )\int ^{\beta }_{\alpha }\int ^{\beta }_{\upsilon }x(s){\mathrm{d}}s{\mathrm{d}}\upsilon \\&\qquad +\, \int ^{\beta }_{\alpha }\dot{f}(\upsilon )\int ^{\beta }_{\upsilon }\int ^{\beta }_{u}x(s){\mathrm{d}}s{\mathrm{d}}u{\mathrm{d}}\upsilon , \end{aligned}$$

and

$$\begin{aligned}&\int ^{\beta }_{\alpha }f(\upsilon )\int ^{\beta }_{\upsilon }x(s){\mathrm{d}}s{\mathrm{d}}\upsilon \\&\quad =f(\alpha )\int ^{\beta }_{\alpha }\int ^{\beta }_{\upsilon }\int ^{\beta }_{u}x(s){\mathrm{d}}s{\mathrm{d}}u{\mathrm{d}}\upsilon \\&\qquad +\int ^{\beta }_{\alpha }\dot{f}(\upsilon )\int ^{\beta }_{\upsilon }\int ^{\beta }_{u}\int ^{\beta }_{w}x(s){\mathrm{d}}s{\mathrm{d}}w{\mathrm{d}}u{\mathrm{d}}\upsilon . \end{aligned}$$

Then the following equalities are derived

$$\begin{aligned}&\int ^{\beta }_{\alpha }l_1(\upsilon )\mu (\upsilon ){\mathrm{d}}\upsilon =\pi _2-\pi _1,\\&\quad \int ^{\beta }_{\alpha }l_2(\upsilon )\mu (\upsilon ){\mathrm{d}}\upsilon ={\bar{\pi }}_1,\ \int ^{\beta }_{\alpha }l_3(\upsilon )\mu (\upsilon ){\mathrm{d}}\upsilon =-{\bar{\pi }}_2. \end{aligned}$$

Denote ${\hat{l}}(\upsilon )={\mathrm{col}}\{l_0(\upsilon ),l_1(\upsilon ),l_2(\upsilon ),l_3(\upsilon )\},\mathcal T={\mathrm{col}}\{T_1,T_2,T_3,T_4\},$ the following equality is derived

$$\begin{aligned}&\int ^\beta _\alpha \bigg [\begin{array}{c} {\hat{l}}(\upsilon )\chi \\ \mu (\upsilon )\end{array}\bigg ]^T\bigg [\begin{array}{cc} \mathcal TU^{-1}\mathcal T^T &{} \mathcal T \\ *&{} U\end{array}\bigg ]\bigg [\begin{array}{c} {\hat{l}}(\upsilon )\chi \\ \mu (\upsilon )\end{array}\bigg ]{\mathrm{d}}\upsilon \\&\quad =\int ^\beta _\alpha \mu (\upsilon )^TU\mu (\upsilon ){\mathrm{d}}\upsilon \\&\qquad +\, (\beta -\alpha )\sum _{\zeta =1}^{4}\frac{1}{2\zeta -1}\chi ^T\left( T_\zeta U^{-1}T_\zeta ^T\right) \chi \\&\qquad +\, {\mathrm{sym}}\left\{ \chi ^T\left[ T_1\pi _1+T_2(\pi _2-\pi _1)+T_3{\bar{\pi }}_1-T_4{\bar{\pi }}_2 \right] \right\} . \end{aligned}$$

Due to $U>0,$ by Schur Complement, the following inequality holds

$$\begin{aligned}&\bigg [\begin{array}{cc} \mathcal TU^{-1}\mathcal T^T &{} \mathcal T \\ *&{} U\end{array}\bigg ]\ge 0, \end{aligned}$$

thus

$$\begin{aligned} 0&\le \int ^\beta _\alpha \mu (\upsilon )^TU\mu (\upsilon ){\mathrm{d}}\upsilon \\&\quad +\, (\beta -\alpha )\sum _{\zeta =1}^{4}\frac{1}{2\zeta -1}\chi ^T\left( T_\zeta U^{-1}T_\zeta ^T\right) \chi \\&\quad +\, {{\mathrm{sym}}}\left\{ \chi ^T\left[ T_1\pi _1+T_2(\pi _2-\pi _1)+T_3{\bar{\pi }}_1-T_4{\bar{\pi }}_2 \right] \right\} , \end{aligned}$$

which completes the proof.

7 Appendix 2: Proof of Lemma 5

The group of conditions (i), (ii) and (iii) is Lemma 4 ( [45]). Now we prove the group of conditions (i), (ii) and (iii)$'.$ For $a_2\ge 0,\ f(x)$ is convex. So, (i) and (ii) ensure $f(x)<0, \forall x\in [\alpha ,\beta ].$ Otherwise, $a_2<0,\ f(x)$ is concave. $\dot{f}(x)=2a_2x+a_1,\ \dot{f}(\alpha )=2a_2\alpha +a_1,\ \ddot{f}(x)=2a_2<0.$ By Maclaurin formula, there exists real scalar $\theta$ between x and $\alpha$ such that

$$\begin{aligned} f(x)&=f(\alpha )+\dot{f}(\alpha )(x-\alpha )+\frac{1}{2}\ddot{f}(\theta )(x-\alpha )^2\\ \le&f(\alpha )+\dot{f}(\alpha )(x-\alpha )\\ &=a_0-a_2\alpha ^2+(2a_2\alpha +a_1)x:=g(x). \end{aligned}$$

Notice that g(x) is convex about x. Thus $g(\alpha )=f(\alpha )<0$ follows from (i) and $g(\beta )=-(\beta -\alpha )^2a_2+f(\beta )<0$ from (iii)$'$. Thus we have $g(x)<0, \forall x\in [\alpha ,\beta ].$ From $f(x)\le g(x),$ this completes the proof of Lemma 5.

8 Appendix 3: Proof of Theorem 1

Based on Assumption 1, the following inequality is correct for any $j\in {\mathcal {N}}$ and $\varsigma ,\zeta \in {\mathbb {R}}$ with $\varsigma \ne \zeta$

$$\begin{aligned} 0&\ge \big [k_j(\varsigma )-k_j(\zeta )-k^-_j(\varsigma -\zeta )\big ]\\&\quad \times \, \left[ k_j(\varsigma )-k_j(\zeta )-{k^+_j}(\varsigma -\zeta )\right] . \end{aligned}$$

Thus, for any positive scalar $u^{\imath }_{pj} ({\imath }=1,2;p=1,2,\ldots ,m-1;\ j\in {\mathcal {N}})$ the following inequalities hold

$$\begin{aligned} 0&\le -u^{\imath }_{pj}k^-_j{k^+_j}[y_{pj}(t)-y_{p+1,j}(t)]^2\\&\quad -\, u^{\imath }_{pj}[k_j(y_{pj}(t))-k_j(y_{p+1,j}(t))]^2+(k^-_j+{k^+_j})\\&\quad u^{\imath }_{pj}[y_{pj}(t)-y_{p+1,j}(t)][k_j(y_{pj}(t))-k_j(y_{p+1,j}(t)). \end{aligned}$$

Denoting $U^{\imath }_{p}={\mathrm{diag}}\{u^{\imath }_{p1},u^{\imath }_{p2},\ldots ,u^{\imath }_{pn}\}({\imath }=1,2;$ $p=1,2,\ldots ,m-1),$ the following inequalities are derived

$$\begin{aligned} 0&\le -[k(y_{p}(t))-k(y_{p+1}(t))]^T\\&\quad \times \, U^{\imath }_{p}[k(y_{p}(t))-k(y_{p+1}(t))]-[y_{p}(t)\\&\quad -\, y_{p+1}(t)]^TU^{\imath }_{p}K_1[y_{p}(t)-y_{p+1}(t)]+2[y_{p}(t)\\&\quad -\, y_{p+1}(t)]^TU^{\imath }_{p}K_2[k(y_{p}(t))-k(y_{p+1}(t))]. \end{aligned}$$

Summing both ends of the aforementioned inequalities from $p=1$ to $m-1$ gives

$$\begin{aligned}&u_{\imath }(t):=-({\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t))^TU_{{\imath }}{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t)-({\mathbf {J}}{\mathbf {y}}_t)^TU_{{\imath }}{\mathbf {K}}_1{\mathbf {J}}{\mathbf {y}}_t\nonumber \\&\quad +\, 2({\mathbf {J}}{\mathbf {y}}_t)^TU_{{\imath }}{\mathbf {K}}_2{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t) \ge 0, \end{aligned}$$

(10)

where $U_{{\imath }}={\mathrm{diag}}\{U^{\imath }_{1},U^{\imath }_{2},\ldots ,U^{\imath }_{m-1}\}({\imath }=1,2).$ Similarly the following inequality is true

$$\begin{aligned} w_{\imath }(t):&=({\mathbf {J}}{\mathbf {y}}_t)^TW_{{\imath }}{\mathbf {K}}{\mathbf {J}}{\mathbf {y}}_t-({\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t))^TW_{{\imath }}{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t)\nonumber \\&\ge 0, \end{aligned}$$

(11)

with $W_{{\imath }}={\mathrm{diag}}\{W^{\imath }_{1},W^{\imath }_{2},\ldots ,W^{\imath }_{m-1}\},W^{\imath }_{p}={\mathrm{diag}}\{w^{\imath }_{p1},$ $w^{\imath }_{p2},\ldots ,w^{\imath }_{pn}\}>0\ ({\imath }=1,2;p=1,2,\ldots ,m-1).$

Stimulated by [14] and [31], we consider the following Lyapunov functional

$$\begin{aligned} V(t,{\mathbf {y}}_{t})=\sum ^3_{g=1}V_{g}(t,{\mathbf {y}}_{t}), \end{aligned}$$

where

$$\begin{aligned} V_{1}(t,{\mathbf {y}}_{t})&=\gamma _t^T\mathcal {X}_1\gamma _{t} \\&\quad +{\omega }(t)\eta _{t}^T\mathcal {X}_2\eta _{t}+[{\bar{\omega }}-{\omega }(t)]\nu _t^T\mathcal {X}_3\nu _{t},\\ V_{2}(t,{\mathbf {y}}_{t})&=\int _{t-{{\bar{\omega }}}}^t(s-t+\bar{\omega }) (*)^T(Q_7+\bar{\omega }Q_8) {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\\&\qquad +\, {{\bar{\omega }}}\int _{t-{{\bar{\omega }}}}^t(s-t+\bar{\omega }) (*)^T{\mathcal {Q}}\chi (t,s){\mathrm{d}}s\\&\qquad +\, \frac{1}{2}\int _{t-{\bar{\omega }}}^{t}(s-t+\bar{\omega })^2 (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\\&\qquad +\, \frac{1}{3}\int _{t-{\bar{\omega }}}^{t}(u-t+\bar{\omega })^3 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s,\\ V_{3}(t,{\mathbf {y}}_{t})&=\int _{t-{{\omega }(t)}}^{t}[u_1(s)+w_1(s)]{\mathrm{d}}s\\&\qquad +\, \int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}}[u_2(s)+w_2(s)]{\mathrm{d}}s\\&=\int _{t-{{\omega }(t)}}^{t}\delta _s^T\mathcal {U}_1\delta _s{\mathrm{d}}s+\int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}}\delta _s^T\mathcal {U}_2\delta _s{\mathrm{d}}s, \end{aligned}$$

with

$$\begin{aligned} \gamma _t&={\mathrm{col}}\left\{ {\mathbf {J}}{\mathbf {y}}_{t}, \int _{t-{{\bar{\omega }}}}^{t}{\mathbf {J}}{\mathbf {y}}_s{\mathrm{d}}s,\right. \\&\quad \left. \int _{t-{{\bar{\omega }}}}^{t}(2s-2t+{\bar{\omega }}){\mathbf {J}}{\mathbf {y}}_s{\mathrm{d}}s\right\} ,\\ \eta _t&={\mathrm{col}}\{{\mathbf {J}}{\mathbf {y}}_{t},{\mathbf {J}}{\mathbf {y}}_{\omega },\tau _1\},\\ \nu _t&={\mathrm{col}}\left\{ {\mathbf {J}}{\mathbf {y}}_{\omega },{\mathbf {J}}{\mathbf {y}}_{{\bar{\omega }}},\tau _2\right\} ,\\ \chi (t,s)&= {\mathrm{col}}\left\{ {\mathbf {J}}\dot{{\mathbf {y}}}_s,{\mathbf {J}}{\mathbf {y}}_{s}, \int _{s}^{t}{\mathbf {J}}\dot{{\mathbf {y}}}_v{\mathrm{d}}v\right\} ,\\ \delta _s&= {\mathrm{col}}\{{\mathbf {J}}{\mathbf {y}}_s,{\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_{s})\}. \end{aligned}$$

It follows from the assumptions and inequalities (10)–(11) that $V(t,\omega _{t})\ge 0$ for any $t\ge 0$ with $0\le {\omega }(t)\le {\bar{\omega }}.$

The time derivative of $V(t,{\mathbf {y}}_{t})$ along the system (7) can be calculated as

$$\begin{aligned} \dot{V}(t,{\mathbf {y}}_{t})=\sum ^3_{g=1}\dot{V}_{g}(t,{\mathbf {y}}_{t}), \end{aligned}$$

(12)

where

$$\begin{aligned} \dot{V}_{1}(t,{\mathbf {y}}_{t})&=\xi ^T_t\Big ({\mathrm{sym}}\left\{ \varDelta _1(\omega (t))\mathcal {X}_1\varDelta _2(\omega (t))^T\right\} \nonumber \\&\quad +\, {\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _2^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _4^T\right\} \nonumber \\&\quad +\, \omega (t){\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _5^T-\varUpsilon _3\mathcal {X}_3\varUpsilon _6^T\right\} \nonumber \\&\quad +\, \omega (t)\dot{\omega }(t){\mathrm{sym}}\left\{ -\varUpsilon _1\mathcal {X}_2\varUpsilon _9^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _{10}^T\right\} \nonumber \\&\quad +\, \dot{\omega }(t)\big [{\mathrm{sym}}\left\{ \varUpsilon _1\mathcal {X}_2\varUpsilon _7^T+\varUpsilon _3\mathcal {X}_3\varUpsilon _8^T\right\} \nonumber \\&\quad +\, \varUpsilon _1\mathcal {X}_2\varUpsilon _1^T-\varUpsilon _3\mathcal {X}_3\varUpsilon _3^T\big ]\Big )\xi _t, \end{aligned}$$

(13)

$$\begin{aligned} \dot{V}_{2}(t,{\mathbf {y}}_{t})&=\xi ^T_t\left( {\bar{\omega }}^2\varUpsilon _{11}{\mathcal {Q}}\varUpsilon _{11}^T+\varPi _1\right) \xi _t\nonumber \\&\quad -\, \int _{t-{{\bar{\omega }}}}^t(*)^T(Q_7+\bar{\omega }Q_8) {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad -\, \int _{t-{\bar{\omega }}}^{t}(s-t+\bar{\omega }) (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad -\, \int _{t-{\bar{\omega }}}^{t}(s-t+\bar{\omega })^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad -\, {{\bar{\omega }}}\int _{t-{{\bar{\omega }}}}^t(*)^T{\mathcal {Q}}\chi (t,s){\mathrm{d}}s, \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_{3}(t,{\mathbf {y}}_{t})&=\xi ^T_t\left\{ \varUpsilon _{12}\mathcal {U}_1\varUpsilon _{12}^T-\varUpsilon _{13}\mathcal {U}_2\varUpsilon _{13}^T\right. \nonumber \\&\quad \left. -\, [1-\dot{{\omega }}(t)]\varUpsilon _{14}(\mathcal {U}_1-\mathcal {U}_2)\varUpsilon _{14}^T\right\} \xi _t. \end{aligned}$$

(15)

Based on the fact that $\int _{a}^{b}\dot{f}(s){\mathrm{d}}s = f (b)-f (a) ,$ the equality

$$\begin{aligned} \int _{a}^{b}\frac{\mathrm{d}}{{\mathrm{d}}s}\left[ \rho (s)^TG\rho (s) \right] {\mathrm{d}}s=\rho (b)^TG\rho (b)-\rho (a)^TG\rho (a), \end{aligned}$$

holds for any symmetric matrix G, where $\rho (s)$ is a vector function (see [23]). Thus, the following equality is also true

$$\begin{aligned}&0=\xi ^T_t\left( \varUpsilon _{15}G_1\varUpsilon _{15}^T-\varUpsilon _{16}G_1\varUpsilon _{16}^T\right) \xi _t\nonumber \\&\qquad -\, \int _{t-{{\omega }(t)}}^{t}\frac{\mathrm{d}}{{\mathrm{d}}s}\left[ (*)G_1\psi (t,s)^T\right] {\mathrm{d}}s\nonumber \\&\quad =\xi ^T_t\left( \varUpsilon _{15}G_1\varUpsilon _{15}^T-\varUpsilon _{16}G_1\varUpsilon _{16}^T\right) \xi _t\nonumber \\&\qquad -\, \int _{t-{{\omega }(t)}}^{t} (*)\mathcal {G}_1\chi (t,s)^T{\mathrm{d}}s, \end{aligned}$$

(16)

$$\begin{aligned}&0=\xi ^T_t\left( \varUpsilon _{16}G_2\varUpsilon _{16}^T-\varUpsilon _{17}G_2\varUpsilon _{17}^T\right) \xi _t\nonumber \\&\qquad -\, \int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}}\frac{\mathrm{d}}{{\mathrm{d}}s}\left[ (*)G_2\psi (t,s)^T\right] {\mathrm{d}}s\nonumber \\&\quad =\xi ^T_t\left( \varUpsilon _{16}G_2\varUpsilon _{16}^T-\varUpsilon _{17}G_2\varUpsilon _{17}^T\right) \xi _t\nonumber \\&\qquad -\, \int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}} (*)\mathcal {G}_2\chi (t,s)^T{\mathrm{d}}s, \end{aligned}$$

(17)

where

$$\begin{aligned} \psi (t,s)&={\mathrm{col}}\left\{ {\mathbf {J}}{\mathbf {y}}_{s}, \int _{s}^{t}{\mathbf {J}}\dot{{\mathbf {y}}}_v{\mathrm{d}}v\right\} ,\\ \mathcal {G}_\imath&=\Bigg [\begin{array}{lll}0&{}\quad G_\imath &{}\quad -G_\imath \\ *&{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad 0\end{array}\Bigg ],\imath =1,2. \end{aligned}$$

For $0<{\omega }(t)<{\bar{\omega }},$ applying Wirtinger-based integral inequality (see [30]) to ${\mathcal {Q}}-$ and $\mathcal {G}_1-$ dependent integral terms gives

$$\begin{aligned}&-\int _{t-{{\omega }(t)}}^{t} (*)({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_1)\chi (t,s)^T{\mathrm{d}}s \nonumber \\&\quad \le -\, \frac{1}{{\omega }(t)}(*)^T({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_1){\mathrm{col}}\big \{{\mathbf {J}}{\mathbf {y}}_{t}-{\mathbf {J}}{\mathbf {y}}_\omega ,{\omega }(t)\tau _1,\nonumber \\&\qquad {\omega }(t)({\mathbf {J}}{\mathbf {y}}_{t}-\tau _1)\big \}-\frac{3}{{\omega }(t)}(*)^T({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_1){\mathrm{col}}\big \{2\tau _1\nonumber \\&\qquad -\, {\mathbf {J}}{\mathbf {y}}_{t}-{\mathbf {J}}{\mathbf {y}}_\omega ,{\omega }(t)(\tau _1-\tau _3),\ {\omega }(t)(\tau _3-\tau _1)\big \}\nonumber \\&\quad = \xi _t^T\Big \{ -\frac{{\bar{\omega }}}{{\omega }(t)}\varUpsilon _{18}{\mathcal {Q}}_1\varUpsilon _{18}^T+\varPi _2\nonumber \\&\qquad -\, {\bar{\omega }}{\omega }(t)\big ( \varUpsilon _{19}{\mathcal {Q}}_4\varUpsilon _{19}^T+\varPi _3\big ) \Big \}\xi _t. \end{aligned}$$

(18)

Similarly, for $0<{\omega }(t)<{\bar{\omega }},$ we get

$$\begin{aligned}&-\int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}} (*)({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_2)\chi (t,s)^T{\mathrm{d}}s \nonumber \\&\quad \le -\, \frac{1}{{{\bar{\omega }}}-{\omega }(t)}(*)^T({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_2){\mathrm{col}}\big \{{\mathbf {J}}{\mathbf {y}}_\omega -{\mathbf {J}}{\mathbf {y}}_{{\bar{\omega }}},\ \nonumber \\&\qquad [{{\bar{\omega }}}-{\omega }(t)]\tau _2, [{{\bar{\omega }}}-{\omega }(t)]({\mathbf {J}}{\mathbf {y}}_{t}-\tau _2)\big \}\nonumber \\&\quad -\, \frac{3}{{{\bar{\omega }}}-{\omega }(t)}(*)^T({{\bar{\omega }}}{\mathcal {Q}}+\mathcal {G}_2){\mathrm{col}}\big \{2\tau _2-{\mathbf {J}}{\mathbf {y}}_{\omega } -{\mathbf {J}}{\mathbf {y}}_{{\bar{\omega }}},\nonumber \\&\qquad [{{\bar{\omega }}}-{\omega }(t)](\tau _2-\tau _4), [{{\bar{\omega }}}-{\omega }(t)](\tau _4-\tau _2)\big \}=\nonumber \\&\qquad xi_t^T\Big \{ -\frac{{\bar{\omega }}}{{\bar{\omega }}-{\omega }(t)}\varUpsilon _{20}{\mathcal {Q}}_1\varUpsilon _{20}^T+\varPi _4\nonumber \\&\quad -\, {\bar{\omega }}[{{\bar{\omega }}}-{\omega }(t)]\big ( \varUpsilon _{21}{\mathcal {Q}}_4\varUpsilon _{21}^T+\varPi _5\big ) \Big \}\xi _t. \end{aligned}$$

(19)

Utilizing Lemma 4 and the Leibniz-Newton formula to $Q_7-$ dependent integral term gives

$$\begin{aligned}&-\int _{t-{{\omega }(t)}}^{t}(*)^TQ_7{\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le \xi _t^T\varUpsilon ^T_{18}\bigg \{\mathcal {Y}_1+\mathcal {Y}_1^T+{\omega }(t)\nonumber \\&\qquad \times \, \sum _{l=1}^{4}\frac{1}{2l-1}Y_lQ_7^{-1}Y^T_l\bigg \}\varUpsilon _{18}\xi _t, \end{aligned}$$

(20)

$$\begin{aligned}&-\int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}}(*)^TQ_7{\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le \xi _t^T\varUpsilon ^T_{20}\bigg \{\mathcal {Y}_2+\mathcal {Y}_2^T+[{\bar{\omega }}-{\omega }(t)]\nonumber \\&\qquad \times \, \sum _{l=5}^{8}\frac{1}{2l-9}Y_{l}Q_7^{-1}Y^T_{l}\bigg \}\varUpsilon _{20}\xi _t, \end{aligned}$$

(21)

For $0<{\omega }(t)<{\bar{\omega }},$ utilizing Lemma 3 to $Q_8-$ dependent integral term derives

$$\begin{aligned}&-{\bar{\omega }}\int _{t-{{\omega }(t)}}^{t}(*)^TQ_8{\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le -\frac{{\bar{\omega }}}{{\omega }(t)}\xi _t^T\varUpsilon ^T_{18}{\mathcal {Q}}_8\varUpsilon _{18}\xi _t, \end{aligned}$$

(22)

$$\begin{aligned}&\qquad -\, {\bar{\omega }}\int _{t-{{\bar{\omega }}}}^{t-{{\omega }(t)}}(*)^TQ_8{\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le -\frac{{\bar{\omega }}}{{\bar{\omega }}-{\omega }(t)}\xi _t^T\varUpsilon ^T_{20}{\mathcal {Q}}_8\varUpsilon _{20}\xi _t. \end{aligned}$$

(23)

It is easy to verify the following equations

$$\begin{aligned}&\int _{t-{\omega }(t)}^{t}(s-t+\bar{\omega }) (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad =\int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)] (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\qquad +\, [\bar{\omega }-{\omega }(t)]\int _{t-{\omega }(t)}^{t} (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\qquad +\, \int ^{t-{\omega }(t)}_{t-{\bar{\omega }}}(s-t+\bar{\omega }) (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s, \end{aligned}$$

(24)

$$\begin{aligned}&\int _{t-{\bar{\omega }}}^{t}(u-t+\bar{\omega })^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad =2[\bar{\omega }-{\omega }(t)]\nonumber \\&\qquad \times \, \int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)] (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\qquad +\, \int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)]^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\qquad +\, \int ^{t-{\omega }(t)}_{t-{\bar{\omega }}}(s-t+\bar{\omega })^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\qquad +\, [\bar{\omega }-{\omega }(t)]^2\int _{t-{\omega }(t)}^{t} (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s. \end{aligned}$$

(25)

For $0<{\omega }(t)<{\bar{\omega }},$ applying Lemma 3 to $Q_9-$ and $Q_{10}-$ dependent integral terms gives

$$\begin{aligned} -&\int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)] (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le \xi _t^T\varPi _6\xi _t, \end{aligned}$$

(26)

$$\begin{aligned}&\qquad -\, [\bar{\omega }-{\omega }(t)]\int _{t-{\omega }(t)}^{t} (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le -\frac{\bar{\omega }-{\omega }(t)}{{\omega }(t)}\xi ^T_t\varUpsilon _{18}{\mathcal {Q}}_9\varUpsilon _{18}^T\xi _t, \end{aligned}$$

(27)

$$\begin{aligned}&\qquad -\, \int ^{t-{\omega }(t)}_{t-{\bar{\omega }}}(s-t+\bar{\omega }) (*)^T Q_9 {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le \xi _t ^T\varPi _7\xi _t, \end{aligned}$$

(28)

$$\begin{aligned}&\qquad -\, \int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)]^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le {\omega }(t) \xi _t ^T\varPi _8\xi _t, \end{aligned}$$

(29)

$$\begin{aligned}&\qquad -\, 2[\bar{\omega }-{\omega }(t)]\int _{t-{\omega }(t)}^{t}[s-t+{\omega }(t)] (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le [\bar{\omega }-{\omega }(t)] \xi _t ^T\varPi _9\xi _t, \end{aligned}$$

(30)

$$\begin{aligned}&\qquad -\, [\bar{\omega }-{\omega }(t)]^2\int _{t-{\omega }(t)}^{t} (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le \left\{ [\bar{\omega }-{\omega }(t)]-\bar{\omega }\frac{\bar{\omega }-{\omega }(t)}{{\omega }(t)} \right\} \nonumber \\&\qquad \times \, \xi ^T_t\varUpsilon _{18}{\mathcal {Q}}_{10}\varUpsilon _{18}^T\xi _t, \end{aligned}$$

(31)

$$\begin{aligned}&\qquad -\, \int ^{t-{\omega }(t)}_{t-{\bar{\omega }}}(s-t+\bar{\omega })^2 (*)^T Q_{10} {\mathbf {J}}\dot{{\mathbf {y}}}_s{\mathrm{d}}s\nonumber \\&\quad \le [\bar{\omega }-{\omega }(t)] \xi _t ^T\varPi _{10}\xi _t. \end{aligned}$$

(32)

Denote $\epsilon =\frac{\omega (t)}{{{\bar{\omega }}}},$ for $0<{\omega }(t)<{\bar{\omega }},$ the following inequality holds based on condition (8) ( [25])

$$\begin{aligned} 0\le \xi _t^T&\bigg [\begin{array}{c}\sqrt{{\epsilon }/({1-\epsilon })}\varUpsilon _{18}^T \\ -\sqrt{(1-\epsilon )/{\epsilon }}\varUpsilon _{20}^T \end{array}\bigg ]^T\\&\times \bigg [\begin{array}{cc}{\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}+{\mathcal {Q}}_{9}+\bar{\omega }{\mathcal {Q}}_{10} &{} {\mathcal {Q}}_{2}\\ *&{} {\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}\end{array}\bigg ](*). \end{aligned}$$

Therefore, for $0<{\omega }(t)<{\bar{\omega }},$ we get

$$\begin{aligned}&\xi _t^T(*)^T\bigg [\begin{array}{cc}{\mathcal {Q}}_{1}+{\mathcal {Q}}_{8} &{} {\mathcal {Q}}_{2}\\ *&{} {\mathcal {Q}}_{1}+{\mathcal {Q}}_{8}\end{array}\bigg ]\bigg [\begin{array}{c}\varUpsilon _{18}^T \\ \varUpsilon _{20}^T\end{array}\bigg ]\xi _t\le \nonumber \\&\quad \xi _t^T\left\{ \frac{1}{\epsilon }\varUpsilon _{18}\left[ ({\mathcal {Q}}_{1}+{\mathcal {Q}}_{8})+(1-\epsilon )({\mathcal {Q}}_{9}+\bar{\omega }{\mathcal {Q}}_{10}) \right] \varUpsilon _{18}^T \right. \nonumber \\&\qquad \left. +\, \frac{1}{1-\epsilon }\varUpsilon _{20}({\mathcal {Q}}_{1}+{\mathcal {Q}}_{8})\varUpsilon _{20}^T \right\} \xi _t. \end{aligned}$$

(33)

Also from

$$\begin{aligned}&\int _{t-{{\bar{\omega }}}}^{t}(2s-2t+{\bar{\omega }}){\mathbf {J}}{\mathbf {y}}_s{\mathrm{d}}s\\&\quad = \int _{t-{\omega (t)}}^{t}\big \{2[s-t+\omega (t)]+2[{\bar{\omega }}-\omega (t)]-{\bar{\omega }}\big \}{\mathbf {J}}{\mathbf {y}}_s{\mathrm{d}}s\\&\qquad +\, \int _{t-{{\bar{\omega }}}}^{t-\omega (t)}[2(s-t+{\bar{\omega }})-{\bar{\omega }}]{\mathbf {J}}{\mathbf {y}}_s{\mathrm{d}}s\\&\quad = \omega (t)[{\bar{\omega }}-2\omega (t)]\tau _1\\&\qquad -\, {\bar{\omega }}[{\bar{\omega }}-\omega (t)]\tau _2+\omega ^2(t)\tau _3+[{\bar{\omega }}-\omega (t)]^2\tau _4, \end{aligned}$$

for any matrix M with proper dimension we get

$$\begin{aligned} 0&=2\xi ^T_t\varDelta _3(\omega (t))Me_{16}^T\xi _t. \end{aligned}$$

(34)

Similar to (10)–(11), we propose

$$\begin{aligned} f_g(s,t)&:=\delta ^T(s)\bigg [\begin{array}{cc}-{F}_{g}(t){\mathbf {K}}_1 &{}F_g(t){\mathbf {K}}_2\\ *&{} -{F}_{g}(t)\end{array}\bigg ]\delta (s)\ge 0,\\ r_g(s,t)&:=\delta ^T(s)\bigg [\begin{array}{ll}{R}_g(t){\mathbf {K}} &{}\quad 0\\ 0 &{}\quad -{R}_g(t)\end{array}\bigg ]\delta (s)\ge 0, \end{aligned}$$

with ${F}_g(t)=\omega (t)F_{1g}+[{\bar{\omega }}-\omega (t)]F_{2g},{R}_g(t)=\omega (t)R_{1g}+[{\bar{\omega }}-\omega (t)]R_{2g},g=1,2,3.$

Thus the following inequalities are acquired

$$\begin{aligned} 0&\le f_1(t,t)+f_2(t-\omega (t),t)+f_3(t-{\bar{\omega }},t)\nonumber \\&\quad +\, r_1(t,t)+r_2(t-\omega (t),t)+r_3(t-{\bar{\omega }},t)\nonumber \\ &=\xi ^T_t\Big \{\omega (t)\big ( \varUpsilon _{12}{\mathcal {F}}_{11}\varUpsilon _{12}^T+\varUpsilon _{14}{\mathcal {F}}_{12}\varUpsilon _{14}^T\nonumber \\&\quad +\, \varUpsilon _{13}{\mathcal {F}}_{13}\varUpsilon _{13}^T\big )+[{\bar{\omega }}-\omega (t)]\big ( \varUpsilon _{12}{\mathcal {F}}_{21}\varUpsilon _{12}^T\nonumber \\&\quad +\, \varUpsilon _{14}{\mathcal {F}}_{22}\varUpsilon _{14}^T+\varUpsilon _{13}{\mathcal {F}}_{23}\varUpsilon _{13}^T\big )\Big \}\xi _t. \end{aligned}$$

(35)

Noticing networks (5), the following zero equality holds for any positive matrix H

$$\begin{aligned} 0&= 2\dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T{\mathbf {H}}{\mathbf {J}} \big \{-{\mathbf {A}}{\mathbf {y}}_t+{\widetilde{\mathbf {B}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}_t)+{\widetilde{\mathbf {C}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}_\omega ) \nonumber \\&\quad +\, {\mathbf {D}}_1{\mathbf {y}}_t+{\mathbf {D}}_2{\mathbf {y}}_\omega +{\mathbf {v}}(t)+{\mathbf {e}}-\dot{{\mathbf {y}}}_t\big \}. \end{aligned}$$

(36)

By Lemmas 1 and 2, we have: ${\mathbf {J}}{\mathbf {A}}={\mathbf {A}}'{\mathbf {J}}=J\otimes A,\ {\mathbf {J}}{\mathbf {v}}(t)=0.$

As $D_1,D_2\in {\mathcal {T}}({\mathbb {R}},0),$ applying Lemma 2 yields that $JD_{\imath }=(J{D_\imath }P)J,\imath =1,2.$ On the basis of Lemmas 1 and 2, the following equalities are correct: ${\mathbf {J}}{\mathbf {D}}_\imath =(J\otimes I_n)({D}_\imath \otimes {\varLambda _\imath })=(J{D_\imath })\otimes {\varLambda _\imath }=[(J{D_\imath }P)J]\otimes ({\varLambda _\imath }I_n)=[(J{D_\imath }P)\otimes {\varLambda _\imath }](J\otimes I_n)={{\mathbf {D}}'_\imath }{\mathbf {J}}.$

Note that

$$\begin{aligned}&\dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T{\mathbf {H}}{\mathbf {J}}{\widetilde{\mathbf {B}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}_t)\nonumber \\&\quad = \sum _{i=1}^{m-1}\big [\dot{y}_i(t)-\dot{y}_{i+1}(t)\big ]^TH \big [{\widetilde{B}}(y_i(t))k(y_i(t))\nonumber \\&\qquad -\, {\widetilde{B}}(y_{i+1}(t))k(y_{i+1}(t))\big ]\nonumber \\&\quad = \sum _{i=1}^{m-1}\big [\dot{y}_i(t)-\dot{y}_{i+1}(t)\big ]^TH \Big \{\bar{B}[k(y_i(t))-k(y_{i+1}(t))]\nonumber \\&\qquad +\, \big [{B}(y_i(t))-\bar{B}\big ]k(y_i(t)) +\big [\bar{B}-{B}(y_{i+1}(t))\big ]\nonumber \\&\qquad \times \, k(y_{i+1}(t))+E[N_{1i}(t)L_1k(y_i(t)) \nonumber \\&\qquad -\, N_{1,i+1}(t)L_1k(y_{i+1}(t))]\Big \}, \end{aligned}$$

(37)

and

$$\begin{aligned}&\sum _{i=1}^{m-1}\big [\dot{y}_i(t)-\dot{y}_{i+1}(t)\big ]^TH\bar{B}[k(y_i(t))-k(y_{i+1}(t))]\nonumber \\&\quad =\dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T\left( I_{m-1}\otimes H{\bar{B}}\right) {\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_t), \end{aligned}$$

(38)

$$\begin{aligned}&\sum _{i=1}^{m-1}\big [\dot{y}_i(t)-\dot{y}_{i+1}(t)\big ]^TH \big \{\big [{B}(y_i(t))-\bar{B}\big ]\nonumber \\&\qquad \times \, k(y_i(t)) +\big [\bar{B}-{B}(y_{i+1}(t))\big ]k(y_{i+1}(t))\big \}\nonumber \\&\quad =\sum _{i=1}^{m-1}\sum _{j=1}^{n}\big [\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)\big ]h_j\nonumber \\&\qquad \times \, \sum _{l=1}^{n}\Big \{\big [b_{jl}(y_i(t)) -\bar{b}_{jl}\big ] k_l(y_{il}(t))\nonumber \\&\qquad +\, \big [\bar{b}_{jl}-b_{jl}(y_{i+1}(t))\big ]k_l(y_{i+1,l}(t))\Big \}\nonumber \\&\quad \le \sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\sum _{l=1}^{n}2{\bar{k}}_l{\hat{b}}_{jl}|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|\nonumber \\&\quad =\sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\varrho _j|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|, \end{aligned}$$

(39)

$$\begin{aligned}&\sum _{i=1}^{m-1}\big [\dot{y}_i(t)-\dot{y}_{i+1}(t)\big ]^TH\nonumber \\&\qquad \times \, E[N_{1i}(t)L_1k(y_i(t))-N_{1,i+1}(t)L_1k(y_{i+1}(t))]\nonumber \\&\quad \le 2\sum _{i=1}^{m-1}{\bar{k}}||E||_1||L_1||_1||H[\dot{y}_i(t)-\dot{y}_{i+1}(t)]||_1\nonumber \\&\quad = 2\sum _{i=1}^{m-1}{\bar{k}}||E||_1||L_1||_1\nonumber \\&\qquad \times \, \sum _{j=1}^{n}h_j|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|. \end{aligned}$$

(40)

Similarly we obtain

$$\begin{aligned}&\dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T{\mathbf {H}}{\mathbf {J}}{\widetilde{\mathbf {C}}}({\mathbf {y}}){\mathbf {k}}({\mathbf {y}}_\omega )\nonumber \\&\quad \le \dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T\left( I_{m-1}\otimes H{{\bar{C}}}\right) {\mathbf {J}}{\mathbf {k}}({\mathbf {y}}_\omega )+\sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\nonumber \\&\qquad \times \, (\vartheta _j+ 2{\bar{k}}||E||_1||L_2||_1)|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|. \end{aligned}$$

(41)

In addition

$$\begin{aligned}&\dot{{\mathbf {y}}}_t^T{\mathbf {J}}^T{\mathbf {H}}{\mathbf {J}}{\mathbf {e}} \nonumber \\&\quad = \sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\theta _j\big [\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)\big ]\sum _{l=1}^{n}\Big \{\varsigma _{il}{\mathrm{sign}}\nonumber \\&\qquad \big [\dot{y}_{lj}(t)-\dot{y}_{ij}(t)\big ] -\varsigma _{i+1,l}{\mathrm{sign}}\big [\dot{y}_{lj}(t)-\dot{y}_{i+1,j}(t)\big ]\Big \}\nonumber \\&\quad = \sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\theta _j\bigg \{-(\varsigma _{i,i+1}+\varsigma _{i+1,i})|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|\nonumber \\&\qquad +\big [\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)\big ]\bigg (\sum _{l=1,l\ne i+1}^{n}\varsigma _{il}{\mathrm{sign}}\big [\dot{y}_{lj}(t)\nonumber \\&\qquad -\dot{y}_{ij}(t)\big ]-\sum _{l=1,l\ne i}^{n}\varsigma _{i+1,l}{\mathrm{sign}}\big [\dot{y}_{lj}(t)-\dot{y}_{i+1,j}(t)\big ]\bigg )\bigg \}\nonumber \\&\quad \le -\sum _{i=1}^{m-1}\sum _{j=1}^{n}h_j\theta _j\mu _{i}|\dot{y}_{ij}(t)-\dot{y}_{i+1,j}(t)|. \end{aligned}$$

(42)

Applying inequalities (9) and (37)-(42) to equality (36) yields

$$\begin{aligned} 0\le&\xi _t^T\varPi _{11}\xi _t. \end{aligned}$$

(43)

Combining (12)–(35) and (43) gives

$$\begin{aligned} \dot{V}(t,{\mathbf {y}}_{t})\le \xi _t^T \big \{{\varXi }(\omega (t),\dot{\omega }(t)) +\varGamma (\omega (t))\big \}\xi _t, \end{aligned}$$

(44)

where $\varGamma (r)=({{\bar{\omega }}}-r)\varGamma _1+r\varGamma _2$ with

$$\begin{aligned} \varGamma _2&=\varGamma _4=\varUpsilon ^T_{18}\sum _{l=1}^{4}\frac{1}{2l-1}Y_lQ_7^{-1}Y^T_l\varUpsilon _{18},\\ \varGamma _1&=\varGamma _3=\varUpsilon ^T_{20}\sum _{l=5}^{8}\frac{1}{2l-9}Y_{l}Q_7^{-1}Y^T_{l}\varUpsilon _{20}. \end{aligned}$$

From Lemma 3, it is easy to verify that inequality (44) still holds for ${\omega }(t)=0$ or ${\omega }(t)={\bar{\omega }}.$

As ${\varXi }(\omega (t),\dot{\omega }(t))+\varGamma (\omega (t))$ is linear in $\dot{\omega }(t),$ condition ${\varXi }(\omega (t),\dot{\omega }(t))+\varGamma (\omega (t))<0$ is equal to two boundary ones ${\varXi }(\omega (t),\omega _\imath )+\varGamma (\omega (t))<0\ (\imath =1,2),$ one for $\dot{\omega }(t)=\omega _1,$ and the other for $\dot{\omega }(t)=\omega _2.$ Obviously, for fixed $\imath =1,2,$ ${\varXi }(\omega (t),\omega _\imath )+\varGamma (\omega (t))$ is a quadratic matrix function of $\omega (t),$ based on Lemma 5, condition ${\varXi }(\omega (t),\omega _\imath )+\varGamma (\omega (t))<0$ can be assured by any one of the two groups of conditions: one is $\varXi _{\rho \imath }+\varGamma _\rho <0$ with $\rho =1,2,3,$ and the other one with $\rho =1,2,4.$

From Schur complement Lemma, for allocated $\imath =1,2,$ $\varXi _{\rho \imath }+\varGamma _\rho <0$ is equal to inequality ${\widetilde{\varXi }}_{\rho \imath }<0,\ \rho =1,2,3,4.$ Thus, the criteria of Theorem 1 mean $\dot{V}(t,{\mathbf {y}}_{t})<0$ for all $t\ge 0.$ Therefore system (7) is globally robustly synchronized. This finishes the proof of Theorem 1.