1 Introduction

In the coupled systems, synchronization is an important collective dynamical behavior [1]. In recent years, the synchronization problem of coupled neural networks has attracted great attention due to its vast application prospects in secure communications [2], pattern recognition [3], associative memory [4] and optimization [5]. Up to now, many results about the synchronization of coupled neural networks have been obtained [6,7,8,9,10,11,12]. Especially, the pinning synchronization of coupled neural networks was investigated in [11] via impulsive control, and the authors of [12] studied the finite-time synchronization of switched coupled neural networks.

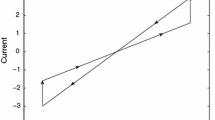
As we know, resistor, capacitor and inductor are three basic circuit elements, which reflect the relations between four fundamental electrical quantities: voltage, current, charge and flux. Specifically, resistor reflects the relationship between voltage and current, capacitor reflects the relationship between charge and voltage, and inductor reflects the relationship between flux and current. In 1971, the concept of memristor was proposed by Chua [13] as the fourth basic circuit element. Memristor has attracted considerable attention since it was prototyped in 2008 [14]. Memristor, which is the abbreviation of memory resistor, reflects the relationship between flux and charge (see Fig. 1). The memristance of memristor varies with the quantity of the passed charge [15], so memristor has the function of memory. In the circuit implementation of neural network, synapses are usually simulated by resistors. However, we know that the synapses play an important part in the formation of memory, but the common resistors don’t have the function of memory. If the resistors used in the circuit implementation of neural network are replaced by memristors, the usual artificial neural network becomes a memristor-based neural network, which is the suitable candidate for simulating the human brain [16]. So far, considerable achievements have been made in the field of memristive neurodynamics, such as stability and synchronization [17,18,19,20,21,22].

Fig. 1
figure 1

The relations among resistor (R), capacitor (C), inductor (L), memristor (M), voltage (v), current (i), charge (q) and flux (\(\varphi \)): \(dv=Rdi\), \(dq = Cdv\), \(d\varphi = Ldi\) and \(d\varphi = Mdq\)

Full size image

Recently, the research on synchronization problem has been extended to CMNNs [23,24,25]. In [23], some sufficient conditions that can guarantee the exponential synchronization of CMNNs with delays and nonlinear coupling were derived. [24, 25] investigated the synchronization problem of CMNNs with delays. Additionally, stochastic effects inevitably exist in nervous systems and the signal transmission between synapses is a noisy process in fact. When there exist stochastic perturbations in networks, it is more difficult to achieve the synchronization of networks. So it is necessary to study the networks with stochastic perturbations [26,27,28]. As far as we know, there have been some results on the drive-response synchronization of memristor-based neural networks with stochastic perturbations [29, 30]. What’s more, the synchronization of CMNNs with delays and stochastic perturbations has also been investigated in [31, 32]. In [31], the global synchronization of CMNNs with delays and stochastic perturbations was studied via pinning impulsive control. In [32], the pth moment exponential synchronization of CMNNs with mixed delays and stochastic perturbations was investigated via the delayed impulsive controllers. However, it should be pointed out that both the controllers used in [31] and [32] were very complex and difficult to be manipulated.

Motivated by the above analysis, in this paper, the feedback control is firstly used to study the synchronization of CMNNs with mixed delays and stochastic perturbations. By designing simple feedback controllers and utilizing a lemma given in [33], some novel sufficient conditions ensuring the exponential synchronization of CMNNs with mixed delays and stochastic perturbations in mean square are derived. Adaptive control can be used even when there is no perfect knowledge of the coupled systems, and the adaptive control can reduce the control gains effectively. By designing suitable adaptive feedback controllers and utilizing stochastic LaSalle invariance principle, the asymptotic synchronization of CMNNs with mixed delays and stochastic perturbations in mean square can be achieved. We believe that the methods used in this paper can also be applied to analyze the synchronization control of other stochastic systems and coupled systems.

The rest of this paper is organized as follows. In Sect. 2, some necessary preliminaries are introduced. We derive the main results of the paper in Sect. 3. In Sect. 4, numerical simulations are presented to verify the effectiveness of the theoretical results. Conclusions are given in Sect. 5.

2 Preliminaries

A memristor-based neural network with mixed delays can be described as follows:

$$\begin{aligned} \begin{aligned} \frac{dz(t)}{dt}&=-D(z(t))z(t)+A(z(t))f(z(t))+B(z(t))f(z(t-\tau _{1}(t)))+J\\&\quad +\,C(z(t))\int _{-\infty }^{t}K(t-s)f(z(s))ds, \end{aligned} \end{aligned}$$
(1)

where \(z(t)=(z_{1}(t),z_{2}(t),\ldots ,z_{n}(t))^{T}\) is the state vector; \(D(z(t))=diag\left( d_{1}(z_{1}(t)),\right. \left. d_{2}(z_{2}(t)),\ldots , d_{n}(z_{n}(t))\right) \), where \(d_{i}(\cdot )\,{>}\,0, i=1,2,\ldots ,n,\) denote the neuron self-inhibitions; \(A(z(t))=(a_{rj}(z_{r}(t)))_{n\times n}\), \(B(z(t))=(b_{rj}(z_{r}(t)))_{n\times n}\) and \(C(z(t))=(c_{rj}(z_{r}(t)))_{n\times n}\) are the memristive connection weight matrices; \(f(z(\cdot ))=\left( f_{1}(z_{1}(\cdot )),\right. \left. f_{2}(z_{2}(\cdot )),\ldots ,f_{n}(z_{n}(\cdot ))\right) ^{T}\), where \(f_{i}(\cdot ), i=1,2,\ldots ,n\), are the activation functions; \(J=(J_{1},J_{2},\ldots ,J_{n})^{T}\), where \(J_{i}, i=1,2,\ldots ,n\), are external inputs; \(\tau _{1}(t)\) is the time-varying discrete delay; \(K\,{:}[0,+\infty )\rightarrow [0,+\infty )\) is the delay kernel of the unbounded distributed delay; \(d_{r}(z_{r}(t))\), \(a_{rj}(z_{r}(t))\), \(b_{rj}(z_{r}(t))\) and \(c_{rj}(z_{r}(t))\) are defined as

$$\begin{aligned} \begin{aligned}&d_{r}(z_{r}(t))=\left\{ \begin{aligned} d_{r}^{*},&\quad \left| z_{r}(t)\right| \le T_{r}, \\ d_{r}^{**},&\quad \left| z_{r}(t)\right|> T_{r}, \end{aligned} \right. \quad a_{rj}(z_{r}(t))=\left\{ \begin{aligned} a_{rj}^{*},&\quad \left| z_{r}(t)\right| \le T_{r}, \\ a_{rj}^{**},&\quad \left| z_{r}(t)\right|> T_{r}, \end{aligned} \right. \\&b_{rj}(z_{r}(t))=\left\{ \begin{aligned} b_{rj}^{*},&\quad \left| z_{r}(t)\right| \le T_{r}, \\ b_{rj}^{**},&\quad \left| z_{r}(t)\right|> T_{r}, \end{aligned} \right. \quad c_{rj}(z_{r}(t))=\left\{ \begin{aligned} c_{rj}^{*},&\quad \left| z_{r}(t)\right| \le T_{r}, \\ c_{rj}^{**},&\quad \left| z_{r}(t)\right| > T_{r}, \end{aligned} \right. \end{aligned} \end{aligned}$$
(2)

for \(r,j=1,2,\ldots ,n\), where \(T_{r}>0\), \(d_{r}^{*},d_{r}^{**}, a_{rj}^{*},a_{rj}^{**},b_{rj}^{*},b_{rj}^{**},c_{rj}^{*},c_{rj}^{**}\) are known constants. The interested readers can refer to some published works [34, 35], which gave detailed explanations about how to build memristor-based neural networks.

A memristor-based neural network with mixed delays and stochastic perturbations can be written in the following form:

$$\begin{aligned} \begin{aligned} dz(t)&=\Bigg [-D(z(t))z(t)+A(z(t))f(z(t))+B(z(t))f(z(t-\tau _{1}(t)))+J\\&\quad +\,C(z(t))\int _{-\infty }^{t}K(t-s)f(z(s))ds\Bigg ]dt+\beta (t,z(t),z(t-\tau _{2}(t)))d\omega (t), \end{aligned} \end{aligned}$$
(3)

where \(\tau _{2}(t)\) is a time-varying delay satisfying \(0\le \tau _{2}(t)\le \tau _{2}\); \(\beta :R^{+}\times R^{n}\times R^{n}\rightarrow R^{n\times n}\) represents the noise intensity function matrix; \(\omega (t)=(\omega _{1}(t),\omega _{2}(t),\ldots ,\omega _{n}(t))^{T}\) is a n-dimensional Brown notion. The initial value of system (3) is \(z(s)=\varphi (s)\in C((-\infty ,0],R^{n})\), where \(C((-\infty ,0],R^{n})\) is the Banach space of all continuous functions that map \((-\infty ,0]\) into \(R^{n}\).

CMNNs with mixed delays and stochastic perturbations can be described by the following differential equations:

$$\begin{aligned} \begin{aligned} dx_{i}(t)&=\Bigg [-D(x_{i}(t))x_{i}(t)+A(x_{i}(t))f(x_{i}(t))+B(x_{i}(t))f(x_{i}(t-\tau _{1}(t)))+J\\&\quad +\,C(x_{i}(t))\int _{-\infty }^{t}K(t-s)f(x_{i}(s))ds+h_{i}(x_{1}(t),x_{2}(t),\ldots ,x_{N}(t))\Bigg ]dt\\&\quad +\beta (t,x_{i}(t),x_{i}(t-\tau _{2}(t)))d\omega (t),~ i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(4)

where \(x_{i}(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in}(t))^{T}\); \(D(x_{i}(t))=diag\left( d_{1}(x_{i1}(t)),d_{2}(x_{i2}(t)),\right. \left. ..,d_{n}(x_{in}(t))\right) \); \(A(x_{i}(t))=(a_{rj}(x_{ir}(t)))_{n\times n}\), \(B(x_{i}(t))=(b_{rj}(x_{ir}(t)))_{n\times n}\), \(C(x_{i}(t)) =(c_{rj}(x_{ir}(t)))_{n\times n}\); \(h_{i}:R^{nN}\rightarrow R^{n}\) is the coupling function, which satisfies \(h_{i}(z(t),z(t),\ldots ,z(t))=0\); \(d_{r}(x_{ir}(t))\), \(a_{rj}(x_{ir}(t))\), \(b_{rj}(x_{ir}(t))\) and \(c_{rj}(x_{ir}(t))\) are defined as

$$\begin{aligned} \begin{aligned}&d_{r}(x_{ir}(t))=\left\{ \begin{aligned} d_{r}^{*},&\quad \left| x_{ir}(t)\right| \le T_{r}, \\ d_{r}^{**},&\quad \left| x_{ir}(t)\right|> T_{r}, \end{aligned} \right. \quad a_{rj}(x_{ir}(t))=\left\{ \begin{aligned} a_{rj}^{*},&\quad \left| x_{ir}(t)\right| \le T_{r}, \\ a_{rj}^{**},&\quad \left| x_{ir}(t)\right|> T_{r}, \end{aligned} \right. \\&b_{rj}(x_{ir}(t))=\left\{ \begin{aligned} b_{rj}^{*},&\quad \left| x_{ir}(t)\right| \le T_{r}, \\ b_{rj}^{**},&\quad \left| x_{ir}(t)\right|> T_{r}, \end{aligned} \right. \quad c_{rj}(x_{ir}(t))=\left\{ \begin{aligned} c_{rj}^{*},&\quad \left| x_{ir}(t)\right| \le T_{r}, \\ c_{rj}^{**},&\quad \left| x_{ir}(t)\right| > T_{r}, \end{aligned} \right. \end{aligned} \end{aligned}$$
(5)

for \(r,j=1,2,\ldots ,n\). The initial value of CMNNs (4) is \(x_{i}(s)=\phi _{i}(s)\in C((-\infty ,0],R^{n})\).

In order to synchronize all the states of CMNNs (4) onto z(t) of system (3), suitable controllers will be needed. The controlled CMNNs are presented as

$$\begin{aligned} \begin{aligned} dx_{i}(t)&=\Bigg [-D(x_{i}(t))x_{i}(t)+A(x_{i}(t))f(x_{i}(t))+B(x_{i}(t))f(x_{i}(t-\tau _{1}(t)))+J\\&\quad +\,C(x_{i}(t))\int _{-\infty }^{t}K(t-s)f(x_{i}(s))ds+h_{i}(x_{1}(t),x_{2}(t),\ldots ,x_{N}(t))+R_{i}(t)\Bigg ]dt\\&\quad +\beta (t,x_{i}(t),x_{i}(t-\tau _{2}(t)))d\omega (t), ~i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(6)

where \(R_{i}(t),~i=1,2,\ldots ,N,\) are the controllers that will be designed.

It is noticed that systems (3) and (6) are discontinuous systems since they switch in view of states. Considering that their solutions in the conventional sense do not exist, we can discuss their solutions in the sense of Filippov. Next, we will give the definition of Filippov solution.

Consider the following differential equation:

$$\begin{aligned} \begin{aligned} \dot{x}(t)=f(x(t)),\quad ~x(0)=x_{0}, \end{aligned} \end{aligned}$$
(7)

where \(x(t)\in R^{n}\), \(f{:}\,R^{n}\rightarrow R^{n}\) is discontinuous and locally measurable.

Definition 1

[36]. The set-valued map of f(x) at \(x\in R^{n}\) is defined by

$$\begin{aligned} K[f](x)=\bigcap _{\delta >0}\bigcap _{\mu (N)=0}\overline{co}[f(B(x,\delta )\backslash N)], \end{aligned}$$

where \(\overline{co}[E]\) is the convex closure of set E, \(\mu (N)\) denotes the Lebesgue measure of set N, and \(B(x,\delta )=\{y{:}\,\Vert y-x\Vert \le \delta \}\).

Definition 2

[37]. A vector function x(t) defined on interval [0, T) is said to be a Filippov solution of system (7) if it is absolutely continuous on any compact subinterval of [0, T) and satisfies differential inclusion \(\dot{x}(t)\in K[f](x(t))\) for almost all \(t\in [0,T)\).

Throughout this paper, set \(\underline{d}_{r}=\min \{d_{r}^{*},d_{r}^{**}\}, {a}_{rj}^{+}=\max \Big \{|a_{rj}^{*}|,|a_{rj}^{**}|\}\), \({b}_{rj}^{+}=\max \{|b_{rj}^{*}|,|b_{rj}^{**}|\}\), \({c}_{rj}^{+}=\max \{|c_{rj}^{*}|,|c_{rj}^{**}|\Big \}\), for \(r,j=1,2,\ldots ,n\).

The synchronization errors are defined as \(e_{i}(t)=x_{i}(t)-z(t),i=1,2,\ldots ,N\). From (3) and (6), it follows that:

$$\begin{aligned} \begin{aligned} de_{i}(t)&=\left[ -D(x_{i}(t))x_{i}(t)+D(z(t))z(t)+F_{i}(t)+H_{i}(e_{1}(t),e_{2}(t),\ldots ,e_{N}(t))\right. \\&\quad \left. +\,R_{i}(t)\right] dt+\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))d\omega (t),\quad ~i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(8)

where \(\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))=\beta (t,x_{i}(t),x_{i}(t-\tau _{2}(t)))-\beta (t,z(t),z(t-\tau _{2}(t))),\) \(H_{i}(e_{1}(t),e_{2}(t),\ldots ,e_{N}(t))=h_{i}(x_{1}(t),x_{2}(t),\ldots ,x_{N}(t))-h_{i}(z(t),z(t),\ldots ,z(t)),\)

$$\begin{aligned} \begin{aligned} F_{i}(t)=&\,A(x_{i}(t))f(x_{i}(t))-A(z(t))f(z(t))+B(x_{i}(t))f(x_{i}(t-\tau _{1}(t)))\\&-B(z(t))f(z(t-\tau _{1}(t)))+C(x_{i}(t))\int _{-\infty }^{t}K(t-s)f(x_{i}(s))ds\\&-C(z(t))\int _{-\infty }^{t}K(t-s)f(z(s))ds. \end{aligned} \end{aligned}$$
(9)

The initial value of system (8) is \(e_{i}(s)=\phi _{i}(s)-\varphi (s)\in C((-\infty ,0],R^{n})\).

The following assumptions will be used in this paper.

\((A_{1})\) :

\(\dot{\tau }_{2}(t)\le \sigma _{2}<1\), where \(\sigma _{2}\) is a positive constant.

\((A_{2})\) :

Activation functions are bounded, that is, there exist constants \(M_{j}>0,~j=1,2,\ldots ,n\), such that \(\left| f_{j}(\cdot )\right| \le M_{j}\).

\((A_{3})\) :

There are some constants \(\gamma _{ij}\ge 0, i,j=1,2,\ldots ,N,\) such that

$$\begin{aligned} \Vert h_{i}(x_{1}(t),x_{2}(t),\ldots ,x_{N}(t))-h_{i}(z(t),z(t),\ldots ,z(t))\Vert \le \sum \limits _{j=1}^{N}\gamma _{ij}\Vert x_{j}(t)-z(t)\Vert . \end{aligned}$$
\((A_{4})\) :

For \(x_{1},y_{1},x_{2},y_{2}\in R^{n}\), there exist constants \(\rho _{1}\ge 0\) and \(\rho _{2}\ge 0\) such that

$$\begin{aligned} \begin{aligned}&\mathrm{trace}\left\{ \left[ \beta (t,x_{1},y_{1})-\beta (t,x_{2},y_{2})\right] ^{T}\left[ \beta (t,x_{1},y_{1})-\beta (t,x_{2},y_{2})\right] \right\} \\ \le&\rho _{1}\Vert x_{1}-x_{2}\Vert ^{2}+\rho _{2}\Vert y_{1}-y_{2}\Vert ^{2}. \end{aligned} \end{aligned}$$
(10)
\((A_{5})\) :

There is a constant \(K>0\) such that \(\int _{0}^{+\infty }K(s)ds\le K\).

Lemma 1

$$\begin{aligned} sign(e_{ij}(t))(-d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t))\le -\underline{d}_{j}\left| e_{ij}(t)\right| +T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| . \end{aligned}$$

Proof

We consider the following four cases:

  1. (1)

    When \(\left| x_{ij}(t)\right| <T_{j}\) and \(\left| z_{j}(t)\right| <T_{j}\),

    $$\begin{aligned} \begin{aligned}&sign(e_{ij}(t))(-d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t))\\&\quad =-sign(e_{ij}(t))(d_{j}^{*}x_{ij}(t)-d_{j}^{*}z_{j}(t))\\&\quad =-d_{j}^{*}\left| e_{ij}(t)\right| \le -\underline{d}_{j}\left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
    (11)
  2. (2)

    When \(\left| x_{ij}(t)\right| >T_{j}\) and \(\left| z_{j}(t)\right| >T_{j}\),

    $$\begin{aligned} \begin{aligned}&sign(e_{ij}(t))(-d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t))\\&\quad =-d_{j}^{**}\left| e_{ij}(t)\right| \le -\underline{d}_{j}\left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
    (12)
  3. (3)

    When \(\left| x_{ij}(t)\right| \ge T_{j}\) and \(\left| z_{j}(t)\right| \le T_{j}\),

    $$\begin{aligned} \begin{aligned}&sign(e_{ij}(t))(-d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t))\\&\quad =-sign(e_{ij}(t))[d_{j}(x_{ij}(t))e_{ij}(t)+(d_{j}(x_{ij}(t))-d_{j}(z_{j}(t)))z_{j}(t)]\\&\quad \le -\underline{d}_{j}\left| e_{ij}(t)\right| +T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| . \end{aligned} \end{aligned}$$
    (13)
  4. (4)

    When \(\left| x_{ij}(t)\right| \le T_{j}\) and \(\left| z_{j}(t)\right| \ge T_{j}\),

    $$\begin{aligned} \begin{aligned}&sign(e_{ij}(t))(-d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t))\\&\quad =-sign(e_{ij}(t))[(d_{j}(x_{ij}(t))-d_{j}(z_{j}(t)))x_{ij}(t)+d_{j}(z_{j}(t))e_{ij}(t)]\\&\quad \le -\underline{d}_{j}\left| e_{ij}(t)\right| +T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| . \end{aligned} \end{aligned}$$
    (14)

The proof is completed. \(\square \)

Lemma 2

Let \(F_{i}(t)=(F_{i1}(t),F_{i2}(t),\ldots ,F_{in}(t))^{T}\), then \(\left| F_{ij}(t)\right| \le \Lambda _{j},\) where \(\Lambda _{j}=\sum \nolimits _{l=1}^{n}2(a_{jl}^{+}+b_{jl}^{+}+c_{jl}^{+}K)M_{l}\), for \(i=1,2,\ldots ,N\), \(j=1,2,\ldots ,n\).

Proof

In view of Assumptions \(A_{2}\) and \(A_{5}\), the proof is obvious. \(\square \)

Lemma 3

[33]. Suppose that the continuous function V(t) satisfies \(V(t)\ge 0,~ \forall t\in (a-\theta ,+\infty )\) and

$$\begin{aligned} \dot{V}(t)\le -k_{1}V(t)+k_{2}\sup \limits _{t-\theta \le s\le t}V(s),~ t\ge a, \end{aligned}$$

where \(k_{1}>k_{2}>0\). Then V(t) satisfies

$$\begin{aligned} V(t)\le \sup \limits _{a-\theta \le s\le a}V(s)e^{-\gamma (t-a)},~ t\ge a, \end{aligned}$$

where \(\gamma \) is the unique positive solution of the equation \(\gamma -k_{1}+k_{2}e^{\gamma \theta }=0\).

Definition 3

CMNNs (6) are said to be exponentially synchronized onto the system (3) in mean square, if there exist constants \(\varpi >0\) and \(\alpha >0\) such that

$$\begin{aligned} \sum \limits _{i=1}^{N}E[\Vert e_{i}(t)\Vert ^{2}]\le \varpi \cdot \sup \limits _{s\le 0}\sum \limits _{i=1}^{N}E[\Vert e_{i}(s)\Vert ^{2}]e^{-\alpha t},~t\ge 0. \end{aligned}$$

Definition 4

CMNNs (6) are said to be asymptotically synchronized onto the system (3) in mean square, if we can derive

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\sum \limits _{i=1}^{N}E[\Vert e_{i}(t)\Vert ^{2}]=0. \end{aligned}$$

3 Main Results

In order to synchronize all the solutions of CMNNs (6) onto z(t) of system (3), we design the following feedback controllers:

$$\begin{aligned} \begin{aligned} R_{i}(t)=-\xi e_{i}(t)-\eta sign(e_{i}(t)),\quad ~ i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(15)

where \(\xi \) is a constant and \(\eta =diag(\eta _{1},\eta _{2},\ldots ,\eta _{n})\) is a matrix.

Theorem 1

Suppose Assumptions \(A_{2}\)–\(A_{5}\) hold. For given constant \(\lambda \ge 0\), if \(\xi >\frac{1}{2}(\lambda +\rho _{1}+\rho _{2}e^{\lambda \tau _{2}})-\min \limits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert \) and \(\eta _{j}\ge T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j},~j=1,2,\ldots ,n\), CMNNs (6) can be exponentially synchronized onto the system (3) in mean square under the controllers (15).

Proof

We design the following Lyapunov function:

$$\begin{aligned} \begin{aligned} V(t)=\sum _{i=1}^{N}\frac{e^{\lambda t}}{2}e_{i}^{T}(t)e_{i}(t),\quad ~ \lambda \ge 0. \end{aligned} \end{aligned}$$
(16)

Differentiating V(t) along system (8), we have

$$\begin{aligned} dV(t)=LV(t)dt+\sum _{i=1}^{N}e^{\lambda t}e_{i}^{T}(t)\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))d\omega (t), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} LV(t)=&\frac{\lambda e^{\lambda t}}{2}\sum _{i=1}^{N}e_{i}^{T}(t)e_{i}(t)+e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)\left[ -D(x_{i}(t))x_{i}(t)\right. \\&\left. +\,D(z(t))z(t)+F_{i}(t)+H_{i}(e_{1}(t),e_{2}(t),\ldots ,e_{N}(t))+R_{i}(t)\right] \\&+\frac{e^{\lambda t}}{2}\sum _{i=1}^{N}\mathrm{trace}\left[ \varrho ^{T}(t,e_{i}(t),e_{i}(t-\tau _{2}(t)))\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))\right] . \end{aligned} \end{aligned}$$
(17)

According to Lemma 1,

$$\begin{aligned} \begin{aligned}&e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)\left[ -D(x_{i}(t))x_{i}(t)+D(z(t))z(t)\right] \\&\quad =e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}e_{ij}(t)\left[ -d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t)\right] \\&\quad =e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}\left| e_{ij}(t)\right| \cdot sign(e_{ij}(t))\left[ -d_{j}(x_{ij}(t))x_{ij}(t)+d_{j}(z_{j}(t))z_{j}(t)\right] \\&\quad \le e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}\left| e_{ij}(t)\right| \cdot \left[ -\underline{d}_{j}\left| e_{ij}(t)\right| +T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| \right] \\&\quad \le -\min \limits _{j}\left\{ \underline{d}_{j}\right\} e^{\lambda t}\sum _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}+e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| \cdot \left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(18)

According to Lemma 2,

$$\begin{aligned} \begin{aligned}&e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)F_{i}(t)\\&\quad \le e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}\left| e_{ij}(t)\right| \cdot \left| F_{ij}(t)\right| \le e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}\left| e_{ij}(t)\right| \Lambda _{j}. \end{aligned} \end{aligned}$$
(19)

Let \(\Gamma =(\gamma _{ij})_{N\times N}\) and \(\zeta =(\Vert e_{1}(t)\Vert ,\Vert e_{2}(t)\Vert ,\ldots ,\Vert e_{N}(t)\Vert )^{T}\), we have

$$\begin{aligned} \begin{aligned}&e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)H_{i}(e_{1}(t),e_{2}(t),\ldots ,e_{N}(t))\\&\quad \le e^{\lambda t}\sum _{i=1}^{N}\Vert e_{i}(t)\Vert \cdot \Vert H_{i}(e_{1}(t),e_{2}(t),\ldots ,e_{N}(t))\Vert \\&\quad \le e^{\lambda t}\sum _{i=1}^{N}\Vert e_{i}(t)\Vert \sum _{j=1}^{N}\gamma _{ij}\Vert e_{j}(t)\Vert \\&\quad =e^{\lambda t}\zeta ^{T}\Gamma \zeta \le e^{\lambda t}\Vert \Gamma \Vert \cdot \Vert \zeta \Vert ^{2}=e^{\lambda t}\Vert \Gamma \Vert \sum _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}, \end{aligned} \end{aligned}$$
(20)

where Assumption \(A_{3}\) has been used.

It is obvious that

$$\begin{aligned} \begin{aligned}&e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)R_{i}(t)=e^{\lambda t}\sum _{i=1}^{N}e_{i}^{T}(t)\left[ -\xi e_{i}(t)-\eta sign(e_{i}(t))\right] \\&\quad =-e^{\lambda t}\sum _{i=1}^{N}\xi \left\| e_{i}(t)\right\| ^{2}-e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}e_{ij}(t)\cdot \eta _{j}sign(e_{ij}(t))\\&\quad =-e^{\lambda t}\sum _{i=1}^{N}\xi \Vert e_{i}(t)\Vert ^{2}-e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}\eta _{j}\left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(21)

According to Assumption \(A_{4}\),

$$\begin{aligned} \begin{aligned}&\frac{e^{\lambda t}}{2}\sum _{i=1}^{N}\mathrm{trace}\left[ \varrho ^{T}(t,e_{i}(t),e_{i}(t-\tau _{2}(t)))\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))\right] \\&\quad \le \frac{e^{\lambda t}}{2}\sum _{i=1}^{N}\left[ \rho _{1}\Vert e_{i}(t)\Vert ^{2}+\rho _{2}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}\right] . \end{aligned} \end{aligned}$$
(22)

Then we have

$$\begin{aligned} \begin{aligned} LV(t)&\le e^{\lambda t}\sum _{i=1}^{N}\left( \frac{\lambda }{2}-\min \limits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert -\xi +\frac{\rho _{1}}{2}\right) \Vert e_{i}(t)\Vert ^{2} +e^{\lambda t}\sum _{i=1}^{N}\frac{\rho _{2}}{2}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}\\&\quad +e^{\lambda t}\sum _{i=1}^{N}\sum _{j=1}^{n}(T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j}-\eta _{j})\left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(23)

Since \(\eta _{j}\ge T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j},j=1,2,\ldots ,n\), it follows that

$$\begin{aligned} \begin{aligned} LV(t)\le e^{\lambda t}\sum _{i=1}^{N}\left( \frac{\lambda }{2}-\min \limits _{j}\{\underline{d}_{j}\}+\Vert \Gamma \Vert -\xi +\frac{\rho _{1}}{2}\right) \Vert e_{i}(t)\Vert ^{2} +e^{\lambda t}\sum _{i=1}^{N}\frac{\rho _{2}}{2}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}. \end{aligned} \end{aligned}$$
(24)

Taking mathematical expectation yields

$$\begin{aligned} \begin{aligned} \frac{dEV(t)}{dt}\le (\lambda -2\min \limits _{j}\left\{ \underline{d}_{j}\right\} +2\Vert \Gamma \Vert -2\xi +\rho _{1})EV(t) +\rho _{2}e^{\lambda \tau _{2}}EV(t-\tau _{2}(t)). \end{aligned} \end{aligned}$$
(25)

That means

$$\begin{aligned} \begin{aligned} \frac{dEV(t)}{dt}\le (\lambda -2\min \limits _{j}\left\{ \underline{d}_{j}\right\} +2\Vert \Gamma \Vert -2\xi +\rho _{1})EV(t) +\rho _{2}e^{\lambda \tau _{2}}\sup \limits _{t-\tau _{2}\le s\le t}EV(s). \end{aligned} \end{aligned}$$
(26)

Since \(\xi >\frac{1}{2}(\lambda +\rho _{1}+\rho _{2}e^{\lambda \tau _{2}})-\min \limits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert \), we can derive from Lemma 3 that

$$\begin{aligned} \begin{aligned} EV(t)\le&\sup \limits _{-\tau _{2}\le s\le 0}EV(s)e^{-\mu t},\quad ~ t\ge 0, \end{aligned} \end{aligned}$$
(27)

where \(\mu \) is the unique positive solution of the equation

$$\begin{aligned} \mu +\lambda -2\min \limits _{j}\left\{ \underline{d}_{j}\right\} +2\Vert \Gamma \Vert -2\xi +\rho _{1}+\rho _{2}e^{(\lambda +\mu ) \tau _{2}}=0. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned} \frac{e^{\lambda t}}{2}\sum _{i=1}^{N}E[\Vert e_{i}(t)\Vert ^{2}]&\le \sup \limits _{-\tau _{2}\le s\le 0}\frac{e^{\lambda s}}{2}\sum _{i=1}^{N}E[\Vert e_{i}(s)\Vert ^{2}]e^{-\mu t}\\&\le \frac{1}{2}\sup \limits _{-\tau _{2}\le s\le 0}\sum _{i=1}^{N}E[\Vert e_{i}(s)\Vert ^{2}]e^{-\mu t},~ t\ge 0. \end{aligned} \end{aligned}$$
(28)

Therefore,

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N}E[\Vert e_{i}(t)\Vert ^{2}]\le \sup \limits _{-\tau _{2}\le s\le 0}\sum _{i=1}^{N}E[\Vert e_{i}(s)\Vert ^{2}]e^{-(\mu +\lambda )t},~ t\ge 0. \end{aligned} \end{aligned}$$
(29)

This completes the proof. \(\square \)

In Theorem 1, the control gains of feedback controllers (15) may be much larger than those needed actually because of the conservativeness of theoretical analysis. Since adaptive feedback controllers can avoid the high control gains perfectly, we will consider adaptive feedback controllers in Theorem 2.

Theorem 2

If Assumptions \(A_{1}\)–\(A_{5}\) hold, CMNNs (6) will be asymptotically synchronized onto the system (3) in mean square under the adaptive feedback controllers:

$$\begin{aligned} \begin{aligned} R_{i}(t)=-\xi _{i}(t)e_{i}(t)-\eta _{i}(t)sign(e_{i}(t)),\quad ~i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(30)

where \(\eta _{i}(t)=diag(\eta _{i1}(t),\eta _{i2}(t),\ldots ,\eta _{in}(t))\), \(\xi _{i}(t)\) and \(\eta _{ij}(t)\) satisfy

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\dot{\xi }_{i}(t)=p_{i}\Vert e_{i}(t)\Vert ^{2},\quad \xi _{i}(0)=0,\\&\dot{\eta }_{ij}(t)=q_{ij}\left| e_{ij}(t)\right| , \quad \eta _{ij}(0)=0, \end{aligned} \right. \end{aligned} \end{aligned}$$
(31)

for \(i=1,2,\ldots ,N,j=1,2,\ldots ,n,\) where \(p_{i}>0\) and \(q_{ij}>0\) are constants.

Proof

We design the following Lyapunov function:

$$\begin{aligned} \begin{aligned} V(t)=V_{1}(t)+V_{2}(t)+V_{3}(t), \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned}&V_{1}(t)=\frac{1}{2}\sum _{i=1}^{N}e_{i}^{T}(t)e_{i}(t),\\&V_{2}(t)=\sum _{i=1}^{N}\frac{\rho _{2}}{2(1-\sigma _{2})}\int _{t-\tau _{2}(t)}^{t}\Vert e_{i}(s)\Vert ^{2}ds,\\&V_{3}(t)=\sum _{i=1}^{N}\frac{1}{2p_{i}}(\xi _{i}(t)-r)^{2}+\sum _{i=1}^{N}\sum _{j=1}^{n}\frac{1}{2q_{ij}}(\eta _{ij}(t)-s_{j})^{2}. \end{aligned} \end{aligned}$$
(33)

Differentiating V(t) along system (8), we get that

$$\begin{aligned} \begin{aligned} dV(t)=LV(t)dt+\sum _{i=1}^{N}e_{i}^{T}(t)\varrho (t,e_{i}(t),e_{i}(t-\tau _{2}(t)))d\omega (t), \end{aligned} \end{aligned}$$
(34)

where \(LV(t)=LV_{1}(t)+LV_{2}(t)+LV_{3}(t)\).

Similarly to the proof of Theorem 1, it can be derived that

$$\begin{aligned} \begin{aligned} LV_{1}(t)&\le \sum _{i=1}^{N}\left( -\min \limits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert -\xi _{i}(t)+\frac{\rho _{1}}{2}\right) \Vert e_{i}(t)\Vert ^{2} +\sum _{i=1}^{N}\frac{\rho _{2}}{2}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}\\&\quad +\sum _{i=1}^{N}\sum _{j=1}^{n}\left( T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j}-\eta _{ij}(t)\right) \left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(35)

Based on Assumption \(A_{1}\),

$$\begin{aligned} \begin{aligned} LV_{2}(t)&= \frac{\rho _{2}}{2(1-\sigma _{2})}\sum _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}-\frac{\rho _{2}(1-\dot{\tau }_{2}(t))}{2(1-\sigma _{2})}\sum _{i=1}^{N}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}\\&\le \frac{\rho _{2}}{2(1-\sigma _{2})}\sum _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}-\frac{\rho _{2}}{2}\sum _{i=1}^{N}\Vert e_{i}(t-\tau _{2}(t))\Vert ^{2}. \end{aligned} \end{aligned}$$
(36)

It is obvious that

$$\begin{aligned} \begin{aligned} LV_{3}(t)=&\sum _{i=1}^{N}\frac{2(\xi _{i}(t)-r)}{2p_{i}}\cdot p_{i}\Vert e_{i}(t)\Vert ^{2}+\sum _{i=1}^{N}\sum _{j=1}^{n}\frac{2(\eta _{ij}(t)-s_{j})}{2q_{ij}}\cdot q_{ij}\left| e_{ij}(t)\right| \\ \le&\sum _{i=1}^{N}(\xi _{i}(t)-r)\Vert e_{i}(t)\Vert ^{2}+\sum _{i=1}^{N}\sum _{j=1}^{n}(\eta _{ij}(t)-s_{j})\left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(37)

It follows that

$$\begin{aligned} \begin{aligned} LV(t)\le&\sum _{i=1}^{N}\left( -\min \limits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert -r+\frac{\rho _{1}}{2}+\frac{\rho _{2}}{2(1-\sigma _{2})}\right) \Vert e_{i}(t)\Vert ^{2} \\&+\sum _{i=1}^{N}\sum _{j=1}^{n}\left( T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j}-s_{j}\right) \left| e_{ij}(t)\right| . \end{aligned} \end{aligned}$$
(38)

Choose \(r\ge -\min \nolimits _{j}\left\{ \underline{d}_{j}\right\} +\Vert \Gamma \Vert +\frac{\rho _{1}}{2}+\frac{\rho _{2}}{2(1-\sigma _{2})}+\varepsilon \) and \(s_{j}\ge T_{j}\left| d_{j}^{*}-d_{j}^{**}\right| +\Lambda _{j},j=1,2,\ldots ,n,\) where \(\varepsilon >0\).

Then we have

$$\begin{aligned} LV(t)\le -\varepsilon \sum _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$

According to LaSalle invariance principle for stochastic delayed differential equations [38,39,40], we have \(\lim \nolimits _{t\rightarrow +\infty }e_{i}(t)=0\), \(i=1,2,\ldots ,N\), which means that \(\lim \nolimits _{t\rightarrow +\infty }\sum \nolimits _{i=1}^{N{}^{\phantom {{1}}}}E\left[ \Vert e_{i}(t)\Vert ^{2}\right] =0\). Based on Definition 4, we can derive that CMNNs (6) can be asymptotically synchronized onto the system (3) in mean square.

This completes the proof. \(\square \)

Remark 1

The CMNNs model studied in this paper is the same as that of [32]. In [32], the upper bounds of the solutions of the isolated node system are assumed to be known in advance, i.e., there exist some known positive constants \(M_{j}^{z}\) such that \(\left| z_{j}(t)\right| \le M_{j}^{z}\), \(j=1,2,\ldots ,n\). However, in our paper, we don’t need the assumption that the upper bounds of the solutions of the isolated node system are known in advance. Moreover, the activation functions \(f_{j}(\cdot ),~j=1,2,\ldots ,n\), in our paper are only required to be bounded, while in [32] they are assumed to be bounded and satisfy the Lipschitz condition.

Remark 2

It should be pointed out that only the asymptotic synchronization of CMNNs (6) is proved in Theorem 2, while Theorem 1 gives the exponential synchronization criteria of CMNNs (6). Furthermore, the proof of Theorem 2 requires an extra assumption condition \(\dot{\tau }_{2}(t)\le \sigma _{2}<1\), while the proof of Theorem 1 doesn’t need this assumption condition.

Remark 3

In this paper, feedback controllers are used in Theorem 1. Because of the conservativeness of theoretical analysis, the control gains of feedback controllers (15) may be much larger than those needed actually. To overcome this drawback, the adaptive control is a good choice. In Theorem 2, we utilize adaptive feedback controllers, which can reduce the control gains effectively.

Remark 4

There have been many results about the synchronization control of memristor-based neural networks, such as [21, 22]. For CMNNs (6) and system (3), if we set \(\beta (t,\cdot ,\cdot )=0\) and \(N=1\), then the results of this paper can be generalized to the drive-response synchronization of common memristor-based neural networks. In this sense, compared with the memristor-based neural networks model considered in [21, 22], the model of our paper is more general. However, the finite time synchronization is also investigated in [21], while only the asymptotic synchronization and exponential synchronization are studied in this paper. Hence, the finite time synchronization of CMNNs will be our future research direction.

4 Numerical Simulations

In this section, an example is given to illustrate the effectiveness of the theoretical results in this paper.

Consider the following 2-dimensional memristor-based stochastic neural network, which is a special case of system (3).

$$\begin{aligned} \begin{aligned} dz(t)&=\Bigg [-D(z(t))z(t)+A(z(t))f((z(t)))+B(z(t))f(z(t-\tau _{1}(t)))+J\\&\quad +\,C(z(t))\int _{-\infty }^{t}K(t-s)f((z(s)))ds\Bigg ]dt+\beta (t,z(t),z(t-\tau _{2}(t)))d\omega (t), \end{aligned} \end{aligned}$$
(39)

where \(z(t)=(z_{1}(t),z_{2}(t))^{T}\), \(f_{1}(v)=f_{2}(v)=\frac{\left| v+1\right| -\left| v-1\right| }{2}\), \(\tau _{1}(t)=2+sint\), \(\tau _{2}(t)=1+0.3cost\), \(J=(0,0)^{T}\), \(K(t)=e^{-0.5t}\), \(T_{1}=T_{2}=1\), \(d_{1}^{*}=0.9\), \(d_{1}^{**}=1.1\), \(d_{2}^{*}=1.1\), \(d_{2}^{**}=0.9\), \(a_{11}^{*}=3.4\), \(a_{11}^{**}=2.9\), \(a_{12}^{*}=-0.4\), \(a_{12}^{**}=-0.22\), \(a_{21}^{*}=4.2\), \(a_{21}^{**}=3.9\), \(a_{22}^{*}=5.2\), \(a_{22}^{**}=5\), \(b_{11}^{*}=-1.4\), \(b_{11}^{**}=-1.2\), \(b_{12}^{*}=0.2\), \(b_{12}^{**}=-0.1\), \(b_{21}^{*}=0.5\), \(b_{21}^{**}=-0.2\), \(b_{22}^{*}=-9.2\), \(b_{22}^{**}=-6\), \(c_{11}^{*}=-1.3\), \(c_{11}^{**}=-1.18\), \(c_{12}^{*}=0.12\), \(c_{12}^{**}=0.05\), \(c_{21}^{*}=-0.3\), \(c_{21}^{**}=-0.2\), \(c_{22}^{*}=-1.2\), \(c_{22}^{**}=-0.6\), \(\beta (t,z(t),z(t-\tau _{2}(t)))=0.6diag(z_{1}(t),z_{2}(t-\tau _{2}(t)))\). Then we have \(M_{1}=M_{2}=1\), \(\sigma _{2}=0.3\), \(K=2\), \(\rho _{1}=\rho _{2}=0.36\).

Fig. 2
figure 2

Trajectories of \(z_{1}(t)\) and \(z_{2}(t)\)

Full size image
Fig. 3
figure 3

Evolutions of \(\Vert e_{i}(t)\Vert \) without control inputs, \(i=1,2,3,4\)

Full size image
Fig. 4
figure 4

Evolutions of \(\Vert e_{i}(t)\Vert \) with controllers (30), \(i=1,2,3,4\)

Full size image
Fig. 5
figure 5

Evolutions of control gains \(\xi _{1}(t), \eta _{11}(t)\) and \(\eta _{12}(t)\) of controllers (30)

Full size image
Fig. 6
figure 6

Evolutions of control gains \(\xi _{2}(t), \eta _{21}(t)\) and \(\eta _{22}(t)\) of controllers (30)

Full size image
Fig. 7
figure 7

Evolutions of control gains \(\xi _{3}(t), \eta _{31}(t)\) and \(\eta _{32}(t)\) of controllers (30)

Full size image
Fig. 8
figure 8

Evolutions of control gains \(\xi _{4}(t), \eta _{41}(t)\) and \(\eta _{42}(t)\) of controllers (30)

Full size image

The initial value of system (39) is \(\varphi (t)=(0.5,0.2)^{T}\) for \(t\in [-5,0]\) and \(\varphi (t)=(0,0)^{T}\) for \(t\in (-\infty ,-5).\) The trajectories of \(z_{1}(t)\) and \(z_{2}(t)\) are presented in Fig. 2.

This is the controlled CMNNs with mixed delays and stochastic perturbations, which is a special case of CMNNs (6).

$$\begin{aligned} \begin{aligned} dx_{i}(t)&=\Bigg [-D(x_{i}(t))x_{i}(t)+A(x_{i}(t))f(x_{i}(t))+B(x_{i}(t))f(x_{i}(t-\tau _{1}(t)))+J\\&\quad +\,C(x_{i}(t))\int _{-\infty }^{t}K(t-s)f(x_{i}(s))ds+h_{i}(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))+R_{i}(t)\Bigg ]dt\\&\quad +\beta (t,x_{i}(t),x_{i}(t-\tau _{2}(t)))d\omega (t), ~i=1,2,3,4, \end{aligned} \end{aligned}$$
(40)

where \(x_{i}(t)=(x_{i1}(t),x_{i2}(t))^{T}\). The initial value of system (40) is \(\phi _{1}(t)=(0.2,0.6)^{T{}^{\phantom {\frac{1}{2}}}}\), \(\phi _{2}(t)=(-0.3,1.2)^{T}\), \(\phi _{3}(t)=(1,-0.5)^{T}\), \(\phi _{4}(t)=(1.3,-0.6)^{T}\) for \(t\in [-5,0]\), and \(\phi _{i}(t)=(0,0)^{T}\) for \(t\in (-\infty ,-5), i=1,2,3,4.\)

Suppose \(h_{i}(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))\) satisfies \(h_{i}(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))=0.1diag(x_{i1}(t)-x_{i+1,1}(t),x_{i2}(t)-x_{i+1,2}(t)),\) \(i=1,2,3,4,\) where \(x_{5}(t)=x_{1}(t)\). Figure 3 presents the evolutions of \(\Vert e_{i}(t)\Vert \) , \(i=1,2,3,4\), without control inputs.

Since \(\Vert h_{i}(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))-h_{i}(z(t),z(t),z(t),z(t))\Vert ^{2} \le 0.02(\Vert e_{i}(t)\Vert +\Vert e_{i+1}(t)\Vert )^{2},\) we obtain that \(\Vert h_{i}(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))-h_{i}(z(t),z(t),z(t),z(t))\Vert \le 0.1\sqrt{2}(\Vert e_{i}(t)\Vert +\Vert e_{i+1}(t)\Vert )\), \(i=1,2,3,4\). So Assumption \(A_{3}\) holds.

Choose \(p_{i}=q_{ij}=1\), \(i=1,2,3,4,j=1,2\). Figure 4 shows the evolutions of \(\Vert e_{i}(t)\Vert \), \(i=1,2,3,4\), with controllers (30). It is obvious that systems (39) and (40) achieve the asymptotic synchronization. The evolutions of the control gains \(\xi _{i}(t), \eta _{i1}(t)\) and \(\eta _{i2}(t)\), \(i=1,2,3,4\), of controllers (30) are given in Figs. 5, 6, 7 and 8, respectively. It should be pointed out that the control gains are all very small.

5 Conclusions

This paper is concerned with the synchronization control problem of CMNNs with mixed delays and stochastic perturbations. Some novel sufficient conditions guaranteeing the exponential synchronization of CMNNs with mixed delays and stochastic perturbations in mean square are derived via feedback controllers. Additionally, by using adaptive feedback controllers and stochastic LaSalle invariance principle, the asymptotic synchronization of CMNNs with mixed delays and stochastic perturbations in mean square can also be achieved. Numerical simulations are given to illustrate the validity and the effectiveness of our theoretical results.