1 Introduction

Fractional calculus, memristor and neural network are all hot topics in the scientific community. Scientists have obtained many results in the three fields above, respectively. So now, it is well known that the study of the combination of three, memristor-based fractional-order neural networks, is a potential research direction.

Fractional calculus, as another branch of the calculus, is the promotion and generation of the common integer-order calculus, dating from about 300 years ago. Lots of scientists threw themselves into fractional calculus for many years. But due to the lack of application background and its complexity in various fields, fractional calculus was studied only in the area of mathematics for such a long time. But recently, facts proved that the theory of fractional-order differential equations offers an excellent tool in modeling in various fields of physics, mathematics, engineering and so on [1–3]. The descriptions of some dynamical systems in the study using fractional-order models are superior to the integer-order systems [4]. It is not difficult for us to perceive that many researchers have turned their attention to the fractional calculus and built fractional-order models, proposing some good results. A method based on the state observer design for a class of nonlinear fractional-order systems (FOSs) with the fractional-order \(0<\alpha <1\) is presented and the asymptotic stability conditions of closed-loop control nonlinear systems are derived by Fractional Lyapunov direct method in Ref. [5]. The synchronization method of two identical fractional-order chaotic systems is developed with lower order than the existing fractional order 3 by designing suitable sliding mode control and a new cryptosystem is derived for an image encryption and decryption based on the synchronized lowest fractional-order 2.01 chaotic systems in Ref. [6].

As far as we know, the neural networks can be constructed by nonlinear circuit which are designed to emulate the function of the human brain. In recent years, the neural networks have enjoyed a high popularity for the reason that their widespread applications in the fields of pattern recognition, optoelectronics, associative memory, remote sensing, optimization, modeling and control (see [7–9]). In Refs [10, 11], the neural networks are applied to approximate solutions of the differential equations of fractional orders. And as for the dynamics analysis of the neural networks, there already have some results. In Ref. [12], the state synchronization and the exponential synchronization are achieved for a class of chaotic neural networks with or without delays based on the drive-response concept and Lyapunov stability method and the Halanay inequality lemma, respectively. And the modified function projective synchronization is achieved between two chaotic neural networks with delays based on the nonlinear state observer and the drive-response concept in Ref. [13]. In Ref. [14], the exponential synchronization for master-slave chaotic delayed neural network with limited communication capacity and network bandwidth based on event trigger control scheme is concerned. Most of all, we know that the fractional-order systems, in comparison with the integer-order parts, have one significant feature that is their infinite memory based on the properties of the fractional-order calculus. Hence, scientists start to incorporate a memory term into a neural network model, named fractional-order artificial neural networks. As a peculiar kind of neural networks, the fractional-order neural networks have received more and more attention and some important results about the models have been investigated in Refs. [15–18].

Memristor, according to the equation deduced, is first introduced in Chuas seminal paper [19] in 1971. It is the representative of the fourth perfect electrical element which can describe the relationship between the flux and the charge with alterable resistance. But it was not clearly experimentally demonstrated until 2008, that the scientists at Hewlett Packard Labs proudly announced the real implementation of the memristor physically with an official publication in Nature [20, 21]. Recently, the memristor, serving as a nonvolatile memory, enjoys some good properties and plays an important role in the modeling (see [22–26]). The reason why the memristor can enjoy a high popularity is because its nanometer dimensions and the memory characteristic. Based on the previous work, it is well known that the memristor performs the same as the neurons in the human brain. If we use the memristors instead of resistors to act as the connection weights and the self-feedback connection weights among the neurons, then there creates the memristor-based neural networks, which is a state-dependent switching system. As for the dynamics analysis of the memristor-based neural networks, there already have some results. In Ref. [27], the existence, uniqueness, and stability of memristor-based synchronous switching neural networks with time delays are studied by introducing multiple Lyapunov functions. In Ref. [28], the paper addresses the problem of circuit design and global exponential stabilization of memristive neural networks with time-varying delays and general activation functions. By using an impulsive delayed differential inequality and Lyapunov function, the exponential stability of the impulsive delayed memristor-based recurrent neural networks is investigated in Ref. [29]. And there are more results in Refs. [30–35].

According to the above discussion, it is significant for us to analysis the dynamic behaviors of the memristor-based fractional-order neural networks, which enjoy the advantages of both fractional-order neural networks and memristor-based neural networks. There are already some researches about this new system. In Ref. [36], the authors analyze the global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. And the global asymptotic stability and synchronization of a class of fractional-order memristor-based delayed neural networks are investigated in Ref. [37]. In Ref. [38], the paper investigated the projective synchronization of fractional-order memristor-based neural networks in the sense of Caputo’s fractional derivation and by combining a fractional-order differential inequality. In Ref. [39], by using Laplace transform, the generalized Gronwalls inequality, Mittag-Leffler functions and linear feedback control technique, some new sufficient conditions are derived to ensure the finite-time synchronization of a class of fractional-order memristor-based neural networks (FMNNs) with time delays for fractional order: \(1<\alpha <2\) and \(0<\alpha <1\), respectively. In the Ref. [40], the synchronization error system is formulated on the basis of the theory of fractional differential equations and the theory of differential inclusion and by employing Hölder inequality, \(C_{p}\) inequality and Gronwall-Bellman inequality, several sufficient criteria are proposed to ensure the quasi-uniform synchronization for the considered delayed fractional-order memristor-based neural networks (FMNNs). However, the effect of parameter uncertainties are not taken into consideration in the above researches, which are unavoidable in our actual life due to some reasons, such as external disturbance, temperature difference, measure errors, and so on. Therefore, make certain the two chaotic systems can also realize the stability or synchronization with respect to these uncertainties in the design or in the applications of neural networks is very necessary and significant. In other words, the design neural network should be robust under such uncertainties. It is well known that the Hopfield neural network is a kind of rather important nonlinear circuit networks because of their wide applications in various fields of optimization problem, associative memory, pattern recognition, etc. There are some results about the fractional-order Hopfield neural networks [16]. And the results of the memristor-based fractional-order Hopfield neural network are very few. Actually, the memristor-based fractional-order Hopfield neural network, compared with the common memristor-based fractional-order neural networks, show more superiority and overcome the defect that computationally restrictive which has been found in some existing memristor-based fractional-order networks. Synchronization is always a hot topic among the neural networks and the feature of the memristor. In Ref. [41], Huang et al. focus on the hybrid effects of parameter uncertainty, stochastic perturbation, and impulses on global stability of delayed neural networks. In Ref. [42], Wong et al. investigated robust synchronization of fractional-order complex dynamical networks with parameter uncertainties. And Wang et al. [43], studied the exponential synchronization problem of a class of memristive chaotic neural networks with discrete, continuously distributed delays and different parametric uncertainties. Motivated by the above, there are few results on synchronization problem of memristor-based fractional-order Hopfield neural networks considering parameter uncertainties, showing the robust of such system. So in this letter, based on the above works, we will study robust synchronization of the memristor-based fractional-order Hopfield neural networks with parameter uncertainties by a simple controller. Based on the fractional-order Lyapunov direct method, a suitable Lyapunov function and some sufficient conditions are presented to achieve the robust synchronization between the two memristor-based fractional-order Hopfield neural networks with the parameter uncertainties by analyzing the Mittag-Leffler stability of the error system. Besides, in the help of the numerical simulations, it can be proved that the system we study is chaotic, so the synchronization between the same master-slave systems is meaningful.

The rest of this paper is organized as follows. Some basic definitions and relevant lemmas are introduced firstly in Sect. 2. Then, the fractional-order Hopfield neural networks with parameter uncertainties based on memristor are given and based on the Lyapunov function, robust synchronization is achieved in Sect. 3. At last, numerical simulations are proposed to show the correctness of the theoretical results in Sect. 4.

2 Preliminaries

To begin with, we would like to introduce some basic definitions and relevant lemmas. The fractional-order calculus is the promotion of the integer-order calculus, and it acts as an important role in the nonlinear science. The fractional-order calculus has three common definitions, such as Grunwald–Letnikov, Riemann–Liouville, and Caputo definitions [1]. As we know, the Caputo fractional-order derivative is the improvement of the Grunwald–Letnikov, having the same initial condition with the integer-order derivatives, which has clear physical meaning. Thus, we employ the Caputo fractional-order derivative in this paper.

Definition 1

The Caputo fractional-order derivative is defined as:

$$\begin{aligned} _{t_{0}}D^{\alpha }_{t}f(t)=\frac{1}{\Gamma (n-\alpha )}\int ^{t}_{t_{0}}\frac{f^{(n)}(\tau )}{(t-\tau )^{\alpha +1-n}}{\mathrm{d}}\tau , \end{aligned}$$
(1)

where n is a positive integer and meets \(n-1<\alpha \le n\), \(\Gamma (\cdot )\) denotes the Gamma function.

Property 1

C is any constant, then \(_{t_{0}}D^{\alpha }_{t}C=0\) holds.

Property 2

There are two any constants \(\mu\) and \(\nu\), Caputo fractional-order derivative has the following linearity:

$$\begin{aligned} _{t_{0}}D^{\alpha }_{t}(\mu f(t)+\nu g(t))=\mu ~ _{t_{0}}D^{\alpha }_{t}f(t)+\nu ~ _{t_{0}}D^{\alpha }_{t}g(t). \end{aligned}$$

Just like the role of the exponential function in the integer-order system, Mittag-Leffler function is often used in the solutions of fractional-order differential equations.

Definition 2

[1] The Mittag-Leffler function having two parameters is defined as:

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum ^{\infty }_{k=0}\frac{z^{k}}{\Gamma (\alpha k+\beta )}, \end{aligned}$$

where \(\alpha >0\), \(\beta >0\) and \(z\in C\). When \(\beta =1\), we have:

$$\begin{aligned} E_{\alpha }(z)=\sum ^{\infty }_{k=0}\frac{z^{k}}{\Gamma (\alpha k+1)}=E_{\alpha ,1}(z), \end{aligned}$$

Next, some relevant lemmas will be given. Consider the following n-dimensional Caputo fractional-order dynamic system

$$\begin{aligned} \left\{ \begin{array}{l} _{t_{0}}D^{\alpha }_{t}x(t)=f(t,x(t))\\ x(t_{0})=x_{t_{0}}, \end{array} \right. \end{aligned}$$
(2)

where \(\alpha \in (0, 1)\), \(x=(x_{1}, x_{2}, \ldots , x_{n})^{T}\in R^{n}\), \(t_{0}\ge 0\) is the initial time and \(f:[0,+\infty )\times R^{n}\rightarrow R^{n}\) is piecewise continuous on t satisfying locally Lipschitz condition on x.

Definition 3

(Mittag-Leffler stability [44]) The solution of system (2) is said to be Mittag-Leffler stable in the case \(\bar{x}=0\) is an equilibrium point of system (2) if

$$\begin{aligned} \Vert x(t)\Vert \le [m(x_{t_{0}})E_{\alpha }(-\lambda (t-t_{0})^{\alpha })]^{b}. \end{aligned}$$
(3)

where \(\lambda >0\), \(b>0\), \(m(0)=0\), \(\Vert \cdot \Vert\) denotes an arbitrary norm and \(m(x)\ge 0\) satisfies locally Lipschitz condition on \(x\in R^{n}\), \(m_{0}\) denotes the Lipschitz constant.

Remark 1

Based on the relationship of the stability, we can know that Mittag-Leffler stability includes asymptotic stability i.e. \(\Vert x(t)\Vert \rightarrow 0\) with \(t\rightarrow +\infty\).

Remark 2

The common phenomenon is that \(\bar{x}\ne 0\), so at this time, the solution of system (2) is said to be Mittag-Leffler stable if

$$\begin{aligned} \Vert x(t)-\bar{x}\Vert \le [m(x_{t_{0}}-\bar{x})E_{\alpha }(-\lambda (t-t_{0})^{\alpha })]^{b}, \end{aligned}$$

and \(x(t)\rightarrow \bar{x}\) when \(t\rightarrow +\infty\).

To analyze Mittag-Leffler stability of system (2), the fractional-order Lyapunov direct method is introduced as follows.

Lemma 1

(Fractional-order Lyapunov direct method [44]) For the initial time\(t_{0}=0\), the fractional-order dynamic system (2) is Mittag-Leffler stable at the equilibrium point\(\bar{x}=0\)if there exists a continuously differentiable functionV(t, x(t)) satisfies

$$\begin{aligned}&\alpha _{1}\Vert x\Vert ^{a}\le V(t,x(t))\le \alpha _{2}\Vert x\Vert ^{ab}, \end{aligned}$$
(4)
$$\begin{aligned}&_{0}D^{\beta }_{t}V(t,x(t))\le -\alpha _{3}\Vert x\Vert ^{ab}. \end{aligned}$$
(5)

where\(V(t,x(t)): [0, \infty )\times D\rightarrow R\)satisfies locally Lipschitz condition onx; \(D\subset R^{n}\)is a domain containing the origin;\(t\ge 0\), \(\beta \in (0, 1)\), \(\alpha _{1}\), \(\alpha _{2}\), \(\alpha _{3}\), aandbare arbitrary positive constants. On the other hand, if the assumptions hold globally on\(R^{n}\), then\(\bar{x}=0\)is globallyMittag-Leffler stable.

Remark 3

According to Ref. [44], the conditions in Lemma 1 can be weakened, that is if inequality (5) holds almost everywhere, the result of Lemma 1 is also correct.

Lemma 2

[36]. If\(h(t)\in C^{1}([0,+\infty ),R)\)is a continuously differentiable function, then the following inequality holds almost everywhere.

$$\begin{aligned} _{0}D^{\alpha }_{t}|h(t)|\le {\mathrm{sgn}}(h(t)) _{0}D^{\alpha }_{t}h(t),\quad 0<\alpha <1. \end{aligned}$$
(6)

3 Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties

In this section, two chaotic memristor-based fractional-order Hopfield neural networks with parameter uncertainties are given firstly. The systems we introduced are ideal models and frequently encountered in applications and in life. Then, a suitable Lyapunov function and some sufficient conditions on robust synchronization of the systems are established by using fractional-order Lyapunov direct method.

Consider the following two n-dimensional memristor-based Caputo fractional-order Hopfield neural networks with the parameter uncertainties:

$$\begin{aligned}&\begin{array}{l} _{0}D^{\alpha }_{t}x(t)=-\,(A+\Delta A(t))x(t)+(B+\Delta B(t))f(x(t))+w,\\ a_{i}= {\left\{ \begin{array}{ll} a_{i}^{'},&{}\quad |x_{i}(t)|\le T\\ a_{i}^{''},&{}\quad |x_{i}(t)|>T. \end{array}\right. }~~~ b_{ij}= {\left\{ \begin{array}{ll} b_{ij}^{'},&{}\quad |x_{i}(t)|\le T\\ b_{ij}^{''},&{}\quad |x_{i}(t)|>T. \end{array}\right. } \end{array} \end{aligned}$$
(7)
$$\begin{aligned}&\begin{array}{l} _{0}D^{\alpha }_{t}y(t)=-(A+\Delta A(t))y(t)+(B+\Delta B(t))f(y(t))+w+u(t),\\ a_{i}= {\left\{ \begin{array}{ll} a_{i}^{'},&{}\quad |y_{i}(t)|\le T\\ a_{i}^{''},&{}\quad |y_{i}(t)|>T. \end{array}\right. }\quad b_{ij}= {\left\{ \begin{array}{ll} b_{ij}^{'},&{}\quad |y_{i}(t)|\le T\\ b_{ij}^{''},&{}\quad |y_{i}(t)|>T. \end{array}\right. } \end{array} \end{aligned}$$
(8)

where \(\alpha \in (0, 1)\), \(x(t)=(x_{1}(t), x_{2}(t), \ldots , x_{n}(t))^{T}\in R^{n}\), \(y(t)=(y_{1}(t), y_{2}(t), \ldots , y_{n}(t))^{T}\in R^{n}\), \(f(x(t))=(f_{1}(x_{1}), f_{2}(x_{2}), \ldots , f_{n}(x_{n}))^{T}\in R^{n}, f(y(t))=(f_{1}(y_{1}), f_{2}(y_{2}), \ldots , f_{n}(y_{n}))^{T}\in R^{n}\), \(A={\mathrm{diag}}\{a_{1}, a_{2}, \ldots , a_{n}\}\), and \(B=(b_{ij})_{n\times n}\). For \(i,j = 1,2,\ldots ,n\), \(x_{i}(t)\), \(y_{i}(t)\) are the state of the ith unit at time t of the system (7) and the system (8), respectively, \(f_{i}(x_{i})\), \(f_{i}(y_{i})\) denote the activation function of the ith neuron, \(a_{i}>0\) denotes the charging rate for the ith neuron, and \(b_{ij}\) is the constant connection weight of the jth neuron on the ith neuron. \(\Delta A(t)={\mathrm{diag}}\{\Delta a_{1}(t), \Delta a_{2}(t), \ldots , \Delta a_{n}(t)\}\) and \(\Delta B(t)=(\Delta b_{ij}(t))_{n\times n}\) are matrices with time-varying parametric uncertainties. \(w=(w_{1}, w_{2}, \ldots , w_{n})^{T}\) is the constant external input vector, \(u(t)=(u_{1}(t), u_{2}(t),\ldots , u_{n}(t))^{T}\) is the control law:

$$\begin{aligned} u(t)=-k(y(t)-x(t)). \end{aligned}$$

where k is a positive constant.

In the rest of this paper, \(\Vert Q\Vert\) denotes the 1-norm of corresponding vector Q or matrix Q. When \(Q=(Q_{1}, Q_{2}, \ldots , Q_{m})^{T}\in R^{m}\) is a vector, \(\Vert Q\Vert =|Q_{1}|+|Q_{2}|+\ldots +|Q_{m}|\). If \(Q\in R^{m\times m}\) is a matrix, \(\Vert Q\Vert ={\mathrm{sup}}\{\Vert Qx\Vert : \forall x\in R^{m}, \Vert x\Vert \le 1\}\).

Definition 4

(Robust Synchronization). If the error system \(e(t)=y(t)-x(t)\) between the two systems tends to 0 as the time \(t\rightarrow +\infty\), then the two systems are said to realize robust synchronization, that is:

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }~||e(t)||=\lim \limits _{t\rightarrow +\infty }~||y(t)-x(t)||=0. \end{aligned}$$

In order to achieve robust synchronization between the two systems (7) and (8), the following four assumptions are given:

(\({\mathrm{A}}_{1}\)) There exist two constants \(M_{A}, M_{B}>0\), the time-varying parameter uncertainty matrices \(\Delta A(t)\) and \(\Delta B(t)\) are both bounded and the inequalities hold \(\Vert \Delta A(t)\Vert \le M_{A}\) and \(\Vert \Delta B(t)\Vert \le M_{B}\).

\((A_{2})\) The activation functions \(f_{i}\) are continuous and satisfy Lipschitz condition on R with Lipschitz constant \(l_{i}>0\), i.e.,

$$\begin{aligned} |f_{i}(x)-f_{i}(y)|\le l_{i}|x-y|. \end{aligned}$$

for all \(x,y\in R\) and \(i=1,2,\ldots ,n\).

\((A_{3})\) There exist positive constants \(\lambda\) and \(\beta _{i}(i=1,2,\ldots ,n)\), k, and the following inequality holds

$$\begin{aligned} (kI+\underline{A}-L|B_{\mathrm{max}}|^{T})\left( \begin{array}{l} \beta _{1} \\ \beta _{2} \\ \vdots \\ \beta _{n} \\ \end{array} \right) \ge (M_{A}\Vert \beta \Vert +M_{B}\Vert L\Vert \Vert \beta \Vert +\lambda )\left( \begin{array}{l} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} \right) , \end{aligned}$$
(9)

where \(\underline{A}={\mathrm{diag}}(\underline{a_{1}}, \underline{a_{2}}, \ldots , \underline{a_{n}})\), \(\underline{a_{i}}=\min \{a_{i}^{'}, a_{i}^{''}\}\). \(|B_{\mathrm{max}}|=(\max \{|b_{ij}^{'}|, |b_{ij}^{''}|\})_{n\times n}\), \(L={\mathrm{diag}}(l_{1}, l_{2}, \ldots , l_{n})\) and \(\beta ={\mathrm{diag}}(\beta _{1}, \beta _{2}, \ldots , \beta _{n})\).

\((A_{4})\) For i, j = 1, 2,…, n

$$\begin{aligned}&a_{i}(y_{i}(t))y_{i}(t)-a_{i}(x_{i}(t))x_{i}(t)\subseteq [\underline{a_{i}}, \overline{a_{i}}](y_{i}(t)-x_{i}(t)),\\&b_{ij}(y_{i}(t))f(y_{j}(t))-b_{ij}(x_{i}(t))f(x_{j}(t))\subseteq [\underline{b_{ij}}, \overline{b_{ij}}](f(y_{j}(t))-f(x_{j}(t))). \end{aligned}$$

\(\underline{a_{i}}=\min \{a_{i}^{'}, a_{i}^{''}\}\), \(\overline{a_{i}}=\max \{a_{i}^{'}, a_{i}^{''}\}\), \(\underline{b_{ij}}=\min \{b_{ij}^{'}, b_{ij}^{''}\}\), \(\overline{b_{ij}}=\max \{b_{ij}^{'}, b_{ij}^{''}\}\).

Theorem 1

The robust synchronization can be realized for the systems (7) and (8), if the assumptions (\({\mathrm{A}}_{1}\))–(\({\mathrm{A}}_{4}\)) are satisfied.

Proof

Firstly, for system (7) and system (8), the error system can be derived,

$$\begin{aligned} _{0}D^{\alpha }_{t}e_{i}(t)= & {} -(a_{i}(y_{i}(t))y_{i}(t)-a_{i}(x_{i}(t))x_{i}(t))-\Delta a_{i}(t)(y_{i}(t) \\&\,-x_{i}(t))+\sum ^{n}_{j=1}[(b_{ij}(y_{i}(t))f_{j}(y_{j}(t))-b_{ij}(x_{i}(t))f_{j}(x_{j}(t))) \\&\,+\Delta b_{ij}(t)(f_{j}(y_{j}(t))-f_{j}(x_{j}(t)))] -k(y_{i}(t)-x_{i}(t)). \end{aligned}$$

by \((A_{4})\), the error system can be simplified as

$$\begin{aligned}_{0}D^{\alpha }_{t}e_{i}(t)&\in -[\underline{a_{i}}, \overline{a_{i}}]e_{i}(t)-\Delta a_{i}(t)e_{i}(t)\\&\quad +\,\sum ^{n}_{j=1}[[\underline{b_{ij}}, \overline{b_{ij}}](f_{j}(y_{j}(t))-f_{j}(x_{j}(t))) ,\\&\quad +\,\Delta b_{ij}(t)(f_{j}(y_{j}(t))-f_{j}(x_{j}(t)))]-ke_{i}(t). \end{aligned}$$

Now let \(\theta _{i}\in [\underline{a_{i}}, \overline{a_{i}}]\), \(\nu _{ij}\in [\underline{b_{ij}}, \overline{b_{ij}}]\), we have

$$\begin{aligned} _{0}D^{\alpha }_{t}e_{i}(t)= & {} -\,(k+\theta _{i}+\Delta a_{i}(t))e_{i}(t)+\sum ^{n}_{j=1}(\nu _{ij}\nonumber \\&+\,\Delta b_{ij}(t))(f_{j}(y_{j}(t))-f_{j}(x_{j}(t))) \end{aligned}$$
(10)

i.e.

$$\begin{aligned} _{0}D^{\alpha }_{t}e(t)= & {} -\,(kI+\theta +\Delta A(t))e(t)+(\nu +\Delta B(t))\nonumber \\&\quad (f(y(t))-f(x(t))). \end{aligned}$$
(11)

According to the fractional-order Lyapunov direct method, a Lyapunov function is constructed as

$$\begin{aligned} V(t,e(t))=\sum ^{n}_{i=1}\beta _{i}|e_{i}(t)|. \end{aligned}$$
(12)

It is obvious that the Lyapunov functional (12) satisfies the condition of inequality (4). Then, we are going to prove that the Lyapunov functional (12) also satisfies the condition of inequality (5) almost everywhere.

From Definition 1 and \(e_{i}(t)\in C^{1}([0,+\infty ),R)\), by (\({\mathrm{A}}_{1}\))–(\({\mathrm{A}}_{3}\)) and Lemma 2, the following inequality holds almost everywhere:

$$\begin{aligned} \begin{aligned} _{0}D^{\alpha }_{t}V(t,e(t)) =&\sum ^{n}_{i=1}\beta _{i}~_{0}D^{\alpha }_{t}|e_{i}(t)| \le \sum ^{n}_{i=1} \beta _{i}{\mathrm{sgn}}(e_{i}(t))~_{0}D^{\alpha }_{t}e_{i}(t)\\ =&\sum ^{n}_{i=1}\beta _{i} {\mathrm{sgn}}(e_{i}(t)) [-(k+\theta _{i}+\Delta a_{i}(t))e_{i}(t)\\&+\,\sum ^{n}_{j=1}(\nu _{ij}+\Delta b_{ij}(t))(f_{j}(y_{j}(t))-f_{j}(x_{j}(t)))]\\ \le&\sum ^{n}_{i=1} \beta _{i}[-k|e_{i}(t)|-\theta _{i}|e_{i}(t)|+|\Delta a_{i}(t)||e_{i}(t)|\\&+\,\sum ^{n}_{j=1}l_{j}(|\nu _{ij}|+|\Delta b_{ij}(t)|)|e_{j}(t)|]\\ =&\sum ^{n}_{i=1}\beta _{i}(-k|e_{i}(t)|-\theta _{i}|e_{i}(t)|+|\Delta a_{i}(t)||e_{i}(t)|)\\&+\,\sum ^{n}_{i=1}\sum ^{n}_{j=1}\beta _{j}l_{i}(|\nu _{ji}|+|\Delta b_{ji}(t)|)|e_{i}(t)|\\ =&-\,\sum ^{n}_{i=1} \left( k\beta _{i}+\theta _{i}\beta _{i}-\sum ^{n}_{j=1}|\nu _{ji}|\beta _{j}l_{i} -\,|\Delta a_{i}(t)|\beta _{i}\right. \\&\left. -\sum ^{n}_{j=1}|\Delta b_{ji}(t)|\beta _{j}l_{i}\right) |e_{i}(t)|\\ \le&-\,\sum ^{n}_{i=1} \left( k\beta _{i}+\theta _{i}\beta _{i}-\sum ^{n}_{j=1}|\nu _{ji}|\beta _{j}l_{i} -\,\Vert \Delta A(t)\beta \Vert \right. \\&\left. -\Vert \beta \Delta B(t)L\Vert \right) |e_{i}(t)|\\ \le&-\sum ^{n}_{i=1} \left( k\beta _{i}+\theta _{i}\beta _{i}-\sum ^{n}_{j=1}|\nu _{ji}|\beta _{j}l_{i} -M_{A}\Vert \beta \Vert \right. \\&\left. -\,M_{B}\Vert L\Vert \Vert \beta \Vert \right) |e_{i}(t)|. \end{aligned} \end{aligned}$$

According to the assumption \((A_{3})\), we have

$$\begin{aligned} k\beta _{i}+\underline{a_{i}}\beta _{i}-\sum ^{n}_{j=1}|b_{ji}|_{\mathrm{max}}l_{i}\beta _{i} \ge (M_{A}\Vert \beta \Vert +M_{B}\Vert L\Vert \Vert \beta \Vert +\lambda ). \end{aligned}$$

Then

$$\begin{aligned} k\beta _{i}+\theta _{i}\beta _{i}-\sum ^{n}_{j=1}l_{i}|\nu _{ji}|\beta _{j}\ge & {} k\beta _{i}+\underline{a_{i}}\beta _{j}-\sum ^{n}_{j=1}l_{i}|b_{ji}|_{\mathrm{max}}\beta _{j}\\\ge & {} M_{A}\Vert \beta \Vert +M_{B}\Vert L\Vert \Vert \beta \Vert +\lambda . \end{aligned}$$

Thus

$$\begin{aligned} \begin{aligned} _{0}D^{\alpha }_{t}V(t,e(t)) \le&-\,\sum ^{n}_{i=1} \left( k\beta _{i}+\theta _{i}\beta _{i}-\sum ^{n}_{j=1}|\nu _{ji}|\beta _{j}l_{i}\right. \\&\left. -\,M_{A}\Vert \beta \Vert -M_{B}\Vert L\Vert \Vert \beta \Vert \right) |e_{i}(t)|\\ \le&-\,\lambda \Vert e(t)\Vert . \end{aligned} \end{aligned}$$

By the Lemma 1, the error system (10) is Mittag-Leffler stable, that is

$$\begin{aligned} \Vert e(t)\Vert \le V(0,e(0))E_{\alpha }(-\lambda t^{\alpha }). \end{aligned}$$
(13)

Then, the equilibrium point of the error system, \(\overline{e}=0\) is Mittag-Leffler stable, which imply asymptotic stability, so

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }~||e(t)||=0. \end{aligned}$$
(14)

To sum up, according the definition 4, the robust synchronization between the systems (7) and (8) is achieved. The proof completes. \(\square\)

4 Numerical simulations

In this section, two examples are given to demonstrate the above results.

4.1 Chaos numerical simulation

The first example is given to display that the memristor-based fractional-order Hopfield neural networks with parameter uncertainties are the chaotic systems.

For system (7) and system (8), \(n=3\), \(w=(0,0,0)^{T}\), \(f(x)=({\mathrm{tanh}}(x_{1}), {\mathrm{tanh}}(x_{2}), {\mathrm{tanh}}(x_{3}))^{T}\), \(A={\mathrm{diag}}(a_{1}, a_{2}, a_{3})\), \(B=(b_{ij})_{n \times n}\), \(\Delta A = \Delta B= 0.1e^{-t}I\), and

$$\begin{aligned} a_{1}= & {} {\left\{ \begin{array}{ll} 1.00,&{}\quad |x_{1}(t)|\le 1\\ 1.05,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\quad a_{2}= {\left\{ \begin{array}{ll} 1.0,&{}\quad |x_{2}(t)|\le 1\\ 0.95,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\\ a_{3}= & {} {\left\{ \begin{array}{ll} 1.00,&{}\quad |x_{3}(t)|\le 1\\ 0.95,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\quad b_{11}= {\left\{ \begin{array}{ll} 2.00,&{}\quad |x_{1}(t)|\le 1\\ 2.05,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\\ b_{12}= & {} {\left\{ \begin{array}{ll} -1.2,&{}\quad |x_{1}(t)|\le 1\\ -1.1,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\quad b_{13}= {\left\{ \begin{array}{ll} 0,&{}\quad |x_{1}(t)|\le 1\\ 0,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\\ b_{21}= & {} {\left\{ \begin{array}{ll} 1.80,&{}\quad |x_{2}(t)|\le 1\\ 1.75,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\quad b_{22}= {\left\{ \begin{array}{ll} 1.710,&{}\quad |x_{2}(t)|\le 1\\ 1.715,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\\ b_{23}= & {} {\left\{ \begin{array}{ll} 1.15,&{}\quad |x_{2}(t)|\le 1\\ 1.10,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\quad b_{31}= {\left\{ \begin{array}{ll} -4.75,&{}\quad |x_{3}(t)|\le 1\\ -4.70,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\\ b_{32}= & {} {\left\{ \begin{array}{ll} 0,&{}\quad |x_{3}(t)|\le 1\\ 0,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\quad b_{33}= {\left\{ \begin{array}{ll} 1.10,&{}\quad |x_{3}(t)|\le 1\\ 1.05,&{}\quad |x_{3}(t)|>1. \end{array}\right. } \end{aligned}$$

The corresponding master-slave systems can be obtained:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} _{0}D^{\alpha }_{t}x_{1}=-(a_{1}+0.1e^{-t})x_{1}+(b_{11}+0.1e^{-t}){\mathrm{tanh}}(x_{1})\\ \qquad +\,b_{12}{\mathrm{tanh}}(x_{2}),\\ _{0}D^{\alpha }_{t}x_{2} =-(a_{2}+0.1e^{-t})x_{2}+b_{21}{\mathrm{tanh}}(x_{1})+(b_{22}\\ \qquad +\,0.1e^{-t}){\mathrm{tanh}}(x_{2})+b_{23}{\mathrm{tanh}}(x_{3}),\\ _{0}D^{\alpha }_{t}x_{3}=-(a_{3}+0.1e^{-t})x_{3}+b_{31}{\mathrm{tanh}}(x_{1})+(b_{33}\\ \qquad +\,0.1e^{-t}){\mathrm{tanh}}(x_{3}). \end{array}\right. } \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} _{0}D^{\alpha }_{t}y_{1}=-(a_{1}+0.1e^{-t})y_{1}+(b_{11}+0.1e^{-t}){\mathrm{tanh}}(y_{1})\\ \qquad +\,b_{12}{\mathrm{tanh}}(y_{2})-k(y_{1}-x_{1}),\\ _{0}D^{\alpha }_{t}y_{2}=-(a_{2}+0.1e^{-t})y_{2}+b_{21}{\mathrm{tanh}}(y_{1})+(b_{22}\\ \qquad +\,0.1e^{-t}){\mathrm{tanh}}(y_{2})+b_{23}{\mathrm{tanh}}(y_{3})-k(y_{2}-x_{2}),\\ _{0}D^{\alpha }_{t}y_{3}=-(a_{3}+0.1e^{-t})y_{3}+b_{31}{\mathrm{tanh}}(y_{1})+(b_{33}\\ \qquad +\,0.1e^{-t}){\mathrm{tanh}}(y_{3})-k(y_{3}-x_{3}). \end{array}\right. } \end{aligned} \end{aligned}$$
(16)

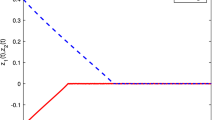
Choose the initial value \(x(0)=(2,-\,5,3)^{T}\), \(y(0)=(10,8,-\,9)^{T}\), \(L={\mathrm{diag}}(1,1,1)\), \(\Vert L\Vert =1\), \(\beta ={\mathrm{diag}}(3,1,1)\), \(\Vert \beta \Vert =3\), \(k=5\), \(\lambda =1.7\), \(\alpha =0.98\) to get Figs. 1, 2, 3, 4.

Fig. 1
figure 1

The states of systems (15) and (16) with chaotic behaviors

Full size image
Fig. 2
figure 2

The state of the master system (15)

Full size image
Fig. 3
figure 3

The state of the slave system (16)

Full size image
Fig. 4
figure 4

The state of the error system between (15) and (16)

Full size image

Figure 1 displays that the memristor-based fractional-order Hopfield neural networks with parameter uncertainties are chaotic, which means that it is significant to study the synchronization between the systems. And the next three figures show that the synchronization is realized (Figs. 5, 6, 7).

4.2 Synchronization numerical simulation

Next, this example can further prove that the robust synchronization is realized for the two memristor-based fractional-order Hopfield neural networks with parameter uncertainties.

For system (7) and system (8), \(n=3\), \(w=(0,0,0)^{T}\), \(f(x)=({\mathrm{tanh}}(x_{1})\), \({\mathrm{tanh}}(x_{2}), {\mathrm{tanh}}(x_{3}))^{T}\),

$$\begin{aligned} a_{i}&= {} {\left\{ \begin{array}{ll} 1.0,&{}\quad |x_{i}(t)|\le 1\\ 1.1,&{}\quad |x_{i}(t)|>1. \end{array}\right. }\qquad A={\mathrm{diag}}(a_{1}, a_{2}, a_{3}).\\ b_{11}&= {} {\left\{ \begin{array}{ll} 2.0,&{}\quad |x_{1}(t)|\le 1\\ 1.9,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\qquad b_{12}= {\left\{ \begin{array}{ll} -\,1.1,&{}\quad |x_{1}(t)|\le 1\\ -\,1.2,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\\ b_{13}&= {} {\left\{ \begin{array}{ll} 0,&{}\quad |x_{1}(t)|\le 1\\ 0,&{}\quad |x_{1}(t)|>1. \end{array}\right. }\qquad b_{21}= {\left\{ \begin{array}{ll} 1.80,&{}\quad |x_{2}(t)|\le 1\\ 1.75,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\\ b_{22}&= {} {\left\{ \begin{array}{ll} 1.71,&{}\quad |x_{2}(t)|\le 1\\ 1.70,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\qquad b_{23}= {\left\{ \begin{array}{ll} 1.15,&{}\quad |x_{2}(t)|\le 1\\ 1.10,&{}\quad |x_{2}(t)|>1. \end{array}\right. }\\ b_{31}&= {} {\left\{ \begin{array}{ll} -\,4.75,&{}\quad |x_{3}(t)|\le 1\\ -\,4.70,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\qquad b_{32}= {\left\{ \begin{array}{ll} 0,&{}\quad |x_{3}(t)|\le 1\\ 0,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\\ b_{33}&= {} {\left\{ \begin{array}{ll} 1.0,&{}\quad |x_{3}(t)|\le 1\\ 1.1,&{}\quad |x_{3}(t)|>1. \end{array}\right. }\\ \Delta A(t)&= {} {\mathrm{diag}}(0.5\sin (t), 0, 0.2\cos (t)),\\ \Delta B&= {} \left[ {\begin{array}{ccc} {{0}} &{}\quad {{0.2\cos (t)}}&{}\quad {{0}} \\ {{0.1\sin (t)}} &{}\quad {{0}} &{}\quad {{0}} \\ {{0}} &{}\quad {{0}} &{}\quad {{0.3\cos (t)}} \end{array}} \right] . \end{aligned}$$

The master-slave system are also obtained:

$$\begin{aligned}&{\left\{ \begin{array}{ll} _{0}D^{\alpha }_{t}x_{1}=-(a_{1}+0.5\sin (t))x_{1}+b_{11}{\mathrm{tanh}}(x_{1})\\ \qquad +\,(b_{12}+0.2\cos (t)){\mathrm{tanh}}(x_{2}),\\ _{0}D^{\alpha }_{t}x_{2}=-a_{2}x_{2}+(b_{21}+0.1\sin (t)){\mathrm{tanh}}(x_{1})\\ \qquad +\,b_{22}+{\mathrm{tanh}}(x_{2})+b_{23}{\mathrm{tanh}}(x_{3}),\\ _{0}D^{\alpha }_{t}x_{3}=-(a_{3}+0.2\sin (t))x_{3}+b_{31}{\mathrm{tanh}}(x_{1})\\ \qquad +\,(b_{33}+0.3\cos (t)){\mathrm{tanh}}(x_{3}). \end{array}\right. }\end{aligned}$$
(17)
$$\begin{aligned}&{\left\{ \begin{array}{ll} _{0}D^{\alpha }_{t}y_{1}=-(a_{1}+0.5\sin (t))y_{1}+b_{11}{\mathrm{tanh}}(y_{1})\\ \qquad +\,(b_{12}-0.2\cos (t)){\mathrm{tanh}}(y_{2})-ke_{1},\\ _{0}D^{\alpha }_{t}y_{2}=-a_{2}y_{2}+(b_{21}+0.1\sin (t)){\mathrm{tanh}}(y_{1})\\ \qquad +\,b_{22}{\mathrm{tanh}}(y_{2})+b_{23}{\mathrm{tanh}}(y_{3})-ke_{2},\\ _{0}D^{\alpha }_{t}y_{3}=-(a_{3}+0.2\sin (t))y_{3}+b_{31}{\mathrm{tanh}}(y_{1})\\ \qquad +\,(b_{33}+0.3\cos (t)){\mathrm{tanh}}(y_{3})-ke_{3}. \end{array}\right. } \end{aligned}$$
(18)

Choose the initial value \(x(0)=(3,-\,4,2)^{T}\), \(y(0)=(-\,4,1,-\,1)^{T}\), \(L={\mathrm{diag}}(1,1,1)\), \(\Vert L\Vert =1\), \(\alpha =0.98\), \(\beta ={\mathrm{diag}}(3,1,1)\), \(\Vert \beta \Vert =3\), for the control law, \(k=5\), \(\lambda =0.69\), it is obvious that the assumptions (\({\mathrm{A}}_{1}\))–(\({\mathrm{A}}_{3}\)) hold, then get the following figures:

Fig. 5
figure 5

The state of the master system (17)

Full size image
Fig. 6
figure 6

The state of the slave system (18)

Full size image
Fig. 7
figure 7

The state of the error system between (17) and (18)

Full size image

From the figures above, we can further know that the robust synchronization is truly realized for two memristor-based fractional-order Hopfield neural networks with parameter uncertainties and the control law is effective.

5 Conclusion

The memristor, as a new fourth electrical element, is a hot topic in the science since its the real implementation. Many scientists focus much attention on it and try to build the relevant model with memristor. Fractional calculus and neural networks both enjoy high popularity because of their widespread applications in various fields. The dynamics behaviors of the memristor-based neural networks and the fractional-order neural networks are both the hot topic in the scientific community. So in this paper, it is necessary for us to analysis the dynamics of the memristor-based fractional-order neural networks which can accurately emulate the human brain. Moreover, the fractional-order Lyapunov direct method is employed to achieve the robust synchronization between the two memristor-based fractional-order Hopfield neural networks with parameter uncertainties which needs less calculation, and finally, the numerical simulations show the systems we argued are chaotic and the control law in the slave system is effective.

The memristor-based fractional-order neural networks are meaningful. It is necessary for us to do more future work about it and explore better method to handle the error system, to make it more accurate, which is an ongoing topic in research area.