1 Introduction

It is well known that, in the past decade, based on the approximating capability of fuzzy logic systems or neural networks, many adaptive fuzzy and NN state feedback control design methods have been proposed for uncertain nonlinear systems in the strict-feedback form [1–12]. The authors in [1–8] presented several adaptive fuzzy or NN control schemes for uncertain MIMO nonlinear systems in strict-feedback form, in which the system model is different from the statements in [9, 10]. Meanwhile, authors in [11, 12] investigated adaptive fuzzy and NN decentralized control design problem for uncertain large-scale nonlinear systems in strict-feedback form. However, the above-mentioned control schemes are all required that the full-state information must be measurable. To relax the restriction in [1–12], the observer-based adaptive fuzzy and NN output-feedback control design problem has been developed, and many interesting research results have also been obtained [13–17], where the works in [13–15] are for a class of uncertain MIMO nonlinear systems and the works in [16, 17] are for a class of uncertain nonlinear interconnected systems.

It should be mentioned that all the aforementioned results are feasible under presupposition that the considered systems have a strict-feedback form or pure-feedback form. Therefore, they cannot be employed in controlling the uncertain nonlinear systems with nonstrict-feedback form. Recently, the control problem of the nonstrict-feedback systems has attracted a great deal of attention, for example in [18–23]. To overcome the difficulty in the traditional adaptive backstepping control design, by utilizing the monotonously increasing property of the bounding functions, authors in [18, 19] developed the variables separation technique, and subsequently proposed two adaptive fuzzy control design methods for single-input and single-output (SISO) and MIMO nonstrict-feedback nonlinear systems, respectively. Then in [20–22], authors proposed different control methods for SISO and MIMO nonstrict-feedback nonlinear systems with input nonlinearity. More recently, the observer-based adaptive NN output-feedback control schemes have been developed in [23, 24] for the SISO nonstrict-feedback nonlinear systems, and the immeasurable state problem of SISO nonstrict-feedback systems has been solved, but the situation of MIMO nonstrict-feedback nonlinear systems is not considered. And also the above-mentioned results are based on the assumption that the unknown functions must satisfy the monotonously increasing property of the bounding functions, which are not suitable for many practical engineering systems. Although the authors in [25] proposed an observer-based adaptive fuzzy control design method for SISO nonlinear system in nonstrict-feedback form, the proposed control method cannot be applied to control the MIMO nonstrict-feedback nonlinear systems considered in this paper. In addition, the controlled nonstrict-feedback nonlinear systems considered in [18–25] did not contain the input quantization.

As stated in [26–28], since many practical engineering systems contain the quantized control input, such as hydraulic systems, hybrid systems, and automotive networked control systems, it is necessary to investigate the control design problem for quantized systems. The work in [28] first proposed a control design method for nonlinear systems with the input quantization. By using backstepping design technique, the authors in [29] proposed the adaptive quantized control method for a class of SISO uncertain nonlinear systems in strict-feedback form. It should be pointed out that [28, 29] only considered the nonlinear uncertainties, and also the nonlinear functions are required to be known or can be linearly parameterized. To eliminate the above limitations, the authors in [30] presented a novel fuzzy adaptive controller for a class of stochastic nonlinear systems, and the authors in [31] extended the results in [30] to a class of uncertain switched nonlinear systems with unmeasured states. Although the results on the adaptive quantized control design have achieved some progress, the controlled plants in the above-mentioned results are strict-feedback nonlinear systems, and they cannot solve the control design problem for the nonlinear systems in nonstrict-feedback form.

Based on the above presentations, an observer-based adaptive fuzzy control problem is studied in this paper for MIMO nonstrict-feedback nonlinear systems. The considered uncertain MIMO nonstrict-feedback systems contain unmeasurable states, unknown nonlinearities, and input quantization. By utilizing fuzzy logic systems to identify the unknown nonlinear functions, a fuzzy state observer is constructed to obtain the unmeasurable states. By transforming the hysteretic quantized input into a new nonlinear decomposition and based on DSC control design, an observer-based adaptive fuzzy quantized control method is presented. It is proved that the closed-loop system is stable in the sense of Lyapunov function stability theory. Compared to the previous works, the following contributions are worth to be emphasized as follows.

  1. 1.

    The adaptive fuzzy control scheme proposed in this paper has solved the unmeasured states and quantized input problems for MIMO nonstrict-feedback systems. Although the references [26–31] also investigated the input quantization design problem, they all required that the states must be available for measurement. Moreover, the controlled plants are SISO strict-feedback nonlinear systems, not the MIMO nonstrict-feedback systems under consideration in this study.

  2. 2.

    The proposed adaptive quantized fuzzy control design method only utilizes the property of fuzzy basis functions, instead of the restrictive assumption in the literature [18–24] that the unknown functions must satisfy the monotonously increasing property of the bounding functions. Therefore, this paper has reduced the conservatism of the control schemes in [18–24].

  3. 3.

    The proposed control scheme has overcome the problem of “explosion of complexity” by introducing into DSC technique into the fuzzy adaptive quantized control design. Therefore, the control structure of this paper is much simpler than those of the previous literature [18–30].

The rest of the paper is organized as follows: the problem formulations and preliminaries are present in Sect. 2. Adaptive quantized control design is given in Sect. 3. In Sect. 4, the simulation study is shown with the aim to validate the effectiveness of the proposed method. Section 5 contains the conclusion.

2 Problem formulation and preliminaries

2.1 System descriptions

Consider the uncertain MIMO nonstrict-feedback systems:

$$\left\{ \begin{aligned} \dot{x}_{{j,i_{j} }}& = f_{{j,i_{j} }} (X) + x_{{j,i_{j} + 1}} + d_{{j,i_{j} }} (t),\quad i_{j} = 1, \ldots ,m_{j} - 1, \hfill \\ \dot{x}_{{j,m_{j} }}& = f_{{j,m_{j} }} (X,\underline{u}_{j - 1} ) + q_{j} (u_{j} ) + d_{{j,m_{j} }} (t) \hfill \\ y_{j} &= x_{j,1} \hfill \\ \end{aligned} \right.$$
(1)

where u j  ∊ R and y = [y 1, y 2, …, y n ]T ∊ R n are the input and output for the first jth subsystem, respectively, with u j-1 = [u 1, …, u j−1]T ∊ R j−1, and q j (u j ) ∊ ℜ is the output of the hysteresis quantizer; \(\underline{x}_{{j,i_{j} }} = [x_{j,1} , \ldots ,x_{{j,i_{j} }} ]^{\text{T}} \in R^{{i_{j} }}\), (j = 1, …, n, i j  = 1, …, m j ), is the state vector of the first i j differential equations of the jth subsystem; \(d_{{j,i_{j} }} (t)\) is the external disturbance bounded by an unknown constant \(d_{{j,i_{j} }}^{*}\), i.e., \(\left| {d_{{j,i_{j} }} (t)} \right| \le d_{{j,i_{j} }}^{*}\); \(f_{{j,i_{j} }} ( \cdot )\) is an unknown smooth nonlinear function. X = [x T1 , …, x T n ]T with \(x_{j} = [x_{j,1} , \ldots ,x_{{j,m_{j} }} ]^{\text{T}}\).

In this paper, a hysteresis quantizer method is adopted to avoid the chattering problem. q j (u j ) denotes a quantized input signal. Similar to [28–30], the quantized input in this paper is described as:

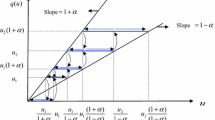
$$q_{j} (u_{j} )\mathop = \limits^{\Delta } \left\{ \begin{array}{ll} u_{i,j} \text{sgn} (u_{j} ),& \quad {\text{if}}\;\;\frac{{u_{i,\sigma (t)} }}{{1 + \delta_{j} }} < \left| {u_{j} } \right| \le u_{i,j} ,\dot{u}_{j} < 0,\;{\text{or}} \hfill \\&\qquad u_{i,j} < \left| {u_{j} } \right| \le \frac{{u_{i,j} }}{{1 - \delta_{j} }},\dot{u}_{j} > 0 \hfill \\ u_{i,j} (1 + \delta_{j} )\text{sgn} (u_{j} ),& \quad{\text{if}}{\kern 1pt} \;u_{i,j} < \left| {u_{j} } \right| \le \frac{{u_{i,j} }}{{1 - \delta_{j} }},\dot{u}_{j} < 0,\;{\text{or}} \hfill \\ & \qquad \frac{{u_{i,j} }}{{1 - \delta_{j} }} \le \left| {u_{j} } \right| \le \frac{{u_{i,j} (1 + \delta_{j} )}}{{1 - \delta_{j} }},\dot{u}_{j} > 0 \hfill \\ 0,& \quad \,{\text{if}}\;\;0 \le \left| {u_{j} } \right| < \frac{{u_{\hbox{min} } }}{{1 + \delta_{j} }},\dot{u}_{j} < 0,\;{\text{or}} \hfill \\ &\qquad \frac{{u_{\hbox{min} } }}{{1 + \delta_{j} }} \le \left| {u_{j} } \right| \le u_{\hbox{min} } ,\dot{u}_{j} > 0 \hfill \\ q_{j} (u_{j}^{{}} (t^{ - } )),& \quad {\text{othercase}} \hfill \\ \end{array} \right.$$
(2)

where u j  = ρ (1−i) u 0,j with integer i = 1, 2, … and \(\delta_{j} = \frac{{1 - \rho_{j} }}{{1 + \rho_{j} }}\) with parameters u 0,j  > 0 and 0 < ρ < 1. q j (u j ) is in the set U = {0, ± u i,j , ± u i,j (1 − δ j )}. \(u_{\hbox{min} } = \frac{{u_{0,j} }}{{1 + \delta_{j} }}\) is the bound of the dead zone for q j (u j ). The map of the hysteretic quantizer q j (u j ) for u j  > 0 is shown in Fig. 1.

Fig. 1
figure 1

Map of q j (u j ) for u j  > 0

Full size image

Remark 1

The parameter ρ j can be seen as a measure of quantization density. If ρ j is smaller, then the quantizer will become coarser. Note that when ρ j  → 0, δ j  → 1, then q j (u j ) will have fewer quantization levels as u j ranges over that interval. The control action for the hysteretic quantizer (2) should be satisfied in terms of existence and uniqueness of solution of the closed-loop systems. The parameter ρ j in (2) is not given a prior since that system (1) is uncertain. Instead, it can be chosen by using a guideline to guarantee that the closed-loop system is stable.

In order to propose a suitable control scheme, we decompose the hysteretic quantizer q j (u j ) into the following form:

$$q_{j} (u_{j} ) = D_{j} (u_{j} )u_{j} + s_{j} (t)$$
(3)

where D j (u j ) and s j (t) denote nonlinear functions. In view of the nonlinearity D j (u j ) and s j (t), the following lemma is needed.

Lemma 1 [29 30 ]

The nonlinearities D j (u j ) and s j (t) satisfy

$$1 - \delta_{j} \le D_{j} \left( {u_{j} } \right) \le 1 + \delta_{j} , \, \left| {s_{j} \left( t \right)} \right| \le u_{ \hbox{min} }$$
(4)

Proof

From Fig. 1 and sector bound property, for |u j | ≥ u min, one has

$$1 - \delta_{j} \le s_{j} (u_{j} ) \le 1 + \delta_{j}$$
(5)

where \(s_{j} (u_{j} ) = \frac{{q_{j} (u_{j} )}}{{u_{j} }}\).

For |u j | ≤ u jmin, q j (u j ) = 0 from the definition (3), we have

$$0 = D_{j} (u_{j} )u_{j} + s_{j} (t)$$
(6)

Define

$$D_{j} (u_{j} ) = \left\{ \begin{aligned} s_{j} (u_{j} ),\;\;\left| {u_{j} } \right| > u_{\hbox{min} } \hfill \\ 1,\;\;\quad \quad \left| {u_{j} } \right| \le u_{\hbox{min} } \hfill \\ \end{aligned} \right.$$
(7)

and

$$s_{j} (t) = \left\{ \begin{aligned} 0,\;\;\quad \;\left| {u_{j} } \right| > u_{\hbox{min} } \hfill \\ - u_{j} ,\;\;\left| {u_{j} } \right| \le u_{\hbox{min} } \hfill \\ \end{aligned} \right.$$
(8)

Then, q j (u j ) = D j (u j )u j  + s j (t) holds, where D j (u j ) and s j (t) satisfy (4), respectively. The proof is completed.

Control objective: The control objective of this paper is to develop the suitable adaptive quantized control inputs u j for systems (1), so that all the variables are bounded, and the systems output y j (t) can track the desired trajectories y j,r (t), regardless of the unknown function \(f_{{j,i_{j} }} (X),\) unmeasured states x i , and quantized input signal q j (u j ), j = 1, …, n, i j  = 1, …, m j .

Assumption 1 ([18–21])

The desired trajectories y j,r (t) are continuous and have the following property

$$\varPi_{j,0} = \{ (y_{j,r} ,\dot{y}_{j,r} ,\ddot{y}_{j,r} ):y_{j,r}^{2} + \dot{y}_{j,r}^{2} + \ddot{y}_{j,r}^{2} \le \varXi_{j,0} \}$$

where Ξ j,0 is a positive constant.

2.2 Fuzzy logic systems

A fuzzy logic system consists of four parts: the knowledge base, the fuzzifier, the fuzzy inference engine working on fuzzy rules, and the defuzzifier. The knowledge base for FLS comprises a collection of fuzzy if–then rules, which can be described as follows:

R i : if x 1 is F l1 , and x 2 is F l2 and …and, x n is F l n , then y is G l, l = 1, 2, …, N. where x = (x 1, …, x n )T and yare the FLS input and output, respectively. Fuzzy sets F l i and G l are associated with the fuzzy functions \(\mu_{{F_{i}^{l} }}\) and \(\mu_{{G^{l} }}\), respectively. N is the rules number.

According to the singleton function, center average defuzzification, the FLS becomes

$$y(x) = \frac{{\sum\nolimits_{l = 1}^{N} {\bar{y}_{l} \prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )} } }}{{\sum\nolimits_{l = 1}^{N} {[\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{l} }} (x_{i} )]} } }}$$
(9)

where \(\bar{y}_{l} = \max_{y \in R} \mu_{{G^{l} }} (y)\).

Let the fuzzy basis functions are

$$\varphi_{l} (x) = \frac{{\mathop \prod \nolimits_{i = 1}^{n} \mu_{{F_{i}^{l} }} (x_{i} )}}{{\sum\nolimits_{i = 1}^{N} {[\mathop \prod \nolimits_{i = 1}^{n} \mu_{{F_{i}^{l} }} (x_{i} )]} }} .$$
(10)

Denoting \(\theta^{T} = (\bar{y}_{1} ,\bar{y}_{2} , \cdots ,\bar{y}_{N} ) = (\theta_{1} ,\theta_{2} , \cdots ,\theta_{N} )\) and φ(x) = (φ 1(x), …, φ N (x))T, then FLS (10) can be rewritten as

$$y(x) = \theta^{\text{T}} \varphi (x)$$
(11)

Lemma 2 ([32])

Let f(x) be a continuous function defined on a compact set Ω. Then, for any constant ɛ > 0, there exists a fuzzy logic system (11) such as

$$\mathop {\sup }\limits_{x \in \varOmega } \left| {f(x) - \theta^{\text{T}} \varphi (x)} \right| \le \varepsilon$$
(12)

3 Adaptive quantized control design

In the following section, a fuzzy state observer will be designed first, then an adaptive fuzzy quantized tracking control method will be developed by utilizing the DSC backstepping design method, and the stability of the control system will be proved.

Assume that the FLSs are as follows:

$$\begin{aligned} \hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }} } \right.) = \theta_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\hat{X}),i_{j} = 1,2, \ldots ,m_{j} - 1 \hfill \\ \hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }} } \right.) = \theta_{{j,m_{j} }}^{\text{T}} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ),j = 1,2, \ldots ,n \hfill \\ \end{aligned}$$
(13)

Then, the optimal approximated parameter vectors \(\theta_{{j,i_{j} }}^{*}\) and \(\theta_{{j,m_{j} }}^{*}\) are defined as

$$\begin{aligned} \theta_{{j,i_{j} }}^{*} &= \arg \min_{{\theta_{{j,i_{j} }} \in \varOmega_{{j,i_{j} }} }} [\sup_{{(\hat{X}) \in U_{{j,i_{j} }} }} \left| {\hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }} } \right.) - f_{{j,i_{j} }} (X)} \right|] \hfill \\ \theta_{{j,m_{j} }}^{*} &= \arg \min_{{\theta_{{j,m_{j} }} \in \varOmega_{{j,m_{j} }} }} [\sup_{{(\hat{X},\underline{u}_{j - 1} ) \in U_{{j,m_{j} }} }} \left| {\hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }} } \right.)} \right.\left. { - f_{{j,m_{j} }} (X,\underline{u}_{j - 1} )} \right|] \hfill \\ \end{aligned}$$

where \(\varOmega_{{j,i_{j} }}\), \(U_{{j,i_{j} }}\), \(\varOmega_{{j,m_{j} }}\), and \(U_{{j,m_{j} }}\) are compact regions for \(\theta_{{j,i_{j} }}\), \(\hat{X}\), \(\theta_{{j,m_{j} }}\), and \((\hat{X},\underline{u}_{j - 1} )\), respectively.

Use the FLSs \(\hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }} } \right.)\) and \(\hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }} } \right.)\) to approximate the nonlinear functions in systems (1), and let the approximation errors \(\varepsilon_{{j,i_{j} }}\) as

$$\varepsilon_{{j,i_{j} }} = f_{{j,i_{j} }} (X) - \hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }}^{ * } } \right.)$$
$$\varepsilon_{{j,m_{j} }}^{{}} = f_{{j,m_{j} }} (X,\underline{u}_{j - 1} ) - \hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }}^{ * } } \right.)$$

where \(\varepsilon_{{j,i_{j} }}\) is bounded by the unknown constant \(\varepsilon_{{j,i_{j} }}^{ * }\), i.e., \(\left| {\varepsilon_{{j,i_{j} }} } \right| \le \varepsilon_{{j,i_{j} }}^{ * }\) j = 1, …, n, i j  = 1, …, m j .

Rewrite (1) as

$$\left\{ \begin{aligned} \dot{x}_{j} = \,& A_{0} x_{j} + \sum\nolimits_{{i_{j} = 1}}^{{m_{j} - 1}} {B_{{j,i_{j} }} f_{{j,i_{j} }} (X)} + B_{{j,m_{j} }} [f_{{j,m_{j} }} (X,\underline{u}_{j - 1} ) + q_{j} (u_{j} )] + d_{j} (t) \\ y_{j} =\, & C_{j} x_{j} \\ \end{aligned} \right.$$
(14)

where \(A_{j} = \left[ {\begin{array}{*{20}c} 0 & {} & {} & {} \\ \vdots & {} & I & {} \\ 0 & 0 & \cdots & 0 \\ \end{array} } \right] ,\) \(B_{{m_{j} }} = [0\;\; \cdots \;\;1]^{\text{T}}\),\(B_{{j,i_{j} }} = [\underbrace {0 \cdots 0\;1}_{{i_{j} }} \cdots 0]^{\text{T}}\), \(d_{j} (t) = [\begin{array}{*{20}c} {d_{j,1} } & \cdots & {d_{{j,m_{j} }} } \\ \end{array} ]^{\text{T}}\), C j  = [1···0].

Similar to the state observer in [15, 16], in this paper, we design the following state observer

$$\begin{aligned} \dot{\hat{x}}_{j}& = A_{j} \hat{x}_{j} + K_{j} y_{j} + \sum\limits_{{i_{j} = 1}}^{{m_{j} - 1}} {B_{{j,i_{j} }} \hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }} } \right.)} \hfill \\\quad+ B_{{j,m_{j} }} \hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }} } \right.) + B_{{j,m_{j} }} q_{j} (u_{j} ) \hfill \\ \hat{y}_{j} &= C_{j} \hat{x}_{j} \hfill \\ \end{aligned}$$
(15)

where \(A_{j} = \left[ {\begin{array}{*{20}c} { - k_{j,1} } & {} & {} & {} \\ \vdots & {} & I & {} \\ { - k_{{j,m_{j} }} } & 0 & \cdots & 0 \\ \end{array} } \right] ,\) \(K_{j} = [k_{j,1} \cdots k_{{j,m_{j} }} ]^{\text{T}}\), and \(\hat{X}\) is designed to estimate the state vector X.

Let the vector K j to satisfy matrix A j be a strict Hurwitz matrix. Then, choose a matrix Q j  = Q T j  > 0, there will be a matrix P j  = P T j  > 0 satisfying

$$A_{j}^{\text{T}} P_{j} + P_{j} A_{j} = - Q_{j}$$
(16)

The observer error vector e j is designed as

$$e_{j} = [e_{j,1} ,e_{j,2} , \cdots ,e_{{j,m_{j} }} ]^{\text{T}} = x_{j} - \hat{x}_{j}$$
(17)

Then, from (14) and (16), we can obtain

$$\begin{aligned} \dot{e}_{j} &= A_{j} e_{j} + \sum\limits_{{i_{j} = 1}}^{{m_{j} - 1}} {B_{{j,i_{j} }} } [f_{{j,i_{j} }} (\left. {\hat{X}} \right|\theta_{{j,i_{j} }}^{*} ) - \hat{f}_{{j,i_{j} }} (\hat{X}\left| {\theta_{{j,i_{j} }} } \right.) + \varepsilon_{j} + d_{j} (t)] \\& \quad + B_{{j,m_{j} }} [f_{{j,m_{j} }} (\hat{X},\left. {\underline{u}_{j - 1} } \right|\theta_{{j,m_{j} }}^{*} ) - \hat{f}_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} \left| {\theta_{{j,m_{j} }} } \right.)] \\ &= A_{j} e_{j} + \sum\limits_{{i_{j} = 1}}^{{m_{j} }} {B_{{j,i_{j} }} } \tilde{\theta }_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} + \varepsilon_{j} + d_{j} (t) \\ \end{aligned}$$
(18)

where \(\varepsilon_{j} = [\varepsilon_{j,1,} , \ldots ,\varepsilon_{{j,m_{j} }} ]^{\text{T}}\) and \(\tilde{\theta }_{{j,i_{j} }} = \theta_{{j,i_{j} }}^{*} - \theta_{{j,i_{j} }}\).

We choose the Lyapunov function candidate V 0 for (18) as V 0 = ∑  n j=1 V j,0 = ∑  n j=1 e T j P j e j , and then from (15) and (18), the time derivative of V 0 follows that

$$\dot{V}_{0} \le \sum\limits_{j = 1}^{n} {\bigg[ - p_{j,0} \left\| {e_{j} } \right\|^{2} } + \frac{1}{{\sigma_{j} }}\sum\limits_{{i_{j} = 1}}^{{m_{j} }} {\tilde{\theta }_{{j,i_{j} }}^{\text{T}} \tilde{\theta }_{{j,i_{j} }} } + L_{j,0} \bigg]$$
(19)

where p j,0 = λ min(Q j ) − r j  − 1 − (σ j  + 1)m j ‖P j ‖2, λ min(Q j ) is the smallest eigenvalue of matrix Q j , \(L_{j,0} = \left\| {P_{j} } \right\|^{2} \left\| {\varepsilon_{j}^{*} } \right\|^{2} + \sum\nolimits_{{i_{j} = 1}}^{{m_{j} }} {d_{{j,i_{j} }}^{*2} }\).

In the following, the process of controller design has been divided into m j steps, and each step is based on the following change of coordinates:

$$z_{j,1} = y_{j} - y_{j,r} ,z_{{j,i_{j} }} = \hat{x}_{{j,i_{j} }} - \vartheta_{{j,i_{j} }}$$
(20)
$$\chi_{{j,i_{j} }} = \vartheta_{{j,i_{j} }} - \alpha_{{j,i_{j} - 1}} ,$$
(21)

where \(z_{{j,i_{j} }}\)(\(j = 1, \ldots ,n; \, \;i_{j} = 2, \ldots ,m_{j}\)) is error surface, \(\vartheta_{{j,i_{j} }}\) is a state variable which will be defined later,\(\alpha_{{j,i_{j} - 1}}\) are intermediate control functions, and \(\chi_{{j,i_{j} }}\) is called the output error of the first-order filter.

  • Step 1 Since \(x_{j,2} = \hat{x}_{j,2} + e_{j,2}\), we can easily obtain the time derivative of z j,1 as

    $$\begin{aligned} \dot{z}_{j,1} =& z_{j,2} + \chi_{j,2} + \alpha_{j,1} + \theta_{1,k}^{\text{T}} \varphi_{1,k} (\hat{x}_{1} ) + \theta_{j,1}^{*T} \varphi_{j,1} (\hat{X}) - \theta_{1,k}^{{*{\text{T}}}} \varphi_{1,k} (\hat{x}_{1} ) \\ &+ \tilde{\theta }_{1,k}^{\text{T}} \varphi_{1,k} (\hat{x}_{1} ) + e_{j,2} - \dot{y}_{j,r} + \varepsilon_{j,1} + d_{j,1} \\ \end{aligned}$$
    (22)

    where \(\tilde{\theta }_{j,1} = \theta_{j,1}^{*} - \theta_{j,1}\). Choose the Lyapunov function candidate as

    $$V_{1} = \sum\limits_{j = 1}^{n} {V_{j,1} } = \sum\limits_{j = 1}^{n} {\bigg(V_{j,0} + \frac{1}{2}z_{j,1}^{2} + \frac{1}{{2\gamma_{j,1} }}\tilde{\theta }_{j,1}^{\rm T} \tilde{\theta }_{j,1} + \frac{1}{{2r_{j,1} }}\tilde{\varTheta }_{j,1}^{2} } \bigg)$$
    (23)

    where γ j,1 > 0 and δ j,1 > 0 are design parameters, and \(\tilde{\varTheta }_{{j,i_{j} }} = \varTheta_{{j,i_{j} }}^{*} - \varTheta_{{j,i_{j} }}\), \(\varTheta_{{j,i_{j} }}^{*} = \left\| {\theta_{{j,i_{j} }}^{ * } } \right\|^{2}\), \(\varTheta_{{j,i_{j} }}\) is the estimate of \(\varTheta_{{j,i_{j} }}^{*}\).

    From (22) and (23), the time derivative of V 1 satisfies

    $$\begin{aligned} \dot{V}_{1} &\le \, \dot{V}_{0} + \sum\limits_{j = 1}^{n} {\bigg(z_{j,1} (} z_{j,2} + \chi_{j,2} + \alpha_{j,1} + \theta_{j,1}^{\text{T}} \varphi_{j,1} (\hat{x}_{j,1} ) + \theta_{j,1}^{{*{\text{T}}}} \varphi_{j,1} (\hat{X}) - \theta_{j,1}^{{*{\text{T}}}} \varphi_{j,1} (\hat{x}_{j,1} ) \\& \quad + \tilde{\theta }_{j,1}^{\text{T}} \varphi_{j,1} (\hat{x}_{j,1} ) + e_{j,2} - \dot{y}_{j,r} \\ & \quad+\,\varepsilon_{j,1} + d_{j,1} ) + \frac{1}{{\gamma_{j,1} }}\tilde{\theta }_{j,1}^{\rm T} \dot{\tilde{\theta }}_{j,1} + \frac{1}{{r_{j,1} }}\tilde{\varTheta }_{j,1}^{\rm T} \dot{\tilde{\varTheta }}_{j,1} \bigg) \\ \end{aligned}$$
    (24)

By using the completing squares, we have

$$z_{j,1} (e_{j,2} + \varepsilon_{j,1} + d_{j,1} ) \le \frac{3}{2}z_{j,1}^{2} + \frac{1}{2}\left\| {e_{j} } \right\|^{2} + \frac{1}{2}\varepsilon_{j,1}^{ * 2} + \frac{1}{2}d_{j,1}^{*2}$$
(25)
$$z_{j,1} (\theta_{j,1}^{{*{\text{T}}}} \varphi_{j,1} (\hat{X}) - \theta_{j,1}^{{*{\text{T}}}} \varphi_{j,1} (\hat{x}_{j,1} )) \le \frac{{\sigma_{j} }}{2}z_{j,1}^{2} \varTheta_{j,1}^{*} + \frac{2}{{\sigma_{j} }}$$
(26)

where σ j  > 0 is a design parameter.

Substituting (25)–(26) and \(\dot{V}_{0}\) into (24), it yields

$$\begin{aligned} \dot{V}_{1} \le & \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } + z_{j,1} \bigg(\frac{3}{2}z_{j,1} + \chi_{j,2} + \alpha_{j,1} + \frac{{\sigma_{j} }}{2}z_{j,1} \varTheta_{j,1} - \dot{y}_{j,r} \\& + \theta_{j,1}^{T} \varphi_{j,1} (\hat{x}_{j,1} )) + \tilde{\theta }_{j,1}^{\rm T} (z_{j,1} \varphi_{j,1} (\hat{x}_{1} ) - \frac{1}{{\gamma_{j,1} }}\dot{\theta }_{j,1} \bigg) \\ & + \tilde{\varTheta }_{j,1}^{\rm T} \bigg(\frac{{\sigma_{j} }}{2}z_{j,1}^{2} - \frac{1}{{r_{j,1} }}\dot{\varTheta }_{j,1} \bigg) + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + L_{j,1} \bigg\} \\ \end{aligned}$$
(27)

where \(p_{j,1} = p_{j,0} - \frac{1}{2}\), \(L_{j,1} = L_{j,0} + \frac{1}{2}\varepsilon_{j,1}^{*2} + \frac{1}{2}d_{j,1}^{*2} + \frac{2}{{\sigma_{j} }}\).

Design the intermediate control function α j,1 and the parameter adaptation functions θ j,1 and Θ j,1 as

$$\alpha_{j,1} = - \beta_{j,1} z_{j,1} - \frac{3}{2}z_{j,1} + \dot{y}_{j,r} - \frac{{\sigma_{j} }}{2}z_{j,1} \varTheta_{j,1} - \theta_{j,1}^{\rm T} \varphi_{j,1} (\hat{x}_{1} )$$
(28)
$$\dot{\theta }_{j,1} = \gamma_{j,1} z_{j,1} \varphi_{j,1} (\hat{X}) - \tau_{j,1} \theta_{j,1}$$
(29)
$$\dot{\varTheta }_{j,1} = r_{j,1} \frac{{\sigma_{j} }}{2}z_{j,1}^{2} - \bar{\tau }_{j,1} \varTheta_{j,1}$$
(30)

where β j,1 > 0, τ j,1 > 0, and \(\bar{\tau }_{j,1} > 0\) are design parameters.

Substituting (28)–(30) into (27), it follows that

$$\begin{aligned} \dot{V}_{1} \le & \, \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } - \beta_{j,1} z_{j,1}^{2} + z_{j,1} \chi_{j,2} + \frac{{\tau_{j,1} }}{{\gamma_{j,1} }}\tilde{\theta }_{j,1}^{\rm T} \theta_{j,1} + \frac{{\bar{\tau }_{j,1} }}{{r_{j,1} }}\tilde{\varTheta }_{j,1}^{\rm T} \varTheta_{j,1} \hfill \\ & + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{T} \tilde{\theta }_{j,k} } + L_{j,1} \bigg\} \hfill \\ \end{aligned}$$
(31)

Given the newly defined state variable ϑ j,2, and let α j,1 pass through a first-order filter with a constant ζ j,2, we have

$$\varsigma_{j,2} \dot{\vartheta }_{j,2} + \vartheta_{j,2} = \alpha_{j,1} ,\quad \vartheta_{j,2} (0) = \alpha_{j,1} (0)$$
(32)

Define χ j,2 = ϑ j,2 − α j,1, and it yields \(\dot{\vartheta }_{j,2} = - \frac{{\chi_{j,2} }}{{\varsigma_{j,2} }}\) and

$$\dot{\chi }_{j,2} = \dot{\vartheta }_{j,2} - \dot{\alpha }_{j,1} = - \frac{{\chi_{j,2} }}{{\varsigma_{j,2} }} + H_{j,2}$$
(33)

where the continuous function H j,2(·) consists of z j,1, z j,2, χ j,2,\(y_{j,r} ,\dot{y}_{j,r} ,\ddot{y}_{j,r}\), Θ j,1 and θ j,1 with the following expression

$$\begin{aligned} H_{j,2} ( \cdot ) = & \beta_{j,1} \dot{z}_{j,1} + 2\dot{z}_{j,1} + \frac{{\sigma_{j} }}{2}\dot{z}_{j,1} \varTheta_{j,1} + \frac{{\sigma_{j} }}{2}z_{j,1} \dot{\varTheta }_{j,1} + \frac{{\theta_{j,1}^{\rm T} \partial \varphi_{j,1} (\hat{x}_{j,1} )}}{{\partial \hat{x}_{j,1} }}\dot{\hat{x}}_{j,1} \\ & + \dot{\theta }_{j,1}^{\text{T}} \varphi_{j,1} (\hat{x}_{1} ) - \ddot{y}_{j,r} \\ \end{aligned}$$
(34)

  • Step i j (2 ≤ i j  ≤ m j  − 1) Similar to Step 1, we have

    $$\dot{z}_{{j,i_{j} }} = z_{{j,i_{j} }} + \chi_{{j,i_{j} + 1}} + k_{{j,i_{j} }} e_{j,1} + \alpha_{{j,i_{j} }} + \theta_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\hat{X}) - \dot{\vartheta }_{{j,i_{j} }}$$
    (35)

Given the newly defined state variable \(\vartheta_{{j,i_{j} + 1}}\), and let \(\alpha_{{j,i_{j} }}\) pass through a first-order filter with time constant \(\varsigma_{{j,i_{j} + 1}}\), we have

$$\varsigma_{{j,i_{j} + 1}} \dot{\vartheta }_{{j,i_{j} + 1}} + \vartheta_{{j,i_{j} + 1}} = \alpha_{{j,i_{j} }} ,\quad \vartheta_{{j,i_{j} + 1}} (0) = \alpha_{{j,i_{j} }} (0)$$
(36)

Let \(\chi_{{j,i_{j} + 1}} = \vartheta_{{j,i_{j} + 1}} - \alpha_{{j,i_{j} }}\), and it yields \(\dot{\vartheta }_{{j,i_{j} + 1}} = - \frac{{\chi_{{j,i_{j} + 1}} }}{{\varsigma_{{j,i_{j} + 1}} }}\) and

$$\dot{\chi }_{{j,i_{j} + 1}} = \dot{\vartheta }_{{j,i_{j} + 1}} - \dot{\alpha }_{{j,i_{j} }} = - \frac{{\chi_{{j,i_{j} + 1}} }}{{\varsigma_{{j,i_{j} + 1}} }} + H_{{j,i_{j} + 1}}$$
(37)

where the continuous function \(H_{{j,i_{j} + 1}} ( \cdot )\) consists of \(\, z_{j,1} , \ldots ,\,z_{{j,i_{j} }} ,\) \(\,\chi_{j,2} , \ldots ,\,\chi_{{j,\rlap{--} i_{l} + 1}}\),\(\,y_{j,r} ,\,\dot{y}_{j,r}\), \(\, \ddot{y}_{j,r}\), \(\varTheta_{j,1} , \ldots ,\varTheta_{{j,i_{j} }}\), and \(\theta_{j,1} , \ldots ,\theta_{{j,i_{j} }}\) with the following expression

$$\begin{aligned} H_{{j,i_{j} + 1}} ( \cdot ) = & \beta_{{j,i_{j} }} \dot{z}_{{j,i_{j} }} + \sigma_{j} \dot{z}_{{j,i_{j} }} + \frac{{\sigma_{j} }}{2}\dot{z}_{{j,i_{j} }} \varTheta_{{j,i_{j} }} + \frac{{\sigma_{j} }}{2}z_{{j,i_{j} }} \dot{\varTheta }_{{j,i_{j} }} + \frac{{\theta_{{j,i_{l} }}^{\text{T}} \partial \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} )}}{{\partial \underline{{\hat{x}}}_{{j,i_{j} }} }}\underline{{\dot{\hat{x}}}}_{{j,i_{j} }} \\& + \dot{\theta }_{{j,i_{j} }}^{T} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) + k_{{j,i_{j} }} \dot{e}_{j,1} + \frac{{\chi_{{j,i_{j} }} }}{{\varsigma_{{j,i_{j} }} }} \\ \end{aligned}$$
(38)

Choose the Lyapunov function candidate \(V_{{i_{j} }}\) as

$$V_{{i_{j} }} = \sum\limits_{j = 1}^{n} {V_{{j,i_{j} }} } = \sum\limits_{j = 1}^{n} {\bigg(V_{{j,i_{j} - 1}} + \frac{1}{2}z_{{j,i_{j} }}^{2} + \frac{1}{{2\gamma_{{j,i_{j} }} }}\tilde{\theta }_{{j,i_{j} }}^{\text{T}} \tilde{\theta }_{{j,i_{j} }} } + \frac{1}{{2r_{{j,i_{j} }} }}\tilde{\varTheta }_{{j,i_{j} }}^{2} + \frac{1}{2}\chi_{{j,i_{j} }}^{2} \bigg)$$
(39)

where \(\gamma_{{j,i_{j} }} > 0\) and \(r_{{j,i_{j} }}\) are design parameters. We can easily obtain the time derivative of \(V_{{j,i_{j} }}\) as

$$\begin{aligned} \dot{V}_{{i_{j} }} = & \dot{V}_{{i_{j} - 1}} + \sum\limits_{j = 1}^{n} \bigg\{ z_{{j,i_{j} }} [\alpha_{{j,i_{j} }} - \tilde{\theta }_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\hat{X}) + \theta_{{j,i_{j} }}^{{*{\text{T}}}} \varphi_{{j,i_{j} }} (\hat{X}) - \theta_{{j,i_{j} }}^{{*{\text{T}}}} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) \\&+ \tilde{\theta }_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) + \theta_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) + \chi_{{j,i_{j} + 1}} + k_{{j,i_{j} }} e_{j,1} - \dot{\vartheta }_{{j,i_{j} }} ] \\ & + \frac{1}{{\gamma_{{j,i_{j} }} }}\tilde{\theta }_{{j,i_{j} }}^{\text{T}} \dot{\tilde{\theta }}_{{j,i_{j} }} + \frac{1}{{r_{{j,i_{j} }} }}\tilde{\varTheta }_{{j,i_{j} }}^{\text{T}} \dot{\tilde{\varTheta }}_{{j,i_{j} }} + \chi_{{j,i_{j} }} \dot{\chi }_{{j,i_{j} }} \bigg\} \\ \end{aligned}$$
(40)

where \(\tilde{\theta }_{{j,i_{j} }} = \theta_{{j,i_{j} }}^{*} - \theta_{{j,i_{j} }}\). In the view of the derivations in Step 1, it yields

$$\begin{aligned} z_{{j,i_{j} }} (\theta_{{j,i_{j} }}^{{*{\text{T}}}} \varphi_{{j,i_{j} }} (\hat{X}) - \tilde{\theta }_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\hat{X}) - \theta_{{j,i_{j} }}^{{*{\text{T}}}} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} )) \hfill \\ \le \frac{1}{2}z_{{j,i_{j} }}^{2} + \frac{1}{2}\tilde{\theta }_{{j,i_{j} }}^{\text{T}} \tilde{\theta }_{{j,i_{j} }} + \frac{2}{{\sigma_{j} }} + \frac{{\sigma_{j} }}{2}z_{{j,i_{j} }}^{2} \varTheta_{{j,i_{j} }}^{*} \hfill \\ \end{aligned}$$
(41)

where σ j is a design parameter.

Substituting (41) into (40) yields

$$\begin{aligned} \ell V_{{i_{j} }} \le & \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } + z_{{j,i_{j} }} (\alpha_{{j,i_{j} }} + k_{{j,i_{j} }} e_{j,1} - \dot{\vartheta }_{{j,i_{j} }} + \theta_{{j,i_{j} }}^{\text{T}} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) + \frac{1}{2}z_{{j,i_{j} }} + \frac{{\sigma_{j} }}{2}z_{{j,i_{j} }} \varTheta_{{j,i_{j} }} ) \\& - \sum\limits_{k = 1}^{{i_{j} - 1}} {\beta_{j,k} z_{j,k}^{2} } + \tilde{\theta }_{{j,i_{j} }}^{\text{T}} \bigg(z_{{j,i_{j} }} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) - \frac{1}{{\gamma_{{j,i_{j} }} }}\dot{\theta }_{{j,i_{j} }} \bigg) + \tilde{\varTheta }_{{j,i_{j} }}^{\text{T}} (\frac{{\sigma_{j} }}{2}z_{{j,i_{j} }}^{2} - \frac{1}{{r_{{j,i_{j} }} }}\dot{\varTheta }_{{j,i_{j} }} ) \\& + \sum\limits_{k = 1}^{{i_{j} - 1}} {\frac{{\tau_{j,k} }}{{\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \theta_{j,k} } + \frac{1}{2}\sum\limits_{k = 2}^{{i_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + \sum\limits_{k = 1}^{{i_{j} - 1}} {\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} } + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } \\& + \sum\limits_{k = 1}^{{i_{i} - 1}} {\chi_{j,k + 1} \bigg( - \frac{{\chi_{j,k + 1} }}{{\varsigma_{j,k + 1} }} + H_{j,k + 1} \bigg)} + \sum\limits_{k = 1}^{{i_{j} }} {z_{j,k} \chi_{j,k + 1} } + L_{{j,i_{j} }} \bigg\} \\ \end{aligned}$$
(42)

where \(L_{{j,i_{j} }} = L_{{j,i_{j} - 1}} + \frac{2}{{\sigma_{j} }}\).

Design the following intermediate control function \(\alpha_{{j,i_{j} }}\), and the adaptation function \(\theta_{{j,i_{j} }}\) as

$$\alpha_{{j,i_{j} }} = - \beta_{{j,i_{j} }} z_{{j,i_{j} }} - \frac{1}{2}z_{{j,i_{j} }} - \frac{{\sigma_{j} }}{2}z_{{j,i_{j} }} \varTheta_{{j,i_{j} }} - k_{{j,i_{l} }} e_{j,1} - \theta_{{j,i_{j} }}^{\rm T} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) + \dot{\vartheta }_{{j,i_{j} }}$$
(43)
$$\dot{\theta }_{{j,i_{j} }} = \gamma_{{j,i_{j} }} z_{{j,i_{j} }} \varphi_{{j,i_{j} }} (\underline{{\hat{x}}}_{{j,i_{j} }} ) - \tau_{{j,i_{j} }} \theta_{{j,i_{j} }}$$
(44)
$$\dot{\varTheta }_{{j,i_{j} }} = r_{{j,i_{j} }} \frac{{\sigma_{j} }}{2}z_{{j,i_{j} }}^{2} - \bar{\tau }_{j,1} \varTheta_{{j,i_{j} }}$$
(45)

where \(\beta_{{j,i_{j} }} > 0\), \(\tau_{{j,i_{j} }} > 0\), and \(\bar{\tau }_{{j,i_{j} }} > 0\) are design parameters. Substituting (43)–(45) into (42) yields

$$\begin{aligned} \dot{V}_{{i_{j} }} \le & \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } - \sum\limits_{k = 1}^{{i_{l} }} {\beta_{j,k} z_{j,k}^{2} } + \sum\limits_{k = 1}^{{i_{l} }} {\frac{{\tau_{j,k} }}{{\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \theta_{j,k} } + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + \sum\limits_{k = 1}^{{i_{j} }} {\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} } \\& + \frac{1}{2}\sum\limits_{k = 2}^{{i_{l} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + \sum\limits_{k = 1}^{{i_{l} - 1}} {\chi_{j,k + 1} \bigg( - \frac{{\chi_{j,k + 1} }}{{\varsigma_{j,k + 1} }} + H_{j,k + 1} \bigg)} + \sum\limits_{k = 1}^{{i_{l} }} {z_{j,k} \chi_{j,k + 1} } + L_{{j,i_{j} }} \bigg\} \\ \end{aligned}$$
(46)

  • Step m j In this step, the quantized control input u j will appear. Similar to the step i j , we can obtain the time derivative of \(z_{{j,m_{j} }}\) as follows:

$$\begin{aligned} \dot{z}_{{j,m_{j} }} = &\, q_{j} (u_{j} ) + k_{{j,m_{j} }} e_{j,1} + \theta_{{j,m_{j} }}^{\rm T} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) - \dot{\vartheta }_{{j,m_{j} }} \\ = &\, G_{j} (u_{j} )u_{j} + s_{j} (t) + k_{{j,m_{j} }} e_{j,1} + \theta_{{j,m_{j} }}^{\rm T} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) - \dot{\vartheta }_{{j,m_{j} }} \\ \end{aligned}$$
(47)

Consider the overall Lyapunov function as

$$V = \sum\limits_{j = 1}^{n} {V_{{j,m_{j} }} } = \sum\limits_{j = 1}^{n} {\left( {V_{{j,m_{j} - 1}} + \frac{1}{2}z_{{j,m_{j} }}^{2} + \frac{1}{{2\gamma_{{j,m_{j} }} }}\tilde{\theta }_{{j,m_{j} }}^{\text{T}} \tilde{\theta }_{{j,m_{j} }} + \frac{1}{2}\chi_{{j,m_{j} }}^{2} } \right)}$$
(48)

where \(\gamma_{{j,m_{j} }} > 0\) is the design parameter and \(\tilde{\theta }_{{j,m_{j} }} = \theta_{{j,m_{j} }}^{*} - \theta_{{j,m_{j} }}\).

By using (3), (47), and (48), one has

$$\begin{aligned} \dot{V} & = \dot{V}_{{m_{j} - 1}} + \sum\limits_{j = 1}^{n} \{ z_{{j,m_{j} }} [D_{j} (u_{j} )u_{j} + s_{j} (t) + k_{{j,m_{j} }} e_{j,1} - \dot{\vartheta }_{{j,m_{j} }} + \theta_{{j,m_{j} }}^{\text{T}} \phi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} )] \\& \quad + \frac{1}{{\gamma_{{j,m_{j} }} }}\tilde{\theta }_{{j,m_{j} }}^{\text{T}} \dot{\tilde{\theta }}_{{j,m_{j} }} + \chi_{{j,m_{j} }} \dot{\chi }_{{j,m_{j} }} \} \\ \end{aligned}$$
(49)

where \(\tilde{\theta }_{{j,m_{j} }} = \theta_{{j,m_{j} }}^{*} - \theta_{{j,m_{j} }}\).

From (4), and in the view of the derivations in Step i j , it yields

$$\begin{aligned} \dot{V} \le & \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } - \sum\limits_{k = 1}^{{m_{j} - 1}} {\beta_{j,k} z_{j,k}^{2} } + z_{{j,m_{j} }} [D_{j} (u_{j} )u_{j} + \frac{3}{2}z_{{j,m_{j} }} + k_{{j,m_{j} }} e_{j,1} - \dot{\vartheta }_{{j,m_{j} }} \\ \quad + \theta_{{j,m_{j} }}^{\text{T}} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} )] + \tilde{\theta }_{{j,m_{j} }}^{\text{T}} \bigg(z_{{j,m_{j} }} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) - \frac{1}{{\gamma_{{j,m_{j} }} }}\dot{\theta }_{{j,m_{j} }} \bigg) \\ \quad + \sum\limits_{k = 1}^{{m_{j} - 1}} {\frac{{\tau_{j,k} }}{{\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \theta_{j,k} } + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + \sum\limits_{k = 1}^{{m_{j} - 1}} {\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} } + \frac{1}{2}\sum\limits_{k = 2}^{{m_{j} - 1}} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } \\ \quad + \sum\limits_{k = 1}^{{m_{j} - 2}} {\chi_{j,k + 1} \bigg( - \frac{{\chi_{j,k + 1} }}{{\varsigma_{j,k + 1} }} + H_{j,k + 1} \bigg)} + \sum\limits_{k = 1}^{{i_{l} }} {z_{j,k} \chi_{j,k + 1} } + L_{{j,m_{j} }} \bigg\} \\ \end{aligned}$$
(50)

where \(L_{{j,m_{j} }} = L_{{j,m_{j} - 1}} + \frac{2}{{\sigma_{j} }} + \frac{1}{2}u_{\hbox{min} }^{2}\).

Design the controller u j and the adaptation function \(\theta_{{j,m_{j} }}\) as follows:

$$u_{j} = \frac{1}{{1 - \delta_{j} }}\bigg( - \beta_{{j,m_{j} }} z_{{j,m_{j} }} - \frac{3}{2}z_{{j,m_{j} }} - k_{{j,m_{j} }} e_{j,1} - \theta_{{j,m_{j} }}^{\rm T} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) + \dot{\vartheta }_{{j,m_{j} }} \bigg)$$
(51)
$$\dot{\theta }_{{j,m_{j} }} = \gamma_{{j,m_{j} }} z_{{j,m_{j} }} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) - \tau_{{j,m_{j} }} \theta_{{j,m_{j} }}$$
(52)

where \(\tau_{{j,m_{j} }} > 0\) and \(\beta_{{j,m_{j} }} > 0\) are design constants.

Note that, from (4) and (51), and by completing the square, we can obtain

$$D_{j} (u_{j} )u_{j} \le - \beta_{{j,m_{j} }} z_{{j,m_{j} }} - z_{{j,m_{j} }} - k_{{j,m_{j} }} e_{j,1} \quad - \theta_{{j,m_{j} }}^{\rm T} \varphi_{{j,m_{j} }} (\hat{X},\underline{u}_{j - 1} ) + \dot{\vartheta }_{{j,m_{j} }}$$
(53)
$$\tilde{\theta }_{{j,m_{j} }}^{T} \theta_{{j,m_{j} }} \le - \frac{1}{2}\tilde{\theta }_{{j,m_{j} }}^{\text{T}} \tilde{\theta }_{{j,m_{j} }} + \frac{1}{2}\theta_{{i,m_{j} }}^{{*{\text{T}}}} \theta_{{i,m_{j} }}^{*}$$
(54)

Substituting (53)–(54) into (50) yields

$$\begin{aligned} \dot{V} \le & \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } - \sum\limits_{k = 1}^{{m_{j} }} {\beta_{j,k} z_{j,k}^{2} } + \frac{1}{{\sigma_{j} }}\sum\limits_{k = 1}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } + \sum\limits_{k = 1}^{{m_{j} }} {\frac{{\tau_{j,k} }}{{\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \theta_{j,k} } + \frac{1}{2}\sum\limits_{k = 2}^{{m_{j} }} {\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } \\ \quad + \sum\limits_{k = 1}^{{m_{j} }} {z_{j,k} \chi_{j,k + 1} } + \sum\limits_{k = 1}^{{m_{j} - 1}} {\chi_{j,k + 1} \bigg( - \frac{{\chi_{j,k + 1} }}{{\varsigma_{j,k + 1} }} + H_{j,k + 1} \bigg)} + \sum\limits_{k = 1}^{{m_{j} - 1}} {\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} } + L_{{j,m_{j} }} \bigg\} \\ \end{aligned}$$
(55)

Let

$$\begin{aligned} \varXi_{j,k} = & \bigg\{ \bigg(e_{j} ,z_{j,k} ,\theta_{j,k} ,\varTheta_{j,k} ,\chi_{j,k} \bigg):\sum\limits_{j = 1}^{n} {\bigg[e_{j}^{\text{T}} Pe_{j} } + \frac{1}{2}\sum\limits_{k = 1}^{{m_{j} }} {z_{j,k}^{2} + \sum\limits_{k = 1}^{{m_{j} }} {\frac{1}{{2\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \tilde{\theta }_{j,k} } } + \sum\limits_{k = 1}^{{m_{j} - 1}} {\frac{1}{{2r_{j,k} }}\tilde{\varTheta }_{j,k}^{2} } \\ + \frac{1}{2}\sum\limits_{k = 2}^{{m_{j} }} {\chi_{j,k}^{2} } \bigg] \le D_{j,k} \bigg\} \\ \end{aligned} ,$$

where D j,k is a known positive constant.

Since Ξ j,k is a compact set and H j,k+1 is a continuous function, there exists a positive constant M j,k+1 such that |H j,k+1| ≤ M j,k+1 on Ξ j,k . Consequently, we have

$$\left| {\chi_{j,k + 1} H_{j,k + 1} } \right| \le \frac{1}{2}\chi_{j,k + 1}^{2} + \frac{1}{2}M_{j,k + 1}^{2}$$
(56)

By completing the square for each parameter estimate:

$$z_{j,k}^{{}} \chi_{j,k + 1} \le \frac{1}{2}\chi_{j,k + 1}^{2} + \frac{1}{2}z_{j,k}^{2}$$
(57)
$$\frac{{\tau_{j,k} }}{{\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\text{T}} \theta_{j,k} \le - \frac{{\tau_{j,k} }}{{2\gamma_{j,k} }}\tilde{\theta }_{j,k}^{\rm T} \tilde{\theta }_{j,k} + \frac{{\tau_{j,k} }}{{2\gamma_{j,k} }}\left\| {\theta_{j,k}^{*} } \right\|^{2}$$
(58)
$$\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} \le - \frac{{\bar{\tau }_{j,k} }}{{2r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \tilde{\varTheta }_{j,k} + \frac{{\bar{\tau }_{j,k} }}{{2r_{j,k} }}\left\| {\varTheta_{j,k}^{*} } \right\|^{2}$$
(59)

Then, (55) can be written as

$$\begin{aligned} \dot{V} \le \sum\limits_{j = 1}^{n} {\bigg\{ - p_{j,1} \left\| {e_{j} } \right\|^{2} } - \sum\limits_{k = 1}^{{m_{j} }} {\bigg(\beta_{j,k} - \frac{1}{2}\bigg)z_{j,k}^{2} } + \sum\limits_{k = 1}^{{m_{j} }} {\frac{{\tau_{j,k} }}{{2\gamma_{j,k} }}\left\| {\theta_{j,k}^{*} } \right\|^{2} } - \sum\limits_{k = 2}^{{m_{j} }} {\bigg(\frac{{\tau_{j,k} }}{{2\gamma_{j,k} }} - \frac{2}{{\sigma_{j} }}\bigg)\tilde{\theta }_{j,k}^{\rm T} \tilde{\theta }_{j,k} } \hfill \\ \quad - \bigg(\frac{{\tau_{j,1} }}{{2\gamma_{j,1} }} - \frac{1}{{\sigma_{j} }}\bigg)\tilde{\theta }_{j,1}^{\text{T}} \tilde{\theta }_{j,1} \quad - \sum\limits_{k = 1}^{{m_{j} - 1}} {\bigg(\frac{1}{{\varsigma_{j,k + 1} }} - 1\bigg)\chi_{j,k + 1}^{2} } + \sum\limits_{k = 1}^{{m_{j} - 1}} {\frac{{\bar{\tau }_{j,k} }}{{r_{j,k} }}\tilde{\varTheta }_{j,k}^{\rm T} \varTheta_{j,k} } \hfill \\ + L_{{j,m_{j} }} + \frac{1}{2}\sum\limits_{k = 1}^{{m_{j} - 1}} {M_{j,k + 1}^{2} } \bigg\} \hfill \\ \end{aligned}$$
(60)

Choose p j,1 > 0,\(\beta_{j,k} - \frac{1}{2} > 0\), (k = 1, …, m j ),\(\frac{{\tau_{j,1} }}{{2\gamma_{j,1} }} - \frac{2}{{\sigma_{j} }} > 0\),\(\frac{1}{{\varsigma_{j,k + 1} }} - 1 > 0\), (k = 1, …, m j  − 1) and \(\frac{{\tau_{j,k} }}{{2\gamma_{j,k} }} - \frac{1}{{\sigma_{j} }} > 0\), and define

\(\begin{aligned} C = & \mathop {\hbox{min} }\nolimits_{\begin{subarray}{l} 1 \le j \le n \\ 1 \le k \le m_{j} \end{subarray} } \{ 2\beta_{j,k} ,(1 \le k \le m_{j} ),\;\tau_{j,k} - \frac{{4\gamma_{j,k} }}{{\sigma_{j} }},\frac{2}{{\varsigma_{j,k + 1} }} - 2,(1 \le k \le m_{j} - 1),\tau_{j,1} - \frac{{2\gamma_{j,1} }}{{\sigma_{j} }}, \\ 2\bar{\tau }_{j,k} ,{{p_{j,1} } \mathord{\left/ {\vphantom {{p_{j,1} } {\lambda_{\hbox{min} } (P_{j} )}}} \right. \kern-0pt} {\lambda_{\hbox{min} } (P_{j} )}}\} \\ \end{aligned}\) and \(D = \sum\nolimits_{j = 1}^{n} {(L_{{j,m_{j} }} + \frac{1}{2}\sum\nolimits_{k = 1}^{{m_{j} - 1}} {M_{j,k + 1}^{2} } } )\).

Then, (60) can be further rewritten as

$$\dot{V} \le - CV + D$$
(61)

Integrating (61) over [0, T], we can easily obtain that

$$0 \le V(T) \le \bigg(V(0) - \frac{D}{C}\bigg)e^{ - CT} + \frac{D}{C}$$
(62)

which means that all the signals in the closed-loop systems are bounded, such as \(\mathop {\lim }\nolimits_{t \to \infty } \quad \left\| {e_{j} } \right\| \le \sqrt {{{(V(0) + \frac{D}{C})} \mathord{\left/ {\vphantom {{(V(0) + \frac{D}{C})} {\lambda_{\hbox{max} } (P_{j} )}}} \right. \kern-0pt} {\lambda_{\hbox{max} } (P_{j} )}}}\), and \(\mathop {\lim }\nolimits_{t \to \infty } \quad \left| {z_{{j,_{{i_{j} }} }} } \right| \le \sqrt {2V(0) + 2\frac{D}{C}}\).

Moreover, the observer and the tracking errors can converge to a small neighborhood of the origin by suitably choosing the following parameters \(\beta_{{j,i_{j} }}\), \(k_{{j,i_{j} }}\),\(\tau_{{j,i_{j} }}\),\(r_{{j,i_{j} }}\),\(\gamma_{{j,i_{j} }}\), \(\bar{\tau }_{{j,i_{j} }}\), and σ j .

The aforementioned design and analysis procedures are summarized in the following theorem.

Theorem 1

For MIMO nonstrict-feedback nonlinear systems (1), under Assumption 1, the controller (51), and state observer (16), together with the intermediate controls (28), (43), and the adaptation functions (29–30), (44–45) and (52), guarantee that all variables in the closed-loop systems are bounded. Furthermore, the observer and the tracking errors can converge to a small neighborhood of the origin by appropriate choosing the design parameters.

From the previous discussions, the control design procedures and the guideline of the parameter selections are given as follows:

  1. Step 1:

    specify the vector L j such that matrix A j is a strict Hurwitz matrix, positive definite matrices Q j and by solving the Lyapunov Eq. (16), positive definite matrices P j are obtained.

  2. Step 2:

    select appropriately design parameters such that \(\beta_{{j,i_{j} }} > 0\), \(\tau_{{j,i_{j} }} > 0\) and \(\bar{\tau }_{{j,i_{j} }} > 0\), and the determine intermediate control functions α j,1(28), \(\alpha_{{j,i_{j} }}\)(43), and the parameters adaptation laws θ j,1 (29), Θ j,1 (30), \(\theta_{{j,i_{j} }}\) (44), and \(\varTheta_{{j,i_{j} }}\) (45), i j  = 1, …, m j  − 1.

  3. Step 3:

    select appropriately design parameters \(\beta_{{j,m_{j} }} > 0\), \(\tau_{{j,m_{j} }} > 0\) and \(\bar{\tau }_{{j,m_{j} }} > 0\), actual controller u j , and adaptive update law θ j,k m j , \(\varTheta_{{j,m_{j} }}\).

4 Simulation study

In this section, we provide a simulation example with the aim to evaluate the control performance of the proposed control strategy.

Example

We consider the following MIMO nonstrict-feedback system:

$$\left\{ \begin{aligned} \dot{x}_{1,1} =\,& x_{1,2} + f_{1,1} (X) + d_{1,1} (t) \\ \dot{x}_{1,2} =\,& q_{1} (u_{1} ) + f_{1,2} (X) + d_{1,2} (t) \\ y_{1} =\,& x_{1,1} \\ \end{aligned} \right.$$
(63)
$$\left\{ \begin{aligned} \dot{x}_{2,1} =\,& x_{2,2} + f_{2,1} (X) + d_{2,1} (t) \\ \dot{x}_{2,2} =\,& q_{2} (u_{2} ) + f_{2,2} (X,u_{1} ) + d_{2,2} (t) \\ y_{2} =\,& x_{2,1} \\ \end{aligned} \right.$$
(64)

where f 1,1(X) = x 1,1 sin 2(x 1,2) + sin (x 2,1) cos (x 2,2),\(f_{1,2} (X) =\,\frac{{x_{1,1}^{2} e^{{ - x_{1,2}^{2} }} }}{{1 + x_{1,1}^{2} }} + x_{1,1} \sin (x_{2,1} x_{2,2} )\), \(d_{1,1} (t) = 0.2\sin (t)\), d 1,2(t) = 0.2 cos (t), \(f_{2,1} (X) = \frac{{x_{2,1} }}{{1 + x_{1,1}^{2} }} + 0.1\sin (x_{2,1} )\cos (x_{2,2} )\), f 2,2(X, u 1) = 0.2x 2,1 x 21,2  + cos (x 2,1 x 22,2 ), d 2,1 = 0.5 sin (t),\(d_{2,2} (t) = \frac{{x_{2,1}^{2} e^{{ - x_{2,2}^{2} }} }}{{1 + x_{2,1}^{2} }}\). The reference signals are y 1,r (t) = sin (0.5t) and y 2,r (t) = sin (0.4t). Choose the parameters in hysteresis quantizer (2) as δ 1 = 0.5, δ 2 = 0.1, and u jmin = 0.8 (j = 1, 2).

Choose the fuzzy membership functions as

\(\mu_{{F_{j,i}^{l} }} = \exp \bigg[ - \frac{{(\hat{x}_{j,1} - 3 + l)^{2} }}{16}\bigg]\), \(\mu_{{F_{j,2}^{l} }} = \exp \bigg[ - \frac{{(\hat{x}_{j,2} - 6 + 2l)^{2} }}{4}\bigg]\) j = 1, 2; l = 1, …, 5.

According to [31], the FLS can be constructed as

$$\hat{f}_{j,1} (\hat{X}\left| {\theta_{j,1,k} } \right.) = \sum\limits_{k = 1}^{5} {\theta_{j,1,k} } \varphi_{j,1,k} (\hat{X})$$
$$\hat{f}_{j,2} (\hat{X},u_{j,1} \left| {\theta_{j,2,k} } \right.) = \sum\limits_{k = 1}^{5} {\theta_{j,2,k} } \varphi_{j,2,k} (\hat{X},u_{j,1} ),j = 1,2$$

Setting the parameters k 1,1 = 4, k 2,1 = 4, k 1,2 = 3, and k 2,2 = 3, the state observer is constructed as

$$\left\{ \begin{aligned} \dot{\hat{x}}_{1,1}& = \hat{x}_{1,2} + \hat{f}_{1,1} (\hat{X}\left| {\theta_{1,1} } \right.) + 4(x_{1,1} - \hat{x}_{1,1} ) \hfill \\ \dot{\hat{x}}_{1,2}& = q_{1} (u_{1} ) + \hat{f}_{1,2} (\hat{X}\left| {\theta_{1,2} } \right.) + 4(x_{1,1} - \hat{x}_{1,1} ) \hfill \\ \hat{y}_{1} &= \hat{x}_{,1,1} \hfill \\ \end{aligned} \right.$$
(65)
$$\left\{ \begin{aligned} \dot{\hat{x}}_{2,1} &= \hat{x}_{2,2} + \hat{f}_{2,1} (\hat{X}\left| {\theta_{1,1} } \right.) + 3(x_{2,1} - \hat{x}_{2,1} ) \hfill \\ \dot{\hat{x}}_{2,2}& = q_{2} (u_{2} ) + \hat{f}_{2,2} (\hat{X},u_{1} \left| {\theta_{2,2} } \right.) + 3(x_{2,1} - \hat{x}_{2,1} ) \hfill \\ \hat{y}_{2}& = \hat{x}_{2,1} \hfill \\ \end{aligned} \right.$$
(66)

Choose the design parameters in the controllers u j (51), the intermediate controls α j,1 (28) the adaptive laws θ j,1 (29) and θ j,2 (52) as

β 1,1 = β 2,1 = 1, β 1,2 = β 2,2 = 4, γ 1,1 = γ 1,2 = γ 2,1 = γ 2,2 = 0.1, r 1,1 = r 1,2 = r 2,1 = r 2,2 = 0.5, τ 1,1 = τ 1,2 = τ 2,1 = τ 2,2 = 0.5, \(\bar{\tau }_{1,1} = \bar{\tau }_{1,2} = \bar{\tau }_{2,1} = \bar{\tau }_{2,2} = 0.5\).

The initial values of the variables x i,j (i, j = 1, 2) are chosen as x 1,1(0) = 0.1, x 1,2(0) = 0.1, x 2,1(0) = 0.1, x 2,2(0) = 0.1,\(\hat{x}_{1,1} (0) = 0.1\), \(\hat{x}_{1,2} (0) = 0.1\), \(\hat{x}_{2,1} (0) = 0.1\), and the others initial values are zeros.

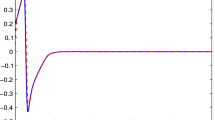
By applying the proposed adaptive quantized fuzzy control approach to systems (63)–(64), the simulation results are shown in Figs. 2, 3, 4, 5, 6, 7, and 8, where Figs. 2 and 3 show the trajectories of the systems output y j and tracking signal y j,r , respectively; Figs. 4 and 5 show the trajectories of x j,1 and their estimates \(\hat{x}_{j,1}\), respectively; Fig. 6 shows the trajectories of the observer errors e j,2; and Figs. 7 and 8 show the control input u j and the quantized input signal q j (u j ), j = 1, 2.

Fig. 2
figure 2

Curves of y 1 (blue) and y 1,r (red)

Full size image
Fig. 3
figure 3

Curves of x 1,1 (blue) and \(\hat{x}_{1,1}\) (red)

Full size image
Fig. 4
figure 4

Curves of y 1 (blue) and y 2,r (red)

Full size image
Fig. 5
figure 5

Curves of x 2,1 (blue) and \(\hat{x}_{2,1}\) (red)

Full size image
Fig. 6
figure 6

Curves of e 1,2 (blue) and e 2,2 (red)

Full size image
Fig. 7
figure 7

Curves of u 1 (blue) and q 1(u 1) (red)

Full size image
Fig. 8
figure 8

Curves of u 2 (blue) and q 2(u 2) (red)

Full size image

Figures 2, 3, 4, 5, 6, 7, and 8 show that the proposed control approach can guarantee the stability of the MIMO nonstrict-feedback systems, and the boundedness of the tracking and observer errors regardless of the existence of uncertain nonlinearities, unmeasurable states, and hysteretic quantized input.

Remark 2

It is worth noting that the authors in [26–31] investigated the input quantization control problem for a class of SISO nonlinear systems. However, the work in [26–31] did not consider the problem of states immeasurable and “explosion of complexity”. Therefore, they cannot be applied to control the MIMO nonstrict-feedback nonlinear systems (63)–(64) for example.

5 Conclusions

A new fuzzy-based adaptive quantized DSC control method has been proposed for uncertain MIMO nonstrict-feedback nonlinear systems with input quantization. The hysteretic quantized input has been decomposed by using two bounded nonlinear functions, and the fuzzy logic systems and a fuzzy state observer have been adopted to identify the uncertain nonlinear functions and to estimate the unmeasurable states, respectively. The investigated adaptive fuzzy quantized control scheme not only guarantees the stability of the MIMO nonstrict-feedback systems, and the boundedness of the tracking and observer errors, but also solves the problem of hysteretic quantized input. Future researches will be concentrated on a fuzzy adaptive quantized optimal control design for nonstrict-feedback nonlinear systems. Further research will concentrate on adaptive fuzzy control for MIMO nonlinear affine or nonaffine systems with time-varying and input delay based on this paper and the results of [33–37].