Observer-based adaptive fuzzy finite time control for non-strict feedback nonlinear systems with unmodeled dynamics and input delay

Abstract

In this paper, we consider observer-based adaptive fuzzy finite time control scheme for non-strict feedback uncertain nonlinear systems with unmodeled dynamics and input delay. A fuzzy state observer is employed to estimate the unmeasurable states and the unknown nonlinearities are identified by the fuzzy logic systems in each step. The design difficulty caused by the unmodeled dynamics and input delay is tackled by a dynamic signal and a compensation signal, respectively. Based on the proposed compensation signal, the considered input delay can be unknown and time varying. To decrease the computational burden, the dynamic surface control (DSC) scheme is adopted in the design process. In the framework of finite time Lyapunov theory, an effective adaptive fuzzy finite time controller has been obtained by combining the idea of backstepping technology with DSC scheme. The proposed method not only solves the algebraic loop problem, but also realizes the finite time stability performance constraint in the presence of input delay, unmodeled dynamics and unmeasurable states. Finally, the stability analysis shows that all signals of the closed-loop systems are bounded in finite time. Simulation results show the superiority of the devised scheme.

1 Introduction

Over the past years, the idea of approximated-based control schemes for nonlinear systems by using fuzzy logic systems (FLS) or neural networks (NNS) has been considerable attention by the researchers [1,2,3,4,5]. The main reason is that the unknown nonlinearity inevitably exists in actual system, and it is difficult to get the accurate information of the unknown nonlinearity, which makes the nonlinear system control very difficult [6]. Particularly, some common phenomena, such as external disturbance [1, 7], unmodeled dynamics [8, 9], time delay [10, 11], non-smooth nonlinearity [12, 13] and state constraint [14, 15], make the control design of nonlinear systems more complicated. Recently, to overcome these design difficulties, dramatic adaptive neural/fuzzy backstepping control schemes have been proposed in [16,17,18]. Nevertheless, the above-mentioned approaches are limited to the strict feedback nonlinear systems which cannot be extended to nonlinear systems with non-strict feedback form. Regarding non-strict feedback nonlinear systems, the functions of the system are related to all the states, which can cause the algebraic loop problem for the traditional adaptive backstepping control technique [19]. Thus, Chen et al. proposed a variable separation approach for non-strict feedback systems in [20]. Furthermore, based on FLS or NNS, many effective adaptive control schemes have been proposed to overcome this problem (see [20,21,22,23]). However, the aforementioned results are only provided that the system states are all measurable.

In practice, the state variables are usually difficult to be measured, due to the technique difficulty and/or costly expense of measuring [24]. Thus, it is hard to obtain all the information of the system states, which limits the application of the aforementioned approaches. In this case, the idea of output feedback control approach is an alternative effective approach, which is more in line with the actual demand [25, 26]. Considering the non-strict feedback nonlinear systems with unmeasurable states and time delay, Chen et al. proposed a linear state observer-based output feedback control scheme in [27]. Furthermore, by using a linear state observer to estimate the unmeasurable states in non-strict feedback stochastic nonlinear systems, the authors in [28, 29] considered adaptive fuzzy/neural output-feedback control schemes, respectively. Recently, in [30] Wang et al. proposed an event-triggered fuzzy output-feedback control approach via linear observer. Nevertheless, the linear observer is independent on the controlled systems, it cannot get the effective estimations of the unmeasurable state variables for practical systems. Thus, Tong et al. proposed a fuzzy state observer-based control approach for stochastic nonlinear strict feedback systems in [31], which is constructed according to the system and the unknown nonlinear functions are identified by the FLS. In [32], the authors considered adaptive fuzzy backstepping control for nonlinear systems with sampled and delayed measurements. In [33], regarding switched strict feedback nonlinear systems with dead-zone and unmeasurable states which is investigated by using fuzzy state observer. In [24], based on fuzzy observer, Wang considered repetitive tracking control for strict feedback nonlinear systems. However, as mentioned above, the algebraic loop problem for non-strict feedback nonlinear systems is inevitable for adaptive backstepping technique. To overcome this limitation, by using the property of the fuzzy basis functions, Tong et al. proposed a fuzzy state observer-based control approach for SISO non-strict feedback systems in [34]. Following this study, Wang et al. considered the actuator failures and unmeasurable states in non-strict feedback systems and proposed a composite adaptive fuzzy control via fuzzy state observer in [35]. However, the aforementioned research results are based on the problem of asymptotic stability in infinite time. Unlike the infinite time stability, finite time control shows higher tracking performance, better disturbance-rejection ability and faster transient response for nonlinear systems. So, it is very significant for us to consider the finite time control scheme for non-strict feedback systems with unmeasurable states.

In recent years, the idea of finite time stability has been widely concerned in strict or pure feedback nonlinear systems, for example, see [36,37,38,39,40,41,42,43]. Furthermore, based on the assumption that all the state variables are measurable in non-strict feedback nonlinear systems, the authors proposed the approximated-based finite time control schemes in [44,45,46,47,48,49], respectively. However, as mentioned above, the system states are usually unmeasured and it is difficult to get the full information about the system states. Therefore, the aforementioned finite time control schemes are not suitable to non-strict feedback systems with unmeasured states. To overcome this drawback, observer-based finite time control schemes for non-strict feedback systems with unmeasured states were discussed in [50,51,52,53,54,55]. Based on FLS, Li et al. investigated the finite-time adaptive fuzzy control for MIMO non-strict feedback systems via a fuzzy observer in [50]. Furthermore, considering the actuator faults and saturations in MIMO non-strict feedback systems, Ji et al. considered finite time fuzzy tracking control problem in [51]. Regarding non-strict feedback nonlinear systems with unmeasurable states, the authors in [52,53,54,55] studied the phenomena of output constraint, state constraint, prescribed performance constraint and input saturation for finite time control schemes, respectively. Nevertheless, the unmodeled dynamics problem was unconsidered in the aforementioned results. The unmodeled dynamics is inevitable existing in practical systems, due to modeling errors, model simplification and measurement noises. As a result, it is difficult to obtain their accurate information, and the difficulty of system control increases sharply. However, the above-mentioned finite time control schemes are useless for the unmodeled dynamics. By introducing a dynamic signal or small-gain theorem, the problem of unmodeled dynamics has been widely considered in infinite time control of nonlinear systems, for example, in [17, 56,57,58,59,60,61,62]. However, from the perspective of finite time control strategy, this problem is rarely considered in output feedback mechanism. Particularly, for non-strict feedback systems, the aforementioned results cannot be extended to this issue. Recently, Sui et al. considered finite time control of stochastic systems with unmodeled dynamics in [63]. Nevertheless, due to the repeated differentiations of virtual controller, which lead to high computational complexity. On the other hand, the input delay problem has not been considered in above research results. It is known that the control forces provided by the actuators are limited in practice. Particularly, the output provided by the observer cannot be used when input delay appears. Thus, the aforementioned results are invalid if the input delay exists in practical systems.

As a kind of time delay, input delay is a common and inevitable phenomenon in practical control systems, such as chemical processes [64], vehicle active suspension system [65] and uncertain mechanical systems [66]. When input delay occurs, the performance of the closed-loop system will be damaged or even be disastrous if the control signal cannot feedback the information provided by the observer in time. To tackle linear systems with input delay, the predictor-based techniques such as smith predictor and truncated predictor feedback are often used. However, it is difficult to deal with nonlinear systems with input delay, due to the unknown nonlinearities exist in actual systems. Thus, the authors in [67,68,69] extended the predictor-based control approach to tackle nonlinear systems with input delay. Unfortunately, most of these results depend on the exact model information of the nonlinear control plant. It should be noted that the unmodeled dynamics and other uncertainties often exist in actual systems which make the aforementioned results difficult to be applied in practice. In addition, for the predictor-based control methods, the state variables of system are difficult to predict. Based on Laplace transform technique, the Pade approximation is employed to deal with nonlinear systems with input delay. For example, Li [70] investigated strict-feedback systems with input delay and output constraint by combing FLS and the idea of Pade approximation. Furthermore, by combing NNS with Pade approximation, the authors in [71] considered adaptive tracking control approach for strict feedback systems with full state constrained and input delay. Nevertheless, the proposed methods are only applicable to strict feedback nonlinear systems, and the Pade approximation approach is invalid for long input delay. Recently, by using a compensation mechanism to deal with input delay, Wang et al. considered adaptive neural control for non-strict feedback systems in [72]. However, the proposed method is only suitable to known constant delay and the state variables are measurable, which might lead to some design conservatism. For the unknown input delay, [73] developed a prediction-based control method based on the exact model assumption of the nonlinear dynamics. Furthermore, [74] proposed proportional integral differential controller for uncertain nonlinear systems. Unfortunately, the considered system model depends on the system model, and the approach is useless when the system model changes. By using finite integral to construct auxiliary signal, Wang et al. considered strict-feedback systems with time-varying input delay and proposed adaptive fuzzy tracking control approach in [75]. Recently, the authors in [76] considered event-triggered dynamic surface control for pure-feedback systems with unknown input time delay and quantized input. However, the aforementioned methods are invalid if the state variables are not measurable or the unmodeled dynamics exist in practice systems. From above narrations, one can observe that no literature is involved in discussion finite time control for non-strict feedback nonlinear systems with unknown time varying input delay. What is more, if this issue involves unmeasured state variables and unmodeled dynamics, the existing results are invalid, which prompt us to carry out this study.

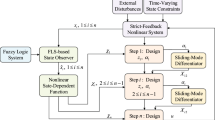
Motivated by above observations, observer-based adaptive fuzzy finite time control for non-strict feedback uncertain nonlinear systems with unknown time varying input delay, unmodeled dynamics and unmeasurable states is investigated in this paper. Fuzzy logical systems are introduced to approximate the unknown nonlinearities and a fuzzy state observer is employed to estimate the unmeasurable state variables. A compensation signal is introduced to tackle the design difficulty caused by the unknown time varying input delay. The unmodeled dynamics is tackled by introduced a dynamical signal and the DSC scheme is employed to tackle the computational burden. Based on the backstepping technique, an effective finite time adaptive fuzzy controller has been obtained in the framework of finite time Lyapunov theory. The main work of this paper is listed as follows:

• (1) In the framework of finite time stability, adaptive fuzzy finite time control for non-strict feedback nonlinear systems with unknown time varying input delay, unmodeled dynamics and unmeasurable states is proposed for the first time. Compared with the nonlinear systems with strict feedback or pure feedback form in [36,37,38,39,40,41,42,43], the proposed method can be applied for a more general structure with unmeasurable states. Compared with the finite time control schemes in [50,51,52,53,54,55, 63], the proposed controller takes into account the unmodeled dynamics and input delay so as to achieve better control performance in practical engineering.

• (2) For the unknown and time varying input delay, a compensation signal is introduced to tackle the design difficulty. Compared with the results in [70,71,72], the restrictions of input delay to be known or constant are removed, compared with [73, 74] the assumption of exact model limitation is eliminated, so that the design conservatism is reduced.

• (3) The structure of the non-strict feedback system is simplified by using the FLS, and the DSC scheme is adopted in the design process of backstepping technique. Compared with [44,45,46,47,48,49, 63], the computational burden, complexity and difficulty of finite time controller design are reduced. The proposed scheme not only solves the algebraic loop problem, but also realizes the finite time stability performance constraint in the presence of unknown input delay, unmodeled dynamics and unmeasurable states.

The paper is organized as follows: Sect. 2 presents the problem and the preliminary results. Section 3 discusses the design process of the controller and the stability analysis. The simulation examples are considered in Sect. 4. Finally, Sect. 5 gives a brief conclusion.

Notations

The following notations will be used throughout this paper $\Vert \cdot \Vert$ denotes the 2-norm for a matrix or a vector, $| \cdot |$ denotes the absolute value for a scalar, and the symbol $\circ$ denotes the composition operator between two functions.

2 Problem formulation

Consider the following dynamic system

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}&= q(x,z) \\ \dot{x}_i&= x_{i + 1} + f_i( x ) + \varDelta _i (x,z),\, i = 1,2, \cdots ,n - 1 \\ \dot{x}_n&= u(t - \tau (t) ) + f_n (x) + \varDelta _n (x,z) \\ y&= x_1 \\ \end{aligned} \right. \end{aligned}$$

(1)

where the state variable $x = [x_1, x_2, \cdots , x_n ]^T$ and all variables except $x_1$ are not measured, z denotes the unmodeled dynamics and $\varDelta _i (x,z)$ represents the unknown dynamic disturbance, $f_i ( \cdot )$ is unknown smooth nonlinear function, $u(t - \tau (t)) \in R$ is the control input with $\tau (t)$ being the unknown time varying delay, and $y(t) \in R$ is the system output.

Remark 1

In practice, many systems can be described or transformed as the system (1), such as one-link manipulator with motor [53, 58], electromechanical system [34] and so on. Compared with the existing results [70,71,72,73,74,75,76] which only work on input delay for nonlinear systems with all state variables are measurable, the finite time control problem is unconsidered. In addition, the considered input delay is known and constant or the proposed method depends on the systems model. Compared with the finite time control approaches in [50,51,52,53,54,55], the design difficulties caused by the phenomena of input delay and unmodeled dynamics are ignored by the authors.

Assumption 1

[62, 63] The unknown dynamic disturbance $\varDelta _i (x,z)$ satisfy

$$\begin{aligned} \left| {\varDelta _i (x,z)} \right| \le q_i^* \psi _{i1} (y) + q_i^* \psi _{i2} (\left| z \right| ) \ \ \ \ 1 \le i \le n\nonumber \\ \end{aligned}$$

(2)

where $q_i^*$ is the unknown positive constant, and $\psi _{i1}(\cdot )$ and $\psi _{i2}(\cdot )$ denote the known non-negative smooth functions.

Assumption 2

[62, 63] The unmodeled dynamic $\dot{z} = q(x,z)$ in (1) exists an input-to-state practically stable (ISpS) Lyapunov V(z) which yields

$$\begin{aligned} \pi _1 (|z|)&\le V(z) \le \pi _2 (|z|) \end{aligned}$$

(3)

$$\begin{aligned} \frac{{\partial V(z)}}{{\partial z}}&\le - a V(z) +\kappa (|x|) + b_0 \end{aligned}$$

(4)

where $\pi _1$, $\pi _2$ and $\kappa$ are $K_\infty -$functions, and the constants $a>0$ and $b_0>0$.

Lemma 1

[63] Assume that for a controlled system, if (3) and (4) hold, then for any constant $\bar{a}$ in $(0, a_0)$, function ${{\bar{\kappa }}}(x) \le \kappa (|x|)$, and initial value $x_0$= $x_0(0)$, there exists a finite $T_0 = T_0(\bar{a}, r_0, z_0)$, $D(t) \ge 0$ for all $t \ge 0$ and a dynamical signal r which described by

$$\begin{aligned} \dot{r} =-{\bar{a}}r + {{\bar{\kappa }}} (x_1(t)) + b_0, r(0)=r_0 \end{aligned}$$

(5)

satisfying $D(t)=0$, $\forall t \ge T_0$

$$\begin{aligned} V(z(t)) \le r(t) + D(t, t_0), \ \ \forall t \ge 0 \end{aligned}$$

(6)

The smooth function ${{\bar{\kappa }}} (\cdot )$ is selected as $\bar{\kappa }(s)=s^2 \kappa _0(s^2)$. Then, (6) becomes

$$\begin{aligned} \dot{r}=- {{\bar{a}}} r + x_1^2 \kappa _0(x_1^2) + b_0, \ \ r(0)=r_0 \end{aligned}$$

(7)

where $\kappa _0(x_1^2)>0$ is a smooth function.

Assumption 3

[34] Let ${\hat{x}}=[{\hat{x}}_1, {\hat{x}}_2, \cdots , {\hat{x}}_n]^T$ be the estimation of $x=[ x_1, x_2, \cdots , x_n]^T$, and $l_i$ $(1\le i \le n)$ be a known constant which satisfying $|f_i(x)-f_i({\hat{x}})| \le l_i ||x-{\hat{x}}||$, where $\Vert \cdot \Vert$ denotes the 2-norm of a vector.

Remark 2

Assumption 3 is commonly adopted in the literatures (Similar assumptions can be found in [27, 29, 34, 35]), which is a common basic assumption in the design of nonlinear systems using output feedback. In absence of Assumption 3, it would be extremely difficult to verify the stability of the overall system. As far as the function $f_i(x)$ in (1) which satisfies local Lipschitz condition, Assumption 3 can be relaxed to satisfy the local Lipschitz condition according to the relevant theories, See [28, 31, 32, 59]. In order to make the description of the problem convenient, we employ this Lemma defined in [34].

Assumption 4

[74] For the slowly varying delay $\tau (t)$, there exists a known constant ${{\hat{\tau }}} >0$ satisfying $\tau (t) <{{\hat{\tau }}}$. $\forall t \in R$, $|{{\dot{\tau }}} (t)|<\eta <1$, and $\eta >0$ is the unknown constant.

Definition 1

[45] Suppose that the equilibrium point of nonlinear system $\dot{x}(t) = f(x(t))$ is $x=0$. If for any initial condition $x(t_0 ) = x_0$, there exists a settling time $T(\varepsilon ,x_0 ) < + \infty$ and $\varepsilon > 0$ which yields $\forall t > t_0 + T$, then $\dot{x}(t) = f(x(t))$ is called semiglobal practical finite-time stable(SGPFS).

Lemma 2

[45] For system ${\dot{x}}(t) = f(x(t))$ is SGPFS, if there exist some scalars $c > 0,0< \beta < 1$, $d>0$ and a smooth function $V(x(t))>0$ which yields ${\dot{V}}(x(t)) \le - cV^\beta (x(t) ) + d$, when $t \ge 0$.

Lemma 3

[45] Let $\omega$ be a real number and $0 \le \omega \le 1$, $x_{i(1 \le i \le m)} \in R$, such that

$$\begin{aligned} \left( {\sum \nolimits _{i = 1}^m {|x_i |} } \right) ^\omega \le \sum \nolimits _{i = 1}^m {|x_i |} ^\omega \le m^{(1 - p)} \left( {\sum \nolimits _{i = 1}^m {|x_i |} } \right) ^\omega . \end{aligned}$$

(8)

Lemma 4

[45] Let x and y be real variables, for any given positive constants $\vartheta _1$, $\vartheta _2$, and $\vartheta _3$, then

$$\begin{aligned} \left| x \right| ^{\vartheta _1} \left| y \right| ^{\vartheta _2}&\le \frac{\vartheta _1}{{\vartheta _1 + \vartheta _2}}{\vartheta _3}|x|^{\vartheta _1 + \vartheta _2} \nonumber \\&\quad + \frac{\vartheta _1}{{\vartheta _1 + \vartheta _2}}{\vartheta _3}^{-\frac{\vartheta _1}{\vartheta _2}} |y|^{\vartheta _1 + \vartheta _2}. \end{aligned}$$

(9)

The purpose of this paper is to design a unified framework of observer-based adaptive fuzzy finite time control scheme for non-strict feedback nonlinear systems with unknown input delay, unmodeled dynamics and unmeasurable state variables such that all signals of the closed-loop systems are SGPFS.

In the following design process, FLS can be employed to identify the unknown continuous nonlinear functions.

Lemma 5

[34] $f\left( x \right)$ is continuous and defined on a compact set $\varOmega$ and can be approximated by a fuzzy logic system $\theta ^T\phi (x)$. Then for any constant $\varepsilon$, which yields

$$\begin{aligned} \mathop {\sup }\limits _{x \in \varOmega } |f(x) - \theta ^{T}\varphi (x)| \le \varepsilon \end{aligned}$$

(10)

where $\theta ^T= [\theta _1 ,\theta _2, \cdots , \theta _N ]^T$ denotes the optimal weight vector with $N>1$ being the number of the fuzzy rules. $\varphi (x) = [\varphi _1 (x), \varphi _2 (x), \cdots ,$ $\varphi _N (x)]^T$ is the membership function vector with

$$\begin{aligned} \varphi _l (x) = \frac{{\prod \nolimits _{i = 1}^n {\mu _{F_i^l (x_i )} } }}{{\sum \nolimits _{l = 1}^N {\left[ {\prod \nolimits _{i = 1}^n {\mu _{F_i^l (x_i )} } } \right] } }} \end{aligned}$$

and $\mu _{F_i^l (x_i )}$ is the membership function of inference antecedent variable of $x_i$ in IF-then rules.

3 Control design

Based on the idea of backstepping technique, the design process of adaptive controller will be discussed in this section.

3.1 Fuzzy observer design

Firstly, let ${\hat{x}}$ be the estimation of state variable x, then system (1) can be transformed as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}_1 = x_2 + f_1 ({\hat{x}}) + \varDelta f_1+ \varDelta _1 (x,z) \\ {\dot{x}}_i = x_ {i+1} + f_i ({\hat{x}}) + \varDelta f_i + \varDelta _i (x,z) \\ {\dot{x}}_n = u(t - \tau (t) ) + f_n ({\hat{x}}) + \varDelta f_n +\varDelta _n (x,z) \\ y = x_1 \\ \end{array} \right. \end{aligned}$$

(11)

where $\varDelta f_i = f_i (x) - f_i ({\hat{x}}),i = 1,2, \cdots ,n$.

For $1 \le i \le n$, according to the idea of approximation in Lemma 5, the unknown function $f_i ({\hat{x}})$ in system (1) can be modeled by a FLS ${\hat{f}}_i ({\hat{x}})=\hat{\theta }_i^T \varphi _i ({\hat{x}})$, i.e.,

$$\begin{aligned} f_i ({\hat{x}})=\varepsilon _i ({\hat{x}}) + {\hat{f}}_i ({\hat{x}})= \varepsilon _i ({\hat{x}}) + \theta _i^{*T} \varphi _i ({\hat{x}}), \ \ \mathrm{{|}}\varepsilon _i \mathrm{{|}} \le \varepsilon _i^* \end{aligned}$$

(12)

where $\varepsilon _i ({\hat{x}})$ is the minimum approximation error, $\varepsilon _i^*$ is an unknown constant, and $\theta _i^*$ denotes the optimal parameter vector, which defined as

$$\begin{aligned} \theta _i^* = \arg \mathop {\min }\limits _{ {{\hat{\theta }}} _i \in \varOmega _i } [\mathop {\sup }\limits _{{\hat{x}} \in U} |{\hat{f}}_i ({\hat{x}}) - f_i ({\hat{x}})|] \end{aligned}$$

(13)

with ${\hat{\theta }} _i$ being the estimation of $\theta ^*_i$, $\varOmega _i$ and U being the compact regions for ${{\hat{\theta }}} _i$ and ${\hat{x}}$, respectively.

Substituting (12) into (11), and rewriting system (11) as

$$\begin{aligned} {\dot{x}}&= Ax + Ly + \sum \limits _{i = 1}^n {B_i \theta _i^{*T} } \varphi _i ({\hat{x}}) + \varepsilon \nonumber \\&\quad + \varDelta F + B_n U(t- \tau (t)) +\varDelta _{xz} \nonumber \\ y&= Cx \end{aligned}$$

(14)

where

$$\begin{aligned} A= & {} \left[ {\begin{array}{*{20}c} { -l_1 } &{} {} &{} {} &{} {} \\ \vdots &{} {} &{} {I_{n - 1} } &{} {} \\ { - l_n } &{} 0 &{} \cdots &{} 0 \\ \end{array}} \right] , L = \left[ {\begin{array}{*{20}c} { l_1 } \\ \vdots \\ {l_n } \\ \end{array}} \right] , \\ \varDelta F= & {} \left[ {\begin{array}{*{20}c} {\varDelta f_1 } \\ \vdots \\ {\varDelta f_n } \\ \end{array}} \right] , C = [1, \cdots ,0], \\ \varepsilon= & {} [\varepsilon _1, \cdots ,\varepsilon _n ]^T, B_i = [\begin{array}{*{20}c} 0 &{} \cdots &{} 1 &{} {\begin{array}{*{20}c} \cdots &{} 0 \\ \end{array}} \\ \end{array}]^T ,\\ \varDelta _{xz}= & {} [\varDelta _1 (x,z), \varDelta _2 (x,z) ,\cdots ,\varDelta _n (x,z) ]^T. \end{aligned}$$

Next, we define the fuzzy state observer as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\hat{x}}}_1 = {\hat{x}}_2 +{{\hat{\theta }}} _1^T \varphi _1 ({\hat{x}}) +l_1 (x_1 - {\hat{x}}_1 ) \\ \dot{{\hat{x}}}_i = {\hat{x}}_{i+1} +{{\hat{\theta }}} _i^T \varphi _i ({\hat{x}})+ l_i (x_1 - {\hat{x}}_1 ) \\ \dot{{\hat{x}}}_n = u(t - \tau (t) )+{{\hat{\theta }}} _n^T \varphi _n ({\hat{x}}) + l_n (x_1 - {\hat{x}}_1 ) \\ y = {\hat{x}}_1 \\ \end{array} \right. \end{aligned}$$

(15)

Remark 3

The linear observer proposed in [27,28,29,30], which is independent on the controlled systems. This results in the limited information obtained by the linear observer, especially the unmodeled dynamics phenomena exist in real systems. In contrast, the fuzzy state observer (15) uses the information of the controlled system in the design process, which can obtain more system information and achieve better estimations of the unmeasurable states.

Furthermore, system (15) can be described as

$$\begin{aligned} \dot{{\hat{x}}}&= A{\hat{x}} + Ly + \sum \limits _{i = 1}^n {B_i {{\hat{\theta }}} _i^T \varphi _i ({\hat{x}})} \nonumber \\&\quad + B_n U(t-\tau (t)) y = Cx \end{aligned}$$

(16)

Let the estimation error e be

$$\begin{aligned} e = \frac{1}{q^*} [e_1 ,e_2, \cdots ,e_n ]^T = \frac{1}{q^*}(x - {\hat{x}}) \end{aligned}$$

(17)

where $q^*=max \{1, q_1^*, q_2^{*2}| 1 \le i \le n \}$.

Based on (14) and (16), one can describe the dynamics of the observer error as

$$\begin{aligned} \dot{e} = Ae + \frac{1}{q^*} \left( \sum \limits _{i = 1}^n {B_i \tilde{\theta }_i^T \varphi _i ({\hat{x}}) + \varepsilon + \varDelta F +\varDelta _{xz}} \right) \end{aligned}$$

(18)

where the estimation error ${{\tilde{\theta }}} _i = \theta _i^* - {\hat{\theta }} _i$.

According Assumption 1 and Lemma 1, we define the transformations as

$$\begin{aligned} {{\bar{e}}}=\varGamma (r) e \end{aligned}$$

(19)

with

$$\begin{aligned} \varGamma (r)=\left( 1+4 \sum \limits _{i = 1}^n [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ]^2 \right) ^{-\frac{1}{2}}. \end{aligned}$$

(20)

Obviously, $\varGamma ^2 (r) \le 1$, and ${{\dot{\varGamma }}} (r)$ can be described as

$$\begin{aligned} \begin{aligned} {\dot{\varGamma }} (r)&= - \left( {1 + 4\sum \limits _{i = 1}^n {[\psi _{i2} \circ \pi _1^{ - 1} (2r)]^2 } } \right) ^{ - \frac{3}{2}}\\&\quad 4\sum \limits _{i = 1}^n {[\psi _{i2} \circ \pi _1^{ - 1} (2r)]^2 \frac{{\partial (\psi _{i2} \circ \pi _1^{ - 1} (2r))}}{{\partial (2r)}}} 2\dot{r} \\&= - \varGamma ^3 (r)4\sum \limits _{i = 1}^n [\psi _{i2} \circ \pi _1^{ - 1} (2r)]^2 \\&\quad \frac{{\partial (\psi _{i2} \circ \pi _1^{ - 1} (2r))}}{{\partial (2r)}} 2\dot{r}. \end{aligned} \end{aligned}$$

(21)

From (18) and (21), one has

$$\begin{aligned} \begin{aligned} \dot{{{\bar{e}}}}&= \varGamma (r)\dot{e} + e{{\dot{\varGamma }}} (r) \\&= \varGamma (r)\dot{e} + \varGamma ^{ - 1} (r){{\bar{e}}}{{\dot{\varGamma }}} (r)\\&= \varGamma (r) \left( Ae + \frac{1}{q^*} \left( \sum \limits _{i = 1}^n {B_i {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}}) + \varepsilon + \varDelta F +\varDelta _{xz}} \right) \right) \\&\quad + \varGamma ^{ - 1} (r){{\bar{e}}}{{\dot{\varGamma }}} (r)\\&= A {{\bar{e}}} + \frac{1}{q^*} \varGamma (r) \left( \sum \limits _{i = 1}^n {B_i {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}}) + \varepsilon + \varDelta F +\varDelta _{xz}} \right) \\&\quad -\varGamma ^{2} (r) 4 \sum \limits _{i = 1}^n [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ] \\&\quad \frac{{\partial ( [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ] )\,}}{{\partial (2r)}}2\dot{r}{{\bar{e}}}. \end{aligned} \end{aligned}$$

(22)

By selecting vector, L which yields matrix A is a strict Hurwitz matrix. Then, for any given matrix $Q = Q^T > 0$, there exists $P = P^T > 0$ which yields $A^T P + PA = - Q$.

Consider the Lyapunov function $V_0 = {{\bar{e}}}^T P {{\bar{e}}}$ , one has

$$\begin{aligned} \begin{aligned}&{\dot{V}}_0 \le - \lambda _{\mathrm{{min}}} (Q)|| {{\bar{e}}}||^2 + \frac{2 {\bar{e}}^T P }{q^*} \varGamma (r) \\&\quad \left( \sum \limits _{i = 1}^n {B_i {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}}) +\varepsilon + \varDelta F +\varDelta _{xz} }\right) \\&\quad -\varGamma (r)^{2} 4 \sum \limits _{i = 1}^n [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ] \\&\quad \frac{{\partial ( [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ] )\,}}{{\partial (2r)}}4\dot{r}{{\bar{e}}}^TP {{\bar{e}}} . \end{aligned} \end{aligned}$$

(23)

By using the complete squares formula and the property of $0 < \varphi _i^T ({\hat{x}})\varphi _i ({\hat{x}}) \le 1$, one can get the following results

$$\begin{aligned}&\frac{2}{q^*}\varGamma (r) {{\bar{e}}}^T P\sum \limits _{i = 1}^n {B_i {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}})} \nonumber \\&\quad \le ||P||^2 \sum \limits _{i = 1}^n {{{\tilde{\theta }}} _i^T {{\tilde{\theta }}} _i } + n|| {{\bar{e}}}||^2 \end{aligned}$$

(24)

$$\begin{aligned}&\frac{2}{q^*} \varGamma (r) {{\bar{e}}}^T P (\varepsilon +\varDelta F) \nonumber \\&\quad \le 2 ||{{\bar{e}}}||^2 + ||P||^2 ||\varepsilon ^* ||^2 + ||P||^2 ||\varDelta F||^2\nonumber \\&\quad \le 2|| {{\bar{e}}}||^2 + ||P||^2 ||\varepsilon ^* ||^2 + ||P||^2 \left( \sum \limits _{j = 1}^n {l_j^2 || {{\bar{e}}}||^2 } \right) . \end{aligned}$$

(25)

Based on Assumption 2 and Lemma 1, one can get $|z| \le \pi _1^{-1} (r + D_0)$. Furthermore, by using Assumption 1 and the complete squares formula, one can have

$$\begin{aligned} \begin{aligned}&\frac{2}{q^*}\varGamma (r) {{\bar{e}}}^T P \varDelta _{xz} \\&\quad \le 2 ||{{\bar{e}}}|| ||P|| \left( \sum \limits _{i = 1}^n \psi _{i1} (y) + \sum \limits _{i = 1}^n \psi _{i2} (\left| z \right| ) \right) \\&\quad \le n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y^2+ 2 ||P||^2 ||{\bar{e}}||^2\\&\qquad + n \varGamma ^2 (r) \sum \limits _{i = 1}^n ( {\psi } _{i2} \circ \pi _1^{-1} (2r) )^2 \\&\qquad + n \varGamma ^2 (r) \sum \limits _{i = 1}^n ( {\psi } _{i2} \circ \pi _1^{-1} (2 D) )^2\\&\quad \le n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y^2+2 ||P||^2 ||{\bar{e}}||^2+ n + d_0 \end{aligned} \end{aligned}$$

(26)

where $\varGamma ^2 (r) \sum \limits _{i = 1}^n ( {\psi } _{i2} \circ \pi _1^{-1} (2r) )^2 \le 1$, $d_0= n \sum \limits _{i = 1}^n ( {\psi } _{i2} \circ \pi _1^{-1} (2 D) )^2$, ${\bar{\psi }} _{i1} (y)$ is a smooth function and $y {\bar{\psi }} _{i1} (y)= \psi _{i1} (y)$.

Substituting (24)–(26) into (23) and based on the fact $\frac{{\partial ( [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ] )\,}}{{\partial (2r)}} > 0$ and ${{\bar{e}}}^T P {{\bar{e}}} >0$, one can get

$$\begin{aligned} {\dot{V}}_0&\le - \lambda _0 ||{{\bar{e}}}||^2 + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} \nonumber \\&\quad + n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y^2 + \varUpsilon _0 \end{aligned}$$

(27)

where $\lambda _0 \mathrm{{ = }}\lambda _{\min } (Q) - ||P||^2 (\sum \limits _{j = 1}^n {l_j^2 ) -2 ||P||^2 - 2 - n }$ and $\varUpsilon _0 = ||P||^2 ||\varepsilon ^*||^2 +n+d_0$.

3.2 Controller design

Firstly, the following change of coordinate is employed in the process of backstepping designing

$$\begin{aligned} \begin{array}{l} z_1 = x_1 \\ z_i ={\hat{x}}_i -\omega _i, \begin{array}{*{20}c} {} &{} {i = 2,3, \cdots ,n} \\ \end{array} \\ \end{array} \end{aligned}$$

(28)

where $\omega _i$ is the first-order filter output signal, which is defined as

$$\begin{aligned} \xi _i {{\dot{\omega }}} _i + \omega _i = \alpha _{i - 1}, \omega _i (0) = \alpha _{i - 1} (0), \ \ \ i = 2,3, \cdots ,n \end{aligned}$$

(29)

with $\xi _i$ being design parameter and $\alpha _i$ being the first-order filter input signals. The filter errors are given by

$$\begin{aligned} \chi _i = \omega _i - \alpha _{i - 1} \begin{array}{*{20}c}, {} \ \ \ \ &{} {i = 2,3, \cdots ,n} \\ \end{array} \end{aligned}$$

(30)

According to the previous change of coordinate, the specific design steps as follows.

Step 1: Based on (28) and (29), the derivative of $z_1$ is obtained that

$$\begin{aligned} \begin{aligned} \dot{z}_1&= \dot{x}_1 \\&=x_2+f_1 ({\hat{x}}) + \varDelta f_1 +\varDelta _1 (x,z) \\&=\hat{x}_2+ q^* e_2+ \theta _1^{*T} \varphi _1 ({\hat{x}}) \\&\quad + \varepsilon _1 + \varDelta f_1 +\varDelta _1 (x,z) . \end{aligned} \end{aligned}$$

(31)

For (31), a desired virtual input $\alpha _1$ can be derived to take place of ${\hat{x}}_2$ based on $z_2 = {\hat{x}}_2 -\omega _2$ and $\chi _2 = \omega _2 - \alpha _1$, we can get

$$\begin{aligned} \begin{aligned} \dot{z}_1&= z_2+ \chi _2+ q^* e_2 +\alpha _1 + \theta _1^{*T} \varphi _1 ({\hat{x}}) \\&\quad + \varepsilon _1 + \varDelta f_1 +\varDelta _1 (x,z) \\&=z_2+ \chi _2 + q^* e_2 +\alpha _1+ \theta _1^{*T} \varphi _1 ({\hat{x}}) \\&\quad +{\hat{\theta }}_1^{T} \varphi _1 ({\hat{x}}_1) - \theta _1^{*T} \varphi _1 ({\hat{x}}_1) + {\tilde{\theta }}_1^{T} \varphi _1 ({\hat{x}}_1) \\&\quad + \varepsilon _1 + \varDelta f_1 + \varDelta _1 (x,z) . \end{aligned} \end{aligned}$$

(32)

Let the Lyapunov function candidate be

$$\begin{aligned} V_{\omega 1}&= V_0 + \frac{1}{2}z_1^2 + \frac{1}{{2\gamma _1}}{{\tilde{\theta }}} _1^T {{\tilde{\theta }}} _1 \nonumber \\&\quad + \frac{1}{{2 {{\bar{\gamma }}}_1}}{{\tilde{\varTheta }}} _1^2 + \frac{1}{2}{\tilde{q}}^2 + \frac{r}{\gamma _0} \end{aligned}$$

(33)

where ${{\tilde{\varTheta }}} _1 = \varTheta ^* _1 - {\hat{\varTheta }} _1$ and ${{\tilde{q}}} = q^* - {\hat{q}}$ represent the estimation errors, ${\hat{\varTheta }} _1$ and ${\hat{q}}$ are the estimations of $\varTheta ^* _1 =||\theta ^*_1||^2$ and $q^*$, respectively. The design parameters $\gamma _1 > 0$, ${{\bar{\gamma }}} _1 > 0$ and $\gamma _0 > 0$.

Differentiating $V_{\omega 1}$, then

$$\begin{aligned} \begin{aligned} \dot{V}_{\omega 1}&\le \dot{V_0 } + z_1 \dot{z}_1 - \frac{1}{{\gamma _1 }}{{\tilde{\theta }}} _1^T \dot{{\hat{\theta }}} _1 \\&\quad - \frac{1}{{{{\bar{\gamma }}} _1 }}{{\tilde{\varTheta }}} _1 \dot{{\hat{\varTheta }}} _1 + {\tilde{q}} \dot{ {\tilde{q}}} + \frac{1}{\gamma _0} {\dot{r}} \\&\le - \lambda _0 ||{{\bar{e}}}||^2 + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} - \frac{1}{{\gamma _1 }}{{\tilde{\theta }}} _1^T \dot{{\hat{\theta }}} _1 \\&\quad + n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y^2 + \varUpsilon _0 - \frac{1}{{{{\bar{\gamma }}} _1 }}{{\tilde{\varTheta }}} _1 \dot{{\hat{\varTheta }}} _1 \\&\quad + z_1 (z_2+ \chi _2 + q^* e_2 + \alpha _1 + \theta _1^{*T} \varphi _1 ({\hat{x}}) \\&\quad + {\hat{\theta }}_1^{T} \varphi _1 ({\hat{x}}_1) + {\tilde{\theta }}_1^{T} \varphi _1 ({\hat{x}}_1) \\&\quad - \theta _1^{*T} \varphi _1 ({\hat{x}}_1) + \varepsilon _1 + \varDelta f_1 +\varDelta _1 (x,z) ) \\&\quad - {\tilde{q}} \dot{ \hat{q}} +\frac{1}{\gamma _0}(- {{\bar{a}}} r + x_1^2 \kappa _0(x_1^2) + b_0). \end{aligned} \end{aligned}$$

(34)

Based on the completion of squares and Assumption 1, one can get the following results

$$\begin{aligned}&z_1( q^* e_2+ \varepsilon _1 + \varDelta f_1 + \chi _2 ) \nonumber \\&\quad \le \frac{3}{2} z_1^2 + \frac{ z_1^2 q^* }{2 \varGamma ^2 (r)}+\left( \frac{1 }{2}+ \frac{l_1^2}{2 \varGamma ^2 (r)} \right) ||{{\bar{e}}}||^2 \nonumber \\&\qquad + \frac{1 }{2}\varepsilon _1^{*2}+ \frac{1}{2}\chi _2^2 \end{aligned}$$

(35)

$$\begin{aligned}&z_1 \left( \theta _1^{*T} \varphi _1 ({\hat{x}}) - \theta _1^{*T} \varphi _1 ({{\hat{x}}} _1 ) \right) \le \frac{\varsigma _1}{2}z^2_1 \varTheta _1^{*} + \frac{2}{\varsigma _1 } \end{aligned}$$

(36)

where $\varsigma _1 >0$ is a design parameter.

From (2) and (3), one can get

$$\begin{aligned} \begin{aligned} z_1 \varDelta _1 (x,z)&\le \frac{1}{4} [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ]^2 z_1 ^2 q^* +1+ \frac{1}{4}z_1 ^2 q^*\\&\quad + 4 [ { \psi } _{i2} \circ \pi _1^{-1} (2D) ]^2 + {\bar{\psi }} _{i1} (y) y z_1 q^*. \end{aligned} \end{aligned}$$

(37)

Furthermore, substituting (35)–(37) into (34), we can have

$$\begin{aligned} \begin{aligned} \dot{V}_{\omega 1}&\le - \lambda _1||{{\bar{e}}}||^2 +{{\tilde{\theta }}}_1^T \left( \varphi _1 ({\hat{x}}_1)z_1 - \frac{1}{{\gamma _1 }}\dot{{\hat{\theta }} }_1 \right) \\&\quad +{{\tilde{\varTheta }}}_1 \left( \frac{\varsigma _1}{2}z^2_1 - \frac{1}{{{{\bar{\gamma }}} _1 }}\dot{{\hat{\varTheta }}} _1 \right) \\&\quad + z_1 \left( \frac{3}{2} z_1+ \alpha _1 + z_2 +\frac{z_1 \kappa _0(x_1^2) }{\gamma _0}+ \frac{\varsigma _1 {\hat{\varTheta }}_1 z_1 }{2} \right. \\&\quad + n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y + {{\hat{\theta }}}_1^T \varphi _1 ({\hat{x}}_1) \\&\quad \left. + \delta _1 \hat{q} \right. ) + {\tilde{q}} (\delta _1 y - \dot{ \hat{q}} ) +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} + \frac{1}{2}\chi _2^2 + {{\bar{\varUpsilon }}}_1 \end{aligned} \end{aligned}$$

(38)

where $\lambda _1= \lambda _0 - (\frac{1 }{2}+ \frac{l_1^2}{2 \varGamma ^2 (r)})$, $\delta _1 = \frac{ z_1 }{2 \varGamma ^2 (r)} + \frac{1}{4} [ { \psi } _{i2} \circ \pi _1^{-1} (2r) ]^2 z_1 + \frac{1}{4}z_1 + {\bar{\psi }} _{i1} (y) y$ and ${{\bar{\varUpsilon }}}_1=\varUpsilon _0 + \frac{2}{\varsigma _1 } + \frac{1 }{2}\varepsilon _1^{*2} +1 + 4 [ { \psi } _{i2} \circ \pi _1^{-1} (2D) ]^2$.

Now, we design the virtual control signal as

$$\begin{aligned} \begin{aligned} \alpha _1&=- \frac{3}{2} z_1 - k_1 z_1^{2\beta - 1} -\frac{z_1 \kappa _0(x_1^2) }{\gamma _0}- \frac{\varsigma _1 {\hat{\varTheta }}_1 z_1 }{2}\\&\quad - n^2 \sum \limits _{i = 1}^n {\bar{\psi }} _{i1}^2 (y) y - {{\hat{\theta }}}_1^T \varphi _1 ({\hat{x}}_1) - \delta _1 \hat{q} \end{aligned}\nonumber \\ \end{aligned}$$

(39)

with the adaptive laws $\dot{{\hat{\theta }}}_1$ and $\dot{\hat{\varTheta }}_1$ as

$$\begin{aligned} \dot{{\hat{\theta }}}_1&= \gamma _1 \phi _1^T ({\hat{x}}_1 )z_1-\varsigma _1 {{\hat{\theta }}}_1 \end{aligned}$$

(40)

$$\begin{aligned} \dot{{\hat{\varTheta }}}_1&= \frac{1}{2} {{\bar{\gamma }}} _1\varsigma _1 z_1^2 - {{\bar{\varsigma }}}_1 {{\hat{\varTheta }}}_1 \end{aligned}$$

(41)

and the turning function $\zeta _1$ as

$$\begin{aligned} \zeta _1=\delta _1 z_1 - \varpi \hat{q} \end{aligned}$$

(42)

where the design parameters $k_1 > 0$, $\varsigma _1 > 0$, $\bar{\varsigma }_1 > 0$ and $\varpi >0$.

From (38)–(40), the following result can be obtained

$$\begin{aligned} \begin{aligned} \dot{V}_{\omega 1}&\le - \lambda _1||{{\bar{e}}}||^2 - k_1 z_1^{2\beta } + z_1z_2 + \frac{\varsigma _1 {{\tilde{\theta }}} _1^T {\hat{\theta }} _1}{{\gamma _1 }} \\&\quad + \frac{ {{\bar{\varsigma }}} _1 {{\tilde{\varTheta }}} _1 {\hat{\varTheta }} _1 }{{{{\bar{\gamma }}} _1 }} + \varpi _1 {\tilde{q}} \hat{q} \\&\quad - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _1 ) +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} + \frac{1}{2}\chi _2^2 +{{\bar{\varUpsilon }}}_1. \end{aligned} \end{aligned}$$

(43)

To deal with the problem of “explosion of complexity” caused by repeatedly differentiating $\alpha _{1}$, let $\alpha _{1}$ pass through a given low-pass filter $\omega _2$, which defined in (29) with the filter time design parameter $\xi _2$ and the filter error $\chi _2$ defined in (30). Then, one can get

$$\begin{aligned} {{\dot{\omega }}}_2=\frac{{ - \chi _2 }}{{\xi _2 }} \end{aligned}$$

(44)

and

$$\begin{aligned} \begin{aligned} {{\dot{\chi }}}_2&= {{\dot{\omega }}} _2 - {{\dot{\alpha }}} _1 = \frac{{ - \chi _2 }}{{\xi _2 }} - {{\dot{\alpha }}} _1 \\&= \frac{{ - \chi _2 }}{{\xi _2 }} + M_2 (\cdot ) \end{aligned} \end{aligned}$$

(45)

where $M_2 (\cdot )$ is a continuous function, and $M_2 (z_1 ,z_2 , \chi _2 , {{\hat{\theta }}}_1 , {{\hat{\varTheta }}}_1, y_d ,\dot{y}_d ,\ddot{y}_d ,\mu _1 ) = - (\frac{{\partial \alpha _1 }}{{\partial {\hat{x}}_1 }}\dot{\hat{x}}_1$ $+ \frac{{\partial \alpha _1 }}{{ \partial z_1 }}\dot{z}_1 + \frac{{\partial \alpha _1 }}{\partial {{\hat{\theta }}} _1} \dot{{{\hat{\theta }}}}_1 + \frac{{\partial \alpha _1 }}{\partial {{\hat{\varTheta }}} _1} \dot{\hat{\varTheta }}_1 + \frac{{\partial \alpha _1 }}{{\partial y_d }}\dot{y}_d + \frac{{\partial \alpha _1 }}{{\partial \mu _1 }}{{\dot{\mu }}} _1)$. Furthermore, for any given $B_0$ and $\sigma$, the sets $H_0 : = \{ (y_d ,\dot{y}_d ,\ddot{y}_d ):(y_d )^2 + (\dot{y}_d )^2 + (\ddot{y}_d )^2 \le B_0 \}$ is compact in $R^3$, and $H_2 : = \{ \sum \nolimits _{j = 1}^2 {z_j^2 + \gamma _1 ^{-1} {{\tilde{\theta }}}_1^T {{\tilde{\theta }}}_1 + {{\bar{\gamma }}} _1 ^{-1} {{\tilde{\varTheta }}}_1^T {{\tilde{\varTheta }}}_1 +\chi _2^2 } \le 2 \sigma \}$ is compact in $R^{N_1+3}$ with $N_1$ being the dimension of ${{\tilde{\theta }}}_1^T$. According [77], $M_{2}$ has a maximum value $B_{2}$. Thus,

$$\begin{aligned} \begin{aligned} \chi _2 {{\dot{\chi }}}_2&= \chi _2 ({{\dot{\omega }}} _2 - {{\dot{\alpha }}} _1 ) \\&= \chi _2 \left( \frac{{ - \chi _2 }}{{\xi _2 }}\right) \\&\quad + \chi _2 M_2 (z_1 ,z_2 , \chi _2 , {{\hat{\theta }}}_1 , {{\hat{\varTheta }}}_1, y_d ,\dot{y}_d ,\ddot{y}_d ,\mu _1 )\\&\le - \frac{1}{{\xi _2 }}\chi _{_2 }^2 + \frac{1}{2}\chi _{_2 }^2 + \frac{1}{2}B_{_2 }^2. \end{aligned} \end{aligned}$$

(46)

Let the first Lyapunov function of the system be

$$\begin{aligned} V_{1}=V_0+V_{\omega 1}+\frac{1}{2} \chi _2 ^2. \end{aligned}$$

(47)

From (43)–(47), one can get

$$\begin{aligned} \begin{aligned} \dot{V}_{1}&=\dot{V}_0 + \dot{V}_{\omega 1} + \chi _2 {{\dot{\chi }}}_2 \\&\le - \lambda _1 || {{\bar{e}}}||^2 - k_1 z_1^{2\beta } + z_1z_2 \\&\quad + \frac{\varsigma _1 {{\tilde{\theta }}} _1^T {{\hat{\theta }}} _1}{{\gamma _1 }} + \frac{ {{\bar{\varsigma }}} _1 {{\tilde{\varTheta }}} _1 {{\hat{\varTheta }}} _1 }{{{{\bar{\gamma }}} _1 }} + \varpi {\tilde{q}} \hat{q} \\&\quad - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _1 ) +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} + \left( 1-\frac{1}{\xi _2}\right) \chi _2^2 + \varUpsilon _1 \end{aligned} \end{aligned}$$

(48)

where $\varUpsilon _1= {{\bar{\varUpsilon }}}_0+ \frac{1}{2}B_{_2 }^2$.

Step i ($2 \le i \le n - 1$) : Based on $z_{i+1} ={\hat{x}}_{i+1} -\omega _{i+1}$ and $\chi _{i+1} = \omega _{i+1} - \alpha _i$, from (28)–(30), differentiating $z_i$ then

$$\begin{aligned} \begin{aligned} {\dot{z}}_i&= \dot{{\hat{x}}}_i - {{\dot{\omega }}}_i \\&= {\hat{x}}_{i+1} + {{\hat{\theta }}} _i^T \varphi _i ({\hat{x}})+ l_i q^*(x_1 - {\hat{x}}_1 ) - {{\dot{\omega }}}_i\\&= z_{i+1} + \chi _{i+1} +\alpha _i + l_i q^*e_1 - {{\dot{\omega }}}_i \\&\quad - {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}}) + {{\tilde{\theta }}} _i^T \varphi _i (\underline{{\hat{x}}} _i ) \\&\quad + {\hat{\theta }} _i^T \varphi _i (\underline{{\hat{x}}} _i ) - \theta _i^{*T} \varphi _i (\underline{{\hat{x}}} _i ) + \theta _i^{*T} \varphi _i ({\hat{x}}) \end{aligned} \end{aligned}$$

(49)

where $\underline{\hat{x}}_i=[\hat{x}_1,\hat{x}_2, \cdots , \hat{x}_i ]$.

Let the following Lyapunov function candidate be

$$\begin{aligned} V_{\omega i} = V_{i-1}+ \frac{1}{2}z_i^2 + \frac{1}{{2\gamma _i }}{{\tilde{\theta }}} _i^T{{\tilde{\theta }}} _i + \frac{1}{{2 \bar{\gamma }_i}}{{\tilde{\varTheta }}} _i^2 \end{aligned}$$

(50)

where the estimation error is ${{\tilde{\varTheta }}} _i = \varTheta _i^* - {{\hat{\varTheta }}} _i$ and ${{\hat{\varTheta }}} _i$ represents the estimation of $||\theta _i^*||^2$. The design parameters $\gamma _i > 0$ and ${{\bar{\gamma }}} _i > 0$.

Thus, differentiating $V_{\omega i}$ one has

$$\begin{aligned} \dot{V}_{\omega i}&\le - \lambda _{i-1} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{i-1} k_{j} z_{j}^{2\beta } + z_{i-1}z_i \nonumber \\&\quad + \sum \limits _{j = 1}^{i-1} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} + \sum \limits _{j = 1}^{i-1}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} + \varpi {\tilde{q}} \hat{q} \nonumber \\&\quad + z_{i} ( z_{i+1} + \chi _{i+1} +\alpha _i + l_i q^* e_1 - {{\dot{\omega }}}_i \nonumber \\&\quad - {{\tilde{\theta }}} _i^T \varphi _i ({\hat{x}}) + {{\tilde{\theta }}} _i^T \varphi _i (\underline{{\hat{x}}} _i ) - \theta _i^{*T} \varphi _i (\underline{{\hat{x}}} _i ) \nonumber \\&\quad + {\hat{\theta }} _i^T \varphi _i (\underline{{\hat{x}}} _i ) + \theta _i^{*T} \varphi _i ({\hat{x}}) ) - \frac{1}{{\gamma _i }}{{\tilde{\theta }}} _i ^T \dot{{\hat{\theta }}}_i \nonumber \\&\quad - \frac{1}{{{{\bar{\gamma }}} _i }}{{\tilde{\varTheta }}} _i \dot{{\hat{\varTheta }}} _i - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _{i-1} ) + \sum \limits _{j = 2}^{i-1} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2}\nonumber \\&\quad +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} \nonumber \\&\quad + \sum \limits _{j = 1}^{i-1} \left( 1-\frac{1}{\xi _{j+1}}\right) \chi _{j+1}^2 + \varUpsilon _{i-1}. \end{aligned}$$

(51)

Based on the completion of squares, one has

$$\begin{aligned} z_{i} \chi _{i+1}&\le \frac{1}{2}z_{i}^2 + \frac{1}{2}\chi _{i+1}^2 \end{aligned}$$

(52)

$$\begin{aligned} z_i q^*l_i e_1&\le \frac{ z_i^2 l_i^2 q^* }{2 \varGamma ^2 (r)}+\frac{1 }{2} ||{{\bar{e}}}||^2 \end{aligned}$$

(53)

$$\begin{aligned} -z_i {{\tilde{\theta }}}_i^{T} \varphi _i ({\hat{x}})&\le \frac{1}{2}z_{i}^2 + \frac{1}{2}{{\tilde{\theta }}}_i^{T} {{\tilde{\theta }}}_i \end{aligned}$$

(54)

$$\begin{aligned} z_i (\theta _i^{*T} \varphi _i ({\hat{x}}) - \theta _i^{*T} \varphi _i ( \underline{{\hat{x}}} _i ) )&\le \frac{\varsigma _i}{2}z^2_i \varTheta _i^{*} + \frac{2}{\varsigma _i } \end{aligned}$$

(55)

where $\varsigma _i>0$ is a design parameter.

Based on (51)–(55), we can obtain that

$$\begin{aligned} \begin{aligned} \dot{V}_{\omega i}&\le - \lambda _{i} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{i-1}k_{j} z_{j}^{2\beta } + z_{i-1}z_i \\&\quad + \sum \limits _{j = 1}^{i-1} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} + \sum \limits _{j = 1}^{i-1}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} + \varpi {\tilde{q}} \hat{q} \\&\quad + z_{i} (z_i+ z_{i+1} +\alpha _i + \frac{\varsigma _i}{2}z_i {{\hat{\varTheta }}}_i + {\hat{\theta }} _i^T \varphi _i (\underline{{\hat{x}}} _i ) \\&\quad + \delta _i {\hat{q}} - {{\dot{\omega }}}_i ) - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _{i} ) \\&\quad +{{\tilde{\theta }}}_i^T \left( \varphi _i ( \underline{{\hat{x}}}_i)z_i - \frac{1}{{\gamma _i }}{{\dot{\theta }}} _i \right) + \sum \limits _{j = 1}^{i-1} \left( 1-\frac{1}{\xi _{j+1}}\right) \chi _{j+1}^2 \\&\quad + \frac{1}{2}\chi _{i+1}^2 + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} \\&\quad +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) +{{\tilde{\varTheta }}}_i \left( \frac{\varsigma _i}{2}z^{2}_{i+1} - \frac{1}{{{{\bar{\gamma }}} _i }}\dot{{\hat{\varTheta }}}_i \right) \\&\quad + \sum \limits _{j = 2}^{i} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2} + \frac{2}{\varsigma _i } + \varUpsilon _{i-1} \end{aligned} \end{aligned}$$

(56)

where $\lambda _{i}= \lambda _{i-1}+ \frac{1}{2}$ and $\delta _i= \frac{ z_i l_i^2 }{2 \varGamma ^2 (r)}$.

Then, design the virtual control input signal as

$$\begin{aligned} \alpha _i&= -z_{i-1} -z_i - k_i z_i^{2\beta - 1} - \frac{\varsigma _i}{2}z_i {{\hat{\varTheta }}}_i \nonumber \\&\quad - {{\hat{\theta }}} _i^T \varphi _i (\underline{{\hat{x}}} _i ) - \delta _i {\hat{q}}+ {{\dot{\omega }}}_i \end{aligned}$$

(57)

with the adaptive laws $\dot{{\hat{\theta }}}_i$ and $\dot{\hat{\varTheta }}_i$ as

$$\begin{aligned} \dot{{\hat{\theta }}}_i&= \gamma _i \phi _i^T (\underline{{\hat{x}}}_i )z_i-\varsigma _i {{\hat{\theta }}}_i \end{aligned}$$

(58)

$$\begin{aligned} \dot{{\hat{\varTheta }}}_i&= \frac{1}{2} {{\bar{\gamma }}} _i\varsigma _i z_i^2 - {{\bar{\varsigma }}}_i {{\hat{\varTheta }}}_i \end{aligned}$$

(59)

and the turning function $\zeta _{i}$ as

$$\begin{aligned} \zeta _{i}=\zeta _{i-1}+\delta _i z_i \end{aligned}$$

(60)

where the design parameters $k_i > 0$, $\varsigma _i > 0$ and ${{\bar{\varsigma }}}_i > 0$.

Furthermore, substituting (57)–(60) into (56), we can have

$$\begin{aligned} \begin{aligned} \dot{V}_{\omega i}&\le - \lambda _{i} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{i}k_{j} z_{j}^{2\beta } + z_i z_{i+1} \\&\quad + \sum \limits _{j = 1}^{i} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} + \sum \limits _{j = 1}^{i}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} + \varpi {\tilde{q}} \hat{q} \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _{i} ) \\&\quad +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) \\&\quad + \sum \limits _{j = 1}^{i-1} \left( 1-\frac{1}{\xi _{j+1}}\right) \chi _{j+1}^2 + \frac{1}{2}\chi _{i+1}^2 \\&\quad + \varUpsilon _{i-1} + \frac{2}{\varsigma _i } + \sum \limits _{j = 2}^{i} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2}. \end{aligned} \end{aligned}$$

(61)

As in step 1, let $\alpha _{i}$ pass through a given low-pass filter $\omega _{i+1}$, which defined in (29) with the filter time design parameter $\xi _{i+1}$ and the filter error $\chi _{i+1}$ defined in (30). Then, one can get

$$\begin{aligned} {{\dot{\omega }}}_{i+1}=\frac{{ - \chi _{i+1} }}{{\xi _{i+1} }} \end{aligned}$$

(62)

and

$$\begin{aligned} \begin{aligned} {{\dot{\chi }}}_{i+1} = \frac{{ - \chi _{i+1} }}{{\xi _{i+1} }} + M_{i+1} (\cdot ) \end{aligned} \end{aligned}$$

(63)

where $M_{i+1} (\cdot )$ is a continuous function, and $M_{i+1} (z_1, \cdots , z_{i+1} , \chi _1, \cdots , \chi _{i+1} , \hat{\theta }_1, \cdots , {{\hat{\theta }}}_{i} ,$ ${{\hat{\varTheta }}}_1, \cdots , {{\hat{\varTheta }}}_{i} , y_d , \dot{y}_d , \ddot{y}_d , \mu _1, \cdots , \mu _{i} ) = - (\frac{{\partial \alpha _i }}{{\partial {\hat{x}}_i }}\dot{\hat{x}}_i + \frac{{\partial \alpha _i }}{{ \partial z_i }}\dot{z}_i + \frac{{\partial \alpha _i }}{\partial {{\hat{\theta }}} _i} \dot{{{\hat{\theta }}}}_i + \frac{{\partial \alpha _i }}{\partial {{\hat{\varTheta }}} _i} \dot{{{\hat{\varTheta }}}}_i + \frac{{\partial \alpha _i }}{{\partial y_d }}\dot{y}_d + \frac{{\partial \alpha _i }}{{\partial \mu _i }}{{\dot{\mu }}} _i)$. Furthermore, for any given $B_0$ and $\sigma$, the sets $H_0 : = \{ (y_d ,\dot{y}_d ,\ddot{y}_d ):(y_d )^2 + (\dot{y}_d )^2 + (\ddot{y}_d )^2 \le B_0 \}$ is compact in $R^3$, and $H_i : = \{ \sum \nolimits _{j = 1}^i {z_j^2 + \gamma _i ^{-1} {{\tilde{\theta }}}_i^T {{\tilde{\theta }}}_i + {{\bar{\gamma }}} _i ^{-1} {{\tilde{\varTheta }}}_i^T {{\tilde{\varTheta }}}_i + \chi _i^2 } \le 2 \sigma \}$ is compact in $R^{N_1+3}$ with $N_1$ being the dimension of ${{\tilde{\theta }}}_i^T$. According [77], $M_{i+1}$ has a maximum value $B_{i+1}$. Thus,

$$\begin{aligned} \begin{aligned} \chi _{i+1} {{\dot{\chi }}}_{i+1}&= \chi _{i+1} ({{\dot{\omega }}} _{i+1} - {{\dot{\alpha }}} _i ) \\&= \chi _{i+1} \left( \frac{{ - \chi _{i+1} }}{{\xi _{i+1} }}\right) + \chi _{i+1} M_{i+1} (\cdot )\\&\le - \frac{1}{{\xi _{i+1} }}\chi _{i+1}^2 + \frac{1}{2}\chi _{i+1}^2 + \frac{1}{2}B_{i+1}^2 . \end{aligned} \end{aligned}$$

(64)

Let the ith Lyapunov function be

$$\begin{aligned} V_{i}= V_{\omega i}+\frac{1}{2} \chi _{i+1} ^2 . \end{aligned}$$

(65)

Then, from (61), (64) and (65) we have

$$\begin{aligned} \begin{aligned} \dot{V}_{i}&= \dot{V}_{\omega i}+\chi _{i+1} {{\dot{\chi }}}_{i+1}\\&\le - \lambda _{i} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{i}k_{j} z_{j}^{2\beta } + z_i z_{i+1} \\&\quad + \sum \limits _{j = 1}^{i} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} + \varpi {\tilde{q}} \hat{q} + \sum \limits _{j = 1}^{i}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} \\&\quad + \sum \limits _{j = 1}^{i} (1-\frac{1}{\xi _{j+1}})\chi _{j+1}^2 - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _{i} ) \\&\quad +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) + \varUpsilon _{i} \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} + \sum \limits _{j = 2}^{i} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2} \end{aligned} \end{aligned}$$

(66)

where $\varUpsilon _i=\varUpsilon _{i-1}+ \frac{2}{\varsigma _i } + \frac{1}{2}B_{i+1 }^2$.

Step n: In this step, a compensation signal $\mu$ is devised to tackle the effect of input delay, and the compensate signal $\mu$ is designed as

$$\begin{aligned} {{\dot{\mu }}}= - h \mu +u(t) - u(t - {{\hat{\tau }}} (t)) . \end{aligned}$$

(67)

Furthermore, we redefine the signal $z_n$ as follows

$$\begin{aligned} z_{n}= {{\hat{x}}}_n - \omega _n + \mu . \end{aligned}$$

(68)

Based on (67) and (68), differentiating $z_{n}$

$$\begin{aligned} \begin{aligned} \dot{z}_{n}&= \dot{{\hat{x}}}_n - {{\dot{\omega }}} _n + {{\dot{\mu }}} \\&= u(t - \tau (t))+ {{\hat{\theta }}} _n^T \varphi _n ({\hat{x}}) + l_nq^*e_1 \\&\quad - {{\dot{\omega }}} _n - h \mu - u(t - {{\hat{\tau }}} ) + u(t). \end{aligned} \end{aligned}$$

(69)

Then, let the Lyapunov function be

$$\begin{aligned} V_n&=V_{n-1}+ \frac{1}{2}z_{n}^2 + \frac{1}{2}\mu ^2 + \frac{1}{{2\gamma _n }}{{\tilde{\theta }}} _n^T {{\tilde{\theta }}} _n\nonumber \\&\quad +D_1 +D_2 + D_3 +D_4 \end{aligned}$$

(70)

where $D_1 = \frac{1}{2(1-\eta ) } {\int _{t- \tau (t)} ^t ||u(s)||^2 \mathrm{d}s }$, $D_2 = \frac{1}{ 1- \eta }\int _{t- \tau (t)}^t {\int _\theta ^t ||u(s)||^2 \mathrm{d}s\mathrm{d}\theta }$, $D_3 = \int _{t- {{\hat{\tau }}}} ^t$ $||u(s)||^2 \mathrm{d}s$, and $D_4 =2 \int _{t- {{\hat{\tau }}}}^t {\int _\theta ^t ||u(s)||^2 \mathrm{d}s\mathrm{d}\theta }$. The derivatives of $D_1$, $D_2$, $D_3$, and $D_4$ can be described as follows

$$\begin{aligned} {\dot{D}}_1&= \frac{1}{2(1-\eta ) } \nonumber \\&\quad \left( ||u(t)||^2 - ||u(t- \tau (t))||^2 (1- {{\dot{\tau }}}(t)) \right) \end{aligned}$$

(71)

$$\begin{aligned} {\dot{D}}_2&= \frac{1}{1-\eta } \nonumber \\&\quad \left( ||u(t)||^2\tau (t) - (1- \dot{\tau }(t)) \int _{t- \tau (t)}^t {||u(s)||^2 \mathrm{d}s } \right) \end{aligned}$$

(72)

$$\begin{aligned} {\dot{D}}_3&= ||u(t)||^2 - ||u(t- {{\hat{\tau }}})||^2 \end{aligned}$$

(73)

$$\begin{aligned} {\dot{D}}_4&= 2 \left( ||u(t)||^2 {{\hat{\tau }}} - \int _{t- \hat{\tau }}^t {||u(s)||^2 \mathrm{d}s } \right) . \end{aligned}$$

(74)

Differentiating $V_n$ as in step i, it is clearly that

$$\begin{aligned} {\dot{V}}_n&={\dot{V}}_{n-1}+ z_n {\dot{z}}_n +\mu {{\dot{\mu }}} + \frac{1}{{\gamma _n }}{{\tilde{\theta }}} _n^T \dot{{{\tilde{\theta }}}} _n\nonumber \\&\quad +\dot{D}_1 +\dot{D}_2 +\dot{D}_3 +\dot{D}_4 \nonumber \\&\le {\dot{V}}_{n-1}+ z_n (u(t - \tau (t) )+ {{\hat{\theta }}} _n^T \varphi _n ({\hat{x}}) + l_nq^* e_1 \nonumber \\&\quad - {{\dot{\omega }}} _n - h \mu + u(t) - u(t - {{\hat{\tau }}} ) ) \nonumber \\&\quad + \mu ( - h \mu +u(t) - u(t - {{\hat{\tau }}} ) ) - z_n {{\tilde{\theta }}} _n^T \varphi _n ({\hat{x}}) \nonumber \\&\quad +{{\tilde{\theta }}}_n^T \left( \varphi _n ( {{\hat{x}}}_n)z_n - \frac{1}{{\gamma _n }}\dot{{{\hat{\theta }}} }_n \right) \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + 2 {{\hat{\tau }}} + 1 \right) ||u(t)||^2 \nonumber \\&\quad - \int _{t- \tau (t)}^t {||u(s)||^2 \mathrm{d}s } \nonumber \\&\quad - 2 \int _{t- {{\hat{\tau }}}}^t {||u(s)||^2 \mathrm{d}s } - ||u(t- {{\hat{\tau }}})||^2 \nonumber \\&\quad - \frac{1}{2 } ||u(t- \tau (t))||^2 . \end{aligned}$$

(75)

It is easy to get the following results

$$\begin{aligned}&z_n q^*l_n e_1 \le \frac{ z_n^2 l_n^2 q^* }{2 \varGamma ^2 (r)}+\frac{1 }{2} ||{{\bar{e}}}||^2 \end{aligned}$$

(76)

$$\begin{aligned}&z_n ( u(t - \tau (t)) - u(t - {{\hat{\tau }}} ) ) \nonumber \\&\quad \le z_n^2 + \frac{1}{2}||u(t - \tau (t) )||^2 \nonumber \\&\quad + \frac{1}{2}||u(t - {{\hat{\tau }}} )||^2 \end{aligned}$$

(77)

$$\begin{aligned}&\mu ( u(t) - u(t - {{\hat{\tau }}} ) ) \nonumber \\&\quad \le \mu ^2 +\frac{1}{2} ||u(t)||^2 + \frac{1}{2} ||u(t - {{\hat{\tau }}} )||^2 \end{aligned}$$

(78)

$$\begin{aligned}&- z_n {{\tilde{\theta }}} _n^T \varphi _n ({\hat{x}}) \le \frac{1}{2}z_n^2 +\frac{1}{2} {{\tilde{\theta }}} _n^T {{\tilde{\theta }}} _n. \end{aligned}$$

(79)

Furthermore, one has

$$\begin{aligned} \int _{t - \tau (t) }^t {\int _\theta ^t {||u(s)||^2 \mathrm{d}s\mathrm{d}\theta } } \le \tau (t) \int _{t - \tau (t) }^t {||u(s)||^2 \mathrm{d}s}. \end{aligned}$$

(80)

Substituting (76)–(80) into (75), one can get

$$\begin{aligned} {\dot{V}}_n&\le - \lambda _{n} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{n-1}k_{j} z_{j}^{2\beta } + \sum \limits _{j = 1}^{n-1} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} \nonumber \\&\quad + \sum \limits _{j = 1}^{n-1}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} + \varpi {\tilde{q}} \hat{q} \nonumber \\&\quad + z_n ( z_{n-1} + \frac{3}{2} z_n + {{\hat{\theta }}} _n^T \varphi _n ({\hat{x}}) \nonumber \\&\quad + \delta _n {\hat{q}} - {{\dot{\omega }}} _n - h \mu + u(t) ) \nonumber \\&\quad +{{\tilde{\theta }}}_n^T \left( \varphi _n ( {{\hat{x}}}_n)z_n - \frac{1}{{\gamma _n }}{{\dot{\theta }}} _n \right) \nonumber \\&\quad - {\tilde{q}} (\dot{{\hat{q}}} - \zeta _{n} ) + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} \nonumber \\&\quad +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0) + \sum \limits _{j =1}^{n-1} \left( 1-\frac{1}{\xi _{j+1}}\right) \chi _{j+1}^2 \nonumber \\&\quad - (h-1) \mu ^2 \nonumber \\&\quad - (1-\eta ) D_1 - \frac{1}{2{{\hat{\tau }}}} D_2 - D_3 \nonumber \\&\quad - \frac{1}{2{{\hat{\tau }}}} D_4 + \sum \limits _{j = 2}^{n} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 + \varUpsilon _{n} \end{aligned}$$

(81)

where $\lambda _{n}= \lambda _{n-1}+ \frac{1}{2}$, $\delta _n= \frac{ z_n l_n^2 }{2 \varGamma ^2 (r)}$ and $\varUpsilon _{n}=\varUpsilon _{n-1} + \frac{2}{\varsigma _n }$.

Therefore, the real controller and the adaptive laws are designed as

$$\begin{aligned} u(t)&= -z_{n-1} - \frac{3}{2} z_n - k_n z_n^{2\beta - 1}\nonumber \\&\quad - \hat{\theta }_n^T \varphi _n ({\hat{x}}) - \delta _n {\hat{q}} \nonumber \\&\quad + {\dot{\omega }}_n +h \mu \end{aligned}$$

(82)

$$\begin{aligned} {\dot{{\hat{\theta }}}}_n&= \gamma _n\phi _n^T ({\hat{x}}) z_n-\varsigma _n {{\hat{\theta }}}_n \end{aligned}$$

(83)

$$\begin{aligned} \dot{{\hat{q}}}&=\zeta _{n-1}+\delta _n z_n \end{aligned}$$

(84)

where the design parameters $k_n > 0$ and $\varsigma _n > 0$.

Consequently, from (81), (82), (83) and (84), we have the following result

$$\begin{aligned} {\dot{V}}_n&\le - \lambda _{n} || {{\bar{e}}}||^2 - \sum \limits _{j = 1}^{n}k_{j} z_{j}^{2\beta } + \sum \limits _{j = 1}^{n} \frac{\varsigma _{j} {{\tilde{\theta }}} _{j}^T {{\hat{\theta }}} _{j}}{{\gamma _{j}}} \nonumber \\&\quad + \sum \limits _{j = 1}^{n-1}\frac{ {{\bar{\varsigma }}} _{j} {{\tilde{\varTheta }}} _{j} {{\hat{\varTheta }}} _{j} }{{{{\bar{\gamma }}} _{j} }} + \varpi {\tilde{q}} \hat{q} \nonumber \\&\quad + ||P||^2 \sum \limits _{j = 1}^n {{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j} +\frac{1}{\gamma _0}(- {{\bar{a}}} r + b_0)\nonumber \\&\quad + \sum \limits _{j = 1}^{n-1} \left( 1-\frac{1}{\xi _{j+1}}\right) \chi _{j+1}^2 - (h-1) \mu ^2 \nonumber \\&\quad - (1-\eta ) D_1 - \frac{1}{2{{\hat{\tau }}}} D_2 - D_3 \nonumber \\&\quad - \frac{1}{2{{\hat{\tau }}}} D_4 + \sum \limits _{j = 2}^{n} \frac{{{\tilde{\theta }}}_j^{T} {{\tilde{\theta }}}_j }{2} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 + \varUpsilon _{n} \end{aligned}$$

(85)

where $\lambda _{n}= \lambda _{n-1}+ \frac{1}{2}$, $\delta _n= \frac{ z_n l_n^2 }{2 \varGamma ^2 (r)}$ and $\varUpsilon _{n}=\varUpsilon _{n-1} + \frac{2}{\varsigma _n }$.

3.3 Stability analysis

Based on the above design process, the stability and boundedness of all signals will be discussed in this section.

Theorem 1

Considered system (1) in the presence of unmodeled dynamic, unknown time varying input delay and unmeasurable states, based on Assumptions 1-3, for the initial conditions $V(0) \le H$ and the real controller defined in (82), associated with the virtual signals defined in (39), (57) for $1 \le i \le n - 1$ , the adaptive laws defined in (40), (41), (58), (59), (83), (84) and the turning functions (42), (60), which can ensure that all signals of the closed-loop system are bounded in finite time.

Proof

Firstly, we design the following Lyapunov function.

$$\begin{aligned} V = V_n . \end{aligned}$$

(86)

Based on the definitions of ${{\tilde{\theta }}} _j$, ${{\tilde{\varTheta }}} _j$ and ${\tilde{q}}$, the inequalities $\tilde{\theta }_j ^T {{\hat{\theta }}} _j \le \frac{{1 }}{2} \theta _j^{*T} \theta _{j}^* - \frac{1}{2}{{{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j}$, ${{\tilde{\varTheta }}} _j {{\hat{\varTheta }}} _j \le \frac{{1 }}{2}\varTheta _j^{*2} - \frac{1}{2}{{{\tilde{\varTheta }}} _j^2 }$, and ${\tilde{q}} \hat{q} \le \frac{{1 }}{2}q^{*2} - \frac{1}{2}{{{\tilde{q}}}^2 }$ are used to deal with the terms ${{\tilde{\theta }}} _j ^T {{\hat{\theta }}} _j$, ${{\tilde{\varTheta }}} _j {{\hat{\varTheta }}} _j$ and ${\tilde{q}} \hat{q}$.

Differentiating V, one can get

$$\begin{aligned} {\dot{V}}&\le - \lambda _{n} || {{\bar{e}}}||^2 -\sum \limits _{j = 1}^{n} k_j z_j^{2\beta } \nonumber \\&\quad - \left( \frac{\varsigma _1}{{2\gamma _1 }}- ||P||^2\right) {{\tilde{\theta }}} _1^T {{\tilde{\theta }}} _1 - \sum \limits _{j = 1}^{n-1} \left( \frac{1}{\xi _{j+1}}-1\right) \chi _{j+1}^2 \nonumber \\&\quad - \sum \limits _{j = 2}^{n} \left( \frac{\varsigma _j}{{2\gamma _j }}- \frac{1}{2 }- ||P||^2\right) {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j - \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }} \nonumber \\&\quad - \frac{ \varpi {{\tilde{q}}}^2}{2} - \frac{ {{\bar{a}}} r}{\gamma _0} - (h-1) \mu ^2 \nonumber \\&\quad - (1-\eta ) D_1 - \frac{1}{2{{\hat{\tau }}}} D_2 - D_3 - \frac{1}{2{{\hat{\tau }}}} D_4 \nonumber \\&\quad + \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} \nonumber \\&\quad + \frac{{ \varpi q^{*2} }}{2} + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 \nonumber \\&\quad - \frac{ b_0}{\gamma _0} + \varUpsilon _{n}. \end{aligned}$$

(87)

Let

$$\begin{aligned} \lambda&=\frac{\lambda _n}{\lambda _{max}(P)}>0 \end{aligned}$$

(88)

$$\begin{aligned} {{\hat{\gamma }}} _1&= \varsigma _1- 2\gamma _1 ||P||^2>0 \end{aligned}$$

(89)

$$\begin{aligned} {{\hat{\gamma }}} _j&=\varsigma _j- \gamma _j-2\gamma _j ||P||^2 >0 , \ \ \ \ j=2,3, \cdots ,n \end{aligned}$$

(90)

$$\begin{aligned} {{\hat{\xi }}}_{j+1}&= \frac{1}{\xi _{j+1}}-1 >0 , \ \ \ \ j=1,2, \cdots ,n-1 \end{aligned}$$

(91)

Substituting (88)–(91) into (87 )

$$\begin{aligned} {\dot{V}}&\le - \lambda {{\bar{e}}}^T P {{\bar{e}}} -\sum \limits _{j = 1}^{n} k_j z_j^{2\beta } - \sum \limits _{j = 1}^{n} \frac{ {{\hat{\gamma }}} _j}{ 2 \gamma _j} {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j \nonumber \\&\quad - \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }} - \sum \limits _{j = 1}^{n-1} {{\hat{\xi }}}_{j+1} \chi _{j+1}^2 - \frac{ \varpi {{\tilde{q}}}^2}{2} \nonumber \\&\quad - \frac{{{\bar{a}}} r}{\gamma _0} - (h-1) \mu ^2 - (1-\eta ) D_1 - \frac{D_2 }{2{{\hat{\tau }}}} \nonumber \\&\quad - D_3 - \frac{ D_4}{2{{\hat{\tau }}}} + \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} \nonumber \\&\quad + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} + \frac{{ \varpi q^{*2} }}{2} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 - \frac{ b_0}{\gamma _0} + \varUpsilon _{n} \nonumber \\&\le - c {{\bar{e}}}^T P {{\bar{e}}} - c\sum \limits _{j = 1}^{n} z_j^{2\beta } - c \sum \limits _{j = 1}^{n} \frac{ 1}{ 2 \gamma _j } {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j \nonumber \\&\quad - c \sum \limits _{j = 1}^{n-1} \frac{ {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }} - c \sum \limits _{j = 1}^{n-1} \frac{1}{2} \chi _{j+1}^2 - c \frac{{\tilde{q}}^2}{2} \nonumber \\&\quad - c \frac{ r}{\gamma _0} - c \frac{ \mu ^2 }{2} -c D_1 - c D_2 - c D_3 - c D_4 \nonumber \\&\quad + \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} + \frac{{ \varpi q^{*2} }}{2} - \frac{ b_0}{\gamma _0} + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 + \varUpsilon _{n} \end{aligned}$$

(92)

where $c = \min \{ \lambda , 2k_{j} , {{\hat{\gamma }}} _j : 1 \le j \le n , {{\bar{\varsigma }}} _j, 2{{\hat{\xi }}}_{j+1} : 1 \le j \le n-1 , \varpi , {{\bar{a}}} , 2(h-1), 1-\eta , \frac{1}{2\hat{\tau }}\}$.

Let $x={\bar{e}}^T P {{\bar{e}}}, y = 1,\vartheta _1 = \beta ,\vartheta _2 = 1 - \beta , \vartheta _3 = \beta ^{ - 1}$, from Lemma 3, one can get

$$\begin{aligned} ({{\bar{e}}}^T P {{\bar{e}}} )^\beta \le {{\bar{e}}}^T P {{\bar{e}}} + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(93)

Furthermore, similar to (93), by using Lemma 3, one can get the following results.

$$\begin{aligned} \left( \sum \limits _{j = 1}^{n} \frac{ 1}{ 2 } {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j \right) ^\beta&\le \sum \limits _{j = 1}^{n} \frac{ 1}{ 2 } {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(94)

$$\begin{aligned} \left( \sum \limits _{j = 1}^{n-1} \frac{ {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }}\right) ^\beta&\le \sum \limits _{j = 1}^{n-1} \frac{ {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }}+ (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(95)

$$\begin{aligned} \left( \sum \limits _{j = 1}^{n-1} \frac{1}{2} \chi _{j+1}^2\right) ^\beta&\le \sum \limits _{j = 1}^{n-1} \frac{1}{2} \chi _{j+1}^2+ (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(96)

$$\begin{aligned} \left( \frac{{{\tilde{q}}}^2}{2} \right) ^\beta&\le \sum \limits _{j = 1}^{n-1} \frac{1}{2} {{\tilde{q}}}^2 + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(97)

$$\begin{aligned} \left( \frac{ r}{\gamma _0}\right) ^\beta&\le \frac{ r}{\gamma _0} + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(98)

$$\begin{aligned} \left( \frac{ \mu ^2 }{2} \right) ^\beta&\le \frac{ \mu ^2 }{2} + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \end{aligned}$$

(99)

$$\begin{aligned} D_i^\beta&\le D_i + (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} , i =1, 2, 3,4. \end{aligned}$$

(100)

Substituting (93)–(100) into (92) and by using Lemma 3, one can get

$$\begin{aligned} {\dot{V}}&\le - c ({{\bar{e}}}^T P {{\bar{e}}})^\beta - c \left( \sum \limits _{j = 1}^{n} z_j^{2} \right) ^\beta \nonumber \\&\quad - c \left( \sum \limits _{j = 1}^{n} \frac{ 1}{ 2 } {{\tilde{\theta }}} _j^T {{\tilde{\theta }}} _j \right) ^\beta - c \left( \sum \limits _{j = 1}^{n-1} \frac{ {{\tilde{\varTheta }}} _j^2}{{2 {{\bar{\gamma }}} _j }}\right) ^\beta \nonumber \\&\quad -c \left( \sum \limits _{j = 1}^{n-1} \frac{1}{2} \chi _{j+1}^2\right) ^\beta -c \left( \frac{{\tilde{q}}^2}{2}\right) ^\beta \nonumber \\&\quad -c \left( \frac{ r}{\gamma _0} \right) ^\beta -c \left( \frac{ \mu ^2 }{2} \right) ^\beta -c D_1^\beta \nonumber \\&\quad -c D_2^\beta -c D_3^\beta -cD_4^\beta + \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} \nonumber \\&\quad + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} + \frac{{ \varpi q^{*2} }}{2} - \frac{ b_0}{\gamma _0} \nonumber \\&\quad + \varUpsilon _{n} + 11 (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 \nonumber \\&\le - cV^\beta + \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} \nonumber \\&\quad + \frac{{ \varpi q^{*2} }}{2} - \frac{ b_0}{\gamma _0} + \varUpsilon _{n} + 11 (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}} \nonumber \\&\quad + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) ||u(t)||^2 . \end{aligned}$$

(101)

If $V(t) < H$, then the error signals $z_j(t)$, $\tilde{\theta }_j(t)$, ${{\bar{e}}}_j(t)$, ${{\tilde{\varTheta }}}_{j}(t)$, $\chi _{j+1}(t)$, and ${{\tilde{q}}}(t)$, the dynamic signal r(t) and the compensation signal $\mu (t)$ are all bounded. It is easy to prove the boundedness of ${{\hat{\theta }}}_i(t)$, ${\hat{\varTheta }}_j(t)$, ${\hat{q}}(t)$, and $e_i(t)$ . Furthermore, from (39), (57) and (82) one can get that $\alpha _i$ and u(t) are all bounded. Therefore, we can get

$$\begin{aligned} \begin{aligned}&\dot{V}(t) \le - cV(t)^\beta + d \end{aligned} \end{aligned}$$

(102)

where $d = \sum \nolimits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} + \frac{{ \varpi q^{*2} }}{2} - \frac{ b_0}{\gamma _0} + \varUpsilon _{n} + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) u_{max} +11 (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}}$ and $u_{max}$ is the upper bound of $||u(t)||^2$.

Based on Lemma 2, the trajectory of the closed-loop system will be derived into $V(t)^\beta \le \frac{d}{{(1 - \rho )c}}$ in finite time $T_{R}$ , and $T_{R}$ can be computed by

$$\begin{aligned} T_{R}&= \left( {\frac{1}{{(1 - \beta )c\rho }}} \right) \nonumber \\&\quad \left[ {V(0)^{1 - \beta } - \left( {\frac{d}{{(1 - \rho )c}}} \right) ^{\frac{{1 - \beta }}{\beta }} } \right] \end{aligned}$$

(103)

where, V(0) is the initial value of V(t).

If $V(t) = H$, based on the boundedness of $z_j(t)$, $\tilde{\theta }_j(t)$, ${{\bar{e}}}_j(t)$, ${{\tilde{\varTheta }}}_{j}(t)$, $\chi _{j+1}(t)$, and ${{\tilde{q}}}(t)$, we also can get $\dot{V}(t) \le - cV(t)^\beta + d$ with $d = \sum \limits _{j = 1}^{n} \frac{\varsigma _j \theta _j^{*T} \theta _j^*}{{2 \gamma _j }} + \sum \limits _{j = 1}^{n-1} \frac{ {{\bar{\varsigma }}} _j \varTheta _j^{*2}}{{2 {{\bar{\gamma }}} _j }} + \frac{{ \varpi q^{*2} }}{2} - \frac{ b_0}{\gamma _0} + \varUpsilon _{n} + \left( \frac{1 + 2 \tau (t) }{2(1-\eta ) } + \frac{3}{2} + 2 {{\hat{\tau }}} \right) u_{max} +11 (1 - \beta )\beta ^{\frac{\beta }{{1 - \beta }}}$. If we choose $c> \frac{d}{ H^\beta }$, then the derivative of satisfies $\dot{V}(t) < 0$. This means that the trajectory of will not escape the boundedness of H . That is to say $V(t) \le {H}$, $\forall t \ge 0$ for $V(0) \le {H}$. Then, based on (102) and Lemma 2, all signals will be derived into $V(t)^\beta \le \frac{d}{{(1 - \rho )c}}$ in finite time.

From above discussion, all signals are SGPFS for $V(0) \le {H}$. The proof is completed. $\square$

Remark 4

Compared with the existing results [50,51,52,53,54,55, 63, 70,71,72] , which only work on the nonlinear system with small input delay or ignoring input delay for finite time control, the proposed scheme in this paper can tackle the problem of finite time control for non-strict feedback uncertain nonlinear systems with unknown time-varying input delay.

Remark 5

The proposed compensation signal can be constructed, which is independent on the system model. The compensation signal is bounded in finite time and the design procedures have nothing to do with the input delay. The fuzzy observer and the dynamical signal function can be easily designed to deal with unmeasurable states and unmodeled dynamics, respectively. In addition, the finite time stability of the closed-loop system can also be guaranteed by choosing the appropriate Lyapunov function and the setting parameters. Thus, the proposed method is tractable for fuzzy finite time control.

4 Examples

In this section, two examples are utilized to show the effectiveness and characteristics of the proposed approach.

Example 1

Consider a second-order system with unmodeled dynamics and input delay described as the following form:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{z}} = -2z+ 0.25 x_1 ^2 \\ {\dot{x}}_1 = x_2+ \frac{ x_2cos (x_1^2)+sin( x_1 x_2)}{sin^2( x_1)+1} +\varDelta _1 \\ {\dot{x}}_2 =u(t- \tau (t)) +\frac{x_2}{1+ x_1^2x_2^2 } + \varDelta _2\\ y = x_1 \\ \end{array} \right. \end{aligned}$$

(104)

where $\varDelta _1=0.5z^2$, $\varDelta _2=z^2$ and $\tau (t)=0.4+0.1sin(t)s$.

Let $\psi _{i1}= y$, $\psi _{i2}=z^2$ for $i=1,2$, it can be easily to prove Assumption 1. Choosing $V(z) =z^2$, one has

$$\begin{aligned} {\dot{V}}(z) =-2z^2+0.25z_1x_1^2 \le -1.6z^2 + 2.5x_1^4+0.625. \end{aligned}$$

Let $a=1.6$, $\kappa (|x|)=2.5x_1^4$, $b_0=0.625$, $\pi _1=0.5z^2$ and $\pi _2=1.6z^2$ then Assumption 2 is true.

By selecting ${{\bar{a}}}=1.2 \in (0,a)$ and according to Lemma 1 the dynamical signal function r can be designed as

$$\begin{aligned} {\dot{r}} =-1.2r+2.5x_1^4 +0.625. \end{aligned}$$

The virtual control input $\alpha _1$ and u are designed as (39) and (82), $\dot{{\hat{\theta }}} _1$, $\dot{{\hat{\theta }}} _2$, $\dot{ {\hat{\varTheta }}} _1$, and $\dot{{\hat{q}}}$ are designed as (40), (41), (83), (84), and the turning function $\zeta _1$ is designed as (42).

In the simulation, $\mu _{F_i^j (\underline{{\hat{x}}}_i )}=\exp [ - 0.5(\underline{{\hat{x}}}_i + 3 - j)]$ , for $i=1,2$, $j=1,2,\cdots , 5$. The observer parameters are selected as $l_1=30$ and $l_2=150$. Selecting $Q=6I$, one can get

$$\begin{aligned} P= \left[ {\begin{array}{*{20}c} 0.1007 &{} \ \ 0.0200 \\ 0.0200 &{} \ \ 15.7000 \\ \end{array}} \right] . \end{aligned}$$

Let the initial conditions $x_1 (0)=x_2 (0)=0.2$, ${\hat{x}}_1 (0) = {\hat{x}}_2 (0)=0$, $r (0)=0$, $\mu (0)=0$, $\omega _2 (0)=0$, ${{\hat{\theta }}} _1 (0)={{\hat{\theta }}} _2 (0)=[0,0,0,0,0]$, ${{\hat{\varTheta }}} _1 (0)=0$ , ${\hat{q}} (0)=0$ and $z (0)=0.2$. The other parameters are taken as $k_1=8$, $k_2=15$, $\gamma _1= \gamma _2 ={{\bar{\gamma }}}_1={{\bar{\gamma }}}_2 =2$, $\gamma _0=1$, $\varsigma _1=1$, $\varsigma _2=5$, ${{\bar{\varsigma }}}_1=5$, $\bar{\varsigma }_2=6$, $\varpi =100$, $\xi _1=0.01$, $h=2$, $\beta =0.92$ and ${\hat{\tau }}=0.5$. The simulation time is 10s, and the simulation results are shown in Figs. 1, 2, 3, 4 and 5.

Figures 1 and 2 draw the trajectories of the state variables $x_1$ and $x_2$ and their estimated values ${\hat{x}}_1$ and ${\hat{x}}_2$ , respectively.

Fig. 1

The trajectories of $x_1$ and ${\hat{x}}_1$ in example 1

Fig. 2

The trajectories of $x_2$ and ${\hat{x}}_2$ in example 1

From Figs. 1 and 2, one can observe that the state trajectories of ${\hat{x}} _1$ and ${\hat{x}} _2$ can track the state variables $x _1$ and $x _2$ quickly, which means that the sate observer can effectively estimate the unmeasurable states by using the proposed fuzzy observer. In addition, it can be seen from Figs. 1 and 2 that the proposed adaptive fuzzy finite-time controller can effectively stabilize the closed-loop systems under the time varying input delay, unmodeled dynamics and unmeasurable states.

Figure 3 depicts the trajectories of auxiliary variable $\mu$.

Fig. 3

The trajectory of $\mu$ in example 1

From Fig. 3, one can observe that under the time varying input delay $\tau (t)=0.4+0.1sin(t)s$, the compensation signal $\mu$ is bounded in finite time. This means that the proposed compensation signal is bounded in finite time, although there are unmodeled dynamics in the real system. On the other hand, Fig. 3 shows that the proposed compensation mechanism cannot destroy the stability of the closed-loop systems.

Figure 4 draws the trajectory of unmodeled dynamics z.

Fig. 4

The trajectory of unmodeled dynamics z in example 1

From Fig. 4, one can observe that the trajectory of unmodeled dynamics z is bounded by using the proposed adaptive fuzzy finite time controller.

The control signals $u(t- \tau (t))$ and u(t) are shown in Fig. 5.

Fig. 5

The trajectories of $u(t- \tau (t))$ and u(t) in example 1

From the simulation results in Figs. 1, 2, 3, 4 and 5, one can obtain that for the time varying input delay, unmodeled dynamics and unmeasurable states, all the signals of the closed-loop systems are bounded by using the proposed adaptive fuzzy finite time controller.

In what follows, two cases are considered to verify the effectiveness of the proposed scheme for the unmodeled dynamics and unknown time varying input delay.

Fig. 6

The trajectories of $x_1$ and ${\hat{x}}_1$ in example 1(Case 1)

Fig. 7

The trajectories of $x_2$ and ${\hat{x}}_2$ in example 1(Case 1)

Case 1. The unmodeled dynamics exists in the considered system (104) and without unknown time varying input delay, i.e., $\tau (t)=0$. If the dynamical signal r does not employed for controller design, then finite time control scheme cannot guarantee the stability of the system. To test this, the compensation signal for unknown time varying input delay is omitted, i.e., $\mu =0$ and the other parameters are designed as above for system (104), the trajectories of $x_1$, ${\hat{x}}_1$, $x_2$, ${\hat{x}}_2$ and z are shown in Figs. 6, 7 and 8.

Fig. 8

The trajectory of unmodeled dynamics z in example 1(Case 1)

From Figs. 6, 7 and 8, it can be observed that for the finite time control scheme, all signals of the closed-loop system become unstable if the dynamic signal is not used to deal with the unmodeled dynamics.

Fig. 9

The trajectories of $x_1$ and ${\hat{x}}_1$ in example 1(Case 2)

Case 2. To test the validity of the compensation mechanism for unknown time varying input delay, both the unmodeled dynamics and the unknown time varying input delay are included in the considered system (104). Under such a condition, only the dynamical signal is employed to tackle the unmodeled dynamics, and the compensation signal for unknown time varying input delay is ignored, i.e., $\mu =0$.

The dynamical signal r and the other parameters are designed as above for system (104), the trajectories of $x_1$, ${\hat{x}}_1$, $x_2$, ${\hat{x}}_2$ and z are shown in Figs. 9, 10 and 11.

Fig. 10

The trajectories of $x_2$ and ${\hat{x}}_2$ in example 1(Case 2)

Fig. 11

The trajectory of unmodeled dynamics z in example 1(Case 2)

From Figs. 9, 10 and 11, one can observe that the finite time control scheme also cannot ensure the stability of the closed-loop system when the compensation mechanism for unknown time varying input delay is ignored for the controller design. In addition, from the trajectory of unmodeled dynamics z in Figs. 8 and 11, one can observer that the unmodeled dynamics z does not change sharply when the dynamical signal is used in Fig. 11. However, due to the existence of unknown time varying input delay, the finite time controller cannot stabilize the closed-loop system.

From the above simulation results, one can observe that the proposed method in this paper can tackle finite time control for non-strict feedback systems with unmeasurable states, unknown time varying input delay and unmodeled dynamics.

Example 2

Consider an application example the one-link manipulator with motor dynamics and disturbances used in [53, 58]. The dynamics model of the system is described as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D\ddot{q} + B\dot{q} + N \sin (q)= I+I_d \\ M\dot{I} + H I = - K_m \dot{q} + V\\ \end{array} \right. \end{aligned}$$

(105)

where q is the link position, $\dot{q}$ is the velocity, and $\ddot{q}$ is the acceleration. I denotes the torque produced, $I_d=sin (\dot{q} ) cos (I )$ denotes the torque disturbance, and V denotes the input control electromechanical torque. The parameters are selected as $D=1$ kg $\text {m}^2$, $B=1 \ \text {Nm} \ \text {s}/ \text {rad}$, $N=10 \ \text {Nm}$, $M=0.3 \ \text {H}$, $H=1.0 \ \varOmega$ and $Km=2 \ \text {Nm/A}$ .

It is assumed that the time varying input delay, the disturbance and the unmodeled dynamics exist in the system (104). Let $x_1=q$, $x_2=\dot{q}$, $x_3=I/D$ and $u(t - \tau (t)) =V(t - \tau (t) )/DM$ then system (105) can be written as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{z}} =-2 z+0.25 x_1^2 \\&{\dot{x}}_1 = x_2 + \varDelta _1 \\&{\dot{x}}_2 = x_3 - \frac{N}{D}\sin (x_1 ) - \frac{B}{D}x_2 \\&\quad \qquad + \frac{1}{D}sin(x_2) cos(D x_3) + \varDelta _2 \\&{\dot{x}}_3 = - \frac{{K_m }}{MD}x_2 - \frac{H}{MD}x_3 + u(t - \tau (t) ) + \varDelta _3 \\&y = x_1 \\ \end{aligned} \right. \end{aligned}$$

where $\varDelta _1=z^2x_1sin(x_1)$, $\varDelta _2=z^2x_1x_2$, $\varDelta _3=zx_1x_2x_3$, and $\tau (t) = 0.4+0.1sin(t) s$.

Let $\psi _{i1}= y$, $\psi _{i2}=z^2$ for $i=1,2,3$, then Assumption 1 holds. Choosing $V(z) =z^2$, one has $\dot{V}(z) =-2z^2+0.5z_1x_1^2 \le -1.5z^2 + 2.5x_1^4+0.625$ . Let $a=1.5$, $\kappa (|x|)=2.5x_1^4$, $b_0=0.625$, $\pi _1=0.5z^2$ and $\pi _2=1.5z^2$ then Assumption 2 is true.

By selecting ${{\bar{a}}}=1.2 \in (0,a)$, and from Lemma 1 the dynamical signal function r can be designed as

$$\begin{aligned} {\dot{r}} =-1.2r+2.5x_1^4 +0.625. \end{aligned}$$

The virtual control input $\alpha _1$, $\alpha _2$ and u are designed as (39), (57) and (82), $\dot{{\hat{\theta }}} _1$, $\dot{{\hat{\theta }}} _2$, $\dot{\hat{\theta }} _3$, $\dot{ {\hat{\varTheta }}} _1$, $\dot{ {\hat{\varTheta }}} _2$, and $\dot{{\hat{q}}}$ are designed as (40), (41) , (58), (59),(83) and (84), the turning function $\zeta _1$ and $\zeta _2$ are designed as (42) and (60).

In the simulation, $\mu _{F_i^j (\underline{{\hat{x}}}_i )}=\exp [ - 0.5(\underline{{\hat{x}}}_i + 3 - j)]$ for $i=1,2,3, j=1,2,\cdots , 5$. The observer parameters are selected as $l_1=80, l_2=2, l_3=2$. Selecting $Q=I$, one can get

$$\begin{aligned}P= \left[ {\begin{array}{*{20}c} {{\mathrm{0.1361}}} &{} { {\mathrm{10.3861}}} &{} {{\mathrm{0.2500}}} \\ {{\mathrm{10.3861}}} &{} {{\mathrm{830.908}}} &{} {{\mathrm{20.2722}}} \\ {{\mathrm{0.2500}}} &{} {{\mathrm{20.2722}}} &{} {{\mathrm{21.2722}}} \\ \end{array}} \right] . \end{aligned}$$

Let the initial conditions $x_1 (0)=x_2(0)=0.5$, $x_3(0)=-0.5$, ${\hat{x}}_1 (0)={\hat{x}}_2(0)={\hat{x}}_3(0)=0$, ${\hat{\theta }} _1 (0)={{\hat{\theta }}} _2 (0)={{\hat{\theta }}} _3 (0)=[0,0,0,0,0]$, ${{\hat{\varTheta }}} _1 (0)={{\hat{\varTheta }}} _2 (0)=0$, $r (0)=0$, $\mu (0)=0$, $\omega _2 (0)=\omega _3 (0)=0$, ${\hat{q}} (0)=0$, $z (0)=0.5$. The other parameters are taken as $k_1=15$, $k_2=15$, $k_3=12$, $\gamma _1=3$, $\gamma _2 =1$, $\gamma _3=3$, $\bar{\gamma }_1={{\bar{\gamma }}}_2 ={{\bar{\gamma }}}_3=3$, $\gamma _0=2$, $\varsigma _1=2$, $\varsigma _2=4$, $\varsigma _3=3$, $\bar{\varsigma }_1=2$, ${{\bar{\varsigma }}}_2=4$, ${{\bar{\varsigma }}}_3=3$, $\varpi =100$, $\xi _1=2$, $\xi _2=0.2$, $h=4$, $\beta =0.95$, ${\hat{\tau }}=0.5$. The simulation time is 10s, and the simulation results are shown in Figs. 12, 13, 14, 16, 15 and 17.

Figures 12, 13 and 14 draw the trajectories of $x_1$, ${\hat{x}}_1$, $x_2$, ${\hat{x}}_2$, $x_3$ and ${\hat{x}}_3$.

Fig. 12

The trajectories of $x_1$ and ${\hat{x}}_1$ in example 2

From Figs. 12, 13 and 14, one can observe that under the time varying input delay $\tau (t)=0.4+0.1sin(t)s$ and the unmodeled dynamics and disturbance, the proposed fuzzy state observer can effectively estimate the unmeasurable states and all state variables are bounded.

Fig. 13

The trajectories of $x_2$ and ${\hat{x}}_2$ in example 2

Fig. 14

The trajectories of $x_3$ and ${\hat{x}}_3$ in example 2

The trajectories of auxiliary variable $\mu$ are depicted in Fig. 15, which shows that the compensation signal $\mu$ is bounded in finite time.

Fig. 15

The trajectory of $\mu$ in example 2

From the simulation result in Fig. 15, one can conclude that the proposed compensation signal is bounded in finite time, although there are unmodeled dynamics in the real system.

Figure 16 draws the trajectory of the unmodeled dynamics z.

Fig. 16

The trajectory of unmodeled dynamics z in example 2

From Fig. 16, one can observer that the trajectory of unmodeled dynamics z is bounded. This means that the unmodeled dynamics can be effectively suppressed by introducing dynamic signal mechanism in the design process of adaptive fuzzy finite time controller.

Figure 17 shows that the control signals $u(t- \tau )$ and u(t) are bounded.

Fig. 17

The trajectories of $u(t- \tau (t))$ and u(t) in example 2

From the simulation results in Figs. 12, 13, 14, 16, 15 and 17, one can conclude that for time varying input delay, unmodeled dynamic and unmeasurable states, all signals are bounded by using the proposed adaptive fuzzy finite time controller.

Remark 6

We considered the one-link manipulator with motor dynamics, disturbances, unmodeled dynamics and unknown time varying input delay. The system model is a non-strict feedback form and the finite time control performance includes the time varying input delay, which will cause great difficulty to design finite time controller. The proposed compensation mechanism effectively solves the input delay problem, and the design process does not make the controller design complicated. The effective control performance is verified by the simulation results.

Furthermore, in order to demonstrate the effectiveness of the proposed compensation mechanism to deal with time input delay, a comparison with the Pade approximation method employed in [70, 71] is carried out to test the control performance. The simulation results are shown in Figs. 18, 19 and 20.

Fig. 18

The trajectories of $x_1$ and ${\hat{x}}_1$ in example 2 ( Pade approximation method)

Fig. 19

The trajectories of $x_2$ and ${\hat{x}}_2$ in example 2 ( Pade approximation method)

Fig. 20

The trajectories of $x_3$ and ${\hat{x}}_3$ in example 2 ( Pade approximation method)

From Figs. 18, 19 and 20, one can observe that the fuzzy observer cannot effectively estimate the unmeasurable states, and all state variables of the closed-loop systems are unstable when time varying input delay occurs for Pade approximation method. The simulation results show that the control signal is completely invalid when the input delay occurs. This means that the Pade approximation method is invalid for long time varying input delay.

Comparative explanations The proposed method in this paper gives an effective way for adaptive fuzzy finite time control of non-strict feedback nonlinear systems with unmodeled dynamics, unknown time varying input delay and unmeasurable states. Compared with the existing results [17, 36,37,38,39,40,41,42,43, 56,57,58,59,60,61,62,63, 70, 71], the main advantages of the proposed scheme can be summarized in three aspects.

• (1) The proposed compensation mechanism can effectively overcome the design difficulty caused by the unknown time varying input delay. Unlike the Pade approximation method in [70, 71], which is invalid once the input delay is long, the proposed method can tackle long unknown time varying input delay. In addition, the proposed method does not depend on the system model.

• (2) The algebraic loop problem has been overcome and the complexity of the non-strict feedback system is reduced for finite time controller design. Specially, the proposed method is also suitable for nonlinear systems with strict-feedback form. Unlike [36,37,38,39,40,41,42,43], the considered finite time control schemes are limited to the strict feedback nonlinear systems or all state variables are measurable, the proposed method is more general.

• (3) Compared with the results in [17, 56,57,58,59,60,61,62,63], the unmodeled dynamics and unknown input delay problem are both considered in finite time control schemes, which can improve the robustness of the closed-loop system in practical applications. Most of the existing general finite time control schemes are invalid for this issue. In addition, the computational burden for finite time controller design is reduced by using the idea of DSC scheme.

5 Conclusions

In this paper, observer-based adaptive fuzzy finite time control for non-strict feedback uncertain nonlinear systems has been addressed. A novel compensation mechanism and dynamical signal function are introduced to solve the challenges caused by unknown time varying input delay and unmodeled dynamics, respectively. A fuzzy state observer is designed to estimate the unknown state variables based on the approximation ability of FLS. The non-strict feedback structure is simplified by using the property of FLS. Moreover, the relationship between input delay $\tau (t)$ and the convergence time $T_R$ will be further studied in future work.