A manifold framework of multiple-kernel learning for hyperspectral image classification

Abstract

Manifold learning is a promising intelligent data analysis method, and the manifold learning preserves the local embedding features of the data in manifold mapping space. Manifold learning has its limitations on extracting the nonlinear features of the data in many applications. For example, hyperspectral image classification needs to seek the nonlinear local relationships between spectral curves. For that, researchers applied the kernel trick to manifold learning in the previous works. The kernel-based manifold learning was developed, but still endures the problem that the inappropriate kernel model reduces the system performance. In order to solve the problem of kernel model selection, we propose a manifold framework of multiple-kernel learning for the application of hyperspectral image classification. In this framework, the quasiconformal mapping-based multiple-kernel model is optimized based on the optimization objective equation, which maximizes the class discriminant ability of data. Accordingly, the discriminative structure of data distribution is achieved for classification with the quasiconformal mapping-based multiple-kernel model.

1 Introduction

Manifold learning promotes dimensionality reduction of intelligent data analysis. Dimensionality reduction is to map a high-dimensional data into a lower-dimensional space with linear transformation matrix, and the data in low-dimensional space are easily analyzed. Manifold learning preserves the nonlinear manifold and constructs a smooth and graded mesh of data. Manifold-based learning seeks the natural geometric dimensionality reduction of data for the excellent classification performance. The most popular methods are principal component analysis (PCA) [1], linear discriminant analysis (LDA) [2], principal curves [3], and principal surfaces [4]. The main manifold learning methods include self-organizing mapping (SOM) [5], visualization-induced SOM (ViSOM) [6], locally linear embedding (LLE) [7], Isomap [8], locality preserving projection (LPP) [9, 10], and class-wise locality preserving projection (CLPP) [11]. These methods have the different criterions of dimensionality reduction as follows. Firstly, SOM learns a nonparametric model with a topological constraint of lines, squares, or hexagonal grids [12, 13]. Secondly, ViSOM constructs a smooth and graded mesh of data as the discrete version of principal curve or surface. Thirdly, LLE preserves the geometrical perspective, and Isomap preserves the geometric relationships and neighborhoods of the data. Finally, LPP locates both training sample and the test data point, and CLPP preserves the local structure of the original data together with the class information.

Kernel CLPP is developed with kernel trick for feature extraction [11]. Researchers present an alternative framework of kernel LPP (KLPP) to develop a framework of KPCA + LPP [5, 8] for image for target recognition, and other improved kernel-based LPP methods were presented in the previous works [6, 13, 14]. As the kernel learning methods, kernel manifold learning still endures the kernel model selection. The geometrical structure of the data distribution is determined by the kernel function. The discriminative ability may be worse under the inappropriate kernel selection [15–17]. Selecting the optimal parameter does not change the geometry structure of data distribution. So, some kernel optimization methods are proposed to improve the performances of kernel learning machines, for example, data-depend kernel [18], kernel-adaptive support vector machine [19–21], sparse multiple-kernel learning [22], large-scale multiple-kernel learning [23], Lp-norm multiple-kernel learning [24].

As the above discussion, the kernel-based manifold learning framework includes two stages: kernel mapping and manifold projection. Multiple-kernel learning methods aim to construct a kernel model with a linear combination of fixed base kernels. Learning the kernel then consists of learning the weighting coefficients for each base kernel. There are two advantages: (1) multiple-kernel learning combines the kernel functions with the different characteristics of the data, so it preserves the nonlinear mapping characteristics of kernel functions; (2) quasiconformal kernel has its ability to change the data structure. So, we propose a manifold framework of multiple-kernel learning for hyperspectral image classification, and the framework is to solve the problems of the determination of the kernel function and its parameters of kernel manifold learning for the practical application system.

2 Proposed scheme

2.1 Motivation

Kernel-based manifold learning is an effective method on the applications of solving the nonlinear problems. As the important indexes of system performances, recognition accuracy or prediction accuracy is largely increased by the nonlinear kernel trick. However, the performance of kernel-based manifold learning system is largely influenced by the function and parameter of kernel. Only optimizing the parameters is not effective, because the data distribution is not changing with the changing of the parameter of kernel function. Researchers have proposed alternative kernel function to solve this problem, for example, multiple kernel and quasiconformal kernel. Firstly, multiple-kernel learning combines the kernel functions with the different characteristics of the data. Accordingly, MKL combines many features and is better to describe the data features than the single feature extraction method. Multiple-kernel learning preserves the nonlinear mapping characteristics of kernel functions. And it shows the possibility of using different kernel functions for kernel-based manifold learning. Secondly, quasiconformal kernel has its ability to change the data structure. It is feasible to improve kernel-based manifold learning through adjusting the quasiconformal.

In this paper, we improve the kernel-based manifold learning through considering enough the advantages of multiple-kernel learning and quasiconformal kernel learning. A manifold framework of multiple-kernel learning is proposed for hyperspectral image classification. Based on the traditional kernel-based manifold learning, the quasiconformal mapping-based multiple-kernel model is solved with the constrained optimization. The framework maximizes the class discriminant ability of data in the nonlinear kernel-based manifold feature space. The kernel-based manifold learning system is improved.

2.2 Framework

In the section, we present a framework of kernel manifold learning with one example of kernel locality preserving projection (KLPP). KLPP preserves the local structure of the data in a low-dimensional mapping space. The objective function of KLPP is defined as

$$\hbox{min} \sum\limits_{i,j}^{n} {\left\| {z_{i}^{\varPhi } - z_{j}^{\varPhi } } \right\|^{2} S_{ij}^{\varPhi } }$$

(1)

where $S_{ij}^{\varPhi }$ is a similarity matrix which measures the likelihood of two data points in the Hilbert space $\varPhi \left( X \right) = \left[ {\varPhi \left( {x_{1} } \right),\varPhi \left( {x_{2} } \right), \ldots ,\varPhi \left( {x_{n} } \right)} \right]$. The similarity matrix has the different meanings in the practical applications, for example, in hyperspectral image, and the similarity matrix describes the similarity of the different hyperspectral curves. $z_{i}^{\varPhi } = \left( {w^{\varPhi } } \right)^{T} \varPhi (x_{i} )$ is the low-dimensional representation of $\varPhi \left( {x_{i} } \right)$ with the a projection vector $w^{\varPhi }$. On the similarity matrix $S_{ij}^{\varPhi }$, many methods are proposed to construct it in the previous work [11], and in this paper, we use the following formulation:

$$S_{ij}^{\varPhi } = \left\{ {\begin{array}{*{20}l} {\frac{{k(x_{i}^{{}} ,x_{j} )}}{{\sqrt {k(x_{i} ,x_{i} )} \sqrt {k(x_{j} ,x_{j} )} }}} \hfill & {{\text{if }}x_{i} {\text{ and }}x_{j} {\text{ belong to the same class;}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \,$$

(2)

Accordingly, Eq. (1) is changed to

$$\tfrac{1}{2}\sum\limits_{i,j}^{n} {\left\| {z_{i}^{\varPhi } - z_{j}^{\varPhi } } \right\|^{2} S_{ij}^{\varPhi } } = \beta^{T} K\left( {D^{\varPhi } - S^{\varPhi } } \right)K\beta ,$$

(3)

where $K$ is kernel matrix calculated with the training samples, i.e., $K = Q^{T} Q$, and $D^{\varPhi } = diag\left[ {\sum\nolimits_{j} {S_{1j}^{\varPhi } } ,\sum\nolimits_{j} {S_{2j}^{\varPhi } } , \ldots ,\sum\nolimits_{j} {S_{nj}^{\varPhi } } } \right]$. The matrix $D^{\varPhi }$ measures the importance of the data points. The element of the similarity matrix is larger, and the relationship of the data is more important. The relationship describes the manifold structure of two training samples. The multikernels-based quasiconformal kernel performs higher than the single quasiconformal kernel on the data distribution.

The hyperspectral image classification system classifies the curves from the different training with the similarity matrix. Accordingly, on kernel-based LPP, the constraint $\left( {Z^{\varPhi } } \right)^{T} D^{\varPhi } Z^{\varPhi } = 1$ can be rewritten as $\beta^{T} KD^{\varPhi } K\beta = 1$. So, the minimization problem is transformed to

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{\beta } \beta^{T} KL^{\varPhi } K\beta \\ & {\text{Subject}}\;{\text{to}}\;\beta^{T} KD^{\varPhi } K\beta = 1 \\ \end{aligned}$$

(4)

where $L^{\varPhi } = D^{\varPhi } - S^{\varPhi }$. QR decomposition of matrix $K$ is considered as $K = P\varLambda P^{T}$, where $P = \left[ {r_{1} ,r_{2} , \ldots ,r_{m} } \right]$, and $\varLambda = diag\left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)$, and $r_{1} ,r_{2} , \ldots ,r_{m}$ are $K$’s orthonormal eigenvectors corresponding to m largest nonzero eigenvalue $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m}$.

As above discussion, the previous work [11] proposed kernel locality preserve projections (KLPP) to improve locality preserve projections (LPP) on the nonlinear feature extraction. But KLPP still endures kernel model selection and parameters, and the performance is influenced by the kernel and parameters. Based on the basic framework of KLPP [11], we propose a manifold framework of multiple-kernel learning based on the quasiconformal mapping-based multiple-kernel model, and the parameter optimization method is proposed based on the optimization equation. The optimization objective equation is created to maximize the class discriminant ability of data in the nonlinear manifold feature space.

Secondly, as the excellent work [25], Lin presented supervised kernel-optimized LPP (SKOLPP) for face recognition and palm biometrics. The recognition performance is to maximize the class separability in kernel learning for feature extraction of image database. The excellent performances were reported on ORL, Yale, AR, and Palmprint databases. In this work, authors apply the data-dependent kernel to SKLPP, and authors claimed that the nonlinear features extracted by SKOLPP had larger discriminative ability compared with SKLPP. Lin’s work testified the feasibility of enhancing the recognition performance with adjusting the kernel parameters of kernel model. So, the Lin’s work aims to enhance the recognition performance of manifold learning, and we also aim to enhance the manifold learning recognition only with the different ideas as follows. SKOLPP applied the single-kernel method to supervised manifold learning, while our work applies multiple-kernel models. From the viewpoint of kernel optimization, quasiconformal multiple kernels have more discriminative ability than single-kernel learning.

So, the manifold framework of quasiconformal kernels learning is defined as

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{\beta } \beta^{T} K^{{(\alpha^{*} )}} L^{\varPhi } K^{{(\alpha^{*} )}} \beta \\ & {\text{Subject}}\;{\text{to}}\;\beta^{T} K^{{(\alpha^{*} )}} D^{\varPhi } K^{{(\alpha^{*} )}} \beta = 1 \\ \end{aligned}$$

(5)

where the optimal projection $\beta$ is the main projection vector to construct the projection matrix, $K^{{(\alpha^{*} )}}$ is the kernel matrix with the optimal $\alpha^{*}$ of multikernels-based quasiconformal kernel $k(x,x^{{\prime }} ) = K_{f} \left( {k_{0,i} (x,x^{{\prime }} ),{\mathbf{d}},{\varvec{\upalpha}}} \right)$, so in this version, $\alpha^{*} = \{ {\mathbf{d}}^{*} ,{\varvec{\upalpha}}^{*} \}$, where ${\mathbf{d}},{\varvec{\upalpha}}$ are adjusted for the classification task.

The optimal projection $\beta^{*}$ is the manifold projection vector, and $\alpha^{*}$ is vector of the optimal kernel parameters. In the computing stages, we solve the $\alpha^{*}$ to obtain the optimal kernel matrix K^(α*) and then solve $\beta^{*}$ the under the optimal kernel matrix K^(α*). The dimensions of the two vectors are determined by the practical applications. The optimal projection $\beta^{*}$ will determine the feature vector after the dimensionality reduction of the data. And then the vector of optimal kernel parameters $\alpha^{*}$ is determined by the vector of expansion vector. The different number of the expansion vectors has the heavy influence on optimization performance of the learning system. The larger dimension increases the large computation stress. Accordingly, the computation efficiency is increased by the large-dimensional vectors.

2.3 Procedural steps

In this section, as the proposed framework of the kernel-based manifold learning, we solve the $\alpha^{*}$ to obtain the optimal kernel matrix K^(α*) and then solve $\beta^{*}$ the under the optimal kernel matrix K^(α*). Accordingly, the procedure is described two steps: Step 1. solving $\alpha^{*} = \{ {\mathbf{d}}^{*} ,{\varvec{\upalpha}}^{*} \}$ ; Step 2. solving the optimal projection $\beta^{*}$. The detailed information is listed as follows.

• Step 1. Solving $\alpha^{*} = \{ {\mathbf{d}}^{*} ,{\varvec{\upalpha}}^{*} \}$

Following the work in [11], we extend the quasiconformal kernel to quasiconformal multikernels. Different from the single quasiconformal kernel, only the expansion parameters need to be computed by constrained optimization equation. While on the quasiconformal multikernels, the weight parameter and expansion coefficient ${\mathbf{d}},{\varvec{\upalpha}}$ are computed through the optimization equation, and the quasiconformal multikernels model has the higher ability on describing the data distribution than the quasiconformal kernel. According to the definition of the quasiconformal kernel [11], the geometrical structure of the data in the kernel mapping space is determined by the expansion coefficients with the determinative XVs and the free parameter. The structure is the data distributions in the empirical mapping space, and the kernel mapping space is empirical mapping space. The multikernels-based quasiconformal kernel has the higher ability on describing the data distribution than the quasiconformal kernel. The quasiconformal multikernels model is defined as

$$k(x,x^{{\prime }} ) = f(x)\sum\limits_{i = 1}^{m} d_{i} k_{0,i} (x,x^{{\prime }} )f(x^{{\prime }} ),$$

(6)

where $k_{0,i} (x,x^{{\prime }} )$ is the $i$ th basic kernel of polynomial kernel and Gaussian kernel, and $m$ is the number of basic kernels for combination, $a_{i} \ge 0$ is the weight for the ith basic kernel function, $q( \cdot )$ is the factor function defined by $f(x) = \alpha_{0} + \sum\nolimits_{i = 1}^{n} \alpha_{i} k_{0} ({\mathbf{x}},a_{i} )$, where $k_{0} (x,a_{i} ) = e^{{ - \gamma \left\| {{\mathbf{x}} - a_{i} } \right\|^{2} }}$, $a_{i} \in R^{d}$, $\alpha_{i}$ is the coefficient for the combination, $\{ a_{i} ,i = 1,2, \ldots ,n\}$ are selected by the training samples. The extended definition will not influence the characters of kernel matrix, and $k(x,x^{{\prime }} )$ satisfies the Mercer condition. Supposed that ${\mathbf{d}} = [d_{1} ,d_{2} , \ldots ,d_{m} ]$, ${\varvec{\upalpha}} = [\alpha_{0} ,\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ]$, the quasiconformal multikernels model is defined as

$$k(x,x^{{\prime }} ) = K_{f} \left( {k_{0,i} (x,x^{{\prime }} ),{\mathbf{d}},{\varvec{\upalpha}}} \right),$$

(7)

where ${\mathbf{d}},{\varvec{\upalpha}}$ are the adjusted for the classification task. So, the jointly convex formulation can be described as

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{{{\mathbf{d}},{\varvec{\upalpha}}}} F_{c} (K_{0} ,{\mathbf{d}},{\varvec{\upalpha}}) \\ & {\text{Subject}}\;{\text{to}}\;\left\| {\mathbf{d}} \right\| = 1,\left\| {\varvec{\upalpha}} \right\| = 1, \\ \end{aligned}$$

(8)

$F_{c} (.)$ measures the class discriminative ability, and we can solve ${\mathbf{d}},{\varvec{\upalpha}}$ with the two stages, one is to solve ${\mathbf{d}}$, and second is to solve ${\varvec{\upalpha}}$. In the first stage, the centered kernel alignment [26] is applied to create the objective optimization function, and in the second stage, Fisher-based and Margin-based optimization function is created to solve ${\varvec{\upalpha}}$.

• Step 1.1. Optimize the weights of multiple kernels d

The parameter vector ${\mathbf{d}} = [d_{1} ,d_{2} , \ldots ,d_{m} ]$ is computed with centered kernel alignment [26] as follows.

$$\begin{aligned} &\hbox{max} O_{c} (K_{0}^{(C)} ,K^{*} ) \hfill \\& {\text{Subject}}\;{\text{to}}\;K_{0}^{(C)} = \sum\limits_{i = 1}^{m} d_{i} K_{0,i}^{(C)} ,\;tr(K_{{\mathbf{0}}} ) = 1,\;d_{i} \ge 0,\;\forall i \hfill \\ \end{aligned}$$

(9)

where $O_{c} (K_{0}^{(C)} ,K^{*} )$ is the optimization objective function, and there are many methods to construct this equation, where $K^{*} (x,x^{{\prime }} ) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;y = y^{{\prime }} } \hfill \\ { - 1/(c - 1)} \hfill & {{\text{if}}\;y \ne y^{{\prime }} } \hfill \\ \end{array} } \right.$ is the ideal target kernel, $tr$ denotes the trace of a matrix. $K_{0}^{(C)} = \left[ {I - \tfrac{{{\mathbf{11}}^{T} }}{m}} \right]K_{0} \left[ {I - \tfrac{{{\mathbf{11}}^{T} }}{m}} \right]$ is the centered kernel matrix of $K_{0}$, $I$ is the identity matrix, ${\mathbf{1}}$ is a vector with all entries equal to 1. Accordingly, $K_{0,i}^{(C)} = \left[ {I - \tfrac{{{\mathbf{11}}^{T} }}{m}} \right]K_{0,i} \left[ {I - \tfrac{{{\mathbf{11}}^{T} }}{m}} \right]$ is the centered kernel matrix of $K_{0,i}$, $i = 1,2, \ldots ,m$. The objective function $O_{c} (K_{0}^{(C)} ,K^{*} ) = \frac{{\left\langle {K_{0}^{(C)} ,K^{*} } \right\rangle_{F} }}{{\left\| {K_{C}^{*} } \right\|_{F} \left\| {K_{0}^{(C)} } \right\|_{F} }}$, $K_{C}^{*}$ is the centered kernel matrix of $K^{*}$, where $\left\langle { \cdot , \cdot } \right\rangle_{F}$ is the Frobenius norm between two matrices, i.e., $\left\langle {D,E} \right\rangle_{F} = \sum\nolimits_{i = 1}^{m} \sum\nolimits_{j = 1}^{m} d_{ij} e_{ij} = tr(DE^{T} )$.$\left\| {K_{C}^{*} } \right\|_{F}$ is a unchanged value in the practical machine learning, while the trace constraint is to fix the scale invariance of KA. So, in the practical applications, we can consider the denominator $\left\| {K_{C}^{*} } \right\|_{F}$ as the unchanged value for the classification task. So, in the optimization equation of maximizing the numerator $\left\langle {K_{0}^{(C)} ,K^{*} } \right\rangle_{F}$, and it can be removed during solving the equation.

Based on this, centered kernel alignment-based optimization problem can be transformed into a quadratic programming (QP) problem [27, 28], which is effectively solved with OPTI toolbox [26]. Supposed that ${\mathbf{d}} = [d_{1} ,d_{2} , \ldots ,d_{m} ]$, the optimized solution ${\mathbf{d}}^{*}$ can be obtained through solving the following QP problem [26],

$$\begin{aligned} & \hbox{min} \;v^{T} {\mathbf{T}}v - 2v^{T} {\varvec{\upeta}} \\ & {\text{Subject}}\;{\text{to}}\;vi \ge 0,\forall i \\ \end{aligned}$$

(10)

where ${\mathbf{d}}^{*} = v^{*} /\left\| {{\mathbf{d}}^{*} } \right\|_{2}$, ${\varvec{\upeta}} = \left[ {\left\langle {K_{0,1}^{(C)} ,K^{*} } \right\rangle_{F} \left\langle {K_{0,2}^{(C)} ,K^{*} } \right\rangle_{F} , \ldots ,\left\langle {K_{0,m}^{(C)} ,K^{*} } \right\rangle_{F} } \right]^{T}$, and ${\mathbf{T}}$ is a symmetric matrix defined by ${\mathbf{T}}_{ij} = \left\langle {K_{0,i}^{(C)} ,K_{0,j}^{(C)} } \right\rangle_{F} ,i,j = 1,2, \ldots ,m$.

• Step 1.2. Optimize the coefficients of quasiconformal kernel α

Fisher-based and margin-based optimization function is created to solve α. In the practical application, we can choose any method. The detail procedure is defined as follows.

Based on Fisher criterion [11], this step is to optimize the coefficients ${\varvec{\upalpha}} = [b_{1} ,b_{2} , \ldots ,b_{n} ]$ of the quasiconformal multikernels based on Fisher criterion. Fisher criterion is to measure the class discriminative ability of the different class data, and this equation is increasing with the increasing of the class ability of data. The function is defined as

$$J_{{_{Fisher} }} \left( {\varvec{\upalpha}} \right) = {\mathbf{(\alpha }}^{{\mathbf{T}}} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E\alpha )/(\alpha }}^{{\mathbf{T}}} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E\alpha )}}$$

(11)

where ${\mathbf{E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E}}$ and ${\mathbf{E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E}}$ are constant matrices of training samples, and the objective function based on Fisher criterion is to measure the ability of the class discriminant. Then $\frac{{\partial J_{{_{Fisher} }} ({\varvec{\upalpha}})}}{{\partial {\varvec{\upalpha}}}} = \frac{2}{{{\mathbf{J}}_{2}^{2} }}({\mathbf{J}}_{2} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E}} - {\mathbf{J}}_{1} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E}}){\varvec{\upalpha}}$, where $J_{Fisher}$ is solved through solving the eigenvalue problem of ${\mathbf{(E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E)}}^{{{\mathbf{ - 1}}}} {\mathbf{(E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E)}}$, and the eigenvector is the expansion coefficients ${\varvec{\upalpha}}$. However, in many applications, the matrix ${\mathbf{(E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E)}}^{{{\mathbf{ - 1}}}} {\mathbf{(E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E)}}$ is not symmetrical, or the matrix ${\mathbf{E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E}}$ is singular. Supposed that learning rate $\varepsilon \left( n \right) = \varepsilon_{0} (1 - \frac{n}{N})$ of the initialized learning rate $\varepsilon_{0}$, the current iteration $n$, the total iterations $N$. The optimal ${\varvec{\upalpha}}$ is solved as

$${\varvec{\upalpha}}^{(n + 1)} = {\varvec{\upalpha}}^{(n)} + \varepsilon \left( {\frac{1}{{J_{2} }}{\mathbf{E}}^{{\mathbf{T}}} {\mathbf{B}}_{{\mathbf{0}}} {\mathbf{E}} - \frac{{J_{Fisher} }}{{J_{2} }}{\mathbf{E}}^{{\mathbf{T}}} {\mathbf{W}}_{{\mathbf{0}}} {\mathbf{E}}} \right){\varvec{\upalpha}}^{(n)}$$

(12)

Based on maximum margin criterion [11], the objective function is defined as

$$\begin{aligned} & \hbox{max} \;{\varvec{\upalpha}}^{{\mathbf{T}}} \left( {2{\tilde{\mathbf{S}}}_{{\mathbf{B}}} - {\tilde{\mathbf{S}}}_{{\mathbf{T}}} } \right){\varvec{\upalpha}} \\ & {\text{Subject}}\;{\text{to}}\;{\varvec{\upalpha}}^{{\mathbf{T}}} {\varvec{\upalpha}} - 1 = 0 \\ \end{aligned}$$

(13)

The optimal expansion coefficient ${\varvec{\upalpha}}^{*}$ is the eigenvector of $2{\tilde{\mathbf{S}}}_{{\mathbf{B}}} - {\tilde{\mathbf{S}}}_{{\mathbf{T}}}$. $\left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{S}}}_{{\mathbf{B}}} = {\mathbf{X}}_{{\mathbf{B}}} {\mathbf{X}}_{{\mathbf{B}}}^{{\mathbf{T}}} } \\ {{\tilde{\mathbf{S}}}_{{\mathbf{T}}} = {\mathbf{X}}_{{\mathbf{T}}} {\mathbf{X}}_{{\mathbf{T}}}^{{\mathbf{T}}} } \\ \end{array} } \right.$, $\left\{ {\begin{array}{*{20}l} {{\mathbf{X}}_{{\mathbf{T}}} = ({\mathbf{Y}}_{0} - \frac{1}{{\mathbf{m}}}{\mathbf{Y}}_{0} {\mathbf{1}}_{\text{m}}^{{\mathbf{T}}} {\mathbf{1}}_{{\mathbf{m}}} ){\mathbf{E}}} \hfill \\ {{\mathbf{X}}_{{\mathbf{B}}} = {\mathbf{Y}}_{{\mathbf{0}}} {\mathbf{M}}^{{\mathbf{T}}} {\mathbf{E}}} \hfill \\ \end{array} } \right.$, ${\mathbf{M}} = {\mathbf{M}}_{1} - {\mathbf{M}}_{2}$ and M ₁, M ₂ are defined as

$$M_{1} = \left[ {\begin{array}{*{20}c} {\left[ {\frac{1}{{\sqrt {m_{1} } }}} \right]_{{m_{1} \times m_{1} }} } & {0_{{m_{1} \times m_{2} }} } & \cdots & {0_{{m_{1} \times m_{c} }} } \\ {0_{{m_{2} \times m_{1} }} } & {\left[ {\frac{1}{{\sqrt {m_{2} } }}} \right]_{{m_{2} \times m_{2} }} } & \cdots & {0_{{m_{2} \times m_{c} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {0_{{m_{c} \times m_{1} }} } & {0_{{m_{c} \times m_{2} }} } & \cdots & {\left[ {\frac{1}{{\sqrt {m_{c} } }}} \right]0_{{m_{c} \times m_{c} }} } \\ \end{array} } \right]\;{\text{and}}\;M_{2} = \left[ {\begin{array}{*{20}c} {\frac{{\sum\limits_{j}^{c} {\sqrt {m_{j} } } }}{m}} & 0 & \cdots & 0 \\ 0 & {\frac{{\sum\limits_{j}^{c} {\sqrt {m_{j} } } }}{m}} & {} & {} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\frac{{\sum\limits_{j}^{c} {\sqrt {m_{j} } } }}{m}} \\ \end{array} } \right].$$

${\mathbf{Y}}_{0} = {\mathbf{K}}_{{\mathbf{0}}} {\mathbf{P}}_{{\mathbf{0}}} {\varvec{\Lambda}}_{0}^{ - 1/2} ,\;{\mathbf{K}}_{0} = {\mathbf{P}}_{{\mathbf{0}}} {\varvec{\Lambda}}_{0}^{{\mathbf{T}}} {\mathbf{Y}}_{0}^{{\mathbf{T}}}$, and K ₀ is the basic matrix. So

$$\left\{ {\begin{array}{*{20}l} {{\text{trace}}({\text{SB}}) = {\varvec{\upalpha}}^{{\mathbf{T}}} {\mathbf{X}}_{{\mathbf{B}}}^{{\mathbf{T}}} {\mathbf{X}}_{{\mathbf{B}}} {\varvec{\upalpha}}} \hfill \\ {{\text{trace}}({\text{S}}_{\text{T}} ) = {\varvec{\upalpha}}^{{\mathbf{T}}} ({\mathbf{X}}^{{\mathbf{T}}} )^{{\mathbf{T}}} {\mathbf{X}}_{{\mathbf{T}}} {\varvec{\upalpha}}} \hfill \\ \end{array} } \right.$$

(14)

Supposed that ${\tilde{\mathbf{S}}}_{{\mathbf{B}}} = {\mathbf{X}}_{{\mathbf{B}}} {\mathbf{X}}_{{\mathbf{B}}}^{{\mathbf{T}}}$ and ${\tilde{\mathbf{S}}}_{{\mathbf{T}}} = {\mathbf{X}}_{{\mathbf{T}}} {\mathbf{X}}_{{\mathbf{T}}}^{{\mathbf{T}}}$ and then

$$Dis({\varvec{\upalpha}}) = {\mathbf{trace}}\left( {{\varvec{\upalpha}}^{{\mathbf{T}}} \left( {2{\tilde{\mathbf{S}}}_{{\mathbf{B}}} - {\tilde{\mathbf{S}}}_{{\mathbf{T}}} } \right){\varvec{\upalpha}}} \right)$$

(15)

So, maximizing $Dis({\varvec{\upalpha}})$ is equal to obtain the objective function through calculating eigenvalue equation of matrix $2{\tilde{\mathbf{S}}}_{{\mathbf{B}}} - {\tilde{\mathbf{S}}}_{{\mathbf{T}}}$, the column vector of P is the eigenvalue matrix of $2{\tilde{\mathbf{S}}}_{{\mathbf{B}}} - {\tilde{\mathbf{S}}}_{{\mathbf{T}}}$, the eigenvalue is 2Λ − I.

• Step 2. solving the optimal projection $\beta^{*}$

After computing, $K^{{(\alpha^{*} )}}$ is computed by the kernel matrix with the optimal $\alpha^{*}$ of multikernels-based quasiconformal kernel $k(x,x') = K_{f} \left( {k_{0,i} (x,x'),{\mathbf{d}},{\varvec{\upalpha}}} \right)$. Then we solve the manifold optimization (5), $\mathop {\hbox{min} }\limits_{\beta } \beta^{T} K^{{(\alpha^{*} )}} L^{\varPhi } K^{{(\alpha^{*} )}} \beta$, subject to $\beta^{T} K^{{(\alpha^{*} )}} D^{\varPhi } K^{{(\alpha^{*} )}} \beta = 1$, where the optimal projection $\beta$ is the main projection vector to construct the projection matrix. QR decomposition of matrix $K^{{(\alpha^{*} )}}$ is considered as $K^{{(\alpha^{*} )}} = P\varLambda P^{T}$, where $P = \left[ {r_{1} ,r_{2} , \ldots ,r_{m} } \right]$, and $\varLambda = diag\left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)$, and $r_{1} ,r_{2} , \ldots ,r_{m}$ are $K^{{(\alpha^{*} )}}$’s orthonormal eigenvector corresponding to m largest nonzero eigenvalue $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m}$.

2.4 Procedural flowchart

The procedure is shown in Fig. 1. The procedure includes three procedures of multiple kernels optimization, training and testing for general kernel-based manifold learning application. This proposed procedure costs more time to solve the optimization equation than KLPP without optimizing kernel function. But the kernel optimization procedure can be implemented off-line. In the practical applications, the kernel optimization procedure is implemented offline, and in the application it needs the additional less time consumption. So, it has the little influence on the learning efficiency in the online application. The optimization equation is solved by iteration method and eigenvalue decomposition method, and they are the most popular methods of solving the optimization equation. Other methods also are the one of the two kinds of optimization method.

Fig. 1

Procedure of multiple kernels-based manifold learning

The advance beyond the state-of-the-art comes from the two points. (1) A manifold framework of quasiconformal multikernels learning is proposed for hyperspectral data on dimensionality reduction. Compared to the traditional kernel-based manifold learning, the proposed quasiconformal multikernels manifold learning achieves the class discriminant ability of data for the data classification. (2) The quasiconformal mapping-based multiple-kernel model is proposed for kernel mapping, and the model can adaptively change the kernel mapping structure of data distribution. The proposed kernel-based manifold learning has the more ability of describing the data mapping than the traditional kernel and data-dependent kernel model, because the data distribution structure can be adaptively adjusted.

2.5 Discussion

The proposed kernel-based manifold learning is based on the kernel-based machine. The theoretical bounds also come from quasiconformal multikernels. The application system is also to optimize accuracy in predicting the test data based on train test. Supposed that the training and test sets have the same size of data set, we can show a performance guarantee that holds with high probability over uniformly chosen training/test partitions.

For a function $f:\chi \to R$, the proportion of errors on the test data of a threshold version of $f$ can be written as

$$er(f) = \frac{1}{n}\left| {\left\{ {n + 1 \le i \le 2n:y_{i} f(x_{i} ) \le 0} \right\}} \right|$$

(16)

where the kernel classifiers were obtained by thresholding kernel expansions of the form, with the bounded norm,

$$\left\| w \right\|^{2} = \sum\limits_{i,j = 1}^{2n} {\alpha_{i} \alpha_{j} k(x_{i} ,x_{j} )} = {\varvec{\upalpha}}^{T} K{\varvec{\upalpha}} \le \frac{1}{{\gamma^{2} }}$$

(17)

where $K$ is the quasiconformal multikernel.

It also holds with high probability over the choice of the training and test data because permuting the sample leaves the distribution unchanged. Here we provide an upper bound on the error of a kernel classifier on the test data over the training data of a certain margin cost function with properties of the kernel matrix. In this paper, we focus on the 1-norm soft margin classifier after manifold-based feature extraction [26].

For every $\gamma > 0$ with probability at least $1 - \delta$ over the data $\left( {x_{i} ,y_{i} } \right)$, every function $f \in F_{k}$ has $er(f)$ no more than

$$\frac{1}{n}\sum\limits_{i = 1}^{n} {\hbox{max} (1 - y_{i} f(x_{i} )) + \frac{1}{\sqrt n }\left( {4 + \sqrt {2\log (1/\delta )} + \sqrt {\frac{\varsigma (k)}{{n\gamma^{2} }}} } \right)}$$

(18)

where $\varsigma ({\mathbf{\rm K}}) = E\mathop {\hbox{max} }\limits_{{K \in {\mathbf{\rm K}}}} \sigma^{T} K\sigma$ with the expectation over $\sigma$. So,

$$\varsigma ({\mathbf{\rm K}}) = cE\mathop {\hbox{max} }\limits_{{K \in {\mathbf{\rm K}}}} \sigma^{T} \frac{K}{trace(K)}\sigma$$

(19)

then

$$\varsigma ({\mathbf{\rm K}}) \le c\hbox{min} \left( {m,n\mathop {\hbox{max} }\limits_{j} \frac{{\lambda_{j} }}{{trace(K_{j} )}}} \right)$$

(20)

where $\lambda_{j}$ is the largest eigenvalue of $K_{j}$. So, the test error is bounded by a sum of the average over the training data of a margin cost function plus a complexity penalty term that depends on the ratio between the trace of the quasiconformal multikernel kernel matrix and the squared margin parameter, $\gamma^{2}$.

3 Experimental results

3.1 Experimental and procedural parameters setting

We evaluate the performances on the databases, and the recognition accuracy is evaluated as the performance index. The average recognition accuracy of ten times of experiments is used to evaluate the classification performance. The experiments are implemented in the MATLAB platform (Version 6.5) with the computer of Pentium 3.0 GHz, 512 MB RAM. On the selection of the procedural parameters, the cross-validation method is applied to select the procedure parameters. We choose the kind of basic kernel functions for the different application systems, and the parameter of basic kernel is chosen with cross-validation method.

3.2 Performance on ORL and Yale databases

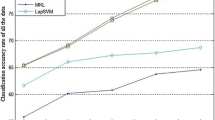
In this section, some experiments on YALE and ORL databases were implemented to evaluate the unified framework of multiple kernels manifold learning. YALE database from the YALE Center for Computational Vision and Control contains 165 grayscale images of 15 individuals, and ORL database was developed at the Olivetti Research Laboratory that consisted of 400 images from 40 individuals. The original ORL face images of 112 × 92 pixels are resized to 48 × 48 pixels. On the Yale database, we divide the database into 5 sub-databases through selecting randomly 5 samples as the training set, and the rest samples as the test sample. The sub-datasets are denoted with T1, T2, T3, T4, and T5. We implement LPP [11], CLPP [11], KCLPP [11], and our method to evaluate the performance, and the experimental results are shown in Table 1, and the procedural parameters were chosen through the cross-validation. Similarly, on ORL database, the quasiconformal kernel-based manifold learning methods are comprehensively evaluated compared with LPP, CLPP, and KCLPP. As shown in Table 2, the proposed framework achieves the highest recognition accuracy because the data structure is adaptively changed for the input data.

Table 1 Recognition performance on Yale databases (%)

Table 2 Recognition performance on ORL databases (%)

Some evaluations are implemented on the randomly selection, and the experimental result is shown in Table 3. The 10 times of experiments are implemented, and averaged recognition accuracy is considered as the index of performance. As experimental results, the proposed kernel optimization method performs better than other methods.

Table 3 Recognition performance on ORL and Yale databases on randomly selection (%)

3.3 Application to hyperspectral image classification

The framework of hyperspectral image classification system is shown in Fig. 2. Hyperspectral imagery is the most popular remote sensing technology on satellite platform, with the prospective applications in military monitoring, energy exploration, geographic information, and so on. The development of hyperspectral instruments with hundreds of contiguous spectral channels promotes collecting remote imagery data. The size of the data is largely increased with the high resolutions of spectral and space. Two problems occur in the practical applications: (1) the bandwidth of the communication channel limits the transmission of the full hyperspectral image data for the further processing and analysis on the ground; (2) the demand of the real-time processing for some applications. Data compression is feasible to solve the transmission problem, but is still endure the limitation on real-time analysis. So, based on the real-time image analysis, machine learning-based data analysis technology is feasible and effective to produce one image from the full band of hyperspectral images. The classification is to classify the spectrum curve based on the spectrum data of each object. The hyperspectral data machine learning system is implemented on the satellite platform. After the hyperspectral data collection, each pixel is classified and denoted to the different objects based on the spectrum database. The spectrum data in database are collected in advance, so it has inconsistency between the spectrums with the data collection. The inconsistency can be considered the nonlinear changing. The relationship between spectral curves is the classical nonlinear relationship. So the classification is the nonlinear and complex classification problem. Researches show that kernel learning method is not effective to hyperspectral sensing data. Kernel-based manifold learning is applied to hyperspectral sensing data classification.

Fig. 2

Application framework of kernel-based manifold learning

Based on the application framework, we evaluate the proposed algorithm on Indian Pines and Washington, D.C. Mall databases. The two databases have the various spectral and spatial resolutions under the different environments of remote sensing.

Indian Pines dataset is collected based on airborne platform on June 1992 and has the various spectral and spatial resolutions, and the spectral curves denote the different remote sensing environments. The airborne visible/infrared imaging spectrometer (AVIRIS) data cube has 224 bands of spectral resolution, and it has the spatial resolution of 20 m per pixel. In our experiments, we removed the noisy and water–vapor absorption bands and 200 bands of images are used in the experiments. The whole scene is consists of 145 × 145 pixels, and 16 classes of interested objects rang the size from 20 to 2468 pixels, but only 9 classes of objects are selected in the experiments. Some examples are shown in Fig. 3.

Fig. 3

One example of Indian Pines data in He & Li [29]. a Three band false color composite, b spectral signatures

D.C. Mall data were acquired under the airborne with hyperspectral digital imagery collection experiment (HYDICE) sensor on August 23, 1995. The image has 1280 × 307 pixels, and it has the spatial resolution of 1.5 m, and 210 spectral bands are in the 0.4–2.4-μm region. In the experiments, several bands influenced by the atmospheric absorption are ignored, and the rest 191 bands are implemented in the experiments. The image is resized to the size of 211 × 307 including 7 classes of land-covers namely roof, grass, street, trees, water, path and shadow. Some examples are shown in Fig. 4.

Fig. 4

One example from D.C. Mall data in He & Li [29]. a Three band false color composite, b spectral signatures

Firstly, we evaluate the proposed algorithm compared with support vector classifier (SVC), kernel sparse representation classifier (KSRC) on data classification. On the basic kernel functions, we compare them in the practical hyperspectral image classification. We test the single-kernel and quasiconformal multikernels for kernel classifiers on SVC and KSRC, that is, PK-SVC: polynomial kernel-SVC, GK-SVC: Gaussian kernel-SVC, QMK-SVC: quasiconformal multikernels-based SVC, PK-KSRC: polynomial kernel-KSRC, GK-KSRC: Gaussian kernel-KSRC, QMK-KSRC: quasiconformal multikernels-based KSRC. For the quantitative comparison, we implement some experiments using polynomial kernel-KCLPP (PK-KCLPP), Guassian kernel (GK-KCLPP), multiple kernel (MK-KCLPP), and quasiconformal multiple kernel-based KCLPP (QMK-KCLPP), PK-SVC, GK-SVC, QMK-SVC, PK-KSRC, GK-KSRC, and QMK-KSRC. The averaged accuracy is to evaluate the performance of the algorithms, and the experimental results are shown in Tables 4 and 5. On the SVC, QMK-SVC performs better than PK-SVC and GK-SVC. On the KSRC, QMK-KSRC outperforms PK-KSRC and GK-KSRC. In particular, the polynomial kernel performs better than Gaussian kernel under SVC and KSRC classifiers. On selection of the basic kernels for multiple-kernel learning, we select the Gaussian kernel and polynomial kernel as the basic kernels.

Table 4 Performance of manifold learning compared with SVC on the Indian Pines data (%)

Table 5 Performance of manifold learning compared with KSRC on the Indian Pines data (%)

Moreover, we also implement some experiments on D.C. Mall data to evaluate the proposed framework including polynomial kernel-KCLPP (PK-KCLPP), Guassian kernel (GK-KCLPP), multiple kernel (MK-KCLPP), and quasiconformal multiple kernel-based KCLPP (QMK-KCLPP). The experimental results are shown in Table 6. The experimental results show that multiple kernels-based manifold learning performs better than the basic kernels, and quasiconformal multiple kernel-based manifold outperform learning performance better than multiple version. So, it is feasible to apply quasiconformal kernel model to improve the kernel manifold learning.

Table 6 Performance on the D.C. Mall data (%)

3.4 Discussion

As experimental results on the performance of manifold learning and other machine learning based on quasiconformal kernel and quasiconformal multiple kernels, we can conclude that, the quasiconformal kernel-based manifold learning performs better than basic kernel-based manifold learning, and quasiconformal multiple kernels outperform other methods. Kernel trick is an effective method to solve the nonlinear problems of machine learning, and the recognition accuracy and prediction accuracy are largely increased with the nonlinear kernel mapping. There is no any kernel which is adaptive to all applications of detecting intrinsic information for the complicate sample data. The multiple kernel-based manifold learning has different kernel representations for the different feature subspaces, and multiple-kernel learning is a feature extraction method of combining many features. So, the multikernel-based manifold learning performs better than the single feature extraction on the data. The proposed framework is to solve the selection of function and parameter of kernel, which have heavy influences on the performance of kernel-based learning system. Quasiconformal single-kernel structure changes the data structure in the kernel empirical space. And then, quasiconformal multiple kernels are combined to more precisely characterize the data for improving performance on solving complex visual learning tasks, so the proposed framework outperforms others in the different datasets.

Moreover, we implement many experiments with the recognition accuracy, and we do not consider the efficiency in the experiments. The procedure includes three procedures of multiple kernels optimization, training and testing for general kernel-based manifold learning application. The optimization procedure costs more time, but the kernel optimization procedure can be implemented off-line. So the kernel optimization-based manifold learning does not cost much time on the online application. In the training steps, the optimal parameters are solved through iteration optimization, and the procedure will cost much time. While in the test stage, it needs the additional less time consuming. So, it has the little influence on the learning efficiency.

4 Conclusion

This paper presents a novel framework of manifold multiple-kernel learning, and it applies quasiconformal multiple-kernel model to increase the data description ability. Some experiments are implemented to evaluate the multiple kernel and quasiconformal kernel. The proposed framework performs better compared with the traditional methods. The framework preserves the good structure of data distribution for classification with the quasiconformal mapping-based multiple-kernel model. And the model has the maximum class discriminant ability of data in the nonlinear manifold feature space. So, the proposed method is a promising dimensionality reduction method on data processing, especially on hyperspectral image processing. The proposed manifold learning is a promising dimensionality reduction method on data processing, especially on hyperspectral data processing, and it preserves the local embedding. The proposed framework can be applied to many applications, for example, image retrieval, video classification, speech recognition, and so on.