1 Introduction

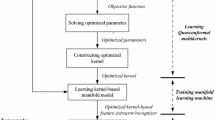
For classification tasks, there are mainly three types: supervised, unsupervised and semi-supervised. Supervised learning has both input and output data, of which the output data are labels of corresponding input data; while, unsupervised learning has only input data. Intuitively, semi-supervised learning has full input data but has partial output data. In the field of supervised classification, many types of classifiers have been proposed. These classifiers are the Bayesian methods, least square linear or non-linear models [1], neural networks [2], decision trees [3], hierarchical methods [4] and so on [5,6,7]. Most of them are based solely on the values or relations of the training data and are solved by learning parameters or a linear system, and a method to estimate the potential geometry within data has not yet been fully developed. In this study, we consider the geometry aspect of data as important information, introducing it into a learning classifier to obtain a more appropriate classifier. As the manifold theory shows, any data assume an intrinsic geometrical structure and, particularly, when \(\left\{ {\left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{n} \in X \times R\), we assume that the marginal probability distribution \(P_{X}\) is supported on the manifold \({\mathcal{M}} \subset X\). Although we may not know the distribution information, the manifold structure can be learned to estimate \(P_{X}\). In order to consider the inner geometrical structure in the classifier, we adopt the manifold regularization technique, one of the important works is proposed by [8], in that work a geometrical framework for solving semi-supervised problem was proposed. Manifold regularization is a geometrically motivated penalty; which considers the classifier \(f\) restricted to \({\mathcal{M}}\) and forces \(f\) to be smooth along \({\mathcal{M}}\). The computation of manifold regularization is based on a graph. The graph is an important tool to represent the similarity of pair-wise data samples and facilitate to extract the geometrical structure within data. When we build a graph, the traditional methods used are unsupervised methods and the relation between vertices is kNN or the Euclidean distance. In supervised classification scenario, the label information is given to the classifier; therefore, we propose a supervised graph method that uses labels. To evaluate the similarity of pair-wise vertices in a graph, we use the Hellinger distance instead of the Euclidean distance as the Hellinger distance can represent distance from four aspects, such as similarity, density, dimension, and orientation [9] and thus provide a comprehensive consideration of data relations. After obtaining the graph, we need to choose the classifier \(f\). Nowadays many datasets are from multiple sources and, have multiple attributes that differ in features and correlate with each other. Therefore, two points should be considered while selecting a classifier: One is that the classifier should be suitable for manifold regularization, and the other is that it should be flexible in dealing with a complicated dataset. Therefore, multiple kernel learning (MKL) is a good option. Unlike a support vector machine (SVM) or a logistic model, MKL searches for a linear combination of the base kernel functions by optimizing the generalized performance evaluation. Given a series of base kernel functions, MKL displays good adaptability and interpretation [10, 11], and thus far, many algorithms for MKL have been developed [12,13,14,15,16]. Moreover we know that regularization techniques are often used in kernel-based methods [5].

In this study, under the assumption that the inner geometrical structure of data improves the performance of a learning machine, we present a classifier based on MKL with the manifold regularization, expecting the regularizer can extract the inner geometrical structure. In the supervised scenario, we propose a supervised graph construction method. This classifier makes use of an intrinsic geometrical structure obtained by using a graph and has the ability to deal with a multiple feature dataset via advanced MKL. The related work is referred to [17], in which a manifold regularization is also added to multiple kernels classifier. The differences between previous study and this study are that previous study adopted an approximated formula-tion while this study is accurate, previous study adopted original manifold regularization while this study applied an improved manifold regularization with Hellinger distance, especially fit for the supervised classification. The main contributions of this paper can be outlined as follows:

  1. (1)

    We propose the supervised manifold regularization using the Hellinger distance, where the Hellinger distance can describe data relationships in details, to address the problem of the supervised classification scenario. The proposed supervised manifold regularization is applied to MKL to construct a reasonable classifier, which can deal with large ranges of datasets.

  2. (2)

    We conduct experiments on several public datasets; the results show that the proposed classifier can achieve competent performances as compared to other methods, leading to results related to the effectiveness and efficiency of the proposed method.

The rest of this paper is organized as follows. In Sect. 2, we present the manifold regularization MKL, and introduce the supervised graph method using the Hellinger distance. In Sect. 3, the classifier is solved, along with a preliminary analysis on complexity; some concerns are also presented in this section. Experimental results are described in Sect. 4. Finally, we present the conclusion and future research directions in Sect. 5.

2 Methodology

2.1 Classifier formulation

Given a supervised dataset \(\left\{ {\left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{n} \in X \times R\), \(x_{i} \in R^{d}\), \(y_{i} = \pm 1\), our task is to find a classifier function \(f\) with the ability to make generalizations. Assume that \(\left( {x,y} \right)\) are drawn from a probability distribution \(P\), and the marginal distribution \(P_{X}\) is supported on a compact manifold \({\mathcal{M}}\); thus, the conditional distribution \(P_{Y|X}\) varies smoothly along the geodesics in the geometry of \({\mathcal{M}}\), which implies that similar \(P\left( {y_{i} |x_{i} } \right)\) and \(P\left( {y_{j} |x_{j} } \right)\) correspond to a close relation between \(x_{i}\) and \(x_{j}\). Therefore, an additional regularization term is needed to control the classification function \(f\) along \({\mathcal{M}}\). This additional regularization is called manifold regularization and we use \(\left\| f \right\|_{I}^{2}\) to note it. In practice, \(P_{X}\) is usually unknown; therefore, \(\left\| f \right\|_{I}^{2}\) is estimated by using a graph [18]. Now, as we use multiple kernel machine to develop \(f\), we first introduce the reproducing kernel Hilbert space (RKHS) [19]. For a Mercer kernel \(K\left( {x,y} \right):X \times X \to R\), there is an RKHS \({\mathcal{H}}\) of functions \(f:X \to R\) with the corresponding norm \(\left\| \cdot \right\|_{{\mathcal{H}}}^{2}\). In \({\mathcal{H}}\), we have the following property,

$$f\left( x \right) = \left( {f\left( \cdot \right),K\left( { \cdot ,x} \right)} \right)$$
(1)

where \(f \in {\mathcal{H}}\) and \(\left( { \cdot , \cdot } \right)\) denotes the inner product defined in \({\mathcal{H}}\). In order to introduce MKL, we use the idea proposed by [13] in SimpleMKL; i.e., any function \(f\) in the multiple kernel space \({\mathcal{H}}\) is a sum of functions \(f_{m} ,m = 1, \ldots ,M\), each belonging to \({\mathcal{H}}_{m}\). The space \({\mathcal{H}}_{m}\) is also an RKHS endowed with an inner product \(\left( { \cdot , \cdot } \right)_{m}\) and a positive definite kernel \(K_{m}\); finally, a classical result on RKHS [19] reveals that \({\mathcal{H}}\) is an RKHS, with the following form:

$$\begin{aligned} K\left( {x,y} \right) = \sum\nolimits_{i = 1}^{M} {d_{m} K_{m} \left( {x,y} \right)} \hfill \\ \sum\nolimits_{i = 1}^{M} {d_{m} } = 1;d_{m} \ge 0,\forall m \hfill \\ \end{aligned}$$
(2)

where we consider the \(\ell_{1}\) norm constraint to the weights \(\left\{ {d_{m} } \right\}_{m = 1}^{M}\). For MKL only, given the data \(\left\{ {\left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{n} \in X \times R\), the following form is considered in the classification task:

$$f^{*} = \arg \mathop {\hbox{min} }\limits_{{f \in {\mathcal{H}}}} C\sum\nolimits_{i = 1}^{n} {V\left( {x_{i} ,y_{i} ,f} \right)} + \gamma \left\| f \right\|_{{\mathcal{H}}}^{2}$$
(3)

where \(V\) denotes a loss function, such as \(\left( {y_{i} - f\left( {x_{i} } \right)} \right)^{2}\) for a least-square model or the hinge loss function for a SVM; \(C\) represents the penalty parameter; and, the RKHS norm \(\left\| \cdot \right\|_{{\mathcal{H}}}^{2}\) forces smoothness conditions on the possible solutions to obtain a better generalization and avoid over-fitting. According to the Representer The-orem [20, 21] and multiple kernels, the optimal function of problem (3) is given by:

$$f^{*} \left( x \right) = \sum\nolimits_{i = 1}^{n} {\alpha_{i} K\left( {x_{i} ,x} \right)} = \sum\nolimits_{i = 1}^{n} {\alpha_{i} d_{m} K_{m} \left( {x_{i} ,x} \right)}$$
(4)

where \(\sum\nolimits_{i = 1}^{M} {d_{m} } = 1;d_{m} \ge 0,\forall m\) and \(\alpha_{i} \in R\), \(\forall i\).

As mentioned earlier, the intrinsic geometrical information is introduced by a regularization form, which is as follows:

$$f^{*} = \arg \mathop {\hbox{min} }\limits_{{f \in {\mathcal{H}}}} C\sum\nolimits_{i = 1}^{n} {V\left( {x_{i} ,y_{i} ,f} \right)} + \gamma_{h} \left\| f \right\|_{{\mathcal{H}}}^{2} + \gamma_{I} \left\| f \right\|_{I}^{2}$$
(5)

where \(\gamma_{h}\) controls the function complexity in the space \({\mathcal{H}}\) and \(\gamma_{I}\) controls the manifold penalty.

We also noted that in (5), the optimal \(f^{*}\) lies in the linear space \({\mathcal{S}} = span\left\{ {K\left( { \cdot ,x} \right)|x \in {\mathcal{M}} \subset X} \right\}\), and for any \(f \in {\mathcal{H}}\), \(f = f_{{\mathcal{S}}} + f_{{\mathcal{S}}}^{ \bot }\), where \(f_{{\mathcal{S}}}\) denotes the projection of \(f\) to \({\mathcal{S}}\) and \(f_{{\mathcal{S}}}^{ \bot }\) represents its orthogonal complement.

Lemma 1. [8] All functions \(f_{{\mathcal{S}}}^{ \bot }\) in \({\mathcal{H}}\) vanish on \({\mathcal{M}}\).

By using lemma 1, we have \(f\left( {x_{i} } \right) = f_{{\mathcal{S}}} \left( {x_{i} } \right)\); on the other hand, \(\left\| f \right\|_{{\mathcal{H}}}^{2} = \left\| {f_{{\mathcal{S}}} } \right\|_{{\mathcal{H}}}^{2} + \left\| {f_{{\mathcal{S}}}^{ \bot } } \right\|_{{\mathcal{H}}}^{2}\). Therefore, \(\left\| f \right\|_{{\mathcal{H}}}^{2} = \left\| {f_{{\mathcal{S}}} } \right\|_{{\mathcal{H}}}^{2}\) and the minimizer \(f^{*}\) is in \({\mathcal{S}}\). And \(f^{*}\) admits the Representer Theorem in (4). This is helpful in reducing the problem and optimizing over the results over a finite dimensional space.

2.2 Supervised graph

Initially, \(\left\| f \right\|_{I}^{2}\) is estimated using a graph. Define a graph \(G = \left( {V,E} \right)\), where \(V\) denotes vertices on all samples, i.e., \(v_{i} = x_{i}\); \(E\) represents the edges linking the adjacency pair, i.e., \(e_{ij} :v_{i} \sim v_{j}\); and ‘\(\sim^{\prime}\) implies that two vertices are adjacent. Two vertices are considered adjacent on the basis of kNN or the Euclidean distance if \(\left\| {x_{i} - x_{j} } \right\| \le \varepsilon\). Further, the edges are weighted by a weight matrix \(W\), whose elements are as follows:

$$\begin{aligned} &w_{ij} = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {v_{i} \sim v_{j} } \\ {\text{otherwise}} \\ \end{array} \hfill \\ & {\text{or }}w_{ij} = \left\{ {\begin{array}{*{20}c} {\exp \left( { - \sigma^{2} \left\| {x_{i} - x_{j} } \right\|^{2} } \right)} \\ 0 \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {v_{i} \sim v_{j} } \\ {\text{otherwise}} \\ \end{array} \hfill \\ \end{aligned}$$
(6)

The natural way to compute manifold regularization is: \(\left\| f \right\|_{I}^{2} = \sum\nolimits_{ij} {\left( {f(x_{i} ) - f(x_{j} )} \right)}^{2} w_{ij}\); this implies that the outputs of \(f\) maintain adjacent relations. By using a Laplacian graph, we obtain the following computations:

$$\begin{aligned} \left\| f \right\|_{I}^{2} = {\text{f}}^{T} L{\text{f}} \hfill \\ L = D - W \hfill \\ \end{aligned}$$
(7)

where \(D\) denotes a diagonal matrix with the entries \(D_{ii} = \sum\nolimits_{j} {w_{ij} }\), and \({\text{f}}^{T} = \left( {f(x_{1} ), \ldots ,f(x_{n} )} \right)\). \(L\) represents a Laplacian graph. This method is unsupervised, and in a supervised setting, it is insufficient from two aspects. One is the loss of useful information, i.e., labels, and the other is the fact that the weights are biased if the adjacent vertices are decided solely on the basis of distance, particularly a scenario where two points are close but they bear different labels.

We propose a graph that uses label information for showing more relations between samples. As we have already seen, the edges on the graph are based on the similarity of vertices; therefore, the more we consider the similarity, the more accurate would be the sample relations. Here, we adopt the Hellinger distance to depict a similarity. As we mentioned above, Hellinger distance can represent data from four aspects: similarity, density, dimension, and orientation. This distance describes data based on the probability where the data is generated from, different from Euclidean distance or Manhattan Distance or Chebyshev distance or Minkowski distance, all of which are based on the coordinate or computation of absolute value, and Mahalanobis distance which emphasizes the distance of covariance. As for manifold assumption, the probability-based measure is proper; therefore, the Hellinger distance is adopted. We notice that the Bhattacharyya distance is also the probability-based distance but it fits for discreet random variables. Kullback–Leibler divergence measures two probabilities but it is not symmetric and mainly for entropy variations.

After the kNN method, we can obtain the neighbors of each sample, for instance, for a point \(x\), \(N\left( x \right)\) is to be a neighbor around \(x\). Define the local sample covariance matrix \(\Delta_{x}\):

$$\Delta_{x} = \sum\nolimits_{{x \in N\left( {x^{\prime}} \right)}} {\frac{{\left( {x^{\prime} - \mu_{x} } \right)\left( {x^{\prime} - \mu_{x} } \right)^{T} }}{{\left( {\left| {N(x)} \right| - 1} \right)}}}$$
(8)

where \(\mu_{x}\) is defined as the neighborhood mean and, \(\left| {N(x)} \right|\) denotes the cardinality, which is a quantity that captures the local geometry feature. We know that initially, the Hellinger distance quantifies the similarity between two probability distributions [22]; therefore, we define two Gaussian distributions, namely \(p\left( {x_{i} } \right) = N\left( {0,\Delta_{{x_{i} }} } \right)\), \(p\left( {x_{j} } \right) = N\left( {0,\Delta_{{x_{j} }} } \right)\), with zero mean and covariance \(\Delta_{{x_{i} }}\), \(\Delta_{{x_{j} }}\). We can get the Hellinger distance of \(x_{i}\), \(x_{j}\) using the following:

$$H_{ij}^{2} = \frac{1}{2}\int {\left( {p^{1/2} (x_{i} ) - p^{1/2} (x_{j} )} \right)}^{2} dx$$
(9)

After obtaining the Hellinger distance matrix \(H\), we need to construct the graph \(G\), which would con-sider the label information. Therefore, \(G\) is split into two graphs \(G_{w}\) and \(G_{b}\); \(G_{w}\) denotes a within-class graph, \(G_{b}\) represents a between-class graph. Let \(\ell \left( {y_{i} } \right)\) be the class label of \(y_{i}\), and \(N\) be the notation of neighbors. Therefore, for each point \(y_{i}\), we define the following:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{w1} = \left\{ {y_{j} |\ell \left( {y_{j} } \right) = \ell \left( {y_{i} } \right),H\left( {\Delta_{{x_{i} }} ,\Delta_{{x_{j} }} } \right) \le \lambda_{1} } \right\}} \\ {N_{w2} = \left\{ {y_{j} |\ell \left( {y_{j} } \right) = \ell \left( {y_{i} } \right),H\left( {\Delta_{{x_{i} }} ,\Delta_{{x_{j} }} } \right) > \lambda_{1} } \right\}} \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}c} {N_{b1} = \left\{ {y_{j} |\ell \left( {y_{j} } \right) \ne \ell \left( {y_{i} } \right),H\left( {\Delta_{{x_{i} }} ,\Delta_{{x_{j} }} } \right) \le \lambda_{2} } \right\}} \\ {N_{b2} = \left\{ {y_{j} |\ell \left( {y_{j} } \right) \ne \ell \left( {y_{i} } \right),H\left( {\Delta_{{x_{i} }} ,\Delta_{{x_{j} }} } \right) > \lambda_{2} } \right\}} \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(10)

It is noted that \(N_{w1}\) denotes within-class neighbors with a low Hellinger distance and, \(N_{w2}\) denotes within-class neighbors with a high Hellinger distance; thus, \(N_{b1}\), \(N_{b2}\) represent between-class neighbors with low and high Hellinger distances. Here, we treat the Hellinger distance differently, i.e., \(\lambda_{1} \le \lambda_{2}\) implying that in a same label occasion we would tighten the bound; otherwise, we would relax the bound. This is done to avoid a bias. Thus, we can adapt the set of neighbors according to the class information and the local geometry similarity between samples.

Let \(W_{w}\) and \(W_{b}\) be the weight matrices of \(G_{w}\) and \(G_{b}\), defined them as follows:

$$\begin{aligned} G_{w} :\left\{ {\begin{array}{*{20}c} {if \, y_{i} \in N_{w1} \left( {y_{j} } \right),w_{w,ij} = 1 \, } \\ {if \, y_{i} \in N_{w2} \left( {y_{j} } \right),w_{w,ij} = \exp \left( { - \left\| {x_{i} - x_{j} } \right\|^{2} } \right)} \\ \end{array} } \right. \hfill \\ G_{b} :\left\{ {\begin{array}{*{20}c} {if \, y_{i} \in N_{b1} \left( {y_{j} } \right),w_{b,ij} = \exp \left( { - r_{ij} \left\| {x_{i} - x_{j} } \right\|^{2} } \right) \, } \\ {if \, y_{i} \in N_{b2} \left( {y_{j} } \right),w_{b,ij} = 0 \, } \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(11)

where \(r_{ij} = \hbox{max} Radius\left\{ {N_{b1} (y_{i} ),N_{b1} (y_{j} )} \right\}\) for the weight between different classes; here, a relatively high similarity needs to be treated as non-zero. Finally, it is easy to show that the global weight matrix \(W\) can be written as \(W = W_{w} + W_{b}\). In terms of manifold regularization, the Laplacian graph is computed in the same way, i.e., \(L = D - W\). To use a different notation, here we denote the Laplacian graph as \(L_{H}\). In the experiment, we use both unsupervised \(L\) and supervised \(L_{H}\) for the manifold regularized MKL classification, to determine their performances. Then, we use only \(L\) for the following formulas to simplify the notation. As shown in (5), by taking the Representer Theorem and (7), we transform (5) into the following:

$$\mathop {\hbox{min} }\limits_{{f \in {\mathcal{H}}}} C\sum\nolimits_{i = 1}^{n} {V\left( {x_{i} ,y_{i} ,f} \right)} + \gamma_{h} \alpha^{T} K\alpha + \gamma_{I} \alpha^{T} KLK\alpha$$
(12)

where \(K = \sum\nolimits_{m = 1}^{M} {d_{m} K_{m} }\) and \(K_{m}\) denotes the Gram-matrix with entry \(K_{m} \left( {x_{i} ,x_{j} } \right)\). Here, (12) extends the model in [8] by using multiple kernels; therefore, (12) has the advantages of both multiple kernels and a manifold regularization.

3 Algorithm and discussion

3.1 Optimization analysis

Using the hinge loss function, we can rewrite (12) as follows:

$$\begin{aligned} \, \mathop {\hbox{min} }\limits_{\alpha ,\xi } C\sum\nolimits_{i = 1}^{n} {\xi_{i} } + \gamma_{h} \alpha^{T} K\alpha + \gamma_{I} \alpha^{T} KLK\alpha \hfill \\ s.t. \, y_{i} \left( {\sum\nolimits_{i = 1}^{n} {\alpha_{j} K\left( {x_{j} ,x_{i} } \right) + b} } \right) \ge 1 - \xi_{i} ; \, \xi_{i} \ge 0,\forall i \hfill \\ \, K = \sum\nolimits_{m = 1}^{M} {d_{m} K_{m} } ,\sum\nolimits_{m = 1}^{M} {d_{m} } = 1; \, d_{m} \ge 0,\forall m \hfill \\ \end{aligned}$$
(13)

Here, \(\alpha^{T} K\alpha = \left\| \alpha \right\|_{K}^{2}\) and \(\alpha^{T} KLK\alpha = \left\| {K\alpha } \right\|_{L}^{2}\). Thus, by adding Lagrangian multipliers to (13), we obtain the following:

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{d,\alpha ,\xi ,b} J\left( d \right) \hfill \\ & s.t. \, \sum\nolimits_{m = 1}^{M} {d_{m} } = 1; \, d_{m} \ge 0,\forall m \hfill \\ & J\left( d \right) = \mathop {\hbox{max} }\limits_{\beta ,\lambda } C\xi + \gamma_{h} \left\| \alpha \right\|_{K}^{2} + \gamma_{I} \left\| {K\alpha } \right\|_{L}^{2} + \hfill \\ & \beta^{T} \left( {{\mathbf{1}} - \xi - Y\left( {K\alpha + b} \right)} \right) - \lambda^{T} \xi \hfill \\ \end{aligned}$$
(14)

where \(\beta\), \(\lambda\) denote the multiplier vectors, \({\mathbf{1}}\) represents a column vector with 1, \(\xi\) denotes a column vector with the entry \(\xi_{i}\), and \(Y\) refers to a diagonal matrix with the entry \(Y_{ii} = y_{i}\).

First, we consider the problem with a temporary fixed \(d\), then take the derivative of \(J\left( d \right)\) w.r.t. primal variables:

$$\begin{aligned} {{\partial J} \mathord{\left/ {\vphantom {{\partial J} {\partial \alpha }}} \right. \kern-0pt} {\partial \alpha }} = 0 \to \left( {2\gamma_{h} K + 2\gamma_{I} KLK} \right)\alpha = KY\beta \hfill \\ {{\partial J} \mathord{\left/ {\vphantom {{\partial J} {\partial \xi_{i} }}} \right. \kern-0pt} {\partial \xi_{i} }} = 0 \to 0 \le \beta_{i} \le C \hfill \\ {{\partial J} \mathord{\left/ {\vphantom {{\partial J} {\partial b}}} \right. \kern-0pt} {\partial b}} = 0 \to \sum\nolimits_{i} {\beta_{i} y_{i} = } 0 \hfill \\ \end{aligned}$$
(15)

By inserting the derivative results back into (14), we obtain the following:

$$\begin{aligned} J\left( d \right) = \mathop {\hbox{min} }\limits_{d} \mathop {\hbox{max} }\limits_{\beta } \sum\nolimits_{i = 1}^{n} {\beta_{i} } - \frac{1}{2}\beta^{T} YKQY\beta \hfill \\ s.t. \, \sum\nolimits_{i = 1}^{n} {\beta_{i} y_{i} } = 0; \, 0 \le \beta_{i} \le C \hfill \\ \end{aligned}$$
(16)

where \(Q = \left( {2\gamma_{h} I + 2\gamma_{I} LK} \right)^{ - 1}\) and \(I\) denotes an identity matrix. (16) can be solved by using a classical SVM solver with fixed \(d\). After getting an intermediate optimal \(\beta^{*}\), we go back to update each \(d_{m}\); this two-layer problem continues until the stop criterion is met. To update each \(d_{m}\), we develop the gradient \({{\partial J} \mathord{\left/ {\vphantom {{\partial J} {\partial d_{m} : = g_{m} }}} \right. \kern-0pt} {\partial d_{m} : = g_{m} }}\) to update \(d\) as follows:

$$g_{m} = - \beta^{ * T} Y\;K_{m} Q/2 - \gamma_{I} KQLK_{m} \;Y\beta^{ * } \;\forall m$$
(17)

It is certain that the minus sign on the right side of (17) denotes the descent direction. Meanwhile, we pay attention to the constraints on \(d\) in order to estimate a feasible descent direction. Therefore, we use the Reduced Gradient Method [23]. Suppose that \(d_{v}\) denotes the maximum element in \(d\) and \(v\) represents the index, then according to the constraint \(\sum {d_{m} } = 1\), the reduced gradient is as follows:

$$g_{m}^{reduced} = \left\{ {\begin{array}{*{20}c} {g_{m} - g_{v} } \\ {0 \, } \\ \end{array} \begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\begin{array}{*{20}c} {m \ne v} \\ {m = v} \\ \end{array}$$
(18)

Therefore, the feasible descent direction can be computed as follows:

$$p = \left\{ {\begin{array}{*{20}c} {p_{m} = \left\{ {\begin{array}{*{20}c} { - g_{m}^{reduced} } \\ { - d_{m} g_{m}^{reduced} } \\ \end{array} \begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {g_{m}^{reduced} \le 0} \\ {g_{m}^{reduced} > 0} \\ \end{array} } \right.} \\ {p_{v} = - \sum\nolimits_{m \ne v} {p_{m} } \, } \\ \end{array} } \right.$$
(19)

After obtaining direction \(p\), we perform a one-dimensional search, and hence, the constraints on \(d\) have to be considered here. Suppose that the update of \(d^{t + 1} = d^{t} + \lambda p\) and, the step length \(\lambda\) is in the range \(\left[ {0,\lambda_{\hbox{max} } } \right]\). Then, we need to pay attention to the maximum admissible step \(\lambda_{\hbox{max} }\) to avoid the violation of the feasible field:

$$\lambda_{\hbox{max} } = \left\{ {\begin{array}{*{20}c} {\hbox{min} \left\{ { - {{d_{m} } \mathord{\left/ {\vphantom {{d_{m} } {p_{m} }}} \right. \kern-0pt} {p_{m} }}} \right\}} \\ {\lambda_{0} \, } \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {p_{m} < 0,d_{m} > 0} \\ {\left\{ {p_{m} < 0,d_{m} > 0} \right\} = \phi } \\ \end{array}$$
(20)

where \(\lambda_{0}\) denotes a pre-defined maximum step.

For (16), we consider the KKT conditions; i.e., we assume that \(J\left( d \right)\) denotes the objective and \(\sum\nolimits_{m} {d_{m} } = 1\) represents the constraints. Then, the first-order optimality conditions can be expressed as follows:

$$\begin{aligned} g_{m} + \delta - \eta_{m} = 0 \, \forall m \hfill \\ \, \eta_{m} \cdot d_{m} = 0 \, \forall m \hfill \\ \end{aligned}$$
(21)

where \(\delta\) and \(\eta_{m}\) denote the Lagrange multipliers for the equality and inequality constraints, respectively. The KKT conditions tell us that for active \(d_{m} > 0\), we have \(g_{m} = \delta\), and for inactive \(d_{m} = 0\), we have \(g_{m} \ge \delta\). Therefore, we define a tolerance \(\varepsilon\) away from \(\delta\), and the necessary optimality conditions could be the following:

$$\begin{aligned} \left| {\mathop {\hbox{min} }\limits_{{d_{m} > 0}} g_{m} - \mathop {\hbox{max} }\limits_{{d_{m} > 0}} g_{m} } \right| \le \varepsilon \hfill \\ g_{\mu } \ge \mathop {\hbox{max} }\limits_{{d_{m} > 0}} g_{m} ,d_{\mu } = 0 \hfill \\ \end{aligned}$$
(22)

Note that for vanishing \(d_{m}\), we put the gradient outside the tolerance tube. Therefore, the stop criterion is decided by (22), and the other way is the norm of the feasible descent direction; i.e., when \(\left\| p \right\|_{2} \le \varepsilon\), the iteration can be terminated.

3.2 Bound

As for the problem of error bounds, we often take two aspects into consideration: one is the sample-based classification accuracy, and the other is the measurement of model complexity. According to [24], the Rademacher complexity is suitable for the case of MKL.

Theorem 1

Let \(P\) be the probability distribution on \(X \times \left\{ { \pm 1} \right\}\) , let \({\mathcal{H}}\) be \(\left\{ { \pm 1} \right\}\) -valued functions defined on \(X\) , and \({\mathcal{T}} = \left\{ {\left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{n}\) be the training samples drawn from \(P\) . With a probability of at least \(1 - \delta\) , every function \(f\) in \({\mathcal{H}}\) satisfies the following:

$$P\left( {Y \ne f\left( x \right)} \right) \le P_{n} \left( {Y \ne f\left( x \right)} \right) + \frac{{R_{n} \left( {\mathcal{H}} \right)}}{2} + \sqrt {\frac{{\ln ({1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-0pt} \delta })}}{2n}}$$
(23)

where \(P_{n}\) denotes the average output of an indicator function, and \(R_{n} \left( {\mathcal{H}} \right)\) represents the Rademacher complexity of \({\mathcal{H}}\) [25]. Let \(\left\| f \right\|_{{\mathcal{H}}}^{2} \le a^{2}\) and the manifold regularization \(\left\| f \right\|_{I}^{2} \le b^{2}\). Thus, by using the Representer Theorem, we obtain \(\alpha^{T} K\alpha \le a^{2}\) and \(\alpha^{T} KLK\alpha \le b^{2}\). We use set \({\mathcal{A}}\) to denote them. Here, \(K\) denotes the Gram matrix over \({\mathcal{T}}\) and the multiple kernel weight \(d\) is still under \(\ell_{1}\) norm constraints. For \({\mathcal{T}}\), the Rademacher complexity can be expressed as follows:

$$R_{n} \left( {\mathcal{H}} \right) = \frac{1}{n}E_{\sigma } \left[ {\mathop {\sup }\limits_{{f \in \left( {\mathcal{H}} \right)}} \sum\limits_{i = 1}^{n} {\sigma_{i} f(x_{i} )} } \right] = \frac{1}{n}E_{\sigma } \left[ {\mathop {\sup }\limits_{{d,\alpha \in {\mathcal{A}}}} \sigma^{T} K\alpha } \right]$$

Here, we take \(\lambda ,\mu \ge 0\) as the Lagrangian multipliers to the inequalities in \({\mathcal{A}}\) and obtain the relation \(\sigma = \left( {\lambda I + \mu KL} \right)\alpha\). Thus, we obtain the following:

$$R_{n} \left( {\mathcal{H}} \right) = \frac{1}{n}E_{\sigma } \left[ {\mathop {\sup }\limits_{d} \sigma^{T} K\left( {\lambda I + \mu KL} \right)^{ - 1} \sigma } \right]$$
(24)

Note that \(\mu_{\sigma }^{m} = \sigma^{T} K_{m} \left( {\lambda I + \mu KL} \right)^{ - 1} \sigma\) and the dual norm \(\sup_{{\left\| u \right\|_{1} \le 1}} u \cdot v = \left\| v \right\|_{\infty }\). Therefore, for any integer \(r \ge 1\), we have the following:

$$R_{n} \left( {\mathcal{H}} \right) = \frac{1}{n}E_{\sigma } \left[ {\mathop {\sup }\limits_{d} \sum\limits_{m = 1}^{M} {d_{m} u_{\sigma }^{m} } } \right] \le \frac{1}{n}E_{\sigma } \left[ {\left\| {u_{\sigma } } \right\|_{r} } \right]$$
(25)

The algorithm computes the inverse of a Gram matrix which has \(O\left( {n^{3} } \right)\) complexity; this is not practical for large data sets. For high-dimensional data, we may use the Laplacian Eigenmap (LE) method for the dimensionality reduction. In this process, we would obtain the Laplacian matrix L; this matrix is just usable in manifold regularization again, which should help to improve the time efficiency. Further, with respect to the algorithm itself, our future work would be to design an efficient algorithm to implement the update of multiple kernel weights \(d\) and the computation of an inverse matrix.

4 Algorithm and discussion

In this section, we will present experimental results on a number of benchmark datasets, which are the UCI dataset [26], USPS dataset [27], Spoken letter dataset and a synthetic dataset.

4.1 Experimental setting

In practice, we fix the value of the hyper-parameter \(C\left( {C = 100} \right)\) and the Hellinger distance parameter \(\lambda \left( {\lambda_{1} = 0.4,\lambda_{2} = 0.6} \right)\). Further, the value of \(\gamma_{h}\) is taken from [10−5,…,10−2] and \(\gamma_{I}\) from [10−6,…,10−2] on the basis of a five-fold cross validation. For multiple kernels, the candidate kernels are divided into two parts: One part is composed of ten Gaussian kernels with 10 different bandwidths [2−4,…,25] and each kernel is set on all variables and on each variable. The other part is composed of three polynomial kernels of degree [1,2,3] on all variables and on each variable. All kernel matrices are a normalized to unit trace. Our algorithm programming refers to SimpleMKL. The neighboring graph vertices are found using the kNN method, where the parameter k is chosen from [6,7,8] with cross-validation along with \(\gamma_{h}\) and \(\gamma_{I}\); a large value of k is not suitable and a small value may correspond to a sparse graph. In an unsupervised Laplacian graph, the weights on the edges are determined by a binary function, and in a supervised Laplacian graph, the weights are decided by using (11). We will use a SVM, the method of [8], i.e., LapSVM, and generic MKL for the sake of comparison. In the case of the SVM, we select two kernels: one is the Gaussian kernel, and the other is the polynomial kernel. The parameters are tuned by using LIBSVM [28], in LapSVM, kernel function is Gaussian, the parameter k in kNN is 7, and in generic MKL, multiple kernels are set in the same way as described above.

4.2 Results

We selected 12 groups of the UCI dataset, and the “g50c” was generated from two unit-covariance normal distributions with equal probabilities. For each group, the experiments were run 30 times with 50% training data and 50% test data each time; the data were randomly chosen. The training data were normalized to zero mean and unit variance, and the test data were normalized using the mean and variance of the training data. The results are shown in Table 1.

Table 1 The classification accuracy (mean ± std. %) in UCI dataset
Full size table

From Table 1, we can see that MKL with manifold regularization could have competent or better accuracy rates. This proves that the potential geometrical information obtained using regularization favors a supervised classification. In the process, we have found that the kernel numbers in the first two methods are more than in the case of generic MKL. We believe that it is implicitly implied that the kernels preserve more information and may be fit for highly relevant data. In the case of the SVM, we elaborate on parameter tuning and obtain good results, but the SVM lacks a mixture of kernels and does not provide much information on sample geometry. Therefore, we expect MKL with the regularization technique to become a useful tool in the case of relatively complicated and multi-source data.

We reported our results of the handwritten digits in the USPS dataset for 3 situations, namely 2 versus 6, 4 versus 9, 5 versus 8 of classification accuracy. Each gray-scale image is scaled 16*16, and we vectorize it into a 256-dimensional sample with normalization. In the first three groups, we select 100 images and set the number of training samples varying between 5 and 20; the rest are considered test data. Further, we run each test 30 times and calculate the average of the results. Lastly, we calculated the average of the final results. When the number of training samples was 5, we assumed tr = 5 and set the kNN neighbor k = 2. Similarly, for tr = 10, we set k = 5, and for tr = 15, 20, 25, we set k = 7. In the case of the SVM, we used a Gaussian kernel with parameter tuning. Tables 2 presents the classification accuracy rates.

Table 2 Classification accuracy (mean ± std. %) of 2 versus 6, 4 versus 9 and 5 versus 8 data
Full size table

From Table 2, we find that manifold regularized MKL classifiers associated with either an unsupervised Laplacian graph or a supervised one remain on the top accuracy level in most of the cases. The results presented in Table 2 imply that the unsupervised Laplacian graph is accurate. This could be attributed to the facts that pairwise digits are almost separable in space and, the weights in the graph are sufficient to define the relations between data.

Isolet database is the letters of English alphabet spoken in isolation from UCI machine learning repository. There are 26 classes containing the utterances of 150 subjects who spoke each alphabet twice. In experiment, we selected 20 samples from each class. The number of training data is from 30 to 70% of all samples. For computation, we adopted Laplacian Eigenmap to reduce the dimension of Isolet from original 618–3 and the loss of information is inevitable, therefore we omitted the method of SVM because of poor performance. We reported the classification accuracy on all the data in Fig. 1.

Fig. 1
figure 1

Isolet experiment: classification accuracy rate of all the data samples

Full size image

Figure 1 shows that the proposed model obtained top classification accuracy. MKL with original manifold regularization also performed good classification ability.

Through the above experimental results, the proposed model benefits from the application of manifold regularization, which introduces the inner geometrical structures within data into the kernel-based classifier. While, the traditional SVM and MKL model do not consider that structure information, losing possible useful information in classifying data. The more detailed formula differences can be seen from formula (3) and (12).

4.3 Time complexity

Assuming there are n data samples with dimension d. We use M different kernels in classifier. First, as for the graph computation, the distances of all samples take time complexity O(nd) and Laplacian graph L has the time complexity O(n2). The hellinger distance of all samples has approximate time complexity O(n2). The combined kernel takes time complexity O(Mnd). In formula (16), there is a dense inverse matrix Q for O(2n3) and calculating the intermediate \(\beta\) would have O(n3). The update of d has O(Mn3) time complexity.

The entire time complexity is \(O(\left( {\left( {M + 1} \right)dn + 2n^{ 2} + \left( { 3 + M} \right){\text{n}}^{ 3} } \right) \times T)\), where T is the number of iterations in optimization process.

5 Conclusion and future

5.1 Conclusion

In this study, we added manifold regularization to a multiple kernel machine for supervised classification; the regularization was computed using a Laplacian graph, which can exploit the potential geometrical distribution of data samples. Further, in the case of a supervised classification, we proposed a supervised Laplacian graph to take the label information into account in order to obtain a good representation of the true data structure, relying on the measures obtained using the Hellinger distance, which help define data relations from the aspects of similarity, density, dimension and orientation. The base classifier that we selected was based on multiple kernels, which showed good adaptability and interpretability. The proposed model is expected to have minimum error as well as maintain the geometrical properties, represented by the assumed manifold. As shown in the experiments, the proposed classifier could achieve competent results. Further, we found that manifold regularization could be applied to supervised and semi-supervised data, particularly to datasets that show an obvious manifold when combined with MKL.

5.2 Future work and application

There are several research directions worthy of being explored further: Choices of parameters in the model and sensitivity analysis; selection of Gaussian widths in MKL; and development of an efficient algorithm to solve the entire optimal problem.

In addition to above works relevant to the model itself, the proposed classifier can be possibly develop to other kernel-based methods, such as signal processing frameworks based on kernel learning [29,30,31]. Moreover, the manifold regularization techniques are useful in analysing data especially for those like covariance features, shape variations and other data with specific structures.