Keywords

1 Introduction

Hyperspectral sensors simultaneously capture hundreds of narrow and contiguous spectral images from a wide range of the electromagnetic spectrum, for instance, the AVIRIS hyperspectral sensor [1] has 224 spectral bands ranging from visible light to mid-infrared areas (0.4–2.5 m). Such numerous numbers of images implicatively lead to high dimensionality data, presenting several major challenges in image classification [2–6]. The dimensionality of input space strongly affects performance of many classification methods (e.g., the Hughes phenomenon [7]). This requires the careful design of primitive algorithms that are able to handle hundreds of such spectral images at the same time minimizing the effects from the “curse of dimensionality”. Nonlinear methods [8–10], are less sensitive to the data’s dimensionality [11] and have already shown superior performance in many machine learning applications. Recently, kernels have a lot of attention in remote-sensed multi/hyperspectral communities [11–16]. However, the full potential of kernels—such as developing customized kernels to integrate a priori domain knowledge—has not been fully explored.

This paper extend traditional linear feature extraction and dimension reduction techniques such as Principal Component Analysis (PCA), Partial Least Squares (PLS), Orthogonal Partial Least Squares (OPLS), Canonical Correlation Analysis (CCA), NMF (Non-Negative Matrix Factorization) and Entropy Component Analysis (ECA) to kernel nonlinear grouped version. Several extensions (linear and non-linear) to solve common problems in hyper dimensional data analysis were implemented and compared in hyperspectral image classification.

We explore and analyze the most representative MVA approaches, Grouped MVA (GMVA) methods and kernel based discriminative feature reduction manners. We additionally studied recent methods to make kernel GMVA more suitable to real world applications, for hyper dimensional data sets. In such approaches, sparse and semi-supervised learning extensions have been successfully introduced for most of the models. Actually, reduction or selection of features that facilitate classification or regression cuts to the heart of semi-supervised classification. We have completed the panorama with challenging real applications with the classification of land-cover classes.

We continue the paper with an exploring the MVA to the Grouped MVA and then extend the Grouped MVA to the Kernel based Grouped MVA algorithms. Section 3 introduces some simulation of extensions that increase the applicability of Kernel Grouped MVA methods in real applications. Finally, we conclude the paper in Sect. 4 with some discussion.

2 Kernel Grouped Multivariate Analysis

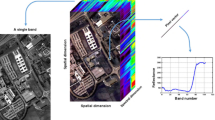
In this section, we first propose the grouping approach and then we extend the linear Canonical Correlation Analysis to kernel based grouped CCA as a sample of kernel based Grouped MVA Methods such as Kernel Grouped Principal Component Analysis (KGPCA), Kernel Grouped Partial Least Squares (KGPLS), Kernel Grouped Orthogonal Partial Least Squares (KGOPLS), and Kernel Grouped Entropy Component Analysis (KGECA). Figure 1 shows the procedure scheme of a simple grouping approach.

Fig. 1.
figure 1

Procedure scheme of a simple grouping approach

Full size image

For a given a set of observations \( \left\{ {\left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{n} \) the grouping algorithm first compute the mean (1) and covariance matrix (2) of entries, where T denotes the transpose of a vector.

$$ \bar{x} = \frac{{\sum\limits_{i = 1}^{N} {x_{i} } }}{N} $$
(1)
$$ \hat{\sum }_{x} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {x_{i} - \bar{x}} \right)\left( {x_{i} - \bar{x}} \right)^{T} } $$
(2)

Then extended data set are sorted and collected in H groups. Then again, the procedure leads to compute the mean (3) and weighted covariance matrix (4) of grouped data when \( n_{h} \) is the number of elements in group h and H is the number of groups and N is the total number of elements.

$$ \bar{x}_{h} = \frac{1}{{n_{h} }}\sum\limits_{i = 1}^{{n_{h} }} {x_{i} } $$
(3)
$$ \hat{\sum }_{W} = \frac{{n_{h} }}{N}\sum\limits_{h = 1}^{H} {\left( {\bar{x}_{h} - \bar{x}} \right)\left( {\bar{x}_{h} - \bar{x}} \right)^{T} } $$
(4)

The last covariance is explored form the mean of groups and the total mean of elements, like Fisher discriminates analysis. The rest of algorithms are similar the conventional formulation and their extensions to nonlinear kernel based analysis. The use of unbiased covariance formula in (2) and (4) is straight forward.

Canonical Correlation Analysis is usually utilized for two underlying correlated data sets. Consider two iid sets of input data, \( x_{1} \) and \( x_{2} \). Classical CCA attempts to find the linear combination of the variables which maximize correlation between the collections. Let

$$ y_{1} = w_{1} x_{1} = \sum\limits_{j} {w_{1j} x_{1j} } $$
(5)
$$ y_{2} = w_{2} x_{2} = \sum\limits_{j} {w_{2j} x_{2j} } $$
(6)

The CCA solves problem of finding values of \( w_{1} \) and \( w_{2} \) which maximize the correlation between \( y_{1} \) and \( y_{2} \), with constrain the solutions to ensure a finite solution.

Let \( x_{1} \) have mean \( \mu_{1} ,x_{2} \) have mean \( \mu_{2} \) and \( \hat{\sum }_{11} ,\hat{\sum }_{22} ,\hat{\sum }_{12} \) are denotation of autocovariance of \( x_{1} \), autocovariance of \( x_{2} \) and covariance of \( x_{1} \) and \( x_{2} \). Then the standard statistical method lies in defining (7). Grouped CCA uses the (4) for computing the covariance of grouped data and K is calculated as (8).

$$ K = \hat{\sum }_{11}^{{ - \frac{1}{2}}} \hat{\sum }_{12} \hat{\sum }_{22}^{{ - \frac{1}{2}}} $$
(7)
$$ K = \hat{\sum }_{W11}^{{ - \frac{1}{2}}} \hat{\sum }_{W12} \hat{\sum }_{W22}^{{ - \frac{1}{2}}} $$
(8)

GCCA then performs a Singular Value Decomposition of K to get

$$ K = \left( {\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{k} } \right)D\left( {\beta_{1} ,\beta_{2} , \ldots ,\beta_{k} } \right)^{T} $$
(9)

where \( \alpha_{i} \) and \( \beta_{i} \) are the eigenvectors of Karush–Kuhn–Tucker (KKT) conditions and Tucker-Karush (KTK) conditions respectively and D is the diagonal matrix of eigenvalues.

The first canonical correlation vectors are given by (10) and (11) and in Grouped CCA the canonical correlation vectors are derived from (12) and (13).

$$ w_{1} = \hat{\sum }_{11}^{{ - \frac{1}{2}}} \alpha_{1} $$
(10)
$$ w_{2} = \hat{\sum }_{22}^{{ - \frac{1}{2}}} \beta_{1} $$
(11)
$$ w_{1} = \hat{\sum }_{W11}^{{ - \frac{1}{2}}} \alpha_{1} $$
(12)
$$ w_{2} = \hat{\sum }_{W22}^{{ - \frac{1}{2}}} \beta_{1} $$
(13)

As an extension of Grouped CCA, the data were transformed to the feature space by nonlinear kernel methods. Kernel methods are a recent innovation predicated on the methods developed for Support Vector Machines [9, 10]. Support Vector Classification (SVC) performs a nonlinear mapping of the data set into some high dimensional feature space. The most common unsupervised kernel method to date has been Kernel Principal Component Analysis [18, 19]. Consider mapping the input data to a high dimensional (perhaps infinite dimensional) feature space. Now the covariance matrices in Feature space are defined by (14) for i = 1, 2 and covariance matrices of grouped data are by (15) where \( \Phi \left( . \right) \) is the nonlinear one-to-one and onto function.

$$ \hat{\sum }_{\varPhi ij} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\Phi \left( {x_{i} } \right) -\Phi \left( {\bar{x}} \right)} \right)\left( {\Phi \left( {x_{j} } \right) -\Phi \left( {\bar{x}} \right)} \right)^{T} } $$
(14)
$$ \hat{\sum }_{W\varPhi ij} = \frac{{n_{h} }}{N}\sum\limits_{h = 1}^{H} {\left( {\Phi \left( {\bar{x}_{ih} } \right) -\Phi \left( {\bar{x}} \right)} \right)\left( {\Phi \left( {\bar{x}_{jh} } \right) -\Phi \left( {\bar{x}} \right)} \right)^{T} } $$
(15)

However the kernel methods adopt a different approach. \( w_{1} \) and \( w_{2} \) exist in the feature space and therefore can be expressed as

$$ w_{1} = \sum\limits_{i = 1}^{2} {\sum\limits_{j = 1}^{M} {\alpha_{ij}\Phi \left( {x_{ij} } \right)} } $$
(16)
$$ w_{2} = \sum\limits_{i = 1}^{2} {\sum\limits_{j = 1}^{M} {\beta_{ij}\Phi \left( {x_{ij} } \right)} } $$
(17)

where \( \alpha_{i} \) and \( \beta_{i} \) are the eigenvectors of SVD of \( K = {\hat{\sum\nolimits}}_{{\Phi 11}}^{{ - \frac{1}{2}}} {\hat{\sum\nolimits}}_{{\Phi 12}} {\hat{\sum\nolimits}}_{{\Phi 22}}^{{ - \frac{1}{2}}} \) Karush–Kuhn–Tucker conditions and Tucker-Karush conditions respectively for KCCA and \( \alpha_{i} \) and \( \beta_{i} \) are the eigenvectors of SVD of \( K = {\hat{\sum\nolimits}}_{{W\Phi 11}}^{{ - \frac{1}{2}}} {\hat{\sum\nolimits}}_{{W\Phi 12}} {\hat{\sum\nolimits}}_{{W\Phi 22}}^{{ - \frac{1}{2}}} \) KKT and KTK conditions respectively for KGCCA where \( K = \left( {\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{k} } \right)D\left( {\beta_{1} ,\beta_{2} , \ldots ,\beta_{k} } \right)^{T} \) and D is the diagonal matrix of eigenvalues. The rest of Kernel Grouped CCA procedure is similar to KCCA method.

This paper implements several MVA methods such as PCA, PLS, CCA, OPLS, MNF and ECA in linear, kernel and kernel grouped manners. Tables 1, 2 and 3 are summarizing maximization target, Constraints and number of feature of different methods for linear, kernel and kernel grouped approaches where \( r\left( A \right) \) returns the rank of the matrix A.

Table 1. Summary of linear MVA methods
Full size table
Table 2. Summary of kernel MVA methods
Full size table
Table 3. Summary of kernel grouped MVA methods
Full size table

Figure 2 shows the projections obtained in the toy problem by linear and modified kernel based MVA methods. Input data was normalized to zero mean and unit variance. Figure 2 shows the features extracted by different MVA methods [20] in an artificial two-class problem using the RBF kernel. Table 1 provides a summary of the MVA methods and Tables 2 and 3 summarized the kernel MVA and KGMVA methods. For each method it is stated the objective to maximize (First row), constraints for the optimization (second row), and maximum number of features (last row).

Fig. 2.
figure 2

Score of various linear MVA, kernel based MVA and kernel grouped MVA methods

Full size image
Fig. 3.
figure 3

Feature extraction methods: PCA, PLS, OPLS, CCA, MNF, KGPCA, KGPLS, KGOPLS, KGCCA, KGMNF and KGECA, Train Sample = 16

Full size image
Fig. 4.
figure 4

Feature extraction methods: PCA, PLS, OPLS, CCA, MNF, KGPCA, KGPLS, KGOPLS, KGCCA, KGMNF and KGECA, Train Sample = 144

Full size image

3 Experimental Results

Following the kernel grouped dimension reduction schemes proposed in Sect. 2, the performance of the KGMVA methods is compared with a standard SVM with no feature reduction kernel, on AVIRIS dataset. False color composition of the AVIRIS Indian Pines scene and Ground truth-map containing 16 mutually exclusive land-cover classes are showed in Fig. 5.

Fig. 5.
figure 5

(Up-Right) False color composition of the AVIRIS Indian Pines scene. (Up-Left) Ground truth-map containing 16 mutually exclusive land-cover classes, (Down-Right) standard SVM, average accuracy = 72.93 % and (Down-Left) SVM with kernel grouped MVA, average accuracy = 79.97, for 64 train samples, 10 classes.

Full size image

The AVIRIS hyperspectral dataset is illustrative of the problem of hyperspectral image analysis to determine land use. However the AVIRIS sensor collects nominally 224 bands (or images) of data, four of these contain only zeros and so are discarded, leaving 220 bands in the 92AV3C dataset. At special frequencies, the spectral images are kenned to be adversely affected by atmospheric dihydrogen monoxide absorption. This affects some 20 bands. Each image is of size 145*145 pixels. The dataset was collected over a test site called Indian Pine in north-western Indiana [1]. The database is accompanied by a reference map; signify partial ground truth, whereby pixels are labeled as belonging to one of 16 classes of vegetation or other land types. Not all pixels are so labeled, presumably because they correspond to uninteresting regions or were too arduous to label. Here, we concentrate on the performance of kernel based grouped MVA methods for classification of hyperspectral images. Experimental results are showed in Figs. 3 and 4, for various numbers of train samples and for supervise and unsupervised methods. We use class 2 and 3 for data samples.

Overall accuracy as a performance measure is depicted v.s. number of prediction for various feature extraction methods such PCA, PLS, OPLS, CCA, MNF, KGPCA, KGPLS, KGOPLS, KGCCA, KGMNF and KGECA. Simulations were repeated for 16 train samples and 144 train samples. Figure 6 shows the average accuracy of different classification approaches, Indiana dataset.

Fig. 6.
figure 6

Average accuracy of different classification approaches, Indiana dataset, 10 classes, 64 train samples. 1. C-SVC, Linear Kernel, 72.93 %, 2. nu-SVC, Linear Kernel, 73.08 %, 3. C-SVC, Polynomial Kernel, 20.84 %, 4. nu-SVC, Polynomial Kernel, 70.52 %, 5. C-SVC, RBF Kernel, 47.10 %, 6. nu-SVC, RBF Kernel, 75.33 %, 7. C-SVC, Sigmoid Kernel, 41.70 %, 8. nu-SVC, Sigmoid Kernel, 50.46 %, 9. Grouped SVM, Linear Kernel, 71.17 %, 10. Grouped SVM, RBF Kernel, 77.74 %, 11. Kernel Grouped SVM, Linear Kernel, 69.89 %, 12. Kernel Grouped SVM, RBF Kernel, 79.97 %, 13. PCA + Grouped SVM, Linear Kernel, 71.17 %, 14. PCA + Grouped SVM, RBF Kernel, 77.74 %, 15. PCA + Kernel Grouped SVM, Linear Kernel, 37.47 %, 16. PCA + Kernel Grouped SVM, RBF Kernel, 37.69 %, 17. KFDA, Linear Kernel, 71.08 %, 18. KFDA, Diagonal Linear Kernel, 45.01 %, 19. KMVA + FDA, Gaussian Kernel, 59.20 %

Full size image

Classification among the major classes can be very difficult [21], which has made the scene a challenging benchmark to validate classification precision of hyperspectral imaging algorithms. Simulations results verified that utilizing the proposed techniques improve the overall accuracy especially kernel grouped CCA in spite of CCA.

4 Discussions and Conclusions

Feature extraction and dimensionality reduction are dominant tasks in many fields of science dealing with signal processing and analysis. This paper provides a kernel based grouped MVA methods. To illustrate the wide applicability of these methods in classification program, we analyze their performance in a benchmark of general available data set, and pay special attention to real applications involving hyperspectral satellite images. In this paper, we have proposed an novel dimension reduction methods for hyperspectral image utilizing kernels and grouping methods. Experimental results showed that, at least for the AVIRIS dataset, the classification performance can be improve to some extent by utilizing either kernel grouped canonical correlation analysis or kernel grouped entropy component analysis. Further work could explore the possibility of localizing grouped of analysis and exploring the algorithms on multiclass datasets. The KGMVA methods were shown to find correlations greater than could be found by linear MVA and also kernel based MVA. However the kernel grouping approach seems to offer a new means of finding such nonlinear and non-stationary correlations and one which is very promising for future research.