1 Introduction

The paper focuses on the exact modal analysis of a sigmoid functionally graded (S-FGM) rectangular plate resting on Winkler–Pasternak foundation by using the dynamic stiffness method (DSM). The present study is of practical relevance as the functionally graded material is now considered to be an advanced class of material used mainly in the design of structural components that are subjected to thermo-mechanical loads. In the design of weight-sensitive structures in aerospace, naval, automotive, and other allied industries, the use of both laminated composite material and functionally graded materials is almost inevitable as they provide superior strength and stiffness properties in comparison with other conventional materials. However, laminated structures often experience issues related to debonding and the development of residual stresses at the interfaces, which eventually leads to the initiation of cracks within the material. To overcome the issue of debonding, the idea of functionally graded material (FGM) had been conceived [1]. In general, FGM plates are produced by proper mixing of metal and ceramic constituents, effectively eliminating the concept of discrete layers in laminates [2], which eventually produces a smooth variation of mechanical properties along the preferred direction [3, 4]. The metal constituents possess superior strength and fracture resistance, whereas ceramic constituents provide high thermal resistance [5]. Furthermore, it offers the added benefit of tailoring the material properties for specific requirements [6]. Due to superior mechanical, electrical, and thermal properties over traditional materials, the structures made of functionally graded material have found their usages in many industrial applications [7]. When operated in external environments, these FGM structures are subjected to severe conditions resulting in excessive noise and vibration. Therefore, the vibration characteristics of FGM materials must be thoroughly studied in order to design the structure properly.

Several micromechanical models based on power-law function (P-FGM) [8,9,10,11], sigmoid function (S-FGM) [12,13,14], and exponential function (E-FGM) [15, 16] are proposed for the estimation of spatial distribution of material constituents along the thickness direction of the FGM plate. Based on these mathematical functions, the effective material properties are determined. A thorough literature study reveals that the static and dynamic analysis of FGM plates based on the power-law micromechanical model is quite significant in number, whereas very few literature are available that carried out the analysis of FGM plate based on the sigmoid micromechanical model. In the sigmoid micromechanical model, the volume fraction is defined using two power-law functions, one from the middle surface to the top surface and other from the bottom surface to the middle surface. The separate functions for the distribution of the volume fraction in each half of the plate ensure the smooth distribution of interfacial stresses and make it more applicable for layered FGM [17] structures. Note that a study of free vibration behavior of S-FGM plate using a classical plate theory (CPT)-based dynamic stiffness method has been attempted by Chauhan et al. in their recent paper [18]. However, a careful analysis reveals that the formulation presented in that paper is inappropriate and the reported numerical results for S-FGM plates are incorrect. In this context, the main objectives of the present study are twofold: (i) To highlight possible mistakes in the CPT-based dynamic stiffness (DS) formulation in recent work of Chauhan et al. [18], and (ii) to present correct results using the dynamic stiffness formulations based on both CPT and FSDT, i.e., the higher-order shear deformation theory. Using the FSDT, the present work advances the previously published work [18], which includes the DS matrix formulation applicable to thicker S-FGM plates by incorporating the important effects of transverse shear deformation and rotatory inertia.

Therefore, the main focus of the present study is to study the free vibration analysis of the S-FGM plate resting on the Winkler–Pasternak foundation using both CPT- and FSDT-based dynamic stiffness method. Plates resting on elastic foundations have been used in many structural applications ranging from railroad tracks to nuclear reactors. Initially, a Winkler model for railroad interaction was developed to investigate the effect of underlying layers on plate vibration. In this model, several independent and unconnected springs are placed beneath the structure to study the effect of elastic foundation [19, 20]. However, the Winkler model does not represent a realistic situation because of the independent and unconnected springs. Later, in Pasternak model a shear layer is introduced to accommodate the longitudinal and lateral displacement of springs [21, 22]. In recent times, the plate supported by the Winkler–Pasternak foundation increasingly found its application in foundation engineering. Several researchers carried out the static and dynamic analysis of isotropic and orthotropic plates resting on Winkler–Pasternak foundation. Xiang [23] presented the closed-form solution of the pre-stressed simply supported plate resting on elastic foundation. Lam et al. [24] analyzed the static and dynamic behavior of the plate using the Green function. Malekzadeh et al. [25] analyzed the free vibration of plate, having continuous thickness variation and supported on a two-parameter foundation, using a FSDT-based differential quadrature method. Baferani et al. [26] employed an analytical method for the free vibration analysis of P-FGM plate based on third-order shear deformation theory. Jung et al. [27] presented a refined higher-order shear deformation theory to analyze the vibration behavior of S-FGM plate resting on elastic foundation. There are several other studies available in the literature which deal with the vibration analysis of plates resting on elastic foundations. However, a careful survey of the past works reveals that a majority of these works adopted different numerical methods such as the finite element method and the finite strip method [28,29,30] for studying the static and dynamic behavior of elastically supported plates. It must be noted that these numerical methods require a large mesh size for the convergence of solutions, which in turn increases the computational cost. Furthermore, these methods provide an approximate solution, especially at higher frequencies, due to several assumptions made en route to the solution. On the contrary, the dynamic stiffness method can be adopted as a solution methodology to obtain very accurate solutions with reasonable computational time [31,32,33,34] and this method is the primary focus of the present work. DSM utilizes the closed-form solutions of the governing differential equation while maintaining the accuracy and exactness of the result as opposed to FEM [35, 36].

In a nutshell, this study presents an exact dynamic stiffness matrix formulations based on both CPT and FSDT and discusses the free vibration results for the elastically supported S-FGM plates in detail. The dynamic stiffness matrix is derived for a Levy-type plate, where two opposite edges are simply supported. It must be noted here that the CPT-based DS matrix formulation presented in the recent work of Chauhan et al. [18] is inappropriate, and it leads to incorrect frequency results for the S-FGM plates resting on elastic foundations. Therefore, the present work should be treated as a correction to the work of Chauhan et al. [18] to apply the dynamic stiffness method for the free vibration analysis of elastically supported S-FGM plates. Over and above, the present study further enriches the existing literature by introducing a FSDT-based dynamic stiffness formulation, for the elastically supported S-FGM plates, which has broader applications than the CPT-based formulation. Thus, the novelty of the present study lies in presenting, first time in the literature, mathematically correct dynamic stiffness formulations based on both CPT and FSDT for the free vibration analysis of FGM plates resting on Winkler–Pasternak elastic foundation. By implementing the exact DSM formulations, very accurate frequency results are obtained for various values of geometric and stiffness parameters of the elastically supported FGM plates and these results can serve as benchmark for any future comparative studies.

2 Scope and contributions of the present work

As discussed earlier, in this work, exact dynamic stiffness formulations based on both CPT and FSDT are presented for the free vibration analysis of S-FGM plate resting on Winkler–Pasternak foundation. The governing differential equations and the boundary conditions are derived using Hamilton’s principle. Assuming Levy-type BCs, a system of linear differential equations is obtained, which leads to the formation of the dynamic stiffness matrix for a plate element. These element stiffness matrices are properly assembled to form the frequency-dependent global dynamic stiffness matrix, which is solved by employing well-known Wittrick–Williams algorithm [37, 38]. Based on the feature of the Sturm sequence, the Wittrick–Williams algorithm makes sure that all the natural frequencies within a given frequency range are computed without missing any single frequency. Using this DSM approach, parametric studies have been carried out to obtain the natural frequencies of S-FGM plate resting on elastic foundation by varying geometrical and stiffness parameters of the plate. In short, the key contributions of the present work can be listed as follows:

  • For the first time in the literature, separate dynamic stiffness matrix formulations based on the kinematic variables of CPT and FSDT are presented for the S-FGM plate resting on Winkler–Pasternak foundation.

  • Due to the transcendental nature of the dynamic stiffness matrix, Wittrick–Williams algorithm is employed in the present work for the accurate computation of natural frequencies for the elastically supported S-FGM plate.

  • Some incorrect frequency results in the published literature [18] are highlighted. The possible reasons for the incorrectness are also discussed in detail.

  • New set of results are obtained for both uniform and non-uniform S-FGM plate resting on elastic foundation by varying different plate parameters and elastic foundation coefficients. These results are presented in both tabulated and graphical forms, and a number of important conclusions are drawn.

With this note, the mathematical details for the DSM formulation are presented below for the vibration analysis of S-FGM plate resting on elastic foundation.

3 Materials and method

In this section, material property variations within the S-FGM plate are described followed by the detailed mathematical formulation for both CPT- and FSDT-based dynamic stiffness approach.

3.1 The plate geometry and the material property description

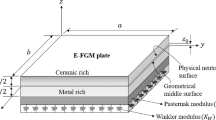
The length, width, and thickness of the functionally graded rectangular plate element, as shown in Fig. 1, are L, b, and h, respectively. As mentioned earlier, the functionally graded materials are made up by varying volume fraction of the material constituents along the thickness direction which also causes change in mechanical properties of the plate. In this study, the idealized mathematical model termed as sigmoid law (S-FGM) has been used to describe the variation of material properties in the thickness direction of the plate.

Fig. 1
figure 1

A functionally graded rectangular plate element supported on elastic foundation showing both the geometric midsurface and the physical neutral surface

Full size image

The volume fractions of the material constituents along the thickness direction in S-FGM plate are defined as:

$$\begin{aligned} \begin{array}{ll} V_t(z) =1-\frac{1}{2}\left( \frac{h-2z}{h}\right) ^p; &{} \quad \text {for } 0\le z\le h/2\\ V_b(z) =\frac{1}{2}\left( \frac{h+2z}{h}\right) ^p; &{} \quad \text {for } -h/2\le z\le 0 \end{array} \end{aligned}$$
(1)

Here, \(0\le p \le \infty \) is a parameter, known as sigmoid-function exponent (or sigmoid volume fraction index), and determines the proportion of ceramic and metal in the thickness direction of the plate. The material constituents vary as one proceeds from bottom to top of the plate. As a function of z-coordinate, the equivalent material properties are calculated using the rule of mixture:

$$\begin{aligned} \begin{array}{ll} X_1(z) =V_t(z)X_c+[1-V_t(z)]X_m; &{} \quad \text {for } 0\le z\le h/2\\ X_2(z) =V_b(z)X_c+[1-V_b(z)]X_m; &{} \quad \text {for } -h/2\le z\le 0 \end{array} \end{aligned}$$
(2)

Here, \(X_c\) and \(X_m\) refer to the material property (e.g., Young’s modulus (E), density (\(\rho \)), Poisson’s ratio (\(\mu \)), etc.) values of the pure ceramic and pure metal, respectively. Interestingly, the behavior of the plate changes from homogeneous isotropic to bimetallic plate as the value of p increases from 0 to \(\infty \). The homogeneous isotropic plate will take the average property of the material constituents, whereas the bimetallic plate consists of ceramic constituent at the top half and metallic counterparts at the bottom half.

3.2 Governing equations derivation

Hamilton’s principle is used for the derivation of the governing equations and the natural BCs, which is expressed as:

$$\begin{aligned} \delta \int _{t_1}^{t_2}(T-P-V_{ef})\textrm{d}t=0. \end{aligned}$$
(3)

Here, T stands for the kinetic energy and expressed as

$$\begin{aligned} T=\frac{1}{2}\int _{A}\int _{z}\rho ({\dot{u}}^2+{\dot{v}}^2+{\dot{w}}^2)\textrm{d}z\textrm{d}A, \end{aligned}$$
(4)

where \(\rho \) represents the equivalent mass density (see Eq. (2)) of the plate, and \((^{.})\) denotes the time derivative. In Eq. (3), P denotes the potential energy which is expressed as

$$\begin{aligned} P=\frac{1}{2}\int _A \int _{z}{\sigma }^{T}\varepsilon \textrm{d}z\textrm{d}A, \end{aligned}$$
(5)

where

$$\begin{aligned} \sigma ^{T}=[\sigma _{xx}{~}\sigma _{yy}{~}\sigma _{xy}{~}\sigma _{yz}{~}\sigma _{xz}]{~}\text {and}{~} \varepsilon ^{T}=[\varepsilon _{xx}{~}\varepsilon _{yy}{~}\gamma _{xy}{~}\gamma _{yz}{~}\gamma _{xz}]. \end{aligned}$$
(6)

The stress–strain constitutive relation used for the development of governing differential equation and natural boundary conditions is mentioned in Appendix A. In Eq. (3), \(V_{ef}\) represents the potential energy associated with the presence of elastic foundation and expressed as:

$$\begin{aligned} \begin{aligned} V_{ef}=\frac{1}{2}\int _A \int _{z}\left( k_ww^2+k_p\left( \left( \frac{\partial {w}}{\partial {x}}\right) ^2+\left( \frac{\partial {w}}{\partial {y}}\right) ^2\right) \right) \textrm{d}z\textrm{d}A, \end{aligned} \end{aligned}$$
(7)

where \(k_w\) and \(k_p\) are the Winkler and Pasternak stiffness coefficients of the elastic foundation, respectively.

In the subsequent sections, the formulations considering the displacement field based on CPT and FSDT are discussed. First, the dynamic stiffness matrix is developed considering the kinematic variables according to CPT and subsequently for FSDT. Figure 2 shows the notations and sign conventions used for the displacement and force components within the plate in a Cartesian coordinate system. For mathematical simplicity, without compromising on the correctness of the method, the concept of physical neutral surface is used for defining the displacement components.

Fig. 2
figure 2

a Displacement field variable and rotation within the plate element. b Notation and the direction used for the forces and moments

Full size image

3.3 Concept of physical neutral surface

Due to the variation in the material stiffness along the thickness direction, the transverse motion and the in-plane displacements are, in general, coupled in FGM plate [39], which increases the complexity of the dynamic stiffness formulation. Abrate [40] observed that by aptly shifting the reference plane from plate’s mid-surface to a new reference surface known as physical neutral surface [41], the stretching-bending coupling in the FGM plate can be avoided. The physical neutral surface position, defined by \(z_{\text {pns}}=z-z_0\) [39], is determined by using the concept that the resultant force in the axial direction is zero. Here, \(z_0\) is the distance between the plate’s geometric mid-surface and the physical neutral surface (see Fig. 1). It can be shown that the net axial force will be zero when the first moment of the material stiffness (i.e., Young’s modulus) about the reference surface is zero. Mathematically, we write

$$\begin{aligned} \begin{aligned} \int _{-h/2-z_0}^{h/2-z_0} z_{\text {pns}}E(z_{\text {pns}})\textrm{d}z_{\text {pns}}=\int _{-h/2}^{h/2}(z-z_0)E(z)\textrm{d}z=0, \end{aligned} \end{aligned}$$
(8)

which leads to,

$$\begin{aligned} \begin{aligned} z_{0}&=\frac{\int _{-h/2}^{h/2}E(z)z\textrm{d}z}{\int _{-h/2}^{h/2}E(z)\textrm{d}z} =\frac{\int _{0}^{h/2}E_1(z)z\textrm{d}z+\int _{-h/2}^{0}E_2(z)z\textrm{d}z}{\int _{0}^{h/2}E_1(z)\textrm{d}z+\int _{-h/2}^{0}E_2(z)\textrm{d}z}\\&=\frac{h(E_c-E_m)}{2(E_c+E_m)}\left[ \frac{1}{2}-\frac{1}{(p+1)(p+2)}\right] \end{aligned} \end{aligned}$$
(9)

3.4 Development of dynamic stiffness matrix based on classical plate theory (CPT)

Taking reference at the physical neutral surface, the displacement field based on the classical plate theory is expressed as:

$$\begin{aligned} \begin{aligned} u&= -z_{\text {pns}}\frac{\partial {w_0}}{\partial {x}}&= -(z-z_0)\frac{\partial {w_0}}{\partial {x}}\\ v&= -z_{\text {pns}}\frac{\partial {w_0}}{\partial {y}}&= -(z-z_0)\frac{\partial {w_0}}{\partial {y}} \\ w&=w_0(x,y,t) \end{aligned} \end{aligned}$$
(10)

Applying the Hamilton’s principle, as described in Sect. 3.2, the governing differential equation is developed for the S-FGM plate resting on elastic foundation as

$$\begin{aligned} D_{\text {sfgm}}(w_{0,xxxx}+2w_{0,xxyy}+w_{0,yyyy})+I_0{\ddot{w}}_0+k_ww_0-k_p(w_{0,xx}+w_{0,yy})=0 \end{aligned}$$
(11)

The natural boundary conditions are:

$$\begin{aligned} \begin{aligned} V_x&:[-D_{\text {sfgm}}(w_{0,xxx}+(2-\mu )w_{0,xyy})+k_p w_{0,x}]\delta {w}\\ M_{xx}&:-D_{\text {sfgm}}(w_{0,xx}+\mu w_{0,yy})\delta {\phi _y} \end{aligned} \end{aligned}$$
(12)

Here, \(D_{\text {sfgm}}\) is the flexural rigidity, and \(I_0\) is the transverse inertia of the S-FGM plate and their expressions are given in Appendix B.

The solution which satisfies the simply supported BCs at \(y=0\) and \(y=L\) is given by:

$$\begin{aligned} w_0(x,y,t)=\sum _{m=1}^{\infty }W_{m}(x)e^{i\omega t}\sin ({\alpha _{m}y}), \end{aligned}$$
(13)

where \(\alpha _m=m\pi /L; (m=1,2,.........,\infty )\). This leads to an ordinary differential equation expressed as:

$$\begin{aligned}{} & {} \frac{\textrm{d}^4W_m(x)}{\textrm{d}x^4}\!-\!\left( 2\alpha _m^2+\frac{k_p}{D_{\text {sfgm}}}\right) \frac{\textrm{d}^2W_m(x)}{\textrm{d}x^2}\!+\!\left( \alpha _m^4+\frac{k_w}{D_{\text {sfgm}}}\!-\!\frac{\alpha _m^2k_p}{D_{\text {sfgm}}}\!-\!\frac{I_0\omega ^2}{D_{\text {sfgm}}}\right) W_m(x)\!=\!0. \end{aligned}$$
(14)

Depending on the nature of the roots, two distinct cases are possible:

Case 1.

$$\begin{aligned} \left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) \ge \sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) } \end{aligned}$$
(15)

In this case, all the four roots are real \((t_{1m},-t_{1m},t_{2m},-t_{2m})\)

$$\begin{aligned} \begin{aligned} t_{1m}&=\sqrt{\left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) +\sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) }}\\ t_{2m}&=\sqrt{\left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) -\sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) }} \end{aligned} \end{aligned}$$
(16)

The solution for the case where all the roots are real is expressed as:

$$\begin{aligned} W_m(x)=A_{1m}\cosh (t_{1m}x)+A_{2m}\sinh (t_{1m}x)+A_{3m}\cosh (t_{2m}x)+A_{4m}\sinh (t_{2m}x) \end{aligned}$$
(17)

Case 2.

$$\begin{aligned} \left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) < \sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) } \end{aligned}$$
(18)

In this case, two real and imaginary roots are possible \((t_{1m},-t_{1m},it_{2m},-it_{2m})\)

$$\begin{aligned} \begin{aligned} t_{1m}&=\sqrt{\left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) +\sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) }}\\ t_{2m}&=\sqrt{-\left( \alpha _m^2+\frac{k_p}{2D_{\text {sfgm}}}\right) +\sqrt{\left( \frac{k_p^2}{4D_{\text {sfgm}}^2}+\frac{I_0\omega ^2}{D_{\text {sfgm}}}-\frac{k_w}{D_{\text {sfgm}}}\right) }} \end{aligned} \end{aligned}$$
(19)

The solution for this case is:

$$\begin{aligned} W_m(x)=A_{1m}\cosh (t_{1m}x)+A_{2m}\sinh (t_{1m}x)+A_{3m}\cos (t_{2m}x)+A_{4m}\sin (t_{2m}x) \end{aligned}$$
(20)

The dynamic stiffness matrix for case 2 is developed here. The formulation of dynamic stiffness matrix for case 1 follows exactly similar procedure, and it is omitted here. Once the displacement \(w_0\) is known, the expressions for the rotation \(\phi _y\), shear force \(V_x\), and the bending moment \(M_{xx}\) are developed. Rotation:

$$\begin{aligned} \begin{aligned} \phi _{ym}&=\Phi _{ym}\sin (\alpha _my)\\&=-[A_{1m}t_{1m}\sinh (t_{1m}x)+A_{2m}t_{1m}\cosh (t_{1m}x)-A_{3m}t_{2m}\sin (t_{2m}x)+A_{4m}t_{2m}\cos (t_{2m}x)] \end{aligned} \end{aligned}$$
(21)

Shear force:

$$\begin{aligned} \begin{aligned} V_x&=-D_{\text {sfgm}}\left( \frac{\textrm{d}^3W_{m}}{\textrm{d}x^2}+(\mu -2)\alpha _m\frac{\textrm{d}W_m}{\textrm{d}x}\right) +k_p\frac{\textrm{d}W_m}{\textrm{d}x}\\&=-D_{\text {sfgm}}\left[ A_{1m}\left( t_{1m}^3-(2-\mu )\alpha _m^2t_{1m}+\frac{k_pt_{1m}}{D_{\text {sfgm}}}\right) \sinh (t_{1m}x)\right. \\&\quad \left. +A_{2m}\left( t_{1m}^3-(2-\mu )\alpha _m^2t_{1m}+\frac{k_pt_{1m}}{D_{\text {sfgm}}}\right) \cosh (t_{1m}x)\right. \\&\quad \left. +A_{3m}\left( t_{2m}^3-(2-\mu )\alpha _m^2t_{2m}+\frac{k_pt_{2m}}{D_{\text {sfgm}}}\right) \sin (t_{2m}x)\right. \\&\quad \left. -A_{4m}\left( t_{2m}^3-(2-\mu )\alpha _m^2t_{2m}+\frac{k_pt_{2m}}{D_{\text {sfgm}}}\right) \cos (t_{2m}x)\right] \end{aligned} \end{aligned}$$
(22)

Bending moment:

$$\begin{aligned} \begin{aligned} M_{{xx}_m}(x,y)&=M_{{xx}_m}\sin (\alpha _my)\\&=-D_{\text {sfgm}}\left[ A_{1m}(t_{1m}^2-\mu \alpha _m^2)\cosh (t_{1m}x)+A_{2m}(t_{1m}^2-\mu \alpha _m^2)\sinh (t_{1m}x)\right. \\&\quad \left. -A_{3m}(t_{2m}^2+\mu \alpha _m^2)\cos (t_{2m}x)-A_{4m}(t_{2m}^2+\mu \alpha _m^2)\sin (t_{2m}x)\right] \end{aligned} \end{aligned}$$
(23)

Now, the displacement BCs are:

$$\begin{aligned} \begin{aligned} \text {At}{~}x=0:{~}W_{m}=\widetilde{W_{1}},\Phi _{y_m}={\widetilde{\Phi }}_{y_1},\\ \text {At}{~}x=b:{~}W_{m}=\widetilde{W_{2}},\Phi _{y_m}={\widetilde{\Phi }}_{y_2}. \end{aligned} \end{aligned}$$
(24)

Similarly, the force BCs:

$$\begin{aligned} \begin{aligned} \text {At } x&=0:{~}V_{xm}=-\widetilde{V_{1}},M_{{xx}_m}=-{\widetilde{M}}_{1},\\ \text {At } x&=b:{~}V_{xm}=\widetilde{V_{2}},M_{{xx}_m}={\widetilde{M}}_{2}. \end{aligned} \end{aligned}$$
(25)

Substituting Eq. (24) into Eqs. (20) and (21) yields the following matrix for the displacement components.

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\widetilde{W}}_{1}\\ {\widetilde{\Phi }}_{y_{1}}\\ {\widetilde{\Phi }}_{x_1}\\ {\widetilde{W}}_{2}\\ \end{bmatrix}= \begin{bmatrix} 1 &{} \quad 0 &{} \quad 1&{} \quad 0\\ 0 &{} \quad -t_{1m} &{} \quad 0 &{}\quad -t_{2m}\\ C_{h_1} &{} \quad S_{h_1} &{} \quad C_2 &{} \quad S_2\\ -t_{1m}S_{h_1} &{}\quad -t_{1m}C_{h_1} &{}\quad t_{2m}S_2 &{} \quad -t_{2m}C_2\\ \end{bmatrix} \begin{bmatrix} A_{1m}\\ A_{2m}\\ A_{3m}\\ A_{4m}\\ \end{bmatrix} \end{aligned} \end{aligned}$$
(26)

i.e.,

$$\begin{aligned} \varvec{\delta }_{{\textrm{e}}} ={\textbf{X}}_{{\textrm{e}}}{\textbf{A}}_{{\textrm{e}}}, \end{aligned}$$
(27)

where \(C_{h_1}=\cosh (t_{im}b)\) and \(S_{h_1}=\sinh (t_{im}b)\) with \(i=1,2\). Again, substituting Eq. (25) into Eq. (22) and (23) yields the following matrix relation for the force components.

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\widetilde{V}}_{1}\\ {\widetilde{M}}_{{xx}_{1}}\\ {\widetilde{V}}_{2}\\ {\widetilde{M}}_{{xx}_2}\\ \end{bmatrix}= \begin{bmatrix} 0 &{} \quad -R_1 &{} \quad 0 &{} \quad R_2\\ -L_1 &{} \quad 0 &{} \quad L_2 &{} \quad 0\\ R_1S_{h_1} &{} \quad R_1C_{h_1} &{} \quad R_2S_2 &{} \quad -R_2C_2\\ L_1C_{h_1} &{}\quad L_1S_{h_1} &{} \quad -L_2S_2 &{}\quad -L_2C_2\\ \end{bmatrix} \begin{bmatrix} A_{1m}\\ A_{2m}\\ A_{3m}\\ A_{4m}\\ \end{bmatrix} \end{aligned} \end{aligned}$$
(28)

i.e.,

$$\begin{aligned} {\mathbf{F_{{\textrm{e}}}}={\textbf{Y}}_{{\textrm{e}}}{\textbf{A}}_{{\textrm{e}}}}, \end{aligned}$$
(29)

where

\(R_i=-D_{\text {sfgm}}\left( t_{im}^3-(2-\mu )\alpha _m^2t_{im}+\frac{k_pt_{im}}{D_{\text {sfgm}}}\right) \) and \(L_i=-D_{\text {sfgm}}(t_{im}^2-\mu \alpha _m^2)\) with \(i=1,2\).

Finally, the dynamic stiffness matrix, \({{\textbf{K}}}_{{\textrm{e}}}\), for a single-plate element is obtained by combining Eqs. (27) and (29) as

$$\begin{aligned} {\textbf{F}}_{{\textrm{e}}}={\textbf{K}}_{{\textrm{e}}} \varvec{\delta }_{{\textrm{e}}}, \end{aligned}$$
(30)

where

$$\begin{aligned} {\textbf{K}}_{{\textrm{e}}}={\textbf{Y}}_{{\textrm{e}}}{\textbf{X}}_{{\textrm{e}}}^{-1}. \end{aligned}$$
(31)

In expanded form, one can write

$$\begin{aligned} \begin{aligned} {\textbf{K}}_{{\textrm{e}}}= \begin{bmatrix} {\widetilde{K}}_{11} &{} \quad {\widetilde{K}}_{12} &{} \quad {\widetilde{K}}_{13} &{} \quad {\widetilde{K}}_{14}\\ &{} \quad {\widetilde{K}}_{22} &{} \quad {\widetilde{K}}_{23} &{}\quad {\widetilde{K}}_{24}\\ {\textbf {Sym}} &{}\quad &{} \quad {\widetilde{K}}_{33} &{}\quad {\widetilde{K}}_{34}\\ &{} \quad &{} \quad &{} \quad {\widetilde{K}}_{44} \\ \end{bmatrix}= \begin{bmatrix} {[}{\widetilde{K}}^{{\textrm{e}}}_{tt}]_{(2*2)} &{}\quad [{\widetilde{K}}^{{\textrm{e}}}_{ts}]_{(2*2)}\\ {[}{\widetilde{K}}^{{\textrm{e}}}_{st}]_{(2*2)} &{} \quad [{\widetilde{K}}^{{\textrm{e}}}_{ss}]_{(2*2)}\\ \end{bmatrix}. \end{aligned} \end{aligned}$$
(32)

The explicit expression for each term of Eq. (32) is not mentioned here due to their larger algebraic expressions.

3.5 Development of dynamic stiffness matrix based on FSDT

Taking reference at the physical neutral surface, the kinematic variables for defining motion of the rectangular plate element are expressed according to the first-order shear deformation theory (FSDT) as [35]:

$$\begin{aligned} \begin{aligned} u&=z_{\text {pns}}\phi _y(x,y,t)=(z-z_0)\phi _y(x,y,t),\\ v&=-z_{\text {pns}}\phi _x(x,y,t)=-(z-z_0)\phi _x(x,y,t),\\ w&=w_0(x,y,t). \end{aligned} \end{aligned}$$
(33)

Here, u, v, and w denote the displacement components within the FGM plate in the respective direction, and \(\phi _x\) and \(\phi _y\) are the rotations of the transverse normals along \(y-\) and \(x-\)axis, respectively. Now, through the application of the Hamilton’s principle, the following three coupled partial differential equations for the transverse motion of the FGM plate are obtained:

$$\begin{aligned} \begin{aligned} {\widehat{A}}_s(w_{0,yy}+w_{0,xx}+\phi _{y_{,x}}-\phi _{x_{,y}})-k_ww_0+k_p(w_{0,xx}+w_{0,yy})&=I_0\ddot{w_0}\\ D_{\text {sfgm}}(\phi _{y_{,xx}}+((1-\mu )/2)\phi _{y_{,yy}}-((1+\mu )/2)\phi _{x_{,xy}})-{\widehat{A}}_s(w_{0,x}+\phi _y)&=I_2\ddot{\phi _y}\\ D_{\text {sfgm}}((1-\mu )/2)\phi _{x_{,xx}}+\phi _{x_{,yy}}-((1+\mu )/2)\phi _{y_{,xy}})+{\widehat{A}}_s(w_{0,y}-\phi _x)&=I_2\ddot{\phi _x} \end{aligned} \end{aligned}$$
(34)

The natural boundary conditions are given as:

$$\begin{aligned} \begin{aligned} Q_{x}&:{\widehat{A}}_s(w_{0,x}+\phi _y)+k_pw_{0,x},\\ M_{xx}&:D_{\text {sfgm}}(\phi _{y_{,x}}-\mu \phi _{x_{,y}})\\ M_{xy}&:D_{\text {sfgm}}((1-\mu )/2)(\phi _{x_{,x}}-\phi _{y_{,y}}) \end{aligned} \end{aligned}$$
(35)

The sign conventions used for defining the displacements and forces are shown in Fig. 2. In these equations, \(D_{\text {sfgm}}\) is the bending stiffness; \(\widehat{A_s}\) is the coefficient of extensional stiffness; \(I_{0}\) and \(I_{2}\) are the transverse and rotational inertia of the plate. Mathematical expression of the stiffness and inertia terms is provided in Appendix B.

The solution of Eqs. (34) and (35) will be expressed for Levy form of BCs, where two distinct sides of the plate at \(y=0\) and \(y=L\) are simply supported (S) and the remaining other two sides at \(x=0\) and \(x=b\) can be either clamped (C), simply supported (S), or free (F).

Solutions that automatically satisfy the Levy-type BCs, i.e., the simply supported condition at both \(y=0\) and \(y=L\) edges, are expressed as:

$$\begin{aligned} \begin{aligned} w_0(x,y,t)=\sum _{m=1}^{\infty }W_{m}(x)e^{i\omega t}\sin ({\alpha _{m}y}),\\ \phi _y(x,y,t)= \sum _{m=1}^{\infty }\Phi _{y_{m}}(x)e^{i\omega t}\sin ({\alpha _{m}y}),\\ \phi _x(x,y,t)= \sum _{m=1}^{\infty }\Phi _{x_{m}}(x)e^{i\omega t}\cos ({\alpha _{m}y}), \end{aligned} \end{aligned}$$
(36)

where \(\omega \) represents the angular frequency of the plate, and \(\alpha _m=\frac{m\pi }{L}\) with \(m=1,2,3,4,....\infty \).

Three coupled ordinary differential equations are obtained after substituting Eq. (36) into Eq. (34), and they can be expressed in matrix form as shown below:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\widehat{A}}_s(\blacktriangle ^2-\alpha _{m}^2)+I_0\omega ^2-k_w+k_p(\blacktriangle ^2-\alpha ^2) &{} {\widehat{A}}_s\blacktriangle &{} {\widehat{A}}_s\alpha _{m}\\ -{\widehat{A}}_s\blacktriangle &{} D_{\text {sfgm}} \left( \blacktriangle ^2-\left( \frac{(1-\mu )}{2}\right) \alpha _{m}^{2}\right) -{\widehat{A}}_s+I_{2}\omega ^2 &{} \frac{(1+\mu )}{2}D_{\text {sfgm}}\alpha _{m}\blacktriangle \\ {\widehat{A}}_s\alpha _{m} &{} -\frac{(1+\mu )}{2}D_{\text {sfgm}}\alpha _{m}\blacktriangle &{} D_{\text {sfgm}}\left( \frac{(1-\mu )}{2}\blacktriangle ^2-\alpha _{m}^2\right) -{\widehat{A}}_s+I_{2}\omega ^2\\ \end{bmatrix} \begin{bmatrix} W_m\\ \Phi _{y_m}\\ \Phi _{x_m}\\ \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix}, \end{aligned}\nonumber \\ \end{aligned}$$
(37)

where \(\blacktriangle =\frac{d}{dx}\) is a differential operator.

The determinant of Eq. (37) leads us to the following differential equation (Eq. (38)):

$$\begin{aligned} (\blacktriangle ^6+p_1\blacktriangle ^4+p_2\blacktriangle ^2+p_3)\ominus =0. \end{aligned}$$
(38)

Here, \(\ominus \) represents \(W_m\) or \(\Phi _{y_m}\) or \(\Phi _{x_m}\), and \(p_1\), \(p_2\), and \(p_3\) are

$$\begin{aligned} \begin{aligned} p_1&=(2\widehat{A_s}^2-D_{\text {sfgm}}(3\alpha _m^2k_p+k_w)(-1+\mu )+(I_2k_p(-3+\mu )+D_{\text {sfgm}}I_0(-1+\mu ))\omega ^2\\&\quad +\widehat{A_s}(-3\alpha _m^2D_{\text {sfgm}}(-1+\mu )-(-3+\mu )(k_p-I_2\omega ^2)))/(D_{\text {sfgm}}(\widehat{A_s}+k_p)(-1+\mu )),\\ p_2&=(\alpha _m^2D_{\text {sfgm}}^2(3\alpha _m^2k_p+2k_w)(-1+\mu )+D_{\text {sfgm}}(-2\alpha _m^2(I_2k_p(-3+\mu )+D_{\text {sfgm}}I_0(-1+\mu )\\&\quad -I_2k_w(-3+\mu ))\omega ^2+I_2(-2I_2k_p+D_{\text {sfgm}}I_0(-3+\mu ))\omega ^4-2\widehat{A_s}(2\alpha _m^2D_{\text {sfgm}}+k_p-I_2\omega ^2)\\&\quad +\widehat{A_s}(D_{\text {sfgm}}(2\alpha _m^2k_p(-3+\mu )+k_w(-3+\mu )+3\alpha _m^4D_{\text {sfgm}}(-1+\mu ))+(4I_2k_p\\&\quad -D_{\text {sfgm}}(I_0+2\alpha _m^2I_2)(-3+\mu ))\omega ^2-2I_2^2\omega ^4)))/(D_{\text {sfgm}}^2(\widehat{A_s}+k_p)(-1+\mu )),\\ p_3&=(2\widehat{A_s}+\alpha _m^2D_{\text {sfgm}}(1-\mu )-2I_2\omega ^2)((\alpha _m^2k_p+k_w-I_0\omega ^2)(\alpha _m^2D_{\text {sfgm}}-I_2\omega ^2)\\&\quad +\widehat{A_s}(\alpha _m^4D_{\text {sfgm}}+\alpha _m^2k_p+k_w-(I_0+\alpha _m^2I_2)\omega ^2)))/(D_{\text {sfgm}}^2(\widehat{A_s}+k_p)(-1+\mu )). \end{aligned} \end{aligned}$$
(39)

Substituting a trial solution in form of \(e^{\delta }\) in Eq. (38), the following auxiliary equation is obtained.

$$\begin{aligned} \delta ^6+p_1\delta ^4+p_2\delta ^2+p_3=0. \end{aligned}$$
(40)

Again, substituting \(\eta =\delta ^2\) into Eq. (40) reduces it into a cubic polynomial.

$$\begin{aligned} \eta ^3+p_1\eta ^2+p_2\eta +p_3=0. \end{aligned}$$
(41)

The three roots of Eq. (41) are given by

$$\begin{aligned} \begin{aligned} \eta _{1}&=-\frac{1}{3}\left( p_1+\root 3 \of {\frac{t_1+\sqrt{t_2}}{2}}+\root 3 \of {\frac{t_1-\sqrt{t_2}}{2}}{~} \right) ,\\ \eta _{2}&=-\frac{1}{3}\left( p_1+\zeta _2\root 3 \of {\frac{t_1+\sqrt{t_2}}{2}}+\zeta _1\root 3 \of {\frac{t_1-\sqrt{t_2}}{2}}{~}\right) ,\\ \eta _{3}&=-\frac{1}{3}\left( p_1+\zeta _1\root 3 \of {\frac{t_1+\sqrt{t_2}}{2}}+\zeta _2\root 3 \of {\frac{t_1-\sqrt{t_2}}{2}}\right) ,\\ \end{aligned} \end{aligned}$$
(42)

with,

$$\begin{aligned} \begin{aligned} \zeta _1&=\frac{i\sqrt{3}-1}{2},{~~~~~}\zeta _2=-\frac{i\sqrt{3}+1}{2}\\ t_1&=2p_1^3-9p_1p_2+27p_3,{~} t_2=t_1^2-4f^3,{~} f=p_1^2-3p_2. \end{aligned} \end{aligned}$$
(43)

Now, the solution of the system of the ordinary differential equations can be written as

$$\begin{aligned} \begin{aligned} W_{m}(x)&=F_{1}e^{m_1x}+F_{2}e^{-m_1x}+F_{3}e^{m_2x}+F_{4}e^{-m_2x}+F_{5}e^{m_3x}+F_{6}e^{-m_3x}\\ \Phi _{y_{m}}(x)&=G_{1}e^{m_1x}+G_{2}e^{-m_1x}+G_{3}e^{m_2x}+G_{4}e^{-m_2x}+G_{5}e^{m_3x}+G_{6}e^{-m_3x}\\ \Phi _{x_{m}}(x)&=H_{1}e^{m_1x}+H_{2}e^{-m_1x}+H_{3}e^{m_2x}+H_{4}e^{-m_2x}+H_{5}e^{m_3x}+H_{6}e^{-m_3x}. \end{aligned} \end{aligned}$$
(44)

where \(m_i=\sqrt{\eta _i}\), and \(F_{1}-F_{6}\), \(G_{1}-G_{6}\), \(H_{1}-H_{6}\) are integration constants. These constants are interrelated to each other, and the relation among the constants is found by substituting Eq. (44) into Eq. (37). Simultaneously, solving all the equations and equating each of the term to zero yields the equation in terms of one set of constants, i.e., \((G_1-G_6)\). The relation between constants is expressed as:

$$\begin{aligned} \begin{aligned} F_{1}&=\Lambda _{1}G_{1},{~~}F_{2}&=-\Lambda _{1}G_{2},{~~}H_{1}&=\Gamma _{1}G_{1},{~~}H_{2}&=-\Gamma _{1}G_{2},\\ F_{3}&=\Lambda _{2}G_{3},{~~}F_{4}&=-\Lambda _{2}G_{4},{~~}H_{3}&=\Gamma _{2}G_{3},{~~}H_{4}&=-\Gamma _{2}G_{4},\\ F_{5}&=\Lambda _{3}G_{5},{~~}F_{6}&=-\Lambda _{3}G_{6},{~~}H_{5}&=\Gamma _{3}G_{5},{~~}H_{6}&=-\Gamma _{3}G_{6}, \end{aligned} \end{aligned}$$
(45)

The extended expressions of \(\Lambda _i\) and \(\Gamma _i\) in terms of material properties are given in Appendix C. Once the relation among the constants (Eq. (45)) is found, the solutions of the system of ordinary differential equation, i.e., Eq. (44), can only be expressed in terms of six integral constants. The solutions in terms of only six integral constant can be expressed as:

$$\begin{aligned} \begin{aligned} W_{m}(x)&=\Lambda _{1}G_{1}e^{m_1x}-\Lambda _{1}G_{2}e^{-m_1x}+\Lambda _{2}G_{3}e^{m_2x}-\Lambda _{2}G_{4}e^{-m_2x}+\Lambda _{3}G_{5}e^{m_3x}-\Lambda _{3}G_{6}e^{-m_3x},\\ \Phi _{y_m}(x)&=G_{1}e^{m_1x}+G_{2}e^{-m_1x}+G_{3}e^{m_2x}+G_{4}e^{-m_2x}+G_{5}e^{m_3x}+G_{6}e^{-m_3x},\\ \Phi _{x_m}(x)&=\Gamma _{1}G_{1}e^{m_1x}-\Gamma _{1}G_{2}e^{-m_1x}+\Gamma _{2}G_{3}e^{m_2x}-\Gamma _{2}G_{4}e^{-m_2x}+\Gamma _{3}G_{5}e^{m_3x}-\Gamma _{3}G_{6}e^{-m_3x}, \end{aligned} \end{aligned}$$
(46)

Similarly, the expression for forces and moments is found by substituting Eqs. (36) and (46) into Eq. (35). Thus, we get

$$\begin{aligned} \begin{aligned} Q_{x_m}(x,y)&=Q_{x_m}(x)\sin (\alpha _{m}y)\\&=(\Lambda _{1}m_{1}(\widehat{A_s}+k_p)+\widehat{A_s})G_{1}e^{m_{1}x}+(\Lambda _{1}m_{1}(\widehat{A_s}+k_p)+\widehat{A_s})G_{2}e^{-m_{1}x}+(\Lambda _{2}m_{2}(\widehat{A_s}+k_p)\\ {}&\quad +\widehat{A_s})G_{3}e^{m_2x}+(\Lambda _{2}m_{2}(\widehat{A_s}+k_p)+\widehat{A_s})G_{4}e^{-m_2x}+(\Lambda _{3}m_{3}(\widehat{A_s}+k_p)+\widehat{A_s})G_{5}e^{m_3x}\\ {}&\quad +(\Lambda _{3}m_{3}(\widehat{A_s}+k_p)+\widehat{A_s})G_{6}e^{-m_3x})\sin (\alpha _{m}y),\\ M_{xx_m}(x,y)&=M_{xx_m}(x)\sin (\alpha _{m}y)\\&=D_{\text {sfgm}}((\mu \alpha _m\Gamma _{1}+m_{1})G_{1}e^{m_1x}-(\mu \alpha _m\Gamma _{1}+m_{1})G_{2}e^{-m_1x}+(\mu \alpha _m\Gamma _{2}+m_{2})G_{3}e^{m_2x}\\&-\quad (\mu \alpha _m\Gamma _{2}+m_{2})G_{4}e^{-m_2x}+(\mu \alpha _m\Gamma _{3}+m_{3})G_{5}e^{m_3x}-(\mu \alpha _m\Gamma _{3}+m_{3})G_{6}e^{-m_3x})\sin (\alpha _{m}y),\\ M_{xy_m}(x,y)&=M_{xy_m}(x)\cos (\alpha _{m}y)\\&=D_{\text {sfgm}}((1-\mu )/2)((\Gamma _{1}m_{1}-\alpha _{m})G_{1}e^{m_1x}+(\Gamma _{1}m_{1}-\alpha _{m})G_{2}e^{-m_1x}+(\Gamma _{2}m_{2}-\alpha _{m})G_{3}e^{m_2x}\\&\quad +(\Gamma _{2}m_{2}-\alpha _{m})G_{4}e^{-m_2x}+(\Gamma _{3}m_{3}-\alpha _{m})G_{5}e^{m_3x}+(\Gamma _{3}m_{3}-\alpha _{m})G_{6}e^{-m_3x})\cos (\alpha _{m}y). \end{aligned} \end{aligned}$$
(47)

Once the expression for displacements and forces is obtained, general BCs in terms of algebraic form are used, which can be formulated as:

$$\begin{aligned} \begin{aligned} \text {At }x=0:{~}W_{m}={\widetilde{W}}_{1},\Phi _{y_m}={\widetilde{\Phi }}_{y_1},\Phi _{x_m}={\widetilde{\Phi }}_{x_1}\\ \text {At }x=b:{~}W_{m}={\widetilde{W}}_{2},\Phi _{y_m}={\widetilde{\Phi }}_{y_2},\Phi _{x_m}={\widetilde{\Phi }}_{x_2}\\ \end{aligned} \end{aligned}$$
(48)
$$\begin{aligned} \begin{aligned} \text {At } x&=0:{~}Q_{x_m}=-{\widetilde{Q}}_1,{~}M_{xx_{m}}=-{\widetilde{M}}_{xx_{1}},{~}M_{xy_{m}}=-{\widetilde{M}}_{xy_{1}}\\ \text {At } x&=b:{~}Q_{x_m}={~}{\widetilde{Q}}_2,{~~}M_{xx_{m}}={~}{\widetilde{M}}_{xx_{2}},{~~}M_{xy_{m}}={~~}{\widetilde{M}}_{xy_{2}} \end{aligned} \end{aligned}$$
(49)

The sign convention used for denoting displacements and force components is shown in Fig. 2. By applying BCs for displacements (i.e., substitution of Eq. (48) into Eq. (46)), the following matrix relation is obtained:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\widetilde{W}}_{1}\\ {\widetilde{\Phi }}_{y_{1}}\\ {\widetilde{\Phi }}_{x_1}\\ {\widetilde{W}}_{2}\\ {\widetilde{\Phi }}_{y_{2}}\\ {\widetilde{\Phi }}_{x_2}\\ \end{bmatrix}= \begin{bmatrix} \Lambda _{1} &{} \quad -\Lambda _{1} &{} \quad \Lambda _{2}&{} \quad -\Lambda _{2} &{} \quad \Lambda _{3} &{} \quad -\Lambda _{3}\\ 1 &{} \quad 1 &{} \quad 1 &{} \quad 1 &{} \quad 1 &{} \quad 1\\ \Gamma _{1} &{} \quad -\Gamma _{1} &{} \quad \Gamma _{2}&{} \quad -\Gamma _{2} &{} \quad \Gamma _{3} &{} \quad -\Gamma _{3}\\ \Lambda _{1}e^{m_1b} &{} \quad -\Lambda _{1}e^{-m_1b} &{} \quad \Lambda _{2}e^{m_2b} &{} -\Lambda _{2}e^{-m_2b} &{} \quad \Lambda _{3}e^{m_3b} &{} -\Lambda _{3}e^{-m_3b}\\ e^{m_1b} &{} \quad e^{-m_{1}b} &{} \quad e^{m_2b} &{} \quad e^{-m_2b} &{} \quad e^{m_3b} &{} \quad e^{-m_3b}\\ \Gamma _{1}e^{m_{1}b} &{} \quad -\Gamma _{1}e^{-m_1b} &{} \quad \Gamma _{2}e^{m_2b} &{} -\Gamma _{2}e^{-m_2b} &{} \quad \Gamma _{3}e^{m_3b} &{} \quad -\Gamma _{3}e^{-m_3b}\\ \end{bmatrix} \begin{bmatrix} G_{1}\\ G_{2}\\ G_{3}\\ G_{4}\\ G_{5}\\ G_{6}\\ \end{bmatrix} \end{aligned} \end{aligned}$$
(50)

i.e.,

$$\begin{aligned} \varvec{\delta }_{{\textrm{e}}} ={\textbf{X}}_{{\textrm{e}}}{\textbf{G}}_{{\textrm{e}}}. \end{aligned}$$
(51)

By applying the force and moment BCs, (i.e., substitution of Eq. (49) into Eq. (47)), the following relationship is obtained:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\widetilde{Q}}_{x_1}\\ {\widetilde{M}}_{xx_1}\\ {\widetilde{M}}_{xy_1}\\ {\widetilde{Q}}_{x_2}\\ {\widetilde{M}}_{xx_2}\\ {\widetilde{M}}_{xy_2}\\ \end{bmatrix}= \begin{bmatrix} -X_{1} &{} \quad -X_{1} &{} \quad -X_{2} &{} \quad -X_{2}&{} \quad -X_{3} &{} \quad -X_{3}\\ -Y_{1} &{} \quad Y_{1} &{} \quad -Y_{2} &{} \quad Y_{2} &{} \quad -Y_{3} &{} \quad Y_{3}\\ -Z_{1} &{} \quad -Z_{1} &{} \quad -Z_{2} &{} \quad -Z_{2} &{} \quad -Z_{3} &{} \quad -Z_{3}\\ X_{1}e^{m_1b} &{} \quad X_{1}e^{-m_1b} &{} \quad X_{2}e^{m_2b} &{} \quad X_{2}e^{-m_2b} &{} X_{3}e^{m_3b} &{} \quad X_{3}e^{-m_3b}\\ Y_{1}e^{m_1b} &{} \quad -Y_{1}e^{-m_1b} &{} \quad Y_{2}e^{m_2b} &{} \quad -Y_{2}e^{-m_2b} &{} Y_{3}e^{m_3b} &{} \quad -Y_{3}e^{-m_3b}\\ Z_{1}e^{m_1b} &{} \quad Z_{1}e^{-m_1b} &{} \quad Z_{2}e^{m_2b} &{} \quad Z_{2}e^{-m_2b} &{} Z_{3}e^{m_3b} &{} \quad Z_{3}e^{-m_3b}\\ \end{bmatrix} \begin{bmatrix} G_{1}\\ G_{2}\\ G_{3}\\ G_{4}\\ G_{5}\\ G_{6}\\ \end{bmatrix} \end{aligned} \end{aligned}$$
(52)

i.e.,

$$\begin{aligned} {\mathbf{F_{{\textrm{e}}}}={\textbf{Y}}_{{\textrm{e}}}{\textbf{G}}_{{\textrm{e}}}}, \end{aligned}$$
(53)

where \(X_{i}=(\Lambda _{i}m_{i}(\widehat{A_s}+k_p)+\widehat{A_s})\), \(Y_{i}=D_{\text {sfgm}}(\alpha _m\mu \Gamma _{i}+m_{i})\), \(Z_{i}=D_{\text {sfgm}}((1-\mu )/2)(\Gamma _{i}m_{i}-\alpha _m)\), with \(i=1,2,3\).

Lastly, the dynamic stiffness matrix, denoted by \({{\textbf{K}}}_{\textrm{e}}\), for a single FGM plate element is derived from Eqs. (51) and (53) as

$$\begin{aligned} {\textbf{F}}_{{\textrm{e}}}={\textbf{K}}_{{\textrm{e}}} \varvec{\delta }_{{\textrm{e}}}, \end{aligned}$$
(54)

where

$$\begin{aligned} {\textbf{K}}_{{\textrm{e}}}={\textbf{Y}}_{{\textrm{e}}}{\textbf{X}}_{{\textrm{e}}}^{-1}. \end{aligned}$$
(55)

In matrix form,

$$\begin{aligned} \begin{aligned} {\textbf{K}}_{{\textrm{e}}}= \begin{bmatrix} {\hat{K}}_{11}^* &{} \quad {\hat{K}}_{12}^* &{} \quad {\hat{K}}_{13}^* &{} \quad {\hat{K}}_{14}^* &{} \quad {\hat{K}}_{15}^* &{} \quad {\hat{K}}_{16}^*\\ &{} \quad {\hat{K}}_{22}^* &{} \quad {\hat{K}}_{23}^* &{} \quad {\hat{K}}_{24}^* &{} \quad {\hat{K}}_{25}^* &{} \quad {\hat{K}}_{26}^*\\ &{} \quad &{} \quad {\hat{K}}_{33}^* &{} \quad {\hat{K}}_{34}^* &{} \quad {\hat{K}}_{35}^* &{} \quad {\hat{K}}_{36}^*\\ &{} \quad &{} \quad &{} \quad {\hat{K}}_{44}^* &{} \quad {\hat{K}}_{45}^* &{} \quad {\hat{K}}_{46}^*\\ &{} \quad {\textbf {Sym}} &{} \quad &{} \quad &{} \quad {\hat{K}}_{55}^* &{} \quad {\hat{K}}_{56}^*\\ &{} \quad &{} \quad &{} \quad &{} \quad &{} \quad {\hat{K}}_{66}^*\\ \end{bmatrix}= \begin{bmatrix} {[}\widehat{K^{{\textrm{e}}}_{tt}}]_{(3*3)} &{} \quad [\widehat{K^{{\textrm{e}}}_{ts}}]_{(3*3)}\\ {[}\widehat{K^{{\textrm{e}}}_{st}}]_{(3*3)} &{} \quad [\widehat{K^{{\textrm{e}}}_{ss}}]_{(3*3)}\\ \end{bmatrix}. \end{aligned} \end{aligned}$$
(56)

The explicit expression for each term of the symmetric dynamic stiffness matrix, \({{\mathbf{K_e}}}\), is not mentioned here due to their larger algebraic expressions.

4 Procedure for the computation of modal characteristics of S-FGM plate

It is apparent that the dynamic stiffness matrix derived above is frequency dependent and transcendental in nature. Therefore, an appropriate procedure is to be followed to compute the frequency values accurately. This section briefly discusses the procedure adopted in the present study to compute natural frequencies and mode shapes of the S-FGM plate. Appropriate boundary conditions are enforced on the global dynamic stiffness matrix, which is obtained after assembling individual dynamic stiffness matrix of the plate segment. Thereafter, the Wittrick–Williams (W–W) algorithm is used for the computation of natural frequencies of S-FGM plate.

4.1 Assembly procedure

This section discusses the procedure used in DSM to assemble the individual dynamic stiffness matrix of each plate segment to form a global dynamic stiffness matrix. The assembly procedure used in DSM is quite similar to that of the assembly procedure used in FEM. In the place of point nodes in FEM, line nodes are used in DSM. A pictorial depiction of the assembly procedure of DSM is presented in Fig. 3.

Fig. 3
figure 3

A pictorial representation of assembly process of DSM

Full size image

It should be noted that DSM results are generally mesh independent, which means that even with a single element for uniform geometry a convergent result can be obtained. In the case of non-uniform geometry, however, very few elements are required to obtain convergent results which reduces the computational cost significantly.

4.2 Application of Levy-type boundary conditions

In Levy form of BCs, two distinct sides of the FGM plate, at \(y=0\) and \(y=L\), are simply supported, whereas two remaining sides of the plate, at \(x=0\) and \(x=b\), can be either clamped (C) or simply supported (S) or free (F). In this study, the penalty method is used to apply these Levy-type boundary constraints. The penalty method allocates a large stiffness to the appropriate term of the leading diagonal of the global dynamic stiffness matrix for the purpose of neutralizing the specific degree of freedom. To be specific, following three cases are considered here.

  • For ‘Free (F)’ edge: No variable needs to be penalized.

  • For ‘Simply supported (S)’ edge: For CPT, \(W_*\) is penalized; for FSDT, \(W_*\) and \({\Phi _x}_*\) are penalized.

  • For ‘Clamped (C)’ edge: For CPT, \(W_*\), and \({\Phi _y}_*\) are penalized; for FSDT, \(W_*\), \({\Phi _y}_*\), and \({\Phi _x}_*\) are penalized.

Here, the letter \(`*\)’ signifies the line node on which the appropriate penalty is to be enforced in order to apply the required boundary constraints.

4.3 Procedure to compute natural frequencies and mode shapes

The assembled global dynamic stiffness matrix is transcendental in nature which leads to the transcendental eigenvalue problem. The well-known Wittrick–Williams algorithm [37, 38] is used to solve such a transcendental eigenvalue problem. The W–W algorithm ensures that no natural frequency, even the coincident one, is missed in a given frequency range. The procedure for the implementation of W–W algorithm and the development of modeshape is described in many previously published literature [35, 36]. Just for the sake of completeness, W–W algorithm is summarized in Fig. 4.

Fig. 4
figure 4

Wittrick–Williams algorithm for the computation of the natural frequency

Full size image

5 Results and discussion

In this section, the natural frequency results for the S-FGM plate resting on elastic foundation for various plate geometries and stiffness parameters are discussed. First, the natural frequencies obtained using DSM based on both CPT and FSDT are validated with the published results. In the subsequent section, the discrepancies in the obtained results and the published results [18] are highlighted. The possible reasons for the mismatch in these results are also discussed. Thereafter, various inferences are made for the free vibration behavior of plates using line diagrams and modeshapes plots.

For better understanding of the results, the following two non-dimensional forms for the natural frequency parameters are used in this study: \({\bar{\omega }}=\omega h\sqrt{\rho _m/E_m}\), \({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c)}\) with \(D_c=E_ch^3/(12(1-\mu ^2))\). And, the non-dimensional form for the elastic foundation parameters is used as: \(K_w=k_wb^4/D_c\) and \(K_p=k_pb^2/D_c\). The material properties considered for the constituents of S-FGM plate are mentioned in Table 1.

Table 1 The material property description of S-FGM plate, adopted from [18]
Full size table

5.1 Comparison with the published results

In this subsection, the natural frequencies results are compared with that of existing literature wherever possible. Table 2 shows the comparison of the natural frequency results of the S-FGM plate obtained using DSM to that of the results mentioned in Kumar and Jana [14]. Kumar and Jana [14] studied the free vibration behavior of the S-FGM plate using a CPT-based DSM approach. It can be seen that the CPT-based DSM computed results agree perfectly with the published results. Table 2 also contains the natural frequency results of the S-FGM plate using FSDT-based DSM. It is noted that the natural frequency results obtained using DSM based on kinematic variables of FSDT are lesser as compared to that of CPT-based DSM results. This is because FSDT includes the effect of the transverse shear deformation on the vibration of the plate, whereas CPT neglects the transverse shear effect.

Table 2 Validation study of the non-dimensional natural frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c))}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of the S-FGM plate with published result for all six BCs [14]. \((b=L, \, \, h=0.05b)\)
Full size table

For the validation of present analysis results, particularly for the case of plate resting on elastic foundation, the results reported in Baferani et al. [26] have been considered. In that reference the results are reported for FGM plate with power-law (P-FGM) material model. For comparison purposes, we also consider the same material model as given in [26] and the comparison is shown in Table 3. It can be noted that Baferani et al. [26] obtained the accurate natural frequency values of the P-FGM plate resting on Winkler–Pasternak foundation using third-order shear deformation theory. In Table 3, the DSM computed natural frequency results of the square P-FGM plate resting on elastic foundation are compared, with that available in [26], for varying plate thickness ratio (h/b), and varying elastic foundation parameters. It can be seen that the FSDT-based DSM results and the published results are in very good agreement.

Table 3 Non-dimensional fundamental frequency \(({\bar{\omega }}=\omega h\sqrt{\rho _m/E_m})\) comparison of a square P-FGM plate resting on elastic foundation for two different BCs with that of the result given in reference [26]
Full size table

Table 4 presents a comparison between the dimensionless fundamental frequency of a SSSS S-FGM plate placed on an elastic foundation and the corresponding values reported in the work of Jung et al. [27]. The comparison considers different coefficients of the elastic foundation (i.e., \(K_w\) and \(K_p\)) and volume fractions (p) of material components. The fundamental frequencies of the S-FGM plates are evaluated using DSM based on CPT and FSDT. It can be seen that the results obtained using DSM are in good agreement with the published result. As expected, it can been observed that the present CPT and FSDT-based DSM results are higher than that of the results reported in Jung et al. [27] which are based on higher-order shear deformation theory (HSDT).

Table 4 Non-dimensional fundamental frequency \(({\bar{\omega }}=\omega h\sqrt{\rho _m/E_m})\) comparison of a square S-FGM plate resting on elastic foundation with that of the result given in Jung et al. [27]
Full size table
Table 5 Comparative study of non-dimensional fundamental frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c))}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of square S-FGM plate resting on elastic foundation with that of the results mentioned in [18]
Full size table

The above three comparative studies establish that the present method has the capability to compute the natural frequency results very accurately for the FGM plates resting on Winkler–Pasternak foundation. We now proceed to highlight some incorrect results in a recently published paper and discuss the possible reasons for this incorrectness.

5.2 Comments on incorrectly published results

It is emphasized here that Chauhan et al. [18] have attempted to present a CPT-based DSM formulation for the natural frequency computation of S-FGM plate resting on the elastic foundation. However, a careful study can reveal that the mathematical formulation presented in [18], particularly for the elastic foundation cases, is inappropriate. For this reason, most of the results especially those related to the elastic foundation cases are incorrect. Hence, an attempt has been made to present the correct results through the present DSM formulation based on both CPT and FSDT. The results are reported in Table 5. From Table 5, it can be observed that the difference in the natural frequency results especially for the plate resting on the elastic foundation parameter is very high. In some cases the difference in both the CPT-based results is as high as 34%. It can be pointed out that this inaccuracy is due to the incorrect mathematical formulation presented in that paper and some of these mistakes are highlighted below.

  • The term \(k_w\frac{\partial ^2 w_0}{\partial {t}^2}\), associated with the Winkler stiffness coefficient, mentioned in Eq. (15) of reference [18] should be \(k_w w_0\) as shown in Eq. (11) of the present paper.

  • The term \(k_p(\frac{\partial ^4 w_0}{\partial {x}^2\partial {t}^2}+\frac{\partial ^4 w_0}{\partial {y}^2\partial {t}^2})\) associated with the Pasternak stiffness coefficient mentioned in Eq. (15) of reference [18] should be \(k_p(\frac{\partial ^2 w_0}{\partial {x}^2}+\frac{\partial ^2 w_0}{\partial {y}^2})\) as shown in Eq. (11) of the present paper.

  • One term associated with the elastic coefficient is missing from the natural BCs equation given in Eq. (16) of reference [18]. The correct expressions are given in Eq. (12) of this paper.

  • For Levy-type plate, the reduced governing differential equation i.e., Eq. (18) of Ref. [18] is also incorrect. The correct form of the equation is shown in Eq. (14) of the present paper.

  • Furthermore, the important inertia term is missing from the rest of the formulation (i.e., from Eq. (19) to (21)) in reference [18]. The correct mathematical expressions are provided in Sect. 3.4 of this paper.

Note that the above mistakes may not be treated as typographical errors as similar mistakes have been found in another recent paper [42] published by the same group of authors. Therefore, in this study, these mistakes in the CPT-based DSM formulation presented in reference [18] have been identified and the correct formulation is presented. For the frequency analysis of S-FGM plate, correct results are obtained using both CPT- and FSDT-based DSM formulation. Importantly, the present DSM results are validated with the available literature and they are found to be in good agreement with that of the published results.

5.3 Parametric study

This section discusses the frequency results for S-FGM plates by changing the plate geometry and stiffness parameters of the elastic foundation. Frequency results for the square S-FGM plates can be found in Table 5 for all six Levy type BCs, whereas Tables 6 and 7 show the natural frequency results of the S-FGM plate resting on elastic foundation for two different aspect ratios i.e., \(L/b = 0.5\) and \(L/b = 2\), respectively. The natural frequency results are shown for varying volume fractions of the material constituents. It can be seen that the natural frequency for the plate with higher aspect ratio \((L/b=2)\) is lesser as compared to that of the plate with smaller aspect ratio \((L/b=0.5)\) as we keep all other parameters same. The reason for this behavior is that the plate with larger dimensions offers lesser bending stiffness as compared to that of the plate with smaller dimensions. One noteworthy point is that the natural frequency results for the DSM based on FSDT are lesser as compared to the result obtained using DSM based on CPT. This trend is as per expectation as FSDT-based formulation considers the shear deformation of the plate, whereas CPT ignores the shear effect.

Table 6 The non-dimensional fundamental frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c)}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of S-FGM rectangular plate (\(L/b=0.5,\ \,h=0.05b\)) resting on elastic foundation for different BCs and varying volume fractions (n) of the material constituents
Full size table
Table 7 The non-dimensional fundamental frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c)}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of S-FGM rectangular plate (\(L/b=2,\ \,h=0.05b\)) resting on elastic foundation for different BCs and varying volume fractions (p) of the material constituents
Full size table

The effect of elastic foundation on the modeshape of the S-FGM plate can be seen from Fig. 5. Here, the modeshape for the SFSF BCs of the S-FGM plate is shown for the varying coefficients of elastic foundation. From the modeshape plots, it can be seen that the plate with shear foundation offers more bending stiffness as compared to the Winkler foundation.

Fig. 5
figure 5

Modeshapes of the SFSF square plate for varying elastic foundation parameters. \((h=0.05b, \, p=2)\)

Full size image

Figure 6 shows the plot of non-dimensional fundamental frequency with varying volume fraction of the material constituents of S-FGM plate for different elastic modulus parameters and BCs. Figure 6a shows the variation of fundamental frequency with volume fraction p of SSSS S-FGM plate for different elastic modulus coefficients. It can be seen that as the volume fraction increases, the fundamental frequency of the plate decreases. This is due to the increase in metal constituents in the plate as the volume fraction increases. Presence of higher metallic constituents leads lower bending stiffness due to its lower value of the Young’s modulus in comparison with that of the ceramic constituent. Figure 6b shows the plot of non-dimensional fundamental frequency for different Levy-type BCs with volume fraction for a plate resting on elastic foundation. It is also observed that the SCSC plate has the highest fundamental frequency and SFSF plate has the lowest.

Fig. 6
figure 6

a Plot of non-dimensional fundamental frequency \(({\tilde{\omega }})\) for different elastic modulus with varying volume fraction of SSSS plate. \((L=b,\, h=0.05b)\). b Plot of non-dimensional fundamental frequency \(({\tilde{\omega }})\) for different boundary conditions with varying volume fraction. For this case, the elastic modulus coefficient is taken as \((K_w, K_p)=(100,{10} )\). \((L=b, \, h=0.05b)\)

Full size image

Figure 7 shows the effect of elastic modulus on the fundamental frequency of a S-FGM plate for varying aspect ratios. Figure 7a shows the variation for the S-FGM plate resting on Winkler foundation, whereas Fig. 7b shows the variation for S-FGM plate resting on Pasternak foundation. It can be observed that the fundamental frequency of the S-FGM plate decreases as the size of the plate increases and this behavior is expected. We know that plate with smaller sizes provides more resistance to bending as compared to that of plate with larger dimensions. Comparison of Fig. 7a and b also shows that the influence of Pasternak foundation on the natural frequency is more as compared to the Winkler foundation. This is due to the fact that the Winkler foundation consists of independent and unconnected springs, whereas the Pasternak foundation has shear layers which exhibits both longitudinal and lateral spring effects leading to higher bending stiffness compared to the Winkler foundation.

Fig. 7
figure 7

Plot of non-dimensional fundamental frequency \(({\tilde{\omega }})\) for elastic modulus with aspect ratio (L/b). a Different Winkler elastic modulus parameter, keeping Pasternak modulus parameter constant vs aspect ratio and b different Pasternak elastic modulus parameter keeping, Winkler elastic modulus parameter constant vs aspect ratio. Here, SSSS plate is considered with \(h=0.05b, \, p=2\)

Full size image

Figure 8 shows the modeshapes for different BCs of a S-FGM plate resting on Winkler–Pasternak foundation. It can be noted that, except SFSF plate, there is no visible change in the modeshape for other BCs when one compares the modeshapes of S-FGM plate with and without the Winkler–Pasternak foundation. Modeshapes plots for all these BCs are not shown here for space constraint.

Fig. 8
figure 8

Mode shape for different BCs of square S-FGM plate resting on Winkler–Pasternak foundation. \((h=0.05b, \, K_w=100, \, K_p=100)\)

Full size image

5.4 Comparison study for different plate configurations

It can be emphasized here that the dynamic stiffness method has a potential advantage in the assembly process where dissimilar plate elements can be suitably assemble to study the vibration behavior of plate having non-uniform configurations. To this end, the present section considers two different S-FGM plate configurations as shown in Fig. 9 and present a comparative study of their free vibration characteristics. Table 8 shows the non-dimensional fundamental frequency of stepped plate without elastic foundation shown in Fig. 9a, whereas Table 9 reports the natural frequencies of the plate resting on partial elastic foundation shown in Fig. 9b. These tables show how the fundamental frequencies vary depending on the boundary conditions, thickness ratios, and various elastic foundation coefficients. The frequency results are computed using the dynamic stiffness method and are evaluated using both classical plate theory and the first-order shear deformation theory. The gradual effect of the step thickness on the fundamental frequency of the S-FGM stepped plate can be observed from Table 8, whereas the effect of the Pasternak foundation is quite noticeable as compared to the Winkler foundation in Table 9. The Pasternak foundation offers higher bending stiffness as compared to the Winkler foundation. Additionally, by comparing the data from Tables 8 and 9, it can be inferred that, when all other parameters are held constant, the frequency value for the stepped thickness \((h_2/h_1)\) is more or less comparable to that of the elastic foundation. It can also be observed that to match the frequency of the partially supported S-FGM plate with \(K_p=100\), a sufficiently higher thickness ratio \((h_2/h_1)\) is required. This is because the Pasternak foundation provides a very high bending stiffness due to the presence of shear layer which exhibits both longitudinal and transverse stiffness effects. Nevertheless, the other effects such as the decrease in fundamental frequency as the volume fraction increases, and the fact that SCSC plate has the highest frequency, while SFSF exhibits the lowest frequency, remain unchanged. The reasons behind these patterns align with explanations provided in the previous section.

Fig. 9
figure 9

Two different non-uniform plate configurations considered in this study: a stepped plate and b plate resting on partial elastic foundation

Full size image
Table 8 The non-dimensional fundamental frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c)}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of S-FGM stepped square plate for different BCs and varying volume fractions (p) of the material constituents. (\(L/b=1,\ \,h=0.05b,\ \,K_w=K_p=0\))
Full size table
Table 9 The non-dimensional fundamental frequency \(({\hat{\omega }}=\omega b^2 \sqrt{(\rho _c h/D_c)}\) with \((D_c=E_ch^3/(12(1-\mu ^2)))\) of S-FGM square plate resting on partial elastic foundation for different BCs and varying volume fractions (p) of the material constituents. (\(L/b=1,\ \,h=0.05b,\ \,b_1=b_2=0.5b\))
Full size table

Figure 10 shows the modal behavior of different configurations of the S-FGM plate. Figure 10a shows the modeshape of the uniform thickness plate without elastic foundation, while Fig. 10b showcases the modeshape of the stepped plate with \(h_2=2h_1\). Evidently, the peak of the modeshape plot of the stepped plate (i.e., Fig. 10b) has shifted to the left side the plate. This shift is attributed to the increased plate thickness, at the right half of the plate, which introduces greater resistance against bending. Figure 10c and d shows the modeshape of the uniform thickness plate resting on homogeneous and non-homogeneous elastic foundation, respectively. The effect of partial elastic foundation on the modeshape of the plate can be clearly seen in Fig. 10c where the peak of modeshape plot of the plate has been shifted toward the unsupported portion of the plate.

Fig. 10
figure 10

Modeshapes of different configurations of square S-FGM plates: a uniform plate without elastic foundation, b stepped plate without elastic foundation \((h_2=2h_1)\), c plate resting on homogeneous elastic foundation \((b_1=0.5b)\), and d plate resting on non-homogeneous elastic foundation. \((L=b,\ \, h=0.05b,\ \,p=2)\)

Full size image

6 Conclusions

This study presents the exact formulation of the dynamic stiffness matrix for the free vibration analysis of S-FGM plate supported on elastic foundation. The distribution of material properties in the thickness of the S-FGM plate is defined using two separate power-law distribution for the two half of the plate which is normally called as sigmoid-law (S-FGM) property distribution. The effective elastic properties are estimated using the rule of mixture. The dynamic stiffness method is applied for two cases where the plate kinematic variables are defined for one case using CPT and for the other case using FSDT. For both these cases, the frequency-dependent dynamic stiffness matrix gives rise to the transcendental eigenvalue problem, which is solved by using the Wittrick and Williams algorithm.

It can be emphasized that the present DSM computed results, for the S-FGM plate resting on elastic foundation, are compared with the available results and an excellent agreement has been found. One important contribution of the present study is that it points out some incorrect mathematical formulation in a recently published paper [18] and discusses all the possible mistakes in detail. It is also shown that the error in the frequency computation in that paper is as high as 34 \(\%\). Therefore, the present paper serves as correction to the work presented in [18]. The present work further enhances the previously published work by implementing a FSDT-based dynamic stiffness formulation for the elastically supported S-FGM plates. As FSDT considers the effect of transverse shear, the reported results will be applicable to thin as well as moderately thick FGM plates.

Furthermore, a thorough parametric analysis of fundamental frequencies influenced by power-law exponent, plate aspect ratios, and elastic foundation stiffness parameters is performed. From this analysis, several inferences are made using different tables and line diagrams. From the reported results, it can be seen that Pasternak foundation adds more restraint to bending compared to the Winkler foundation. This is because, unlike the Winkler model, which consists of independent and unconnected springs, the Pasternak foundation introduces a shear layer that accounts for both longitudinal and transverse spring effects. Furthermore, comparison of the two non-uniform configurations, considered in the study, shows that the introduction of stepped thickness enhances the frequency values. However, the frequency increase due to the presence of partial Pasternak foundation remains higher than that of the stepped plate as the Pasternak foundation provides a very high stiffness due to the presence of the shear layer. Lastly, it is reemphasized that, due to the exact mathematical formulation, the natural frequencies obtained using DSM are considered to be very accurate and these results can be used as a benchmark for future design purposes.