1 Introduction

Functionally graded materials (FGMs) are generally inhomogeneous metal-ceramic composites in which the material properties are continuously varying along the thickness direction from one layer to another layer and decrease the stress concentration to achieve the applicable functionality [1, 2]. The ceramic part of the FGM resists the high temperature due to the low thermal conductivity of the constituent material, and the metallic part reduces the fracture caused and increases the strength of the given material. As a result of these dynamic advantages, FGM plates are widely used in various engineering fields [3]. Some unpredictable external–internal excitations are generally subjected to the product manufacturing working conditions. Due to this, a considerable amount of noise and vibration is produced in the given product or structure. Under these operating conditions, the study of vibration behavior of FGM plates is required to be well understood for designing and manufacturing processes of structural components. As per the available literature, the mechanical property variation of FGM plates generally varies in the transverse direction by using various mathematical methods such as the power-law function, sigmoid-law function, and exponential-law function [4, 5]. The variation of the material property of FGM plates with power-law function and sigmoid-law function is well reported [4,5,6,7,8]. In the present work, an exponential law is considered for material property variation of FGM plate resting on Winkler and Pasternak elastic foundation.

The application of plates resting on elastic foundations has practical applications in mechanical and civil engineering, such as in nuclear reactors, turbo generators, the foundation of railways tracks, tanks, and impact-type machines [9]. Various researchers have projected different elastic foundation models to determine the interaction behavior between the plate and elastic foundation [10]. In this context, Winkler [11] suggested the simplest mathematical one-parameter elastic foundation model where the elastic foundation is assumed to be continuously attached to an independent spring system with no coupling effects and applied normal pressure to investigate the mechanical response of plate resting on elastic foundation. To enhance the interaction between the spring system, Pasternak [12] introduced a two-dependent parameter (normal pressure and shear layer) model and applied the interaction of the shear layer in the spring system. The presence of shear layer interaction between the spring system is achieved by connecting the ends of the springs to the plate that only takes shear deformation in the transverse direction [12]. Winkler and Pasternak mathematical models are widely implemented to construct raft foundations, railroad tracks, concrete slabs, airports, and rigid concrete pavement for highways and motorways [9, 10, 12].

Implementing the dynamic stiffness method is considered an efficient analytical method as an effective alternative to the finite element method (FEM). When comparing both the methods (DSM and FEM), the proposed dynamic stiffness method is a more accurate, reliable, and efficient solution than the FEM [7, 8]. The development of the block assembly mechanism of DSM and FEM is assumed to be exactly similar, but the difference between them is their discretization technique. In the finite element method, the assumed shape function is used for discretizing the single element structure and for generating the separate stiffness-mass matrices. In contrast, DSM implemented a frequency-dependent shape function for a single element structure and developed a single element matrix dependent on both stiffness and mass property and called a dynamic stiffness matrix [7, 8, 13]. Due to these advantages, the obtained DSM results by exact shape function are exact. In this perspective, the recognition of DSM in the last decade is continuously increased. DSM was applied for the first time in the seventies century by the well-known researcher Wittrick and Williams [14] to carry out the buckling and vibration response of isotropic–anisotropic structural components. Banerjee [15] developed dynamic stiffness matrices using a general methodology in the nineteen century and concluded that the qualitative computational time could be saved. Later on, many authors [16,17,18,19,20,21,22] applied DSM to analyze the free vibration and mode shape behavior of the isotropic and composite structures.

This continuation presents a brief review of various methodologies to carry out the natural vibration response of FGM plates resting on an elastic foundation.

Shen et al. [23] used the Rayleigh–Ritz method with Reissner–Mindlin plate theory to study four free edges plates' free and forced vibration resting on a Pasternak elastic foundation. The modal superposition procedure is considered with the Mindlin–Goodman approach to estimate the dynamic behavior of the free edge plate. Omurtag et al. [24] applied Kirchhoff plate theory with the finite element method to analyze the free vibration of the plate resting on the Winkler and Pasternak foundation. Huang et al. [25] implemented a finite strip method to estimate the static and free vibration behavior of a mixed boundary condition plate resting on the Winkler elastic foundation. Continuing previous work, Huang et al. [26] used the state space method considered with the three-dimensional theory of elasticity to estimate the free vibration motion of functionally graded plate resting on the Winkler and Pasternak elastic foundation. Amini et al. [27] applied Ritz and Chebyshev polynomial method to carry out the natural frequency of a rectangular FGM plate resting on an elastic foundation. Thai et al. [28] used higher shear deformation theory with analytical method to analysis the free vibration response of simply supported FGM plate. Xue et al. [29] used Ritz method based on classical plate theory to estimate the natural vibration behavior of the flat stiffened plate with two different boundary conditions. Atmane et al. [30] used higher deformation theory with the Navier method to estimate the free vibration response of a simply-supported FGM plate resting on the Winkler–Pasternak elastic foundation. Baferani et al. [31] applied third-order shear deformation theory with an analytical method to investigate the natural vibration response of FGM plate supported on the Winkler and Pasternak foundation. Chiker et al. [32] applied finite element method along with layer wise shear deformation theory to analyze the natural frequency of the hybrid laminated carbon nanotube reinforced composite plate. Vinh et al. [33] implemented finite element method with first-order shear deformation theory to study the free vibration response of functionally graded sandwich plates. Farid et al. [34] used the quadrature method in conjunction with trigonometric function in the transverse and longitudinal direction to carry out the free vibration response of the initially stressed FGM plate supported on the Winkler and Pasternak foundation. Thai et al. [35] applied the Navier method with refined plate theory to estimate the out-of-plate free vibration response of an FGM plate resting on a two-parameter Pasternak elastic foundation. Thai et al. [36] used the Navier method under refined plate theory to estimate in-plane free vibration of the FGM plate resting on the Pasternak foundation. Kamarian et al. [37] implemented the generalized differential quadrature method considered with a three-dimensional theory of elasticity to characterize the natural vibration behavior of the three-parameter FGM plate structure resting on the Pasternak foundation. Dong et al. [38,39,40,41] applied analytical method with Donnell’s nonlinear shell and first-order shear deformation theory to analyze the free vibration behavior of functionally graded graphene reinforced porous nanocomposite cylindrical shells. Fallah et al. [42] applied Mindlin plate theory with the Kantorovich method to study the free vibration frequency of the moderate thick FGM plate resting on the Winkler elastic foundation under different boundary conditions. Chakraverty et al. [43] applied the classical plate theory with the Rayleigh–Ritz method to extract the natural frequency and mode shape of the FGM plate under different boundary conditions resting on the Winkler model. Continuing his work, Chakraverty et al. [44] used Kirchhoff's plate theory with a framework of the Rayleigh–Ritz method to study the natural vibration and mode shape of the FGM plate under different boundaries conditions. The material properties of the FGM plate are varied exponential-law with temperature-dependent function. Akavci et al. [45] applied a hyperbolic shear deformation approach with the Navier method to carry out the natural frequency of the FGM plate resting on the Pasternak foundation. Bodaghi et al. [46] used Levy-type solution along classical plate theory to investigate the free vibration behavior of functionally graded rectangular plates simply supported on two opposite sides. Malekzadeh et al. [47] applied GDQM based on first-order shear deformation plate theory (FSDT) to analyze the free vibration response supported on an elastic foundation. Continuing his work, Malekzadeh et al. [48] applied the differential quadrature method with a three-dimensional theory of elasticity to study the free vibration behavior of FGM plates resting on the Pasternak foundation. Benferhat et al. [49] implemented the Navier method considering a neutral surface to analyze the free vibration response with a simply supported FGM plate resting on the Winkler–Pasternak foundation. They considered the shear deformation effect by implementing the refined shear deformation theory and developed exact shearing strain, and no shear correction factor is further needed for free vibration analysis of FGM plate. Su et al. [50] used the first-order theory considered with the Fourier–Ritz solution method to carry out the free frequency of the laminated FGM plate resting on an elastic foundation. Mesksi [51] investigated the free vibration behavior of FGM plates supported on elastic foundations. They used the Navier method with novel FSDT to extract the natural frequency of the FGM plate. Various authors Ramu et al. [52], Ozgan et al. [53], Dastjerdi et al. [54], Ansari t al. [55], Aragh et al. [56], Benahmed et al. [57], Jung et al. [58, 59], Gupta et al. [60, 61], Vinh Tran et al. [62], Pridha et al. [63, 64] applied different analytical techniques with different plate theories to carry out the natural frequency of the FGM plates resting on a different combination on elastic foundation with different boundary conditions.

The literature review suggests that computing the natural frequency using DSM for functionally graded plate, whose property distribution is exponential and resting on Winkler and Pasternak elastic foundation, is nearly nonexistent in the literature. It is also noticed from the literature review that most of the researchers have modeled FGM plates based on the geometric mid-surface rather than the neutral surface of the plate [58, 61]. Nevertheless, the material property of the FGM plate is not homogenous and using a mid-surface instead of a neutral surface is not correct (as property varies in the transverse direction). In this study, DSM is developed to compute the natural frequencies of the FGM plate with exponential material distribution using a physical neutral surface (PNS) and is the novel contribution of this paper.

The mechanism of the remaining part of the present study can be explained in the following way. After explaining the introduction, Sect. 2 determines the aimed contribution of the present work. In Sect. 3, the mathematical formulation of the E-FGM plate with material property and modeling of the elastic foundation is reported. Here, the fundamental principle of mathematical modeling of DSM and the motion governing equation of the E-FGM plate, developed by using Hamilton's principle, are highlighted. A dynamic stiffness matrix is generated, and Wittrick and Williams algorithm is applied to carry out the free vibration natural frequencies of the E-FGM plate. Section 4 describes the new set of natural frequency results highlighting the effect of geometric parameters on the natural frequency of an E-FGM plate resting on an elastic foundation. In the last section, 5, conclusions of the present work are reported.

2 Contributions and relevant scope of present work

In the present work, the natural vibration behavior in the thickness direction of the E-FGM plate resting on the Winkler and Pasternak elastic foundation is analyzed, where the material property variation of the FGM plate is explained by using exponential law. Kirchhoff's plate theory describes the E-FGM plate's displacement component or kinematic variables. Hence, the effect of shear deformation of the plate can be neglected, and present work is mainly focused on thin E-FGM plates. The Levy-type (displacement and force) boundary condition is implemented where two opposite sides of the plate are supported, and the other sides are arbitrary conditions (free, clamped, and simply supported). Under the present study's relevant scopes and limitations, the paper's main contributions can be explained as under:

  • The development of DSM to analyze the natural vibration behavior of E-FGM plate resting on Winkler and Pasternak elastic foundation is reported.

  • A well-known W–W algorithm is implemented to extract the natural frequency of the E-FGM plate.

  • For modeling the E-FGM plate, physical neutral surface (PNS) rather than mid-geometry of the plate is applied in this present work.

  • This present study also reported some inaccurate published results and tried to explain the possible reasons behind these inaccurate results.

  • For different density ratios, elastic modulus ratio, material gradient indices, and aspect ratios, a new set of natural frequencies results based on an exponential-law FGM plate resting on an elastic foundation are highlighted.

3 Theoretical modeling of DSM

3.1 Material properties and geometry of E-FGM plate

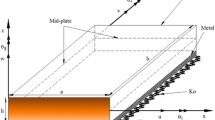
Figure 1 represents the Cartesian coordinate system of a thin rectangular E-FGM plate where the geometric parameters of the plate are explained as length \((a)\), width \((b)\), and plate thickness \((h)\). The FGM plate is made from a combination of ceramic–metal constituents, where the top surface of the FGM plate is ceramic-rich, and the bottom surface of the plate is metal-rich. The material properties of the FGM plate vary along the transverse direction by implementing the exponential law [7, 44] in terms of volume fraction, as explained by Eq. (1).

Fig. 1
figure 1

Schematic representation of thin rectangular exponential law FGM plate on elastic foundation

Full size image

As per the exponential law function [7, 44], the variation of material property along the transverse direction is given by

$$ P(z) = P_{{\text{c}}} e^{{ - \delta \left( {1 - \frac{2z}{h}} \right)}} \;{\text{with}}\;\delta = \frac{1}{2}\ln \left( {\frac{{P_{{\text{c}}} }}{{P_{{\text{m}}} }}} \right) $$
(1)

where \(P\left(z\right)\) represents the material property through the transverse direction of the FGM plate and \({P}_{\mathrm{c}}\) and \({P}_{\mathrm{m}}\), indicate the value of material properties of ceramic and metal constituents, respectively. It is noticed from Eq. (1) that at \(\delta =0\), the value of \({P}_{\mathrm{c}}={P}_{\mathrm{m}}\), and it is considered as if the E-FGM plate behaves like a homogenous isotropic plate with the presence of ceramic constituent. The variation of Young's modulus through the transverse direction of the plate as described in Eq. (1) is shown in Fig. 2.

Fig. 2
figure 2

Exponential law variation of Young’s modulus for FGM plate

Full size image

In this present work, the Poisson's ratio variation through the transverse direction is not considered because the FGM plate is thin (as per Kirchhoff's plate theory), and the variation in Poisson's ratio may be neglected [4, 22, 65,66,67,68,69].

The material property values of ceramic–metal constituents of the FGM plate considered in this research are shown in Table 1 [8, 16].

Table 1 Standard numerical values of ceramic and metal material property of FGM plate
Full size table

3.2 Elastic foundation models

A Winkler model [11] is defined as a closed vertical linear spring system that is mutually independent of each other, and the stiffness of the spring is considered equivalent to the elastic modulus of the medium. Winkler model has been improved by Pasternak [12], where the shear interaction is applied between the spring system, and the whole geometrical configuration is obtained by connecting the spring ends to the E-FGM plate that only undergoes transverse shear deformation as shown in Fig. 1. The advantage of the Pasternak model is that it applies both normal pressure and transverse shear deformation at a given system of the surrounding elastic medium. Due to this advantage, the Pasternak model [70, 71] is widely used for analyzing the structure interaction response of free vibration, supported on an elastic foundation.

The normal force [72] of the elastic foundation can be expressed as:

$${q}_{\text{Winkler}}={k}_{W}w$$
$${q}_{{\text{Pasternak}}}={k}_{W}w-{k}_{P}{\nabla }^{2}w$$
(2)

where the normal force of the foundation is represented by \(q\) and vertical displacement represented by \(w\), \({\nabla }^{2}={\partial }^{2}/\partial {x}^{2}+{\partial }^{2}/\partial {y}^{2}\), \({k}_{W}\) and \({k}_{P}\) represent the modulus of subgrade reaction of the Winkler layer and shear modulus of the shear layer [72], respectively.

3.3 Mathematical formulation of Kirchhoff's theory with a physical neutral surface

As per Fig. 1, the kinematic variable or displacement components of the E-FGM plate are explained by Kirchhoff’s plate theory and can be written as:

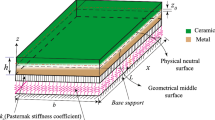
$$ \begin{aligned} u_{x} & = u_{o} (x,y) - z\frac{{\partial w}}{{\partial x}} \\ v_{y} & = v_{o} (x,y) - z\frac{{\partial w}}{{\partial y}} \\ w_{z} & = w(x,y) \\ \end{aligned} $$
(3)

Here, \({u}_{o} \left(x,y\right)\), and \({v}_{o} (x,y)\) represent the mid-surface in-plane displacement component of the E-FGM plate. The main focus of the present work is analyzing the E-FGM plate's out-of-plane free vibration behavior. For small deformation, the in-plane displacement components can be ignored. Hence, the displacement in the transverse (out of plane) direction \(w(x,y)\) is only unknown in Eq. (3). The material property of the E-FGM plate is heterogeneous in the thickness direction, and because of this, a considerable amount of vertical displacement is induced, which cannot be ignored [20]. Due to this, the geometric physical neutral surface (PNS) does not co-exist with the middle surface, as shown in Fig. 1, and therefore, the effect of bending-stretching is present in the E-FGM plate. If the concept of PNS is appropriately applied, the effect of bending-stretching can be ignored [7, 8]. The concept of the new coordinates system \({z}_{\mathrm{ns}}=\left(z-{z}_{0}\right)\) is applied at the neutral surface of the FGM plate; the distance between the neutral surface and the middle surface of the geometry is represented by \({z}_{0}\), as shown in Fig. 1.

By applying the new coordinate system, the vertical displacement components of the E-FGM plate can be expressed as:

$$ \begin{aligned} u_{x} & = - z_{{{\text{ns}}}} \frac{{\partial w}}{{\partial x}} = - \left( {z - z_{0} } \right)\frac{{\partial w}}{{\partial x}} \\ v_{y} & = - z_{{{\text{ns}}}} \frac{{\partial w}}{{\partial y}} = - \left( {z - z_{0} } \right)\frac{{\partial w}}{{\partial y}} \\ w_{z} & = w(x,y) \\ \end{aligned} $$
(4)

The strains constraint related to Eq. (4) can be given by:

$${\varepsilon }_{xx}=-{z}_{\mathrm{ns}}\frac{{\partial }^{2}w}{\partial {x}^{2}}; \quad{\varepsilon }_{yy}=-{z}_{\mathrm{ns}}\frac{{\partial }^{2}w}{\partial {y}^{2}}; \quad{\gamma }_{xy}=-2{z}_{\mathrm{ns}}\frac{{\partial }^{2}w}{\partial xy}$$
(5)

where normal strains in a particular \(x\) and \(y\) direction are represented by \({\varepsilon }_{xx}\) and \({\varepsilon }_{yy}\), respectively, and \({\gamma }_{xy}\) denotes the \(x\)-y plane shear strain.

The FGM plate material constituents follow the basic principle of Hook's law, and as per this law, the relationship of stress and strain is given in the following matrix and is expressed as

$$\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\tau }_{xy}\end{array}\right]=\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {Q}_{12}& {Q}_{22}& 0\\ 0& 0& {Q}_{66}\end{array}\right]\left[\begin{array}{c}{\varepsilon }_{xx}\\ {\varepsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right]$$
(6)

The normal stresses of the plate can be represented as \({\sigma }_{xx}\) and \({\sigma }_{yy}\) in the \(x\) and \(y\) direction, respectively, and the shear stress of \(\mathrm{the} x\)-y plane is represented by \({\tau }_{xy}\). The plate reduced stiffness components \({(Q}_{ij})\) can be expressed as:

$${Q}_{11}={Q}_{22}=\frac{E\left({z}_{\mathrm{ns}}\right)}{1-{v}^{2}};\quad{ Q}_{12}={Q}_{21}=\frac{vE\left({z}_{\mathrm{ns}}\right)}{1-{v}^{2}}\text{ and }\quad{ Q}_{66}=\frac{E\left({z}_{\mathrm{ns}}\right)}{2(1+v)}$$
(7)

To examine the PNS \({(z}_{0}),\) the plate total axial force in the particular \(x, y\)-direction should be zero. Therefore,

$$\sum {F}_{x}={\int }_{-h/2-{z}_{0}}^{h/2-{z}_{0}} {\sigma }_{xx}\mathrm{d}A=0$$
(8)

which gives to

$$ \begin{aligned} \left( {z_{0} } \right) & = \frac{{\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {E\left( z \right)z{\text{d}}z} }}{{\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {E\left( z \right){\text{d}}z} }} \\ & = h\left[ {\frac{ - 1}{{\log \left( {\frac{{E_{c} }}{{E_{m} }}} \right)}} + \frac{{E_{c} + E_{m} }}{{E_{c} - E_{m} }}} \right] = h\left[ {\frac{ - 1}{{\log \left( {E_{\text{rat}} } \right)}} + \frac{{E_{\text{rat}} + 1}}{{E_{\text{rat}} - 1}}} \right] \\ \end{aligned} $$
(9)

The mathematical non-dimensional expression of PNS of the E-FGM plate is represented in Eq. (9), which depends upon Young’s modulus ratio \({E}_{\mathrm{rat}}=\frac{{E}_{c}}{{E}_{m}}\). The variation of \({E}_{rat}\) on a neutral surface is shown in Fig. 3. For a particularly given value of Young's modulus ratio \({(E}_{\mathrm{rat}}=1)\) with \({z}_{0}=0\), the exponential law FGM plate is converted to a homogenous isotropic plate, and at this condition, PNS exactly coincides with the mid surface of the plate. Equation (9) shows that, as Young’s modulus ratio \({(E}_{\mathrm{rat}})\) increases, the corresponding \({z}_{0}\) value also increases. It is obtained from Fig. 3 that as \({E}_{\mathrm{rat}}\) increases, the PNS is moved away from the middle surface of the FGM plate and shifted as for the highly ceramic side of the plate. This phenomenon is due to the higher stiffness value of ceramic constituents at the top part than metal constituents at the bottom part of the exponential-law FGM plate.

Fig. 3
figure 3

Shifting of non-dimensional \({(z}_{0}/h)\) parameter with Young’s modulus ratio \({(E}_{\mathrm{rat}})\)

Full size image

3.4 The governing free vibration equation of motion of FGM plate

The governing motion equation of the FGM plate for free vibration is carried out by applying the standard Hamilton's principle.

As per Hamilton’s principle,

$$\delta \int (T-(U+{U}_{EM})\mathrm{d}t=0$$
(10)

where \(T, U\) represent the kinetic energy strain energy of the plate, and \({U}_{EM}\) represents the strain energy due to the elastic foundation and can be given by

$$T=\frac{1}{2}{\int }_{V} \rho \left({\left(\frac{\partial {u}_{x}}{\partial t}\right)}^{2}+{\left(\frac{\partial {v}_{y}}{\partial t}\right)}^{2}+{\left(\frac{\partial {w}_{z}}{\partial t}\right)}^{2}\right)\mathrm{d}V$$
(11)

The strain energy \((U)\) of the E-FGM plate is expressed as:

$$U=\frac{1}{2}{\int }_{V} \left({\sigma }_{xx}{\varepsilon }_{xx}+{\sigma }_{yy}{\varepsilon }_{yy}+{\tau }_{xy}{\gamma }_{xy}\right)\mathrm{d}V$$
(12)

The exponential-law functionally graded plate is supported on an elastic foundation; therefore, the foundation strain energy \({(U}_{EM})\) is expressed as [35].

$${U}_{EM}={\int }_{\Omega } \left[{k}_{W}w\delta w+{k}_{P}\left(\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}+\frac{\partial w}{\partial y}\frac{\partial \delta w}{\partial y}\right)\right]\mathrm{d}x\mathrm{d}y$$
(13)

The displacement components from Eq. (5) are substituted into Eqs. (10–13) and the relationship of stress–strain of Eqs. (6–7) is substituted into Eq. (12) with applied Hamilton's principle; the equation of motion for free transverse direction vibration of E-FGM plate and general boundary condition can be formulated as given by Eqs. (14) and (15), respectively.

$${D}_{\mathrm{FGM}}\left(\frac{{\partial }^{4}w}{\partial {x}^{4}}+2\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}\right)+{I}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{k}_{W}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{k}_{P}\left(\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}w}{\partial {y}^{2}\partial {t}^{2}}\right)=0$$
(14)

The natural boundary conditions of plate elements are given as represented in Fig. 4.

$$\begin{aligned} V_{x} & = \left[ { - D_{{{\text{FGM}}}} \left( {\frac{{\partial ^{3} w}}{{\partial x^{3} }} + (2 - v)\frac{{\partial ^{3} w}}{{\partial x\partial y^{2} }}} \right)} \right]\delta w \\ M_{{xx}} & = - D_{{{\text{FGM}}}} \left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }} + v\frac{{\partial ^{2} w}}{{\partial y^{2} }}} \right)\delta \phi _{y} \\ \end{aligned} $$
(15)

where \({D}_{\mathrm{FGM}}\) indicates the flexure rigidity and \({I}_{o}\) represents the inertia in the transverse direction of the plate. The analytical mathematical expression of these parameters is explained in Appendix A. In the present study, non-dimensional parameters \({D}_{\mathrm{FGM}}/{D}_{C}\) are introduced where the expression is represented by \({D}_{C}={E}_{c}{h}^{3}/12(1-{\nu }^{2})\). At a particular value of Young's modulus ratio \({E}_{\mathrm{rat}}=1\), the E-FGM plate is advanced as a highly ceramic-rich plate with \({D}_{\mathrm{FGM}}/{D}_{C}=1\), and the corresponding E-FGM plate becomes a homogenous isotropic plate. Figure 5 represents the effect of \({D}_{\mathrm{FGM}}/{D}_{C}\) for seven different values of Young’s modulus ratio \({(E}_{\mathrm{rat}})\). Figure 5 shows that the parametric value of \({D}_{\mathrm{FGM}}/{D}_{C}\) decreases as Young's modulus ratio increases, and the FGM plate's metallic constituents increase, which has a low value of Young's modulus and flexure stiffness than that of ceramic constituents.

Fig. 4
figure 4

Schematic representation of force and displacements boundary conditions for a plate element

Full size image
Fig. 5
figure 5

The non-dimensional parameter \({D}_{\mathrm{FGM}}/{D}_{C}\) with different values of \({E}_{\mathrm{rat}}\)

Full size image

Equation (15) represents the natural boundary conditions of the plate element where the shear force \({(V}_{x})\) of the plate is co-related to the displacement component \((w)\), and the associated bending moment is related to the rotation \({\phi }_{y}=\frac{\partial w}{\partial x}\) of the plate. In developing the DS (dynamic stiffness) matrix, Eq. (15) and Eq. (16) are considered the main elements, and the methodology to obtain the DS matrix is expressed below.

3.5 Levy-type solution for E-FGM plate

The generalized differential equation of Eq. (14) is completely solved by implementing the force–displacement boundary conditions. A Levy solution is used in the present study (where a simply supported boundary condition is applied at the two different edges of the plate, and the other reaming edges are considered simply supported, free, and clamped) to solve Eq. (15) and satisfy the natural boundary condition obtained in Eq. (15) and can be given by:

$$w(x,y,t)=\sum_{m=1}^{\infty } {W}_{m}(x){e}^{i\omega t}\mathrm{sin}\left({\alpha }_{m}y\right)\text{ with }{\alpha }_{m}=m\pi /a;\,(m=\mathrm{1,2},\dots \dots \dots .\infty )$$
(16)

where \(\omega \) represents the unknown frequency.

The obtained Eq. (16) is substituted into Eq. (14); a generalized fourth-order differential equation is obtained as:

$$\frac{{d}^{4}{W}_{m}}{d{x}^{4}}-\left(2{\alpha }_{m}^{2}+\frac{{k}_{P}{\omega }^{2}}{{D}_{\mathrm{FGM}}}\right)\frac{{d}^{2}{W}_{m}}{d{x}^{2}}+\left({\alpha }_{m}^{4}-\frac{{k}_{W}{\omega }^{2}}{{D}_{\mathrm{FGM}}}-\frac{{k}_{P}{\omega }^{2}{\alpha }_{m}^{2}}{{D}_{\mathrm{FGM}}}\right){W}_{m}=0$$
(17)

The developed Eq. (17) produces standard four roots, and based on its nature depends, there are only two feasible solutions obtained and given by:

Case 1

$$\left({\alpha }_{m}^{2}-\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)\ge \sqrt{{\left(\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)}^{2}+\frac{{k}_{W}{\omega }^{2}}{{D}_{\mathrm{FGM}}}}$$

In case 1, all roots are real \({(r}_{1m}, {-r}_{1m,}\) \({r}_{2m}, {-r}_{2m})\) and the expression is given as

$$\begin{array}{c}{r}_{1m}=\sqrt{\left({\alpha }_{m}^{2}-\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)+\sqrt{{\left(\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)}^{2}+\frac{{k}_{W}{\omega }^{2}}{{D}_{\mathrm{FGM}}}}}\\ {r}_{2m}=\sqrt{\left({\alpha }_{m}^{2}-\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)-\sqrt{{\left(\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)}^{2}+\frac{{k}_{W}{\omega }^{2}}{{D}_{\mathrm{FGM}}}}},\end{array}$$
(18)

The solution is

$${W}_{m}(x)={A}_{m}\mathrm{cosh}\left({r}_{1m}x\right)+{B}_{m}\mathrm{sinh}\left({r}_{1m}x\right)+{C}_{m}\mathrm{cosh}\left({r}_{2m}x\right)+{D}_{m}\mathrm{sinh}\left({r}_{2m}x\right)$$
(19)

Case 2

$$\left({\alpha }_{m}^{2}-\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)<\sqrt{{\left(\frac{{k}_{P}{\omega }^{2}}{2{D}_{\mathrm{FGM}}}\right)}^{2}+\frac{{k}_{W}{\omega }^{2}}{{D}_{\mathrm{FGM}}}}$$

In case 2, two roots are real, and two roots are imaginary \({(r}_{1m}, {-r}_{1m,}\) \({r}_{2m}, {-r}_{2m})\) and the expression is given as:

$$ \begin{gathered} r_{{1m}} = \sqrt {\left( {\alpha _{m}^{2} - \frac{{k_{P} \omega ^{2} }}{{2D_{{{\text{FGM}}}} }}} \right) + \sqrt {\left( {\frac{{k_{P} \omega ^{2} }}{{2D_{{{\text{FGM}}}} }}} \right)^{2} + \frac{{k_{W} \omega ^{2} }}{{D_{{{\text{FGM}}}} }}} } \hfill \\ r_{{2m}} = \sqrt { - \left( {\alpha _{m}^{2} - \frac{{k_{P} \omega ^{2} }}{{2D_{{{\text{FGM}}}} }}} \right) + \sqrt {\left( {\frac{{k_{P} \omega ^{2} }}{{2D_{{{\text{FGM}}}} }}} \right)^{2} + \frac{{k_{W} \omega ^{2} }}{{D_{{{\text{FGM}}}} }}} } , \hfill \\ \end{gathered} $$
(20)

The solution is:

$${W}_{m}(x)={A}_{m}\mathrm{cosh}\left({r}_{1m}x\right)+{B}_{m}\mathrm{sinh}\left({r}_{1m}x\right)+{C}_{m}\mathrm{cos}\left({r}_{2m}x\right)+{D}_{m}\mathrm{sin}\left({r}_{2m}x\right)$$
(21)

3.6 Formulation of DS matrix for E-FGM plate

For case 1, the formulation of the DS matrix is explained below. A similar pattern is implemented for case2 but is not explained here for brevity.

By using the natural boundary condition Eq. (15) with displacement \((w\)) relation in Eqs. (16–19), the bending rotation \({\phi }_{y}\), shear force \({V}_{x}\), and moment \({M}_{xx}\) are obtained and are given by Eqs. (22– 24).

$$ \begin{aligned} \phi _{{y_{m} }} (x,y) & = \Phi _{{y_{m} }} \left( x \right){\text{sin}}\left( {\alpha _{m} y} \right) = \frac{{{\text{d}}W_{m} (x)}}{{{\text{d}}x}}{\text{sin}}\left( {\alpha _{m} y} \right) \\ & = - \left( {(A_{m} r_{{1_{m} }} {\text{sinh}}\left( {r_{{1_{m} }} x} \right) + B_{m} r_{{1m}} {\text{cosh}} \left( {r_{{1_{m} }} x} \right) + C_{m} r_{{2m}} {\text{sin}}\left( {r_{{2m}} x} \right)} \right. \\ & \quad \;+ D_{m} r_{{2m}} \cos \left( {r_{{2m}} x} \right)\sin \left( {\alpha _{m} y} \right) \\ \end{aligned} $$
(22)
$$ \begin{aligned} V_{{x_{m} }} \left( {x,y} \right) = & {\mathcal{V}}_{{x_{m} }} \left( x \right)\sin \left( {\alpha _{m} y} \right) \\ = & - D_{{FGM}} \left( {A_{m} \left( {r_{{1m}}^{3} - (2 - \nu ) \alpha _{m}^{2} r_{{1_{m} }} } \right)\sinh \left( {r_{{1m}} x} \right) + B_{m} \left( {r_{{1m}}^{3} - (2 - \nu )\alpha _{m}^{2} r_{{1m}} } \right)\cosh \left( {r_{{1m}} x} \right)} \right. \\ & \left. { + C_{m} \left( {r_{{2m}}^{3} + \left( {2 - \nu } \right)\alpha _{m}^{2} r_{{2m}} } \right)\sin \left( {r_{{2m}} x} \right) + D_{m} \left( {r_{{2m}}^{3} + \left( {2 - \nu } \right)\alpha _{m}^{2} r_{{2m}} } \right) \cos \left( {r_{{2m}} x} \right)} \right)\sin \left( {\alpha _{m} y} \right) \\ \end{aligned} $$
(23)
$$ \begin{aligned} M_{{xx_{m} }} (x,y) = & {\mathcal{M}}_{{xx_{m} }} (x)\sin \left( {\alpha _{m} y} \right) \\ = & - D_{{FGM}} \left( {A_{m} \left( {r_{{1_{m} }}^{2} - \nu \alpha _{m}^{2} } \right){\text{cosh}}\left( {r_{{1_{m} }} x} \right) + B_{m} \left( {r_{{1_{m} }}^{2} - \nu \alpha _{m}^{2} } \right){\text{sinh}}\left( {r_{{1_{m} }} x} \right)} \right. \\ & \left. { + C_{m} \left( {r_{{2,m}}^{2} - \nu \alpha _{m}^{2} } \right)\cos \left( {r_{{2m}} x} \right) + D_{m} \left( {r_{{2_{m} }}^{2} - \nu \alpha _{m}^{2} } \right)\sin \left( {r_{{2m}} x} \right)} \right)\sin \left( {\alpha _{m} y} \right) \\ \end{aligned} $$
(24)

The boundary conditions of displacements are given by:

$$\begin{array}{l}x=0 {W}_{m}={W}_{1}; {\phi }_{{y}_{m}}={\phi }_{{y}_{1}}\\ \\ x=b {W}_{m}={W}_{2}; {\phi }_{{y}_{m}}={\phi }_{{y}_{2}}\end{array}$$
(25)

The force boundary conditions are given by:

$$\begin{array}{l}x=0 {V}_{xm}=-{V}_{1}; {M}_{x{x}_{m}}=-{M}_{1}\\ \\ x=b {V}_{xm}={V}_{2}; {M}_{x{x}_{m}}={M}_{2}\end{array}$$
(26)

The displacement boundary conditions present in Eq. (25) are substituted into solution Eq. (19) and bending rotation Eq. (22) to develop the following matrix.

$$\left[\begin{array}{c}{W}_{1}\\ {\Phi }_{{y}_{1}}\\ {W}_{2}\\ {\Phi }_{{y}_{2}}\end{array}\right]=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& -{r}_{{1}_{1m}}& 0& -{r}_{2m}\\ {C}_{{h}_{1}}& {S}_{{h}_{1}}& {C}_{2}& {S}_{2}\\ -{r}_{{1}_{m}}{S}_{{h}_{1}}& -{r}_{{1}_{m}}{C}_{{h}_{1}}& {r}_{{2}_{m}}{S}_{2}& -{r}_{{2}_{m}}{C}_{2}\end{array}\right]\left[\begin{array}{c}{A}_{m}\\ {B}_{m}\\ {C}_{m}\\ {D}_{m}\end{array}\right]$$
(27)

or,

$${\varvec{\delta}}={\varvec{A}}{\varvec{C}},$$
(28)

where

$$\begin{array}{c}{C}_{{h}_{i}}=\mathrm{cosh}\left({r}_{i}b\right), {S}_{{h}_{i}}=sinh\left({r}_{i}b\right)\\ {C}_{i}=cos\left({r}_{i}b\right),{ S}_{i}=\mathrm{sin}\left({r}_{i}b\right)\, with\, i=\mathrm{1,2}.\end{array}$$
(29)

For force boundary conditions, a similar procedure is to be followed, i.e., Eq. (26) is substituted into shear force Eq. (23) and moment Eq. (24) to obtain the following matrix.

$$\left[\begin{array}{c}{V}_{1}\\ {M}_{1}\\ {V}_{2}\\ {M}_{2}\end{array}\right]=\left[\begin{array}{cccc}0& {R}_{1}& 0& {R}_{2}\\ {L}_{1}& 0& {L}_{2}& 0\\ -{R}_{1}{S}_{{h}_{1}}& -{R}_{1}{C}_{{h}_{1}}& {R}_{2}{S}_{2}& -{R}_{2}{C}_{2}\\ -{L}_{1}{C}_{{h}_{1}}& -{L}_{1}{S}_{{h}_{1}}& -{L}_{2}{C}_{2}& -{L}_{2}{S}_{2}\end{array}\right]\left[\begin{array}{c}{A}_{m}\\ {B}_{m}\\ {C}_{m}\\ {D}_{m}\end{array}\right]$$
(30)

or,

$${\varvec{F}}={\varvec{R}}{\varvec{C}}$$
(31)

where

\({R}_{i}={D}_{FGM}\left[{r}_{im}^{3}-{\alpha }^{2}{r}_{im}(2-v)\right]\), \({L}_{i}={D}_{FGM}\left({r}_{im}^{3}-{\alpha }^{2}v\right)\) (32).with i = 1,2.

For excluding the constant vector value of \(C\), the following relationship can be formed as

$${\varvec{F}}={\varvec{K}}{\varvec{\delta}}$$
(33)

where

$${\varvec{K}}={\varvec{R}}{{\varvec{A}}}^{-1}$$
(34)

In Eq. (34), K indicates the square 4 × 4 symmetric dynamic stiffness (DS) matrix, including the independent terms \({(S}_{vv}, {S}_{vm}, {F}_{vv}, {F}_{vm}, {S}_{mm}, {S}_{vn})\). Therefore, the generated DS matrix of the single plate element can be expressed as

$$ \left[ \user2{K} \right] = \left[ {\begin{array}{*{20}l} {S_{{vv}} } \hfill & {S_{{vm}} } \hfill & {F_{{vv}} } \hfill & {F_{{vm}} } \hfill \\ {S_{{vm}} } \hfill & {S_{{mm}} } \hfill & { - F_{{vm}} } \hfill & {F_{{mm}} } \hfill \\ {F_{{vv}} } \hfill & { - F_{{vm}} } \hfill & {S_{{vv}} } \hfill & { - S_{{vm}} } \hfill \\ {F_{{vm}} } \hfill & {F_{{mm}} } \hfill & { - S_{{vm}} } \hfill & {S_{{mm}} } \hfill \\ \end{array} } \right] $$
(35)

The mathematical expressions of Eq. (35) are explained in Appendix B.

3.7 Dynamic stiffness (DS) matrix assembly procedure with boundary conditions

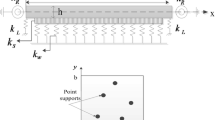
The DS matrix for a single element is given by Eq. (35). The assembly procedures for DS matrix are represented in Fig. 6. This method is very similar to FEM. The only difference from FEM is that the line is taken rather than the point node for each strip connection of plate element, as presented in Fig. 6.

Fig. 6
figure 6

Schematic representation of global assembly formulation of the dynamic stiffness matrix

Full size image

The penalty method is used to suppress line nodes' specific degree of freedom in the global DS matrix.

The penalty method procedure for different boundary conditions is summarized below:

  • Displacement \({(W}_{i})\) is penalized for simply supported (S) boundary conditions.

  • Displacement (\({W}_{i})\) and rotation (\({\phi }_{i})\) are penalized for clamped (C) boundary conditions.

  • No penalty is implemented for the free (F) boundary condition.

where \(i\) represent the suppressed node.

3.8 Application of Wittrick–Williams (W–W) algorithm

For the whole structure, the overall DS matrix is developed with relevant, suitable constraints used to carry out the natural frequency of the E-FGM plate. The algorithm of Wittrick and Williams [73] is applied to carry out the eigenvalues of the plate, and it solves the transcendental behavior of the overall DS matrix, which ensures that no natural frequencies are missed out [8, 16]. The methodology of the W–W algorithm is represented by the flow chart as shown in Fig. 7.

Fig. 7
figure 7

Flowchart representation of the W–W algorithm

Full size image

4 Results and discussion

The analytical methodology of DSM described above has been imported into the MATLAB software program to extract the E-FGM plate's mode shape and natural frequencies. The boundary conditions of the E-FGM plate, such as clamped, free, and simply supported, are represented as the notation of C, F, and S, respectively. It indicates that the boundary condition of SCSF stands as simply supported (at y = 0 and y = a), clamped (at x = 0) and free (at x = b) for a given E-FGM plate. The symbols, \(m\), and \(n\) denote a particular frequency mode shape, where ‘m’ represents the number of half-sine waves in a particular x-direction and ‘n’ represents the nth lower frequency for a corresponding value of ‘m’.

This section compares the natural frequencies formulated by DSM with published results and shows very good agreement with them. The effect of design parameters (material gradient index, elastic modulus, material properties ratio, and aspect ratio) on natural frequency is reported in tables and graphs.

4.1 Comparative study

The following mathematical expression for non-dimensional natural frequency parameters is used to compare DSM results.

$$\overline{\omega }=\omega h\sqrt{{\rho }_{m}/{G}_{m}}, \widetilde{\omega }=\omega h\sqrt{{\rho }_{c}/{E}_{c}}, { \omega }^{*}=\omega {a}^{2}\sqrt{\frac{{\rho }_{c}h}{{D}_{c}}, } {K}_{p}=\frac{{k}_{p}{a}^{4}}{{D}_{c}}{, K}_{w}=\frac{{k}_{w}{a}^{2}}{{D}_{c}}$$
(36)

where \({G}_{m}={E}_{m}/(2\left(1+\nu \right))\) represents the shear modulus of the metal constituent of the plate. The DSM results for the natural frequency of square \((a/b=1.0)\) and rectangular \((a/b=2.0, 5.0)\) isotropic plates with simply supported (SSSS) at all the edges for \(h/a=0.01\) are compared with published literature [69] and are shown in Table 2. It is noted that for a delta equal to zero, the E-FGM plate behaves as an isotropic plate with ceramic-rich and material property values are taken from Table 1. The natural frequencies obtained by DSM are in very good agreement with published results as seen in Table 2.

Table 2 Comparison of natural frequency parameters \(\left(\overline{\omega }=\omega h\sqrt{{\rho }_{m}/{G}_{m}}\right)\) of SSSS homogeneous isotropic plate with a different aspect ratio \((a/b=1.0, 2.0, and \,\, 5.0)\)
Full size table

The natural frequency results computed by the DSM method are in excellent agreement with Ref [7]. as seen in Table 3.

Table 3 Comparison of natural frequencies parameters \(\left({\omega }^{*}=\omega {a}^{2}\sqrt{\frac{{\rho }_{c}h}{{D}_{c}}}\right)\) of E-FGM plate under Levy-type boundary conditions with a different aspect ratio \((a/b=0.5, and 1.5)\)
Full size table

The natural frequencies of the E-FGM plate for two boundary conditions (SSSS, SCSC) obtained by DSM in Table 4 are compared with those published in the literature for \(\delta =0\), and they are in good agreement. It is further emphasized that, for δ = 0, E-FGM behaves as an isotropic plate shown in Fig. 2. For a particular case of E-FGM, for \(\delta =-1/2\mathrm{log}\left({P}_{c}/{P}_{m}\right)\), the first seven natural frequencies for SSSS and SCSC edge conditions are compared in Table 4.

Table 4 Comparison of natural frequencies parameters \(\left({\omega }^{*}=\omega {a}^{2}\sqrt{\frac{{\rho }_{c}h}{{D}_{c}} }\right)\) of SSSS homogeneous isotropic E-FGM plate
Full size table

It is observed from Table 4 that the published frequency results of the E-FGM plate in Ref. [43] are not sufficiently accurate, and the first frequency error is around 11.8%, and for higher mode, the error is around 58.12%. The possible reason for this inaccuracy is that in Ref. [43], the authors considered a geometric middle surface instead of a physical neutral surface as the reference plane of the E-FGM plate, which is not correct. We used a physical neutral surface to compute the natural frequencies in our approach. It is further noted that the computation of natural frequencies of E-FGM plate is scanty in the literature.

4.2 Extraction of the natural frequency of E-FGM plate resting on Winkler–Pasternak foundation

This section highlights the extraction of a new set of natural frequencies for the E-FGM plate developed by DSM under two parametric geometric configurations (one square and another rectangular) resting on the Winkler and Pasternak elastic foundation.

4.2.1 Square E-FGM plate with Winkler–Pasternak foundation

In this subsection, a new set of natural frequency results of a square E-FGM plate for a different combination of Winkler modulus \(\left({K}_{w}=0, 100, 1000\right)\) with Levy-type edge conditions are shown in Table 5. At a particular mode, the natural frequency increases with the Winkler modulus value (\({K}_{w}=\) 0, 100, 1000). This is because of stiffness of the E-FGM plate increases. This table shows that the maximum natural frequency value is obtained for SCSC boundary conditions and the minimum for SFSF boundary conditions. The reason is that by adding more constraints at the SCSC edge condition, the stiffness of the plate increases and gives the maximum value of natural frequency, while for free edge condition SFSF, removing the constraints at the particular edge decreases the plate stiffness and gives the minimum value of natural frequency. Similarly, Table 6 shows the natural frequency results for Pasternak modulus \(\left({K}_{P}=0, 100, 1000\right)\) for the E-FGM plate under Levy-type edge conditions, and natural frequency increases as the Pasternak modulus \(\left({K}_{P}=0, 100, 1000\right)\) of the plate, because of increases in the plate stiffness. It is obtained from Tables 5, 67 that the effect of the Pasternak modulus \({( K}_{w}=0)\) is higher than the Winkler modulus \({( K}_{P}=0)\). The obtained mode shapes for the E-FGM plate, in Fig. 8, are similar to those observed in an isotropic plate.

Table 5 Fundamental frequency parameters \({(\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c})}\) for square E-FGM plate under Levy-type boundary conditions for different values of Winkler parameters for \({K}_{p}=0\) and \(h/a=0.01.\)
Full size table
Table 6 Fundamental frequency parameters \({(\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c})}\) for square isotropic E-FGM plate under Levy-type boundary conditions for different Pasternak parameters for \({K}_{W}=0\) and \(h/a=0.01.\)
Full size table
Table 7 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for square E-FGM plate for different Winkler–Pasternak parameters with different Levy-type boundary conditions and \(h/a=0.01\)
Full size table
Fig. 8
figure 8

Representation of natural mode for square E-FGM plate under simply supported (SSSS) boundary condition for \(h/a=0.01\)

Full size image

4.2.2 Rectangular E-FGM plate resting on Winkler–Pasternak elastic foundation

This subsection reports the fundamental natural frequencies of the E-FGM rectangular plate obtained by DSM. Tables 8, 9, 10, 11, 12, 13 represent the fundamental frequency results for three different values of aspect ratios for Levy-type edge conditions with different combinations of elastic foundation\({(K}_{w}, {K}_{P})\).

Table 8 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SCSC rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table
Table 9 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SCSS rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table
Table 10 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SSSS rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table
Table 11 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SFSC rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table
Table 12 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SSSF rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table
Table 13 Fundamental frequency parameter \({\omega }^{*}=\omega {a}^{2}\sqrt{{\rho }_{c}h/{D}_{c}}\) for SFSF rectangular E-FGM plate with different combinations of \({(K}_{w}, {K}_{P})\) and \(h/a =0.01\)
Full size table

It is illustrated from these tables that the frequency of the plate decreases with an increase in the particular value of elastic foundation and aspect ratio. Besides this, as the aspect ratio increases with elastic foundation, the frequency of the plate increases under all boundary conditions except the SFSF condition. As the aspect ratio increases, natural frequency increases with a change in boundary condition under an elastic foundation because the plate's stiffness increases. Except in the SFSF boundary condition, as the aspect ratio increases, the stiffness of the plate decreases, and consequently, the natural frequency decreases, as seen in Table 13.

4.3 A parametric study

In this section, the variations of the different values of geometrical parameters such as modulus ratio, density ratio, aspect ratio, and Winkler and Pasternak modulus on the natural frequency of the E-FGM plate are reported.

The influence of Winkler and Pasternak elastic modulus \({(K}_{w, }{K}_{P})\) for different modulus ratios (\({E}_{rat}\)) with a fixed value of density ratio (\({\rho }_{rat}=2\)) on the natural frequency of square E-FGM plate under SCSC edge condition is shown in Fig. 9a–d. At a particular mode, it can be seen from these figures that the natural frequency of the E-FGM plate decreases with an increase in Young's modulus ratio (\({E}_{rat}\)) because the plate's stiffness decreases and more metal constituents get introduced in the E-FGM plate and similar trend is shown in Fig. 5 where the parametric value of \({D}_{FGM}/{D}_{C}\) decreases as Young's modulus ratio increases, and the FGM plate's metallic constituents increase, due to this the natural frequency of the plate is decreased.

Fig. 9
figure 9figure 9

a. Effect of \({E}_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{0,0}\right), {\rho }_{\mathrm{rat}}=2, \mathrm{and }h/a=0.01\). Figure 9 b Effect of \({E}_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,0}\right), {\rho }_{\mathrm{rat}}=2, \mathrm{and }h/a=0.01\). Figure 9 c. Effect of \({E}_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{0,100}\right), {\rho }_{\mathrm{rat}}=2, \mathrm{and }h/a=0.01\). Figure 9 d Effect of \({E}_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,100}\right)\),\({\rho }_{\mathrm{rat}}=2, \mathrm{and }h/a=0.01\)

Full size image

This influence of Young's modulus ratio of the E-FGM plate natural frequency is similar as obtained by various authors [46, 47, 56] for other kinds of functionally graded plates. It can also be illustrated that the influence of the Pasternak modulus on natural frequency for a particular mode is significantly high than the Winkler modulus, and a similar observation is also reported by authors [58, 59, 81] for other types of functionally graded plates. At a lower value of Young’s modulus ratio \(({E}_{rat}<10)\), the natural frequency decrease for a particular mode with a fixed elastic modulus value is more evident.

The effect of density ratio \({(\rho }_{rat})\) for a different combination of elastic modulus \({(K}_{w, }{K}_{P})\) under a fixed value of Young's modulus ratio \({(E}_{rat}=2)\) on the natural frequency of square E-FGM plate with SCSC edge condition is highlighted in Fig. 10a–c. As the density ratio increases \({(\rho }_{rat})\), the frequency of the E-FGM plate increases, and its shows that for the lower value of density ratio \({(\rho }_{rat}< 10)\), increases in natural frequencies are significant for a particular value of Winkler and Pasternak elastic modulus. The Pasternak modulus's effect on natural frequency is more significant than the Winkler modulus, and similar observations are also reported by authors [58, 59, 81] for other kinds of FGM plates.

Fig. 10
figure 10figure 10

a Effect of \({\rho }_{rat}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,0}\right), {E}_{rat}=2, \mathrm{and }h/a=0.01\). Figure 10 b Effect of \({\rho }_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{0,100}\right)\),\({E}_{\mathrm{rat}}=2 \mathrm{and }h/a=0.01\). Figure 10 c. Effect of \({\rho }_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,100}\right)\),\({E}_{\mathrm{rat}}=2 \mathrm{and }h/a=0.01\)

Full size image

The variation of Winkler–Pasternak elastic modulus \({(K}_{w, }{K}_{P})\) and different values of \({E}_{rat}\)=\({\rho }_{rat}\) on the natural frequency of E-FGM square plate under SCSC edge conditions are reported in Fig. 11a–c. It is obtained from these figures that as \({E}_{rat}\)=\({\rho }_{rat}\) increases (0 to 40), the plate's natural frequency decreases. The decrease in natural frequency is significant at the lower value of \({E}_{rat}\)=\({\rho }_{rat}\) (say, less than 10).

Fig. 11
figure 11figure 11

a Effect of \({E}_{\mathrm{rat}}\) and \({\rho }_{\mathrm{rat}}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,0}\right),\) \({(E}_{\mathrm{rat}}={\rho }_{\mathrm{rat}}) \mathrm{and }h/a=0.01\). Figure 11 b Effect of \({E}_{\mathrm{rat}}\) and \({\rho }_{rat}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{0,100}\right),\) \({(E}_{\mathrm{rat}}={\rho }_{\mathrm{rat}}) \mathrm{and }h/a=0.01\). Figure 11 c Effect of \({E}_{rat}\) and \({\rho }_{rat}\) on frequency parameter \({(\omega }^{*})\) for square E-FGM plate for constant \(\left({K}_{W},{K}_{p}=\mathrm{100,100}\right),\) \({(E}_{\mathrm{rat}}={\rho }_{\mathrm{rat}}) \mathrm{and }h/a=0.01\)

Full size image

The effect of Winkler–Pasternak modulus \({(K}_{w, }{K}_{P})\) for different values of aspect ratio \((a/b)\) on the natural frequency of rectangular E-FGM plate with SSSS edge condition and \({E}_{rat}=1, {\rho }_{rat}=1\) is shown in Fig. 12a–c. A similar pattern of natural frequency variations is obtained for all boundary conditions (Levy-type); therefore, simply supported (SSSS) boundary condition in Levy solution is shown in Fig. 12a–c.

Fig. 12
figure 12figure 12

a Effect of aspect ratio on frequency parameter \({(\omega }^{*})\) under different combinations of \({K}_{W}\) and fixed \({K}_{p}=0\) for SSSS boundary conditions for \({E}_{\mathrm{rat}}=2, {\rho }_{\mathrm{rat}}=2\) and \(h/a=0.01\). Figure 12 b Effect of aspect ratio on frequency parameter \({(\omega }^{*})\) under different combinations of \({K}_{p}\) and fixed \({K}_{W}=0\) for SSSS boundary conditions for \({E}_{\mathrm{rat}}=2, {\rho }_{\mathrm{rat}}=2\mathrm{ and} h/a=0.01\). Figure 12 c Effect of aspect ratio on natural frequency parameter \({(\omega }^{*})\) under different combinations of \({K}_{W}\) and \({K}_{p}\) for SSSS boundary conditions for \({E}_{\mathrm{rat}}=2, {\rho }_{\mathrm{rat}}=2,\mathrm{ and }h/a=0.01\)

Full size image

It is noticed from these figures that as the aspect ratio \((a/b)\) of the plate increases, the natural frequency of the E-FGM plate increases because of increase in the flexural stiffness of the plate. The obtained frequencies show that the effect of the Pasternak modulus is higher than the Winkler modulus for all aspect ratio values. It is also illustrated that for the high value of aspect ratio, natural frequency does not change with Winkler modulus, but it increases in the case of Pasternak modulus.

5 Conclusions

This present work formulates the dynamic stiffness method for a thin rectangular E-FGM plate resting on Winkler and Pasternak elastic foundation. The concept of a physical neutral surface is applied rather than the geometric middle surface with classical plate theory for the theoretical formulation of a thin E-FGM plate. The partial governing differential motion equation is obtained under the consideration of elastic foundation using Hamilton’s principle. A Levy-type solution is applied with displacement and force boundary conditions at the contrary edge of the plate. The Wittrick–Williams algorithm is implemented as a solution technique for solving the transcendental nature of the dynamic stiffness matrix to find out the natural frequencies of the E-FGM plate resting on the Winkler and Pasternak elastic foundation.

The methodology of DSM is implemented into a MATLAB program. The natural frequencies obtained by DSM are compared with the published results. The present paper contributes a novel set of natural frequencies incorporating Winkler and Pasternak elastic foundation for square and rectangular E-FGM plates. The effect of various material parameters, elastic foundation, and boundary conditions on natural frequency is also highlighted in tables and graphs. It is obtained that the impact of the Pasternak modulus on natural frequency is higher than the Winkler modulus for various material property variations of the E-FGM plate. The obtained natural frequency results by DSM resting on an elastic foundation can be further used as a benchmark solution for future comparison.