Bending analysis of two-directional functionally graded beams using trigonometric series functions

Abstract

In the present paper, Navier’s method based on the first-order shear deformation theory for bending analysis of two-directional functionally graded beams subjected to various sets of boundary conditions is presented. In Navier's method, different trigonometric series functions are proposed for each boundary condition. The accuracy of these proposed functions was investigated and compared with the literature. It is also presented in a parametric study. The governing equations are derived according to Lagrange’s principle. The variation of the components of the beam material in the volume is defined by a power-law rule. The normalized maximum transverse deflections, the normalized axial and transverse shear stresses are obtained for various boundary conditions, gradation exponents (p_x, p_z) in the x- and z-directions, and the slenderness (L/h). The trigonometric series functions used in this study give results that are quite compatible with the literature. In addition, the parametric study contributes to the literature.

1 Introduction

Functionally graded materials (FGMs), which have wide usage areas such as aviation, aircraft and space industry, mechanical, construction, and electrical circuit industry, are preferred because they are highly resistant to thermal changes. Its mechanical properties change smoothly and continuously from one side to the other. It is formed of ceramic and metal phases to reduce thermal stresses due to temperature changes. Due to the constant change in the composition of the component materials, FGMs have many advantages over composites. Therefore, many researchers have studied the mechanical behavior of FGMs.

According to the literature, researchers have conducted a significant number of studies over the past two decades to predict and understand the bending, buckling, and vibration behavior of conventional (one-directional) functionally graded beams (or 1D-FGBs) and plates based on different theories [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

1D-FGMs are unsuitable for meeting technical requirements such as temperature and stress distributions in two or three directions for spacecraft and shuttles. To eliminate the mentioned disadvantage of 1D-FGM, a new type of FGM is needed whose material properties can vary in two or three directions. For this reason, there are many studies in the literature examining the mechanical behavior of two-directional functionally graded beams (2D-FGBs) with numerical and analytical methods according to various beam theories. Among the studies carried out with the finite element method, which is the most widely used numerical method in the literature, we can mention the following: Karamanlı and Vo [19] performed the size-dependent bending analysis of two-directional functionally graded microbeams via a quasi-3D theory and finite element method. Chinh et al. [20] investigated the elastostatic bending behavior of a two-directional functionally graded sandwich beam under various types of non-uniform distributed loads by a finite element model. Chen et al. [21] presented nonlinear free vibration analysis of a rotating two-directional functionally graded porous micro-beam using isogeometric analysis based on the Timoshenko beam theory. Nguyen et al. [22] investigated the dynamic behavior of a two-directional functionally graded sandwich beam made of three different materials due to the non-uniform motion of a moving point load. Viet et al. [23] presented free vibration analysis based on a finite element model of unidirectional and bidirectional functionally graded cantilever beams. Le et al. [24] proposed an efficient third‐order shear deformation beam element for free vibration and buckling analysis of two-directional functionally graded sandwich beams.

Among analytical works, we can mention the following: Lü et al. [25] presented elasticity solutions for bending and thermal deformations of bi-directional FGBs with different end conditions, using the state space-based differential quadrature method. Şimşek [26] investigated free and forced vibration of bi-directional functionally graded Timoshenko beam under the action of a moving load. Şimşek [27] studied buckling of Timoshenko beams composed of 2D-FGBs having different boundary conditions. Nejad et al. [28] presented buckling analysis of arbitrary two-directional functionally graded Euler–Bernoulli nano-beams based on nonlocal elasticity theory. Wang et al. [29] proposed an analytical solution for free vibration of a functionally graded beam with variable material properties along the beam length and thickness. Karamanlı [30,31,32] presented the bending and elastostatic behavior of 2D-FGBs subjected to various sets of boundary conditions by using different shear deformation theories and the Symmetric Smoothed Particle Hydrodynamics method. Karamanlı [33,34,35] investigated free vibration and buckling of 2D-FGBs according to different beam theories using various solution methods. Shanab and Attia [36] studied semi‑analytical solutions for static and dynamic responses of bi‑directional functionally graded non-uniform nanobeams with surface energy effects. Huang [37] investigated bending and free vibration behaviors of bi-directional functionally graded cylindrical beams. Huang and Ouyang [38] presented the exact solution for bending analysis of 2D-FG Timoshenko beams.

Although there are many studies dealing with the mechanical behavior of FGM beams by numerical and analytical methods, the literature review shows that research on 2D-FGBs with employing Navier’s method is limited. The most critical situation that distinguishes the existing studies for Navier's method is the functions used in the solution. In this method, trigonometric functions that satisfy the boundary conditions for the solution should be selected. Due to the difficulty in selecting these functions, studies using Navier's method have generally been limited to simple beams. By the literature survey and authors’ knowledge, there is no study examining the bending behavior of 2D-FGBs with the proposed trigonometric series functions. This study aims to perform a bending analysis of 2D-FGBs with various boundary conditions using trigonometric series functions and to investigate the accuracy of the trigonometric series functions. The difference between Huang and Ouyang [38] used for comparison and the presented study is methods. They used the equilibrium equations for the plane state of elasticity in their research. Proposed trigonometric series functions were used before by Nguyen et al. [39] for static, vibration, and buckling of laminated composite beams. The governing equations are derived according to Lagrange’s principle. A power-law rule defines the variation of the components of the beam material in the volume. The normalized maximum transverse deflections, the normalized axial, and transverse shear stresses are obtained for various boundary conditions, gradation exponents (p_x, p_z) in the x- and z-directions, and the slenderness (L/h). In addition, this study aims to present some benchmark results for the bending behavior of 2D-FGBs subjected to various sets of boundary conditions with employing Navier's method. Some new graphs that can be used as reference data for the future are presented in parametric studies.

2 Theory and formulation

2.1 Material properties

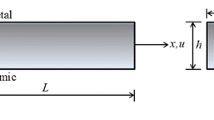
Figure 1 shows a two-directional functionally graded beam of length L, width b, thickness h. The x-, y-, and z-axes are located along the length, width, and thickness of the beam, respectively. The beam is subjected to a uniformly distributed loading q₀ in the same direction as the z-axis. The beam consists of a mixture of two components such as ceramic (Al₂O₃) and metal (Al). According to the rule of mixtures, the effective material properties can be given by

$$ P(x,z) = P_{c} V_{c} \left( {x,z} \right) + P_{m} V_{m} \left( {x,z} \right) $$

(1)

where P_m and P_c are the corresponding material properties of the metal and ceramic constituents, e.g., Young’s modulus E, Poisson’s ratio ν, and mass density ρ, respectively. V_c and V_m are the volume fractions of the ceramic and metal, and they are related by

$$ V_{c} \left( {x,z} \right) + V_{m} \left( {x,z} \right) = 1 $$

(2)

Fig. 1

Geometry of a 2D-FGBs under uniformly distributed loading with the corresponding coordinates

For the 2D-FGBs, the effective material properties are assumed to follow the power-law rule. The volume fraction of ceramic constituent is defined by

$$ V_{c} \left( {x,z} \right) = \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} \left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} $$

(3)

where p_x, and p_z are the gradation exponents (power-law exponents) in the x and z directions. The variation of the volume fraction (V_c) in two dimensions is shown in Fig. 2.

Fig. 2

Variation of the volume fraction (V_c) in x and z directions for a) p_x = p_z = 0, b) p_x = p_z = 1, c) p_x = p_z = 5

Using Eqs. (1, 2 and 3), the effective material properties of the 2D-FGB whose material properties vary continuously through the length and thickness can be found as follows:

$$ P(x,z) = (P_{c} - P_{m} )\left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} \left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} + P_{m} $$

(4)

Based on Eq. (4), one can be expressed for the Young's modulus E and shear modulus G by

$$ \begin{aligned} E(x,z) & = (E_{c} - E_{m} )\left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} \left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} + E_{m} \\ G(x,z) & = (G_{c} - G_{m} )\left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} \left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} + G_{m} \\ \end{aligned} $$

(5)

where E_m, E_c, and G_m, G_c are Young’s modulus and shear modulus of metal and ceramic, respectively.

2.2 Governing Equations and Analytical Solution

The nonzero components of the displacement field of FSDT are given by

$$ \begin{aligned} u(x,z,t) & = u^{0} (x,t) + z\,\phi^{0} (x,t), \\ w(x,z,t) & = w^{0} (x,t) \\ \end{aligned} $$

(6)

Here superscript “0” indicates the variable at the neutral axis. According to the geometrical and physical linearity assumptions, the strain–displacement relations and stresses of the beam take the following form:

$$ \varepsilon_{xx} = \frac{\partial u}{{\partial x}} = u_{,x}^{0} + z\phi_{,x}^{0} ,\quad \gamma_{xz} = \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}} = w_{,x}^{0} + \phi^{0} $$

(7)

$$ \sigma_{xx} = E(x,z)\varepsilon_{xx} ,\quad \tau_{xz} = KG(x,z)\gamma_{xz} $$

(8)

where ε_xx is the normal strain, γ_xz is the shear strains, σ_xx is the normal stress, τ_xz is the shear stress, K is the shear correction factor, E(x, z) is the Young modulus, and G(x, z) is the shear modulus. $( \cdot )_{,x}$ denotes the derivative with respect to x.

The governing equations can be obtained by Lagrange’s equations given by

$$ \frac{d}{dt}\left( {\frac{\partial \Pi }{{\partial \dot{q}_{i} }}} \right) - \frac{\partial \Pi }{{\partial q_{i} }} = 0 $$

(9)

where q_i represents the variables of u_i, w_i and ϕ_i. The Lagrangian functional is expressed in the following form

$$ \Pi = T - (U + V) $$

(10)

The strain energy of the beam can be expressed by

$$ U = \frac{1}{2}\int_{0}^{L} {\int_{A} {(\sigma_{xx} \varepsilon_{xx} + \tau_{xz} \gamma_{xz} )dA} {\kern 1pt} dx} $$

(11)

where A is the cross-sectional area of the beam. If Eqs. (7) and (8) are substituted into Eq. (11) together with Eq. (5), one can obtain the strain energy in the following form

$$ U = \frac{1}{2}\int_{0}^{L} {\left\{ \begin{gathered} (u_{,x}^{0} )^{2} \left\{ {A_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + A_{1} } \right\} + 2u_{,x}^{0} \phi_{,x}^{0} \left\{ {B_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + B_{1} } \right\} \hfill \\ \quad + ({\kern 1pt} \phi_{,x}^{0} )^{2} \left\{ {C_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + C_{1} } \right\} + (w_{,x}^{0} + \phi^{0} )^{2} \left\{ {D_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + D_{1} } \right\} \hfill \\ \end{gathered} \right\}dx} $$

(12)

where the stiffness coefficients are defined as

$$ \begin{gathered} [A_{0} ,B_{0} ,C_{0} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left( {E_{c} - E_{m} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} [1,z,z^{2} ]dz} ,\quad [A_{1} ,B_{1} ,C_{1} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {E_{m} [1,z,z^{2} ]dz} \hfill \\ D_{0} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {K\left( {G_{c} - G_{m} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} dz} ,\quad D_{1} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {KG_{m} dz} \hfill \\ \end{gathered} $$

(13)

The kinetic energy of beam can be given by

$$ T = \frac{1}{2}\int_{0}^{{L_{e} }} {\int_{A} {\rho (x,z)(\dot{u}^{2} + \dot{w}^{2} )dA} {\kern 1pt} } dx $$

(14)

where dot denotes the derivative with respect to time. Taking the derivative of Eqs. (6) with respect to time, and substituting the result into Eq. (14) gives in the following form

$$ T = \frac{1}{2}\int_{0}^{L} {\left\{ \begin{gathered} (\dot{u}^{0} )^{2} \left\{ {I_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{00} } \right\} + 2\dot{u}^{0} \dot{\phi }^{0} \left\{ {I_{1} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{11} } \right\} \hfill \\ \quad + ({\kern 1pt} \dot{\phi }^{0} )^{2} \left\{ {I_{2} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{22} } \right\} + (\dot{w}^{0} )^{2} \left\{ {I_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{00} } \right\} \hfill \\ \end{gathered} \right\}dx} $$

(15)

where the inertia coefficients are

$$ [I_{0} ,I_{1} ,I_{2} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{{p_{z} }} [1,z,z^{2} ]dz} ,\quad [I_{00} ,I_{11} ,I_{22} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\rho_{m} [1,z,z^{2} ]dz} $$

(16)

where $\rho_{m}$ and $\rho_{c}$ are the mass density of metal and ceramic, respectively. The work done by the vertical uniformly distributed loading q₀ can be expressed as

$$ V = \int_{0}^{L} {q_{0} w^{0} dx} $$

(17)

Solutions to $u^{0} (x,t)$, $w^{0} (x,t)$ and $\phi^{0} (x,t)$ can be assumed as

$$ u^{0} (x,t) = \sum\limits_{i = 1}^{m} {\varphi_{i} (x)\,u_{i} (t)} ,\quad w^{0} (x,t) = \sum\limits_{i = 1}^{m} {\psi_{i} (x)\,w_{i} (t)} ,\quad \phi^{0} (x,t) = \sum\limits_{i = 1}^{m} {\theta_{i} (x)\,\phi_{i} (t)} $$

(18)

where $\varphi_{i} (x)$, $\psi_{i} (x)$ and $\theta_{i} (x)$ are trigonometric series functions that change depending on the boundary conditions of the beam, and $u_{i} (t)$, $w_{i} (t)$ and $\phi_{i} (t)$ are the generalized nodal displacements, and m represents the number of trigonometric series. The trigonometric series functions selected to satisfy the boundary conditions for the beams considered in the study are given in Table 1. Here, SS refers to the simply supported beam, CC to the clamped–clamped beam, and CF to the clamped-free beam.

Table 1 Kinematic boundary conditions and trigonometric series functions used in Navier’s method

Substituting Eqs. (12), (15) and (17) into Eq. (9) with considering Eqs. (18) leads to

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{m}}^{11} } & {\mathbf{0}} & {{\mathbf{m}}^{13} } \\ {\mathbf{0}} & {{\mathbf{m}}^{22} } & {\mathbf{0}} \\ {{\mathbf{m}}^{13T} } & {\mathbf{0}} & {{\mathbf{m}}^{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{u}_{i} } \\ {\ddot{w}_{i} } \\ {\ddot{\phi }_{i} } \\ \end{array} } \right\}{\mathbf{ + }}\left[ {\begin{array}{*{20}c} {{\mathbf{k}}^{11} } & {\mathbf{0}} & {{\mathbf{k}}^{13} } \\ {\mathbf{0}} & {{\mathbf{k}}^{22} } & {{\mathbf{k}}^{23} } \\ {{\mathbf{k}}^{13T} } & {{\mathbf{k}}^{23T} } & {{\mathbf{k}}^{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{i} } \\ {w_{i} } \\ {\phi_{i} } \\ \end{array} } \right\}{\mathbf{ = }}\left\{ {\begin{array}{*{20}c} 0 \\ {{\mathbf{f}}_{{\mathbf{2}}} } \\ 0 \\ \end{array} } \right\} $$

(19)

where m, k and f are the mass matrix, the stiffness matrix and the force vector, respectively. m, k and f₂ are explicitly expressed for SS 2D-FGB in the following form

$$ \begin{aligned} {\mathbf{m}}_{ij}^{11} & = \int\limits_{0}^{L} {\left\{ {I_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{00} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx} , \\ {\mathbf{m}}_{ij}^{13} & = \int\limits_{0}^{L} {\left\{ {I_{1} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{11} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx} , \\ {\mathbf{m}}_{ij}^{22} & = \int\limits_{0}^{L} {\left\{ {I_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{00} } \right\}\sin \left( {\frac{i\pi }{L}x} \right)\sin \left( {\frac{j\pi }{L}x} \right)dx} , \\ {\mathbf{m}}_{ij}^{33} & = \int\limits_{0}^{L} {\left\{ {I_{2} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + I_{22} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx} , \\ \end{aligned} $$

$$ \begin{aligned} {\mathbf{k}}_{ij}^{11} & = \int\limits_{0}^{L} {ij\frac{{\pi^{2} }}{{L^{2} }}} \left\{ {A_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + A_{1} } \right\}\sin \left( {\frac{i\pi }{L}x} \right)\sin \left( {\frac{j\pi }{L}x} \right)dx, \\ {\mathbf{k}}_{ij}^{13} & = \int\limits_{0}^{L} {ij\frac{{\pi^{2} }}{{L^{2} }}} \left\{ {B_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + B_{1} } \right\}\sin \left( {\frac{i\pi }{L}x} \right)\sin \left( {\frac{j\pi }{L}x} \right)dx, \\ {\mathbf{k}}_{ij}^{22} & = \int\limits_{0}^{L} {ij\frac{{\pi^{2} }}{{L^{2} }}} \left\{ {D_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + D_{1} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx, \\ {\mathbf{k}}_{ij}^{23} & = \int\limits_{0}^{L} {i\frac{\pi }{L}} \left\{ {D_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + D_{1} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx, \\ {\mathbf{k}}_{ij}^{33} & = \int\limits_{0}^{L} {ij\frac{{\pi^{2} }}{{L^{2} }}} \left\{ {C_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + C_{1} } \right\}\sin \left( {\frac{i\pi }{L}x} \right)\sin \left( {\frac{j\pi }{L}x} \right)dx \\ &\quad + \int\limits_{0}^{L} {\left\{ {D_{0} \left( {1 - \frac{x}{2L}} \right)^{{p_{x} }} + D_{1} } \right\}\cos \left( {\frac{i\pi }{L}x} \right)\cos \left( {\frac{j\pi }{L}x} \right)dx} , \\ \end{aligned} $$

$$ {\mathbf{f}}_{{\mathbf{2}}} = \frac{{Lq_{0} }}{i\pi }\left[ {1 - \cos \left( {i\pi } \right)} \right]\quad {\text{with}}\;\,i = j = 1,2,...,m $$

(20)

The matrix governing equation of the 2D-FGB with the length of L in terms of U can be written as follows

$$ {\bf M}{\ddot{\mathbf U}} + {\bf KU} = {{\bf F}} $$

(21)

where M, K and F are the mass, stiffness matrix and the force vector, respectively. U is the vector of unknowns, and is as follows

$$ {\mathbf{U}} = \{ u_{1} \quad \cdots \quad u_{m} \quad w_{1} \quad \cdots \quad w_{m} \quad \phi_{1} \quad \cdots \quad \phi_{m} \}^{T} $$

(22)

For bending analysis, M is zero (M = 0) in Eq. (21). The system equations given by Eq. (21) has been solved numerically by using any numerical method. After this process, displacements and stresses are calculated.

3 Results and discussion

In this section, some numerical results obtained from the bending analysis of 2D-FGBs with various boundary conditions are presented. Numerical results are obtained with a code written in the MATLAB [40] program. The accuracy of the proposed trigonometric series functions for each boundary condition is investigated. In addition, some new graphs that can be used as reference data for the future are presented as parametric studies. The physical parameters of the beam are L = 1 m and b = 0.1 m. Two different slenderness such that L/h = 5 and 20 are considered. The uniformly distributed loading q₀ is 10,000 N/m. The shear correction factor is considered to be K = 5/6 for rectangular cross sections. A functionally graded beam composed of aluminum (Al) as metal and alumina (Al₂O₃) as ceramic is considered for which E_m = 70GPa, ρ_m = 2702 kg/m³, ν_m = 0.3, E_c = 380GPa, ρ_c = 3960 kg/m³, and ν_c = 0.3. The transverse deflections, axial and shear stresses are given in the following normalized form:

$$ \overline{w} = \frac{{100E_{m} bh^{3} }}{{q_{0} L^{4} }}w\left( {x,0} \right),\quad \overline{\sigma }_{xx} = \frac{bh}{{q_{0} L}}\sigma_{xx} \left( {x,z} \right),\quad \overline{\tau }_{xz} = \frac{bh}{{q_{0} L}}\tau_{xz} \left( {x,z} \right) $$

(23)

3.1 Convergence study

A convergence study is performed to determine the number of trigonometric series that will be sufficient. The normalized maximum transverse deflections of the 2D-FGBs with respect to the number of trigonometric series m for different boundary conditions (u⁰ ≠ 0, L/h = 5, p_x = p_z = 2) are given in Table 2. It is observed that the deflections converge quickly for three boundary conditions. Fourteen trigonometric series (m = 14) seem to be enough for the desired accuracy in numerical calculations. In addition, the results of the proposed solution agree well with the exact solution given by Ref. [38].

Table 2 Convergence studies for normalized maximum transverse deflections of the 2D-FGBs with the different boundary conditions (u⁰ ≠ 0, L/h = 5, p_x = p_z = 2)

3.2 Verification with previous results

Verification studies are carried out to demonstrate the accuracy of the proposed solution and to investigate the responses of 2D-FGBs with various boundary conditions for bending problems. Tables 3 and 4 show a comparison of the normalized maximum transverse deflections of the SS 2D-FGBs for various slenderness (L/h = 5, L/h = 20) and gradation exponents. For u⁰ = 0, the effects of longitudinal displacements are neglected. For u⁰ ≠ 0, it is not neglected. The tables compare the normalized maximum transverse deflections of the SS 2D-FGBs with the results of Huang and Ouyang [38], which is the exact solution based on the Timoshenko beam theory. The results are in good agreement as seen. According to these tables, the smallest normalized displacements occur when p_x = p_z = 0 (fully ceramic) for L/h = 5 and 20. With the increase of the p_x and p_z in both directions, the transverse deflections increase. The normalized maximum transverse deflection decreases as the L/h increases. For p_z = 0, the normalized maximum transverse deflections do not change according to the results of u⁰ = 0 and u⁰ ≠ 0. For p_z ≠ 0, the results of u⁰ = 0 are smaller than the other.

Table 3 Comparison of the normalized maximum transverse deflections of the SS 2D-FGBs for various gradation exponents, L/h = 5

Table 4 Comparison of the normalized maximum transverse deflections of the SS 2D-FGBs for various gradation exponents, L/h = 20

In Tables 5 and 6, the normalized axial and transverse shear stresses of the SS 2D-FGBs are given for u⁰ ≠ 0. There is no difference in mechanical behavior between the u⁰ = 0 and u⁰ ≠ 0. The results of this study are compared with those of Karamanlı [32] based on a four-unknown shear and normal deformation theory and Vo et al. [6] based on FSDT for p_x = 0. The results for axial stresses are in good agreement. For transverse shear stresses, the results do not agree with those of Karamanlı [32] because the theories are different, but they are in good agreement with those of Vo et al. [6]. The transverse shear strain is assumed to be constant in the beam depth direction in the FSDT. In higher-order shear deformation theories, the transverse shear strain is not constant throughout the depth. It is clear that the axial stress decreases as the gradation exponent in the x-direction increases for p_z ≠ 0. In the z-direction, they increase with increasing p_z. The transverse shear stresses increase with the increase of p_x. They decrease with the increase of p_z.

Table 5 The normalized axial stress $\overline{\sigma }_{xx} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-\nulldelimiterspace} 2},{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)$ of the SS 2D-FGBs (u⁰ ≠ 0)

Table 6 The normalized transverse shear stress $\overline{\sigma }_{xz} \left( {0,0} \right)$ of the SS 2D-FGBs (u⁰ ≠ 0)

Comparison of the normalized maximum transverse deflections of the CC 2D-FGBs for various gradation exponents and the slenderness (L/h = 5, L/h = 20) is given in Tables 7 and 8. The results are in good agreement with those of Ref. [38]. It is clear that the deflections increase as the gradation exponents increase.

Table 7 Comparison of the normalized maximum transverse deflections of the CC 2D-FGBs for various gradation exponents, L/h = 5

Table 8 Comparison of the normalized maximum transverse deflections of the CC 2D-FGBs for various gradation exponents, L/h = 20

Verification of the normalized maximum transverse deflections of the CF 2D-FGBs for various gradation exponents and the slenderness is shown in Tables 9 and 10. Here, a good agreement is observed between the results. Also, as it is expected, the largest deflections occur in the CF beam within the considered boundary conditions. As it is seen from Tables 9 and 10, the transverse deflections increase as the p_x and p_z increase due to the lower stiffness.

Table 9 Comparison of the normalized maximum transverse deflections of the CF 2D-FGBs for various gradation exponents, L/h = 5

Table 10 Comparison of the normalized maximum transverse deflections of the CF 2D-FGBs for various gradation exponents, L/h = 20

3.3 Parametric study

This section presents the normalized transverse deflections, axial and shear stresses of 2D-FGBs with various boundary conditions. Since there is no difference in mechanical behavior between neglecting and not ignoring the effects of longitudinal displacements, results are given according to u⁰ ≠ 0. The beams have the slenderness L/h = 5.

Normalized transverse deflections of the SS 2D-FGBs with respect to the normalized coordinate x/L for various gradation exponents are presented in Fig. 3. As can be seen from the figure, it is clear that the transverse deflections increase with the increase in the gradation exponent (i.e., the metallic character of the beam increases). The location of the normalized maximum transverse deflections of the SS 2D-FGBs is at or very close to the mid-section. For p_x = 0, the location of the normalized maximum transverse deflections is at the mid-section (x/L = 0.5). As seen, with the increase of p_x, x/L also increases. Also, when p_z increases for p_x = 5, x/L decreases.

Fig. 3

Normalized transverse deflections of the SS 2D-FGBs with respect to the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0)

Figure 4 shows normalized axial stress of the SS 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents. When p_x and p_z increase, the ceramic ratio of the beam decreases, and the metal ratio increases. Based on this information, the following comments can be made. In any beam cross section in the x-direction, the tensile region is at the top, and the compression region is at the bottom. As it is expected, the normalized absolute maximum stress is at the top surface of the beam. It is clear that the tensile stress increase by increasing of gradation exponent in the z-direction. As it increases p_x, the maximum axial stress decrease, and it moves away from the middle section.

Fig. 4

Normalized axial stress of the SS 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

In Fig. 5, normalized shear stress of the SS 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents are presented. The shear stress distribution is linear for p_z = 0. For nonzero values of p_z, for example, with increasing p_x for p_z = 1, shear stress does not change at the left edge of the beam, while shear stress decreases at the right edge. The reason for this is that with the increase in p_x, the material property of the left edge does not change, while the material property of the right edge approaches metal. When p_x is constant, shear stress increases at the top of the section with increasing p_z. It is observed that the variation of p_z is more effective on shear stress than the p_x.

Fig. 5

Normalized shear stress of the SS 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

Figure 6 shows normalized transverse deflections of the CC 2D-FGBs with respect to the normalized coordinate x/L for various gradation exponents. The normalized transverse deflections increase with increasing p_x and p_z (i.e., decreasing the ceramic ratio of the beam). For p_x = 0, while the maximum deflection is in the middle section of the beam, it moves away from the middle section with the increase of p_x. The comments for the SS beam can be said for this as well.

Fig. 6

Normalized transverse deflections of the CC 2D-FGBs with respect to the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0)

In Fig. 7, the normalized axial stress of the CC 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents is presented. At different values of p_x and p_z, the compression region is above the section at the left and right edges of the beam. In the middle region of the beam (approximately 0.25 x/L 0.8), the tensile region is above the section. The maximum compressive stress occurs at the x/L = 0 and z/h = 0.5 point of the beam. Here, the material property is ceramic. The maximum compressive stress increases with the increase of p_x and p_z. The tensile stress decreases with increasing p_x in the middle section of the beam x/L = 0.5. Here, with the rise of p_z, the tensile stress increases.

Fig. 7

Normalized axial stress of the CC 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

The variations of the normalized shear stress of the CC 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents are given in Fig. 8. For p_x = 0 and p_z = 0, the shear stress is zero in the middle section. The shear stress increases at the left edge and decreases at the right edge with the increase in p_x. Here, the material property is ceramic on the left edge, and the ceramic ratio decreases toward the right end of the beam with the increase in p_x. When p_x is not changed, the maximum shear stress increases with the increase of p_z on the left and right edges.

Fig. 8

Normalized shear stress of the CC 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

In Fig. 9, the normalized transverse deflections of the CF 2D-FGBs are plotted for various p_x and p_z. The gradation exponents in x, z-direction p_x, and p_z are set to 1. The effect of the varying gradation exponents in the x, z-direction p_x, and p_z is observed for the transverse deflections. As the gradation exponent in the x and z-direction increases, the deflections increase. As expected, the increase in p_z affects the deflections more than p_x. The maximum deflections occur at the largest value of p_z (high metal content of the beam). The maximum deflections always occur at the free end of the beam, regardless of material properties.

Fig. 9

Normalized transverse deflections of the CF 2D-FGBs with respect to the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0)

The variations of the normalized axial stress of the CF 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents are given in Fig. 10. When p_x increases, the material property on the left edge does not change, so there is not much change in axial stress. For example, for p_z = 0, 1, 2, and 5, the variation of p_x does not affect their magnitudes, as the maximum compressive stress occurs at the left edge. However, the variation of p_x changes the axial stress distribution in the x, and z-direction of the beam. The compressive stresses increase with the increase of p_z. In addition, in any beam cross section in the x-direction, the compression region is at the top, and the tensile region is at the bottom. As is expected, the normalized absolute maximum stress is generally at the top surface of the beam.

Fig. 10

Normalized axial stress of the CF 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

The variations of the normalized shear stress of the CF 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents are shown in Fig. 11. Since the maximum shear stress is on the left edge, increasing p_x does not change the value of the maximum shear stress. The maximum shear stress increases with the increase of p_z. Here, it is seen that p_z is more effective on shear stress.

Fig. 11

Normalized shear stress of the CF 2D-FGBs with respect to the normalized thickness z/h and the normalized coordinate x/L for various gradation exponents (u⁰ ≠ 0, L/h = 5)

4 Conclusion

A Navier’s method based on FSDT is presented for bending analysis of the 2D-FGBs subjected to various sets of boundary conditions. In Navier's method, different trigonometric series functions are proposed for each boundary condition. The governing equations are derived according to Lagrange’s principle. The variation of the components of the beam material in the volume is defined by a power-law rule. The normalized maximum transverse deflections, the normalized axial and transverse shear stresses are obtained for various boundary conditions, gradation exponents (p_x, p_z) in the x- and z-directions, and the slenderness (L/h). The results show that the gradation exponents, as well as the boundary conditions, play a significant influence on the bending behavior of the 2D-FGBs. According to the study, the following conclusions can be drawn:

• The trigonometric series functions used in the study can accurately predict the transverse deflections and the stresses of 2D-FGBs with different boundary conditions. The accuracy and performance of the present solution in the computation are well enough.

• The transverse deflections increase when the p_x and p_z increase in both directions (i.e., ceramic ratio decreases).

• The location of the maximum deflection in the SS and CC beams depends on the material property (depend on p_x and p_z).

• In CF beams, it has been observed that the material property has no effect on the location of the maximum deflection, but it is quite effective on the magnitude of the maximum deflection.

• Since p_z changes the material properties faster, the variation of p_z is more effective on stresses than the p_x.