Introduction

The surface charge density/surface potential relationship and the electric double-layer potential distribution for colloidal particles in an electrolyte solution, which play essential roles in determining the behaviors of colloidal particles, can be obtained via the Poisson-Boltzmann equation [1,2,3,4,5,6,7,8,9]. The standard Poisson-Boltzmann equation, however, assumes that ions behave like point charges and neglects the effects of ionic size. There are many theoretical studies on the modified Poisson-Boltzmann equation [10,11,12,13,14,15,16], which takes into account the effect of ionic size by introducing the activity coefficients of electrolyte ions [10, 17,18,19]. In a previous paper [20], on the basis of the equation for the ionic activity coefficients given by Carnahan and Starling [19], which is the most accurate among existing theories, we presented a simple algorithm for solving the modified Poisson-Boltzmann equation and derived a simple approximate analytic expression for the surface charge density/surface potential relationship for a planar charged surface. On the basis of the modified Poisson-Boltzmann equation, we also derived analytic expressions for the interaction energy between two colloidal particles [21] and the electrophoretic mobility of a spherical particle [22].

In the present paper, we derive approximate expressions for the surface charge density/surface potential relationship and double-layer potential distribution for a spherical or cylindrical colloidal particle based on the modified Poisson-Boltzmann equation with the help of the previously developed method [23,24,25,26]. We also derive approximate expression for the effective surface potential of a spherical or cylindrical particle and for the electrostatic interaction energy between two spherical or cylindrical particles on the basis of the linear superposition approximation.

Surface charge density/surface potential relationship and double-layer potential distribution around a spherical particle

Consider a spherical particle of radius a in a symmetrical electrolyte solution of valence z and bulk concentration (number density) n. We take a spherical coordinate system with its origin r = 0 placed at the center of the sphere and r is the radial distance from the sphere center so that the region r > a corresponds to the electrolyte solution. The electric double-layer potential ѱ(r) at position r in the electrolyte solution (r > a) obeys the following spherical Poisson equation:

$$ \frac{d^2\psi }{{d r}^2}+\frac{2}{r}\frac{d\psi}{d r}=-\frac{\rho_{\mathrm{el}}(r)}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}} $$
(1)

Here, εr is the relative permittivity of the electrolyte solution, εo is the permittivity of a vacuum, and ρel(r) is the space charge density resulting from the electrolyte ions and is given by

$$ {\rho}_{\mathrm{el}}(r)= ze\left\{{n}_{+}(r)-{n}_{-}(r)\right\} $$
(2)

where n+(r) and n−(r) are, respectively, the concentrations of cations and anions at position r and e is the elementary electric charge. The boundary conditions for ѱ(r) are given by

$$ \psi (a)={\psi}_{\mathrm{o}} $$
(3)
$$ \psi \to 0,\kern0.5em \frac{d\psi}{d r}\to 0\kern0.5em \mathrm{as}\kern0.5em r\to \infty $$
(4)

We assume that the activity coefficients of cations and anions at position r have the same value γ(r). The electrochemical potential μ+(r) of cations and that of anions μ − (r) are thus given by

$$ {\mu}_{\pm }(r)={\mu}_{\pm}^{\mathrm{o}}\pm ze\psi (r)+ kT\ln \left[\gamma (r){n}_{\pm }(r)\right] $$
(5)

where \( {\mu}_{\pm}^{\mathrm{o}} \) are constant terms, k is Boltzmann’s constant, and T is the absolute temperature. The values of μ±(r) must be the same as those in the bulk solution phase, where ѱ(r) = 0, viz.,

$$ {\mu}_{\pm}\left(\infty \right)={\mu}_{\pm}^{\mathrm{o}}+ kT\ln \left({\gamma}^{\infty }n\right) $$
(6)

where γ∞ = γ(∞). By equating μ±(r) = μ±(∞), we obtain

$$ {n}_{\pm }(r)=\frac{\gamma^{\infty }n}{\gamma (r)}\exp \left(\mp \frac{ze\psi (r)}{kT}\right) $$
(7)

Thus, Eq. (1) as combined with Eqs. (2) and (7) becomes the following modified Poisson-Boltzmann equation:

$$ \frac{d^2\psi }{{d r}^2}+\frac{2}{r}\frac{d\psi}{d r}=\frac{2 zen}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}}\cdot \frac{\gamma^{\infty }}{\gamma (r)}\sinh \left(\frac{ze\psi (r)}{kT}\right) $$
(8)

We now assume that cations and anions have the same radius ai. We introduce the volume fraction ø + (r) of cations and that of anions ø − (r) at position r. Then, we have

$$ {\phi}_{\pm }(r)=\left(\frac{4}{3}\pi {a}_{\mathrm{i}}^3\right){n}_{\pm }(r) $$
(9)

The total ion volume fraction ø(x) at position r is thus given by

$$ \phi (r)={\phi}_{+}(r)+{\phi}_{-}(r)=\left(\frac{4}{3}\pi {a}_{\mathrm{i}}^3\right)\left\{{n}_{+},\left(,r,\right),+,{n}_{-},\left(,r,\right)\right\}={\phi}_{\mathrm{B}}\frac{\left\{{n}_{+},\left(,r,\right),+,{n}_{-},\left(,r,\right)\right\}}{2n} $$
(10)

where øB ≡ ø(∞) = (4πai3/3)⋅2n is the total ion volume fraction in the bulk solution phase.

We employ the expression for γ(x) derived by Carnahan and Starling [19], viz.,

$$ \gamma (r)=\exp \left[\frac{\phi (r)\left\{8-9\phi (r)+3{\phi}^2(r)\right\}}{{\left\{1-\phi (r)\right\}}^3}\right] $$
(11)

In a previous paper [20], we have shown that Eq. (11) can be approximated well by

$$ \gamma (r)={\gamma}^{\infty}\left\{1+G{\sinh}^2\left(\frac{ze\psi (r)}{2 kT}\right)\right\} $$
(12)

where G is defined by

$$ G=\frac{16{\phi}_{\mathrm{B}}}{1+8{\phi}_{\mathrm{B}}} $$
(13)

The above approximation (Eq. (12)) is a good approximation with negligible errors for low øB (øB ≤ 0.1) and low-to-moderate potentials (|zeѱo/kT| ≤ 3) [20]. By substituting Eq. (12) into Eq. (8), we obtain the following approximate form for the spherical modified Poisson-Boltzmann equation:

$$ \frac{d^2\psi }{{d r}^2}+\frac{2}{r}\frac{d\psi}{d r}=\frac{2 zen}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}}\cdot \frac{\sinh \left(\frac{ze\psi (r)}{kT}\right)}{1+G{\sinh}^2\left(\frac{ze\psi (r)}{2 kT}\right)} $$
(14)

which is rewritten in terms of the scaled electric potential y(r) = zeѱ(r)/kT:

$$ \frac{d^2y}{dr^2}+\frac{2}{r}\frac{dy}{dr}=\frac{\kappa^2\sinh (y)}{H(y)} $$
(15)

with

$$ H(y)=1+G{\sinh}^2\left(y/2\right) $$
(16)

We introduce f(y) defined by

$$ f(y)=\operatorname{sgn}\left({y}_{\mathrm{o}}\right)\cdot 2\sqrt{\frac{\ln \left(H(y)\right)}{G}} $$
(17)

where yo = zeѱo/kT is the scaled particle surface potential and sgn(yo) = + 1 for yo > 0 and − 1 for yo < 0. Then, Eq. (15) becomes

$$ \frac{d^2y}{dr^2}+\frac{2}{r}\frac{dy}{dr}={\kappa}^2f(y)\frac{df(y)}{dy} $$
(18)

In order to obtain a large κa approximate solution to Eq. (18), we make the change of variables [23,24,25]

$$ s=\frac{a}{r}{e}^{-\kappa \left(r-a\right)} $$
(19)

and rewrite Eq. (18) as

$$ {s}^2\frac{d^2y}{ds^2}+s\frac{dy}{ds}=f(y)\frac{df}{dy}-\frac{2\kappa r+1}{{\left(\kappa r+1\right)}^2}\left\{f(y)\frac{df}{dy}-s\frac{dy}{ds}\right\} $$
(20)

which is subject to the boundary conditions: y = yo at s = 1 and y = dy/ds = 0 at s = 0 (see Eqs. (3) and (4)). This approximation method is excellent for κa ≥ 1 with relative errors less than about 1% [23,24,25].

When κa »1, Eq. (20) reduces to

$$ {s}^2\frac{d^2y}{ds^2}+s\frac{dy}{ds}=f(y)\frac{df}{dy} $$
(21)

which is integrated one to give

$$ s\frac{dy}{ds}=f(y) $$
(22)

We then replace the second term on the right-hand side of Eq. (20) with its large κa limiting form, i.e., κr → κa and sdy/ds → f(y) (Eq. (22)), and integrate Eq. (21) to obtain

$$ s\frac{dy}{ds}={F}_{\mathrm{s}}(y) $$
(23)

with

$$ {F}_{\mathrm{s}}(y)=\frac{\kappa a}{\kappa a+1}f(y){\left[1+\frac{2\left(2\kappa a+1\right)}{{\left(\kappa a\right)}^2}\frac{1}{f^2(y)}{\int}_0^yf(u) du\right]}^{1/2} $$
(24)

The surface charge density σ/surface potential ѱo (or yo) relationship can be obtained by using the following relation:

$$ \sigma =-{\varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}{\left.\frac{d\psi}{d r}\right|}_{r={a}^{+}}=\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}\frac{\kappa a+1}{\kappa a}s{\left.\frac{d y}{d s}\right|}_{s=1}=\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}\frac{\kappa a+1}{\kappa a}{F}_{\mathrm{s}}\left({y}_{\mathrm{o}}\right) $$
(25)

or

$$ \sigma =\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}f\left({y}_{\mathrm{o}}\right){\left[1+\frac{2\left(2\kappa a+1\right)}{{\left(\kappa a\right)}^2}\frac{1}{f^2\left({y}_{\mathrm{o}}\right)}{\int}_0^{y_{\mathrm{o}}}f(u) du\right]}^{1/2} $$
(26)

Equation (23) is integrated again to give

$$ -\ln s={\int}_y^{y_{\mathrm{o}}}\frac{dy}{F_{\mathrm{s}}(y)} $$
(27)

One can numerically calculate Fs(y) from f(y) (Eq. (17)) with the help of Eq. (24) and then calculate y(r) from Eq. (27).

Equations (26) and (27) are the required expressions for the σ/yo relationship and y(r) for a sphere based on the modified Poisson-Boltzmann equation.

Surface charge density/surface potential relationship and potential distribution around a cylindrical particle

The same approximation method as for a spherical particle can be applied to an infinitely long cylindrical particle of radius a [23, 24, 26]. The cylindrical Poisson-Boltzmann equation for the electric potential ѱ(r) around a cylinder of radius a is

$$ \frac{d^2\psi }{{d r}^2}+\frac{1}{r}\frac{d\psi}{d r}=\frac{2 zen}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}}\cdot \frac{\sinh \left(\frac{ze\psi (r)}{kT}\right)}{1+G{\sinh}^2\left(\frac{ze\psi (r)}{2 kT}\right)} $$
(28)

where r is the radial distance from the cylinder axis r = 0. We make the change of variables [24, 26]

$$ c=\frac{K_0\left(\kappa r\right)}{K_0\left(\kappa a\right)} $$
(29)

where K n (z) is the modified Bessel functions of the second kind of order n. It can be shown that Eq. (28) can approximately integrated to give

$$ c\frac{dy}{dc}={F}_{\mathrm{c}}(y) $$
(30)

where

$$ {F}_{\mathrm{c}}(y)=\beta f(y){\left[1+2\left(\frac{1}{\beta^2}-1\right)\frac{1}{f^2(y)}{\int}_0^yf(u) du\right]}^{1/2} $$
(31)

with

$$ \beta =\frac{K_0\left(\kappa a\right)}{K_1\left(\kappa a\right)} $$
(32)

The surface charge density σ of the cylinder can be obtained as follows:

$$ \sigma =-{\varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}{\left.\frac{d\psi}{d r}\right|}_{r={a}^{+}}=\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}\frac{1}{\beta }c{\left.\frac{d y}{d c}\right|}_{c=1}=\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}\frac{1}{\beta }{F}_c\left({y}_{\mathrm{o}}\right) $$
(33)

or

$$ \sigma =\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}{ze}f\left({y}_{\mathrm{o}}\right){\left[1+2\left(\frac{1}{\beta^2}-1\right)\frac{1}{f^2\left({y}_{\mathrm{o}}\right)}{\int}_0^{y_{\mathrm{o}}}f(u) du\right]}^{1/2} $$
(34)

Equation (30) is integrated again to give

$$ -\ln c={\int}_y^{y_{\mathrm{o}}}\frac{dy}{F_{\mathrm{c}}(y)} $$
(35)

which gives y(r) as a function of r for a cylinder of radius a and scaled surface potential yo.

Equations (34) and (35) are the required expressions for the σ/yo relationship and y(r) for a cylinder based on the modified Poisson-Boltzmann equation.

Results and discussion

The principal results of the present paper are Eqs. (26), (27), (34), and (35) for the surface charge density/surface potential relationship and the electric double-layer potential distribution for a spherical or cylindrical colloidal particle in an electrolyte solution. These expressions, which are applicable for |yo| ≤ 3, øB ≤ 0.1, and κa ≥ 1, have been derived on the basis of the modified Poisson-Boltzmann equations (Eqs. (14) and (28)) by taking into account the ionic size effect through the approximate form (Eq. (12)) of the Carnahan-Starling activity coefficient (Eq. (11)). The Carnahan-Starling ionic activity coefficient (Eq. (11)) is the most accurate among the exiting theories and indeed agrees well with simulation results by Attard [27]. It can be seen [20] that Eq. (12) is a good approximation to Eq. (11) for small øB (øB ≤ 0.1) and low-to-moderate values of the electric potential y(x) (|y(x)| ≤ 3). The maximum error of Eq. (12) relative to Eq. (11) is ca. 3% for y(x) = 1, ca. 4% for y(x) = 2, and ca. 7% for y(x) = 3. Even for y(x) = 4, the maximum relative error is ca. 12% at øB = 0.01.

In the limit of small yo, Eqs. (26) and (27) for the sphere case reduce to

$$ {\psi}_{\mathrm{o}}=\frac{\sigma }{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa \left(1+1/\kappa a\right)} $$
(36)
$$ \psi (r)={\psi}_{\mathrm{o}}\frac{a}{r}{e}^{-\kappa \left(r-a\right)} $$
(37)

and Eqs. (34) and (35) for the cylinder case to

$$ {\psi}_{\mathrm{o}}=\frac{\sigma }{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa}\frac{K_0\left(\kappa a\right)}{K_1\left(\kappa a\right)} $$
(38)
$$ \psi (r)={\psi}_{\mathrm{o}}\frac{K_0\left(\kappa r\right)}{K_0\left(\kappa a\right)} $$
(39)

Note that in this limit, the σ/yo relationship and y(r) for a sphere or a cylinder become independent of øB and coincide with those obtained via the standard Poisson-Boltzmann equation.

In the limiting case of øB → 0, Eqs. (26), (27), (34), and (35) for the σ/yo relationship and y(r) for a spherical or cylindrical colloidal particle tend to those obtained via the standard Poisson-Boltzmann equation [24,25,26].

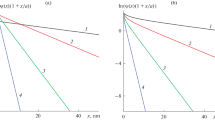
Some examples of the calculation of the σ/yo relationship and y(r) for a spherical particle on the basis of Eqs. (26) and (27) are shown in Figs. 1 and 2. These figures show how the effects of ionic size on the σ/yo relationship and y(r) become appreciable for higher surface charge density σ and higher total ion volume fraction øB. The ionic size effect always gives rise to an increase in the values of surface potential yo and double-layer potential y(r). This is because the ionic concentration becomes lower due to the ionic size effect, leading to a decrease in the ionic shielding effects so that the magnitude of yo and double-layer potential y(r) increases.

Fig. 1
figure 1

Scaled surface potential yo = zeѱo/kT as a function of scaled surface charge density σ* = zeσ/εrεoκkT calculated with Eq. (26) for three values of the total ion volume fraction øB = 0.1 (solid lines), 0.01 (dashed lines), and 0 (dotted lines) at scaled sphere radius κa = 1 and 10

Full size image
Fig. 2
figure 2

Scaled electric potential y(r) = zeѱ(r)/kT as a function of scaled radial distance κr calculated with Eq. (27) for three values of the total ion volume fraction øB = 0.1 (solid lines), 0.01 (dashed lines), and 0 (dotted lines) at scaled surface charge density σ* = zeσ/εrεoκkT = 3 and scaled sphere radius κa = 10

Full size image

The asymptotic form of the potential distribution around a sphere must be

$$ \psi (r)={\psi}_{\mathrm{eff}}\frac{a}{r}{e}^{-\kappa \left(r-a\right)} $$
(40)

where ѱeff is called the effective surface potential and is related to the surface potential ѱo by [25]

$$ {\psi}_{\mathrm{eff}}={\psi}_{\mathrm{o}}\exp \left[{\int}_0^{y_{\mathrm{o}}}\left\{\frac{1}{F_{\mathrm{s}}(y)}-\frac{1}{y}\right\} dy\right] $$
(41)

where Fs(y) is given by Eq. (24). The asymptotic form of the interaction energy, which corresponds to the linear superposition approximation, is given in terms of the effective surface potential. The asymptotic interaction energy Vsp(R) between two spheres at separation R between their centers having radii a1 and a2 and effective surface potentials ѱeff1 and ѱeff2, respectively, is given by

$$ {V}_{\mathrm{sp}}(R)=4\pi {\varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}{a}_1{a}_2{\psi}_{\mathrm{eff}1}{\psi}_{\mathrm{eff}2}\frac{e^{-\kappa \left(R-{a}_1-{a}_2\right)}}{R} $$
(42)

Similarly, the asymptotic form of the potential distribution around a cylinder must be

$$ \psi (r)={\psi}_{\mathrm{eff}}\frac{K_0\left(\kappa r\right)}{K_0\left(\kappa a\right)} $$
(43)

where ѱeff is the effective surface potential and is related to the surface potential ѱo by [26]

$$ {\psi}_{\mathrm{eff}}={\psi}_{\mathrm{o}}\exp \left[{\int}_0^{y_{\mathrm{o}}}\left\{\frac{1}{F_{\mathrm{c}}(y)}-\frac{1}{y}\right\} dy\right] $$
(44)

where Fc(y) is given by Eq. (31). The asymptotic interaction energy Vcl(R) per unit length between two parallel cylinders at separation R between their axes having radii a1 and a2 and effective surface potentials ѱeff1 and ѱeff2, respectively, is given by

$$ {V}_{\mathrm{cl}}(R)=2{\pi \varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}{\psi}_{\mathrm{eff}1}{\psi}_{\mathrm{eff}2}\frac{K_0\left(\kappa R\right)}{K_0\left(\kappa {a}_1\right){K}_0\left(\kappa {a}_2\right)} $$
(45)

Our theory is based on the Poisson-Boltzmann approach. Although various analytic approximations are possible within the frame work of the Poisson-Boltzmann theory, the standard Poisson-Boltzmann theory ignores the ionic size effect and the inter-ion interactions [28]. In the present paper, we have considered only the finite ion size effect. In order to take into account the inter-ion interactions, one has to employ simulation studies or an advanced electrostatic theory, i.e., a classical density functional theory. The readers should refer to recent papers by Zhao [29, 30] and Zhao et al. [31].

Conclusion

We have derived approximate expressions for the surface charge density/surface potential relationship and electric double-layer potential distribution for a spherical or cylindrical colloidal particle in an electrolyte solution (Eqs. (26), (27), (34), and (35)). The obtained expressions are based on an approximate form (Eqs. (14) and (28)) of the modified Poisson-Boltzmann equation taking into account the ion size effects through Carnahan-Starling activity coefficients of electrolyte ions. We further derive approximate expression for the effective surface potential for a spherical or cylindrical particle (Eqs. (41) and (44)) and for the electrostatic interaction energy between two spherical or cylindrical particles on the basis of the linear superposition approximation (Eqs. (42) and (45)).