Introduction

The standard theory of the electrophoretic mobility of a colloidal particle in an electrolyte solution is based on the solution to the Poisson-Boltzmann equation for the electric potential distribution around the particle [1–20]. The original Poisson-Boltzmann equation, however, assumes that ions behave like point-charges and neglect the effects of ionic size. There are many theoretical studies on the modified Poisson-Boltzmann eq. [21–28], which takes into account the effect of ionic size by introducing the activity coefficients of electrolyte ions [21, 29–31]. López-García et al., in particular, presented the numerical results of the electrophoretic mobility of a spherical particle taking into account the ionic size effect [27, 28]. In a previous paper [32], on the basis of the equation for the ionic activity coefficients given by Carnahan and Starling [31], which is the most accurate among existing theories, we presented a simple algorithm for solving the modified Poisson-Boltzmann equation and derive a simple approximate analytic expression for the surface charge density/surface potential relationship for a planar charged surface. We also considered the interaction energy between two colloidal particles in an electrolyte solution based on the modified Poisson-Boltzmann eq. [33].

In the present paper, we present a simple algorithm for the calculation of an approximate electrophoretic mobility of a spherical colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann eq. [32, 33]. We consider only the steric interactions among ions of finite size and do not consider other effects relating to the dielectric permittivity of the electrolyte solution. The mathematical analysis given in this paper is similar to that in our previous papers on the electrophoresis problem based on the standard Poisson-Boltzmann approach [9, 16].

Fundamental electrokinetic equations

Consider a spherical particle of radius a and zeta potential ζ moving with a velocity U in a liquid containing a symmetrical electrolyte with valence z and bulk concentration (number density) n (in units of m−3). The origin of the spherical polar coordinate system (r, θ, ϕ) is held fixed at the center of the particle, and the polar axis (θ = 0) is put parallel to E. Without loss of generality, we may assume that the particle is positively charged (ζ > 0).

The main assumptions in our analysis are as follows: (i) The Reynolds number of the liquid flow is small enough to ignore inertial terms in the Navier-Stokes equation, and the liquid can be regarded as incompressible. (ii) The applied field E is weak so that the particle velocity U is proportional to E and terms of higher order in E may be neglected. (iii) The slipping plane is located on the particle core. (iv) No electrolyte ions can penetrate the particle surface.

The fundamental electrokinetic equations are given by

$$ \eta \nabla \times \nabla \times \boldsymbol{u}+\nabla p+{\rho}_{\mathrm{el}}\nabla \psi =\mathbf{0} $$
(1)
$$ \nabla \cdot \boldsymbol{u}=0 $$
(2)
$$ {\boldsymbol{v}}_{\pm }=\boldsymbol{u}-\frac{1}{\lambda_{\pm }}\nabla {\mu}_{\pm } $$
(3)
$$ \nabla \cdot \left({n}_{\pm }{\boldsymbol{v}}_{\pm}\right)=0 $$
(4)
$$ {\rho}_{\mathrm{el}}\left(\boldsymbol{r}\right)= ze\left\{{n}_{+}\left(\boldsymbol{r}\right)-{n}_{-}\kern0.2em \left(\boldsymbol{r}\right)\right\} $$
(5)
$$ {\mu}_{\pm }(\boldsymbol{r})={\mu}_{\pm}^{\mathrm{o}}+{z}_{\pm } e\psi (\boldsymbol{r})+ k T \ln \left[{\gamma}_{\pm}\left(\boldsymbol{r}\right){n}_{\pm}\left(\boldsymbol{r}\right)\right] $$
(6)
$$ \Delta \psi (r)=-\frac{\rho_{\mathrm{el}}(r)}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}} $$
(7)

where u(r) is the liquid velocity at position r, v + and v − are, respectively, the velocities of cations and anions, λ + and λ − are, respectively, the drag coefficients of cations and anions, p(r) is the pressure, ρ el(r) is the charge density resulting from electrolyte ions given by Eq. (5), ψ(r) is the electric potential, μ +(r) and n +(r) are, respectively, the electrochemical potential and the concentration (the number density) of cations, μ −(r) and n −(r) are those of anions, μ ± o are constant terms in μ ±(r), and γ +(r) and γ -(r) are, respectively, the activity coefficients of cations and anions. The ionic size effects are taken into account through γ ±(r). Equations (1) and (2) are the Navier-Stokes equation and the equation of continuity for an incompressible flow. Equation (3) expresses that the flow v ±(r) of electrolyte ions are caused by the liquid flow u(r) and the gradient of the electrochemical potential μ ±(r), given by Eq. (6). Equation (4) is the continuity equation for electrolyte ions, and Eq. (7) is Poisson’s equation. The ionic drag coefficients λ ± of cations and anions are, respectively, related to the diffusion constant D + and the limiting equivalent conductance \( {\Lambda}_{+}^{\mathrm{o}} \) of cations and those of anions D − and \( {\Lambda}_{-}^{\mathrm{o}} \) by

$$ {\lambda}_{\pm }=\frac{kT}{D_{\pm }}=\frac{N_{\mathrm{A}}{ze}^2}{\Lambda_{\pm}^{\mathrm{o}}} $$
(8)

where N A is Avogadro’s number. We assume that the slipping plane, at which the liquid velocity u relative to the particle is zero coincides the particle core surface at r = a, where r = ∣r∣ (assumption (iii)). Then the above electrokinetic equations must be solved under the following boundary conditions:

$$ \boldsymbol{u}=\mathbf{0}\kern0.5em \mathrm{at}\kern0.5em r= a $$
(9)
$$ \begin{array}{ccc}\boldsymbol{u}\kern.3em \to \kern.3em -\boldsymbol{U}\kern1em & \kern1em \mathrm{as}\kern1em & \kern1em r\kern.3em \to \kern.3em \infty \kern1em \end{array} $$
(10)

In the stationary state the net force acting on the particle or an arbitrary volume enclosing the particle must be zero. Consider a large sphere S of radius r containing the particle (plus the electrical double layer around the particle) at its center. The radius r of S is taken to be sufficiently large so that the net electric charge within S is zero. There is then no electric force acting on S, and we need consider only hydrodynamic force F H, which must be zero, i.e.,

$$ \begin{array}{ccc}\kern1em {\boldsymbol{F}}_{\mathrm{H}}={\int}_S{\boldsymbol{\sigma}}_{\mathrm{H}}\cdot \hat{\boldsymbol{n}} dS\to \mathbf{0}\kern1em & \kern1em \mathrm{as}\kern1em & \kern1em r\to \infty \kern1em \end{array} $$
(11)

where the integration is carried out over the surface of S, σ H is the hydrodynamic stress tensor and \( \widehat{n} \) is the outward normal to S. Finally, the boundary condition for the velocity of the ionic flow v ± is given by

$$ {\operatorname{}{\boldsymbol{v}}_{\pm}\cdot \hat{\boldsymbol{n}}\Big|}_{r= a}=0 $$
(12)

which states that no electrolyte ions can penetrate the particle surface (assumption (iv)).

Linearized equations

Under assumption (ii), we may write

$$ {n}_{\pm }(\boldsymbol{r})={n}_{\pm}^{(0)}( r)+\delta {n}_{\pm }(\boldsymbol{r}) $$
(13)
$$ \psi (\boldsymbol{r})={\psi}^{(0)}( r)+\delta \psi (\boldsymbol{r}) $$
(14)
$$ {\mu}_{\pm }(\boldsymbol{r})={\mu}_{\pm}^{(0)}+{\delta \mu}_{\pm }(\boldsymbol{r}) $$
(15)

where the quantities with superscript (0) refer to those at equilibrium, i.e., in the absence of E, and μ ± (0) is a constant independent of r.

The equilibrium electric potential ψ (0)(r) outside the particle satisfies the Poisson equation and is a function of r only, viz.,

$$ \frac{1}{r^2}\frac{d}{ d r}\left({r}^2\frac{{ d\psi}^{(0)}}{ d r}\right)=-\frac{\rho_{\mathrm{el}}^{(0)}(r)}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}} $$
(16)

with

$$ {\rho}_{\mathrm{el}}^{(0)}(r)=\mathrm{ze}\left\{{n}_{+}^{(0)}(r)-{n}_{-}^{(0)}(r)\right\} $$
(17)

The boundary condition for ψ (0)(r) are

$$ {\psi}^{(0)}(a)=\zeta $$
(18)
$$ \begin{array}{ccc}\hfill {\psi}^{(0)}(r)\to 0\hfill & \hfill \mathrm{as}\hfill & \hfill r\to \infty \hfill \end{array} $$
(19)

Further, symmetry considerations permit us to write

$$ \boldsymbol{u}\left(\boldsymbol{r}\right)=\left(-\frac{2}{r} h(r) E \cos \theta, \frac{1}{r}\frac{d}{ d r}\left( r h(r)\right) E \sin \theta, 0\right) $$
(20)
$$ {\delta \mu}_{\pm }(\boldsymbol{r})=\mp z e{\phi}_{\pm }( r) E \cos \theta $$
(21)

where E = |E|, e is the elementary electric charge, and h(r) and ϕ ±(r) are functions of r. The fundamental electrokinetic eqs. (1)–(4) can be transformed into equations for h(r) and ϕ ±(r), which are expressed as [9]

$$ L{\phi}_{\pm }=-\frac{1}{n_{\pm}^{(0)}}\frac{{ d n}_{\pm}^{(0)}}{ d r}\left(\frac{d{\phi}_{\pm }}{ d r}\mp \frac{2{\lambda}_{\pm }}{e}\frac{h}{r}\right) $$
(22)
$$ L( L h)= G( r) $$
(23)

with

$$ G( r)=\frac{ze}{\eta r}\left(\frac{d{ n}_{+}^{(0)}}{ d r}\cdot {\phi}_{+}-\frac{d{ n}_{-}^{(0)}}{ d r}\cdot {\phi}_{-}\right) $$
(24)

where L = d 2/dr 2 + (2/r)d/dr − 2/r 2. The boundary conditions for u(r) and v ±(r) are expressed in terms of h and ϕ ±(r) as follows:

$$ {\operatorname{}\frac{d{\phi}_{\pm }}{ d r}\Big|}_{r= a}=0 $$
(25)
$$ \begin{array}{ccc}{\phi}_{\pm }(r)\to r\kern1em & \kern1em \mathrm{as}\kern1em & \kern1em r\to \infty \kern1em \end{array} $$
(26)
$$ \begin{array}{ccc} h=\frac{dh}{dr}=0\kern1em & \kern.5em \mathrm{at}\kern1em & \kern.5em r= a\kern1em \end{array} $$
(27)
$$ \begin{array}{ccc}\hfill h(r)\to \frac{U}{2 E} r+ O\left(\frac{1}{r}\right)\hfill & \hfill \mathrm{as}\hfill & \hfill r\to \infty \hfill \end{array} $$
(28)

General expression for electrophoretic mobility

The electrophoretic mobility μ = U/E (where U = |U|) can be calculated from Eq. (28) as

$$ \mu =2\underset{r\to \infty }{ \lim}\frac{h(r)}{r} $$
(29)

The result is [9]

$$ \mu =\frac{a^2}{9}{\int}_a^{\infty}\left(1-\frac{3{r}^2}{a^2}+\frac{2{r}^3}{a^3}\right) G(r) dr $$
(30)

It is to be noted that Eq. (30) takes the same form as that of the general mobility expression based on the standard Poisson-Boltzmann eq. [9, 16]. If the Boltzmann distribution is assumed for the concentrations \( {n}_{\pm}^{(0)}(r) \) of cations and anions at equilibrium, then \( {n}_{\pm}^{(0)}(r) \) is given

$$ {n}_{\pm}^{(0)}( r)= n \exp \left(\mp \frac{ze\psi (r)}{kT}\right) $$
(31)

and Eq. (16) becomes the standard Poisson-Boltzmann equation, viz.,

$$ \frac{1}{r^2}\frac{d}{ d r}\left({r}^2\frac{d}{ d r}\left(\frac{ze{\psi}^{(0)}}{kT}\right)\right)={\kappa}^2 \sinh \left(\frac{\mathrm{ze}{\psi}^{(0)}}{kT}\right) $$
(32)

where

$$ \kappa ={\left(\frac{z^2{e}^2 n}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}} kT}\right)}^{1/2} $$
(33)

is the Debye-Hückel parameter. In this case, Eq. (30) reduces the general mobility expression based on the standard Poisson-Boltzmann approach [9, 16].

Approximate mobility expression for large κa

We derive an approximate expression applicable for large values of κa (≥30) with the help of an approximation method as developed in a previous paper [9, 16]. For large κa, since the principal contribution to the integral in Eq. (30) comes from the region r - a ≈ 1/κ, we may regard (r -a)/a as of the order of 1/κa and expand the integrand of Eq. (30) around r = a, obtaining

$$ \mu =\frac{1}{3}{\int}_a^{\infty }{\left( r- a\right)}^2 G( r) d r+ O\left(\frac{1}{\kappa a}\right). $$
(34)

Also in this case the Poisson eq. (16) can be approximated by the following planar Poisson equation:

$$ \frac{d^2{\psi}^{(0)}}{{d r}^2}=-\frac{\rho_{\mathrm{el}}^{(0)}(r)}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}} $$
(35)

Modified Poisson-Boltzmann equation

In order to calculate the electrophoretic mobility of a spherical colloidal particle, one needs the equilibrium concentrations of electrolyte ions n ± (0)(r) and the equilibrium electric potential ψ (0)(r). In the standard electrophoresis theory one assumes the Boltzmann distribution of electrolyte ions (Eq. (31)) and thus one uses the Poisson-Boltzmann equation for the electric potential (Eq. (32)). Now we employ the modified Poisson-Boltzmann equation instead of the standard Poisson-Boltzmann equation. We take into account the ionic size effects through the ionic activity coefficient γ ±. We assume that cations and anions have the same ionic radius a i and the activity coefficients of cations and anions are the same, γ +(r) = γ −(r) = γ (r). The equilibrium electrochemical potentials μ ±(r) of cations and anions at position r are thus given by

$$ {\mu}_{\pm }( r)={\mu}_{\pm}^o\pm z e\psi ( r)+ k T \ln \left[\gamma (r){n}_{\pm}^{(0)}(r)\right] $$
(36)

The values of μ ±(r) must be the same as those in the bulk solution phase, where ψ(r) = 0, viz.,

$$ {\mu}_{\pm}\left(\infty \right)={\mu}_{\pm}^{\mathrm{o}}+ k T \ln \left({\gamma}^{\infty } n\right) $$
(37)

where γ ∞ = γ(∞). By equating μ ±(r) = μ ±(∞), we obtain

$$ {n}_{\pm}^{(0)}(r)=\frac{\gamma^{\infty } n}{\gamma (r)}{\mathrm{e}}^{\mp y} $$
(38)

with

$$ y( r)=\frac{ze{\psi}^{(0)}(r)}{kT} $$
(39)

where y(r) is the scaled equilibrium electric potential at position r. We use the following Carnahan-Starling ionic activity coefficient [31].

$$ \gamma ( r)= \exp \left[\frac{\phi (r)\left\{8-9\phi (r)+3{\phi}^2(r)\right\}}{{\left\{1-\phi (r)\right\}}^3}\right] $$
(40)

where ϕ(r) is the total ion volume fraction at position r at equilibrium and is given by

$$ \phi ( r)=\left(\frac{4}{3}\pi {a}_{\mathrm{i}}^3\right)\left\{{n}_{+}^{(0)}(r)+{n}_{-}^{(0)}(r)\right\}=\frac{\phi_{\mathrm{B}}\left\{{n}_{+}^{(0)}(r)+{n}_{-}^{(0)}(r)\right\}}{2 n} $$
(41)

and \( {\phi}_{\mathrm{B}}\equiv \phi \left(\infty \right)=\left(4\pi {a}_{\mathrm{i}}^3/3\right)\cdot 2 n \) is the total ion volume fraction in the bulk solution phase. By substituting Eq. (38) into Eq. (41), we obtain

$$ \phi (r)={\phi}_{\mathrm{B}}\frac{\gamma^{\infty } \cosh y}{\gamma (r)} $$
(42)

In a previous paper [32], we have shown that Eq. (40) can be approximated well by

$$ \gamma (r)={\gamma}^{\infty } H(y) $$
(43)

or equivalently

$$ \phi (r)={\phi}_{\mathrm{B}}\frac{ \cosh y}{H(y)} $$
(44)

with

$$ H(y)=1+ B{ \sinh}^2\left(\frac{y}{2}\right) $$
(45)
$$ B=\frac{16{\phi}_{\mathrm{B}}}{1+8{\phi}_{\mathrm{B}}} $$
(46)

Then Eq. (38) becomes

$$ {n}_{\pm}^{(0)}( r)=\frac{{ n e}^{\mp y}}{H(y)} $$
(47)

and thus Eq. (35) gives the following modified Poisson-Boltzmann equation:

$$ \frac{d^2 y}{{d r}^2}=\frac{\kappa^2 \sinh y}{H(y)} $$
(48)

which can be integrated to give

$$ \frac{dy}{dr}=-\frac{2\kappa}{\sqrt{B}}\sqrt{ \ln \left[ H(y)\right]} $$
(49)

which gives the following relationship between the surface charge density σ and the zeta potential ζ = ψ (0)(a) (Eq. (18)):

$$ \sigma =\frac{2{\varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\upkappa kT}{ze}\frac{1}{\sqrt{B}}\sqrt{ \ln \left[ H\left( ze\zeta / kT\right)\right]} $$
(50)

or equivalently

$$ \zeta =\frac{2 kT}{ze}\cdot \mathrm{arcsinh}\left(\frac{1}{\sqrt{B}}\sqrt{\left\{ \exp \left[\left(\frac{B}{4}\right){\left(\frac{ ze\sigma}{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}\kappa kT}\right)}^2\right]-1\right\}}\right) $$
(51)

The above approximation (Eq. (42) or Eq. (43)) is a good approximation with negligible errors for low ϕ B (ϕ B ≤ 0.1) and low-to moderate zeta potentials (ζeψ o/kT ≤ 3).

Approximate electrophoretic mobility expression based on the modified Poisson-Boltzmann equation

By substituting Eqs. (47)–(49) into Eq. (34) and using an approximation method developed in previous papers [9, 16], we finally obtain the following large-κa approximate expression for the electrophoretic mobility μ of a spherical colloidal particle of radius a in an electrolyte solution based on the modified Poisson-Boltzmann equation by neglecting terms of order 1/κa:

$$ \mu =\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}}{2\eta}\left(\frac{kT}{ze}\right)\left({N}_{+}-\frac{N_{-}}{1+ F}\right) $$
(52)

with

$$ {N}_{\pm }=-\frac{B}{4}{\int}_0^{ze\zeta / kT}{\int}_0^y\left\{\frac{e^{\mp {y}^{\prime }}}{H\left({y}^{\prime}\right)}-1\right\}\frac{d{ y}^{\prime }}{\sqrt{ \ln \left[ H\left({y}^{\prime}\right)\right]}}\frac{d y}{\sqrt{ \ln \left[ H(y)\right]}} $$
(53)
$$ F=\frac{2}{\upkappa a}\left(1+3{m}_{-}\right) M $$
(54)
$$ {m}_{-}=\frac{2{\varepsilon}_{\mathrm{r}}{\varepsilon}_{\mathrm{o}} kT}{3{\eta \mathrm{z}}^2{e}^2}{\lambda}_{-} $$
(55)
$$ M=\frac{\sqrt{B}}{4}{\int}_0^{ze\zeta / kT}\left\{\frac{e^y}{H(y)}-1\right\}\frac{dy}{\sqrt{ \ln \left[ H(y)\right]}} $$
(56)

where m − is the scaled drag coefficient of anions (counterions) and F corresponds to Dukhin’s number based on the modified Poisson-Boltzmann approach.

Results and discussion

The principal result of the present paper is Eq. (52) for the electrophoretic mobility μ of a spherical colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann approach (Eqs. (46)–(48)) by taking into account the ionic size effect through the Carnahan-Starling activity coefficient [31]. In the limiting case of ϕ B → 0, Eq. (52) tends to the following electrophoretic mobility expression based on the standard Poisson-Boltzmann approach [9, 16]:

$$ \mu =\frac{\varepsilon_{\mathrm{r}}{\varepsilon}_{\mathrm{o}}}{\eta}\left\{\zeta -\frac{2 F}{1+ F}\left(\frac{kT}{ze}\right) \ln \left[\frac{1+ \exp \left( ze\zeta /2 kT\right)}{2}\right]\right\} $$
(57)

where

$$ F=\frac{2}{\upkappa a}\left(1+3{m}_{-}\right)\left\{ \exp \left(\frac{ze\zeta}{2 kT}\right)-1\right\} $$
(58)

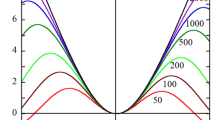
corresponds to the Dukhin number based on the standard Poisson-Boltzmann approach. It is found that Eq. (52) is a good approximation for large particles (κa ≥ 30), low ϕ B (ϕ B ≤ 0.1) and low-to moderate values of ζ (zeζ/kT ≤ 3). Figure 1 shows some examples of the calculation of the scaled electrophoretic mobility E m = (3ηze/2ε r ε o kT)μ obtained via Eq. (52) in an aqueous monovalent electrolyte solution containing cations and anions having radius a i = 0.4 nm and the ionic diffusion coefficient D = 2 × 10−9 m2/s at T = 298 K (z = 1, ε r = 80, η = 0.89 mPa s) as a function of the surface charge density σ for the case where the particle radius a = 0.1 μm and 1 μm and the electrolyte concentration C (in units of M) (which is related to the number density n (in units of m−3) by n = 1000N A C). Since the zeta potential ζ depends on the electrolyte concentration C and the total ion volume fraction ϕ B for given values of σ, we plot μ as a function of σ instead of ζ in Fig. 1. Here σ is calculated from ζ via Eq. (50). Figure 1 also shows the exact numerical results obtained by López-García [27] (given as closed circles). The agreement between the present results (Eq. (52)) and the exact numerical results [27] is good for low-to-moderate values of the particle surface charge density σ (σ ≤ 0.05 C/m2) with relative errors of several percents. We can thus conclude that the present algorithm for the calculation of the electrophoretic mobility of a spherical colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann approach is applicable for most practical cases.

Fig. 1
figure 1

Scaled electrophoretic mobility E m = (3ηze/2ε r ε o kT)μ obtained via Eq. (52) in an aqueous monovalent electrolyte solution containing cations and anions having radius a i = 0.4 nm and the ionic diffusion coefficient D = 2 × 10−9 m2/s at T = 298 K (z = 1, ε r = 80, η = 0.89 mPa.s) as a function of the surface charge density σ. Calculated for the particle radius a = 0.1 μm and 1 μm and the electrolyte concentration C (in units of M) (which is related to the number density n (in units of m−3) is 0.01 M. The exact numerical results obtained by López-García [27] are plotted as closed circles)

Full size image

Conclusion

We have presented a simple algorithm for calculating the approximate electrophoretic mobility of a spherical colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann approach (Eq. (52)), which takes into account the effects of ionic size on the basis of ionic activity coefficient given by Carnahan and Starling [31]. It is shown that the results are in good agreement with the exact numerical results by Lopez-Garcia et al. [27] for most practical cases.