1 Introduction

Composite materials have the advantages of high specific strength, lightweight, and good chemical corrosion resistance, making them well-suited to widespread use in the aircraft industry [1, 2]. During aircraft use, stiffened composite structures are subjected to tensile, compressive, bending, shear, and impact loads that result in complex stress forms, with buckling being a common failure mode [3, 4]. When subjected to axial load, a stiffened composite panel will remain undamaged after buckling and still exhibit sufficient bearing capacity; that is, it has excellent post-buckling strength. The bearing efficiency of a structure can therefore be considerably improved by making full use of this characteristic [5, 6]. The study of the post-buckling reliability of stiffened composite structures thus has important value in engineering applications [7,8,9,10,11,12]. For example, Mohammed et al. [7] proposed a finite element modeling strategy to capture failure modes associated with steel bar buckling and low cycle fatigue. Salami et al. [8] proposed a nonlinear fiber beam-column model, which can simulate a variety of failure modes of reinforced concrete columns under dynamic loads. Huang et al. [9] combined with the random damage constitutive model of concrete, and carried out numerical simulation work on material failure, member fracture and structural buckling.

Many scholars have studied the buckling of stiffened composite panels [13,14,15,16,17,18]. For example, Yu et al. [15] studied the post-buckling behavior of fixed laminated beams under axial compression and shear deformation, and established the analytical solution of the original governing equation. Guo et al. [16] studied the buckling and post-buckling of copper nanobeams under uniaxial compression by theoretical analysis and atomic simulation. Hu et al. [17] studied the axial and eccentric compression behavior of Q420 double angle composite columns. Sun et al. [18] established a seismic vulnerability analysis framework based on machine learning to assess the risk of structures under seismic loading.

In a traditional composite structure design, the mechanical model is first determined [19, 20], then the safety factor method is applied. This design method is able to reduce the instance of structural failure to some extent, but cannot completely prevent it. Indeed, due to the current lack of quantitative analyses on the variability of the relevant design parameters, any applied safety factor cannot accurately reflect the degree of safety of an engineering structure [21, 22]. A particularly large number of uncertainties exist in composite structures, including those related to material properties, geometric parameters, applied loads, and boundary conditions, etc., none of which are typically consistent. These uncertainties will notably have a significant impact on the performance of stiffened composite panels [23, 24]. Therefore, it is necessary to study the reliability of such composite structures [25, 26].

At present, the most commonly used methods for the reliability analysis of composite structures include approximate analytical methods [27] and digital simulation methods [28, 29]. Approximate analytical methods include the first-order second-moment method [30], which requires minimal calculation but results in a large relative error, making it only suitable for the reliability problem of an explicit limit state equation. Among the digital simulation methods, the Monte Carlo method [31] uses the joint probability density function of random variables for sampling. This method is simple, but its sampling efficiency is low so that large-scale calculation is necessary to obtain results that meet most accuracy requirements. The importance sampling method [32] is another type of digital simulation method that takes the design point of the limit state equation as the sampling center, considerably improving the sampling efficiency. However, this design point must be obtained in advance. When determining the post-buckling reliability of a stiffened composite panel, it is difficult to directly obtain the design point of the limit state equation, restricting the direct use of the importance sampling method. Therefore, the use of an adaptive iterative sampling method that is able to continuously optimize the sampling center and estimate the failure probability using pre-sampling is proposed in this paper. In this method, the sampling efficiency—that is, the ratio of the number of samples falling into the failure area to the total number of samples—is defined during the process of sampling to provide a basis for the quantitative evaluation of optimality.

To study the post-buckling characteristics of stiffened composite panels and ensure full utilization of the excellent properties of composite materials, the failure limit stress of stiffened composite panels was calculated using a semi-empirical equation and the results were compared with the corresponding experimental results. A failure analysis of the stiffened composite panel was then conducted using the adaptive iterative sampling method, and the results were discussed. The results of this study indicate that the proposed adaptive iterative sampling method provides higher sampling efficiency, smaller error, and greater accuracy than the conventional Monte Carlo method, demonstrating that it is a more efficient and reliable method for post-buckling reliability research.

Nomenclature

\(D\)

Bending stiffness

Pcr

Euler load

\({{ET}}\)

Tensile and compressive stiffness

Pe

Buckling load

\({{GT}}\)

Shear stiffness coefficient

\(\sigma_{{{\text{co}}}}\)

Failure stress

\({{EI}}\)

Buckling stiffness

Load

Failure load

2 Post-buckling failure model of a stiffened composite panel

2.1 Post-buckling analysis based on semi-empirical equations

A sketch of the stiffened composite panel structure studied in this paper, consisting of a skin plate laminate and stiffeners, is shown in Fig. 1. To define the bending stiffness of the skin plate and overall stiffened panel, in this section, the post-buckling limit load of a stiffened composite panel is first calculated using semi-empirical equations [33] and a buckling analysis is conducted.

Fig. 1
figure 1

Structural diagram of the stiffened composite panel a stiffener and b skin plate laminate

Full size image
  1. (1)

    The stiffness coefficients of the skin plate laminate are calculated by

    $$ A_{ij} = \sum\limits_{k = 1}^{M} {\left( {\overline{Q}_{ij} } \right)_{k} \left( {Z_{k} - Z_{k - 1} } \right)} {\kern 1pt} $$
    (1)
    $$ B_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{M} {\left( {\overline{Q}_{ij} } \right)_{k} \left( {Z_{k}^{2} - Z_{k - 1}^{2} } \right)} {\kern 1pt} $$
    (2)
    $$ D_{ij} = \frac{1}{3}\sum\limits_{k = 1}^{M} {\left( {\overline{Q}_{ij} } \right)_{k} \left( {Z_{k}^{3} - Z_{k - 1}^{3} } \right)} {\kern 1pt} , $$
    (3)

    where \(A_{ij}\) is the in-plane stiffness coefficient of the laminate; \(B_{ij}\) is the tension bending stiffness coefficient of the laminate; \(D_{ij}\) is the bending stiffness coefficient of the laminate; \(i,j\) are the directions of stress, given as 1, 2, and 6; \(M\) is the total number of plies; \(Z_{k}\) and \(Z_{k - 1}\) are the z-direction coordinates of plies k and k—1, respectively; and \((\overline{Q}_{ij} )_{k}\) is the off-axis modulus of the k-th ply.

  2. (2)

    The equivalent bending stiffness D of a symmetric laminate is calculated by

    $$ D_{x} = D_{11} + \frac{{2D_{12} D_{16} D_{26} - D_{22} D_{16}^{2} - D_{12}^{2} D_{66} }}{{D_{22} D_{66} - D_{26}^{2} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$
    (4)
    $$ D_{y} = D_{22} + \frac{{2D_{12} D_{16} D_{26} - D_{11} D_{26}^{2} - D_{12}^{2} D_{66} }}{{D_{11} D_{66} - D_{16}^{2} }} $$
    (5)
    $$ D_{xy} = \frac{{2D_{12} D_{16} D_{26} - D_{11} D_{26}^{2} - D_{22}^{2} D_{16} }}{{D_{11} D_{12} - D_{12}^{2} }}, $$
    (6)

    where \(D_{x}\) is the equivalent bending stiffness of the laminate along the x direction; \(D_{y}\) is the equivalent bending stiffness of the laminate along the y direction; \(D_{xy}\) is the equivalent in-plane bending stiffness of the laminate; and \(D_{11} ,D_{12} ,D_{22} ,D_{66} ,D_{16} ,D_{26}\) are the bending stiffness coefficients of the laminate for each direction of stress.

  3. (3)

    The equivalent in-plane tensile/compressive stiffness coefficients along with the x and y directions, \(({\text{ET}})_{x}\) and \(({\text{ET}})_{y}\), respectively, and shear stiffness coefficient GT of the laminate are calculated by

    $$ ({\text{ET}})_{x} = E_{x} t = A_{11} + \frac{{2A_{12} A_{16} A_{26} - A_{22} A_{16}^{2} - A_{12}^{2} A_{66} }}{{A_{22} A_{66} - A_{26}^{2} }} $$
    (7)
    $$ ({\text{ET}})_{y} = E_{y} t = A_{22} + \frac{{2A_{12} A_{16} A_{26} - A_{11} A_{26}^{2} - A_{12}^{2} A_{66} }}{{A_{11} A_{66} - A_{16}^{2} }} $$
    (8)
    $$ \left( {{\text{GT}}} \right) = G_{xy} t = A_{66} + \frac{{2A_{12} A_{16} A_{26} - A_{22} A_{16}^{2} - A_{11} A_{26}^{2} }}{{A_{11} A_{22} - A_{12}^{2} }}, $$
    (9)

    where t is the thickness of the laminate; \(A_{11}\), \(A_{12}\), \(A_{22}\), \(A_{16}\), \(A_{26}\), and \(A_{66}\) are the in-plane stiffness coefficients of the laminate; \(E_{x}\) and \(E_{y}\) are the equivalent tensile/compressive elastic moduli of the laminate in the x and y directions, respectively; and \(G_{xy}\) is the equivalent in-plane shear modulus of the laminate.

  4. (4)

    The overall buckling stiffness EI of the stiffened panel is calculated by

    $$ {\text{EI}} = \sum\limits_{i = 1}^{n} {\left[ {\left( {D_{11i} - \frac{{D_{12i}^{2} }}{{D_{22i} }}} \right)b_{i} + \left( {A_{11i} - \frac{{A_{12i}^{2} }}{{A_{22i} }}} \right)b_{i} \left( {z_{i} - z_{c} } \right)^{2} } \right]} , $$
    (10)

    where \(b_{i}\) is the width of the i-th strip element; \(z_{c}\) is the position of the neutral axis of the section of the stiffened laminate; and \((z_{i} - z_{c} )\) is the distance from the center of the section of the i-th element to the neutral axis.

  5. (5)

    The overall bearing capacity of the stiffened panel is calculated by

    $$ P_{{{\text{cr}}}} = \frac{{P_{{\text{e}}} }}{{1 + \lambda P_{{\text{e}}} /\left( {G\overline{A} } \right)}} $$
    (11)
    $$ P_{{\text{e}}} = \frac{{c\pi^{2} \left( {{\text{EI}}} \right)}}{{L^{2} }}, $$
    (12)

    where the support coefficient c is 2.04; the shape factor \(\lambda\) is 1.2; \(P_{{{\text{cr}}}}\) is the Euler load; G is the equivalent shear stiffness of the vertical web; \(\overline{A}\) is the area of the vertical web; and \(P_{{\text{e}}}\) is the buckling load.

  6. (6)

    The failure stress \(\sigma_{{{\text{co}}}}\) of the stiffened laminate plate is calculated by

    $$ \sigma_{{{\text{co}}}} = \left[ {1 - \left( {1 - \frac{{\sigma_{{{\text{cr}}}} }}{{\sigma_{{{\text{cc}}}} }}} \right)\frac{{\sigma_{{{\text{cr}}}} }}{{\sigma_{{\text{r}}} }}} \right]\sigma_{{{\text{cc}}}} , $$
    (13)

    where \(\sigma_{{\text{r}}}\) is the global buckling stress of the stiffened laminate calculated by the Euler equation without considering the effect of stiffness reduction after local buckling of either the skin plate or stiffener; \(\sigma_{{{\text{cc}}}}\) is the short-plate compressive failure stress of the stiffened laminate, which is approximately 0.75 times that of the pure compressive failure stress of the skin laminate; \(\sigma_{{{\text{co}}}}\) is the failure stress of the stiffened laminate; and \(\sigma_{{{\text{cr}}}}\) is the local buckling stress of the skin laminate.

  7. (7)

    The failure load of the stiffened composite panel is obtained by

    $$ {\text{Load}} = \sigma_{{{\text{co}}}} A, $$
    (14)

    where \(\sigma_{{{\text{co}}}}\) is the failure stress of the stiffened laminate and A is it's area.

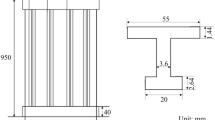
This study employed a composite skin plate thickness of 0.125 mm, ply angle of 0°, skin width a of 710 mm, horizontal edge strip width W1 of 55 mm, horizontal edge strip width W2 of 25 mm, edge strip height H of 45 mm, and the stiffened laminated plate length b of 570 mm, resulting in a post-buckling stiffened composite panel failure load of 1300 kN, as calculated by Eqs. (1)–(14).

2.2 Experimental verification of failure modes

Axial compression tests of stiffened composite panels with the same parameters as those used to calculate the failure load in Sect. 2.1 were then conducted as discussed in this section as shown in Fig. 2. The local buckling of the skin was observed to occur first, followed by the overall buckling failure of the stiffened plate. The test results are shown in the load–displacement curve in Fig. 3, which indicates that the maximum failure load was 1417.89 kN. The calculated failure load is compared with the experimental result in Table 1.

Fig. 2
figure 2

Axial compression test

Full size image
Fig. 3
figure 3

Experimentally obtained load–displacement curve for the stiffened composite panel

Full size image
Table 1 Comparison of results
Full size table

2.3 Post-buckling simulation of composite stiffened panels

Abaqus software is used to simulate the composite stiffened panel with the same parameters for simulation, and the load–displacement curve is obtained, as shown in Fig. 4 below.

Fig. 4
figure 4

Overall displacement-load diagram in Abaqus

Full size image

It can be seen from Fig. 4 that the simulation specimen is damaged at 1589 kN.

The calculated and simulated failure loads are compared with the experimental results in Table 1.

It can be observed in Table 1 that the experimentally obtained value agrees well with the value calculated using the semi-empirical equations, with a relative error of approximately 8.3%. And when using Abaqus software, different people will get different results due to different mesh generation, while there is only one result calculated by semi-empirical equations. This indicates that the semi-empirical equations are highly accurate, establishing a good foundation for the subsequent structural reliability analysis.

3 Reliability analysis of stiffened composite panel post-buckling failure

3.1 Reliability modeling of post-buckling failure

There is a wide range of uncertainties in the structure of a stiffened composite panel, including the distribution of material properties, manufacturing process errors, and structural size deviations. Combining engineering experience and theoretical analysis, the thickness, width, and ply angle of the composite skin plate, as well as the edge strip widths, height, and length of the stiffened composite plate can be regarded as random variables, as defined in Table 2.

Table 2 Probability characteristics of stiffened composite plate parameters
Full size table

The failure load \({\text{Load}}\{ X_{1} ,X_{2} , \ldots ,X_{7} \}\) can be obtained by substituting the relevant composite structure parameters into Eqs. (1)–(14). Combined with the actual load on the subject structure, the post-buckling analysis function is established as:

$$ g({\mathbf{X}}) = {\text{Load}}\{ X_{1} ,X_{2} , \ldots ,X_{7} \} - X_{8} , $$
(15)

where \({\mathbf{X}} = \{ X_{1} ,X_{2} , \ldots ,X_{8} \}\).

When \(g({\mathbf{X}}) < 0\) the post-buckling behavior X falls into the failure domain Rn; when \(g({\mathbf{X}}) \ge 0\), there is no failure, and X falls into the safety region Rs.

3.2 Adaptive iterative sampling method

The adaptive iterative sampling applied in this study is based on the Monte Carlo method. By constantly modifying the sampling center during the calculation process to limit it as much as possible to the “important areas” that have a significant impact on the results, the sampling of irrelevant events is minimized, improving the calculation efficiency.

The traditional method used for sampling in a structural reliability analysis is the Monte Carlo method. The integral equation expressing the Monte Carlo method used to determine failure probability is

$$ P_{{\text{f}}} = \int\limits_{Rn} f ({\mathbf{X}}){\text{d}}{\mathbf{X}}, $$
(16)

where \(f({\mathbf{X}})\) is the joint probability density function, which in this study is based on the variables \({\mathbf{X}} = \left\{ {X_{1} ,X_{2} , \cdots ,X_{8} } \right\}^{{\text{T}}}\); Rn is the failure domain; and \(P_{{\text{f}}}\) is the failure probability, which in this study is the evaluation index of the post-buckling reliability of the stiffened composite panel.

According to the joint probability density function \(f({\mathbf{X}})\), N samples \(\{ {\mathbf{X}}_{1} ,{\mathbf{X}}_{2} , \cdots ,{\mathbf{X}}_{N} \}^{{\text{T}}}\) of input vector variable X are extracted, then the estimated value of failure probability \(\hat{P}_{{\text{f}}}\) is given by

$$ \hat{P}_{{\text{f}}} = \frac{1}{N}\sum\limits_{s = 1}^{N} {I({\mathbf{X}}_{s} )} = \frac{{N_{{\text{f}}} }}{N}, $$
(17)

where \({\mathbf{X}}_{s}\) is the s-th sample \((s = 1,2, \ldots ,N)\) extracted by the joint probability density function \(f({\mathbf{X}})\); \(I({\mathbf{X}})\) is the indicator function; \(I({\mathbf{X}}_{s} ){ = }\left\{ {\begin{array}{*{20}c} 1 & {{\mathbf{X}}_{s} \in Rn} \\ 0 & {{\mathbf{X}}_{s} \notin Rn} \\ \end{array} } \right.\); \(N_{{\text{f}}}\) is the number of samples falling within the failure domain Rn, and N is the total number of samples.

The Monte Carlo method requires a large number of samples to obtain converging results, and its sampling efficiency is very low. Therefore, researchers have proposed improved digital simulation methods [29], of which the importance sampling method is one of the more common. By introducing the importance sampling density function \(h({\mathbf{X}})\), the integral equation for solving the failure probability is transformed into

$$ P_{f} = \int\limits_{Rn} {\frac{{f({\mathbf{X}})}}{{h({\mathbf{X}})}}} h({\mathbf{X}}){\text{d}}{\mathbf{X}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} . $$
(18)

If N samples of input variable X are extracted according to the importance sampling density function \(h({\mathbf{X}})\), the estimated failure probability \(\hat{P}_{f}\) is:

$$ \hat{P}_{{\text{f}}} = \frac{1}{N}\sum\limits_{s = 1}^{N} {\left[ {I\left( {{\mathbf{X}}_{s} } \right)\frac{{f\left( {{\mathbf{X}}_{s} } \right)}}{{h\left( {{\mathbf{X}}_{s} } \right)}}} \right]} . $$
(19)

The challenge when using the importance sampling method to solve the reliability problem of the post-buckling behavior of stiffened composite panels is to select an appropriate importance sampling function \(h({\mathbf{X}})\). The simple explicit function \(g({\mathbf{X}})\) can be obtained by improving the first-order second-moment method. For the post-buckling problem of stiffened composite panels, the form of function \(g({\mathbf{X}})\) is complex, and it is difficult to obtain it directly. Therefore, in this study, the adaptive iterative strategy was used to modify the sampling center and construct the next sampling function.

For the adaptive iterative importance sampling function \(h_{q} ({\mathbf{X}})(q = 1,2, \ldots ,m)\), the number of samples extracted is \(N_{(q)} (q = 1,2, \ldots ,m)\). Therefore,

$$ P_{f(q)} = \int\limits_{Rn} {\frac{{f({\mathbf{X}})}}{{h_{(q)} ({\mathbf{X}})}}} h_{(q)} ({\mathbf{X}}){\text{d}}{\mathbf{X}} $$
(20)
$$ \hat{P}_{f(q)} = \frac{1}{{N_{(q)} }}\sum\limits_{s = 1}^{{N_{(q)} }} {\left[ {I_{F} \left( {{\mathbf{X}}_{(q)s} } \right)\frac{{f\left( {{\mathbf{X}}_{(q)s} } \right)}}{{h_{(q)} \left( {{\mathbf{X}}_{(q)s} } \right)}}} \right]} . $$
(21)

Finally, the failure probability estimation based on the adaptive iterative importance sampling method can be defined as

$$ \hat{P}_{f} = \frac{1}{m}\sum\limits_{q = 1}^{m} {\hat{P}_{f(q)} } $$
(22)

To effectively evaluate the sampling efficiency of the proposed method, the sampling efficiency \(\eta\) is defined as the ratio of the number of samples falling into the failure area Rn to the total number of samples.

The sampling efficiency \(\eta\) of the Monte Carlo method is given by

$$ \eta { = }\frac{{N_{{\text{f}}} }}{N}{ = }P_{{\text{f}}} . $$
(23)

For the adaptive iterative importance sampling method, if the number of samples falling into the failure area in the q-th \((q = 1,2, \ldots ,m)\) sampling is \(N_{(q)f} (q = 1,2, \ldots ,m)\), then the sampling efficiency \(\eta_{q}\) is

$$ \eta_{q} { = }\frac{{N_{(q)f} }}{{N_{(q)} }}. $$
(24)

Thus, the total sampling efficiency \(\eta\) for the adaptive iterative sampling is

$$ \eta { = }\frac{{\sum\nolimits_{q = 1}^{m} {N_{(q)f} } }}{{\sum\nolimits_{q = 1}^{m} {N_{(q)} } }}. $$
(25)

3.3 Obtaining failure probability

According to the principle of the adaptive iterative importance sampling method, the specific steps used to calculate the post-buckling reliability of a stiffened composite panel are as follows.

  1. 1.

    The first importance sampling function is \(h_{(1)} ({\mathbf{X}})\), and the sampling center \({{\varvec{\Delta}}}_{{{\mathbf{X}}(1)}}\) of \(h_{(1)} ({\mathbf{X}})\) is its mean point. The variance vector of the sampling function is consistent with the variance vector of the joint probability density function of the input vector, that is, \({{\varvec{\upmu}}}_{h(1)} = {{\varvec{\upmu}}}_{{\mathbf{X}}}\) and the variance vector \({{\varvec{\upsigma}}}_{h(1)}^{2} = {{\varvec{\upsigma}}}_{{}}^{2}\). According to the importance sampling function \(h_{(1)} ({\mathbf{X}})\), \(N_{(1)}\) samples are selected to judge whether the sample \({\mathbf{X}}_{(1)s} (s = 1,2, \ldots ,N_{(1)} )\) falls into the failure region Rn. For the sampling points falling into Rn, the failure probability is calculated by Eq. (21), and the sample point corresponding to the current maximum value of \(f({\mathbf{X}})\) is marked as \({{\varvec{\updelta}}}*\). The sampling center \({{\varvec{\Delta}}}_{{{\mathbf{X}}(2)}}\) of the second importance sampling function \(h_{(2)} ({\mathbf{X}})\) is thus defined as \({{\varvec{\updelta}}}^{*}\). The variance vector of the second importance sampling function is consistent with the variance vector of the joint probability density function of the input vector.

  2. 2.

    The q-th (q = 2, 3,…, m) importance sampling density function \(h_{(q)} ({\mathbf{X}})\) is normal, and the sampling center is \({{\varvec{\Delta}}}_{{{\mathbf{X}}(q)}}\). The variance vector of this importance sampling density function is consistent with the variance vector of the joint probability density function of the input vector; that is, \({{\varvec{\upmu}}}_{h(q)} = {{\varvec{\Delta}}}_{{{\mathbf{x}}(q)}}\) and the variance vector \({{\varvec{\upsigma}}}_{h(q)}^{2} = {{\varvec{\upsigma}}}_{{}}^{2}\). According to the importance sampling function \(h_{(q)} ({\mathbf{X}})\), \(N_{(q)}\) samples are selected to judge whether sample \({\mathbf{X}}_{(q)s} (s = 1,2, \ldots ,N_{(q)} )\) falls into the failure region Rn. For the sampling points falling into Rn, the failure probability is calculated by Eq. (21), and the sample point corresponding to the current maximum value of \(f({\mathbf{X}})\) is marked as \({{\varvec{\updelta}}}*\). Then, the joint probability density functions \(f({{\varvec{\Delta}}}_{{{\mathbf{X}}(q)}} )\) and \(f({{\varvec{\updelta}}}*)\), respectively corresponding to \({{\varvec{\Delta}}}_{{{\mathbf{X}}(q)}}\) and \({{\varvec{\updelta}}}*\) are compared; if \(f({{\varvec{\updelta}}}*) \ge f({{\varvec{\Delta}}}_{{{\mathbf{X}}(q)}} )\), the sampling center \({{\varvec{\Delta}}}_{{{\mathbf{X}}(q + 1)}}\) of the (q + 1)-th importance sampling function \(h_{{(q{ + }1)}} ({\mathbf{X}})\) is selected as \({{\varvec{\updelta}}}*\); otherwise, the sampling center \({{\varvec{\Delta}}}_{{{\mathbf{X}}(q + 1)}}\) of the (q + 1)-th importance sampling function \(h_{{(q{ + }1)}} ({\mathbf{X}})\) is selected as \({{\varvec{\Delta}}}_{{{\mathbf{X}}(q)}}\).

  3. 3.

    A total of M samplings are conducted. The failure probability \(\hat{P}_{{\text{f}}}\) of the stiffened composite panel structure is calculated by Eq. (22), and the algorithm is finished.

The flow chart for determining the failure probability using the proposed adaptive iterative sampling method is shown in Fig. 5.

Fig. 5
figure 5

Flow chart for determining failure probability using the adaptive iterative sampling method

Full size image

4 Analysis and discussion

The typical method for reliability modeling and analysis primarily relies upon the collection of a large quantity of failure data to design and evaluate the reliability based on probability theory. In this study, a reliability analysis is applied to quantitatively determine the post-buckling reliability of stiffened composite panels based on probability and statistics.

In this study, the adaptive iterative sampling method was used for the reliability analysis. In order to evaluate the calculation accuracy and efficiency of this method, its results are compared with those of the Monte Carlo method in Table 3.

Table 3 Resulting failure probability according to the calculation method
Full size table

It can be seen from the results in Table 3 that for the same total number of samples, the relative error between the results obtained using the adaptive iterative sampling method and those obtained using the Monte Carlo method is only = \(\delta\)(5.6077 × 10–5–5.525 × 10–5)/(5.6077 × 10–5) = 1.47%, which indicates consistent results. It can be seen in Fig. 6 that the failure probability curve corresponding to the adaptive iterative sampling method fluctuates only slightly, while that corresponding to the Monte Carlo method fluctuates relatively large. This demonstrates that compared with the traditional Monte Carlo method, the failure probability obtained by the adaptive iterative sampling method tends to stability much faster. Indeed, the simulation times required to obtain a convergent solution using the proposed method are much less than those using the Monte Carlo method, indicating improved efficiency. Comparing the total sampling efficiency of the adaptive iterative sampling method with that of the Monte Carlo method as reported in Table 3, an improvement of 0.4912/(5.4 × 10–5) = 8.8931 × 103 can be observed. Therefore, the adaptive iterative sampling method is just as accurate as the Monte Carlo method, but much more efficient.

Fig. 6
figure 6

Change in probability of failure with sample size

Full size image

The two-norm describes the linear distance between two vector matrices in space. By calculating the two-norm of the sampling center positions obtained in each iteration of the adaptive iterative sampling process, we can observe the correction of sampling centers between iterations.

In normal space, the two-norm of the sampling center position in the adaptive iterative sampling method can be calculated by.

$$ \frac{{\Delta_{{\varvec{X}}} - {\varvec{\mu}}_{{\varvec{X}}} }}{{\varvec{\sigma}}} $$
(26)

with the results shown per iteration in Table 4 and Fig. 7.

Table 4 Two-norms of sampling center location
Full size table
Fig. 7
figure 7

Change in two-norm of sampling center position according to sample size

Full size image

It can be seen in Table 4 that the two-norm of the sampling center consistently decreases with increasing iterations. Starting at the fourth sampling iteration, the two-norm of the sampling center changes only slightly in the next iteration, indicating that the sampling center is constantly being adaptively adjusted.

It can be seen in Table 4 that after many iterations, the two-norm of the sampling center position in the normal distribution decreases and gradually converges to a stable value. From the plot of two-norm sampling center position in Fig. 7, it can be confirmed that the overall curve shows a decreasing trend with a very small fluctuation, proving that there is an optimal design point. The selection of design point directly affects the efficiency and accuracy of the calculation as the adaptive iterative sampling method depends on the selection of design points. The existence of an optimal design point thus indicates that the results obtained using the adaptive iterative sampling method are reliable, stable, and effective. It is therefore proven that the proposed use of the adaptive iterative sampling method can effectively analyze the post-buckling reliability of stiffened composite panels.

5 Conclusion

In this study, a semi-empirical equation was first derived and used to determine the ultimate load of a stiffened composite panel, which was then experimentally verified; the experimental and semi-empirical results agreed well, and the error is about 8.3%. It was then demonstrated that some processing methods and algorithms for capturing uncertainty in the semi-empirical equations are more effective and accurate than others. Based on the semi-empirical equations, the post-buckling reliability of a stiffened composite panel was then analyzed and discussed using the proposed adaptive iterative sampling method to obtain the failure probability. Compared with the traditional Monte Carlo method, the adaptive iterative sampling method was shown to reduce the sampling of events that are irrelevant to the analysis results, improving the calculation efficiency. Notably, the adaptive iterative sampling method is independent as it did not need to find the sampling center of the panel using any other method. An analysis and discussion of the two-norm of the sampling center position during sampling indicated that after several iterations, its value gradually decreases and converges to stability. This proved that there was an optimal design point, indicating that the adaptive iterative sampling method based on the derived semi-empirical equations is effective and the results obtained are reliable and stable. The results of this research are of significance to the study of the post-buckling reliability of stiffened composite panels and can be used to improve and consolidate the application of composite materials in aircraft.