Post-buckling Reliability and Sensitivity Analysis of Composite Stiffened Plates Based on Adaptive Kriging Method

Abstract

Based on the active learning Kriging (ALK) model and the Hashin failure criterion, this paper proposes a new reliability evaluation model for composite stiffened panels, and conducts a reliability analysis on the ultimate bearing capacity. In addition, this paper studies the importance ranking of input variables. By comparing the calculation results of the reliability model proposed in this paper with those of the Monte Carlo method, the accuracy and efficiency of the ALK model are verified by case studies. Finally, the effects of longitudinal elastic modulus and fiber-direction tensile strength on post-buckling failure probability are discussed, which provides significant reference and guidance for the optimization and design of composite stiffened plates.

1 Introduction

As a kind of advanced material with special properties, composite materials have been widely used in the aerospace field. By increasing the proportion of composite materials in the main and secondary load-bearing components, the weight reduction effect of aircraft becomes obvious. One of the most common failure forms of thin-walled structures, which are typical components of aircraft structures, is the loss of stability.

As a typical structural form, the stability of plate and shell structures has been studied by many scholars for a long time [1,2,3,4]. To analyze the initial failure of composite stiffened plates under axial compression, Orifici et al. [5] adopted the "whole-local" analysis method in the finite element software. Zhou [6] studied the vibration frequency and instability characteristics of ring-stiffened thin-walled cylindrical shells conveying fluid. Additionally, Sun et al. [7] established the topology optimization approach for the stiffener layout of composite stiffened panels based on moving morphable components. These post-buckling analyses of composite stiffened plates are under deterministic conditions, without considering the effect of uncertain parameters.

With the wide application of composite materials, the reliability optimization design of composite materials has been increasingly concerned [8,9,10]. Due to the nonlinearity of calculating the ultimate bearing capacity of complex composite reinforced panels, the reliability analysis of this structure is time-demanding and inefficient. Traditional post-buckling reliability analysis is based on the first-order reliability method (FORM) or response surface methodology, whose computational budget is expensive and performances are limited by the nonlinearity and cost on finite element analysis of composites. In addition, the in-depth analysis of post-buckling reliability and sensitivity based on the ultimate bearing capacity failure is still lacking. Therefore, in this paper, the reliability model is constructed based on the ultimate bearing capacity failure. Then, the efficient active learning Kriging (ALK) method is first employed to solve the failure probability of composite stiffened plates. And the moment-independent global sensitivity based on the generalized sensitivity idea is first introduced to obtain the importance ranking of input variables, which provides a reference for the design and optimization of composite plates.

The representative approximate analytical methods include the FORM and the second-order reliability method (SORM) [11]. The surrogate model has also evolved greatly [12], such as the Kriging model [13]. The two most famous ALK methods are the efficient global reliability analysis method proposed by Bichon et al. [14] and the AK-MCS method proposed by Echard et al. Yang et al. [15] combined the ALK model with an IS method based on kernel density estimation to evaluate low failure probability. Gaspar et al. [16] proposed an adaptive Kriging model combining the active refinement and trust region methods. These methods provided a great solving strategy for reliability analysis and low failure probability problems. At the same time, various add-point strategies, also called the active learning functions, were developed, such as the expected feasibility function (EFF) [14], U function[17], expected risk function (ERF) [18], H function[19], and least improvement function (LIF) [20], and so on [21].

Based on failure probability, global sensitivity analysis (GSA) has been employed to measure the influence of uncertainty in random variables on failure probability. The GSA index can be divided into non-parametric index [22], moment-independent index [23] and variance-based index [24]. There are two kinds of moment-independent sensitivity indices. Borgonovo [23] proposed a moment-independent sensitivity index based on differences between the non-conditional and conditional probability density functions (PDF), while Liu and Homma [25] proposed another moment-independent sensitivity index based on differences between the non-conditional and conditional cumulative distribution functions (CDF). To improve the computational efficiency of sensitivity analysis, Guo et al. [26] proposed the variable sensitivity index based on the generalized sensitivity analysis idea. Because the post-buckling reliability problem of composite stiffened plates needs to utilize time-demanding finite element software, this paper derives the efficient moment-independent sensitivity index based on the generalized sensitivity idea.

This paper is organized as follows. Section 2 establishes the post-buckling reliability model and moment-independent global sensitivity index of composite stiffened plates. Section 3 introduces the ALK method for solving post-buckling failure probability and sensitivity index efficiently. Section 4 provides case studies for analyzing the effects of longitudinal elastic modulus and fiber-direction tensile strength on the post-buckling failure probability. Section 5 concludes this paper.

2 Post-buckling Reliability Analysis and Sensitivity Analysis

2.1 Mechanical Properties

The arc-length method is adopted in most finite element software. At present, the improved arc length method [27, 28] has become one of the most important methods for solving nonlinear buckling equations.

For the nonlinear bending problem of composite stiffened plate, the governing equation is as follows

$$ \left[ {K_{T} } \right]\text{d}\left\{ \Delta \right\} = \text{d}\left\{ P \right\} $$

(1)

where $\left[ {K_{T} } \right]$, $\text{d}\left\{ \cdot \right\}$, $\Delta$ and $P$ represent tangent stiffness matrix, differential operator, deformation and loaded force, respectively.

$$ \left[ {K_{T} } \right] = \left[ {K_{L} } \right] + \left[ {K_{\sigma } } \right] + \left[ {K_{NL} } \right] $$

(2)

where $\left[ {K_{L} } \right]$, $\left[ {K_{\sigma } } \right]$ and $\left[ {K_{NL} } \right]$ indicate linear stiffness matrix, geometric stiffness matrix and initial deformation matrix, respectively.

The Hashin failure criterion is applied to conventional shell elements and continuous shell elements, which can be divided into four failure modes. The detailed expressions are as follows:

Fiber failure mode in tension ($\sigma_{11} > 0$):

$$ F_{ft} = \frac{{\sigma_{11}^{2} }}{{X_{T}^{2} }} + \alpha \left( {\frac{{\sigma_{12} }}{{S_{L} }}} \right)^{2} = 1 $$

(3)

Fiber failure mode in compression ($\sigma_{11} \le 0$):

$$ F_{fc} = \left( {\frac{{\sigma_{11} }}{{X_{C} }}} \right)^{2} = 1 $$

(4)

Matrix failure mode in tension ($\sigma_{22} \ge 0$):

$$ F_{mt} = \left( {\frac{{\sigma_{22} }}{{Y_{T} }}} \right)^{2} + \left( {\frac{{\sigma_{12} }}{{S_{L} }}} \right)^{2} = 1 $$

(5)

Matrix failure mode in compression ($\sigma_{22} \le 0$):

$$ F_{mc} = \left[ {\left( {\frac{{Y_{C} }}{{2S_{T} }}} \right)^{2} - 1} \right]\frac{{\sigma_{22} }}{{Y_{C} }} + \left( {\frac{{\sigma_{22} }}{{2S_{T} }}} \right)^{2} + \left( {\frac{{\sigma_{12} }}{{S_{L} }}} \right)^{2} = 1 $$

(6)

in which, $X_{T}$, $X_{C}$, $Y_{T}$, $Y_{C}$, $S_{L}$ and $S_{T}$ are axial tensile strength, axial compressive strength, transverse tensile strength, transverse compressive strength, axial shear strength and transverse shear strength, respectively. $\alpha$ is the influential factor of shear strength on fiber failure in tension. $\sigma_{11}$, $\sigma_{22}$ and $\sigma_{12}$ are the components of effective stress $\sigma$.

When the coefficient of damage criterion reaches 1, damage appears in the rubber layer, and its expression is:

$$ \left( {\frac{{\left\langle {\sigma_{n} } \right\rangle }}{{N_{\max } }}} \right)^{2} + \left( {\frac{{\sigma_{s} }}{{S_{\max } }}} \right)^{2} + \left( {\frac{{\sigma_{t} }}{{T_{\max } }}} \right)^{2} = 1 $$

(7)

where $\sigma_{n}$, $\sigma_{s}$ and $\sigma_{t}$ are the normal stress, the shear stress in the first direction and the shear stress in the second direction at the opening, respectively. $N_{\max }$, $S_{\max }$ and $T_{\max }$ represent the values of normal tensile strength and shear strength in different directions, respectively. The BK failure criterion is utilized to simulate the failure of the adhesive layer after damage. The expression of BK failure criterion is:

$$ G_{{{\text{{I}}{C}}}} + \left( {G_{\Pi C} - G_{{{\text{{ I}}{C}}}} } \right)\left( {\frac{{G_{\Pi } }}{{G_{{{T}}} }}} \right)^{\eta } = G_{{{{TC}}}} $$

(8)

where $G_{\rm I}$, $G_{\Pi }$ and $G_{T}$ are the energy release rates of type ${\rm I}$, type $\Pi$ and the entire model, respectively, and $G_{{{T}}} = G_{\rm I} + G_{\Pi }$. $G_{{{\text{{I}}{C}}}}$, $G_{\Pi C}$ and $G_{{TC}}$ are the critical energy release rates of type ${\rm I}$, type $\Pi$ and the entire model, respectively, and $G_{{{{TC}}}} = G_{{{\text{{I}}{C}}}} + G_{\Pi C}$.

2.2 Post-buckling Reliability Model

It is assumed that the composite stiffened plate completely fails when its ultimate bearing capacity is reached, so the performance function under axial compression is defined as

$$ G\left( {\varvec{X}} \right) = \eta_{{{u}}} P_{{{u}}} \left( {\varvec{X}} \right) - P $$

(9)

where $G\left( {\varvec{X}} \right)$ is the performance function, ${\varvec{X}}$ is the random variable vector included in the reliability evaluation, $\eta_{{{u}}}$ is the model uncertainty coefficient, $P_{{{u}}}$ is the ultimate bearing capacity, and $P$ is the loaded compression. Eq. (9) contains the ultimate bearing capacity$P_{u}$, which is obtained using the nonlinear finite element method (FEM).

In order to improve the calculation efficiency, the ratio coefficient $K$ is introduced and the ultimate strength $P_{u}$ can be calculated in combination with the buckling load, i.e.

$$ P_{{{u}}} = KP_{{{\text{cr}}}} $$

(10)

According to Eq. (10), a new performance function replacing the ultimate compressive strength with buckling load is established for post-buckling reliability analysis, which is defined as

$$ G\left( {\varvec{X}} \right) = \eta_{u} K\left( {\varvec{X}} \right)P_{\text{cr}} \left( {\varvec{X}} \right) - P $$

(11)

where $P_{\text{cr}}$ indicates the buckling load function, and the ratio coefficient $K\left( {\varvec{X}} \right)$ can be defined as

$$ K\left( {\varvec{X}} \right) = K_{0} h_{0} (\varvec{X}) $$

(12)

where $h_{0} \left( {\varvec{X}} \right)$ is the distribution function of ratio coefficient $K$, and $K_{0}$ is the mean value of coefficient $K$, which is obtained by the following equation

$$ K_{0} = \frac{{\overline{P}_{u} }}{{\overline{{P_{{{\text{cr}}}} }} }} $$

(13)

where $\overline{P}_{u}$ is the mean value of the ultimate compression, and $\overline{P}_{\text{cr}}$ is the mean buckling load. The distribution function $h_{0} (X)$ is a function of variables $X_{{{T}}} ,X_{{{C}}} ,Y_{{{T}}} ,Y_{{{C}}} ,S,R,X_{{{{TC}}}} ,S_{{{C}}}$.

2.3 Moment-Independent Global Sensitivity Analysis

In order to measure the influence of input variable $X_{i}$ on the uncertainty of output response, the moment-independent sensitivity index is defined as follows [23, 29,30,31]

$$ \delta_{i} = \frac{1}{2}E_{{X_{i} }} \left( {s\left( {X_{i} } \right)} \right) = \frac{1}{2}\int {s\left( {x_{i} } \right)} f_{{X_{i} }} \left( {x_{i} } \right)\text{d}x_{i} $$

(14)

where $E_{{X_{i} }} \left( \cdot \right)$ is the expectation operator, $f_{{X_{i} }} \left( {x_{i} } \right)$ indicates the PDF of variable $X_{i}$, and $s\left( {X_{i} } \right)$ is the area difference between the unconditional PDF $f_{Y} \left( y \right)$ and the conditional PDF $f_{{Y\left| {X_{i} } \right.}} \left( y \right)$ of $Y$, which is as follows

$$ s\left( {X_{i} } \right) = \int {\left| {f_{Y} \left( y \right) - f_{{Y\left| {X_{i} } \right.}} \left( y \right)} \right|} {\rm d}y $$

(15)

where $f_{{Y\left| {X_{i} } \right.}} \left( y \right)$ represents the PDF of the model output $Y$ when the input variable $X_{i}$ is fixed at $x_{i}$, while $f_{Y} \left( y \right)$ is the unconditional PDF of $Y$. If $X_{i}$ has greater influence on the uncertainty of $Y$, fixing $X_{i}$ will make the PDF of the model output change more, and then the corresponding distance between $f_{{Y\left| {X_{i} } \right.}} \left( y \right)$ and $f_{Y} \left( y \right)$ will be larger, resulting in a larger $s\left( {X_{i} } \right)$.$\,s\left( {X_{i} } \right)$ is a unary function of $X_{i}$, and the average influence of $X_{i}$ on $Y$ can be measured by taking expectation of $s\left( {X_{i} } \right)$, thus the sensitivity index $\delta_{i}$ can be obtained.

3 Active Learning Kriging Method

As an unbiased estimation model with minimum variance, the Kriging surrogate model combines the global approximation with the local random error.

The Kriging model includes the linear regression model and the stochastic process model, i.e.

$$ g\left( \user2{x} \right) = F\left( {\user2{x},\beta } \right) + z\left( \user2{x} \right) = {\beta } + z\left( \user2{x} \right) $$

(16)

where $g\left( \user2{x} \right)$ represents the unknown function to fit, $\beta$ represents the global estimation of the model, and $z\left( \user2{x} \right)$ denotes the random distribution of the unknown function.

Given the design of experiments (DoE), the predicted value and variance of the Kriging model at the unknown point can be expressed as:

$$ \mu _{g} \left( \user2{x} \right) = \hat{\beta } + \user2{r}\left( {\theta ,\user2{x}} \right)^{{\text{T}}} \user2{R}\left( \theta \right)^{{ - 1}} \left( {\user2{g} - \hat{\beta }{\mathbf{1}}} \right) $$

(17)

$$\sigma _{g}^{2} \left( \user2{x} \right) = \sigma ^{2} \left[ {1 + \frac{{\left( {\user2{1}^{{\text{T}}} \user2{R}\left( \theta \right)^{{ - 1}} {\varvec{r}}\left( {\theta ,\user2{x}} \right) - 1} \right)^{2} }}{{\user2{1}^{{\text{T}}} \user2{R}\left( \theta \right)^{{ - 1}} \user2{1}}} - {\varvec{r}}\left( {\theta ,\user2{x}} \right)^{{\text{T}}} \user2{R}\left( \theta \right)^{{ - 1}} {\varvec{r}}\left( {\theta ,\user2{x}} \right)} \right]$$

(18)

where ${\mathbf{1}}$ is an m-dimensional unit column vector; ${\varvec{r}}\left( {\theta ,{\varvec{x}}} \right)$ represents the correlation function of training points; ${\varvec{R}}\left( \theta \right)$ is a correlation matrix of any pair of training points; $\hat{\beta }$, $\sigma^{2}$ and $\theta$ are parameters of the Kriging model.

With an optimization problem, the estimated value $\theta$ solved for can establish a Kriging model:

$$ \theta^{*} = \arg \mathop {\min }\limits_{\theta } \left( {\left| {{\varvec{R}}\left( \theta \right)} \right|^{\frac{1}{m}} \sigma^{2} } \right) $$

(19)

The Kriging interpolation model is established by random sampling of the points near the predicted ones, so the accuracy of the model is bound to be related to the selected sample points. Since the predicted value $\mu_{G} \left( x \right)$ given by the Kriging model is not the real value, there exists a situation where the symbol of the predicted value is different from the real one. The following is a case for separate consideration. When $\hat{G}\left( x \right) < 0$, i.e., $\mu_{G} \left( x \right) < 0$, then there is a risk with the real value $G(x) > 0$, and the risk index $\Re (x)$ is defined as

$$ \Re (x) = \max \left[ {\left( {G(x) - 0} \right),0} \right] $$

(20)

$\Re (x)$ represents the degree of the true value $G(x) > 0$ when $\mu_{G} \left( x \right) < 0$. Since $G(x)$ is a random variable, $\Re (x)$ is also a random variable. Therefore, the mathematical expectation of $\Re (x)$ is

$$ \begin{aligned} E\left( {\Re \left( x \right)} \right) & = E\left[ {\max \left( {\left( {G(x) - 0} \right),0} \right)} \right] \\ & = \int_{0}^{ + \infty } {G(x)\phi \left( {\frac{{\hat{G}\left( x \right) - \mu_{G} \left( x \right)}}{{\sigma_{G} (x)}}} \right)\text{d}G} \hfill \\ &= \sigma_{G} (x)\phi \left( {\frac{{\mu_{G} \left( x \right)}}{{\sigma_{G} (x)}}} \right) + \mu_{G} \left( x \right)\Phi \left( {\frac{{\mu_{G} \left( x \right)}}{{\sigma_{G} (x)}}} \right) \hfill \\ \end{aligned} $$

(21)

where $\mu_{G} \left( x \right)$ is the mean value of the predicted value at point $x$, and $\sigma_{G} (x)$ is the variance of the predicted value. $\phi \left( \cdot \right)$ is the PDF of the standard normal distribution, and $\Phi \left( \cdot \right)$ is the CDF of the standard normal distribution. Similarly, when $\hat{G}\left( x \right) > 0$,$\,\mu_{G} \left( x \right) > 0$, then there is a risk with the true value $G(x) < 0$.

The expected risk equations in separate conditions can be rewritten in a unified form as follows

$$ \begin{gathered} E\left( {\Re (x)} \right) = - \text{sign}\left( {\mu_{G} \left( x \right)} \right)\mu_{G} \left( x \right)\Phi \left( { - \text{sign}\left( {\mu_{G} \left( x \right)} \right)\frac{{\mu_{G} \left( x \right)}}{{\sigma_{G} \left( x \right)}}} \right) \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} + \sigma_{G} \left( x \right)\phi \left( {\frac{{\mu_{G} \left( x \right)}}{{\sigma_{G} \left( x \right)}}} \right) \hfill \\ \end{gathered} $$

(22)

Equation (22) is called the expected risk function (ERF), also known as the learning equation, which illustrates the possibility that the sign of the function to be fitted is predicted wrongly. The basic steps for calculating the post-buckling failure probability and the variable importance ranking of composite stiffened plates by the ALK method are as follows:

Step 1: According to the variable information, generate 20 sample points $X_{t} = \left( {X_{1,t} ,X_{2,t} , \cdots ,X_{n,t} } \right)\left( {t = 1,2, \cdots ,N,N = 20} \right)$ randomly by the Latin hypercube sampling method and construct the initial set of samples. Then calculate the corresponding values of performance function $G\left( X \right)$ with the initial samples. The initial training points and the corresponding responses of $G\left( X \right)$ constitute the initial DoE.

Step 2: Generate 10⁵ samples randomly in the uncertainty space of input variables as the candidate population.

Step 3: Construct the initial Kriging model with the initial DoE.

Step 4: Predict the values of $\mu_{G} \left( X \right)$ and variances $\sigma_{G}^{2} \left( x \right)$ of the candidate points using the Kriging model, and then calculate the ERF values based on Eq. (22). The point with the maximum ERF value is marked as $X^{*}$.

Step 5: If the maximum value of ERF meets the threshold of convergence condition, then turn to Step 6. The threshold is set as $10^{ - 3}$. Elsewise, add the marked point $X^{*}$ and its response of performance function into the set of training samples. Refresh the Kriging model with the updated DoE and return to Step 4.

Step 6: Based on the established Kriging model, calculate the post-buckling failure probability by the MCS method.

Step 7: Select failure sample $\left\{ {{\varvec{x}}_{1}^{F} ,{\varvec{x}}_{2}^{F} , \cdots ,{\varvec{x}}_{{\varvec{N}_{F} }}^{F} } \right\}$ to estimate the conditional probability density $f_{{x_{j} }} \left( {\left. {x_{j} } \right|F} \right)$ of input variable ${\varvec{x}}_{j}$, and label it as $\widehat{f}_{{x_{j} }} \left( {\left. {x_{j} } \right|F} \right)$, where $N_{F}$ is the number of failure samples.

Step 8: According to Eq. (14), estimate $\delta_{i}^{{}}$.

4 Case Study

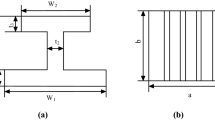
The geometric schematic is shown in Fig. 1. The information of each layer is shown in Table 1, and the thickness of a single layer is 0.12 mm.

Fig. 1

Geometric schematic of the composite stiffened plate

Table 1 Layer information of the composite stiffened plate

The material of this composite stiffened plate is CCF300/BA9916, and the material of interface adhesive layer is J116B. Table 2 shows the material properties of J116B and CCF300/BA9916.

Table 2 Mechanical properties of J116B and CCF300/BA9916

In order to verify the accuracy of the finite element model, the simulation results are compared with the experimental ones in reference [32]. A total of 5 sets of tests were carried out, and 5 sets of failure loads were obtained, the mean value of which was 1188.4 kN [32].

In the finite element model, the stiffener and skin are simulated by the shell element (S4R), the adhesive layer is simulated by the cohesive force element, and the cohesive force element and shell element are connected at common nodes. In order to accurately simulate the failure process of composite materials, the Hashin failure criterion is adopted and the damage evolution law is set. The finite element model and boundary conditions of the composite stiffened plate are shown in Fig. 2. As shown in Fig. 2, it is fixed away from the loading end, and the secondary end boundary is constrained by U1 and U2. The wing rib boundary is constrained by the Y-degree of freedom of the plate, and the non-loading edge is free. In the nonlinear analysis of post-buckling, the ninefold first-order bucking modes and onefold second-order buckling modes are used to replace the initial defects.

Fig. 2

Finite element model and boundary conditions of stiffened composite plate

Figure 3 is the displacement cloud of post-buckling finite element analysis. It can be seen from the figure that the failure area and sequence of finite element analysis are consistent with the experimental results [32].

Fig. 3

Displacement cloud of post-buckling finite element analysis

Figure 4 shows the load–displacement curve of post-buckling analysis, which is obtained by constructing coupling reference points. The final bearing capacity of the structure, i.e., the ultimate load, is 1177.38 kN. And the error of the simulation result compared with the experimental result is $0.93\%$.

Fig. 4

Load–displacement curve of post-buckling analysis

In this paper, all material property parameters of the composite stiffened plate are taken as random variables. Table 3 shows the probabilistic characteristics of each variable. The ultimate strength $P$ is set as 1188.4 kN.

Table 3 Probabilistic properties of fundamental variables

4.1 Effect of Longitudinal Elastic Modulus

Consider four cases of $E_{1}$: (1)$E_{1} = 129\;{\text{GPa}}$, (2)$E_{1} = 140\;{\text{GPa}}$, (3)$E_{1} = 150\;{\text{GPa}}$, and (4)$E_{1} = 170\;{\text{GPa}}$. And the fiber-direction tensile strength $X_{T}$ is set as $1720\;{\text{MPa}}$. The post-buckling failure probability results of these four cases are shown in Table 4. It can be seen that the post-buckling failure probability of composite stiffened plates decreases rapidly with the increase of $E_{1}$. When $E_{1}$ grows to 170 GPa, the failure probability is only 0.0800, which shows that the fiber is a significant load-bearing part in the structure. The ALK method calls the performance function 154 times in total. The comparison between the results of the ALK method and the MCS method fully demonstrates the accuracy and efficiency of the ALK method in dealing with post-buckling reliability problems.

Table 4 Post-buckling failure probability of composite stiffened plate with different $E_{1}$

For purposes of convenience, the importance rankings of input variables obtained by sensitivity analysis with the increase of longitudinal elastic modulus $E_{1}$ are shown in Fig. 5. It can be seen that the sensitivity indices of $G_{12}$, $G_{13}$ and $G_{23}$ are the largest, and $G_{12} > G_{23} > G_{13}$, which validates that the ability to resist shear failure is significant for composite stiffened plates. In addition, as can be seen from Fig. 5, the importance ranking of $E_{1}$ increases with the increase of $E_{1}$. When $E_{1} = 129\;{\text{GPa}}$, $E_{1} < v_{12}$; but when $E_{1} = 150\;{\text{GPa}}$, $E_{1} > v_{12}$. This indicates that the contribution of design variables to the post-buckling failure probability of composite stiffened plates varies under various working conditions. However, the importance rankings of $X_{{{T}}}$,$X_{{{C}}}$,$Y_{{{T}}}$,$Y_{{{C}}}$,$S_{23}$ and $S_{12}$ are smaller and close to zero under various working conditions. In order to verify the rationality of the sensitivity analysis results, the change of failure probability varying with $X_{{{T}}}$ is studied in Sect. 4.2.

Fig. 5

Sensitivity results of input variables

4.2 Effect of Fiber-Direction Tensile Strength

Consider four cases of $X_{{{T}}}$: (1)$X_{{{T}}} = 1720\;{\text{MPa}}$, (2)$X_{{{T}}} = 1750\;{\text{MPa}}$, (3)$X_{{{T}}} = 1900\;{\text{MPa}}$, and (4)$X_{{{T}}} = 2100\;{\text{MPa}}$. And the longitudinal elastic modulus $E_{1}$ is set as $129\;{\text{GPa}}$. The results of post-buckling failure probability of these four cases are shown in Table 5. It can be seen that the failure probability of the composite stiffened plate does not change with the increase of $X_{{{T}}}$, which illustrates that the uncertainty of variable $X_{T}$ has little effect on the failure probability and further demonstrates the rationality and effectiveness of the sensitivity analysis results in Fig. 5. Therefore, researchers do not need to spend a lot of sources on the tensile strength in the process of reliability design for the ultimate strength of composite stiffened plates. Due to little change of post-buckling failure probability with varying $X_{T}$, the sensitivity analysis results with different cases of $X_{T}$ are not shown in this paper.

Table 5 Post-buckling failure probability of composite stiffened plate with different $X_{T}$

5 Conclusion

In this paper, a post-buckling reliability analysis method of composite stiffened plates is proposed based on the ALK model and the Hashin failure criterion. The ALK method is employed to estimate the post-buckling failure probability and sensitivity index of composite stiffened plates. In case studies, the simulation accuracy of the finite element model is first verified by comparing the simulation results with the experimental results. The MCS method is employed to obtain the benchmark results for validating the computational accuracy and efficiency of the ALK method. The results show that the ALK method can reduce the computational cost obviously while ensuring the computational accuracy. Then, the effects of longitudinal elastic modulus $E_{1}$ and fiber-direction tensile strength $X_{{{T}}}$ on the post-buckling failure probability are analyzed. The sensitivity results show that the shear modulus has the largest effect on the post-buckling reliability of the composite stiffened plate. The variables, whose sensitivity indices are close to zero, can be ignored in the design and optimization of composite stiffened plates, which is further demonstrated in the investigation of the effect of fiber-direction tensile strength on the post-buckling reliability. The proposed post-buckling reliability and sensitivity analysis method with the ALK model is significant for the safety assessment and optimization design of composite stiffened plates.