Stochastic bending and buckling analysis of laminated composite plates using Latin hypercube sampling

Abstract

Deterministic and stochastic bending and buckling characteristics of antisymmetric cross-ply and angle-ply laminated composite plates are thoroughly examined. Partial differential equations for cross-ply and angle-ply laminates are derived using the three variable refined shear deformation theory based on the Hamilton principle. Deterministic Navier’s solutions are obtained for specific boundary conditions and numerical results are validated with the first-order and third-order shear deformation theories. Two stochastic sampling methods, namely Monte Carlo simulation and Latin hypercube sampling, are presented and analyzed to determine the optimal one based on convergence studies and criteria of sampling errors. Comprehensive probability characteristics of stochastic bending deflections and stochastic critical buckling loads of antisymmetric cross-ply and angle-ply laminated composite plates are investigated using the optimal sampling technique. Probability distribution functions of various stochastic cases provide good assessments for the effects of each inevitable source uncertainty on the bending and buckling behaviors of the laminated composites. This study presents a good alternative for the classical and expensive Monte Carlo simulations and provides a fundamental understanding of bending and buckling statistics of laminated composites.

1 Introduction

Among different types of composites [1,2,3,4,5,6,7,8], composite laminates are widely used and intensively studied due to their advanced characteristics such as high strength-to-weight ratios, thermal insulation, corrosion resistance, and the ability to be tailored in different working environments. The development of advanced manufacturing techniques makes it possible to use laminated composites in various engineering fields such as aerospace [9,10,11,12,13], automotive [14,15,16,17] industries, and marine structures [18] with more affordable costs. A comprehensive understanding of their behaviors under various working environments is crucial for utilizing the composites safely and effectively. Indeed, a specified structural configuration behaves in a specified manner, called deterministic behaviors [19,20,21], while the behaviors can deviate from deterministic states when uncertain factors exist in reality [22,23,24,25]. We initially performed deterministic bending and buckling analyses of antisymmetric cross-ply and angle-ply laminated composite plates before quantifying their uncertainties for different sources of randomness in geometrical configurations and materials properties.

Deterministic studies on laminated composites have been conducted using different approaches. Köllner et al. [26] analyzed the delamination propagation of thin-film laminated composites under the buckling mechanisms caused by anisotropic effects of the contact, mode-mixing, and sub-laminates. Two analytical models to determine the energy release rate can be used together to characterize ranges of post-buckling stiffness of the laminated composites for accuracy and computational efficiency. Baucke and Mittelstedt [27] analytically investigated the buckling loads of thin rectangular laminated composite plates under uniaxial compressions using the classical plate theory and classical Rayleigh–Ritz method. Symmetric stacking sequences and the coupling between bending and twisting effects were considered. The degradation of the bend-twist coupling on the shear buckling phenomenon of laminated composite plates was investigated by Lee and York [28] by developing the concept of contour maps. In that study, ply contiguity constraints and ply percentages were also adopted, which provided practical design knowledge. Tran et al. [29] conducted an isogeometric finite element analysis (IGA) based on the higher-order shear deformation theory (HSDT) to examine the thermal buckling and bending behaviors of laminated composite plates. The study raised the importance of considering the transverse normal strain in the analysis of laminated composites in thermal environments. Using the Galerkin method, Chen and Qiao [30] investigated the buckling and post-buckling behaviors of laminated composite plates under either pure shear or the coupling of shear and compression. Rotationally restrained edges were modeled with a trigonometric series, and the semi-analytical results were validated with numerical results obtained from finite element analyses in the commercial software ABAQUS. Using isogeometric analysis based on the PHT-splines, Qin et al. [31] studied the vibration and buckling phenomenon of laminated composite plates reinforced by curvilinear stiffeners. The parameters of curvilinear stiffeners, namely, location, dimensions, curvature, and orientations, can be optimized to improve the fundamental frequency and buckling load of the composites. Manickam et al. [32] examined the thermal buckling behaviors of laminated composite plates using the first-order shear deformation theory. The curvilinear variation of fiber angles enables the spatial variation of the composite stiffness and significantly affects the composite thermal buckling behaviors. Using the HSDT, Kharghani and Soares [33] investigated the delamination propagation around the boundary of the embedded delamination region on laminated composite plates subjected to bending loads. The bending stress–strain curves of the plates were characterized and the initiation of delamination propagation was determined by evaluating the strain energy release rate. Theoretical, numerical, and experimental investigations on the buckling of rectangular laminated composite plates [34] were also conducted. Liu et al. [35] studied the nonlinear vibration characteristics of eccentric-rotating laminated shallow cylinders exposed to thermomechanical excitations. The chaotic dynamics and resonant response of the cylinders were obtained by solving nonlinear partial different methods with the Galerkin method.

Stochastic studies on laminated composites have received increasing interest from researchers. Dey et al. [36] studied the stochastic buckling loads and natural frequencies of laminated sandwich plates using a stochastic finite element model based on a higher-order zigzag theory and multivariable adaptive regression splines. The proposed surrogate model characterized the system sensitivity and uncertainty caused by randomness in ply angle, structure thickness, and material properties with more efficiency in comparison with the classical Monte Carlo simulation. Sepahvand and Marburg [37] used the generalized polynomial chaos expansion to estimate Young’s moduli, shear moduli, and Poisson’s ratios of laminated composite plates from eigenfrequencies observed from experiments. The stochastic finite element procedure was used as the model within this non-sampling probability method for the inverse problem. Noh and Park [38] investigated the spatially random effects of Poisson’s ratio on the bending behaviors of laminated composite plates. The constitutive matrix was decomposed using the Taylor series to simplify the representation of Poisson’s ratio in the finite element formulation, which proved to be as efficient as the Monte Carlo simulation. Chen and Soares [39] incorporated the Karhunen–Loève expansion into the spatial discretization of the finite element procedure to study the stochastic bending of laminated composite plates with randomness in material properties and multi-layer effects. The proposed method produced a more reasonable probabilistic estimation than the Monte Carlo simulation due to the enhancement of its convergence due to the preconditioning conjugate gradient technique. Dodwell et al. [40] directly adopted a Monte Carlo simulation at a multilevel framework to characterize failure statistics of laminated composites. The proposed approach proved to be more simple and self-adaptive and was hugely more computationally effective in comparison to the classical Monte Carlo simulation. Using the Karhunen–Loève theorem within the framework of the stochastic assumed mode method, Parviz and Fakoor [41] studied the stochastic free vibration of laminated composite plates with random fields in material properties as well as thermal distribution. This non-intrusive method was more computationally efficient than the intrusive finite element method for stochastic analysis. Gadade et al. [42] examined the buckling and progressive failure of a laminated composite plate with a polymer matrix and reinforced fibers exposed to hygro-thermo-mechanical loads. The statistics of the buckling load, first ply failure strength, and last ply failure strength of the composites whose constituents had random thermal and mechanical properties were predicted based on the mode of failure and the Pucks failure criteria. Chen et al. [43] quantified the uncertainty of elastic mechanical properties of laminated composite plates from initial experimental data whose errors were eliminated using the grey judgment criterion. Feasible intervals of last ply failure loads of the composite subjected to in-plane tensile loads and its structural reliability were evaluated with the obtained statistics of the feasible mechanical properties of laminae. Mahjudin et al. [44] proposed a non-intrusive framework to quantify the bending uncertainty of laminated composite shells. The generalized stresses were assumed to be independent of the randomness of input variability, and the Monte Carlo method was used to generate random parameters and evaluate the deflection statistics. Besides, integrating stochastic sampling techniques with the cell-based smoothed finite element methods [45], isogeometric analyses [46], or the generalized shell elements using the mixed interpolation of tensorial components (MITC) technique [47,48,49,50] shows high potential in stochastic analyses of laminated composites.

The literature clearly shows that different sampling and non-sampling techniques have been developed for stochastic analyses of laminated composites in which Monte Carlo simulations play an important role either as the primary simulation tool or the benchmark for other techniques. Despite its popularity, samples generated from Monte Carlo simulations can be clustered and large unsampled regions may exist [51]. Thus, to have accurate simulation results with Monte Carlo simulations, large samples are often necessary, which makes the method computationally expensive. Among several endeavors being made to either improve or replace Monte Carlo simulations, the Latin hypercube sampling technique is believed to be a good alternative. In this paper, we quantitatively present the advantages of the Latin hypercube sampling technique over Monte Carlo simulations. Initially, we derived deterministic partial differential equations for the bending and buckling phenomena of antisymmetric cross-ply and angle-ply laminated composite plates in the framework of the three variable refined shear deformation theory and Hamilton’s principle. We obtained the deterministic bending deflections and buckling loads and verified them with results from popular theories such as the first-order and third-order shear deformation theories. Then, we compared the convergence characteristics of Monte Carlo simulations and the Latin hypercube sampling technique in different stochastic environments. We used the optimal technique for a comprehensive investigation of the probability of bending deflections and buckling loads of different antisymmetric cross-ply and angle-ply laminated composite plates. The obtained results not only depict the advantages of the Latin hypercube sampling technique in stochastic analysis but also provide a fundamental understanding of the statistics of static behaviors of laminated composites in stochastic environments.

2 Lamina and laminate deterministic configurations

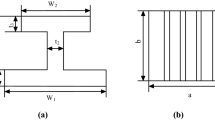
A general laminated composite plate is illustrated in Fig. 1 with gross thickness $h$; $x$-axis length $a$; $y$-axis length $b$; fiber orientations of laminae $\alpha_{1}$, $\alpha_{2}$, …, $\alpha_{N - 1}$, and $\alpha_{N}$; lamina thicknesses $h_{1}$, $h_{2}$, …, $h_{N - 1}$, and $h_{N}$ (see Fig. 1A). Figure 1B shows the cross-section of the laminated composite plate with vertical coordinates $z_{1}$, $z_{2}$, $z_{3}$, …, $z_{N - 1}$, $z_{N}$, and $z_{N + 1}$. Figure 1C presents the configuration of a typical lamina that constitutes the laminated plate. The local coordinates $\left( {x_{1} ,x_{2} ,x_{3} } \right)$ with primary fiber orientations make an angle $\alpha$ with the problem coordinate systems $\left( {x,y,z} \right)$. In the local coordinate of the $i{\text{th}}$ lamina, the plane stress-reduced stiffnesses $C_{pq}^{\left( i \right)}$ can be expressed in terms of engineering constants as follows [52]:

$$\begin{aligned} C_{11}^{\left( i \right)} & = \frac{{E_{1}^{\left( i \right)} }}{{1 - \nu_{12}^{\left( i \right)} \nu_{21}^{\left( i \right)} }},\,\,\,\,\,\,C_{12}^{\left( i \right)} = \frac{{\nu_{12}^{\left( i \right)} E_{2}^{\left( i \right)} }}{{1 - \nu_{12}^{\left( i \right)} \nu_{21}^{\left( i \right)} }},\,\,\,\,\,\,C_{22}^{\left( i \right)} = \frac{{E_{2}^{\left( i \right)} }}{{1 - \nu_{12}^{\left( i \right)} \nu_{21}^{\left( i \right)} }}, \\ C_{44}^{\left( i \right)} & = G_{23}^{\left( i \right)} ,\,\,\,\,\,C_{55}^{\left( i \right)} = G_{13}^{\left( i \right)} ,\,\,\,\,\,C_{66}^{\left( i \right)} = G_{12}^{\left( i \right)} . \\ \end{aligned}$$

(1)

Fig. 1

Laminated composite plates. A Geometry parameters and layer-stacking sequence with arbitrary laminae, where $\alpha_{i}$ represents the fiber orientation of each lamina, $i = 1,...,N$ with $N$ is the number of layers. B Cross-section with vertical coordinates. C A lamina with local $\left( {x_{1} ,x_{2} ,x_{3} } \right)$ and global $\left( {x,y,z} \right)$ coordinate systems

These lamina stiffnesses are transformed to the laminate coordinates as follows:

$$\begin{aligned} \overline{C}_{11}^{\left( i \right)} & = C_{11}^{\left( i \right)} \cos^{4} \alpha + 2\left( {C_{12}^{\left( i \right)} + 2C_{66}^{\left( i \right)} } \right)\sin^{2} \alpha \cos^{2} \alpha + C_{22}^{\left( i \right)} \sin^{4} \alpha , \\ \overline{C}_{12}^{\left( i \right)} & = \left( {C_{11}^{\left( i \right)} + C_{22}^{\left( i \right)} - 4C_{66}^{\left( i \right)} } \right)\sin^{2} \alpha \cos^{2} \alpha + C_{12}^{\left( i \right)} \left( {\sin^{4} \alpha + \cos^{4} \alpha } \right), \\ \overline{C}_{22}^{\left( i \right)} & = C_{11}^{\left( i \right)} \sin^{4} \alpha + 2\left( {C_{12}^{\left( i \right)} + 2C_{66}^{\left( i \right)} } \right)\sin^{2} \alpha \cos^{2} \alpha + C_{22}^{\left( i \right)} \cos^{4} \alpha , \\ \overline{C}_{44}^{\left( i \right)} & = C_{44}^{\left( i \right)} \cos^{2} \alpha + C_{55}^{\left( i \right)} \sin^{2} \alpha , \\ \overline{C}_{45}^{\left( i \right)} & = \left( {C_{55}^{\left( i \right)} - C_{44}^{\left( i \right)} } \right)\cos \alpha \sin \alpha , \\ \overline{C}_{55}^{\left( i \right)} & = C_{55}^{\left( i \right)} \cos^{2} \alpha + C_{44}^{\left( i \right)} \sin^{2} \alpha , \\ \overline{C}_{16}^{\left( i \right)} & = \left( {C_{11}^{\left( i \right)} - C_{12}^{\left( i \right)} - 2C_{66}^{\left( i \right)} } \right)\sin \alpha \cos^{3} \alpha + \left( {C_{12}^{\left( i \right)} - C_{22}^{\left( i \right)} + 2C_{66}^{\left( i \right)} } \right)\sin^{3} \alpha \cos \alpha , \\ \overline{C}_{26}^{\left( i \right)} & = \left( {C_{11}^{\left( i \right)} - C_{12}^{\left( i \right)} - 2C_{66}^{\left( i \right)} } \right)\sin^{3} \alpha \cos \alpha + \left( {C_{12}^{\left( i \right)} - C_{22}^{\left( i \right)} + 2C_{66}^{\left( i \right)} } \right)\sin \alpha \cos^{3} \alpha , \\ \overline{C}_{66}^{\left( i \right)} & = \left( {C_{11}^{\left( i \right)} + C_{22}^{\left( i \right)} - 2C_{12}^{\left( i \right)} - 2C_{66}^{\left( i \right)} } \right)\sin^{2} \alpha \cos^{2} \alpha + C_{66}^{\left( i \right)} \left( {\sin^{4} \alpha + \cos^{4} \alpha } \right). \\ \end{aligned}$$

(2)

3 Deterministic solution procedure

3.1 Displacement, strain, and stress fields

Displacement components of an arbitrary point in the laminated composite plate were obtained using the three variable refined shear deformation theory (TRSDT) [53] as follows:

$$\begin{gathered} u\left( {x,y,z} \right) = u_{{\text{e}}} \left( {x,y} \right) - zw_{{{\text{b}},x}} - f_{z} w_{{{\text{s}},x}} , \hfill \\ v\left( {x,y,z} \right) = v_{{\text{e}}} \left( {x,y} \right) - zw_{{{\text{b}},y}} - f_{z} w_{{{\text{s}},y}} , \hfill \\ w\left( {x,y,z} \right) = w_{{\text{e}}} \left( {x,y} \right) + w_{{\text{b}}} \left( {x,y} \right) + w_{{\text{s}}} \left( {x,y} \right). \hfill \\ \end{gathered}$$

(3)

in which

$$f_{z} = - \frac{z}{4} + \frac{{5z^{3} }}{{3h^{2} }},$$

(4)

and subscripts ${\text{e}}$, ${\text{b}}$, and ${\text{s}}$ denote the extensional, bending, and shear effects, respectively. Subscript commas denote the spatial derivative. It is noted that the bending components of the in-plane displacements were assumed to take the form of the classical plate theory, while the shear components were assumed to have a cubic function that enables the shear stresses to vanish at the top and bottom surfaces. This eliminates the use of the shear correction factor.

Von Karman strain components were derived from the displacement field as follows [52, 53]:

$$\left( {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\varepsilon_{x}^{e} } \\ {\varepsilon_{y}^{e} } \\ {\gamma_{xy}^{e} } \\ {\gamma_{xz}^{e} } \\ {\gamma_{yz}^{e} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {z\kappa_{x}^{b} } \\ {z\kappa_{y}^{b} } \\ {z\kappa_{xy}^{b} } \\ 0 \\ 0 \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {f_{z} \kappa_{x}^{s} } \\ {f_{z} \kappa_{y}^{s} } \\ {f_{z} \kappa_{xy}^{s} } \\ {\left( {1 - f_{z,z} } \right)\gamma_{xz}^{s} } \\ {\left( {1 - f_{z,z} } \right)\gamma_{yz}^{s} } \\ \end{array} } \right),$$

(5)

in which

$$\left( {\begin{array}{*{20}c} {\varepsilon_{x}^{e} } \\ {\varepsilon_{y}^{e} } \\ {\gamma_{xy}^{e} } \\ {\gamma_{xz}^{e} } \\ {\gamma_{yz}^{e} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {u_{{{\text{e}},x}} - r_{x} w + {{w_{,x}^{2} } \mathord{\left/ {\vphantom {{w_{,x}^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {v_{{{\text{e}},y}} - r_{y} w + {{w_{,y}^{2} } \mathord{\left/ {\vphantom {{w_{,y}^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {v_{{{\text{e}},x}} + u_{{{\text{e}},y}} + w_{,x} w_{,y} } \\ {w_{{{\text{e}},x}} } \\ {w_{{{\text{e}},y}} } \\ \end{array} } \right),\quad \left( {\begin{array}{*{20}c} {\kappa_{x}^{b} } \\ {\kappa_{y}^{b} } \\ {\kappa_{xy}^{b} } \\ {\kappa_{x}^{s} } \\ {\kappa_{y}^{s} } \\ {\kappa_{xy}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - w_{{{\text{b}},xx}} } \\ { - w_{{{\text{b}},yy}} } \\ { - 2w_{{{\text{b}},xy}} } \\ { - w_{{{\text{s}},xx}} } \\ { - w_{{{\text{s}},yy}} } \\ { - 2w_{{{\text{s}},xy}} } \\ \end{array} } \right).$$

(6)

In the problem coordinate system, stress components in the $i{\text{th}}$ lamina are written as

$$\left( {\begin{array}{*{20}c} {\sigma_{x}^{\left( i \right)} } \\ {\sigma_{y}^{\left( i \right)} } \\ {\tau_{xy}^{\left( i \right)} } \\ {\tau_{xz}^{\left( i \right)} } \\ {\tau_{yz}^{\left( i \right)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\overline{C}_{11}^{\left( i \right)} } & {\overline{C}_{12}^{\left( i \right)} } & {\overline{C}_{16}^{\left( i \right)} } & 0 & 0 \\ {\overline{C}_{12}^{\left( i \right)} } & {\overline{C}_{22}^{\left( i \right)} } & {\overline{C}_{26}^{\left( i \right)} } & 0 & 0 \\ {\overline{C}_{16}^{\left( i \right)} } & {\overline{C}_{26}^{\left( i \right)} } & {\overline{C}_{66}^{\left( i \right)} } & 0 & 0 \\ 0 & 0 & 0 & {\overline{C}_{44}^{\left( i \right)} } & {\overline{C}_{45}^{\left( i \right)} } \\ 0 & 0 & 0 & {\overline{C}_{45}^{\left( i \right)} } & {\overline{C}_{55}^{\left( i \right)} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( i \right)} } \\ {\varepsilon_{y}^{\left( i \right)} } \\ {\gamma_{xy}^{\left( i \right)} } \\ {\gamma_{xz}^{\left( i \right)} } \\ {\gamma_{yz}^{\left( i \right)} } \\ \end{array} } \right).$$

(7)

3.2 Hamilton’s principle

From the continuum mechanics point of view, the gross energy of an elastic body is constituted by the elastic strain energy $U$, external virtual work $V$, and kinetic energy $K$. Integrals of its variation over an arbitrary period should satisfy Hamilton’s principle as follows:

$$\int\limits_{{T_{0} }}^{T} {\left( {\delta U + \delta V - \delta K} \right){\text{d}}t} = 0,$$

(8)

in which

$$\delta U = \int\limits_{A} {\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\left( {\sigma_{x} \delta \varepsilon_{x} + \sigma_{y} \delta \varepsilon_{y} + \tau_{xy} \delta \gamma_{xy} + \tau_{xz} \delta \gamma_{xz} + \tau_{yz} \delta \gamma_{yz} } \right){\text{d}}z{\text{d}}A} } } ,$$

(9)

$$\delta V = - \int\limits_{A} {q\delta w} \,{\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {N_{x}^{0} \delta w_{,xx} + 2N_{xy}^{0} \delta w_{,xy} + N_{y}^{0} \delta w_{,yy} } \right)} \,{\text{d}}A,$$

(10)

$$\delta K = \int\limits_{A} {\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\rho \left( {\dot{u}\delta \dot{u} + \dot{v}\delta \dot{v} + \dot{w}\delta \dot{w}} \right){\text{d}}z{\text{d}}A} } } .$$

(11)

in which $q$ is the transverse distributed force; $N_{x}^{0}$, $N_{y}^{0}$, and $N_{xy}^{0}$ are in-plane distributed forces. Substituting Eqs. (3), (5), and (7) into Eq. (8) and applying the integration by part leads to the equations of motion for the laminated composite plates as follows:

$$N_{x,x} + N_{xy,y} = \rho_{0} \ddot{u}_{{\text{e}}} ,$$

(12)

$$N_{y,y} + N_{xy,x} = \rho_{0} \ddot{v}_{{\text{e}}} ,$$

(13)

$$N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + Q_{xz,x}^{e} + Q_{yz,y}^{e} + q = \rho_{0} \ddot{w},$$

(14)

$$\begin{aligned} & N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} \\ & \quad + M_{x,xx}^{b} + 2M_{xy,xy}^{b} + M_{y,yy}^{b} + q = \rho_{0} \ddot{w} - \rho_{1} \left( {\ddot{w}_{{{\text{b}},xx}} + \ddot{w}_{{{\text{b}},yy}} } \right), \\ \end{aligned}$$

(15)

$$\begin{aligned} & N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + M_{x,xx}^{s} \\ & \quad + 2M_{xy,xy}^{s} + M_{y,yy}^{s} + Q_{xz,x}^{s} + Q_{yz,y}^{s} + q = \rho_{0} \ddot{w} - \rho_{2} \left( {\ddot{w}_{{{\text{s}},xx}} + \ddot{w}_{{{\text{s}},yy}} } \right), \\ \end{aligned}$$

(16)

in which

$$\left\{ {\rho_{0} ,\,\,\rho_{1} ,\,\,\rho_{2} } \right\} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\rho^{\left( i \right)} \left\{ {1,\,\,z^{2} ,\,\,f_{z} } \right\}{\text{d}}z} } .$$

(17)

For antisymmetric cross-ply laminated plates, the force and moment resultants in Eqs. (12–16) were evaluated as follows:

$$\begin{aligned} N_{x} & = a_{11} \varepsilon_{x}^{e} + a_{12} \varepsilon_{y}^{e} + a_{13} \kappa_{x}^{b} + a_{14} \kappa_{x}^{s} , \\ N_{y} & = a_{21} \varepsilon_{x}^{e} + a_{22} \varepsilon_{y}^{e} + a_{23} \kappa_{y}^{b} + a_{24} \kappa_{y}^{s} , \\ N_{xy} & = a_{31} \gamma_{xy}^{e} , \\ M_{x}^{b} & = b_{11} \varepsilon_{x}^{e} + b_{12} \kappa_{x}^{b} + b_{13} \kappa_{y}^{b} + b_{14} \kappa_{x}^{s} + b_{15} \kappa_{y}^{s} , \\ M_{y}^{b} & = b_{21} \varepsilon_{y}^{e} + b_{22} \kappa_{x}^{b} + b_{23} \kappa_{y}^{b} + b_{24} \kappa_{x}^{s} + b_{25} \kappa_{y}^{s} , \\ M_{xy}^{b} & = b_{31} \kappa_{xy}^{b} + b_{32} \kappa_{xy}^{s} , \\ M_{x}^{s} & = c_{11} \varepsilon_{x}^{e} + c_{12} \kappa_{x}^{b} + c_{13} \kappa_{y}^{b} + c_{14} \kappa_{x}^{s} + c_{15} \kappa_{y}^{s} , \\ M_{y}^{s} & = c_{21} \varepsilon_{y}^{e} + c_{22} \kappa_{x}^{b} + c_{23} \kappa_{y}^{b} + c_{24} \kappa_{x}^{s} + c_{25} \kappa_{y}^{s} , \\ M_{xy}^{s} & = c_{31} \kappa_{xy}^{b} + c_{32} \kappa_{xy}^{s} , \\ Q_{xz}^{e} & = d_{11} \gamma_{xz}^{e} + d_{12} \gamma_{xz}^{s} , \\ Q_{yz}^{e} & = d_{21} \gamma_{yz}^{e} + d_{22} \gamma_{yz}^{s} , \\ Q_{xz}^{s} & = d_{12} \gamma_{xz}^{e} + d_{13} \gamma_{xz}^{s} , \\ Q_{yz}^{s} & = d_{22} \gamma_{yz}^{e} + d_{23} \gamma_{yz}^{s} . \\ \end{aligned}$$

(18)

For antisymmetric angle-ply laminated plates, the force and moment resultants in Eqs. (12–16) were evaluated as follows:

$$\begin{aligned} N_{x} & = a_{11} \varepsilon_{x}^{e} + a_{12} \varepsilon_{y}^{e} + a_{15} \kappa_{xy}^{b} + a_{16} \kappa_{xy}^{s} , \\ N_{y} & = a_{21} \varepsilon_{x}^{e} + a_{22} \varepsilon_{y}^{e} + a_{25} \kappa_{xy}^{b} + a_{26} \kappa_{xy}^{s} , \\ N_{xy} & = a_{31} \gamma_{xy}^{e} + a_{15} \kappa_{x}^{b} + a_{25} \kappa_{y}^{b} + a_{16} \kappa_{x}^{s} + a_{26} \kappa_{y}^{s} , \\ M_{x}^{b} & = b_{16} \gamma_{xy}^{e} + b_{12} \kappa_{x}^{b} + b_{13} \kappa_{y}^{b} + b_{14} \kappa_{x}^{s} + b_{15} \kappa_{y}^{s} , \\ M_{y}^{b} & = b_{26} \gamma_{xy}^{e} + b_{22} \kappa_{x}^{b} + b_{23} \kappa_{y}^{b} + b_{24} \kappa_{x}^{s} + b_{25} \kappa_{y}^{s} , \\ M_{xy}^{b} & = b_{16} \varepsilon_{x}^{e} + b_{26} \varepsilon_{y}^{e} + b_{31} \kappa_{xy}^{b} + b_{32} \kappa_{xy}^{s} , \\ M_{x}^{s} & = c_{16} \gamma_{xy}^{e} + c_{12} \kappa_{x}^{b} + c_{13} \kappa_{y}^{b} + c_{14} \kappa_{x}^{s} + c_{15} \kappa_{y}^{s} , \\ M_{y}^{s} & = c_{26} \gamma_{xy}^{e} + c_{22} \kappa_{x}^{b} + c_{23} \kappa_{y}^{b} + c_{24} \kappa_{x}^{s} + c_{25} \kappa_{y}^{s} , \\ M_{xy}^{s} & = c_{16} \varepsilon_{x}^{e} + c_{26} \varepsilon_{y}^{e} + c_{31} \kappa_{xy}^{b} + c_{32} \kappa_{xy}^{s} , \\ Q_{xz}^{e} & = d_{11} \gamma_{xz}^{e} + d_{12} \gamma_{xz}^{s} , \\ Q_{yz}^{e} & = d_{21} \gamma_{yz}^{e} + d_{22} \gamma_{yz}^{s} , \\ Q_{xz}^{s} & = d_{12} \gamma_{xz}^{e} + d_{13} \gamma_{xz}^{s} , \\ Q_{yz}^{s} & = d_{22} \gamma_{yz}^{e} + d_{23} \gamma_{yz}^{s} . \\ \end{aligned}$$

(19)

Coefficients $a_{ij} ,\,\,b_{ij} ,\,\,c_{ij} ,\,\,d_{ij}$ are presented in the Appendix.

Substituting the strain components in Eqs. (5)–(6) into the force and moment resultants in Eqs. (18)–(19), then substituting the obtained results into Eqs. (12)–(16), we obtained five differential equations for five primary variables $\left( {u,v,w_{{\text{e}}} ,w_{{\text{b}}} ,w_{{\text{s}}} } \right)$. Specifically, for antisymmetric cross-ply laminated plates, we have

$$a_{11} u_{{{\text{e}},xx}} + a_{31} u_{{{\text{e}},yy}} + \left( {a_{12} + a_{31} } \right)v_{{{\text{e}},xy}} - a_{13} w_{{{\text{b}},xxx}} - a_{14} w_{{{\text{s}},xxx}} = \rho_{0} \ddot{u}_{e} ,$$

(20)

$$a_{22} v_{{{\text{e}},yy}} + a_{31} v_{{{\text{e}},xx}} + \left( {a_{12} + a_{31} } \right)u_{{{\text{e}},xy}} - a_{23} w_{{{\text{b}},yyy}} - a_{24} w_{{{\text{s}},yyy}} = \rho_{0} \ddot{v}_{{\text{e}}} ,$$

(21)

$$d_{11} w_{{{\text{e}},xx}} + d_{21} w_{{{\text{e}},yy}} + d_{12} w_{{{\text{s}},xx}} + d_{22} w_{{{\text{s}},yy}} + N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w},$$

(22)

$$\begin{aligned} & b_{11} u_{{{\text{e}},xxx}} + b_{21} v_{{{\text{e}},yyy}} - b_{12} w_{{{\text{b}},xxxx}} \\ & \quad - 2\left( {b_{13} + 2b_{31} } \right)w_{{{\text{b}},xxyy}} - b_{23} w_{{{\text{b}},yyyy}} - b_{14} w_{{{\text{s}},xxxx}} - 2\left( {b_{15} + 2b_{32} } \right)w_{{{\text{s}},xxyy}} \\ & \quad - b_{25} w_{{{\text{s}},yyyy}} + \,N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w} - \rho_{1} \left( {\ddot{w}_{{{\text{b}},xx}} + \ddot{w}_{{{\text{b}},yy}} } \right), \\ \end{aligned}$$

(23)

$$\begin{aligned} & c_{11} u_{{{\text{e}},xxx}} + c_{21} v_{{{\text{e}},yyy}} - c_{12} w_{{{\text{b}},xxxx}} - 2\left( {c_{13} + 2c_{31} } \right)w_{{{\text{b}},xxyy}} - c_{23} w_{{{\text{b}},yyyy}} \\ & \quad - c_{14} w_{{{\text{s}},xxxx}} - 2\left( {c_{15} + 2c_{32} } \right)w_{{{\text{s}},xxyy}} - c_{25} w_{{{\text{s}},yyyy}} + d_{12} w_{{{\text{e}},xx}} + d_{22} w_{{{\text{e}},yy}} + d_{13} w_{{{\text{s}},xx}} + d_{23} w_{{{\text{s}},yy}} \\ & \quad + N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w} - \rho_{2} \left( {\ddot{w}_{{{\text{s}},xx}} + \ddot{w}_{{{\text{s}},yy}} } \right). \\ \end{aligned}$$

(24)

For antisymmetric angle-ply laminated plates, we have:

$$a_{11} u_{{{\text{e,}}xx}} + a_{31} u_{{{\text{e}},yy}} + \left( {a_{12} + a_{31} } \right)v_{{{\text{e}},xy}} - 3a_{15} w_{{{\text{b}},xxy}} - a_{25} w_{{{\text{b}},yyy}} - 3a_{16} w_{{{\text{s}},xxy}} - a_{26} w_{{{\text{s}},yyy}} = \rho_{0} \ddot{u}_{{\text{e}}} ,$$

(25)

$$a_{22} v_{{{\text{e}},yy}} + a_{31} v_{{{\text{e,}}xx}} + \left( {a_{12} + a_{31} } \right)u_{e,xy} - a_{15} w_{{{\text{b}},xxx}} - 3a_{25} w_{{{\text{b}},xyy}} - a_{16} w_{{{\text{s}},xxx}} - 3a_{26} w_{{{\text{s}},xyy}} = \rho_{0} \ddot{v}_{{\text{e}}} ,$$

(26)

$$d_{11} w_{{{\text{e}},xx}} + d_{21} w_{{{\text{e}},yy}} + d_{12} w_{{{\text{s}},xx}} + d_{22} w_{{{\text{s,}}yy}} + N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w},$$

(27)

$$\begin{aligned} & 3b_{16} u_{{{\text{e}},xxy}} + b_{26} u_{{{\text{e}},yyy}} + b_{16} v_{{{\text{e}},xxx}} + 3b_{26} v_{{{\text{e}},xyy}} - b_{12} w_{{{\text{b}},xxxx}} \\ & \quad - 2\left( {b_{13} + 2b_{31} } \right)w_{{{\text{b}},xxyy}} - b_{23} w_{{{\text{b}},yyyy}} - b_{14} w_{{{\text{s}},xxxx}} - 2\left( {b_{15} + 2b_{32} } \right)w_{{{\text{s}},xxyy}} - b_{25} w_{{{\text{s}},yyyy}} \\ & \quad + N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w} - \rho_{1} \left( {\ddot{w}_{{{\text{b}},xx}} + \ddot{w}_{{{\text{b}},yy}} } \right), \\ \end{aligned}$$

(28)

$$\begin{aligned} & 3c_{16} u_{{{\text{e}},xxy}} + c_{26} u_{{{\text{e}},yyy}} + c_{16} v_{{{\text{e}},xxx}} + 3c_{26} v_{{{\text{e}},xyy}} - c_{12} w_{{{\text{b}},xxxx}} - 2\left( {c_{13} + 2c_{31} } \right)w_{{{\text{b}},xxyy}} - c_{23} w_{{{\text{b}},yyyy}} \\ & \quad - c_{14} w_{{{\text{s}},xxxx}} - 2\left( {c_{15} + 2c_{32} } \right)w_{{{\text{s}},xxyy}} - c_{25} w_{{{\text{s}},yyyy}} + d_{12} w_{{{\text{e}},xx}} + d_{22} w_{{{\text{e}},yy}} + d_{13} w_{{{\text{s}},xx}} + d_{23} w_{{{\text{s}},yy}} \\ & \quad + N_{x}^{0} w_{,xx} + 2N_{xy}^{0} w_{,xy} + N_{y}^{0} w_{,yy} + q = \rho_{0} \ddot{w} - \rho_{2} \left( {\ddot{w}_{{{\text{s}},xx}} + \ddot{w}_{{{\text{s}},yy}} } \right). \\ \end{aligned}$$

(29)

3.3 Navier solution

Navier solutions were achieved for cross-ply and angle-ply laminated composite plates with simply supported boundary conditions as presented in Table 1. Satisfying the boundary conditions, the Navier generalized displacements were correspondingly assumed.

Table 1 Simply supported boundary conditions for cross-ply and angle-ply laminated composite plates (listed parameters have zero values)

For the cross-ply laminated composite plates:

$$\begin{gathered} u_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {U_{emn} \cos \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ v_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {V_{emn} \sin \varphi_{m} x} \cos \varphi_{n} y} , \hfill \\ w_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{emn} \sin \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ w_{{\text{b}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{bmn} \sin \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ w_{{\text{s}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{smn} \sin \varphi_{m} x} \sin \varphi_{n} y.} \hfill \\ \end{gathered}$$

(30)

For the angle-ply laminated composite plates:

$$\begin{gathered} u_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {U_{emn} \sin \varphi_{m} x} \cos \varphi_{n} y} , \hfill \\ v_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {V_{emn} \cos \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ w_{{\text{e}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{emn} \sin \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ w_{{\text{b}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{bmn} \sin \varphi_{m} x} \sin \varphi_{n} y} , \hfill \\ w_{{\text{s}}} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{smn} \sin \varphi_{m} x} \sin \varphi_{n} y} . \hfill \\ \end{gathered}$$

(31)

The external pressure applied to the laminated composite plates is presented as

$$q = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {Q_{mn} \sin \varphi_{m} x} \sin \varphi_{n} y} ,$$

(32)

in which $\varphi_{m} = {{m\pi } \mathord{\left/ {\vphantom {{m\pi } a}} \right. \kern-\nulldelimiterspace} a}$ and $\varphi_{n} = {{n\pi } \mathord{\left/ {\vphantom {{n\pi } b}} \right. \kern-\nulldelimiterspace} b}$. Substituting Eq. (30) and Eq. (32) into Eqs. (20)–(24), and substituting Eq. (31) and Eq. (32) into Eqs. (25)–(29), we have

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {g_{11} } & {g_{12} } & {g_{13} } & {g_{14} } & 0 \\ {g_{12} } & {g_{22} } & {g_{23} } & {g_{24} } & 0 \\ {g_{13} } & {g_{23} } & {g_{33} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {g_{34} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {\varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } \\ {g_{14} } & {g_{24} } & {g_{34} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {g_{44} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {g_{45} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } \\ 0 & 0 & {\varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {g_{45} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } & {g_{55} + \varphi_{m}^{2} N_{x}^{0} + \varphi_{n}^{2} N_{y}^{0} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{emn} } \\ {V_{emn} } \\ {W_{bmn} } \\ {W_{smn} } \\ {W_{emn} } \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {\rho_{0} } & 0 & 0 & 0 & 0 \\ 0 & {\rho_{0} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{0} + \rho_{1} \left( {\varphi_{m}^{2} + \varphi_{n}^{2} } \right)} & {\rho_{0} } & {\rho_{0} } \\ 0 & 0 & {\rho_{0} } & {\rho_{0} + \rho_{2} \left( {\varphi_{m}^{2} + \varphi_{n}^{2} } \right)} & {\rho_{0} } \\ 0 & 0 & {\rho_{0} } & {\rho_{0} } & {\rho_{0} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{U}_{emn} } \\ {\ddot{V}_{emn} } \\ {\ddot{W}_{bmn} } \\ {\ddot{W}_{smn} } \\ {\ddot{W}_{emn} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {Q_{mn} } \\ {Q_{mn} } \\ {Q_{mn} } \\ \end{array} } \right\}, \\ \end{aligned}$$

(33)

in which

$$\begin{aligned} g_{11} & = a_{11} \varphi_{m}^{2} + a_{31} \varphi_{n}^{2} ,\,\,\,\,\,g_{12} = \left( {a_{12} + a_{31} } \right)\varphi_{m} \varphi_{n} ,\,\,\,\,\,g_{13} = - a_{13} \varphi_{m}^{3} ,\, \\ g_{14} & = - a_{14} \varphi_{m}^{3} ,\,\,\,\,\,g_{22} = a_{31} \varphi_{m}^{2} + a_{22} \varphi_{n}^{2} ,\,\,\,\,\,g_{23} = a_{23} \varphi_{n}^{3} ,\,\,\,\,\,g_{24} = a_{24} \varphi_{n}^{3} , \\ g_{33} & = b_{12} \varphi_{m}^{4} + 2\left( {b_{13} + 2b_{31} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + b_{23} \varphi_{n}^{4} , \\ g_{34} & = b_{14} \varphi_{m}^{4} + 2\left( {b_{15} + 2b_{32} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + b_{25} \varphi_{n}^{4} , \\ g_{44} & = c_{14} \varphi_{m}^{4} + 2\left( {c_{15} + 2c_{32} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + c_{25} \varphi_{n}^{4} + d_{13} \varphi_{m}^{2} + d_{23} \varphi_{n}^{2} , \\ g_{45} & = d_{12} \varphi_{m}^{2} + d_{22} \varphi_{n}^{2} ,\,\,\,\,\,g_{55} = d_{11} \varphi_{m}^{2} + d_{21} \varphi_{n}^{2} , \\ \end{aligned}$$

(34)

for cross-ply laminated composite plates, and

$$\begin{aligned} g_{11} & = a_{11} \varphi_{m}^{2} + a_{31} \varphi_{n}^{2} ,\,\,\,\,\,g_{12} = \left( {a_{12} + a_{31} } \right)\varphi_{m} \varphi_{n} ,\,\,\,\,\,g_{13} = - 3a_{15} \varphi_{m}^{2} \varphi_{n} - a_{25} \varphi_{n}^{3} ,\, \\ g_{14} & = - 3a_{16} \varphi_{m}^{2} \varphi_{n} - a_{26} \varphi_{n}^{3} ,\,\,\,\,\,g_{22} = a_{31} \varphi_{m}^{2} + a_{22} \varphi_{n}^{2} ,\,\,\,\,\,g_{23} = - a_{15} \varphi_{m}^{3} - 3a_{25} \varphi_{m} \varphi_{n}^{2} ,\, \\ g_{24} & = - a_{16} \varphi_{m}^{3} - 3a_{26} \varphi_{m} \varphi_{n}^{2} , \\ g_{33} & = b_{12} \varphi_{m}^{4} + 2\left( {b_{13} + 2b_{31} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + b_{23} \varphi_{n}^{4} , \\ g_{34} & = b_{14} \varphi_{m}^{4} + 2\left( {b_{15} + 2b_{32} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + b_{25} \varphi_{n}^{4} , \\ g_{44} & = c_{14} \varphi_{m}^{4} + 2\left( {c_{15} + 2c_{32} } \right)\varphi_{m}^{2} \varphi_{n}^{2} + c_{25} \varphi_{n}^{4} + d_{13} \varphi_{m}^{2} + d_{23} \varphi_{n}^{2} , \\ g_{45} & = d_{12} \varphi_{m}^{2} + d_{22} \varphi_{n}^{2} ,\,\,\,\,\,g_{55} = d_{11} \varphi_{m}^{2} + d_{21} \varphi_{n}^{2} , \\ \end{aligned}$$

(35)

for angle-ply laminated composite plates. Navier solutions for both cross-ply and angle-ply laminated composite plates were obtained from Eq. (33). Deterministic bending and buckling results and their verifications are thoroughly presented in upcoming subsections.

3.4 Deterministic bending

In bending problems, cross-ply and angle-ply laminated composite plates were considered subjected to sinusoidal transverse loads with $Q_{mn} = q_{0}$. The in-plane distributed loads were set to zero (i.e., $N_{x}^{0} = N_{y}^{0} = N_{xy}^{0} = 0$) and the time derivative terms in Eq. (33) were omitted, so the equation was solved easily. Obtained transverse deflections are presented in dimensionless form as the following:

$$\overline{w} = \frac{{100E_{2} h^{3} }}{{q_{0} a^{4} }}w\left( {\frac{a}{2},\frac{b}{2}} \right).$$

(36)

Results obtained from the TRSDT were compared with results obtained by implementing the first-order shear deformation theory (FSDT) and the third-order shear deformation theory (TSDT) presented in [52].

Table 2 compares the dimensionless deflections of square and rectangular simply supported multi-layer antisymmetric cross-ply laminated composite plates [0/90/…] denoted as [0/90]_M subjected to sinusoidal transverse loads $q_{0} = 1$. M = 1, 2, 3, and 4 were considered, corresponding to the plate with 2, 4, 6, and 8 laminae. $a = b$ for the square plate, $b = 2a$ for the rectangular plate, and ratio ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = \left\{ {5,\,10,\,20,\,50,\,100} \right\}$ indicating a wide range of the plate thickness. Each lamina was assumed to have engineering constants as $E_{1} = 25$, $E_{2} = 1$, $G_{12} = G_{13} = 0.5$, $G_{23} = 0.2$, and $\nu_{12} = 0.25$. It is clear that the TRSDT results are in good agreement with the FSDT and TSDT results for both square and rectangular plates. The thinner the laminated composite plate, the closer the results obtained using the three theories. For both square and rectangular plates, the dimensionless deflections decreased when the number of lamina layers increased while the gross thickness was constant, which provided useful insight for the design and application of laminated composites. The comparison verified the reliability of the TRSDT in modeling the bending of cross-ply laminated composite plates with variable layups and thickness.

Table 2 Comparison of dimensionless transverse deflections of square and rectangular simply supported antisymmetric cross-ply laminated composite plates [0/90]_M with variable layups subjected to sinusoidal transverse loads

Table 3 compares the dimensionless deflections of square and rectangular simply supported four-layer antisymmetric angle-ply laminated composite plates [α/−α/α/−α] subjected to sinusoidal transverse loads $q_{0} = 1$. α = 30, 45, and 60 were considered. Each lamina was assumed to have engineering constants as $E_{1} = 40$, $E_{2} = 1$, $G_{12} = G_{13} = 0.5$, $G_{23} = 0.6$, and $\nu_{12} = 0.25$. We observed that the TRSDT results agreed well with the FSDT and TSDT results for both square and rectangular plates with variable fiber orientations, except the rectangular plate with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 5$ and $\alpha = 60$. Minor differences among the results of the three theories vanished when ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}$ decreased. The smallest dimensionless deflections of square plates existed at $\alpha = 45$, while the smallest dimensionless deflections of rectangular plates existed at $\alpha = 30$. Thus, the optimal fiber directions in square and rectangular laminated plates were different. The dimensionless deflection of each rectangular plate approximately doubled that of the square plate with similar geometry parameters. The comparison verified the reliability of the TRSDT in modeling the bending of angle-ply laminated composite plates with variable fiber orientations and thickness.

Table 3 Comparison of dimensionless transverse deflections of square and rectangular simply supported antisymmetric angle-ply laminated composite plates [α/−α/α/−α] with variable fiber orientations subjected to sinusoidal transverse loads

3.5 Deterministic buckling

In buckling problems, we considered cross-ply and angle-ply laminated composite plates subjected to the uniaxial distributed force $N_{x}^{0} = - N_{0}$ at edges $x = \left\{ {0,\,a} \right\}$ and other in-plane distributed forces were $N_{y}^{0} = N_{xy}^{0} = 0$. The sinusoidal transverse loads were set to zero (i.e., $Q_{mn} = 0$) and the time derivative terms in Eq. (33) were omitted, so the equation was solved easily. The obtained uniaxial buckling loads are presented in dimensionless form as the following:

$$\overline{N}_{0} = \frac{{a^{2} }}{{E_{2} h^{3} }}N_{0} .$$

(37)

Table 4 compares the dimensionless uniaxial buckling loads of square and rectangular simply supported multi-layer antisymmetric cross-ply laminated composite plates [0/90/…] denoted as [0/90]_M subjected to sinusoidal transverse loads. M = 1, 2, 3, and 4 were considered, corresponding to the plate with 2, 4, 6, and 8 laminae. Each lamina had engineering constants as $E_{1} = 25$, $E_{2} = 1$, $G_{12} = G_{13} = 0.5$, $G_{23} = 0.2$, and $\nu_{12} = 0.25$. It can be seen that the dimensionless uniaxial buckling loads obtained using the TRSDT were in good agreement with the FSDT and TSDT results for both square and rectangular plates. These results converged when the ratio ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}$ increased. For both square and rectangular plates, the dimensionless uniaxial buckling loads increased with the number of lamina layers. This suggests good practice for designing laminated composites with high load-bearing capacity. The square plate had higher uniaxial buckling loads than the corresponding rectangular plate did at each ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}$ value. The comparison verified the reliability of the TRSDT in modeling the buckling of cross-ply laminated composite plates with variable layups and thickness.

Table 4 Comparison of dimensionless uniaxial buckling loads of square and rectangular simply supported antisymmetric cross-ply laminated composite plates [0/90]_M with variable layups subjected to uniaxial distributed forces

Table 5 compares the dimensionless uniaxial buckling loads of square and rectangular simply supported six-layer antisymmetric angle-ply laminated composite plates [α/−α/α/−α/α/−α], denoted as [α/−α]₃ for brevity. α = 30, 45, and 60 were considered. Each lamina had engineering constants as $E_{1} = 40$, $E_{2} = 1$, $G_{12} = G_{13} = 0.5$, $G_{23} = 0.6$, and $\nu_{12} = 0.25$. We observed that the TRSDT results agreed well with the FSDT and the TSDT results for both square and rectangular plates with variable fiber orientations, except for the square plate with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = \left\{ {5,\,10,\,20} \right\}$ and $\alpha = 60$, and the rectangular plate with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = \left\{ {5,\,10} \right\}$ and $\alpha = 60$. The difference among results obtained from the three theories decreased with the increment of the ratio ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}$. For both square and rectangular plates, the dimensionless uniaxial buckling loads decreased with the increment of fiber orientation $\alpha$. It should be noted that $\alpha$ is an angle formed between the fiber and the $x$-axis (i.e., the loading axis in the uniaxial compression). The increment of $\alpha$ certainly decreased the contribution of fibers on the compression load-bearing capacity of the laminated composite, and the uniaxial buckling loads of square plates were higher than that of the corresponding rectangular plates at each ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}$ ratio.

Table 5 Comparison of dimensionless uniaxial buckling loads of square and rectangular simply supported antisymmetric angle-ply laminated composite plates [α/−α/α/−α/α/−α] with variable fiber orientations subjected to uniaxial distributed forces

The bending deflections and critical buckling loads presented in this section are deterministic results wherein the material, geometry, and loading configurations of the laminated composite plates were pre-specified. These deterministic results may become uncertain when disturbances are introduced into the system configurations. As sources of these disturbances are usually unpredictable, an essential understanding of the possible effects of inevitable source uncertainties is helpful and of utmost importance. The upcoming section presents fundamental methods to quantify the uncertainty of a typical engineering system with randomness in its input parameters.

4 Stochastic sampling methods

In a stochastic environment, parameters that define a system can have uncertain values that produce uncertain responses to the system output. We sampled sample points or observations from the statistical population of each uncertain input parameter. If the population was small, the entire population was used for analysis. However, when the population of each uncertain input parameter became very large, the census sampling of the whole population seemed to be impossible and was impractical. In this case, a subset to represent the characteristics of the population should be sampled and its statistics evaluated. From the statistical results of the subset, the characteristics of the whole population were obtained by performing interpolations and extrapolations.

In this study, the actual dispersions of uncertain input parameters were unknown, so it was reasonable to assume their normal distributions, which are the most popular type for random physical entities [54]. Input parameters $s = \left\{ {s_{j} } \right\} = \left( {E_{1} ,E_{2} ,G_{12} ,G_{13} ,G_{23} ,\nu_{12} ,h,a,b,\alpha } \right)$, $j = 1,...,D_{s}$ with $D_{s} = 10$ were considered as random sources and assumed to be independent of each other. The standard deviation $\sigma_{j}$ of the population of each input parameter was assumed to correlate with its population mean as $\sigma_{j} = \mu_{j} \times r_{j}$, where $r_{j}$ is the coefficient of variation or the degree of stochasticity of the input parameter. Fiber angles were an exception due to their wide range of values (i.e., $\alpha = \left\{ {0,30,45,60,90} \right\}$ is presented in this study) such that the standard deviation $\sigma_{\alpha }$ of each fiber angle was assumed to be equal to $\sigma_{\alpha = 45}$. This helped to eliminate privileges towards any fiber angle and treat all uncertain angles equally.

Two sampling techniques, namely, Monte Carlo sampling and Latin Hypercube sampling, were used to generate observations and evaluate the statistics of the output of interest (i.e., bending deflections $\overline{w}\left( s \right)$ and critical buckling loads $\overline{N}_{0} \left( s \right)$). The optimal technique should have the lowest computational cost and fast converged statistical results. The computational cost came mainly from re-executing the deterministic procedure at certain times until its convergence was reached. The stopping point of iterations depended on the characteristics of sampling techniques.

4.1 Monte Carlo sampling

The Monte Carlo simulation (MCS) is the most widely used sampling technique and its results are often considered as benchmarks for other sampling techniques [55,56,57,58]. The MCS can be executed either randomly or according to a specific density function. In this study, we assumed the pseudorandom samples had normal distributions. If $N_{s}$ is the number of sampling points $s^{i} = \left( {E_{1}^{i} ,E_{2}^{i} ,G_{12}^{i} ,G_{13}^{i} ,G_{23}^{i} ,\nu_{12}^{i} ,h^{i} ,a^{i} ,b^{i} ,\alpha^{i} } \right)$, $i = 1,...,N_{s}$, where the subscript $s$ denotes ‘stochastic’, then the output $\mu \left( {O\left( s \right)} \right)$ (i.e., $\overline{w}\left( s \right)$ and $\overline{N}_{0} \left( s \right)$) was evaluated as the mean of $N_{s}$ estimations $O\left( {s^{i} } \right)$ (i.e., $\overline{w}\left( {s^{i} } \right)$ and $\overline{N}_{0} \left( {s^{i} } \right)$) as follows:

$$\mu \left( {O\left( s \right)} \right) = \frac{1}{{N_{s} }}\sum\limits_{i = 1}^{{N_{s} }} {O\left( {s^{i} } \right)} ,$$

(38)

where $s$ in parenthesis represents a whole set of sampling points $s^{i}$, $i = 1,...,N_{s}$. Each component in a sampling point $s^{i}$ is denoted as $s_{j}^{i}$ with $j = 1,\,...,\,D_{s}$ pointing to random input parameters. The standard deviation of $N_{s}$ estimations $O\left( {s^{i} } \right)$, $i = 1,...,N_{s}$ was evaluated as follows:

$$\sigma \left( {O\left( s \right)} \right) = \sqrt {\frac{{{\text{Var}}\left( {\left\{ {O\left( {s^{i} } \right)} \right\}} \right)}}{{N_{s} }}} ,$$

(39)

in which $\left\{ {O\left( {s^{i} } \right)} \right\}$ is a set of $N_{s}$ estimations $O\left( {s^{i} } \right)$, $i = 1,...,N_{s}$. The convergence of the MCS is characterized as follows:

$${\text{Error}} = \Theta \left( {\frac{{\sigma \left( {O\left( s \right)} \right)}}{{\sqrt {N_{s} } }}} \right),$$

(40)

in which $\Theta$ denotes the order notation. It can be seen that the higher the number of sampling points, the lower the simulation error of the MCS method. The convergence of the MCS is independent of the number of random parameters, that is, the stochastic dimensions $\left( {D_{{\text{s}}} } \right)$ [57]. Thus, the MCS can retain its convergence characteristics even for problems with many random input parameters. In this paper $D_{{\text{s}}} = 10$. However, the MCS has poor space-filling properties such as clustering effects (i.e., too close points exist) and large unsampled regions (i.e., non-informative sampling regions) [51].

4.2 Latin hypercube sampling

Since its first introduction by McKay et al. [59] in 1979, Latin hypercube sampling (LHS) has been considered to be a good alternative for the MCS because it ensures that sampled points represent a full range of each input variable and avoids unnecessarily dense sampling regions. Different from the MCS, sampling domains of input parameters are equally divided into many sub-regions, and within each sub-region, only one random point can be sampled. This guarantees that the entire space of random input parameters can be sampled independently and equiprobably.

The output $O\left( s \right)$ (i.e., $\overline{w}\left( s \right)$ and $\overline{N}_{0} \left( s \right)$) using the LHS was similar to the MCS as in Eq. (38). Using the LHS standard deviation of $N_{s}$ estimations $O\left( {s^{i} } \right)$, $i = 1,...,N_{s}$ was evaluated as follows [59]:

$$\sigma \left( {O\left( s \right)} \right) = \sqrt {\frac{{{\text{Var}}\left( {\left\{ {O\left( {s^{i} } \right)} \right\}} \right)}}{{N_{s} }} + \frac{{N_{s} - 1}}{{N_{s} N_{{\text{s}}}^{{{\text{D}}_{{\text{s}}} }} \left( {N_{s} - 1} \right)^{{D_{s} }} }}\sum\limits_{1,\,p \ne q}^{{N_{s} }} {\left( {O\left( {s^{p} } \right) - \mu \left( {O\left( s \right)} \right)} \right)\left( {O\left( {s^{q} } \right) - \mu \left( {O\left( s \right)} \right)} \right)} .}$$

(41)

For a sufficiently large number of pseudorandom samples, the LHS always has a lower variance than the MCS in view of the central limit theorem [60]. Thus, the LHS is appropriate for sampling in high-dimensional problems.

5 Stochastic bending and buckling of laminated composite plates

To determine the optimal sampling method, we compared the statistical modeling performances of the MCS and LHS. The statistical converged results can be compared with the corresponding deterministic values presented in Sects. 3.4 and 3.5 to evaluate the stochastic effects of random sources. We also conducted sensitivity analyses to determine the profound sources of randomness. We then analyzed the statistical characteristics of the stochastic bending and buckling phenomena, which yielded notable observations.

In this study, we considered eleven cases of randomness as follows:

Case 1: Individual randomness in the elastic modulus $E_{1}$.

Case 2: Individual randomness in the elastic modulus $E_{2}$.

Case 3: Individual randomness in the shear modulus $G_{12}$.

Case 4: Individual randomness in the shear modulus $G_{13}$.

Case 5: Individual randomness in the shear modulus $G_{23}$.

Case 6: Individual randomness in Poisson’s ratio $\nu_{12}$.

Case 7: Individual randomness in the thickness $h$.

Case 8: Individual randomness in the $x$-axis dimension $a$.

Case 9: Individual randomness in the $y$-axis dimension $b$.

Case 10: Individual randomness in the fiber angle $\alpha$.

Case 11: Compound randomness in $\left( {E_{1} ,E_{2} ,G_{12} ,G_{13} ,G_{23} ,\nu_{12} ,h,a,b,\alpha } \right)$.

Inevitably, many different partially compound cases with randomness in two or more parameters can exist in reality. However, it seemed to be impossible to evaluate all partially compound cases, so we analyzed only the individual and fully compound cases of randomness. Considering the superposition principle, the random effect of any partially compound case can be evaluated as the sum of the random effects of each case involved.

5.1 Convergence of sampling methods

In each iteration, $N_{s} = 100$ sampling points are generated and the mean of their outputs are recorded as the output of the iteration. The standard deviation of the sample means after certain iterations can be evaluated and considered as the convergence rate or the sampling error. The optimal sampling method should have the lowest sampling error in the convergence results. In this study, we did 10,000 iterations to examine the sampling errors and computational cost of each sampling method. In the convergence studies, we examined composite plates with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to a stochastic environment of compound randomness with $r_{j} = r_{0} = 0.1$.

5.1.1 Bending convergence

This subsection presents the convergence characteristics of the MCS and LHS on the stochastic bending deflection $\overline{w}\left( s \right)$ of cross-ply laminated composite plates [0/90]_M (see Fig. 2 for square $\left( {a = b} \right)$ and Fig. 3 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α] (see Fig. 4 for square $\left( {a = b} \right)$ and Fig. 5 for rectangular $\left( {b = 2a} \right)$ plates). Different layer-schemes (i.e., M = 1, 2, 3, and 4) and fiber angles (i.e., α = 30, α = 45, and α = 60) were considered for cross-ply and angle-ply laminated composite plates.

Fig. 2

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness with $r_{0} = 0.1$

Fig. 3

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness with $r_{0} = 0.1$

Fig. 4

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of square angle-ply laminated composite plates [α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness with $r_{0} = 0.1$

Fig. 5

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of rectangular angle-ply laminated composite plates [α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness with $r_{0} = 0.1$

We observed that the bending deflections evaluated by the LHS and MCS converged and agreed well with each other, and their converged values were different from the corresponding deterministic values although input parameters were randomized around their deterministic states. In terms of mean values, the LHS converged quickly within 500 iterations, while the MCS required 2000–4000 iterations to converge. The same trend held for the convergence of standard deviations (i.e., sampling errors), which were obtained when the LHS converged to much lower values than standard deviations obtained from the MCS in all convergence plots.

To further analyze the performance of the MCS and LHS in different stochastic environments, the means and standard deviations of stochastic bending deflections $\overline{w}\left( s \right)$ of cross-ply laminated composite plates [0/90]_M (see Fig. 6 for square $\left( {a = b} \right)$ and Fig. 7 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α] (see Fig. 8 for square $\left( {a = b} \right)$ and Fig. 9 for rectangular $\left( {b = 2a} \right)$ plates) were evaluated for a range of degrees of stochasticity $r_{0} = 0 - 0.2$. Different layer-schemes (i.e., M = 1, 2, 3, and 4) in cross-ply laminates and different fiber angles (i.e., α = 30, α = 45, and α = 60) in angle-ply laminates were considered.

Fig. 6

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness

Fig. 7

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness

Fig. 8

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of square angle-ply laminated composite plates [α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness

Fig. 9

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic bending behaviors $\overline{w}\left( s \right)$ of rectangular angle-ply laminated composite plates [α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness

We observed that the trend lines of the means and standard deviations obtained from the LHS and MCS agreed well with each other. Generally, the increment of the degree of stochasticity $r_{0}$ widens the fluctuations of both means and standard deviations of the stochastic bending deflection. In terms of mean values, the MCS curves started to fluctuate considerably at $r_{0} = 0.05$ in most cases, or even at lower $r_{0}$ values in Fig. 6A–C. On the other side, the fluctuations of LHS curves were insignificant as long as $r_{0} \le 0.15$. In terms of standard deviations, although the MCS curves started to deviate at a higher $r_{0}$ value, the performance of the LHS was still more stable than the MCS.

5.1.2 Buckling convergence

Convergence characteristics of the MCS and LHS on the stochastic buckling load $\overline{N}_{0} \left( s \right)$ of cross-ply laminated composite plates [0/90]_M (see Fig. 10 for square $\left( {a = b} \right)$ and Fig. 11 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α/α/−α] (see Fig. 12 for square $\left( {a = b} \right)$ and Fig. 13 for rectangular $\left( {b = 2a} \right)$ plates) are presented in this subsection. Different layer-schemes (i.e., M = 1, 2, 3, and 4) and fiber angles (i.e., α = 30, α = 45, and α = 60) were considered for cross-ply and angle-ply laminated composite plates.

Fig. 10

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness with $r_{0} = 0.1$

Fig. 11

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness with $r_{0} = 0.1$

Fig. 12

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of square angle-ply laminated composite plates [α/−α/α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness with $r_{0} = 0.1$

Fig. 13

Convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of rectangular angle-ply laminated composite plates [α/−α/α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness with $r_{0} = 0.1$

Note that although the buckling loads evaluated by the LHS and MCS converged to approximately the same values, the number of iterations required by the MCS was much larger than that required by the LHS. Indeed, the LHS required less than 500 iterations while the MCS required between 2000 and 4000 iterations to have converged results in both means and standard deviation. The converged values of buckling loads deviated from their deterministic values due to the effects of uncertainties. The sampling error is indicated by the converged value of standard deviations. In these plots, the converged standard deviation obtained by the LHS was much lower than that obtained by the MCS, which indicated that the LHS had lower sampling errors.

To further analyze the performance of the MCS and LHS in different stochastic environments, the means and standard deviations of stochastic buckling loads $\overline{N}_{0} \left( s \right)$ of cross-ply laminated composite plates [0/90]_M (see Fig. 14 for square $\left( {a = b} \right)$ and Fig. 15 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α] (see Fig. 16 for square $\left( {a = b} \right)$ and Fig. 17 for rectangular $\left( {b = 2a} \right)$ plates) were evaluated for a range of degrees of stochasticity $r_{0} = 0 - 0.2$. Different layer-schemes (i.e., M = 1, 2, 3, and 4) in cross-ply laminates and different fiber angles (i.e., α = 30, α = 45, and α = 60) in angle-ply laminates were considered.

Fig. 14

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness

Fig. 15

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness

Fig. 16

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of square angle-ply laminated composite plates [α/−α/α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness

Fig. 17

Effects of stochastic environments on convergence characteristics of Monte Carlo simulation (MCS) and Latin hypercube sampling (LHS) in stochastic buckling behaviors $\overline{N}_{0} \left( s \right)$ of rectangular angle-ply laminated composite plates [α/−α/α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to compound randomness

Although the trend lines of both the means and standard deviations obtained from the LHS and MCS agreed well with each other, the MCS curves fluctuated wider than LHS curves do when the degree of stochasticity $r_{0}$ increases. In terms of mean values, the MCS curves started to fluctuate considerably at $r_{0} = 0.05$ while the LHS curves started to fluctuate when $r_{0} > 0.15$. In terms of standard deviations, both the MCS and LHS curves were stable as long as $r_{0} \le 0.15$. As $r_{0} > 0.15$, the LHS curves performed better than the MCS curves.

For both bending and buckling convergence studies, the LHS outperformed the MCS in either computational costs (i.e., fewer iteration to be converged) or accuracy as it produced stable results even in highly stochastic environments, which created lower sampling errors. Thus, for subsequent analyses, we used the LHS for stochastic bending and stochastic buckling analyses.

5.2 Stochastic bending analysis

The sensitivity of the bending deflection $\overline{w}$ of cross-ply laminated composite plates [0/90]_M (see Fig. 18 for square $\left( {a = b} \right)$ and Fig. 19 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α] (see Fig. 20 for square $\left( {a = b} \right)$ and Fig. 21 for rectangular $\left( {b = 2a} \right)$ plates) towards each case of uncertainty with $r_{0} = \left\{ {0.05,\,\,0.10,\,\,0.15} \right\}$ is defined as ${{\sigma_{{\overline{w}}} } \mathord{\left/ {\vphantom {{\sigma_{{\overline{w}}} } {\mu_{{\overline{w}}} }}} \right. \kern-\nulldelimiterspace} {\mu_{{\overline{w}}} }}$ or ${\sigma \mathord{\left/ {\vphantom {\sigma \mu }} \right. \kern-\nulldelimiterspace} \mu }$ for brevity. We investigated different layer-schemes M = {1, 2, 3, 4} and different fiber angles α = {30, 45, 50}.

Fig. 18

Stochastic sensitivity of bending deflection $\overline{w}$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 19

Stochastic sensitivity of bending deflection $\overline{w}$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 20

Stochastic sensitivity of bending deflection $\overline{w}$ of square angle-ply laminated composite plates [α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 21

Stochastic sensitivity of bending deflection $\overline{w}$ of rectangular angle-ply laminated composite plates [α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

The bending deflections are inevitably most sensitive towards the compound randomness. Among cases of individual randomness, case 7 $\left( h \right)$, case 8 $\left( a \right)$, case 9 $\left( b \right)$, and case 1 $\left( {E_{1} } \right)$ in descending order had profound effects on the output of both cross-ply and angle-ply laminated composite plates. The individual randomness in the $y$-axis dimension $b$ (case 9) strongly affected the stochastic bending deflection of square cross-ply laminated composite plates $\left( {a = b} \right)$ but had little effect on rectangular cross-ply laminated composite plates $\left( {b = 2a} \right)$. The individual randomness in the fiber angle $\alpha$ (case 10) had a considerable effect on the angle-ply plates but a negligible effect on the cross-ply laminated composite plates. The higher the degree of stochasticity $r_{0}$, the higher the sensitivity of the bending deflection. It is clear that, while only Young’s modulus $E_{1}$ among six different material parameters had a profound stochastic effect on the bending of the laminated composite plates, all geometrical parameters mattered. We further analyzed these profound parameters to provide comprehensive probability characteristics of the bending behavior of cross-ply and angle-ply laminated composite plates in stochastic environments.

We investigated the probability characteristics of the stochastic bending deflection $\overline{w}$ of cross-ply laminated composite plates [0/90]_M (see Fig. 22 for square $\left( {a = b} \right)$ and Fig. 23 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α] (see Fig. 24 for square $\left( {a = b} \right)$ and Fig. 25 for rectangular $\left( {b = 2a} \right)$ plates) in profound cases of uncertainty $\left( {r_{0} = 0.10} \right)$ as defined previously. We analyzed the correlative stochastic effects of each profound case of randomness from the distribution of these probability density functions. The most concentrated distributions for square $\left( {a = b} \right)$ and rectangular $\left( {b = 2a} \right)$ cross-ply laminated composite plates came from case 1 $\left( {E_{1} } \right)$ (see Fig. 22) and case 9 $\left( b \right)$ (see Fig. 23), respectively. The most concentrated distributions for both square $\left( {a = b} \right)$ and rectangular $\left( {b = 2a} \right)$ angle-ply laminated composite plates came from case 10 $\left( \alpha \right)$ (see Figs. 24, 25). For both cross-ply and angle-ply laminates, case 11 of compound randomness had the widest distribution followed by case 7 $\left( h \right)$. Thus, plate thickness was the strongest randomness source among individual cases.

Fig. 22

Probability of stochastic bending deflection $\overline{w}$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 23

Probability of stochastic bending deflection $\overline{w}$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 24

Probability of stochastic bending deflection $\overline{w}$ of square angle-ply laminated composite plates [α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 25

Probability of stochastic bending deflection $\overline{w}$ of rectangular angle-ply laminated composite plates [α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to profound cases of randomness ($r_{0} = 0.1$)

The distributions of case 8 $\left( a \right)$ and case 9 $\left( b \right)$ were unique for square cross-ply laminates (see Fig. 22), while the distribution of case 8 $\left( a \right)$ was wider than the distribution of case 9 $\left( b \right)$ for rectangular cross-ply laminates (see Fig. 23). Thus, the smaller dimension had a stronger stochastic effect on the bending of the cross-ply laminated composites. This observation was held for rectangular angle-ply laminated composite plates (see Fig. 25) regardless of the effect of fiber angles $\alpha$. The effect of $\alpha$ can be observed in Fig. 24 for square angle-ply laminated composite plates. The distributions of case 8 $\left( a \right)$ and case $\left( b \right)$ were unique and similar to Fig. 22 as $\alpha = 45$ (see Fig. 24B), but different from each other as $\alpha = 30$ (see Fig. 24A) and $\alpha = 60$ (see Fig. 24C).

The effect of fiber angles $\alpha$ on the probability of stochastic bending deflection $\overline{w}$ for square and rectangular laminated composites exposed to compound randomness with $r_{0} = 0.10$ were further investigated in Figs. 26 and 27, respectively. Different fiber angles [0/90]_M, [15/− 15]_M, [30/− 30]_M, [45/− 45]_M, [60/− 60]_M and [75/− 75]_M and different layer-schemes M = {1, 2, 3, 4} were considered. For square laminated composite plates (see Fig. 26), [45/− 45]_M plates had the lowest mean value and the most concentrated distribution. In the contrast, [0/90]_M plates had the highest mean value and the most scattering distribution. Pairs of plates with symmetric fiber angles about $\alpha = 45$ such as [15/− 15]_M and [75/− 75]_M or [30/− 30]_M and [60/− 60]_M had unique distributions. Thus, the [45/− 45]_M plates had the best bending performance among considered square laminated composite plates. For rectangular laminated composite plates (see Fig. 27), the increment of fiber angles $\alpha$ created a widening of probability distribution curves, except for [0/90]_M plates. Thus, [75/− 75]_M plates had the highest mean value and largest probability distributions. The best bending performance among considered rectangular laminated composite plates was the [15/− 15]_M plate, which had the lowest mean values and smallest probability distributions.

Fig. 26

Effects of fiber angles on the probability of bending deflection $\overline{w}$ of square laminated composite plates [0/90]_M and [α/−α]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness ($r_{0} = 0.1$)

Fig. 27

Effects of fiber angles on the probability of bending deflection $\overline{w}$ of rectangular laminated composite plates [0/90]_M and [α/−α]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

5.3 Stochastic buckling analysis

Now we present the sensitivity of the critical buckling load $\overline{N}_{0}$ of cross-ply laminated composite plates [0/90]_M (see Fig. 28 for square $\left( {a = b} \right)$ and Fig. 29 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates [α/−α/α/−α/α/−α] (see Fig. 30 for square $\left( {a = b} \right)$ and Fig. 31 for rectangular $\left( {b = 2a} \right)$ plates) for each case of randomness with $r_{0} = \left\{ {0.05,\,\,0.10,\,\,0.15} \right\}$. Different layer-schemes M = {1, 2, 3, 4} and different fiber angles α = {30, 45, 60} were investigated.

Fig. 28

Stochastic sensitivity of critical buckling load $\overline{N}_{0}$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 29

Stochastic sensitivity of critical buckling load $\overline{N}_{0}$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 30

Stochastic sensitivity of critical buckling load $\overline{N}_{0}$ of square angle-ply laminated composite plates [α/−α/α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

Fig. 31

Stochastic sensitivity of critical buckling load $\overline{N}_{0}$ of rectangular angle-ply laminated composite plates [α/−α/α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$ exposed to different cases of randomness with A $r_{0} = 0.05$, B $r_{0} = 0.10$, and C $r_{0} = 0.15$

The strongest stochastic effects came from the compound randomness (case 11) followed by the individual randomness in the thickness $h$ (case 7). In other words, the individual randomness in the thickness was the strongest among individual cases for both cross-ply and angle-ply laminated composite plates. The randomness in $b$ (case 9) was stronger than the randomness in $a$ (case 8) for square cross-ply and angle-ply laminates, while the reverse occurred for rectangular cross-ply laminates. In rectangular angle-ply laminates, the correlative effects of $a$ (case 8) and $b$ (case 9) depended on fiber angles $\alpha$. The individual randomness in fiber angles $\alpha$ (case 10) had a considerable effect on angle-ply laminated composite plates but not on cross-ply laminated composite plates. Both cross-ply and angle-ply laminates were considerably sensitive to the randomness of Young’s modulus $E_{1}$ (case 1) and not sensitive to the randomness in Young’s modulus $E_{2}$ (case 2), shear moduli $G_{12}$ (case 3), $G_{13}$ (case 4), $G_{23}$ (case 5), and Poisson’s ratio $\nu_{12}$ (case 6). The comprehensive probability characteristics of stochastic critical buckling loads $\overline{N}_{0}$ of the laminated composite plates in profound cases of randomness were then investigated.

We investigated the probability characteristics of the stochastic critical buckling load $\overline{N}_{0}$ of cross-ply laminated composite plates (see Fig. 32 for square $\left( {a = b} \right)$ and Fig. 33 for rectangular $\left( {b = 2a} \right)$ plates) and angle-ply laminated composite plates (see Fig. 34 for square $\left( {a = b} \right)$ and Fig. 35 for rectangular $\left( {b = 2a} \right)$ plates) in profound cases of uncertainty $\left( {r_{0} = 0.10} \right)$. The most concentrated distributions for the square and rectangular cross-ply laminated composite plates came from case 8 $\left( a \right)$ (see Fig. 32) and case 9 $\left( b \right)$ (see Fig. 33), respectively. The most concentrated distributions for the square and rectangular angle-ply laminated composite plates came from case 8 $\left( a \right)$ (see Fig. 34) and case 10 $\left( \alpha \right)$ (see Fig. 35), respectively. As expected, the widest distribution came from the compound randomness (case 11) followed by the individual randomness in the thickness (case 7).

Fig. 32

Probability of stochastic critical buckling load $\overline{N}_{0}$ of square cross-ply laminated composite plates [0/90]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 33

Probability of stochastic critical buckling load $\overline{N}_{0}$ of rectangular cross-ply laminated composite plates [0/90]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 34

Probability of stochastic critical buckling load $\overline{N}_{0}$ of square angle-ply laminated composite plates [α/−α/α/−α/α/−α] (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to profound cases of randomness ($r_{0} = 0.1$)

Fig. 35

Probability of stochastic critical buckling load $\overline{N}_{0}$ of rectangular angle-ply laminated composite plates [α/−α/α/−α/α/−α] (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A α = 30, B α = 45, and C α = 60 exposed to profound cases of randomness ($r_{0} = 0.1$)

For square cross-ply and angle-ply laminated composite plates (see Figs. 32, and 34), the distributions of case 9 $\left( b \right)$ spread wider than the distributions of case 8 $\left( a \right)$. The reverse occurred for rectangular cross-ply laminated composite plates as shown in Fig. 33. It should be noted that the plates were subjected to uniaxial compressions at $x = 0$ and $x = a$ edges. For rectangular angle-ply laminated composite plates (see Fig. 35), the comparative distributions of case 8 $\left( a \right)$ and case 9 $\left( b \right)$ depend on the fiber angles $\alpha$. The curves of case 9 $\left( b \right)$ were distributed wider than the curves of case 8 $\left( a \right)$ when $\alpha = 45$ and $\alpha = 60$, but did not at $\alpha = 30$. There was no case of unique distribution between case 8 $\left( a \right)$ and case 9 $\left( b \right)$ as in the probability distribution of bending flections due to the un-symmetry of the uniaxial buckling analyses.

The effects of fiber angles $\alpha$ on the probability of stochastic critical buckling loads $\overline{N}_{0}$ for square and rectangular laminated composites were further investigated in Figs. 36 and 37. We considered different fiber angles [0/90]_M, [15/− 15]_M, [30/− 30]_M, [45/− 45]_M, [60/− 60]_M and [75/− 75]_M and different layer-schemes M = {1, 2, 3, 4}. For square laminated composite plates (see Fig. 36), [75/− 75]_M plates had the lowest mean value and most concentrated distribution followed by the distributions of [0/90]_M plates. In the contrast, [45/45]_M plates had the highest mean value (i.e., the best buckling resistance) and the widest probability distribution (i.e., the most sensitive case) among square laminated composite plates. For rectangular laminated composite plates (see Fig. 37), the smaller the fiber angles $\alpha$, the higher the mean values and the wider the probability distribution, except for the [0/90]_M plates whose curves were close to the curves of [45/45]_M plates. Among different rectangular laminated composite plates, [15/− 15]_M plates had the highest mean value and largest probability distributions.

Fig. 36

Effects of fiber angles on the probability of critical buckling load $\overline{N}_{0}$ of square laminated composite plates [0/90]_M and [α/−α]_M (a = b) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to compound randomness ($r_{0} = 0.1$)

Fig. 37

Effects of fiber angles on the probability of critical buckling load $\overline{N}_{0}$ of rectangular laminated composite plates [0/90]_M and [α/−α]_M (b = 2a) with ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 50$, A M = 1, B M = 2, C M = 3, and D M = 4 exposed to profound cases of randomness ($r_{0} = 0.1$)

6 Conclusion

In this study, we thoroughly investigated the deterministic and stochastic bending and buckling behaviors of the antisymmetric cross-ply and angle-ply laminated composite plates. Deterministic partial differential equations were derived using the three variable refined shear deformation theory based on Hamilton’s principle. Numerical Navier’s solutions were validated with the first-order and third-order shear deformation theories. Monte Carlo simulation and Latin hypercube sampling were studied to determine the optimal sampling technique for stochastic analyses. We considered eleven scenarios of individual and compound randomness. Convergence studies, sensitivity analyses, and comprehensive probability characteristics of the bending and the buckling phenomenon of laminated composite plates were conducted. We analyzed the detailed results and made several notable observations as follows:

• Among cross-ply laminated plates with the same thickness, plates with more laminae had better bending and buckling performance.

• Square laminated plates had lower bending deflections and higher critical buckling loads in comparison with rectangular laminated plates.

• The Latin hypercube sampling outperformed the conventional Monte Carlo simulation in both computational efficiency and numerical accuracy, even in strongly stochastic environments.

• Most material properties had few stochastic effects on the bending and buckling behaviors of laminated composite plates.

• All geometry parameters had strong stochastic effects on the bending and buckling behaviors of laminated composite plates.

This study provides an efficient approach for understanding deterministic and stochastic structural behaviors, which is crucially important for good practices in the real analysis, design, and utilization of structures.

Appendix

$$a_{11} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{12} = a_{21} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{12}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{13} = b_{11} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z\,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{14} = c_{11} = - \frac{1}{4}a_{13} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{3} \,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{15} = b_{16} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z\,\overline{C}_{16}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{16} = c_{16} = - \frac{1}{4}a_{15} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{3} \,\overline{C}_{16}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{22} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{23} = b_{21} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z\,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{24} = c_{21} = - \frac{1}{4}a_{23} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{3} \,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{25} = b_{26} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z\,\overline{C}_{26}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{26} = c_{26} = - \frac{1}{4}a_{25} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{3} \,\overline{C}_{26}^{\left( i \right)} \,{\text{d}}z} }$$

$$a_{31} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{66}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{12} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{13} = b_{22} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{12}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{14} = c_{12} = - \frac{1}{4}b_{12} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{15} = b_{24} = c_{13} = c_{22} = - \frac{1}{4}b_{13} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{12}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{23} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{25} = c_{23} = - \frac{1}{4}b_{23} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{31} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{66}^{\left( i \right)} \,{\text{d}}z} }$$

$$b_{32} = \,c_{31} = - \frac{1}{4}b_{31} + \frac{5}{{3h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{66}^{\left( i \right)} \,{\text{d}}z} }$$

$$c_{14} = \frac{1}{16}b_{12} - \frac{5}{{6h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{9h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{6} \,\overline{C}_{11}^{\left( i \right)} \,{\text{d}}z} }$$

$$c_{15} = c_{24} = \frac{1}{16}b_{13} - \frac{5}{{6h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{12}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{9h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{6} \,\overline{C}_{12}^{\left( i \right)} \,{\text{d}}z} }$$

$$c_{25} = \frac{1}{16}b_{23} - \frac{5}{{6h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{9h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{6} \,\overline{C}_{22}^{\left( i \right)} \,{\text{d}}z} }$$

$$c_{32} = \frac{1}{16}b_{31} - \frac{5}{{6h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{66}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{9h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{6} \,\overline{C}_{66}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{11} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{55}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{12} = \frac{5}{4}d_{11} - \frac{5}{{h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{55}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{13} = \frac{25}{{16}}d_{11} - \frac{25}{{2h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{55}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{55}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{21} = \sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\overline{C}_{44}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{22} = \frac{5}{4}d_{21} - \frac{5}{{h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{44}^{\left( i \right)} \,{\text{d}}z} }$$

$$d_{23} = \frac{25}{{16}}d_{21} - \frac{25}{{2h^{2} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{2} \,\overline{C}_{44}^{\left( i \right)} \,{\text{d}}z} } + \frac{25}{{h^{4} }}\sum\limits_{i = 1}^{N} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {z^{4} \,\overline{C}_{44}^{\left( i \right)} \,{\text{d}}z} }$$