Thermo-electro-mechanical vibration analysis of size-dependent nanobeam resting on elastic medium under axial preload in presence of surface effect

Abstract

In the present manuscript, a nonclassical beam theory is developed to analyze free vibration of piezoelectric nanobeam by considering surface effects resting on Winkler–Pasternak elastic medium and thermal loading with axial preload. The nonclassical Eringen theory is utilized to incorporate the length-scale parameter to account for the small-scale effect, while the Gurtin–Murdoch model is employed to inject the surface effects including surface elasticity, surface stress and surface density. The governing equations are derived using Hamilton’s principle in the framework of Euler–Bernoulli beam theory. The governing partial differential equations of motions of system are reduced to a set of algebraic equations with the help of differential transformation method as a semi-analytical–numerical. The mathematical derivations and numerical results are presented in detail for various boundary conditions. Some numerical examples are illustrated in order to investigate the effect of several parameters such as the nonlocal parameter, piezoelectric voltage, surface effects, temperature change, axial preload and elastic medium parameters. Moreover, it is also indicated that the numerical results have good agreement with previous studies.

1 Introduction

With the advance of energy harvesting from ambient energy sources to generate other forms of energy such as electricity, MEM and NEM sensors are employed as energy harvesters in different fields. As an example, in tire pressure monitoring systems (TPMS) which directly affect vehicle’s handling [1], one approach for harvesting is to provide sustainable power for wireless sensors, while it will be possible by piezoelectric materials. The piezoelectric materials when subjected in electrical loads will produce mechanical deformations for their intrinsic electro-mechanical coupling effect [2]. Many studies have been done around the macroscopic piezoelectric materials such as works done in Refs. [3–5].

Because of high sensitivity of MEMs/NEMs, investigating their mechanical properties and behavior is crucial to design and manufacture of these structures. It is observed that the piezoelectric nanostructures have different mechanical, electrical and also physical and chemical properties than their bulk. Among all nanostructures, investigating piezoelectric nanobeams’ vibrational behavior is important according to their wide range of application such as nanosensors, actuators, generators, transistors and diodes [6]. Pan et al. [7] reported the ZnO piezoelectric nanostructures among other piezoelectric nanomaterials such as ZnS, PZT, GaN and BaTiO₃, and studying nanostructures has received attention from researchers such as those in [8, 9].

To date, studying buckling and vibration characteristics of nanobeams has been theoretically investigated in the content of size-dependent beam analysis by several researchers. However, it is known that the classical continuum mechanics cannot predict and explain the size-dependent behavior of nanostructures. Therefore, in order to incorporate the size effects in continuum mechanics, there are several higher-order continuum theories, such as the couple stress theory [34], strain gradient theory [10], nonlocal elasticity theory [11], micropolar theory [12] and surface elasticity [13]. But, among all of these theories, the nonlocal elasticity of Eringen [11] is proved to be capable for different analyses on nanostructures. The simplicity in the application of nonlocal elasticity of Eringen resulted in rapid extension of this theory in different static and dynamic analyses for various nanostructures such as those in [14, 15].

As the experimental and atomistic simulations show, the ratio of surface to volume has undeniable role in nanoscale problems [16]. Gurtin and Murdoch [17] represented the surface elasticity theory and also its applications in nanostructures which have a good agreement with experimental measurements [18]. Recently, surface effects on static and dynamic analyses of elastic materials have been extensively studied by researchers, such as works done in [19–22]. Further, the nonlocal and surface effects are two inevitable fields which studied simultaneously. For instance, Hosseini-Hashemi et al. [6] studied the static and dynamic analyses with considering both surface and nonlocal effects on piezoelectric functionally graded nanobeams. In a similar work, they also studied the nonlinear free vibration of piezoelectric functionally graded nanobeams in the framework of the Euler–Bernoulli beam theory [23].

Also, the study of surface and nonlocal effects on buckling and vibrational characteristics of Al and Si nanotubes is done by Ebrahimi et al. [24]. They also used DTM for the first time to investigate the nondimensional natural frequency and buckling loads. In a similar work [25], the influence of various surface effects on fundamental natural frequencies was mentioned.

In addition, investigating the thermal effect in high-temperature conditions has considerable effect on dynamic behavior of nanobeams. Afterward, the effect of temperature changing is studied in different researches, such as Ebrahimi and Salari [26], whom studied thermo-electrical buckling characteristics of functionally graded piezoelectric (FGP) nanobeams based on Timoshenko theory subjected to in-plane thermal loads and applied electrical voltage, while the motion equations have been solved by Navier-type solution. Furthermore, Ansari et al. [27] studied thermo-electro-mechanical vibration of postbuckled piezoelectric nanobeams based on the nonlocal elasticity theory in the framework of Timoshenko beam theory. In a similar work, thermo-electric-mechanical vibration of the piezoelectric nanobeams is done by Ke and Wang [2] based on the nonlocal theory and Timoshenko beam theory. Moreover, Ebrahimi and Barati [28] studied the dynamic modeling of a magneto-thermo-piezoelectrically actuated nanobeam based on the higher-order shear deformation beam theory. And also, study of the electro-mechanical coupling behavior of piezoelectric nanowires in the presence of both surface and small-scale effects based on Euler–Bernoulli beam theory is analyzed by Wang and Wang [29]. So, it can be concluded that it is necessity to consider the thermal effects in vibration analysis of nanostructures and should not be ignored in dynamic analysis.

It is known that studying the mechanical behavior of nanostructures rested in elastic medium is also achieved attention from researchers and is considered in analysis. It should be noted that the Winkler elastic foundation model consists of closely spaced elastic springs which are integrated to the bottom of beam surface. But this model cannot incorporate the continuousness of the elastic environment. Besides, Pasternak model consists of two parameters elastic foundation which is known as Winkler–Pasternak model. This model comprises a Winkler-type elastic spring besides the transverse shear stress as a result of the shear deformation in the medium, while the Winkler model incorporates the normal pressure from surrounding medium [30, 31]. A few investigations have been carried out in the open literature dealing with the elastic medium in dynamic analysis of nanostructures such as [15, 18, 32–34].

Lots of literature works presented the thermo-electro-mechanical vibration of size-dependent piezoelectric nanobeams, whereas investigating both surface and nonlocal effects in Winkler–Pasternak medium with preload is rather limited. This motivated the current work which is concerned with theoretical modeling on thermo-electro-mechanical analysis of piezoelectric nanobeams which is complemented with size-dependent model based on the extended theory of piezoelectricity and Euler–Bernoulli beam theory. The Gurtin–Murdoch model is used to incorporate the surface effects including surface elasticity, surface stress and surface density. The governing motion equations are obtained by Hamilton’s principle using the nonlocal elasticity of Eringen within the framework of Euler–Bernoulli beam theory. The differential transformation method (DTM) is used as a semi-analytical–numerical technique which is simpler with high precision in comparison with other methods. However, implementing the DTM to solve similar works is also rather limited, which is used to solve the current motion equations for various boundary conditions for the first time. Next, the resultant natural frequencies are validated for different boundary conditions as it is shown that they are in good agreement with well-known literature. Finally, through some numerical examples, the influence of various parameters such as nonlocality, surface effects, temperature change, preload and elastic medium is investigated.

2 Governing equations

2.1 Nonlocal effects

The nonlocal elasticity theory introduces information about the forces between atoms in the bulk of material and the internal length scale, the constitutive equations will be obtained which will can used as the material parameters. This theory expresses that the stress at a reference point is a function of the stain at all points in the adjacent region. This assumption can explain some experimental observations of atomic and molecular scales, for example high-frequency vibration and wave dispersion [15]. For a homogeneous and nonlocal piezoelectric solid, the basic equations for stress tensor and electrical displacement at any point x in the bulk of material by neglecting the body forces can be expressed as [29]:

$$\sigma_{ij} - \mu^{2} \nabla^{2} \sigma_{ij} = C_{ijkl} \varepsilon_{kl} - e_{kij} E_{k} - \lambda_{ij}\Delta T$$

(1)

$$D_{i} - \mu^{2} \nabla^{2} D_{i} = e_{ikl} \varepsilon_{kl} + \varepsilon_{ik} E_{k} + p_{i}\Delta T$$

(2)

where $\sigma_{ij} ,\,D_{i}$ are the component of the stress and electrical field, while the $\varepsilon_{kl} ,\,C_{ijkl} ,\,e_{{_{ikl} }} ,\,\lambda_{ij}$ are the strain, elastic constant, piezoelectric constants and thermal moduli. ΔT and p _i are the temperature change and piezoelectric constants; $\mu = (e_{0} a)^{2}$ is the nonlocal constant; moreover, e ₀ a is the scale length which takes the size effect into account on the response of nanostructures.

2.2 Surface effects

The energy which is associated by atoms in the surface layers affects the mechanical properties of nanostructures which have been extensively studied by researchers. So far, Gurtin and Murdoch [17] introduced the continuum framework which represented the influence of the surface elastic stress and strain field. Their model reflects the surface elastic, by assuming the surface layers as a two-dimensional film with zero thickness which is attached to the material body. Assuming that these surface layers are only because of modeling purpose and these layers do not actually exist, so the type of surface is not defined. For the surface of the piezoelectric materials, the local stresses and electrical displacement can be expressed as [29]:

$$\tau_{\alpha \beta }^{sl} = \tau_{\alpha \beta }^{0} + C_{\alpha \beta \gamma \delta }^{s} \varepsilon_{\gamma \delta } - e_{\alpha \beta k}^{s} E_{k}$$

(3)

$$D_{i}^{sl} = D_{i}^{0} + e_{\alpha \beta i}^{s} \varepsilon_{\alpha \beta } + k_{ij}^{s} E_{j}$$

(4)

where $C_{\alpha \beta \gamma \delta }^{s}$, $\varepsilon_{\gamma \delta }$, $e_{\alpha \beta k}^{s}$ and $k_{ij}^{s}$ are surface elastic constant, surface strains, surface piezoelectric constants and surface dielectric constants, respectively. $\tau_{\alpha \beta }^{sl}$ and $\tau_{\alpha \beta }^{0}$ are the nonlocal stress tensor and residual surface stress tensor, respectively.

Assuming the same material properties in top and bottom layers, the relative stress–strain relations for surface layers will be expressed as:

$$\tau_{xx} = \tau_{0} + E^{s} u_{x,x} ,\quad E^{s} = 2\mu_{0} + \lambda_{0} ,\quad \tau_{nx} = \tau_{0} u_{n,x}$$

(5)

The $\mathop \sigma \nolimits_{zz}$ which is often neglected in classical beam theories will be considered to satisfy the equilibrium equations and has linear relation with the beam thickness which can be obtained as:

$$\sigma_{zz} = \frac{2z\nu }{h}\left( {\tau_{o} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{o} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)$$

(6)

2.3 Problem formulation

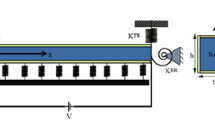
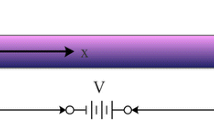
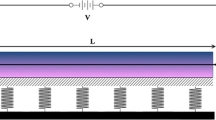
Based on the nonlocal theory and surface effects of piezoelectric material proposed in previous section, the vibration of size-dependent piezoelectric nanobeam under thermo-electro-material in elastic foundation is analyzed. A piezoelectric nanobeam with length L ($0 \le x \le L$), thickness h ($- h/2 \le z \le h/2$) and width b ($- b/2 \le y \le b/2$) is subjected to an applied voltage $\phi (x,z)$ and uniform temperature change ΔT. The Euler–Bernoulli beam theory is utilized to develop the piezoelectric nanobeam. Based on the Euler–Bernoulli beam model, the cross section of nanobeam is assumed to remain plane and normal to the deformed beam axis, and also in this study, the cross section of nanobeam is assumed to be constant along the length of the beam. The coordinate system is often supposed: The x-axis is taken along the length of the beam, the y-axis is taken along the width, while the z-axis is taken along the thickness of beam as shown in Fig. 1.

Fig. 1

Geometry of a nanobeam with length L and thickness h in elastic medium

Following the Euler–Bernoulli beam model, the displacement can be expressed as follows:

$$u_{1} = u - z\frac{\partial w}{\partial x},\quad u_{2} = 0,\quad u_{3} = w(x,t)$$

(7)

where $u(x,t)$ and $w(x,t)$ are axial and lateral displacement components in mid-plane, and t is the time.

The strain relation according to Euler–Bernoulli beam theory is obtained as:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial^{2} x}}$$

(8)

Accordingly, the normal stress ($\sigma_{xx}$) and the surface stress ($\sigma_{\text{s}}$) are functions of surface strain $\varepsilon_{xx}$ which is obtained as follows:

$$\begin{aligned} & \sigma_{xx} = E\varepsilon_{xz} + \upsilon \sigma_{zz} - e_{31} E_{z} \\ & \sigma_{\text{s}} = \tau_{0} + E_{\text{s}} \varepsilon_{xx} \\ \end{aligned}$$

(9)

where e ₃₁ and E _z are the piezoelectric coefficient and z-component of the electrical field, respectively. Also, $\tau_{0}$ and E _s are the surface tension and surface Young’s modulus.

The distribution field of the electrical potential should be assumed for the presented model. The electrical displacement can be defined as [35]:

$$\begin{aligned} & E_{x} = - \frac{\partial \phi }{\partial x};\quad E_{z} = - \frac{\partial \phi }{\partial z}, \\ & D_{x} = \lambda_{11} E_{x} ;\quad D_{z} = e_{31} \varepsilon_{x} + \lambda_{33} E_{z} , \\ & \frac{{\partial D_{x} }}{\partial x} + \frac{{\partial D_{z} }}{\partial z} = 0 \\ \end{aligned}$$

(10)

where λ ₁₁ and λ ₃₃ denote the dielectric constants; D _x and D _z are electrical displacements. Because λ ₁₁ and λ ₃₃ are in the same order and assuming $E_{x} \ll E_{z} ,$ so D _x can be ignored in comparison with D _z . Substituting Eq. (8) into Eq. (10), while the electrical boundary conditions are assumed $\phi (x, - h) = 0,\,\phi (x,h) = 2V$ the electrical potential is obtained as:

$$\phi (x,z) = - \frac{{e_{31} }}{{\lambda_{33} }}\left( {\frac{{z^{2} - h^{2} }}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {1 + \frac{z}{h}} \right)V$$

(11)

So, in this case, the equivalent load to the piezoelectric layers will be obtained as:

$$P_{\text{electric}} (x,t) = b\int\limits_{ - h}^{h} {\sigma_{x}^{*} {\text{d}}z = 2V{\text{be}}_{31} }$$

(12)

with $\sigma_{x}^{*}$ indicating the normal stress due to the piezoelectric property.

The governing motion equations and boundary conditions can be obtained by Hamilton’s principle:

$$\int_{0}^{t} {\delta (U - T + W_{\text{ext}} ){\text{d}}t = 0}$$

(13)

in which, U, T and W _ext indicate the strain energy, kinetic energy and work done by external forces.

The first variation of strain energy is obtained as:

$$U = \int\limits_{0}^{L} {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xz} \delta \gamma_{xz} - D_{x} \delta E_{x} - D_{z} \delta E_{z} } \right){\text{d}}z\,{\text{d}}x} }$$

(14)

Combining Eq. (8) and Eq. (14) leads to:

$$\delta U = \int\limits_{0}^{l} {\int_{ - h/2}^{h/2} {\left[ {N\delta u - M\delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + D_{x} \delta \left( {\frac{\partial \phi }{\partial x}} \right) + D_{z} \delta \left( {\frac{\partial \phi }{\partial z}} \right)} \right]{\text{d}}x} }$$

(15)

where N the axial force and M the bending moment are determined through the following equations:

$$N_{x} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma_{xx} {\text{d}}z,\quad M_{x} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma_{xx} z{\text{d}}z} }$$

(16)

The kinetic energy for piezoelectric nanobeam can be calculated as:

$$\begin{aligned} T & = \frac{1}{2}\rho \iint {\left( {\dot{u}_{1}^{2} + \dot{u}_{2}^{2} + \dot{u}_{3}^{2} } \right){\text{d}}A \cdot {\text{d}}x} \\ & = \frac{1}{2}\rho \int {\left( {I_{1} \left( {\frac{\partial u}{\partial t}} \right)^{2} + I_{2} \left( {\frac{{\partial^{2} w}}{\partial x\partial t}} \right)^{2} + I_{1} \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right)} {\text{d}}x \\ \end{aligned}$$

(17)

where I ₁ and I ₂ are defined:

$$I_{1} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho {\text{d}}z,\quad I_{2} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho z^{2} {\text{d}}z} }$$

(18)

Accordingly, the first variation of Eq. (17) can be obtained as:

$$\delta T = - \int\limits_{0}^{l} {\left( {I_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)\delta (w) - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)\delta (w) + I_{1} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)\delta (u)} \right)} {\text{d}}x$$

(19)

In this study, the axial load which is caused by the elastic medium based on the Winkler–Pasternak foundation is assumed in the following form:

$$f = - k_{\text{w}} w + k_{\text{p}} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$

(20)

And the work done by external forces is given by:

$$\delta W_{\text{ext}} = \int\limits_{0}^{t} {\left( {q_{\text{w}} \delta (w) + q_{\text{u}} \delta (u)} \right)}$$

(21)

where q _w is calculated as:

$$\begin{aligned} q_{\text{w}} & = \left( {H + N_{\text{p}} + N_{\text{T}} + P_{\text{electric}} } \right)\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) \\ & \quad - K_{\text{w}} W + K_{\text{P}} \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) \\ \end{aligned}$$

(22)

In this equation, N _p and N _T are the normal forces which are induced by the biaxial force P ₀ and temperature rise, and H is a constant which is obtained by residual surface stress and the shape of cross section.

$$\begin{aligned} & N_{\text{P}} = P_{0} \\ & N_{\text{T}} = - \lambda_{1} A\Delta T \\ & H = 2b\tau_{0} \\ \end{aligned}$$

(23)

Substituting Eqs. (15), (19) and (21) into Eq. (13) with setting the coefficient of $\delta u$ and $\delta w$ equal to zero, the following equations will be obtained:

$$\frac{\partial N}{\partial x} + q_{\text{u}} - I_{1} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) = 0$$

(24)

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} + q_{\text{w}} + I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) - I_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) = 0$$

(25)

The bending moment for piezoelectric nanobeam with considering surface effects will be calculated by:

$$M = \int {\sigma_{xx} z{\text{d}}A + \int {\tau_{xx} z{\text{d}}A - \int {e_{31} \phi_{z} z{\text{d}}A} } }$$

(26)

$$\begin{aligned} M & = - (EI)^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{2I\nu }{h}\left( {\tau_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ & \quad + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \end{aligned}$$

(27)

where $({\text{EI}})^{*} = E(bh^{3} /12) + E_{\text{s}} (h^{3} /6 + bh^{2} /2)$ is the effective bending stiffness. Using the nonlocal elasticity theory for bending moment:

$$\begin{aligned} M - \mu \frac{{\partial^{2} M}}{{\partial x^{2} }} & = - ({\text{EI}})^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{2I\nu }{h}\left( {\tau_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ & \quad + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \end{aligned}$$

(28)

$$\begin{aligned} M & = \mu \left( { - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - q_{w} } \right) - ({\text{EI}})^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + \frac{2I\nu }{h}\left( {\tau_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \end{aligned}$$

(29)

Substituting Eq. (29) into Eq. (25) the constitutive motion equation will be obtained:

$$\begin{aligned} & \left( {1 - \mu \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left( { - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - q_{w} } \right) - (EI)^{*} \frac{{\partial^{4} w}}{{\partial x^{4} }} \\ & \quad + \frac{2I\nu }{h}\left( {\tau_{0} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \rho_{0} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{4} w}}{{\partial x^{4} }} = 0 \\ \end{aligned}$$

(30)

Assuming the harmonic motion for the free vibration of nanobeam with natural frequency of ω, namely:

$$w(x,t) = W(x){\text{e}}^{i\omega t}$$

(31)

Substituting Eq. (31) into Eq. (30) leads to:

$$\begin{aligned} & \left( {1 - \mu \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left( {\omega^{2} I_{2} \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) - \omega^{2} I_{1} W(x) - q_{w} } \right) - ({\text{EI}})^{*} \frac{{\partial^{4} W}}{{\partial x^{4} }} \\ & \quad + \frac{2I\nu }{h}\left( {\tau_{0} \frac{{\partial^{4} W}}{{\partial x^{4} }} + \rho_{0} \omega^{2} \frac{{\partial^{4} W}}{{\partial x^{2} }}} \right) + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{4} W}}{{\partial x^{4} }} = 0 \\ \end{aligned}$$

(32)

2.4 Solution procedure

In addition, the governing motion equation for piezoelectric nanobeam and associated boundary conditions is discretized using DTM. This method is one of the most useful techniques for solving the differential equations which comes from Taylor’s series expansion. Implementing DTM reduces the governing equations for various boundary conditions to algebraic equations, and finally, all the calculations turn into simple iterative process [36]. The basic definitions are defined as:

$$Y[k] = \frac{1}{k!}\left( {\frac{{{\text{d}}^{k} y(x)}}{{{\text{d}}x^{k} }}} \right)_{{x = x_{0} }}$$

(33)

$$y(x) = \mathop \sum \limits_{k = 0}^{\infty } (x - x_{0} )^{k} Y[k]$$

(34)

Some of the transformation functions in order to transform the constitutive equations and boundary conditions into algebraic equations are listed in Table 1.

Table 1 Some basic theorems of DTM for equations of motion

Apply the mentioned equations in Table 1. Using the DTM to Eq. (32), the resultant equations are obtained as:

$$\begin{aligned} & \left( {({\text{EI}})^{*} + \frac{{2I_{3} \nu }}{h}\tau_{0} - \frac{{e_{31}^{2} }}{{\lambda_{33} }} - \mu^{2} \left( {N_{\text{p}} + N_{\text{T}} + P_{\text{electric}} + H} \right) - \mu^{2} K_{\text{P}} } \right) \\ & \quad \frac{{\left( {k + 4} \right)!}}{k!}W[k + 4] + \left( {\frac{{2I_{3} \nu \,\rho_{0} \omega^{2} }}{h} + \left( {N_{\text{p}} + N_{\text{T}} + P_{\text{electric}} + H} \right) + K_{\text{P}} + \mu^{2} K_{\text{w}} - I_{1} \mu^{2} \omega^{2} } \right) \\ & \quad \frac{(k + 2)!}{k!}W[k + 2] - \left( {K_{w} + I_{1} \omega^{2} } \right)W[k] = 0 \\ \end{aligned}$$

(35)

Simplifying Eq. (35), the following relation can be obtained:

$$\begin{aligned} & W[k + 4] \\ & \quad = \frac{{ - \left( {\frac{{2I_{3} \nu \rho_{0} \omega^{2} }}{h} + \left( {N_{\text{p}} + N_{\text{T}} + P_{\text{electric}} + H} \right) + K_{\text{P}} + \mu^{2} K_{\text{w}} - I_{1} \mu^{2} \omega^{2} } \right)\frac{(k + 2)!}{k!}W[k + 2] + \left( {K_{\text{w}} + I_{1} \omega^{2} } \right)W[k]}}{{\left( {\left( {\text{EI}} \right)^{*} + \frac{{2I_{3} \nu }}{h}\tau_{0} - \frac{{e_{31}^{2} }}{{\lambda_{33} }} - \mu^{2} \left( {N_{\text{p}} + N_{\text{T}} + P_{\text{electric}} + H} \right) - \mu^{2} K_{\text{P}} } \right)\frac{(k + 4)!}{k!}}} \\ \end{aligned}$$

(36)

Also, the resultant equations for boundary conditions by using from Table 2 are given as:

Table 2 Transformed boundary conditions (BC) based on DTM

• Simply–simply supported:

$$\begin{aligned} & W[0] = 0, \quad W[2] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } k(k - 1)W[k] = 0 \\ \end{aligned}$$

(37a)

• Clamped–clamped:

$$\begin{aligned} & W[0] = 0, \quad W[1] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } kW[k] = 0 \\ \end{aligned}$$

(37b)

• Clamped–simply:

$$\begin{aligned} & W[0] = 0, \quad W[1] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } k(k - 1)W[k] = 0 \\ \end{aligned}$$

(37c)

The initial boundary conditions are calculated from the first four W[k]s, and also the higher quantities will be obtained by substituting these equations into recurrence Eq. (36). From Eq. (36) and transformed boundary conditions, the following expression will be obtained:

$$\left[ {\begin{array}{*{20}c} {A_{11} (\omega )} &\quad {A_{12} (\omega )} \\ {A_{21} (\omega )} &\quad {A_{22} (\omega )} \\ \end{array} } \right][C] = 0$$

(38)

The eigenvalue equation is calculated from Eq. (38) as follows:

$$\left| {\begin{array}{*{20}c} {A_{11} (\omega )} &\quad {A_{12} (\omega )} \\ {A_{21} (\omega )} &\quad {A_{22} (\omega )} \\ \end{array} } \right| = 0$$

(39)

Solving Eq. (39), we get $\omega = \omega_{j}^{(n)}$ which $\omega_{j}^{(n)}$ shows the jth natural frequency and for calculating n, the following equation is used:

$$\left| {\omega_{j}^{(n)} - \omega_{j}^{(n - 1)} } \right| \le \varepsilon$$

(40)

in which $\varepsilon$ is the tolerance parameter which is assumed as 0.0001 which means the value of frequencies had four-digit precision. The constitutive equations are solved, and fundamental natural frequencies are obtained.

3 Numerical results and discussion

In this section, the natural frequencies of piezoelectric nanobeam based on the nonlocal Euler–Bernoulli beam theory under thermo-electro-mechanical resting on elastic medium with various boundary conditions are predicted. The Al material properties assumed are listed in Table 3 [28, 37].

Table 3 Al and Si material properties

The selected numerical results are investigated to present the influence of nonlocal parameter (μ), temperature change (ΔT), external electrical voltage (V ₀) and preload (N _p) with various boundary condition including clamped–clamped (C–C), clamped–simply (C–S) and simply–simply supported (S–S).

In order to validate the numerical results and procedure, the comparative studies are presented in this section. The first case study is related to the dimensionless natural frequency; for S–S boundary condition, it is compared with ones presented in Refs. [38, 39] which are tabulated in Table 4. As it is indicated from Table 3, the results are in better agreement with Reddy [39] than Eltaher et al. [38], and this happens because the numerical results in [39] are obtained by analytical method which are more reliable in comparison with those presented in [38] which are obtained by finite element method (FEM). Table 5 also includes nondimensional natural frequencies for C–S and C–C boundary condition presented in Ref. [38], and in the present study, it can be concluded that results are in good agreement with those in [38] with a very slight difference due to solution method.

Table 4 Comparison of the nondimensional fundamental frequency for a nanobeam with various nonlocal parameters with S–S boundary conditions

Table 5 Comparison of the nondimensional fundamental frequency for a nanobeam with various nonlocal parameters with C–S boundary conditions

In the calculation of the natural frequencies by solving the governing motion equations with DTM, the value of natural frequencies after some iteration converges to the constant value. The convergences of first three natural frequencies are investigated in Table 6. As it can be observed from Table 6, the first natural frequency in S–S boundary condition converged after 15 iterations with four-digit precision, while the second natural frequency converged after 25 iterations.

Table 6 Convergence study of nanobeam for the first three natural frequencies (L/h = 100, μ = 2 nm²)

After studying convergence and validation, the influence of temperature and nonlocal parameters with changing voltage for piezoelectric nanobeam is represented in Tables 7, 8 and 9 for S–S, C–S and C–C boundary conditions in the presence of surface effects, respectively. And also according to the previous discussion, the mechanical properties are considered to be constant and all the results are calculated for Al in this section. As indicated in Tables 7, 8 and 9, increasing temperature causes an increase in natural frequency; the reason is that increase in temperature change brings in more increase in the nanobeam stiffness and hence leads to rise in natural frequencies, while increasing the nonlocal parameter and voltage from negative to positive amount decreases the value of natural frequencies. Cause of reducing frequency with growing nonlocal parameter is that the presence of the nonlocal effect tends to decrease the stiffness of nanostructures and decreases natural frequency. Also, the positive voltage tends to decrease natural frequency, while the negative voltage causes an increase in natural frequency. It happens for the fact that the axial compressive and tensile forces are generated in nanobeams by applied positive and negative voltage, respectively. It should be noted that when the nonlocal parameter assumed to be zero, the resultant natural frequencies correspond to classical beam theory.

Table 7 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for S–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h)$

Table 8 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h)$

Table 9 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–C $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h)$

Tables 10, 11 and 12 list the effect of voltage and temperature on elastics medium. Increasing both linear and shear stiffness constants (k _w, k _p) tends to decrease natural frequency. This happens because the foundation elastic affects the stiffness of nanobeams and increasing the value of medium parameters reduces natural frequency. Also, it is clear that the Winkler foundation has less effective than the Pasternak foundation on natural frequency.

Table 10 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for S–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\mu = 2\,{\text{nm}}^{2} )$

Table 11 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\mu = 2\,{\text{nm}}^{2} )$

Table 12 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–C $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\mu = 2\,{\text{nm}}^{2} )$

Effects of voltage and nonlocal parameter via axial preload are shown in Table 13. It can be seen that when the axial comprehensive force is applied, the lower the natural frequency becomes, and for axial tensile force, natural frequency increases. Its reason is because the axial tensile force strengthens the nanobeam stiffness and comprehensive force weakens its stiffness.

Table 13 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h)$

Tables 14, 15 and 16 show nonlocal parameter and voltage effects via length of nanobeam. As the length of nanobeam increases, natural frequency decreases. The influence of surface effects on natural frequencies diminishes from nanoscale to macro-scale.

Table 14 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for S–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\Delta T = 50\,^\circ {\text{C}})$

Table 15 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–S $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\Delta T = 50\,^\circ {\text{C}})$

Table 16 First natural frequency for piezoelectric nanobeam by considering surface and nonlocal effects for C–C $(L = 20\,{\text{nm}},\,h = 0.1L,\,b = 0.5h,\,\Delta T = 50\,^\circ {\text{C}})$

Moreover, Fig. 2 presents the variation of first natural frequency for piezoelectric nanobeam as a function of voltage for different nonlocal parameters in the presence of surface effects by ignoring the Winkler–Pasternak elastic medium and thermal effects. For all values of nonlocal parameter, a descending trend can be observed, while by increasing the voltage from negative to positive amount the difference between curves increases. The piezoelectric field shows increasing effect for negative voltage and decreasing influence for positive voltage amount on fundamental natural frequencies of nanobeam.

Fig. 2

Variation of first natural frequency of S–S for a S–S, b C–S and c C–C piezoelectric nanobeam for different nonlocal parameters in the presence of surface effects for different nonlocal parameters

Next, the variation of natural frequency versus the voltage for various piezoelectric nanobeam lengths is shown in Fig. 3 by considering surface and nonlocal effects in the absence of Winkler–Pasternak elastic medium effect, while the temperature change is considered to be 50 °C. The numerical results imply that the influence of surface and nonlocal effects decreases by increasing voltage in negative region, while they have different manner for positive voltage. And also, it can be discovered that by increasing the beam size the nonlocal and surface with piezoelectric effects have less influence on the natural frequencies.

Fig. 3

Variation of first natural frequency of S–S for a S–S, b C–S and c C–C piezoelectric nanobeam for different nanobeam lengths in the presence of surface effects

4 Conclusion

In the current study, a semi-analytical method of nonlocal piezoelectric surface effect on thermal free vibration of nanobeam lying on Winkler–Pasternak for various boundary conditions with axial preload is presented. The main motivations of this paper are investigating influences of thermal, preload and elastic medium in the presence of electric potential field. As it is presented, governing equation is derived with using Hamilton’s principle for Euler–Bernoulli beam; then, DTM as an efficient and accurate numerical tool was applied to solve vibration of nanobeam subjected to different boundary condition. After presenting the rate of convergence for first three natural frequencies and its validation, some were clarified the influences of piezoelectric, nonlocal and surface effects in combination with other parameters on the vibration of nanobeam. Based on the presented numerical results:

• 1. For all values of nonlocal parameter, voltage and different boundary condition, the influence of surface effects on natural frequencies decreases significantly as the nanobeam length increases.

• 2. Natural frequency increases with increasing thermal effect.

• 3. Increasing voltage parameter tends to decrease fundamental frequency.

• 4. Increasing tension load causes the natural frequency decrease, and increasing comprehension load tends to rise natural frequency .

• 5. Rising elastic medium parameters including Winkler and Pasternak foundations significantly reduces frequency.