1 Introduction

In recent years, numerous researchers are interested in the study and survey of smart structures. It is well known that magneto–electro-elastic materials reveal a particular ability in order to convert the energy of magnetism to electricity or inverse, which does not appear in a single-phase piezoelectric or piezo-magnetic material. For the great coupling effects of magneto–electro-elastic materials, they open towards new interesting and effective applications in many technological fields such as sensing and actuator, vibrations control, energy harvesting and smart structure technologies (Liu et al. 2016b). Hence, it is essential to analyze the behavior of a magneto–electro-elastic beam under mechanical, electrical or magnetic loads. The piezoelectric materials are considered to be a class of smart structure materials which are used widely as sensors and actuators for their fantastic electromechanical properties. It can be found that there are a lot of works about their applications and analysis of piezoelectric materials in fields of vibration, buckling, postbukling and wave propagation for plate (GhorbanpourArani et al. 2015; Kiani 2016; Liu et al. 2016a; Wang et al. 2015; Yao and Li 2016; Zhou et al. 2014), beam (Ebrahimi et al. 2014, 2015a; Farokhi et al. 2016; Marzbanrad et al. 2016; Shaghaghi 2015; Zidour et al. 2012) and wire (Bo and Ronca 1970; Gheshlaghi and Hasheminejad 2012; Haghpanahi et al. 2013).

Functionally graded materials (FGMs) are composite materials whose composition varies continuously along the thickness of the structure. They are usually composed of two different parts ceramic with great properties in heat and corrosive resistances and metal with toughness. For this reason, these materials have incredible properties such as high performance, novel thermos-mechanical properties and resistance under ultra-high temperature. For their novel properties, FGMs have received the significant attention which enables them to be widely used in various researches, which were mainly focused on studying their static, dynamic and vibration characteristics of FG structures (Brischetto et al. 2016; Ebrahimi et al. 2009; Hosseini-Hashemi and Nazemnezhad 2013; Natarajan et al. 2012; Şimşek 2012; Wattanasakulpong and Ungbhakorn 2014).

On the other hand, after discovering carbon nanotubes (CNT) by Iijima (1991), nanoscale engineering materials have attracted more interest in science societies. They have great mechanical, electrical and thermal performances promotion in comparing with conventional materials. Attention is sought toward the development of nanodevices and nanomachines such as beams which are one of the basic components for micro/nano electromechanical systems, biomedical sensors, actuators, transistors, probes, and resonators. Hence understanding and studying the mechanical and physical behaviors of nanobeams made of piezoelectric material is important in the design of nanodevices and nanomachines.

Besides, for the fact that running experiments at the nanoscale is hard, and atomistic modeling is limited to small-scale systems owing to computer resource limitations, continuum mechanics suggest an easy and useful tool for the analysis of MEMs/NEMs. However, the classical continuum models must be developed to consider the nanoscale effects which can be achieved through the nonlocal elasticity theory proposed by Eringen (1972) in order to consider the size-dependent effect. This theory states that the stress at a reference point is a function of strain at all of other points in the body (Eringen 1983). In the field of nonlocal elasticity theory, Ansari et al. (2016) investigated free vibration behavior of piezoelectric Timoshenko nanobeams in the vicinity of postbuckling domain based on the nonlocal elasticity theory. Togun (2016) studied nonlinear free and forced vibration of nanobeam using Euler–Bernoulli theory with attached nanoparticle at the free end based on nonlocal elasticity theory. Moreover, the simplicity in the application of Eringen’s nonlocal elasticity resulted in rapid extensions of this theory in various static and dynamic analyses of nanostructures, such as Ebrahimi et al. (2015c), Malekzadeh and Shojaee (2013), Murmu et al. (2013) and Reddy 2007).

in recent years FGMs and their application have received a considerable attention within the nanotechnology community. Actually, FGM’s applications have been increased in micro and nanoscale systems such as atomic force microscopes (AFMs), micro sensors, nanomotors, and nanomachines. In all of these applications, small-scale effect plays a major roll and must be considered in order to study and investigate mechanical behaviors. Afterward, Chaht et al. (2015) examined the bending and buckling behaviors of size-dependent nanobeams made of FGM including the thickness stretching effect on the basis of the nonlocal continuum model. Moreover, Ebrahimi et al. (2015b) investigated vibrational characteristics of size-dependent FG nanobeams using differential transformation method. Furthermore, free vibration analysis of size-dependent functionally graded rotating nanobeams with considering all surface effects base on the nonlocal continuum model is studied by Ghadiri et al. (2016).

In addition, for the wide range of application of FGMs in sensors and actuators, researchers tend to investigate FG piezoelectric material properties. As, Hashemi-Hosseini et al. (2014) investigated free vibration of FGM nanobeams by considering surface effects as well as the piezoelectric field using nonlocal elasticity theory. In an effort Sabzikar et al. (Boroujerdy and Eslami 2015) developed the buckling analysis of functionally graded piezoelectric spherical shells by considering thermal loading.

On the other hand, thermal effects have considerable influence on mechanical characteristics of FGMs. So, many investigations have been carried out in the open literature dealing with studying the thermal influence on mechanical characteristics of nanostructures such as those in (Ebrahimi and Salari 2015b; Ebrahimi et al. 2016; Zhang et al. 2015). Further, investigating the thermo–electrical buckling of FG piezoelectric Timoshenko nanobeams subjected to in-plane thermal loads and applied electric voltage is presented by Ebrahimi and salari (2015a). The nonlinear thermo-electro-mechanical response of FGM piezoelectric actuators is investigated by Reddy et al. (Komijani et al. 2014). In this study the theoretical formulation is based on the Timoshenko beam theory with the von Kármán nonlinearity and a microstructural length scale is incorporated by means of the modified couple stress theory. And also, Ansari et al. (2015) proposed an exact solution for the nonlinear forced vibration analysis of nanobeams made of FGM subjected to the thermal environment including the effect of surface stress.

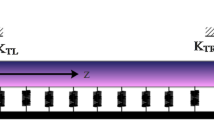
To date, one of the basic terms in MEMs/NEMs is consideration of elastic medium that tends to increase the natural frequency and buckling loads. Therefore, buckling of higher-order shear deformable nanobeams made of functionally graded piezoelectric materials embedded in an elastic medium is examined by Ebrahimi and Barati (2016). After that, Jandaghian and Rahmani (2016) investigated free vibration analysis of magneto–electro–thermo-elastic nanobeams resting on a Pasternak medium based on nonlocal theory and Timoshenko beam theory. Most recently, Marzbanrad et al. (2016) studied the thermo–electro–mechanical vibration analysis of nanobeam rested in Winkler–Pasternak elastic medium by considering surface effects.

Moreover, although the dynamic analysis of piezoelectric FG nanobeams by considering thermal effects is studied, whereas investigating the moisture and preload effects in presence of magnetic field for various boundary conditions on the natural frequencies is rather limited. In the perspective of the above discussion, the current manuscript is concerned with the hygro–thermo–electro–mechanical vibration of nanobeam made of FGM in presence of magnetic field resting on Pasternak medium undergoing preload. The approximate expressions of natural frequencies based on Hamilton’s method in the framework of Euler–Bernoulli beam theory are obtained. A new semi-analytical method called differential transformation method (DTM) is utilized for vibration analysis of size-dependent FG nanobeams. However, implementing the DTM in order to solve similar studies is also rather limited. Comparisons with the results from the well-known references with good agreement between the results of the DTM method and those available in literature validated the presented approach. It is demonstrated that the DTM has high accuracy and precision in dynamic analysis of nanotubes. Finally, through some numerical examples, the influence of various parameters such as a nonlocal parameter, voltage and temperature, elastic medium, power-law index, aspect ratio, preload, magnetic field and moisture effect is investigated.

2 Theory and formulation

2.1 Material gradient of FG nanobeams

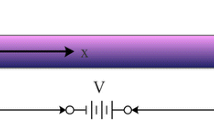
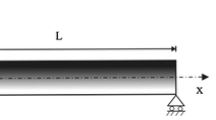
A FG nanobeam with length L, uniform thickness h, and width b having rectangular cross-section is considered as shown in Fig. 1. The coordinate system of FG nanobeam is considered to be located on the central axis of the beam while the x-axis is taken along the central axis, y-axis in the width direction and z-axis in the thickness direction. The effective material properties of FG nanobeam which is made of ceramic and metal such as Young’s modulus \( E \), mass density \( \rho \), poison ratio \( \nu \) and thermal expansion \( \lambda \) are assumed to change continuously in the thickness direction. According to the mixture rule, the effective material properties for FG material, \( P_{f} \), can be defined as (Şimşek 2010a, b):

$$ P_{f} = P_{c} \,V_{c} + P_{m} \,V_{m} $$
(1)

where \( P_{m} \), \( P_{c} \), \( V_{m} \) and \( V_{c} \) are the material properties, accordingly the volume fractions of the metal and the ceramic constituents as (Şimşek 2010b):

$$ V_{c} + V_{m} = 1 $$
(2)
Fig. 1
figure 1

FG nanobeam with Cartesian coordinate and elastic medium

Full size image

The variation of volume fraction is described by a simple power law function which is described as follows:

$$ V_{c} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{P} $$
(3)

which p denotes the non-negative variable parameter of the power-law exponent in order to dictate the material distribution through the thickness of the beam. Also, z is the distance to the mid-plane of the FG beam. When p is assumed to be zero, the FG beam becomes a fully ceramic beam. So from Eqs. (1) to (3), the effective material properties of the FG nanobeam such as Young’s modulus \( E \), mass density \( \rho \), poison ratio \( \nu \) and thermal expansion \( \lambda \) can be obtained as follows:

$$ \begin{aligned} E(z) = (E_{c} - E_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} + E_{m} \hfill \\ \rho (z) = (\rho_{c} - \rho_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} + \rho_{m} \hfill \\ \lambda \left( z \right) = (\lambda_{c} - \lambda_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{2} + \lambda_{m} \hfill \\ \nu \left( z \right) = (\nu_{c} - \nu_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{2} + \nu_{m} \hfill \\ \end{aligned} $$
(4)

In order to model the behavior of FGMs under high temperature effectively, in the material properties the temperature dependency must be considered as follows (Reddy and Chin 1998):

$$ P = P_{0} \left( {\frac{{P_{ - 1} }}{T} + 1 + P_{1} \,T + P_{2} \,T^{2} + P_{3} \,T^{3} } \right) $$
(5)

where \( P_{0} ,P_{ - 1} ,P_{1} ,P_{2} \) and \( P_{3} \) denote the temperature dependent coefficients that are listed in Table 1 for steel and alumina (\( Al_{2} O_{3} \)). The bottom surface of FG nanobeam is considered as pure metal (steel) and the top surface is considered to be pure ceramic (alumina).

Table 1 Some basic theorems of DTM for equations of motion
Full size table

2.2 Nonlocal elasticity theory via piezoelectric materials

The nonlocal elasticity theory expresses that the stress field at a reference point x in an elastic medium is considered to depend on not only the strain at that point but also the strains at all other points in the domain(Eringen 1972). This assumption can explain some experimental observations of atomic and molecular scales for example high-frequency vibration and wave dispersion (Ke et al. 2012). The basic equations for stress-tensor and electric displacement for a homogeneous and nonlocal piezoelectric solid at any point x in the bulk of material by ignoring the body forces obtained as (Wang and Wang 2012):

$$ \sigma_{ij} - \mu^{2} \nabla^{2} \sigma_{ij} = C_{ijkl} \varepsilon_{kl} - e_{kij} E_{k} - \lambda_{ij} \Delta T $$
(6)
$$ D_{i} - \mu^{2} \nabla^{2} D_{i} = e_{ikl} \varepsilon_{kl} + \varepsilon_{ik} E_{k} + p_{i} \Delta T $$
(7)

where \( \sigma_{ij} ,D_{i} \) denote the component of the stress, electric field, and also the \( \varepsilon_{kl} ,C_{ijkl} ,e_{{_{ikl} }} ,\lambda_{ij} \) are the strain, elastic constant, piezoelectric constants, and thermal module. \( \Delta T \) and \( p_{i} \) are the temperature change and piezoelectric constants, while the \( \mu = (e_{0} a)^{2} \) is the nonlocal parameter furthermore \( e_{0} a \) is the scale length to incorporate the size effect for the response of nanostructures.

2.2.1 Euler–Bernoulli beam theory

Component of displacement vector for Euler–Bernoulli beam theory at an arbitrary point can expressed as following:

$$ u_{1} = u(x,t) - z\frac{\partial w(x,t)}{\partial x},\quad u_{2} = 0,\quad u_{3} = w(x,t) $$
(8)

where \( u(x,t) \) and \( w(x,t) \) express axial and transverse displacement components along midplane of the FG nanobeam respectively. The nonzero strains of the EBT are obtained as follows:

$$ \varepsilon_{xx} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial^{2} x}} $$
(9)

Besides the displacement field, in order to satisfy Maxwell’s equation, The electric displacement can be defined as (Samaei et al. 2012):

$$ \begin{aligned} & E_{x} = - \frac{\partial \phi }{\partial x};\quad E_{z} = - \frac{\partial \phi }{\partial z}, \\ & D_{x} = \lambda_{11} E_{x} ;\quad D_{z} = e_{31} \varepsilon_{x} + \lambda_{33} E_{z} , \\ & \frac{{\partial D_{x} }}{\partial x} + \frac{{\partial D_{z} }}{\partial z} = 0 \\ \end{aligned} $$
(10)

where \( \lambda_{11} \) and \( \lambda_{33} \) are the dielectric constants, while \( D_{x} \) and \( D_{z} \) denote the electric displacements. Because the \( \lambda_{11} \) and \( \lambda_{33} \) are in the same order and also by considering \( E_{x} < < E_{z} \), \( D_{x} \) can be neglected in compare with \( D_{z} \) (Hosseini-Hashemi et al. 2014). By substituting Eq. (9) into Eq. (11) and the electrical boundary conditions are \( \phi (x, - h/2) = 0,\,\,\,\,\,\phi (x,h/2) = 2V \), the electrical potential is obtained as (Gheshlaghi and Hasheminejad 2012):

$$ \phi (x,z) = - \frac{{e_{31} }}{{\lambda_{33} }}\left( {\frac{{z^{2} - h^{2} }}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {1 + \frac{z}{h}} \right)V $$
(11)

So, it is assumed that the equivalent load is applied to the piezoelectric layers, this load can be obtained as (Gheshlaghi and Hasheminejad 2012):

$$ P_{electric} (x,t) = b\int\limits_{ - h}^{h} {\sigma_{x}^{*} \,dz} = 2\,V\,b\,e_{31} $$
(12)

The Hamilton’s principle is utilized to derive governing equation of motion and boundary conditions in the framework ok EBT as (Reddy 2007):

$$ \int_{0}^{t} {\delta (U - T + W_{ext} )\,dt = 0} $$
(13)

Here U expresses the strain energy; T denotes kinetic energy and \( W_{ext} \) is the work done by external forces. The first variation of the piezoelectric nanobeams strains energy is obtained as:

$$ \delta U = \int\limits_{0}^{L} {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xz} \delta \gamma_{xz} - D_{x} \delta E_{x} - D_{z} \delta E_{z} } \right)dz\,dx} } $$
(14)

Substituting Eq. (9) into Eq. (14) gives:

$$ \delta U = \int\limits_{0}^{l} {\left[ {N\delta u - M\delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + D_{x} \delta \left( {\frac{\partial \phi }{\partial x}} \right) + D_{z} \delta \left( {\frac{\partial \phi }{\partial z}} \right)} \right]dx} $$
(15)

In which the axial force N and bending moment force M are determined as:

$$ N = \int {\sigma_{xx} dz} \,,M = \int {\,\sigma_{xx} zdz} $$
(16)

The kinetic energy for FG nanobeam is expressed as:

$$ T = \frac{1}{2}\,\iint {\rho (z)(\dot{u}_{1}^{2} + \dot{u}_{2}^{2} + \dot{u}_{3}^{2} )\,}dA.dx $$
(17)

where the first variation of Eq. (17) can be written as:

$$ \delta T = - \int\limits_{0}^{l} {\left( {I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)\delta (w) + I_{0} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)\delta (u) - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)\delta (w) - I_{1} \left( {\frac{{\partial^{3} w}}{{\partial x.\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x.\partial t^{2} }}} \right)} \right)} dx $$
(18)

where

$$ \{ I_{0} ,I_{1} ,I_{2} \} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho (z)\{ 1,z,z^{2} \} \,dz} $$
(19)

Then, the first variation of the work done by external forces can be expressed as:

$$ \delta W_{ext} = \int\limits_{0}^{t} {\left( {f\delta (u) + q\delta (w)} \right)} dt $$
(20)

where \( f \) is calculated as:

$$ f = (N_{p} + N_{T} + P_{electric} + K_{P} + q_{z} + N^{H} )\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) - K_{w} \,W $$
(21)

where \( N_{p} ,N_{T} ,P_{electric} ,K_{P} ,K_{w} ,q_{z} \) and \( N^{H} \) are a normal force, thermal force, external electric potential, Pasternak foundation, Winkler foundation, magnetic field and moisture effect. This can be expressed as:

$$ \begin{aligned} N_{P} & = P_{0} \, \\ N_{T} & = - \int\limits_{ - h/2}^{h/2} {E(z)\lambda (z)\,b\,\Delta T\,dz} \\ q_{z} & = \int_{A} {f_{z} \,dz} = \eta \,A\,H_{x}^{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ N^{H} & = - \int\limits_{A} {E\,\beta \,\Delta H\,dA} = - E\,\beta \,\Delta H\,dA \\ \end{aligned} $$
(22)

By utilizing Hamilton’s principle and substituting Eqs. (15), (18) and (20) into Eq. (13), the equations of motion are obtained as following:

$$ \frac{\partial N}{\partial x} + f - I_{0} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{3} w}}{{\partial x.\partial t^{2} }}} \right) = 0 $$
(23a)
$$ \frac{{\partial^{2} M}}{{\partial x^{2} }} + q - I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x.\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right) = 0 $$
(23b)

For FG nanobeam with piezoelectric properties, nonlocal equations can be developed as following (Jandaghian and Rahmani 2016):

$$ N - \mu \frac{{\partial^{2} N}}{{\partial x^{2} }} = A_{xx} \frac{\partial u}{\partial x} - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2Vb $$
(24a)
$$ M - \mu \frac{{\partial^{2} M}}{{\partial x^{2} }} = B_{xx} \frac{\partial u}{\partial x} - C_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(24b)

where

$$ \left\{ {A_{xx} ,B_{xx} ,C_{xx} } \right\} = \int_{A} {E(z)\,\,\left\{ {1,z,z^{2} } \right\}\,} dA $$
(25)

The explicit relations for axial force and bending moment force can be written by substituting Eqs. (23a, 23b) into Eqs. (24a, 24b) as:

$$ N = A_{xx} \frac{\partial u}{\partial x} - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2Vb + \mu \left( {\frac{\partial f}{\partial x} + I_{0} \left( {\frac{{\partial^{3} u}}{{\partial x.\partial t^{2} }}} \right) - I_{1} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right)} \right) $$
(26a)
$$ M = B_{xx} \frac{\partial u}{\partial x} - C_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu \left( {q + I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x.\partial t^{2} }}} \right) - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right)} \right) $$
(26b)

Accordingly, by substituting Eqs. (26a, 26b) into Eqs. (24a, 24b), the nonlocal governing equations of the Euler–Bernoulli FG nanobeam can be derived:

$$ \begin{aligned} A_{xx} \frac{{\partial^{2} u}}{{\partial x^{2} }} - B_{xx} \frac{{\partial^{3} w}}{{\partial x^{3} }} + \mu \left( {\frac{{\partial^{2} f}}{{\partial x^{2} }} + I_{0} \left( {\frac{{\partial^{4} u}}{{\partial x^{2} .\partial t^{2} }}} \right) - I_{1} \left( {\frac{{\partial^{5} w}}{{\partial x^{3} .\partial t^{2} }}} \right)} \right) - f - I_{0} \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) \hfill \\ + I_{1} \left( {\frac{{\partial^{3} w}}{{\partial x.\partial t^{2} }}} \right) = 0 \hfill \\ \end{aligned} $$
(27a)
$$ \begin{aligned} B_{xx} \frac{{\partial^{3} u}}{{\partial x^{3} }} - C_{xx} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I\frac{{\partial^{4} w}}{{\partial x^{4} }} + \mu \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + I_{0} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right)} \right. \hfill \\ \left. { + I_{1} \left( {\frac{{\partial^{5} u}}{{\partial x^{3} .\partial t^{2} }}} \right) - I_{2} \left( {\frac{{\partial^{6} w}}{{\partial x^{4} .\partial t^{2} }}} \right)} \right) - q - I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x.\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right) = 0 \hfill \\ \end{aligned} $$
(27b)

By neglecting terms of time-dependent and forces and nonlocal parameter in Eq. (27a) and also by substituting Eq. (27a) into Eq. (27a), governing equation is obtained as follows:

$$ \begin{aligned} & \left( {\frac{{B_{xx}^{2} }}{{A_{xx} }} - C_{xx} + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \mu \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + I_{0} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right) + I_{1} \frac{{B_{xx} }}{{A_{xx} }}\left( {\frac{{\partial^{6} w}}{{\partial x^{4} .\partial t^{2} }}} \right) - I_{2} \left( {\frac{{\partial^{6} w}}{{\partial x^{4} .\partial t^{2} }}} \right)} \right) \\ & \quad - q - I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - I_{1} \frac{{B_{xx} }}{{A_{xx} }}\left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} .\partial t^{2} }}} \right) = 0 \\ \end{aligned} $$
(28)

2.3 Differential transformation method

Among all numerical methods which are used to solve the resultant motion equations such as finite element method, Galerkin method or analytical methods, DTM is one of the useful techniques. Differential transformation (DT) technique is a method which utilized to solve ordinary differential equations. The polynomial form is used as an approximation to the exact solution which comes to the Taylor series expansion. But the main difference between the DTM and Taylor series method is that the Taylor series requires computations of higher order derivatives, while DTM involves iterative procedures instead. Applying the DTM in solving free vibration problems generally requires two transformations, namely, differential transformation (DT) and inverse differential transformation (IDT). The definitions of DT and IDT are expressed as (Hassan 2002):

$$ {\text{DT:Y}}\left( {\text{k}} \right) = \frac{1}{{{\text{k}}!}}\left[ {\frac{{{\text{d}}^{\text{k}} }}{{{\text{dx}}^{\text{k}} }}{\text{y}}\left( {\text{x}} \right)} \right]_{{{\text{x}} = 0}} $$
(29)
$$ IDT:y(x) = \sum\limits_{k = 0}^{\infty } {Y_{k} (x - x_{0} )} $$
(30)

Some of the basic transformation functions which are used to transform the constitutive equations and also boundary conditions into algebraic equations are listed in Tables 1 and 2, respectively.

Table 2 Transformed boundary conditions (BC) based on DTM
Full size table

After applying transformation operations introduced in Table 1, the Eq. (28) will be transformed as follows:

$$ W[k + 4] = \frac{{\left( \begin{aligned} \mu \left( { - K_{w} + K_{p} - I_{0} \omega^{2} } \right) - (N_{p} + N_{T} + P_{electric} ) \hfill \\ - K_{p} - \eta AH_{x}^{2} + I_{1} \omega^{2} \frac{{B_{xx} }}{{A_{xx} }} - I_{2} \omega^{2} \hfill \\ \end{aligned} \right)\frac{(k + 2)!}{k!}W[k + 2] + (K_{w} + I_{0} \omega^{2} )W[k]}}{{\left( {\frac{{B_{xx}^{2} }}{{A_{xx} }} - C_{xx} + \frac{{e_{31}^{2} }}{{\lambda_{33} }}I + \mu ((N_{p} + N_{T} + P_{electric} ) + \eta AH_{x}^{2} - I_{1} \omega^{2} \frac{{B_{xx} }}{{A_{xx} }} + I_{2} \omega^{2} )} \right)\frac{(k + 4)!}{k!}}} $$
(31)

By applying DTM to various boundary conditions according to Table 2, following equations will be obtained:

  • Simply–simply supported:

    $$ \begin{aligned} & W[0] = 0,\quad {\text{W}}[2] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } k(k - 1)W[k] = 0 \\ \end{aligned} $$
    (32a)

  • Clamped–clamped:

    $$ \begin{aligned} & {\text{W}}[0] = 0,\quad {\text{W}}[1] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } k W[k] = 0 \\ \end{aligned} $$
    (32b)

  • Clamped–simply:

    $$ \begin{aligned} & {\text{W}}[0] = 0,\quad {\text{W}}[1] = 0 \\ & \mathop \sum \limits_{k = 0}^{\infty } W[k] = 0,\quad \mathop \sum \limits_{k = 0}^{\infty } k(k - 1)W[k] = 0 \\ \end{aligned} $$
    (32c)

3 Numerical results

The FG material properties for steel as metal and alumina as ceramic are written in Table 3 (Reddy and Chin 1998).

Table 3 Temperature dependent coefficients of Young’s modulus, density, poison ratio, thermal expansion (Reddy and Chin 1998)
Full size table

The numerical results are investigated to examine the influence of nonlocal parameter (\( \mu \)), power-law index, temperature change (\( \Delta T \)), external electric voltage (\( V_{0} \)), preload (\( N_{p} \)), length effect (L), moisture effect and magnetic field with various boundary conditions including simply–simply supported (S–S), clamped–simply (C–S) and clamped–clamped (C–C).

In the calculation of natural frequencies by utilizing DTM, the value of natural frequency converges to a constant value after some iteration. First three natural frequencies of piezoelectric FG nanobeam for different boundary conditions are given in Table 4 for different iteration. As indicated, the first frequencies of nanobeam converge after 21st, 19th and 15th iterations with four digit precisions, while the second frequencies converge after 31th, 29th, and 25th itereations and the third frequencies after 37th, 39th and 31th converge to a constant value for C–C, C–S, and S–S, respectively. Therefore, a number of iterations are selected as k = 30 for results reported here for first natural frequencies for all boundary conditions.

Table 4 Convergence study of nanobeam for the first three natural frequencies of FG nanobeam (\( L/h = 20\;,L = 10\ {\rm nm},\; \) \( \mu = 2\ {\text{nm}}^{2} ,p = 0,b = h \))
Full size table

After that, in order to validate and check the accuracy of resultant natural frequencies and procedure in the FG nanobeam, the results obtained from present work are compared with results given by Eltaher et al. (Eltaher et al. 2012) for various boundary conditions. Table 5 presents non-dimensional natural frequency, \( \hat{\omega } = \omega L^{2} \sqrt {{\uprho }_{c} \,{\text{A}}/{\text{E}}_{c} \,{\text{I}}} \), of piezoelectric FG nanobeams for power-law index equal to 0.1 and 5 by varying aspect ratio and nonlocal parameter. It is clear that the obtained results are in good agreement with results given by Eltaher et al. (2012).

Table 5 Comparison of non-dimensional fundamental natural frequencies of simply supported beams (L = 10 nm, h = b)
Full size table

After the convergence study and validation of results, the influences of the power-law index, aspect ratio, and nonlocal parameter are examined in Table 6 for various boundary conditions. It is observed when power-law index and nonlocal parameter increase, natural frequency declines while as the aspect ratio grows, natural frequency increases. In addition, it should be noted that in the case that the nonlocal parameter assumed to be zero, the resultant natural frequencies correspond to the classical beam theory.

Table 6 First natural frequency for piezoelectric FG nanobeam \( (L = 20 \ {\text{nm,}}\,{\text{b = 0}} . 5 {\text{h,V = }} -0. 5 ) \)
Full size table

Influences of temperature and nonlocal parameter change on natural frequency are examined while the voltage is varying between −0.5 and 0.5 for various boundary conditions and the results are listed in Table 7 for all boundary conditions. It is observed when temperature increases, natural frequency decrease, the reason is that, increasing temperature causes the stiffness to decrease which is followed by a decrease in natural frequency. On the other hand, as the nonlocal parameter grows the natural frequency decline, that its reason is similar with increasing frequency which reduces the stiffness of FG nanobeam. Also varying Voltage between −0.5 and 0.5 leads to decline natural frequency. As indicated in obtained results, it can be considered that influence of Voltage on natural frequency is less than nonlocal parameter and temperature change. And also it should be noted that the positive voltage causes the natural frequencies to decrease, while the negative voltage tends to increase the natural frequency. These phenomena happen for the fact that by applying a positive and negative voltage to the nanobeam the axial compressive and tensile forces are generated which affect the natural frequencies.

Table 7 First natural frequency for piezoelectric FG nanobeam \( (L = 10 \ {\text{nm,}}\,{\text{h = L/20}},{\text{b = 0}} . 5 {\text{h,}}\,p = 1 ) \)
Full size table

Table 8 reveals natural frequency for varying preload from −10 to 10 with considering power law index, voltage and nonlocal parameter changes for various boundary conditions. From obtained results, it can be deduced that as the preload parameter increases, natural frequency increases. With increasing comprehensive load, frequency declines and with increasing tensile preload, the natural frequency of FG nanobeam decreases. It happens for the fact that as the FG nanobeam locates under tension, it becomes stiffer and when it puts into compression, it becomes softer.

Table 8 First natural frequency for piezoelectric nanobeam \( (L = 50\ {\text{nm,}}\,{\text{h = L/20,}}\,{\text{b = 0}} . 5 {\text{h,}}\mu {\text{ = 2 \ nm}}^{2} ) \)
Full size table

Table 9 presents the natural frequency for various boundary conditions in order to investigate the influence of Pasternak medium, temperature change and voltage on natural frequency. As seen, when the nanobeam is assumed to rest in an elastic medium, natural frequency rises; In other words, elastic medium leads to improvement stiffness of FG nanobeam. As mentioned, rising temperature and voltage decrease natural frequency.

Table 9 First natural frequency for piezoelectric FG nanobeam \( (L = 10 \ {\text{nm,}}\,{\text{h = L/20,}}\,p = 1,{\text{b = 0}} . 5 {\text{h}}) \)
Full size table

Moreover, the influences of length on natural frequency via power-law index and voltage for different boundary conditions are illustrated in Table 10. From the resultant natural frequencies, it can be deduced when length increase, results are converging to a certain value. Effect of various parameters such as voltage, magnetic field, and the power-law index is investigated in Table 11. It is observed when magnetic field increases, natural frequency inverse power-law index and voltage rises and FG nanobeam become stiffer.

Table 10 First natural frequency for piezoelectric FG nanobeam for various length \( ({\text{h = L/20,}}\,{\text{b = 0}} . 5 {\text{h,}}\,\Delta T = 20^\circ C,\mu = 2 \ {\text{nm}}^{2} ) \)
Full size table
Table 11 First natural frequency for piezoelectric FG nanobeam by considering magnetic field \( (L = 10\ {\rm nm},{\text{h = L/20,}} \) \( \,{\text{b = 0}} . 5 {\text{h,}} \) \( \,\Delta T = 0^\circ C,\mu = 2 \ {\text{nm}}^{2} ) \)
Full size table

Table 12 depicts the variation of natural frequency versus the moisture expansion coefficients and power-law index for various nonlocal parameter values. As the moisture expansion coefficient increases the natural frequency decrease which is assign that the stiffness of the nanobeam is reduced and the nanobeam becomes softer. Similar to the moisture expansion coefficients the increase in the nonlocal parameter for all values of moisture expansion coefficients results in a reduction in natural frequencies.

Table 12 First natural frequency for piezoelectric FG nanobeam by considering magnetic field and hygro parameter \( (L = 10 \ {\rm nm},{\text{h = L/20,}} \) \( \,{\text{b = 0}} . 5 {\text{h,}} \) \( \,\Delta T = 10^\circ C) \)
Full size table

The variation of the natural frequency of piezoelectric FG nanobeam versus power-law index for various voltages and different boundary conditions where the temperature effects are ignored is illustrated in Fig. 2. It can be discovered that when the voltage increases, natural frequency declines for all values of voltage. And also when power-law index grows, for all values of voltage, natural frequency decreases.

Fig. 2
figure 2

Variation of natural frequency of piezoelectric FG nanobeam versus gradient index for different voltages (L = 10 nm, L/h = 20, b = 0.5 h, ∆T = 0, µ = 2 nm2). a Simply supported--simply supported, b clamped--simply supported, c clamped--clamped

Full size image

Figure 3 reveals the variation of the natural frequency of piezoelectric FG nanobeam versus length for various voltages and different boundary conditions. As seen, with increasing length of FG nanobeam, natural frequency increase for all voltage values and also tends to reach its local value and nonlocal effect with voltage can be neglected in macrosize.

Fig. 3
figure 3

Variation of natural frequency of piezoelectric FG nanobeam versus length of nanobeam for different voltages (L/h = 20, b = 0.5 h, ∆T = 0, µ = 2 nm2, P = 1). a Simply supported--simply supported, b clamped--simply supported, c clamped--clamped

Full size image

Finally, Fig. 4 depicts a variation of the natural frequency of FG nanobeam versus external voltage for different boundary conditions and various nonlocal parameters. According to Fig. 4, by increasing the value of external voltage from negative to positive the natural frequency tends to decrease. Because increasing external voltage decreases the stiffness of the FG nanobeam.

Fig. 4
figure 4

Variation of natural frequency of piezoelectric FG nanobeam versus voltage external for different nonlocal parameter (L = 10 nm, L/h = 20, b = 0.5 h, ∆T = 0,p = 1). a Simply supported--simply supported, b clamped--simply supported, c clamped--clamped

Full size image

4 Conclusion

A piezo-nonlocal beam model is utilized to study hydro–thermo–electro–mechanical vibration response of functionally graded material nanobeam in presence of magnetic field and preload resting in the elastic medium for various boundary conditions. The governing equations are obtained with Hamilton’s principle and solved with DTM. Frequency analysis is carried out for different nonlocal parameters, power-law index, temperature changes, voltage externals, magnetic fields, preload parameter, aspect ratio, moisture effect and length. Based on obtained results:

  1. 1.

    Increasing nonlocal parameter leads to decrease natural frequency.

  2. 2.

    Rising temperature decreases natural frequency.

  3. 3.

    Increasing external voltage causes the natural frequency to decrease.

  4. 4.

    Considering preload and increasing tension loads leads to increase the natural frequency and increasing compression load leads to decline natural frequency.

  5. 5.

    Elastic medium causes FG nanobeam becomes stiffer which tends to increase natural frequency.

  6. 6.

    With increasing length of FG nanobeam, results are converging to a certain value.

  7. 7.

    With rising moisture effect, frequencies of Piezoelectric FG nanobeam decline.