Bubbly Markov equilibria

Abstract

Bubbly Markov equilibria (BME) are recursive equilibria on the natural state space which admit a non-trivial bubble. The present paper studies the existence and properties of BME in a general class of overlapping generations economies with capital accumulation and stochastic production shocks. Using monotone methods, we develop a general approach to construct Markov equilibria and provide necessary and sufficient conditions for these equilibria to be bubbly. Our main result shows that a BME exists whenever the bubbleless equilibrium is Pareto inefficient due to either overaccumulation of capital or inefficient risk sharing between generations.

1 Introduction

A bubble is an intrinsically worthless asset which trades at a positive price such as fiat money or a bond with infinite maturity that never pays any dividends. Bubbly equilibria in which bubbles occur as an equilibrium outcome in the presence of rational investors only exist if the equilibrium price system satisfies certain conditions. If investors are infinite-lived, these conditions can only hold if there are frictions such as borrowing constraints. In models with overlapping generations of investors, however, bubbles can occur even in the absence of such frictions which makes this class an attractive framework to study the existence and properties of bubbly equilibria.

The general contribution of this paper is to conduct such a study in a stochastic overlapping generations model with production. To our knowledge, we are the first to offer a comprehensive study of this type. Specifically, we state explicit conditions for the existence of bubbly equilibria in terms of the pricing kernel and provide a recursive method to construct them. Our main existence condition takes the form of an inefficiency property of the bubbleless equilibrium which recovers several existing results in the literature as special cases.

The emergence of a bubble in our setup has two important macroeconomic effects. First, it affects the formation of capital by providing an alternative investment opportunity to investors. Second, it creates an additional insurance possibility which affects the risk sharing arrangements among consumers. With these features, our setup encompasses previous studies of bubbly equilibria in OLG models for the case of a deterministic production economy as studied in Tirole (1985) or Bose and Ray (1993) as well as stochastic models with pure exchange as in Manuelli (1990), Aiyagari and Peled (1991), or Magill and Quinzii (2003). By construction, these studies neglect either the investment or the risk sharing effect of bubbles. In this sense, our framework contains these models as special cases and we will discuss which role the previous existence results play in our extended setup.

The stochastic OLG model with production has been studied in Wang (1993, 1994) and, more recently, in Morand and Reffett (2007), McGovern et al. (2013), and Hillebrand (2014). These studies focus on a particular class of equilibria in which the equilibrium variables are determined by time-invariant mappings on the minimal or ‘natural’ state space. Following Kübler and Polemarchakis (2004), such equilibria will be called Markov equilibria (ME) in this paper.

All results on the existence and properties of ME in Wang (1993, 1994) and the aforementioned and related papers are derived under the assumption that capital is the only asset available to consumers. This excludes the existence of a bubbly asset from the outset. However, as bubbly equilibria can potentially emerge in these economies without any change in fundamentals or the behavioral characteristics of agents, any characterization of the set of equilibria and their properties remains incomplete unless bubbly equilibria are also taken into account. Filling this gap is therefore the main contribution relative to Wang (1993) and similar studies of ME. Extending the terminology from Kübler and Polemarchakis (2004), we call a ME which admits a bubble a bubbly Markov equilibrium (BME). Identifying conditions under which a BME exists and characterizing its properties are the general objectives of this paper.

The first part of our analysis lays out a general method to construct potentially bubbly ME. This sets the stage to establish a general existence theorem for BME in the second part. A first major obstacle to construct ME in our setup is that the pointwise methods employed in Wang (1993) are no longer applicable. For this reason, our construction is based on monotone methods from functional analysis similar to Coleman (1991, 2000), or Greenwood and Huffman (1995). This approach was successfully applied in Morand and Reffett (2007) to study bubbleless ME, and we will show how it can be extended to study BME as well. The method to be developed is also constructive and can directly be employed to compute BME numerically in applications of our results.

The goal of the second part is to provide necessary and sufficient conditions under which the ME constructed is bubbly. Our main result shows that this is the case whenever the bubbleless equilibrium is Pareto inefficient. Such an inefficiency can be the result of dynamic inefficiency due to overaccumulation of capital as studied in Zilcha (1990) but may also be the result of inefficient intertemporal risk sharing between generations (see Barbie et al. 2007 for details). In such cases, a bubbly asset can be welfare improving by permitting state-contingent transfers between generations that otherwise would not be possible.¹

The welfare concept employed in this paper is that of interim or conditional Pareto optimality which evaluates each consumer’s utility conditional on the state at birth (see Demange 2002 for an exploration of different optimality concepts for stochastic OLG models). In our model with time-additive utility and two-period lived consumers, this implies that utility from first period consumption is evaluated ex post, i.e., after the current state is observed, while utility from second period consumption is evaluated in expected terms, i.e., before the state in this period is observed. This asymmetry is a key to obtain a welfare improvement by state-dependent transfers which change the risk structure of first and second period consumption.

A crucial difference to the deterministic result in Tirole (1985) is therefore that bubbles can emerge in stochastic economies which are dynamically efficient but suffer from inefficient risk sharing. While this result may sound intuitive, it requires new methods and proofs inherently different from those used in deterministic studies or stochastic exchange economies.² Thus, our paper also offers a methodological contribution.

One of the major challenges to establish our existence result is that it requires a workable criterion to determine when an equilibrium allocation is Pareto inefficient. Building on the results from Chattopadhyay and Gottardi (1999), a complete characterization of Pareto optimality in stochastic OLG production economies is provided in Barbie et al. (2007). The criterion employed in our paper essentially combines their results with the recursive formulations of Pareto optimality/suboptimality developed in Barbie and Kaul (2015) who provided dominant root-type criteria necessary and sufficient for inefficiency in a stationary exchange economy with continuous state space. Similar criteria for efficiency/inefficiency are derived in Demange and Laroque (2000). By exploiting certain monotonicity properties, our framework allows us to extend the results in Barbie and Kaul (2015) and Demange and Laroque (2000) and offer a complete characterization of inefficiency under a standard condition (Feller continuity) on the endogenous transition probability on the natural state space.

Based on this criterion, we establish our existence result by constructing a sequence of economies with a dividend-paying asset whose dividends converge to zero.³ Each such economy is known to have only efficient ME. Under some additional restrictions, the limiting ME of the benchmark economy with zero dividends is also efficient. Thus, a BME necessarily exists whenever the bubbleless equilibrium is known to be Pareto inefficient.

We expect our existence result to have many promising and interesting applications. One such application concerns the sustainability of government debt which is rolled over indefinitely between any two successive generations and is formally equivalent to a bubble. The sustainability of debt in the deterministic case was first analyzed in Diamond (1965). In the stochastic case, Ball et al. (1998) argued that, roughly speaking, rollover is possible when debt offers a riskless return lower than the growth rate of the economy. Our characterization which is based on the pricing kernel of the economy offers a clean theoretical foundation of this argument and permits to extend it to debt returns with a general stochastic structure. Further, our construction of BME provides an algorithm for explicitly determining sustainable debt policies and the optimal risk indexation of debt returns. These findings could also be valuable for applied studies, e.g., in the current discussion about sustainable debt levels, low interest rates and secular stagnation. Further potential applications, e.g., in the context of social security systems as studied in Gottardi and Kübler (2011) are discussed below.

Bubbles can also emerge in models with heterogeneous, infinitely lived households in the presence of borrowing constraints which are self-enforcing. A recent paper representative of this literature is Hellwig and Lorenzoni (2009). They show that if borrowing constraints are positive and sustainable, they behave like a bubble in the sense that the resulting equilibrium allocation is the same as in an economy with unbacked public debt (see Theorem 2 in Hellwig and Lorenzoni 2009). Similar to the OLG literature, bubbles in their model can only occur if equilibrium interest rates are sufficiently low (see their Proposition 3).

A final large and growing branch of the literature studies the existence and properties of bubbly equilibria in the presence of financial frictions. Representatives of this literature are Farhi and Tirole (2012), Martin and Ventura (2012), and, more recently, Ikeda and Phan (2016) or Miao et al. (2016). In the present paper, we choose not to include such frictions for at least three reasons. First, we would like to retain the deterministic case studied in Tirole (1985) as a natural reference point for our existence conditions. Second, as explained above, we will formulate our existence conditions in terms of the welfare properties of the bubbleless equilibrium based on criteria which are well understood only in the frictionless case. Third, an important reason for introducing frictions in the first place was to explain the emergence of bubbles in dynamically efficient economies. Thus, an important contribution of our paper to the literature with frictions is that bubbles can emerge in dynamically efficient economies even in the absence of such frictions.

The paper is organized as follows. Section 2 introduces the model and defines the concept of a Markov equilibrium. Section 3 develops a general approach to construct these equilibria. Section 4 contains the main results which state necessary and sufficient conditions under which the ME constructed is bubbly. Section 5 concludes; technical proofs and derivations are relegated to Mathematical Appendices A and B.

2 The model

This section introduces the structure and assumptions of the basic model and formalizes the concept of a Markov equilibrium which will be at the core of the subsequent analysis.

2.1 Production sector

The production side is represented by a unit mass continuum of perfectly competitive firms which operate a linear homogeneous technology to produce an all-purpose output commodity using capital and labor as inputs. In addition, production in period t is subjected to an exogenous aggregate random production shock $\theta _t>0$. At equilibrium, labor supply will be constant and normalized to unity. Given the shock, the intensive form production function $f:\mathbb {R}_+ \longrightarrow \mathbb {R}_+$ determines production output $y_t$ in period t from the existing stock of capital $k_t \ge 0$ as

$$\begin{aligned} y_t = \theta _t f(k_t). \end{aligned}$$

As in Wang (1993), shocks are i.i.d. over time with (marginal) distribution $\nu$ supported on the compact set $\varTheta \subset \mathbb {R}_{++}$. Let $\theta _{\mathrm{min}}$ denote the minimal and $\theta _{\mathrm{max}}$ the maximal realization of the shock. The formal arguments in Sect. 4 assume that $\varTheta$ is a finite set. The process $\{\theta _t\}_{t \ge 0}$ induces a probability space $(\Omega , \mathcal {F}, \mathbb {P})$ on which all random variables are defined and a filtration $\{\mathcal {F}_t\}_{t \ge 0}$ such that $\theta _t$ is $\mathcal {F}_t$-measurable. Throughout, the notion of an adapted stochastic process $\{\xi _t\}_{t \ge 0}$ refers to this filtration and implies that each $\xi _t$ can depend only on random variables $\theta _{n}$, $n \le t$. Moreover, $\mathbb {E}_t[\cdot ]:= \mathbb {E}[\cdot |\mathcal {F}_t]$ is the conditional expectations operator.

The following restrictions on f are standard and will be imposed throughout the paper.

Assumption 1

The map $f:\mathbb {R}_+ \longrightarrow \mathbb {R}_+$ is $C^2$ with derivatives $f''<0<f'$ and $\lim _{k \rightarrow 0}f'(k) = \infty$. Moreover, there exists an upper bound $\bar{k}>0$ such that $\theta _{\mathrm{max}} f(k) < k$ whenever $k> \bar{k}$.

The previous restrictions ensure that f is strictly increasing, strictly concave, and satisfies the so-called left-side Inada condition of an infinite capital return at zero. The final restriction excludes unbounded growth and ensures that any feasible allocation of capital, output, and consumption in our model is uniformly bounded.

Market clearing and profit maximizing behavior imply that the equilibrium wage $w_t$ and capital return $r_t$ are determined by the capital stock $k_t>0$ and the shock as $\theta _t \in \varTheta$ as

$$\begin{aligned} w_t = W(k_t, \theta _t):= & {} \theta _t \left[ f(k_t) - k_t f'(k_t)\right] \end{aligned}$$

(1a)

$$\begin{aligned} r_t = R(k_t, \theta _t):= & {} \theta _t \, f'(k_t). \end{aligned}$$

(1b)

Economically, Eqs. (1a) and (1b) equate the prices of labor and capital to their marginal product in production which also implies that equilibrium profits are zero.

2.2 Consumption sector

The consumption sector consists of overlapping generations of consumers who live for two periods. For simplicity, there is no population growth and the size of each generation is normalized to unity. Young consumers earn income from supplying one unit of labor inelastically to the labor market, while old consumers earn the proceeds on their investments made during the previous period.

To transfer income to the second period of life, there are two investment possibilities available to a young consumer in period t. First, she can invest in capital to earn the uncertain capital return $r_{t+1}$ in the next period per unit invested at time t. Second, she can invest in assets given by retradable shares of a fruit tree (Lucas tree) which pay a constant non-random dividend $d \ge 0$ in each period. Let $p_t \ge 0$ denote the asset price per share in period $t \ge 0$. The total supply of shares is normalized to unity.

A young consumer in period t observes her labor income $w_t>0$ and the buying price of shares $p_t \ge 0$ while taking the selling price $p_{t+1}\ge 0$ and the capital return $r_{t+1}>0$ as given random variables in her decision. The consumer chooses the desired investments in capital s and in shares z to maximize expected lifetime utility. Assuming an additive von Neumann–Morgenstern utility function $U(c^y, c^o) = u(c^y) + v(c^o)$ over lifetime consumption, the decision problem reads:

$$\begin{aligned}&\max _{z,s}\Bigl \{u(w_t - z\, p_t - s ) + \mathbb {E}_t \bigl [ v \bigl ( z \, (p_{t+1} + d ) + s\, r_{t+1} \bigr ) \bigr ] \bigl |\, \nonumber \\&\quad \qquad s\ge 0, z \ge 0, z\, p_t + s \le w_t \Bigr \}. \end{aligned}$$

(2)

Throughout, we impose the following standard restrictions on the utility functions.

Assumption 2

Both $g \in \{u,v\}$ are $C^2$ with derivatives satisfying $g''< 0 < g'$ and $\lim _{c \rightarrow 0}g'(c) = \infty$. Moreover, second period utility satisfies the following property $(U): c |v''(c)| \le v'(c)$ for all $c \in ]0, c_{\mathrm{max}}]$.⁴

The previous restrictions imply that utility functions in both periods are strictly increasing and concave and their boundary behavior excludes equilibrium allocations with zero consumption in any period of life. Furthermore, property (U) confines risk aversion of second period utility to the unit interval which is again a standard although more restrictive condition also imposed in Magill and Quinzii (2003), Morand and Reffett (2007) or McGovern et al. (2013). In deterministic models such as Galor and Ryder (1989), it ensures that savings are an increasing function of the expected capital return.

Capital investment $s_t$ in period t determines the capital stock $k_{t+1}$ of the following period. Combining this with the first-order conditions of the decision problem (2), one obtains the following Euler equations which must hold in each period t at equilibrium:

$$\begin{aligned} u'(w_t - p_t - k_{t+1})= & {} \mathbb {E}_{t}\bigl [r_{t+1}v'(p_{t+1} + d + k_{t+1} r_{t+1}) \bigr ] \end{aligned}$$

(3a)

$$\begin{aligned} u'(w_t - p_t - k_{t+1})p_t= & {} \mathbb {E}_{t}\bigl [(p_{t+1} + d)v'(p_{t+1} + d + k_{t+1} r_{t+1}) \bigr ]. \end{aligned}$$

(3b)

Some results will require an additional joint restriction on the production technology f and second period utility v. To introduce this restriction, let $E_\phi (z) := |\frac{z \phi '(z)}{\phi (z)}|$, $z \in \mathbb {R}$ the (absolute) elasticity of a differentiable function $\phi \ne 0$. Using this notation, define

$$\begin{aligned} {E}^{\mathrm{max}}_{v'}:= & {} \sup \Bigl \{ E_{v'}(c) | \; c \in ]0, c_{\mathrm{max}}] \Bigr \} \end{aligned}$$

(4a)

$$\begin{aligned} {E}^{\mathrm{min}}_{v'}:= & {} \inf \Bigl \{ E_{v'}(c) | \; c \in ]0, c_{\mathrm{max}}]\Bigr \}. \end{aligned}$$

(4b)

The values in (4) define upper and lower bounds on risk aversion $E_{v'}(c) = \frac{c |v''(c)|}{v'(c)}$. The following assumption uses these values to obtain a lower bound on the elasticity of $f'$.

Assumption 3

The production technology f and second period utility v satisfy the joint restriction

$$\begin{aligned} E_{f'}(k) \ge \frac{{E}^{\mathrm{max}}_{v'}-{E}^{\mathrm{min}}_{v'}}{1+{E}^{\mathrm{max}}_{v'}- {E}^{\mathrm{min}}_{v'}} \end{aligned}$$

(5)

for all $k \in \mathbb {K}= ]0, k_{\mathrm{max}}]$ with $k_{\mathrm{max}}$ to be determined below and ${E}^{\mathrm{max}}_{v'}$ and ${E}^{\mathrm{min}}_{v'}$ by (4).

Unlike Assumptions 1 and 2, Assumption 3 is a non-standard restriction which will be needed for the monotone methods employed in this paper. Essentially, condition (5) imposes a uniform lower bound on the curvature of the function f measured by $E_{f'}$ which increases with the range of risk aversion ${E}^{\mathrm{max}}_{v'}-{E}^{\mathrm{min}}_{v'}$. It holds automatically if $v'$ displays constant relative risk aversion in which case ${E}^{\mathrm{max}}_{v'} = {E}^{\mathrm{min}}_{v'}$, an assumption widely used in applied macroeconomic models. Further, since $0 \le E_{v'}^{\mathrm{max}} - {E}^{\mathrm{min}}_{v'} \le {E}^{\mathrm{max}}_{v'} \le 1$ due to Assumption 2, the r.h.s. in (5) is uniformly bounded from above by $\frac{1}{2}$. Thus, (5) holds for any production technology with $E_{f'}$ uniformly bounded from below by $\frac{1}{2}$. An example is the Cobb–Douglas case $f(k)= k^{\alpha }$ with capital elasticity $0<\alpha \le \frac{1}{2}$ which is a standard restriction imposed in virtually any empirical application. These observations reveal that Assumption 3 can be satisfied by restricting either the production or the consumer side of the economy. Also note that we do not impose an upper bound on $E_{f'}$. Thus, we completely avoid the restrictive capital income monotonicity condition $E_{f'} \le 1$ which is often imposed in the literature, cf. Wang (1993), Hauenschild (2002), and others. Finally, we remark that we could further relax Assumption 3 if some restrictions on the distribution $\nu$ were imposed. In this paper, we decided not to impose such restrictions.

2.3 Markov equilibria (ME)

The dividend payment $d \ge 0$ will be a key parameter in our analysis. For a given value $d \ge 0$, the economy is summarized by the list $\mathscr {E}_{d}=\langle u, v, f, \nu , d \rangle$ plus initial conditions for capital $k_0>0$ and the shock $\theta _0 \in \varTheta$. Specifically, we refer to the economy $\mathscr {E}:= \mathscr {E}_{0}$ in which dividend payments are zero as the benchmark economy in our framework. Note that $\mathscr {E}$ essentially corresponds to the economy studied in Wang (1993).

The following definition is standard and provides the most general notion of equilibrium which reconciles market clearing and optimal behavior of all market participants with rational, self-confirming expectations of consumers.

Definition 1

Given initial values $k_0>0$ and $\theta _0 \in \varTheta$, a sequential equilibrium (SE) of $\mathscr {E}_d$ is an adapted stochastic process $\bigl \{w_t, r_t, p_t, k_{t+1}\bigr \}_{t \ge 0}$ which satisfies (1a, 1b) and (3a, 3b) for all $t \ge 0$.

Using the consumers’ budget constraints, the equilibrium consumption processes are given by $c_t^y = w_t - p_t - k_{t+1}$ and $c_t^o = k_t r_t + p_t + d = \theta _t f(k_t) + d - c_t^y - k_{t+1}$ for all $t \ge 0$.

In this paper, we focus on a particular class of equilibria where all equilibrium variables are determined by time-invariant functions of some state variable $x_t$ which takes values in the state space $\mathbb {X}$. In the literature, such equilibria are called recursive equilibria (RE). We confine ourselves to a particular class of recursive equilibria where the state variable is $x_t = (k_t, \theta _t)$. The underlying state space $\mathbb {X}$ is called the natural state space. Note that the factor price mappings W and R from (1a, 1b) already satisfy this property. Following the terminology of Kübler and Polemarchakis (2004), RE on the natural state space are called Markov equilibria (ME). In the following definition, $\mathbb {X} \subset \mathbb {R}_{++} \times \varTheta$ is a non-empty Borel set which will be constructed explicitly in the next section.

Definition 2

A SE of $\mathscr {E}_d$ is called a Markov equilibrium (ME) on $\mathbb {X}$ if there exists measurable mappings $K^\mathrm{E}_d:\mathbb {X} \longrightarrow \mathbb {R}_{++}$ and $P^\mathrm{E}_d:\mathbb {X} \longrightarrow \mathbb {R}_{+}$ such that $k_{t+1} = K^\mathrm{E}_d(k_t, \theta _t)$ and $p_t = P^\mathrm{E}_d(k_t, \theta _t)$ for all $t \ge 0$ and all $x_0 =(k_0, \theta _0) \in \mathbb {X}$.

A primary goal of this paper is to study ME $(K^\mathrm{E}, P^\mathrm{E})$ of the benchmark economy $\mathscr {E}=\mathscr {E}_0$ where dividend payments are zero (we will occasionally drop the subscript if $d=0$). In particular, we ask whether such equilibria admit a bubble, i.e., can be supported by a nonzero asset price process. Extending the previous terminology, we refer to a ME which admits a bubble as a bubbly Markov equilibrium (BME). Formally, we have

Definition 3

A ME $(K^\mathrm{E}, P^\mathrm{E})$ of $\mathscr {E}$ is called bubbly if $P^\mathrm{E} \ne 0$ and bubbleless if $P^\mathrm{E} =0$.

Below we show that any BME satisfies $P^\mathrm{E}>0$, i.e., the price of the bubbly asset is everywhere positive. Note that by adding the Euler equations (3a, 3b), one could also re-interpret the bubbly asset as a bubble on capital, i.e., a deviation from its fundamental value rather than being a separate asset. Intuitively, one can imagine that the firm issues a combined asset which subsumes both investment in capital and the bubble. In this way, we can attach a bubble to any existing asset by adding its price to the fundamental price of the asset.

In addition to their theoretical appeal, bubbly ME have several important applications and admit various alternative interpretations. One such application concerns the sustainability and optimal risk structure of governmental debt. Suppose in each period t, a government issues one-period bonds with unit price and (risk-indexed) return $r_{t+1}^{*}$ to finance its current debt $b_t>0$. Then, the process $\{b_t\}_{t \ge 0}$ which evolves as $b_{t+1} = r_{t+1}^{*}b_t$ is formally equivalent to a bubble in our previous framework. Exploiting this equivalence, the value $P^\mathrm{E}(x_t)$ defines the maximum level of debt that is sustainable if the current fundamental state is $x_t \in \mathbb {X}$. Further, the optimal risk structure of the return offered in period t needed to sustain this maximum level is determined by the random variable

$$\begin{aligned} r_{t+1}^{*} := R^{*}(x_t, \cdot ) = \frac{P^\mathrm{E}\left( K^\mathrm{E}(x_t), \cdot \right) }{P^\mathrm{E}(x_t)}. \end{aligned}$$

(6)

The existence of a BME is therefore equivalent to a positive equilibrium level of debt that can be sustained without further stabilization such as taxation. Also note that (6) would permit to explicitly compute the Arrow–Debreu prices of risk at equilibrium.

An alternative interpretation of a BME is that of a monetary equilibrium in which a fixed quantity $M>0$ of fiat money is exchanged between successive generations. In this case, the price $p_t>0$ corresponds to real money balances in period t.

One can also interpret a BME as an equilibrium with a social security system in which $p_t>0$ represents the transfers from young to old consumers in period $t \ge 0$. A particular appealing feature that follows from the Euler equation (3b) is that such a system is time-consistent in the sense that no generation has an incentive to change it (see Hillebrand 2011 for an application of this concept). Thus, a BME directly implies the existence of a time-consistent social security system.

In the following section we show that the properties of the (unique) bubbleless ME of $\mathscr {E}$ are key to construct the state space $\mathbb {X}$ associated with any ME of $\mathscr {E}_d$ where $d \ge 0$.

2.4 Restricting the state space

It is shown in Hillebrand (2014) that property (U) from Assumption 1 is already sufficient for the benchmark economy $\mathscr {E}$ to possess a unique bubbleless ME. In this case, the equilibrium mappings are given by $P_0^\mathrm{E} \equiv 0$ and $K_0^\mathrm{E} = K_0 \circ W$ where $K_0:\mathbb {R}_{++} \longrightarrow \mathbb {R}_{++}$ determines the unique solution $k= K_0(w)$ to the implicit condition

$$\begin{aligned} G_0(k, w) := u'(w-k) - \mathbb {E}_{\nu } \left[ R(k, \cdot ) v'\left( k R(k,\cdot )\right) \right] =0. \end{aligned}$$

(7)

Note that the implicit function theorem implies that ${K}_0$ is $C^1$, strictly increasing, and $0< {K}_0(w) < w$ for all $w >0$. The capital process along the bubbleless ME evolves as

$$\begin{aligned} k_{t+1} = K_0^\mathrm{E}(k_t, \theta _t) = {K}_0 \circ W(k_t, \theta _t). \end{aligned}$$

(8)

Equation (8) is precisely the representation of equilibrium studied in Wang (1993). To rule out degenerate cases in which capital converges to zero with positive probability, he imposes the additional restriction $\lim _{k \searrow 0} \partial _{k} K_0^\mathrm{E}(k, \theta _{\mathrm{min}}) >1$, cf. Theorem 4.3 in Wang (1993). It ensures existence of a lower bound $\underline{k}>0$ such that $K^\mathrm{E}(k, \theta )>k$ for all $\theta \in \varTheta$ whenever $k \le \underline{k}$. For most of the following analysis, however, it suffices to work with a weaker condition which only excludes that capital converges to zero with probability one. Only later will the stronger requirement of Wang (1993) be necessary.

Before introducing such restrictions formally, a crucial observation is that the bubbleless ME is fully described by the map $K_0$ defined on the one-dimensional set $\mathbb {W} \subset \mathbb {R}_{++}$ of equilibrium wages. We will show in the next section that the same structure obtains in the bubbly case and also along any ME of $\mathscr {E}_{d}$, $d>0$. In each case, the equilibrium mappings in Definition 2 take the form $P^\mathrm{E}_d = P_d \circ W$ and $K^\mathrm{E}_d = K_d \circ W$ with $P_d$ and $K_d$ defined on $\mathbb {W}$. Thus, any ME is completely described by mappings defined on a one-dimensional set $\mathbb {W}$ which we will refer to as the reduced state space. For this reason, the pair $(P_d, K_d)$ will also be referred to as a ME of $\mathscr {E}_d$.

It will be convenient to impose restrictions on the reduced state space $\mathbb {W}$ rather than $\mathbb {X}$ directly. For this reason, we state the aforementioned boundary properties in terms of the wage process along the bubbleless equilibrium which evolves as

$$\begin{aligned} w_{t+1} = W_{0}^\mathrm{E}(w_t, \theta _{t+1}) := W\left( K_0(w_t), \theta _{t+1}\right) {.} \end{aligned}$$

(9)

Mathematically, this representation of the equilibrium dynamics is equivalent to (8). The following assumption rules out that the wage process (9) converges to zero with probability one.

Assumption 4

The map $W_0^\mathrm{E}$ defined in (9) satisfies $\liminf _{w \searrow 0}W_0^\mathrm{E}(w, \theta _{\mathrm{max}})/w >1$.

Assumption 4 does not seem too restrictive, as it essentially excludes only economies for which capital converges to zero with probability one. In our view, such economies are not very interesting for the primary objective of this paper to study bubbly equilibria.

Assumptions 1 and 4 together with continuity of $W_0^\mathrm{E}$ ensure that the set of fixed points of $W_0^\mathrm{E}(\cdot , \theta _{\mathrm{max}})$ is non-empty and compact. Thus, defining

$$\begin{aligned} w_{\mathrm{max}} := \min \Bigl \{w >0 \Bigl | w = W_0^\mathrm{E}(w, \theta _{\mathrm{max}})\Bigr \} \end{aligned}$$

(10)

allows us to use $\mathbb {W} := ]0, w_{\mathrm{max}}]$ as the reduced state space. Note that $\mathbb {W}$ is self-supporting in the sense that $w \in \mathbb {W}$ implies $W_{0}^\mathrm{E}(w, \theta ) \in \mathbb {W}$ for all $\theta \in \varTheta$. Further, $W_0^\mathrm{E}(\cdot , \theta _{\mathrm{max}})$ has $w_{\mathrm{max}}$ as its unique fixed point which is globally asymptotically stable on $\mathbb {W}$.⁵

Setting $k_{\mathrm{max}} := K_0(w_{\mathrm{max}})$ and $\mathbb {K} = ]0, k_{\mathrm{max}}]$ permits to define $\mathbb {X}:= \mathbb {K} \times \varTheta$ as the natural state space from Definition 2 along the bubbleless ME. In the next section, we show that these choices for $\mathbb {W}$ and $\mathbb {X}$ extend to the bubbly case and any ME of $\mathscr {E}_d$ if $d>0$. Thus, a major advantage of Assumption 4 is that it permits a bounded state space.

Some results of Sect. 4 will even require that $\mathbb {W}$ and $\mathbb {X}$ can be chosen compact along the bubbleless ME. In such cases, the following stronger restriction is imposed which rules out that the wage process (9) converges to zero even with positive probability.

Assumption 5

There exists $\underline{w}>0$ such that $W_0^\mathrm{E}(w, \theta _{\mathrm{min}}) >w$ for all $w \le \underline{w}$ with $W_0^\mathrm{E}$ defined in (9).

Assumption 5 ensures that $W_0^\mathrm{E}(\cdot , \theta _{\mathrm{min}})$ has at least one positive fixed point. Defining

$$\begin{aligned} w_{\mathrm{min}} := \min \Bigl \{w >0 \Bigl | w = W_0^\mathrm{E}(w, \theta _{\mathrm{min}})\Bigr \} \end{aligned}$$

(11)

ensures that $\overline{\mathbb {W}}:=[w_{\mathrm{min}}, w_{\mathrm{max}}]$ is a compact self-supporting set for the dynamics (9). While this would also permit to choose the state space $\mathbb {X}$ compact along the bubbleless ME, these choices extend neither to the bubbly case nor to a ME of $\mathscr {E}_d$ if $d>0$.

A direct implication of Assumption 5 is $\liminf _{w \searrow 0} W_0^\mathrm{E}(w, \theta _{\mathrm{min}})/w \ge 1$, which is mathematically essentially equivalent to (although slightly weaker than) the condition in Wang (1993) discussed above. Further, since shocks in (9) are multiplicative, Assumption 5 implies Assumption 4 whenever $\theta _{\mathrm{max}} > \theta _{\mathrm{min}}$.

A potential problem with both Assumptions 4 and 5 is that they refer to derived objects and are not stated in terms of the primitives of the model. For this reason, we present two additional results which state restrictions on the primitives under which the stronger Assumption 5 holds. These restrictions should also be easy to verify in any numerical or empirical application of the model. As they are sufficient but not necessary, we will continue to work with Assumptions 4 and 5 in the following analysis.

Lemma 1

In addition to Assumptions 1 and 2, let the following conditions hold:

$$\begin{aligned} (\mathrm{a}) \, \liminf _{k \searrow 0} \dfrac{W(k, \theta _{\mathrm{min}})}{k}>1 \qquad \qquad \qquad (\mathrm{b}) \, \liminf _{k \searrow 0} \dfrac{\mathbb {E}_{\nu }[R(k, \cdot )v'(k R(k, \cdot ))]}{u'(W(k, \theta _{\mathrm{min}})-k)} >1. \end{aligned}$$

Then, Assumption 5 is satisfied.

Condition (a) is necessary for Assumption 5, as it excludes a poverty trap in which capital would converge to zero under the minimal shock $\theta _{\mathrm{min}}$, independently of any restriction on preferences. A sufficient restriction under which (a) holds is the so-called strengthened Inada (SI) condition $\lim _{k \searrow 0} k f''(k)=\infty$ introduced in Galor and Ryder (1989). Note that this condition is implied by the left-side Inada condition from Assumption 1 whenever $E_{f'}$ is bounded away from zero. Thus, it holds automatically under our Assumption 3 whenever there is some variation in risk aversion of second period utility. As $\lim _{k \searrow 0} f'(k)=\infty$, condition (b) requires that $\mathbb {E}_{\nu } \left[ \frac{\mathrm{id}_{\varTheta }(\cdot ) v'(k R(k, \cdot ))}{u'(W(k, \theta _{\mathrm{min}})-k)}\right]$ is either bounded below or at least does not converge to zero ‘too fast’ as capital converges to zero [here, $\mathrm{id}_{\varTheta }(\cdot )$ is the identity map on $\varTheta$]. As $\theta \mapsto \theta v'(\theta f'(k) k)$ is non-decreasing due to $E_{v'} \le 1$, a sufficient condition for (b) is therefore

$$\begin{aligned} \liminf _{k \searrow 0} \frac{v'\left( k R(k, \theta _{\mathrm{min}})\right) }{u'\left( W(k, \theta _{\mathrm{min}})-k\right) }>0 \end{aligned}$$

(12)

which is similar to the existence conditions in Li and Lin (2012) for the deterministic case.

An alternative restriction to enforce (a) is the so-called non-vanishing labor share (NLS) condition $\liminf _{k \searrow 0} \frac{f(k)}{kf'(k)}>1$ which is generally stronger and implies SI whenever $f(0)=0$.⁶ The NLS condition is again satisfied if $E_{f'}$ is bounded away from zero. Importantly, in the special case often studied in the literature where $v(c) = \beta u(c)$ for some discount factor $\beta >0$, NLS combined with Assumptions 1 and 2 also implies (12) and, therefore, condition (b). The same is true if instead $f(0)>0$ which holds, e.g., with CES production and an elasticity of substitution larger than one. As we did not find these last results in the literature, we state them in the following lemma.⁷

Lemma 2

Under Assumptions 1 and 2, suppose $\liminf _{k \searrow 0} \frac{f(k)}{kf'(k)}>1$. Then, condition (a) from Lemma 1 holds. Moreover, if either $v(c) = \beta u(c)$ for all $c \in ]0, c_{\mathrm{max}}]$ or $f(0)>0$, then (b) is also satisfied.

3 Constructing Markov equilibria

The pointwise construction of ME employed in Wang (1993) and the previous section is available only in the bubbleless case. For this reason, the following sections develop a more general approach which is based on methods from functional analysis similar to Morand and Reffett (2007). It is shown in Hillebrand (2014) that this approach is equivalent to the pointwise construction in Wang (1993) in the bubbleless case. Our method permits to construct ME of the general class of economies $\mathscr {E}_d$, $d\ge 0$ introduced in the previous section. Identifying conditions under which the solution obtained for $d=0$ defines a bubbly ME of the benchmark economy $\mathscr {E}$ then becomes a separate issue to be explored in Sect. 4.

The following sections throughout impose Assumptions 1, 2, and 4. Using the results from Sect. 2.4, define $w_{\mathrm{max}}$ as in (10) and the reduced state space $\mathbb {W}=]0, w_{\mathrm{max}}]$, $k_{\mathrm{max}} := K_0(w_{\mathrm{max}})$ by (7), $\mathbb {K}=]0, k_{\mathrm{max}}]$, and the natural state space $\mathbb {X}=\mathbb {K} \times \varTheta$.

3.1 Defining an operator $T_d$

Given $d\ge 0$, the following analysis aims to construct ME of $\mathscr {E}_d$ as fixed points of an operator $T_d$ defined on some suitably chosen function space $\mathscr {G}$. To restrict the class of candidate equilibrium functions $\mathscr {G}$, a first and crucial observation is that the current state $x_t = (k_t, \theta _t)$ enters the Euler equations (3a, 3b) only through the wage $w_t = W(x_t)$.⁸ Therefore, we conjecture that, similar to the bubbleless equilibrium, the mappings from Definition 2 can be written as $K_d^\mathrm{E} = {K}_d \circ W$ and $P^\mathrm{E}_d = {P}_d \circ W$ where $K_d:\mathbb {W} \longrightarrow \mathbb {K}$ and $P_d:\mathbb {W} \longrightarrow \mathbb {R}_+$. Under this hypothesis, the problem of determining a ME is equivalent to determining the two functions $(K_d, P_d)$ consistent with the Euler equations (3a, 3b). Moreover, we will show below that any solution $P_d$ uniquely determines the associated capital function $K_d$. Thus, we are essentially left to determine the function $P_d$. We restrict our search for this solution to the function space

$$\begin{aligned} \mathscr {G}:= \left\{ P: \mathbb {W} \longrightarrow \mathbb {R}_{+} \, \left| \, \begin{array}{l} P \text{ is } \text{ continuous } \\ w\mapsto P(w) \text{ is } \text{ weakly } \text{ increasing } \\ w\mapsto w - P(w) \text{ is } \text{ weakly } \text{ increasing } \end{array} \right. \right\} . \end{aligned}$$

(13)

The space $\mathscr {G}$ is endowed with the usual pointwise ordering, i.e., $P_1 \ge P_2$ ($P_1 > P_2$) iff $P_1(w) \ge P_2(w)$ ($P_1(w) > P_2(w)$) for all $w \in \mathbb {W}$.

The previous insights greatly simplify the construction of ME because they permit to reduce the problem of determining two functions $(P^\mathrm{E}_d, K^\mathrm{E}_d)$ both defined on $\mathbb {X}$ to finding a single function $P_d$ defined on the one-dimensional space $\mathbb {W}$. In the sequel we will construct $P_d$ as a fixed point of some operator $T_d$ defined on $\mathscr {G}$. The additional monotonicity restrictions in (13) will be necessary for this operator to be well defined.

Let $d \ge 0$ be arbitrary but fixed. The key ingredient to construct the operator $T_d$ is the Euler equations (3a, 3b). The idea is as follows: At some fixed point in time, suppose next period’s asset price is determined by some function $P \in \mathscr {G}$ of next period’s wage. Then, for any current state $w \in \mathbb {W}$, the current asset price p and capital investment k must solve the Euler equations (3a, 3b). Given $P \in \mathscr {G}$ and some fixed $w \in \mathbb {W}$, let

$$\begin{aligned} H^1 (k, p; w, P, d) := & {} \, u'(w - p - k) \nonumber \\&-\,\mathbb {E}_{\nu } \bigl [ R (k, \cdot ) v' \bigl ( P(W(k, \cdot ))+\, d + k R (k, \cdot ) \bigr )\bigr ] \end{aligned}$$

(14a)

$$\begin{aligned} H^2 (k, p; w, P, d) := & {} \, u'(w - p - k) p \nonumber \\&-\, \mathbb {E}_{\nu } \bigl [(P(W(k, \cdot )) + d ) v' \bigl ( P(W(k, \cdot ))+\, d + k R (k, \cdot ) \bigr ) \bigr ]\nonumber \\ \end{aligned}$$

(14b)

which are defined for all $0<k<k_{\mathrm{max}}$ and $p \ge 0$ such that $k+p < w$. Then, for any fixed $\tilde{w} \in \mathbb {W}$, the problem is to determine $\tilde{k} \in \mathbb {K}$, and $\tilde{p} \ge 0$ such that $\tilde{k}+\tilde{p} < \tilde{w}$ and

$$\begin{aligned} H^1\left( \tilde{k}, \tilde{p}; \tilde{w}, P, d\right) = H^2\left( \tilde{k}, \tilde{p}; \tilde{w}, P, d\right) =0. \end{aligned}$$

(15)

First, consider the problem (15) for $d=0$. For this case, we have the following result.

Lemma 3

Let Assumptions 1, 2, and 4 be satisfied and suppose $d=0$. Then, for any $P \in \mathscr {G}$ and $\tilde{w} \in \mathbb {W}$, there is a unique solution $\tilde{p} \ge 0$ and $\tilde{k} \in \mathbb {K}$ to (15).

Lemma 3 permits to define functions $TP: \mathbb {W} \longrightarrow \mathbb {R}_{+}$ and $K_{P}: \mathbb {W} \longrightarrow \mathbb {R}_{++}$ which determine the unique solution to (15) if $d=0$, i.e., $T P(\tilde{w}):= \tilde{p}$ and $K_{P}(\tilde{w}) := \tilde{k}$ for each $\tilde{w} \in \mathbb {W}$. This induces an operator T on $\mathscr {G}$ which associates with any function $P \in \mathscr {G}$ the new function $T(P) := T P$. We also denote by $K_{\bullet }$ the operator on $\mathscr {G}$ which assigns to $P \in \mathscr {G}$ the function $K_{P}$.⁹

The following result shows that T maps $\mathscr {G}$ into itself and establishes several additional properties. Here, the additional restriction (5) from Assumption 3 is needed to ensure that T maps monotonic functions to monotonic functions.

Lemma 4

In addition to Assumptions 1, 2, and 4, let Assumption 3 hold. Then, $T:\mathscr {G} \longrightarrow \mathscr {G}$. Further, for each $P \in \mathscr {G}$ the following holds:

• (i) $T(P) < \mathrm{id}_{\mathbb {W}}$, $P>0$ implies $T(P) >0$, while $P =0$ implies $T(P) =0$.

• (ii) $K_{P}$ is continuous and increasing, $K_{P} \le K_0 < \mathrm{id}_{\mathbb {W}}$ and $P>0$ implies $K_{P} < K_0$.

In a second step, consider now the problem (15) for $d>0$. Observe that this problem is identical to the case where $d=0$ if P is replaced by the function $\hat{P}=P+d$, i.e., $\hat{P}(w):= P(w) + d$ for all $w \in \mathbb {W}$. Clearly, $P\in \mathscr {G}$ implies $P+d \in \mathscr {G}$ for all $d\ge 0$. Thus, define for each fixed $d \ge 0$ the operator $T_d$ on $\mathscr {G}$ as

$$\begin{aligned} T_d (P) = T (P + d). \end{aligned}$$

(16)

Then, by Lemmas 3 and 4, for each $P \in \mathscr {G}$, $\tilde{w} \in \mathbb {W}$ and fixed $d \ge 0$, the unique solution to (15) is given by $\tilde{p}=T_d P(\tilde{w})$ and $\tilde{k}=K_{P+d}(\tilde{w})$. In particular, $T_0 =T$. The relation (16) shows that $T_d$ inherits all properties derived above for T. In particular, $T_d$ maps $\mathscr {G}$ into itself and $T_d(P) < {\mathrm{id}}_{\mathbb {W}}$ for all $P \in \mathscr {G}$.

3.2 Monotonicity properties of $T_d$

We conjecture—and prove in the next subsection—that a fixed point of $T_d$, i.e., a function $P_d^{*} \in \mathscr {G}$ such that $P_d^{*}= T_d P_d^{*}$ together with the induced capital function $K_d^{*} = K_{P_d^{*} + d}$ define a ME of $\mathscr {E}_d$. In this regard, the last result from Lemma 4 implies $K_d^{*} \le K_0$ with the latter defined by (7). This property permits to employ $\mathbb {W}=]0, w_{\mathrm{max}}]$ as the reduced state space and $\mathbb {X} = \mathbb {K} \times \varTheta$ as the natural state space along any ME.

Our ultimate goal in this paper is to prove the existence of a BME which corresponds to a non-trivial fixed point $P_0^{*} >0$ of T. Unfortunately, however, Lemma 4 already showed that the trivial solution $P =0$ is always a fixed point of T, so a mere existence result will not help. Instead, we will explicitly construct fixed points as pointwise limits of sequences of function. The method is similar to the one developed in Greenwood and Huffman (1995), see also Morand and Reffett (2003, 2007).

A key property for this construction to be successful is that $T_d$ be monotonic which by (16) is equivalent to monotonicity of T which we will consider first. A major obstacle to establish this property globally on $\mathscr {G}$ is that the methods from differential calculus including the implicit function theorem are not available for all functions in $\mathscr {G}$. To remedy this problem, we will temporarily restrict ourselves (respectively T) to the smaller set

$$\begin{aligned} \mathscr {G}' := \left\{ P \in \mathscr {G} \, | \, P \text{ is } C^1\right\} \end{aligned}$$

(17)

of continuously differentiable functions in $\mathscr {G}$. Observe that $\mathscr {G}'$ still contains the trivial solution $P \equiv 0$. The next result shows that T maps $\mathscr {G}'$ into itself.

Lemma 5

Under the hypotheses of Lemma 4, $P \in \mathscr {G}'$ implies $TP \in \mathscr {G}'$.

The following result now establishes the monotonicity of T on $\mathscr {G}'$ which will turn out to be sufficient to apply the construction principle below. In addition, we show that $K_{\bullet }$ is strictly decreasing on $\mathscr {G}'$ which resembles the usual crowding-out effect of assets.

Lemma 6

Let Assumptions 1, 2, and 4 hold. Then, T is monotonically increasing on $\mathscr {G}'$, i.e., for any $P_0, P_1 \in \mathscr {G}'$, $P_1 \ge P_0$ implies $T(P_1) \ge T(P_0)$ and $P_1 > P_0$ implies $T(P_1) > T(P_0)$. Moreover, $K_{\bullet }$ is monotonically decreasing on $\mathscr {G}'$.

It follows directly from (16) that the operator $T_d$ inherits again all previous properties from T. In particular, $T_d$ is monotonic on $\mathscr {G}'$ and maps this subclass into itself. In addition, the map $d \mapsto T_d$ is monotonic in the sense that $d_1 \ge d_0$ implies $T_{d_1} P \ge T_{d_0} P$ for all $P \in \mathscr {G}'$. For later reference, we state these properties formally in the next result.

Corollary 1

Under the hypotheses of Lemma 6, $T_d$ satisfies the following monotonicity properties:

• (i) For all $d \in \mathbb {R}_{+}$ and $P_0, P_1 \in \mathscr {G}'$: $P_1 \ge (>) P_0$ implies $T_{d} P_1 \ge (>) T_{d} P_0$.

• (ii) For all $P \in \mathscr {G}'$ and $d_0, d_1 \in \mathbb {R}_{+}$: $d_1 \ge (>) d_0$ implies $T_{d_1} P \ge (>) T_{d_0} P$.

3.3 Constructing ME as fixed points of $T_d$

Let $d \ge 0$ be arbitrary but fixed. We are now in a position to construct ME of $\mathscr {E}_d$ as fixed points of $T_d$. For $m \in \mathbb {N}$, let $T_d^m$ denote the m-fold composition of $T_d$ with itself, i.e., $T_d^m = T_d \circ T_d^{m-1}$. As $T_d P = T(P+d) < {\mathrm{id}}_{\mathbb {W}}$ for all $P \in \mathscr {G}$ by Lemma 4, the identity map ${\mathrm{id}}_{\mathbb {W}} \in \mathscr {G}'$ defines a natural upper bound for any fixed point of $T_d$. Thus, define the sequence of functions $(P_d^m)_{m \ge 0}$ recursively by setting $P_d^0 \equiv P_0 := {\mathrm{id}}_{\mathbb {W}}$ and $P_d^{m}:= T_d(P_d^{m-1}) = T_d^{m} P_0$. By Lemma 5, this sequence is well defined and $P_d^m \in \mathscr {G}'$ for all $m \ge 0$. Further, $P_d^1 < P_d^0$ implies $P_d^{m+1} < P_d^m$ for all $m\ge 0$ by monotonicity of $T_d$, i.e., $(P_d^m)_{m \ge 0}$ is strictly decreasing. Thus, the pointwise limit

$$\begin{aligned} P_{d}^{*}(w):= \lim _{m \rightarrow \infty } P_d^{m}(w) = \lim _{m \rightarrow \infty } T_d^{m}P_0(w) \end{aligned}$$

(18)

is well defined for all $w \in \mathbb {W}$ as $(P_d^m(w))_{m \ge 0}$ is a strictly decreasing sequence of real numbers bounded by zero. We show that the limiting function satisfies $P_d^{*} \in \mathscr {G}$. For each $m \ge 1$, $P_d^m \in \mathscr {G}$ implies that $w \mapsto P_d^m(w)$ and $w \mapsto w-P_d^m(w)$, $w \in \mathbb {W}$ are both increasing. Thus, for any $0<w_1 < w_2 \le w_{\mathrm{max}}$ the inequalities $P_d^m(w_1) \le P_d^m(w_2)$ and $w_1 - P_d^m(w_1) \le w_2 - P_d^m(w_2)$ being true for all $m \ge 1$ also hold in the limit and imply that $P_d^{*}$ inherits the previous monotonicity properties. Using an argument developed and proved in (Morand and Reffett 2003, p.1369), these properties already imply continuity of $P_d^{*}$. Thus, ${P}_d^{*} \in \mathscr {G}$. Note, however, that we cannot be certain that $P_d^{*} \in \mathscr {G}'$.

The previous findings lead to the following main result.

Theorem 1

Let Assumptions 1, 2, 3, and 4 hold. Then, for each $d \ge 0$ the functions $P_d^{*}$ defined in (18) and $K_d^{*} := K_{P_d^{*} + d}$ satisfy the following:

• (i) $P_d^{*}$ is a fixed point of $T_d$ which satisfies $P_d^{*}>0$ for $d>0$ and either $P_0^{*}>0$ or $P_0^{*}=0$ if $d=0$. Moreover, $d > d' \ge 0$ implies $P_d^{*} \ge P_{d'}^{*}$ and $K_d^{*} < K_{d'}^{*}$.

• (ii) Both mappings $P_d^{*}$ and $K_d^{*}$ are continuous and increasing.

• (iii) $K_d^\mathrm{E}:= K_{d}^{*}\circ W$ and $P_d^\mathrm{E}:= P_d^{*} \circ W$ is a ME of $\mathscr {E}_d$ on $\mathbb {X} = \mathbb {K} \times \varTheta$.

Theorem 1 shows that our algorithm delivers a unique ME for each $d \ge 0$ with asset prices being strictly positive whenever $d>0$. Moreover, (i) shows that these prices increase with dividend payments, which is certainly what one would expect. Further, higher asset prices and dividends reduce capital formation, which is the usual crowding-out effect. Intuitively, consumers form less capital when asset pay-offs in the second period are higher. Assertion (ii) shows that both capital and asset prices increase with first period income, i.e., higher income increases investment in both capital and assets.

For $d=0$, the previous construction also delivers a unique ME $(K^{*}_0, P^{*}_0)$ of $\mathscr {E}$. However, it may be the case that $P_0^{*}=0$ . Clearly, this would imply $K_0^{*}= K_0$ defined by (7) which yields precisely the bubbleless equilibrium studied in Sect. 2.4. Therefore, the main question to be answered in the remainder of the paper is when does $P^{*}_0>0$ hold?

Before exploring this question in the next section, we present an alternative way to construct the ME from Theorem 1 for the benchmark economy $\mathscr {E}$. The proof of our main existence result will be based on this construction. The idea is to obtain the ME of $\mathscr {E}$ as the limit of ME of dividend economies $\mathscr {E}_d$ as d goes to zero. Formally, let $(d_n)_{n \ge 1}$ be a decreasing sequence of dividends such that $d_n \ge 0$ for all n and $\lim _{n \rightarrow \infty } d_n =0$. By Theorem 1, for each $n \ge 1$ the functions $P_{d_n}^{*}$ defined by (18) and $K_{d_n}^{*}=K_{P_{d_n}^{*} + d_n}$ define a ME of $\mathscr {E}_{d_n}$. The following result shows that the sequence of ME constructed in this fashion indeed converges (pointwise) to the ME of $\mathscr {E}$ defined by Theorem 1.

Lemma 7

For any positive dividend sequence $(d_n)_{n \ge 1}$ converging monotonically to zero, the induced sequence of ME $(K_{d_n}^{*}, P_{d_n}^{*})_{n \ge 1}$ from Theorem 1 converges pointwise to $(K_{0}^{*}, P_{0}^{*})$.

4 Existence of bubbly Markov equilibria

In this section we establish necessary and sufficient conditions under which the ME $(K_0^{*}, P_0^{*})$ constructed in Theorem 1 is bubbly, i.e., $P_0^{*}>0$. Our main result stated as Theorem 2 below shows that this is the case whenever the bubbleless equilibrium derived in Sect. 2.4 is Pareto inefficient. As the proof requires that the (reduced) state space can be chosen compact along this equilibrium, the following sections replace our previous Assumption 4 by the stronger Assumption 5. In addition, the formal arguments in the proofs of Lemma 8 and Theorem 2 below assume that the shock space $\varTheta$ is finite without explicit notice. These restrictions allow us to directly use the characterization of Pareto inefficiency along with Proposition 4 from Barbie et al. (2007). While we are confident that an extension of these results to infinite shock spaces would, in principle, be possible and could be obtained along the lines of the proof of Proposition 1 in Barbie and Kaul (2015), we decided to restrict ourselves here to results that are already available. All other arguments and proofs in this section are formulated and hold also for the general case where $\varTheta$ is an interval.

In this section, define $w_{\mathrm{max}}$ by (10) and $w_{\mathrm{min}}$ by (11). As a notational convention, a superscript $^{*}$ identifies functions associated with the ME constructed in Theorem 1.

4.1 Pareto efficiency, dynamic efficiency, and risk sharing

Our concept of Pareto optimality corresponds to Interim Pareto Optimality (IPO) as defined and studied, for example, in Demange and Laroque (2000) or Conditional Pareto Optimality (CPO) as in Chattopadhyay and Gottardi (1999). The following definition formalizes this concept for the class of economies $\mathscr {E}_d$ defined above for a fixed value $d \ge 0$. To identify and distinguish the potential sources of Pareto inefficiency below, we also introduce the concept of dynamic efficiency as studied in Zilcha (1990) and others.

Definition 4

• (i) Given $x_0 = (k_0, \theta _0) \in \mathbb {X}$, a feasible allocation of $\mathscr {E}_d$ is an adapted stochastic process $a=\{k_{t+1}, c_t^y, c_t^o\}_{t \ge 0}$ with values in $\mathbb {R}^3_{+}$ which satisfies the resource constraint

  $$\begin{aligned} k_{t+1} + c_t^y + c_t^o = f(k_t, \theta _t) + d \end{aligned}$$

  for all $t \ge 0$. The set of feasible allocations of $\mathscr {E}_d$ is denoted $\mathbb {A}_d(x_0)$.

• (ii) Allocation $a \in \mathbb {A}_d(x_0)$ (Pareto) dominates allocation $\tilde{a} \in \mathbb {A}_d(x_0)$ if $c_0^o \ge \tilde{c}_0^o$ and

  $$\begin{aligned} u_t := \mathbb {E}_t \left[ u(c_t^y) + v (c_{t+1}^o)\right] \ge \mathbb {E}_t \left[ u(\tilde{c}_t^y) + v (\tilde{c}_{t+1}^o)\right] =: \tilde{u}_t \end{aligned}$$

  for all $t \ge 0$ and for some $t \ge 0$ there exists a non-empty set $A \in \mathcal {F}_t$ such that $u_t(\omega )> \tilde{u}_t(\omega )$ for all $\omega \in A$.

• (iii) Allocation $a \in \mathbb {A}_d(x_0)$ is called Pareto optimal or efficient if it is not dominated by any other allocation in $\mathbb {A}_d(x_0)$. Otherwise, it is called inefficient.

• (iv) Allocation $a \in \mathbb {A}_d(x_0)$ is called dynamically efficient if there is no other allocation $\tilde{a} \in \mathbb {A}_d(x_0)$ such that

  $$\begin{aligned} {c}_t := \theta _t f(k_t)-k_{t+1} \le \theta _t f(\tilde{k}_t)-\tilde{k}_{t+1} =: \tilde{{c}}_t \end{aligned}$$

  for all $t \ge 0$ and for some $t \ge 0$ there exists a non-empty set $A \in \mathcal {F}_t$ such that ${c}_t(\omega )< {\tilde{c}}_t(\omega )$ for all $\omega \in A$. Otherwise, it is called dynamically inefficient.

For the class of stochastic OLG economies with production studied in this paper, there are two potential reasons why equilibrium allocations may be Pareto inefficient. The first one is dynamic inefficiency corresponding to an overaccumulation of capital. This concept was originally introduced in Cass (1972) for the deterministic case and extended to the stochastic case by Zilcha (1990). If an allocation is dynamically inefficient, a small reduction in initial capital formation leads to a Pareto improvement by increasing aggregate consumption in all future periods and under any possible path of shocks. If an allocation is dynamically inefficient, the introduction of a bubbly asset offers an alternative investment opportunity to consumers which induces an additional income transfer from young to old consumers and may be Pareto improving by crowding-out capital investment. For the deterministic case, this is the result from Tirole (1985).

A complete characterization of dynamic inefficiency of feasible allocations is possible based on the process of capital returns $\{\theta _t f'(k_t)\}_{t \ge 0}$ supporting the allocation, cf. Zilcha (1990). Intuitively, it requires these returns to be smaller than unity ‘sufficiently often’ along any possible path of shocks which generalizes the well-known deterministic results.

A second source of inefficiency arises from potentially inefficient risk sharing between generations. In such cases, a Pareto improvement can be accomplished by redistributing aggregate income between young and old consumers via state-dependent transfers. A bubbly asset which accomplishes this can be seen as a form of government debt with state-dependent return rolledover indefinitely generalizing the basic idea of Samuelson (1958). In a stochastic world, however, the conditions under which such a rollover is possible depend not only on the absolute level of intergenerational transfers but also on their relative size in different states of the world. Therefore, a bubbly asset not only redistributes resources between young and old consumers, but also changes the stochastic structure of their incomes. If the latter increases utility of each generation, we call this an improvement in risk sharing.

Intuitively, a bubbly asset can improve risk sharing by allowing for state-contingent transfers that otherwise would not be possible. For example, along the bubbleless equilibrium studied in Sect. 2.4, the risk to which consumption in the first and second period of life is exposed is exclusively determined by the risk structure of wages and capital returns. In our model, due to the multiplicative structure of shocks in (1), consumption of both generations in each period is perfectly correlated. Introducing a bubbly asset with a return imperfectly correlated with the return on capital (e.g., offering a riskless return) allows to change the risk structure of first and second period consumption which may increase utility of each generation. In fact, this positive effect may overcompensate the crowding-out effect of the bubble and lead to a Pareto improvement even if the initial allocation is dynamically efficient. In Sect. 4.5 we present an example where the bubbleless equilibrium is dynamically efficient but Pareto inefficient due to inefficient risk sharing in this sense. The relation between the previous concepts for competitive equilibrium allocations has also been examined in Barbie et al. (2007).

A characterization of Pareto inefficiency cannot be merely based on capital returns supporting the allocation but must take into account how each generation is willing to substitute incomes today and tomorrow in different states of the world. Based on this idea, the first part of this chapter uses the pricing kernel to obtain a complete characterization of Pareto inefficiency for equilibrium allocations defined recursively on the natural state space. Our main result in Theorem 2 below then establishes that the benchmark economy $\mathscr {E}=\mathscr {E}_0$ has a BME whenever the bubbleless equilibrium allocation is Pareto inefficient. Stating this result formally requires the concept of a Markovian equilibrium allocation which is introduced in the next section.

4.2 Markovian equilibrium allocations (MEA)

For fixed $d \ge 0$, identify a ME of $\mathscr {E}_d$ with the mappings (K, P) on $\mathbb {W}=]0, w_{\mathrm{max}}]$ constructed as in the previous sections (here and in the sequel we drop the subscript d when convenient). We seek to derive the induced mappings which determine the consumption process along a ME. It will be convenient to define these mappings on the reduced state space $\mathbb {W}$ rather than $\mathbb {X}$ and to identify the state at time t by $w_t$. For this reason, we fix the realization of the initial shock $\theta _0 \in \varTheta$ ¹⁰ and define the consumption mappings associated with a ME (K, P) as

$$\begin{aligned} \begin{array}{llcl} C^y:\mathbb {W} \longrightarrow \mathbb {R}_{++},&{} C^y(w) &{}:=&{} w - K(w) - P(w) \\ C^o:\mathbb {W} \times \varTheta \longrightarrow \mathbb {R}_{++}, &{} C^o(w, \theta ) &{}:=&{} P\left( W\left( K(w), \theta \right) \right) + d + K(w) R\left( K(w), \theta \right) . \end{array}\nonumber \\ \end{aligned}$$

(19)

We call the triple $A = (K, C^y, C^o)$ a Markovian equilibrium allocation (MEA). The pricing kernel associated with A is defined as the map $m_{A}:\mathbb {W} \times \varTheta \longrightarrow \mathbb {R}_{++}$,

$$\begin{aligned} m_{A}(w, \theta ) := \frac{v'\left( C^o(w, \theta )\right) }{u'\left( C^y(w)\right) }. \end{aligned}$$

(20)

For each $w_0 \in \mathbb {W}$, a MEA determines a unique feasible allocation $a^\mathrm{E}(w_0) \in \mathbb {A}_d(x_0)$ where $k_{t+1} = K(w_t)$, $c_t^y= C^y(w_t)$, $c_{t+1}^o = C^o(w_t, \theta _{t+1}) = C^o(w_t, w_{t+1}/W(K(w_t),1)$ for $t \ge 0$, while old-age consumption $c_0^o$ in $t=0$ follows from the aggregate resource constraint. Consequently, we adopt the following notions of efficiency/inefficiency for MEA.¹¹

Definition 5

A MEA $A = (K, C^y, C^o)$ is called

• (i) efficient/inefficient at $w_0 \in \mathbb {W}$ if $a^\mathrm{E}(w_0)$ is efficient/inefficient.

• (ii) efficient/inefficient on $\overline{\mathbb {W}} \subset \mathbb {W}$ if A is efficient/inefficient at all $w_0 \in \overline{\mathbb {W}}$.

• (iii) efficient/inefficient if it is efficient/inefficient at each $w_0 \in \mathbb {W}$.¹²

The previous formulation permits consumption and capital along the ME to be expressed as functions of the (reduced) state process $\{w_t\}_{t \ge 0}$. Given $w_0 \in \mathbb {W}$, the statistical evolution of this process is determined by a time-invariant transition probability Q (see ‘Appendix B’ for details). Therefore, the lifetime utility $u_t$ of generation t from Definition 4 (ii) also depends exclusively on the state $w_t$. Combining results from Barbie et al. (2007) and Barbie and Kaul (2015), these properties will allow us to characterize the (in-)efficiency of MEA in terms of mappings defined on a one-dimensional state space which greatly simplifies this characterization. To obtain these results, the following additional restrictions on MEA will be employed.

Definition 6

Let $A=(K, C^y, C^0)$ be a MEA defined as above.

• (i) We call A continuous if the mappings K, $C^y$, and $C^o$ are all continuous.

• (ii) We call a subset of the form $\overline{\mathbb {W}} = [\underline{w}, w_{\mathrm{max}}] \subset \mathbb {W}$ a stable set and $\underline{w}>0$ a lower bound (of A) if $w \in \overline{\mathbb {W}}$ implies $W(K(w), \theta ) \in \overline{\mathbb {W}}$ for all $\theta \in \varTheta$.

• (iii) We call A bounded, if for each $w_0 \in \mathbb {W}$ there is some stable set $\overline{\mathbb {W}}$ containing $w_0$.

The existence of a stable set excludes cases where the state variable converges to zero under some unfavorable sequence of shocks. A stable set can always be chosen as a compact state space because states in this set stay in it under any realization of shocks.

For each $d \ge 0$, denote by $A_d^{*} = (K_d^{*}, C_d^{y,*}, C_d^{o*})$ the MEA associated with the ME $(K_d^{*}, P_d^{*})$ from Theorem 1. Further, let $A_0 = (K_0, C^y _0, C^o_0)$ be the MEA associated with the bubbleless ME of $\mathscr {E}$ derived in Sect. 2.4. That is, $K_0$ is defined by (7), $C^y_0(w):= w - K_0(w)$, and $C_0^o(w, \theta ):= K_0(w) R(K_0(w), \theta )$ for all $w\in \mathbb {W}$ and $\theta \in \varTheta$. Note that $A_0^{*}$ coincides with $A_0$ if and only if $(K_0^{*}, P_0^{*})$ is bubbleless, i.e., $P_0^{*} =0$. This observation will play a key role in the next section. Also observe that $A_0$ and each $A_d^{*}$ are continuous by the results from Sect. 2.4 and Theorem 1(ii) and that $A_0$ is bounded under the additional restriction from Assumption 5.

4.3 A general existence theorem

We are now in a position to state our main existence result in the following theorem.

Theorem 2

Let Assumptions 1, 2, 3, and 5 hold. If $A_0$ is inefficient, then $(K_0^{*}, P_0^{*})$ defines a BME of $\mathscr {E}$, i.e., $P_0^{*}>0$.

The intuition behind the proof of Theorem 2 is straightforward. Consider a monotonic sequence of strictly positive dividend payments $(d_n)_{n \ge 1}$ which converges to zero. For each $n\ge 1$, construct the ME $(K_{d_n}^{*}, P_{d_n}^{*})$ of $\mathscr {E}_{d_n}$ as in Theorem 1 and denote by $A_{d_n}^{*}$ the induced MEA defined as above. It is well known that each $A_{d_n}^{*}$, being an equilibrium allocation of an economy with a dividend-paying asset, is efficient. Intuitively, one would expect that this efficiency also holds in the limit such that the sequence $(A^{*}_{d_n})_{n \ge 1}$ cannot converge to $A_0$ if $A_0$ is inefficient. Thus, $A_0 \ne A_0^{*}$ which is only possible if $P_0^{*}>0$, i.e., $(K_0^{*}, P_0^{*})$ is bubbly.¹³

We preface the proof of Theorem 2 by the following three lemmata. The first result is a sort of unit root condition, which is used in OLG models with finitely many states to characterize the Pareto optimality of stationary competitive equilibria. The proof of part (i) is an adaption of the results from Barbie et al. (2007) and Barbie and Kaul (2015). Part (ii) goes beyond the previous results and provides together with Lemma 9 and Lemma 10 a complete characterization of inefficiency. This part makes use of our monotonicity assumptions to obtain the more general result. The proofs are relegated to ‘Appendix B.’ Also note the similarity of (21) below to the conditions for inefficiency in Demange and Laroque (2000) or Magill and Quinzii (2003).

Lemma 8

Let $A = (K, C^y, C^o)$ be a bounded and continuous MEA and define $m_A$ as in (20).

• (i) If A is inefficient, there is an upper-semicontinuous function $\eta :\mathbb {W} \longrightarrow ]0,1]$ such that

  $$\begin{aligned} \mathbb {E}_{\nu }\left[ \eta (W(K(w), \cdot )) \, m_{A}(w, \cdot ) \right] > \eta (w) \text{ for } \text{ all } w \in {\mathbb {W}}\text{. } \end{aligned}$$

  (21)

• (ii) If $m_A$ is increasing, then $\eta$ in (i) can be chosen continuous. Moreover, if A is inefficient at some $w_0 \in \mathbb {W}$, it is also inefficient for all $w_0' \ge w_0$.

Let $m_0 := m_{A_0}$ be the pricing kernel associated with the bubbleless allocation $A_0$. Our next result ensures that $\eta$ in (21) can be chosen continuous whenever $A_0$ is inefficient.

Lemma 9

If Assumptions 1, 2, 3, and 4 hold, then $m_0$ is increasing.

Finally, we have the following sufficient condition for inefficiency. This condition also appears as part of Theorem 1 of Barbie and Kaul (2015) and as Theorem 1 in Demange and Laroque (2000). The proof we give here is similar to the ones given in these papers.

Lemma 10

Let $A = (K, C^y, C^o)$ be continuous and $\overline{\mathbb {W}}$ be a stable set of A. If a continuous function $\eta :\overline{\mathbb {W}} \longrightarrow ]0,1]$ satisfies (21) for all $w \in \overline{\mathbb {W}}$, then A is inefficient on $\overline{\mathbb {W}}$.

We are now in a position to prove Theorem 2 in five steps.

Step 1:

Let $w_0 \in \mathbb {W}$ be arbitrary and $\overline{\mathbb {W}}=\overline{\mathbb {W}}_{A_0}=[\underline{w}, w_{\mathrm{max}}]$ be a stable set of $A_0$ containing $w_0$ such that $W(K_0(\underline{w}), \theta _{\mathrm{min}})/\underline{w}>1$. Assumption 5 ensures that such a set exists. By hypothesis, $A_0$ is inefficient at $w_0$. Thus, invoking Lemmas 8 and 9, there exists a continuous function $\eta :\mathbb {W}\rightarrow ]0,1]$ such that for all $w \in \overline{\mathbb {W}}$:

$$\begin{aligned} \mathbb {E}_{\nu }\bigl [\eta (W(K_0(w), \cdot )) m_0(w, \cdot ) \bigr ] >\eta (w). \end{aligned}$$

(22)

Step 2:

Define the sequence $(d_n)_{n \ge 1}$ as $d_n := \bar{d}/n$ for $n \ge 1$ with $\bar{d}>0$ specified below. For each $n \ge 1$, let $(K^{*}_{d_n}, P^{*}_{d_n})$ be the ME of $\mathscr {E}_{d_n}$ from Theorem 1 and define the induced MEA $A_{d_n}^{*}= (K_{d_n}^{*}, C_{d_n}^{y*}, C_{d_n}^{o*})$ as in Sect. 4.2. By Lemma 7, the sequence $(K^{*}_{d_n}, P^{*}_{d_n})_{n \ge 1}$ converges pointwise to the ME $(K^{*}_{0}, P^{*}_{0})$ of $\mathscr {E}$ which satisfies either $P_0^{*} =0$ or $P^{*}_0 >0$. We will show that the first case is impossible under the hypotheses of the theorem. Thus, with the aim of obtaining a contradiction, the remainder assumes $P_0^{*} =0$ which implies $K_0^{*} = K_0$. Then, the sequence $(A_{d_n}^{*})_{n \ge 1}$ converges pointwise to $A_0 = (K_0, C^y_0, C^o_0)$ defined above. Further, the sequence $(m_n)_{n \ge 1}$ of pricing kernels $m_n := m_{A_{d_n}^{*}}$ associated with $A_{d_n}^{*}$ defined in (20) converges pointwise to $m_0= m_{A_0}$.

Step 3:

We choose $\bar{d}>0$ such that $\overline{\mathbb {W}}=[\underline{w}, w_{\mathrm{max}}]$ is stable for each $A^{*}_{d_n}$. Since $(K^{*}_{d_n})_{n \ge 1}$ is increasing by Theorem 1(i), it suffices to specify $\bar{d}$ such that $\overline{\mathbb {W}}$ is stable for $A_{d_1}^{*}$. As $\delta := W(K_0(\underline{w}), \theta _{\mathrm{min}})/\underline{w}>1$ and $K^{*}_{d_1} = K^{*}_{\bar{d}}$ converges pointwise to $K_0$ for $\bar{d} {\searrow } 0$ due to Lemma 7, choosing $\bar{d}>0$ small ensures $W(K^{*}_{\bar{d}}(\underline{w}), \theta _{\mathrm{min}})/\underline{w}>1$. Then, $w \ge \underline{w}$ implies $W(K^{*}_{d_n}(w), \theta ) \ge W(K^{*}_{d_1}(w), \theta _{\mathrm{min}}) \ge W(K^{*}_{d_1}(\underline{w}), \theta _{\mathrm{min}}) >\underline{w}$, i.e., $\overline{\mathbb {W}}$ is stable for $A_{d_n}^{*}$.

Step 4:

Standard arguments imply that each $A_{d_n}^{*}$ is efficient on $\overline{\mathbb {W}}$. To see this, define for $n \ge 1$ the continuous function $R_n^{*}(w,\theta ):= (P^{*}_{d_n}(W(K_{d_n}^{*}(w),\theta ))+d_n)/P^{*}_{d_n}(w)$ which satisfies $\mathbb {E}_{\nu } \left[ m_n(w, \cdot ) R_n^{*}(w, \cdot )\right] =1$ for all $w\in \overline{\mathbb {W}}$. Thus, $R_n^{*}$ is a return in the sense of Barbie et al. (2007), cf. their Eq. (5). For all $N>0$ and $w_0 \in \overline{\mathbb {W}}$, monotonicity of $P^{*}_{d_n}$ implies $\Pi _{t=1}^N R_n^*(w_{t-1}, \theta _t) \ge P_{d_n}^{*}(w_N)/P^{*}_{d_n} (w_0) \ge P^{*}_{d_n}(\underline{w})/P^{*}_{d_n}(w_{\mathrm{max}})=:M$ for any realization of shocks $\theta _1, \ldots , \theta _N$ where $w_t = W(K_{d_n}^{*}(w_{t-1}), \theta _t)$. Note that M is independent of N and the shocks. Using Proposition 4(a) in Barbie et al. (2007), this implies that $A_{d_n}^{*}$ is interim Pareto efficient on $\overline{\mathbb {W}}$.¹⁴

Step 5:

Combining the previous result with Lemma 10 shows that for each $n \ge 1$ there exists some $w_n \in \overline{\mathbb {W}}$ such that

$$\begin{aligned} \mathbb {E}_{\nu }\bigl [\eta (W(K^{*}_{d_n}(w_n), \cdot )) m_n(w_n, \cdot )\bigr ] \le \eta (w_n). \end{aligned}$$

(23)

Since $\overline{\mathbb {W}}$ is compact, the sequence $(w_n)_{n \ge 1}$ contains a subsequence converging to some $w^*\in \mathbb {W}$. Denote this sequence again by $(w_n)_{n\ge 1}$. Clearly, $\lim _{n \rightarrow \infty } \eta (w_n) = \eta (w^{*})$ by continuity of $\eta$. We would like to show that for all $\theta \in \varTheta$

$$\begin{aligned} \lim _{n \rightarrow \infty } \eta \left( W\left( K^{*}_{d_n}(w_n), \theta \right) \right) m_n(w_n, \theta ) = \eta \left( W(K_0(w^{*}), \theta )\right) m_0\left( w^{*}, \theta \right) . \end{aligned}$$

(24)

Since all functions in (24) are continuous, it suffices to show that $\lim _{n \rightarrow \infty } P^{*}_{d_n}(w_n) =0$ and $\lim _{n \rightarrow \infty } K^{*}_{d_n}(w_n) = K_0(w^{*})$. We have that $\lim _{n \rightarrow \infty } \sup \{P^{*}_{d_n}(w) \, | \, w \in \overline{\mathbb {W}}\}=0$ by Theorem A in Buchanan and Hildebrandt (1908)¹⁵, which immediately gives the result for $P^{*}_{d_n}$. Also by Theorem A in Buchanan and Hildebrandt (1908), $(K^{*}_{d_n})_{n \ge 1}$ being a sequence of strictly monotonic functions converges uniformly to $K_0$ on the compact interval $\overline{\mathbb {W}}$. Combined with continuity of $K_0$, for any $\delta >0$ there exists $n_0$ such that $n > n_0$ implies

$$\begin{aligned} |K^{*}_{d_n}(w_n) - K_0(w^{*})| \le |K^{*}_{d_n}(w_n) - K_0(w_n)| + |K_0(w_n) - K_0(w^{*})| < \delta . \end{aligned}$$

This proves (24). Further, $\eta$ is bounded as a continuous function on the compact set $\overline{\mathbb {W}}$, while $0< m_n(w_n, \theta ) < v'(K_{\bar{d}}(\underline{w}) R(K_0(w_{\mathrm{max}}), \theta _{\mathrm{min}}))/u'(w_{\mathrm{max}})$ for each $\theta \in \varTheta$. Thus, by the Lebesgue-dominated convergence theorem, (23) and (24) imply

$$\begin{aligned} \mathbb {E}_{\nu }\bigl [ \eta (W(K_0(w^{*}), \cdot )) m_0(w^{*}, \cdot ) \bigr ] \le \eta (w^{*}). \end{aligned}$$

(25)

But this contradicts (22) and proves the claim that $P_0^{*}>0$.

The previous construction also suggests that the limiting MEA $A_0^{*}$ associated with the BME $(K^{*}_0, P^{*}_0)$ is efficient. Clearly, if $A_0^{*}$ is bounded, this follows immediately from the same arguments used in Step 4. We thus have the following result.

Proposition 1

If the limiting allocation $A_0^{*}$ associated with the BME $(K^{*}_0, P^{*}_0)$ constructed above is bounded, then it is efficient.

Unfortunately, however, boundedness of $A_0^{*}$ is not guaranteed even if the bubbleless equilibrium satisfies Assumption 5.

Under the hypotheses of Theorem 2, suppose the shock process is non-degenerate, i.e., $\theta _{\mathrm{min}} < \theta _{\mathrm{max}}$ or, equivalently, $w_{\mathrm{min}} < w_{\mathrm{max}}$ defined by (10) and (11). Then, for any initial value $w_0 \in \mathbb {W}$, the dynamics (9) takes values in the ergodic set $[w_{\mathrm{min}}, w_{\mathrm{max}}]$ after finitely many periods with positive probability. In this case, global inefficiency of $A_0$ is equivalent to inefficiency on the ergodic set which by Lemma 8(ii) and 9 is equivalent to $A_0$ being inefficient at $w_{\mathrm{min}}$. Thus, we obtain the following existence result as a corollary to Theorem 2.

Corollary 2

Let Assumptions 1, 2, 3, and 5 hold. If $w_{\mathrm{min}} < w_{\mathrm{max}}$ and $A_0$ is inefficient at $w_{\mathrm{min}}$, then $(K_0^{*}, P_0^{*})$ is a BME of $\mathscr {E}$, i.e., $P_0^{*}>0$.

4.4 Conditions for inefficiency of $A_0$

In this section we provide necessary and sufficient conditions for $A_0$ to be inefficient as required in Theorem 1 which are simple and easy to verify. As in the previous section, we impose the stronger Assumption 5 and define $w_{\mathrm{max}}$ by (10) and $w_{\mathrm{min}}$ by (11).

Define the bubbleless MEA $A_0=(K_0, C_0^y, C_0^o)$ as before. The pricing kernel $m_0 = m_{A_0}$ defined in (20) induces a map $M:\mathbb {W} \longrightarrow \mathbb {R}_{++}$,

$$\begin{aligned} M(w) := \mathbb {E}_{\nu } \bigl [ m_0(w, \cdot )\bigr ]. \end{aligned}$$

(26)

Economically, the value 1 / M(w) can be interpreted as the riskless return in state $w \in \mathbb {W}$. Using (7) and the definition (20) of $m_0$, M can equivalently be written as

$$\begin{aligned} M(w) = \frac{\mathbb {E}_{\nu }\left[ v'\left( C_0^o(w, \cdot )\right) \right] }{\mathbb {E}_{\nu }\left[ R\left( K_0(w), \cdot \right) v'\left( C_0^o(w, \cdot )\right) \right] }, \quad w \in \mathbb {W}. \end{aligned}$$

(27)

The representation in (27) reveals directly that M is continuously differentiable and satisfies $0 \le M(w) \le 1/R(K_0(w); \theta _{\mathrm{min}})$ for all w. The latter implies $\lim _{w \searrow 0} M(w) = 0$.

Our first result states a simple sufficient condition under which $A_0$ is inefficient. Note that the additional restriction from Assumption 3 is not required here.

Lemma 11

Let Assumptions 1, 2, and 5 hold and define M as in (26). If $M(w)>1$ for all $w \in [w_{\mathrm{min}}, w_{\mathrm{max}}]$, then $A_0$ is inefficient.

Proof

We construct a continuous function $\eta : ]0, w_{\mathrm{max}}] \longrightarrow \mathbb {R}_{++}$ which satisfies (22) for all $w \in \mathbb {W}$. By Lemma 10, this implies inefficiency of $A_0$ on any stable set $[\underline{w}, w_{\mathrm{max}}]$ which implies inefficiency on $\mathbb {W}$.

Defining $W_{0}^\mathrm{E}$ as in (9), note that $W_{0}^\mathrm{E}(\cdot ; \theta _{\mathrm{min}})$ is strictly increasing and, therefore, invertible on its range. Denote the inverse by $\varLambda$. By continuity of M, there exists $\delta >0$ such that $M(w)>1$ for all $w \in [w_{\mathrm{min}} - \delta , w_{\mathrm{max}}]$. Construct a sequence $(w_n)_{n \ge 0}$ by setting $w_0 := w_{\mathrm{min}} - \delta$ and $w_n := \varLambda (w_{n-1}) = \varLambda ^n(w_0)$ for $n \ge 1$. Note that $(w_n)_{n \ge 0}$ is strictly decreasing and, due to Assumption 5, converges to zero.

Now construct $\eta$ as follows. For $w \in [w_0, w_{\mathrm{max}}]$, let $\eta (w) \equiv 1$. Then,

$$\begin{aligned} \mathbb {E}_{\nu } \left[ \eta \left( W_{0}^\mathrm{E}(w, \cdot )\right) m_0(w, \cdot )\right] = M(w) > 1 =\eta (w) \end{aligned}$$

for all $w \in [w_0, w_{\mathrm{max}}]$. Second, for $w \in [w_1, w_0[$ let $\eta (w) := M(w)/M(w_0)$. Then,

$$\begin{aligned} \mathbb {E}_{\nu } \left[ \eta \left( W_{0}^\mathrm{E}(w, \cdot )\right) m_0(w, \cdot )\right] = M(w) > M(w)/M(w_0) =\eta (w) \end{aligned}$$

for all $w \in [w_1, w_0[$. Now proceed inductively for $n \ge 1$ by defining for $w \in [w_n, w_{n-1}[$

$$\begin{aligned} \eta (w) := \mathbb {E}_{\nu } \left[ \eta \left( W_{0}^\mathrm{E}(w, \cdot )\right) m_0(w, \cdot ) \right] /M(w_0). \end{aligned}$$

By construction, $\eta$ is a continuous function which satisfies (22). Since $[w_0, w_{\mathrm{max}}] \cup (\cup _{n \ge 1} [w_{n}, w_{n-1}[) = ]0, w_{\mathrm{max}}]$, the construction covers the entire interval $\mathbb {W}$.$\square$

A partial converse to Lemma 11 is the following result.

Lemma 12

Let Assumptions 1, 2, and 5 hold. If $A_0$ is inefficient, then $M(w)>1$ for at least one $w \in [w_{\mathrm{min}}, w_{\mathrm{max}}]$.

Proof

By contradiction, suppose $A_0$ is inefficient but $M(w) \le 1$ for all $w \in [w_{\mathrm{min}}, w_{\mathrm{max}}]$. By Lemma 8, there is an upper-semicontinuous function $\eta :\mathbb {W} \longrightarrow \mathbb {R}_{++}$ such that

$$\begin{aligned} \mathbb {E}_{\nu }\left[ \eta \left( W_{0}^\mathrm{E}(w, \cdot )\right) m_0(w, \cdot ) \right] > \eta (w) \end{aligned}$$

for all $w \in [w_{\mathrm{min}}, w_{\mathrm{max}}]$. By Theorem 2.43 in (Aliprantis and Border 2007, p. 44), $\eta$ attains a maximum on any compact set and the set of maximizers is compact. Let $w^{*}\in [w_{\mathrm{min}}, w_{\mathrm{max}}]$ be a value for which $\eta (w^{*})=\eta _{\mathrm{max}}:= \max \{\eta (w) \, | \, w \in [w_{\mathrm{min}}, w_{\mathrm{max}}]\}$. Then,

$$\begin{aligned}&\mathbb {E}_{\nu }\left[ \eta \left( W_{0}^\mathrm{E}(w^{*}, \cdot )\right) m_0(w^{*}, \cdot ) \right] \\&\quad \le \eta _{\mathrm{max}} \mathbb {E}_{\nu }\left[ m_0(w^{*}, \cdot ) \right] = \eta _{\mathrm{max}} M(w^{*}) \le \eta _{\mathrm{max}}= \eta (w^{*}) \end{aligned}$$

which is a contradiction. $\square$

The previous conditions take an even simpler form under the additional restriction from Assumption 3. In this case, monotonicity of $m_0$ due to Lemma 9 implies that M is strictly increasing. Combining Lemmas 11 and 12 then yields the following result.

Theorem 3

Under Assumptions 1, 2, 3, and 5, the following holds:

• (i) If $M(w^{\mathrm{min}})>1$, then $A_0$ is inefficient.

• (ii) If $A_0$ is inefficient, then $M(w^{\mathrm{max}}) >1$.

In the deterministic case where $w_{\mathrm{min}} = w_{\mathrm{max}}$, the two conditions from Theorem 3 reduce to $M(w_{\mathrm{min}}) >1$ which is equivalent to a capital return $\bar{R}<1$ at the bubbleless steady state. This is precisely the condition in Tirole (1985) which is sufficient and necessary in the deterministic case. In the present stochastic case, the condition $M>1$ requires an ‘average’ capital return less than unity on the ergodic set $[w_{\mathrm{min}}, w_{\mathrm{max}}]$.

4.5 Two example economies

The following examples illustrate the construction of ME of $\mathscr {E}$ developed in Sect. 3 and the previous conditions under which the ME is bubbly. The first example permits to compute all solutions explicitly and also demonstrates that the condition $M(w_{\mathrm{min}})>1$ from Theorem 3 is not necessary for a BME to exist. The second example illustrates our main result that a BME can exist in dynamically efficient economies by constructing an economy in which the bubbleless equilibrium suffers from inefficient risk sharing.

Example 1

Let $f(k) = k^{\alpha }$, $0<\alpha <1$, $u(c)=\log (c)$, and $v(c) = \beta u(c)$, $\beta >0$. This parameterization is widely studied in the literature, cf. Michel and Wigniolle (2003) or Demange and Laroque (2000). Rangazas and Russell (2005) provided a detailed discussion on the (dynamic) efficiency properties of the bubbleless equilibrium allocation in this case.

One verifies directly that Assumptions 1, 2, and 3 hold and the factor price mappings (1) take the form

$$\begin{aligned} W(k, \theta )= & {} \theta (1-\alpha ) k^{\alpha } \end{aligned}$$

(28a)

$$\begin{aligned} R(k, \theta )= & {} \theta \alpha k^{\alpha -1}. \end{aligned}$$

(28b)

The mapping $K_0$ associated with the bubbleless ME of $\mathscr {E}$ defined by (7) computes explicitly as $K_0(w) = \frac{\beta }{1+\beta }w$ such that $W^\mathrm{E}_{0}$ defined in (9) takes the form

$$\begin{aligned} W_0^\mathrm{E}(w, \theta ) = \theta (1-\alpha ) \left( \frac{\beta }{1+\beta } w \right) ^{\alpha }. \end{aligned}$$

(29)

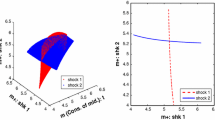
Direct computations reveal that $W_0^\mathrm{E}(\cdot , \theta _{\mathrm{max}})$ has a unique non-trivial fixed point given by $w_{\mathrm{max}}= [(1-\alpha ) \theta _{\mathrm{max}}\left( \beta /(1+\beta ) \right) ^{\alpha }]^{\frac{1}{1-\alpha }}$ which is stable. Further, $W_0^\mathrm{E}(\cdot , \theta _{\mathrm{min}})$ also has a unique fixed point $w_{\mathrm{min}} = [(1-\alpha ) \theta _{\mathrm{min}}\left( \beta /(1+\beta ) \right) ^{\alpha }]^{\frac{1}{1-\alpha }}$ and Assumption 5 is satisfied. For later reference, let $k_{\mathrm{max}}:=K_0(w_{\mathrm{max}})$ denote the maximum capital stock and $R_{\mathrm{max}}:=R(k_{\mathrm{max}}, \theta _{\mathrm{max}})$ the associated capital return under the high shock. Again, these values can be obtained explicitly as $k_{\mathrm{max}}= \left[ \frac{\beta }{1+\beta }(1-\alpha ) \theta _{\mathrm{max}}\right] ^{\frac{1}{1-\alpha }}$ and $R_{\mathrm{max}}=\frac{1+\beta }{\beta } \frac{\alpha }{1-\alpha }$.

Applying the construction principle from Sect. 3.3, let $P_0 = {\mathrm{id}}_{\mathbb {W}}$ and consider the sequence $(P_n)_{n \ge 0}$ defined as $P_n=T(P_{n-1})$, $n \ge 1$. As $P(w) = \delta w$ implies $TP(w)=[R_{\mathrm{max}} + \delta \frac{1+\beta }{\beta }]^{-1}P(w)$ for $w \in \mathbb {W}$, the operator T maps linear functions onto linear functions. Thus, each $P_n$ is linear and can be computed explicitly as

$$\begin{aligned} P_n(w) = \dfrac{w}{R_{\mathrm{max}}^n + \frac{1+\beta }{\beta } \sum _{m=0}^{n-1} R_{\mathrm{max}}^m}, n \ge 0. \end{aligned}$$

For each $w \in \mathbb {W}$, the limit $P_0^{*}$ defined in (18) is given by

$$\begin{aligned} P_0^{*}(w) = \left\{ \begin{array}{cl} \left( \frac{\beta }{1+\beta } - \frac{\alpha }{1-\alpha }\right) w &{}\quad \text{ if } R_{\mathrm{max}} <1 \\ 0 &{} \quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

(30)

Thus, in this example, the ME constructed is bubbly, if and only if $R_{\mathrm{max}}<1$ which is equivalent to $A_0$ being Pareto inefficient. To relate this result to the condition in Theorem 3(ii), consider the function M defined in (27) which can be computed as

$$\begin{aligned} M(w) = \mathbb {E}_{\nu } \left[ \left( R(K_0(w), \cdot )\right) ^{-1}\right] . \end{aligned}$$

(31)

Direct computations reveal that $M(w_{\mathrm{max}}) = \frac{1}{R_{\mathrm{max}}}\mathbb {E}_{\nu } [\theta _{\mathrm{max}}/\mathrm{id}_{\varTheta }(\cdot )]$ and $M(w_{\mathrm{min}}) = \frac{1}{R_{\mathrm{max}}}\mathbb {E}_{\nu } [\theta _{\mathrm{min}}/\mathrm{id}_{\varTheta }(\cdot )]$. As $\mathbb {E}_{\nu } [\theta _{\mathrm{max}}/\mathrm{id}_{\varTheta }(\cdot )] >1$, $R_{\mathrm{max}}<1$ implies $M(w_{\mathrm{max}})>1$. On the other hand, one can easily choose a distribution $\nu$ such that $\mathbb {E}_{\nu } [\theta _{\mathrm{min}}/\mathrm{id}_{\varTheta }(\cdot )]< R_{\mathrm{max}}<1$. In this case, the fixed point (30) satisfies $P_0^{*}>0$ and $\mathscr {E}$ has a BME but $M(w_{\mathrm{min}}) < 1$.

In the previous example, the bubble is a linear function of the wage and, therefore, possesses the same risk structure as capital investment since shocks are multiplicative. That is, the returns on capital and the bubble asset are perfectly correlated. In such cases, it seems intuitively clear that the bubble cannot enhance risk sharing between generations and can induce a Pareto improvement only if the bubbleless equilibrium allocation is dynamically inefficient. This suspicion is correct. In fact, dynamic inefficiency and Pareto inefficiency of the bubbleless MEA $A_0$ are equivalent in this example.¹⁶

Example 2

The second example constructs an economy in which the bubbleless equilibrium allocation $A_0$ suffers from inefficient risk sharing, i.e., is dynamically efficient but Pareto inefficient. Thus, by Theorem 2, the ME constructed as above is bubbly, i.e., $P_0^*>0$.

We maintain the assumption of Cobb–Douglas production $f(k)=k^{\alpha }$ from the previous example such that factor prices are again determined by (28). The utility functions u and v are chosen as $u(c) = \frac{c^{1-\sigma } -1 }{1-\sigma }$ and $v(c) = \beta u(c)$ for some $\beta >0$ where $\sigma >0$ quantifies relative risk aversion. For $\sigma =1$ we recover the economy from the previous example. Under the additional restriction $\sigma \le 1$ needed for property (U) to hold, all Assumptions 1, 2, and 3 are satisfied. Moreover, since f satisfies the NLS property $\lim _{k \searrow 0} \frac{f(k)}{k f'(k)} = \frac{1}{\alpha }>1$ and $v(c) = \beta u(c)$, an application of Lemma 4 shows that Assumption 5 is also satisfied. Hence, the values $w_{\mathrm{max}}$ and $w_{\mathrm{min}}$ from (10) and (11) are well defined. As before, denote the associated capital stocks as $k_{\mathrm{max}}:= K_0(w_{\mathrm{max}})$ and $k_{\mathrm{min}}:= K_0(w_{\mathrm{min}})$ with $K_0$ defined implicitly by (7).

As in the previous example, the wage dynamics (9) or, equivalently, the capital dynamics (8) possess a unique non-trivial fixed point $\bar{k}_{\theta }>0$ for any fixed $\theta \in \varTheta$ which is globally asymptotically stable. To see this, note that any fixed point of the capital dynamics (8) solves $\bar{k} = K^\mathrm{E}_0(\bar{k}, \theta )$ which is equivalent to $G(\bar{k}, W(\bar{k}, \theta ))=0$ with G defined as in (7). Using (28) and the particular form of the utility functions, the latter condition can equivalently be written as

$$\begin{aligned} \tilde{G}(\bar{k}):= \bar{k}^{1-\alpha } \left( \theta (1-\alpha )-\bar{k}^{1-\alpha }\right) ^{-\sigma } - \beta \alpha ^{1-\sigma } \mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot )^{1-\sigma }\right] =0. \end{aligned}$$

Since $\tilde{G}$ is a strictly increasing function, this proves uniqueness of the fixed points. Thus, both mappings $K_0^\mathrm{E}(\cdot , \theta )$ and $W_0^\mathrm{E}(\cdot , \theta )$ possess unique fixed points $\bar{k}_{\theta }$ and $\bar{w}_{\theta }:= W(\bar{k}_{\theta }, \theta )$ for each $\theta \in \varTheta$ which are globally stable on $\mathbb {K}$ respectively $\mathbb {W}$. This implies that under a constant shock path $\theta _t \equiv \theta$, the equilibrium sequences of capital and wages defined by (8) and (9) converge to $\bar{k}_{\theta }$ and $\bar{w}_{\theta }$ for any initial values $k_0 \in \mathbb {K}$ and $w_0 \in \mathbb {W}$.

Equipped with these preparations, we now choose a particular set of parameter values such that the bubbleless ME is dynamically efficient but Pareto inefficient, i.e., suffers from inefficient risk sharing. The specification is as follows. There are two shocks $\varTheta = \{\theta _{\mathrm{min}}, \theta _{\mathrm{max}}\}$ with associated probabilities $\nu _{\mathrm{min}} := \nu (\{ \theta _{\mathrm{min}}\})$ and $\nu _{\mathrm{max}} := \nu (\{\theta _{\mathrm{max}}\})$. Specifically, we choose the following parameter values:

$$\begin{aligned} \theta _{\mathrm{min}}=\frac{3}{2}, \quad \theta _{\mathrm{max}}=\frac{9}{5}, \quad \nu _{\mathrm{min}} = \frac{9}{10}, \quad \nu _{\mathrm{max}} = \frac{1}{10}, \quad \alpha = \frac{3}{10}. \end{aligned}$$

(32)

Thus, there is a low probability for the favorable shock to occur. The value adopted for the production elasticity $\alpha$ is consistent with most empirical applications.

We now specify target values for the fixed points $k_{\min }:= \bar{k}_{\theta _{\mathrm{min}}}$ and $k_{\max }:= \bar{k}_{\theta _{\mathrm{max}}}$ of the capital dynamics under the low and high shock, respectively. Using (28) and the young consumer’s budget constraint, we then infer the associated values for wages $w_{\mathrm{min}}= W(k_{\mathrm{min}}, \theta _{\mathrm{min}})$, $w_{\mathrm{max}} = W(k_{\mathrm{max}}, \theta _{\mathrm{max}})$ and first period consumption $c_{\mathrm{min}}:=w_{\mathrm{min}} - k_{\mathrm{min}}$ and $c_{\mathrm{max}}:=w_{\mathrm{max}} - k_{\mathrm{max}}$ at the respective fixed points. The values we use are

$$\begin{aligned} k_{\mathrm{min}}= & {} 1/3, \quad w_{\mathrm{min}} \approx 0.7552, \quad c_{\mathrm{min}} \approx 0.4219\end{aligned}$$

(33)

$$\begin{aligned} k_{\mathrm{max}}= & {} 2/5, \quad w_{\mathrm{max}} \approx 0.9572, \quad c_{\mathrm{max}} \approx 0.5572. \end{aligned}$$

(34)

We now determine the parameter values $\sigma$ and $\beta$ such that the target value $k_{\min }$ is indeed a fixed point of the capital dynamics (8) under the low shock and $k_{\max }$ a fixed point of (8) under the high shock, i.e., $k_{\mathrm{min}} = K_0^\mathrm{E}(k_{\mathrm{min}}, \theta _{\mathrm{min}})$ and $k_{\mathrm{max}}= K_0^\mathrm{E}(k_{\mathrm{max}}, \theta _{\mathrm{max}})$. Defining the map G as in (7), these conditions are equivalent to $G(k_{\mathrm{min}}, w_{\mathrm{min}}) = 0 = G(k_{\mathrm{max}}, w_{\mathrm{max}})$ which, under the present parameterization, take the form

$$\begin{aligned} c_{\mathrm{min}}^{-\sigma } k_{\mathrm{min}}^{1-\alpha (1-\sigma )} = \alpha ^{1-\sigma } \beta \mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot )^{1-\sigma }\right] = c_{\mathrm{max}}^{-\sigma } k_{\mathrm{max}}^{1-\alpha (1-\sigma )}. \end{aligned}$$

(35)

Given the parameter values from (32) and the target values from (33), conditions (35) can uniquely be solved to obtain

$$\begin{aligned} \sigma ^*= & {} \frac{(1-\alpha )\log (k_{\mathrm{max}}/k_{\mathrm{min}})}{\log (c_{\mathrm{max}}/c_{\mathrm{min}}) - \alpha \log (k_{\mathrm{max}}/k_{\mathrm{min})} }\approx 0.5710\end{aligned}$$

(36a)

$$\begin{aligned} \beta ^*= & {} \frac{c_{\mathrm{min}}^{-\sigma ^*} k_{\mathrm{min}}^{1-\alpha (1-\sigma ^*)}}{\alpha ^{1-\sigma ^*} \mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot )^{1-\sigma ^*}\right] }\approx 0.8782. \end{aligned}$$

(36b)

Thus, for the parameter choices defined in (32) and (36), the values $k_{\mathrm{min}}$ and $k_{\mathrm{max}}$ are fixed points of the capital dynamics (8), while $w_{\mathrm{min}}$ and $w_{\mathrm{max}}$ are fixed points of the wage dynamics (9). Moreover, since all these fixed points are unique, $[k_{\mathrm{min}}, k_{\mathrm{max}}]$ and $[w_{\mathrm{min}}, w_{\mathrm{max}}]$ are the unique minimal stable sets of the capital and wage dynamics.

We now claim that the MEA $A_0$ is dynamically efficient, i.e., for any $w_0 \in \mathbb {W}$, the allocation $a^\mathrm{E}_0(w_0)$ is dynamically efficient. To see this, we can apply the generalized Cass criterion developed in Zilcha (1990) (see also Rangazas and Russell 2005 and Barbie and Kaul 2009). According to this criterion, a sufficient condition for dynamic efficiency is $R(k, \theta _{\mathrm{max}}) >1$ for all $k \in ]0, k_{\mathrm{max}}]$ or, equivalently, $R(k_{\mathrm{max}}, \theta _{\mathrm{max}}) >1$. This may be viewed as a generalization of the well-known deterministic result requiring a steady-state return $\bar{R} >1$. Using the values from (32) and (33) in (28b) gives

$$\begin{aligned} R(k_{\mathrm{max}}, \theta _{\mathrm{max}}) = \theta _{\mathrm{max}}\alpha k_{\mathrm{max}}^{\alpha -1} = \frac{9}{5}\frac{3}{10} \left( \frac{2}{5}\right) ^{-\frac{7}{10}} \approx 1.02554 >1. \end{aligned}$$

(37)

The intuition why (37) implies dynamic efficiency is as follows. Dynamic inefficiency would require aggregate consumption to increase under any possible realization of shocks which is possible only if the capital return is (asymptotically) less than unity. Thus, it suffices to find a particular path for which this is not possible to prove dynamic efficiency. In the present case, consider the constant shock path where $\theta _t = \theta _{\mathrm{max}}$ for all $t \ge 0$. In this case, the induced equilibrium sequence of capital converges to the maximum fixed point $k_{\mathrm{max}}$ which has a capital return $R(k_{\mathrm{max}}, \theta _{\mathrm{max}}) >1$. Thus, an initial reduction in capital formation in fact reduces aggregate consumption along any path where the shock $\theta _{\mathrm{max}}$ occurs ‘sufficiently often.’ Intuitively, capital productivity in the good state is always high enough such that aggregate consumption cannot be increased in each period and under any shock path. Hence, one cannot Pareto improve the bubbleless equilibrium allocation by simply crowding-out capital investment.

We also claim that $A_0$ is Pareto inefficient, i.e., $a_0^\mathrm{E}(w_0)$ is inefficient for all $w_0 \in \mathbb {W}$. Invoking Theorem 3, it suffices to show that $M(w_{\mathrm{min}})>1$ with M defined as in (27). Under the present specification of v and f, this function takes the form

$$\begin{aligned} M(w) = \frac{K_0(w)^{1-\alpha }}{\alpha } \frac{\mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot )^{-\sigma }\right] }{\mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot )^{1-\sigma }\right] }. \end{aligned}$$

(38)

Using $K_0(w_{\mathrm{min}}) = k_{\mathrm{min}} = \frac{1}{3}$ together with the parameter values from (32) and (36) gives

$$\begin{aligned} M(w_{\mathrm{min}})= & {} \frac{k_{\mathrm{min}}^{1-\alpha }}{\alpha } \frac{\nu _{\mathrm{min}} \theta _{\mathrm{min}}^{-\sigma } + \nu _{\mathrm{max}} \theta _{\mathrm{max}}^{-\sigma }}{\nu _{\mathrm{min}} \theta _{\mathrm{min}}^{1-\sigma } + \nu _{\mathrm{max}} \theta _{\mathrm{max}}^{1-\sigma }} \\= & {} \frac{10 \cdot 3^{-0.7}}{3}\frac{9 (1.5)^{-0.571} + (1.8)^{-0.571}}{9 (1.5)^{1-0.571} + (1.8)^{1-0.571}} \approx 1.012 >1. \end{aligned}$$

Thus, even though $A_0$ does not suffer from capital overaccumulation, a BME exists and can be constructed by following the principle devised above. Unlike the solution from Example 1, however, this solution cannot be obtained in closed form. However, one can show that operator T now maps linear function to nonlinear functions which implies that the fixed point $P^*_0$ will be a nonlinear function of the wage and, therefore, of the shock $\theta$. Thus, a potential Pareto improvement can occur by improving the way in which production risk is shared via young and old generations through trading of the bubble. Note that if this is the case, aggregate consumption will at least among some shock paths be lower due to the crowding-out effect of bubbles and the dynamic efficiency of the bubbleless equilibrium. However, if the BME constitutes a Pareto improvement, this effect is overcompensated by the improvement in risk sharing.

To further understand the nature of inefficient risk sharing and how a bubbly asset with an appropriate risk structure can potentially lead to a Pareto improvement, it is instructive to study how feasible transfers with different risk structures affect the utility of different generations in this example. Consider first a transfer payment from young to old consumers which has exactly the same risk structure as capital investment, i.e., is perfectly correlated with the shock $\theta _t$. To ensure feasibility of the scheme in each state $w \in \mathbb {W}$, suppose the transfer is a constant fraction $\tau \ge 0$ of the wage chosen sufficiently small. Since shocks in (1) are multiplicative, transfers and capital returns are perfectly correlated and the utility of a young consumer with wage w depending on $\tau$ is

$$\begin{aligned} U(w; \tau )= & {} u(w - K_0(w) - \tau w) \nonumber \\&+ \mathbb {E}_{\nu }\left[ v\left( \tau W(K_0(w), \cdot ) +\, K_0(w) R(K_0(w), \cdot )\right) \right] . \end{aligned}$$

(39)

To evaluate the potential welfare effects of introducing this transfer scheme, consider the derivative $\partial _{\tau } U(w; \tau )$ evaluated at $\tau =0$. Using the Euler equation (7) and exploiting that shocks are multiplicative give

$$\begin{aligned} \partial _{\tau } U(w; 0) = V(w) w/\theta _{\mathrm{max}} \mathbb {E}_{\nu }\left[ \mathrm{id}_{\varTheta }(\cdot ) v'\left( K_0(w) R(K_0(w), \cdot )\right) \right] \end{aligned}$$

(40)

where $V(w):= W(K_0(w), \theta _{\mathrm{max}})/w- R(K_0(w), \theta _{\mathrm{max}})$ determines the sign of the derivative. Since $K_0(w_{\mathrm{max}}) = k_{\mathrm{max}}$, $W(k_{\mathrm{max}}, \theta _{\mathrm{max}}) =w_{\mathrm{max}}$ and $R(k_{\mathrm{max}}, \theta _{\mathrm{max}})>1$, it follows directly that $V(w)<0$ for w sufficiently close to $w_{\mathrm{max}}$. But this implies that the previous transfer scheme does not lead to a Pareto improvement: Under the constant path $\theta _t \equiv \theta _{\mathrm{max}}$, the economy converges to $w_{\mathrm{max}}$ for any initial condition and any generation with income w close to $w_{\mathrm{max}}$ will be worse-off. Note that the negative effect arises from $R(k_{\mathrm{max}}, \theta _{\mathrm{max}})>1$ which is exactly what makes this economy dynamically efficient. The intuition is therefore that transfers which are perfectly correlated with capital returns cannot improve risk sharing and, therefore, do not lead to a Pareto improvement.

As a second case, consider a transfer scheme which is not perfectly correlated with the capital return. Specifically, suppose that transfers from young to old consumers are state- and time-independent and given by some constant $\bar{\tau } \ge 0$ chosen sufficiently small. As a consequence, capital returns and transfers are uncorrelated and the utility of a consumer born with wage w depending on $\bar{\tau }$ is

$$\begin{aligned} \overline{U}(w; \bar{\tau }) = u\left( w - K_0(w) - \bar{\tau }\right) + \mathbb {E}_{\nu }\left[ v\left( \bar{\tau } + K_0(w) R\left( K_0(w), \cdot \right) \right) \right] . \end{aligned}$$

(41)

Exploiting again the Euler equation (7), the marginal change in utility is

$$\begin{aligned} \partial _{\bar{\tau }} \overline{U}(w; 0) = u'\left( w - K_0(w)\right) \left( M(w)-1\right) \end{aligned}$$

(42)

where the function M is defined as in (27) and given by (38). Recall that $M(w_{\mathrm{min}}) >1$ in this example which implies $M(w)>1$ for all $w \ge w_{\mathrm{min}}$ and that the state dynamics (9) converge to the set $[w_{\mathrm{min}}, w_{\mathrm{max}}]$ under any realization of shocks. Thus, the previous transfer scheme can induce a Pareto improvement when introduced once the wage exceeds the critical level $w_{\mathrm{crit}}$ at which $M(w_{\mathrm{crit}})=1$. The intuition is that transfers redistribute incomes from young to old across different states in a clever way which increases utility even if capital formation remains unchanged and an increase in aggregate consumption is not possible. It is precisely this effect we call an ‘improvement in risk sharing.’ The function $\eta$ in Lemmas 8–10 formalizes the idea that finding transfers with the right risk structure characterizes a Pareto improvement in our economy.

4.6 Dynamics along a BME

Suppose the ME $(K_0^{*}, P_0^{*})$ of $\mathscr {E}$ constructed in Theorem 1 is bubbly, i.e., $P_0^{*}>0$. We seek to deduce several qualitative properties of the equilibrium dynamics along a BME.

Given the initial state $x_0 = (k_0, \theta _0) \in \mathbb {X}$, all equilibrium variables can be expressed as continuous functions of the equilibrium wage process $\{w_t\}_{t \ge 0}$ which evolves as

$$\begin{aligned} w_{t+1} = W^\mathrm{E}\left( w_t, \theta _{t+1}\right) := W\left( K_0^{*}(w_t), \theta _{t+1}\right) . \end{aligned}$$

(43)

It will again be convenient to study (43) rather than the mathematically equivalent capital dynamics generated by $K^\mathrm{E} = K_0^{*} \circ W$.

As $P_0^{*}>0$ implies $K_0^{*} < K_0$, a first observation is that $W^\mathrm{E} < W_0^\mathrm{E}$ where the latter is defined in (9). Thus, the sequence generated by (43) is bounded by the wage process (9) along the bubbleless equilibrium under any path of the shock process $\{\theta _t\}_{t \ge 0}$.

A second observation that follows from the Euler equations (3a, 3b) is that in each period the return on the bubbly asset must (weakly) exceed the capital return (1b) in at least one future state. Thus, for each $w \in \mathbb {W}$ there exists some $\theta ' \in \varTheta$ such that

$$\begin{aligned} \frac{P_0^{*}\left( W^\mathrm{E}(w, \theta ')\right) }{P_0^{*}(w)} \ge R\left( K_0^{*}(w), \theta '\right) . \end{aligned}$$

(44)

As $\lim _{w \rightarrow 0} R(K_0^{*}(w), \theta ') = \infty$ for all $\theta ' \in \varTheta$ and the left side in (44) is increasing in the shock, there exists a lower bound $\underline{w}'>0$ such that $R(K_0^{*}(w), \theta _{\mathrm{min}})>1$ and $P_0^{*}(W^\mathrm{E}(w, \theta _{\mathrm{max}})) > P_0^{*}(w)$ for all $w\le \underline{w}'$. Thus, by monotonicity of $P_0^{*}$

$$\begin{aligned} W^\mathrm{E}(w, \theta _{\mathrm{max}}) > w \end{aligned}$$

(45)

for all $w\le \underline{w}'$. As $W^\mathrm{E}(w_{\mathrm{max}},\theta _{\mathrm{max}}) < W_0^\mathrm{E}(w_{\mathrm{max}},\theta _{\mathrm{max}}) = w_{\mathrm{max}}$, (45) also shows that $W^\mathrm{E}(\cdot , \theta _{\mathrm{max}})$ has at least one stable fixed point which lies in the interval $]\underline{w}', w_{\mathrm{max}}[$. In fact, since $\theta _{\mathrm{max}}$ belongs to the support of $\nu$, (45) and continuity of $W^\mathrm{E}$ imply that for each $w\le \underline{w}'$ there exists a measurable set $\varTheta _w \subset \varTheta$ of positive measure $\nu (\varTheta _w)>0$ such that $W^\mathrm{E}(w, \theta ) > w$ holds for all $\theta \in \varTheta _w$. Thus, defining $\underline{p}^{*}:= P_0^{*}(\underline{w}')$, one observes that the bubbly asset price process $\{p_t\}_{t\ge 0}$ along the BME is persistent in the sense that whenever $p_t < \underline{p}^{*}$ there is a positive probability that $p_{t+n} > \underline{p}^{*}$ for some finite $n \ge 1$.

An open question is whether this last result can be strengthened in the sense that $p_t < \underline{p}^{*}$ implies $p_{t+n} > \underline{p}^{*}$ for some finite $n \ge 1$ with probability one. Essentially, this holds when the wage dynamics (43) admits a uniform lower bound $\underline{w}'>0$ such that $W^\mathrm{E}(w, \theta )>w$ for all $\theta \in \varTheta$ whenever $w\le \underline{w}'$. Example 1 from Sect. 4.5 satisfies this condition. If such a lower bound exists, the bubble price processes and in fact all equilibrium variables remain bounded away from zero with probability one. Clearly, Assumption 5 is a necessary precondition for this to hold, but is it sufficient? This question becomes particularly relevant for studying the existence of stationary distributions associated with the state process defined by (43) which we leave for future research.

4.7 Stochastically bursting bubbles

By construction, the bubble along a BME never bursts. Asset bubbles which have a constant probability of bursting in each period were first studied in Weil (1987) using an otherwise deterministic framework similar to Tirole (1985). It is now straightforward to modify the previous setting along these lines to study ME with bursting bubbles in our setup as well.

Setting $d=0$, suppose that in each period t, there is a constant exogenous probability for the bubble to burst in the following period. Thus, the future selling price of the bubbly asset in period t is $p_{t+1}$ with some probability q and zero otherwise. Under this modification, the equilibrium mappings (14a) and (14b) now take the following form (with q replacing the dividend parameter $d=0$)

$$\begin{aligned} H^1 (k, p; w, P, q) =&\, u'(w - p - k) - q \mathbb {E}_{\nu } \left[ R (k, \cdot ) v' \left( P\left( W(k, \cdot )\right) + k R (k, \cdot ) \right) \right] \nonumber \\&- (1- q) \mathbb {E}_{\nu } \left[ R (k, \cdot ) v' \left( k R (k, \cdot ) \right) \right] \end{aligned}$$

(46a)

$$\begin{aligned} H^2 (k, p; w, P, q) =&\, u'(w - p - k) p \nonumber \\&- q \mathbb {E}_{\nu } \left[ \left( P\left( W(k, \cdot )\right) \right) v' \left( P\left( W(k, \cdot )\right) + k R (k, \cdot ) \right) \right] . \end{aligned}$$

(46b)

The case studied in the previous sections is recovered by setting $q=1$.

It seems now straightforward to repeat the entire analysis of Sect. 3 based on (46a) and (46b) rather than (14a) and (14b) and construct such modified Markov equilibria for $q<1$ as fixed points of some operator $T_{q}:\mathscr {G} \longrightarrow \mathscr {G}$ defined by (46a) and (46b) in the exact same fashion as before. As establishing the rather technical Lemmas 2.1–2.4 for the case $q<1$ seems quite tedious, we choose not to work through this case here.

We will, however, show that our existence result derived above for $q=1$ does not necessarily imply the existence of a BME for any $q<1$. To show this, we focus on the first example discussed in Sect. 4.5 where $f(k) = k^{\alpha }$, $0<\alpha <1$, $u(c)=\log (c)$, and $v(c) = \beta u(c)$, $\beta >0$. Clearly, the bubbleless equilibrium is exactly the same as before and is inefficient if and only if $R_{\mathrm{max}} =\frac{1+\beta }{\beta } \frac{\alpha }{1-\alpha } <1$.

Applying the construction principle from Sect. 3.3 for $T_q$, set $P_0 = {\mathrm{id}}_{\mathbb {W}}$ and consider the sequence $(P_n)_{n \ge 0}$ defined as $P_n=T_q(P_{n-1})$, $n \ge 1$. In this example, the operator $T_q$ again maps linear functions onto linear functions and can be derived explicitly. One verifies that $P(w) = \delta w$, $\delta \ge 0$ implies $T_qP(w)=[R_{\mathrm{max}}/q + \delta \frac{1+\beta }{\beta q}]^{-1}P(w)$ for $w \in \mathbb {W}$. Thus, each $P_n$ is linear and can be computed explicitly as

$$\begin{aligned} P_n(w) = \dfrac{w}{(R_{\mathrm{max}}/q)^n + \frac{1+\beta }{\beta q} \sum _{m=0}^{n-1} (R_{\mathrm{max}}/q)^m},\quad n \ge 0. \end{aligned}$$

For each $w \in \mathbb {W}$, the pointwise limit $P_0^{*}(w) := \lim _{n \rightarrow \infty } P_n(w)$ is given by

$$\begin{aligned} P_0^{*}(w) = \left\{ \begin{array}{cl} \left( \frac{\beta }{1+\beta }q - \frac{\alpha }{1-\alpha }\right) w &{}\quad \text{ if } R_{\mathrm{max}} <q \\ 0 &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

(47)

Thus, in this example a BME with $q<1$ exists if and only if $R_{\mathrm{max}} < q$. While this restriction also requires inefficiency of the bubbleless equilibrium, the probability of bursting $1-q$ must, in addition, be sufficiently small. Essentially the same result is obtained in Weil (1987) for a deterministic economy. We conjecture that a similar conclusion also holds in the general case and that only stochastic bubbles which enjoy a sufficiently high level of confidence can occur in Pareto inefficient economies.

5 Conclusions

This paper developed a general approach to construct potentially bubbly Markov equilibria for a general class of frictionless OLG economies with stochastic production. Our main result shows that a BME exists whenever the bubbleless equilibrium is inefficient. This type of inefficiency can be the result of an overaccumulation of capital but also due to inefficient risk sharing between consumers. The deterministic result of Tirole (1985) therefore constitutes a special case of our existence theorem. Our existence result also completes the characterization of the equilibrium set for the class of economies studied in Wang (1993) and related papers by providing conditions under which additional bubbly equilibria exist in these models.

To focus on this existence result and keep the technical part bearable, we deliberately limited the underlying class of economies to a setup with i.i.d. TFP shocks and additive consumer utility. We believe that these restrictions are inessential and easy to dispense with at a cost of a more complex structure and notation. Potential extensions of the previous framework include non-additive utility, non-multiplicative and correlated production shocks, and non-classical production technologies. Models with these features were employed, for example, in Wang (1994), Morand and Reffett (2007), McGovern et al. (2013), or Hillebrand (2014) to study the existence and properties of bubbleless ME. Since all these papers rely on methods similar to those employed in this paper, we believe that the previous construction of a BME should be amendable to these extensions. This constitutes a first major objective of future research.

In addition, several issues remain to be studied even within the framework of this paper. For instance, an open question is if the bubbly equilibrium is always efficient and, related to that, whether it constitutes a Pareto improvement relative to the bubbleless equilibrium. The characterization of Pareto optimality developed in Sect. 4 should be key to answer these questions. Another avenue of future research is whether the state dynamics along the BME converge to a stationary distribution on the endogenous state space. Since our equilibrium mappings are all monotonic, we view the recent results of Kamihigashi and Stachurski (2014) as tailor-made for studying the existence, uniqueness, and stability of stationary distributions along a BME.

Appendices

A Mathematical Appendix

1.1 A.1 Proof of Lemma 1

For convenience, define the numerator in (b) as $D(k) := \mathbb {E}_{\nu }[R(k, \cdot )v'(k R(k, \cdot ))]$ which, as shown in the proof of Lemma 3 below is strictly decreasing under property (U) from Assumption 2. Conditions (a) and (b) permit to choose a lower bound $\underline{k}>0$ such that $W(k, \theta _{\mathrm{min}})>k$ and $H(k) := u'(W(k, \theta _{\mathrm{min}}) - k) - D(k) < 0$ for all $0<k \le \underline{k}$. Now define $\underline{w} := W(\underline{k},\theta _{\mathrm{min}})$ and choose an arbitrary value $\hat{w} \in ]0, \underline{w}]$. By monotonicity of W, there exists a unique $\hat{k} \in ]0, \underline{k}]$ such that $W(\hat{k}, \theta _{\mathrm{min}}) = \hat{w}$. Then, $H(\hat{k})<0$ and the properties of D and $u'$ permit to choose a unique $\hat{k}_1$ such that $\hat{k}<\hat{k}_1<\hat{w}$ and $u'(\hat{w} - \hat{k}_1) = D(\hat{k}_1)$ which is equivalent to $\hat{k}_1 = K_0(\hat{w})$ defined by (7). Then, by monotonicity of $W(\cdot , \theta _{\mathrm{min}})$,

$$\begin{aligned} \hat{w} = W\left( \hat{k}, \theta _{\mathrm{min}}\right) < W\left( \hat{k}_1, \theta _{\mathrm{min}} \right) = W\left( K_0(\hat{w}), \theta _{\mathrm{min}} \right) = W_0^\mathrm{E}\left( \hat{w}, \theta _{\mathrm{min}}\right) . \end{aligned}$$

Since $\hat{w} \in ]0, \underline{w}]$ was arbitrary, this proves Assumption 5. $\square$

1.2 A.2 Proof of Lemma 2

By (1), $\frac{f(k)}{k f'(k)} = \frac{W(k, \theta _{\mathrm{min}})}{k R(k, \theta _{\mathrm{min}})}+1$. Thus, NLS implies $\liminf _{k \searrow 0} \frac{W(k, \theta _{\mathrm{min}})}{k R(k, \theta _{\mathrm{min}})}>0$. Using this and the boundary behavior of R, we can choose values $\bar{B}> 1> \bar{b}>0$ and a lower bound $\underline{k}_1>0$ such that $R(k, \theta _{\mathrm{min}})> \frac{\bar{B}}{\bar{b}}$ and $W(k, \theta _{\mathrm{min}})> \bar{b} R(k, \theta _{\mathrm{min}}) k > \bar{B} k$ for all $0<k \le \underline{k}_1$. Clearly, this implies $\liminf _{k \searrow 0} \frac{W(k, \theta _{\mathrm{min}})}{k} > \bar{B}$ and condition (a).

To establish (b), suppose first that $u = \beta ^{-1} v$. Note that $\liminf _{k \searrow 0} \frac{W(k, \theta _{\mathrm{min}})}{k R(k, \theta _{\mathrm{min}})}>0$ and $\lim _{k \searrow 0} \frac{k}{k R(k, \theta _{\mathrm{min}})}=0$ imply $\liminf _{k \searrow 0} \frac{W(k, \theta _{\mathrm{min}}) - k}{k R(k, \theta _{\mathrm{min}})}>0$. Thus, there exists $0<\underline{k}_{2} \le \underline{k}_1$ and $\bar{b}_1>0$ such that for all $0<k \le \underline{k}_{2}$ we have

$$\begin{aligned} W(k, \theta _{\mathrm{min}}) - k \ge \bar{b}_1 k R(k, \theta _{\mathrm{min}}). \end{aligned}$$

(A.1)

Suppose $\bar{b}_1 \ge 1$. Then, $u'(W(k, \theta _{\mathrm{min}}) - k) \le u'(k R(k, \theta _{\mathrm{min}}))$ for all $0<k \le \underline{k}_{2}$ yields

$$\begin{aligned} \liminf _{k \searrow 0} \frac{v'\left( k R\left( k, \theta _{\mathrm{min}}\right) \right) }{u'\left( W\left( k, \theta _{\mathrm{min}}\right) -k\right) } \ge \frac{1}{\beta } >0. \end{aligned}$$

Second, suppose $\bar{b}_1 <1$. From Assumption 2 (which holds for $u=\beta ^{-1} v$), we infer that

$$\begin{aligned} \bar{b}_1 u'\left( W\left( k, \theta _{\mathrm{min}}\right) - k\right) \le u'\left( \bar{b}_1^{-1}\left( W\left( k, \theta _{\mathrm{min}}\right) - k\right) \right) \end{aligned}$$

(A.2)

for all $0<k \le \underline{k}_{2}$. To see this, define for fixed $c>0$ the map $H(a) := a v'(a c)$. Then, $H(1) = v'(c)$ and $H'(a) = v'(ac) + ac v''(ac) \ge 0$. Thus, H is non-decreasing and $H(a)\ge H(1)$ for all $a>1$. Setting $c = W(k, \theta _{\mathrm{min}}) - k$ and $a=\bar{b}_1^{-1}>1$, this proves (A.2) which, combined with (A.1), gives

$$\begin{aligned} \bar{b}_1 u'\left( W\left( k, \theta _{\mathrm{min}}\right) - k\right) \le u'\left( \bar{b}_1^{-1}\left( W\left( k, \theta _{\mathrm{min}}\right) - k\right) \right) \le u'\left( k R\left( k, \theta _{\mathrm{min}}\right) \right) \end{aligned}$$

(A.3)

for all $0<k \le \underline{k}_{2}$ which implies

$$\begin{aligned} \liminf _{k \searrow 0} \frac{v'\left( k R(k, \theta _{\mathrm{min}})\right) }{u'\left( W(k, \theta _{\mathrm{min}})-k\right) } \ge \frac{\bar{b}_1}{\beta } >0. \end{aligned}$$

Finally, let $f(0)>0$. Then, NLS implies $\lim _{k \searrow 0} W(k, \theta _{\mathrm{min}}) = \theta _{\mathrm{min}} f(k) (1 - \frac{k f'(k)}{f(k)}) >0$ and, therefore, $\lim _{k \searrow 0} u'(W(k, \theta _{\mathrm{min}})-k) >0$ in (12). As the numerator diverges, this implies (b). $\square$

1.3 A.3 Proof of Lemma 3

Let $P\in \mathscr {G}$ be given and $w\in \mathbb {W}$ be arbitrary but fixed. For each $k \in \mathbb {K}=]0, k_{\mathrm{max}}]$ and $\theta \in \varTheta$, set $c(k, \theta ) := P(W(k, \theta ) ) + k R (k, \theta ).$ Define the functions

$$\begin{aligned} V(k) := \dfrac{\mathbb {E}_{\nu } \bigl [ P(W(k,\cdot ) ) v' \bigl ( c(k,\cdot ) \bigr ) \bigr ] }{\mathbb {E}_{\nu } \bigl [ R (k,\cdot ) v' \bigl ( c(k,\cdot ) \bigr ) \bigr ] } =: \frac{N(k)}{D(k) } , \quad k \in \mathbb {K} \end{aligned}$$

(A.4)

and

$$\begin{aligned} S(k) := k + V(k) = \dfrac{\mathbb {E}_{\nu } \bigl [ c(k,\cdot )v'\bigl ( c(k,\cdot ) \bigr ) \bigr ] }{\mathbb {E}_{\nu } \bigl [ R (k,\cdot ) v'\bigl ( c(k,\cdot ) \bigr ) \bigr ] } =: \frac{M(k) }{D(k) }, \quad k \in \mathbb {K}. \end{aligned}$$

(A.5)

Since P is continuous, so are the mappings V, N, D, L, and S. The first part of the proof establishes certain monotonicity properties and the boundary behavior of the previously defined functions. First, we will show that D is strictly decreasing and S is strictly increasing. Fixing an arbitrary interior point $k \in \mathbb {K}$, it suffices to show $D(k+\Delta )< D(k)$ and $S(k+\Delta )> S(k)$ for any $0<\Delta \le k_{\mathrm{max}} - k$. Since P and W and are weakly increasing and $v'$ strictly decreasing,

$$\begin{aligned} D(k+ \Delta ) \le \tilde{D}(\Delta ) := \mathbb {E}_{\nu } \bigl [ R (k+\Delta ,\cdot ) v'\bigl ( \tilde{c}(\Delta , \cdot ) \bigr ) \bigr ] \end{aligned}$$

(A.6)

where $\tilde{c}(\Delta , \theta ) := P(W(k, \theta ) ) + (k+\Delta ) R (k+\Delta , \theta )$. Likewise, property (U) from Assumption 2 implies that the map $a \mapsto (a+b) v'( a + b)$, $a>0$ is weakly increasing for any $b \ge 0$. Therefore,

$$\begin{aligned} M(k+\Delta ) \ge \tilde{M}(\Delta ) := \mathbb {E}_{\nu } \bigl [ \tilde{c}(\Delta , \cdot ) v'\bigl ( \tilde{c}(\Delta , \cdot ) \bigr ) \bigr ]. \end{aligned}$$

(A.7)

This and (A.6) combined show that

$$\begin{aligned} S(k+\Delta ) \ge \tilde{S}(\Delta ) := \frac{\tilde{M}(\Delta )}{\tilde{D}(\Delta )}. \end{aligned}$$

(A.8)

Since $\tilde{D}(0) = D(k)$ and $\tilde{S}(0) = S(k)$, it suffices to establish monotonicity of $\tilde{D}$ and $\tilde{S}$. The major advantage is that, unlike L, D, and S, the maps $\tilde{L}$, $\tilde{D}$, and $\tilde{S}$ are all differentiable. Dropping arguments when convenient, the derivative of $\tilde{D}$ computes

$$\begin{aligned} \nonumber \tilde{D}'(\Delta )= & {} -\frac{E_{f'}(k+\Delta )}{k+\Delta }\mathbb {E}_{\nu } \Bigl [ R (k+\Delta ,\cdot ) \bigl (v'(\cdot ) - (k+\Delta ) R(k+\Delta , \cdot ) |v''(\cdot )| \bigr ) \Bigr ] \\&-\, \mathbb {E}_{\nu } \bigl [ R (k+\Delta ,\cdot )^2 |v''(\cdot )| \bigr ] \end{aligned}$$

(A.9)

where we have used that $\partial _{\Delta }\tilde{c}(\Delta , \theta ) = R (k+\Delta , \theta )(1 - E_{f'}(k+\Delta ))$. Property (U) from Assumption (2) implies that the expectation in the first term is nonnegative and, therefore, $\tilde{D}'(\Delta )<0$ and monotonicity of D. By (A.8), the sign of $\tilde{S}'$ is determined by $H(\Delta ) := (k+\Delta )\bigl (\tilde{M}'(\Delta ) \tilde{D}(\Delta ) - \tilde{M}(\Delta ) \tilde{D}'(\Delta )\bigr )$. Noting that $\tilde{M}(\Delta ) \ge (k+\Delta ) \tilde{D}(\Delta )$ and using $\tilde{D}'(\Delta )<0$, it suffices to show that $\tilde{M}'(\Delta ) > (k+\Delta ) \tilde{D}'(\Delta )$. The derivative of $\tilde{M}$ computes as

$$\begin{aligned} \tilde{M}'(\Delta ) = \left( 1-E_{f'}(k+\Delta )\right) \mathbb {E}_{\nu } \Bigl [ R (k+\Delta ,\cdot ) \bigl (v'(\cdot ) - \tilde{c}(\Delta , \cdot ) |v''(\cdot )| \bigr ) \Bigr ] \end{aligned}$$

(A.10)

For brevity, define

$$\begin{aligned} A_1(\Delta ):= & {} \mathbb {E}_{\nu } \Bigl [ R (k+\Delta ,\cdot ) \bigl (v'(\cdot ) - \tilde{c}(\Delta , \cdot ) |v''(\cdot )| \bigr ) \Bigr ] \\ A_2(\Delta ):= & {} \mathbb {E}_{\nu } \Bigl [ R (k+\Delta ,\cdot ) \bigl (v'(\cdot ) - (k+\Delta ) R(k+\Delta , \cdot ) |v''(\cdot )| \bigr ) \Bigr ]. \end{aligned}$$

Note that property (U) from Assumption 2 implies $0 \le A_1(\Delta ) \le A_2(\Delta )$. Further, note from (A.9) that $-(k+\Delta )\tilde{D}'(\Delta ) > E_{f'}(k+\Delta ) A_2(\Delta )$. Using this property and (A.10) gives the desired result

$$\begin{aligned} \tilde{M}'(\Delta ) - (k+\Delta ) \tilde{D}'(\Delta )> A_1(\Delta ) + E_{f'}(k+\Delta )\left( A_2(\Delta ) - A_1(\Delta ) \right) > 0. \end{aligned}$$

Since $\varTheta$ is compact and $k \le k_{\mathrm{max}}$, consumption $c(k, \theta )$ is uniformly bounded from above (e.g., by $c_{\mathrm{max}}:= P(w_{\mathrm{max}}) + \theta _{\mathrm{max}} f(k_{\mathrm{max}})$) and so is M defined in (A.5) (e.g., by $c_{\mathrm{max}} v'(c_{\mathrm{max}})$). The boundary conditions from Assumptions 1 and 2 then imply

$$\begin{aligned}&\lim _{k \searrow 0} D(k) = \infty . \end{aligned}$$

(A.11)

$$\begin{aligned} \quad \hbox {and}\quad \quad \quad 0\le & {} \lim _{k \searrow 0} V(k) \le \lim _{k \searrow 0} S(k) =\lim _{k \searrow 0}\frac{M(k) }{D(k) } = 0. \end{aligned}$$

(A.12)

Having established the properties necessary for the proof, define

$$\begin{aligned} G(k;w) := u'\left( w - S(k)\right) - D(k). \end{aligned}$$

(A.13)

Then, the desired solution $\tilde{k}$ solves $G(\tilde{k}; {w})=0$. Observe that $G(\cdot ; w)$ is a strictly increasing function which follows from the monotonicity of S and D and $u'$. Thus, any zero is necessarily unique. Also observe the boundary behavior $\lim _{k \searrow 0}G(k; w) = -\infty$ due to (A.11). By continuity, it suffices to find a $k < w$ such that $G(k; w) \ge 0$. Suppose $P \equiv 0$. Then, the solution is $\tilde{k} = k_0 := K_0(w)$ defined by (7) and $\tilde{p} =0$. If $P \ne 0$, consider the following two cases. First, $S(k_0) \ge w$. Then, by (A.12) and monotonicity and continuity of S, there exists a unique value $0<\hat{k} \le k_0$ such that $S(\hat{k})=w$ which implies $\lim _{k \nearrow \hat{k}}G(k; w) = \infty$. Second, suppose $S(k_0) < w$. Then, $\lim _{k \nearrow k_0}G(k; w) = u'(w - S(k_0)) - D(k_0) \ge G_0(k_0; w) =0$ with $G_0$ defined by (7). Thus, in either case, there exists a solution $0<\tilde{k} \le k_0 < w$. Setting $\tilde{p}= V(\tilde{k})$ completes the proof. $\square$

1.4 A.4 Proof of Lemma 4

Let $P \in \mathscr {G}$ be arbitrary. As shown in the previous proof, $T P = V \circ K_{P}$ where V is defined in (A.4) and, for $w \in \mathbb {W}$, $k = K_{P}(w)$ is the unique solution to $G(k; w) = 0$ defined in (A.13). Clearly, $K_P$ is continuous. Note from (A.4) that $T P \ge 0$, $P >0$ implies $T P >0$ and $P =0$ implies $T P =0$. As G in (A.13) is increasing in P and V, $K_P \le K_0$ for all P with strict inequality if $P>0$. By definition of $K_{P}$ and (A.13), $w> S(K_{P}(w)) > V(K_{P}(w)) = T P (w)$ for $w \in \mathbb {W}$ which proves $TP < \mathrm{id}_{\mathbb {W}}$.

To show that $w \mapsto w - T P (w)$ is (even strictly) increasing, let $w \in \mathbb {W}$ be an arbitrary interior point and choose $\Delta >0$ such that $w + \Delta \in \mathbb {W}$. We show that $T P (w + \Delta ) < T P (w) + \Delta$. By contradiction, suppose $T P (w + \Delta ) \ge T P (w) + \Delta$. Note that G defined in (A.13) is strictly decreasing in w and strictly increasing in k by strict monotonicity of D and S. These properties imply that $K_{P}$ is strictly increasing which gives $K_{P}(w + \Delta ) > K_{P}(w)$. Further, as shown in the previous proof, the function D defined in (A.5) is strictly decreasing which gives $D(K_{P}(w+ \Delta ))<D(K_{P}(w))$. But by (A.13) and our hypothesis

$$\begin{aligned} D\left( K_{P}(w + \Delta )\right)= & {} u'\left( w + \Delta - T P (w + \Delta ) - K_{P}(w+\Delta ) \right) \\\ge & {} u'\left( w - T P (w) - K_{P}(w+\Delta )\right) \\> & {} u'\left( w - T P (w) - K_{P}(w)\right) \\= & {} D(K_{P}(w)) \end{aligned}$$

which is a contradiction and proves that $w \mapsto w - T P (w)$ is increasing.

Next, we show that TP is increasing. As $T P = V \circ K_{P}$ and we have already shown that $K_{P}$ is strictly increasing, it remains to show that V defined in (A.4) is increasing as well. To avoid trivialities, assume in the remainder that $P>0$. Adjusting the arguments to the case where $P \ge 0$ is straightforward. Let $k \in \mathbb {K}$ be an arbitrary but fixed interior point. We show that $V(k + \Delta ) \ge V(k )$ for any $0<\Delta < k_{\mathrm{max}} - k$. By property (U) from Assumption 2, the map $a \mapsto a v'( a + b)$, $a>0$ is increasing for any $b \ge 0$. Thus, by monotonicity of $P \circ W$ the numerator in (A.4) satisfies

$$\begin{aligned} N(k+\Delta ) \ge \tilde{N}(\Delta ) := \mathbb {E}_{\nu } \bigl [ P(W(k,\cdot ) ) v' \bigl ( P(W, k, \cdot ) + (k+\Delta ) R(k+\Delta , \cdot ) \bigr ) \bigr ].\nonumber \\ \end{aligned}$$

(A.14)

Furthermore, by Eq. (A.6), the denominator in (A.4) satisfies $D(k+\Delta ) \le \tilde{D}(\Delta )$. Thus, defining $\tilde{V}(\Delta ):= \frac{\tilde{N}(\Delta )}{\tilde{N}(\Delta )}$, we have $V(k+\Delta ) \ge \tilde{V}(\Delta )$ and $\tilde{V}(0) = V(k)$. It therefore suffices to show that $\tilde{V}$ is increasing. Observe that unlike V, $\tilde{V}$ is $C^1$ and, by direct computation, the derivative satisfies $\tilde{V}'(\Delta ) \ge 0$, if and only if

$$\begin{aligned} A(\Delta ) := (k+\Delta )^2 \tilde{N}'(\Delta ) \tilde{D}(\Delta ) - (k+\Delta )^2 \tilde{D}'(\Delta ) \tilde{N}(\Delta ) \ge 0. \end{aligned}$$

(A.15)

To establish that $A(\Delta ) \ge 0$, let $0<\Delta \le k_{\mathrm{max}} -k$ be arbitrary but fixed and, for the sake of brevity, define the nonnegative random variables

$$\begin{aligned} X:= & {} (k+\Delta )R(k+\Delta , \cdot ) |v''(P(k,\cdot ) + (k+\Delta )R(k+\Delta ,\cdot ))|^{\frac{1}{2}} \end{aligned}$$

(A.16a)

$$\begin{aligned} Y:= & {} P(k,\cdot ) |v''(P(k,\cdot ) + (k+\Delta )R(k+\Delta , \cdot ))|^{\frac{1}{2}} \end{aligned}$$

(A.16b)

both defined on the probability space $(\varTheta , \mathscr {B}(\varTheta ), \nu )$. Then, by direct computation again, the derivative of $\tilde{N}$ defined in (A.14) can be expressed as

$$\begin{aligned} (k+\Delta ) \tilde{N}'(\Delta ) = -(1- E_{f'}(k+\Delta )) \mathbb {E}_{\nu } \bigl [ X Y \bigr ] \end{aligned}$$

(A.17)

while the derivative of $\tilde{D}$ computed in (A.9) satisfies

$$\begin{aligned} -(k+\Delta )^2 \tilde{D}'(\Delta ) = E_{f'}(k+\Delta ) (k+\Delta ) \tilde{D}(\Delta ) + (1- E_{f'}(k+\Delta ))\mathbb {E}_{\nu }[X^2].\nonumber \\ \end{aligned}$$

(A.18)

Suppose $E_{f'}(k+\Delta ) \ge 1$. Then, by (A.17) $\tilde{N}'(\Delta ) \ge 0$ while, as shown in (A.9), $\tilde{D}'(\Delta ) < 0$. Thus, all terms in (A.15) are positive implying $A(\Delta )>0$ in this case. Therefore, the remainder assumes $E_{f'}(k+\Delta ) < 1$. Note from (4) that $\tilde{N}(\Delta ) \ge \frac{\mathbb {E}_{\nu }[Y^2 + XY]}{E_{v'}^{\mathrm{max}}} \ge \frac{\mathbb {E}_{\nu }[XY]}{E_{v'}^{\mathrm{max}}}$. Using this together with (A.17) and (A.18) in (A.19) gives

$$\begin{aligned} A(\Delta )\ge & {} - (k+\Delta ) \tilde{D}(\Delta )\mathbb {E}_{\nu } \bigl [ X Y \bigr ] \left( 1- E_{f'}(k+\Delta )\frac{1+E_{v'}^{\mathrm{max}}}{E_{v'}^{\mathrm{max}}}\right) \nonumber \\&+\, B(\Delta ) \end{aligned}$$

(A.19)

where

$$\begin{aligned} B(\Delta ) := \frac{\mathbb {E}_{\nu }[Y^2 + XY]\mathbb {E}_{\nu }[X^2]}{E_{v'}^{\mathrm{max}}}\left( 1- E_{f'}(k+\Delta )\right) . \end{aligned}$$

(A.20)

By Hölder’s inequality [see Aliprantis and Border (2007, p. 463) for the special case $p=q =2$ implying $\frac{1}{p} + \frac{1}{q} =1$], we have $\mathbb {E}_{\nu } \bigl [{X}^2 \bigr ] \mathbb {E}_{\nu } \bigl [{Y}^2 \bigr ] \ge (\mathbb {E}_{\nu } \bigl [{X}Y \bigr ])^2$ which implies $\mathbb {E}_{\nu }[Y^2 + XY]\mathbb {E}_{\nu }[X^2] = \mathbb {E}_{\nu }[Y^2]\mathbb {E}_{\nu }[X^2] + \mathbb {E}_{\nu }[ XY]\mathbb {E}_{\nu }[X^2] \ge \mathbb {E}_{\nu }[XY]\mathbb {E}_{\nu }[X (Y+X)]$. Further, using (A.16) and the bounds defined in (4) gives $\mathbb {E}_{\nu }[X (X+Y)]\ge E_{v'}^{\mathrm{min}} (k+\Delta ) \tilde{D}(\Delta )$. Using both results in (A.20) gives

$$\begin{aligned} B(\Delta ) \ge \frac{(k+\Delta ) \tilde{D}(\Delta ) \mathbb {E}_{\nu }[XY]E_{v'}^{\mathrm{min}}}{E_{v'}^{\mathrm{max}}}(1- E_{f'}(k+\Delta )). \end{aligned}$$

(A.21)

Finally, using (A.21) in (A.19) gives the desired result

$$\begin{aligned} A(\Delta )\ge & {} - \frac{(k+\Delta ) \tilde{D}(\Delta )\mathbb {E}_{\nu } \bigl [ X Y \bigr ]}{E_{v'}^{\mathrm{max}}} \left( E_{v'}^{\mathrm{max}}- E_{v'}^{\mathrm{min}} - E_{f'}(k+\Delta ) (1 + E_{v'}^{\mathrm{max}}- E_{v'}^{\mathrm{min}}\right) \\\ge & {} 0 \end{aligned}$$

where the last inequality follows from condition (5) in Assumption 3. This proves that $\tilde{V}$ is weakly increasing which implies the desired result $V(k + \Delta ) \ge \tilde{V}(\Delta ) \ge \tilde{V}(0) = V(k)$. Finally, adopting an argument used and proved in Morand and Reffett (2003, p. 1360), monotonicity of TP and $w \mapsto w - T P(w)$, $w \in \mathbb {W}$ imply continuity of TP. $\square$

1.5 A.5 Proof of Lemma 5

Let $P \in \mathscr {G}'$ be arbitrary. We need to show that TP is $C^1$. Since P is $C^1$, so are the mappings $\tilde{P}$, S, D, and $\tilde{N}$ defined in (A.4) and (A.5) and G defined in (A.13). Recall that for each $w \in \mathbb {W}$, $K_{P}$ determines the unique zero of $G(\cdot ; w)$. Since $\partial _k G (k;w) >0$, $K_{P}$ is $C^1$ by the implicit function theorem. Thus, $T P = \tilde{P} \circ K_{P}$ is $C^1$ as well.$\square$

1.6 A.6 Proof of Lemma 6

We only prove the strict inequalities, as the proof of the weak inequalities is analogous. Given $P_1, P_0 \in \mathscr {G}'$, suppose $P_1 > P_0$. For $\lambda \in [0,1]$, define $P_{\lambda }:= \lambda P_1 + (1-\lambda ) P_0$. Since $\mathscr {G}'$ is convex, $P_{\lambda } \in \mathscr {G}'$ and, using the monotonicity properties in (13), the derivative satisfies $0 \le P_{\lambda }' \le 1$ for all $\lambda$. Moreover, the map $\lambda \mapsto P_{\lambda } = P_0 + \lambda \Delta$ where $\Delta := P_1 -P_0 >0$ is strictly increasing (with respect to the pointwise ordering on $\mathscr {G}$).

Let $w \in \mathbb {W}$ be arbitrary but fixed. By Lemma 3 (and a slight abuse of notation), for each $\lambda \in [0,1]$ there exists a unique pair $(k_{\lambda }, p_{\lambda })$ which solves $H_1(k_{\lambda }, p_{\lambda }; w, \lambda ) = H_2(k_{\lambda }, p_{\lambda }; w, \lambda ) =0$. We will now show that $\lambda \mapsto k_{\lambda }$, $\lambda \in [0,1]$ is strictly decreasing and $\lambda \mapsto p_{\lambda }$, $\lambda \in [0,1]$ is strictly increasing. This implies $p_1 > p_0$ and $k_1 < k_0$ and the claim.

Employing the same definitions and notation as in the proof of Lemma 3, write $c_{\lambda }(k, \theta ) := P_{\lambda }(W(k, \theta )) + k R(k, \theta )$. Then, the pair $(k_{\lambda }, p_{\lambda })$ satisfies $p_{\lambda } = \tilde{P}(k_{\lambda }, \lambda )$ where

$$\begin{aligned} \tilde{P}(k, \lambda ) := \dfrac{\mathbb {E}_{\nu } \bigl [ P_{\lambda }(W(k, \cdot ) ) v' \bigl ( c_{\lambda }(k, \cdot ) \bigr ) \bigr ] }{\mathbb {E}_{\nu } \bigl [ R (k, \cdot ) v' \bigl ( c_{\lambda }(k, \cdot ) \bigr ) \bigr ] } =: \frac{{N}(k, \lambda )}{ {D}(k, \lambda )}, \quad k \in \mathbb {K}, \lambda \in [0,1].\qquad \quad \end{aligned}$$

(A.22)

To compute the partial derivatives of D and N, note that $\partial _k W(k, \theta ) = E_{f'}(k) R(k, \theta ) >0$ by (1a, 1b) which implies

$$\begin{aligned} \partial _k c_{\lambda }(k,\theta ) = R(k, \theta ) \bigl ( E_{f'}(k) P_{\lambda }'(-) + 1 - E_{f'}(k)) \ge - R(k, \theta )E_{f'}(k).\quad \end{aligned}$$

(A.23)

Taking the derivative of (A.22) one obtains, exploiting property (U) and suppressing arguments when convenient

$$\begin{aligned} \partial _k {N}(k, \lambda )= & {} \mathbb {E}_{\nu } \Bigl [ P_{\lambda }'(\cdot ) E_{f'}(k) R(k,\cdot ) v'(\cdot ) - P_{\lambda }(\cdot )|v''(\cdot )|\partial _k c_{\lambda }(k,\cdot ) \Bigr ]\end{aligned}$$

(A.24)

$$\begin{aligned} \partial _{\lambda }{N}(k, \lambda )= & {} \mathbb {E}_{\nu } \bigl [\Delta (k,\cdot )\bigl ( v'(\cdot ) -P_{\lambda }(W(k,\cdot ) ) |v''(\cdot )| \bigr ) \bigr ] >0 \end{aligned}$$

(A.25)

$$\begin{aligned} \partial _k {D}(k, \lambda )= & {} -\frac{1}{k}\mathbb {E}_{\nu } \Bigl [E_{f'}(k) R(k,\cdot ) v'(\cdot ) + k R(k,\cdot ) |v''(\cdot )|\partial _k c_{\lambda }(k,\cdot ) \Bigr ] \end{aligned}$$

(A.26)

$$\begin{aligned} \partial _{\lambda }{D}(k, \lambda )= & {} -\mathbb {E}_{\nu } \bigl [\Delta (k,\cdot ) R (k,\cdot ) |v'' (\cdot )| \bigr ] <0 \end{aligned}$$

(A.27)

where $\Delta (k, \theta ):= P_1(W(k, \theta )) - P_0(W(k, \theta ))>0$ for all $k \in \mathbb {K}$ and $\theta \in \varTheta$. Using (A.23) and property (U) from Assumption 2 in (A.26), we infer that

$$\begin{aligned} \partial _k {D}(k, \lambda ) < -\frac{E_{f'}(k)}{k}\mathbb {E}_{\nu } \Bigl [R(k,\cdot ) \Bigl (v'(\cdot ) - k R(k,\cdot ) |v''(\cdot )|\Bigr ) \Bigr ] \le 0. \end{aligned}$$

(A.28)

We show that $\frac{\hbox {d} k_{\lambda }}{\hbox {d} \lambda }<0$. As $k_{\lambda }$ is the unique solution to $G(k,\lambda ) := u'(w-k-\tilde{P}(k, \lambda )) - {D}(k, \lambda )=0$, the implicit function theorem yields the derivative

$$\begin{aligned} \frac{\hbox {d} k_{\lambda }}{\hbox {d} \lambda } = - \frac{\partial _{\lambda }G (k, \lambda ) }{\partial _k G(k, \lambda ) }\Bigl |_{k= k_{\lambda }} = - \frac{|u''(\cdot )| \partial _{\lambda } \tilde{P}(k_{\lambda },\lambda ) - \partial _{\lambda }{D}(k_{\lambda }, \lambda ) }{|u''(\cdot )|\left( 1+ \partial _k \tilde{P}(k_{\lambda },\lambda )\right) - \partial _{k}{D}(k_{\lambda }, \lambda ) }.\quad \end{aligned}$$

(A.29)

As shown in the proof of Lemma 3, the map $S(k,\lambda ) := k+\tilde{P}(k,\lambda )$ is strictly increasing in k and, therefore, satisfies $\partial _{k}{S}(k,\lambda ) = 1+\partial _{k} \tilde{P}(k,\lambda ) \ge 0$. Further, combining (A.22) with (A.25) and (A.27) shows that $\partial _{\lambda } \tilde{P}(k,\lambda )>0$. This together with (A.27) and (A.28) shows that all terms determining the fraction in (A.29) are positive which gives $\frac{d k_{\lambda }}{d \lambda }<0$.

Second, we show that $\frac{\hbox {d} p_{\lambda }}{\hbox {d} \lambda }>0$. As $p_{\lambda } = \tilde{P}(k_{\lambda }, \lambda )$ one obtains the derivative

$$\begin{aligned} \frac{\hbox {d} p_{\lambda }}{\hbox {d} \lambda } = \partial _k \tilde{P}(k_{\lambda }, \lambda ) \frac{\hbox {d} k_{\lambda }}{\hbox {d} \lambda } + \partial _{\lambda } \tilde{P}(k_{\lambda }, \lambda ). \end{aligned}$$

(A.30)

Using (A.29), the derivative (A.30) can equivalently be written as

$$\begin{aligned} \frac{\hbox {d} p_{\lambda }}{\hbox {d} \lambda } = \frac{|u''(\cdot )|\partial _{\lambda } \tilde{P}(k_{\lambda },\lambda ) + Z(k_{\lambda },\lambda )}{|u''(\cdot )|\left( 1+\partial _{k} \tilde{P}(k_{\lambda },\lambda )\right) - \partial _{k}{D}(k_{\lambda }, \lambda ) } \end{aligned}$$

(A.31)

where $Z(k,\lambda ):= \partial _{\lambda } D(k,\lambda ) \partial _{k} \tilde{P}(k,\lambda ) - \partial _{k} D(k,\lambda ) \partial _{\lambda } \tilde{P}(k,\lambda )$. By (A.26) and our previous result, both the denominator and the first term in the numerator in (A.31) are strictly positive. Hence, it suffices to show that $M(k_{\lambda },\lambda ) \ge 0$. Using the explicit form of the derivatives $\partial _{k} \tilde{P}$ and $\partial _{\lambda } \tilde{P}$ computed from (A.22), this last expression can be written as

$$\begin{aligned} Z(k,\lambda ) = \frac{\partial _{\lambda }{D}(k, \lambda ) \partial _{k}{N}(k, \lambda ) - \partial _{k}{D}(k, \lambda ) \partial _{\lambda }{N}(k, \lambda )}{{D}(k, \lambda )}. \end{aligned}$$

Using property (U), (A.25), and (A.27) gives $\partial _{\lambda }{N}(k, \lambda ) \ge - k \partial _{\lambda }{D}(k, \lambda )$. Thus, it suffices to show $\partial _k N(k, \lambda ) + k \partial _k D(k, \lambda ) \le 0$. By (A.24) and (A.26), recalling that $0 \le P_{\lambda }' \le 1$,

$$\begin{aligned}&-\partial _k N(k, \lambda ) - k \partial _k D(k, \lambda )\\&\quad = \mathbb {E}_{\nu } \bigl [\bigl (1-P_{\lambda }'(\cdot )\bigr ) E_f'(k) R(k,\cdot ) v'(\cdot ) +\, c_{\lambda }(k, \cdot ) |v''(\cdot )| \partial _k c_{\lambda }(k, \cdot ) \bigr ] \\&\quad > E_f'(k) \mathbb {E}_{\nu } \bigl [\bigl (1-P_{\lambda }'(\cdot )\bigr ) R(k,\cdot ) \bigl (v'(\cdot ) -\, c_{\lambda }(k, \cdot )|v''(\cdot )|\bigr ) \bigr ] \ge 0 \end{aligned}$$

where the last inequality exploits (A.23). This proves $Z(k_{\lambda },\lambda ) >0$ and the claim. $\square$

1.7 A.7 Proof of Corollary 1

• (i) $T_{d} P_1 = T(P_1 + d) \ge T(P_0 + d) = T_{d} P_0$.

• (ii) $T_{d_1} P = T(P + d_1) \ge T(P + d_0) = T_{d_0} P$. $\square$

1.8 A.8 Proof of Theorem 1

(i) We show the fixed point property for $d=0$. The proof for $d>0$ is analogous. For convenience, we drop the subscript $d=0$ and denote the sequence $(T^n P_0)_{n \ge 0}$ simply as $(P_n)_{n \ge 0}$ and its pointwise limit by $P^*$. Also, for the sake of brevity we abuse our notation by writing $P(k, \theta )$ instead of $P(W(k, \theta ))$.

Let $w\in \mathbb {W}$ be arbitrary but fixed. As $(P_n)_{n}$ is a decreasing sequence of functions in $\mathscr {G}'$, monotonicity of $K_{\bullet }$ due to Lemma 6 implies that the sequence $k_n := K_{P_{n}}(w)$, $n \ge 0$ is strictly increasing and converges to some limit $0<k^{*} \le K_0(w) \le k_{\mathrm{max}}$. The claim will follow if we show that $k^{*}$ and $p^{*}:= P^{*}(w)$ satisfy (15), i.e., $H_1(k^{*}, p^{*}; w, P^{*}, 0) = H_2(k^{*}, p^{*}; w, P^{*}, 0) =0$. Uniqueness of the solution to (15) then implies $k^{*} = K_{P^{*}}(w)$.

Let $\theta \in [\theta _{\mathrm{min}}, \theta _{\mathrm{max}}]$ be arbitrary but fixed. We show that $\lim _{n \rightarrow \infty }P_{n}(k_n, \theta ) = P^{*}(k^{*}, \theta )$. As $(P_n)_{n \ge 0}$ is a sequence of increasing functions which converges pointwise to the continuous function $P^{*}$, convergence is uniform on $\overline{\mathbb {W}}:=[W(k_0,\theta _{\mathrm{min}}), w_{\mathrm{max}}] \subset \mathbb {W}$ by Theorem A in Buchanan & Hildebrandt (1908). Note that $W(k_n, \theta ) \in \overline{\mathbb {W}}$ for $n \ge 0$. Thus, for each $\delta >0$, there is $n_0 \ge 0$ such that $\vert P_{n}(k_n, \theta ) - P^{*}(k_n,\theta )\vert < \delta /2$ for all $n \ge n_0$. Further, by continuity of W and $P^{*}$ there is $n_0'>0$ such that $n \ge n_0'$ implies $\vert P^{*}(k_n, \theta ) - P^{*}(k^{*}, \theta )\vert < \delta /2$. Combining both insights, we have for all $n \ge \max \{n_0, n_0' \}$:

$$\begin{aligned} \vert P_{n}(k_n, \theta ) - P^{*}(k^{*}, \theta )\vert \le \vert P_{n}(k_n, \theta ) - P^{*}(k_n,\theta ) \vert + \vert P^{*}(k_n, \theta ) - P^{*}(k^{*}, \theta )\vert < \delta . \end{aligned}$$

For $\theta \in [\theta _{\mathrm{min}}, \theta _{\mathrm{max}}]$, define the functions

$$\begin{aligned} \phi ^1_n(\theta ):= & {} R(k_n,\theta )v'\left( P_{n}(k_n,\theta )+k_n R(k_n,\theta )\right) \\ \phi ^2_n(\theta ):= & {} P_{n}(k_n,\theta )v'\left( P_{n}(k_n,\theta )+k_n R(k_n,\theta )\right) . \end{aligned}$$

The previous result and continuity of $v'$ and R imply for each $\theta \in [\theta _{\mathrm{min}}, \theta _{\mathrm{max}}]$

$$\begin{aligned} \lim _{n \rightarrow \infty } \phi ^1_n(\theta )= & {} \phi ^1_{*}(\theta ) := R(k^{*},\theta )v'\left( P^{*}(k^{*},\theta )+k^{*} R(k^{*},\theta )\right) \\ \lim _{n \rightarrow \infty } \phi ^2_n(\theta )= & {} \phi ^2_{*}(\theta ) := P^{*}(k^{*},\theta ) v'\left( P^{*}(k^{*},\theta )+k^{*} R(k^{*},\theta )\right) . \end{aligned}$$

As $\phi ^1_n(\theta ) < R(k_1,\theta _{\mathrm{max}})v'(k_1 R(k_{\mathrm{max}},\theta _{\mathrm{min}}))$ and $\phi ^2_n(\theta ) < w_{\mathrm{max}} v'(k_1 R(k_{\mathrm{max}},\theta _{\mathrm{min}}))$ for all n, the Lebesgue-dominated convergence theorem implies $\lim _{n \rightarrow \infty } \mathbb {E}_{\nu }[\phi ^i_n(\cdot )] = \mathbb {E}_{\nu }[\phi ^i_{*}(\cdot )]$, $i=1,2$. This, $\lim _{n \rightarrow \infty } P_n(w) =p^{*}$ and $\lim _{n \rightarrow \infty } u'(w - P_n(w) - k_n) = u'(w - p^{*} - k^{*})$ imply that (15) is satisfied. Since w was arbitrary, $P^{*}$ is a fixed point of T.

That $d>0$ implies $P_d^{*}>0$ follows directly from the Euler equations (14a, 14b) resp. (15).

To prove the stated properties of $P_0^{*}$, we show that $P_0^{*}(w)=0$ for some $w\in \mathbb {W}$ implies $P_0^{*}(w)=0$ for all $w\in \mathbb {W}$. Let $w_0 \in \mathbb {W}$ be arbitrary and suppose $P_0^{*}(w_0)=0$. If $w_0= w_{\mathrm{max}}$, the claim follows from monotonicity of $P_0^{*}$, so suppose $w_0< w_{\mathrm{max}}$. By (14b) and (15), $P_0^{*}(w_0)=0$ implies $P_0^{*}(W(K_{P_0^{*}}(w_0), \theta ))=0$ $\nu$–a.s. As $\theta _{\mathrm{max}}$ is contained in the support of $\nu$, continuity of $P_0^{*}$ yields $P_0^{*}(W(K_0^{*}(w_0), \theta _{\mathrm{max}}))=0$. Moreover, (14a) and (15) imply $K_0^{*}(w_0) = K_0(w_0)$, the latter being defined by (7). Thus, under Assumption 4, $w_1 := W(K_0^{*}(w_0), \theta _{\mathrm{max}})$ satisfies $w_1= W(K_0(w_0), \theta _{\mathrm{max}}) > w_0$ and $P_0^{*}(w_1) =0$.

Let $w_1 \le w_n< w_{\mathrm{max}}$ be any value for which $P_0^{*}(w_n)=0$. Repeating the previous argument shows that $w_{n+1} := W(K_0^{*}(w_{n}), \theta _{\mathrm{max}}) = W(K_0(w_{n}), \theta _{\mathrm{max}})>w_n$ and $P_0^{*}(w_{n+1}) =0$. Due to Assumption 4, the sequence $(w_n)_{n \ge 1}$ converges monotonically to $w_{\mathrm{max}}$ and $P_0^{*}(w_n)=0$ for all $n \ge 1$ implies $P_0^{*}(w_{\mathrm{max}})=0$ due to continuity of $P_0^{*}$.

The remaining inequalities follow as limits from the monotonicity of $K_{\bullet }$ and $T_{\cdot }$ due to Lemma 6 and Corollary 1 which imply $P_d^m > P_{d'}^m$ and $K_{P_d^m + d} < K_{P_{d'}^m + d'}$ for all m which must (weakly) also hold in the limit. As for each $w \in \mathbb {W}$, $K_d^{*}(w)$ is the unique zero k of $G_d(k;w)= u'(w - k - P_d^{*}(w)) - \mathbb {E}_{\nu }[R(k,\cdot ) v'( P_d^{*}(W(k,\cdot )) + d + k R(k,\cdot )) ]$ which is strictly increasing in d, the second inequality even holds strictly.

• (ii) Follows directly from $P_d^{*} \in \mathscr {G}$ as shown in the main text and Lemma 4(ii).

• (iii) Follows directly from the previous results and Definitions 1 and 2. $\square$

1.9 A.9 Proof of Lemma 7

Let $(d_n)_{n \ge 0}$ be a sequence converging monotonically to zero. For each $n \ge 1$, define $(P_{d_n}^m)_{m \ge 1}$ as $P_0 = \mathrm{id}_\mathbb {W}$ and $P_{d_n}^m = T_{d_n}^m P_0 \in \mathscr {G}'$ for $m \ge 1$. This sequence is strictly monotonic and converges pointwise to $P_{d_n}^{*} \in \mathscr {G}$ defined in (18). It follows from Theorem 1(i) that the sequence of limits $(P_{d_n}^{*})_{n \ge 1}$ is decreasing such that the limiting function

$$\begin{aligned} P^{**}_0(w) := \lim _{n \rightarrow \infty } P_{d_n}^{*}(w) \end{aligned}$$

(A.32)

is well defined for all $w \in \mathbb {W}$. Denote by $P_0^{*}$ the limit in (18) for $d=0$, i.e.,

$$\begin{aligned} P_0^{*}(w) = \lim _{m \rightarrow \infty } T^m P_0(w) \end{aligned}$$

(A.33)

for $w \in \mathbb {W}$. We would like to show that $P^{**}_0 = P_0^{*}$.

As $T_d$ is increasing in d by Corollary 1, $P_{d_n}^m = T_{d_n}^m P_0 \ge T^m P_0 = P_0^m$ for all m which implies $P_{d_n}^{*} \ge P_0^{*}$ for all n. Therefore, $P_0^{**} \ge P_0^{*}$. We therefore need to show $P_0^{**} \le P_0^{*}$.

Suppose $d_n =0$ for all $n \ge n_0$. In this case $n \ge n_0$ implies $P_{d_n}^m = T_{d_n}^m P_0 = T^m P_0 = P_0^m$ for all $m \ge 1$ and, therefore, $P_0^{**} = P_0^{*}$. The remainder of the proof therefore assumes that the dividend sequence is strictly positive, i.e., $d_n>0$ for all n and strictly decreasing.

We first show that $P_0^{**}$ in (A.32) is independent of the particular dividend sequence. For $i=1,2$, let $(d_n^i)_{n \ge 1}$ be a strictly positive sequence converging monotonically to zero. Denote by $P^{**, i}_0$ the pointwise limit (A.32) induced by $(d_n^i)_{n \ge 1}$. Now, for each $n \ge 1$ there exists $k \ge 0$ such that $d_n^1 > d_{n+m}^2$ for all $m \ge k$. By Theorem 1(i), this implies $P^{*}_{d_n^1} \ge P^{*}_{d_{n+m}^2}$ and, therefore, $P_{d_n^1}^{*}(w) \ge \lim _{m \rightarrow \infty } P^{*}_{d_{n+m}^2}(w)= P^{**, 2}_0(w)$ for all $w \in \mathbb {W}$. Since n was arbitrary, $P^{**, 1}_0 \ge P^{**, 2}_0$. Reversing the argument gives $P^{**, 2}_0 \ge P^{**, 1}_0$.

We show that $P > P^{**}_0$ implies $T P > P^{**}_0$ for any $P \in \mathscr {G}'$. As $P_0> P^{**}_0$ and $P_0\in \mathscr {G}'$, we then obtain by simple induction that $T^m P_0 > P^{**}_0$ for all m which proves $P^{*}_0 \ge P^{**}_0$.

Let $P\in \mathscr {G}'$ satisfy $P > P^{**}_0$ and $\hat{w} \in \mathbb {W}$ be arbitrary. We show $TP (\hat{w}) > P^{**}_0(\hat{w})$.¹⁷ Given $\hat{w}$, define the compact set $\overline{\mathbb {W}}_{\hat{w}} := [W(K_P(\hat{w}), \theta _{\mathrm{min}}), w_{\mathrm{max}}] \subset \mathbb {W}$. We will construct a function $\tilde{P}\in \mathscr {G}'$ such that $P>\tilde{P}$ on $\overline{\mathbb {W}}_{\hat{w}}$. Noting that only the behavior of P and $\tilde{P}$ on the interval $\overline{\mathbb {W}}_{\hat{w}}$ is relevant to compute $TP(\hat{w})$ and $T \tilde{P}(\hat{w})$, the same arguments as in the proof of Lemma 6 can then be used to show $TP(\hat{w}) > T \tilde{P}(\hat{w})$.¹⁸

In order to construct such a $\tilde{P}$, set $\delta := \min _{w \in \overline{\mathbb {W}}_{\hat{w}}} \{P(w) - P^{**}_0(w)\}>0$. By Theorem A in Buchanan and Hildebrandt (1908), there exists a $d>0$ such that $\Vert P^*_d(w)-P^{**}_0(w)\Vert _{\infty }<\frac{\delta }{3}$ on $\overline{\mathbb {W}}_{\hat{w}}$ as $P^*_d$ converges montonically to $P^{**}_0$ for $d {\searrow } 0$ (here $\Vert \cdot \Vert _{\infty }$ denotes the supremum norm). By the same argument, there exists $m\in \mathbb {N}$ such that $\Vert T^m_d P_0(w)-P^*_d(w)\Vert _{\infty }<\frac{\delta }{3}$ on $\overline{\mathbb {W}}_{\hat{w}}$ as $(T^m_d P_0)_{m \ge 0}$ converges pointwise to $P_d^{*}$. Define $\tilde{P}:=T^m_d P_0$ and note that $\Vert \tilde{P}-P^{**}_0\Vert _{\infty }<\frac{2 \delta }{3}$ on $\overline{\mathbb {W}}_{\hat{w}}$. Further, $P_0^{**}<T^{m+1}_{\tilde{d}} P_0<T_{\tilde{d}}\circ T^m_d P_0$ on $\mathbb {W}$ for any $0<\tilde{d}<d$. Thus, $P_0^{**}<T_{\tilde{d}}\tilde{P}$ for any $\tilde{d}>0$ which implies $P^{**}_0 \le T\tilde{P}$. This last result uses that

$$\begin{aligned} \lim _{n \rightarrow \infty } T_{d_n} P(w) = T P(w) \end{aligned}$$

for all $P \in \mathscr {G}'$, $w \in \mathbb {W}$ and any monotonic sequence $(d_n)_{n}$ converging to zero.¹⁹ Combining these results we get $TP(\hat{w})>T\tilde{P}(\hat{w})\geqslant P^{**}_0 (\hat{w})$ for any $\hat{w} \in \mathbb {W}$.

To show that $\lim _{n \rightarrow \infty } K^{*}_{d_n}(w) = K_0^{*}(w)$ for each $w \in \mathbb {W}$, note that $(K^{*}_{d_n}(w))_{n}$ is increasing by Theorem 1(i) and converges to some limit $k^{*} \le K_0(w)$. By the same arguments used in the proof of Theorem 1(i), $k^{*}$ and $p^{*}:= P_0^{*}(w)$ satisfy the Euler equations at $P=P_0^{*}$ and $d=0$ which implies $k^{*} = K_{P_0^{*}}(w)$ by uniqueness of the solution to (15). $\square$

B Efficiency and inefficiency of MEA

In this appendix, we review the recursive characterization of interim Pareto optimality for stationary exchange economies obtained in Barbie and Kaul (2015) and adapt their results to characterize the optimality of MEA in a stochastic production economy. As large parts of the analysis holds almost unchanged and requires mainly notational changes, we will frequently refer to Barbie and Kaul (2015) for the details and proofs and just repeat the core facts. To adapt the results, we need the characterization of interim optimality for production OLG models from Barbie et al. (2007) who extended the pure exchange case in Chattopadhyay and Gottardi (1999).

1.1 B.1 Notation and definitions

Let $A= (K, C^y, C^o)$ be a continuous, bounded MEA defined as in Sect. 4.2 and $\overline{\mathbb {W}}=[\underline{w}, w_{\mathrm{max}}]$ be a stable set of A. Fixing the initial shock $\theta _0 \in \varTheta$ permits $\overline{\mathbb {W}}$ to be used as the state space which corresponds to the set S in Barbie and Kaul (2015). To adapt our notation to their setup, note that any two successive states w and $w'$ permit to recover the shock in the second period via $\theta ' = w'/W(K(w),1)$. Thus, define the (modified) pricing kernel $m:{\overline{\mathbb {W}}} \times {\overline{\mathbb {W}}} \longrightarrow \mathbb {R}_{++}$

$$\begin{aligned} m(w, w'):= \dfrac{v'\left( C^o(w, w'/W(K(w), 1))\right) }{u'(C^y(w))}. \end{aligned}$$

(B.1)

Denote by $\mathscr {B}(\overline{\mathbb {W}})$ the Borel-$\sigma$ algebra on $\overline{\mathbb {W}}$. As shocks are i.i.d., function K defines a transition probability $Q:\overline{\mathbb {W}} \times \mathscr {B}(\overline{\mathbb {W}}) \longrightarrow [0,1]$,

$$\begin{aligned} Q(w, G) := \nu (\{ \theta \in \varTheta \, | \, W(K(w), \theta ) \in G. \}). \end{aligned}$$

(B.2)

Note that Q has the Feller property since the function $W\circ K$ is continuous. By the change-of-variable formula, the inequality (21) can be written as

$$\begin{aligned} \int _{\overline{\mathbb {W}}} \eta (w') m(w, w') Q(w, \mathrm{d}w') > \eta (w). \end{aligned}$$

(B.3)

To adapt their formal arguments the remainder follows Barbie et al. (2007) by assuming that the shock process is finite-valued, i.e., $\varTheta =\{\theta _1, \ldots , \theta _N\}$. Thus, if $w_t\in \overline{\mathbb {W}}$ is the state in period t, there are N successive states $w_{t+1} = W(K(w_t), \theta _{t+1})$. If $w^{\prime }\in \overline{\mathbb {W}}$ is a such a successor, we write $w^{\prime }\succ w_{t}$. With this notation, an integral of the form (B.3) can be written as $\sum _{w' \succ w} \eta (w') m(w, w') Q(w, w')$.

Given some initial state $w_0 \in \overline{\mathbb {W}}$, denote by $W^t(w_0)$ the set of histories $w^t=(w_0,\ldots , w_t)$ observed up to time t, i.e., $w_{n} \succ w_{n-1}$ for all $n=1, \ldots , t$. Further, let $W^{\infty }(w_0)$ denote the set of all infinite histories $w^{\infty } = (w_t^{\infty })_{t \ge 0}$, i.e., $w^{\infty }_{t} \succ w^{\infty }_{t-1}$ for all $t \ge 1$ and $w^{\infty }_0=w_0$. For any infinite path $w^{\infty }\in W^{\infty }(w_0)$, denote by $\left( w^{\infty }\right) ^{t}$ the induced history up to time $t \ge 0$ along this path, i.e., $\left( w^{\infty }\right) ^{t}=\left( w_{0}^{\infty },w_{1}^{\infty },\ldots ,w_{t}^{\infty }\right) \in W^t(w_0)$.

Similar to Chattopadhyay and Gottardi (1999), define for each $w^{t} \in W^t(w_0)$ the set weights ²⁰

$$\begin{aligned} \mathcal {U}( w^{t}) = \left\{ \lambda (w^{t},w^{\prime }) \in \mathbb {R}_+ \left| \right. w^{\prime }\succ w_t, \sum _{w^{\prime }\succ w_t}\lambda (w^{t},w^{\prime }) Q( w_{t},w^{\prime }) =1\right\} . \end{aligned}$$

Given some $w_0 \in \overline{\mathbb {W}}$, define $\mathcal {U}^{\infty }\left( w_{0}\right)$ to be the family of weights $\lambda ^{\infty } = (\lambda (w^t, \cdot ))_{t \ge 1}$ where $w^t \in W^t(w_0)$ and $\lambda (w^t, \cdot ) \in \mathcal {U}(w^t)$ for all t.

1.2 B.2 Recursive characterization of inefficiency

Barbie et al. (2007) derived a condition for interim Pareto inefficiency in a stochastic Diamond model. For a MEA A which satisfies the restrictions from Lemma 8, the necessary part of this result can be stated as follows.

Lemma 13

If $A=(K, C^y, C^o)$ is inefficient at $w_0\in \overline{\mathbb {W}}$, there exists a family of weights $\lambda ^{\infty } \in \mathcal {U}^{\infty }\left( w_{0}\right)$ and a constant $C\ge 0$ such that for each path $w^{\infty } \in W^{\infty }(w_0)$

$$\begin{aligned} \sum _{i=0}^{\infty }\prod _{j=0}^{i}\frac{\lambda \left( (w^{\infty })^{j},w_{j+1}^{\infty }\right) }{m\left( w_{j}^{\infty },w_{j+1}^{\infty }\right) }\le C . \end{aligned}$$

(B.4)

As noted in Barbie and Kaul (2015), the condition (B.4) can be restated as a minimax problem. The max-part is taking the supremum over all possible paths, the min-part is taking the infimum over all possible weights. For any $w_{0}\in \overline{\mathbb {W}}$, define the value function

$$\begin{aligned} {J^{*}\left( w_{0}\right) := } \underset{\lambda ^{\infty }\in \mathcal {U}^{\infty }\left( w_{0}\right) }{ \inf }\ \ \underset{w^{\infty }\in W^{\infty }(w_0)}{\sup } \left\{ \ \ 1+\sum _{i=0}^{\infty }\prod _{j=0}^{i}\frac{\lambda \left( \left( w^{\infty }\right) ^{j},w_{j+1}^{\infty }\right) }{m\left( w_{j}^{\infty },w_{j+1}^{\infty }\right) } \right\} . \end{aligned}$$

(B.5)

The next result follows immediately from Lemma 13 and (B.5).

Corollary 3

If A is inefficient at $w_0 \in \overline{\mathbb {W}}$, then $J^*(w_0)<\infty$.

Following Barbie and Kaul (2015) we show that (B.5) defines a recursive structure permitting $J^{*}$ to be computed as a fixed point of some operator Z. For each $w\in \overline{\mathbb {W}}$, denote the set of all stationary weights

$$\begin{aligned} \mathcal {U}(w) = \left\{ \lambda (w,w^{\prime }) \in \mathbb {R}_+ \, | \, w' \succ w, \sum _{w^{\prime }\succ w}\lambda (w,w^{\prime }) Q( w,w^{\prime }) =1 \right\} . \end{aligned}$$

Define the operator Z which associates with any nonnegative extended real-valued function $J:\overline{\mathbb {W}} \longrightarrow \mathbb {R}_+ \cup \{+ \infty \}$ the new function ZJ defined for all $w \in \overline{\mathbb {W}}$ as

$$\begin{aligned} Z J(w) :=1+\underset{{\lambda \left( w, \cdot \right) } \in \mathcal {U}\left( w\right) }{\inf } \ \ \underset{w^{\prime }\succ w}{\sup } \left\{ \frac{\lambda \left( w,w^{\prime }\right) }{m\left( w,w^{\prime }\right) } \cdot J\left( w^{\prime }\right) \right\} . \end{aligned}$$

(B.6)

Note that Z is monotonic, i.e., $J_1 \ge J_2$ implies $Z J_1 \ge Z J_2$. The operator Z can now be used to compute a value function that solves the functional Eq. (B.6). Construct the sequence $(J_n)_{n \ge 0}$ of functions $J_n$ defined on $\overline{\mathbb {W}}$ recursively by setting $J_{0}\equiv 1$ and $J_n = Z J_{n-1}$ for $n \ge 1$. For each $w\in \overline{\mathbb {W}}$, define the function

$$\begin{aligned} J_{\infty }\left( w\right) := \lim _{n \rightarrow \infty } J_n(w). \end{aligned}$$

(B.7)

Note that the pointwise limit in (B.7) exists since the sequence $(J_n)_{n \ge 0}$ is increasing. We now have the following result. The proof is the same as the ones of Theorem 1 and Proposition 2 in Barbie and Kaul (2015) (with the appropriate notational changes).

Lemma 14

The function $J_{\infty }$ defined in (B.7) is a fixed point of Z that coincides with the value function $J^{*}$ defined in (B.5), i.e., $J_{\infty } = Z J_{\infty } = J^{*}$.

1.3 B.3 Proof of Lemma 8(i)

By Corollary 3, if A is inefficient then $J^*(w_0)< {\infty }$ for all $w_0 \in \overline{\mathbb {W}}$. Set $\eta (w):= 1{/}J^{*}(w)$ for $w \in \overline{\mathbb {W}}$. It follows from the same arguments as in the proofs of Proposition 4 and Theorem 2(a) in Barbie and Kaul (2015) that $\eta$ is a strictly positive, upper-semicontinuous function which takes values in the unit interval (since $J^{*}>1$) and satisfies (B.3) for all $w\in \overline{\mathbb {W}}$. As boundedness of A permits to choose the lower bound $\underline{w}$ arbitrarily small, the previous construction of $\eta$ can be extended to the entire interval $\mathbb {W}=]0, w_{\mathrm{max}}]$. $\square$

1.4 B.4 Proof of Lemma 8(ii)

In this section we present a new additional sufficient condition under which the function $\eta$ constructed as in the previous subsection is continuous, not just upper-semicontinuous. We will then argue that this condition is satisfied if the kernel $m_A$ exhibits the monotonicity property required in Lemma 8(ii). We have the following result:

Lemma 15

Suppose $J^{*}=J_{\infty }$ defined in (B.7) is uniformly bounded on $\overline{\mathbb {W}}$, i.e., there exists a constant $M \ge 0$ such $J^{*}(w) \le M$ for all $w\in \overline{\mathbb {W}}$. Then, $\eta =1/J^{*}$ is continuous.

Proof

Construct the sequence $(J_n)_{n \ge 0}$ as above by setting $J_0 \equiv 1$ and $J_n = Z J_{n-1}$ for $n \ge 1$. Recall that $J_1 > 1 = J_0$ and monotonicity of Z imply that $(J_n)_{n \ge 0}$ is strictly increasing, i.e., $J_n > J_{n-1}$ for all $n \ge 0$. By Lemma 14, we know that the pointwise limit $J^*$ defined in (B.7) is a fixed point of Z. We will show that under the hypotheses of Lemma 15, $(J_n)_{n \ge 1}$ is a Cauchy sequence in the space of bounded continuous functions on $\overline{\mathbb {W}}$. As this space is complete, the sequence must converge to some bounded continuous function, which coincides with the pointwise limit $J^*$.

First, we show that each $J_n$ is of the form $J_n(w) = 1 + c_n^{*}(w)$ for some continuous function $c_n^{*}:\overline{\mathbb {W}} \longrightarrow \mathbb {R}_+$. Clearly, this holds trivially for $n=0$ and $c_0^{*} \equiv 0$. By induction, suppose $J_{n-1}(w) = 1+c_{n-1}^{*}(w)$ for some $n \ge 1$. For each $w\in \overline{\mathbb {W}}$ and $w' \succ w$, define the function

$$\begin{aligned} \lambda _n^{*}(w, w'):= \frac{m(w, w')}{J_{n-1}(w')}c_n^{*}(w) \end{aligned}$$

(B.8)

where $c_n^{*}$ is chosen such that $\sum _{w^{\prime }\succ w}\lambda _n^{*} (w,w^{\prime }) Q( w,w^{\prime }) =1$ for all $w \in \overline{\mathbb {W}}$, i.e.,

$$\begin{aligned} c_{n}^{*}(w) : = \left[ \sum _{w^{\prime }\succ w} \frac{m(w,w^{\prime })}{J_{n-1}(w')} Q( w,w^{\prime })\right] ^{-1}. \end{aligned}$$

(B.9)

Note that $\lambda _n^{*}$ is continuous and attains the infimum in (B.6). Hence,

$$\begin{aligned} J_{n}(w) = 1 + \max _{w'\succ w} \frac{\lambda _n^{*}(w, w')}{m(w, w')} J_{n-1}(w') = 1+c_{n}^{*}(w). \end{aligned}$$

(B.10)

As continuity of $c_{n-1}^{*}$ implies continuity of $c_n^{*}$, this proves that each $J_n$ is continuous and, therefore, bounded on the compact set $\overline{\mathbb {W}}$.

Defining $\lambda _n^{*}$ by (B.8) for each $n\ge 1$ we can now use the first equality in (B.10) to expand $J_n$ for all $w_0 \in \overline{\mathbb {W}}$ as

$$\begin{aligned} J_{n}(w_0)= & {} 1 + \max _{w_1\succ w_{0}} \frac{\lambda _n^{*}(w_{0}, w_{1})}{m(w_{0}, w_1)}\left[ 1 + \max _{w_{2}\succ w_{1}} \frac{\lambda _{n-1}^{*}(w_1, w_2)}{m(w_1, w_2)}J_{n-2}(w_2) \right] \nonumber \\ \nonumber= & {} 1 + \max _{w_1\succ w_{0}} \frac{\lambda _n^{*}(w_{0}, w_{1})}{m(w_{0}, w_1)}\left[ 1 + \max _{w_{2}\succ w_{1}} \frac{\lambda _{n-1}^{*}(w_1, w_2)}{m(w_1, w_2)} \biggl [ \ldots \right. \nonumber \\&\left. \left. \left[ 1+ \max _{w_n\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_n)} \right] \ldots \right] \right] . \end{aligned}$$

(B.11)

The final term in (B.11) satisfies $1+\max _{w_n\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_n)} = J_1(w_{n-1}) = 1+c_1^{*}(w_{n-1})$.

Clearly, $\lambda _{n}^{*}$ does not necessarily attain the infimum when defining $J_{n+1}$ by (B.6). Therefore, for all $w_0 \in \overline{\mathbb {W}}$, recalling that $J_1(w) = 1+c_1^{*}(w)$

$$\begin{aligned} J_{n+1}(w_0)= & {} 1+ \max _{w_1\succ w_0} \frac{\lambda _{n+1}^{*}(w_0, w_1)}{m(w_0, w_1)} J_{n}(w_1) \nonumber \\\le & {} 1+ \max _{w_1\succ w_0} \frac{\lambda _n^{*}(w_0, w_1)}{m(w_0, w_1)} J_{n}(w_1) \nonumber \\\le & {} 1 + \max _{w_1\succ w_{0}} \frac{\lambda _n^{*}(w_{0}, w_{1})}{m(w_{0}, w_1)}\left[ 1 + \max _{w_{2}\succ w_{1}} \frac{\lambda _{n-1}^{*}(w_1, w_2)}{m(w_1, w_2)} \biggl [ \ldots \right. \nonumber \\&\left. \left. 1+\,\max _{w_{n-1}\succ w_{n-2}} \frac{\lambda _2^{*}(w_{n-2}, w_{n-1})}{m(w_{n-2}, w_{n-1})}\left[ \right. \right. \right. \nonumber \\&\left. \left. \left. 1+\, \max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})}\left( 1+c_1^{*}(w_n)\right) \right] \ldots \right] \right] . \end{aligned}$$

(B.12)

By elementary observations,²¹ the final term in (B.12) satisfies for any $w_{n-2} \in \overline{\mathbb {W}}$

$$\begin{aligned}&\max _{w_{n-1}\succ w_{n-2}} \frac{\lambda _2^{*}(w_{n-2}, w_{n-1})}{m(w_{n-2}, w_{n-1})}\left[ 1+ \max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})}\left( 1+c_1^{*}(w_n)\right) \right] \\&\quad \le \max _{w_{n-1}\succ w_{n-2}} \frac{\lambda _2^{*}(w_{n-2}, w_{n-1})}{m(w_{n-2}, w_{n-1})} \left[ 1\right. +\,\max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})} \nonumber \\&\qquad +\left. \max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})} c_1^{*}(w_n) \right] \\&\quad \le \max _{w_{n-1}\succ w_{n-2}} \frac{\lambda _2^{*}(w_{n-2}, w_{n-1})}{m(w_{n-2}, w_{n-1})} \left[ 1+\max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})} \right] \\&\qquad +\, \max _{w_{n-1}\succ w_{n-2}} \frac{\lambda _2^{*}(w_{n-2}, w_{n-1})}{m(w_{n-2}, w_{n-1})} \max _{w_{n}\succ w_{n-1}} \frac{\lambda _1^{*}(w_{n-1}, w_{n})}{m(w_{n-1}, w_{n})} c_1^{*}(w_n). \end{aligned}$$

Solving (B.12) in this recursive fashion and using (B.11) we obtain for all n and $w_0 \in \overline{\mathbb {W}}$

$$\begin{aligned} J_{n+1}(w_0) \le J_n(w_0) + \max \limits _{w_1\succ w_0} \frac{\lambda ^*_n(w_0,w_1)}{m(w_0,w_1)} \cdots \max \limits _{w_n\succ w_{n-1}} \frac{\lambda ^*_{1}(w_{n-1},w_n)}{m(w_{n-1},w_n)}c_1^{*}(w_n).\nonumber \\ \end{aligned}$$

(B.13)

Using (B.8) and (B.10) in (B.13) we obtain for all $n \in \mathbb {N}$ and $w_0 \in \overline{\mathbb {W}}$

$$\begin{aligned} J_{n+1}(w_0)-J_n (w_0)&\leqslant \max \limits _{w_1\succ w_0}\frac{c^*_n(w_0)}{1+c^*_{n-1}(w_1)}\\&\quad \times \max \limits _{w_2\succ w_1}\frac{c^*_{n-1}(w_1)}{1+c^*_{n-2}(w_2)}\ldots \max \limits _{w_n\succ w_{n-1}}c^*_1(w_{n-1})\cdot c^*_1(w_n)\\&=c^*_n(w_0)\cdot \max \limits _{w_1\succ w_0}\frac{c^*_{n-1}(w_1)}{1+c^*_{n-1}(w_1)}\ldots \max \limits _{w_{n-1}\succ w_{n-2}}\frac{c^*_1(w_{n-1})}{1+c^*_1(w_{n-1})}\\&\quad \times \max \limits _{w_n\succ w_{n-1}}c^*_1(w_n). \end{aligned}$$

Since $M\geqslant J^*(w)\geqslant J_n(w)=1+c^*_n(w)>c^*_n(w)$ for any $w\in \overline{\mathbb {W}}$ and $n\in \mathbb {N}$, we get

$$\begin{aligned} 0<&J_{n+1}(w)-J_n (w)\leqslant M^2\cdot \left( \frac{M}{1+M}\right) ^{n-1} \end{aligned}$$

for all $w\in \overline{\mathbb {W}}$. But this means that

$$\begin{aligned} \Vert J_{n+1} - J_n \Vert _{\infty }\leqslant B\left( \beta \right) ^{n-1} \end{aligned}$$

where $\Vert \cdot \Vert _{\infty }$ is the supremum norm on the space of bounded continuous functions on $\overline{\mathbb {W}}$ and $B>0$ and $0<\beta <1$. By standard arguments, this implies

$$\begin{aligned} \Vert J_{n+m} -J_n\Vert _{\infty }\leqslant B \beta ^{n-1}\frac{1}{1-\beta } \end{aligned}$$

for all $n,m>0$ and so $(J_n )_{n \ge 0}$ is a Cauchy sequence, as was to be shown.$\square$

Now suppose $m_A$ defined in (20) is monotonically increasing. We show that this implies the hypothesis of Lemma 15. Using the change-of-variable formula in (B.9) yields

$$\begin{aligned} \frac{1}{c_n^{*}(w)} = \sum _{w^{\prime }\succ w} \frac{m(w,w^{\prime })}{1+c_{n-1}^{*}(w')} Q( w,w^{\prime }) = \mathbb {E}_{\nu }\left[ \frac{m_A(w, \cdot )}{1+c_{n-1}^{*}\left( W(K(w), \cdot )\right) } \right] . \end{aligned}$$

As the term to the far right is a strictly increasing function whenever $c_{n-1}^{*}$ is decreasing, it follows by induction that each $J_n(w) = 1 + c_n^{*}(w)$, $w \in \overline{\mathbb {W}}$ is strictly decreasing which implies $J_n(w) \le J_n(\underline{w})$ for all n. Taking the limit gives $J^{*}(w) \le J^{*}(\underline{w})$ for all $w \in \overline{\mathbb {W}}$. Finally, if A is inefficient at $w_0$, monotonicity of $J^{*}$ implies $J^{*}(w_0') \le J^{*}(w_0) <\infty$ also for $w_0 \ge w_0'$, i.e., A is also inefficient for all $w_0 \ge w_0'$. $\square$

1.5 B.5 Proof of Lemma 9

For each $w \in \mathbb {W}$ and $\theta \in \varTheta$, define $C_0^o(w, \theta ):= K_0(w) R(K_0(w), \theta )$ and $\tilde{m}(w) := \mathbb {E}_{\nu }[R(K_0(w), \cdot ) v'(C_0^o(w; \cdot ))]$. Using (7), the pricing kernel $m_0$ can be written as

$$\begin{aligned} m_0 (w, \theta ) = v'\left( C_0^o(w, \theta )\right) /\tilde{m}(w). \end{aligned}$$

Let $w \in \mathbb {W}$ and $\theta \in \varTheta$ be arbitrary but fixed and set $c_0 := C_0^o(w, \theta )$ and $k_0 := K_0(w)$. Then, by direct computations $\frac{\partial m_0}{\partial w}(w, \theta ) = \frac{K_0'(w) v'(c_0)}{k_0 \tilde{m}(w)} H(w)$ where

$$\begin{aligned} H(w):= & {} E_{f'}(k_0) + (1-E_{f'}(k_0))\nonumber \\&\times \left( \frac{ \mathbb {E}_{\nu }\left[ R(k_0, \cdot )C_0(w, \cdot ) |v''\left( C_0(w, \cdot )\right) |\right] }{\tilde{m}(w)} - E_{v'} (c_0)\right) \end{aligned}$$

(B.14)

determines the sign of $\frac{\partial m_0}{\partial w}(w, \theta )$. Using (4), we have $0 \le E_{v'}^{\mathrm{min}} \le E_{v'} (c_0) \le E_{v'}^{\mathrm{max}} \le 1$ and

$$\begin{aligned} E_{v'}^{\mathrm{min}} \tilde{m}(w) \le \mathbb {E}_{\nu }[R(k_0, \cdot )C_0(w, \cdot ) |v''(C_0(w, \cdot ))|] \le E_{v'}^{\mathrm{max}} \tilde{m}(w). \end{aligned}$$

Using these bounds in (B.14), we obtain

$$\begin{aligned} H(w) \ge E_{f'}(k_0) + E_{v'}^{\mathrm{min}} - E_{v'}^{\mathrm{max}} - E_{f'}(k_0) \left( E_{v'}^{\mathrm{max}} - E_{v'}^{\mathrm{min}}\right) . \end{aligned}$$

(B.15)

As the r.h.s in (B.15) is nonnegative due to (5) in Assumption 3, the claim follows.

$\square$

1.6 B.6 Proof of Lemma 10

As both $C^y$ and $C^{o}$ are continuous, strictly positive functions on their compact domains $\overline{\mathbb {W}}$ and $\overline{\mathbb {W}}\times \varTheta$, respectively, we can choose $\overline{\alpha }>0$ such that the ‘perturbed’ allocation $(K, C^y_{\alpha },C^{o}_{\alpha })$ defined as $C^y_{\alpha }(w):=C^y(w)-\alpha \eta (w)$ and $C^{o}_{\alpha }(w,\theta )=C^{o}(w,\theta )+\alpha \eta (W(K(w), \theta ))$ is strictly positive and feasible for all $\alpha \in [-\overline{\alpha }, \overline{\alpha }]$ and $w \in \overline{\mathbb {W}}$. Thus, given $w\in \overline{\mathbb {W}}$, the map $h(\alpha ; w):=u(C^y_{\alpha }(w))+\mathbb {E}_\nu [v(C^{o}_{\alpha }(w, \cdot ))]$ is well defined and determines the utility of a generation born in state $w\in \overline{\mathbb {W}}$ under the perturbation $\alpha \in [-\overline{\alpha }, \overline{\alpha }]$.

We will determine $\alpha ^{*}>0$ such that $h(\alpha ^{*};w) - h(0; w)>0$ for all $w\in \overline{\mathbb {W}}$, i.e., the perturbed allocation improves the utility of any generation. Let $w \in \overline{\mathbb {W}}$ be fixed. As $h(\cdot ; w)$ is twice continuously differentiable on the open interval $]-\overline{\alpha }, \overline{\alpha }[$, we have

$$\begin{aligned} h(\alpha ;w)-h(0;w)=h'(0;w)\alpha +\frac{1}{2}h''(\xi ;w) \alpha ^2 \end{aligned}$$

for $0 \le \alpha \le \overline{\alpha }$ and some $0<\xi <\alpha$ that may depend on both w and $\alpha$. By hypothesis,

$$\begin{aligned} h'(0;w)=-u'\left( C^y(w)\right) \eta (w)+\mathbb {E}_\nu \left[ v'\left( C^{o}(w, \cdot )\right) \eta \left( W\left( K(w, \cdot )\right) \right) \right] >0 \end{aligned}$$

for all w. Further, using the Lebesgue-dominated convergence theorem

$$\begin{aligned} h''(\xi ;w)=u''\left( C^y_{\xi }(w)\right) \left( \eta (w)\right) ^2+\mathbb {E}_\nu \left[ v''\left( {C^{o}_{\xi }(w, \cdot )}\right) \left( \eta \left( W\left( K(w),\cdot \right) \right) \right) ^2\right] <0. \end{aligned}$$

By the Lebesgue-dominated convergence theorem again, both mappings $w \mapsto h'(0; w)$ and $(\xi ; w) \mapsto h''(\xi ; w)$ are continuous on $\overline{\mathbb {W}}$ and $[0,\overline{\alpha }] \times \overline{\mathbb {W}}$, respectively. Thus, there exist $\Delta _1>0$ and $\Delta _2<0$ such that $h(\alpha ;w)-h(0;w)\geqslant \Delta _1 \alpha +\Delta _2 \alpha ^2$ for all $w\in \overline{\mathbb {W}}$ and $\alpha \in [0,\overline{\alpha }]$. Choosing $\alpha ^{*}>0$ sufficiently small therefore ensures that $h(\alpha ^{*};w)>h(0;w)$ for all $w\in \overline{\mathbb {W}}$. $\square$