Generalized integer aperture estimation for partial GNSS ambiguity fixing

Abstract

In satellite navigation, the key to high precision is to make use of the carrier-phase measurements. The periodicity of the carrier-phase, however, leads to integer ambiguities. Often, resolving the full set of ambiguities cannot be accomplished for a given reliability constraint. In that case, it can be useful to resolve a subset of ambiguities. The selection of the subset should be based not only on the stochastic system model but also on the actual measurements from the tracking loops. This paper presents a solution to the problem of joint subset selection and ambiguity resolution. The proposed method can be interpreted as a generalized version of the class of integer aperture estimators. Two specific realizations of this new class of estimators are presented, based on different acceptance tests. Their computation requires only a single tree search, and can be efficiently implemented, e.g., in the framework of the well-known LAMBDA method. Numerical simulations with double difference measurements based on Galileo E1 signals are used to evaluate the performance of the introduced estimation schemes under a given reliability constraint. The results show a clear gain of partial fixing in terms of the probability of correct ambiguity resolution, leading to improved baseline estimates.

1 Introduction

For satellite-based positioning, two types of measurements are available at the receiver: the code-based pseudoranges and the carrier-phases. In order to enable highly precise state estimates, the carrier-phase measurements are employed, which are two orders of magnitude less noisy, but ambiguous by an unknown number of complete cycles. Resolving these unknown ambiguities as integers is known as integer ambiguity resolution. Successful ambiguity resolution enables the carrier-phases to act as very precise pseudoranges. Classical options for that task are the class of integer estimators, e.g., bootstrapping [BS, see Blewitt (1989), Teunissen (2001), also referred to as Babai solution in lattice theory, Babai (1986)] or integer least squares [ILS, also maximum likelihood in the Gaussian case, finds the closest lattice point, Agrell et al. (2002)]. A very efficient implementation of the latter principle is given by the Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) (Teunissen 1995). Within that class, all ambiguities are fixed to integer values, regardless of the strength of the underlying system model. This may prevent the state estimates to reach higher quality, if the fixing is not successful. For that reason, ambiguity validation is a very important issue. Different tests can be used to decide, whether or not to accept the integer solution. Examples are the ratio test (Euler and Schaffrin 1991), the difference test (Tiberius and De Jonge 1995), the F ratio test (Frei and Beutler 1990), the W ratio test (Wang et al. 1998), and the projector test (Han 1997). An overview and evaluation of these tests can be found in Verhagen (2004a, b), Wang et al. (2000), and Li and Wang (2012).

The class of integer aperture (IA) estimators, introduced in Teunissen (2003a), provides a general framework for ambiguity validation. Each of the mentioned tests can be interpreted as a member of this class. For a given, tolerable rate of incorrect ambiguity fixing, IA estimators can serve as an overall estimation and validation process, suitable for scenarios, which require a certain reliability (Verhagen and Teunissen 2006; Teunissen and Verhagen 2009).

For a low predefined rate of wrong fixing, the probability of fixing the ambiguities at all can be very small. To overcome this problem, a subset of ambiguities can be fixed to partially benefit from the low carrier-phase noise level. Different approaches were proposed in the literature. In Teunissen et al. (1999), the set of ambiguities to be fixed is selected by the BS success rate. This scheme is extended by a position domain-based acceptance test in Khanafseh and Pervan (2010). In Dai et al. (2007), those ambiguities are fixed, which are equal in the best and second best set of ambiguity estimates, where best is defined in the least-squares sense. The algorithms in Parkins (2011) and Verhagen et al. (2011) are iterative procedures, where in each iteration a different subset is chosen. The ILS ambiguity estimates for the chosen subset are computed and tested for acceptance. The iteration terminates once a valid solution is found. In Verhagen et al. (2011) it is shown, that the selection of the subset of ambiguities should be based not only on the stochastic system model but also on the actual measurements.

In this paper, a new class of algorithms is introduced, which combines a predefined requirement on the probability of wrong fixing with partial ambiguity estimation. The difference w.r.t. Verhagen et al. (2011) is that the new approach only needs a single tree search. The determination of the subset as well as the search for the ambiguity solution itself is accomplished jointly in one single search process, thus providing only slightly increased complexity compared to the ILS solution. The method can be interpreted as a generalized form of IA estimators. The key lies in providing separate reliability information for each scalar ambiguity estimate from an integer estimator, not only for the complete set of ambiguities, as is done in IA estimation.

The detection problem in multiple-input multiple-output (MIMO) communication systems is similar to carrier-phase ambiguity resolution. The counterpart to the decision feedback equalizer (also successive interference cancellation) is integer BS. The sphere decoder, e.g., Viterbo and Boutros (1999), is an efficient solution to the maximum-likelihood detection problem, which corresponds to ILS. Generalized IA estimation as presented in this paper has some similarities with soft-output sphere decoding (Studer et al. 2008; Studer and Bölcskei 2010).

Outline: The remainder of the paper is organized as follows. In Sect. 2, the mathematical description used for global navigation satellite system (GNSS) parameter estimation is introduced. A short review of the principles of IA estimation is given. The novel class of generalized IA estimators is presented in Sect. 3. Two specific realizations of that class are shown in Sect. 4 along with implementation aspects aiming at low complexity. Numerical results based on simulated double difference measurements are presented in Sect. 5.

2 GNSS parameter estimation

2.1 System model and estimation strategy

The problem of carrier-phase-based GNSS state estimation, like positioning, attitude determination, or the estimation of atmospheric or instrumental delays can be written as a system of linear(ized) equations in the form

$$\begin{aligned} {\varvec{y}} = {\varvec{A}}{\varvec{a}} + {\varvec{B}}{\varvec{b}} + \varvec{\eta }, \end{aligned}$$

(1)

where ${\varvec{y}} \in \mathbb {R}^q$ is the measurement vector with undifferenced, single-differenced or double-differenced carrier-phase and/or pseudorange measurements. The vectors ${\varvec{a}} \in \mathbb {Z}^n$ and ${\varvec{b}} \in \mathbb {R}^p$ denote the set of unknown integer ambiguities and the remaining unknown real-valued states, respectively, and the corresponding matrices ${\varvec{A}} \in \mathbb {R}^{q\times n}$ and ${\varvec{B}} \in \mathbb {R}^{q\times p}$ represent the known full rank linear system model. Finally, $\varvec{\eta } \in \mathbb {R}^q$ is an additive Gaussian noise with zero mean and covariance matrix ${\varvec{Q}}_{\varvec{\eta }} \in \mathbb {R}^{q\times q}$.

The process of estimating ${\varvec{a}}$ and ${\varvec{b}}$ can be divided into three steps (e.g., Teunissen 1995, 2003a, c). In the first step the fact, that the entries in ${\varvec{a}}$ are integer valued, is disregarded, which leads to the so-called float solutions $\hat{{\varvec{a}}}$ and $\hat{{\varvec{b}}}$ following from a linear least-squares adjustment

$$\begin{aligned} \hat{{\varvec{a}}}&= \left( \bar{{\varvec{A}}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} \bar{{\varvec{A}}} \right) ^{-1} \bar{{\varvec{A}}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} {\varvec{y}} \nonumber \\ \hat{{\varvec{b}}}&= \left( \bar{{\varvec{B}}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} \bar{{\varvec{B}}} \right) ^{-1} \bar{{\varvec{B}}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} {\varvec{y}}, \end{aligned}$$

(2)

with $\bar{{\varvec{A}}} = {\varvec{P}}_{{\varvec{B}}}^\perp {\varvec{A}}$, $\bar{{\varvec{B}}} = {\varvec{P}}_{{\varvec{A}}}^\perp {\varvec{B}}$, and the two orthogonal projection matrices

$$\begin{aligned} {\varvec{P}}_{{\varvec{A}}}^\perp&= {\varvec{I}}_q - {\varvec{A}} \left( {\varvec{A}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} {\varvec{A}} \right) ^{-1} {\varvec{A}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} \nonumber \\ {\varvec{P}}_{{\varvec{B}}}^\perp&= {\varvec{I}}_q - {\varvec{B}} \left( {\varvec{B}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1} {\varvec{B}} \right) ^{-1} {\varvec{B}}^\mathrm{T} {\varvec{Q}}_{{\varvec{y}}}^{-1}. \end{aligned}$$

(3)

The covariance matrix ${\varvec{Q}}_{{\varvec{y}}}$ follows from the law of error propagation and system model (1) as ${\varvec{Q}}_{{\varvec{y}}} = {\varvec{Q}}_{\varvec{\eta }}$.

In the second step, a non-linear mapping $S(\cdot ) :\mathbb {R}^n \mapsto \mathbb {R}^n$ is introduced, which allocates to each float ambiguity vector $\hat{{\varvec{a}}}$ the estimate

$$\begin{aligned} \check{{\varvec{a}}} = S\left( \hat{{\varvec{a}}} \right) , \end{aligned}$$

(4)

which somehow takes the integer nature of the ambiguities into account. In case $S(\cdot )$ represents an integer estimator like BS or ILS, $\check{{\varvec{a}}} \in \mathbb {Z}^n$ is usually referred to as the fixed solution. In the following that term will be used regardless of the structure of $S(\cdot )$.

In the last step the fixed ambiguity estimate $\check{{\varvec{a}}}$ is used to obtain the fixed estimate for the real-valued parameters $\check{{\varvec{b}}}$ from its conditional estimate

$$\begin{aligned} \check{{\varvec{b}}} = \hat{{\varvec{b}}}\!\mid \!{\varvec{z}} \big |_{{\varvec{z}} = \check{{\varvec{a}}}} = \hat{{\varvec{b}}} - {\varvec{Q}}_{\hat{{\varvec{b}}}\hat{{\varvec{a}}}} {\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1} \left( \hat{{\varvec{a}}} - \check{{\varvec{a}}} \right) , \end{aligned}$$

(5)

where ${\varvec{Q}}_{\hat{{\varvec{a}}}}$ denotes the covariance matrix of $\hat{{\varvec{a}}}$ and ${\varvec{Q}}_{\hat{{\varvec{b}}}\hat{{\varvec{a}}}}$ the covariance matrix of $\hat{{\varvec{b}}}$ and $\hat{{\varvec{a}}}$.

This three-step procedure is motivated by a decomposition of the cost function

$$\begin{aligned} J\left( \varvec{\alpha },\varvec{\beta }\right) = \left\| {\varvec{y}} - {\varvec{A}}\varvec{\alpha } - {\varvec{B}}\varvec{\beta } \right\| ^2_{{\varvec{Q}}_{{\varvec{y}}}^{-1}} \end{aligned}$$

(6)

of the ILS problem corresponding to (1) (Teunissen 1995; Hassibi and Boyd 1998). The degree of freedom in the design of an estimation scheme is given by the choice of the mapping function $S(\cdot )$. Three well-known classes of estimators are: integer estimators, integer equivariant estimators (Teunissen 2003b), and IA estimators. In Sect. 3, a generalized version of the latter class is introduced. In the remainder of this paper, only the design of this mapping function $S(\cdot )$ will be considered. For the sake of simplicity, $S(\cdot )$ will be referred to as the estimator, although it represents only one of the three steps of the actual estimation process.

2.2 Integer aperture estimation

In contrast to integer estimators, which necessarily fix all entries of $\check{{\varvec{a}}}$ to integer values, IA estimators (Teunissen 2003a) comprise a validation step. This provides for the possibility to either fix $\check{{\varvec{a}}}$ to an integer vector or to remain with the float solution $\check{{\varvec{a}}} = \hat{{\varvec{a}}}$, if a fixing is not sufficiently reliable based on the system model and the actual realization $\hat{{\varvec{a}}}$. Such an estimator is fully characterized by its pull-in regions $\varOmega _{{\varvec{z}}}, \forall {\varvec{z}} \in \mathbb {Z}^n$, and given by

$$\begin{aligned} S\left( \hat{{\varvec{a}}} \right) = \sum _{{\varvec{z}} \in \mathbb {Z}^n} {\varvec{z}} \, w_{{\varvec{z}}}\! \left( \hat{{\varvec{a}}}\right) + \hat{{\varvec{a}}} \left( 1- \sum _{{\varvec{z}} \in \mathbb {Z}^n} w_{{\varvec{z}}}\! \left( \hat{{\varvec{a}}}\right) \right) \end{aligned}$$

(7)

with the binary indicator function

$$\begin{aligned} w_{{\varvec{z}}}\! \left( {\varvec{x}}\right) = {\left\{ \begin{array}{ll} 1 &{}\text {if } {\varvec{x}}\in \varOmega _{{\varvec{z}}} \\ 0 &{}\text {else.} \end{array}\right. } \end{aligned}$$

(8)

In order for the IA estimator to be admissible, its characterizing pull-in regions have to fulfill the following properties:

$$\begin{aligned} \begin{array}{cl} (i) &{} \bigcup _{{\varvec{z}} \in \mathbb {Z}^n} \varOmega _{{\varvec{z}}} = \varOmega \\ (ii) &{} \varOmega _{{\varvec{z}}} \cap \varOmega _{{\varvec{u}}} = \emptyset ,\quad \forall {\varvec{z}},{\varvec{u}} \in \mathbb {Z}^n, \quad {\varvec{z}} \ne {\varvec{u}} \\ (iii) &{} \varOmega _{{\varvec{z}}} = \varOmega _\mathbf {0} + {\varvec{z}}, \quad \forall {\varvec{z}} \in \mathbb {Z}^n. \end{array} \end{aligned}$$

(9)

Condition $(i)$ defines the aperture space $\varOmega \subseteq \mathbb {R}^n$, which is assembled by the pull-in regions $\varOmega _{{\varvec{z}}}$. Condition $(ii)$ ensures that the pull-in regions do not overlap, which is important for $S(\cdot )$ to be unique, and condition $(iii)$ states the translational invariance of the pull-in regions, i.e., each $\varOmega _{{\varvec{z}}}$ is a shifted version of $\varOmega _\mathbf {0}$. This property makes possible to use carrier phase measurements from a phase tracking loop with arbitrary initialization.

From (9) follow three different cases for IA estimation, which are helpful in order to evaluate the performance of the estimator:

$$\begin{aligned} S\left( \hat{{\varvec{a}}}\right) = {\left\{ \begin{array}{ll} {\varvec{a}} &{}\quad \text {if } \hat{{\varvec{a}}}\in \varOmega _{{\varvec{a}}} \quad \text {(success)}\\ {\varvec{z}}\in \mathbb {Z}^n {\setminus } {\varvec{a}} &{}\quad \text {if } \hat{{\varvec{a}}}\in \varOmega _{{\varvec{z}}},{\varvec{z}} \ne {\varvec{a}} \quad \text {(failure)}\\ \hat{{\varvec{a}}} &{}\quad \text {if } \hat{{\varvec{a}}} \notin \varOmega \quad \text {(undecided).}\\ \end{array}\right. } \end{aligned}$$

(10)

The probabilities, which correspond to the three events of (10), follow from integrating the probability density function of $\hat{{\varvec{a}}}$ over the respective sets and are given by the success rate $P_\mathrm{s}$, the failure rate $P_\mathrm{f}$, and the rate for the undecided event $P_\mathrm{u} = 1 - P_\mathrm{s} - P_\mathrm{f}$.

In practice, the size and shape of $\varOmega _\mathbf {0}$, which uniquely define an IA estimator, are often inherently determined by testing the best integer vector ${\varvec{z}}_1$ against the second best integer vector ${\varvec{z}}_2$, where best is defined in the way of minimizing

$$\begin{aligned} {\varvec{z}}_1 = \mathrm {arg}\min _{{\varvec{z}}\in \mathbb {Z}^n} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| _{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}^2. \end{aligned}$$

(11)

Different tests of that form were mentioned in Sect. 1. In Verhagen (2004a) and Li and Wang (2013) it is shown, that these tests are valid members of the IA class.

3 Generalized integer aperture estimation

As described in the previous section, IA estimators either fix all entries of $\check{{\varvec{a}}}$ to integer values or completely remain with the float solution. This property is now relaxed, and it is rather allowed to fix a subset of ambiguities to integers, while the estimates for the remaining ambiguities, which cannot be fixed reliably, remain real valued.

Let the set of indexes of those ambiguities, which are fixed to integer values by the estimator be defined as

$$\begin{aligned} {\mathcal {I}} \subseteq \left\{ 1,\dots ,n \right\} , \quad {\mathcal {I}} \in {\mathfrak {I}}, \end{aligned}$$

(12)

where ${\mathfrak {I}}$ denotes the set of all possible index sets ${\mathcal {I}}$, i.e., the cardinality of ${\mathfrak {I}}$ is given by $\left| {\mathfrak {I}}\right| = 2^n$ (there are two choices for each ambiguity–fixing or not fixing). The complementary set $\bar{\mathcal {I}} \in {{\mathfrak {I}}}$ with

$$\begin{aligned} {\mathcal {I}} \cap \bar{\mathcal {I}} = \emptyset ,\quad {\mathcal {I}} \cup \bar{\mathcal {I}} = \left\{ 1,\dots ,n \right\} \end{aligned}$$

(13)

represents the subset of ambiguities, which is not fixed to integer values.

Each index set $\mathcal {I}$ is uniquely coupled with a generalized aperture region $\varOmega _{\mathcal {I}}$. The generalized IA estimator is given by

$$\begin{aligned} S\left( \hat{{\varvec{a}}} \right)&= \sum _{{\varvec{z}} \in \mathbb {Z}^n} \underset{i=1,\dots ,n}{\mathrm {diag}} \!\left[ w_{i,{\varvec{z}}}\! \left( \hat{{\varvec{a}}} \right) \right] {\varvec{z}} \nonumber \\&\quad + \left( {\varvec{I}}_n - \sum _{{\varvec{z}} \in \mathbb {Z}^n} \underset{i=1,\dots ,n}{\mathrm {diag}} \!\left[ w_{i,{\varvec{z}}} \!\left( \hat{{\varvec{a}}} \right) \right] \right) \hat{{\varvec{a}}}, \end{aligned}$$

(14)

with the binary indicator function

$$\begin{aligned} w_{i,{\varvec{z}}}\! \left( {\varvec{x}} \right) = {\left\{ \begin{array}{ll} 1 &{}\text {if } {\varvec{x}} \in \varOmega _{{\mathcal {I}},{\varvec{z}}} \text { and } i \in \mathcal {I} \\ 0 &{}\text {else}. \end{array}\right. } \end{aligned}$$

(15)

In (15), $\varOmega _{{\mathcal {I}},{\varvec{z}}}$ represents the generalized pull-in region for the integer vector ${\varvec{z}}\in \mathbb {Z}^n$ corresponding to the generalized aperture space $\varOmega _{\mathcal {I}}$. Essentially, if $\hat{{\varvec{a}}}\in \varOmega _{{\mathcal {I}},{\varvec{z}}}$, all ambiguities with index $i\in {\mathcal {I}}$ are fixed to the $i$th entry in ${\varvec{z}}$, whereas for the remaining ambiguities with index $i \in \bar{\mathcal {I}}$ the float solution of $\hat{{\varvec{a}}}$ is kept. Note that the undecided case of Sect. 2, where $S\left( \hat{{\varvec{a}}}\right) = \hat{{\varvec{a}}}$, is represented by the index set $\mathcal {I}=\emptyset$ and the region $\varOmega _\emptyset$.

Similar to (9), there are some attributes and desirable properties the generalized pull-in regions and aperture regions have to fulfill:

$$\begin{aligned} \begin{array}{cl} (i) &{} \bigcup _{{\varvec{z}} \in \mathbb {Z}^n} \varOmega _{{\mathcal {I}},{\varvec{z}}} = \varOmega _{\mathcal {I}}, \quad \forall \mathcal {I} \in {\mathfrak {I}}\\ (ii) &{} \bigcup _{{\mathcal {I}}\in {\mathfrak {I}}} \varOmega _{\mathcal {I}} = \mathbb {R}^n \\ (iii) &{} \varOmega _{{\mathcal {I}},{\varvec{z}}} \cap \varOmega _{{\mathcal {J}},{\varvec{u}}} = \emptyset , \\ &{}\qquad \left\{ \begin{array}{l} \forall {\mathcal {I}},{\mathcal {J}} \in {\mathfrak {I}} \\ \forall {\varvec{z}},{\varvec{u}} \in \mathbb {Z}^n \end{array}\right\} \Big \backslash \!\!\! \left( {\mathcal {I}} = {\mathcal {J}} \text { and } {\varvec{z}} = {\varvec{u}} \right) \\ (iv) &{} \varOmega _{{\mathcal {I}},{\varvec{z}}} = \varOmega _{{\mathcal {I}},\mathbf {0}} + {\varvec{z}},\quad \forall {\mathcal {I}}\in {\mathfrak {I}}, \forall {\varvec{z}} \in \mathbb {Z}^n. \end{array} \end{aligned}$$

(16)

The first property defines the generalized aperture region $\varOmega _{\mathcal {I}}$ for subset ${\mathcal {I}}$, which is composed of the generalized pull-in regions $\varOmega _{{\mathcal {I}},{\varvec{z}}}$. Condition $(ii)$ demands from the union of all $\varOmega _{\mathcal {I}}$ to cover the whole $\mathbb {R}^n$, which ensures that $S(\cdot )$ is defined for every possible value of $\hat{{\varvec{a}}}$. Condition $(iii)$ guarantees that $S(\cdot )$ is uniquely defined. Finally, condition $(iv)$ states the translational invariance of the generalized pull-in regions $\varOmega _{{\mathcal {I}},{\varvec{z}}}$ for each possible subset $\mathcal {I}$. As a counterpart to $(i)$, it is also possible to define

$$\begin{aligned} \bigcup _{{\mathcal {I}}\in {\mathfrak {I}}} \varOmega _{{\mathcal {I}},{\varvec{z}}} = \varOmega _{{\varvec{z}}}, \quad \forall {\varvec{z}} \in \mathbb {Z}^n. \end{aligned}$$

(17)

Note that $\varOmega _{{\varvec{z}}}$ as defined by (17) does not conform with the definition of $\varOmega _{{\varvec{z}}}$ in Sect. 2. With definitions $(ii)$–$(iv)$ from (17) it gets clear that $\varOmega _{{\varvec{z}}}$ rather describes the pull-in regions of admissible integer estimators like BS or ILS. In the examples for generalized IA estimators presented in Sect. 4, $\varOmega _{{\varvec{z}}}$ is equivalent to the ILS pull-in region of ${\varvec{z}}$.

For generalized IA estimators, the definition of the events success, failure, and undecided with their respective rates is not that clear as in the case of IA estimation. There are now cases which are partially undecided, and where only a subset of ambiguities is fixed correctly or incorrectly. The following three cases are defined¹:

$$\begin{aligned} \begin{array}{ll} \text {Success:} &{} \hat{{\varvec{a}}} \in \varOmega _{{\mathcal {I}}, {\varvec{z}}}, {\mathcal {I}}\in {\mathfrak {I}} {\setminus } \emptyset , {\varvec{z}} \in \mathbb {Z}^n \mid {\varvec{z}}_{({\mathcal {I}})} = {\varvec{a}}_{(\mathcal {I})} \\ \text {Failure:} &{} \hat{{\varvec{a}}} \in \varOmega _{{\mathcal {I}}, {\varvec{z}}}, \mathcal {I}\in {\mathfrak {I}} {\setminus } \emptyset , {\varvec{z}} \in \mathbb {Z}^n \mid {\varvec{z}}_{(\mathcal {I})} \ne {\varvec{a}}_{(\mathcal {I})}\\ \text {Undecided:} &{} \hat{{\varvec{a}}} \in \varOmega _{\emptyset }. \end{array} \end{aligned}$$

(18)

That is, whenever all ambiguities with index $i\in \mathcal {I}$ are fixed correctly, given that at least one ambiguity is fixed at all, this event is called success, whereas if only a single ambiguity is fixed wrongly, the event is called a failure. If no ambiguity is fixed at all, the event is called undecided. In the practical design of a generalized IA estimator, the failure rate $P_\mathrm{f}$, i.e., the probability of the event failure, is used to construct the size and shape of the different generalized pull-in regions.

4 Two exemplary generalized integer aperture estimators

In the previous section, the theoretical principles of generalized IA estimation were introduced along with the properties, which an admissible estimator of that class has to fulfill. Now, the question arises, how to actually construct the shape and size of the generalized pull-in regions. In accordance with Teunissen and Verhagen (2009) and Verhagen and Teunissen (2013), a predefined value for the failure rate $P_\mathrm{f}$ is given and the pull-in regions have to be defined such that this failure rate is not exceeded.

From the first step of the three step estimation framework in Sect. 2 the float ambiguity solution $\hat{{\varvec{a}}}$ is given. It is Gaussian distributed with deterministic, but unknown mean value ${\varvec{a}}$ and known covariance matrix ${\varvec{Q}}_{\hat{{\varvec{a}}}}$. The likelihood function for estimating the ambiguity vector ${\varvec{a}}$ based on the realization $\hat{{\varvec{a}}}$ is thus given by

$$\begin{aligned} L\left( \hat{{\varvec{a}}};{\varvec{z}}\right)&= \frac{1}{\sqrt{\left( 2\pi \right) ^n \left| {\varvec{Q}}_{\hat{{\varvec{a}}}} \right| }} \exp \left( -\frac{1}{2} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| ^2_{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}} \right) ,\quad {\varvec{z}} \in \mathbb {Z}^n.\nonumber \\ \end{aligned}$$

(19)

In the following, two generalized IA estimation schemes are presented. The first one is based on log-likelihood ratios (LLRs), a well-known tool for soft decisions in iterative algorithms for communication systems (see, e.g., Hagenauer et al. 1996), while the second one is based on the ratio of log-likelihood values (RLLs) for each single ambiguity. These two approaches turn out to correspond to a generalized version of the distance test and ratio test mentioned in Sect. 1.

4.1 LLR-based generalized integer aperture estimation

For each single ambiguity in the vector ${\varvec{a}}$ the computation of reliability information in form of a LLR is required. The LLR for the $i$th ambiguity is defined as

$$\begin{aligned} l_i \!\left( \hat{{\varvec{a}}}\right) = \log \frac{L\left( \hat{{\varvec{a}}};{\varvec{z}}_1\right) }{L\left( \hat{{\varvec{a}}};\bar{{\varvec{z}}}_{i} \right) },\quad i = 1,\dots ,n, \end{aligned}$$

(20)

where ${\varvec{z}}_1 \in \mathbb {Z}^n$ denotes the integer vector, which maximizes the likelihood function (19)

$$\begin{aligned} {\varvec{z}}_1 = \mathrm {arg}\max _{{\varvec{z}} \in \mathbb {Z}^n} L\left( \hat{{\varvec{a}}};{\varvec{z}}\right) , \end{aligned}$$

(21)

i.e, ${\varvec{z}}_1$ denotes the ILS ambiguity solution, which does not depend on the index $i$. The so-called counter-hypothesis $\bar{{\varvec{z}}}_{i}$ follows from the maximization problem

$$\begin{aligned} \bar{{\varvec{z}}}_{i} = \mathrm {arg}\max _{{\varvec{z}} \in \bar{\mathcal {Z}}_i} L\left( \hat{{\varvec{a}}};{\varvec{z}}\right) , \end{aligned}$$

(22)

where the set $\bar{\mathcal {Z}}_i$ is defined as ($z_{(i)}$ refers to the $i$th element of ${\varvec{z}}$)

$$\begin{aligned} \bar{\mathcal {Z}}_i = \left\{ {\varvec{z}} \in \mathbb {Z}^n \mid z_{(i)} \ne z_{1,(i)} \right\} . \end{aligned}$$

(23)

From (23), the chosen term counter-hypothesis should become clear: it is sought for the best possible integer vector (in terms of maximizing the likelihood function, i.e., the vector closest to the float solution $\hat{{\varvec{a}}}$), which differs in the $i$th ambiguity from the overall best integer vector ${\varvec{z}}_1$. In contrast to the unique ${\varvec{z}}_1$, the counter-hypotheses $\bar{{\varvec{z}}}_{i}$ can of course be different for each ambiguity. Combining (19), (20), (21), (22), (23), and considering the monotonicity of the logarithm, the problem of computing the LLR values reads

$$\begin{aligned} 2 l_i\!\left( \hat{{\varvec{a}}}\right) = \min _{{\varvec{z}} \in \bar{\mathcal {Z}}_i} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| ^2_{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}} - \min _{{\varvec{z}} \in \mathbb {Z}^n} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| ^2_{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}. \end{aligned}$$

(24)

According to (24), a first problem of LLR-based generalized IA estimation is to efficiently determine the ILS ambiguity solution, the counter-hypotheses for all $n$ ambiguities, and the respective weighted squared distances. This is further discussed in Sect. 4.3.

Once the $n$ LLR values $l_i\!\left( \hat{{\varvec{a}}}\right) ,\, i=1,\dots ,n,$ are determined, the index set $\mathcal {I}$ for the generalized pull-in regions is defined as

$$\begin{aligned} \mathcal {I} = \left\{ i=1,\dots ,n \mid l_i\!\left( \hat{{\varvec{a}}}\right) \ge l_\mathrm{th} \right\} , \end{aligned}$$

(25)

where $l_\mathrm{th} \ge 0$ is a predefined scalar threshold. From (14) and (15) follow the mapping of the float ambiguity vector $\hat{{\varvec{a}}}$ to the generalized IA ambiguity estimates. The size and shape of the generalized aperture regions $\varOmega _{\mathcal {I}}$ are inherently defined by (24) and (25), whereas the generalized pull-in regions $\varOmega _{{\mathcal {I}},{\varvec{z}}}$ are defined as

$$\begin{aligned} \varOmega _{{\mathcal {I}},{\varvec{z}}} = \lbrace {\varvec{x}} \in \mathbb {R}^n \mid \,&l_i\!\left( {\varvec{x}} \right) \ge l_\mathrm{th},\quad \forall i\in {\mathcal {I}} \nonumber \\&\text {and } l_i\!\left( {\varvec{x}} \right) < l_\mathrm{th},\quad \forall i\in \bar{\mathcal {I}} \nonumber \\&\text {and } {\varvec{z}} = \mathrm {arg}\max _{{\varvec{z}}' \in \mathbb {Z}^n} L\left( {\varvec{x}};{\varvec{z}}'\right) \rbrace . \end{aligned}$$

(26)

That is, all ambiguities $i$, which fulfill the requirement of the LLR value $l_i\!\left( \hat{{\varvec{a}}} \right)$ to be greater or equal as $l_\mathrm{th}$, are fixed to the ILS solution.

One way to choose the threshold $l_\mathrm{th}$ is to use a fixed value based on empirical studies, which is often proposed in the literature for IA acceptance tests [a summary of proposed values can be found in Li and Wang (2012)]. Preferably, $l_\mathrm{th}$ is chosen such that a fixed value for the resulting failure rate $P_\mathrm{f}$ is achieved. This is possible, as the threshold $l_\mathrm{th}$ defines the size (and, to some extend, also the shape) of the generalized pull-in regions. The failure rate is monotonically decreasing with increasing threshold $l_\mathrm{th}$ [see definition of failure in (18) and combine with (25)]. Following the latter approach, $l_\mathrm{th}$ is determined for the actual system model through a combination of Monte-Carlo simulations and a bisection method. An initial interval for $l_\mathrm{th}$, chosen sufficiently large to contain the sought for value, is iteratively divided in half by evaluating the (approximate) failure rate based on the simulations for $l_\mathrm{th}$ chosen as the center of the interval. Contrary to the LLR-based IA estimator, the success rate $P_\mathrm{s}$ of the LLR-based generalized IA estimator is not necessarily decreasing with increasing threshold $l_\mathrm{th}$.

It is to prove that the so-defined generalized pull-in regions $\varOmega _{{\mathcal {I}},{\varvec{z}}}$ form an admissible generalized IA estimator as defined by (16).

Proof From (17), with the three conditions of (26), and $l_i(\cdot ): \mathbb {R}^n \mapsto \mathbb {R}, i=1,\dots ,n$, $\varOmega _{{\varvec{z}}}$ is the ILS pull-in region.

With property $(i)$, condition $(ii)$ is automatically fulfilled, as ${\mathfrak {I}}$ covers all possible states of $\mathcal {I}$, and, therefore, all possible float solutions in $\mathbb {R}^n$.

With $\varOmega _{{\mathcal {I}},{\varvec{z}}} \cap \varOmega _{{\mathcal {J}},{\varvec{u}}} = \left( \varOmega _{\mathcal {I}} \cap \varOmega _{{\varvec{z}}}\right) \cap \left( \varOmega _{\mathcal {J}} \cap \varOmega _{{\varvec{u}}}\right)$, $\varOmega _{{\varvec{z}}} \cap \varOmega _{{\varvec{u}}} = \emptyset , \text {if } {\varvec{z}} \ne {\varvec{u}}$ (ILS pull-in regions do not overlap), and $\varOmega _{\mathcal {I}} \cap \varOmega _{\mathcal {J}} = \emptyset , \text {if } \mathcal {I} \ne \mathcal {J}$ and $l_\mathrm{th} \ge 0$, (iii) follows.

Finally, let ${\varvec{z}}_1$ and $\bar{{\varvec{z}}}_i$ denote the ILS solution and counter-hypothesis of (24), then the problem $l_i\left( \hat{{\varvec{a}}} + {\varvec{u}}\right) ,$ $\forall {\varvec{u}} \in \mathbb {Z}^n$, has the ILS solution ${\varvec{z}}'_1 = {\varvec{z}}_1 + {\varvec{u}}$ due to the translational invariance of the ILS pull-in regions, and counter-hypothesis $\bar{{\varvec{z}}}'_i = \bar{{\varvec{z}}}_i + {\varvec{u}}$, due to the regularity of the integer grid. Accordingly, a shift of $\hat{{\varvec{a}}}$ by an arbitrary integer vector ${\varvec{u}}$ leaves the LLRs invariant, i.e., $\mathcal {I}$ stays invariant, and thus with (26) $\varOmega _{{\mathcal {I}},{\varvec{z}}+{\varvec{u}}} = \varOmega _{{\mathcal {I}},{\varvec{z}}} + {\varvec{u}}, \forall {\varvec{u}} \in \mathbb {Z}^n$, which concludes the proof. $\square$

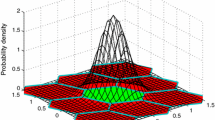
In Fig. 1, the four generalized aperture regions for the two-dimensional case are illustrated. The shape of the Gaussian distribution of $\hat{{\varvec{a}}}$ is characterized by the hexagonal ILS pull-in regions. The aperture region $\varOmega _{\lbrace 1,2 \rbrace }$ is equivalent to the aperture region of the classical IA estimator. The two generalized aperture regions $\varOmega _{\lbrace 1\rbrace }$ and $\varOmega _{\lbrace 2 \rbrace }$ are characterized by covering the area around the respective integer axes, where the statistical properties of the float solution are still considered.

Fig. 1

Shape of generalized aperture regions based on LLRs for the two-dimensional case. All $\hat{{\varvec{a}}}$ that fall in $\varOmega _{\lbrace 1,2 \rbrace }$, are fixed to the respective integer vector ${\varvec{z}}$, for all $\hat{{\varvec{a}}}$ in $\varOmega _{\lbrace 1 \rbrace }$/$\varOmega _{\lbrace 2 \rbrace }$, only the first/second component is fixed, while the float solution is kept if $\hat{{\varvec{a}}}$ falls in $\varOmega _{\lbrace \rbrace }$

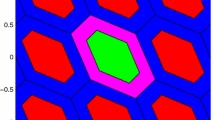
The regions of the three events success, failure, and undecided as defined in (18) are illustrated in Fig. 2 for a two-dimensional example. The region, for which the (partial) fixing is called successful, is now not only the hexagon $\varOmega _{\lbrace 1,2 \rbrace , {\varvec{a}}}$ but also the generalized pull in regions along the $a_{(1)}$ axis, where only $\check{a}_{(1)}$ is fixed correctly, and along $a_{(2)}$, where $\check{a}_{(2)}$ is fixed correctly. The failure region is characterized by at least one wrongly fixed ambiguity.

Fig. 2

The regions of the three events success, failure, and undecided as defined in (18) based on LLRs for the two-dimensional case

4.2 RLL-based generalized integer aperture estimation

Instead of using the LLRs for constructing a generalized IA estimator, the RLLs can be used alternatively. The RLL for the $i$th ambiguity is defined as

$$\begin{aligned} r_i' \left( \hat{{\varvec{a}}} \right) = \frac{\log L\left( \hat{{\varvec{a}}}; {\varvec{z}}_1 \right) }{\log L\left( \hat{{\varvec{a}}}; \bar{{\varvec{z}}}_i \right) },\quad i=1,\dots , n, \end{aligned}$$

(27)

where ${\varvec{z}}_1 \in \mathbb {Z}^n$ again denotes the ILS solution, which maximizes the likelihood function (19), cf. (21), and $\bar{{\varvec{z}}}_i \in \bar{\mathcal {Z}}_i$ the counter-hypothesis, cf. (22), (23).

The problem of computing the ratio values can be rewritten as

$$\begin{aligned} r'_i \left( \hat{{\varvec{a}}} \right) = \frac{\max _{{\varvec{z}} \in \mathbb {Z}^n} \left( -\frac{1}{2} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| _{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}^2\right) - c}{\max _{{\varvec{z}} \in \bar{\mathcal {Z}}_i} \left( -\frac{1}{2} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| _{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}^2\right) - c}, \end{aligned}$$

(28)

where $c$ denotes the constant term resulting from the normalization factor of the Gaussian distribution. A different version of the ratio is used in the following, i.e., this constant term $c$ is discarded, which causes slightly different ratio values:

$$\begin{aligned} r_i \left( \hat{{\varvec{a}}} \right) = \frac{\min _{{\varvec{z}} \in \mathbb {Z}^n} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| _{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}^2}{\min _{{\varvec{z}} \in \bar{\mathcal {Z}}_i} \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| _{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}^2}. \end{aligned}$$

(29)

Again, this problem reduces to efficiently determine the ILS solution and the counter-hypothesis for each ambiguity with the respective weighted squared distances to the float solution $\hat{{\varvec{a}}}$. The index set $\mathcal {I}$, which defines in which generalized aperture region the float solution falls, is defined by

$$\begin{aligned} \mathcal {I} = \left\{ i = 1,\dots ,n \mid r_i\left( \hat{{\varvec{a}}} \right) \le r_\mathrm{th} \right\} , \end{aligned}$$

(30)

with $0 < r_\mathrm{th} \le 1$ a predefined threshold. For the generalized pull-in region $\varOmega _{{\mathcal {I}},{\varvec{z}}}$ follows

$$\begin{aligned} \varOmega _{{\mathcal {I}},{\varvec{z}}} = \lbrace {\varvec{x}} \in \mathbb {R}^n \mid \,&r_i\!\left( {\varvec{x}} \right) \le r_\mathrm{th},\quad \forall i\in \mathcal {I} \nonumber \\&\text {and } r_i\!\left( {\varvec{x}} \right) > r_\mathrm{th},\quad \forall i\in \bar{\mathcal {I}} \nonumber \\&\text {and } {\varvec{z}} = \mathrm {arg}\max _{{\varvec{z}}' \in \mathbb {Z}^n} L\left( {\varvec{x}};{\varvec{z}}'\right) \rbrace . \end{aligned}$$

(31)

The proof that the so-defined generalized IA estimator is admissible follows the proof in 4.1. Figures 3 and 4 show the generalized pull-in regions of the RLL-based generalized IA estimator and the regions for the events success, failure, and undecided, respectively (cf. Figs. 1, 2). The borders of the different generalized aperture regions are defined by intersecting ellipsoids [see Verhagen and Teunissen (2006)]. Compared to the LLR-based scheme, the curvature of the ellipsoids mainly affects the result toward the boundaries of the ILS pull-in regions, especially for rather restrictive values of $r_\mathrm{th}$, which leads to the gaps of $\varOmega _{\lbrace 1 \rbrace }$ and $\varOmega _{\lbrace 2 \rbrace }$ in the given example. For ratio values $r_i(\hat{{\varvec{a}}})$ as defined in (29), the failure rate $P_\mathrm{f}$ is increasing with $r_\mathrm{th}$, which allows for the fixed failure rate approach. Again, this does not hold for the success rate $P_\mathrm{s}$ as it would for the RLL-based classical IA estimator.

Fig. 3

Shape of generalized aperture regions based on RLLs for the two-dimensional case, cf. Fig. 1

Fig. 4

The regions of the three events success, failure, and undecided as defined in (18) based on RLLs for the two-dimensional case

4.3 Low complexity tree search formulation

The problems of finding the ILS ambiguity solution and the $n$ counter-hypotheses for the computation of the ratio values $l_i\left( \hat{{\varvec{a}}}\right)$ in (24) and $r_i\left( \hat{{\varvec{a}}}\right)$ in (29) are addressed. With the Cholesky decomposition of the inverse covariance matrix ${\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1} = {\varvec{G}}^\mathrm{T}{\varvec{G}}$, with ${\varvec{G}} \in \mathbb {R}^{n \times n}$ a right upper triangular matrix, the weighted squared distances can be expressed in the recursive form

$$\begin{aligned} d\left( {\varvec{z}}\right) = \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| ^2_{{\varvec{Q}}_{\hat{{\varvec{a}}}}^{-1}}&= \sum _{i=1}^n \left( \sum _{j=i}^n G_{(i,j)} \left( \hat{a}_{(j)} - z_{(j)} \right) \right) ^2 \nonumber \\&= \sum _{i=1}^n e_i(z_{(n)},\dots ,z_{(i)} ). \end{aligned}$$

(32)

The computation of the expression in the parentheses for the $i$th element depends only on all elements $z_{(j)}$ with $j\ge i$ ($G_{(i,j)} = 0, \forall j<i$). Starting with level $i=n$, the partial squared distance $d_i\left( z_{(n)},\dots ,z_{(i)} \right)$ can be expressed as

$$\begin{aligned} d_i\left( z_{(n)},\dots ,z_{(i)} \right)&= d_{i+1}\left( z_{(n)},\dots ,z_{(i+1)} \right) \nonumber \\&+\, e_i(z_{(n)},\dots ,z_{(i)}), \end{aligned}$$

(33)

with initial value $d_{n+1} = 0$ and $d_1 ({\varvec{z}}) = d({\varvec{z}})$. With all distance increments $e_i\left( \cdot \right)$ being non-negative, solving problems (24) and (29) can be considered tree search problems. Nodes of the search tree correspond to partial distances $d_i(\cdot )$ and branches, which correspond to different values for the respective ambiguity, to distance increments $e_i(\cdot )$. The tree is restrained to nodes within a radius $\chi ^2$ around $\hat{{\varvec{a}}}$. The search is performed depth first following the Schnorr-Euchner strategy, i.e., smallest distance increments $e_i\left( \cdot \right)$ first (Schnorr and Euchner 1994).

Two basic questions arise from that formulation: How to choose an efficient tree traversal strategy, and how to determine the search radius $\chi ^2$ around the float solution $\hat{{\varvec{a}}}$, such that the number of integer grid points within that radius $\chi ^2$ is as small as possible.

4.3.1 Tree traversal strategies

There are two fundamentally different strategies on how to search the tree corresponding to (32) for solving problems (24) and (29). The first possibility is to perform a repeated tree search. Thereby, the tree is first searched for the integer candidate ${\varvec{z}}$ with the smallest weighted squared distance $d({\varvec{z}})$ (which is the ILS solution ${\varvec{z}}_1$). After ${\varvec{z}}_1$ has been found, $n$ additional search runs are performed for all counter-hypotheses $\bar{{\varvec{z}}}_i$. The restriction to the set $\bar{\mathcal {Z}}_i$ is equivalent to blocking all branches, which correspond to $z_{1,(i)}$ of the ILS solution.

Obviously, such a repeated search implies a high computational burden, which can be considerably decreased by the single tree search approach, which guarantees that each node of the tree is at most visited once. This approach is based on the administration of a list, which stores the best candidates for the ILS estimate and all counter-hypotheses found so far. Whenever a leaf ${\varvec{z}}$ of the tree is reached, following cases have to be distinguished:

• 1. $d({\varvec{z}}) < d({\varvec{z}}_1)$: An improved candidate for the ILS solution is found, i.e., update $\bar{{\varvec{z}}}_i \leftarrow {\varvec{z}}_1, \forall i \mid z_{1,(i)} \ne z_{(i)}$, and ${\varvec{z}}_1 \leftarrow {\varvec{z}}$.

• 2. $d({\varvec{z}}) > d({\varvec{z}}_1)$: Check, if counter-hypotheses have to be updated, i.e., $\bar{{\varvec{z}}}_i \leftarrow {\varvec{z}}, \forall i \mid z_{(i)} \ne z_{1,(i)} \text { and } d({\varvec{z}})< d(\bar{{\varvec{z}}}_i)$.

All distances $d(\bar{{\varvec{z}}}_i), i=1,\dots ,n$, and $d({\varvec{z}}_1)$ are initialized with infinity. A similar strategy has been developed in the context of MIMO detection in Studer and Bölcskei (2010) and Jaldén and Ottersten (2005).

4.3.2 Setting the search radius

Only the single tree search strategy is considered. If it was just to find the ILS solution ${\varvec{z}}_1$, the goal would be to determine the radius $\chi ^2$ of the search space such that exactly one candidate lies within that radius—the ILS solution itself. However, as not only the ILS solution ${\varvec{z}}_1$ has to be found, but also $n$ counter-hypotheses $\bar{{\varvec{z}}}_i, i=1,\dots ,n$, a larger value for $\chi ^2$ has to be considered.

Actually, it is not really necessary to compute the true ratios $l_i(\hat{{\varvec{a}}})$ or $r_i(\hat{{\varvec{a}}})$ for all ambiguities $i=1,\dots ,n$, as it is only decisive, if the ratio $l_i(\hat{{\varvec{a}}}) \ge l_\mathrm{th}$ or $r_i(\hat{{\varvec{a}}}) \le r_\mathrm{th}$, respectively [cf. (25) and (30)]. As a consequence, if no counter-hypothesis $\bar{{\varvec{z}}}_i$ is found within the search space with radius

$$\begin{aligned} \chi ^2 = d({\varvec{z}}_1) + l_\mathrm{th}\quad \text {and}\quad \chi ^2 = \frac{d({\varvec{z}}_1)}{r_\mathrm{th}} \end{aligned}$$

(34)

for the LLR- and RLL-based approach, respectively, it automatically follows

$$\begin{aligned} l_i(\hat{{\varvec{a}}}) \ge l_\mathrm{th} \quad \text {and}\quad r_i(\hat{{\varvec{a}}}) \le r_\mathrm{th}. \end{aligned}$$

(35)

The unknown value $d({\varvec{z}}_1)$ can be upper bounded by $d({\varvec{z}}_\mathrm{BS})$, with ${\varvec{z}}_\mathrm{BS}$ the easily computable BS ambiguity estimate (also simple, component-wise rounding of $\hat{{\varvec{a}}}$ is a viable option). An illustration for setting the size of the search space is provided in Fig. 5.

Fig. 5

The fundamental relation between the squared distance of ILS solution and float solution $d({\varvec{z}}_1)$, the given ratio thresholds $l_\mathrm{th}$ and $r_\mathrm{th}$, and the radius $\chi ^2$ of the search ellipse is illustrated. For the RLL-based approach, $l_\mathrm{th}$ is replaced by $d({\varvec{z}}_1)\left( \frac{1}{r_\mathrm{th}}-1\right)$

The complexity of the tree search can be further minimized by optimized tree pruning, i.e., by shrinking the search space, when a new candidate for ${\varvec{z}}_1$ has been found, or as soon as a valid counter-hypothesis $\bar{{\varvec{z}}}_i$ has been found $\forall i=1,\dots ,n$.

4.3.3 Integer decorrelation/lattice reduction

A substantial complexity reduction is to be expected through the use of a prior integer decorrelation ${\varvec{Z}} \in \mathbb {Z}^{n\times n}$, such as the iterative transformation of the LAMBDA method in Teunissen (1995) or the LLL lattice reduction in Lenstra et al. (1982). The decorrelation possibly comprises a sorting of the float ambiguity estimates according to their precision, which allows for removing large parts of the search tree, if the search is started with the most precise estimates. Such a transformation does not change the weighted squared distances

$$\begin{aligned} d({\varvec{z}}) = \left\| \hat{{\varvec{a}}} - {\varvec{z}} \right\| ^2_{{\varvec{Q}}^{-1}_{\hat{{\varvec{a}}}}} = \left\| {\varvec{Z}} \hat{{\varvec{a}}} - {\varvec{z}}' \right\| ^2_{{\varvec{Q}}^{-1}_{{\varvec{Z}}\hat{{\varvec{a}}}}},\quad \forall {\varvec{z}} \in \mathbb {Z}^n, \end{aligned}$$

(36)

with ${\varvec{Z}}$ any unimodular matrix (${\varvec{Z}}$ invertible and ${\varvec{Z}}^{-1} \in \mathbb {Z}^{n\times n}$), ${\varvec{z}}' = {\varvec{Z}} {\varvec{z}}$, and ${\varvec{Q}}_{{\varvec{Z}}\hat{{\varvec{a}}}} = {\varvec{Z}} {\varvec{Q}}_{\hat{{\varvec{a}}}} {\varvec{Z}}^\mathrm{T}$. Therefore, the results of the LLR- and RLL-based IA estimators, which only depend on the two closest integer vectors (e.g., Verhagen 2004a), are not affected by the use of ${\varvec{Z}}$.

The situation for generalized IA estimation is quite different. The result of the estimator completely changes, if the counter-hypotheses $\bar{{\varvec{z}}}_i, i=1,\dots ,n,$ are found for the transformed ambiguities ${\varvec{Z}} \hat{{\varvec{a}}}$ instead for the original ambiguities $\hat{{\varvec{a}}}$. In case the original space is used, the search can still be done in the decorrelated space with low complexity. Each integer candidate, which is found in the search, has to be back-transformed before building up the list of candidates for the counter-hypotheses of the single tree search approach.

The preferable strategy is to compute the estimates after decorrelating as far as possible. In the original space of ambiguities it is not unlikely that the best candidate ${\varvec{z}}_1$ and the second-best candidate differ in many or even all entries, which causes equal LLR or RLL values for many ambiguities. This reduces the advantage of the generalized IA scheme compared to conventional IA estimation.

4.4 Conditioning

If the failure rate is chosen sufficiently small, the precision of the estimate of the real-valued parameter vector ${\varvec{b}}$ can be further increased by conditioning the ambiguity estimates with indexes $\bar{\mathcal {I}}$, which are not fixed to integers, on the fixed ambiguities, instead of just keeping the float solution $\hat{{\varvec{a}}}_{(\bar{\mathcal {I}})}$:

$$\begin{aligned} \check{{\varvec{a}}}_{(\bar{\mathcal {I}})}&= \hat{{\varvec{a}}}_{(\bar{\mathcal {I}})} \!\mid \! {\varvec{z}} \big |_{{\varvec{z}} = \check{{\varvec{a}}}_{\left( \mathcal {I} \right) }} \nonumber \\&= \hat{{\varvec{a}}}_{(\bar{\mathcal {I}})} - {\varvec{Q}}_{\hat{{\varvec{a}}},(\bar{\mathcal {I}},{\mathcal {I}})} {\varvec{Q}}^{-1}_{\hat{{\varvec{a}}},({\mathcal {I}}, {\mathcal {I}})} \left( \hat{{\varvec{a}}}_{\left( \mathcal {I} \right) } - \check{{\varvec{a}}}_{\left( \mathcal {I}\right) } \right) . \end{aligned}$$

(37)

This additional step is primarily recommended before the back-transformation from the decorrelated space to the original space via ${\varvec{Z}}^{-1}$, i.e., if the counter-hypotheses are found for the decorrelated ambiguities. Otherwise, the estimates $\hat{{\varvec{a}}}_{( \bar{\mathcal {I}} )}$ can be treated as additional entries of $\hat{{\varvec{b}}}$ in (5).

5 Numerical results

The results are based on simulated single epoch, single frequency pseudorange and carrier-phase measurements for two receivers located in Munich. Galileo E1 signals with a frontend bandwidth of $20\,\mathrm {MHz}$ are used. The strength of the system model is varied by choosing a subset of $k$ satellites out of the $11$ visible satellites as seen by the receivers (Fig. 6). The noise of the undifferenced measurements is assumed as additive white Gaussian noise with standard deviations $\sigma _\rho$ and $\sigma _\varphi$ for pseudorange and carrier-phase measurements, respectively. In the system model (1), ${\varvec{y}}$ contains $k-1$ double difference pseudorange and $k-1$ double difference carrier-phase measurements. The $k-1$ double difference ambiguities are stacked in ${\varvec{a}}$, and ${\varvec{b}}$ is the three-dimensional baseline vector. The differencing removes all receiver- and satellite-dependent biases. Atmospheric delays are assumed to be sufficiently suppressed because of a short baseline. The noise vector $\varvec{\eta }$ is Gaussian distributed, where the covariance matrix ${\varvec{Q}}_{\varvec{\eta }}$ follows from the diagonal covariance matrix of the undifferenced measurements through the double difference operator. Table 1 summarizes the simulation parameters and states the failure rates of ILS for the six given satellite selections. For each scenario, $2\cdot 10^6$ random samples are drawn.

Fig. 6

Skyplot of Galileo constellation as used in the simulations

Table 1 System parameters for 11 visible satellites, the subscripts for $k=8$ refer to different satellite geometries

For the practical use of classical and generalized IA estimators with a fixed failure rate, the corresponding success rate is an important measure. The success rates $P_\mathrm{s}$ as a function of the failure rate $P_\mathrm{f}$ are shown in Fig. 7 for $k=6$, $k=7$, and $k=8$ (scenario $8_1$) satellites. For generalized IA estimation, the counter-hypotheses are found in the decorrelated space of integers using the ${\varvec{Z}}$ transformation of the LAMBDA method. For all three scenarios, and both for LLR- and RLL-based estimation, the gain of the novel schemes compared to classical IA estimation is remarkable. This is in particular the case for low values of the failure rate, which is the desired operating point. As already described, Fig. 7 confirms that the success rate of generalized IA estimators does not necessarily decrease with decreasing failure rate. The results indicate that the LLR-based generalized IA scheme is more powerful than the RLL-based scheme.

Fig. 7

Success rates as a function of the failure rate for generalized IA estimators (GIA) and IA estimators, based on both LLR and RLL values. The three subfigures represent from left to right $k=6$, $k=7$, and $k=8$ (scenario $8_1$) satellites

Note that the last subfigure has a different scale. This is caused by the strength of the system model, which excludes failure rates of $P_\mathrm{f} \ge 3.52\,\%$ for the considered schemes.

However, for choosing an estimation scheme, the success rate is not the decisive quantity, but rather the precision of the estimate of ${\varvec{b}}$. If all ambiguities are fixed correctly, this precision is driven by the highly precise carrier-phase measurements. Hence, also the average number of fixed ambiguities is a criterion. For generalized IA estimation this number is given by $\mathrm {E}\left[ \left| \mathcal {I}\right| \right]$, for IA estimation by $n(P_\mathrm{s}+P_\mathrm{f})$. In Table 2, these numbers are presented for a fixed failure rate of $P_\mathrm{f} = 0.1\,\%$. Table 2 also indicates a slight advantage of the LLR-based generalized IA scheme over the RLL-based scheme, and a clear gain compared to IA estimation.

Table 2 Average number of fixed double difference ambiguities, failure rate $P_\mathrm{f} = 0.1\,\%$

Finally, Figs. 8, 9, 10 show the complementary cumulative distribution function of the norm of the baseline error

$$\begin{aligned} P_e = \mathrm {Pr} \left( \Vert \tilde{{\varvec{b}}} - {\varvec{b}} \Vert _2^2 \ge e \right) , \end{aligned}$$

(38)

where $\tilde{{\varvec{b}}}$ is either the float solution $\hat{{\varvec{b}}}$, or $\check{{\varvec{b}}}$ from ILS, IA or generalized IA estimation. For a fixed failure rate of $P_\mathrm{f} = 0.1\,\%$, it is aimed at minimizing this tail distribution function. The most interesting cases – for the given failure rate – are the ones with $k=8$ satellites and ILS failure rates between $3.52\,\%$ and $0.58\,\%$. For $k<8$ and $k>8$, the fixed failure rate of $P_\mathrm{f} = 0.1\,\%$ would have to be adapted in order to account for the strength of the system model to see a clear distinction of the (generalized) IA estimators compared to the float and ILS solution, respectively. Figure 8 shows that the probability $P_e$ of the ILS solution drops very soon due to the relatively high probability of correct fixing, but there is also a high error floor for $e \ge 1\,\mathrm {m}$. Compared to ILS, the two IA estimators are characterized by higher values of $P_e$ for very small errors $e$, but show much better performance for large errors $e \ge 1\,\mathrm {m}$. Generalized IA estimation outperforms classical IA estimation practically over the whole error range. Thereby, the gain of the LLR-based scheme is roughly one order of magnitude for $0.3\,\mathrm {m}\le e \le 1\,\mathrm {m}$, while the RLL-based scheme still shows a gain of roughly half a order of magnitude. All in all, the LLR-based schemes clearly outperform the RLL-based schemes for a wide range of errors. Yet, for $e\ge 1.25\,\mathrm {m}$, RLL starts to show better performance.

Fig. 8

The probability of the norm of the baseline error to exceed $e$ for generalized IA (GIA) and IA estimators, for $k=8$ satellites (scenario $8_1$) and fixed failure rate $P_\mathrm{f} = 0.1\,\%$

Fig. 9

Corresponding to Fig. 8 for scenario $8_2$; $k=8$ satellites; failure rate $P_\mathrm{f} = 0.1\,\%$

Fig. 10

Corresponding to Fig. 8 for scenario $8_3$; $k=8$ satellites; failure rate $P_\mathrm{f} = 0.1\,\%$

With increasing strength of the underlying system model, i.e., with decreasing ILS failure rate ($1.26\,\%$ for Fig. 9 and $0.58\,\%$ for Fig. 10), some interesting effects can be observed. As Fig. 7 and Table 2 already indicate, the differences between IA and GIA schemes get smaller, but are still present, albeit for a smaller error range. Compared to Fig. 8, the RLL-based schemes show better performance for stronger system models, which is practically equal to the performance of the LLR-based schemes for scenario $8_3$ in Fig. 10.

6 Conclusion

A new class of integer ambiguity estimators was introduced, which extends the concept of IA estimation to partial ambiguity fixing. After a general definition of this class, two specific, low-complexity realizations were provided. Both of them are capable of the fixed failure rate approach. The performance gain compared to IA estimation for a predefined failure rate was examined through numerical simulations. So far, the threshold values for selecting the subset of ambiguities to be fixed with the given failure rate constraint were determined based on Monte-Carlo simulations. For a practical implementation, the use of a look-up table as proposed in Verhagen and Teunissen (2013) for IA estimation is a promising tool.

The two realizations of GIA estimators as presented in this paper can be quite easily integrated in the popular LAMBDA method. After the threshold value $l_\mathrm{th}$ or $r_\mathrm{th}$ has been determined, the search radius follows from (34). The search algorithm of the LAMBDA method (see De Jonge and Tiberius 1996) has to be modified in the way that not the best integer candidates are stored, but rather the list of candidates as described in 4.3.1. From this list and the acceptance tests (25) or (30) follow the final ambiguity estimates.