1 Introduction

Topology optimization obtains an optimal material layout for a structural design problem for an objective subject to a constraint or set of constraints [1, 2] while additive manufacturing (AM) is a layer-by-layer process of joining material from a 3D model data [3, 4]. Years of development and innovation have introduced a synergistic relationship between topology optimization and additive manufacturing. Before this unique connection was formed, topology optimization was relegated to theoretical formulations [5, 6] because the resultant optimal structures often consist of complex features that are difficult or sometimes impossible to produce by traditional manufacturing technologies. Many AM technologies can handle the production of components with intricate features [7,8,9,10] although there are both process- and structural-based challenges that can either reduce print quality or inhibit print success altogether. A combination of topology optimization and additive manufacturing has ensured that both technologies attain their full potential [11,12,13,14,15].

Some manufacturing challenges in AM that researchers have attempted to resolve using topology optimization and related solutions are overhanging features [16,17,18,19,20,21,22,23,24,25,26], minimum feature size or size control [27,28,29], cavity or void filling [30,31,32,33,34], build orientation optimization [35,36,37,38], anisotropy control [39,40,41], support structure optimization [42,43,44,45,46,47], residual stress and/or distortion minimization [48,49,50]. This study focuses on overhang feature elimination since it directly impacts printability and down-skin surface roughness; these are some reasons it has garnered arguably the most attention from researchers of all structural-based manufacturing constraints. Many efforts to restrict overhang features can be broadly divided into topology optimization integrated approaches and post-topology optimization approaches. Integrated approaches are built into topology optimization models either by formulating some overhang restrictive filters [12, 13, 16, 51], overhang constraints [6, 52], or additional objective functions [10]. Gaynor and Guest [12] transformed the independent physical density variable in density-based topology optimization to a dependent variable defined by a support density function and an independent density design variable. In their formulation, the support density function is a projection of the densities of elements below an element under investigation and within a prescribed angle region. Their methodology produces quality results but several parameters require tuning depending on the design problem. Also, the methodology is dependent on the optimizer (MMA in this case) like many integrated approaches are. In a similar fashion as Gaynor and Guest [12], Langelaar [13] introduced a printed density variable as a function of an independent blueprint density and a printed density of supporting elements. However, in contrast, Langelaar [13] defined the printed density of supporting elements as a smooth approximation of the maximum density of three supporting elements (in the 2D case) since the max or min of several numbers is not differentiable. Unfortunately, this methodology is limited to an overhang angle threshold of 45°. Van de Ven et. al. [21] introduced an overhang filter by detecting overhanging features using a front propagation method that tracks a curve or surface as it evolves. Garaigordobil et.al. [6] and Zhao [52] formulated overhang constraints added to the material volume constraint in their topology optimization problem definition. In the former, after contour detection is done, the constraint is computed as a ratio of the number of self-supported contours to the total number of acceptable and unacceptable contours. The latter work by Zhao constituted the overhang constraint by summing the density squares of unsupported elements. Using Bi-directional Evolutionary Structural Optimization (BESO), Minghao et.al. [53] developed a layer-wise overhang restriction constraint within the updating scheme. The framework using uniform cuboid voxels can achieve 45° overhang thresholds while arbitrary angle thresholds can be implemented by changing the aspect ratio of the voxels. Wang et.al. [10] formulated a consolidated objective function comprising compliance and an overhang function and then attempted to simultaneously minimize both. In this case, instead of eliminating overhangs, their results included some unsupported features as might be expected in an only compliance minimization scheme.

Post-topology optimization approaches involve identifying and modifying overhanging features after topology optimization is carried out; the pioneering work on this was done by Leary et.al. [17]. In the methodology by Leary et.al. [17], they identify infeasible domains in the optimized topology and introduce support-free trusses. They also optimize the build orientation by assessing the manufacturing time and mass of several viable orientations. Their methodology is implemented outside the voxel field of the optimized topology and therefore, theoretical performance characterization of the manufacture-enabled design might be difficult. Also, there is a significant increase in the volume when support-free trusses are added thereby violating the volume constraint to the design problem. There have been other ingenious efforts put into solving the overhang feature problem: one is by Mass and Amir [18] using a virtual skeleton being the discrete optimization of a truss system considering an overhang angle threshold which is then projected to a design field that influences a continuum optimization stage. Another innovative work done by Guo et.al. [19] achieves overhang elimination by optimizing a set of geometric parameters based on Moving Morphable Components (MMC) and Moving Morphable Volume (MMV) in an explicit topology optimization framework.

This research centers on the enhancement of topology-optimized structures to possess inherent self-supporting characteristics. The primary objective is to relieve the iterative optimization process from the task of establishing internal structural support. In this new post-topology optimization method, every stage of transforming theoretically optimal structures to manufacture-enabled structures from the identification of unsupported features to the introduction of support-free trusses is done within the density voxel field of the optimized topology. Also, to eliminate the increase in material volume which naturally characterizes post-topology optimization methods, a volume correction stage is included and is optional depending on the user’s preferences. Another key importance of post-topology optimization methods is their independence from optimizers, interpolations functions, and other ‘tuning’ parameters that may affect the optimization process. The overhang elimination process will be presented for 2D cases in this article and will be extended to 3D cases in the future.

2 Description of methodology

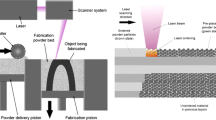
In this study, Laser Powder-Bed Fusion (LPBF) AM is considered since support structures are typically imperative in this technology. LPBF, as shown in Fig. 1 uses metal powder in a bed as feedstock which a laser selectively scans layer by layer (likened to a micro-welding process [54]) till the part is printed from bottom to top [55, 56]. A foremost design rule for this technology is introducing sacrificial supports for overhanging features with inclination angles less than 40° to the build plate for print success [57] and for limiting poor surface roughness on the down skin [58, 59]. Leary et. al. [60] identified three distinct zones for overhanging features in FDM: Robust zone, \(\upphi \ge 40^\circ\) with features having no identifiable defect, compromised zone, \(30^\circ \le\upphi <40^\circ\), with features having identifiable defects and failed zone, \(\upphi <30^\circ\) with features that are completely not self-supporting. In many cases, the minimum overhanging feature angle applied during pre-processing for LPBF and other AM technologies that require support structures can range between 35° and 50°. In the current methodology, support trusses inclined at a specified minimum angle are introduced into the optimized topology in unsupported areas.

Fig. 1
figure 1

The layout of a typical LPBF machine showing major components

Full size image

2.1 Detecting overhanging features

The process of detecting overhanging features is done in two major steps: first, identifying the boundary of the topologically optimized design using mesh nodes, and second, extracting nodes from boundary nodes that define overhanging or unsupported features according to an imposed self-supporting angle threshold. The density-based gradient topology optimization method is adopted in this study and homogenous, uniform four-node bilinear shapes are the element type.

2.1.1 Boundary identification

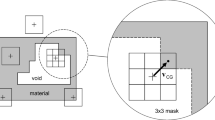
The topological boundary is defined by boundary nodes that are selected by comparing the mean density of elements around a mesh node with a threshold value. As observed in Fig. 2, node \(n\) is surrounded by elements with density \({x}_{n,i}\); the mean density value, \({\overline{x} }_{n,i}\) is compared to a threshold density value \({f}_{th}\). If \({\overline{x} }_{n,i}\) is lower than \({f}_{th}\), node \(\mathrm{n}\) is selected as a boundary node. \({f}_{th}\) in this study is 0.1 and it can be tightened or relaxed depending on the contrast of the topological boundary. Furthermore, for optimal designs that might have a significant number of intermediate-density elements, elements \({x}_{sn,l}\) associated with nodes \(Sn\) surrounding node \(n\) are also used in the selection of boundary nodes. \({x}_{n,i}\) is a vector of density elements surrounding node \(n\) for \(i\) ranging from 1 to 4 for 2D quadrilateral elements and 1 to 12 for 3D hexahedral elements while \({x}_{sn,l}\) is the corresponding vector of density elements surrounding node \(Sn\) for \(\mathrm{l}\) from 1 to 4. For every node \(n\), there are four \(Sn\) nodes in the 2D domain and six in the 3D domain. Boundary nodes in a 2D domain can be chosen by the selection criteria [61]:

Fig. 2
figure 2

Identifying a boundary node and its surrounding nodes in a topological boundary

Full size image
$$\mathrm{b}n=\left\{\begin{array}{cc}n& \langle \forall ({\overline{x} }_{sn,l}<{f}_{th})\in \left[\mathrm{1,2}\right]\rangle \parallel \langle \left\{\forall ({x}_{n,i}>0)=2\right\}\wedge \left({\overline{x} }_{n,i}>{f}_{th}\right)\rangle \\ \mathrm{Nil}& \mathrm{any\;other\;case}\end{array}\right.$$
(1)

2.1.2 Identifying unsupported features

The angles subtended by the tangents to the topological boundary at every boundary node obtained in 2.1.1 are computed. Using an optimized half MBB beam, these tangent angles defined in (2) are graphically described in Fig. 3

Fig. 3
figure 3

Boundary nodes (blue squares) of an optimized design with an enlarged portion showing coordinates C1 (\({u}_{1},{v}_{1}\)) and C2 (\({u}_{2},{v}_{2}\)) of the line tangent at a node bn

Full size image
$${\theta }_{bn}={\mathrm{tan}}^{-1}\left(\frac{{v}_{2}-{v}_{1}}{{u}_{2}-{u}_{1}}\right)$$
(2)

In (2), for a boundary node \(bn\), C1 (\({u}_{1}\),\({v}_{1})\) is the cartesian coordinate of the closest node (apart from those that are one element away from \(\mathrm{bn}\) along \(\overrightarrow{u}\)) on the left of \(\mathrm{bn}\); the same analogy follows for C2. Equation (2) is calculated for all boundary nodes and each angle is compared with the overhang angle threshold. To select nodes that define overhanging edges or surfaces, the selection criteria are applied:

$$ovn=\begin{array}{cc}bn& \left\{({\theta }_{bn}<{\theta }_{thresh})\wedge \left({\overline{x} }_{bn+\xi ,i}<0.1{f}_{th}\right)\right\}\\ \mathrm{Nil}& \mathrm{any\;other\;case}\end{array}$$
(3)

In (3), \(ovn\) is a set of nodes that define overhanging edges, \({\theta }_{thresh}\) is the feature inclination angle limit or overhanging angle threshold while \(\xi\) is a small movement from a node in \(ovn\) to another mesh node vertically downwards. The parameter \(\xi\) which is elaborately described in [61] is in this study assigned as two nodes away from the \(ovn\) node under investigation in the downward vertical direction. Overhanging features in the optimized topology in Fig. 3 can be observed in Fig. 4 for a 45° angle threshold. To maintain a definite edge in the overhanging regions, a continuous connection of the overhanging nodes is made as observed in the enlarged portion of Fig. 4. We recall that the overhang nodes, \(ovn\) are drawn from boundary nodes \(bn\) which are located at the element vertices or mesh grid of the design domain. Moving forward, these nodes are repositioned to element centers for convenience.

Fig. 4
figure 4

Nodes in orange showing overhanging edges for the optimized topology in Fig. 3. The enlarged region shows an edge connection made in purple

Full size image

Once unsupported features are identified, the next step of adding self-supported trusses is initiated.

2.2 Introducing support-free trusses

To introduce support-free trusses into an optimized topology, geometrical forms of topology-optimized designs against overhang elimination in literature are first analyzed. Most of these studies in literature have results with geometrically similar internal features [6, 12, 13, 17, 51, 62]. Results from three studies [12, 13, 17] are shown in Fig. 5

Fig. 5
figure 5

Optimized topologies considering overhang elimination from studies by (a) Gaynor and Guest [13], (b) Langelaar [14], (c) Leary [16]. Similar self-supporting internal structures are highlighted in green and yellow

Full size image

The geometrical similarities in Fig. 5 can be observed in the internal features which consistently have two parts: the highlighted green portion which will be designated as a ‘root’ and a yellow portion designated as a ‘stem’. A combination of the root and stem will represent a self-supported truss member to be introduced in an unsupported optimal topology for overhang elimination. Therefore, the focus will be drawn on modeling this root and stem for every truss member.

  1. i.

    Modeling the root: In the enlarged portion in Fig. 4, the nodes that form the edge connection are used to define the new truss’s root, and these nodes are shown in Fig. 6(a) again. The base length of the root is determined by two nodes which are a distance \(\chi\) nodes apart, in Fig. 6(a), \(\chi\) is 5 nodes. Invariably, a longer χ translates to a larger truss root while a shorter \(\upchi\) to a smaller truss root. The angle of inclination of a line joined by these two nodes is calculated and will be designated as \({\theta }_{\chi }\). If the overhang angle threshold is \({\theta }_{thresh}\), as shown in Fig. 6(b), projections of \({\theta }_{thresh}-{\theta }_{\chi }\) and \({{\theta }_{thresh}+\theta }_{\chi }\) are made on the design elements from the two nodes. The elements in the intersection (Fig. 6(c)) of these projections form the truss root in Fig. 6(d) and are assigned as solids with a density value of 1. All elements that form the root of the self-supported truss are shown in green in Fig. 6.

  2. ii.

    Modeling the stem: First, the lowest element in the root is identified, then all other elements inclined at approximately \({\theta }_{thresh}\) downwards from this element are identified and assigned as solids (Fig. 6(e,f)). The direction of projection from the lowest element is made the same as that of the overhang nodes for the first support-free truss on the overhanging feature. As observed in Fig. 6(g), this direction is changed for the next truss stem but the same angle \({\theta }_{thresh}\) is maintained.

Fig. 6
figure 6

Stages in modeling support-free trusses for an overhanging feature. a-d modeling the root (e, f) modeling the stem g introducing a second truss

Full size image

From the steps, we can expect a ‘checkerboard’ density distribution of the additional support-free trusses as shown in Fig. 6(g), therefore further fine-tuning is carried out to obtain smoother boundaries. The densities of elements that define the support-free trusses are filtered in (4) and thresholded by a Heaviside function in (5).

$${\widetilde{x}}_{st}= \frac{\sum_{j\in {N}_{st}}{H}_{st,j}{x}_{j}}{\sum_{j\in {N}_{st}}{H}_{st,j}}$$
(4)
$${\widetilde{x}}_{st}=\frac{\mathrm{tanh}\left(\beta \eta \right)+\mathrm{tanh}\left(\beta \left({\overline{x} }_{st}-\eta \right)\right)}{\mathrm{tanh}\left(\beta \eta \right)+\mathrm{tanh}\left(\beta \left(1-\eta \right)\right)}$$
(5)

While \(st\) denotes the additional support-free elements in (4) and (5), \({\widetilde{x}}_{st}\) and \({\widehat{x}}_{st}\) are the filtered and physical densities respectively of st elements, Nst is a set of neighboring elements whose center-to-center distance, \(\Delta (st,j)\) to a support-free element is less than a specified filter radius, rmin. The density filter is a linear filter used here to control the size of features obtained during and post optimization. The choice of value for the filter radius is dependent on several factors not limited to the minimum feature size resolution of the AM technology, functional requirements of the optimized structure, etc. \(\beta\) is the sharpness factor while \(\eta\) is a threshold parameter. \({H}_{st,j}\) is a weight factor for support-free truss (\(st\)) elements expressed as

$${H}_{st,j}=\mathrm{max}(0,{r}_{min}-\Delta (st,j))$$
(6)

Figure 7 highlights the implementation of the proposed methodology which commences with obtaining an optimized topology for a particular design case, then a boundary identification is done according to Eq. (1). Thereafter, overhanging features are determined by identifying overhanging nodes from boundary nodes according to Eq. (3), then support-free trusses are added underneath overhanging features following the procedure in Sect. 2.1.2, finally, a density filter and Heaviside projection are applied to the introduced support-free trusses.

Fig. 7
figure 7

The post-process methodology showing the major stages (a) An optimized topology (b) boundary identification of optimized topology (c) identification of overhang features subtended less than 45° to the build plate (build plate is assumed to be just below the horizontal bottom surface of the structure) (d) inclusion of support-free trusses to identified overhanging features (e) applying the density filter and Heaviside projection to support-free trusses

Full size image

3 Experiment

The load–displacement responses of the as-built topologically optimized AM samples are experimentally investigated and compared to numerical results. Besides the cantilever problem, the MBB beam is a widely adopted case study for most topology optimization algorithms or models [6, 12, 20, 63,64,65] for both numerical and experimental studies. In this study, the dimensioned beam problem described in Fig. 8(a) is first topologically optimized by the SIMP method [66,67,68] based on compliance minimization for a volume fraction of 0.5. Thereafter, the post-topology optimization algorithm is carried out on the density map to eliminate overhanging features. In this study, three categories of optimized beams are studied: without overhang elimination (WOE), with different minimum feature sizes (\(na\) – where \(n\) is an integer multiple of half the finite element length—\(a\)—used in the optimization), and with different overhang angle thresholds (\(\theta\)). The MBB beam problem is shown in Fig. 8(a), where load and support locations are presented while Fig. 8(b) shows an input image file of half the domain used in IBIPP [69] for the optimization. IBIPP [69] is an open-source program that has been developed to initialize free-form design domains for topology optimization and generate STL files for printing.

Fig. 8
figure 8

a The MBB problem showing the load and support locations and domain dimensions b the half MBB initial design domain used for optimization in ibipp.m [69]. Dimensions are in mm

Full size image

In Fig. 8, a preserved region (shown in black in (a) and green in (b)) around the supports is added to improve stability during the bending tests. The problem is discretized using \(270\times 77\) (\(20790\)) bilinear homogenous square elements with a finite element length of \(2a=0.4 mm\). The Optimality Criteria Method [70] was used as the gradient optimizer and a convergence criterion of 0.01 or 0.1 after 250 iterations was imposed. Altogether, 12 optimized designs were generated: two designs without overhang elimination, of minimum feature radii—\(5a\) and \(7a\) conveniently named \(5a\)-WOE and \(7a\)-WOE respectively, 10 designs having overhang angle thresholds at \(45^\circ ,50^\circ , 55^\circ ,60^\circ ,\) and \(65^\circ\) with minimum feature radii of \(5a\) and \(7a\) respectively. Figure 9 shows the different optimized designs in 2D and extruded 3D:

Fig. 9
figure 9

Optimized designs showing the reference designs without overhang elimination (WOE) for minimum size 5a and 7a (middle figures), (a-e) 5a and (f-j) 7a with angles 45°, 50°, 55°, 60°, and 65° respectively

Full size image

3.1 Sample production

An EOS M290 LPBF machine equipped with a Ytterbium fiber was used to produce the tensile and topologically optimized samples. The printing was done under an argon environment and the build plate temperature was \(80^\circ C.\) The Hastelloy x powders were gas-atomized, and they were supplied by EOS GmbH. Other process parameters are shown in Table 1. Three repetitions of the optimized beam samples in Fig. 9 were printed with their build orientations as shown in the figure. Tensile samples oriented at \(0^\circ , 45^\circ ,\) and \(90^\circ\) to the plane of the substrate or build platform were printed for tensile testing as shown in Fig. 10. The dimensions of the tensile samples were according to ASTM E8 [71] and can be seen in [72, 73]. The printed samples are shown in Fig. 11. Note, the tensile samples oriented at \(0^\circ\) and \(90^\circ\) are not shown in Fig. 11.

Table 1 LPBF process parameters used for residual stress and bending tests
Full size table
Fig. 10
figure 10

Tensile samples in different orientations

Full size image
Fig. 11
figure 11

Printed tensile and optimized beam samples. Note that only 3 repeats of the tensile dogbone samples inclined at 45° are shown in this figure. Other orientations described in Fig. 10 were printed in other build beds that are not shown

Full size image

3.2 Mechanical testing

Room temperature quasi-static tensile tests were done using the Instron® 8874 servo-hydraulic machine in the displacement control mode at a crosshead speed of 0.45 mm/min following ASTM E8 standard [71]. The load capacity of the testing machine was \(\pm 25kN\) and an Instron® 2630–120 extensometer with a gauge length and travel of \(8 mm\) and \(\pm 4 mm\) respectively was used. Thereafter, 3-point bending tests were carried out on the sample size using a crosshead speed of 1.5 mm/min. All tensile and bending samples were carried out under the same experimental conditions. The tensile and bending test setups are shown in Fig. 12.

Fig. 12
figure 12

a Tensile and b bending test setups

Full size image

4 Results and discussion

To investigate the feasibility of the proposed methodology, some structures are topologically optimized with and without overhang elimination while examining some aspects of the post-T.O. process. First, overhang elimination considering volume correction is studied, second, the effects of feature size limitation and angle threshold on compliance and volume fraction of the resultant support-free structure are investigated. Third, the benefit of the proposed methodology’s independence from the iterative process of topology optimization is displayed through its computational effectiveness. Finally, experimental and numerical load–displacement relationships for varying overhang angle thresholds and minimum feature sizes are investigated and compared. The core strength of the proposed post-T.O. process is its adaptability to any and every class of T.O. using uniform quad elements in a discretized domain.

4.1 Overhang elimination with volume correction

A consequence of adding support-free trusses to overhanging features is an increase in the desired volume fraction. In Fig. 7, there is a 7% increase in volume fraction from (a) to (e). This volume increase potentially becomes larger when the truss thickness and/or angle are increased. For example, the increase in volume fraction in Fig. 7 rises from 7 to 10% when the filter radius is increased from \(4a\) to \(5a\): \(a\) is half the length of a finite square element. Also, Leary et. al. [17] realized over 30% increase in volume fraction for 60° support-free trusses. Therefore, it is necessary to correct this volume fraction for designs subject to strict material requirements. To achieve this, a volume correction according to (7) is proposed and computed after the step in Fig. 7(e)

$${f}_{new}=f-\gamma \left({f}_{old}-f\right)$$
(7)

\(f\) is the required volume fraction, \({f}_{old}\) is the volume fraction after support-free trusses have been added, \({f}_{new}\) is the new computed volume fraction for the forthcoming step and \(\gamma\) is a correction factor that typically ranges from 1 to 1.5 after several numerical investigations.

A second topology optimization process is done using the newly obtained \({f}_{new}\) which gives a topology with a volume less than that of the original topology. Thereafter, steps (b) to (e) in Fig. 6 are carried out to end up with a topology having a volume fraction closely matching the required value.

In Table 2, comparisons are made between overhang-restricted topologies with and without volume correction. We observe up to 22% increase without volume correction and after correction is done, the original volume fraction is maintained although slight changes may be obtained such as the 3% increase in the second orientation. A fallout from volume correction is an increase in compliance; this is expected because in attempting to correct the volume, a lower volume fraction is used in the second topology optimization process resulting in a higher compliance history compared to the first T.O. process as observed in Fig. 13. Another observation from Table 2 is that part orientation greatly affects the volume of support-free trusses needed for overhang elimination and final compliance value. In Fig. 13, although the compliance after the 1st T.O. process without volume correction is the lowest in all scenarios, there is a significant jump in the volume fraction. However, the volume fraction after the 2nd T.O. process with volume correction is right at the originally specified value while the compliance is at an intermediate value between the 1st and 2nd T.O. processes. In conclusion, going for volume correction or not is dependent on which requirement between strength and volume is more stringent for the designer.

Table 2 Overhang elimination with and without volume correction for an optimized topology at different orientations. The red lines show the location of the build plate
Full size table
Fig. 13
figure 13

Compliance, \(C\), and volume fraction, \(f\) history with and without volume correction. T.O. – topology optimization, V.C. – volume correction, required \(f\) is 0.5

Full size image

The workflow of this methodology is shown in the schematic diagram in Fig. 14.

Fig. 14
figure 14

Workflow of post-topology optimization overhang elimination scheme

Full size image

4.2 Effects of minimum feature thickness and angle threshold

In structural design for AM using T.O., controlling the minimum feature size is important because of manufacturability restrictions on the AM technology. Theoretically, the minimum feature size for LPBF can be as low as the laser’s beam diameter but in practice, it should be a multiple of the diameter. In the case of FDM, in theory, minimum feature thickness can assume the size of the nozzle but in practice, an integer multiple is recommended [74]. Minimum values of 0.3 mm and 1 mm have been recommended for LPBF and FDM respectively [57, 74]. Likewise, the printability of overhanging features is dependent on the angle of inclination and AM technology. In literature, several research efforts [12, 57, 74, 75] have identified between \(40^\circ\) to \(50^\circ\) as the range of minimum angle threshold to successfully print overhanging features without support structures in LPBF and FDM. Notwithstanding, this angle threshold can be varied depending on the feature thickness. Typically, smaller feature thicknesses can allow a relatively small feature to be printed at much lower angles (\(<30^\circ )\) [12]. Nonetheless, this might adversely affect the part quality or increase the surface roughness of downfacing surfaces. It is, therefore, necessary to ensure feature thickness and angle of inclination are flexible parameters for a robust overhang elimination procedure. In this methodology, \({r}_{min}\) and \({\theta }_{thresh}\) are the controlling parameters; Fig. 15(a-b) shows different values of these parameters and how they influence compliance and corrected volume fraction.

Fig. 15
figure 15

Effect of (a) filter radius, \({r}_{min}\) at \({\theta }_{thresh}=45^\circ\) and (b) overhanging angle threshold, \({\theta }_{thresh}\) at \({r}_{min}=6a\) on compliance and volume fraction for γ = 1.2 and \(a=2\times {10}^{-4} m (0.2 mm)\)

Full size image

It is observed that an increase in feature thickness and overhang angle threshold in Fig. 15(a-b) translates to an increase in compliance. There is an approximately 19% increase in compliance in both cases from left to right because as feature thickness or angle increases, there is more material relatively assigned to the additional ‘inefficient’ trusses. This trend is not seen in volume fraction because it is a corrected parameter. However, there is a small increase in the volume fraction in Fig. 15(b) but this can be adjusted by increasing the correction factor \(\gamma\) slightly.

4.3 Computational effectiveness

A unique characteristic of a post-process overhang elimination method is its detachment from the iterative optimization process; therefore, it does not contribute to expensive nested chain rule derivatives as an additional overhang elimination or self-supporting filter or a constraint. Using 48,500 four-node square elements on an intel core i7, 16 Gb RAM, the time duration for the optimization of the hook problem in Fig. 16 is investigated for a case without overhang elimination, with overhang elimination by Langelaar’s AMfilter [13] and with overhang elimination by the new post-TO method. Using the post-TO method with volume correction, the time was limited to under 200 s from over 450 s needed by the AMfilter. This time will further significantly reduce to under 100 s if volume correction is ignored.

Fig. 16
figure 16

The time taken to optimize a hook problem without overhang elimination, with overhang elimination using the AMfilter by Langelaar [13], and with overhang elimination using the new post-TO methodology

Full size image

4.4 Quasi-static response

The engineering stress–strain curve and yield stress plots of the tensile samples printed in three orientations are shown in Fig. 17. In Fig. 17 (a), the vertical sample experiences more ductility than other orientations although the yield stress is the lowest in Fig. 17(b). Similar trends for the reduction in mechanical strength as the build orientation moves towards \(90^\circ\) can be seen in [76, 77]. However, since Hastelloy is a very ductile material [72, 73] with a very high elongation observed at lower yield strengths. The Young’s Modulus is highest at \(90^\circ\) with a value of \(158 \mathrm{MPa}\) and while this is in the range of reported additively manufactured Hastelloy X parts at \(153\pm 5.5 \mathrm{GPa}\) [72, 73], the Young’s Modulus for \(0^\circ\) and \(45^\circ\) fell a little short at 141 and 136 MPa respectively. The same trend of Young’s Modulus can also be noticed in [78] although the samples reported were printed using DSM Somos 14120 and Stereolithography (SLA). In this study, the yield stress drops slightly with an increase in the build orientation angle; the mean yield stress value is 455 MPa. The slight reduction in the yield stress (rather than an increase) with an increase in the orientation angle can be attributed to a small noisiness in the engineering stress–strain results. The mean of the Young’s Modulus and yield stress were taken and used in an FEA simulation and the computation of the final compliance of the optimized beam structures.

Fig. 17
figure 17

Quasi-static tensile responses for Hastelloy X (a) Engineering stress–strain curves (b) Yield stress and Young’s Modulus plots

Full size image

The load–displacement plots of the optimized beams for minimum feature sizes \(5a\) and \(7a\) are shown in Fig. 18. For the optimized beams without overhang elimination (WOE) the load–displacement plots are quite similar, and this is not far-fetched from their similar structural topology seen in Fig. 9 with only insignificant feature differences. These WOE beams can overcome more work compared to the optimized beams with overhang elimination. Since no manufacturability constraint (overhang elimination) was placed on them, their structural optimality is higher than those optimized under the constraint, consequently performing better functionally. For each minimum feature size, the higher the overhang angle threshold, the less work is overcome. Also, it is observed that at a particular angle threshold, a move from \(5a\) to \(7a\) slightly decreases the performance of the beam samples. It is expected that this decline in performance will be exacerbated by a further increase in the minimum feature size. Therefore, while considering manufacturability, limiting the overhang angle threshold and minimum feature size to a minimum is recommended. Therefore, for relatively simple topologies, only build orientation optimization may be considered to minimize overhanging regions. However, when dealing with significantly complex parts, introducing support-free trusses might be more beneficial to avoid complications in printability and support removal since build orientation optimization, only, might not eliminate overhanging regions.

Fig. 18
figure 18

Load–displacement plots for the optimized MBB beams with a minimum feature size of (a) 5a (b) 7a

Full size image

4.5 Numerical and experimental comparisons

Finally, the maximum forces in the load–displacement results obtained in the previous section are compared with the compliance values obtained after optimization. Additionally, two FEA simulations for samples 5a-WOE and 7a-WOE are carried out in Solidworks to observe the similarities between numerical and experimental deformations of the optimized beams. Figure 19 shows the influence of the overhang angle threshold and minimum feature size on numerically obtained compliance values and the maximum force from the load–displacement response. An increase in compliance invariably results in a decrease in the maximum load possible for the structure. A similar trend for different topologies is seen in [78]. From Fig. 19, when the manufacturability of a structure is considered by thresholding the overhanging feature angle and minimum feature size, there is more than a 40% increase in the compliance and a 30% decrease in the maximum load carried by the structure for \(65^\circ\) angle threshold and \(7a\) minimum feature size. Between angle and feature size thresholds, from this study, the overhang angle threshold appears to influence the compliance and performance more, however, it should be noted that the marginal difference between successive angles and feature sizes is \(5^\circ\) and \(4a\) respectively. Also note that the feature size is the diameter of the linear density filter which is twice the filter radius (\(2\times {r}_{min}\)), therefore \(5a\) and \(7a\) represent diameters of \(10a\) and 14a respectively. The maximum change resulting from a change in the minimum feature size is between \(5a 55^\circ\) and \(7a 55^\circ\) beams with a 9% increase in compliance from 2700 to 2950 Nm. Although there is also a 9% maximum increase between successive angle thresholds from \(60^\circ\) to \(65^\circ\), there is an 18% increase in compliance when moving from a structure without overhang elimination (WOE) to one with a \(45^\circ\) angle threshold.

Fig. 19
figure 19

Influence of overhang angle threshold and minimum feature size on numerically obtained compliance values and the maximum force from the load–displacement response

Full size image

In Fig. 20, the deformed beams representing \(7a\) WOE and \(5a 45^\circ\) from simulation and experiment are shown. The simulation was carried out in Solidworks®’s static analysis and the material properties investigated in the experimental study were used. A maximum force of 8750 N was applied in the middle of the top surface of the beam (where the load for the bending test was located). The matching deformation profile in both cases is noticed and areas of high-stress concentration at the top and bottom features are consistent with the deformed locations in the tested beams. The \(5a 45^\circ\) beam experiences comparatively higher stresses and deformation further substantiating the effects of manufacturing constraints in a design.

Fig. 20
figure 20

Deformed optimized MBB beam for (a) 7a WOE – simulation (b) 7a WOE – experiment (c) 5a 45° – simulation (d) 5a 45° – experiment

Full size image

5 Conclusion

In this study, a novel and alternative post-topology optimization method for dealing with the overhanging feature problem in many AM technologies such as LPBF and FDM has been presented. First, topology optimization is carried out on the design problem, secondly, boundary identification [61] and overhang detection as outlined in Sect. 2.1 are done. Thirdly and finally, additional structural elements subject to a specified feature thickness and angle are introduced to support previously detected unsupported features. This addition can result in as much as a 22% increase in the volume fraction and a 4% decrease in compliance. For strict design volume adherence, a volume fraction (\(f\)) correction can be introduced to obtain a new and lower \(f\) which will be used in the final topology optimization, boundary identification, and overhang elimination stages. Several key reasons why this methodology is attractive are:

  1. i.

    Although the proposed method is post-topology optimization, there is a seamless workflow from topology optimization because the type and number of design elements, density variables, feature size limit, and other controlling parameters are inputs. There is, therefore, no data conversion or transformation needed, and consequently, both tools (topology optimization and overhang elimination) can be deployed easily as one.

  2. ii.

    There is complete independence from several aspects of the topology optimization process such as sensitivity analysis, optimizers, parameter tuning, and others. Due to the nature of many integrated overhang elimination methods, they may either perform poorly or break down completely when major changes are introduced in the topology optimization scheme [6, 10, 12, 13, 52].

  3. iii.

    This methodology allows for ample design expression regarding the geometrical properties of the additional support-free struts. In other words, the user or designer can dictate strict strut requirements such as thickness, orientation or angle, space between strut roots, and size of strut root (which in turn influences the number of struts added).

  4. iv.

    A direct consequence of post-topology optimization overhang elimination schemes is an increased final volume of the design. This is addressed by a volume correction step in this proposed methodology.

  5. v.

    There is as much as a 30% decrease in the maximum load carried by an optimized beam structure constrained by a steep overhang angle threshold of \(65^\circ\) and a 40% increase in its compliance compared to an optimized structure without overhang elimination. However, these percentages can be reduced by less than half when a \(\le 45^\circ\) angle threshold is considered instead.

Notwithstanding the several benefits, there are a few challenges and limitations this methodology offers. In 3D design problems which will be more valuable, designing the struts’ roots will not be as straightforward as presented here; the base of each strut, prismatically shaped, will be defined by \({\upchi }_{1}\) and \({\upchi }_{2}\) along the overhanging downfacing surface. Also, the direction of strut inclination will become more complicated and might require some optimization. The major limitation of this methodology is the shape of the finite element used. Currently, homogenous square (in 2D cases) or hex (the case for 3D problems) elements are utilized. Although this is a popular type of element used in most topology optimization algorithms, the proposed methodology must be tweaked to accommodate other shapes. Moving forward, 3D extensions of the proposed methodology will be implemented and presented in the future.