Optimizing supports for additive manufacturing

Abstract

In additive manufacturing process, support structures are often required to ensure the quality of the final built part. In this article, we present mathematical models and their numerical implementations in an optimization loop, which allow us to design optimal support structures. Our models are derived with the requirement that they should be as simple as possible, computationally cheap, and, yet, based on a realistic physical modelling. Supports are optimized with respect to two different physical properties. First, they must support overhanging regions of the structure for improving the stiffness of the supported structure during the building process. Second, supports can help in channeling the heat flux produced by the source term (typically a laser beam) and thus improving the cooling down of the structure during the fabrication process. Of course, more involved constraints or manufacturability conditions could be taken into account, most notably removal of supports. Our work is just a first step, proposing a general framework for support optimization. Our optimization algorithm is based on the level set method and on the computation of shape derivatives by the Hadamard method. In a first approach, only the shape and topology of the supports are optimized, for a given and fixed structure. In a second and more elaborated strategy, both the supports and the structure are optimized, which amounts to a specific multiphase optimization problem. Numerical examples are given in 2D and 3D.

1 Introduction

Additive manufacturing (AM) refers to the construction of objects using a layer by layer deposition system. Such fabrication processes have the advantage of being able to build complex or unique structures starting from a given design. Additive manufacturing offers multiple advantages over classical fabrication techniques, like moulding or casting. In particular, the complexity of the structure is only limited by the precision given by the width of the layers, while there are no topological constraints. Moreover, the design can be modified at any moment in the fabrication process, allowing the immediate correction of eventual design errors. Recent developments in technologies regarding AM processes based on melting metal powder with the aid of a laser (or electron) beam provide great opportunities for the usage of these technologies in various industrial branches like aeronautics, automotive, biomedical engineering, etc. (Barlier and Bernard 2016; Gibson et al. 2015).

As already underlined in many works (Cacace et al. 2017; Calignano 2014; Dumas et al. 2014; Gan and Wong 2016; Hu et al. 2015; Huang et al. 2008; Hussein et al. 2013; Kuo et al. 2018; Langelaar 2016, 2018; Mirzendehdel and Suresh 2016; Mumtaz et al. 2011; Strano et al. 2013; Vanek et al. 2014) a recurring issue when dealing with AM processes is the conformity of the printed structures to the original design. Indeed, it has been observed that structures which have large portions of surfaces which are close to being horizontal and are unsupported tend to be distorted after the manufacturing process. Such horizontal regions are called overhangs. These deformations, which were not in the original design, may have multiple sources. Firstly, the overhang sections may be rough or deformed because the melted powder is not supported. This constraint is linked to the angle of normals to overhang surfaces with the build direction and it varies with the material or machines involved. As a rule of thumb, it is agreed that angles greater than 45–60^∘ (depending on the 3D printer technology) are admissible in order to be able to build the structures. Secondly, the uneven temperature distribution in the structure, which is due to the path of the heating laser (or electron) beam, may create thermal residual stresses or thermal dilation of the structure in various directions. In order to avoid such undesired deformations, the structure can either be redesigned taking into consideration the limitation of the overhang regions and of the thermal effects, or support parts can be added with the goal of improving the construction process, which will be removed after the fabrication is finished.

Shape and topology optimization is by now a well-known technique to automatically design structures with optimal mechanical or thermal properties (Allaire 2007a; Bendsøe and Sigmund 2004). Recently, there has been a growing interest in extending these techniques in the framework of additive manufacturing. There are at least two main directions of research in this context.

First, structures can be optimized, not only for their final use but also for their behaviour during the building process, without requiring the addition of supports. In general, the main goal is to limit the apparition of overhang parts during the design optimization and very often it is achieved by enforcing a geometric constraint on the overhang angle. In the framework of the SIMP method, the topology optimization of support-free structures was proposed in Leary et al. (2014). Unfortunately, relying only on a penalization of the overhang angle is not enough. An horizontal overhanging part can be replaced by a zig-zag structure, which passes the angle penalization but is still globally an overhang. This is called the dripping effect. It shows that mechanical properties should be taken into account. In the framework of the level set method, it is achieved by a combination of geometric and mechanical constraints in Allaire et al. (2017a, b). The minimization of thermal residual stresses or thermal deformations has been considered in Allaire and Jakabcin (2018). The optimization of the orientation of the shape was studied in Morgan et al. (2016), Zhang et al. (2015).

Second, for given structures (optimal or not) one can optimize the placement of supports to improve the building process and avoid any of the possible defects, previously mentioned, like overhang deformations or residual stresses. There are many more works in this second class of problems. Various ways of optimizing the supports were proposed, like sloping wall structures (Huang et al. 2008), tree-like structures (Vanek et al. 2014; Gan and Wong 2016), periodic cells (Strano et al. 2013), lattices (Hussein et al. 2013) and support slimming (Hu et al. 2015). A procedure for the automatic design of supports under the form of bars, with applications to polymer 3D printers was presented in Dumas et al. (2014). An approach to optimize the topological structure of supports using the SIMP method was considered in Gardan and Schneider (2015). The optimization of supports was also addressed in Langelaar (2016), where mechanical properties and geometric aspects were consider in the optimal design process. In Bruggi et al. (2017) the authors consider the optimization of supports under mechanical stresses, using the SIMP method in dimension 2. Still in the framework of the SIMP method, but adding the ease of removal as an additional constraint, the optimal design of supports was studied in Kuo et al. (2018). The addition of supports via a level set method in order to limit the overhang regions was studied in Cacace et al. (2017) for some 2D tests. A model for optimizing supports using compliance minimization for the linearized elasticity using the SIMP method was proposed in Mezzadri et al. (2018).

Of course, the two approaches can be combined in a simultaneous optimization of shape and support. Topology optimization coupled with support structure design was considered in Mirzendehdel and Suresh (2016). In Langelaar (2018) the simultaneous optimization of the shape, support and orientation is treated.

In the present paper we are concerned with the second approach, i.e. optimizing the supports for a given structure. The main novelty of our research is to propose a general framework for optimizing supports rather than just one single specific model. Inside this framework, several models are discussed for support optimization. Either one can optimize the support distribution for maximizing the rigidity of the supported structure with a fixed structure, or both the support and the structure can be optimized in a multiphase topology optimization setting. Thermal properties of the support can also be optimized in order to facilitate the evacuation of heat produced by the additive manufacturing process. A combination of both mechanical and thermal properties can be taken into account. Following the lead of Allaire et al. (2017a, b) it is also possible to mimick the building process and optimize supports in a layer by layer model. The common point of all these models and the main characteristic of our framework is that we choose to evaluate the support performance in terms of physical models (based on partial differential equations) rather than in terms of simple geometrical measures. To the best of our knowledge, apart from the notable exception (Kuo et al. 2018), our work is the first to systematically use such a physical modelling of the supports in their optimization. Furthermore, we are not aware of any previous work on support optimization based on thermal properties. Although we insist on a physical modelling of supports, in the mean time, having in mind to limit the computational cost, we deliberately choose simple enough models so that support optimization is cheap and easy to implement into automatic design software. Our goal is thus not to model very accurately the building process and the behaviour of supports but rather to obtain a global and approximate performance of the supports which is easily taken into account in an optimization algorithm. In particular, if supports are finely spaced and form a very heterogeneous structure, our model consider them as an equivalent homogenized material which avoids a precise description and meshing of all geometrical details. Of course, our models, objective functions and resulting optimized supports should be assessed by comparison with experimental results. In this respect, a crucial issue is the removal of supports after printing. This may be a very intricate process, especially for complex 3-d shapes. One possibility is to add geometric constraints (in the spirit of Allaire et al. 2016a, b) ensuring that any contact zone between supports and the actual shape is accessible from the outside along a straight tubular hole, allowing for the passage of some tool able to cut the supports. This is the topic of future work which is clearly out of the scope of the present paper. In particular, it may well be that new objective functions or models arise, based on experimental evidence (for example to take into account thermal residual stresses as in Allaire and Jakabcin 2018). One advantage of our approach is that such new ingredients can easily be cast in our framework. Nevertheless, we make comparison of our optimized supports with the one obtained in Kuo et al. (2018) and those obtained by classical geometric criteria.

The content of our paper is the following. In Section 2 we focus on minimizing the mechanical effects of overhangs, without taking into account a thermal model. In Section 2.1 the shape is assumed to be fixed and only the supports are optimized by using a mechanical criterion. More precisely we minimize a weighted sum of the support volume and of the compliance for the union of the shape and its support, submitted to gravity. Of course, under such a load, overhang regions of the shape will have a tendency to get supported during the optimization process. In Section 2.2 we extend our analysis to the simultaneous optimization of the shape and support. It involves two state equations: one for the final use of the shape (without supports) and another one for gravity effects during the building process. It is therefore a multiphase optimization problem and we rely on the method proposed in Allaire et al. (2014). Section 2.3 makes a comparison with the more involved layer by layer model, introduced in Allaire et al. (2017a, b), restricted here to the case of a fixed shape.

Section 3 turns to the support optimization in order to facilitate the evacuation of the heat coming from the laser or electron beam. In this case the model is the stationary heat equation or its long-time behaviour, given by the first eigenmode, posed in the union of the shape and its support. Thermal compliance is minimized for a given source term supported only in the shape since thermal deformations of the support are not important. As is well known, minimizing thermal compliance can be interpreted as maximizing heat evacuation.

As explained in Section 4, our main numerical tool is the level set method (Sethian 1999). Shape derivatives, computed by Hadamard method, are the velocities in the transport Hamilton-Jacobi equation (Allaire et al. 2004). Our optimization algorithm is a simple Augmented Lagrangian method (Birgin and Martínez 2014). Dealing with the level set method needs certain specific tools regarding the reinitialization and the advection of the level set function. We rely on the publicly available tools MshDist (Dapogny and Frey 2012) and Advect (Bui et al. 2012) from the ICSD Toolbox available online: https://github.com/ISCDtoolbox. Our partial differential equations models are solved by finite elements in the FreeFem++ software (Hecht 2012) which is well suited for multiphysics simulation (and is a publicly available tool too).

Eventually, Section 5 contains our numerical test cases. At first, a few examples concerning supports which maximize the rigidity of the structure under gravity loads are presented, using the ideas of Section 2. Numerical examples in dimensions two and three show that our algorithm can handle complex cases. Then, some simulations concerning the optimization of the supports with respect to their thermal properties are displayed in the framework of Section 3. Of course, it is possible to optimize the supports for both thermal and elastic loads, as in Section 5.3. The simultaneous optimization of the shape and its support, as discussed in Section 2.2, is also illustrated. The behaviour of the support with respect to the orientation of the shape is also considered in Section 5.5. Finally, for the sake of comparison, the layer by layer algorithm, presented in Section 2.3, is tested for 2- and 3D test cases. The resulting optimal supports are not very different from the ones obtained with the simpler algorithm of Section 2, showing the interest of the present approach, which is much cheaper in terms of CPU time. Comparisons with other methods for generating supports, like the model considered in Kuo et al. (2018) or the simple geometrical criterion adding vertical supports under overhanging regions, can be found in Section 5.1.

Concluding remarks and perspectives are given in Section 6. As already said, our approach has to be validated by experiments which will possibly indicate other possible objective functions and models which may be useful for support optimization. Other constraints or objectives on supports include mitigation of thermal deformations, ease of removal, a precise geometric description of the supports not based on equivalent homogenized properties: they are not treated here and will be addressed in future works. The main point of our work, as well as any optimization approach, is to progressively replace the expert intuition and knowledge by an automatic process of support design, based on a physical, albeit simplified, modelling.

2 Shape optimization for minimizing the mechanical effects of overhangs

2.1 Optimizing the support when the shape is fixed

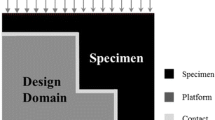
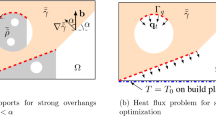
Let us consider a shape ω, which has to be printed, together with its supports S. Both S and ω are open sets of ℝ^d (with d = 2 or 3 in practice) and are not necessarily made of the same material. In a first stage the shape ω will be fixed and only the support S will be the optimized. In a second stage (see the next subsection), both the support S and the shape ω will be optimized. Our numerical framework could be used for arbitrary build directions. In our computations, however, we always suppose that the build direction is the vertical one: a structure is built from the bottom towards its top. A point in ℝ^d is denoted by x = (x₁,...,x_d) and the vertical direction is e_d = (0,...,0,1). The supported structure is denoted by Ω = S ∪ ω and is assumed to be contained in a given computational domain D, which can be interpreted as the build chamber. For simplicity, the build chamber will always be a rectangular box. The build chamber D always contains the baseplate as its bottom boundary, denoted by Γ_D. By definition, the bottom boundary Γ_D corresponds to x_d = 0. We assume that the support S is clamped on the boundary Γ_D of the computation domain D. The other regions of the boundary of the supported structure Ω are traction-free, denoted by Γ_N. In the following for an open domain Ω ⊂ ℝ^d and a (d − 1)-dimensional set Γ we consider the space

$$ H_{\Gamma}^{1}({\Omega})^{d} = \{ u \in H^{1}({\Omega})^{d} : u = 0 \text{ on } {\Gamma}\} $$

(1)

The deformation of the supported structure Ω is governed by the equations of linearized elasticity. Following Allaire et al. (2017b) only gravity forces are applied to Ω. Then, optimizing the support S for minimizing the compliance of Ω will induce minimal overhang regions. The elastic displacement u_spt of the supported structure Ω = ω ∪ S is the unique solution in the space $H^{1}_{{\Gamma }_{D}}({\Omega })$ (defined in (1)) to the mechanical system

$$ \left\{ \begin{array}{cl} -\operatorname{div}(Ae(u_{\text{spt}})) = \rho g & \text{ in }{\Omega} ,\\ u_{\text{spt}} = 0 & \text{ on }{\Gamma}_{D} ,\\ Ae(u_{\text{spt}}) n = 0 & \text{ on } {\Gamma}_{N} . \end{array} \right. $$

(2)

In (2), $e(u) = \frac {1}{2} (\nabla u + \nabla u^{T})$ is the linearized strain tensor associated with the displacement u, g is the (vertical) gravity vector and n denotes the unit normal vector to Ω. We denote by ρ(x) the density of the structure Ω and by A(x) its Hooke’s tensor, which may both vary with respect to the position x. Typically, these material properties may be different in the shape ω and in the support S, which happens often in practice. Indeed, supports are often not bulk pieces of metal but rather are some kind of lattice-thin-wall structures. However, for optimization purposes it is out of the question to model all these fine details and rather it is replaced here by a homogeneous effective material (or equivalent homogenized material) with different material properties from those of the shape. More precisely we have Ae(u) = 2μe(u) + λ div u Id, where Id is the identity matrix and μ,λ are the Young modulus and Poisson ratio, respectively. If μ_ω, λ_ω, ρ_ω are the mechanical parameters for the shape ω and μ_S, λ_S, ρ_S are the corresponding parameters for the support, then

$$\mu = \mu_{\omega} \chi_{\omega} + \mu_{S} \chi_{S},\ \ \lambda = \lambda_{\omega} \chi_{\omega} + \lambda_{S} \chi_{S}, \ \ \rho = \rho_{\omega} \chi_{\omega} + \rho_{S} \chi_{S}. $$

We evaluate the mechanical performance of the supported structure Ω in terms of its structural compliance

$$ J(S) = {\int}_{\omega \cup S} Ae(u_{\text{spt}})\cdot e(u_{\text{spt}})\ dx ={\int}_{\omega \cup S} \rho g \cdot u_{\text{spt}}\ dx . $$

(3)

Other objective functions would be possible. This objective function is minimized in the set $\mathcal U_{ad}$ of admissible supports defined by

$$\mathcal U_{ad} = \{ S \subset (D\setminus\omega ) \text{ such that }, {\Gamma}_{D} \cap \partial S \neq \emptyset, \partial \omega \cap \partial S \neq \emptyset \} . $$

If we do not impose any constraints then the optimization procedure will not produce relevant supported structures since the support S will simply fill the space under the shape ω in D. In order to prevent this we add a constraint on the volume of the support S. This is of course relevant from a physical point of view, since we wish to obtain optimal structures which do not use too much material.

The constraint can be incorporated in the functional by using a Lagrange multiplier ℓ. Therefore we will consider problems of the form

$$ \min_{S \in \mathcal U_{ad}} J(S) + \ell \operatorname{Vol}(S), $$

(4)

where ℓ is either a given penalization parameter or a parameter which changes during the optimization process in order to reach the equality in the volume constraint at the end of the optimization process. When we wish to work with a volume constraint, an Augmented Lagrangian method is used, as described in Section 4.

In order to find numerical solutions to the problem (4), we use algorithms which are based on the derivatives of the compliance J(S) and the volume Vol(S). In the shape optimization context, these shape derivatives are computed by the Hadamard method (Allaire 2007a; Pironneau 1984). Given a vector field 𝜃 ∈ W^1,∞(ℝ^d, ℝ^d), we consider variations of the set S induced by 𝜃 of the form

$$\theta \mapsto S_{\theta} = (\text{Id}+\theta)(S) .$$

Definition 2.1

A function F(S) of the domain is shape differentiable at S if the underlying map 𝜃↦F(S_𝜃) from W^1,∞(ℝ^d, ℝ^d) into ℝ, defined above, is Fréchet differentiable at 0. The corresponding derivative is denoted by F^′(S) and the following asymptotic expansion holds in a neighbourhood of 0:

$$\begin{array}{@{}rcl@{}} F(S_{\theta}) &=& F(S) + F^{\prime}(S) (\theta) + o(\theta),\\&& \text{ where } \frac{|o(\theta)|}{\|\theta \|_{W^{1,\infty}(\Bbb{R}^{d},\Bbb{R}^{d})}} \stackrel{\theta \to 0}{\longrightarrow} 0 . \end{array} $$

Computing the shape derivative of the compliance is a classical result (see e.g. Allaire et al. 2004). Recall that the shape ω is fixed and only the support S may vary. Note also that, from a mechanical point of view, the support S always lies outside the shape ω and cannot move inside ω. Therefore, for most results in the following we make the following assumption.

Assumption 2.2

The interface ∂S ∩ ∂ω is assumed to be fixed. Therefore, all vector fields 𝜃 in the shape derivatives are assumed to satisfy 𝜃 ⋅ n = 0 on ∂S ∩ ∂ω.

Proposition 2.3

Under Assumption 2.2, the shape derivative of the compliance (3) is given by

$$J^{\prime}(S)(\theta) = {\int}_{\partial S \cap \omega^{c}} \left( - Ae(u_{\text{spt}})\cdot e(u_{\text{spt}})+ 2\rho g\cdot u_{\text{spt}}\right) \theta \cdot n \ ds $$

where u_spt is the solution of (2) and ω^c = D ∖ ω and ∂S ∩ ω^c = ∂S ∖ ∂ω.

This follows at once from (Allaire et al. 2004, Theorem 7). The shape derivative is carried merely by ∂S ∩ ω^c because the normal components of the vector fields 𝜃 vanish on the interface ∂S ∩ ∂ω. This result is a particular case of the more general result, Proposition 2.5, proved in the following section.

Eventually, it is well known that the shape derivative of the volume is given by

$$\operatorname{Vol}^{\prime}(S)(\theta) = {\int}_{\partial S \cap \omega^{c}} \theta \cdot n ds. $$

2.2 Simultaneous optimization of the support and the shape

In a second stage, we consider the simultaneous optimization of the shape and the support. While in the previous subsection, the support S was optimized only for counter-balancing the gravity effects during the building process, now the shape ω has also to be optimized for its final use, independently of the support S. Therefore, in addition to the state (2), accounting for gravity effects on the supported structure S ∪ ω, we now add another state equation for ω only, which takes into account its final use with new loads and boundary conditions. Figure 1 displays the different type of boundary conditions for these two state equations on an example which will be studied later in Section 5. From now on, the elastic displacement, the solution of the first state equation for the supported structure during its building process, is denoted u_spt, while the other elastic displacement, solution of the second state equation for the shape during its final use, is denoted u_fin.

Fig. 1

Different boundary conditions for the final use of the shape (left) and for the supported structure (right)

For its final use, the shape ω is clamped on a boundary $\tilde {\Gamma }_{D}$ and is loaded on another boundary Γ₀ by some surface loads by f_fin. The rest of the boundary denoted $\tilde {\Gamma }_{N}$ is traction-free. The mechanical properties of ω with respect to the final functionality of the shape is described by the following second state equation

$$ \left\{ \begin{array}{cl} -\operatorname{div}(Ae(u_{\text{fin}})) = 0 & \text{ in }\omega , \\ u_{\text{fin}} = 0 & \text{ on } \tilde {\Gamma}_{D} ,\\ Ae(u_{\text{fin}})n = f_{\text{fin}} & \text{ on } {\Gamma}_{0},\\ Ae(u_{\text{fin}})n = 0 & \text{ on } \tilde {\Gamma}_{N} . \end{array} \right. $$

(5)

As already said, the boundary conditions and loadings are not the same for the two states (2) and (5) (see Fig. 1).

The objective function to be optimized is now the sum of the compliance for (5) and that for (2)

$$ J_{2}(\omega,S) = {\int}_{\omega \cup S} \rho g \cdot u_{\text{spt}} dx +{\int}_{{\Gamma}_{0}} f_{\text{fin}} \cdot u_{\text{fin}} ds . $$

(6)

Of course, more general objective functions for (5) could be studied, at the expense of introducing an adjoint equation. This new objective function is minimized in the set $\mathcal U_{ad}$ of combined admissible shapes and supports defined by

$$\begin{array}{@{}rcl@{}} \mathcal U_{ad} &=& \left\{\vphantom{\tilde{\Gamma}_{D}} (\omega,S) \subset D \text{ such that } \omega\cap S = \emptyset, {\Gamma}_{D} \cap \partial S \neq \emptyset,\right.\\ && \left.\tilde{\Gamma}_{D} \cap \partial\omega \neq \emptyset, \partial \omega \cap \partial S \neq \emptyset \right\} . \end{array} $$

Adding volume constraints on both S and ω, we consider the following optimization problem

$$ \min_{(\omega,S) \in \mathcal U_{ad}} J_{2}(\omega,S) + \ell_{S} \operatorname{Vol}(S) + \ell_{\omega} \operatorname{Vol}(\omega) , $$

(7)

where ℓ_S, ℓ_ω are two Lagrange multipliers for the volume constraints on S and ω, respectively. Contrary to the previous section, the interface between the support S and the shape ω can now be optimized. Therefore, the vector fields 𝜃 in the shape derivatives do not necessarily vanish on the interface ∂S ∩ ∂ω. In other words, the problem (7) is a two-phase optimization problem because the material properties are usually not the same in the support and in the shape.

It is well known (see e.g. Allaire et al. 2014) that computing shape derivatives for an interface between two phases is a delicate issue and that the resulting formulas are complicated to use in numerical optimization. Typically, because of different mechanical properties A and ρ between ω and S, there will be jumps of discontinuous quantities on the interface in the shape derivative formula. However, as already underlined in Allaire et al. (2014, Section 2.2), shape derivatives are much simpler if we suppose that the (2) and (5) are solved for u_spt, u_fin in some finite dimensional subspaces. Therefore, in the following, we make the following simplifying assumption, which remains valid in our numerical computations based on finite element methods.

Assumption 2.4

Let V_h and W_h be finite dimensional subspaces of $H_{\tilde {\Gamma }_{D}}^{1}(\omega )^{d}$ and $H_{{\Gamma }_{D}}^{1}({\Omega })^{d}$ (see(1) for their definition), respectively. Let $u_{\text {fin}}^{h}$ be the solution of the approximate variational formulation of (5) in V_h and $u_{\text {spt}}^{h}$ be the solution of the approximate variational formulation of (2) in W_h. In the following, we work with these discrete solutions, and for the simplicity of notation, we drop the discrete index h.

We now give the shape derivative of J₂(ω,S) when both the shape and the support are deformed by a vector field 𝜃.

Proposition 2.5

Under Assumption 2.4, for any vector field 𝜃 ∈ W^1,∞(ℝ^d, ℝ^d), the shape derivative of J₂(ω,S), defined by (6), is given by

$$\begin{array}{@{}rcl@{}} J_{2}^{\prime}(\omega,S)(\theta) &=& {\int}_{\partial \omega \setminus \partial S} j_{1} \theta\cdot n \ ds+{\int}_{\partial \omega \cap \partial S} j_{2} \theta\cdot n \ ds \\&&+ {\int}_{\partial S \setminus \partial \omega} j_{3} \theta\cdot n \ ds, \end{array} $$

where the integrands j₁, j₂, j₃ are given by

$$\begin{array}{@{}rcl@{}} j_{1} \!& =&\! -Ae(u_{\text{fin}})\cdot e(u_{\text{fin}})-Ae(u_{\text{spt}})\cdot e(u_{\text{spt}})+ 2\rho g \cdot u_{\text{spt}} \\ j_{2} \!& =&\! -[A]e(u_{\text{spt}})\cdot e(u_{\text{spt}}) + 2 [\rho] g\cdot u_{\text{spt}}-Ae(u_{\text{fin}})\cdot e(u_{\text{fin}}) \\ j_{3} \!& =&\! -Ae(u_{\text{spt}})\cdot e(u_{\text{spt}})+ 2\rho g\cdot u_{\text{spt}} \end{array} $$

(8)

and the notation [ξ] denotes the jump of a quantity ξ through the interface ∂ω ∩ ∂S.

We choose an orientation on ∂ω ∩ ∂S such that the normal vector points outwards ω. In this case [ξ] = ξ_ω − ξ_S where ξ_ω andξ_S are the valuesof ξ on the two sides of ∂ω ∩ ∂S. For details we refer to Allaire et al. (2014).

Proof

We simply sketch the proof which is a variant of that of Proposition 2.5 in Allaire et al. (2014). Under Assumption 2.4, the discrete solutions u_fin of (5) in V_h and u_spt of (2) in W_h are shape differentiables. The shape derivative of (6) is computed by Céa’s method (Céa 1986). Introduce a Lagrangian defined for $(\omega ,S) \in \mathcal U_{ad}$ and $\hat u_{\text {fin}},\hat p_{\text {fin}} \in H^{1}_{\tilde {\Gamma }_{D}}(\omega )^{d}, \hat u_{\text {spt}},\hat p_{\text {spt}} \in H^{1}_{{\Gamma }_{D}}({\Omega })^{d}$ by

$$\begin{array}{@{}rcl@{}} \mathcal{L}(\hat u_{\text{fin}},\hat u_{\text{spt}},\hat p_{\text{fin}},\hat p_{\text{spt}},\omega,S)\!& =&\! {\int}_{\omega} A e(\hat u_{\text{fin}}) \cdot e(\hat p_{\text{fin}}) \ dx\\ && \!-{\int}_{{\Gamma}_{0}} f_{\text{fin}} \cdot \hat p_{\text{fin}} \ ds \\ && \!+ {\int}_{\omega \cup S} A e(\hat u_{\text{spt}}) \cdot e(\hat p_{\text{spt}}) \ dx\\ && \!-{\int}_{\omega \cup S} \rho g\cdot \hat p_{\text{spt}} \ dx \\ && \!+{\int}_{\omega \cup S} \rho g \cdot \hat u_{\text{spt}} \ dx\\ &&\!+{\int}_{{\Gamma}_{0}} f_{\text{fin}} \cdot \hat u_{\text{fin}} \ ds. \end{array} $$

The variables in the Lagrangian are denoted with a hat, since this functional is defined for general variables, which are not the solutions of the state and adjoint equations. As usual, the Lagrangian is the sum of the objective function and of the weak forms of (5) and (2). Differentiating with respect to $\hat p_{\text {fin}}$ and $\hat p_{\text {spt}}$ yield the weak forms of (5) and (2). Differentiating with respect to $\hat u_{\text {fin}}$, we obtain the adjoint equation

$$\left\{\begin{array}{cl} -\operatorname{div} Ae(p_{\text{fin}}) = 0 & \text{ in } \omega ,\\ Ae(p_{\text{fin}})n = -f_{\text{fin}} & \text{ on } {\Gamma}_{0} ,\\ p_{\text{fin}} = 0 & \text{ on } \tilde {\Gamma}_{D} ,\\ Ae(p_{\text{fin}})n = 0 & \text{ on } \tilde {\Gamma}_{N} . \end{array}\right.$$

Therefore, the adjoint state is simply p_fin = −u_fin. In the same manner, it is found that the adjoint state p_spt is equal to − u_spt. We now differentiate $\mathcal {L}$ with respect to the variables ω and S in the direction of a vector field 𝜃. Note that the mechanical properties A and the density ρ may have jumps when passing from ω to S. These jumps are denoted by [A] and [ρ] and will appear when computing the shape derivative on ∂ω ∩ ∂S. We refer to Allaire et al. (2014) for a detailed analysis of moving interfaces corresponding to jumps in the material properties. Therefore, we deduce

$$\begin{array}{@{}rcl@{}} \frac{\partial \mathcal L}{\partial \omega,S }(\theta) & =& -{\int}_{\partial \omega} Ae(u_{\text{fin}})\cdot e(u_{\text{fin}}) \theta \cdot n \ ds + {\int}_{\partial \omega \setminus \partial S}\\ && -Ae(u_{\text{spt}})\cdot e(u_{\text{spt}}) \theta \cdot n \ ds\\ && + {\int}_{\partial \omega \cap \partial S} - [A] e(u_{\text{spt}}) \cdot e(u_{\text{spt}}) \theta \cdot n\ ds \\ &&+ {\int}_{\partial \omega \cap \partial S} [\rho] g\cdot u_{\text{spt}} \theta \cdot n\ ds \end{array} $$

$$\begin{array}{@{}rcl@{}} &&{\kern42pt} + {\int}_{\partial \omega \setminus \partial S} \rho g\cdot u_{\text{spt}} \theta \cdot n\ ds \\ &&{\kern42pt} + {\int}_{\partial \omega \setminus \partial S} \rho g \cdot u_{\text{spt}} \theta \cdot n\ ds \\ &&{\kern42pt} + {\int}_{\omega \cap \partial S} [\rho] g\cdot u_{\text{spt}} \theta \cdot n\ ds\\ &&{\kern42pt} - {\int}_{\partial S \setminus \partial \omega} A e(u_{\text{spt}})\cdot e(u_{\text{spt}})\theta \cdot n\ ds \\ &&{\kern42pt} + {\int}_{\partial S \setminus \partial \omega} \rho g \cdot u_{\text{spt}} \theta \cdot n\ ds\\ &&{\kern42pt} + {\int}_{\partial S \setminus \partial \omega} \rho g\cdot u_{\text{spt}} \theta \cdot n\ ds \end{array} $$

Regrouping the integrals on the different parts of the boundaries ∂ω ∖ ∂S,∂S ∖ ∂ω and ∂S ∩ ∂ω, we obtain the desired result. □

2.3 Layer by layer model for optimizing the support

We come back to the case where the shape ω is fixed and only the support is optimized. Our goal is to consider a more detailed modelling of the additive manufacturing process, featuring a layer by layer model as in Allaire et al. (2017a, b). As before, the build chamber D is a rectangle and its height in the vertical (and built) direction is denoted by h.

Let 0 = x₀ < h₁ < ... < h_N = h be an equi-distant subdivision of [0,h], corresponding to a number N of slices. Of course, the number N of layers in our model is not the exact number of layers in the actual AM process (which is of the order of 1000) but is much smaller for the sake of computational cost. This is a classical lumping trick which is used in AM simulation and is all the more necessary in an optimization loop. For each i = 1,...,N, define Ω_i = {x ∈ (ω ∪ S) such that 0 < x_d < h_i} as the intermediate domain corresponding to the first i stages in the AM process. The slice number i, or equivalently the last layer in Ω_i, is defined as R_i = {x ∈Ω_i such that h_i− 1 < x_d < h_i}. For each intermediate domain, Ω_i is associated with a state equation, characterizing the mechanical system. Following Allaire et al. (2017a), in order to minimize the effect of overhang regions, the loading in Ω_i is just gravity. However, for taking each layer into account only once, gravity forces are restricted to the last layer R_i, assuming somehow that the previous layers are stable. Such a model was already shown in Allaire et al. (2017a) to produce relevant numerical results. In other words, the state equation in Ω_i is

$$ \left\{ \begin{array}{cl} -\operatorname{div}(Ae(u_{i})) = \rho g_{i} & \text{ in } {\Omega}_{i} \\ u_{i} = 0 & \text{ on }{\Gamma}_{D} \\ Ae(u_{i}) n = 0 & \text{ on } \partial {\Omega}_{i}\setminus {\Gamma}_{D} \end{array} \right. $$

(9)

where $g_{i} = (0,0,...,-1)\chi _{R_{i}}$, where $\chi _{R_{i}}$ is the characteristic function of the last layer R_i. Note that the powder is completely neglected in (9). For each intermediate structure Ω_i we compute its compliance

$${\int}_{{\Omega}_{i}} Ae(u_{i})\cdot e(u_{i}) \ dx ={\int}_{{\Omega}_{i}} f_{i}\cdot u_{i} \ dx,$$

and we minimize their sum, or total compliance,

$$ J_{3}(S) = \sum\limits_{i = 1}^{N} {\int}_{{\Omega}_{i}} f_{i} \cdot u_{i} dx $$

(10)

with a volume constraint on the support S implemented via a Lagrange multiplier. Working under Assumption 2.2, the shape derivative of (10) is given by

$$J_{3}^{\prime}(S)(\theta) = \sum\limits_{i = 1}^{N} {\int}_{\partial S\cap {\Omega}_{i}} \left( - Ae(u_{i})\cdot e(u_{i})+ 2f_{i} \cdot u_{i}\right) \theta \cdot n ds . $$

3 Optimization of supports for thermal evacuation

3.1 Heat equation model

In some cases, support structures are not only necessary for avoiding overhangs, but also for evacuating or regulating the heat inside the structure shape/support in order to reduce thermal residual stresses and deformations. Thus, we suggest another criterion for optimizing supports, which is based on the minimization of the temperature, supposing that the source term is given and the heat conductivity properties of the shape and support are known. As before, the shape to be built is denoted ω and its supports S. We assume that the heat is regulated on the boundary Γ_D of the structure, by imposing a Dirichlet condition on Γ_D. On other boundaries of the structure, we may consider Fourier-type conditions or Neumann conditions, since the conductivity of the powder is significantly smaller than the conductivity of the fused structure.

In the following, we denote by k = k_ωχ_ω + k_Sχ_S the conductivity throughout the structure. Here k_ω is the constant conductivity in the shape ω and k_S that in the support S. These two values k_ω and k_S may be different since the support can be an equivalent homogenized material, with distinct properties from the bulk material occupying the shape. The source term f is assumed to be supported inside the shape ω. Fourier boundary conditions may be considered, in view of the fact that the heat may dissipate in the powder region or by radiation in the upper layer. However, since it is considered that the main source of heat evacuation is through the baseplate, we simplify our model by considering homogeneous Neumann boundary conditions. Thus, the thermal model reads

$$ \left\{ \begin{array}{rll} -\operatorname{div} (k \nabla T)& = f\chi_{\omega} & \text{ in } S \cup \omega \\ k(x) \nabla T \cdot n &= 0 & \text{ on } {\Gamma}_{N} \\ T& = 0 & \text{ on } {\Gamma}_{D} \end{array} \right. $$

(11)

The shape ω is assumed to be fixed and thermal compliance is minimized for all admissible supports

$$ \min_{S \in \mathcal U_{ad}} \mathcal F(S) = {\int}_{\omega} fT {dx}. $$

(12)

The volume constraint is added using a Lagrange multiplier.

Proposition 3.1

Under Assumption 2.2 the shape derivative of the thermal compliance (12) related to the system (11) is given by

$$ \mathcal{F}^{\prime}(S)(\theta) = -{\int}_{\partial S \setminus \partial \omega} k|\nabla T|^{2} \theta \cdot n ds. $$

(13)

Proof

This is a classical result and we briefly sketch the main idea of the proof. Consider the Lagrangian defined for $S \in \mathcal U_{ad}$ and $\hat T,\hat p \in H_{{\Gamma }_{D}}^{1}(D)$ by

$$\mathcal{L}(\hat T,\hat p,S) = {\int}_{S \cup \omega} k \nabla \hat T \cdot \nabla \hat p dx -{\int}_{\omega} fp dx +{\int}_{\omega} fT dx $$

obtained by summing the variational form of (11) with the functional $\mathcal {F}(S)$. The partial derivative of $\mathcal {L}$ with respect to p gives the state equation and the partial derivative with respect to T yields the adjoint equation. This is a self-adjoint case and the adjoint is simply p = −T. The partial derivative of $\mathcal L$ with respect to S gives the shape derivative of $\mathcal {F}$ given in (13). □

3.2 Spectral model

In truth, heat evacuation is a transient phenomenon, which is governed by the heat equation

$$\left\{ \begin{array}{rcll}\displaystyle \rho\frac{\partial u}{\partial t} -\operatorname{div} (k \nabla u) & = & 0 &\text{ in } S\cup \omega\\ u(t = 0) & = & u_{0} &\text{ in } S\cup \omega \\ u & = & 0 & \text{ on }{\Gamma}_{D} \\ k\nabla u \cdot n & = & 0 & \text{ on } {\Gamma}_{N} , \end{array} \right. $$

where ρ = ρ_ωχ_ω + ρ_Sχ_S is the product of density by specific heat and k = k_ωχ_ω + k_Sχ_S is the conductivity. Since the heat operator is self-adjoint with compact resolvent, its spectrum consists of an increasing sequence of eigenvalues. Furthermore, the associated eigenfunctions form a Hilbert basis for the space $H_{{\Gamma }_{D}}^{1}({\Omega })$. In the following, λ_k and $\mathfrak w_{k}$ denote the eigenvalues and eigenvectors of the heat operator. It is well known (see, for example, Allaire 2007b) that if the initial data admits the decomposition $u_{0} = {\sum }_{k = 1}^{\infty } {u_{k}^{0}} \mathfrak w_{k}$, then the solution of the heat equation is

$$u(t,x) = \sum\limits_{k = 1}^{\infty} {u_{k}^{0}} e^{-\lambda_{k} t} \mathfrak w_{k}(x) . $$

Thus, in the absence of a source term, the decay of the temperature u(t,x) as t →∞ is independent of the initial condition u₀ and is given by the first (smallest) eigenvalue of the heat operator. Moreover, in order to achieve the best cooling rate the first eigenvalue λ₁ should be maximized. Based on this analysis, for achieving the best asymptotic heat evacuation, the following spectral problem is considered

$$ \left\{ \begin{array}{rll} -\operatorname{div} (k \nabla T)& =\lambda_{1} \rho T& \text{ in } S \cup \omega \\ k \nabla T \cdot n &= 0 & \text{ on } {\Gamma}_{N} \\ T& = 0 & \text{ on } {\Gamma}_{D}, \end{array} \right. $$

(14)

where λ₁ ≡ λ₁(S) is the first eigenvalue (which depends on the support S). As explained above and in Michailidis (2014), in order to optimize the evacuation of heat, one can maximize the first eigenvalue of (14)

$$\max_{S \in \mathcal U_{ad}} \mathcal{F}(S) = \lambda_{1}(S). $$

Recall that the first eigenvalue of (14) is simple and therefore it is shape differentiable (see for example Chapter 5, Henrot and Pierre 2005).

Proposition 3.2

Under Assumption 2.2, the shape derivative of the first eigenvalue of (14) is given by

$$\begin{array}{@{}rcl@{}} \lambda^{\prime}_{1}(S)(\theta) = {\int}_{\partial S \setminus \omega} \left( k |\nabla T|^{2} - \rho T^{2}\right) \theta\cdot n ds \end{array} $$

(15)

where T is an eigenfunction of the first eigenvalue of (14) normalized such that ${\int }_{\omega } \rho T^{2} dx= 1$.

Proof

To justify this known classical result, introduce the Lagrangian defined for $S \in \mathcal U_{ad}$, $\hat T,\hat p \in H_{{\Gamma }_{D}}^{1}$ and $\hat \lambda \in \Bbb {R}$ by

$$\mathcal{L}(\hat T,\hat p,S,\hat\lambda) = {\int}_{S\cup \omega} k \nabla \hat T \cdot \nabla\hat p dx - \hat\lambda {\int}_{S \cup \omega}\rho \hat T\hat p dx + \hat\lambda , $$

obtained by summing the variational form of the state (14) and the functional $\mathcal {F}(S) = \lambda (S)$. The partial derivative of $\mathcal L$ with respect to $\hat p$ gives the state equation, while the derivative with respect to $\hat T$ gives the adjoint equation. In this case, we obtain that the adjoint p is a multiple of T. The derivative with respect to λ gives

$${\int}_{S\cup\omega} \rho Tp dx = 1,$$

which establishes the multiplicative constant between T and the adjoint state p. Finally, the partial derivative of $\mathcal {L}$ with respect to S yields the shape derivative formula of the eigenvalue shown in (15). □

4 Numerical framework

4.1 The level set method

In order to be able to describe complex structures, including possible topology changes, and to use a fixed computational mesh of the domain D, containing the variable shapes, we use the level set method (Sethian 1999). The boundary of a generic shape Ω ⊂ D is defined via a level set function ψ : D → ℝ such that

$$\left\{ \begin{array}{cl} \psi(x) < 0 & \text{ in }{\Omega},\\ \psi(x) = 0 & \text{ on } \partial {\Omega} ,\\ \psi(x) > 0 & \text{ in } D\setminus {\Omega} . \end{array} \right. $$

During the optimization process the shape evolves according to a scalar normal velocity V (x). In other words, its level set function is the solution of the following advection or transport equation, which is a Hamilton-Jacobi equation,

$$ \frac{\partial \psi}{\partial t}+V|\nabla \psi| = 0. $$

(16)

Our computations rely on the software Advect (Bui et al. 2012) from the ICSD Toolbox in order to solve (16). The algorithm of Bui et al. (2012) solves a linearization of (16) by the method of characteristics. It has the advantage of being able to handle unstructured meshes.

A particular level set function associated to the set Ω is its signed distance function d_Ω. The signed distance function allows us to recover geometric properties of the shape Ω by performing simple computations. For example, the unit normal vector to ∂Ω at x is simply ∇ψ(x) and to compute the curvature of ∂Ω at x it is enough to compute the Laplacian Δψ at a point x ∈ ∂Ω. See (Osher and Fedkiw 2003, Chapter 2) for more facts and proofs regarding the geometry of objects defined via signed distance functions. Therefore, it is important to keep the level set ψ equal to the signed distance function in order to have immediate access to geometric properties of ∂Ω. It is classical to initialize the level set to a signed distance function at the beginning of the optimization process. However, when advecting the shape via the Hamilton-Jacobi equation (16) the resulting level set is not necessarily a signed distance function anymore. Therefore, at every iteration, we perform a redistancing procedure in order to keep the level set equal to the signed distance function to the actual set Ω. This redistancing procedure is done efficiently with the toolbox MshDist (Dapogny and Frey 2012) or with the distance function in FreeFem++ (Hecht 2012).

4.2 Optimization algorithm

In the optimization procedure, we use the following ingredients.

• Initialization. The initial level set function is chosen with sufficiently rich topology in 2D (uniformly distributed holes), or as the whole computational domain in 3D.

• Optimization loop. Given the current shape, represented by the level set function, we compute the corresponding cost functional and its shape derivative. This gives the perturbation field V to be used in the Hamilton-Jacobi equation (16) in order to advect the level set function. If the value of the cost function decreases, up to a certain tolerance, the iteration is accepted, if not, the step size is decreased and the current step is computed again. An iteration is accepted if the relative decrease is below a certain tolerance ranging from 0.001 to 0.01. This tolerance is decreased during the optimization algorithm to ensure the convergence to a local minimum. For all accepted iterations the level set function is reinitialized as a signed distance function.

• Termination. We terminate the algorithm once we observe that the cost functional does not decrease further, or when a prescribed number of iterations is reached. The number of iterations is chosen high enough such that convergence is achieved. Of course, a better termination criterion could be added regarding the non-decrease of the cost function or the verification of an optimality condition.

As usual, the holes or the exterior of the shape, inside the computational domain, is filled by an ersatz material which has typically mechanical parameters 10^− 3 smaller than those of the structure. In our computation, there are thus three phases: the shape, the support and the ersatz material.

In general, when not stated otherwise, a fixed Lagrange multiplier is used for the volume constraint. When a prescribed volume constraint is imposed, we use an augmented Lagrangian approach. It amounts to solve problems of the type

$$\min_{c(\omega) = 0} \mathcal{F}(\omega) $$

by minimizing at each iteration k an unconstrained functional

$$\mathcal{F}(\omega)-Y_{k} c(\omega) + \frac12 R_{k} c(\omega)^{2} ,$$

where the Lagrange multipliers are updated as follows: Y_k+ 1 = Y_k − R_k ⋅ c(ω_k). The penalization multiplier R is initialized to the value 0.1 in our computations and is increased using the formula R ← 1.1R every 5 iterations, as long as the absolute value of the constraint is above a certain threshold, for example |c(ω)| > 0.01. More details concerning Augmented Lagrangian methods can be found in Birgin and Martínez (2014).

5 Simulations

All our numerical computations are performed with the freeware software FreeFem++ (Hecht 2012). The figures in this paper were plotted with Matlab, xd3d or Paraview. Although the shape and its support could have different mechanical properties, here we restrict ourselves to the case of equal Young’s module (normalized to 1) and Poisson’s ratio, equal to 0.3, with one exception: in Test Case 3, where different Young moduli are considered in the shape and the support. However, their densities and thermal conductivities can be different. The build direction for additive manufacturing is always vertical. As shown in Fig. 1, when solving the state equations associated to the supported structure, Dirichlet boundary conditions are considered on the baseplate which corresponds to the bottom of the computation domain. When dealing with linearized elasticity systems this corresponds to the fact that supports are fixed on the baseplate while for the heat equation the baseplate has a fixed temperature for regulation purposes.

In the following, two approaches are used in order to handle the volume constraint. The first one is to use a prescribed Lagrange multiplier chosen experimentally so that the objective function and the constraint are well balanced in the optimization process. The second approach consists in using an augmented Lagrangian where the Lagrange multiplier is updated in order to reach at convergence the prescribed value of the constraint. In the test cases presented below, the volume is considered as a constraint and an objective function related to the compliance is optimized. From a mathematical and numerical point of view it is completely equivalent to consider the compliance as a constraint and to minimize the volume of supports. If one wants to fix a constraint on the compliance, an issue is to find a physically sound maximal value of the compliance. One possible choice is to fix a maximal displacement, assume that it is attained everywhere in the shape and compute the resulting compliance under gravity load, which will be the maximal value of the constraint.

The computational parameters are chosen experimentally in order to illustrate the behaviour of the models described in the paper. It is known that in shape and topology optimization, initial conditions are important and influence the final result. In dimension two, particular care needs to be given to the initial shape, since no new holes can appear during the optimization process. In dimension three there are less restrictions on the initial design, since the topology can change and new holes can appear during the optimization process. In view of these aspects the initialization is chosen as follows:

• dimension 2: the initial design is chosen as either the complement of a union of equally spaced disks corresponding to vertically aligned holes, or as the level set given by an expression coming from a product of cosines of the form cos(2nπx)cos(2nπy) − 0.5, corresponding to diagonally aligned holes. The parameter n controls the number of holes in the second case. For the 2D computations, the initializations are displayed or explicitly referenced.

• dimension 3: the initial condition is chosen as full subset or as the whole computational domain. In some cases some balls may be removed in order to enrich the topology of the final result. In each of the computations below we describe the initialization used in the computations.

The computational time depends on the dimension, on the size of the discretization and on the number of optimization iterations. For example, performing 300 iterations for the 2D computations presented in the Test Cases 1 and 2 below takes less than half an hour. For the 3D computations with 150 iterations the computational time is around 3 h for both Test Cases 5 and 6 when dealing with roughly 10⁵ degrees of freedom. The computations were made on an Intel Xeon 8 core processor, with 32 RAM and on an Intel i7 quad-core laptop with 16GB of RAM.

5.1 Minimizing compliance with a fixed shape

In this subsection, the shape ω is fixed and we only optimize the support S for minimal compliance under gravity loads (see Section 2.1). In all the following cases we take g = (0,− 1) in dimension two and g = (0,0,− 1) in dimension three.

Test Case 1 (MBB beam)

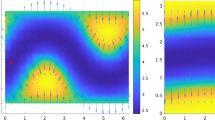
The fixed shape ω is a MBB beam obtained by compliance minimization for a volume V = 1.13, without any further constraint (see e.g. Allaire et al. 2017a, b for details). The fixed shape, theinitial and optimal supports are shown in Fig. 2. Gravity does not apply to the support S, namelyρ_S = 0. The supports are obtained for the density ρ_ω = 2.5 and the optimization procedure has 300 iterations. The computational domain is of size3 × 1 corresponding to half of the beam and a symmetry condition on the vertical symmetry axis is imposed by making the horizontal displacement equal to zero. The computational domain D is discretized using a grid of size301 × 101 with 30401 nodes and ℙ₁ finite elements are used for solving (2). In this simulation, the support and the fixed shape have the same mechanical parameters.

Fig. 2

The fixed shape and the initialization used for Test Case 1 (MBB beam)

In order to illustrate the behaviour of the algorithm, two versions of the optimization procedure are used here: fixed Lagrange multiplier (Fig. 3) and augmented Lagrangian (Fig. 4). The initial condition is the same and the target volume for the augmented Lagrangian is chosen as the final volume of the structure obtained at the end of the optimization with fixed Lagrange multiplier. Note the differences in the convergence histories between the two algorithms. Convergence is monotone for all terms in the optimization process with a fixed Lagrange multiplier. On the other hand, with the augmented Lagrangian approach, compliance first increase until the volume constraint is satisfied, and later it decreases. The final volume of the support structure is 0.4620 and the final compliances are 1.4648 for the fixed Lagrange multiplier and 1.4330 for the augmented Lagrangian approach. The augmented Lagrangian approach finds a structure which performs better and is topologically different from the one obtained with a fixed Lagrange multiplier, starting from the same initial condition and using the same mechanical parameters.

Fig. 3

Optimal supports and convergence curves for Test Case 1 with a fixed Lagrange multiplier ℓ = 1. Fixed shape and initialization given in Fig. 2

Fig. 4

Optimal supports and convergence curves for Test Case 1 with a volume constraint and an augmented Lagrangian algorithm. Fixed shape and initialization given in Fig. 2

The interest of Test Case 1 is that the initial MBB beam has large horizontal parts. These horizontal parts cannot be produced using additive manufacturing processes, unless they are supported. Notice that the optimal support S is distributed in such a way that overhang regions are indeed supported. Moreover, the results obtained with our algorithm resemble those presented in Allaire et al. (2017a), where the additive manufacturing constraints imposed in the optimization process lead to a self-supporting structure.

In order to evaluate the performance of the support with respect to its volume constraint, we plot in Fig. 5 the computed optimal compliances as a function of the support volume. As expected, the optimal compliance is decreasing with respect to the volume constraint. A small amount of support improves a lot the rigidity of the supported structure, but the improvement is saturating when adding more and more supports.

Fig. 5

Optimal compliance of the supported structure as a function of the support volume constraint for Test Case 1

Test Case 2 (M-shape)

The fixed shape and the initial and optimal support are displayed in Fig. 6. The M-shape consists of two thin vertical bars, connected by a thicker part. The computational domain has size3.1 × 3 and the mesh has 156 × 151 degrees of freedom. We consider ρ_ω = 5 for the fixed shape and we optimize the objective function (4) with a fixed Lagrange multiplierℓ = 150. The convergence history of the algorithm for 300 iterations can be seen on Fig. 7.

Fig. 6

Numerical results for Test Case 2. From left to right, fixed M-shape, initial and final supports

Fig. 7

Convergence history of the cost function, the volume and the compliance for Test Case 2 (M-shape)

The motivation for Test Case 2 comes from the fact the M-shape successfully passes the geometric constraint of an angle between the boundary normal and the build direction less than 45^∘, although the overall structure is clearly overhanging. Such a M-shape is hard to manufacture without support since the lower angle of the M start right in the middle of the powder bed. Thus it requires some support. Moreover, in order to have the desired stability as the layers are added, the support should be strong enough to hold the start surface and the subsequent layers, until they join with the other parts of the structure. With our model, optimal supports distribute as expected in order to provide enough resistance for the part of the shape which starts to be fabricated from the powder bed.

Test Case 3 (MBB beam with different phases)

In order to illustrate the behaviour of the algorithm when different mechanical parameters are present in the shape and the support, the same configuration as in Test Case 1 is considered, but the support is allowed to have different material properties from the shape. In this case, the mesh has301 × 101 nodes. The Young modulus of the shape is set to be equal to 1, while the Young modulus of the support has the values 0.5, 0.9 and 1. The optimization algorithm uses an augmented Lagrangian approach and the combined volume of the shape and support is set to converge to 1.7. Results, histories of convergence and final values of the compliances can be visualized in Fig. 8.

Fig. 8

Test Case 3: optimal supports and convergence histories obtained when varying the Young modulus of the support. The Young modulus of the support is equal to 1,0.9 and 0.5 (from top to bottom), while for the shape it is kept at 1

The goal of Test Case 3 is to test the influence of a different stiffness of the support with respect to the shape. As expected, supports tend to be more massive when its Young modulus is smaller. Since the same initial condition is used for all three computations, the topological structure of the result is not radically different in the result. Nevertheless, the convergence curves for the compliances which can be seen in Fig. 8 show that the stiffness of the supported structure decreases when weaker materials are used for supports.

The goal of the next computation is to make a comparison between our model and the one presented by Kuo et al. in Kuo et al. (2018) which does not feature the same loading conditions. Their surface loads are reproduced in Fig. 9 and compared to the bulk loads which are used in this work. Recall that in Kuo et al. (2018) the authors also used techniques in order to facilitate the removal of supports and that these ideas are not implemented in the models proposed here.

Fig. 9

(top row) Loadings considered for the Test Case 4 inspired from Kuo et al. (2018). On the left, bulk loads as proposed in the present work, while on the right, for the sake of comparison, surface loads as proposed in Kuo et al. (2018). (bottom row): initial support (left), result for the model proposed in this article using bulk loads (centre), result for the model using surface loads on the upper boundary as in Kuo et al. (2018) (right)

Test Case 4 (Kuo et al.)

The fixed shape is represented in Fig. 9. Since the model used in Kuo et al. (2018) is different from the ones proposed in this article, two loading cases are considered: one surface load corresponding to the model in Kuo et al. (2018) and one bulk load corresponding to the model proposed in Section 2.1. The optimization is done with an augmented Lagrangian approach with target volume 0.7 for the combined structure part/supports. The parameters considered areρ_ω = 2, ρ_S = 0. The initial design and the optimized ones for each of the loading cases are shown in Fig. 9. In view of the fact that the mesh and shape parameters, loading cases and mechanical properties are not the same in the two models, no precise quantitative comparison of the results can be made. From a qualitative point of view, it can be noted that when using volumic forces, supports tends to concentrate under the more massive parts of the structure. The model proposed in Kuo et al. (2018) allows a more uniform distribution of supports, but for more general and complex shapes it is not clear on which surfaces should the surface load be applied.

Test Case 5 (3D chair)

The fixed shape and the optimal support are displayed in Fig. 10. The computational domain is the union of the rectangular boxes [0,6] × [0,2] × [0,6] and [0,2] × [0,2] × [6,12]. The domain is meshed using 343201 nodes. The initial support fills the whole domain outside the shape. The density is ρ_ω = 3.7, the volume of the chair structure represents 5% of the computational domain and the Lagrange multiplier is chosen so that the final volume of the support is3% of the volume of the computational domain. The optimization procedure has 150 iterations.

Fig. 10

Test Case 5 (3D chair): fixed shape (left) and two views of the optimal supports

Test Case 5 is inspired from Allaire and Jouve (2005), where the 3D chair shape was obtained by compliance minimization.

Test Case 6 (3D beam)

The fixed shape and the optimal support are displayed on Fig. 11. Due to the symmetry we work on a quarter of the box containing the shape. The computational domain is[0,3] × [0,0.5] × [0,1] which is discretized using finite elements. The discretization contains 104181 nodes and 576000 tetrahedra. The density isρ_ω = 3.5 in the fixed shape and we adapt the Lagrange multiplier in order that the final support occupies4% of the computational box (equal to 0.24). The optimization procedure has 300 iterations. The fixed MBB beam was obtained by compliance minimization and occupies10% of the computational domain. The initial support, the result of the optimization and the convergence histories are represented in Fig. 11. Note that these graphs correspond to computations made on one quarter of the domain with symmetry conditions.

Fig. 11

Test Case 6 (3D beam): fixed shape and initial (left) and the optimized support (right) together with the convergence curves

In order to automatically generate support structures, most commercial or proprietary software propose methods based on geometric criteria. One such criterion is to detect all surfaces which are sufficiently close to being horizontal. An inclination angle α₀ is given and it is decided that all structure boundaries which make an angle smaller than α₀ with the horizontal plane have to be supported. We implemented this simple idea and define vertical supports under all overhanging regions given by the angle α₀. In the following, the case of the 3D MBB Beam is studied and supports are calculated for multiple values of α₀. In the left column of Fig. 12 our results, obtained for α₀ ∈{21.5^∘,30^∘,45^∘}, are provided. The corresponding support volumes are 0.24, 0.48 and 0.80, respectively. In particular, note that the solution obtained for α₀ = 21.5^∘ has the same volume as the one used as a target in the Test Case 6. In view of the results presented in Fig. 11, this kind of supports based on simple geometric assumptions can be further optimized, showing again the interest in modelling the optimization of supports.

Fig. 12

(left) Vertical supports generated under the overhang regions for the fixed beam shape shown in Fig. 11 for limiting angle α₀ ∈{21.5^∘,30^∘,45^∘}. (right) Supports generated by the freeware software Ultimaker Cura for the same angles

For the sake of comparison, the free software Ultimaker Cura¹ was also used in order to generate supports for the same angles α₀ as above. The resulting support structures, generated with default parameters of the software, are shown in the right column of Fig. 12 for an easy comparison with our results, obtained with the simple geometrical method described in the previous paragraph. Clearly, the supports of both columns of Fig. 12 are qualitatively similar, which is a confirmation that only geometric information is used to generate supports in Ultimaker Cura.

5.2 Thermal evacuation

In the following, results obtained for the optimization of supports for heat evacuation are presented. The theoretical aspects concerning the objective functions and shape derivatives used can be found in Section 3. The heat (11) with a constant source term f in the fixed shape ω is considered and the support structure S is optimized such that the thermal compliance is minimized. In practice, this would correspond to an optimal evacuation or regulation of the heat produced by the additive manufacturing process. In the following test cases a Dirichlet condition T = 0 is imposed on some parts of the boundary of the computational domain. It is expected that supports will connect the shape ω to these parts of the boundary. Since the conductivity of the powder is orders of magnitude smaller than the conductivity of the shape or the support, Neumann boundary conditions are imposed on ∂(S ∪ ω). Here, only simple test cases in dimension two are performed. More complex situations can be handled with no additional difficulties: for example, different thermal conductivities in the structure and the support, non-constant source terms.

In this subsection, the fixed shape ω is a cantilever, obtained by compliance minimization with volume 0.8 in a 2 × 1 rectangular box with a vertical point load at the middle of the right side and a clamped left side. In all the test cases of this subsection the optimization procedure has 300 iterations.

Test Case 7

A cantilever shape is considered in a2 × 1 rectangular box with Dirichlet condition on the baseplate (bottom of the domain). The conductivity in the fixed shape and the support is set to 0.5 and the constant source term f is equal to 2 in the fixed shape. The optimization is done using an augmented Lagrangian method: the final support has volume 0.35. The initialization and the result of the optimization can be seen in Fig. 13.

Fig. 13

Test Case 7: initial and optimal supports for thermal evacuation

In industrial practice, only connections to the baseplate (lower boundary) of the build chamber can be considered as solid contact, which could efficiently evacuate the heat. Nevertheless, the next test case investigates other boundaries where to apply Dirichlet boundary condition, for the sake of comparison and since the role of supports for heat evacuation is still in debate. Note also that supports are often used to connect the structure to the baseplate: thus, contrarily to the Test Case 7, the structure is placed slightly above the baseplate so that supports must appear between the structure and the baseplate. It is thus not surprising that the optimal supports are different between Test Cases 7 and 8.

Test Case 8

In this test case the behaviour of the algorithm with respect to different boundary conditions is investigated. In Fig. 14 a slightly enlarged box of size2.2 × 1.2 is considered around the cantilever and it is placed such that it is not in contact with any of the boundaries. In this case the behaviour of the algorithm with respect to different boundary conditions is investigated. As expected, supports optimized in order to reduce the temperature tend to connect to the parts of the boundary which are regulated through the Dirichlet boundary condition.

Fig. 14

Test Case 8: Optimal supports for thermal evacuation with different boundary conditions: bottom, top-bottom, top-bottom-right and left-right

Test Case 9

In order to optimize the behaviour of the structure concerning the heat evacuation, the maximization of the fundamental eigenvalue of the system given in (14) is considered. The conductivities are set to 0.5 and the density isρ_ω = 1. Dirichlet boundary conditions are imposed on the lower boundary of the domain. The optimization is done using an augmented Lagrangian method: the final support has volume 0.35. The initial support is the same as the one in Test Case 7 and is shown in Fig. 13. The result of the optimization is presented in Fig. 15.

Fig. 15

Test Case 9: Maximization of the first eigenvalue for the heat equation

The optimal support of Test Case 9 is quite similar to that of Test Case 7 which indicates some kind of robustness of this design to the chosen model.

5.3 Mixing elastic and thermal constraints

We now consider an objective function which takes into account both mechanical and thermal constraints: the average of the elastic and thermal compliancesset functions are. In order to perform the optimization, one simply needs to solve both the elastic system (2) and the thermal system (11) and combine the corresponding shape derivatives.

Test Case 10

The fixed shape is a MBB beam (same as in Test Case 1). The parameters are as follows. The mesh consists of a301 × 101 grid which is triangulated, representing half the beam, by symmetry. The source is 2.5 in the beam and the conductivity is k = 0.5χ_ω + χ_S. The mechanical parameters are the same as in other computations in the previous subsection: Young modulus is 1 and the Poisson ratio is 0.3. A fixed Lagrange multiplierℓ = 1 is used and the optimization procedure has 300 iterations. The optimal supports obtained are shown in Fig. 16. The initial support is initialized with a grid of15 × 4 vertically aligned holes.

Fig. 16

Test Case 10: Optimal supports with respect to the average of mechanical and thermal compliances

5.4 Simultaneous optimization of the shape and the support

Following the theoretical results stated in Section 2.2, the optimization of the shape and the support at the same time is illustrated below. The difficulty here is to be able to represent numerically both the shape and the support and to evolve through the Hamilton-Jacobi equation the corresponding parts of ∂ω and ∂S following the derivatives given in (8). In order to represent both the fixed shape ω and the support S and to distinguish easily between boundaries ∂ω ∖ ∂S, ∂S ∖ ∂ω and ∂ω ∩ ∂S, two-level set functions are used, following classical ideas from Vese and Chan (2002), Wang and Wang (2004). These techniques were already used when dealing with the optimization of structures made of multiple materials in Allaire et al. (2014). In our case two level sets ψ₁, ψ₂ : D → ℝ are needed. The mechanical shape ω and the support S are represented with the aid of the level set functions ψ₁, ψ₂ as follows

$$\begin{array}{rcl} x \in \omega & \Leftrightarrow & \psi_{1}(x)\leq 0 \\ x \in S & \Leftrightarrow & \psi_{1}(x) >0 \ \text{ and } \ \psi_{2}(x) \leq 0\\ x \in D\setminus (\omega \cup S) & \Leftrightarrow & \psi_{1}(x)>0 \ \text{ and } \ \psi_{2}(x)>0. \end{array} $$

This helps decide how to implement the shape derivatives formulas found in (8). The vector field 𝜃, giving a descent direction, is chosen as follows

$$\begin{array}{@{}rcl@{}} \begin{array}{rll} x \in \partial \omega \setminus \partial S & \Leftrightarrow \psi_{1}(x)= 0 \ \text{ and } \ \psi_{2}(x)>0 & \Rightarrow \theta (x) \\&= -j_{1}(x) n\\ x \in \partial \omega \cap \partial S & \Leftrightarrow \psi_{1}(x)= 0 \ \text{ and } \ \psi_{2}(x)\leq 0 & \Rightarrow \theta (x) \\&= -j_{2}(x) n\\ x \in \partial S \setminus \partial \omega & \Leftrightarrow \psi_{1}(x)= 0 \ \text{ and } \ \psi_{2}(x)>0 & \Rightarrow \theta (x) \\&= -j_{3}(x) n, \end{array} \end{array} $$

where the expressions of j₁, j₂ and j₃ can be found in (8) and n is the normal vector to the considered surfaces. On ∂ω ∩ ∂S the normal vector n is chosen pointing outwards ω. In view of the shape derivative formulas (8), the choice of a vector field perturbation 𝜃 gives a corresponding descent direction for the functional we wish to optimize. The volume constraints on ω and S are implemented via Lagrange multipliers. In order to allow different behaviours concerning the shape or the support, two different Lagrange multipliers ℓ_ω, ℓ_S are used and the functional to be optimized is the following:

$$\begin{array}{@{}rcl@{}} J_{2}(\omega,S)&+&\ell_{\omega} \text{Vol}(\omega) + \ell_{S} \text{Vol}(S) = {\int}_{{\Gamma}_{0}} f_{\text{fin}}\cdot u_{\text{fin}} ds\\ & +& {\int}_{\omega \cup S} \rho g\cdot u_{\text{spt}} dx\\ &+&\ell_{\omega} \text{Vol}(\omega) + \ell_{S} \text{Vol}(S). \end{array} $$

(17)

The initialization for the two level sets ψ₁, ψ₂ needs also particular care. In order to have rich enough structures for the shape and the support one should place the holes such that the boundaries of S and ω do not coincide so that the shape derivatives corresponding to parts ∂ω ∖ S,∂ω ∩ ∂S and ∂S ∖ ∂ω are all active. An example of initialization is given in Fig. 17.

Fig. 17

Test Case 11: Simultaneous optimization of a MBB beam and its supports together with the initialization of the two level sets used to represent S and ω

Test Case 11

We minimize (17) simultaneously with respect to S and ω. In Fig. 17 the initial configuration of the two level sets, as well as the result of the optimization algorithm are displayed (see the previous paragraph for a justification of the choice of the initial support and shape). The MBB beam is optimized under a standard centre load with sliding boundary conditions at the lower corners and the support is optimized under the gravity loads of the beam. The Lagrange multipliers areℓ_ω = 1.4 for the beam and ℓ_S = 0.5 for the support. The vertical load for the mechanical properties of the final shape is equal tof_fin = 2.5e_d and the density of the shape used in (2)) is ρ_ω = 2.5 (ρ_S = 0). The optimization procedure took 200 iterations.

5.5 Towards an optimized orientation

In practice when given a shape ω to be printed, before searching for a support strategy one needs to find the proper orientation of the shape which ensures that the need for supports is minimal. In the following, our algorithm is applied to a fixed cantilever shape under different orientations. The capabilities of FreeFem++ (Hecht 2012) are used in order to rotate the level set and construct a new mesh containing it so that the quality of the level set function is preserved under rotation. We perform the exact rotation of the mesh using the command movemesh with the vector field

$${\Phi} = (x \cos \alpha-y \sin \alpha,x \sin \alpha +y \cos \alpha),$$

corresponding to an exact rotation of angle α. In this way, a new rectangular mesh containing the rotated shape is constructed and the level set is interpolated on this new mesh. Furthermore, the mesh is truncated so that the unnecessary parts of the mesh which lie above the rotated shape are not considered in the computation. Finally, the width of the mesh coincides with the width of the rotated shape.

Optimized supports for a cantilever shape under different orientations are presented below. The minimal compliance model presented in Section 2 is used in order to optimize the supports in this case. The results given in Fig. 18 correspond to rotation angles 0^∘,30^∘,45^∘,60^∘ and 90^∘. More precisely, the compliance of the structure ω ∪ S, given by (3), is optimized with a fixed volume constraint, implemented as an augmented Lagrangian. The convergence curves for the volume, compliance and the cost function are shown in Fig. 19, noticing that we have the desired convergence of the volume. Various computations are performed for all angles, multiples of 7.5^∘, between 0^∘ and 90^∘ for different volume constraints and the final compliance of the structure for each angle is represented in Fig. 20. For comparison, the compliance of the structure without supports is also presented. Of course, compliance is greatly diminished when adding supports. The behaviour of compliance with respect to the support volume is also indicated by three different curves. Again, compliance is decreased by adding more supports. It is striking to check that, without support, the minimal compliance is obtained for the vertical orientation of the cantilever, while, with support, it is the horizontal orientation which yields the smallest compliance (whatever the tested volume of support).

Fig. 18

Optimal supports for different orientations 0^∘,30^∘,45^∘,60^∘ and 90^∘ of the fixed shape. The support has fixed volume in all computations. The cantilever shapes have the same size, but the pictures are rescaled to have a fixed height

Fig. 19

Convergence history of the volume and compliance when optimizing the supports for the horizontal orientation of the cantilever presented in Fig. 18. The volume constraint is implemented using an augmented Lagrangian approach

Fig. 20

Final compliance of the structure ω ∪ S with respect to the orientation angle for the rotated cantilevers in Fig. 18. Different curves correspond to different volume constraints for the support

Remark 5.1

The computations described above were made for a fixed family of angles. An immediate perspective of this work is to consider the angle as a parameter in the optimization process. The sensitivity with respect to the angle parameter is classical. However, there are some choices regarding the coupling between the support and the rotated shape. Either the shape and its support are rotated together or the shape is rotated, while the support remains fixed. We favor the last choice, but close attention needs to be given in order to prevent the separation of the structure and its support.

5.6 Layer by layer model

In the following, results concerning the minimization of the functional (10), which models the layer by layer AM process, are presented (see Section 2.3 for details and notations). Recall that the number of layers, denoted by N, is much smaller in our model than in reality, for minimizing the computational cost. Given the computational domain D and the number of slices, meshes are constructed for D and for each region D_i = D ∩{x_d ≤ h_i}. In order to compute the objective function modelling the layer by layer process (10), N partial differential equations of the type (9) need to be solved. Ideally, the mesh chosen in the whole computational domain D will have meshes D_i as sub-meshes which will be computed only once, before starting the optimization algorithm in FreeFem++. Each of the solutions u_i is then interpolated on D by extending it with zero on the region {x_d > h_i}. The extensions of u from D_i to D are denoted by $\tilde u_{i}$. Finally, the vector field giving the descent direction for the level set optimization algorithm, is given by

$$\theta = -\sum\limits_{i = 1}^{N} \left( - Ae(\tilde u_{i})\cdot e(\tilde u_{i})+ 2f_{i}\cdot\tilde u_{i}\right) n, $$

where n is the normal vector to ∂S.

Test Case 12

In dimension two the MBB beam structure is used (same as in Test Case 1) and the objective function (10) is minimized for 10 and 50 slices. Shape optimization problems tend to have multiple local minima, therefore the solution found by the optimization algorithm depends on the initial choice. The results of the optimization algorithm for two different initializations are shown in Fig. 21. The computation is made for a fixed volume constraint and comparing the final costs given by (10) it can be noticed that structures corresponding to the vertical alignment of holes in the initial condition give a slightly lower cost function. The mechanical parameters and the fixed beam are the same as in Test Case 1. The optimization algorithm takes 150 iterations.

Fig. 21

Test Case 12: Optimization of the supports for a MBB beam for 10 (middle line) and 50 slices (bottom line), for different initial conditions at fixed volume (top line). The optimized designs on the left, giving rise to vertical bar structures, have a lower value of the cost function

A strong resemblance between our results and the self supporting structures obtained in Allaire et al. (2017a, b) can be observed.

Test Case 13

In dimension three the layer by layer algorithm is applied to the chair structure used before in the Test Case 5 for 5, 10 and 20 slices. The mechanical and optimization parameters are the same. The results obtained are shown in Fig. 22. As the number of slices increases, it can be noticed that the structure of supports modifies slightly so that there is a more uniform supporting of overhang surfaces.

Fig. 22

Test Case 13: Optimization of the supports for the 3D chair structure for 5,10 and 20 slices

The computational cost for the layer by layer model is important since we need to solve the state equation for each slice. In general, for N slices, the computational cost is multiplied by N, since most of the time in the optimization algorithm is spent solving the elasticity systems. 2D computations for 50 slices take about 3 h, while the 3D computations for 20 slices took 2 days of computational time.

6 Conclusion

This paper introduces several models and algorithms for the optimization of supports in additive manufacturing. Our mathematical models are based on the mechanical and thermal properties regarding the combined structure shape/support. Yet, they are simple enough so that their computational cost remains reasonable. They allow to successfully detect and support overhang regions without relying only on geometrical information. We also consider the simultaneous optimization of the shape and its support in a multiphase optimization framework. The numerical computations were performed with the freeware software FreeFem++ (Hecht 2012), in reasonable computational times. For example a typical 2D optimization with 300 iterations on a mesh of size 300 × 100 takes less than half an hour on a laptop (Intel i7 quad-core laptop with 16GB of RAM), while a 3D optimization with 150 iterations on a mesh consisting of around 10⁵ nodes costs around 3 h of CPU time. We believe that our algorithms, coupled with more optimized finite element solvers (for example, using parallel computing), could be easily implemented and used for industrial purposes. A parallel version of our algorithm is a work in progress and it could significantly improve computational times in dimension three. In a future work, we plan to handle the optimization of the shape orientation, combined with that of the supports. We also want to incorporate other manufacturability constraints, including accessibility issues related to the removal of supports. The removal of supports may pose difficulties, especially for complex 3D shapes. To guarantee the ease of removal, any contact zone between supports and the actual shape should be accessible from the outside along a straight line. This can be added as a constraint in the optimization process. Another constraint relevant to supports is the penalization of the unnecessary contact zone between the support and the shape. The optimal orientation with respect to the area of overhang regions and the volume under overhang regions is also a relevant aspect regarding the support structures. All these issues are the topic of an ongoing work. Of course, it is crucial to assess our optimized supports with experiments. This will be the topic of a future collaboration with industrial partners in the SOFIA project.