1 Introduction

Additive manufacturing (AM) is an umbrella term used to describe any process that adds material together to produce a final part. This manufacturing technology was formerly seen only as a rapid prototyping tool; however, the recognition of its ability to create complex designs has led to its use in a widespread range of applications. The evolution of this manufacturing process has included the use of multiple different material groups such as polymer, metal, and composite. AM technology is being pursued by various industries including aerospace, who are interested in high-performance, reliable, and lightweight designs. In 2018, the global additive manufacturing market was valued at US$ 8.44 billion and is expected to grow to US$ 36.61 billion by 2027, growing at a compound annual growth rate of 17.7% (Research and Markets 2019). Further development will increase use by industry, allowing them to realize complex designs.

Topology optimization (TO) is a mathematical design tool used to determine the optimal distribution of material within a given design space. As first proposed by Bendsøe and Kikuchi (1988), the objective is to minimize compliance, subject to a volume constraint. The high-performance designs produced by TO have led to implementation by multiple industry sectors, including aerospace and automotive (Li et al. 2015; Wong et al. 2018). Research efforts have aimed to increase the practicality of the resulting geometries and the utility of the design tool, such as limiting intermediate element densities, imposing manufacturing or symmetry constraints, and the ability to admit multi-material designs (Sigmund and Petersson 1998; Harzheim and Graf 2006; Woischwill and Kim 2018; Florea et al. 2019).

While TO has the potential to produce lightweight and efficient designs, the results are often complex and difficult to manufacture. The layer-wise nature of AM facilitates greater design freedom compared to traditional manufacturing; therefore, it is an ideal method to fabricate the designs generated by TO. Full integration of the two techniques, specifically ways to address the high costs associated with AM, is still on-going. Decreasing these costs will assist in the ability for industries to maximize the benefits of topology optimization.

A major design challenge encountered in AM is the existence of overhanging features that require support structures in the manufacturing process. In common industrial AM processes, such as selective laser melting (SLM), the self-supporting threshold angle is approximately 45° (Wang et al. 2013). If the angle between a surface on the part and the build plate is less than the self-supporting threshold angle, support material is required. The support material may significantly contribute to the total cost of manufacturing through three categories:

  1. 1.

    Cost of material used

  2. 2.

    Increased build time

  3. 3.

    Cost of support material removal: the surface where support material interfaces with the part requires additional post-processing steps to remove the support material and improve the surface finish

The primary approach to limit support material is to change the topology of the design. Brackett et al. (2011) were able to identify the major issues associated in AM-related TO and proposed possible solutions. Leary et al. (2014) modified a previously optimized topology by adding structures in a post-processing step that ensures a self-supporting design. The added structures are implemented to be part of the final design, as opposed to sacrificial support structures, leading to increased weight. Instead of changing the topology after generating an optimal design, Gaynor and Guest (2016) incorporated an AM constraint into sensitivity-based topology optimization. The constraint effectively eliminated all supported surfaces and, therefore, support material. Similarly, Ryan and Kim (2019) and Sabiston and Kim (2019) implemented sensitivity expressions for support material in the topology optimization procedure, but employed the support material as an objective as opposed to a constraint in 2D and 3D, respectively. It was shown that significant decreases in support material could be achieved, but at the expense of structural performance. Langelaar (2016, 2017) implemented a bottom-up approach achieving self-supporting structures in both 2D and 3D. A filter that relies on the existence of a uniform regular mesh is used to ensure that elements in the layer above are supported by elements below, following a user-defined self-supporting threshold angle. In the context of optimization, changing the topology of a design by including AM considerations will reduce design freedom.

Another approach to limit support material is optimizing the support structures. For example, Vanek et al. (2014) use tree-like designs to support overhanging surfaces, while Hussein et al. (2013) and Strano et al. (2013) implement lattice and cellular support structures, respectively. The benefit to these approaches is the potential to significantly reduce support material, without compromising the structural performance; however, the surfaces that require support material remain unchanged.

Furthermore, changing the build orientation can significantly influence the support material needed for a design. Generally, the build orientation is determined logically by the designer or a brute force approach is utilized to determine the optimal orientation. Within topology optimization, Langelaar (2018) adapted the previously conceived AM filter to simultaneously optimize part topology, support layout, and build orientation. A continuation scheme was implemented by considering several user-defined build orientations, each with a corresponding support layout, and eliminating the uncompetitive orientations throughout the optimization. Guo et al. (2017) also combined part topology and build orientation optimization, incorporating the moving morphable voids approach. This approach requires the user to specify an initial number of voids within the design domain and then utilize shape optimization techniques to optimize a set of geometrical parameters. Allowing variable build orientation can significantly decrease the amount of support material; however, the optimal build orientation is not always intuitive.

Research efforts have been directed toward the various methods to minimize support material. The best approaches often include a hybrid of two or more of the way to reduce support material such as changing part topology and incorporating variable build orientation. Minimizing support material in AM can lead to significant cost savings, but often at the expense of structural performance.

Of the existing research, most methods are developed in 2D and rely heavily on the finite element discretization scheme; however, these findings do not directly translate to practical 3D problems, leading to a knowledge gap. Additionally, a significant portion of the research aiming to minimize the amount of supported surface area relies on the level set topology optimization method (Mirzendehdel and Suresh 2016; Allaire et al. 2017). Developing a method that utilizes density-based topology optimization will further assist implementation of TO by industry.

Ideally, all support material and supported surfaces are eliminated or significantly reduced while having no impact on structural performance. As previously mentioned, Ryan and Kim (2019) were successful in reducing support material through implementing one of the methods to reduce support material: changing part topology. Incorporating build orientation into the optimization procedure allows increased design freedom, leading to the potential for better designs.

The objective of this paper is to develop a 3D approach for the combined optimization of part topology and build orientation with AM considerations. The structural objective is compliance, while the AM objectives are supported surface area and support material. Ryan and Kim (2019) have previously developed a method to minimize these AM objectives by changing the part topology with a fixed build orientation. Therefore, the novel aspects in this paper are implementing variable build orientation into the optimization procedure. In many cases, the optimal build orientation is intuitive; however, when solving complex geometries, it is advantageous to have a numerical design tool that determines the optimal build orientation. The formulation is constructed in a way that both the part topology and build orientation are considered throughout the entire optimization process. Both 2D and 3D academic problems are solved, as well as a practical test problem.

The ensuing sections are organized as follows. Section 2 describes the proposed approach to simultaneously consider part topology and build orientation. Section 3 explains the numerical implementation and the analytical sensitivities are validated in Section 4. Numerical results are presented in Section 5, with relevant discussions in Section 6. Lastly, Section 7 consists of conclusions.

2 Formulation

2.1 Spatial density gradient method for computation of supported surface area and support material

The topology optimization framework includes many modifications to the standard topology optimization problem statement to achieve the goal of minimizing supported surface area and support material, via changing the part topology. The use of the Helmholtz PDE density filtering operation, simultaneously proposed by Lazarov and Sigmund (2011) and Kawamoto et al. (2011), provides a means to efficiently control checkerboarding and promote a defined topological boundary, while conveniently providing nodal density information. Conversion between the element densities and nodal densities is given by (1) (note: first-order tensors are denoted by a lowercase character and under-tilde, \( \underset{\sim }{x} \), and second-order tensors are denoted by an uppercase character and under-tilde, \( \underset{\sim }{K} \)):

$$ {\underset{\sim }{K}}_{\mathrm{f}}\overset{\sim }{\underset{\sim }{\rho }}={\underset{\sim }{T}}_{\mathrm{f}}\underset{\sim }{x} $$
(1)

where \( \overset{\sim }{\underset{\sim }{\rho }} \) is the filtered nodal design variables, \( {\underset{\sim }{K}}_{\mathrm{f}} \) is a global filter matrix related to the structural stiffness matrix, and \( {\underset{\sim }{T}}_{\mathrm{f}} \) converts the element design variables, \( \underset{\sim }{x} \), to a nodal representation as described by Lazarov and Sigmund (2011).

To counteract the negative artifacts of applying Neumann boundary conditions at the limits of the design domain, as conventionally done when using a Helmholtz PDE filter, a boundary extension method is used. The boundary extension method is similar to that proposed by Clausen and Andreassen (2017), but uses a block of solid elements at areas where loads or supports are located to remove the risk of singular matrices (Sabiston and Kim 2019).

The calculation of total support material was performed using a similar four-step process to Ryan and Kim (2019):

  1. 1.

    Spatial gradient calculation

  2. 2.

    Identification of surface area

  3. 3.

    Identification of supported surface area

  4. 4.

    Support material computation

To obtain accurate information about the topological boundary, the spatial density gradient of the nodal density variables is calculated using (2):

$$ \nabla {\rho}_e=\sum \limits_{j=1}^{N_{\mathrm{d}}}{\underset{\sim }{B}}_e^j\underset{\sim }{\overset{\sim }{\rho }}{\hat{e}}_j $$
(2)

where ∇ρe is the spatial density gradient of the e − th element, \( {\underset{\sim }{B}}_e^j \) is the derivative of the e − th element’s shape function vector with respect to the j − th spatial dimension, Nd is the number of spatial dimensions, \( \underset{\sim }{\overset{\sim }{\rho }} \) is the vector of nodal design variables, and \( {\hat{e}}_j \) is the basis vector of the j − th spatial dimension. Areas where the spatial gradient is high indicate a transition from solid to void or void to solid elements, whereas a low spatial gradient value indicates a region of constant density. The surface area condition number of the e − th element can then be calculated using the spatial density gradient magnitude by (3):

$$ {\varphi}_e=\left\Vert \nabla {\rho}_e\right\Vert =\sqrt{\sum \limits_{j=1}^{N_{\mathrm{d}}}{\left({\nabla}_j{\rho}_e\right)}^2} $$
(3)

where φe is the surface area condition number of the e − th element.

With the surface elements determined, identification of an element’s supported surface condition number can be calculated with the use of the spatial density gradient direction. A smoothed Heaviside function, similar to that proposed by Qian (2017), is used to formulate a differentiable function, as opposed to having a strict 0 or 1 solution, depending on if the self-supporting threshold angle is exceeded by the spatial density gradient direction. The implementation of the smoothed Heaviside step function to calculate the supported surface condition number yields (4):

$$ {\psi}_e={H}_{\overline{\alpha}}\left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \underset{\sim }{b}\right){\varphi}_e=\frac{1}{1+{e}^{-2\beta \left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \underset{\sim }{b}-\cos \left(\overline{\alpha}\right)\right)}}\left\Vert \nabla {\rho}_e\right\Vert $$
(4)

where ψe is the supported surface condition number of the e − th element, \( {H}_{\overline{\alpha}} \) is the Heaviside step function, \( \overline{\alpha} \) corresponds to the self-supporting threshold angle, \( \underset{\sim }{b} \) is the build direction unit vector, and β is a constant controlling the steepness of the smoothed Heaviside step projection. A mathematical representation of the supported surface condition number for all elements is given by (5):

$$ \left[\underset{\sim }{\psi}\right]=\left[\begin{array}{c}{\psi}_1\\ {}{\psi}_2\\ {}\vdots \\ {}{\psi}_N\end{array}\right] $$
(5)

where N is the number of elements. The total supported surface area, Ψ, can then be approximated as (6):

$$ \varPsi ={\left[\underset{\sim }{V}\right]}^T\left[\underset{\sim }{\psi}\right] $$
(6)

where \( \left[\underset{\sim }{V}\right] \) is a vector of element volumes. As a result, the supported surface area is a volumetric quantity in both 2D and 3D implementations.

Using the surface area and supported surface area information, the support material can be calculated. Elements are grouped into linear columns that extend up from the build plate in the build direction. Following Ryan and Kim (2019), a peak finding algorithm is then used to identify where supported surface elements are located within that column as well as if supporting elements are present, which indicates that the support material attaches onto the part itself as opposed to the build plate. The support material columns are then calculated by integrating between the supported surface elements, be, and the supporting surface elements, ae, in the linear column \( {\overrightarrow{z}}_i(t) \) as (7):

$$ {\lambda}_e=\underset{a_e}{\overset{b_e}{\int }}\underset{\sim }{V}\left({\overrightarrow{z}}_i(t)\right)\left(1-\underset{\sim }{\rho}\left({\overrightarrow{z}}_i(t)\right)\right)\mathrm{d}t $$
(7)

where λe is the support material column for the e − th supported element, be and ae are the upper and lower integration limits, \( \underset{\sim }{V}\left({\overrightarrow{z}}_i(t)\right) \) and \( \underset{\sim }{\rho}\left({\overrightarrow{z}}_i(t)\right) \) correspond to the volume and density of an element in the column, with integral quantity t. The total support material is then found by summing all the support material columns as (8):

$$ \varLambda =\sum \limits_{e=1}^N{\lambda}_e $$
(8)

where Λ is the support material for all N elements. Like supported surface area, support material is a volumetric quantity in both 2D and 3D.

2.2 Implementing build orientation as a design variable

The supported surfaces and, therefore, the support material are dependent on build orientation. Therefore, an equation for supported surface area that is smooth and differentiable with respect to build orientation is necessary for gradient-based optimization. To do this, a novel approach that utilizes transformation laws is used. A rotation matrix is integrated into the supported surface area calculation that allows the build direction vector to be rotated by an angle. All rotations are relative to a reference build direction unit vector, \( \underset{\sim }{b} \), that is fixed and set in the positive y-direction, as shown in Fig. 1. Since the reference build direction vector does not change, even when the build direction is rotated to a new vector, subsequent rotations are still with reference to the initial configuration.

Fig. 1
figure 1

Reference build direction vector for 2D and 3D

Full size image

The implementation of the rotation matrix is represented as (9):

$$ \left[\overset{\sim }{\underset{\sim }{b}}\right]={\left[\underset{\sim }{R}\right]}^T\left[\underset{\sim }{b}\right] $$
(9)

where \( \overset{\sim }{\underset{\sim }{b}} \) is the transformed build direction vector and \( \underset{\sim }{R} \) is a rotation matrix. In 2D, the equation simply represents a positive rotation about the z-direction, described by the right-hand coordinate system, with \( \underset{\sim }{R} \) defined as (10):

$$ \left[{\underset{\sim }{R}}^{2\mathrm{D}}\left(\theta \right)\right]=\left[\begin{array}{cc}\cos \left(\theta \right)& \sin \left(\theta \right)\\ {}-\sin \left(\theta \right)& \cos \left(\theta \right)\end{array}\right] $$
(10)

where θ is the angle of rotation between the reference and transformed build direction vector shown in Fig. 2.

Fig. 2
figure 2

Rotation of the reference build direction vector, \( \underset{\sim }{b} \), to the transformed build direction vector, \( \tilde{\underset{\sim }{b}} \), by θ. Build plate omitted for clarity

Full size image

In 3D, there is now a possibility for the build direction vector to rotate about the x-, y-, or z-axis and a global rotation matrix is used. All possible build direction vectors can be obtained by a combination of any rotations about just two axes. Therefore, to simplify the problem, only rotations about the x- and z-axes in the reference configuration are used. The global rotation matrix is given by (11):

$$ \left[{\underset{\sim }{R}}^{3\mathrm{D}}\left(\underset{\sim }{\theta}\right)\right]=\left[{\underset{\sim }{R}}_z\left({\theta}_z\right)\right]\left[{\underset{\sim }{R}}_x\left({\theta}_x\right)\right] $$
(11)

where Rz contributes a rotation about the z-axis and Rx contributes a rotation about the x-axis. In 3D, \( \underset{\sim }{\theta } \) is now a vector (12):

$$ \left[\underset{\sim }{\theta}\right]=\left[\begin{array}{c}{\theta}_x\\ {}{\theta}_z\end{array}\right] $$
(12)

where θx and θz are the angles of rotation between the reference and transformed build direction vector about the reference x- and z-axes. Since (11) is not associative, the order of multiplication matters, and the results must be interpreted as such. The rotation matrices are then defined as (13):

$$ {\displaystyle \begin{array}{c}\left[{\underset{\sim }{R}}_x\right]=\left[\begin{array}{ccc}1& 0& 0\\ {}0& \cos \left({\theta}_x\right)& \sin \left({\theta}_x\right)\\ {}0& -\sin \left({\theta}_x\right)& \cos \left({\theta}_x\right)\end{array}\right]\\ {}\left[{\underset{\sim }{R}}_z\right]=\left[\begin{array}{ccc}\cos \left({\theta}_z\right)& \sin \left({\theta}_z\right)& 0\\ {}-\sin \left({\theta}_z\right)& \cos \left({\theta}_z\right)& 0\\ {}0& 0& 1\end{array}\right]\end{array}} $$
(13)

Again, the rotations are relative to the reference build direction vector, which does not change when the build direction vector is transformed.

With the build direction vector defined as a function of the design variable \( \underset{\sim }{\theta } \) (θ in 2D), (4) can be modified to allow variable build orientation by replacing \( \underset{\sim }{b} \) with \( \overset{\sim }{\underset{\sim }{b}} \) as (14):

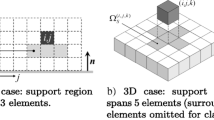
$$ {\psi}_e={H}_{\overline{\alpha}}\left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \overset{\sim }{\underset{\sim }{b}}\right){\varphi}_e=\frac{1}{1+{e}^{-2\beta \left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \overset{\sim }{\underset{\sim }{b}}-\cos \left(\overline{\alpha}\right)\right)}}\left\Vert \nabla {\rho}_e\right\Vert $$
(14)

When the build direction vector is transformed, the elements are still grouped into columns that extend from the build plate as described in Section 2.1. This strategy ensures that the proposed method does not rely on a regular pixel or voxel mesh for the support material calculation as shown in Fig. 3. Challenges may arise if there are significant changes between the column widths and the element sizes. For example, two elements at the same height could be grouped into a single column if the columns are significantly larger than the element size.

Fig. 3
figure 3

Element grouping method for when the build direction vector is transformed. The blue rectangle represents the grouping column. Only three columns are shown in each case for clarity

Full size image

In the following sections, the build direction design variables will also be referred to as 1 and 2, such that (15):

$$ \left[\begin{array}{c}{\theta}_x\\ {}{\theta}_z\end{array}\right]=\left[\begin{array}{c}{\theta}_1\\ {}{\theta}_2\end{array}\right] $$
(15)

2.2.1 Optimization problem statement

The structural objective evaluated in this work is compliance (C), while the AM objectives are supported surface area (Ψ) and support material (Λ). The mathematical problem statement is formulated following the conventional SIMP material definition (Bendsøe and Sigmund 1999), and using a bi-objective function subject to volume constraints as (16):

$$ {\displaystyle \begin{array}{cc}\operatorname{minimize}:& J=w\frac{C\left(\underset{\sim }{x}\right)}{C_0}+\left(1-w\right)\left(\frac{\varPsi \left(\underset{\sim }{x},\underset{\sim }{\theta}\right)}{\varPsi_0}\ \mathrm{OR}\ \frac{\varLambda \left(\underset{\sim }{x},\underset{\sim }{\theta}\right)}{\varLambda_0}\right)\\ {}\mathrm{subject}\ \mathrm{to}:& \left(\sum \limits_{e=1}^NE\left({x}_e\right){\underset{\sim }{K}}_e^0\right)\underset{\sim }{u}=\underset{\sim }{f}\\ {}& \sum \limits_{e=1}^N{x}_e{V}_e\le \gamma {V}_0\\ {}& \begin{array}{c}0\le {x}_e\le 1\kern0.75em \forall e\in \varOmega \\ {}0{}^{\circ}\le {\theta}_k<360{}^{\circ}\begin{array}{c}k=1\left(2\mathrm{D}\right)\\ {}k=1,2\left(3\mathrm{D}\right)\end{array}\end{array}\end{array}} $$
(16)

where \( \underset{\sim }{x} \) and \( \underset{\sim }{\theta } \) represent vectors of the element density and build orientation design variables, respectively. A weighting factor, w, controls the influence of either objective on the final design. C0, Ψ0, and Λ0 are used to normalize the objective functions; N is the number of elements; and xe represents the e − th element density design variable that interpolates the Young’s modulus for the given material represented by E. The element level stiffness matrix is represented by \( {\underset{\sim }{K}}_e^0 \), while \( \underset{\sim }{u} \) and \( \underset{\sim }{f} \) are the nodal displacement and load vectors, respectively. Additionally, Ve is the element volume, V0 is the total volume in the design space, and γ is the volume fraction.

The element density and build orientation design variables are simultaneously considered throughout the entire optimization process. In the initial stages of optimization, little to no topological boundaries exist due to the vast amount of intermediate element densities. Thus, attempts were made to begin the build orientation optimization once the topology resembled the final geometry. This resulted in worse performance, likely due to better local optimum being initially overlooked.

In the present mathematical problem statement (16), only one of the AM objectives (supported surface area or support material) can be activated. This is simply so that the results can be more meaningfully evaluated, but it may be beneficial to include both AM objectives into the optimization problem. Furthermore, only a single, user-defined build direction can be initialized per optimization run. As a result, the solution may produce a poor-quality local optimum since the build orientation problem generally has several solutions or local optima present. This means that the solution, and therefore quality of the local optima, for the optimizer may be different depending on where the build direction is initialized. To improve the optimality of the final solutions, a continuation scheme similar to that presented by Langelaar (2018), which initially considers multiple build orientations and eliminates the uncompetitive designs throughout the optimization process, could be implemented with the existing formulation; however, in 3D, the computational expense is increased; thus, this method becomes less feasible.

2.2.2 Sensitivity analysis with respect to build orientation

Sensitivity analysis was performed with respect to the build orientation design variables with the intention of solving the optimization problem using gradient-based methods. As previously mentioned, the two objectives that include build orientation as a design variable are supported surface area and support material. The sensitivities for supported surface area are solved analytically, and the finite difference method (FDM) is used to obtain the sensitivities for total support material. The sensitivities for the additive manufacturing–based objective functions with respect to the element density design variables were previously derived by Ryan and Kim (2019).

The derivative of the supported surface area objective function, given by (14), with respect to the build orientation design variable vector, \( \underset{\sim }{\theta } \), is represented as (17):

$$ {\displaystyle \begin{array}{c}\frac{\partial \varPsi }{\partial \underset{\sim }{\theta }}\\ {}\left[1\times k\right]\end{array}}={\displaystyle \begin{array}{c}{\underset{\sim }{V}}^T\\ {}\left[1\times N\right]\end{array}}{\displaystyle \begin{array}{c}\frac{\partial \underset{\sim }{\psi }}{\partial \underset{\sim }{\theta }}\\ {}\left[N\times k\right]\end{array}} $$
(17)

where k represents the number of build orientation design variables (two in 3D, one in 2D). The derivative of the e − th supported surface condition number with respect to the k − th build orientation design variable is then defined as (18):

$$ \frac{\partial {\psi}_e}{\partial {\theta}_k}=\frac{\partial }{\partial {\theta}_k}\left({H}_{\overline{\alpha}}\left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \overset{\sim }{\underset{\sim }{b}}\right){\varphi}_e\right) $$
(18)

For clarity, since there are two build orientation design variables in 3D, each element contributes two sensitivities to the supported surface area sensitivity calculation as (19):

$$ \frac{\partial {\psi}_e}{\partial {\theta}_k}=\left[\frac{\partial {\psi}_e}{\partial {\theta}_1}\kern0.5em \frac{\partial {\psi}_e}{\partial {\theta}_2}\right] $$
(19)

Expanding the smoothed Heaviside step function yields (20):

$$ \frac{\partial {\psi}_e}{\partial {\theta}_k}=\frac{\partial }{\partial {\theta}_k}\left(\frac{1}{1+{e}^{-2\beta \left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \left({\underset{\sim }{R}}^T\left(\underset{\sim }{\theta}\right)\cdot \underset{\sim }{b}\right)-\cos \left(\overline{\alpha}\right)\right)}}{\varphi}_e\right) $$
(20)

Using the chain rule, the sensitivity of this expression can be written as (21):

$$ \frac{\partial {\psi}_e}{\partial {\theta}_k}=\left(\frac{2\left\Vert \nabla {\rho}_e\right\Vert \beta {e}^{-2\beta \left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \left({\underset{\sim }{R}}^T\left(\underset{\sim }{\theta}\right)\cdot \underset{\sim }{b}\right)-\cos \left(\overline{\alpha}\right)\right)}}{{\left(1+{e}^{-2\beta \left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \left({\underset{\sim }{R}}^T\left(\underset{\sim }{\theta}\right)\cdot \underset{\sim }{b}\right)-\cos \left(\overline{\alpha}\right)\right)}\right)}^2}\right)\left(\frac{\nabla {\rho}_e}{\left\Vert \nabla {\rho}_e\right\Vert}\cdot \left(\frac{\partial {\underset{\sim }{R}}^T\left(\underset{\sim }{\theta}\right)}{\partial {\theta}_k}\cdot \underset{\sim }{b}\right)\right) $$
(21)

For support material, FDM was used to calculate the sensitivities with respect to build orientation. In topology optimization, calculating sensitivities with respect to the density design variables using this method is infeasible due to the large number of design variables (> 100,000 elements/design variables in some cases). With there being at most two design variables in 3D for build orientation, FDM becomes feasible. Another consideration is the calculation of support material is independent from the finite element analysis operation, which is the most computationally expensive operation in the TO procedure. Therefore, the proposed approach remains efficient with the use of FDM, described as (22):

$$ \frac{\varDelta \varLambda}{\varDelta \underset{\sim }{\theta }}={\left[\begin{array}{c}\frac{\varDelta \varLambda}{\varDelta {\theta}_1}\\ {}\frac{\varDelta \varLambda}{\varDelta {\theta}_2}\end{array}\right]}^{\prime }={\left[\begin{array}{c}\frac{\varLambda \left(\underset{\sim }{\theta}\right)-\varLambda \left(\underset{\sim }{\theta }-\varDelta {\theta}_1\right)}{\varDelta {\theta}_1}\\ {}\frac{\varLambda \left(\underset{\sim }{\theta}\right)-\varLambda \left(\underset{\sim }{\theta }-\varDelta {\theta}_2\right)}{\varDelta {\theta}_2}\end{array}\right]}^{\prime } $$
(22)

2.2.3 Visualization

To assist with visualizing the results, the build direction is always displayed as “up the page.” As such, in 2D, since θ represents a positive angle of rotation between the reference and transformed build direction vector, the part is rotated by −θ as shown in Fig. 4. The same process for visualization is applied in 3D. The build plate is displayed in blue and will remain so throughout the following sections. The build direction is always normal to the build plate.

Fig. 4
figure 4

Visualization of build orientation results. a The raw results. b The part rotated by −θ

Full size image

3 Numerical implementation

In this study, three examples are used to demonstrate the proposed approach: a single 2D academic problem and two 3D problems, one of which is a practical example (Fig. 5). The 2D academic example consists of a cantilever beam with the load applied in the bottom right corner. A similar academic cantilever beam problem is solved in 3D, with the load placed at the mid-node in the z-direction. The 3D practical problem is modeled after an aircraft landing gear door hinge, which includes a circular nondesign space used for hinge attachment onto the interior of the aircraft. An additional nondesign region is used as a mounting plate for the landing gear door. Although the boundary padding elements are omitted for visualization purposes, during implementation they would be added to the outsides of the design domains. The number of boundary layers is equal to the nearest ceiling whole number of the filter radius.

Fig. 5
figure 5

Example problems: a 2D cantilever beam, b 3D cantilever beam, c 3D aircraft landing gear door hinge

Full size image

Separate optimization codes were implemented for each dimensionality (2D and 3D) in MATLAB. For the 2D case, four-node bi-linear quadrilateral elements are used, while the 3D case uses eight-node tri-linear hexahedral elements. The academic problems have element side lengths of 1 mm, whereas the practical 3D example has side lengths of 1.5 mm. For all cases, the self-supporting threshold angle is set at \( \overline{\alpha}=45{}^{\circ} \), the Young’s modulus is set at E0 = 1 N/mm2, and the Poisson’s ratio is v = 0.3.

Again for both 2D and 3D cases, the method of moving asymptotes (MMA) is used (Svanberg 1987). As well, an adaptive penalization scheme is implemented, initially setting p equal to 4. Once the convergence criterion is met, the penalization is increased to a more aggressive value of 6 to further mitigate intermediate densities. Convergence is defined as having less than 1% change in the objective function over the past 5 iterations. Upon final convergence, a volume-preserving sharpening step is completed to obtain discrete element values that are physically meaningful. The effect of the sharpening step is shown in Appendix 1.

The applied perturbation used to calculate the support material sensitivities with respect to the build orientation design variables is Δθk = 0.1. It is noted that the magnitude of the sensitivities depends on the selected applied perturbation; however, the sign or direction that the sensitivity would change the design variable does not depend on the amount of perturbation.

4 Sensitivity verification

To validate the analytical sensitivities for the supported surface condition number, FDM is used with Δθk = 0.1. The analysis was conducted on the 3D cantilever beam with a preconverged topology optimization solution to simulate more practical results. Figure 6 shows the preconverged topology for the data provided in Table 1. The analysis demonstrates excellent agreement between all analytical and FDM sensitivities.

Fig. 6
figure 6

3D preconverged TO solution (sharpened for visualization) of the 3D cantilever beam test problem used for verification of the analytical sensitivity analysis (40 × 22 × 22): a iso-metric view and b side view

Full size image
Table 1 3D sensitivity analysis verification of the supported surface condition number of element e. Separate verification is shown for both θx and θz
Full size table

5 Results

The ideal outcome for any optimization process is to determine the global optimum for a given design domain. Addition of build orientation as a design variable presents challenges associated with topology optimization, since both are nonconvex in nature. To assist with assessing the proposed approach, optimization 4, three reference cases are used for comparison. The problem statements are summarized in Table 2. Optimization 1 performs compliance-only minimization with a fixed build orientation, while the addition of either support material (a) or supported surface area minimization (b) with respect to the build orientation design variable occurs in optimization 2. As such, the topology and, therefore, compliance produced by optimization 1 and optimization 2 are identical. Optimization 3 investigates the combined optimization of compliance and support material with respect to the element densities; therefore, build orientation remains unchanged. Lastly, the proposed approach to simultaneously optimize the element densities and build orientation with the combined objective of compliance and support material is given by optimization 4.

Table 2 Summary of problem statements for the reference optimizations and proposed approach
Full size table

Optimization 3 and optimization 4 are only completed with support material as the AM objective. Preliminary studies show that when minimizing the supported surface area with respect to the element density design variables, \( \varPsi \left(\underset{\sim }{x}\right) \), the results are not physically meaningful (Fig. 7). These findings are consistent with the boundary oscillation effect observed previously by Qian (2017). The optimization tends to remove the surface boundaries that require support material. Simply stated, if no clear boundary exists, then the boundary cannot contribute to the total supported surface area value. Although this makes sense from an optimization standpoint, the result is undesirable from a practical perspective and the significant amount of intermediate element densities makes for an infeasible design.

Fig. 7
figure 7

Boundary oscillation effect on the 2D cantilever beam due to minimizing the supported surface area with respect to element density design variables, \( \Psi \left(\underset{\sim }{x}\right) \)

Full size image

In the following subsections, three test problems are investigated. For each test problem, the reference optimizations are compared to the proposed approach. Since support material is designed as a sacrificial structure that is removed in the post-processing steps, it has no influence on the structural compliance. All reported values for \( \underset{\sim }{\theta } \) are to be interpreted following Section 2.2.3 with reference build directions corresponding to the positive y-directions indicated in Fig. 5.

5.1 2D cantilever beam

The first test problem used to demonstrate the proposed approach is a 2D cantilever beam with a mesh size of 126 × 66 elements. A volume fraction of 0.35 and filter radius of 3 are used. When the AM objective is activated using the element densities as the design variable (optimizations 3–4), the weighting factor is set to w = 0.5 and does not change throughout the optimization.

5.1.1 Support material minimization

The three reference optimizations and the proposed approach are shown in Figs. 8, 9, and 10, with corresponding θ initializations of 60°, 180°, and 300°, respectively. Each θ initialization (four optimizations) is considered a set. The support material is shown in red.

Fig. 8
figure 8

2D cantilever beam–support material minimization. Optimization set initialized at θ = 60°

Full size image
Fig. 9
figure 9

2D cantilever beam–support material minimization. Optimization set initialized at θ = 180°

Full size image
Fig. 10
figure 10

2D cantilever beam–support material minimization. Optimization set initialized at θ = 300°

Full size image

As depicted in Figs. 8, 9, and 10, a significant amount of support material is needed for optimization 1 in all three sets. Optimization 2a reduces support material by including variable build orientation in the problem statement, while maintaining the same compliance value as optimization 1 (topology remains the same). This is achieved by reducing surfaces that require support material, as well as reducing the length of support material columns. Employing a different method, the topology of optimization 3 is influenced by the AM objective with a fixed build orientation. The support material tends to be reduced by pulling the supported surfaces toward the build plate, reducing support height. The topology of the proposed approach, optimization 4, is influenced by the AM objective, as well as includes variable build orientation. Comparing the optimizations within each set, optimization 4 appears to have the least amount of support material and therefore produces the best designs.

The combined objective values for all optimizations in each set are calculated following (16) and are shown in Fig. 11. Each objective has been normalized to the best objective achieved for all sets, J∗. A similar trend is seen between optimization sets where optimization 4 has the best objective, followed by optimization 2a, optimization 3, and optimization 1.

Fig. 11
figure 11

Normalized objective values for the 2D cantilever beam–support material minimization

Full size image

Analyzing the objectives separately (not shown), there is a trade-off between compliance and support material. Optimization 1 and optimization 2a have the lowest values for compliance since the topology is not influenced by the AM objective. When comparing optimization 4 (proposed approach) to optimization 1, at the best combined objective achieved (θ initialized at 60°), there is a 38.6% reduction in support material at the expense of 4.7% increased compliance. For the worst combined objective achieved by the proposed approach (θ initialized at 300°), the support material is decreased by 58.0%, with an increase of 3.4% in compliance. Although the support material savings are greater with a smaller increase in compliance for θ initialized at 300°, the combined local optimum is still of poorer quality than when θ is initialized at 60°.

5.1.2 Supported surface area minimization

A similar process is used to demonstrate the effect of supported surface area minimization. As previously discussed (Fig. 7), only optimization 1 and optimization 2b produce meaningful results and, therefore, are the only optimizations explored. Consistent θ initializations of 60°, 180°, and 300° are shown in Figs. 12, 13, and 14, respectively. The supported surfaces are shown in orange.

Fig. 12
figure 12

2D cantilever beam-supported surface area minimization. Optimization set initialized at θ = 60°

Full size image
Fig. 13
figure 13

2D cantilever beam-supported surface area minimization. Optimization set initialized at θ = 180°

Full size image
Fig. 14
figure 14

2D cantilever beam-supported surface area minimization. Optimization set initialized at θ = 300°

Full size image

In all three sets, optimization 1 contains more supported surface area than optimization 2b. Allowing variable build orientation leads to a design where more of the elements satisfy the self-supporting threshold value, \( \left(\overline{\alpha}\right) \). The same final value for θ is obtained by optimization 2b with the starting θ initializations of 180° and 300°, suggesting a global optimum is achieved with respect to build orientation. This is confirmed in Fig. 15 by manually plotting the supported surface area values as a function of θ. The design consists of two apparent local optima at 91° and 268°, validating the effectiveness of supported surface area minimization.

Fig. 15
figure 15

2D cantilever beam manual rotations for supported surface area

Full size image

Since the topology, and therefore compliance, remains the same between the two optimizations, the two approaches can be compared directly by analyzing the amount of supported surface area, Ψ. The objectives have been normalized to the lowest supported surface area achieved in all sets, Ψ∗, shown in Fig. 16. A large difference in performance can be seen when comparing each optimization set. For example, optimization 1 initialized at 60° already produces a design with a small amount of supported surface area and there is not much opportunity for reduction, whereas at 180°, there is a significant amount of supported surface area that can be minimized from optimization 1. The reduction in supported surface area within each optimization set is 17, 76, and 47% for the initializations at 60°, 180°, and 300°, respectively.

Fig. 16
figure 16

Normalized supported surface area values for the 2D cantilever beam

Full size image

5.2 3D cantilever beam

The proposed approach is extended to 3D and demonstrated using a cantilever beam similar to the 2D test problem. The 3D problem is solved with an element mesh size of 126 × 66 × 26, filter radius of 3, and a volume fraction of 0.15. The weighting factor is set and held constant at w = 0.85 upon the AM objective being activated using the element densities as the design variable (optimizations 3–4).

5.2.1 Support material minimization

The three reference optimizations as well as the proposed approach are completed at six unique \( \underset{\sim }{\theta } \) initializations. Two of these optimization sets with and without support material are shown in Figs. 17 and 18. Again, the support material is shown in red. Convergence history for the proposed approach (optimization 4) of Fig. 17 is provided in Appendix 2.

Fig. 17
figure 17

3D cantilever beam–support material minimization. Optimization set initialized at θx = 60; θz = 60

Full size image
Fig. 18
figure 18

3D cantilever beam–support material minimization. Optimization set initialized at θx = 180; θz = 60

Full size image

The optimization 1 topology in 3D, which does not change between initializations, is very similar to the 2D cantilever beam; however, the members have a solid cylindrical bar shape requiring a significant amount of support material. Optimization 2a can reduce the support material by rotating the build direction by both θx and θz. The topological influence by the AM objective in optimizations 3 and 4 is less noticeable compared with 2D. Depending on the build direction, significant support material savings can be achieved through minor topology changes, such as slimming the members. For example, the top edge of the topology in optimization 1 and optimization 2a (the same for Figs. 17 and 18) flares out emulating an I-beam. In optimization 4 of Fig. 17, significant support material savings are made by lessening the amount of I-beam overhang.

The combined objective values for all six unique build orientations are calculated following (16) and are shown in Fig. 19. Each objective has been normalized to the best objective achieved for all sets, J∗. The same trend between optimization sets that was found in the 2D cantilever beam can be seen, where optimization 4 has the best objective, followed by optimization 2a, optimization 3, and optimization 1.

Fig. 19
figure 19

Normalized objective values for the 3D cantilever beam–support material minimization

Full size image

Depending on where \( \underset{\sim }{\theta } \) is initialized, the decrease in combined objective value within each set for optimization 4 when compared to optimization 1 can vary significantly (Fig. 19). This can be shown more clearly, when studying the objective values separately (not shown). At a build direction initialization of θx = 60; θz = 60, the support material decreased by 93.2% with a 3.0% increase in compliance, while at an initialization of θx = 180; θz = 60, the support material reduction was only 80.2% with a 1.8% increase in compliance.

5.2.2 Supported surface area minimization

The same \( \underset{\sim }{\theta } \) initializations for support material minimization are shown for supported surface area minimization in Figs. 20 and 21. The supported surfaces in 3D are shown in green.

Fig. 20
figure 20

3D cantilever beam-supported surface area minimization. Optimization set initialized at θx = 60; θz = 60

Full size image
Fig. 21
figure 21

3D cantilever beam-supported surface area minimization. Optimization set initialized at θx = 180; θz = 60

Full size image

In 3D, the potential surfaces that require support material are greater than in 2D. When comparing optimization 1 and optimization 2b, the reduction in supported surface area in Fig. 20 is more apparent than in Fig. 21. This is attributed to the design being initialized at a favorable build direction in Fig. 21. Quantitative comparison is shown in Fig. 22, with additional \( \underset{\sim }{\theta } \) initializations. The objectives have been normalized to the lowest supported surface area achieved in all sets, Ψ∗.

Fig. 22
figure 22

Normalized supported surface area values for the 3D cantilever beam

Full size image

With the exclusion of the optimization set initialized at θx = 60; θz = 180, all values for optimization 2b result in similar supported surface area values. This indicates that high-quality local optima are being obtained, regardless of build direction initialization.

5.3 3D landing gear door hinge

A landing gear door hinge industry test problem is used to assess the practicality of the proposed approach. The 3D problem is solved with an element mesh size of 111 × 71× 27, filter radius of 2, and a volume fraction of 0.2. When the AM objective is activated using the element densities as the design variable (optimizations 3 and 4), the weighting factor is set and held constant at w = 0.7.

5.3.1 Support material minimization

The same set of optimizations is completed at the six \( \underset{\sim }{\theta } \) initializations investigated for the 3D cantilever beam. Two of these optimization sets with and without support material are shown in Figs. 23 and 24. The topologies generated for the landing gear door hinge are more complex than the 3D cantilever beam resulting in the ideal build directions being more difficult to determine directly. Visually, Fig. 23 shows substantial support material differences when variable build orientation is included (optimization 2a and optimization 4), whereas the changes in Fig. 24 are less prominent. Small topology differences can be perceived when influenced by the AM objective. For example, in Fig. 24, an entire feature requiring support material that is present in optimization 1 and optimization 2a is filled in for optimizations 3 and 4.

Fig. 23
figure 23

3D landing gear door hinge support material minimization. Optimization set initialized at θx = 60; θz = 60

Full size image
Fig. 24
figure 24

3D landing gear door hinge support material minimization. Optimization set initialized at θx = 180; θz = 60

Full size image

Supplementary build direction initializations were studied and are included in Fig. 25. Alike the other test problems, each objective has been normalized to the best objective achieved for all sets, J∗, and the trend observed in previous test problems is maintained.

Fig. 25
figure 25

Normalized objective values for the 3D landing gear door hinge support material minimization

Full size image

The combined objective values for all initializations are within a similar range. Further analysis on the objective values separately shows that support material decreases by 81.3% with a 4.4% increase in compliance when comparing the proposed approach (optimization 4) to optimization 1 at a build direction initialization of θx = 60; θz = 60. At θx = 180; θz = 60, the support material reduction was 21.1% with a 5.4% compliance trade-off.

5.3.2 Supported surface area minimization

Figures 26 and 27 demonstrate the effect of supported surface minimization on the landing gear door hinge with different \( \underset{\sim }{\theta } \) initializations.

Fig. 26
figure 26

3D landing gear door hinge-supported surface area minimization. Optimization set initialized at θx = 60; θz = 60

Full size image
Fig. 27
figure 27

3D landing gear door hinge-supported surface area minimization. Optimization set initialized at θx = 180; θz = 60

Full size image

The increased topological complexity of this test problem makes it more difficult to minimize supported surface area. During optimization, by varying the build direction, some of the surfaces become self-supporting, while other locations of the design become supported surfaces. Like the 3D cantilever beam, the performance improvement for optimization 2b, over optimization 1, depends on where the build direction is initialized. This is further shown by the normalized supported surface area values in Fig. 28.

Fig. 28
figure 28

Normalized supported surface area values for the 3D landing gear door hinge

Full size image

When comparing the landing gear door hinge to the 3D cantilever beam, there is a larger distribution in the final values for supported surface area. The complex topology increases the multimodal nature of the optimization for this test problem, creating more local optima possibilities. Nevertheless, optimization 2b produces better objective values than optimization 1 for all build direction initializations.

6 Discussion and future works

The results for all three test cases demonstrate the best designs for support material minimization (lowest combined objective) are produced by the proposed approach, which includes variable build orientation with topology influenced by the AM objective. In regard to supported surface area, topology was not influenced by the AM objective due to the lack of physically meaningful results; however, build orientation was still able to be optimized. Although the quality of the results varied between the test problems, all problems showed considerable reduction for both support material and supported surface area, with a minimal impact on structural performance (no impact during supported surface minimization).

By minimizing support material, cost savings are achieved through using less material and reducing the time required to manufacture the support structures. As a result of minimizing the supported surface area, there is generally less support material and there are less post-processing operations required, saving time and effort.

The trade-off between structural performance and the AM objective is governed by the weighting factor, w. As the focus in this work is incorporating build orientation as an additional design variable, the reader is directed to the works of Ryan and Kim (2019) in 2D and Sabiston and Kim (2019) in 3D for an in-depth analysis of these trade-offs. Within each test problem, the weighting factor was held constant and strategically chosen to ensure a relatively small impact on structural performance. Different weighting values will impact the results accordingly and are able to be selected depending on the needs of the user.

A variation to the optimization problem statement could be implemented by using the AM formulations as constraints, as opposed to objectives in the current formulation. This would require a user to pre-set the amount of support material or supported surface area that the optimizer could admit. Although feasible, each test problem can inherently have significantly different support material requirements, leading to the user needing to have prior knowledge for that particular test problem. Having both the structural and AM quantities as objectives leads to a more robust design tool that reduces the possibility for drastic design outcomes if the user has not priorly investigated the test problem.

As commonly found with nonconvex optimization problems, substandard local optima were obtained in the results. For example, in Fig. 19, the proposed approach (optimization 4) produced a better optimum when initialized at θx = 60; θy = 60 versus θx = 180; θy = 180. Despite this, the designs produced by the proposed approach still have a combined objective value that is less than all reference optimizations, but this may not be the case for other starting \( \underset{\sim }{\theta } \) initializations. Contributing to the difficulties in obtaining a quality local optimum, the support material (7) produces a discontinuous function with respect to build orientation. This is attributed to entire support material columns being activated or deactivated when the build direction is rotated. Upon looking at the supported surface area minimization (Figs. 16, 22, and 28), the final values for optimization 2a are in relatively close proximity. This is a result of the implementation of the smoothed Heaviside step function on the supported surface area (14) ensuring a continuous response. Future works may look to improve the stability of the support material calculation to make it more suitable for gradient-based optimization.

Other future works include the following:

  • Introducing or developing methodologies to mitigate the boundary oscillation effect observed when the element densities are used as design variables for supported surface area minimization.

  • Investigation of more test problems to further reveal the strengths and weaknesses of the proposed approach. The support material and supported surfaces required in each optimization are dependent on the test problem; therefore, the benefit of adding AM considerations into topology optimization may vary. A focus on solving problems with nonintuitive build orientations will fully showcase the benefits of the proposed approach.

  • Expanding design freedom by implementing another method to reduce support material: optimizing the support structures. This can include changing the support structure volume (Vanek et al. 2014), or utilizing lattice or porous structures (Hussein et al. 2013; Strano et al. 2013). Careful thermal considerations would be needed, as support structures in metal AM are necessary to transfer heat to the build plate. Ignoring thermal-related stress can lead to costly part build failure.

  • Developing a more accurate cost model. The authors recognize that build height is a very influential parameter on AM build time and cost. This is not considered in the approach as currently formulated. An objective that includes element height as a design variable could be implemented or element penalization methods could be utilized.

7 Conclusion

The method proposed in this study provides a way to implement AM considerations into density-based topology optimization. The aim is to minimize AM cost and time associated with the amount of supported surface area and support material, while maximizing the design freedom of the optimizer. This is accomplished by simultaneously using element density and build orientation design variables to minimize the combined structural and AM objectives.

A 2D and 3D implementation of the proposed approach are tested on numerical examples, showing the effectiveness. The results demonstrate significant savings in supported surface area and support material, with small trade-offs in structural performance. A simplified landing gear door hinge test problem validates that the method can be applied to real-world practical problems. Although the test problems had reasonably intuitive optimal build orientations, the approach is most beneficial when implemented on complex problems where the optimal build orientation may be elusive.

Although the proposed method generates the best designs compared to all reference optimizations, a global optimum is not guaranteed. The quality of the final design is dependent on where the build orientation is initialized. An adaptive continuation strategy similar to Langelaar (2018) could be implemented into the existing formulation, increasing the likelihood of obtaining the best possible design, but at the expense of computational time.