1 Introduction

With the rapid development of aerospace technology, marine exploration, railway cars, and renewable energy, a large number of key components with complex shapes, difficult processing procedures, and demanding performance indicators have emerged. Five-axis machining is an important means to achieve the efficient and accurate machining of these complex parts [1, 2]. Recently, the hybrid robot (or hybrid machine) has become the core unit for the specific in situ machining of large parts due to its ability to provide high rigidity and precision, large working space, and reconfigurability [3], e.g., Tricept [4], Exechon [5], and TriMule [6] devices. These robots are composed of a 1T2R (T---Translation, R---Rotation) parallel mechanism plus an A/C-type wrist that is serially connected to the platform. Therefore, the kinematics characteristics of hybrid robots are posture-dependent, and there exists a strong nonlinear mapping relationship between the operation space and joint space. Therefore, it faces the challenges to schedule the trajectory and feedrate of the hybrid robot. If the toolpath is not continuous or the feedrate is inappropriate, the actuated joints may move violently, which will deteriorate the machining accuracy (MA) and even damage the equipment. In order to make a balance between the MA and machining efficiency (ME), the primary task of the computer numerical control (CNC) system for high-speed machining is to generate a smooth and efficient tool motion trajectory that satisfies (a) the high-order continuous toolpath without dramatic motion in cutter axis orientation; and (b) the smooth and achievable movement of actuated joints constrained by drive capability.

In current commercial CNC systems and industrial robot systems, a programming format of small line segments is still the most commonly used motion instruction. However, the processing file of this programming format is large, and the discontinuous machining toolpath requires the frequent acceleration and deceleration of the cutter, which can potentially cause the machining equipment to resonate [7]. Parametric interpolation, which describes the toolpath by parametric curves such as the NURBS curve and polynomial curve, has been developed instead of discrete cutter location (CL) data [8, 9]. A five-axis toolpath contains information about the cutter tip position and cutter axis orientation, and the cutter tip motion is treated as the main motion while the cutter axis orientation follows through the curve parameter [10,11,12]. Although the synchronization method generates a high-order continuous toolpath, the cutter axis motion is not restricted. To avoid the above phenomenon, the most commonly used methods in the industry are to assign a conservative and constant value to the feedrate, which results in low ME. Therefore, as a key input of parametric interpolation, feedrate scheduling needs to be performed offline or online considering the drive constraints of the machining equipment as well as the geometry constraints of the predefined toolpath. How to schedule a feedrate profile, which is not only reliable and flexible for a predefined toolpath but also easy to implement in the CNC system, is worthy of ongoing research for robot machining [13].

Feedrate scheduling was first studied in robotics for point-to-point motion, where a time-optimal feedrate profile was generated considering the dynamics of the robot [14, 15]. However, robot machining is a continuous trajectory following task, and the research of feedrate scheduling is usually performed in the operation space owing to the nonlinear kinematics of the machining robot. Although the solutions to feedrate scheduling can be achieved using different methods, the goal of feedrate scheduling is basically to find an effective and achievable feedrate profile under predefined constraints. Furthermore, feedrate scheduling is usually performed offline if more constraints are considered. Yeh et al. regarded the chord error constraint of toolpath and proposed an adaptive interpolation algorithm [16]. Xu et al. proposed a feedrate-scheduling algorithm by establishing the mathematical relationship between the curvature of the cutter tip position and the feedrate [17]. Conway demonstrated improvements in the contouring accuracy of CNC machines using the curvature-dependent feedrate profile in experiments [18]. To improve MA, Erkorkmaz et al. proposed a fifth-order spline interpolation algorithm considering the tangential jerk constraints of cutter tip position [19]. Lin et al. proposed a real-time acceleration and deceleration (Acc/Dec) scheduling method based on the S curve while considering chord error, cutter tip curvature, and contour error constraints [20]. Jia et al. proposed a feedrate-scheduling algorithm with constant feedrate in feedrate-sensitive regions [21]. It can be found that these methods cannot be directly implemented in robot machining due to the ignorance of the drive capability of the equipment.

Barre studied the effects of the jerks of actuated joints on the vibration of mechanical structures and noted that limiting the jerks of the actuated joints can generate the smooth and achievable movement for the machining equipment and avoid mechanical structural resonance [22]. Lu et al. proposed a genetic algorithm-based S-curve Acc/Dec scheme for five-axis machining that considers the joint motion constraints [23]. Sencer et al. considered the jerks of actuated joints and obtained the time-optimized feedrate profile by transforming the scheduling problem into an optimal problem for the control points of a B-spline curve [24]. Beudaert et al. first established the approximate relationship between actuated joint jerk and the feedrate, and then proposed an iterative feedrate-scheduling algorithm to obtain the time-optimized feedrate profile [25, 26]. Sun et al. described the feedrate profile in a B-spline form, and then adjusted the control points of the B-spline curve through a proportional adjustment and curve evolution strategy iteratively until all the constraints were satisfied [27, 28]. However, the scheduled feedrate profile may exhibit local oscillation characteristics, which is not desirable in high-speed machining. To obtain a smooth jerk-limited feedrate profile, the algorithms proposed by Chen et al., Lu et. al, Liu et al., and Liang et al. [13, 29,30,31] require a large number of iterative calculations to guarantee a feasible solution as well. Lu et al. proposed a jerk-limited time-optimal motion planning method for robot machining of sculptured surfaces considering joint motion and cutter tip kinematic constraints [32]. Sang et al. proposed an improved feedrate-scheduling algorithm considering the geometric and drive constraints to balance the MA and ME [33]. Wang et al. proposed a feedrate scheduling algorithm with constant feedrate in feedrate-sensitive regions and the S-curve Acc/Dec strategy is adopted [34]. In these approaches, the feedrate profile described by a parametric curve with a large number of control points may exhibit high-frequency feedrate fluctuation and increase the computational burden. Besides, the accelerations and jerks of the actuated joints may violate the predefined constraints during the Acc/Dec stage when the S-curve or sine Acc/Dec strategy is applied.

To compromise the MA and ME of the hybrid robot, a feedrate-scheduling algorithm for robot machining considering drive constraints is proposed in this paper. By adding a dimension of the curve parameter, the feedrate profile described using a cubic uniform B-spline is mapped into a two-dimensional (2D) curve with the least number of control points. Then, the feedrate can be directly scheduled by iteratively modulating the control points of the 2D feedrate profile based on feedrate-constant intervals and transition intervals, respectively. The proposed algorithm can avoid high-frequency feedrate fluctuation, remain constant in most parameter intervals, and change smoothly in transition intervals without violating any constraints. Furthermore, the computational burden of the CNC system can be reduced by this approach. The rest of this paper is organized as follows. The “Parametric toolpath and parametric interpolation for robot machining” section introduces the parameterization of the five-axis toolpath and parametric interpolation strategy for robot machining. The “Feedrate-scheduling algorithm” section derives the feedrate constraint equations first and introduces the proposed scheduling algorithm in detail. In the “Simulation and experimental results” section, simulations and experiments are carried out on the in-house developed TriMule600/800 machining platform to validate the correctness and effectiveness of the proposed algorithm. Finally, conclusions are summarized in the “Conclusions” section.

2 Parametric toolpath and parametric interpolation for robot machining

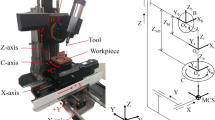
In this section, a parametric interpolation strategy for robot machining is introduced briefly, taking the TriMule600 robot shown in Fig. 1 for example. The cutter location (CL) data generated by computer-aided manufacturing (CAM) is composed of the position vector \( {\left\{{\boldsymbol{P}}_i\right\}}_{i=1}^N={\left({X}_i,{Y}_i,{Z}_i\right)}^{\mathrm{T}} \) and the unit orientation vector \( {\left\{{\boldsymbol{O}}_i\right\}}_{i=1}^N={\left({O}_{i,x},{O}_{i,y},{O}_{i,z}\right)}^{\mathrm{T}} \), where N denotes the number of generated CL points. Similar to the post-processing of the AB-type five-axis machine tool, the attitude angle vectors \( {\left\{{\boldsymbol{\psi}}_i\right\}}_{i=1}^N \) are adopted here to define cutter axis orientation \( {\left\{{\boldsymbol{O}}_i\right\}}_{i=1}^N \). Note that ψi = (Ai, Bi)T is a 2D vector. The coordinates Ai and Bi denote rotational motions around the x axis and y axis of the part coordinate system (PCS), respectively. The mapping relationship between the unit orientation vector Oi and the 2D vector ψi is expressed as:

$$ {\boldsymbol{\psi}}_i=\left(\begin{array}{c}{A}_i\\ {}{B}_i\end{array}\right)=\left(\begin{array}{c}-{\sin}^{-1}\left({O}_{i,y}\right)\\ {}{\tan}^{-1}\left({O}_{i,x}/{O}_{i,z}\right)\end{array}\right) $$
(1)
Fig. 1
figure 1

Kinematic configuration of TriMule600 robot

Full size image

Then, the dual NURBS toolpath is introduced to parameterize the five-axis toolpath as shown in Fig. 2. Here, a NURBS curve fitting method with arc-length parameterization [35] is implemented. The parametric toolpath composed of a position spline P(u) and an attitude angle spline ψ(u) is expressed as

$$ \Big\{{\displaystyle \begin{array}{c}\boldsymbol{P}(u)=\sum \limits_{i=0}^n{\omega}_{1i}{\boldsymbol{p}}_i{N}_{i,k}(u)/\sum \limits_{i=0}^n{\omega}_{1i}{N}_{i,k}(u)\\ {}\boldsymbol{\psi} (u)=\sum \limits_{i=0}^n{\omega}_{2i}{\boldsymbol{o}}_i{N}_{i,k}(u)/\sum \limits_{i=0}^n{\omega}_{2i}{N}_{i,k}(u),u\in \left[0,1\right]\end{array}}\operatorname{} $$
(2)

where u denotes the curve parameter, n + 1 is the number of control points, k is the order of the NURBS curve, and pi and oi are the control points. ω1i and ω2i are weight factors. The B-spline basis functions Ni, k(u) are functions of parameter u and node vector U = (u0, u1, ⋯, un + k + 1) with the following definition:

$$ {\displaystyle \begin{array}{c}{N}_{i,0}(u)=\left\{\begin{array}{cc}1,& {u}_i\le u<{u}_{i+1}\\ {}0,& \mathrm{others}\end{array}\right.\\ {}{N}_{i,k}(u)=\frac{u-{u}_i}{u_{i+k}-{u}_i}{N}_{i,k-1}(u)+\frac{u_{i+k+1}-u}{u_{i+k+1}-{u}_{i+1}}{N}_{i+1,k-1}(u)\end{array}} $$
(3)
Fig. 2
figure 2

Toolpath smooth using a dual NURBS curve. a The parameterization five-axis toolpath. b The spline curve of attitude angle defined in the 2D plane

Full size image

After the NURBS fitting process, the inverse mapping of Eq. (1) is used to calculate the unit orientation vector O(u), that is:

$$ \boldsymbol{O}(u)=\left(\begin{array}{c}\mathit{\cos}\left(A(u)\right)\mathit{\sin}\left(B(u)\right)\\ {}-\mathit{\sin}\left(A(u)\right)\\ {}\mathit{\cos}\left(A(u)\right)\mathit{\cos}\left(B(u)\right)\end{array}\right) $$
(4)

Note that the magnitude of the orientation vector ‖O(u)‖ is unity regardless of the value of u. In CNC post-processing, the inverse kinematic transformation is applied to generate the pulses of actuated joints based on the CL data, that is:

$$ \boldsymbol{q}(u)={f}^{-1}\left(\boldsymbol{x}(u)\right) $$
(5)

where f−1 denotes the inverse kinematics of the TriMule600 robot, q(u) = (q1(u), q2(u), q3(u), θ4(u), θ5(u))T denotes the vector of actuated joint variable and x(u) = (X(u), Y(u), Z(u), A(u), B(u))T denotes the vector of cutter location.

To implement the parametric interpolation strategy, the core is to efficiently solve the interpolation point parameter ui + 1 in the next interpolation period based on the current parameter ui and the feedrate F(ui). The second-order Taylor expansion method, which achieves a good balance between computational efficiency and computational accuracy, is adopted here:

$$ {u}_{i+1}={u}_i+\frac{F\left({u}_i\right)}{\left\Vert {\boldsymbol{P}}^{\prime}\left({u}_i\right)\right\Vert }{T}_s+\frac{1}{2}\left(\frac{F^{\prime}\left({u}_i\right)F\left({u}_i\right)}{{\left\Vert {\boldsymbol{P}}^{\prime}\left({u}_i\right)\right\Vert}^2}-\frac{{\boldsymbol{P}}^{{\prime\prime}}\left({u}_i\right)\cdot {\boldsymbol{P}}^{\prime}\left({u}_i\right)}{{\left\Vert {\boldsymbol{P}}^{\prime}\left({u}_i\right)\right\Vert}^4}{F}^2\left({u}_i\right)\right){T_s}^2 $$
(6)

where F(u) denotes the feedrate profile with respect to u, superscript “′” denotes the first derivative with respect to u, and Ts denotes the interpolation period of CNC system.

3 Feedrate-scheduling algorithm

The flowchart of the proposed feedrate-scheduling algorithm is illustrated in Fig. 3. The system input is composed of the parametric toolpath and the form of feedrate profile. The feedrate profile is first expressed in a cubic uniform B-spline form and then mapped into a 2D curve with the redefined control points. The adjustment strategy of control points is conduct after deriving the feedrate constraint equations. First, the parameter set \( {\left\{{u}_i^{\ast}\right\}}_{i=1}^{N_{sp}} \) of sampling points is obtained by the equal arc-length sampling method with supplementary parameters considering the curvature of curve P(u) and the change rate of curve O(u). Second, the initial control points \( {\left\{{\boldsymbol{F}}_{1,i}\right\}}_{i=0}^{M-1} \) are generated according to the process constraint, and F1(u) is obtained subsequently. Then, control points \( {\left\{{\boldsymbol{F}}_{1,i}\right\}}_{i=0}^{M-1} \) are adjusted to meet the neighbor-independent (NI) constraints, and \( {\left\{{\boldsymbol{F}}_{f,i}\right\}}_{i=0}^{M-1} \) are generated. Note that the feedrate profile Ff(u) is composed of feedrate-constant intervals and transition intervals. Finally, control points \( {\left\{{\boldsymbol{F}}_i\right\}}_{i=0}^{M-1} \) are generated iteratively to meet the neighbor-dependent (ND) constraints, and the scheduled feedrate profile F(u) is transferred to the CNC system. Specifically, the adjustment of control points \( {\left\{{\boldsymbol{F}}_{f,i}\right\}}_{i=0}^{M-1} \) contains two parts: (a) the adjustment based on feedrate-constant intervals with control points \( {\left\{{\boldsymbol{F}}_{s,i}\right\}}_{i=0}^{M-1} \) generated; and (b) the adjustment based on transition intervals. The detailed algorithm will be presented as follows.

Fig. 3
figure 3

Flowchart of the proposed feedrate-scheduling algorithm

Full size image

3.1 Feedrate constraint equations

Feedrate constraints are used to determine the maximal feasible feedrate at an arbitrary sampling point. As shown in Table 1, two types of feedrate constraints are considered in this paper, named the NI constraints and the ND constraints [27]. The NI constraints are only related to the feedrate of the target CL point and the maximum feasible feedrate can be obtained by only one-time calculation. The ND constraints are related to both the feedrate of the target CL point and its derivatives; iterative solution methods are usually applied here to generate the desired feedrate profile.

Table 1 Constraints considered in the proposed feedrate-scheduling algorithm
Full size table

3.1.1 Geometric toolpath constraints

Chord error constraint

The chord error δ(u) refers to the error caused by using the small straight segment to approach curve P(u) in the CNC machining [16]. Given the limit value δlim, the maximum feasible feedrate Vce(u) is derived as:

$$ {V}_{\mathrm{ce}}(u)=\frac{2}{T_s}\sqrt{2\rho (u){\delta}_{\mathrm{lim}}} $$
(7)

where ρ(u) is the curvature of curve P(u), and Ts is the interpolation period of CNC system.

Tangential acceleration and jerk constraints

The tangential acceleration A(u) and jerk J(u) of the cutter tip position are calculated as:

$$ A(u)=\dot{F}(u)={F}^{\prime }(u)\frac{F(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert } $$
(8)
$$ J(u)={F}^{{\prime\prime} }(u)\frac{F^2(u)}{{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}^2}+{F}^{\prime }(u)\frac{A(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert }-{F}^{\prime }(u)\frac{{\boldsymbol{P}}^{{\prime\prime} }(u)\cdotp {\boldsymbol{P}}^{\prime }(u)}{{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}^4}{F}^2(u) $$
(9)

where superscript “⋅” denotes the derivative with respect to time t, and superscript “′” and “′′” denote the first and second derivative with respect to parameter u, respectively. The above representation applies to the full text unless otherwise stated. The feedrate constraint equations are derived based on the limit values Alim and Jlim as follows:

$$ \left|A(u)\right|\le {A}_{\mathrm{lim}},\left|J(u)\right|\le {J}_{\mathrm{lim}} $$
(10)

where “|⋅|” denotes the absolute value.

Angular velocity and acceleration constraints

The angular velocity ω(u) and angular acceleration ωA(u) of the cutter axis are derived below [27]:

$$ \omega (u)=\left\Vert {\boldsymbol{O}}^{\prime }(u)\right\Vert \frac{F(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert } $$
(11)
$$ {\omega}_A(u)=\left|\frac{{\boldsymbol{O}}^{{\prime\prime} }(u)\cdot {\boldsymbol{O}}^{\prime }(u)}{\left\Vert {\boldsymbol{O}}^{\prime }(u)\right\Vert}\frac{F^2(u)}{{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}^2}+\left\Vert {\boldsymbol{O}}^{\prime }(u)\right\Vert \frac{A(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}\right| $$
(12)

In addition, the first derivatives of P(u) and ψ(u) with respect to time t are derived as

$$ \left\{\begin{array}{c}\dot{\boldsymbol{P}}(u)={\boldsymbol{P}}^{\prime }(u)\frac{du}{dt}=F(u)\frac{{\boldsymbol{P}}^{\prime }(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}\\ {}\dot{\boldsymbol{\psi}}(u)={\boldsymbol{\psi}}^{\prime }(u)\frac{du}{dt}=F(u)\frac{{\boldsymbol{\psi}}^{\prime }(u)}{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert}\end{array}\right. $$
(13)

Then, the feedrate constraint equation is derived based on the limit value ωA, lim:

$$ {\omega}_A(u)\le {\omega}_{A,\mathit{\lim}} $$
(14)

Similarly, the maximum feasible feedrate Vw(u) is derived based on the limit value ωlim,:

$$ {V}_w(u)=\frac{\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert }{\left\Vert {\boldsymbol{O}}^{\prime }(u)\right\Vert }{\omega}_{\mathrm{lim}} $$
(15)

3.1.2 Drive constraints

As mentioned above, it is hard to establish the mapping relationship between continuous curve q(u) and x(u) for TriMule600 robot considering its posture-dependent characteristics and the strong nonlinear mapping relationship between operation space and joint space. Therefore, the drive constraint equations are derived based on the discrete velocity analysis in this paper:

$$ \dot{\boldsymbol{q}}(u)={\boldsymbol{J}}_a^{-1}(u)\dot{\boldsymbol{x}}(u)={\boldsymbol{J}}_a^{-1}(u)\left(\begin{array}{c}\dot{\boldsymbol{P}}(u)\\ {}\dot{\boldsymbol{\psi}}(u)\end{array}\right) $$
(16)

where Ja denotes the [5 × 5] Jacobian matrix and \( {\boldsymbol{J}}_a^{-1} \) denotes its inverse matrix. Furthermore, \( \ddot{\boldsymbol{q}}(u) \) and \( \overset{\dddot{}}{\boldsymbol{q}}(u) \) can be derived using acceleration analysis and jerk analysis [36] which is not the focus of this paper. Subsequently, the feedrate constraint equations are derived based on the limit values \( {\hat{\boldsymbol{A}}}_{\mathrm{lim}} \) and \( {\hat{\boldsymbol{J}}}_{\mathrm{lim}} \):

$$ \left|{\ddot{q}}_j(u)\right|\le {\hat{A}}_{\mathit{\lim},j},\left|{\overset{\dddot{}}{q}}_j(u)\right|\le {\hat{J}}_{\mathit{\lim},j},j=1,2,\dots, 5 $$
(17)

where variable j denotes of the index of the actuated joints. Similarly, the maximum feasible feedrate Vaa(u) is derived based on the limit value \( {\hat{\boldsymbol{V}}}_{\mathrm{lim}} \):

$$ {V}_{\mathrm{aa}}(u)=\mathit{\min}\left\{{V}_{\mathrm{aa},j}(u)\left|j=1,2,\dots, 5\right.\right\} $$
(18)

where

$$ {\displaystyle \begin{array}{c}{V}_{\mathrm{aa},j}(u){\left({\boldsymbol{J}}_a^{-1}{\boldsymbol{x}}^{\prime }(u)\right)}_j=\left\Vert {\boldsymbol{P}}^{\prime }(u)\right\Vert {\hat{V}}_{\mathit{\lim},j},j=1,\dots, 5\\ {}{\boldsymbol{x}}^{\prime }(u)=\left(\begin{array}{c}{\boldsymbol{P}}^{\prime }(u)\\ {}{\boldsymbol{\psi}}^{\prime }(u)\end{array}\right)\end{array}} $$
(19)

3.2 Adjustment strategy of control points

The feedrate profile F(u) is expressed in a cubic B-spline form:

$$ F(u)=\sum \limits_{i=0}^{M-1}{f}_i{N}_{i,k}(u) $$
(20)

where \( {\left\{{f}_i\right\}}_{i=1}^{M-1} \) are the control points, and M denotes the number of control points. Ni, k(u) is the B-spline basis function, where k denotes the order of the B-spline curve. The node vector Uf is uniformly distributed as

$$ {\boldsymbol{U}}_f=\left(\underset{k+1}{\underbrace{0,..,0}},\frac{1}{M-k},\frac{2}{M-k},\dots, \frac{M-k-1}{M-k},\underset{k+1}{\underbrace{1,\dots, 1}}\right). $$
(21)

Note that the position spline P(u) and the attitude angle spline ψ(u) are parameterized with respect to the normalized arc-length parameter s, and the sampling points are selected by the equal arc-length sampling method. Therefore, there is at least one sampling point in arbitrary node interval of the node vector Uf when M is less than the number of sampling points. To visualize the adjustment process of the feedrate profile, the original control points \( {\left\{{f}_i\right\}}_{i=1}^{M-1} \) are extended to the 2D control points \( {\left\{{\boldsymbol{F}}_i\right\}}_{i=0}^{M-1} \) as shown in Fig. 4. Figure 4a shows the distribution of the control points along the parameter u. \( {\left\{{c}_i\right\}}_{i=0}^{M-1} \), which are the added dimension values, are defined as

$$ \left(\begin{array}{c}u\\ {}F(u)\end{array}\right)=\sum \limits_{i=0}^{M-1}\left(\begin{array}{c}{c}_i\\ {}{f}_i\end{array}\right){N}_{i,k}(u)=\sum \limits_{i=0}^{M-1}{\boldsymbol{F}}_i{N}_{i,k}(u) $$
(22)
Fig. 4
figure 4

Feedrate profile described by a cubic B-spline curve. a The distribution of the control points along the parameter u. b The distribution of the added dimension ci given the node vector Uf

Full size image

By deriving the first derivative of Eq. (22) with respect to u, \( {\left\{{c}_i\right\}}_{i=0}^{M-1} \) can be calculated by Eq. (23).

$$ {\left(\sum \limits_{i=0}^{M-1}{c}_i{N}_{i,k}(u)\right)}^{\prime}\equiv 1\Rightarrow \frac{k}{{\boldsymbol{U}}_f\left(i+4\right)-{\boldsymbol{U}}_f\left(i+1\right)}\left({c}_{i+1}-{c}_i\right)\equiv 1 $$
(23)

Specifically, the formula Δc = ci + 1 − ci = 1/(M − k) always holds when the condition k − 1 ≤ i ≤ M − k is satisfied. Figure 4b shows the distribution of \( {\left\{{c}_i\right\}}_{i=0}^{M-1} \) given the node vector Uf. From the figure, we can see that the distribution of \( {\left\{{c}_i\right\}}_{i=0}^{M-1} \) is approximately linear with respect to parameter u when variable M is much greater than k. As parameter u is the normalized arc-length parameter of curve P(u), it is reasonable to think that the control points \( {\left\{{\boldsymbol{F}}_i\right\}}_{i=0}^{M-1} \) are approximately uniformly distributed with respect to the arc-length parameter s. Therefore, it is feasible to realize the feedrate-scheduling process by modulating the control points \( {\left\{{\boldsymbol{F}}_i\right\}}_{i=0}^{M-1} \). Note that the proposed method is general and can be applied to arbitrary five-axis parameterized toolpath.

3.2.1 Parameter set of the sampling points

The parameters \( {\left\{{u}_i^{\ast}\right\}}_{i=1}^{N_{\mathrm{sp}}} \) of the sampling points are obtained by the equal arc-length sampling method and dominant point selection scheme. First, the total arc length St of curve P(u) is calculated by the Simpson method [37], and a series of data pairs \( \left(\tilde{u}_{j},{S}_j\right) \) are generated subsequently, where Sj represents the total arc length of P(u) in the parameter interval \( \left[0,\tilde{u}_{j}\right] \). Second, a seventh-order polynomial combination curve [12] is adopted to fit data \( \left(\tilde{u}_{j},{S}_j\right) \). Finally, the parameter set is obtained by substituting [0, Δs, …, St]T into the combination polynomials, where Δs denotes the interval of arc length used in the equal arc-length sampling method.

Considering the strong nonlinear mapping relationship between the operation space and joint space, dominant points that can characterize the shape of the parametric toolpath are also selected, such as the change rate of the cutter axis orientation σ(u) = ‖O′(u)‖/‖P′(u)‖ and the curvature κ(u) of curve P(u). Given parameter set \( {\left\{{u}_{r,i}\right\}}_{i=1}^{N_{dp}} \) with the same parameter increment, the supplementary parameters are obtained if variables κ(ur, i) and σ(ur, i) meet the following conditions:

$$ \left\{\begin{array}{c}\kappa \left({u}_{r,i}\right)>\kappa \left({u}_{r,i+1}\right)\\ {}\kappa \left({u}_{r,i}\right)>\kappa \left({u}_{r,i-1}\right)\\ {}\kappa \left({u}_{r,i}\right)\ge {\kappa}_{\mathrm{lim}}\end{array}\right.\ \boldsymbol{or}\ \left\{\begin{array}{c}\sigma \left({u}_{r,i}\right)>\sigma \left({u}_{r,i+1}\right)\\ {}\sigma \left({u}_{r,i}\right)>\sigma \left({u}_{r,i-1}\right)\\ {}\sigma \left({u}_{r,i}\right)\ge {\sigma}_{\mathrm{lim}}\end{array}\right.,i=1,\dots {N}_{dp} $$
(24)

where κlim and σlim denote the filtering thresholds, which can be determined according to the geometric characteristics of the toolpath. Ndp denotes the parameter number used for searching dominant points. Consequently, the sampling point parameters \( {\left\{{u}_i^{\ast}\right\}}_{i=1}^{N_{sp}} \) are obtained for feedrate-scheduling.

3.2.2 Initial adjustment of control points

The ordinate values of the 2D control points \( {\left\{{\boldsymbol{F}}_{1,i}\right\}}_{i=0}^{M-1} \) are set as \( {\left\{{f}_{1,i}\right\}}_{i=0}^{M-1}={V}_{p,\mathit{\lim}} \) initially. Subsequently, a curve scanning process is carried out, and the maximum feasible feedrate \( {V}_{\mathrm{sp}}\left({u}_i^{\ast}\right) \) for parameter set \( {\left\{{u}_i^{\ast}\right\}}_{i=1}^{N_{\mathrm{sp}}} \) considering the NI constraints is derived by combining Eq. (7), Eq. (15), and Eq. (18):

$$ {V}_{sp}\left({u}_i^{\ast}\right)=\mathit{\min}\left\{{V}_{ce}\left({u}_i^{\ast}\right),{V}_{\omega}\left({u}_i^{\ast}\right),{V}_{aa}\left({u}_i^{\ast}\right),{V}_{p,\mathit{\lim}}\right\} $$
(25)

where Vp, lim denotes the process feedrate. If existing a parameter interval [ua, ub] where \( {V}_{\mathrm{sp}}\left({u}_i^{\ast}\right)<{V}_{p,\mathit{\lim}} \) is always satisfied for \( {u}_i^{\ast}\in \left[{u}_s,{u}_e\right] \), then the interval [us, ue] is defined as the feedrate-sensitive interval. The adjustment process of control points \( {\left\{{\boldsymbol{F}}_{1,i}\right\}}_{i=0}^{M-1} \) is illustrated in Fig. 5, and the detailed procedure is summarized as follows:

  1. 1.

    Find all the feedrate-sensitive intervals \( {\left\{\left[{u}_{s,j},{u}_{e,j}\right]\right\}}_{j=1}^{N_{\mathrm{fc}}} \) which are also named as feedrate-constant intervals, and Nfc denotes the interval number.

  2. 2.

    Search the minimum subintervals \( {\left\{{\prod}_j\right\}}_{j=1}^{N_{\mathrm{fc}}} \) in node vector Uf that contain \( {\left\{\left[{u}_{s,j},{u}_{e,j}\right]\right\}}_{j=1}^{N_{\mathrm{fc}}} \), and the parameter domain of ∏j is defined as [Uf (aj), Uf (bj)].

  3. 3.

    Adjust the control points \( {\left\{{\boldsymbol{F}}_{1,i}\right\}}_{i=0}^{M-1} \) which are associated with intervals \( {\left\{{\prod}_j\right\}}_{j=1}^{N_{\mathrm{fc}}} \) based on the local adjustment characteristics of the B-spline curve:

Fig. 5
figure 5

Initial adjustment of control points

Full size image
$$ \left\{\begin{array}{c}{\left\{{\boldsymbol{F}}_{f,i}\right\}}_{i=0}^{M-1}=\left\{\begin{array}{c}{\left({c}_i,{V}_{\mathrm{sp},j}^{\ast}\right)}^{\mathrm{T}},\mathrm{if}i={a}_j-k,\dots, {b}_j-1\\ {}{\boldsymbol{F}}_{1,i},\mathrm{other}\end{array}\right.\\ {}{V}_{\mathrm{sp},j}^{\ast }=\mathit{\min}\left\{{V}_{\mathrm{sp}}(u)\left|u\in \left[{u}_{a,j},{u}_{b,j}\right]\right.\right\},j=1,\dots, {N}_{\mathrm{fc}}\end{array}\right. $$
(26)

where \( {\left\{{V}_{\mathrm{sp},j}^{\ast}\right\}}_{j=1}^{N_{\mathrm{fc}}} \) denotes the maximum feasible feedrate of intervals \( {\left\{{\prod}_j\right\}}_{j=1}^{N_{\mathrm{fc}}} \) considering the NI constraints.

3.2.3 Iterative adjustment of control points based on the feedrate-constant intervals

The profile Ff(u) generated after the initial adjustment is composed of the feedrate-constant intervals \( {\left\{{\prod}_i\right\}}_{i=1}^{N_{\mathrm{fc}}} \) and transition intervals, Nfc denotes the interval number. In feedrate-constant intervals, where \( {\left\{{F}_{\mathrm{fc},i}\right\}}_{i=1}^{N_{\mathrm{fc}}} \) denote the constant feedrate values, A(u) = 0, J(u) = 0 are always satisfied. If modulating Ffc, i by multiplying a coefficient η ∈ (0, 1), then:

$$ \left\{\begin{array}{c}{\omega}_A^{\ast }(u)={\eta}^2{\omega}_A(u)\\ {}{\ddot{\boldsymbol{q}}}^{\ast }(u)={\eta}^2\ddot{\boldsymbol{q}}(u);{\overset{\dddot{}}{\boldsymbol{q}}}^{\ast }(u)={\eta}^3\overset{\dddot{}}{\boldsymbol{q}}(u)\end{array}\right. $$
(27)

From Eq. (27), it can be seen that reducing the value of Ffc, i can reduce the value of the ND constraints proportionally. Based on the above conclusion, the iterative adjustment strategy of feedrate profile Ff(u) considering the ND constraints is illustrated in Fig. 6, and the detailed procedure is presented as follows:

  1. 1.

    Search the parameters of sampling points in the set \( {\left\{{u}_i^{\ast}\right\}}_{i=1}^{N_{\mathrm{sp}}} \) that belong to the feedrate-constant internals \( {\left\{{\prod}_i\right\}}_{i=1}^{N_{\mathrm{fc}}} \).

  2. 2.

    Evaluate the values of the ND constraints at the selected parameters by curve scanning. Then parameters which violate the predefined constraints are recorded. Subsequently, the minimum subintervals \( {\left\{\Big[{\boldsymbol{U}}_f\left({c}_j\right),{\boldsymbol{U}}_f\left({d}_j\right)\Big]\right\}}_{j=1}^{N_{\mathrm{pa}}} \) that contain the recorded parameters are determined in the node vector Uf, Npa denotes the interval number.

  3. 3.

    Adjust the 2D control points of Ff(u) iteratively according to Eq. (28), and Fs(u) is generated subsequently.

Fig. 6
figure 6

Iterative adjustment of control points based on the feedrate-constant intervals

Full size image
$$ \left\{\begin{array}{c}{\left\{{\boldsymbol{F}}_{s,i}\right\}}_{i=0}^{M-1}=\left\{\begin{array}{c}{\left({c}_i,{\eta}^{\tau_j}{f}_{f,i}\right)}^{\mathrm{T}},\mathrm{if}i={c}_j-k,\dots, {d}_j-1\\ {}{\boldsymbol{F}}_{f,i},\mathrm{others}\end{array}\right.\\ {}j=1,2,\dots, {N}_{\mathrm{pa}}\end{array}\right. $$
(28)

where τj denotes the number of iterative adjustments for the jth subinterval, η denotes the proportional adjustment coefficient, and \( {\left\{{f}_{f,i}\right\}}_{i=0}^{M-1} \) are the ordinate values of the control points \( {\left\{{\boldsymbol{F}}_{f,i}\right\}}_{i=0}^{M-1} \). Finally, the feedrate-constant intervals \( {\left\{{\prod}_i\right\}}_{i=1}^{N_{\mathrm{fc}}} \) are updated with the parameter domain [Uf (ai), Uf (bi)] and the constant feedrate value Ffc, i, Nfc denotes the number of the updated intervals \( {\left\{{\prod}_i\right\}}_{i=1}^{N_{\mathrm{fc}}} \).

3.2.4 Iterative adjustment of control points based on the transition intervals

The purpose of the feedrate adjustment in transition intervals iteratively is to reduce F′(u) and F″(u) considering the ND constraints between two adjacent feedrate-constant intervals. For convenience, the feature data set of interval ∏i is defined as {Mfc, i, Ffc, i, Mf, i, Mb, i}, where Mfc, i denotes the control point number associated with this interval, Ffc, i denotes the constant feedrate value, Mf, i denotes the number of control points that needs to be adjusted in the acceleration stage, and Mb, i in the deceleration stage. As shown in Fig. 7, a bidirectional scanning method is applied first to determine the parameters Mf, i and Mb, i. If the parameter domain [Uf(ai), Uf(bi)] is too small to meet the Acc/Dec requirements, which means Mfc, i − Mf, i − Mb, i ≤ k, then the interval ∏i will be merged with the adjacent interval ∏i − 1 or ∏i + 1 subsequently. The forward scanning procedure is presented as follows:

  1. 1.

    Let i = 1 and Mf, i = 0;

  2. 2.

    Judge whether an acceleration process exists from interval ∏i to ∏i + 1. If not, let Mf, i + 1 = 0, then go to Step 6. Otherwise, go to Step 3.

  3. 3.

    If Mf, i + 1 ≥ Mfc, i + 1 − k, which means the parameter domain of ∏i + 1 is small, then go to Step4; otherwise, calculate Mf, i + 1 by Eq. (29), then go to Step 6;

Fig. 7
figure 7

Linear adjustment of control points based the transition intervals by the bidirectional scanning method

Full size image
$$ {M}_{f,i+1}=\left({F}_{fc,i+1}-{F}_{fc,i}\right)/\gamma $$
(29)

where γ denotes the difference between the ordinates of two adjacent 2D control points during the linear adjustment as shown in Fig. 7. Note that γ has the same unit as Ffc, i, and is iteratively adjusted considering the ND constraints.

  1. 4.

    If i + 2 = Nfc, then emerge intervals ∏i and ∏i + 1 into a new feedrate-constant interval ∏∗. The parameter domain is updated as [Uf (ai), Uf (bi + 1)], the constant feedrate is set as \( {F}_{\mathrm{fc}}^{\ast }={F}_{\mathrm{fc},i} \), the number of feedrate-constant intervals is updated as Nfc = Nfc − 1. Subsequently, the feature data sets {Mfc, i, Ffc, i, Mf, i} are updated, end the program; otherwise, go to step 5.

  2. 5.

    If Ffc, i > Ffc, i + 2, as shown in Fig. 8a, then emerge intervals ∏i and ∏i + 1 into a new feedrate-constant interval ∏∗. The parameter domain is updated as [Uf(ai), Uf(bi + 1)], and the constant feedrate is set as \( {F}_{\mathrm{fc}}^{\ast }={F}_{\mathrm{fc},i} \); otherwise, emerge intervals ∏i + 1 and ∏i + 2 into a new interval ∏∗ with updated parameter domain [Uf(ai + 1), Uf(bi + 2)] and feedrate \( {F}_{\mathrm{fc}}^{\ast }={F}_{\mathrm{fc},i+2} \), as shown in Fig. 8b. Note that the number of feedrate-constant intervals is updated as Nfc = Nfc − 1. Subsequently, update the feature data set {Mfc, i, Ffc, i, Mf, i}, then go to Step 2.

  3. 6.

    If i = Nfc, end the program; otherwise, let i = i + 1, then go to step 2.

    Fig. 8
    figure 8

    Interval merging in the forward scanning process when interval ∏i is small

    Full size image

The backward scanning procedure is similar to the forward scanning procedure and is not presented here for brevity. Based on the bidirectional scanning method, the feature data set {Mfc, i, Ffc, i, Mf, i, Mb, i} of interval ∏i is obtained consequently. Then, F′(u) and F″(u) in the transition intervals can be reduced by linearly modulating the selected control points. Specifically, the control points \( {\left\{{\boldsymbol{F}}_p\right\}}_{p=0}^{M-1} \) of the feedrate profile F(u) are adjusted according to Eq. (30) in the acceleration stage:

$$ \left\{\begin{array}{c}{f}_p={F}_{\mathrm{fc},i}+\frac{F_{\mathrm{fc},i+1}-{F}_{\mathrm{fc},i}}{M_{f,i}}\cdot j\\ {}p={M}_{\mathrm{ct},i-1}+j,j=1,\dots, {M}_{f,i}\end{array}\right. $$
(30)

where Mct, i − 1 represents the index of the last control point associated with interval ∏i, which is expressed as

$$ {M}_{\mathrm{ct},i-1}=\sum \limits_{j=1}^{i-1}{M}_{\mathrm{fc},j} $$
(31)

Similarly, the control points \( {\left\{{\boldsymbol{F}}_p\right\}}_{p=0}^{M-1} \) are adjusted according to Eq. (32) for the deceleration stage:

$$ \left\{\begin{array}{c}{f}_p={F}_{\mathrm{fc},i+1}+\frac{F_{\mathrm{fc},i}-{F}_{\mathrm{fc},i+1}}{M_{b,i}}\cdot j,\\ {}p={M}_{\mathrm{ct},i}-j,j=1,\dots, {M}_{b,i}\end{array}\right. $$
(32)

After bidirectional scanning and control point adjustment, the feedrate profile F(u) is generated. Subsequently, whether the ND constraints are satisfied for all the sampling points is judged. If yes, then feedrate profile F(u) is acceptable for the CNC machining. Otherwise, update \( {\left\{{M}_{f,i}\right\}}_{i=1}^{N_{\mathrm{fc}}} \) and \( {\left\{{M}_{b,i}\right\}}_{i=1}^{N_{\mathrm{fc}}} \) by changing the value of γ in Eq. (29) and repeat the above process until the ND constraints are not violated. The initial value of γ can be set as γ = Vp, lim/2 and is adjusted by the dichotomy method between (0, Vp, lim/2] in each iteration. Figure 9 shows the block diagram of the iterative adjustment of the 2D control points. To schedule a more effective feedrate profile, different values of γ can be selected either in the acceleration or deceleration process.

Fig. 9
figure 9

Block diagram of the iterative adjustment of control points based on transition intervals

Full size image

As the feedrate profile F(u) is composed of feedrate-constant intervals and transition intervals, the number of control points can be further reduced according to the local adjustment property of the B-spline curve, which is beneficial to the CNC system of machining robot. Furthermore, the finite difference method, which can reduce the computational complexity of the proposed algorithm, is implemented to calculate the value of ND constraints below:

$$ \left\{\begin{array}{c}A\left({u}_i^{\ast}\right)\approx \left(F\left({u}_{i1}^{\ast}\right)-F\left({u}_i^{\ast}\right)\right)/{T}_s\\ {}J\left({u}_i^{\ast}\right)\approx \left(F\left({u}_i^{\ast}\right)-2F\left({u}_{i1}^{\ast}\right)+F\left({u}_{i2}^{\ast}\right)\right)/{T}_s^2\\ {}\begin{array}{c}\ddot{\boldsymbol{q}}\left({u}_i^{\ast}\right)\approx \left(\dot{\boldsymbol{q}}\left({u}_{i1}^{\ast}\right)-\dot{\boldsymbol{q}}\left({u}_i^{\ast}\right)\right)/{T}_s\\ {}\overset{\dots }{\boldsymbol{q}}\left({u}_i^{\ast}\right)\approx \left(\dot{\boldsymbol{q}}\left({u}_i^{\ast}\right)-2\dot{\boldsymbol{q}}\left({u}_{i1}^{\ast}\right)+\dot{\boldsymbol{q}}\left({u}_{i2}^{\ast}\right)\right)/{T}_s^2\end{array}\end{array}\right. $$
(33)

where \( {u}_i^{\ast } \) is the parameter of targeted sampling point, \( {u}_{i1}^{\ast } \) and \( {u}_{i2}^{\ast } \), which can be calculated by Eq. (6), are the curve parameters of the P(u) at time t + Ts and t + 2Ts, respectively.

4 Simulation and experimental results

In this section, simulations and experiments are carried out by the TriMule600 and TriMule800 machining platforms [38] (see Fig. 10). The dimensional parameters of two robots are listed in Table 2. The TriMule600 (TriMule800) has a maximum movement capability of 0.83 m/s (1.17 m/s) in velocity and 10 m/s2 (16 m/s2) in acceleration. The hardware part of the CNC system of the robot is built upon the Turbo PMAC-PCI motion controller and the software part is developed by NI LabVIEW®. Compared with carving, the flank milling needs larger cutting force. Therefore, we use TriMule600 platform for carving and TriMule800 platform for flank milling in the simulation. The simulation environment consists of Intel Core i5-8250 1.80 GHz personal computer, and the simulation program is developed by MATLAB®. Detailed parameters of the kinematic and dynamic constraints used in the feedrate-scheduling algorithm are presented in Table 3.

Fig. 10
figure 10

The layout of TriMule600 machining platform

Full size image
Table 2 Dimensional parameters of the TriMule robot
Full size table
Table 3 Parameters used in the simulation of the proposed feedrate-scheduling algorithm
Full size table

4.1 Simulation and experiment of the three-axis toolpath for carving

Figure 11a shows a butterfly-shaped NURBS curve for carving with a sharp curvature change, and its detailed parameters are shown in [37]. The cubic NURBS curve contains 51 control points and its total arc-length is 382.86 mm. The direction of the cutter axis always follows the positive direction of the zw-axis in {PCS} during the machining process. As shown in Fig. 11b, there are eight points marked C1 to C8 whose curvature is larger than 0.5 mm−1, and the above points should be chosen as sampling points for feedrate scheduling. The sampling points are obtained by setting arc-length Δs as 0.4 mm and threshold κlim as 0.5 in Eq. (24). As a result, 971 sampling points are selected. Note that the greater number of control points that exist in the feedrate profile, the stronger the curve adjustment ability is. To achieve a good balance between computational complexity and curve adjustment ability, the number of control points of F(u) is initially set as 400 and the coefficient η in Eq. (28) is set as 0.85. The results of feedrate scheduling are illustrated in Fig. 12. From this figure, it can be seen that the feedrate profile is composed of feedrate-constant intervals and transition intervals. In addition, the feedrate value is reduced in the region with a large curvature, such as C1 to C8, and increased in the region with small curvature. According to the local adjustment characteristics of the B-spline curve, the number of control points associated with feedrate-constant intervals is reduced, and the final feedrate profile contains 206 control points.

Fig. 11
figure 11

The butterfly-like NURBS curve for simulation. a Geometric model. b Variation profile of curve curvature

Full size image
Fig. 12
figure 12

Simulation results of butterfly-like NURBS curve by the proposed feedrate-scheduling method. a Scheduled feedrate profile. b Scheduled feedrate value shown on the position spline

Full size image

Furthermore, to verify the effectiveness of the presented feedrate-scheduling algorithm, Jia’s algorithm [21] is employed for comparison study. The MA is evaluated by the jerks of actuated joints, and the ME is measured by the machining time. Similar to the proposed method, the feedrate profile generated by Jia’s method is composed of feedrate-constant intervals and transition intervals. The largest difference between two methods is the ND constraints considered in the transition intervals. Specifically, only tangential acceleration and tangential jerk are considered in Jia’s method, and S-curve Acc/Dec strategy is applied for transition. Meanwhile, the NI constraints considered in both methods are the same.

The obtained feedrate profile by Jia’s method is compared with that by the proposed method as shown in Fig. 13, while the resulted jerk profiled of actuated joints are compared in Fig. 14. Due to the adopted adjustment strategy of control points and the consideration of drive constraints in this paper, the ME is inevitably sacrificed compared to Jia’s method. It can be seen that although the machining time of Jia’s method is 15.4% shorter than the proposed method, the kinematic and drive constraints of the proposed method are more effective. The average acceleration value obtained by the proposed method is 37.6% smaller than that obtained by Jia’s method, and the average jerk value is 49.7% smaller. Furthermore, Jia’s method cannot control the acceleration and jerk of the actuated joints in transition intervals, which causes the joint motion to exceed the drive constraints in the region around C1, C4, C5, and C8 as shown in Fig. 14, while the proposed method can effectively solve this problem. Therefore, it is reasonable to consider that the proposed method can achieve a good balance between the MA and ME.

Fig. 13
figure 13

Comparing results of the kinematics of cutter tip position with Jia’s method and the proposed method. a Scheduled feedrate profile. b Scheduled acceleration profile. c Scheduled jerk profile

Full size image
Fig. 14
figure 14

Comparing results of the kinematics of the actuated joints with Jia’s method and the proposed method

Full size image

On the basis of simulation, experiments are performed on the TriMule600 machining platform. The parametric toolpath is initially interpolated with 3 ms in Cartesian space, and converted into joint commands via inverse kinematics with servo feedback rate of 2 kHz in real implementation subsequently. Figure 15 shows the machining result for the butterfly-like toolpath using a flat-bottomed cylindrical milling cutter whose diameter is 8 mm, and the total machining time is 18.6 s. Building upon encoder signals acquired by DSP at 20-ms intervals in the motion controller, it is easy to see that continuous and smooth joint movement can be achieved. As shown in Fig. 16, the real feedrate profile computed by velocity analysis based on the collected velocity signal of actuated joints is in line with the simulated profile shown in Fig. 12. The measured jerk profiles of the actuated profiles are identical to those shown in Fig. 14, and therefore not displayed here. Since the friction compensation is not realized in the control system, feedrate fluctuation due to the reversal of three telescopic legs of the TriMule600 robot appears in the region with large curvature. The focus of follow-up research will be based on friction compensation to reduce feedrate fluctuation. Based upon the encoder signals acquired by DSP in the motion controller, Fig. 17 shows that the tracking errors of the five actuated joints and smooth joint movement are achieved after feedrate scheduling, resulting in a tracking error less than 0.015 mm for the telescopic legs and 4 × 10−5 rad for the A/C wrist. According to the robot’s absolute positioning accuracy of 50 μm, a tracking error smaller than 0.02 mm for the telescopic legs and 1 × 10−4 rad for the A/C wrist are acceptable for machining. Therefore, the experimental results further validate the correction and effectiveness of the proposed algorithm for feedrate scheduling.

Fig. 15
figure 15

Machining results for the butterfly-like NURBS curve by the proposed feedrate-scheduling algorithm

Full size image
Fig. 16
figure 16

The measured feedrate profile during machining process

Full size image
Fig. 17
figure 17

Tracking errors of the actuated joints vs. time during machining

Full size image

4.2 Simulation and experiment of the five-axis toolpath for flank milling

Figure 18 shows a five-axis toolpath for the flank milling of a non-developable ruled surface in [11], and it contains one region marked as R1 where the orientation of cutter axis changes dramatically. Simulation and experiment are carried out in the TriMule800 machining platform. First, a flat-bottom milling cutter with a diameter of 16 mm is used, and the small line segments are obtained by multi-axis machining mode in UG NX10. Second, the dual B-spline toolpath is generated by the parameterization method shown in the “Parametric toolpath and parametric interpolation for robot machining” section. The total arc-length of position spline P(u) is 291.04 mm. The sampling points are obtained by setting arc-length Δs as 0.4 mm, the threshold κlim as 0.15 mm−1, and σlim as 0.007 mm−1. As a result, 750 sampling points are selected. The number of control points of feedrate profile is initially set as 200, and it is reduced to 115 after feedrate scheduling. The coefficient η in Eq. (28) is set as 0.85 for iterative adjustment of the control points. The simulation results of feedrate scheduling by the proposed method are illustrated in Fig. 19. It can be found that the feedrate profile is mainly limited by the chord error, and the constant feedrate value in the region R1 is closed to 10 mm/s. Comparing the proposed method with Jia’s method, it can be found that a good balance between the MA and ME can be obtained. The conclusions are identical to those drawn in the “Simulation and experiment of the three-axis toolpath for carving” section. Therefore, the results are not displayed here for brevity. The simulation results verify the correctness and effectiveness of the proposed feedrate-scheduling algorithm.

Fig. 18
figure 18

Five-axis toolpath and its parameterization for simulation and experiment

Full size image
Fig. 19
figure 19

Simulation results of five-axis toolpath by the proposed feedrate-scheduling method. a Scheduled feedrate profile. b Scheduled feedrate value shown on the ruled surface

Full size image

Figure 20 shows the machining results for the five-axis toolpath. The feedrate profile generated by Jia’s method will violate drive constraints in some regions. Therefore, a comparative experiment with the conservative feedrate [39], which is the common practice in industry, is carried out to further verify the effectiveness of the proposed method. The same toolpath is used for two machining experiments. The comparing results between the conservative feedrate profile and the scheduled feedrate profile computed by velocity analysis based on the collected signals of actuated joint velocity are shown in Fig. 21. The total machining time with the scheduled feedrate profile is 14.754 s, while that with the conservative feedrate profile is 30.824 s. The results show that machining time is reduced by half without sacrificing the MA compared to the conservative feedrate profile usually used in the industry. Figure 22 shows the tangential acceleration, tangential jerk, angular velocity, and angular acceleration profiles of the cutter tip position by the proposed method. The jerk profiles of the actuated joints measured by DSP at 20-ms intervals in the motion controller are illustrated in Fig. 23. It can be seen that the magnitudes of constraints are both confined below the maximum allowable value. The considered constraints are far lower than the given limitations in the comparative experiment [39]. Hence, the results of the comparative experiment are not displayed here. Figure 24 shows the comparison of the tracking errors with the scheduled feedrate profile and the conservative feedrate profile. The tracking errors of the actuated joint are related to both its motion trajectory and control strategy. Since the measured velocity, acceleration, and jerk of the actuated joints with the scheduled feedrate profile are much greater than those with the conservative feedrate profile, the tracking error of each actuated joint with the scheduled feedrate profile is slightly larger. According to the robot’s absolute positioning accuracy of 80 μm, the tracking error less than 0.03 mm for the telescopic legs and 1.5 × 10−4 rad for the A/C wrist are acceptable for machining. The maximum tracking errors measured with feedrate scheduling is 0.03 mm for the telescopic legs and 1 × 10−4 rad for the A/C wrist. The experiment results further validate the correction and effectiveness of the proposed feedrate-scheduling algorithm in balancing the MA and ME.

Fig. 20
figure 20

Machining results of five-axis toolpath by the proposed feedrate-scheduling algorithm

Full size image
Fig. 21
figure 21

Comparison of machining time for five-axis toolpath with the scheduled feedrate profile and the conservative feedrate profile

Full size image
Fig. 22
figure 22

Tangential acceleration, jerk profile of cutter tip position and angular velocity, and acceleration of cutter axis orientation by the proposed method for the five-axis toolpath

Full size image
Fig. 23
figure 23

The measured jerk profiles of the actuated joints by the proposed method

Full size image
Fig. 24
figure 24

Comparison of tracking errors for five-axis toolpath with the scheduled feedrate profile and the conservative feedrate profile

Full size image

5 Conclusions

In this paper, an offline feedrate-scheduling algorithm considering the geometry and drive constraints for hybrid machines is proposed. The following conclusions are drawn.

  1. 1.

    The general five-axis toolpath for machining robot is described in a dual NURBS form as similar to the A-B-type five-axis machine tool. The motion of the cutter tip is the main motion, while the orientation of the cutter axis defined by attitude angle follows the cutter tip through the curve parameter.

  2. 2.

    By adding a dimension of the curve parameter, the feedrate profile expressed by a cubic uniform B-spline is mapped into a 2D curve with redefined control points. The adjustment strategy of control points is presented to realize the feedrate scheduling of a hybrid robot.

  3. 3.

    The feedrate constraint equations are derived by considering the geometric and drive constraints. Specifically, the NI constraints are used to adjust the redefined control points of the feedrate profile to the desired location by only one-time calculation, while the ND constraints are used in the iteration adjustment process. The scheduled feedrate profile can avoid high-frequency feedrate fluctuation, remain constant in most parameter intervals, and change smoothly in transition intervals.

  4. 4.

    The proposed algorithm has been integrated into the CNC system, and simulations and experiments for three-axis carving and five-axis flank milling are carried out on the TriMule600 and TriMule800 machining platform, respectively. The simulation results of the butterfly-shaped NURBS curve compared to Jia’s method show that the average jerk can be reduced by 49.7% without violating any constraint, although the machining time is increased by 15.4%. The machining results of the five-axis toolpath show that the machining time is reduced by half with acceptable tracking errors compared to that without feedrate scheduling. It is reasonable to conclude that the proposed algorithm can achieve a balance between the MA and ME.

  5. 5.

    The proposed algorithm can be employed for other five-axis machining equipment. However, the scheduled feedrate profile is not time-optimal, and the dynamics of the hybrid robot are not taken into account, which will be intensively studied in our future work.