1 Introduction

In modern processing industry, the parametric curves are extensively applied for workpieces of various fields, such as aerospace, transportation, automobile, and so on. For this reason, many parameter interpolation algorithms have been proposed to generate reference positions as the input of motor controllers. Direct approximation method with Taylor’s expansion is widely employed in the interpolation process. The first-order Taylor expansion is usually adequate. If it is not adequate, the second-order approximation could be adopted. In order to further improve the approximation accuracy, the Adams-Bashforth method (ABM) and fourth-order Runge-Kutta method are applied instead of Taylor’s expansion [1]. By introducing the concept of “feedback,” the predictor-corrector method is presented to avoid directly calculating the first- or second-order derivatives of the parametric curve [2]. Since some parametric curves are not parameterized by arc length, some unexpected feedrate fluctuations may appear during the interpolation. The interpolation method of feed correction polynomial is proposed [3]. This method is further improved by introducing the adaptive quadrature length method [4] and the multiple inverse length function method [5].

However, no matter which interpolation method is used, the appropriate feedrate is needed before interpolation. Conservative constant feed can not make full use of the performance of machine tools, which may lead to larger chord error in places with larger curvature. So, the algorithms which can adjust the feedrate adaptively have been extensively researched. By considering the chord error, curvature, and contour error, an integrated look-ahead dynamics-based algorithm is proposed [6]. This method can reduce the feedrate when the chord error exceeds the tolerance value or the curvature is too large. In addition, if the contour error estimated through high-order transfer function is greater than the error bound, the algorithm will re-plan the feedrate profile. Sun et al. present a method of adaptive feedrate for improving precision of five-axis computer numerical control (CNC) machining [7]. This method takes consideration of both the confined nonlinear geometric error and the angular feedrate. Hence, tangential velocity at sensitive regions can be adjusted based on geometric error with bi-directional scan algorithm. Another online speed profile generator is developed for industrial machine tools based on neuro-fuzzy network [8]. In this literature, it is assumed that the machining mission must be divided into several parts due to the capacity of NC system. The feedrate is adjusted adaptively according to different feed limits which are caused owing to changing the spindle speed for processing each part.

Generally, a smooth feed profile is generated by restraining the jerk. However, most of jerk-limited methods with adaptive feedrate require an initial command feedrate which is empirical and conservative. The optimal feedrate profile can not be generated. Therefore, optimization methods are introduced to the trajectory planning by some researchers. For example, two optimal time-jerk trajectory planning methods are analyzed and validated for robotic manipulators [9]. In the two algorithms, both the time and jerk square are included in the objective function, so as to satisfy the need of fast execution and the need of a smooth trajectory simultaneously. Through modifying two weights of the jerk square and time, optimal time-jerk trajectory could satisfy kinds of requirements. Zhang et al. propose an algorithm which can generate the smooth time-optimal trajectory for cartesian computer numerical control (CNC) manufacturing systems [10]. In this algorithm, smooth minimum time feed profile is obtained by solving a nonlinear program (NLP) with constraints of axial feeds, axial accelerations, and axial jerks. Considering G01 paths, Lin et al. present a trajectory planning model combining fitting error constraints and dynamic constraints [11]. In this literature, the cubic B-spline fitting with confined error and speed planning method are combined together instead of traditional sequential implementation.

To further reduce the planning time, linear programming is applied to solve the optimization problem of feedrate. In order to obtain an optimal motion trajectory for a robotic manipulator, a robust planning algorithm based on linear programming is addressed, since the manipulator dynamics and torque parameters are uncertain [12]. Considering the feedrate bound, axis acceleration bounds, and axis tracking errors, Guo et al. transform feedrate planning into an optimal control problem [13]. In order to solve the optimal problem with linear programming, some constraints are simplified and jerk bounds are not considered. For integrating jerk constraints into an optimization problem, Liu et al. firstly obtain an upper bound of feedrate for spline curve tool paths [14]. Secondly, the jerk constraints are approximated as linear ones based on the upper bound. Finally, the linear programming method can be adopted to solve the optimization problem. Ye et al. extend the feedrate planning method based on optimization to the Frenet-Serret frame by re-parameterizing parametric tool paths [15]. Afterwards, a time optimal method for parametric trajectory generation is proposed based on linear programming algorithm.

However, most of optimal trajectory planning methods are mainly concerned about feedrate planning. There is few mention about the interpolation method which is very important for generating servo controlling commands. Although a method of interpolation point generation for robotic manipulators is developed [16], it is time consuming since high-order derivative of parameter is required.

In this paper, a two-stage feedrate scheduling scheme (TFSS) is proposed to obtain smooth profile. The first stage constructs a problem of minimum time trajectory planning (MTTP) in order to fully utilize the performance of the machine tool. Then, the MTTP problem is transformed into a linear programming problem for further improving the computation efficiency. According to the solution of MTTP, the second stage re-plan the feedrate based on a bell-shape profile. The final feedrate is suitable for real-time interpolation. In the second stage, in order to deal with the overlapping phenomenon, known as “ripple effect” [1] at the sharp corners, the jerk-limited method of eliminating interaction (JMEI) is proposed. Since the feedrate is re-planned by the JMEI in the time domain, the results of JMEI can be directly used for interpolation of feed correction polynomial. Finally, the reference positions calculated by the interpolation method are sent to servo controllers. The flowchart of the TFSS and feed correction polynomial is shown as Fig. 1, where Si+ 1 and Si denote displacements in the (i + 1)th and the i th interpolation period, respectively, Vi is a planned feedrate in the i th period, T is the interpolation period and mi+ 1 is curve parameter yielded by feed correction polynomial in the (i + 1)th period.

Fig. 1
figure 1

Flowchart of TFSS and feed correction polynomial

Full size image

The left portions of this paper are organized as follows. In Section 2, MTTP for a cartesian 3-axis system is formulated, imposing the constraints of the resultant feedrate, the axial accelerations, and the chord error. Then, this MTTP problem is discretized with direct transcription method and reformulated as a linear programming problem. These are illustrated in Section 3. The method of smooth feedrate generation, namely JMEI, is proposed in Section 4. Machining results of simulation and experiment for two NURBS tool paths are shown in Section 5. Section 6 concludes the whole paper finally.

2 MTTP problem

Let C = [x(m) y(m) z(m)], m ∈ [0,1] be a curve path, where m denotes the path parameter. The MTTP problem aims to make the machine tool traverse the entire tool path in the shortest time, so the objective of the MTTP problem can be written as

$$ \min\limits_{\textbf{v}} \quad T ={\int}_{t_{0}}^{t_{n}}{1 \ dt} $$
(1)

where v = [vxvyvz] denotes velocity vector of the cutter tip at any one point on the path. The velocity vector needs to be planned to minimize the objective function. While the velocity is planned, the acceleration of each axis is also planned and let a = [axayaz] be the axial acceleration vector.

Define the derivative of an arbitrary variable w with respect to parameter m as \(w^{\prime }\) and the derivative with respect to time t as \(\dot {w}\). For example, \(\dot {x} = \frac {dx}{dt} \) represents derivative of displacement along x axis w.r.t time t, and \(x^{\prime } = \frac {dx}{dm} \) indicates derivative of displacement along the x axis w.r.t parameter m. They have the following relationship:

$$ \dot{x} = \frac{dx}{dt} = \frac{dx}{dm}\frac{dm}{dt} = x^{\prime}\dot{m} $$
(2)

Obviously, the MTTP problem must be subject to the predefined path and other constraints, such as the feedrate, axial accelerations, and the chord error. According to differential relations of displacement, velocity, and acceleration, the following equation can be derived as

$$ \dot{\textbf{C}}(t) = {\textbf{v}}, {\dot{\textbf{v}}}(t) = {\textbf{a}} $$
(3)

From Eqs. 2 and 3, the feedrate can be obtained from the velocity vector

$$ v(t) = \left\| {\textbf{v}} \right\| = \left\| {\dot{\textbf{C}}} \right\| = \left\| {{\textbf{C}^{\prime}}} \right\|\dot m \leq v_{F} $$
(4)

where vF denotes the command feedrate, and ∥∙∥ is the 2-norm. In addition, the acceleration for each axis also is limited because of the capacity of a machine tool, which is described as

$$ \left\{ \begin{array}{l} {{\textbf{a}}_{{\textbf{min}}}} \le {\textbf{a}} \le {{\textbf{a}}_{{\textbf{max}}}}\\ {\textbf{a}} = {\dot{\textbf{v}}} = {\textbf{C}^{\prime}} \ddot{m} + {\textbf{C}^{\prime\prime}}{\dot{m}^{2}} \end{array} \right. $$
(5)

Meanwhile, in actual machining, two adjacent interpolation points are not connected by an arc, but a short straight line. The chord error represents the maximum distance between the straight line and the arc, which is an important part of machining error in a NC system. According to the definition of the chord error [18], there is the following relationship shown as

$$ {v^{2}}(t) \le \frac{{8\delta \rho (t) - 4{\delta^{2}}}}{T^{2}} \approx \frac{{8\delta \rho (t)}}{T^{2}} = \frac{{8\delta }}{{\kappa (t){T^{2}}}} $$
(6)

where δ is the chord error bound, κ denotes the curvature, and ρ is the radius of curvature. Let ch(t) denotes the chord error, when the tangential velocity is v(t), there is

$$ \text{ch}(t) = \frac{{\kappa (t){T^{2}}{v^{2}}(t)}}{8} \le \delta $$
(7)

Since the centripetal acceleration of the cutter tip is defined as ac(t) = κ(t)v2(t), from Eqs. 6 and 7, the chord error constraint can be transformed to the centripetal acceleration constraint. Hence, the centripetal acceleration is restrained as follows:

$$ {a_{c}}(t) \le \mu \quad \text{with} \quad \mu = \frac{{8\delta }}{{{T^{2}}}} $$
(8)

In view of a parametric path, the curvature at parameter value m can be described as

$$ \kappa (m) = \frac{{\left| {{\textbf{C}^{\prime}}(m) \times {\textbf{C}^{\prime\prime}}(m)} \right|}}{{{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}^{3}}}} $$
(9)

By substituting Eqs. 4 and 9 into Eq. 8, the centripetal acceleration constraint can be rewritten as the following function of parameter m:

$$ {a_{c}}(m) = \frac{{\left| {{\textbf{C}^{\prime}}(m) \times {\textbf{C}^{\prime\prime}}(m)} \right|}}{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}}{\dot m^{2}} \le \mu $$
(10)

Thus, the constraints of the feedrate, the axial acceleration, and the chord error are all transformed into the functions of parameter velocity and parameter acceleration. Therefore, MTTP with these three constraints is formulated as an optimal control problem about parameter, while multi-variable optimization problem is reduced to a problem where only one parameter variable needs to be optimized. Imposing boundary conditions and system dynamic, the time optimal control problem can be formulated as

$$ \begin{array}{@{}rcl@{}} &&\min\limits_{\ddot{m}} \quad T ={\int}_{t_{0}}^{t_{n}}{1 \ dt}\\ &&{\text{s}}{\text{.t}}{\text{. }}\left\{ \begin{array}{l} \frac{dm}{dt} = \dot m(t),\frac{d \dot m}{dt} = \ddot m(t)\\ m({t_{0}}) = 0,m({t_{n}}) = 1,\dot m({t_{0}}) = {{\dot m}_{0}},\dot m({t_{n}}) = {{\dot m}_{n}}\\ \| {{\textbf{C}^{\prime}}(m)} \|^{2}{{\dot m}^{2}} \le {v_{F}}^{2}\\ {{\textbf{a}}_{\min }} \le {\textbf{C}^{\prime}}\ddot m + {\textbf{C}^{\prime\prime}}{{\dot m}^{2}} \le {{\textbf{a}}_{\max }}\\ \frac{{\left| {{\textbf{C}^{\prime}}(m) \times {\textbf{C}^{\prime\prime}}(m)} \right|}}{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}}{{\dot m}^{2}} \le \mu \end{array} \right. \end{array} $$
(11)

where \({\dot m_{0}} = \frac {{{v_{0}}}}{{\left \| {{\textbf {C}^{\prime }}(0)} \right \|}},{\dot m_{n}} = \frac {{{v_{n}}}}{{\left \| {{\textbf {C}^{\prime }}(1)} \right \|}}\) are constraints of the start point and the end point, respectively. In Eq. 11, system dynamic is linear while process constraints are nonlinear. Therefore, the formulation is actually a time optimal control problem for a linear system with constraints of nonlinear equality and inequality.

3 Solution of MTTP problem

Equation 11 is an optimal control of second-order dynamic system with nonlinear constraints. In addition, the final time is free. Parameter \(\dot {m}\) obviously becomes the state variable, and constraints are nonlinear functions of parameter velocity \(\dot {m}\). Since constraints have strong nonlinearity, Eq. 11 is difficult to solve efficiently. To solve such a problem, it is best to convert the free time into fixed time by introducing a time scale factor. Then the free time optimal control problem is transformed to the corresponding fixed time one. As the parametric formula of the tool path is known, Eq. 11 can be mapped from the time domain t ∈ [t0, tn] to the parameter domain m ∈ [0,1], which can effectively weaken nonlinearity.

3.1 Dynamic system model reduction

Since \(\dot m = \frac {dm}{dt}\), the objective function of Eq. 11 can be rewritten as

$$ \min J = {{\int}_{0}^{1}} {\frac{1}{\dot m}\ dm} $$
(12)

Define new variables [19, 20]

$$ \alpha (m) = {\dot m^{2}},\beta (m) = \ddot m $$
(13)

Then, constraints of the feed, the axial accelerations, and the centripetal acceleration can be rewritten as the linear functions of (α, β)

$$ \left\{ \begin{array}{l} {\|{\textbf{C}^{\prime}}(m)\|^{2}}\alpha \le {v_{F}}^{2}\\ {{\textbf{a}}_{{\min}}} \le {\textbf{C}^{\prime\prime}}\alpha + {\textbf{C}^{\prime}}\beta \le {{\textbf{a}}_{\max }}\\ \frac{{\left| {{\textbf{C}^{\prime}}(m) \times {\textbf{C}^{\prime\prime}}(m)} \right|}}{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}}\alpha \le \mu \end{array} \right. $$
(14)

The following differential relations can also be derived as

$$ \alpha^{\prime}(m) = \frac{{{\text{d}}{{\dot m}^{2}}}}{{{\text{d}}m}} = 2\dot m\frac{{{\text{d}}\dot m}}{{{\text{d}}m}} = 2\dot m\frac{{{\text{d}}\dot m}}{{{\text{d}}t}}\frac{{{\text{d}}t}}{{{\text{d}}m}} = 2\ddot m = 2\beta (m) $$
(15)

Taking parameter acceleration β as the optimized variable, Eq. 11 can be reformulated as Eq. 16:

$$ \begin{array}{@{}rcl@{}} &&\min\limits_{\beta} J = {{\int}_{0}^{1}} {\frac{1}{{\sqrt \alpha }}} \ {dm}\\ &&{\text{s}}{\text{.t}}{\text{. }}\left\{ \begin{array}{l} \alpha '(m) = 2\beta (m),\alpha (0) = {\alpha_{0}},\alpha (1) = {\alpha_{1}}\\ {\left\| {{\textbf{C}^{\prime}}(m)} \right\|^{2}}\alpha \le {v_{F}}^{2}\\ {{\textbf{a}}_{\min }} \le {\textbf{C}^{\prime\prime}}\alpha + {\textbf{C}^{\prime}}\beta \le {{\textbf{a}}_{\max }}\\ \frac{{\left| {{\textbf{C}^{\prime}}(m) \times {\textbf{C}^{\prime\prime}}(m)} \right|}}{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}}\alpha \le \mu \end{array} \right. \end{array} $$
(16)

Equation 16 is actually the convex optimal control problem of the first-order linear system [20], which has much weaker nonlinearity and lower system order compared with Eq. 11. Because Eq. 16 is convex, local optimal solution for Eq. 16 is just the global one. Furthermore, the optimal solution of Eq. 16 is unique and maximum among all feasible solutions at any time [13, 21].

Although Eq. 16 can be efficiently solved by approaches based on gradient, we still want to find a more efficient method like linear programming [13]. Considering minimum processing time may need maximum feed profile, the optimal control Eq. 16 can be replaced with

$$ \mathop {\max }\limits_{\beta} J = {{{\int}_{0}^{1}} {\left\| {{\textbf{C}^{\prime}}(m)} \right\|}^{2}}{v^{2}}{\text{d}}m = {{{\int}_{0}^{1}} {\left\| {{\textbf{C}^{\prime}}(m)} \right\|}^{4}}\alpha {\text{(}}m{\text{)d}}m $$
(17)

Note that constraints of Eq. 17 is omitted, because they are the same as that of Eq. 16. Actually, solution of Eq. 17 is just that of Eq. 16, which can be proved by theorem 1.

Theorem 1

Equation 17has the same and unique optimal solution with Eq. 16.

Before proving the theorem, two assumptions must be stated.

Assumption 1 The predefined path C(m) is bounded and has a two-order continuous derivative.

Assumption 2 The predefined path C(m) doesn’t present singularity.

Proof

Consider that γ∗(m) is the optimal solution of Eq. 16. Since Eq. 17 has the same constraints with Eq. 16, γ∗(m) is also a feasible solution to Eq. 17. Let Rn be the space of all the feasible solutions. Since the optimal solution is unique and maximum among all feasible solutions, so as to an arbitrary γf(m) ∈ Rn, there is \({\gamma ^{*}}(m) \ge {\gamma _{f}}(m),m \in \left [ {0,1} \right ]\). Then, with regard to the objective function of Eq. 17, there is

$$ {{\int}_{0}^{1}} {{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}^{4}}{\gamma^{*}}(m){\text{d}}m} > {{\int}_{0}^{1}} {{{\left\| {{\textbf{C}^{\prime}}(m)} \right\|}^{4}}{\gamma_{f}}(m){\text{d}}m} $$
(18)

As a consequence, γ∗(m) is also the optimal solution of Eq. 17 , and the theorem is proved. Theorem 1 allows to conclude that minimum time feedrate trajectory can be generated by solving a simpler linear optimal control problem. In the next section, through discretizing the state and controlled variables, Eq. 17 can be rewritten as the standard linear programming formulation. □

3.2 Linear programming–based formulation

An effective method of numerical solution, namely direct transcription method, which discretizes both the state and controlled variables, may be proper for Eq. 17. Since the system dynamic of Eq. 17 is a first-order linear system, radial basis functions can be applied to parameterize the state variable [22]. The state variable can be approximated by

$$ \alpha (m) \approx \hat \alpha (m) = \sum\limits_{i = 1}^{L} {{N_{i}}(m)} {\xi_{i}} $$
(19)

where \({N_{i}}(m) = exp\left ({ - {{(m - {{\bar m}_{i}})}^{2}}/2{\delta ^{2}}} \right ) > 0\) is the i th radial basis function, and ξi is the i th weight coefficient. The scope of each radial basis function can be restricted by the function center \({\bar m_{i}}\) and the width parameter δ. Subsisting Eq.19 into Eq.15, the control variable can be derived as

$$ \beta (m) = \hat \beta (m) = \frac{1}{2}\sum\limits_{i = 1}^{L} {{{N^{\prime}}_{i}}(m)} {\xi_{i}} $$
(20)

where \({N_{i}}^{\prime } (m) = - \frac {{(m - {{\bar m}_{i}})}}{{{\delta ^{2}}}}\exp \left ({ - \frac {{{{(m - {{\bar m}_{i}})}^{2}}}}{{2{\delta ^{2}}}}} \right )\).

Function centers of radial basis functions may or may not coincide with grid points, and this paper assumes that they are the same. The grid sequences can be described as

$$ {\textbf{m}} = \left[ {{{\bar m}_{1}}, {\ldots} ,{{\bar m}_{L}}} \right] $$
(21)

where \(0 < {\bar m_{1}} < {\bar m_{2}} < {\cdots } < {\bar m_{L}} < 1\). Because the grid points are uniformly distributed, each interval between two adjacent grids is equal to Δm = 1/(L + 1). All the constraints including path constraints are estimated at grid points. This method is known as point-wise discretization which has been proved convergent [23]. Meanwhile, the system dynamic is eliminated.

Take the weight coefficient vector \({\xi } = {\left [ {{{\bar \xi }_{1}}, {\cdots } ,{{\bar \xi }_{L}}} \right ]^{T}}\) as optimized variables, the maximum objective function of Eq. 17 can be deduced as

$$ \begin{array}{@{}rcl@{}} \max J &\approx& \sum\limits_{j = 1}^{L} {\left( {{{\left\| {{\textbf{C}^{\prime}}({{\bar m}_{j}})} \right\|}^{4}}\sum\limits_{i = 1}^{L} {{N_{i}}({{\bar m}_{j}}){\xi_{i}}} {\varDelta} m} \right)}\\ &=&\sum\limits_{j = 1}^{L} {\left( {\sum\limits_{i = 1}^{L} {{{\left\| {{\textbf{C}^{\prime}}({{\bar m}_{j}})} \right\|}^{4}}{\varDelta} m{N_{i}}({{\bar m}_{j}}){\xi_{i}}} } \right)}\\ &=&{\textbf{F}\xi} \end{array} $$
(22)

where

$$ \left\{ \begin{array}{lll} &{\textbf{F}} = \left[ {\begin{array}{*{20}{c}} {{F_{1}}}&{{F_{2}}}& {\cdots} &{{F_{L}}} \end{array}} \right]\\ &{F_{i}} = \sum\limits_{j = 1}^{L} {{{\left\| {{\textbf{C}^{\prime}}({{\bar m}_{j}})} \right\|}^{4}}{\varDelta} m{N_{i}}({{\bar m}_{j}})} \end{array} \right. $$

The feedrate constraint can be approximated as \({\textbf {B}\xi } \le {v_{F}}^{2}{\textbf {I}}\), where

$$ \left\{ \begin{array}{lll} &{\textbf{B}} = {\left[ {{{{\mathrm{B}}}_{1}} {\cdots} {{{\mathrm{B}}}_{L}}} \right]^{T}}\\ &{{\textbf{B}}_{j}} = d({\bar m_{j}})\left[ {{N_{1}}({{\bar m}_{j}}) {\cdots} {N_{L}}({{\bar m}_{j}})} \right]\\ &d({\bar m_{j}}) = {\left\| {{\textbf{C}^{\prime}}({{\bar m}_{j}})} \right\|^{2}} \end{array} \right. $$

Similarly, the centripetal acceleration constraint can also be written as Hξ ≤ μI. Since two axes have the same form of acceleration constraint, we take the x axis for example. The approximation formula of x axis acceleration constraint is given as

$$ {a_{x\min }}{\textbf{I}} \le {{\textbf{A}}_{x}}{{\xi}} \le {a_{x\max }}{\textbf{I}} $$
(23)

where

$$ \left\{ \begin{array}{llll} &{{\textbf{A}}_{x}} = {\left[ {\begin{array}{*{20}{c}} {{{\textbf{A}}_{x{\textbf{1}}}}}&{{{\textbf{A}}_{x{\textbf{2}}}}}& {\cdots} &{{{\textbf{A}}_{x{\textbf{L}}}}} \end{array}} \right]^{T}}\\ &{{\textbf{A}}_{xj}} = {\left[ {\begin{array}{*{20}{c}} {x^{\prime\prime}({{\bar m}_{j}}){N_{1}}({{\bar m}_{j}}) + \frac{1}{2}x^{\prime}({{\bar m}_{i}}){{N^{\prime}}_{1}}({{\bar m}_{j}})}\\ {\vdots} \\ {x^{\prime\prime}({{\bar m}_{j}}){N_{L}}({{\bar m}_{j}}) + \frac{1}{2}x^{\prime}({{\bar m}_{j}}){{N^{\prime}}_{L}}({{\bar m}_{j}})} \end{array}} \right]^{T}} \end{array} \right. $$

In the same way, the constraint on y axis can be obtained as

$$ {a_{y\min }}{\textbf{I}} \le {{\textbf{A}}_{y}}{{\xi }} \le {a_{y\max }}{\textbf{I}} $$
(24)

Until now all constraints have been converted to linear functions of ξ, and Eq. 17 is easily reformulated to the standard form of linear programming

$$ \begin{array}{@{}rcl@{}} &&\max\limits_{\xi} {\text{ }}{\textbf{F}\xi}\\ &&{\text{s}}{\text{.t}}{\text{. }}\left\{ \begin{array}{l} {a_{x\min }}{\textbf{I}} \le {{\textbf{A}}_{x}}{{\xi }} \le {a_{x\max }}{\textbf{I}}\\ {a_{y\min }}{\textbf{I}} \le {{\textbf{A}}_{y}}{{\xi }} \le {a_{y\max }}{\textbf{I}}\\ {\textbf{B}\xi} \le {v_{F}}{\textbf{I}}\\ {\textbf{H}\xi} \le \mu {\textbf{I}} \end{array} \right. \end{array} $$
(25)

where \({\textbf {I}} \in \mathbb {R}^{L\times 1}\) is unit column vector, \({{\textbf {A}}_{x}} \in \mathbb {R}^{L \times L}\), \({{\textbf {A}}_{y}} \in \mathbb {R}^{L \times L}\), \({\textbf {B}} \in \mathbb {R}^{L \times L}\) and \({\textbf {H}} \in \mathbb {R}^{L \times L}\) denote Jacobian matrices with the sparse structure.

Solving Eq. 25 with linear programming, the optimal coefficient vector ξo is obtained. Substituting ξo into Eq. 19, the optimal parameter speed at any parameter can be estimated. Therefore, the optimal feedrate profile is easily gained according to Eq. 4. This feedrate profile needs to be interpolated to generate reference positions for servo controllers. But the feedrate profile is a function of parameter, not the time. The interpolation methods developed for this kind of feedrate either unstable or time consuming. Moreover, jerk constraints are not considered. Hence, the feedrate gained by solving MTTP is taken as an initial feedrate, since it is the maximum in the feasible region and has “bang-bang” structures [13, 17, 21]. we re-plan the feedrate on time domain considering jerk constraints in next section.

4 Feedrate re-planning and NURBS interpolation

In this section, the JMEI method is presented to re-plan the feedrate, which can simultaneously consider the influence of acceleration and jerk. Moreover, the “ripple effect” is eliminated.

4.1 Feedrate profile of bell shape

If the feedrate profile has discontinuity during the processing, dents and defects will appear on the surface of workpieces. So the feedrate profile needs to be smoothed, and bell-shape profile are proved to be efficient to limit the acceleration and jerk within the abilities of the machine tool. A complete bell-shape profile covers the acceleration segment, the constant speed segment, and the deceleration segment. Three segments consist of seven substages at most. Here, the acceleration segment is taken as an example, which is divided into three substages or two substages. Three sub-stages are increasing acceleration stage, constant acceleration stage, and decreasing acceleration stage, as shown in Fig. 2a. V1 and V2 denote the starting speed and terminal speed, respectively. Am is the maximum acceleration and Jm is the maximum jerk. If \(|V_{1}-V_{2}| \leq \frac {{A_{m}}^{2}}{J_{m}}\), there is no constant acceleration substage, and the acceleration segment becomes what is shown in Fig. 2b. And \({A_{m}}^{\prime }=\sqrt {|V_{1}-V_{2}|J_{m}}\) denotes the maximum acceleration which can be achieved during the acceleration segments, satisfying \({A_{m}}^{\prime } \leq A_{m}\).

Fig. 2
figure 2

The feedrate, acceleration, and jerk of acceleration segment: a three substages and b two substages

Full size image

4.2 Proposed feedrate scheduling algorithm

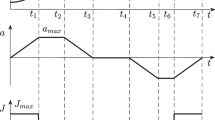
The proposed feedrate scheduling algorithm makes sure that the acceleration and the jerk are limited within allowable ranges, and meanwhile considers the maximum initial feedrate obtained from MTTP. Moreover, the “ripple effect” shown in Fig. 3 also is handled, which represents the overlap between adjacent sharp corners. A sharp corner represents a local minimum point of speed on the feedrate profile. The local minimum points of speed are the results of reducing the speed greatly to satisfy kinds of constraints when the MTTP is solved. Generally, the larger command feedrate is given, the “ripple effect” more easily appears. The reason can be stated as follows. On the one hand, the higher command feedrate leads to more sharp corners on the initial feedrate profile. On the other hand, the distance of two adjacent sharp corners along the tool path becomes smaller when higher command feedrate is required. And the distance is not long enough to complete the feedrate planning of the bell-shape profile. We divide the sharp corners into three types according to the severity of “ripple effect”, that is, the severe overlap (such as corner 4, 5, and 6), the slight overlap (such as corner 1 and 2 ), and no overlap (such as corner 7 and 8).

Fig. 3
figure 3

The overlapping phenomenon

Full size image

Therefore, the JMEI searches the sharp corners, distinguishes the types of “ripple effect,” and re-plans the feedrate near them. To realize these functions, the JMEI method is composed of three main steps: the severe overlap detection, the slight overlap detection, and no overlap replanning.

When the cutter encounters the corners with severe overlap, it cannot even accelerate or decelerate from one sharp corner to another adjacent one according to Fig. 2. The sharp corners involved in severe overlap needs to be combined together through reducing the speed at each corner to the minimum value of all. Algorithm 1 is presented to detect the severe overlap corners and to merge them.

figure a

After applying algorithm 1 to the initial feedrate, the sharp corners involved in severe overlap are detected and merged. For example, corners 4, 5, and 6 are merged into one corner. Hence, the number of sharp corners drop to M + 1. The new arc length array \({\textbf {P}^{\prime }}\) is easily obtained from P by simple addition operation. Let \(\mathbf {{V_{l}}^{\prime }}\) be the new feedrate array at M + 1 sharp corners. And the corresponding array of parameters is stored in \(\mathbf {{m_{l}}^{\prime }}\). As a result, the slight overlap corners and no overlap corners are left. The slight overlap generally consists of two adjacent sharp corners. Take corners 1 and 2 for example, the cutter can accelerate to a certain peak feedrate from corner 1 and then decelerate to corner 2. But the peak feedrate of the cutter cannot reach the boundary value. The peak feedrate attainable needs to be searched. Algorithm 2 is proposed to find the peak feedrate.

figure b

After applying algorithm 2, slight overlap corners have been transformed into no overlap. No overlap means the cutter can reach the boundary value when motions between two adjacent sharp corners. The proper boundary value array \(\mathbf {F_{m}}^{\prime }\) has been determined by algorithm 2. Until now, for the two adjacent j th and (j + 1)th sharp corners, we have known the acc/dec structures of motion, starting feedrate, terminal feedrate, arc length, and boundary value between them. When we re-plan the feedrate according to the method in Section 4.1, the mathematical expression of Fig. 2 can be obtained through solving equations [24, 25]. The re-planned feedrate profile is a function of time, which is convenient to adopt in real-time interpolation.

4.3 Interpolation with feed correction polynomial

Since some NURBS curves are not parameterized by arc length, the mapping relationship between NURBS parameter and the displacement of cutter tip along the curve is not accurate, and feedrate fluctuations appear [26].

In order to avoid the fluctuations of feedrate, feed correction polynomial is employed for interpolation [27]. In view of a non-arc-length parameterized NURBS curve, the adaptive quadrature method [28] are used to split the curve. As a result, a set of (mi, Si) pairs is obtained, where mi is the parameter and Si is the arc length between 0 and mi, i = 1,2,⋯ , N. Different with previous methods, we go on calculating \(\tilde {S}_{j}\) which is the arc length from 0 to \(\tilde {m}_{j}\), where

$$ \tilde{m}_{j}=\frac{m_{k}+m_{k+1}}{2}\quad j,k\in{1,2,\cdots,N-1} $$
(28)

Hence, we have another set of \((\tilde {m}_{j},\tilde {S}_{j})\) pairs, which will be used to test the feed correction polynomial. Then, the arc length is normalized with the following formula:

$$ \lambda_{i}=\frac{S_{i}-S_{0}}{S_{N}-S_{0}} $$
(29)

These pairs of (mi, λi) are used to evaluate the coefficients of the 7-order polynomial. Suppose the polynomial f(λ) is approximated as

$$ f(\lambda)=\tau_{0}\lambda^{7}+\tau_{1}\lambda^{6}+\tau_{2}\lambda^{5}+\tau_{3}\lambda^{4}+\tau_{4}\lambda^{3}+\tau_{5}\lambda^{2}+\tau_{6}\lambda+\tau_{7} $$
(30)

The first and second derivatives with respect to S are deduced as

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} \frac{df}{dS}=\frac{7\tau_{0}\lambda^{6}+6\tau_{1}\lambda^{5}+5\tau_{2}\lambda^{4}+4\tau_{3}\lambda^{3}+3\tau_{4}\lambda^{2}+2\tau_{5}\lambda+\tau_{6}}{S_{N}-S_{0}}\\ \frac{d^{2} f}{dS^{2}}=\frac{42\tau_{0}\lambda^{5}+30\tau_{1}\lambda^{4}+20\tau_{2}\lambda^{3}+12\tau_{3}\lambda^{2}+6\tau_{4}\lambda+2\tau_{5}}{{(S_{N}-S_{0})}^{2}} \end{array} \right. \end{array} $$
(31)

Hence, the parameter value of a NURBS curve m could be predicted with Eq. 30, and the matrix form is written as

$$ \mathbf{\widehat{m}}= \left[ \begin{array}{ll} 0\\ \widehat{m_{1}} \\ \widehat{m_{2}}\\ \vdots\\ \widehat{m_{N}} \end{array} \right] = \underbrace{\left[ \begin{array}{lllll} 0\quad &0\quad &0\quad &\cdots\quad &1\\ {\lambda_{1}^{7}} \quad &{\lambda_{1}^{6}}\quad &{\lambda_{1}^{5}}\quad &{\cdots} \quad &1\\ {\lambda_{2}^{7}} \quad &{\lambda_{2}^{6}}\quad &{\lambda_{2}^{5}}\quad &\cdots\quad &1\\ \vdots\quad &\vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ 1\quad &1\quad &1\quad &\cdots\quad &1 \end{array} \right]}_{\varTheta} \cdot \underbrace{ \left[ \begin{array}{ll} \tau_{0}\\ \tau_{1} \\ \vdots\\ \tau_{6}\\ \tau_{7} \end{array} \right] }_{\mathbf{\tau}} $$
(32)

where \(\mathbf {\widehat {m}}\) denotes the predicted parameter value, Θ the regression matrix, and τ the coefficient vector. Then, the vector of prediction errors is expressed as

$$ \mathbf{e}=\mathbf{m}-\mathbf{\widehat{m}} $$
(33)

In order to gain the optimal τ, the quadratic cost function is defined as

$$ J=\frac{1}{2}\mathbf{e}^{T}\mathbf{e}=\frac{1}{2}(\mathbf{m}-{\varTheta} {{\tau}})^{T}(\mathbf{m}- {\varTheta} {\tau}) $$
(34)

As to the NURBS curve, the differentials of arc length with respect to parameter are deduced as

$$ \left\{ \begin{array}{l} \frac{dS}{dm}=\sqrt{x^{\prime}(m)^{2}+y^{\prime}(m)^{2}+z^{\prime}(m)^{2}}\\ \frac{d^{2}S}{dm^{2}}=-\frac{x^{\prime}(m)x^{\prime\prime}(m)+y^{\prime}(m)y^{\prime\prime}(m)+z^{\prime}(m)z^{\prime\prime}(m)}{x^{\prime}(m)^{2}+y^{\prime}(m)^{2}+z^{\prime}(m)^{2}} \end{array} \right. $$
(35)

Through imposing the boundary conditions at start and end points, the continuity between connecting segments can be ensured. Therefore, the derivatives at the boundary obtained with Eq. 35 should be equal to what are evaluated with Eq. 31. Let mb and me denote the parameters of boundary points. Then, the following expressions can be obtained:

$$ \underbrace{ \left[ \begin{array}{ll} m^{b}\\ (S_{N}-S_{0}){m_{s}^{b}} \\ (S_{N}-S_{0})^{2} m_{ss}^{b}\\ m^{e} \\ (S_{N}-S_{0}) {m_{s}^{e}} \\ (S_{N}-S_{0})^{2} m_{ss}^{e} \end{array} \right]}_{\mathbf{\zeta}} = \underbrace{\left[ \begin{array}{llllllll} 0 &0 &0 &0 \ &0\ &0\ &0\ &1\ \\ 0 &0 &0 &0 \ &0\ &0\ &1\ &0\ \\ 0 &0 &0 &0 \ &0\ &2\ &0\ &0\ \\ 1 &1 &1 &1 \ &1\ &1\ &1\ &1\ \\ 7 &6 &5 &4 \ &3\ &2\ &1\ &0\ \\ 42 &30 &20 &12 \ &6\ &2\ &0\ &0\ \end{array} \right]}_{\varGamma} \cdot \underbrace{\left[ \begin{array}{ll} \tau_{0}\\ \tau_{1} \\ \vdots\\ \tau_{6}\\ \tau_{7} \end{array} \right] }_{\mathbf{\tau}}\\ $$
(36)

where

$$ \left\{ \begin{array}{l} {m_{s}^{b}}=\frac{dS}{dm} |_{m=m^{b}},\ m_{ss}^{b}=\frac{d^{2} S}{dm^{2}} |_{m=m^{b}}\\ \\ {m_{s}^{e}}=\frac{dS}{dm} |_{m=m^{e}},\ m_{ss}^{e}=\frac{d^{2} S}{dm^{2}} |_{m=m^{b}} \end{array} \right. $$
(37)

The constrained optimization problem is constructed by minimizing the cost function Eq. 34 and taking Eq. 36 as the constraint. The method of multipliers is applied to solve the problem, and the following linear equation system is gained:

$$ \left[ \begin{array}{ll} {\varTheta}^{T} {\varTheta} & \quad {\varGamma}^{T}\\ \\ {\varGamma} & \quad \mathbf{0} \end{array} \right] \times \left[ \begin{array}{ll} \mathbf{\tau}\\ {\varLambda} \end{array} \right] =\left[ \begin{array}{ll} {\varTheta}^{T} \mathbf{m}\\ \mathbf{\zeta} \end{array} \right] $$
(38)

where Λ is the multiplier vector. The linear equation system can be easily solved, and coefficients of the polynomial is included in vector τ.

One feed correction polynomial may not reflect the relationship between the parameter and the arc length accurately. If one polynomial can not fit all (mi, Si) pairs, the multiple 7th-order polynomials are adopted to improve the accuracy [4]. In this section, whether multiple polynomials are adopted or not depends on the difference between the predictive value \(\hat {\tilde {m}}_{j}\) and the test value \(\tilde {m}_{j}\). The difference can be computed with

$$ \sum \limits_{j = 1}^{N_{\text{sub}}} \frac{|\tilde{m}_{j}-\hat{\tilde{m}}_{j}|}{N_{\text{sub}}} \leq \varepsilon $$
(39)

where Nsub is the total numbers of \((\tilde {m}_{j},\tilde {S}_{j})\) pairs and ε is the tolerance. If Eq. 39 is not satisfied, the (mi, Si) pairs are divided into two sets of the same size, so is the \((\tilde {m}_{j},\tilde {S}_{j})\) pairs. Then, the fitting and testing steps above are implemented again. The subdivision terminates when Eq. 39 is satisfied or (mi, Si) pairs are equal to the order of polynomial.

Figure 4 shows the comparison of three interpolation method: the first-order Taylor approximation, the improved robust fast interpolator [5], and the proposed interpolation method. The maximum fluctuation ratio [29, 30] of the three methods are 2.48%, 0.25%, and 2%, respectively. From Fig. 4, the presented method get the minimal fluctuations.

Fig. 4
figure 4

Comparison of three interpolation techniques

Full size image

5 Simulation and experimental examples

Two curves are used to evaluate the performance of the proposed method. One is a star pattern for simulation. The simulation is performed by MATLAB installed on a PC. The PC is equipped with 4G memory and AMD A8 processor. The other is a fan pattern for experiment. The experiment is implemented on a typical 3-axis CNC machine.

5.1 Simulation results for star curve

The star curve is a single NURBS curve with five control points as shown in Fig. 5a. In this example, the bound of feedrate is set to 500 mm/s and the tolerance of chord error is set to 0.1 μ m. The maximum acceleration/deceleration of each axis is 2500 mm/s2, and the maximum jerk is 50000 mm/s3. The tracking error bound for each axis is set to 0.05 mm. The contour error bound is set to 0.05mm, too. For comparison, the feedrate is generated with three methods: sharp corner detection (SCD) [6], confined tracking error (CTE) [13], and the proposed scheme (TFSS).

Fig. 5
figure 5

Simulation results of star curve with SDC, CTE, and TFSS. a Star curve. b Resultant feedrate profiles. c Axial feedrate profiles. d Axial acceleration profiles. e Axial jerk profiles. f Chord error profiles

Full size image

Figure 5b shows the feedrate profiles planned by the three methods. Compared with the profile obtained by CTE, SCD, and TFSS can both get smoother feedrate which is favorable to improve processing quality. Figure 5c shows the profiles of axial feedrates, and the axial acceleration profiles are plotted in Fig. 5d. The accelerations of CTE always reach bounds, while acceleration profiles of the other two methods don’t. That is because CTE does not consider jerk limits but tracking errors which are easily transformed into linear constraints. Hence, the jerk profiles of CTE exceed the boundary value as shown in Fig. 5e. The jerk profiles of SCD and TFSS are bounded, since the jerk-limited module is introduced. The profiles of chord errors are evaluated according to Eq. 7, which are shown in Fig. 5f. The chord error profile of CTE is still beyond the boundary value because the chord error constraint is not considered. The chord error profile of SCD far below the boundary value, since the conservative feed, is adopted. From these figures, the TFSS scheme has the best performance.

Other comparison of performances are all listed in Table 1. Both the planning time and machining time are listed. The whole time spent on machining and planning by the three methods are 1.902 s, 1.243 s, and 1.693 s. The CTE method spends shortest time on machining. That is because it has highest feed owing to the unlimited jerks. The SCD method takes the least planning time owing to no optimization progress. Therefore, the feed of SCD is not optimized, which leads to the conservative feed and long machining time. Comparing with the other two methods, the TFSS takes both processing time and planning time into account. Certainly, we can further decrease the planning time by reducing the grid points. But too few grid points may lead to incorrect results. Of course, adaptive strategy can be used to obtain ideal grid number. In the simulation, 252 grids are adopted for both the CTE and TFSS. In addition, the contour errors of three methods are also estimated according to Zhang et al. [17]. The contour errors of SCD (without dynamics module) and TFSS are very similar. They can all get the smaller contour error than CTE.

Table 1 Performance comparison for SCD, CTE, and TFSS for the star curve
Full size table

5.2 Experimental results for fan curve

The experiment is implemented on a typical 3-axis CNC machine, which was updated to meet the needs of implementing new algorithms. The structure of the experimental platform is illustrated in Fig. 6. The reference positions for each axis is generated by a PC with a MATLAB environment. Then, these positions are sent to the motion controller equipped with PID algorithm through a parallel communication card installed in a PCIE slot. In this experiment, the maximum axial acceleration of the platform is set to 800 mm/s2 and the maximum axial jerk is set to 1000 mm/s3. The chord error tolerance is set to 1 μ m. And the real-time machining is not considered, all the reference positions are generated by MATLAB off-line. The processed curve is a fan-shape pattern which has 45 control points as shown in Fig. 7a.

Fig. 6
figure 6

The experimental platform

Full size image
Fig. 7
figure 7

Experimental results of fan curve based on TFSS when the maximum feedrate is set to 4800 mm/min and 6000 mm/min. a Fan curve. b Resultant feedrate profiles. c Profiles of resultant acceleration, resultant jerk, and chord error when the maximum feedrate is 4800 mm/min. d Profiles of resultant acceleration, resultant jerk, and chord error when the maximum feedrate is 6000 mm/min

Full size image

In order to fully evaluate the effectiveness of the proposed scheme, the command feedrate is set to 4800 mm/min and 6000 mm/min in succession. The resultant feedrate profiles of two different command speeds are represented with solid lines in Fig. 7b, where MTTP constraints are indicated with dashed lines. The machining time for two command feedrate is 5.554 s and 4.847 s, respectively. The lower command feedrate takes 14.5% more time than a higher one. Figure 7 c and d show resultant accelerations, resultant jerks, and chord errors of two different command feedrates, respectively. In the experiment, the dynamics of axes are not identified. Hence, the chord error estimated is applied for investigating the accuracy. The chord errors for two command feedrates are far lower than the required tolerance. The maximum chord error for lower feedrate is reduced 10.3% than that for a higher one. They are 0.122 μ m and 0.136 μ m, respectively. So the feedrate should be chosen based on the trade off between machining time and precision.

6 Conclusion

In this paper, a complete scheme of smooth minimum time trajectory planning is proposed, and the numerical simulation and the experiment are employed to verify the effectiveness and practicability of the proposed scheme. Initially, the MTTP problem for curve machining is discretized with the direct transcription method, and then the discrete MTTP problem is transformed into linear programming by employing a proper objective function. The linear programming form of MTTP could greatly improve the efficiency of solving MTTP. Moreover, jerk constraints are not considered in MTTP, which further reduce the computation cost. To smooth the feedrate profile, the jerk-limited method of eliminating interaction (JMEI) is applied to re-plan the feedrate. Since JMEI is introduced, the planning problem in the parameter domain is transferred to that in the time domain. A bridge between optimal programming in the parameter domain and real-time interpolation is built by this transferring process. Therefore, the interpolation of a feed correction polynomial can be used to minimize the fluctuations. Finally, results of simulation and experiment demonstrate that the proposed scheme can balance time consumed and precision.