1 Introduction

In nature and engineering, cylindrical structures immerged in cross flows such as wind and water current are ubiquitous, such as the trunk of trees, stalk of aquatic or terrestrial plants, overhead electric transmission lines, offshore risers, tubes in power plant and heat exchangers, tall chimneys and cables of cable-stayed bridges, to name a few. In general, Reynolds numbers of incoming flows with respect to the diameters of these cylindrical structures are well above the threshold of vortex shedding, leading to oscillating fluids loads and flow-induced vibrations (FIVs). Because FIVs may cause fatigue problem in long term or broken and damage in short term, studying the underlying physics of fluid–structure interaction (FSI) of these cylindrical structures is of great importance [1].

In last decades, FIV of an isolated cylindrical structure has been widely investigated, as seen in reviews by Sarpkaya [2], Williamson and Govardhan [3], and Williamson and Govardhan [4]. For an isolated circular cylinder, ‘lock-in’ appears when the structure’s natural frequency approaches the vortex shedding frequency. In ‘lock-in’ region, the vibrating amplitude is amplified significantly, and the structure’s vibration dominates the vortex shedding process. For Y-DOF model only allowing transverse response, there are two branches on the amplitude curve at high Reynolds numbers and large mass ratio, namely the ‘initial’ and ‘lower’ branches, which are related to the 2S and 2P vortex modes, respectively [5, 6]. At small mass ratio, an ‘upper’ branch with a maximum amplitude over 1D appears, which generates the deformed 2P vortex mode in the wake [7,8,9]. At low Reynolds number, however, only the ‘initial’ and ‘lower’ branches can be observed, and the maximum amplitude is always below 0.6D[3]. For XY-DOF model having both streamwise and transverse responses, the structure exhibits slightly larger response than the Y-DOF model following an ‘8’ trajectory [10,11,12], and a ‘super-upper’ branch with a maximum transverse amplitude up to 1.5D can be observed along with a 2T vortex mode when the mass ratio drops below \(m^{*}=6\) [13, 14].

In various engineering applications, cylindrical structures usually appear in group and undergo strong flow interference. To study FIVs in such scenario, flow fields and dynamic behaviors of the two-cylinder model have been studied extensively. Zdravkovich [15] , Xu and Zhu [16], and Zhou and Yiu [17] investigated systematically the unsteady flow past two tandem stationary circular cylinders at different Reynolds numbers and center-to-center distances. According to the flow patterns observed, three flow regimes are roughly divided, that is, ‘extended body,’ ‘reattachment’ and ‘co-shedding’ regimes. Since fluid loads on the two cylinders change significantly among different flow regimes, dynamic behaviors of the two cylinders are quite different in three regimes as well. Brika and Laneville [18], Hover and Triantafyllou [19], Assi et al. [20,21,22], Carmo et al. [23] and Mysa et al. [24, 25] investigated FIV of an elastically supported or flexible circular cylinder behind a fixed circular cylinder. The downstream one was found to exhibit much larger transverse response than the one-cylinder model. In ‘co-shedding’ regime, the downstream cylinder usually undergoes VIV at small \(U_{\mathrm{r}}\) while galloping-like wake-induced vibration (WIV) at high \(U_{\mathrm{r}}\), which is characterized by the gradual built-up of vibration amplitude. In ‘extended body’ and ‘reattachment’ regimes, the onset \(U_{\mathrm{r}}\) of WIV reduces and combined VIV and WIV or sole WIV occurs. Zdravkovich [26], Laneville and Brika [27], Papaioannou et al. [28], Prasanth and Mittal [29], Borazjani and Sotiropoulos [30], Huera-Huarte and Bearman [31], Lin et al. [32], Griffith et al. [33] and Qin et al. [34] investigated the scenario that both cylinders are free to oscillate. In ‘co-shedding’ regime, the upstream cylinder exhibits similar response to the one-cylinder model, while the downstream cylinder experiences larger-amplitude response as in the scenario behind a fixed upstream cylinder. In ‘extended body’ and ‘reattachment’ regimes, the upstream cylinder could display galloping-like vibration and attain larger vibration amplitude, depending on the flow state in the gap between two cylinders.

For the two-tandem-cylinder model, an interesting phenomenon observed is WIV, which leads to more violent response on the downstream cylinder. To explain the underlying physics of WIV, Assi et al. [21, 22] indicated that WIV of the downstream cylinder is dependent on the unsteady wake of the upstream cylinder, and WIV occurs when the ‘wake stiffness’ dominates over the structure stiffness at high \(U_{\mathrm{r}}\). Carmo et al. [23] and Mysa et al. [23] stated that WIV of the downstream cylinder is highly related to the shift of its front stagnation point under effect of the unsteady wake behind the upstream cylinder.

Based on studies on the two-cylinder model, some investigations have also been conducted on FIVs of the three-cylinder model. Yu et al. [35] computed FIVs of three tandem circular cylinders at \(L/D=4\) and \(\text {Re}=\)100 and 150. It was found that the response of the three-cylinder model is quite different from the two-cylinder model, and the maximum transverse vibration amplitude is increased by about 25% compared with the two-cylinder model under the same condition. Shaaban and Mohany [36] studied numerically FIVs of three tandem circular cylinders in uniform stream with \(\text {Re}=200\). In their research, an elastically supported cylinder was put behind two fixed cylinders; the distance between the first and third cylinders was fixed at 4D, while the spacing between the first and second cylinders varied in 1.05D–2.95D. They found that the most downstream cylinder experiences more violent response than the case with only one fixed cylinder upstream. Chen et al. [37] simulated dynamic responses of three tandem circular cylinders at \(L/D= \) 1.2–5 and \(\text {Re}=100\). As L/D is increased, two types of vibrating modes were revealed, namely WIV at \(L/D=1.2\) and VIV at \(L/D=\)1.5–5.

Recently, Hosseini et al. [38] conducted numerical studies on the case with more circular cylinders. In their work, effects of cylinder number (\(n=\) 2–100) and center-to-center gap (\(L/D=\) 1.1–10) on the flow around an array of stationary circular cylinders are investigated systematically at \(\text {Re}< 200\), and a self-similar cascade of flow regimes was recorded, namely fluctuation development, vortex shedding, two-row vortex structure (2RVS) and breaking of 2RVS into fluctuation of longer length scale. As long as the tandem array contains sufficient cylinders, this cascade repeats as the flow progresses downstream. For cases with larger gap (\(L/D> 4.4\)) and \(\text {Re}< 200\), a complete cascade of flow regimes was observed when the total number of cylinders was increased beyond four. It means that, to understand dynamic behaviors of an array of tandem circular cylinders under effect of the cascade of flow regimes, FIV model containing at least five cylinders should be investigated. To the best of our knowledge, however, little work has been done on this subject.

In present paper, WIVs of five circular cylinders in tandem arrangement are studied numerically. In our five-cylinder model, all five cylinders are elastically mounted and allowed to oscillate in both streamwise and transverse directions. The Reynolds number and damping coefficient are fixed at \(\text {Re}=100\) and \(\zeta =0\), respectively. The mass ratio is set as \(m^{*}=5\), 10 and 15, the center-to-center distance is changed among \(L/D=4\), 6 and 8, and the reduced velocity varies in \(U_{\mathrm{r}}=\) 2–18. By numerical experiments, dynamic responses of the tandem circular cylinders in one cascade of flow regimes as mentioned above are analyzed in detail using the computed fluid loads, vibrating amplitudes, vibrating frequencies, flow patterns and their relationships. Special attention is paid to the sub-harmonic WIV of the downstream cylinders. This work could reveal new dynamic characteristics of an array of tandem circular cylinders under effect of flow interference, which is insightful for understanding FIVs of a group of cylindrical structures encountered frequently in various engineering applications.

Fig. 1
figure 1

Mechanics model of FIVs of five tandem circular cylinders in a cross flow

Full size image

2 Mathematical formulation

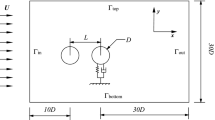
Figure 1 illustrates the FIV model involving five tandem circular cylinders. As seen in the figure, the incoming flow is uniform with a streamwise velocity of U. All cylinders are elastically mounted on fixed foundations and allowed to oscillate in both transverse and streamwise directions. Five cylinders have the same mass ratio, damping coefficient and natural frequency. The distance between the neighbor cylinders is L.

For an isolated cylinder, Barkley and Henderson [39] found that the wake turns to weakly three-dimensional at \(\text {Re} \approx 190\). For two tandem circular cylinders, Carmo et al. [40] revealed that the flow is still two-dimensional (2D) at \(\text {Re}< 180\). In present five-cylinder model as shown in Fig. 1, the Reynolds number of the incoming flow is set as \(\text {Re}=100\), which is well below above critical Reynolds numbers. Therefore, the 2D incompressible Navier–Stokes equations are employed as the governing equations of the flow field, the non-dimensional form of which can be expressed as

$$\begin{aligned}&\displaystyle \frac{\partial u_{1}}{\partial x} +\frac{\partial u_{2}}{\partial y}=0 \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \frac{\partial u_{1}}{\partial t}+u_{1} \frac{\partial u_{1}}{\partial x} +u_{2} \frac{\partial u_{1} }{\partial y}=-\frac{\partial p}{\partial x} +\frac{1}{Re}\left( {\frac{\partial ^{2}u_{1} }{\partial x^{2}} +\frac{\partial ^{2}u_{1} }{\partial y^{2}}} \right) \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \frac{\partial u_{2} }{\partial t}+u_{1} \frac{\partial u_{2}}{\partial x} +u_{2} \frac{\partial u_{2} }{\partial y}=-\frac{\partial p}{\partial y} +\frac{1}{Re}\left( {\frac{\partial ^{2}u_{2} }{\partial x^{2}} +\frac{\partial ^{2}u_{2} }{\partial y^{2}}} \right) \end{aligned}$$
(3)

The vibration of each circular cylinder is described by the spring–mass–damper model. The non-dimensional equations in streamwise and transverse directions can be expressed, respectively, as

$$\begin{aligned}&\ddot{{X}}+4\pi F_{\mathrm{N}} \zeta \dot{{X}}+({2\pi F_{\mathrm{N}}})^{2}X =\frac{2C_{\mathrm{D}}}{\pi m^{*}} \end{aligned}$$
(4)
$$\begin{aligned}&\ddot{{Y}}+4\pi F_{\mathrm{N}} \zeta \dot{{Y}}+\left( {2\pi F_{\mathrm{N}} } \right) ^{2}Y=\frac{2C_{\mathrm{L}}}{\pi m^{*}} \end{aligned}$$
(5)

The flow field governed by Eqs. (1)–(3) and the structure field governed by Eqs. (4) and (5) interact with each other. The drag and lift forces, i.e., \(C_{\mathrm{D}}\) and \(C_{\mathrm{L}}\), in Eqs. (4) and (5) are obtained from the flow field. In turn, the boundary conditions of Eqs. (1)–(3) are decided by the displacements (X and Y) and velocities (\(\dot{X}\) and \(\dot{Y}\)) on each cylinder. On the fluid–cylinder interfaces, the displacements, velocities and stresses of the flow and structure field are identical.

3 Numerical methods

To simulate precisely FIV of each cylinder, three physical processes should be carefully treated, namely the flow around the cylinder array, the vibration of each cylinder and the interaction between the flow and structure. Unlike the traditional flow problems, in the present model the flow boundaries corresponding to five cylinders’ surfaces move with time due to FIVs. To solve this problem, an implicit flow solver proposed in our previous studies is employed to compute Eqs. (1)–(3), which combines the modified characteristic-based split (CBS) finite element method (FEM) for moving-boundary flows [41], dual-time stepping (DTS) method [42] and spring analogy technique [43]. In this flow solver, following the CBS FEM, Eqs. (1)–(3) are discretized in time first by three steps and then integrated spatially by the standard Galerkin FEM employing linear triangular elements. Subsequently, Eqs. (4) and (5) are solved implicitly by the Generalized-\(\alpha \) method [44]. Finally, the loosely coupled partitioned scheme is introduced to combine the flow and structure solvers. In laminar flow regime and at high structure mass ratio, such FSI solution procedure has been proved to have good stability and accuracy in simulating VIV of a membrane wing [45,46,47], VIV of a flexible splitter plate in the wake of a cylinder [48, 49], FIV of a circular-plate assembly [50] and WIVs of two circular cylinders in tandem arrangement [51]. More details of the employed FSI solution procedure can be found in references [45, 50, 52], and will not be discussed in detail here.

4 Code validations

4.1 Flow past five fixed circular cylinders in tandem

To examine the accuracy of our flow solver, flow around five fixed circular cylinders in tandem arrangement is computed first. The Reynolds number and gap distance are set as \(\text {Re}=200\) and \(L/D=5\), respectively, which are as same as those in the five-cylinder model reported by Hosseini et al. [38] for purpose of comparison. For this model, a completely varying process of flow structures including the vortex shedding, the 2RVS and breaking of 2RVS into fluctuation of longer length scale has been observed. Figure 2 illustrates the computational model for this flow problem. For convenience, the five cylinders are marked briefly as C1, C2, C3, C4 and C5, respectively.

Three meshes are employed to simulate this flow model to obtain a grid-independence result, with a fixed dimensionless time step of \(\Delta t=0.01\). Table 1 provides grid information along with the computed fluid loads (\(C_{\mathrm{L},\mathrm{max}}\), \(C_{\mathrm{D},\mathrm{mean}}\)) and dominant vortex shedding frequency (St) at each cylinder, which are also displayed in Fig. 3. As shown in Table 1 and Fig. 3, the numerical results are barely improved when the grid density is further increased from Mesh_02 to Mesh_03. Moreover, the numerical results obtained by our flow solver agree well with those computed by Hosseini et al. [38].

Fig. 2
figure 2

Solution domain and boundary conditions for the five-stationary-cylinder model

Full size image
Table 1 Numerical results from the five-stationary-cylinder model at \(\text {Re} = 200\) and \(L/D = 5\)
Full size table
Fig. 3
figure 3

Fluid loads and vortex shedding frequency from the five-stationary-cylinder model at \(\text {Re}=200\) and \(L/D=5\)

Full size image

4.2 FIVs of one and two-tandem circular cylinders

To validate the FSI solver employed, FIVs of the one-cylinder and two-tandem-cylinder models are computed next. Figure 4 shows the flow domains and boundary conditions for two cases. As seen in two figures, the computational models are very similar to that in Fig. 2 except that the cylinder is no longer stationary and the flow has same velocity with the oscillating cylinder on the fluid–cylinder interface.

Fig. 4
figure 4

Solution domain and boundary conditions for FIVs of the elastically supported circular cylinder: a one-cylinder model, and b two-tandem-cylinder model

Full size image

For the one-cylinder model, the flow and structural parameters are defined as Re \(=100\), \(m^{*}=10\), \(U_{\mathrm{r}} =6\) and \(\zeta =0\). For the two-tandem-cylinder model, the flow and structural parameters are Re \(=100\), \(m^{*} =10\), \(L/D=5.5\), \(U_{\mathrm{r}} =5.5\) and \(\zeta =0\). In each case, the grid-independence test is conducted with the time step always kept constant at \(\Delta t=0.01\). Tables 2 and 3 present the mesh information and computed vibration parameters of the one-cylinder and two-cylinder models, respectively. As displayed in two tables, for the one-cylinder and two-cylinder models the grid-independence results are obtained at Mesh_12 and Mesh_22, respectively. Again, our results exhibit a very good consistency with those computed by other researchers [29, 53, 54].

Table 2 Numerical results of FIV of the one-cylinder model
Full size table
Table 3 Numerical results of FIVs of the two-tandem-cylinder model
Full size table

5 FIVs of five tandem circular cylinders

Using validated FSI solution procedure, FIVs of five tandem circular cylinders with large gap distance are studied. For purpose of comparison to the one-cylinder model and two-cylinder model as presented in Sect. 4.2, the Reynolds number of this five-cylinder model is fixed at Re \(=100\). The mass ratio is changed among \(m^{*}=5\), 10 and 15, the dimensionless gap distance is set as \(L/D=4\), 6 and 8, and the reduced velocity varies in \(U_{\mathrm{r}} =\) 2–18. Moreover, the damping coefficient is set as \(\zeta =0\) to induce large-amplitude response on each cylinder.

5.1 Grid independence test

Figure 5 illustrates the computational model for FIV of the five-tandem-cylinder model. As seen in the figure, the solution domain and boundary conditions are identical to those shown in Fig. 2, except that the location and velocity of the flow-cylinder interface become dependent on the cylinders’ responses. To examine the effect of grid density on this model, responses of five cylinders at Re \(=100\), \(m^{*} =10\), \(\zeta =0\), \(L/D=6\) and \(U_{\mathrm{r}}=5.5\) are computed by three meshes of different grid densities. Table 4 presents the mesh information and calculated maximum transverse amplitude (\(Y_{\mathrm{max}}\)) of each cylinder. Figure 6 displays the time histories of transverse displacements of C1 and C5 in \(t=\) 600–800. As shown in Table 4 and Fig. 6, the improvement turns to very limited between Mesh_32 and Mesh_33. Therefore, Mesh_32 is applied to the rest of simulations. As shown in Fig. 7, the grids around and behind the cylinder array are refined to compute more precisely the vortex structures in these regions.

Fig. 5
figure 5

Computational model for FIVs of the five-tandem-cylinder model

Full size image
Table 4 Numerical results of FIVs of the five-tandem-cylinder model at Re \(=100\), \(m^{*}=10\), \(\zeta =0\), \(L/D=6\) and \(U_{\mathrm{r}} =5.5\)
Full size table
Fig. 6
figure 6

Instantaneous transverse displacements at Re \(=100\), \(m^{*}=10\), \(\zeta =0\), \(L/D=6\) and \(U_{\mathrm{r}} =5.5\): a C1 and b C5

Full size image
Fig. 7
figure 7

Computational mesh (Mesh_32) for FIVs of the five-tandem-cylinder model

Full size image

5.2 Dynamic response

Figure 8 displays the transverse vibrating amplitude and frequency of each cylinder at \(\text {Re}=100\), \(L/D=6\), \(m^{*}=10\), \(\zeta =0\) and \(U_{\mathrm{r}}=\) 2–18. As seen in Fig. 8a, all five cylinders exhibit VIV-like vibrations with first-increase-then-decrease vibration amplitude, while the galloping-like response featured by amplitude build-up with respect to the reduced velocity does not appear. In \(\textit{U}_{\mathrm{r}}=\) 2–4.5, all five cylinders exhibit FIVs of negligible amplitudes. The responses of C1–C4 are dominated by the vortex shedding frequency of C1 (\(\text {St}_{1}=0.155\)), while the vibration of C5 is dominated by the sub-harmonic frequency of \(\text {St}_{2}=0.0775\). In \(\textit{Ur}=\) 4.5–5.2, the dominant vibration frequencies of all five cylinders jump to the natural frequency. C1 attains the maximum transverse displacement of \(Y_{\mathrm{max}}=0.58D\) at \(U_{\mathrm{r}}=5.2\), while C2–C5 exhibit local peaks in their \(Y_{\mathrm{max}}\) curves. For C1–C4, their vibration frequencies begin to be locked to the natural frequency. For C5, however, the vibration frequency drops back to the sub-harmonic branch at \(U_{\mathrm{r}}=5.2\). As Ur further increases, the dominant vibration frequencies of C1–C4 decrease simultaneously with the natural frequency, while the dominant vibration frequency of C5 first increases slowly toward \(\text {St}_{2}=0.0775\) while then jumps to the natural frequency at \(U_{\mathrm{r}}=6.8\). Meanwhile, C2–C5 obtain large-scale responses sequentially. At \(U_{\mathrm{r}}=\)7, the transverse amplitude of C2 jumps to the high branch, attaining a maximum value of \(Y_{\mathrm{max}}=1.05D\), and second local peaks appear in the \(Y_{\mathrm{max}}\) curves of C3–C5. Near \(U_{\mathrm{r}}=8\), C3 attains its maximum transverse amplitude of \(Y_{\mathrm{max}}=1.1D\), which also induces local peaks on the \(Y_{\mathrm{max}}\) curves of C4 and C5. At \(U_{\mathrm{r}}=8.8\), the transverse response of C4 jumps to the high branch, attaining a transverse amplitude of \(Y_{\mathrm{max}}=1.19D\). At \(U_{\mathrm{r}}=9.5\), the response of C5 is amplified greatly, leading to a transverse displacement of \(Y_{\mathrm{max}}=1.29D\). At \(U_{\mathrm{r}}=12\), C4 and C5 attain the maximum transverse amplitudes of \(Y_{\mathrm{max}}=1.34D\) and 1.49D, respectively. Once the reduced velocity rises above the critical point, the synchronization of each cylinder ends. For different cylinders, the critical points are different. As illustrated in Fig. 8b, C1 leaves the ‘lock-in’ regime at \(U_{\mathrm{r}}=8.2\) where its dominant vibration frequency jumps back to \(\text {St}_{1}=0.155\). For C2, the synchronization ends at \(U_{\mathrm{r}}=14\) and the vibration frequency also turns back to \(\text {St}_{1}=0.155\). For C3, the vibration frequency first approaches the sub-harmonic branch of \(\text {St}_{2}=0.0775\) at \(U_{\mathrm{r}}=14\) while then jumps back to \(\text {St}_{1}=0.155\) at \(U_{\mathrm{r}}=15\). For C4 and C5, however, their dominant vibration frequencies eventually approach \(\text {St}_{2}=0.0775\) after they depart from the natural frequency curve.

In general, C1–C3 exhibit similar dynamic response, which is dominated by the structural natural frequency in the ‘lock-in’ region while by \(\text {St}_{1}=0.155\) out of the ‘lock-in’ region. This is consistent to the vibration of the three-cylinder model at Re \(=100\) and \(L/D=5\) as reported by Chen et al. [37]. Unlike C1–C3, C5 enters the ‘lock-in’ regime at a higher \(U_{\mathrm{r}}\) and experiences a lower oscillating frequency of about \(\text {St}_{2}=0.0775\) in the un-synchronization region, which is near the subharmonic of the usual Strouhal number of \(\text {St}_{0}=0.17\). FIV of C4 can be taken as a transition between above two responses. In the pre-synchronization region, C4 vibrates at a dominant frequency of \(\text {St}_{1}=0.155\). In the post-synchronization region, however, its vibration is dominated by \(\text {St}_{2}=0.0775\). Such sub-harmonic WIV of C4 and C5 has not been found in the two-cylinder or three-cylinder model before.

Fig. 8
figure 8

Responses of the five-tandem-cylinder model at \(\text {Re}=100\), \(L/D=6\) and \(m^{*}=10\): a maximum transverse vibration amplitude, b dominant transverse vibration frequency

Full size image

5.3 Fluid loads

To understand the sub-harmonic response of C4 and C5 in the five-tandem-cylinder model, the fluid load on each cylinder is studied in this section. Figure 9 illustrates the oscillating frequency of the lift on each cylinder, where \(f_{\mathrm{CL}}\) is the frequency components extracted from the oscillating lift coefficient using Fast Fourier Transform (FFT) method and the contour with color shifting from white to black indicates the dimensionless amplitude of each frequency component. Since the lift on each cylinder is strongly associated with the vortex shedding process, \(f_{\mathrm{CL}}\) can also be taken as the vortex shedding frequency.

As shown in Fig. 9a, the oscillating frequency of \(C_{\mathrm{L}}\) on C1 has a similar trend to its vibration frequency as seen in Fig. 8b. In synchronization region, \(f_{\mathrm{CL}}\) jumps to the natural frequency, while in the un-synchronization state \(f_{\mathrm{CL}}\) approaches \(\text {St}_{1}=0.155\). At most points only one frequency component dominates the lift of C1, while near the upper boundary of synchronization (\(U_{\mathrm{r}}=\) 7.5–8.5) some harmonic frequency components appear. As illustrated in Fig. 9b, the tendency of C2’s \(f_{\mathrm{CL}}\) is almost the same with C1’s, except that two sub-harmonic frequency components are observed near the lower boundary of synchronization (\(U_{\mathrm{r}}=\) 4.5–5). As displayed in Fig. 9c, more harmonic frequency branches appear in the spectrogram of C3’s \(C_{\mathrm{L}}\). In \(U_{\mathrm{r}}=\) 5.5–6.5 and \(U_{\mathrm{r}}=\) 13–15, the effect of \(\text {St}_{2}=0.0775\) begins to emerge. In \(U_{\mathrm{r}}=\) 8–13, three higher harmonic branches and three lower harmonic branches are observed above and below the \(\text {St}_{1}\) line, respectively. As displayed in Fig. 9d, for C4 the strength of the sub-harmonic component (\(\text {St}_{2}=0.0775\)) is increased significantly. In \(U_{\mathrm{r}}=\) 2–4.5, the effect of \(\text {St}_{2}=0.0775\) becomes comparable to that of \(\text {St}_{1}=0.155\), while in \(U_{\mathrm{r}}=\) 14–18 \(\text {St}_{2}=0.0775\) starts to dominate the lift oscillation of C4. Besides, a new branch with three times the natural frequency appears near the top right corner of Fig. 9d. As observed in Fig. 9e, for C5 the influence brought by frequency component \(\text {St}_{1}=0.155\) decreases a lot, while \(\text {St}_{2}=0.0775\) dominates the lift oscillation in the pre and post ‘lock-in’ regions.

Therefore, for C1–C3 the lift load is dominated by \(\text {St}_{1}=0.155\) near the Strouhal number in the un-synchronization region and by the natural frequency of the structure in the synchronization region, respectively, leading to the same vibrating frequencies in two regions. For C4, a sub-harmonic frequency (\(\text {St}_{2}=0.0775\)) of comparable strength to \(\text {St}_{1}=0.155\) appears in the lift spectrum and results in the sub-harmonic vibration in the post ‘lock-in’ region. For C5, \(\text {St}_{2}=0.0775\) dominate the lift oscillation over \(\text {St}_{1}=0.155\), leading to the sub-harmonic response in pre- and post-synchronization region.

Fig. 9
figure 9

Spectrograms of lift coefficient of each cylinder with respect to \(U_{\mathrm{r}}\) at \(\text {Re}=100\), \(L/D=6\) and \(m^{*}=10\): a C1; b C2; c C3; d C4; e C5

Full size image

5.4 Flow patterns

To understand the sub-harmonic lift oscillating frequency on C4 and C5, instantaneous flow pattern around the cylinder array is further analyzed. Figure 10 displays the vorticity contours around the five-tandem-cylinder system at representative reduced velocities of \(U_{\mathrm{r}}=4\), 5.2, 7, 7.7, 8.8, 9.5, 12 and 14, when the cylinder having the largest transverse amplitude is moving up and passing the equilibrium state with \(Y=0\) and \(\dot{Y}>0.\) For comparison, the instantaneous flow pattern around five stationary cylinders is also given in Fig. 10a.

As seen in Fig. 10a, for the case with five stationary cylinders at \(\text {Re}=100\) and \(L/D=6\), C1 behaves as an isolated cylinder and sheds a pair of vortices with opposite signs alternatively, generating the 2S vortex mode in the first gap. Subsequently, the vortices formed in the first gap impinge on the second cylinder (C2), merge with the shear layers from C2 itself and then separate from C2, forming a two-row vortex structure (2RVS). As reported by Hosseini et al. [55], 2RVS is convectively instable and can only carry disturbances downstream as long as they are not close to C2. Therefore, C3 does not exhibit influence on the upstream flow. Additionally, because the flow in the wake centerline of C2 is almost stationary and C3 further decreases the flow velocity, the presence C3 does not bring significant disturbance to the downstream flow either. As a result, C3 is completely immersed in the two-row vortex structure. As transported downstream, 2RVS begins to fluctuate due to the secondary instability (breaking of 2RVS), resulting in the elongated recirculation in the gap behind C4. Finally, 2RVS completely disappears near C5, and an elongated 2S vortex mode appears in C5’s wake. In summary, a cascade of flow regimes around the five-tandem-cylinder model includes 2S, 2RVS, breaking of 2RVS and elongated 2S. As reported by Hosseini et al. [38], if we put more cylinders behind C5, such cascade of flow regimes repeats, forming a self-similarity flow pattern around the cylinder array.

Fig. 10
figure 10

Instantaneous vorticities around five circular cylinders in tandem at \(\text {Re}=100\), \(L/D=6\), \(m^{*}=10\) and a stationary; b \(U_{\mathrm{r}} =4\); c \(U_{\mathrm{r}} =5.2\); d \(U_{\mathrm{r}} =7\); e \(U_{\mathrm{r}} =7.7\); f \(U_{\mathrm{r}} =8.8\); g \(U_{\mathrm{r}} =9.5\); h \(U_{\mathrm{r}} =12\); i \(U_{\mathrm{r}} =14\)

Full size image

As seen in Fig. 10b, at \(U_{\mathrm{r}} =4\) FIVs of all five cylinders are too weak to show significant effect on the flow around them. Therefore, the flow pattern in Fig. 10b is close to that in the stationary scenario as seen in Fig. 10a. At \(U_{\mathrm{r}}=5.2\), C1 attains the maximum transverse amplitude and the vortex street between C1 and C2 becomes wider than that at \(U_{\mathrm{r}}=4\), as observed in Fig. 10c. In this case, the vortices behind C1 no longer impinge directly on C2 but pass by its upper and lower sides. As a result, a broader 2RVS appears behind C2, and the length scales of the fluctuation structure behind C4 and the elongated 2S vortex structures behind C5 increase accordingly. At \(U_{\mathrm{r}}=7\), a large-amplitude response of C2 is excited. As shown in Fig. 10d, C2 begins to shed vortices independently. The vortices shed from C2 merge with the vortices shed from C1, generating a pseudo 2S vortex mode of the tadpole-like configuration behind C2. Subsequently, the ‘tail’ part of merged vortex impinges directly on C3 while the ‘head’ part flows around it, generating a 2RVS behind C3. Compared with that at \(U_{\mathrm{r}}=5.2\), the 2RVS in this case is much wider, so that it completely embraces C4 and C5 and extends to the far wake. At \(U_{\mathrm{r}}=7.7\), C3 also exhibits large-scale response. As illustrated in Fig. 10e, the interaction between C3 and the vortices behind C2 is more significant and the shear layers on C3 itself begin to shed. Under C3’s disturbance, the 2RVS becomes more unstable and breaks just behind C5, generating the elongated 2S vortex mode in the near wake. At \(U_{\mathrm{r}}=8.8\), the flow pattern around the cylinder array becomes more complex. With drops of the vibration amplitudes of C1 and C2, the interference between the vortices behind C1 and shear layers on C2 is amplified, as displayed in Fig. 10f. Two vortex pairs are shed into the gap behind C2 in each period, indicating the appearance of 2P vortex mode. Subsequently, the 2P vortex structure impinges on C3 and results in the pseudo 2S vortex mode behind it. Finally, 2RVS forms behind C4 due to its large-scale response and breaks into the 2S vortex mode behind C5. At \(U_{\mathrm{r}}=9.5\), C5 attains large vibration amplitude. As seen in Fig. 10g, 2RVS appears behind C5 and extends to the near wake. At \(U_{\mathrm{r}}=12\), both C4 and C5 attain the maximum transverse amplitude. As displayed in Fig. 10h, the vortices behind C4 and C5 are elongated a lot by the large-scale displacement of the two cylinders. In this case, 2RVS disappears and a 2S-like vortex mode is observed behind C5. At \(U_{\mathrm{r}}=14\), the response of the downstream cylinders as well as their effect on the flow field drops a lot, and the vortex pattern around the cylinders almost returns back to that at \(U_{\mathrm{r}}=4\), as shown in Fig. 10i.

At most representative reduced velocities, the cascade of flow regimes including the 2S, 2RVS, breaking of 2RVS and elongated 2S vortex structures still appears. In addition, new flow structures such as the pseudo 2S and 2P vortex modes are also observed under effect of large-scale vibrations. From Figs. 9 and 10, it is clear that the fluid load on each cylinder is strongly correlated to the flow pattern around it. The more vortices one cylinder interacts, the more frequency components appear in its lift spectrogram. The longer length scale a vortex structure is, the lower the frequency of perturbation it introduces. Moreover, the sub-harmonic oscillating frequency (\(\text {St}_{2}=0.0775\)) in the lift spectrum of C4 and C5 is associated to the breaking of 2RVS and forming of the elongated 2S vortex structure.

5.5 Effect of mass ratio

As it is well known, mass ratio is a key factor for the dynamic behavior of the cylindrical structure experiencing external flow. To study its effect on the present five-tandem-cylinder model, FSI simulations at Re \(=100\), \(L/D=6\), \(\zeta =0\), \(U_{\mathrm{r}} =\) 2–18 and \(m^{*}=5\) and 15 are further computed. Figures 11 and 12 display the transverse vibrating amplitudes and dominate frequencies at \(m^{*}=5\) and 15, respectively. As seen in the figures, the transverse response curve of each cylinder at \(m^{*}=5\) and 15 exhibits similar trend as that at \(m^{*}=10\). As decrease of the mass ratio, transverse vibrating amplitude of each cylinder is gradually amplified and the ‘lock-in’ region becomes wider. At lower mass ratio of \(m^{*}=5\), the vibrating frequency of C4 and C5 is increased slightly in the post-synchronization region, while in the pre-synchronization region the sub-harmonic response does not change much. At \(m^{*}=15\), the response of C4 is dominated by \(\text {St}_{2}=0.0775\) at \(U_{\mathrm{r}}=2\) and 3, which is different from that at \(m^{*}=5\) and 10. As discussed in Sects. 5.3 and 5.4, the fluid load on C4 is affected by both the vortices separated from the upstream cylinders and the breaking of the 2RVS, and \(\text {St}_{1}=0.155\) and \(\text {St}_{2}=0.0775\) show comparable effects on it. Therefore, the vibrating state of C4 is more unstable than other cylinders and is more sensitive to the mass ratio.

Fig. 11
figure 11

Responses of the five-tandem-cylinder model at \(\text {Re}=100\), \(L/D=6\), \(m^{*}=5\): a maximum transverse vibration amplitude, b dominant transverse vibration frequency

Full size image
Fig. 12
figure 12

Responses of the five-tandem-cylinder model at \(\text {Re}=100\), \(L/D=6\), \(m^{*}=15\): a maximum transverse vibration amplitude, b dominant transverse vibration frequency

Full size image

5.6 Effect of cylinder spacing

To study effect of cylinder spacing in ‘co-shedding’ regime, FIV of the five-tandem-cylinder model at Re \(=100\), \(\zeta =0\), \(m^{*}=10\), \(U_{\mathrm{r}} =\) 2–18 and \(L/D=4\) and 8 are further considered. Figures 13 and 14 provide the transverse vibrating amplitudes and dominate frequencies at \(L/D=4\) and 8, respectively. Comparing Figs. 13 and 14 with Figs. 8, 11 and 12, it can be found that the center-to-center distance has larger effect on the dynamic response of the five-tandem-cylinder model than the mass ratio does. At \(L/D=4\), the onset point of ‘lock-in’ of each cylinder is postponed a lot to \(U_{\mathrm{r}}=5.5\), and all cylinders experience much lower oscillating frequency than the one-cylinder model, as seen in Fig. 13. Moreover, five cylinders almost have the same oscillating frequency except in the de-synchronization region, and the sub-harmonic response branch appearing at \(L/D=6\) is not observed. At \(L/D=8\), the effect of downstream cylinder on the upstream cylinder is decreased, and C1 exhibits almost the same dynamic behavior as the one-cylinder model does, as seen in Fig. 14. As seen in Fig. 14b, the sub-harmonic response branch turns to stronger than that at \(L/D=6\). In pre-synchronization region, both C4 and C5 oscillate at the sub-harmonic frequency. In post-synchronization region, besides C4 and C5, C3 also follows the sub-harmonic response branch.

To understand effect of cylinder spacing as presented above, Figs. 15 and 16 display the instantaneous flow patterns at \(L/D=4\) and \(L/D=8\), respectively. At \(L/D=4\), the breaking of 2RVS always happens in the wake of C5, as seen in Fig. 15. In most cases, the elongated 2S associated with the sub-harmonic frequency does not interact with any of the cylinder. Therefore, the sub-harmonic response branch is not observed in Fig. 13b. At \(L/D=8\), however, the breaking of 2RVS occurs in advance in the gap between C3 and C4, as seen in Fig. 16. Therefore, C4 and C5 always interact with the elongated 2S vortex structure and experience the sub-harmonic WIV, and C3 also exhibit sub-harmonic response in the post-synchronization region, as seen in Fig. 14b.

Fig. 13
figure 13

Responses of the five-tandem-cylinder model at \(\text {Re}=100\), \(m^{*}=10\), \(L/D=4\): a maximum transverse vibration amplitude, b dominant transverse vibration frequency

Full size image
Fig. 14
figure 14

Responses of the five-tandem-cylinder model at \(\text {Re}=100\), \(m^{*}=10\), \(L/D=8\): a maximum transverse vibration amplitude, b dominant transverse vibration frequency

Full size image
Fig. 15
figure 15

Instantaneous vorticities around five circular cylinders in tandem at \(\text {Re}=100\), \(L/D=4\), \(m^{*}=10\) and a stationary; b \(U_{\mathrm{r}} =4\); c \(U_{\mathrm{r}} =5.6\); d \(U_{\mathrm{r}} =7\); e \(U_{\mathrm{r}} =10\); f \(U_{\mathrm{r}} =15\)

Full size image
Fig. 16
figure 16

Instantaneous vorticities around five circular cylinders in tandem at \(\text {Re}=100\), \(L/D=8\), \(m^{*}=10\) and a stationary; b \(U_{\mathrm{r}} =4\); c \(U_{\mathrm{r}} =4.8\); d \(U_{\mathrm{r}} =7.2\); e \(U_{\mathrm{r}} =11\); f \(U_{\mathrm{r}} =15\)

Full size image

6 Conclusions

Flow-induced vibrations of five elastically supported circular cylinders in a tandem arrangement at \(\text {Re}=100\), \(L/\hbox {D}=4\), 6 and 8, \(\zeta =0\), \(m^{*}=5\), 10 and 15, and \(U_{\mathrm{r}}=\) 2–18 are investigated using FSI simulation. The followings summarize the many observations made in the article:

  1. (1)

    In the range of parameters considered, all five cylinders exhibit VIV-like responses, with the transverse amplitude showing a first-increase-then-decrease trend and vibrating frequency locked to the natural frequency in the ‘lock-in’ region, and the downstream cylinder can attain higher transverse displacement. For the most upstream cylinder, the response is almost the same as VIV of the one-cylinder model at large cylinder spacing of \(L/D=6\) and 8. For four downstream cylinders, however, the vortex shedding frequency is not always locked to the natural frequency in the ‘lock-in’ region because of the flow interference effect, which is inconsistent with the typical ‘lock-in’ process of the one-cylinder model.

  2. (2)

    For the three upstream cylinders (C1–C3), the responses are similar to those of the three-tandem-cylinder model as reported by Yu et al. [35] and Chen et al. [37], with the vibration frequency jumping between the vortex shedding frequency of \(\text {St}_{1}=0.155\) and the natural frequency. For the two most downstream cylinders (C4 and C5), however, their responses are affected significantly by the sub-harmonic frequency of \(\text {St}_{2}=0.0775\) induced by the breaking of 2RVS and appearing of the elongated 2S vortex mode.

  3. (3)

    As decrease of the mass ratio, the vibrating amplitude of each cylinder in the five-tandem-cylinder model is increased, and the ‘lock-in’ region of each cylinder is broadened slightly, which is similar to the scenario of one-cylinder or two-tandem-cylinder model.

  4. (4)

    Compared with the mass ratio, the cylinder spacing shows more significant effect on the dynamic response of the five-tandem-cylinder model. At smaller cylinder spacing of \(L/D=4\), the breaking of 2RVS occurs in the wake of the cylinder array, and the sub-harmonic response branch is not observed. At cylinder spacing of \(L/D=6\), the breaking of 2RVS appears in the gap between the last two cylinders (C4 and C5), leading to sub-harmonic response on C5 in the un-lock region and on C4 in the post-synchronization region. At larger cylinder spacing of \(L/D=8\), the breaking of 2RVS move upstream to the gap between the third and fourth cylinders (C3 and C4), leading to sub-harmonic response on C4 and C5 in the un-lock region and on C3 in the post-synchronization region.