Nonlinear dynamic responses of a perimeter-reinforced membrane wing in laminar flows

Abstract

Dynamic responses of a two-dimensional (2D) perimeter-reinforced (PR) membrane wing in laminar viscous flows are investigated numerically. The 2D Navier–Stokes equations and a one-dimensional nonlinear equation for membrane vibration are coupled to describe the flow-induced vibrations of the membrane wing in laminar flows. The modified characteristic-based split scheme, Galerkin finite element method, spring analogy technique and loosely coupled partitioned approach are employed, respectively, for the flow simulation, computation of the membrane response, mesh movement of the flow domain and fluid–structure interaction. The accuracy and stability of the proposed numerical method and corresponding codes are validated using a benchmark model of fluid–membrane interaction. Finally, the bifurcation characteristics of the membrane dynamic response and vortex structure near the membrane wing with respect to the angle of attack, Reynolds number, rigidity and pre-strain are analysed in detail. This paper could give people more information about the dynamic behaviours of the PR membrane wing in the laminar flow regime.

1 Introduction

Inspired by the natural flyers such as flies, bees, dragonflies and bats, many studies have been carried out on the flexible membrane wings in the past decades to improve the maneuverability, agility and stability of the Micro Air Vehicles (MAVs). According to the distribution of the rigid mounts and membrane skin attached to them, the membrane wing can be divided into two types, namely the batten-reinforced (BR) membrane wing and perimeter-reinforced (PR) membrane wing [1, 2]. For the BR design, the membrane is attached to the rigid mounts at the leading and two side edges while left unconstrained at the trailing edge, and some rigid battens oriented in the chordwise direction are imbedded in the membrane. For the PR design, however, the membrane is attached to the rigid mounts at both of the leading and trailing edges but there is no batten imbedded in the membrane. Different from the traditional rigid wings, both BR and PR membrane wings are allowed to deform and vibrate under the aerodynamic load and the fluid–structure interaction (FSI) is utilized to improve the aerodynamic performance at low Reynolds numbers [2,3,4,5,6].

In general, the effect of FSI on the aerodynamic performance of a fixed membrane wing comes from two aspects. First, when air flows around a membrane wing with positive angles of attack, the membrane wing will deform towards the leeside due to the pressure difference between the lower and upper surfaces and form a mean camber. The mean camber could further increase the pressure difference between the two surfaces, make the flow attached longer and change the action point of the aerodynamic load. For the BR membrane wings, it has been found that the mean camber could delay the stall [1, 7], increase the mean lift [8, 9] and improve the adaptability to the wind gust [1]. For the PR membrane wings, this camber effect could improve at the same time the stall and mean lift [10,11,12,13,14,15,16,17] and increase the pitching stability [1, 16, 17].

Besides the camber effect, the unsteady interaction between the flexible membrane and surrounding viscous flow also has a great influence on the aerodynamic performance of the membrane wings. In the past decade, this influence factor has received considerable attention and many studies on the flow-induced vibration (FIV) of the fixed BR or PR membrane wings have been carried out. For example, Waszak et al. [7] proposed a novel MAV model with fixed BR membrane wing and studied the effect of batten arrangement by wind tunnel test, and the high-frequency vibration with an order of 100 Hz was observed on the entire wing at ${ Re}=9 \times 10^{4}$. Subsequently, dynamic response of the same membrane model was analysed numerically by Lian et al. [4]. Comparable vibration frequency was obtained and considerable vertical component of velocity was observed on the membrane surface. Johnston et al. [18] revealed experimentally more details of the FIV of the BR membrane wing. In their study, the onsets of the limit cycle oscillation (LCO) of the BR membrane wing at three small angles of attack were captured by increasing gradually the inflow speed, and the effects of the pre-strain, number of battens and angle of attack on the flutter onset speed, maximum amplitude and dominant frequency were investigated. Coupling a nonlinear finite element model for the dynamic response of the flexible membrane and a vortex lattice model for the aerodynamics, Attar et al. [19] confirmed numerically the flutter and LCO characteristics of the BR membrane wing model with two membrane cells used by Johnston et al. [18]. Hubner and Hicks [8] found that the trailing-edge scalloping could improve the aerodynamic efficiency and increase the peak frequency of the FIV of the BR membrane wing. Scott et al. [20] showed by experiments that the BR membrane wing is not stationary but vibrating before flutter onset, although in this case the amplitude is much smaller than that of the LCO and the coherence is very low between the membrane vibration and flow perturbation. In the study of Attar et al. [21], the effect of structural pre-strain on the FIV of the BR membrane wing at moderate-to-high angles of attack was investigated.

For a PR membrane wing with tip and root unconstrained, Galvao et al. [22] observed in their experiments that, in a certain band of inflow speeds and angles of attack, FIVs of the tested membrane wing will be amplified due to the resonance between the separated leading-edge vortices and the compliant membrane, and the vibrating mode is changed with the inflow speed and angle of attack. In the work of Song et al. [10], the transition of the dynamic response of the PR membrane wing model proposed in [22] among several vibration states with different modes was revealed in detail. Rojratsirkul et al. [23, 24] proposed a benchmark PR membrane wing model and investigated its unsteady aerodynamic performance in their experiments. It was found that FIVs of the membrane could excite the shear layer and result in the roll-up of the large-scale vortices over the wing at higher angles of attack, which was thought playing an important role in decreasing the separation region and drag and delaying the stall. In their subsequent experimental studies [13, 25], the effects of the pre-strain, excess length and aspect ratio on the unsteady FSIs of this PR membrane wing model were further analysed. Coupling a sixth-order Navier–Stokes (NS) solver with a nonlinear membrane structural model, Gordnier [11], Gordnier and Attar [16, 26] and Visbal et al. [12] confirmed numerically the unsteady characteristics reported by Rojratsirkul et al. [13, 23,24,25]. In addition, Arbós-Torrent et al. [14] found that the shape of the leading- and trailing-edge supports will affect greatly the unsteady response of the PR membrane wing; Curet et al. [27] revealed that imposing a forced harmonic oscillation on the membrane could further increase the mean lift of the PR membrane wing; Sun and Zhang [28] studied the effects of the reinforced leading or trailing edge on the aerodynamics of the fixed PR membrane wing at low Reynolds number.

Fig. 1

Schematic of the 2D PR membrane wing model proposed by Rojratsirkul et al. [23, 24]

As mentioned above, for the BR membrane wing many studies have been done on the onset of the flutter/LCO as well as the transition between the vibration states with different modes. For the PR membrane wing, Gordnier [11] showed that at ${ Re} = 2500$ the membrane is nominally stationary at $\alpha =4^{^{\circ }}$, in a third mode standing wave response at $\alpha =8^{^{\circ }}$ and in the chaotic responses at $\alpha =12^{^{\circ }},16^{^{\circ }}$ and $20^{^{\circ }}$. Besides the angle of attack, the Reynolds number, rigidity and pre-strain were also found having great influence on the vibration states of the PR membrane wing. Unfortunately, since only 3 or 5 points were selected for each parameter in [11], the onset of the flutter/LCO and critical points between different vibration states were not captured. To describe more accurately the bifurcation characteristics of the dynamic response of the PR membrane wing, finer increments of the flow and structure parameters should be selected. In our previous work [29], the influence of the structure parameters on the nonlinear dynamic response of the nonlinear membrane model reported in [11] was studied and a variety of nonlinear vibration states were revealed. However, the membrane model was not coupled with the real flow in this work and the aerodynamic load was supposed to be uniformed and periodic.

In this paper, the onset of the flutter/LCO and bifurcation of the dynamic response of the fixed two-dimensional (2D) PR membrane wing proposed by Rojratsirkul et al. [23, 24] with respect to the angle of attack, Reynolds number, rigidity and pre-strain are investigated numerically by selecting much finer increment for each parameter. Besides the structural response, the changes of the transient flow structure and mean aerodynamic performances at each bifurcation points are also analysed. This paper could reveal more details of the unsteady FSIs of the PR membrane wing in the laminar flow regime.

2 Mathematical model

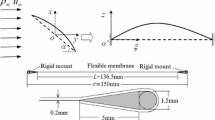
The 2D PR membrane wing model proposed by Rojratsirkul et al. [23, 24] is utilized in this paper. As shown in Fig. 1, the wing is formed by gluing a rectangular latex sheet to two small rigid mounts at the leading and trailing edges. Because the root and tip edges are left free and the sheet has a much longer span, both of the membrane and the surrounding flow exhibit 2D characteristics at small Reynolds numbers.

Considering the FIVs of the PR membrane wing at the Reynolds numbers below $10^{4}$ are investigated, the flow field is supposed to be laminar everywhere and the transitions in the boundary layer and free shear layer are not concerned. Hence, the incompressible Navier–Stokes (NS) equations are taken as the governing equations, the non-dimensional form of which can be expressed as

$$\begin{aligned}&\frac{\partial u_i }{\partial x_i }=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u_i }{\partial t}+u_{j} \frac{\partial u_i }{\partial x_j }=-\frac{\partial p}{\partial x_i }+\frac{1}{\textit{Re}}\frac{\partial ^{2}u_i }{\partial x_j \partial x_j }, \end{aligned}$$

(2)

where the summation convention is used and the effect of body force is ignored.

As illustrated in Fig. 1, when fluid flows around the membrane wing, the flexible membrane will be subjected to both fluid and structural forces. In principle, the membrane wing is subjected to both normal and shear stresses from the fluid and deformed in both $\xi$ and z directions. However, compared with the pressure difference between the lower and upper surfaces $(\Delta p=p^{-}-p^{+})$, the shear stress $(\tau ^{+}$ and $\tau ^{-})$ and other components of the normal stress are much smaller and can be ignored. Therefore, it is assumed that the membrane is only driven by $\Delta p$ and its response is restricted in z direction. In addition, considering the thickness of the membrane is very small when compared with the chord length, the shear forces and bending moments at each membrane section and the effect of gravity are also ignored. Based on the above assumptions, the dynamic response of the membrane wing in Fig. 1 can be described by [11, 28,29,30,31]

$$\begin{aligned} \rho _\mathrm{S} h\frac{\partial ^{2}z}{\partial t^{2}}+\rho _\mathrm{S} C_\mathrm{d} \frac{\partial z}{\partial t}-T\frac{\partial ^{2}z}{\partial \xi ^{2}}\left[ {1+\left( \frac{\partial z}{\partial \xi }\right) ^{2}} \right] ^{-\frac{3}{2}}=\Delta p,\nonumber \\ \end{aligned}$$

(3)

In Eq. (3), the tension T is uniform along the membrane and can be computed by

$$\begin{aligned} T=Eh\left( {\delta _0 +\bar{\delta }} \right) , \end{aligned}$$

(4)

where

$$\begin{aligned} \bar{\delta }=\frac{L_\mathrm{S} -L}{L} \end{aligned}$$

(5)

and

$$\begin{aligned} L_\mathrm{S} =\int _0^L {\sqrt{1+\left( \frac{\partial z}{\partial \xi }\right) ^{2}}} \hbox {d}\xi . \end{aligned}$$

(6)

Considering the displacement z is only dependent on one spatial coordinate $\xi$, Eq. (3) is a one-dimensional (1D) vibration equation. In the work of Jaworski and Gordnier [32], this 1D computational model has been compared with a 2D membrane wing model taking the shear stress and deformation in the tangential direction into account. The numerical results from the two membrane wing model are very close. More details about the derivation process of Eq. (3) can be found in Sun and Zhang [29].

The flow field governed by Eqs. (1) and (2) and the membrane structure governed by Eqs. (3)–(6) interact with each other on the fluid–membrane interface. To solve Eq. (3), the fluid force $\Delta p$ should be obtained from the flow field. In turn, the displacement and velocity of the membrane surface will change the solution domain and boundary conditions of the flow field when solving Eqs. (1) and (2).

3 Numerical method

The modified characteristic-based split (CBS) finite element method (FEM) for the moving mesh proposed in our previous study [33] is utilized to solve the flow field. The dual-time stepping (DTS) method is employed to increase the stability and the freedom in selecting the time step of the flow solver. Moreover, the segment spring analogy method [33, 34] is taken as the moving mesh method for the unstructured triangular grids in the fluid domain. According to the DTS method proposed by Jameson [35], adding a derivative term of $u_i$ with respect to the pseudo time $\tau$ to Eq. (2) yields

$$\begin{aligned} \frac{\partial u_i }{\partial \tau }+\frac{\partial u_i }{\partial t}+u_j \frac{\partial u_i }{\partial x_j }=-\frac{\partial p}{\partial x_i }+\frac{1}{\textit{Re}}\frac{\partial ^{2}u_i }{\partial x_j \partial x_j }. \end{aligned}$$

(7)

Then, discretizing Eq. (7) in the pseudo time using the characteristic-Galerkin (CG) method [36], we have

$$\begin{aligned} \begin{array}{l} u_i^{m+1} -u_i^m =-\Delta \tau \left[ {u_j^m \frac{\partial u_i^m }{\partial x_j }-\frac{1}{\textit{Re}}\frac{\partial ^{2}u_i^m }{\partial x_j \partial x_j }+\frac{\partial p^{m+\theta }}{\partial x_i }} \right] \\ \quad +\frac{\Delta \tau ^{2}}{2}u_k^m \frac{\partial }{\partial x_k }\left[ {u_j \frac{\partial u_i }{\partial x_j }+\frac{\partial p}{\partial x_i }} \right] ^{m}-\Delta \tau \frac{3u_i^m -4u_i^n +u_i^{n-1} }{2\Delta t}, \end{array}\nonumber \\ \end{aligned}$$

(8)

where the superscripts m and n stand for the number of the pseudo and real time steps, respectively, and the last term is a discretized form of the term ${\partial u_i }/{\partial t}$ in Eq. (7). In each real time interval $[t^{n}, t^{n+1}]$, taking $u_i^0 =u_i^n$ and $p^{0} =p^{n}$ as the initial conditions and solving Eq. (8) iteratively, unknowns $u_i^{n+1}$ and $p^{n+1}$ at $t^{n+1}$ can be obtained when $u_i^{m+1} =u_i^m$ and $p^{m+1} =p^m$.

Using the CBS algorithm, Eq. (8) can be solved by three steps:

Step 1::

$$\begin{aligned}&u_i^{*} =u_i^{m} -\Delta \tau \left[ {u_j \frac{\partial u_i}{\partial x_j}-\frac{1}{\textit{Re}}\frac{\partial ^{2}u_i }{\partial x_j \partial x_j }} \right] ^{m}\nonumber \\&\quad +\,\frac{\Delta \tau ^{2}}{2}u_k^m \frac{\partial }{\partial x_k }\left[ {u_j \frac{\partial u_i }{\partial x_j }} \right] ^{m} \end{aligned}$$

(9)

where $u_i^*$ are the intermediate velocity components.

Step 2::

$$\begin{aligned}&\theta \frac{\partial }{\partial x_i }\left( {\frac{\partial p^{m+1}}{\partial x_i }} \right) \nonumber \\&\quad =\frac{1}{\Delta \tau }\frac{\partial }{\partial x_i }\left[ u_i^*-\Delta \tau (1-\theta )\frac{\partial p^{m}}{\partial x_i }\right] \end{aligned}$$

(10)

Step 3::

$$\begin{aligned}&u_i^{m+1} =u_i^*-\Delta \tau \frac{\partial p^{m+\theta }}{\partial x_i }\nonumber \\&\quad +\frac{\Delta \tau ^{2}}{2}u_k^m \frac{\partial }{\partial x_k }\left( {\frac{\partial p}{\partial x_i }} \right) ^{m}\nonumber \\&\quad -\Delta \tau \frac{3u_i^m -4u_i^n +u_i^{n-1} }{2\Delta t} \end{aligned}$$

(11)

In Eqs. (9)–(11), $u_i^*, u_i^m, u_i^{m+1}$, $u_i^{n+1}$, $p^{m}$, $p^{m+1}$ and $p^{n+1}$ are unknowns at each grid node at time instant $t^{n+1}$, while $u_i^n, p^{n}$ and $u_i^{n-1}$ are the unknowns at the same spatial coordinates at time $t^{n}$ and $t^{n-1}$. For the traditional problems with fixed boundaries, the mesh is not moved during computation and $u_i^n$, $p^{n}$ and $u_i^{n-1}$ are also node values. For the moving boundary problems encountered here, however, the mesh is moved during computation and $u_i^n, p^{n}$ and $u_i^{n-1}$ are no longer node values. Hence, $u_i^n, p^{n}$ and $u_i^{n-1}$ in Eqs. (9)–(11) are approached by the node values $\left. {u_i^n } \right| _I$,$\left. {p^n } \right| _I$ and $\left. {u_i^{n-1} } \right| _I$ at time $t^{n}$ and $t^{n-1}$ using the Taylor expansions as

$$\begin{aligned} \left\{ {\begin{array}{l} u_i^n =\left. {u_i^n } \right| _I +\delta _j \frac{\partial \left. {u_i^n } \right| _I }{\partial x_j }+o\left( \left| {\varvec{\delta }} \right| ^{2}\right) ; \\ p^n =\left. {p^n } \right| _I +\delta _j \frac{\partial \left. {p^n } \right| _I }{\partial x_j }+o\left( \left| {\varvec{\delta }} \right| ^{2}\right) ; \\ u_i^{n-1} =\left. {u_i^{n-1} } \right| _I +{\delta }'_j \frac{\partial \left. {u_i^{n-1} } \right| _I }{\partial x_j }+o\left( \left| {{\varvec{\delta }}^{\prime }} \right| ^{2}\right) \\ \end{array}} \right. \end{aligned}$$

(12)

where ${\varvec{\delta }}$ and ${\varvec{\delta }}^{\prime }$ are the displacements of the grid node I in the time intervals $[t^{n}, t^{n+1}]$ and $[t^{n-1}, t^{n+1}]$, respectively. The unstructured triangular grid with linear shape function is used for both velocity and pressure to discretize the flow domain, and then, the standard Galerkin FEM is employed to solve Eqs. (9)–(11), as reported earlier by Zienkiewicz et al. [36] and Sun et al. [33]. Moreover, the convergence criterion of the flow solver is taken as

$$\begin{aligned}&\frac{\sqrt{\sum _{I=1}^{n_\mathrm{P} } {\left[ {\left( {u_1^{m+1} } \right) _I -\left( {u_1^m } \right) _I } \right] ^{2}} }}{\sqrt{\sum _{I=1}^{n_\mathrm{P} } {\left( {u_1^{m+1} } \right) _I^2 } }}<10^{-6},\nonumber \\&\frac{\sqrt{\sum _{I=1}^{n_\mathrm{P} } {\left( {p_I^{m+1} -p_I^m } \right) ^{2}} }}{\sqrt{\sum _{I=1}^{n_\mathrm{P} } {\left( {p_I^{m+1} } \right) ^2 } }}<10^{-5}. \end{aligned}$$

(13)

To solve the dynamic responses of the membrane wing, the Galerkin FEM is utilized first to discretize Eq. (3) spatially. The flexible membrane is divided equally into $n_{M }$ elements and at each element the Hermite polynomial is used as the interpolation function. Following the Galerkin FEM, the spatially discretized form of Eq. (3) can be obtained as

$$\begin{aligned} \mathbf{M} \ddot{\mathbf{X}}+\mathbf{C}\dot{\mathbf{X}}+\mathbf{K}(\mathbf{X})\mathbf{X}=\mathbf{Q} \end{aligned}$$

(14)

where

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{X}=[z_1 ,\left( {{\partial z}/{\partial \xi }} \right) _1 ,z_2 ,\left( {{\partial z}/{\partial \xi }} \right) _2 \ldots z_{(n_\mathrm{M} +1)} ,\\ \qquad \left( {{\partial z}/{\partial \xi }} \right) _{(n_\mathrm{M} +1)} ]^{\mathrm{T}}, \\ \mathbf{M}=\rho _\mathrm{S} h\int _0^L {\mathbf{N}^{\mathrm{T}}{} \mathbf{N}\hbox {d}\xi } ,\quad \mathbf{C}=\rho _\mathrm{S} C_\mathrm{d} \int _0^L {\mathbf{N}^{\mathrm{T}}{} \mathbf{N}\hbox {d}\xi } , \\ \mathbf{K(X)}=\int _0^L {\frac{\partial }{\partial \xi }\left\{ {\mathbf{N}^{\mathrm{T}}T\left[ {1+\left( {\frac{\partial \mathbf{N}\cdot \mathbf{X}}{\partial \xi }} \right) ^{2}} \right] ^{-\frac{3}{2}}} \right\} \frac{\partial \mathbf{N}}{\partial \xi }\hbox {d}\xi } \\ \mathbf{Q}=\int _0^L {\mathbf{N}^{\mathrm{T}}\Delta p{\text {d}}\xi } ,\quad \mathbf{N}=[N_1 ,N_2,\ldots ,N_{2(n_\mathrm{M} +1)} ].\\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(15)

Equation (14) is a group of nonlinear ordinary differential equations and is then discretized in time using the Generalized-$\alpha$ method [37]. Finally, the nonlinear algebra equations obtained from the Generalized-$\alpha$ method are solved by the Newton–Raphson method. More details about the structural solver can be found in Sun and Zhang [29].

The flow and structure solvers are coupled by the loosely coupled partitioned approach. The grid nodes of the membrane and fluid are distributed overlapping each other on the fluid–membrane interface to increase the accuracy of the information transfer between the two solvers. The same time step is utilized for the flow and structure solvers. In summary, the FSI solution procedure at each time interval $[t^{n}, t^{n+1}]$ can be divided mainly into five steps:

• 1. Compute $\Delta p$ at each grid node of the membrane using the flow pressure at $t^{n}$;

• 2. Solve Eq. (14) to obtain the displacement and velocity of the flexible membrane at $t^{n+1}$;

• 3. Adjust the mesh of the flow domain using the segment spring analogy method;

• 4. Compute $u_i^n,p^{n}$ and $u_i^{n-1}$using Eq. (12);

• 5. Solve iteratively Eqs. (9)–(11) on the new mesh until the convergence criteria in Eq. (13) is approached.

4 Examples and discussions

4.1 Code validation

Figure 2 shows the solution domain and boundary conditions of the flow field. As seen in the figure, the inlet and two side boundaries of the flow domain are all located at 8c from the membrane centre point, and the free-stream velocity components, namely $u_1=1$ and $u_2 =0$, are imposed on them. The outlet of the flow domain is placed at 16c downstream and the pressure on this boundary is supposed to be zero. The no-slip boundary condition is imposed on the surface of the membrane wing. On the surfaces of the two rigid mounts, both of the velocity components $u_{1}$ and $u_{2}$ are equal to zero; on the upper and lower surfaces of the flexible membrane, the fluid has the same displacement and velocity with the membrane.

Fig. 2

Schematic of the solution domain and boundary conditions for the flow around a flexible membrane wing

To test the accuracy of the proposed numerical method for the fluid–membrane interaction in laminar flow region, the aerodynamic performance of the 2D PR membrane wing presented in Fig. 1 is computed first at ${ Re}=2500, E=50{,}000, {\rho }_\mathrm{S} =589, C_\mathrm{d} =0$, $h=0.001$ and $\text {AOA}=8^{\circ }$. In this case and the computations hereafter, the computational time step is taken as $\Delta t=0.01$, the simulation is carried out from $t=0$–400 and the mean characteristics are obtained using the data in $t=300$–400.

Table 1 Grid information and computed mean aerodynamic characteristics at ${ Re}=2500$ and $\text {AOA}=8^{\circ }$

Fig. 3

Mean deflection and pressure distribution of the 2D PR membrane wing at ${ Re}=2500$ and $\alpha =8^{\circ }$: a deflection; b pressure coefficient on the membrane surface

Fig. 4

Initial mesh (Mesh_2) for the laminar flow around the 2D PR membrane wing at $\alpha =8^{\circ }$

Three meshes are used to examine the effect of the grid density on the numerical results of this FSI problem. In Table 1, the grid information and computed mean lift coefficients, drag coefficients and lift-to-drag ratios are presented and compared with the results reported by Gordnier [11]. As shown in the table, the largest relative changes of $\bar{C}_{L}, \bar{C}_{D}$ and $\overline{L/D}$ between the three meshes are only 0.2%, 0.88% and 0.45%, respectively, and the computed $\bar{C}_{L}$ has a very good agreement with that provided in the reference. In Fig. 3, the mean deflection and pressure coefficients of the flexible membrane are also displayed. It can be seen from both Fig. 3a, b that the numerical results from Mesh_2 and Mesh_3 are very close and agree well with the existing results. Hence, the Mesh_2 with 80 elements on the flexible membrane is taken as the computation mesh in the following sections. As shown in Fig. 4, for Mesh_2 the body-fitted grids are generated near the membrane surface and the grids in the wake of the wing are refined for the purpose of capturing more accurately the boundary layer, flow separation and vortex shedding in these regions. Moreover, in the following sections when the effect of one parameter is investigated, the other parameters will remain unchanged as those in this section.

In Fig. 5, the time-averaged non-dimensional pressure, shear stress and other normal components of the normal stress on the membrane surface are presented and compared with each other. As seen in the figures, the pressure at ${ Re}=2500$ and $\alpha =8^{\circ }$ has much larger magnitude than the shear stress and other normal components of the normal stress at most points of the membrane. Hence, the assumptions introduced into the membrane model in Sect. 2, which suppose that the flexible membrane is only driven by the pressure differences between the lower and upper surfaces and ignore the effects of the shear stress and other normal components, will not lead to large discrepancy when compared with the 2D membrane model, as reported by Jaworski and Gordnier [32].

Fig. 5

Time-averaged pressure, stress and other components of the normal stress on the surfaces of the flexible membrane at ${ Re}=2500$ and $\alpha =8^{\circ }$: a upper surface; b lower surface

Fig. 6

Mean aerodynamic characteristics of the 2D PR membrane wing at ${ Re}=2500$ and different angles of attack: a lift coefficient; b drag coefficient; c lift-to-drag ratio

4.2 Effect of angle of attack

The effect of the angle of attack on the mean and dynamic behaviours of the 2D PR membrane wing at ${ Re}=2500$ is studied first. Unlike the previous work of Gordnier [11] which has studied the cases with $\alpha =4^{\circ }, 8^{\circ }, 12^{\circ }, 16^{\circ }$ and $20^{\circ }$, a much finer increment of $\Delta \alpha =1^{\circ }$ is utilized to capture the bifurcation of the structure response and flow structure at $\alpha =1^{\circ }$–20$^{\circ }$.

Figure 6 gives the mean lift coefficients, drag coefficients and lift-to-drag ratios at different angles of attacks. As shown in Fig. 6, when $\alpha$ is increased from $1^{\circ }$ to $8^{\circ }$, the mean lift coefficient of the membrane wing is increased almost linearly from 0.366 to 0.998 and the drag coefficient is increased slightly from 0.068 to 0.113, which in combination increase the mean lift-to-drag ratio to a maximum value near $\alpha =8^{\circ }$. When $\alpha$ is changed from $8^{\circ }$ to $10^{\circ }$, the slopes of both of the mean lift and drag curves are increased but the mean lift-to-drag ratio begins to decrease. Then, further increasing $\alpha$ from $10^{\circ }$ to $11^{\circ }$, the increase in the mean drag coefficient in Fig. 6b becomes more apparent. As a result, a larger drop of the mean lift-to-drag ratio from 8.35 to 7.02 can be found in Fig. 6c. Finally, when $\alpha$ is increased from $11^{\circ }$ to $20^{\circ }$, both of the mean lift and drag coefficients are increased gradually while the mean lift-to-drag ratio is further decreased. The effects of the angle of attack on the mean aerodynamic characteristics could be explained by the time-dependent vortex structures and dynamic response of the membrane wing, which will be discussed in detail later. In Fig. 6a, the mean lift coefficients computed by Gordnier [11] are also presented for comparison. As shown in the figure, again, our results agree very well with those reported in the reference.

Fig. 7

Bifurcation diagram at the centre point of the membrane wing at ${ Re}=2500$ with respect to $\alpha$

In Fig. 7, the instantaneous positions of the membrane centre point in $t\in [300, 400]$ when its velocity becomes zero (or changes direction) are presented to illustrate the effect of the angle of attack on the dynamic response of the membrane wing. In fact, the points in Fig. 7 can also be taken as a Poincare map of the phase portraits by taking the plane $\dot{z}=v=0$ as the Poincare section. As shown in Fig. 7, only one point is observed in the bifurcation diagram at $\alpha =1^{\circ }$–7$^{\circ }$ because the membrane is either stationary or its maximum amplitude from the mean deflection is very small. At $\alpha =8^{\circ }$, however, periodic response with apparent amplitude is found in Fig. 7, which indicates the Hopf bifurcation as well as the onset of the flutter/LCO. Figure 8a displays the phase portrait and spectrogram of the centre point at $\alpha =8^{\circ }$. As seen in the figures, the vibration state is period 1 and the non-dimensional dominant frequency is 1.53 at $\alpha =8^{\circ }$. At $\alpha =9^{\circ }$ and $10^{\circ }$, the Poincare map of the centre point are very similar with that at $\alpha =8^{\circ }$ except that the mean deformation is increased slightly. However, it can be seen from Fig. 8b that the stability of the LCO as well as the dominant frequency is decreased and a harmonic frequency of 2.27 appears at $\alpha =10^{\circ }$. Then, when $\alpha$ is increased slightly from $10^{\circ }$ to $11^{\circ }$, the dynamic response of the membrane centre is changed greatly. As seen in Figs. 7 and 8c, the maximum amplitude of the membrane centre is increased by about ten times from $2.64 \times 10^{-3}$ to 0.0275 and the vibration becomes irregular at $\alpha =11^{\circ }$. In this case, the spectrogram becomes almost continuous with several peaks, which might indicate the appearance of the chaotic vibration. Finally, the vibration state at the membrane centre is not changed very much with further increase of $\alpha$ from $11^{\circ }$ to $20^{\circ }$, although the dominant frequency is decreased gradually from 0.79 to 0.7, as shown in Figs. 7 and 8d.

To investigate the dynamic response along the whole membrane wing, the $\xi$–t diagram showing the difference between the instantaneous and mean deformations of the flexible membrane is analysed. Compared with the bifurcation diagram in Fig. 7, the $\xi$–t diagram has revealed more details and five different types of response are found when $\alpha$ is increased from $1^{\circ }$ to $20^{\circ }$. At $\alpha =1^{\circ }$ and $2^{\circ }$, the whole membrane is found eventually staying at the mean deflection position and the static equilibrium state is obtained, as shown in Fig. 9a. At $\alpha =3^{\circ }$–6$^{\circ }$, $7^{\circ }$–$8^{\circ }$ and $9^{\circ }$–$10^{\circ }$, the fourth, third and second mode standing wave responses are observed, respectively, as shown in Fig. 9b–d. Strictly speaking, the point of Hopf bifurcation or onset of flutter/LCO is near $\alpha =3^{\circ }$. However, because the maximum amplitudes are below $10^{-3 }$ at $\alpha =3^{\circ }$–$7^{\circ }$ and the effects of the FIVs on the aerodynamic performance are very small, $\alpha =8^{\circ }$ with apparent FIV amplitude is taken as the onset point of the flutter/LCO here. When $\alpha$ is larger than $10^{\circ }$, it can be seen from Fig. 9e, f that the vibration state of the membrane wing is changed from the standing wave response to the irregular mode. This is in agreement with the findings in Fig. 7. In general, the mode number and stability of the membrane response are decreased with the increase in the angle of attack. In Fig. 9g, the mean deflections of the membrane wing at different angles of attack are also presented. As seen in the figure, with increase in the angle of attack, the deflection of the whole membrane is increased continuously and the point with maximum deflection is moved upward, which are also found in the numerical study of Gordnier [11].

Fig. 8

Phase portraits and spectrograms of the membrane centre at ${ Re}=2500$ and different angles of attack: a $\alpha =8^{\circ }$; b $\alpha =10^{\circ }$; c $\alpha =11^{\circ }$; d $\alpha =20^{\circ }$

Fig. 9

$\xi$–t diagram for vibration from the mean membrane deflection at different angles of attack: a $\alpha =2^{\circ }$; b $\alpha =5^{\circ }$; c $\alpha =8^{\circ }$; d $\alpha =10^{\circ }$; e $\alpha =11^{\circ }$ ; f $\alpha =20^{\circ }$; g mean deflections (in the legend of each figure, the right side of the contour plot corresponds to the font)

The change of the membrane response with respect to the angle of attack is believed closely related to the change of the vortex structure around the membrane wing. To reveal this, the instantaneous streamlines near the membrane wing at different angles of attack are presented in Fig. 10. As shown in Fig. 10a, the membrane wing is cambered up slightly and a small vortex can be observed near the trailing edge at $\alpha =1^{\circ }$–$2^{\circ }$. Since the trailing-edge vortex is not shed, the flow field is not changed with time in Fig. 10a. As a result, the membrane wing is in a static equilibrium in Fig. 9a. At $\alpha =3^{\circ }$–$6^{\circ }$, however, a pair of trailing-edge vortices appears. Moreover, the trailing-edge vortices are no longer always attached to the wing but begin to shed alternatively and periodically, as seen in Fig. 10b. Under the periodic excitation of the shedding vortices, the fourth mode standing wave response is observed in Fig. 9b. When $\alpha$ is increased gradually from $6^{\circ }$ to $10^{\circ }$, a small vortex is formed at the leading edge, and the shedding position of the trailing-edge vortex rotating in the clockwise direction (we will call it “separation bubble” hereafter for convince) is moved gradually towards the leading edge along the upper surface, as shown in Fig. 10b–d. Because the region fluctuated directly by the shedding vortices is enlarged, the dynamic response of the membrane is changed gradually from the fourth to the third and second modes, as displayed in Fig. 9b–d. At  $\alpha =11^{\circ }$, the leading-edge vortex begins to shed in Fig. 10e. In this case, a vortex chain with larger scale and strength is formed on the upper surface and the membrane is interacting, at most time instants, with two vortices with comparable strength. This might be the key reason why the dynamic response of the membrane wing becomes very irregular at $\alpha =11^{\circ }$. Then, with further increase of $\alpha$ from $11^{\circ }$ to $20^{\circ }$, the scales of both of the leading-edge vortices and the vortex chain are increased gradually, as shown in Fig. 10e, f. As a result, the maximum amplitude of the membrane response is further increased as seen in Fig. 9f.

Fig. 10

Instantaneous streamlines around the membrane wing at different angles of attack: a $\alpha =2^{\circ }$; b $\alpha =5^{\circ }$; c $\alpha =8^{\circ }$; d $\alpha =10^{\circ }$; e $\alpha =11^{\circ }$; f $\alpha =20^{\circ }$

4.3 Effect of Reynolds number

The aerodynamic performances and dynamic responses of the 2D PR membrane wing at $\alpha =8^{\circ }$ and ${ Re}=100$–10, 000 are computed to investigate the effect of the Reynolds number. The increment in the Reynolds number is taken as 100 for ${ Re}=100$–1000 while 500 for ${ Re}=1000$–10,000. Figure 11 displays the computed mean lift coefficients, drag coefficients and lift-to-drag ratios at the computed Reynolds numbers. As shown in Fig. 11a, the curve of the mean lift coefficient can be divided roughly into three regions with different characteristics, namely ${ Re}=100$–900, 900–5000 and 5000–10,000. First, when Re is increased from 100 to 900, the mean lift coefficient of the membrane wing is first increased continuously from 0.678 to 0.781 at $\textit{Re}=100$–600 and then becomes nearly unchanged at $\textit{Re}=600$–900. Subsequently, the mean lift coefficient jumps abruptly from 0.78 to 0.814 when Re is increased from 900 to 1000 and then is increased almost linearly from 0.814 to 1.23 at $\textit{Re}=1000$–5000. Finally, the mean lift coefficient is dropped suddenly from 1.23 to 1.18 near ${ Re}=5000$ and then not changed very much at $\textit{Re}=5000$–10,000. Different from the mean lift, both of the mean drag and lift-to-drag ratio are changed monotonously with the Reynolds number. As shown in Fig. 11b, the mean drag coefficient is reduced by about 65.5% from 0.415 to 0.143 at $\textit{Re}=100$–1000 while then decreased much slower at $\textit{Re}=1000$–10,000. As shown in Fig. 11c, the curve of the lift-to-drag ratio is very close to a parabolic curve in the whole range of Reynolds number computed.

Fig. 11

Mean aerodynamic characteristics of the 2D PR membrane wing at different Reynolds numbers: a lift coefficient; b drag coefficient; c lift-to-drag ratio

The bifurcation diagram at the membrane centre with respect to the Reynolds number is presented in Fig. 12. As seen in the figure, the membrane centre is eventually stayed at a static equilibrium position at $\textit{Re}=100$–900. Its mean deflection is first increased from 0.062 to 0.064 at $\textit{Re}=100$–500 and then decreased slightly at $\textit{Re}=500$–900. WhenRe is increased from 900 to 1000, the mean deflection at the membrane centre jumps abruptly and the final state is changed from stationary to period-1, as shown in Figs. 12 and 13a. This indicates that the Hopf bifurcation or flutter/LCO of the computed membrane wing at $\alpha =8^{\circ }$ appears near ${ Re}=1000$. With further increase of Re from 1000 to 4500, both of the mean deflection and vibrating amplitude are increased, as seen in Figs. 12 and 13b. Moreover, an additional harmonic frequency of 2.14 appears in the spectrogram at ${ Re}=4500$. When Re is further increased from 4500 to 5000, the stability of the LCO is reduced and the dynamic response becomes quasi-periodic, as shown in Figs. 12 and 13c. In this case, it can be seen from Fig. 13c that several irrational frequency peaks appears in the spectrogram besides the harmonic frequencies. Then, when Re is further increased from 5000 to 5500 and 6000, the mean deflection at the membrane centre is decreased slightly and the vibrating state is changed from quasi-periodic to period-3 and period-6, as displayed in Figs. 12, 13d, e. Finally, the response of the membrane centre turns to irregular at $\textit{Re}=6500$–10,000, as shown in Figs. 12 and 13f.

Similar with the angle of attack, the Reynolds number is also found having great effect on the response mode of the membrane wing. As seen in Fig. 14a, the whole membrane wing is stationary when Re <1000. At ${ Re}=1000$, however, the response becomes the second mode standing wave with very small amplitude, as shown in Fig. 14b. Subsequently, the dynamic response becomes the third mode standing wave at $\textit{Re}=1500$–3000 and then turns back to the second mode at $\textit{Re}=3000$–5000, as seen in Fig. 14c–e. Compared Fig. 14d with Fig. 14e, it can be also found that the membrane wing exhibits more properties of travelling wave near the trailing edge when Re is larger than 3000.Then, when Re is further increased from 5000 to 5500 and 6000, the response mode is changed significantly. As seen in Fig. 14f, the FIV of the membrane has become more unstable at ${ Re}=5500$. Finally, the $\xi$–t diagram becomes very irregular at $\textit{Re}=6500$–10,000 as displayed in Fig. 14g, h. It can be seen from Fig. 14 that, with the increase of Re, the membrane response will generally become unstable and exhibit more and more properties of travelling wave. In Fig. 14i, the mean deflections of the membrane wing at different Reynolds numbers are presented. As shown in the figure, the deflection of the membrane is increased first when Re is increased from 100 to 5000 but then not changed much at $\textit{Re}=5000$–10,000.

Fig. 12

Bifurcation diagram at the centre point of the membrane wing with respect to Re

Fig. 13

Phase portraits and spectrograms of the membrane centre at $\alpha =8^{\circ }$ with different Reynolds numbers: a ${ Re}=1000$; b ${ Re}=4500$; c ${ Re}=5000$; d ${ Re}=5500$; e ${ Re}=6000$; f ${ Re}=6500$

Fig. 14

$\xi$–t diagram for vibration from the mean membrane deflection at $\alpha =8^{\circ }$ and different Reynolds numbers: a $\textit{Re}=900$; b $\textit{Re}=1000$; c $\textit{Re}=1500$; d $\textit{Re}=3000$; e $\textit{Re}=5000$; f $\textit{Re}=5500$; g $\textit{Re}=6500$; h $\textit{Re}=10{,}000$; i mean deflections

Fig. 15

Instantaneous streamlines around the membrane wing at $\alpha =8^{\circ }$ with different Reynolds numbers: a $\textit{Re}=900$; b $\textit{Re}=1000$; c $\textit{Re}=1500$; d $\textit{Re}=3000$; e $\textit{Re}=5000$; f $\textit{Re}=5500$; g $\textit{Re}=6500$; h $\textit{Re}=10{,}000$

To explain the change of the vibrating state discussed above, Fig. 15 displays the instantaneous streamlines near the membrane wing at $\alpha =8^{\circ }$ with different Reynolds numbers. As shown in Fig. 15a, the flow is steady and the trailing-edge vortex is not changed with time when Re is less than 900. Therefore, the response of the membrane wing is also stationary in Fig. 14a. At ${ Re}=1000$, however, the pair of trailing-edge vortices begins to shed from the upper surface of the wing in Fig. 15b, which has triggered the periodic dynamic response of the structure in Fig. 14b. Compared with that in Fig. 10b, the scale of the shedding trailing-edge vortices themselves as well as their affecting region are much larger in Fig. 15b. As a result, the response of the membrane is the second mode standing wave in Fig. 14b when the LCO/flutter is on set, not the fourth mode standing wave as shown in Fig. 9b. At ${ Re}=1500$, since the scale of the trailing-edge vortex is reduced slightly in Fig. 15c, the response of the membrane is changed from the second mode to the third mode. When Re is increased from 1500 to 3000, one of the trailing-edge vortices (the separation bubble) is moved upstream. As a result, the dynamic response turns back to the second mode standing wave. Then, with further increase of Re from 3000 to 5000, the shedding point of the separation bubble is further moved towards the leading edge. At ${ Re}=5000$, the separation bubble is moved so upward that it begins to interact with the leading-edge vortex in Fig. 15e. Moreover, a small-scale secondary vortex appears between the leading-edge vortex and separation bubble at some time instants in this case. This could be the reason why the response of the membrane wing becomes quasi-periodic at ${ Re}=5000$, as shown in Figs. 13c and 14e. In Fig. 15e, it can also be found that the leading-edge vortex has not been shed yet at ${ Re}=5000$, although its size is changed with time during the shedding process of the separation bubble. At ${ Re}=5500$ and 6000, the secondary vortex between the leading-edge vortex and separation bubble disappears, as seen in Fig. 15f. As a result, the response of the membrane is stabilized and changed from quasi-periodic to period-3 and period-6, as presented in Fig. 13c–e. When Re is increased from 6000 to 6500, the leading-edge vortex begins to shed. As seen in Fig. 15g, the scale and strength of leading-edge and shedding vortices on the upper surface are increased a lot in this case. Excited at the same time by several shedding vortices, the response of the membrane wing becomes very irregular as shown in Figs. 13f and 14g. Finally, when Re is further increased from 6500 to 10,000, the fluctuation of the flow field becomes more apparent and more small-scale vortices appear on the upper surface, as seen in Fig. 15h. In this range of Re, the irregular response of the membrane is not only induced by the shedding leading-edge vortices but also by the fluctuation of the flow.

Fig. 16

Mean aerodynamic characteristics of the 2D PR membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with different rigidities: a lift coefficient; b drag coefficient; c lift-to-drag ratio

4.4 Effect of rigidity

The effect of rigidity (Eh) on the FIVs of the 2D PR membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ is investigated by changing Eh from 10 to 100 with an increment of 5. Figure 16 presents the mean aerodynamic performances of the membrane wing at different rigidities. As shown in Fig. 16a, the mean lift coefficient is first dropped by 17.4% from 1.21 to 1.0 when Eh is increased from 10 to 40 while then changed much slowly at ${ Eh}=40$–55. Then, an abrupt drop of the lift curve appears at ${ Eh}=60$. At ${ Eh}=65$, the mean lift coefficient jumps from 0.968 to 1.02, but then the mean lift is almost unchanged at ${ Eh}=65$–100. Similar with the mean lift coefficient, the mean drag coefficient of the membrane wing is also decreased generally when Eh is increased in ${ Eh}=10$–100. As seen in Fig. 16b, the mean drag is decreased smoothly first at ${ Eh}=10$–55 while then not changed much at ${ Eh}=65$–100. At ${ Eh}=60$, an abrupt drop of the mean drag is also observed. Different from the mean lift and drag, the mean lift-to-drag ratio is increased generally with the rigidities. As shown in Fig. 16c, the mean lift-to-drag ratio is first increased from 6.66 to 8.85 at ${ Eh}=10$–60 and then jumps to a higher value near 9.1 at ${ Eh}=65$–100.

Fig. 17

Bifurcation diagram at the centre point of the membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with respect to Eh

Fig. 18

Phase portraits and spectrograms of the membrane centre at $\alpha =8^{\circ }$ and ${ Re}=2500$ with different rigidities: a ${ Eh}=10$; b ${ Eh}=55$; c ${ Eh}=60$; d ${ Eh}=65$; e ${ Eh}=100$

Fig. 19

$\xi$–t diagram for vibration from the mean membrane deflection at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with different rigidities: a $Eh=10$; b $Eh=40$; c $Eh=55$; d $Eh=60$; e $Eh=65$; f $Eh=100$; g mean deflections

Fig. 20

Instantaneous streamlines around the membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with different rigidities: a $Eh=10$; b $Eh=40$; c $Eh=55$; d $Eh=60$; e $Eh=65$ ; f $Eh=100$

Figures 17 and 18 display, respectively, the bifurcation diagram at the membrane centre when Eh is increased from 10 to 100 and the phase portraits and spectrograms at several rigidities. As seen in Fig. 17, as expected, the mean deflection at the membrane centre is decreased continuously with the enhancement of the membrane rigidity. With the increase of Eh, the vibrating amplitude is first decreased at ${ Eh}=10$–17, then increased to a maximum value at ${ Eh}=17$–60 and eventually decreased at ${ Eh}=60$–100. Moreover, the dynamic response at the membrane centre is period 1 at all computed points except at ${ Eh}=60$, which is period 2, as shown in Figs. 17 and 18. It seems that the resonance is triggered near ${ Eh}=60$ when the dominant frequency of the shedding vortices approaches the natural frequency of the membrane structure.

The $\xi$–t diagram showing the difference between the instantaneous and mean deformations of the flexible membrane is also utilized to study the effect of the rigidity on the dynamic response of the whole membrane structure. As shown in Fig. 19, three types of response mode have been found in the computed rigidity range. First, the third mode standing wave response is observed at ${ Eh}=10$–55, as displayed in Fig. 19a–c. Compared Fig. 19a, b, it can also be found that the membrane has larger amplitude near the trailing edge at Eh $=$ 10 but then the vibrating amplitudes near the centre and leading edge are increased with the increase of Eh. Then, the response of the membrane becomes the second mode at ${ Eh}=60$. As shown in Fig. 19d, when Eh is increased from 55 to 60, the response of the membrane near the leading edge is not changed very much. Near the trailing edge, however, the positive and negative peaks no longer appear iteratively. When Eh is increased from 60 to 65, the response of the membrane wing turns to the second mode standing wave in Fig. 19e. Finally, further change of the response mode is not found at ${ Eh}=65$–100 although the amplitude near the trailing edge is decreased gradually. Comparing Fig. 19 with Figs. 9 and 14, it can be found that the rigidity has smaller effect on the dynamic response of the membrane wing when compared with the angle of attack and Reynolds number. Figure 19g displays the time-averaged membrane deflections at different rigidities. As shown in the figure, with increase of Eh, the deflection of the whole membrane is decreased continuously and the point with maximum deflection is moved towards the leading edge.

The instantaneous streamlines near the membrane wing at different rigidities are given in Fig. 20. As shown in Fig. 20a, the flow-induced deflection of the membrane wing is very large when the membrane is very flexible at ${ Eh}=10$. Under the effect of the structure deflection, a pair of large-scale vortices are formed and shed iteratively near the trailing edge, which results in the larger response of the membrane near the trailing edge in Fig. 19a. When Eh is increased from 10 to 40, the mean camber of the membrane wing is decreased and the shedding point of the separation bubble is moved forward to the membrane centre, as seen in Fig. 20b. At ${ Eh}=40$, because the excitations from the flow are comparable near the centre point and trailing edge, the amplitudes of the three peaks on the membrane become much closer in Fig. 19b. When Eh is further increased from 40 to 55, the vortex structure is not changed very much as seen in Fig. 20c. At ${ Eh}=60$, however, the shedding point of the separation bubble is moved forward a lot to the 40% chord length from the leading edge in Fig. 20d. With the increase in the influence region of the shedding vortex, the dynamic response is changed to the second mode in Fig. 19d. With further increase of Eh from 60 to 65 and 100, the shedding point of the separation bubble is not moved much, while its strength and scale are increased slightly, as shown in Fig. 20e, f.

Fig. 21

Mean aerodynamic characteristics of the 2D PR membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with different pre-strains: a lift coefficient; b drag coefficient; c lift-to-drag ratio

4.5 Effect of pre-strain

The effect of the pre-strain on the dynamic response of the 2D PR membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ is studied in this section. The range of the pre-strain considered here is [0, 0.1] and the increment is taken as 0.005. In Fig. 21, the computed mean aerodynamic performances of the membrane wing are presented. As shown in Fig. 21a, the mean lift coefficient is increased slightly first from 0.998 to 1.02 when $\delta _{0}$ is increased from 0 to 0.005 and then decreased almost linearly from 1.02 to 0.970 at $\delta _{0} =0.005$–0.02. Then, it jumps suddenly by 8.2% from 0.97 to 1.05 at $\delta _{0}=0.025$ and then decreased generally at $\delta _{0}=0.025$–0.06. At $\delta _{0}=0.065$, the mean lift coefficient is dropped significantly from 1.0 to 0.923. Finally, it is decreased continuously from 0.923 to 0.820 when $\delta _{0}$ is further changed from 0.06 to 0.1. Similar with the lift curve in Fig. 21a, three branches are also observed in the drag curve in Fig. 21b. As seen in the figure, the mean drag coefficient of the membrane wing is first decreased slightly and then increased at $\delta _{0}=0$–0.02. When $\delta _{0}$ is increased a little bit from 0.02 to 0.025, the mean drag coefficient is increased greatly from 0.116 to 0.132. Then, it is changed nearly linearly from 0.132 to 0.153 at $\delta _{0}=0.025$–0.06. At $\delta _{0}=0.065$, the mean drag coefficient is dropped by 9.2% from 0.153 to 0.139 and at last it is decreased smoothly from 0.139 to 0.133 when $\delta _{0}$ is further increased from 0.065 to 0.1. Different from the mean lift and drag coefficients, large jump or drop of the mean lift-to-drag ratio is not found in the computed range of the pre-strain. As shown in Fig. 21c, the mean lift-to-drag ratio is increased slightly from 8.84 to 9.16 when $\delta _{0}$ is increased from 0 to 0.005. Then, it is decreased gradually from 9.16 to 6.14 in the rest of the pre-strain range computed.

Fig. 22

Bifurcation diagram at the centre point of the membrane wing at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ with respect to $\delta _{0}$

Fig. 22 displays the bifurcation diagram at the membrane centre when the pre-strain is increased from 0 to 0.1. As shown in the bifurcation diagram, the state of the dynamic response of the membrane at $\alpha =8^{\circ }$ and $\textit{Re}=2500$ varies a lot at $\delta _{0}=0$–0.1. First, when $\delta _{0}$ is increased from 0 to 0.02, the vibrating state at the membrane centre is not changed although its mean deflection and amplitude are decreased continuously. Then, with slight increase of $\delta _{0}$ from 0.02 to 0.025, however, the amplitude is amplified by about 19 times while the dominant frequency is decreased by 62.7% from 1.26 to 0.47, as shown in Figs. 22, 23a, b. Such change of the vibration state from one LCO to another LCO is very similar with that observed in our previous work [29]. It seems that there are two stable LCOs near $\delta _{0}$ =0.02 and the system jumps from one to the other when $\delta _{0}$ is increased from 0.02 to 0.025. Then, the stability of the LCO with larger amplitude is deteriorated with further increase in the pre-strain in $\delta _{0}=0.025$–0.06. As displayed in Figs. 22 and 23c, d, the dynamic response becomes quasi-periodic near $\delta _{0}=0.03$ and irregular at $\delta _{0} =0.035$–0.06. Then, the system becomes more and more stable when $\delta _{0}$ is increased from 0.06 to 0.075. As seen in Figs. 22 and 23e, f, the vibrating state turns back to quasi-periodic near $\delta _{0}=0.065$ and period 1 near $\delta _{0}=0.075$, respectively. Finally, the state of the dynamic response at the membrane centre is no longer changed at $\delta _{0}=0.075$–0.1.

Fig. 23

Phase portrait and spectrogram of the membrane centre at $\alpha =8^{\circ }$ and ${ Re}=2500$ with different pre-strains: a $\delta _{0}=0.02$; b $\delta _{0}=0.025$; c $\delta _{0}=0.03$; d $\delta _{0}=0.06$; e $\delta _{0}=0.065$; f $\delta _{0}=0.075$

In Fig. 24, the $\xi$–t diagrams at different pre-strains are presented to illustrate the effect of the pre-strain on the dynamic response of the whole membrane wing at $\alpha =8^{\circ }$ and ${ Re}=2500$. As shown in Fig. 24a, b, the response of the membrane is changed from the third mode standing wave to the second mode standing wave when a very small pre-strain of $\delta _{0}=0.005$ is imposed on the membrane. Then, the second mode response is not affected very much except that the amplitude near the trailing edge is decreased slightly at $\delta _{0}= 0.005$–0.02, as seen in Fig. 24b, c. At $\delta _{0}=0.025$, the vibrating state turns to the first mode standing wave and the maximum amplitude is increased abruptly from 0.006 to 0.02 in Fig. 24d. Then, the first mode response becomes more and more unstable when $\delta _{0}$ is further increased from 0.025 to 0.06, as shown in Fig. 24e, f. When $\delta _{0}$ is increased slightly from 0.06 to 0.065, the response over the membrane becomes more regular and the increase in the dominant frequency is apparent in Fig. 24g. Finally, vibration of the membrane wing turns back to the stable first mode standing wave at $\delta _{0}=0.07$–0.1, as shown in Fig. 24h. It can be seen from Fig. 24 that, in general, increasing the pre-strain will decrease the mode number; however, its effect on the stability of the membrane response is not apparent. Fig. 24i also presents the mean membrane deflections at different pre-strains. As seen in the figure, with increase of $\delta _{0}$, the membrane deflection is decreased continuously and the point with maximum deflection is moved towards the leading edge. It seems that the pre-strain and rigidities have similar effect on the time-averaged deflection of the PR membrane wing.

Fig. 24

$\xi$–t diagram for vibration from the mean membrane deflection at different pre-strains: a $\delta _{0}=0$; b $\delta _{0}=0.005$; c $\delta _{0}=0.02$; d $\delta _{0}=0.025$; e $\delta _{0}=0.03$; f $\delta _{0}=0.06$; g $\delta _{0}=0.065$; h $\delta _{0}=0.075$; i mean deflections

Figure 25 shows the instantaneous streamlines at $\alpha =8^{\circ }$ and ${ Re}=2500$ with different pre-strains. Comparing Fig. 25a with Fig. 25b, it can be found that the shedding point of the separation bubble is moved forward a lot when very small pre-strain of $\delta _{0}=0.005$ is imposed on the membrane. Again, since this has increased the fluctuating region on the upper surface, the response of the membrane wing is changed from the third mode sanding wave to the second mode standing wave. When $\delta _{0}$ is increased from 0.005 to 0.02, the flow patterns around membrane wing is not changed very much except that the shedding point of the separation bubble is further moved towards the leading edge and the scale of the leading-edge vortex is increased, as shown in Fig. 25b, c. As a result, the dynamic response of the membrane wing at $\delta _{0}=0.02$ is similar with that at $\delta _{0}=0.005$, as seen in Fig. 24b, c. When $\delta _{0}$ is further increased from 0.02 to 0.025, the vortex structure is changed a lot and three vortices appear near the leading edge. In this case, only one of the leading-edge vortices is shed periodically and its excitation on the membrane structure is dominant. Therefore, the response of the membrane in Fig. 24d becomes the first mode. At $\delta _{0}=0.03$, all of the three leading-edge vortices begin to shed with time and the evolution of the vortices on the upper surface of the membrane wing becomes more complex, as shown in Fig. 25e. This change in flow flied has resulted in the quasi-periodic response of the membrane wing in Figs. 23c and 24e. With further increase of $\delta _{0}$ from 0.03 to 0.06, the vortex structure becomes more and more complex and the response of the membrane wing also becomes more irregular, as shown in Figs. 24e, f and 25e, f. At $\delta _{0}=0.065$, not all but only one of the leading-edge vortices is shed in Fig. 25g, which is very similar with the case at $\delta _{0}=0.025$ in Fig. 25d. In response, the vibrating state in Fig. 24g turns back to the first mode. Finally, the vortex structure is observed nearly unchanged at $\delta _{0}=0.07$–0.1, as seen in Fig. 25h. As a result, the first mode response is also not changed when $\delta _{0}$ is further increased from 0.07 to 0.1, as shown in Fig. 24h.

Fig. 25

Instantaneous streamlines around the membrane wing at different pre-strains: a $\delta _{0}=0$; b $\delta _{0}=0.005$; c $\delta _{0}=0.02$; d $\delta _{0}=0.025$; e $\delta _{0}=0.03$; f $\delta _{0}=0.06$; g $\delta _{0}=0.065$; h $\delta _{0}=0.075$

5 Conclusions

Bifurcations of the nonlinear dynamic responses of a fixed 2D PR membrane wing with respect to the flow and structure parameters are investigated numerically using a CBS-based FSI algorithm. It can be found from the numerical results that the angle of attack, Reynolds number, rigidity and pre-strain have great influence on the unsteady FSI process of the fixed PR membrane wing in the laminar flow regime considered. At very small angles of attack or Reynolds numbers, the flow field around the membrane wing is steady and the membrane wing will eventually stay at a static equilibrium position. With increase in the angle of attack or Reynolds number, the trailing-edge vortices will be shed first. Under their periodic excitation, the membrane wing will vibrate in the form of standing wave. Moreover, the mode number of the standing wave response will be decreased with the increase in the angle of attack, Reynolds number, rigidity or pre-strain, due to the movement of the shedding points of one of the trailing-edge vortices (or separation bubble) towards the leading edge. Therefore, the Hopf bifurcation or onset of the flutter/LCO of the fixed 2D PR membrane wing is triggered by the shedding of the trailing-edge vortices. In addition, it is also found that the shedding of the leading-edge vortex at higher angles of attack, Reynolds number and pre-strain will change significantly the vortex structure on the upper surface of the PR membrane wing and lead to very irregular response of the membrane structure with much larger amplitude. At high Reynolds numbers, the irregular response of the membrane wing is partly due to the fluctuation of the flow.