Numerical study of flow-induced vibrations of cylinders under the action of nonlinear energy sinks (NESs)

Abstract

An isolated two-dimensional circular cylinder with two linear degrees of freedom, parallel and perpendicular to the free-stream direction, and owning a nonlinear energy sink (NES) is investigated by fluid–structure interaction (FSI) simulations to assess vortex-induced vibrations (VIV) at moderate Reynolds numbers. Subsequently, the wake-induced vibration (WIV) of a pair of identical cylinders under the action of two NES in a tandem arrangement and in a proximity–wake interference regime is explored using the same approach. The NES parameters (mass, nonlinear stiffness and damping) are investigated to determine their effects on the dynamic response of a single degree of freedom (in transverse flow direction) coupled system by a reduced-order model based on an experimentally validated van der Pol oscillator. The CFD model coupled with FSI method is also validated against VIV experimental data for an isolated cylinder in a uniform flow. The study is aimed to investigate the effect of the passive suppression NES device on VIV and WIV. The amplitude response, trajectories of cylinder motion and temporal evolutions of vortex shedding are obtained by conducting a series of numerical simulations. It is found that placing a tuned NES in the cylinders can provide good suppression effect; however, the effectiveness is function of the reduced velocity.

1 Introduction

Vortex-induced vibration (VIV) is a flow-induced vibration (FIV) phenomenon occurring when a structure is driven by cyclic loads produced by vortex shedding [1]. VIV commonly occurs in ocean and civil engineering structures; it is due to flows past ocean risers, cables, bridges, chimneys and buildings, just to name but a few. In case where the vortex shedding frequency ($f_\mathrm{v} )$ is in the vicinity of the structure natural frequency of oscillation ($f_\mathrm{n} )$, the system may respond with a “lock-in” or “synchronization” phenomenon that produces high-amplitude vibration and could cause severe fatigue and critical failure of structural elements [2,3,4,5,6]. Wake-induced vibration (WIV) produced on a downstream structure occurs in tandem arrangement, and it is also a typical FIV phenomenon. The structure located upstream is exposed to a free uniform current, and Reynolds number (Re) of these two structures is decided by the current velocity of the upstream structure.

Assuming, for example, two cylinders in tandem arrangement, vortices shed from the front cylinder not only will impact on the rear cylinder, but also will interfere with its own vortex shedding process forming the downstream wake. Consequently, the rear cylinder is immersed in a disturbed flow region which is created by the wake of the front cylinder. The response of the rear cylinder is dissimilar to the typical VIV, but a type of vibration that is influenced by the wake coming from the upstream cylinder and featured by the amplitude response continue to grow during high reduced velocities ($U_\mathrm{r} )$, and normally the maximum amplitude response is larger than that of a typical VIV [1, 5, 7,8,9,10]. The reduced velocity is defined as $U_\mathrm{r} =U/f_\mathrm{n} {}D$, where U, D and $f_\mathrm{n}$ are the flow speed, cylinder diameter and cylinder natural frequency in still water or air, respectively. Since FIV may lead to structural fatigue or damage, VIV and WIV of cylindrical structures and their suppression are of critical importance for practitioners. Indeed, in the past 20 years, many approaches have been proposed in order to suppress VIV responses, including active [11,12,13,14] and passive [15,16,17,18,19,20,21,22] suppression solutions. Often excessive power and complex actuation limit the practical application of active control technologies [11, 12]. Most of the passive suppression mechanisms resource to the addition of appendages to the external cylinder, including the use of small rods [16, 17], helical [20], faring [21] and shroud [22] which may lead to undesirable structural issues of their own, including the increase in mass ratio and possible increase in the drag coefficient.

A nonlinear energy sink (NES) is a strongly nonlinear local attachment that can pump energy from the primary system is linked to and to reduce the vibration amplitude of such a system without changing its natural frequencies. NES solutions have been developed to reduce unwanted structural vibration in different engineering applications given their ability to mitigate vibrations in a broad frequency range [23,24,25,26,27,28]. Since the NES can absorb the vibration energy generated by general broadband transient excitations, it is an attractive control strategy for structural vibration suppression. In recent years, Tumkur et al. [29,30,31] introduced an NES passive control approach to suppress the VIV response of a sprung cylinder. The authors used a variational multiscale finite-element methodology to study the VIV of the flow cylinder–NES coupled system and demonstrated that the NES played a significant role in suppressing the VIV response with suitable NES parameters. Mehmood et al. [32] investigated the effects of NES parameters (mass and damping) on the VIV response of a cylinder system by computational fluid dynamics (CFD) model coupled with structure and NES. Significant suppressing effects of the NES were obtained with properly tuned parameters. Dai et al. [33] further investigated the passive suppression mechanism of VIV of the cylinder by NES, and a numerical model was established using a van der Pol oscillator coupling to the structural dynamics with NES. The results showed that the coupled system dynamic behaves are periodic, aperiodic and multiple stable responses, which depended upon the values of the NES parameters. The significant reductions in the VIV responses were obtained with properly tuned NES parameter.

It is worth noting that the research performed by Tumkur et al. [29,30,31], Mehmood et al. [32] and Dai et al. [33] about VIV suppression was limited to one degree of freedom (1-DOF) vibration of the cylinder. However, in more realistic conditions, the cylinder can also vibrate in the inflow direction, which may lead to an effect on the cross-flow (CF) direction response [34]. It also should be noted that research by Tumkur et al. [29,30,31] and Mehmood et al. [32] was performed at very low Reynold’s number ($Re < 140$) and one or two Re from the “lock-in” range, which is clearly inadequate if the intent is to assess the dynamics behavior of the entire “lock-in” region when considering the influence of NES parameters.

To properly understand the dynamic behavior and effect of the NES and its parameters on the VIV of the cylinder within the selected $U_\mathrm{r}$ region which includes in and out the typical “lock-in” region, further investigations are warranted. As such, the dynamic behavior of VIV and WIV of cylinders under the action of NESs for selected $U_\mathrm{r}$ and turbulent flows (Re from 2300 to 5600) based on more accuracy models, considering also the inflow direction vibration motion, constitutes the topic of this paper. The NES parameters are, firstly, studied efficiently on the basis of the van der Pol oscillator coupled with structure and NES. Then, the dynamics of two- degrees-of-freedom (2-DOF) VIV of one cylinder with and without NES for a range of $U_\mathrm{r}$ is investigated by fluid–structure interaction (FSI) model coupled with NES. Finally, the dynamic behavior of WIV of a pair of identical cylinders under the action of two NESs is preliminarily explored using the same approach.

The rest of the paper is organized as follows. In Sect. 2, the problem description of three different models is introduced. In Sect. 3, the modeling of these three models and validations is discussed. Section 4.1 presents the effect of NES parameters on this coupled flow cylinder and NES system, Sect. 4.2 illustrates the dynamic behaviors of 2-DOF VIV of the single cylinder under the action of NES, while Sect. 4.3 explores the dynamic behaviors of 2-DOF WIV of a pair of cylinders in a tandem arrangement under the action of NES. Finally, in Sect. 5 concluding remarks are offered.

2 Problem description

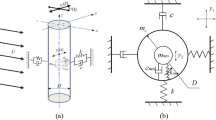
In order to obtain appropriate NES parameters for 2-DOF VIV and WIV FSI model as to explore the circular cylinders dynamic response behavior, the reduced model proposed in [33] is considered first. This model assumes a single circular cylinder constrained to oscillate transversely (y-direction) in a uniform current of free-stream velocity U (x-direction) following the van der Pol oscillator dynamics. This model is proposed here also to explore NES parameters, including structural mass, damping and nonlinear stiffness. The model, named Model I, having 1-DOF is shown in Fig. 1a. The circular cylinder of diameter D is supported by the spring and damper. In order to suppress the VIV of the single cylinder, an NES consisting of mass $m_\mathrm{nes}$, nonlinear stiffness $k_\mathrm{nes}$ and a linear damper $c_\mathrm{nes}$ is considered. It should be noted that the NES is placed inside of the cylinder to avoid the influence of the flow on the NES system. Moreover, the mass of the cylinder is reduced as to maintain unchanged both the combined mass of the cylinder and NES and the natural frequency of the coupled system. To establish a more accurate model and study the trajectories of cylinder motion, the amplitude response and the temporal evolution of the vortex shedding of the cylinder under the action of the NES, the in-line (IL) flow direction vibration on the VIV or WIV of the cylinders is considered in Models II and III. These models are established using CFD models coupled with FSI and NES and are both shown in Fig. 1b, c. Close-up view of the cylinder with NES which have 2-DOF is shown in Fig. 1d. Boundary conditions used in the CFD simulations are also specified in Fig. 1b, c. For both Models II and III, the computational domain is a rectangle region in which the Re #, based on upstream cylinder velocity, diameter of the cylinder and kinematic viscosity of fluid, changes within the range 2300–5600. The mass, stiffness, structural damping ratio and diameter of the cylinder are $m= 15.708\, \hbox {kg}$, $k = 2530.1 \,\hbox {N}/\hbox {m}$, $\varsigma = 0.0013$ and $D= 0.02\, \hbox {m}$, respectively. The natural frequency in still water is $f_\mathrm{n} = 2 \,\hbox {Hz}$. As a result, in the carried simulations the speed $U_\mathrm{r}$ changes from 3 to 7, which correspond to a Re # within the range 2300–5600.

Fig. 1

Sketch of fluid flow over cylinders under action of NES: a Model I; b computational domain with boundary conditions for the single cylinder of Model II; c computational domain with boundary conditions for a pair of cylinders of Model III; and d close-up view of the 2-DOF vibration cylinder with NES

Nine different $U_\mathrm{r}$ values are considered to examine the effect of flow velocity on the VIV response of the cylinders with and without NES. As shown in Fig. 1c, d, the center of the upstream cylinder is 10 times the diameter of the cylinder (10D) from the inlet boundary, while the outlet boundary is placed aft at 30D. In addition, the lateral boundaries are placed at 10D from the centerline, and the overlapping meshes zone around the cylinder cover 3D. For Model 3, the distance between upstream cylinder and downstream cylinder is 5D. No-slip boundary condition is imposed on the cylinders, and the top and bottom boundary conditions are of slip-wall type with $\partial u/\partial y = 0$ and $v = 0$, where u and v are velocity in x-and y-directions, respectively. The model inflow and outflow boundaries are velocity inlet and pressure outlet, respectively.

3 Mathematical modeling and numerical approach

Using Newton’s second law, the governing equations of VIV for the elastically mounted cylinders coupled with NES, as shown in Fig. 1, and subjected to the external fluid forces are given as:

$$\begin{aligned}&m{\ddot{x}}_1 +c{\dot{x}}_1 +kx_1 =F_\mathrm{D} (t) \end{aligned}$$

(1)

$$\begin{aligned}&(m-m_\mathrm{nes} ){\ddot{y}}_1 +c{\dot{y}}_1 +ky_1 +c_\mathrm{nes} ({\dot{y}}_1 \nonumber \\&\quad -{\dot{y}}_2 )+k_\mathrm{nes} (y_1 -y_2 )^{3}=F_\mathrm{L} (t) \end{aligned}$$

(2)

$$\begin{aligned}&m_\mathrm{nes} {\ddot{y}}_2 +c_\mathrm{nes} ({\dot{y}}_2 -{\dot{y}}_1 )+k_\mathrm{nes} (y_2 -y_1 )^{3}=0 \end{aligned}$$

(3)

where ($\cdot )$ implies derivative with respect to the dimensional time t. The parameters m, c, and k are the mass, damping and stiffness of the cylinder, respectively, while $m_\mathrm{nes}$, $c_\mathrm{nes}$ and $k_\mathrm{nes}$ are the mass, damping and nonlinear stiffness of the NES, respectively. $F_\mathrm{D} (t)$ and $F_\mathrm{L} (t)$ represent the time-dependent external forces (drag and lift, respectively) exerted by the fluid flow on the cylinder. In addition, $x_1 , {\dot{x}}_1$ and ${\ddot{x}}_1$ denote the IL flow direction displacement, velocity and acceleration of the cylinder, respectively, while $y_1 , {\dot{y}}_1 , {\ddot{y}}_1$ and $y_2 , {\dot{y}}_2 , {\ddot{y}}_2$ represent the same quantities associated with the CF direction motion of the cylinder and NES. It should be noted that mass, damping and stiffness parameters are defined per unit length since all models are in two-dimensional. As indicated earlier, the mass of the cylinder has been reduced to ensure the combined mass of the cylinder and NES remains constant [23].

Fig. 2

Validation of Model I for two different mass ratio ($m^{*})$ using van der Pol oscillator: a comparison of non-dimensional maximum displacement amplitudes ($|y_1 |_{\max } /D)$ of the cylinder versus reduced velocity with experiments from [34]; b time histories of the vibration displacement ($y_1 /D)$ of the cylinder when $U_\mathrm{r} =7$; c power spectra for the cylinder in the case of $U_\mathrm{r} =7$; d frequency ratio of the cylinder versus reduced velocity

The motions of the cylinders under the action of the NES are described by the following equations:

$$\begin{aligned}&{\ddot{x}}_1 +2\varsigma \omega _0 {\dot{x}}_1 +\omega _0 ^{2}x_1 =\frac{F_\mathrm{D} (t)}{m} \end{aligned}$$

(4)

$$\begin{aligned}&(1-\beta ){\ddot{y}}_1 +2\varsigma \omega _0 {\dot{y}}_1 +\omega _0 ^{2}y_1 \nonumber \\&\qquad +\,2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_1 -{\dot{y}}_2 )+\frac{\gamma }{D^{2}}\omega _0 ^{2}(y_1 -y_2 )^{3} \nonumber \\&\quad =\frac{F_\mathrm{L} (t)}{m} \end{aligned}$$

(5)

$$\begin{aligned}&\beta {\ddot{y}}_2 +2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_2-{\dot{y}}_1 )+\frac{\gamma }{D^{2}}\omega _0 ^{2}(y_2 -y_1 )^{3}=0 \end{aligned}$$

(6)

in which

$$\begin{aligned} \omega _0= & {} \sqrt{\frac{k}{m}}, \quad \zeta =\frac{c}{2\sqrt{km}}, \quad \zeta _\mathrm{nes} =\frac{c_\mathrm{nes} }{2\sqrt{km}}, \nonumber \\ \beta= & {} \frac{m_\mathrm{nes} }{m}, \quad \gamma =\frac{k_\mathrm{nes} \cdot D^{2}}{k} \end{aligned}$$

(7)

For simplicity, the variable $\xi ={\varsigma _\mathrm{nes} }/\varsigma$ will be used later.

3.1 Mathematical modeling of model I and validation

3.1.1 Mathematical modeling of model I

The van der Pol oscillator [35, 36] is used to compute the cylinder wake and to express the VIV force in Model I (Fig. 1a). Such model also provides an efficient characterization of the dynamic behavior of VIV response under the action of NES with various NES parameters. The VIV loads of the cylinder include two elements; one is the basic fluid effects which are related to the drag coefficient and the vibration velocity of the cylinder; the other one is the effects of vortices, which are associated with the unsteady lift coefficient on the cylinder. As a result, the vortex-induced force $F_\mathrm{L} (t)$ of equation (2) can be empirically expressed as [33]:

$$\begin{aligned} F_\mathrm{L} (t)=-\frac{1}{2}C_\mathrm{D} \rho _\mathrm{f} DU{\dot{y}}_1 +\frac{1}{4}C_{\mathrm{L}_0 } \rho _\mathrm{f} DU^{2}q(t) \end{aligned}$$

(8)

where $C_\mathrm{D}$ and $C_{\mathrm{L}_0 }$ are the mean sectional drag coefficients and steady lift coefficients in the transverse direction, taken as 1.2 and 0.3 [36] in the region of well-developed wakes, respectively; $\rho _\mathrm{f}$ is the density of fluid flow; q(t) is defined as the reduced lift coefficient, which describes the behavior of the near wake and can be modeled by the following van der Pol equation [36]:

$$\begin{aligned} {\ddot{q}}+\lambda \omega _s (q^{2}-1){\dot{q}}+\omega _s^2 q=\frac{P}{D}{\ddot{y}}_1 \end{aligned}$$

(9)

Herein, $\omega _s$ is the vortex shedding frequency defined as $\omega _s =2\pi \cdot S_t \cdot U/D$, $S_t$ is the Strouhal number, and the value chosen in the present study is 0.2, consistent with the Re # range of 2300–5600. The values found for the empirical parameters $\lambda$ and P are 0.24 and 15, respectively, similarly to what reported in [36]. According to Eqs. (5), (6), (8) and (9), the governing equations of Model I which only have 1-DOF can be expressed as:

$$\begin{aligned}&(1-\beta ){\ddot{y}}_1 +2\varsigma \omega _0 {\dot{y}}_1 +\omega _0^2 y_1 +2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_1 -{\dot{y}}_2)\nonumber \\&\qquad +\,\gamma \frac{\omega _0^2 }{D^{2}}(y_1 -y_2 )^{3} \nonumber \\&\quad =-\frac{1}{2m}C_\mathrm{D} \rho _\mathrm{f} DU{\dot{y}}_1 +\frac{1}{4m}C_{\mathrm{L}_0 } \rho _\mathrm{f} DU^{2}q(t) \end{aligned}$$

(10)

$$\begin{aligned}&{\ddot{q}}+\lambda \omega _s (q^{2}-1){\dot{q}}+\omega _s^2 q=\frac{P}{D}{\ddot{y}}_1 \end{aligned}$$

(11)

$$\begin{aligned}&\beta {\ddot{y}}_2 +2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_2 -{\dot{y}}_1 )+\gamma \frac{\omega _0^2 }{D^{2}}(y_2 -y_1 )^{3}=0 \end{aligned}$$

(12)

Equations (10–12) can be solved by ordinary differential equations (ODE-45) time marching scheme. The initial conditions are set equal to $y_1 = 0.000001$, $y_2 ={\dot{y}}_1 ={\dot{y}}_2 =q={\dot{q}}=0$, and the selected time step is 0.01 s. It should be noted that the initial conditions have significant effect on the response of the primary circular cylinder [32].

3.1.2 Validation of model I

The usefulness of the model should be demonstrated as the first logical step. To validate the van der Pol oscillator and the coupling scheme, the present simulation results have been compared with the experimental data of Stappenbelt et al. [34]. For this purpose, the response of the cylinder without the NES was considered using the same parameters of the experimental work reported in [34]. It is noted that the mass m of Eq. (10) of Model I should take into account both the mass of the cylinder and the added fluid mass. The mass ratio is defined as $m^{*}=m/m_\mathrm{f} -1$, where fluid added mass $m_\mathrm{f} =0.25\rho _\mathrm{f} \pi D^{2}$ [34]. The mass ratio parameter is therefore the ratio of the oscillating cylinder mass to the displaced fluid mass. For the cylinder of experimental work [34], one group physical parameters are $D = 0.0554\, \hbox {m}$, $\zeta = 0.0056$, $\omega _0 = 7.486$ rad/s, $m^{*} = 6.54$, and another group of parameters are D = 0.0554 m, $\zeta = 0.0057$, $\omega _0 = 6.0276 \,\hbox {rad/s}$, $m^{*} = 10.63$. Figure 2a shows the comparison of non-dimensional maximum displacement amplitudes ($|y_1 |_{\max } /D)$ of the cylinder versus $U_\mathrm{r}$ with the experimental measurements of Stappenbelt et al. [34] for two different values of mass ratios. It follows from the predicted numerical results of Fig. 2a that van der Pol oscillator can capture the resonance characteristics of the cylinder compared with the experiment data [34]. However, the magnitudes of VIV amplitudes are quite different from that of experimental results, especially at the $U_\mathrm{r}$ region from 3 to 6. This is because there are few empirical parameters in the van der Pol oscillator model, and the simulation results depend heavily on the selection of these parameters. The vibration displacement ($y_1 /D)$ time history of the cylinder for two mass ratios and $U_\mathrm{r} = 7$ is shown in Fig. 2b, while their frequency spectrum curves are depicted in Fig. 2c. The shedding frequency was $f_\mathrm{v} = 1.24 \,\hbox {Hz}$ for $m^{*}= 6.54$ with a cylinder natural frequency $f_\mathrm{n} = 1.1914\, \hbox {Hz}$ and $f_\mathrm{v} = 0.99\, \hbox {Hz}$ for $m^{*} = 10.63$ with a cylinder natural frequency $f_\mathrm{n} = 0.9593\, \hbox {Hz}$. The two simulations imply that $f_\mathrm{v} /f_\mathrm{n}$ = 1.0408 and 1.0320, respectively. The flow passing over the cylinder leads to separation of the boundary layer with alternating vortices shed with a specific frequency in the wake region. Similarly, all the shedding frequencies of the cylinder in the cases of various $U_\mathrm{r}$ from 2 to 16 are obtained. The “lock-in” phenomenon can be observed from the frequency responses. The vortex shedding frequency is extremely close to the cylinder natural frequency (i.e., $f_\mathrm{v} /f_\mathrm{n} \sim 1$) at a $U_\mathrm{r}$ range from 4 to 8 as shown in Fig. 2d, which causes the cylinder to oscillate with a high amplitude, as shown in Fig. 2a. Consequently, the wake oscillator model, describing the fluctuating lift force, can capture quite well the dynamic behavior of VIV response of the elastically mounted cylinder.

Fig. 3

Computational mesh: a close-up view of overset component and background meshes before (a) and after (b) hole cutting; c entire grid (background and overset component meshes) of Model II; d entire grid (background and a pair of overset component meshes) of Model III

Fig. 4

Validation of CFD model: a trajectories of the isolated 2-DOF cylinder at different $U_\mathrm{r}$; b and c power spectra for the cylinder for various $U_\mathrm{r}$; d and e comparison of amplitude and frequency ratio responses of the cylinder versus $U_\mathrm{r}$ with experiment data

Fig. 5

Temporal evolution of vortex shedding for flow over the elastic supported cylinder at $U_\mathrm{r} = 5$

Fig. 6

Effect of the mass ratios on the maximum oscillating amplitudes of a the cylinder; b the relative motion between the cylinder and the NES as a function of $U_\mathrm{r}$ when $\xi = 0.8$ and $\gamma = 0.8$.

Fig. 7

Time histories of the non-dimensional displacements ($y_1 /D, y_2 /\hbox {D})$ (a, c, e) and power spectral density (b, d, f) in the cases of $\beta = 0.03$ for a, b; $\beta = 0.1$ for c, d; and $\beta = 0.5$ for e, f when $U_\mathrm{r} = 5$, $\xi = 0.8$ and $\gamma = 0.8$

Fig. 8

Comparison of frequency ratios of the cylinder versus $U_\mathrm{r}$: a the $y_1$ and $y_2$ displacements responses’ frequency ratio in case of $\beta = 0.1$; b the $y_1$ displacement responses’ frequency ratio in cases of variable mass ratios

Fig. 9

Effect of the non-dimensional stiffness ratios on the maximum oscillating amplitudes of the cylinder and the relative motion between the cylinder and the NES as a function of $U_\mathrm{r}$: a, b when $\beta = 0.1$ and $\xi = 0.8$; c, d when $\beta = 0.03$ and $\xi = 0.8$

Fig. 10

Comparison of frequency ratios of the cylinder versus $U_\mathrm{r}$, the $y_1$ and $y_2$ displacements responses’ frequency ratio in case of $\gamma = 0.8$: a $\beta = 0.1$; c $\beta = 0.03$; the $y_1$ displacement responses’ frequency ratio in cases of non-dimensional stiffness ratios: b $\beta = 0.1$; d $\beta = 0.03$

3.2 Mathematical modeling and validation of models II and III

3.2.1 Mathematical modeling of models II and III

CFD is as a methodology able to predict quite accurately the aero/hydro dynamic loads for a range of fluid dynamic phenomena related to many geometrically complex, single or interacting multiple bluff bodies [1, 5,6,7, 16, 17]. In order to establish a more accurate cylindrical model with NES accounting for IL flow direction vibration effect and flow interaction between the cylinders, CFD methodology is coupled with the ODE model governing the motions of the cylinders and NES. The commercial available FLUENT$^{{\textregistered }}$ version 17.0 [37], its user-defined functions (UDFs) and overlapping meshes technology are used in this study. All simulations are run over 2 CPUs in parallel using the HP Z820 workstation. The flow over the cylinders is treated as unsteady and incompressible flow with constant fluid properties. The 2-D, time-dependent, incompressible Reynolds-averaged Navier–Stokes (RANS) equations, including equations for mass and momentum conservation, are formulated as follows:

Fig. 11

Response of the cylinder and NES ($y_1 /D,\;y_2 /D)$ in the cases of a $\gamma = 0.3$; b $\gamma = 0.8$; c $\gamma = 2$, and d $\gamma = 4$, when $U_\mathrm{r} = 5$, $\beta = 0.1$ and $\xi = 0.8$

$$\begin{aligned}&\frac{\partial \bar{{u}}_i }{\partial x_i }=0 \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial \bar{{u}}_i }{\partial t}+\frac{\partial \bar{{u}}_i \bar{{u}}_j }{\partial x_j }=-\frac{1}{\rho _\mathrm{f} }\frac{\partial \bar{{p}}}{\partial x_i }+\upsilon \nabla ^{2}\bar{{u}}_i -\frac{\partial {\bar{{u}}}'_i {\bar{{u}}}'_j }{\partial x_j } \end{aligned}$$

(14)

in which,

$$\begin{aligned} \overline{u_i^{\prime } u_j^{\prime } } ==\upsilon _t \left( {\frac{\partial u_i }{\partial x_j }+\frac{\partial u_j }{\partial x_i }} \right) +\frac{2}{3}k_t \delta _{ij} \end{aligned}$$

(15)

where $u_i$ represents the transient velocity component in i direction, while ${u}'_i$ is the fluctuation velocity component in i direction, and $u_i$ or ${u}'_i$ with a top bar represents its time average one; $x_i$, t, p and $\upsilon$ are the Cartesian coordinate in i direction, time, pressure and kinematic viscosity of fluid, respectively. In addition, $\upsilon _t$ is the turbulent viscosity and $k_t$ is the turbulent energy. The shear stress transport (SST) $k-\omega$ turbulence model developed by Menter [38] gives good predictions in simulating flows with adverse pressure gradients and flow separations, and it is carried out for closing the RANS equations [39, 40]. The details of SST$k-\omega$ turbulence model can be found in Menter [38]. Once the flow field is obtained, the drag coefficient $C_\mathrm{D}$ and lift coefficient $C_\mathrm{L}$ can be calculated from the surface pressure of oscillation cylinder boundary. The drag ($F_\mathrm{D} )$ and lift ($F_\mathrm{L} )$ forces per unit length acting on the cylinder can be expressed as:

$$\begin{aligned} F_\mathrm{D}= & {} \frac{1}{2}C_\mathrm{D} \rho _\mathrm{f} U^{2}D \end{aligned}$$

(16)

$$\begin{aligned} F_\mathrm{L}= & {} \frac{1}{2}C_\mathrm{L} \rho _\mathrm{f} U^{2}D \end{aligned}$$

(17)

Fig. 12

Effect of the damping ratios on the maximum oscillating amplitudes (a, c) and frequency ratios (b, d) of the cylinder as a function of $U_\mathrm{r}$ in the cases of $\beta = 0.1$ for a, b and $\beta = 0.03$ for c, d when $\gamma = 0.8$

Fig. 13

Various models’ simulation results: a maximum oscillating amplitude; b frequency ratios of the cylinder with and without NES versus $U_{r}$

Fig. 14

Trajectories of 2-DOF VIV of one isolated cylinder at different $U_\mathrm{r}$ in cases of various conditions: a without NES; b with NES, $\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8$; c with NES, $\beta = 0.1$, $\gamma = 2$, $\xi = 0.8$; d with NES, $\beta = 0.5$, $\gamma = 0.8$, $\xi = 0.8$

Thus, according to equation (4–6), (16) and (17), the governing equations for Model II and III are cast as:

$$\begin{aligned}&{\ddot{x}}_1 +2\varsigma \omega _0 {\dot{x}}_1 +\omega _0 ^{2}x_1 =\frac{1}{2}\frac{C_\mathrm{D} \rho _\mathrm{f} U^{2}D}{m} \end{aligned}$$

(18)

$$\begin{aligned}&(1-\beta ){\ddot{y}}_1 +2\varsigma \omega _0 {\dot{y}}_1 +\omega _0 ^{2}y_1 +2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_1 -{\dot{y}}_2 )\nonumber \\&\quad +\frac{\gamma }{D^{2}}\omega _0 ^{2}(y_1 -y_2 )^{3} =\frac{1}{2}\frac{C_\mathrm{L} \rho _\mathrm{f} U^{2}D}{m} \end{aligned}$$

(19)

$$\begin{aligned}&\quad \beta {\ddot{y}}_2 +2\varsigma _\mathrm{nes} \omega _0 ({\dot{y}}_2 -{\dot{y}}_1 ) +\frac{\gamma }{D^{2}}\omega _0 ^{2}(y_2 -y_1 )^{3}=0\nonumber \\ \end{aligned}$$

(20)

Runge–Kutta fourth-order (RK4) method [41, 42] is employed to solve ODE Eqs. (18–20) for the cylinders with RANS equations (Eqs. 13, 14) to obtain the velocity ${\dot{x}}_1 ,{\dot{y}}_1 ,{\dot{y}}_2$ and position $x_1 ,y_1 ,y_2$ of the cylinder and the NES. All the FSI equations with NES are coded in the UDF of CFD software FLUENT$^{{\textregistered }}$, and the UDF code are presented in Appendix. The initial conditions are set equal to $x_1 (0)={\dot{x}}_1 (0)=y_1 (0)={\dot{y}}_1 (0)=y_2 (0)={\dot{y}}_2 (0)=0$, and the time step is 0.01s.

Fig. 15

Maximum oscillating amplitude of the cylinder (a) and the relative motion between the cylinder and NES (b) versus $U_\mathrm{r}$ when $\xi = 0.8$

In this situation, the dynamic mesh technology should be carried out to perform mesh deformation based on the motion of the cylinder boundaries. In order to update grid successfully, computational domain from overlapping meshes, which also known as Chimera or overset methodology, is adopted, and it is shown in Fig. 3.

This technology offered a facile way to build the complete mesh which can avoid the negative mesh problem due to the large motion of the cylinder [37]. The moving overlapping grids used for the rectangular fluid domain around the cylinders are composed of a static background grid and overset component meshes.

Fig. 16

Comparison of frequency ratios of the cylinder versus $U_\mathrm{r}$, $y_1$, $y_2$ and $C_\mathrm{L}$ responses’ frequency ratio in case of a $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$; b $y_{1}$ responses’ frequency ratio in various conditions

Figure 3a shows an overset mesh before the hole has been cut. Hole cutting is a process by which lying outside of the flow region (that is, inside bodies and outside of the computational domain) are marked as dead cells. This is achieved by marking all the grids that are cut by physical boundary zones, and marking seed cells determined to lie outside the flow region for subsequent flood filling of dead cells. The result of this flood filling is a valid overset mesh with maximum mesh overlap [37].

Fig. 17

Temporal evolution of vortex formations for flow over an isolated cylinder with and without NES at $U_\mathrm{r} = 5$: a without NES; b with NES, $\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8$

Fig. 18

Time histories of the non-dimensional displacements ($y_1 /D{}\;\hbox {,}\;y_2 /D)$ (a, c, e) and power spectral density (b, d, f) in the cases of $U_\mathrm{r}= 3.5$ for a, b; $U_\mathrm{r}= 5$ for c, d; and $U_\mathrm{r} = 7$ for e, f when $\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8$

Figure 3b shows an overset mesh after hole cutting process and have valid mesh transition regions, which can offer high-quality data interpolation between background and overset component meshes. For one cylinder, one overset component grid is assigned. Model II has one overset component mesh (see Fig. 3c), while Model III has a pair of overset component mesh (see Fig. 3d). The overset component mesh of cylinders with high quality is used to simulate the viscous flows and wake in near field. The grid utilizes 15,731 cells background mesh for Model II and 22,035 cells background mesh for Model III, with 5262 cells overset component mesh, while the location of the first row of cells is such that $Y^{+}<1$. Moreover, since the flow is incompressible, the pressure- based algorithm is selected and the coupled algorithm is chosen to solve the pressure–velocity coupling scheme. The second-order upwind method is used for spatial discretization. The convergence criteria for the residual of each parameter are smaller than $10^{-5}$.

Fig. 19

Time histories of the non-dimensional displacements ($y_1 /D)$ (a) and power spectral density; b in the cases of $U_\mathrm{r} = 3.5$, 5 and 7 when $\beta = 0.5$, $\gamma = 0.8$ and $\xi = 0.8$

3.2.2 Model validation

To confirm the accuracy of the CFD numerical model, 2-DOF VIV of a single cylinder with elastic supports in a uniform current is investigated against the experimental results by Khalak and Williamson [4]. The parameters selected for this validation are $m = 2.7325\, \hbox {kg}$, $\varsigma = 0.00542$, $k = 17.26\, \hbox {N/m}$ and $f_\mathrm{n} = 0.4\, \hbox {Hz}$ [4]. In the present work simulations and the experiment that performed in [4], $U_\mathrm{r}$ is increased from 0 to 16, which corresponds to a Re # ranging from 0 to 7000. The time step chosen for the validation simulations is 0.005 s.

Figure 4a shows the trajectories of the isolated 2-DOF cylinder at various $U_\mathrm{r}$. The combination of IL and CF directions vibrations is such the cylinder displays a figure “8” motion. The synchronization region is from $U_\mathrm{r}$ = 4–10, where the amplitude of oscillation is higher than for other speeds. The temporal evolution of the vortex shedding from t = 75–78.5 s for the elastically supported cylinder at $U_\mathrm{r} = 5$ is presented in Fig. 5. It displays P+S vortex shedding pattern (sheds a single vortex and a vortex pair per cycle) which has the relation with large-amplitude vibration of the cylinder in the wake. The initial position of the cylinder (marked as dotted line in Fig. 5) is used to recognize the cylinder’s displacement. The trajectory of the cylinder from t = 75–78.5 s (every 0.25 s mark location of the center of the circle as a point) in case of $U_\mathrm{r} = 5$ is shown as figure “8” motion in Fig. 5. All of these dynamic behaviors are also found in the study by Bao et al. [43, 44]. Figure 4b, c shows the exhibitions of the power spectra for the cylinder CF directions vibrations response in the case of various $U_\mathrm{r}$. Figure 4d, e shows $|y_1 |_{\max } /D$ and $f_\mathrm{v} /f_\mathrm{n}$ responses of the elastically mounted cylinder versus $U_\mathrm{r}$. The simulation results show the three branches, including initial, upper and lower branches (see Fig. 4d) which is presented by Khalak and Williamson [41]. The “lock-in” phenomenon ($f_\mathrm{v} /f_\mathrm{n} \approx 1)$ can be seen from the frequency ratio responses within the $U_\mathrm{r}$ range from 4 to 10 in Fig. 4e. As discussed above, the amplitude, frequency responses and the dynamic behaviors are in good agreement with experiment evaluations, which provides confidence in the accuracy of the CFD coupled FSI model.

Fig. 20

Trajectories of 2-DOF VIV of the cylinders at different $U_\mathrm{r}$ in cases of various conditions: a upstream cylinder without NES; b downstream cylinder without NES; c upstream cylinder with NES ($\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8)$; d downstream cylinder with NES ($\beta = 0.5$, $\gamma =2$, $\xi = 0.8)$

4 Results and discussion

4.1 Influences of the NES and its parameters on the dynamic responses of the cylinder

The extensive use of CFD and FSI simulations to evaluate the influence of the NES parameters on the dynamic responses of the elastically supported cylinders can be considered a paramount task. Since this is an expensive task, more efficiently, the van der Pol oscillator [35, 36] can be used as an empirical mean of computing the VIV forces necessary in Model I and as to assess the NES parameters effect on the VIV response of the cylinder.

Fig. 21

Variation of the maximum vibration amplitudes versus $U_\mathrm{r}$ for cylinders with and without NES: a upstream cylinder and b downstream cylinder. Case 1: $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (upstream cylinder), $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (downstream cylinder); case 2: $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (upstream cylinder), $\beta = 0.5$, $\gamma = 0.8$ and $\xi = 0.8$ (downstream cylinder)

4.1.1 Effect of the mass ratio on the dynamic responses of the cylinder and NES

The non-dimensional NES parameter mass ratio $\beta$ effect on the VIV response of the cylinder is examined when keeping other NES non-dimensional parameters constant. In this subsection, $\beta$ is varied over the range $0.01\le \beta \le 0.5$, and the damping ratio $\xi$ and stiffness ratio $\gamma$ are both set equal to 0.8. Figure 6 shows that the maximum oscillation amplitudes of the cylinder and the relative motion between the cylinder and the NES as a function of $U_\mathrm{r}$ in the cases of various mass ratios. Figure 6a shows the lock-in region is in the range of $U_\mathrm{r}$ from 4.5 to 5.5 for a cylinder without NES. When the values of $\beta$ are 0.01 and 0.03, the lock-in range is unaffected by the NES, e.g., results are virtually identical with or without the NES. The lock-in ranges shown a right shift with the increase in $\beta$, a phenomenon which was also observed by Dai et al. [33]. The maximum amplitudes of the cylinder are significantly influenced by $\beta$. When the mass ratio is 0.01, it resulted hard to suppress the VIV of the cylinder. On the other hand, with $\beta$ set to 0.1, the cylinder has the lowest resonant amplitude compared to other mass ratios, and no optimization was carried for this value of the mass ratio. Figure 6b shows the maximum relative motion is about 40% of the cylinder’s diameter. It should be noted that in the practical implementation, the size of the NES which is placed inside the cylinder should be considered appropriately due to the maximum relative motion amplitude that must be lower than 0.5D. Figure 7 shows the dynamic behaviors of the cylinder and NES for selected values of $\beta$, namely 0.03, 0.1 and 0.5, when $U_\mathrm{r} = 5$. The cylinder and NES have synchronized periodic vibrations, and the NES starts to pump the energy from the cylinder at t= 11.5s when $\beta = 0.03$ as shown in Fig. 7a. Therefore, the cylinder’s amplitude is a bit lower than that of the case without NES. When $\beta$ increased to 0.1, as shown in Fig. 7c, the cylinder and NES start showing aperiodic responses. As a result, the VIV energy is transferred to the NES, leading to high vibration amplitudes ($y_2 /D)$ for the NES, as shown in Fig. 7c. In addition, significant decrease in the cylinder’s oscillating amplitude is observed. Figure 7e shows that the cylinder and NES return to the periodic responses but in the asynchronous manner when $\beta = 0.5$. It is noted that the vibration amplitudes of both cylinder and NES are very small due to lock-in region and have a large shift to the right when $\beta$= 0.5. Consequently, $U_\mathrm{r} = 5$ is not in the lock-in region (see Fig. 6a). To further investigate and understand the dynamic response of the cylinder and NES, the frequency spectrum curves are depicted in Fig. 7b, d, f. It is clearly observed that periodic responses take place when $\beta = 0.03$ and 0.5, while aperiodic responses take place when $\beta = 0.1$. In addition, NES and the cylinder show the identical displacement responses’ frequencies in the $U_\mathrm{r}$ range from 3 to 7 and for different $\beta$ as illustrated in Figs. 7b, d, f and 8a.

The sequence of simulations illustrate that the NES has a critical feature of mitigating vibrations in a broad frequency range. Figure 8b illustrates the cylinder displacement responses’ frequency ratios versus $U_\mathrm{r}$ in the cases of variable mass ratios. According to Figs. 6a and 8b, it can be seen that when the value of $\beta$ equals 0.01 and 0.03, the frequency ratio values are still close to 1 similarly to the case without NES during lock-in region ($U_\mathrm{r}$ from 4.5 to 5.5). Thus, the cases $\beta = 0.01$ and 0.03 suppress the VIV amplitude only marginally. However, when $\beta >0.06$ and the $f_\mathrm{v} /f_\mathrm{n}$ ratio is greater than 1, for $U_\mathrm{r}$ in the range from 4.5 to 5.5, a more significant VIV suppression occurs in the lock-in region. It is also evident from the same figure that the $f_\mathrm{v} /f_\mathrm{n}$ values are remarkably higher and levels to constant values for $U_\mathrm{r}$ in the range 6 to 7 and for = 0.3, 0.4 and 0.5. Therefore, the lock-in regions have obvious right shift. From the assessment of performance using selected value of mass ratios, one can observe that the mass ratios have a significant effect on the alteration of lock-in regions and the VIV amplitudes.

4.1.2 Effect of the non-dimensional stiffness ratio on the dynamic responses of the cylinder and NES

The maximum amplitudes of the cylinder and NES for various values of $\gamma$ are plotted in Fig. 9 for selected conditions, namely $\beta = 0.1$, $\xi = 0.8$ in Fig. 9a, b and $\beta = 0.03$, $\xi = 0.8$ in Fig. 9c, d. In order to better understand the non-dimensional stiffness ratios effect on the dynamic behaviors of the cylinder under the action of NES, the frequency ratios of the entire $U_{r}$ range for the cases of distinct $\gamma$ are depicted in Fig. 10b, d which correspond to the ones presented in Fig. 9a, c. Clearly, Fig. 9a shows that with the increase in $\gamma$, the maximum amplitude of the cylinder significantly decreases. Moreover, a very small shift in the lock-in region to higher reduced speed is discovered when NES parameters designed as $\beta = 0.1$ and $\xi = 0.8$. Figure 10 shows the comparisons of frequency ratios of the cylinder versus $U_\mathrm{r}$ for different $\gamma$ where $\beta$= 0.1, $\xi = 0.8$ in Fig. 10a, b and $\beta = 0.03$, $\xi = 0.8$ in Fig. 10c, d. It is easy to recognize that frequency ratio $f_\mathrm{v} /f_\mathrm{n}$ of the synchronization region has significantly increased with the increase in $\gamma$ which contributes to the decrease in the VIV response of the cylinder in the lock-in range (see Fig. 10b). In addition, the slope of the frequency ratio response curves is reduced in the range of $U_\mathrm{r}$ from 5 to 6, explaining the right shift of the amplitude peak displayed in Fig. 9a. Figure 11 shows the response of the cylinder and NES ($y_1 /D\;,\;y_2 /D)$ in the cases of various $\gamma$, when $U_\mathrm{r} = 5$, $\beta = 0.1$ and $\xi = 0.8$. Inspecting Fig. 11a, the cylinder and NES show asynchronous periodic responses for $\gamma = 0.3$, with a vibration amplitude of the NES lower than the cylinder, implying that the NES does not reach the desired effect of pumping energy. On the other hand, with the increase in the value $\gamma$, the cylinder and NES show aperiodic motion which contributes to a lower vibration amplitude for the cylinder, as presented in Fig. 11b, c, d. However, Fig. 9c shows a slight decrease in the maximum vibration amplitude of the cylinder when $\beta = 0.03$ and $\xi = 0.8$. It can be explained by Fig. 10d that $f_\mathrm{v} /f_\mathrm{n}$ values are in close proximity to 1 with the increase in $\gamma$ within the lock-in region. While the mass ratios have a significant effect on VIV of the coupled NES–cylinder system, the nonlinear stiffness ratios do not have much influence on the shift of the lock-in region. Figure 9b, d both shows that the relative motion between the cylinder and NES is less than 0.5D. The cylinder and NES maintain the same displacement responses’ frequency in case of $\gamma = 0.8$ as shown in Fig. 10a, c which reveals that the NES suppression mechanism is resonance capture pumping energy from the cylinder to the NES. From the above results, it can be found that increasing the nonlinear stiffness ratio helps in suppressing the VIV response of the cylinder quite significantly when an appropriate NES parameter mass ratio is selected.

Fig. 22

Temporal evolution of vortex formations for flow over a pair of cylinders without NES at a $U_\mathrm{r} = 5.5$; b $U_\mathrm{r} = 7$

4.1.3 Effect of the non-dimensional damping ratio

Another parameter of the coupled NES-cylinder system is non-dimensional damping ratio $\xi$. To determine the effect of $\xi$ on the VIV response of the cylinder, selected values of $\xi$ are investigated while keeping other parameters constant. Figure 12 shows the effect of $\xi$ on maximum oscillating amplitudes (see Fig. 12a, c) and frequency ratios (see Fig. 12b, d) of the cylinder as a function of $U_{r}$ in various conditions, namely $\beta = 0.1$, $\gamma = 0.8$ in Fig. 12a, b and $\beta = 0.03$, $\gamma = 0.8$ in Fig. 12c, d. It follows from Fig. 12a that the NES is unable to effectively suppress VIV response of the cylinder when $\xi = 0.1$ and 0.3. With the increase in $\xi$, the oscillation amplitudes of the cylinder decrease when $\beta = 0.1$ and $\gamma = 0.8$. In addition, the lock-in regions have a slight right shift (see Fig. 12a, b) which is similar to the modulated dynamic behavior discussed above. However, it is clear that $\xi$ has a negligible impact on the maximum amplitudes of the cylinder and the lock-in region in case of $\beta = 0.03$, $\gamma = 0.8$, as shown in Fig. 12c. The displayed results show that for small damping ratios and given mass ratios, the NES is not able to reduce the oscillation amplitude of the cylinder, and the damping ratios have no influence on the movement of lock-in region.

4.2 Dynamic behaviors of 2-DOF VIV of the cylinder under the action of NES

Generally speaking, the empirical model has many limitations. The classical van der Pol oscillator model cannot handle cylinders’ interference problem, the model with complex geometry shapes and cylinders with multiple degrees of freedom. Its accuracy depends on the empirical parameters selected to match the experimental parameters. In order to better understand the FIV dynamic behavior of the cylinders under the action of NES, more fidelity CFD model considering IL flow direction vibration effect and cylinders’ interference is carried out to simulate the FIV dynamic behavior of the cylinders with and without NESs. Figure 13 shows the CF vibration amplitudes and frequency ratios of the cylinder with and without NES versus $U_\mathrm{r}$ based on various numerical models (van der Pol model, 1-DOF CFD model and 2-DOF CFD model). It is observed that the maximum oscillating amplitude values for the cylinders with 1-DOF and 2-DOF CFD models are higher than the one obtained from the van der Pol model simulations (see Fig. 13a). Moreover, the lock-in region produced for a 1-DOF CFD model’s simulation result is quite similar to that of van der Pol model, while the lock-in region has a slight right shift for the 2-DOF CFD simulation results when compared with the results of van der Pol model (see Fig. 13a, b). One can argue that the van der Pol simulation results can be reasonable by ignoring the IL direction vibration effect and by properly selecting the empirical parameters of the van der Pol model. For the fixed cylinder, the vortex shedding frequency is proportional to the current speed [3]. It is observed that frequency ratios are proportional to the reduced velocities when using 1-DOF or 2-DOF CFD models with NES. That means the CFD model results show the vibration of the cylinder during lock-in region under the action of NES is very weak. However, the van der Pol model results show the frequency ratios tend to be quite proportional to the $U_\mathrm{r}$.

Fig. 23

Comparison of frequency ratios of the cylinder versus $U_\mathrm{r}$: a upstream cylinder; b downstream cylinder

Fig. 24

Temporal evolution of vortex formations for flow over a pair of cylinders with NES (upstream cylinder’s NES: $\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8$; downstream cylinder’s NES: $\beta = 0.5$, $\gamma = 0.8$, $\xi = 0.8$) at a $U_\mathrm{r} = 5.5$; b $U_\mathrm{r} = 7$

In this paper, 2-DOF CFD model simulations are also carried out to study the dynamic responses of one isolated circular cylinder without NES. As the flow passes over a cylinder, vortices are formed in the wake and shed with a specific frequency. The trajectories, maximum oscillating amplitudes, frequency ratios and temporal evolution of vortex formations of 2-DOF VIV of one isolated cylinder with and without NES versus $U_\mathrm{r}$ are shown in Figs. 14, 15, 16 and 17. Figure 14a shows the trajectories of the vibration at different $U_\mathrm{r}$. The combined IL and CF directions vibrations of the cylinder typically present a figure “8” motion under most conditions. The lock-in region is from $U_\mathrm{r}$ = 5–6, where the amplitudes are higher than other areas (see Figs. 14a and 15a). Frequency synchronization ($f_\mathrm{v} /f_\mathrm{n} \approx 1)$ occurs at $U_\mathrm{r}$ = 5–6 in which the vortex shedding frequency is extremely close to the natural frequency of the cylinder (see Fig. 16, the case without NES). The temporal evolution of vortex shedding from t = 35–35.5 s of the cylinder without NES at $U_\mathrm{r} = 5$ is presented in Fig. 17a, and it displays a 2P vortex shedding pattern (sheds two vortex pair per cycle) in the wake which is a vortex structure shedding phenomenon that occurs when the cylinder vibration is violent.

The dynamic behavior of the VIV of the cylinder under the action of NES is generally well understood from the above simulation results of van der Pol model. Herein, simulations of 2-DOF VIV of one isolated cylinder with the addition of three sets of NES parameters based on model II are also performed. The trajectories of 2-DOF VIV of the cylinder with NES (set I: $\beta = 0.1$, $\gamma = 0.8$, $\xi = 0.8$; set II: $\beta = 0.1$, $\gamma = 2$, $\xi = 0.8$; set III: $\beta = 0.5$, $\gamma = 0.8$, $\xi = 0.8$) at different $U_\mathrm{r}$ are shown in Fig. 14b, c, d. The CF direction vibration is distinctly decreased when $U_\mathrm{r}$ is in the range 5–6 in comparison with the case without NES. Figure 14b, c shows that the trajectories of the cylinder with set I and II NES parameters are chaotic when $U_\mathrm{r}$ is in the range 5 to 6.5, but regular figure “8” motion when $U_\mathrm{r}$ outside of the lock-in region. Figure 14d shows all the trajectories of the cylinder are figure “8” motion when $U_\mathrm{r}$ is in the range 3–7. The VIV amplitude increases constantly for increasing $U_\mathrm{r}$ as reported in Fig. 14d. The NES significantly suppresses the vibration amplitude using these three set NES parameters. The lock-in regions have sight right shift when set I and II NES parameters are chosen. The trends are similar to the simulation results in Fig. 9a. In addition, the maximum amplitudes of the cylinder decrease when the stiffness ratios increase for the equivalent mass ratio (see Fig. 15a). In this case, the maximum relative motion is less than 0.5D as shown in Fig. 15b. As expected, the VIV cylinder amplitudes with and without NES all are different, similarly to what shown in Sect. 4.1B. Nevertheless, the dynamic behaviors are very similar to the one reported for van der Pol model in the same section. Frequency responses of the cylinder with NES are also reported in Fig. 16 and are obtained through a power spectral density analysis of CF direction displacements and lift coefficients signals using fast Fourier transform process. The NES, cylinder displacement responses and the lift coefficients show the identical signal responses’ frequencies when $U_\mathrm{r}$ ranges from 3–7 in the cases of $\beta = 0.1$, $\xi = 0.8$ and $\gamma = 0.8$ (see Fig. 16a). The NES is essentially a strong nonlinear passive control device lacking an inherent linearized natural frequency. Depending on the driving force energy and frequency content, the NES can engage in resonance capture with the cylinder, leading to dissipation of the vibration energy of the cylinder system. It may point out that these behaviors have similar trends as shown in Figs. 8a and 10a, c. Figure 16b shows the cylinder displacement responses’ frequency ratios versus $U_\mathrm{r}$ for three sets of NES parameters. During the lock-in region ($U_\mathrm{r}$ = 5–6), the frequency ratios have a slight increase due to the increase in stiffness ratio. In addition, all the values of $f_\mathrm{v} /f_\mathrm{n}$ are sufficiently far from 1 for $U_\mathrm{r}$ in the range 5–6, relative to the case without NES, so that the VIV of the cylinder in the lock-in region can be suppressed. Moreover, the coupled response’s frequencies are constantly increasing until $U_\mathrm{r}$= 6 and then increase more slowly as shown in Fig. 16b for the case with NES and $\beta = 0.5$, $\gamma = 0.8$, $\xi = 0.8$. This illustrates that the lock-in region has a significantly right shift when set III NES parameters are considered. Vorticities due to the flow process from time 35 to 35.5 s of the case $\beta = 0.1$, $\xi = 0.8$ and $\gamma = 0.8$ when $U_\mathrm{r} = 5$ are shown in Fig. 17b. The cylinder’s vibration amplitude is slight relatively to the initial position of the cylinder which is marked as dotted line in Fig. 17b. It displays a 2S vortex shedding mode (two single vortices being formed in one cycle) in the wake which is a vortex structure shedding phenomenon that occurs when the cylinder vibration is slight.

When the elastic supported cylinder under the action of NES, the CF displacement responses may show type I synchronous and type II asynchronous periodic and type III aperiodic behavior. The VIV suppression mechanism is essentially changing the coupled responses’ frequencies as to avoid the natural frequency of the cylinder in the lock-in region. For example, Fig. 18 shows the time series of CF vibration ($y_1 /D$, $y_2 /D)$ along with the corresponding power spectral density curves for the cases of $U_\mathrm{r} = 3.5$, 5 and 7 when $\beta = 0.1$, $\xi = 0.8$ and $\gamma = 0.8$. Periodic response takes place when $U_\mathrm{r} = 3.5$ and 7 (see Fig. 18a, b, e, f), while the aperiodic response takes place when $U_\mathrm{r} = 5$ (see Fig. 18c, d). Figure 18c shows that the maximum amplitude of oscillation of the cylinder with NES ($y_1 /D$ (NES)) is approximately 0.13D, compared to the steady periodic amplitude of 0.55D for the cylinder without the NES ($y_1 /D$ (without NES)). Thus, a 76.4% reduction in the maximum displacement can be attributed to the NES. The resonant vibration of the NES ($y_2 /D$(NES)) is observed in Fig. 18c. The vortex shedding pattern in the wake displays as 2S mode which is a flow phenomenon that occurs when the cylinder vibration is very weak. The non-dimensional displacements response and power spectral density curves are presented in Fig. 19a, b. Clearly, periodic responses are observed in the cases of $U_\mathrm{r} = 3.5$, 5 and 7 when $\beta = 0.5$, $\xi = 0.8$ and $\gamma = 0.8$.

Fig. 25

Time histories of the non-dimensional displacements ($y_1 /D$,$y_2 /D)$ (a, c) and power spectral density (b, d) in the cases of $U_\mathrm{r}$= 5.5 for a, b upstream cylinder; c, d downstream cylinder

4.3 Dynamic behaviors of 2-DOF WIV of two tandem cylinders under the action of NES

The previous CFD coupled FSI and NES technique is adopted in this section to compute the vibration amplitudes of a pair of identical tandem cylinders with and without NES in the proximity–wake interference regime. The dynamic responses of two tandem circular cylinders without NES are considered firstly. The distance between the upstream cylinder (cylinder 1) and downstream cylinder (cylinder 2) is 5D. Figure 20 shows the trajectories of the two tandem springs supported cylinders with and without NES in the cases of various $U_\mathrm{r}$. A figure “8” trajectory is shown by the front cylinder; however, the combined IL and CF directions motion affects the rear cylinder modes of vibration due to the induced wake interference effect (see Fig. 20a, b, the case without NES). Figure 21a, b shows the CF vibration amplitude with $U_\mathrm{r}$ for the two cylinders with and without NES arranged in tandem. The results for a single cylinder without NES are also included for comparison. The maximum vibration amplitudes of the cylinder 1 without NES are observed at an identical reduced velocity $U_\mathrm{r} = 5.5$ with a magnitude of $|y_1 |_\mathrm{max} /D\approx 0.56$ which is similar to the displacement $|y_1 |_\mathrm{max} /D$ of the single cylinder. In contrast to the behavior of the front cylinder, the effect of the wake interactions between the couple of cylinders on the vibration amplitude responses of the rear cylinder is evident. The maximum CF vibration amplitude of cylinder 2 is about $|y_1 |_\mathrm{max} /D\approx$ 0.69 when $U_\mathrm{r} = 6.5$. The cylinder 1 shows a typical VIV response with very small vibration amplitudes at high $U_\mathrm{r}$ ($U_\mathrm{r}$ = 6–7). In contrast, for the present study (the distance between the two cylinders is 5D), the fully detached vortices from cylinder 1 shown in Fig. 22 cause the WIV of cylinder 2 with relatively large-amplitude vibration being maintained up until the maximum $U_\mathrm{r}$ considered. The vortex shedding contours of the two tandem cylinders at different time instants when $U_\mathrm{r} = 5.5$ and 7 are shown in Fig. 22a, b, respectively. A variation of the vortex shedding patterns around cylinders 1 and 2 is discovered. The vortices from behind the cylinder 1 interact with the shear layers of cylinder 2 when they reach the cylinder 2 surface. 2P vortex shedding pattern is observed behind cylinder 1 and also cylinder 2, and they are interacting with each other when $U_\mathrm{r} = 5.5$. The vortex shedding exhibits a 2S mode behind cylinder 1 where the vibration of the cylinder is weak when $U_\mathrm{r} = 7$. Meanwhile, a 2P mode associated with the large-amplitude vibration of the cylinder occurs behind cylinder 2 and interacts with the wake from cylinder 1 when $U_\mathrm{r} = 7$. This confirms the observation from the trajectories of the cylinders’ motion as shown in Figs. 20a, b and 21 the cases without NES.

Figure 23, also a case without NES, shows the comparison of frequency ratios ($f_\mathrm{v} /f_\mathrm{n} )$ between the single cylinder and the two tandem cylinders. The lock-in range of the single cylinder in terms of $U_\mathrm{r}$ is from 5 to 6 based on the synchronization between $f_\mathrm{v}$ and $f_\mathrm{n}$. For two tandem flexible cylinders, the lock-in range of cylinder 1 occurs for $U_\mathrm{r}$= 5–5.5 (see Fig. 23a, cylinder 1 without NES). The synchronization of the cylinder 2 also starts from $U_\mathrm{r} = 5$ until the maximum $U_\mathrm{r}$ considered in the present simulation (see Fig. 23b, cylinder 2 without NES, $f_\mathrm{v} /f_\mathrm{n} \approx 1$ in the $U_\mathrm{r}$ region from 5 to 7). It should also be noted that the frequency ratio of cylinder 2, in the $U_\mathrm{r}$ range from 3 to 5.5, is similar as the corresponding frequency ratio of cylinder 1. From the previous simulation results based on the van der Pol model and CFD model, the fundamental dynamic behaviors of the single cylinder under the action of NES are obtained. The mass ratio had a significantly effect on the alteration of lock-in regions and the VIV amplitudes. Thus, selecting a suitable mass ration is very important to the simulation. During this section study, it observed that the lock-in region of the downstream cylinder without NES extends to the right until the maximum selected $U_\mathrm{r}$ is reached.

In order to preliminarily explore the dynamic behaviors and suppress the FIV amplitude of the two tandem cylinders under the action of NESs, two cases of NES parameters (case 1: $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (upstream cylinder), $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (downstream cylinder); case 2: $\beta = 0.1$, $\gamma = 0.8$ and $\xi = 0.8$ (upstream cylinder), $\beta$= 0.5, $\gamma = 0.8$ and $\xi = 0.8$ (downstream cylinder)) are selected for the simulation of WIV of the two tandem cylinders under the action of the NES. In case 1, the NES parameters are identical for upstream and downstream cylinder. However, in case 2, only cylinder 2 NES parameter $\beta$ is increased relative to the NES parameters of cylinder 1. The maximum displacement amplitude of the cylinders with NES (cases 1 and 2) as a function of $U_\mathrm{r}$ defines the lock-in curve shown in Fig. 21. It follows from that the oscillating amplitudes of the upstream cylinder are significantly decreased in case 1, while there is almost no effect on the WIV amplitudes of the downstream cylinder. More interestingly, the WIV amplitudes of both front and rear cylinders significantly decrease in case 2. The greatest performances are observed for a $U_\mathrm{r} = 5.5$ (front cylinder), with a 76.3% reduction, and a $U_\mathrm{r} = 6.5$ (downstream cylinder) with an 88.5% reduction in the transverse vibration response. This can also be confirmed by the observation from the trajectories of the cylinders’ motion as shown in Fig. 20c, d. Clearly, the trajectories of the front cylinder in case 2 mostly exhibit a figure “8” mode but show a chaotic trajectory when $U_\mathrm{r} = 5.5$. The frequency ratios of the cylinders 1 and 2 in case 2 are almost identical independently of $U_\mathrm{r}$ (see Fig. 23a, b) for $f_\mathrm{v} /f_\mathrm{n}$ outside the lock-in region. This illustrates that the vibration of the cylinder 2 is quite weak during lock-in and the NES is effective in suppressing the vibration of cylinder 2. Moreover, the trajectories of the rear cylinder show more disordered behavior relative to the case without NES when $U_\mathrm{r} = 5.5$. Figure 24a, b shows the temporal evolution of vortex shedding for case 2 at $U_\mathrm{r} = 5.5$ and 7, respectively. It is found that the front and rear cylinder’s vibration amplitudes are slightly relative to the initial position of the cylinder, and the vortex shedding pattern displays 2S mode behind the front and rear cylinders when $U_\mathrm{r} = 5.5$. The vortex shedding exhibits a 2S mode behind the upstream cylinder and a weak 2P mode behind the downstream cylinder when $U_\mathrm{r} = 7$. Figure 25 shows CF vibration ($y_1 /D$, $y_2 /D)$ responses and power spectral density curves of the front and rear cylinder in case 2 when $U_\mathrm{r} = 5.5$. It is observed that aperiodic responses take place on cylinder 1 (see Fig. 25a, b), while periodic responses take place on cylinder 2 (see Fig. 25c, d). Consequently, a 76.3% reduction in the maximum displacement of cylinder 1 and 84.5% reduction in maximum displacement of cylinder 2 can be attributed to the effectiveness of the NES.

5 Conclusions

The dynamics of a single and a tandem arrangement of two-dimensional circular cylinders is investigated by fluid–structure interaction (FSI) simulations to assess low Reynolds number vortex-induced (VIV) and wake-induced vibration (WIV). The suppression of FIV of elastically supported single and two-degrees-of-freedom circular cylinders by utilizing NES based on various numerical models has been investigated. At first, a van der Pol model is used to explore the effect of the NES parameters on the dynamic behavior of the VIV of a single cylinder. Then, a CFD coupled FSI model is adopted to determine FIV dynamic behaviors of an isolated and a tandem cylinders arrangement with and without van der Pol modeled NES. The NES is a strong nonlinear passive control device without inherent linearized natural frequency. Its characteristics depend upon the driving force energy and frequency content; hence, the NES can engage in resonance capture with the cylinders, leading to the dissipation of the cylinder’s vibration energy. The NES suppression mechanism is resonance capture, and then, the energy is transferred from the cylinder to NES. The mass ratios affect significantly the lock-in regions and the VIV amplitudes, while the nonlinear stiffness ratios have virtually no influence on the shift of the lock-in region. However, by increasing the nonlinear stiffness ratio, the amplitude of the VIV response of the cylinder can be reduced significantly when an appropriate NES parameter mass ratio is identified. On the other hand, with small damping and ineffective mass ratios, the NES is not capable of reducing the oscillation amplitude of the cylinder, and the damping ratio has no influence on the shift of the lock-in region. When the NES pumps the energy from the cylinder to NES, the cross-flow displacement responses will show type I synchronous and type II asynchronous periodic and type III aperiodic behavior. The VIV suppression mechanism is essentially changing the coupled responses’ frequencies to avoid approaching the natural frequency of the cylinder in the lock-in region. Within the lock-in region, the wake behind the cylinders nearly displays a 2P vortex shedding patterns if the cylinder does not have an NES. However, the vortex shedding mode in the wake displays as 2S mode when the cylinder has a properly tuned NES. It is found that placing a tuned NES in the cylinders can suppress the FIV amplitude quite well. The best performance is obtained at $U_\mathrm{r} = 5$ for a single isolated cylinder, with a 76.4% reduction in the transverse vibration response compared to a case without NES. For the tandem arrangement, the greatest performance is observed at $U_\mathrm{r} = 5.5$ for the front cylinder, with a 76.3% transverse vibration response reduction, and at $U_\mathrm{r} = 6.5$ for the downstream cylinder with a 88.5% reduction.

Appendix

The UDF codes of VIV of 2-DOF cylinder under action with NES are shown as follows: