1 Introduction

Uncertainties widely exist in engineering problems, such as inhomogeneous materials (Bai and Kang 2021), manufacturing errors (Zhao et al. 2019; Qiao et al. 2021), random loads (Liu et al. 2021a; Wu and Law 2012), and so on. Uncertain parameters can lead to large fluctuations in the structural response and lead to reliability problems. Therefore, it is necessary to determine the distributional properties of the response function and provide the probability density function of the response function for reliability optimization design (Liu et al. 2021b; Wang and Luo 2019; Tian et al. 2022; Tang et al. 2022). Uncertainty propagation methods are commonly developed based on probability statistics theory, which can obtain the uncertainty information of the response function, such as the probability density function (PDF), cumulative distribution function (CDF), mean, and variance. At present, numerous significant achievements have been made for uncertainty propagation problems, which can be roughly divided into two categories: sampling-based methods and moment-based methods. The sampling-based methods, such as the Monte Carlo simulation (MCS) method (Grigoriu 1984; Marseguerra et al. 1998), are extensively used in uncertainty propagation. A large number of samples are used to compute the response function. They can achieve satisfactory computational accuracy, but are relatively less computationally efficient. Therefore, they are not suitable for practical problems. Some modified methods, such as importance sampling methods (Mori and Kato 2003) and subset simulation (Au and Beck 2001; Bourinet et al. 2011), have been proposed to improve the computational efficiency of the sampling-based methods. However, the low computational efficiency has been a problem for these methods. Therefore, the moment-based methods have been proposed with satisfactory computational efficiency.

Moment-based methods include numerical integration methods, function expansion methods, and local expansion methods. Numerical integration methods are used to compute the statistical moments of the response function based on a limited number of integration points and weights, which include the dimension reduction methods (Rahman and Xu 2004; Xu and Rahman 2004) and sparse grid methods (Nobile et al. 2008; Wu et al. 2021). Function expansion methods, such as polynomial chaos expansion (Bhattacharyya 2022, 2020, 2023; Jacquelin et al. 2019; Shao et al. 2017; Guo et al. 2019), introduce orthogonal polynomials to construct efficient surrogate models of the response function. Local expansion methods (Hu et al. 2021; Breitung 1984) require a first- or second-order Taylor expansion of the response function at the reference points to efficiently compute the mean and variance. In addition, some PDF approximation methods have been proposed based on the statistical moments of the response function. They can be divided into five categories: Johnson systems (Trenkler 1994), Pearson family distributions (Pearson and I.X. 1916), saddlepoint approximation methods (Du 2007), generalized lambda distributions (Asquith 2007), and maximum entropy methods (Livesey and Brochon 1987).

In the above uncertainty propagation analysis, random variables are mainly considered as the unimodal distributions, such as normal, uniform, and Weibull distributions. However, random variables may follow multimodal distributions in engineering problems. For example, the fatigue lifetimes of safety cut specimens in aircraft structure follow a bimodal lognormal distribution after repair (Zeng et al. 2020). In long-term stress monitoring of steel bridges, the stress distribution follows a multimodal distribution (Ni et al. 2010). In the reliability optimization design, the unimodal distribution neglects the features of the multimodal distribution, which leads to insufficient accuracy. In areas with strict reliability requirements, such as the nuclear industry and the aerospace industry, insufficient accuracy can lead to serious disasters. Therefore, it is essential to develop efficient uncertainty propagation methods for multimodal distributions. There has been a small amount of research work on multimodal distribution problems. In terms of computational accuracy, sampling-based methods have been able to achieve satisfactory computational accuracy. However, they are widely known to be computationally demanding. As a result, they are difficult to apply to engineering problems involving complex simulation models. In terms of computational efficiency, moment-based methods have been developed. Du (Hu and Du 2018) introduced a first-order approximation method for bimodal distributions. The saddlepoint approximation method is used to obtain the reliability analysis results. Chen (Li et al. 2021) proposed a novel direct probability integration method (DPIM), which can be used to calculate the response function’s PDF involved multimodal distributions. Zhang (Zhang et al. 2019) proposed a multimodal uncertainty propagation method based on univariate dimension reduction method (UDRM). In this method, UDRM is used to compute higher-order statistical moments. The PDF of the response function is computed using an adaptive framework based on the maximum entropy method. These methods are computationally efficient compared to sampling-based methods, but they may fail to provide satisfactory accuracy and efficiency when the response function is deeply nonlinear or complex. Thus, it is relatively difficult to consider both computational efficiency and accuracy at present.

This study presents a multimodal uncertainty propagation method that takes into account both computational efficiency and accuracy. Unimodal decomposition strategy and arbitrary polynomial chaos expansion improve the computational accuracy while ensuring computational efficiency. The study is organized as follows: In Sect. 2, the probability density function of multimodal random variables is established. In Sect. 3, elements are constructed where input random variables are unimodal distributions. In Sect. 4, the PDF of the response function in each element is computed and then the PDF of the response function in the complete probability space is obtained. In Sect. 5, the computational efficiency and accuracy of the proposed method are demonstrated by examples.

2 Uncertainty modeling of input multimodal random variables

Gaussian mixture model (GMM) can be used to determine the probability density function of the multimodal random variable \(X\), which is expressed as follows (Figueiredo and Jain 2002):

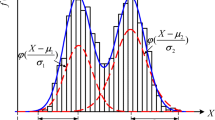
$$f\left( {x|{{\varvec{\Theta}}}} \right) = \sum\limits_{{{\text{i}} = 1}}^{N} {\omega_{{\text{i}}} \varphi \left( {x|{\varvec{\theta}}_{{\text{i}}} } \right)}$$
(1)

where \(N\) is the number of Gaussian components, which can be obtained by direct observation or integral square difference (ISD)(Valverde et al. 2012); \({{\varvec{\Theta}}} = \left( {\omega_{1} ,{\varvec{\theta}}_{1} ,\omega_{2} ,{\varvec{\theta}}_{2} , \ldots ,\omega_{{\text{N}}} ,{\varvec{\theta}}_{{\text{N}}} } \right)\) is the parameter set of GMM; \({\varvec{\theta}}_{{\text{i}}} = \left( {\mu_{{\text{i}}} ,\sigma_{{\text{i}}}^{2} } \right)\) represents the mean and variance at the \(i{\text{th}}\) Gaussian component; \(\omega_{i}\) and \(\varphi \left( {x|{\varvec{\theta}}_{{\text{i}}} } \right)\) denote the coefficient and probability density function at the \(i{\text{th}}\) Gaussian component, respectively. \(\omega_{i}\) also satisfies \(\omega_{i} \ge 0\) and \(\sum\limits_{i = 1}^{N} {\omega_{i} } = 1\). A Gaussian mixture model of a multimodal distribution with four components is shown in Fig. 1.

Fig. 1
figure 1

Gaussian mixture model of multimodal distribution with four components

Full size image

Therefore, the parameter set \({{\varvec{\Theta}}}\) is required to be computed and applied to obtain the probability density function of \(X\). Maximum likelihood estimation is a widely used method for parameter estimation. A sample set \({\varvec{s}} = \left\{ {s_{1} ,s_{2} , \ldots ,s_{h} } \right\}\) is obtained, where a latent variable set \({\varvec{\gamma}} = \left\{ {\gamma_{1} ,\gamma_{2} , \ldots ,\gamma_{N} } \right\}\) is introduced for each sample. \(\gamma_{i} = 1\) denotes the sample located at the \(i{\text{th}}\) Gaussian component and the probability of the sample being located at this Gaussian component can be written as follows:

$$p\left( {\gamma_{i} = 1} \right) = \omega_{i}$$
(2)

Hence, the probability of the sample \(s_{j}\) can be expressed as follows:

$$p\left( {s_{{\text{j}}} } \right) = \sum\limits_{i = 1}^{N} {p\left( {\gamma_{{\text{i}}} } \right)p\left( {s_{{\text{j}}} |\gamma_{{\text{i}}} } \right)} = \sum\limits_{{{\text{i}} = 1}}^{N} {\omega_{{\text{i}}} \varphi \left( {s_{{\text{j}}} |{\varvec{\theta}}_{{\text{i}}} } \right)}$$
(3)

The logarithmic form of the joint probability density function for each sample is considered as a log-likelihood function:

$$\log L\left( {\mathbf{\Theta }} \right) = \log \left( {\prod\limits_{{{\text{j}} = 1}}^{{\text{h}}} {\sum\limits_{{{\text{i}} = 1}}^{{\text{N}}} {\omega _{i} \varphi \left( {s_{j} |\varvec{\theta }_{i} } \right)} } } \right) = \sum\limits_{{{\text{j}} = 1}}^{{\text{h}}} {\log \sum\limits_{{{\text{i}} = 1}}^{{\text{N}}} {\omega _{{\text{i}}} \varphi \left( {s_{{\text{j}}} |\varvec{\theta }_{{\text{i}}} } \right)} }$$
(4)

Set the derivation of Eq. (4) equal to 0, and the parameter set \(\Theta\) is calculated as follows:

$${\hat{\mathbf{\Theta }}} = \arg \mathop {\max }\limits_{{{\varvec{\Theta}}}} \left\{ {\log L\left( {{\varvec{\Theta}}} \right)} \right\}$$
(5)

In fact, it is difficult to directly calculate \({{\varvec{\Theta}}}\) based on the formula (5). Therefore, the expectation–maximization algorithm (Castillo-Barnes et al. 2020) is often used to search for the local maximum of \(\log L\left({\varvec{\varTheta}}\right)\).

3 Unimodal decomposition strategy

In early research, a decomposition method is proposed for multimodal random variables (Nouy 2010). This method decomposed a partition of \(\left[ {0,\left. 1 \right)} \right.\) into multiple discrete intervals and constructed the desired partitions of a multimodal random variable based on them. The purpose of the unimodal decomposition strategy is also to transform multimodal random variables into a set of unimodal random variables. The difference is that the method is based on a direct decomposition of multimodal random variables in terms of minimum points, and it is aimed at the multidimensional multimodal random variables. Three steps are involved in unimodal decomposition strategy: (i) determining the division points of the multimodal random variables, (ii) decomposing multimodal random variables by division points and constructing unimodal elements, and (iii) computing the response function’s PDF.

Division points can be used in the decomposition of multimodal random variables, and the computational accuracy of the division points can affect the effect of the decomposition. The division point is defined at the lowest point between two neighboring components of the multimodal distribution. The probability density functions of the multimodal random variables are treated as objective functions and the division points are considered as local minima of them. According to the mathematical properties of local minima, the points around the division points satisfy the following conditions:

$$\nabla f\left( a \right) < 0,\,\nabla f\left( b \right) > 0$$
(6)

where \(\nabla f\) is the derivation of the objective function. \(a\) and \(b\) are the points to the left and right of the division point, respectively. The search intervals of the minimum points are determined based on Eq. (6), and then the local minimum point of each interval is calculated by the univariate optimization methods. The division points of the multimodal random variables are used to define disjoint division intervals. Each multimodal random variable \(X\) can be decomposed into a set of random variables, where each random variable follows a unimodal distribution. The decomposition procedure for a multimodal distribution with four components is shown in Fig. 2.

Fig. 2
figure 2

The decomposition of multimodal distribution

Full size image

This is essential for reconstructing uncertainty propagation problems after decomposition of multimodal random variables. All sets of random variables are chosen to construct elements \(B_{k}\), each of which contains various independent random variables. The elements are disjoint and satisfy the following conditions:

$$\left\{ \begin{gathered} B_{k} = \left[ {X_{k,1} ,X_{k,2} , \ldots ,X_{k,d} } \right] \hfill \\ B = \bigcup\limits_{k}^{{N_{1} }} {B_{k} } \hfill \\ B_{{k_{1} }} \cap B_{{k_{2} }} = \phi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if{\kern 1pt} {\kern 1pt} {\kern 1pt} k_{1} \ne k_{2} \hfill \\ \end{gathered} \right.$$
(7)

where \(X_{k,i}\) is a random variable in the \(i{\text{th}}\) set and an element \(B_{k}\). d is the number of independent multimodal random variables. \(N_{1}\) is the number of elements. Thus, \(N_{1}\) disjoint elements are constructed based on the decomposition of the multimodal distribution. The construction of the elements in the two-dimensional probability space is described using Fig. 3.

Fig. 3
figure 3

The construction of elements in a two-dimensional probability space

Full size image

The above method transforms the uncertainty propagation for multimodal distributions into a set of uncertainty propagation for unimodal distributions. In this way, elements are treated as multidimensional uncertainty propagation problems and PDFs of various response functions are included. The PDF of the response function \(f\left( y \right)\), for a multimodal distribution, can be determined based on the elements. The statistical moments of the response function \(m_{i}\) are decomposed into various statistical moments in the elements and the procedure can be stated as follows:

$$m_{i} = \int_{{\text{X}}} {g\left( {\varvec{x}} \right)} f_{{\text{X}}} \left( {\varvec{x}} \right)dx = \sum\limits_{k = 1}^{{N_{1} }} {{\varvec{P}}\left( {B_{{\text{k}}} } \right)\int_{{X_{{\text{k}}} }} {g\left( {{\varvec{x}}_{k} } \right)} f_{{X_{{\text{k}}} }} \left( {{\varvec{x}}_{{\text{k}}} } \right)d{\varvec{x}}_{{\text{k}}} } = \sum\limits_{k = 1}^{{N_{1} }} {{\varvec{P}}\left( {B_{{\text{k}}} } \right)m_{{{\text{k}},{\text{i}}}} }$$
(8)

where \(P\left( {B_{{\text{k}}} } \right)\) is the probability of element \(B_{k}\). \({\varvec{X}} = \left( {X_{1} ,X_{2} , \ldots ,X_{d} } \right)\) denotes the vector of \(d\) independent multimodal random variables. \(m_{k,i}\) is the \(i{\text{th}}\)-order statistical moment in element \(B_{k}\). The PDF of the response function in each element based on \(m_{k,i}\) is estimated using the maximum entropy method. Hence, \(f\left( y \right)\) is decomposed as follows:

$$f\left( y \right) = \sum\limits_{k = 1}^{{N_{1} }} {P\left( {B_{{\text{k}}} } \right)f_{{\text{k}}} \left( y \right)}$$
(9)

where \(f_{k} \left( y \right)\) is the PDF of the response function in element \(B_{k}\). Let \(F_{k} \left( y \right) = P\left( {B_{k} } \right)f_{k} \left( y \right)\), and Eq. (9) can be rewritten as follows:

$$f\left( y \right) = \sum\limits_{k = 1}^{{N_{1} }} {F_{k} \left( y \right)}$$
(10)

The uncertainty propagation based on the unimodal decomposition strategy is shown in Fig. 4. The random variables follow unimodal distributions in each element, and then \(f_{k} \left( y \right)\) can be estimated from the first 4th-order statistical moments. Specific computation methods are shown in Sect. 4. Thus, it can be found that the first 4th-order statistical moments are required to determine \(f\left( y \right)\) in this method.

Fig. 4
figure 4

The uncertainty propagation based on unimodal decomposition strategy

Full size image

Equation (9) indicates that P(Bk) are also required to be determined and the computation process is shown as follows: First, MCS is used to produce n samples and they can be divided into various elements. Second, an indicator function \(I_{{B_{k} }}\), which is used to determine whether the samples belong to the element \(B_{k}\), is initially defined for them.

$$I_{{{\text{B}}_{{\text{k}}} }} = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}\,\,\user2{x}_{{{\text{B}}_{{\text{k}}} }} \in B_{{\text{k}}} \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{otherwise}} \hfill \\ \end{gathered} \right.$$
(11)

It can be found that \(I_{{B_{k} }} = 1\) indicates that the sample is located at the element \(B_{k}\). The distribution ratios of the samples are considered as P(Bk), and they can be expressed as follows:

$$P\left( {B_{{\text{k}}} } \right) = P\left( {I_{{{\text{B}}_{{\text{k}}} }} = 1} \right) = \frac{{n_{{\text{k}}} }}{n}$$
(12)

where \(n_{k}\) is the number of samples located at element \(B_{k}\).

4 Uncertainty propagation in unimodal elements

In this section, uncertainty propagation is performed for unimodal random variables in each element, where the arbitrary polynomial chaos expansion and maximum entropy method are involved.

4.1 Calculating the statistical moments of the response function

Based on the random variables \({\varvec{X}}_{k}\) in the elements, the surrogate model of response function \(Y{ = }g\left( {{\varvec{X}}_{k} } \right)\) can be constructed by polynomial chaos expansion (PCE) (Sachdeva et al. 2006):

$$\hat{g}\left( {{\varvec{X}}_{{\text{k}}} } \right) \approx \sum\limits_{i = 0}^{P} {\alpha_{{{\text{k}},{\text{i}}}} \Phi_{{\text{i}}} \left( {{\varvec{X}}_{{\text{k}}} } \right)}$$
(13)

where p is the number of truncated expansion terms. \(\alpha_{i}\) denotes a polynomial coefficient. \(\Phi_{i} \left( {{\varvec{X}}_{k} } \right)\) stands for the multivariable PCE basis, which can be expressed as follows:

$$\Phi_{{\text{i}}} \left( {{\varvec{X}}_{{\text{k}}} } \right) = \prod\limits_{{{\text{j}} = 1}}^{d} {\phi_{{{\text{i}}_{{\text{j}}} }} \left( {X_{{{\text{k}},{\text{j}}}} } \right)}$$
(14)

where \(\phi_{{{\text{i}}_{{\text{j}}} }} \left( {X_{{{\text{k}},{\text{j}}}} } \right)\) is the one-dimensional orthogonal polynomial chaos basis of the random variable \(X_{{{\text{k}},{\text{j}}}}\). Therefore, \(\alpha_{{{\text{k}},{\text{i}}}}\) and \(\phi_{{{\text{i}}_{{\text{j}}} }} \left( {X_{{{\text{k}},{\text{j}}}} } \right)\) are required to be computed to determine the surrogate model \(\hat{g}\left( {{\varvec{X}}_{{\text{k}}} } \right)\).

A moment-based analysis (Oladyshkin and Nowak 2012) is used to construct a multivariable PCE basis for arbitrary distributions. The kth-order one-dimensional orthogonal polynomial chaos basis \(\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {\text{k}} \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right)\) can be defined as follows:

$$\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {\text{k}} \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right){ = }\,\sum\limits_{{{\text{m}} = 0}}^{{\text{K}}} {\beta_{{\text{m}}}^{{\left( {\text{K}} \right)}} X_{{{\text{k}},{\text{j}}}}^{{\text{m}}} }$$
(15)

where \(\beta_{{\text{m}}}^{{\left( {\text{K}} \right)}}\) are unknown parameters. \(X_{{{\text{k}},{\text{j}}}}^{{\text{m}}}\) are \(m{\text{th}}\) power of \(X_{{{\text{k}},{\text{j}}}}\). \(\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {{\text{K}}_{1} } \right)}} \left( {X_{{\text{j}}} } \right)\) and \(\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K_{2} } \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right)\) satisfy the following requirements:

$$\left\langle {\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K_{1} } \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right),\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K_{2} } \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right)} \right\rangle = \int_{{X_{{{\text{k}},{\text{j}}}} }} {\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K_{1} } \right)}} \left( {x_{{{\text{k}},{\text{j}}}} } \right)\phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K_{2} } \right)}} \left( {x_{{{\text{k}},{\text{j}}}} } \right)f\left( {x_{{{\text{k}},{\text{j}}}} } \right)dx_{{{\text{k}},{\text{j}}}} = 0} ,\,\forall K_{1} \ne K_{2}$$
(16)

The \(K{\text{th}}\)-order statistical moment of a random variable \(X_{k,j}\) can be expressed as follows:

$$\mu_{K} = \int_{{X_{{{\text{k}},{\text{j}}}} }} {x_{{{\text{k}},{\text{j}}}}^{K} f\left( {x_{{\text{k,j}}} } \right)dx_{{{\text{k}},{\text{j}}}} }$$
(17)

Equation (16) is transformed into matrix form based on Eq. (15) and Eq. (17):

$$\left[ {\begin{array}{*{20}l} {\mu_{0} } \hfill & {\mu_{1} } \hfill & \ldots \hfill & {\mu_{K} } \hfill \\ {\mu_{1} } \hfill & {\mu_{2} } \hfill & \ldots \hfill & {\mu_{K + 1} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\mu_{K - 1} } \hfill & {\mu_{K} } \hfill & \ldots \hfill & {\mu_{2K - 1} } \hfill \\ 0 \hfill & 0 \hfill & \ldots \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\beta_{0}^{\left( K \right)} } \hfill \\ {\beta_{1}^{\left( K \right)} } \hfill \\ \vdots \hfill \\ {\beta_{K - 1}^{\left( K \right)} } \hfill \\ {\beta_{K}^{\left( K \right)} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{array} } \right]$$
(18)

\(\beta_{i}^{\left( K \right)}\) is determined based on Eq. (18) and \(\Phi_{i} \left( {{\varvec{X}}_{k} } \right)\) can be constructed based on Eq. (14).

The polynomial coefficients \(\alpha_{k,i}\) can be written as follows:

$$\alpha_{{{\text{k}},{\text{i}}}} = \int_{{X_{{\text{k}}} }} {g\left( {{\varvec{x}}_{{\text{k}}} } \right)\Phi_{{\text{i}}} \left( {{\varvec{x}}_{{\text{k}}} } \right)f\left( {{\varvec{x}}_{{\text{k}}} } \right)d{\varvec{x}}_{{\text{k}}} }$$
(19)

Equation (19) is a multivariate integral problem and sparse grid method is applied to calculate the multivariate integral in this study. It is necessary to determine the integration points and weights of the random variables. The Hankle positive definite matrix \({\varvec{H}}\) is built from the statistical moments of the random variables \(\mu_{K} ,K = 1,2, \ldots ,2p_{1}\). The upper triangular matrix \({\varvec{C}}\) is constructed from the Cholesky decomposition \({\varvec{H}} = {\varvec{C}}^{{\text{T}}} {\varvec{C}}\):

$${\varvec{C}} = \left[ {\begin{array}{*{20}c} {c_{1,1} } & {c_{1,2} } & \ldots & {c_{{1,p_{1} + 1}} } \\ {} & {c_{2,2} } & \ldots & {c_{{2,p_{1} + 1}} } \\ {} & {} & \ddots & \vdots \\ {} & {} & {} & {c_{{p_{1} + 1,p_{1} + 1}} } \\ \end{array} } \right]$$
(20)

\(\phi_{{{\text{i}}_{{\text{j}}} }}^{\left( K \right)} \left( {X_{{{\text{k}},{\text{j}}}} } \right),K = 1,2, \ldots ,p_{1}\) (Ahlfeld et al. 2016) satisfy the following equation:

$$X_{{{\text{k}},{\text{j}}}} \phi_{{{\text{i}}_{{\text{j}}} }}^{\left( K \right)} \left( {X_{{{\text{k}},{\text{j}}}} } \right) = b_{K - 1} \phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K - 2} \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right) + a_{k,K} \phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K - 1} \right)}} \left( {X_{{{\text{k}},{\text{j}}}} } \right) + b_{K} \phi_{{{\text{i}}_{{\text{j}}} }}^{{\left( {K - 1} \right)}} \left( {X_{{{\text{k}}.{\text{j}}}} } \right)$$
(21)

where the parameters \(a_{K}\) and \(b_{K}\) are expressed as:

$$a_{{\text{K}}} = \frac{{c_{{{\text{K}},{\text{K}} + 1}} }}{{c_{{{\text{K}},{\text{K}}}} }} - \frac{{c_{{{\text{K}} - 1,{\text{K}}}} }}{{c_{{{\text{K}} - 1,{\text{K}} - 1}} }}{\kern 1pt} ,\,b_{{\text{K}}} = \frac{{c_{{{\text{K}} + 1,{\text{K}} + 1}} }}{{c_{{{\text{K}},{\text{K}}}} }},\,c_{0,0} = 1,\,c_{0,1} = 0$$
(22)

Equation (21) can be rewritten as a positive definite symmetric tridiagonal Jacobi matrix \(J\):

$$J = \left[ {\begin{array}{*{20}l} {a_{1} } \hfill & {b_{1} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {b_{1} } \hfill & {a_{2} } \hfill & {b_{2} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {b_{2} } \hfill & {a_{3} } \hfill & {b_{3} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {b_{{p_{1} - 2}} } \hfill & {a_{{p_{1} - 1}} } \hfill & {b_{{p_{1} - 1}} } \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {b_{{p_{1} - 1}} } \hfill & {a_{{p_{1} }} } \hfill \\ \end{array} } \right]$$
(23)

The integration points and weights of the random variables are determined by the eigenvalues and the corresponding normalized eigenvectors of the matrix \(J\), respectively. Special tensor product operations (Smolyak 1963) are then performed to determine the configuration points and weights used to compute the polynomial coefficients. The \(1{\text{st}}\)-order statistical moment can be determined as follows:

$$E\left[ {g\left( {\user2{X}_{{\text{k}}} } \right)} \right]\, = \,\alpha _{{{\text{k}},0}}$$
(24)

where \(\alpha_{0}\) is the first polynomial coefficients. The \(l{\text{th}}\)-order statistical moment \(E\left[ {g^{l} \left( {{\varvec{X}}_{{\text{k}}} } \right)} \right]\) can also be calculated using this equation. Defining formula as follows:

$$G\left( {\user2{X}_{{\text{k}}} } \right)\, = \,g^{{\text{l}}} \left( {\user2{X}_{{\text{k}}} } \right)$$
(25)

Thus, the \(l{\text{th}}\)-order statistical moment of \(Y{ = }g\left( {{\varvec{X}}_{{\text{k}}} } \right)\) is transformed into the 1st-order statistical moment of \(Y{ = }G\left( {{\varvec{X}}_{{\text{k}}} } \right)\).

4.2 Computing the probability density function of the response function

Based on the statistical moments, the PDF of the response function in the elements is computed using the maximum entropy method. The first 4th-order statistical moments are applied to estimate the probability density function of the random variable. The entropy value indicates the estimation accuracy of the probability density function. In order to estimate a more accurate probability density function, the response function \(Y_{k}\) needs to be normalized. The constrained optimization problem (Sobczyk and Trcebicki 1999) can be written as follows:

$$\left\{ \begin{gathered} \mathop {\max }\limits_{{f_{k} }} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S\left( {f_{{\text{k}}} } \right) \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{Y_{{\text{k}}} }} {\left( {\frac{{y - \mu_{{Y_{{\text{k}}} }} }}{{\sigma_{{Y_{{\text{k}}} }} }}} \right)^{i} f_{{\text{k}}} \left( y \right)dy} = m_{{{\text{k}},{\text{i}}}}^{\prime } ,i = 0,1, \ldots ,4 \hfill \\ \end{gathered} \right.$$
(26)

where \(\mu_{{Y_{{\text{k}}} }}\) and \(\sigma_{{Y_{{\text{k}}} }}\) denote the mean and variance of the response function in element \(B_{{\text{k}}}\), respectively. \(f_{{\text{k}}} \left( y \right)\) represents the estimated PDF of the response function. \(S\left( {f_{{\text{k}}} } \right)\) is the entropy value of \(f_{{\text{k}}} \left( y \right)\):

$$S\left( {f_{{\text{k}}} } \right) = \int_{{Y_{{\text{k}}} }} {f_{{\text{k}}} \left( y \right)\ln \left( {f_{{\text{k}}} \left( y \right)} \right)dy}$$
(27)

\(m_{{{\text{k}},{\text{i}}}}^{\prime }\) indicates a non-standard central moment that is determined by the original statistical moment \(m_{k,i}\):

$$m_{{{\text{k}},{\text{i}}}}^{\prime } = \frac{1}{c!}\left[ {\sum\limits_{{{\text{j}} = 1}}^{{{\text{i}} + 1}} {\left( { - 1} \right)^{{{\text{j}} + 1}} C_{{\text{i}}}^{{\text{j}}} \left( {m_{1} } \right)^{{{\text{j}} - 1}} m_{{{\text{i}} - {\text{j}} + 1}} } } \right],i = 0,1, \ldots ,4$$
(28)

where \(C_{{\text{i}}}^{{\text{j}}} = \left( {\begin{array}{*{20}c} i \\ {j - 1} \\ \end{array} } \right)\) is binomial coefficient. \(m_{{{\text{k}},0}}\) represents the \(0{\text{th}}\)-order statistical moment in element \(B_{{\text{k}}}\). \(c\) denotes the proportional factor of \(m_{{{\text{k}},{\text{i}}}}^{\prime }\). The response function’s PDF can be estimated by the constrained optimization problem in Eq. (26). After obtaining the response function’s PDF \(f_{{\text{k}}} \left( y \right)\) in all elements, the response function’s PDF \(f\left( y \right)\) is calculated by using Eq. (9) and Eq. (12).

4.3 Numerical procedure

In the proposed method, elements are constructed and the probabilities of elements are computed in Sect. 3. The PDF of the response function in the elements is then computed in Sect. 4. The PDF of the response function for the multimodal distribution is determined based on the probabilities of the elements and the PDF of the response function in the elements. The numerical procedure of the proposed method is illustrated in Fig. 5, and the detailed procedure is presented below:

Fig. 5
figure 5

Flow chart of the proposed method

Full size image
Step 1:

Determine the number of division points \(M\), the total number of elements \(N_{1}\) and initialize the current element number \(k = 0\).

Step 2:

Decompose the multimodal random variables \(X\) based on the division points and obtain the unimodal random vectors \({\varvec{X}} = \left[ {X_{1} ,X_{2} , \ldots ,X_{M + 1} } \right]\).

Step 3:

Construct elements \(B_{k}\) based on Eq. (7).

Step 4:

Let \(k = k + 1\).

Step 5:

Calculate the probability of the current element \(P\left( {B_{{\text{k}}} } \right)\) by samples using Eq. (12).

Step 6:

Calculate orthogonal polynomial chaos basis \({{\varvec{\Phi}}}\left( {{\varvec{X}}_{{\text{k}}} } \right)\) using Eq. (14) and polynomial coefficient \({\varvec{\alpha}}_{{\text{k}}}\) using Eq. (19) in the current element.

Step 7:

Calculate the statistical moments of the response function \(m_{{{\text{k}},{\text{i}}}} ,i = 0,1, \ldots ,4\) in the current element using Eq. (24) and Eq. (25).

Step 8:

Calculate the response function’s PDF \(f_{{\text{k}}} \left( y \right)\) in the current element using Eq. (26) based on statistical moments \(m_{{{\text{k}},{\text{i}}}}\).

Step 9:

If \(k \le N_{1}\), repeat step 2 to step 8. Otherwise, go to step 9.

Step 10:

Output the response function’s PDF \(f\left( y \right)\) for the multimodal distribution using Eq. (9).

5 Numerical examples

In this section, three examples are used to verify the computational accuracy and efficiency of the proposed method, and MCS is used as a validation method to verify the computational accuracy and efficiency. The method UDRM (Zhang et al. 2019) has the requirement of computing higher-order statistical moments. Thus, it is used as a comparison method. The relative error (RE) \(\varepsilon_{RE}\) and Kullback–Leibler divergence (KLD) \(\varepsilon_{{{\text{KL}}}}\) are used for accuracy analysis, where RE is defined as:

$$\varepsilon_{{{\text{RE}}}} = \frac{{\left| {V - V_{{{\text{MCS}}}} } \right|}}{{V_{{{\text{MCS}}}} }} \times 100\%$$
(29)

where \(V_{{{\text{MCS}}}}\) is the solution at a certain value of the CDF computed by MCS; \(V\) is a solution computed by other methods.

\(\varepsilon_{{{\text{KL}}}}\) is defined as:

$$\varepsilon_{{{\text{KL}}}} \left( {P||Q} \right) = \sum\limits_{{{\text{x}} \in \chi }} {P\left( x \right)\log \left( {\frac{Q\left( x \right)}{{P\left( x \right)}}} \right)}$$
(30)

where \(P\) and \(Q\) are the PDFs obtained by MCS and other methods, respectively; \(\chi\) is probability space.

5.1 Linear elastic cantilever beam force problem

A linear elastic cantilever beam is loaded with one distributed load and two concentrated loads as illustrated in Fig. 6. In this example, the displacement PDF at point \(B\) is determined. The displacement at point \(B\) is denoted as:

$$\Delta _{B} \, = \,f\left( {q,F_{1} ,F_{2} ,E,I,L} \right) = \frac{{qL^{4} }}{{8EI}} + \frac{{5F_{1} L^{3} }}{{48EI}} + \frac{{F_{2} L^{3} }}{{3EI}}$$
(31)

where \(q\) is distributed load. \(F_{1}\) and \(F_{2}\) represent various concentrated loads. \(E\), \(I\) and \(L\) denote the elastic modulus of material, the moment of inertia of beam section and the length of linear elastic cantilever beam, respectively.

Fig. 6
figure 6

Circular section column model (Fan et al. 2016)

Full size image

\(F_{2}\), \(I\) , and \(L\) are determined parameters that \(F_{2} { = }100\, \times \,10^{3} N\), \(L{ = }3000mm\) and \(I{ = 5}{\text{.3594}}\, \times \,{10}^{8} mm^{4}\). \(q\), \(F_{1}\) , and \(E\) are multimodal random variables. Distributional properties of random variables are presented by a large amount of observational data. Therefore, a GMM with four Gaussian components is used to construct the probability density function of multimodal random variables, as illustrated in Fig. 7. The distribution parameters of the multimodal random variables are listed in Table 1.

Fig. 7
figure 7

Distribution of multimodal random variables

Full size image
Table1 Distribution parameters of multimodal random variables
Full size table

Based on the multimodal random variables \(q\), \(F_{1}\) , and \(E\), the displacement PDF at point \(B\) is computed using the proposed method. The decomposition of the multimodal random variables into multiple random variables based on the division points is illustrated in Fig. 8.

Fig. 8
figure 8

Decomposition of multimodal random variables

Full size image

Multimodal random variables are decomposed into four random variables. Therefore, three sets of random variables are obtained. The random variables are chosen to form the elements, and a total of 64 elements are constructed in this example. MCS is continuously used to verify the accuracy of the proposed method based on a large number of samples (\(1\, \times \,10^{6}\)), which are generated using the probability density functions of the multimodal random variables \(q\), \(F_{1}\) , and \(E\).

The results of uncertainty propagation are determined by the proposed method, UDRM, and MCS. They are illustrated in Fig. 9. The PDF and CDF obtained by the proposed method are very close to MCS. For illustration, the CDF values and RE of the proposed method, UDRM, are listed in Table 2, where four locations are considered. The frequency histograms of the response functions constructed by MCS with UDRM and the proposed method are shown in Fig. 10. Then, \(\varepsilon_{KL}\) can be calculated by Eq. (30).

Fig. 9
figure 9

The uncertainty propagation results of proposed method, UDRM, and MCS

Full size image
Table 2 CDF values and RE of different locations
Full size table
Fig. 10
figure 10

Frequency histograms of MCS with different methods

Full size image

It can be found that the proposed method obtains better computational accuracy at these locations. The RE of the proposed method is considerably lower than that of UDRM. The largest RE of the proposed method and the UDRM are both located at y = 7.5, with values of 0.0297% and 8.5706%, respectively. The KLD of MCS and UDRM is 0.0441. The KLD of MCS and the proposed method is smaller, with a value of 0.0013. Hence, the proposed method has the best computational accuracy among them. Computation of higher-order statistical moments not only increases the computational error, but also increases the computational complexity. The proposed method requires the first 4th-order statistical moments, while UDRM requires the first 12th-order statistical moments to construct the PDF of the response function. In addition, UDRM needs to call the response function to calculate 31 times, the proposed method needs to call the response function to calculate 1792 times and MCS needs to call the response function to calculate \(1 \times 10^{6}\) times. Therefore, UDRM and the proposed method are more computationally efficient than MCS. However, the proposed method has the best performance among them, considering both computational accuracy and efficiency.

5.2 The uncertainty propagation problem of RV reducer

RV reducer are an integral part of industrial robots and are widely used in the industrial robotics field. For light industrial robots, the RV reducer only considers the first to the fourth joint. However, for heavy industrial robots, all joints of the RV reducer need to be considered. The mechanism of the RV reducer mainly includes the central gear with input shaft, planetary gear, crank shaft, RV gear, pin gear, pin wheel housing, tapered roller bearing, gasket, needle bearing, angular contact ball bearing and output mechanism. The structure diagram is illustrated in Fig. 11.

Fig. 11
figure 11

RV reducer structure diagram (Yang et al. 2021)

Full size image

The gear teeth of the planetary gear are required to satisfy the contact fatigue strength of the tooth surface. Therefore, the response function of the contact fatigue strength of the planetary gear teeth is defined as follows:

$$Y = g\left( {d,X} \right)\,{ = 297}{\text{.6064}}\sqrt {\frac{7161.8144}{{X_{1} d_{1} d_{2} }}\left( {d_{2} + d_{3} } \right)} - 1100$$
(32)

where \(d_{1}\), \(d_{2}\), \(d_{3}\) , and \(X_{1}\) represent modulus, number of central gear, number of planetary gear, and width of planetary gear, respectively. Parameter \(d_{1}\), \(d_{2}\), \(d_{3}\) , and \(X_{1}\) are multimodal random variables. Distributional properties of random variables are presented by a large amount of observational data. Therefore, GMM with two Gaussian components is used to construct the probability density function of multimodal random variables. Distribution parameters of random variables \(d_{1}\),\(d_{2}\),\(d_{3}\) , and \(X_{1}\) are listed in Table 3.

Table 3 Distribution parameters of random variables
Full size table

Based on the probability density functions of the multimodal random variables \(d_{1}\), \(d_{2}\), \(d_{3}\) , and \(X_{1}\), the proposed method is employed to compute the probability density function of the contact fatigue strength of the planetary gear tooth \(Y\). Each multimodal random variable is decomposed into two random variables and four sets of random variables are constructed, as illustrated in Fig. 12. Thus, a total of 16 elements are determined in this example.

Fig. 12
figure 12

The decomposition of multimodal random variables

Full size image

The computational accuracy of the statistical moments in the elements may change with the order of the polynomial \(P\). The \(\log {\text{RE}}\) of the statistical moments with the orders of the polynomial \(P\) are illustrated in Fig. 13. It follows that \(\log {\text{RE}}\) is extremely large when \(P = 1\). Then, the \(\log {\text{RE}}\) becomes extremely small and remains stable when \(P \ge 2\). Therefore, when \(P{ = }2\), the optimal computational accuracy can be achieved with the proposed method.

Fig. 13
figure 13

The \(\log {\text{RE}}\) with the orders of polynomial

Full size image

The results of uncertainty propagation are calculated using the proposed method, UDRM, and MCS and are illustrated in Fig. 14. It can be found that the PDF and CDF obtained by the proposed method are highly close to MCS, but the results obtained by UDRM are different from MCS. The CDF values and relative errors of the proposed method, UDRM, are listed in Table 4, where four locations are considered. The frequency histogram of the response function constructed by MCS with UDRM and the proposed method is shown in Fig. 15. Then, \(\varepsilon_{KL}\) can be calculated by formula (30).

Fig. 14
figure 14

The uncertainty propagation results of the proposed method, UDRM, and MCS

Full size image
Table 4 CDF values and relative errors of different locations
Full size table
Fig. 15
figure 15

Frequency histograms of MCS with different methods

Full size image

The RE of the proposed method is less than 1% at these locations, with the smallest being 0.0729%. However, the RE of UDRM is considerably larger than that of the proposed method, with a minimum of 3.4575%. The KLD of MCS and UDRM is 0.0288. The KLD of MCS and the proposed method is smaller, with a value of 0.0018. Hence, the proposed method has the best computational accuracy among them. The proposed method and UDRM require the first 4th-order statistical moments and first 8th-order statistical moments to construct the PDF of the response function, respectively. Computing the statistical moments of the UDRM is more complicated than the proposed method. UDRM needs to call the response function to calculate 41 times to estimate the PDF, the proposed method needs to call the response function to calculate 720 times and MCS needs to call the response function to calculate \(1 \times 10^{6}\) times to compute the PDF. The computational efficiency of the proposed method is lower than UDRM but higher than MCS. However, the proposed method requires fewer statistical moments. Therefore, the proposed method has the best performance among them, considering both computational accuracy and efficiency.

5.3 Vehicle collision problem

Lightweight design is employed in the vehicle industry and improves the energy consumption performance of the vehicle. However, a lightweight design may weaken the vehicle’s crashworthiness. Therefore, collision analysis is used to verify crashworthiness. The structure diagram and simulation model of the vehicle are illustrated in Fig. 16. The failure analysis for high-speed frontal impact of a vehicle is performed at a speed of 56.4 km/h. In high-speed collisions, it is necessary to retain a relatively safe space to reduce passenger injuries. Hence, the intrusion of the marker points under the left back chair \(I_{L}\) is a highly valuable indicator.

Fig. 16
figure 16

Structure diagram and simulation model of vehicle (Huang et al. 2016)

Full size image

The thickness of the front bumper \(X_{1}\), the inner plate of the anti-collision box \(X_{2}\), the outer plate of the anti-collision box \(X_{3}\), the inner plate of the front longitudinal beam \(X_{4}\) , and the outer plate of the front longitudinal beam \(X_{5}\) lead to a large influence on the intrusion of the marked point \(I_{L}\), which mathematically can be expressed as follows:

$$I_{L} \left( \varvec{X} \right) = g{\text{ }}\left( {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} } \right)$$
(33)

The response surface of the intrusion quantity for the landmark under the left back chair \(I_{L}\) is established by finite element sampling points and the uncertainty propagation is performed for the intrusion quantity \(I_{L}\) in the vehicle collision problem:

$$\begin{aligned} I_{L} \,{ = } & \,51.820X_{1} { - }9.242X_{2} { + }8.394X_{3} { - }79.998X_{4} { - }64.932X_{5} { - }5.156X_{1} X_{2} \\ & + 6.211X_{2} X_{3} + 14.747X_{1} X_{5} - 5.878X_{2} X_{4} - 9.894X_{2} X_{5} - 8.811X_{3} X_{4} \\ & - 2.477X_{3} X_{5} { + }7.152X_{4} X_{5} { - }15.196X_{1}^{2} { + }6.761X_{2}^{2} { + }20.438X_{4}^{2} { + }7.471X_{5}^{2} \\ & { + 275}{\text{.327}} \\ \end{aligned}$$
(34)

Random variables are multimodal distributions based on observed data, and GMM is used to determine the probability density function of multimodal random variables. The distribution parameters of \(X_{1}\),\(X_{2}\),\(X_{3}\),\(X_{4}\) , and \(X_{5}\) are listed in Table 5

Table 5 Distribution parameters of random variables
Full size table

Each multimodal random variable is decomposed into two random variables and five sets of random variables are constructed. Thus, a total of 32 elements are obtained in this example. The uncertainty propagation results of the proposed method are illustrated in Fig. 17.

Fig. 17
figure 17

The uncertainty propagation results of the proposed method, UDRM, and MCS

Full size image

As shown in Fig. 17, the PDF and CDF of the response function obtained by the proposed method are very close to MCS, but the results obtained by UDRM are different from MCS. In addition, the proposed method requires the first 4th-order statistical moments and UDRM requires the first 8th-order statistical moments to construct the PDF of the response function. To illustrate the computational accuracy of the proposed method, the relative errors of CDF for the proposed method and UDRM are listed in Fig. 18. Four locations (\(I_{L} { = }147,150,153,156\)) are used to represent the computational accuracy.

Fig. 18
figure 18

Relative errors of CDF of the proposed method and UDRM

Full size image

The relative errors of the proposed method are smaller than that of UDRM in these locations, and their relative errors are less than 0.5% in these locations. The highest relative error of the proposed method is located at \(I_{L} { = }150\), and the highest relative error of the UDRM is located at \(I_{L} { = }147\). The KLD of MCS and UDRM is 0.0085. The KLD of MCS and the proposed method is smaller, with a value of 0.0004. Hence, the proposed method has the best computational accuracy among them. The proposed method and UDRM are computationally efficient compared to MCS and they compute the response functions for 2112, 51, and \(1 \times 10^{6}\) times, respectively. UDRM is the most computationally efficient, followed by the proposed method and MCS is the least efficient. Therefore, the proposed method has the best performance among them, considering both computational accuracy and efficiency.

6 Conclusion

This study proposes an uncertainty propagation method for multimodal distributions through unimodal decomposition strategy. First, the GMM is used to establish the probability density functions of the multimodal random variables. Second, a unimodal decomposition strategy is proposed for uncertainty propagation for multimodal distributions. A set of unimodal elements is constructed and the PDF of the response function in the elements is estimated using an arbitrary polynomial chaos expansion and the maximum entropy method. Third, the PDF of the response function in the complete probability space is obtained based on the elements. The analytical results of the three examples demonstrate that the proposed method can accurately and efficiently obtain the PDF of the response function for the uncertainty propagation of the multimodal distribution. The proposed method avoids computing higher-order statistical moments and the first 4th-order statistical moments can meet the engineering requirements. As a result, errors in the calculation of higher-order statistical moments can be avoided. However, the limitation of this method is that more multimodal random variables or modes need to construct more elements. In this way, they lead to a decrease in computational efficiency. Further research should be done to apply the sensitivity analysis to reduce the number of input random variables and improve the computational efficiency.