Enhanced Gaussian-mixture-model-based nonlinear probabilistic uncertainty propagation using Gaussian splitting approach

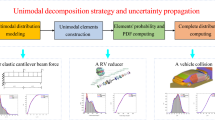
Abstract

Practical engineering problems often involve stochastic uncertainty, which can cause substantial variations in the response of engineering products or even lead to failure. The coupling and propagation of uncertainty play a crucial role in this process. Hence, it is imperative to quantify, propagate and control stochastic uncertainty. Different from most traditional uncertainty propagation methods, the proposed method employs Gaussian splitting method to divide the input random variables into Gaussian mixture models. These GMMs have a limited number of components with very small variances. As a result, the input Gaussian components can be conveniently propagated to the response and remain Gaussian distributions after nonlinear uncertainty propagation, which is able to provide an effective method for high-precision nonlinear uncertainty propagation. Firstly, the probability density function of input random variable is reconstructed by Gaussian mixture models. Secondly, the K-value criterion is proposed for selecting split direction, taking into account both the nonlinearity and variance. The components of input random variables are then divided into a Gaussian mixture model with small variance along the direction determined by the K-value. Thirdly, the individual components of the Gaussian mixture model are propagated one by one to obtain the probability density function of the response. Finally, the convergence criterion based on Shannon entropy is developed to ensure the accuracy of uncertainty propagation. The efficacy of the method is verified using three numerical examples and two engineering examples.

1 Introduction

Practical engineering problems (Vanmarcke et al. 1986; Guo et al. 2019) frequently involve uncertainties that arise from various sources, including the structure’s geometry, material properties, manufacturing and assembly faults, and random loads. The performance of mechanical structures can be affected by multiple sources of uncertainty, which can spread and amplify, resulting in fluctuations or even failures (Schuëller and Jensen 2008; Du and Chen 2000). The measurement, propagation and control of uncertainties are important tools to ensure the safety and reliability of engineering structures (Yao et al. 2011; Balu and Rao 2014).

Uncertainty is commonly categorized into two separate categories: epistemic uncertainty and aleatory uncertainty (Helton et al. 2010; Brevault et al. 2016). Epistemic uncertainty emerges from limited data or information during the modeling process, including model uncertainty and uncertainty in variable distribution parameters caused by insufficient objective knowledge (Jakeman et al. 2010; Jiang et al. 2016). The occurrence of this issue might be attributed to insufficient accuracy in measuring a quantity, failure or incomplete understanding of the modeling process, or inadequate comprehension of the system’s motion mechanism. The main approaches to modeling epistemic uncertainty are: evidence theory (Barnett 2008; L Chen et al. 2023), fuzzy set theory (Dodagoudar and Venkatachalam 2000; Kabir and Papadopoulos 2018), and interval theory (Rao and Berke 1997; Qiu et al. 2008). Aleatory uncertainty represents the randomness that exists in nature or physical phenomena, which cannot control or reduce such randomness, also called statistical uncertainty, and probability theory is used to research it.

Aleatory uncertainty is modeled by a probability model (Chen et al. 2018; Meng et al. 2021) to derive the probability density function (PDF), failure probability, and statistical characteristics of output based on distribution information of random variables. A substantial amount of probabilistic uncertainty propagation analysis method has been devised, which can be broadly arranged in four groups: Sampling-based methods, Moment-based methods, Local expansion-based methods, Surrogate-based models. Sampling-based methods mainly include Monte Carlo simulation (MCS) (Cox and Siebert 2006) and the unscented transform (UT) (Julier and Uhlmann 2004; Kandepu et al. 2008). MCS generates a substantial number of randomly sampled points to acquire uncertainty information of the system’s response. Although MCS is highly adaptable and accurate, it incurs high computational costs. For the purpose of enhancing the efficiency of propagating uncertainty, some special methods of sampling have been proposed, including Latin hypercube sampling (Helton and Davis 2003), importance sampling (Mori and Kato 2003), adaptive sampling (Bucher 1988; Brookes and Listgarten 2018). The UT generates sigma points based on the distribution of random variables, and then weights response values of the sigma points on the performance function to acquire the statistical moments.

Moment-based methods employ a numerical integration approach to compute statistical moments of output response. They use probabilistic evolutionary methods (maximum entropy principle (Xi et al. 2012)) to acquire the response PDF, such as sparse grid numerical integration (Jia et al. 2019), univariate dimension reduction method (Rahman and Xu 2004; Z Zhang et al. 2019). Nevertheless, low-order moments are inadequate in capturing the non-Gaussian properties of the output response. Additionally, the nonlinearity of the performance function has a substantial impact on the accuracy of higher-order statistical measures. Local expansion-based approaches require approximation of performance function by Taylor expansion at reference point, such as first order reliability method (FORM) (Low and Tang 2007) and second-order reliability method (SORM) (Junfu Zhang and Du 2010). FORM makes a linear approximation with very high computational efficiency, but only for weakly nonlinear uncertainty problems. SORM performs a second-order approximation, considering its second-order curvature. However, FORM and SORM both are required to compute partial derivatives of performance function. Surrogate-based models approximate the performance function by constructing a numerical model. Typical surrogate models are Kriging (Kaymaz 2005), support vector machines (Noble 2006), artificial neural networks (Srivaree-Ratana et al. 2002), etc. Due to its lower cost relative to the original performance function, the surrogate model is extensively utilized in various domains such as aviation and transportation networks. This leads to a significant reduction in computational expenses. However, Surrogate-based model can introduce uncertainty of the numerical models.

The samples of MCS method describing the PDF are the same as the Dirac delta function with infinitesimal variance. In contrast, Gaussian mixture model (GMM) use Gaussian sum instead of infinitesimal sample point to describe the PDF (Psiaki et al. 2015). To perform uncertainty propagation using GMM, the output GMM entails being estimated from the GMM of the input uncertainty variables. Although each Gaussian component is easy to propagate by multiple methods, it is still a challenge to determine the weights and number of components. Terejanu et al. (Terejanu et al. 2008) pointed out that when covariance of input Gaussian distribution is infinitesimal, the weights of Gaussian components through nonlinear performance function remain constant. They introduce two different methods to update weights of the GMM components. Although updating weights can improve accuracy of uncertainty propagation, it remains a problem to determine the optimal number of initial Gaussian components. Huber et al. (Huber 2011) proposed a method based on GMM component weights and covariance traces to select Gaussian components that need to be split. However, this approach ignores the effect of nonlinearity of the performance function on the output response. Vittaldev et al. (Vittaldev and Russell 2016) greatly expanded the number of splits of Gaussian distributions and proposed the idea of simultaneous splits along multiple directions judged by Stirling criterion. However, when there are multiple extremums of the performance function, the splitting direction judged by the criterion may be incorrect. Demars et al. (DeMars et al. 2013) detected the nonlinearity of the Gaussian distribution by the difference between the entropy of the linearization and UT, and splitting was performed along the eigenvector when it exceeded a certain threshold. Although the method accurately finds the component to be split, it uses both linearization and UT for propagation, which increases the computational burden. Zhang et al. (Bin Zhang and Shin 2021) proposed an uncertainty propagation method for artificial neural networks, which selects the Gaussian components to be split based on the KL divergence. The initial input random variable of some existing method is a Gaussian distribution (Huber 2011; DeMars et al. 2013; Vittaldev and Russell 2016). Therefore, it cannot be used with other types of distributions, such as Beta distribution or Gamma distribution.

Different from most traditional uncertainty propagation method, we split the input variable into a weighted combination of a series of small variance Gaussian components. The response of Gaussian component with small variance remains Gaussian through the nonlinear performance function. This property ensures that the uncertainty propagation of a single Gaussian component is straightforward, efficient, and accurate. Consequently, the nonlinear uncertainty propagation becomes a series of simple and efficient uncertainty propagation of a single Gaussian component.

This study presents a novel uncertainty propagation method based on Gaussian mixture models. Additionally, a new criterion is introduced to determine the direction of splitting. The subsequent segments of this paper are organized as follows: In Sect. 2, a Gaussian mixture model is employed to reconstruct PDF of input random variables. In Sect. 3, Gaussian components are split into Gaussian mixture models with small variance along the direction judged by K-value criterion. In Sect. 4, each component of the GMM is propagated using UT to obtain the output response PDF. In Sect. 5, the difference in the entropy of response PDF is used to determine the number of splits, which ensures accuracy of uncertainty propagation. Section 6 discusses three numerical examples and two engineering examples, and Sect. 7 summarizes some conclusions.

2 Uncertainty variable reconstruction based on Gaussian mixture model

As mentioned above, the method based on input random variable splitting is aimed at the Gaussian distribution. Since the components of the GMM are Gaussian and GMM can approximate any non-Gaussian PDFs with a sufficient number of components (Vlassis and Likas 2002), the GMM is employed to reconstruct the PDF of input random variables. The optimal number of GMM components is selected using the AIC criterion.

2.1 Gaussian mixture model

GMM find extensive application in statistics, machine learning, computer vision, data mining. They are employed for various tasks including feature extraction, anomaly detection, speech recognition, and reconstruction of PDF. The GMM is a probabilistic model that uses a linear combination of multiple Gaussian distributions to model uncertainty, and it is expressed as follows

$$f\left( {x;\theta } \right) = \sum\limits_{k = 1}^{K} {\alpha_{k} \varphi \left( {x;\mu_{k} ,\Sigma_{k} } \right)}$$

(1)

where: $\alpha_{k}$ denotes weight of the $k{\text{th}}$ component, $\phi \left( {x;\mu_{k} ,\Sigma_{k} } \right)$ denotes the $k{\text{th}}$ component of Gaussian mixture model, $\mu_{k}$ and $\Sigma_{k}$ denote mean and covariance, respectively. To satisfy the properties of the probability density function (PDF is greater than or equal to 0, and sum of integrals is 1), so the weights satisfy the conditions $\alpha_{k} \ge 0$ and $\sum\limits_{{k=1}}^{K} {\alpha_{k} } = 1$. The parameters of GMM:$\theta = \left\{ {\alpha_{k} ,\mu_{k} ,\Sigma_{k} } \right\}_{k = 1}^{K}$.

To ascertain PDF of the Gaussian mixture model, the model parameters $\theta$ need to be estimated. Suppose that a data set $x = \left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} ,...,x^{\left( m \right)} } \right)$ containing $m$ samples is collected. The samples in data set $x$ are independent of each other, the probability that we draw this samples simultaneously are the product of probability of drawing each sample, which is the joint probability of the sample set. This joint probability is the likelihood function, as in Eq. (2):

$$L\left( \theta \right) = L\left( {x^{(1)} ,x^{(2)} ,x^{(m)} ;\theta } \right) = \prod\limits_{i = 1}^{m} f \left( {x^{(i)} ;\theta } \right)$$

(2)

The maximum likelihood method is usually chosen to estimate parameters $\theta$:

$$\theta = \arg \mathop {\max }\limits_{\theta } \prod\limits_{i} f (x^{(i)} |\theta )$$

(3)

Substitute the expression of the GMM into the Eq. (3) and take the logarithm as follows:

$$\begin{aligned} In(L(x|\theta )) & = \sum\limits_{i} I n[f(x^{(i)} \left| \theta \right.)] \\ & = \sum\limits_{i} I n[\sum\limits_{k} {\alpha_{k} } \varphi (x^{(i)} ,\mu_{k} ,\Sigma_{k} )] \\ \end{aligned}$$

(4)

To tackle the challenge of directly solving the optimization problem in Eq. (4), expectation maximization (EM) algorithm is utilized to iteratively explore and identify the local maximum of $In(L(x|\theta )).$. In order to promote the process of iterative algorithms, the EM algorithm introduces the hidden variables $z$, which represents the likelihood of the sample $x^{\left( i \right)}$ pertained to the $z{\text{th}}$ Gaussian model. For each iteration, the distribution of hidden variables $z$ is first calculated using parameters from the previous iteration, and then target parameters are estimated by updating the likelihood function using $z$. The EM algorithm consists of two steps: E-step and M-step.

Step E: The goal of step E is to calculate the values of the hidden variables $z$, which is tantamount to calculating probability of belonging to each Gaussian component separately for each data point. As a result, the hidden parameters $w$ form a $N \times K$ matrix. After each iteration, it can be updated with the latest Gaussian parameters $\left. {\theta = \left( {\begin{array}{*{20}c} {\alpha_{k} ,\mu_{k} ,\Sigma_{k} } \\ \end{array} } \right.} \right)$.

$$w_{i,k}^{t} = \frac{{\alpha_{k}^{t} p\left( {x^{(i)} |\mu_{k}^{t} ,\Sigma_{k}^{t} } \right)}}{{\sum\limits_{{\dot{k}}} {\alpha_{k}^{t} } p\left( {x^{(t)} |\mu_{k}^{t} ,\Sigma_{k}^{t} } \right)}}$$

(5)

The updated expression for the objective function $Q\left( {\theta ,\theta^{t} } \right)$ is obtained by substituting the updated $w$ into likelihood function.

$$Q(\theta ,\theta^{t} ) = E[In \, p(x,z|\theta )|x,\theta^{t} ] = In(p(x,w^{t} |\theta ))$$

(6)

Step M: The step M is to search the extreme value of the function $Q\left( {\theta ,\theta^{t} } \right)$ for $\theta$, which is to search the model value for new iteration.

$$\theta^{(t + 1)} = \arg \mathop {\max }\limits_{\theta } Q(\theta ,\theta^{(t)} )$$

(7)

By using the function $Q\left( {\theta ,\theta^{t} } \right)$ to find the partial derivative of $\mu_{k}$,$\Sigma_{k}$ and making it equal to 0, we can obtain $\hat{\mu }_{k}$,$\hat{\Sigma }_{k}$ To obtain $\hat{\alpha }_{z}$, we need to get the partial derivative under the condition $\mathop \sum \limits_{k=1}^{K} \alpha_{{{\kappa }}} = 1$ and make it equal to 0.

2.2 Akaike information criterion

When employing EM algorithm to estimate parameter of the GMM, it is necessary to predefine the number of GMM components. In real-world scenarios, it is common to have access to only a subset of data, with no existing categorization of the data. To address this problem, the number of GMM components is estimated by Akaike Information Criterion (AIC). AIC, a metric for estimating prediction error and evaluating the relative quality of statistical models, is employed to assess both model complexity and goodness of fit (Burnham and Anderson 2004). Equation (8) presents its formulation.

$$AIC = 2K - 2In(L(\theta ))$$

(8)

where: $K$ denote number of parameters, $L\left( \theta \right)$ represent the value of likelihood function. Generally speaking, as the overall sample size increases, the likelihood function $L\left( \theta \right)$ also increases, leading to a decrease in the value of AIC. Nevertheless, if the sample size is too massive, the model will be overfitting. Hence, it is essential to balance model complexity and goodness of fit, ensuring that the selected model strikes the right trade-off. The optimal model is determined by choosing the one with the smallest AIC value.

Through the above process, arbitrary input random variables can be characterized and modeled by GMM. Nevertheless, the individual Gaussian components of GMM may exhibit a significant variance. This can lead to a response that deviates from a Gaussian distribution and ultimately diminishes the computational accuracy when nonlinear uncertainty is propagated. To enhance the precision and effectiveness of uncertainty propagation for each individual Gaussian component, the subsequent measure involves diminishing the variance of each Gaussian component.

3 Gaussian splitting oriented to reduce the variance

It is shown that when the covariance of all Gaussian components is infinitesimal, uncertainty propagation is achieved by locally approximating behavior of performance function. So the response of the Gaussian component remains Gaussian after nonlinear uncertainty propagation, and the weights and number of components remain constant (Terejanu et al. 2008). Using the fundamental concepts mentioned above, the Gaussian components of the GMM can be divided iteratively until the covariance of each component reaches a sufficiently small value. This ensures that the performance function approaches linearity, so the response of the Gaussian components after uncertainty propagation can also be approximated as a Gaussian distribution.

Given a input random variable x described by a GMM $f\left( {\varvec{x}} \right) = \sum\limits_{i = 1}^{K} {\alpha_{i} N\left( {{\varvec{x}};{\varvec{\mu}}_{{\varvec{i}}} ,{\varvec{\varSigma}}_{{\varvec{i}}} } \right)}$ and the kth Gaussian component is split, as in Eq. (9):

$$\alpha_{k} N\left( {{\varvec{x}};{\varvec{\mu}}_{{\varvec{k}}} ,{\varvec{\varSigma}}_{{\varvec{k}}} } \right) \approx \sum\limits_{j = 1}^{L} {\alpha_{k,j} N\left( {{\varvec{x}};{\varvec{\mu}}_{k,j}{\varvec{\varSigma}}_{{\varvec{k,j}}} } \right)}$$

(9)

where $L$ indicates that there are L Gaussian components and $L > 1$; there are $L$ weights $\alpha_{k,j}$, $L$ means ${\varvec{\mu}}_{{\varvec{k,j}}}$, $L$ covariance ${\varvec{\varSigma}}_{{\varvec{k,j}}}$, and a total of $3L$ free parameters, much larger than the number of given conditions, which is an undetermined problem. It can be extracted by attenuating the difference between $\alpha_{k} N\left( {{\varvec{x}};{\varvec{\mu}}_{k} ,{\varvec{\varSigma}}_{k} } \right)$ and $\sum\nolimits_{j = 1}^{L} {\alpha_{k,j} N\left( {{\varvec{x}};{\varvec{\mu}}_{k,j}{\varvec{\varSigma}}_{k,j} } \right)}$.

3.1 Splitting of univariate Gaussian component

To streamline the process of solving the splitting problem, the initial focus is on studying the splitting of univariate Gaussian distribution, which can be easily extended to splitting of multivariate Gaussian distribution. The splitting of standard Gaussian distribution is performed firstly in order to create a library of splits, thus facilitating the subsequent propagation of uncertainty. Whereas input variables are characterized by non-standard Gaussian distributions, their components can be transformed into each other by a coordinate transformation that can transform the non-standard normal distribution into a standard normal distribution. In order to simplify the task of solving the aforementioned splitting problem, certain constraints are imposed: all Gaussian mixture models have the same covariance,$\sigma_{\kappa ,j} = \sigma$; the means are negatively symmetrically distributed along the mean $\mu$ of the initial Gaussian component; and the weights are symmetrically distributed along mean $\mu$ of initial Gaussian distribution. The imposed constraints are as in Eq. (10). Then the total number of free parameters is reduced to $L - 1$. The univariate splitting library in this paper is derived from the reference (Vittaldev and Russell 2016).

$$\begin{gathered} \mu_{0} = 0,\mu_{j} = - \mu_{ - j} \, j = 1,2,...,(L - 1)/2 \hfill \\ \alpha_{j} = \alpha_{ - j} ,\sum\limits_{j = 1}^{L} {\alpha_{j} } = 1 \, j = 1,2,...,(L - 1)/2 \hfill \\ \sigma_{j} = \sigma \, j = 1,2,...,L \hfill \\ \end{gathered}$$

(10)

3.2 Splitting of multivariate Gaussian component

For multivariate uncertainty problems, it becomes essential to extend the splitting methodology from univariate Gaussian distribution to multivariate Gaussian distribution. To accomplish this, the eigenvalue decomposition of the covariance matrix is employed for a multivariate Gaussian distribution $N\left( {{\varvec{x}}|{\varvec{\mu}},{\varvec{\varSigma}}} \right)$, as shown in Eq. (11)..

$${\varvec{\varSigma}}= \varvec{V\Lambda V}^{T}$$

(11)

$${\varvec{V}} = \left[ {V_{1} ,V_{2} ...,V_{k} } \right] \,{\varvec{\varLambda}}{\text{ = diag}}\left[ {\lambda_{1} ,\lambda_{2,} ...,\lambda_{k} } \right]$$

(12)

where: $\lambda_{i}$ denotes the eigenvalue and $V_{i}$ denotes the corresponding eigenvector. The matrix ${\varvec{V}}$ denotes a rotation matrix, and the rotation and translation transformations are in Eq. (13).

$${\varvec{x}} = {\varvec{\mu}} + \sqrt{\varvec{\varLambda}}\cdot {\varvec{V}} \cdot {\varvec{y}}$$

(13)

Then the transformed PDF of Gaussian distribution is:

$$f\left( {\varvec{y}} \right) = N\left( {{\varvec{y}};{\varvec{o}},{\varvec{I}}} \right) = \prod\limits_{j = 1}^{L} {N\left( {y;0,1} \right)}$$

(14)

where ${\varvec{I}}$ is identity matrix, ${\varvec{o}}$ is zero matrix. Since the covariance of $f\left( {\varvec{y}} \right)$ is a diagonal matrix, corresponding eigenvectors align with the coordinate axes, respectively, while each independent distribution is also standard normal.

In the scenario when the inputs consist of multivariate distributions, the nonlinearity of the performance function and the variance of variables vary in different directions. Consequently, splitting in different directions yields distinct effects on the output results. Hence, it is imperative to divide in the direction that exerts the most significant influence on the output response. For this reason, we propose the K-value criterion, as in Eq. (15). This criterion enables the simultaneous consideration of both the impact of performance function’s nonlinearity and covariance of input variables on propagation of uncertainty.

$$\begin{gathered} \varphi = \frac{{f\left( {{\varvec{\mu}} + h\widehat{{\varvec{a}}}} \right) + f\left( {{\varvec{\mu}} - h\widehat{{\varvec{a}}}} \right) - 2f({\varvec{\mu}})}}{{h^{2} }} \hfill \\ K = \varphi \varvec{\lambda /2} \hfill \\ \end{gathered}$$

(15)

where ${\varvec{\lambda}}$ denotes eigenvector of the covariance matrix ${\varvec{\varSigma}}$, and $h$ denotes a specified constant, $\widehat{{\varvec{a}}}$ is a unit vector representing the split direction. $\varphi$ denotes the second-order derivative of the performance function in the direction $\widehat{{\varvec{a}}}$. In general, $h$ can take a specific value in practical engineering. The nonlinearity of a function can be described in terms of curvature, which is positively correlated with the second-order derivative. Therefore, when the value of $\varphi$ is larger, the performance function is more nonlinear. $\lambda$ denotes the magnitude of variance of random variable. Correspondingly, as the value of $\lambda$ increases, the variance also increases.

The direction of $i{\text{th}}$ eigenvector is selected as splitting direction by the K-value criterion, and the univariate splitting library mentioned in the previous section is also applied to split the input variable, as in Eq. (16).

$$N_{i} \left( {y_{i} ;0,1} \right) \approx \sum\limits_{k = 1}^{K} {\alpha_{k} N\left( {y_{i} ;\mu_{k} ,\sigma_{k}^{2} } \right)}$$

(16)

Substituting Eq. (16) into Eq. (14), the split Gaussian mixture model is obtained.

$$f\left( y \right) = \sum\limits_{k = 1}^{K} {\alpha_{k} N\left( {y_{i} ;\mu_{k} ,\sigma_{k} } \right)} \prod\limits_{j = 1,j \ne i}^{L} {N\left( {y_{j} ;0,1} \right)}$$

(17)

The mixture model of Eq. (17) is rotated and translated into the space of coordinate systems of the initial Gaussian distribution by the inverse transformation of Eq. (13): ${\varvec{y}} = \left( {\sqrt{\varvec{\varLambda}}{\varvec{V}}} \right)^{ - 1} \left( {{\varvec{x}} - {\varvec{\mu}}} \right)$. Then the multivariate GMM after splitting can be obtained: the weights remain constant and the means and covariances are as follows:

$$\begin{gathered} {\varvec{\mu}}_{{\varvec{k}}} = {\varvec{\mu}} + {\varvec{\mu}}_{k} \sqrt {{\varvec{\lambda}}_{i} } {\varvec{V}}_{i} \hfill \\{\varvec{\varLambda}}_{{\varvec{k}}} = {\text{diag}}\left\{ {\lambda_{1} ,...,\sigma_{k}^{2} \lambda_{i} ,...,\lambda_{L} } \right\} \hfill \\{\varvec{\varSigma}}_{{\varvec{k}}} = {\varvec{V}}^{T}{\varvec{\varLambda}}_{k} {\varvec{V}} \hfill \\ \end{gathered}$$

(18)

4 Uncertainty propagation for Gaussian components with small variance

Nonlinear performance functions can cause the initial Gaussian distribution to transform into a non-Gaussian distribution during uncertainty propagation. Nevertheless, research conducted by (Terejanu et al. 2008) has shown that even after nonlinear uncertainty propagation, the response of the GMM component continues to adhere to the Gaussian distribution when the GMM reconstructs it with a sufficiently small covariance. The reason is that nonlinear performance function is almost linear in each small variance component of the GMM. Considering that output response of small variance Gaussian component is approximately Gaussian, it becomes sufficient to calculate the response of a finite number of points to fit the mean variance and thus obtain a more accurate normal distribution of the response. Thus, this paper employs UT (Julier and Uhlmann 2004) as an uncertainty propagation method.

The PDF of n dimensional input random variables can be represented by a GMM $f\left( {\varvec{x}} \right) = \sum\nolimits_{k = 1}^{K} {\alpha_{k} P\left( {{\varvec{x}};{\varvec{\mu}}_{k} ,{\varvec{\varSigma}}_{k} } \right)}$ after splitting, and propagate the uncertainty for the $k{\text{th}}$ component.

Firstly, calculate the $2n + 1$ weights of the sigma points, as follows:

$$\begin{gathered} W_{m,k}^{{^{\left( i \right)} }} = \left\{ {\begin{array}{*{20}c} {\frac{\lambda }{n + \lambda }} & {i = 0} \\ {\frac{1}{2(n + \lambda )}} & {i = 1,...,2n} \\ \end{array} } \right. \hfill \\ W_{c,k}^{\left( i \right)} = \left\{ {\begin{array}{*{20}c} {\frac{\lambda }{n + \lambda } + 1 - \tau^{2} + \beta } & {i = 0} \\ {\frac{1}{{2\left( {n + \lambda } \right)}}} & {i = 1,...,2n} \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(19)

where: $W_{m,k}^{\left( i \right)}$ denotes the sigma point weight for calculating the approximate mean, $w_{c,k}^{\left( i \right)}$ denotes the sigma point weight for calculating the approximate covariance, and the parameters $\lambda$ satisfy:

$$\lambda = \tau^{2} \left( {n + t} \right) - n$$

(20)

where: the parameters $\tau$ and $t$ serve as scaling factors that determine the spread of sigma points away from mean. $\tau$ satisfies $10^{ - 4} \le \tau \le 1$, which is usually taken as a small value to avoid the problem of nonlocal effects in strongly nonlinear systems.$t \ge 0$, as usually $t = 3 - n$ or $t = 0$.

Generally speaking, sigma points are positioned at the mean and are symmetrically dispersed based on the covariance of the primary axes. The point set matrix ${\varvec{\chi}}^{\left( i \right)}$ is obtained by the $2n + 1$ sigma points, as follows:

$${\varvec{\chi}}^{\left( i \right)} = \left\{ {\begin{array}{*{20}l} {{\varvec{\mu}}_{x} } \hfill & {i = 0} \hfill \\ {{\varvec{\mu}}_{x} + \left( {\sqrt {\left( {n + \lambda } \right){\varvec{\varSigma}}_{x} } } \right)^{{\left( {i - 1} \right)}} } \hfill & {i = 1,...,n} \hfill \\ {{\varvec{\mu}}_{x} - \left( {\sqrt {\left( {n + \lambda } \right){\varvec{\varSigma}}_{x} } } \right)^{{\left( {i - n - 1} \right)}} } \hfill & {i = n + 1,...,2n + 1} \hfill \\ \end{array} } \right.$$

(21)

where $\left( {\sqrt {\left( {n + \lambda } \right)\sum {_{{\varvec{x}}} } } } \right)^{i - 1}$ denotes the $(i - 1){\text{th}}$ column of lower triangular matrix after Cholesky decomposition of matrix $\left( {n + \lambda } \right)\sum {_{{\varvec{x}}} }$, and $\left( {\sqrt {\left( {n + \lambda } \right)\sum {_{{\varvec{x}}} } } } \right)^{i - n - 1}$ denotes $(i - n - 1){\text{th}}$ column of the lower triangular matrix.

Substitute each sigma point into performance function $y = g\left( {\varvec{x}} \right)$ to obtain the set of points $y^{\left( i \right)} = g\left( {{\varvec{\chi}}^{\left( i \right)} } \right)$. Then mean $\mu_{y,k}$ and covariance $\Sigma_{y,k}$ of $k{\text{th}}$ Gaussian component after UT transformation are as follows:

$$\begin{gathered} {\varvec{u}}_{y,k} = \sum\limits_{i = 0}^{i = 2n} {W_{m,k}^{\left( i \right)} y^{\left( i \right)} } \hfill \\ \sum {_{{\varvec{y,k}}} } = = \sum\limits_{i = 0}^{i = 2n} {W_{c,k}^{\left( i \right)} \left[ {y^{\left( i \right)} - \mu_{k} } \right]\left[ {y^{\left( i \right)} - \mu_{k} } \right]^{T} } \hfill \\ \end{gathered}$$

(22)

When the UT is used to propagates uncertainty on the split Gaussian components, we assume that the weights of Gaussian components keep unchanged and Gaussian components remain as Gaussian after the uncertainty propagation. Therefore, the response PDF $f_{Y} \left( {\varvec{y}} \right)$ is:

$$f_{Y} \left( {\varvec{y}} \right) = \sum\limits_{k = 1}^{K} {\alpha_{k} N\left( {{\varvec{y}};{\varvec{\mu}}_{y,k} ,{\varvec{\varSigma}}_{y,k} } \right)}$$

(23)

5 Convergence criterion

For the proposed approach, the input Gaussian distribution require to be split in Sect. 3. And subsequently, the components of the GMM are propagated one by one using the UT in Sect. 4 to obtain the response PDF. However, the task of determining the optimal splitting number of input random variable remains an unresolved yet significant challenge. On the one hand, the response PDF is non-Gaussian distribution through a nonlinear performance function. Therefore, input random variables require to be split and represented by a Gaussian mixture model. When confronted with a highly nonlinear performance function, accurately calculating the response PDF using only a limited number of splitting becomes challenging Alternatively, it should be noted that increasing the number of splits does not necessarily lead to improved precision in uncertainty propagation, as this sometimes requires significant processing resources.

As splitting number of input random variables raises, the estimated response PDF gradually approximates the true PDF, and its Shannon’s entropy eventually approaches a stable value. Therefore, we introduce an iterative strategy to gradually improve the precision of PDF estimation by progressively increasing the number of splits until uncertainty propagation requirement is satisfied. This approach can effectively control the computational complexity during the solving process.

For a continuous random variable $X$, the definition of Shannon’s entropy is as follows:

$$H\left( X \right) = - \int\limits_{\Omega } p \left( x \right)In \, p_{X} \left( x \right)dx$$

(24)

where $\Omega$ is domain of PDF $p\left( x \right)$. When the random variable is Gaussian distribution $p_{X} \left( x \right) = N(x,\mu ,\Sigma )$, there exists an analytic solution for the information entropy.

$$H\left( x \right) = \frac{1}{2}\log \left| {2\pi {\text{e}}\Sigma } \right|$$

(25)

When $p_{X} \left( x \right) = \sum\limits_{i = 1}^{N} {c_{i} } p_{i} \left( x \right)$ is a Gaussian mixture model, the expression of Shannon’s entropy is as follows:

$$H(x) = - \int {\left( {\sum\limits_{i = 1}^{N} {c_{i} } p_{i} (x)} \right)} In\left( {\sum\limits_{i = 1}^{N} {c_{i} } p_{i} (x)} \right)$$

(26)

From Eq. (26), it is clear that there is no analytical solution. For this reason, when the probability distribution function is GMM, the value of its Shannon entropy needs to be estimated using the approximate value (Kolchinsky and Tracey 2017).

$$H\left( X \right) \approx \hat{H}_{HD} \left( X \right) = H\left( {X|C} \right) - \sum\limits_{i} {c_{i} } In\sum\limits_{j} {c_{j} } e^{{ - BD\left( {p_{i} ||p_{j} } \right)}}$$

(27)

where:$H\left( {X|C} \right)$ is the conditional entropy, as in Eq. (28); $BD\left( {p_{i} \parallel p_{j} } \right)$ is the Bhattacharyya distance, as in Eq. (29).

$$H\left( {X\left| C \right.} \right) = \sum\limits_{i} {c_{i} } H\left( {p_{i} } \right)$$

(28)

$$BD(p\parallel q) = - In\int {\sqrt {p(x)q(x)} dx}$$

(29)

The flow of nonlinear probabilistic uncertainty propagation algorithm based on Gaussian mixture model is shown in the Fig. 1.The detailed steps are outlined below:

• (1) If input variable $X$ is a Gaussian distribution or Gaussian mixture model, go directly to step (3), otherwise go to next step.

• (2) Select the best Gaussian mixture model to approximate non-Gaussian PDF by EM algorithm and the AIC criterion, using Eq. (5) to (8).

• (3) Calculate K-value $\phi_{k}$ of the performance function $Y = f\left( x \right)$ in all directions, using Eq. (15).

• (4) Based on size of K-value $\phi_{k}$ calculated in step (3), select the splitting direction $m$, set the initial value $n$ of the splitting number and the error limit $\varepsilon$.

• (5) Along the selected splitting direction $m$, the Gaussian component is split into a Gaussian mixture model with smaller variance.

• (6) Uncertainty propagation of the Gaussian components after splitting is performed by the UT, using Eq. (19) to Eq. (23).

• (7) Calculate approximate value of entropy value of PDF $p\left( y \right)$, using Eq. (27) to Eq. (29).

• (8) Check whether the convergence condition is satisfied, and if so, proceed to the next step. If not, $n = n + 2$, repeat step (4) to (7).

• (9) Output the final response PDF.

Fig. 1

Flowchart of the proposed method

6 Examples of algorithm performance

In this section, we validate effectiveness of the proposed method by using three numerical examples and two engineering examples. At the same time, uncertainty propagation results of the proposed method are compared with those of the multidirectional GMM (MGMM) [37] and MCS.

6.1 Example 1: Mathematical problems where the input distribution is Gaussian

Consider a performance function with two output components:

$$y = \left\{ {\begin{array}{*{20}l} {r\cos (\theta )} \hfill \\ {r\sin (\theta )} \hfill \\ \end{array} } \right.$$

(30)

The distributions of input random variables $\left( {r,\theta } \right)$ are Gaussian distributions with mean $\mu$ and covariance $\Sigma$ as in Eq. (31), and the eigenvalues and eigenvectors are in Eq. (32).

$$\left. {\mu = \left[ {\begin{array}{*{20}c} {10} \\ {\pi /2} \\ \end{array} } \right.} \right] \, \Sigma = \left[ {\begin{array}{*{20}c} 8 & {0.5} \\ {0.5} & {1.21\pi^{2} } \\ \end{array} } \right]$$

(31)

$$\begin{gathered} \lambda_{1} = 7.9376\quad v_{1} = \left[ {\begin{array}{*{20}c} { - 0.9923} & {0.1239} \\ \end{array} } \right]^{7} \hfill \\ \lambda_{2} = 12.0046\quad v_{2} = \left[ {\begin{array}{*{20}c} {0.1239} & {0.9923} \\ \end{array} } \right]^{7} \hfill \\ \end{gathered}$$

(32)

We employed the proposed method, in conjunction with the MGMM and MCS, to investigate the uncertainty propagation of the performance function $y\left( {r,\theta } \right)$. For the proposed method: since input Gaussian distribution is a multivariate GMM with 1 component, the K-value $\phi_{k}$ in each direction (the direction of the eigenvector) is first calculated: $\phi_{{K_{1} }} = 1.1428$, $\phi_{{K_{2} }} = 45.9205$. Given that the K-value in the $v_{2}$ direction is approximately 36 times more than in the $v_{1}$ direction, the K-value in the $v_{1}$ direction has a negligible effect on the performance function and the splitting is done only along the $v_{2}$ direction. Secondly, the input Gaussian distribution is split into a Gaussian mixture model with smaller covariance along direction $v_{2}$. Third, we perform uncertainty propagation on each Gaussian component of the GMM to obtain the PDF of performance function and calculate its corresponding Shannon’s entropy. Finally, the number of splits is increased until the disparity in Shannon entropy is below a given error limit $\varepsilon$. For the MGMM, the value of Stirling criterion $\phi_{s}$ is calculated:$\phi_{{S_{1} }} = 1.0913$,$\phi_{{S_{2} }} = 0.1951$. Similarly, since the $\phi_{s}$ along the $v_{1}$ direction is 5.5 times that in the $v_{2}$ direction, the splitting is done only along the $v_{1}$ direction. For MCS, we generate a substantial number of $\left( {1 \times 10^{5} } \right)$ random samples and the values on the performance function $y\left( {r,\theta } \right)$ are directly calculated. Thus, the outcomes derived from the MCS can serve as a benchmark for assessing precision of the proposed approach.

From Fig. 2, it is clear that entropy difference of the proposed method gradually drops progressively as number of splits rises. Additionally, the number of splits along direction v₂ converges to $N = 21 \times 3 = 63$, given a specific accuracy $\varepsilon = 4 \times 10^{ - 3}$. Error limit $\varepsilon$ needs to be chosen adaptively according to the specific problem. Generally speaking, a large K-value indicates that the nonlinearity of the performance function and covariance of random variables have a greater influence on the response. In order to ensure the accuracy of uncertainty propagation, the Gaussian components need to be split more when the K-value is large. Therefore, the error limit $\varepsilon$ should be set relatively small. Conversely, the relatively large error limit $\varepsilon$ can also ensure the accuracy of uncertainty propagation when the K-value is small. For comparison with the K-value of the proposed method, the number of splits of MGMM along the direction $v_{1}$ is 113. Figure 3 illustrates uncertainty propagation outcomes of MCS method, the proposed method, the MGMM method. It can be derived from Fig. 3a that the PDF 2D surface diagram of the MCS method has a comparable "barrel shape". Meanwhile, it can be concluded from Fig. 3b that the shape of the PDF 2D surface obtained by proposed method is highly analogous to the MCS method. However, from Fig. 3a and c, it can be inferred that PDF calculated by MGMM differs very much from MCS.

Fig. 2

The difference of entropy by proposed method

Fig. 3

Comparison of PDFs by MCS, the proposed method, and MGMM. a The PDF of MCS with $10^{5}$ samples. b The PDF by proposed method. c The PDF by MGMM method

To provide a comprehensive assessment of computational accuracy of the proposed method and the MGMM method, Table 1 presents the joint CDF of multiple response functions $y(r,\theta ) - \overline{y}$ and corresponding relative errors. $\overline{y}$ represents the boundary value of the joint CDF of the response function. The joint CDF outcomes of the proposed method show minimal discrepancies when compared to those obtained by the MCS across all five cases. For instance, when $\overline{y} = (0, - 5)$, the maximum relative error of the proposed method is merely 2.95%. In the remaining cases, the CDF results of the proposed method closely align with those derived from the MCS method. However, the MGMM has a minimum error of 44% and a maximum error of 432%. Consequently, the analysis of the response PDF and CDF confirms that the proposed method achieves a notable degree of precision in this specific example.

Table 1 Comparison of joint CDF by MCS, the proposed method, and MGMM

The cost of proposed method is discussed next. In this example, we use MCS and MGMM as a comparison of the proposed method. The MCS is used as a benchmark and calls the performance function $10^{5}$ times. For MGMM, the number of splits is 113 and the number of times it calls the performance function is 565. Although the number of calls to the performance function is much smaller than the MCS, the accuracy is insufficient since it chooses the wrong direction of the split. For proposed method, the number of splits is 63 and the number of calls to the performance function is 315. Compared to MGMM, it calls fewer performance function and the accuracy of uncertainty propagation is higher. In this paper, the calculation cost is related to the number of dimensions and splits. For cases with a high number of dimensions or a large number of splits, the computational burden will be larger. But at the same time, uncertainty propagation accuracy will also increase.

6.2 Example 2: Mathematical problems with Gaussian and non-Gaussian

Consider the following performance function:

$$y = \cos \left( {x_{1} - 10.4} \right) + \cos \left( {x_{2} } \right) + 0.08*x_{2}$$

(33)

where $x_{1}$ and $x_{2}$ are independent of each other, and their parameters are shown in Table 2.

Table 2 Distribution type and parameters of random variables

For normal distribution, parameter 1 is mean $\mu$ and parameter 2 is standard variance $\sigma$; for Gamma distribution, parameter 1 is shape parameter $\alpha$ and parameter 2 is scale parameter $\beta$.

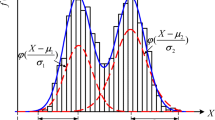
For a non-Gaussian distribution of input random variables, it needs to be reconstructed with a Gaussian mixture model. First, we generate 1000 sample points based on the non-Gaussian distribution $x_{1}$, and EM algorithm is used to estimate parameters of GMM, while gradually increasing the number of Gaussian components. Based on the multiple GMMs, the one with the smallest AIC value is chosen as the best GMM using the AIC criterion. In this example, the best GMM consisting of two Gaussian components is used to reconstruct the PDF of the Gamma distribution, and Table 3 presents the parameters of this model. The approximate GMM PDF of $x_{1}$ and the PDF of the original distribution are shown in Fig. 4, from which it can be observed that the GMM PDF is almost identical to the original Gamma distribution PDF.

Table 3 GMM parameters for Gamma distribution

Fig. 4

Reconstruction of input variables PDF of $x_{1}$

Prior to uncertainty propagation, it is necessary to combine the marginal distributions of $x_{1}$ and $x_{2}$ into a joint PDF. The joint PDF can be obtained by multiplying each marginal distributions since the two input random variables are independent, then the number of components of the joint PDF is $n = 2 \times 1 = 2$. Subsequently, the Stirling criterion of MGMM and the K-value of the proposed method are employed to ascertain direction of splitting, as outlined in Table 4. It is observable that for K-value, since the $\phi_{K}$ of the two components of the GMM in the direction 2 is approximately 5 times that in direction 1, both components of the GMM are split along direction 2. However, for the Stirling criterion, the $\phi_{s}$ in the direction 1 is approximately 2 times that in the direction 2, both components of the GMM are split along direction 1.According to the splitting direction of the two methods, the splitting is carried out separately, and then uncertainty propagation is performed, while the MCS method is also used to calculate the response PDF as a reference, and the outcomes are depicted in Fig. 5a. In contrast to the MGMM method, response PDF curve by proposed method agrees better with MCS method. Meanwhile, the CDF of the output response is shown in Fig. 5b. For the proposed method, the CDF of response is highly analogous to MCS method, while the MGMM method significantly diverges from the MCS.

Table 4 The splitting direction of the variable and the splitting number

Fig. 5

Response PDF, CDF by MCS, the proposed method, and MGMM. a The output response PDF. b The output response CDF

Furthermore, Table 5 displays joint CDF of multiple response functions and corresponding relative errors. Upon examining all five situations, it is evident that the proposed method consistently achieves a small relative error. For instance, the proposed method has a maximum relative error of only 7.6% when $\mathop y\limits^{ - } = 0$, and the smallest relative error is only 0.04% when $\overline{y} = 2$. However, the minimum error of the MGMM method is 8.11%, and the maximum error is 914%. The accuracy of the response PDF and CDF illustrates that the proposed method effectively propagates uncertainty with good accuracy in this particular instance.

Table 5 Joint CDF by MCS, the proposed method, and MGMM

6.3 Example 3: Mathematical problems where the input distributions are non-Gaussian

The performance functions are as follows:

$$f(x) = \sqrt[7]{\begin{gathered} \left( {x_{1} - 4.9536} \right)*\left( {x_{1} - 5.7897} \right)*\left( {x_{1} - 6.9} \right) \hfill \\ + \left( {\left( {x_{2} - 14.2474} \right)*\left( {x_{2} - 18.4091} \right)} \right)^{2} \hfill \\ \end{gathered} }$$

(34)

where $x_{1}$ and $x_{2}$ are independent and their parameters are in Table 6.

Table 6 The distribution of the random variable and related parameters

For Log-normal distribution, the log-mean is represented by parameter 1, while parameter 2 denotes the log-variance. For Gamma distribution, the shape parameter is represented by parameter 1, and parameter 2 denotes scale parameter. Since input random variables $x_{1}$ and $x_{2}$ are both non-Gaussian, they need to be reconstructed by GMMs respectively. The GMM of $x_{1}$ consists of 5 components, while the GMM of $x_{2}$ consists of 3 components. The parameters are shown in Table 7. The PDF of the GMM and the original distribution are shown in Fig. 6. It is evident that the PDF curves of the GMM closely resemble those of the original distributions $x_{1}$ and $x_{2}$.

Table 7 The approximate GMM parameters of $x_{1}$ and $x_{2}$

Fig. 6

Reconstruction of input variables PDF of $x_{1}$ and $x_{2}$. a Random variable $x_{1}$. b Random variable $x_{2}$

The joint PDF can be obtained by multiplying each marginal distributions since the two input random variables $x_{1}$ and $x_{2}$ are independent. Thus, the number of components of the joint PDF is $n = 5 \times 3 = 15$. Under the K-value of the proposed method, both components of the GMM are split along direction 2. In contrast, the Stirling criterion of the MGMM requires splitting along direction 1 for component 1, 4, 7, and 13, while the remaining components are split along direction 2.

Figure 7 displays outcomes of uncertainty propagation obtained from MCS, the proposed method, the MGMM. Response PDF acquired by the MCS shows an obvious bimodal pattern, with distinct peaks at $y \approx - 2.{1}$,$y \approx {1}{\text{.4}}$. The PDF by the proposed method well match MCS, and column 3 of Table 8 displays the splitting count for each Gaussian component. Conversely, the response PDF under the MGMM can only displays the initial peak, while the second peak appears excessively smooth and exhibits a greater degree of inaccuracy when compared to MCS. Meanwhile, CDF of output response is shown in Fig. 7b. The response CDF derived from the proposed method demonstrates good consistency with MCS method, while MGMM has a very large deviation compared with the MCS method.

Fig. 7

Response PDF and CDF by MCS, the proposed method, and MGMM. a PDF of output response. b PDF of output response

Table 8 The splitting direction and splitting number of input random variables

Furthermore, Table 9 presents the joint CDF outcomes of multiple response functions, together with their related relative errors. Upon examining all five situations, the proposed method achieves a negligible relative error. For instance, the proposed method has a maximum relative error of only 3.6% when $\overline{y} = 1.5$.However, the maximum relative error of the MGMM is 85%. The accuracy of the response PDF and CDF illustrates that the proposed method effectively propagates uncertainty with high accuracy in this particular instance.

Table 9 The joint CDF by MCS, the proposed method, and MGMM

6.4 Example 4: RV reducer

RV reducer typically consists of a 2-stage reduction mechanism that offers a substantial transmission ratio, smooth transmission, small inertia, large output torque, small size, high precision, high reliability and high impact resistance, etc. Therefore, it is widely used in industrial machinery, aerospace and automotive industries, robotics, medical equipment and precision instruments to achieve high precision control and transmission. RV reducer is primarily composed of shell, input shaft, planetary gear set, ring gear, output shaft, bearings, seals, lubrication system, support structure. The detailed structure as shown in the Fig. 8 (Yang et al. 2021).

Fig. 8

The structure of RV reducer (Yang et al. 2021)

The performance function of the contact functional fatigue strength of the planetary gear teeth is shown in Eq. (35), and the parameters $d_{1}$,$d_{2}$,$d_{3}$ and $X_{1}$ denote the modulus, the number of central gears, the number of planetary gears, and the width of the planetary gears, respectively. Each random variable obeys a multimodal distribution, and GMM is used to model the random variables, whose distribution parameters are shown in Table 10.

$$Y = g\left( {d,X} \right) = 297.6064\sqrt {\frac{7161.8144}{{X_{1} d_{1}^{2} d_{3}^{3} }}(d_{2} + d_{3} )} - 1100$$

(35)

Table 10 Parameters of individual random variable

The joint PDF of input random variables can be obtained by multiplying each marginal distribution. The number of components of the joint PDF is $n = 2 \times 2 \times 2 \times 2 = 16$. The K-value criterion is applied to each Gaussian component of the joint GMM, and the splitting is performed along the direction with the largest K-value, all the splitting directions are direction 1, and all the number of splitting is 5, then the number of splitting is $n = {16} \times {5} = {80}$. The response PDF of the MCS and the proposed method are shown in Fig. 9a. The response PDF calculated by the proposed method is very close to the PDF derived from MCS, which achieves nonlinear uncertainty propagation with high precision. Meanwhile, it can be observed from Fig. 9b that response CDF of the proposed method is also in total accordance with the outcomes acquired by the MCS.

Fig. 9

Response PDF and CDF by the proposed method and MCS. a The PDF by proposed method and MCS. b The CDF by proposed method and MCS

Furthermore, Table 11 presents CDF of multiple response functions together with their related relative error. Upon examining all five situations, the proposed method achieves a small relative error. For instance, the proposed method has a maximum relative error of only 2.0% when $\overline{Y} = - 1015.18$, and the minimum relative error is 0.02% when $\overline{Y} = - 860$. The accuracy of the response PDF and CDF illustrates that the proposed method effectively propagates uncertainty with high accuracy in this particular instance.

Table 11 Relative errors of the CDF between MCS and the proposed method

6.5 Example 5: NASA challenging problem

In 2014, NASA released a publication on the complex issue of uncertainty propagation in spacecraft and system design (Crespo et al. 2014), as shown in Fig. 10. The structural performance function is a two levels of uncertainty propagation process. The first level is to propagate uncertainty parameters to the subsystem response (intermediate variable $x$), after obtaining uncertainty information of the intermediate variable $x$, it is used to the second level uncertainty propagation to obtain uncertainty information of final performance function $g$.

Fig. 10

NASA challenge problems

The inputs of first-level uncertainty problem are 21 uncertain variables, which are expressed in Eq. (36). Because the input variables $p$ is mainly classified into three types: random uncertainty, epistemic uncertainty, and stochastic and epistemic mixed uncertainty. And this paper only studies the stochastic uncertainty problem, so this complex uncertainty parameter is simplified and only stochastic uncertainty is considered. Additionally, some parameters are held constant, as shown in Tables 12 and 13.

$$\left\{ {\begin{array}{*{20}l} {x_{1} = h_{1} (p_{1} ,p_{2} ,p_{3} ,p_{4} ,p_{5} )} \hfill \\ {x_{2} = h_{2} (p_{6} ,p_{7} ,p_{8} ,p_{9} ,p_{10} )} \hfill \\ {x_{3} = h_{3} (p_{11} ,p_{12} ,p_{13} ,p_{14} ,p_{15} )} \hfill \\ {x_{4} = h_{4} (p_{16} ,p_{17} ,p_{18} ,p_{19} ,p_{20} )} \hfill \\ {x_{5} = p_{21} } \hfill \\ \end{array} } \right..$$

(36)

where: $p$ is a random variable; $h$ is the first level model of the system and $x$ is an intermediate variable; $d$ is the design variable.

Table 12 Parameters of random variable

Table 13 Parameters of deterministic variable

In this example, the PDF of $p_{8} ,p_{15} ,p_{17}$ is reconstructed by a 3-component GMM. The optimal number of GMM components is 1 for $p_{21}$, and the specific parameters are shown in Table 14. The GMM PDF of random variables and original distribution are shown in Fig. 11. from which it can be seen that the PDF curve of GMM closely resembles that of the original Gamma distribution.

Table 14 Approximate GMM parameters for the random variables $p_{8} ,p_{15} ,p_{17} ,p_{21}$

Fig. 11

PDF curve with Gamma distribution and GMM

The joint PDF can be obtained by multiplying each marginal distribution. Given that input random variables are independent, the number of components of the joint PDF is determined to be $n = 3 \times 3 \times 3 = 27$. Due to the five-dimensional nature of the output response PDF, it is not possible to visually represent the joint PDF using 3D graphics. Therefore, the marginal PDFs of the response are displayed individually. The PDFs of the first-level uncertainty problem using the proposed method and the MCS are shown in Fig. 12, from which it can be seen that the PDF of $x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5}$ by the proposed method and MCS coincide almost exactly.

Fig. 12

Joint PDF of intermediate variable x by proposed method and MCS

Furthermore, Table 15 presents the joint CDF of multiple response functions and their accompanying relative errors. Upon examining all five situations, the proposed method achieves a small relative error. For instance, the proposed method has a maximum relative error of only 5.6% and the minimum relative error is 2.2%. The accuracy of the response PDF and CDF illustrates that the proposed method effectively propagates uncertainty with good accuracy for the first-level uncertainty propagation problem.

Table 15 Relative errors of the joint CDF by MCS and the proposed method

Since the result of first-level uncertainty propagation is the joint PDF, the GMM of intermediate variable $x$ is directly used as the input probability distribution for the second-level uncertainty problem. The PDFs of the second-level uncertainty derived from MCS and the proposed method are shown in Fig. 13, respectively. Based on the analysis of Fig. 13, it can be inferred that the proposed method exhibits certain discrepancies when compared with the MCS method for ${\text{g}}_{1} ,g_{2} ,g_{3}$.However, the PDF curve is globally comparable to the MCS. And in the other variables, the PDF curves obtained from MCS and the proposed method are in complete agreement.

Fig. 13

Joint PDF of output $g$ calculated by MCS and the proposed method

Furthermore, Table 16 presents the joint CDF of multiple response functions and their accompanying relative errors. Upon examining all five situations, the proposed method achieves a small relative error. For instance, the proposed method has a maximum relative error of only 5.1% and the minimum relative error is 1.4%. The accuracy of the response PDF and CDF illustrates that the proposed method effectively propagates uncertainty with good accuracy for the second-level uncertainty propagation problem.

Table 16 Relative errors of the joint CDF by MCS and the proposed method

7 Conclusion and outlook

This paper develops a new method for propagating uncertainties in the presence of nonlinear performance functions. When the input follows multivariate Gaussian distribution, a K-value criterion is proposed, which can select the direction of splitting. The criterion can take into account the influence of the nonlinearity of performance function and the variance of the input variables on the response. The appropriate number of components for Gaussian distribution splitting can be determined by using the approximate entropy of the output response as the criterion for convergence. Based on the outcomes of multiple cases, it is found that the accuracy of the proposed method is relatively high. Therefore, this method can serve as a valuable approach for effectively propagating uncertainties with a high degree of precision. Furthermore, it can be expanded and applied to multi-level uncertainty propagation of intricate products. Inaccurate multi-level uncertainty propagation might result in error accumulation, necessitating a high-precision method for uncertainty propagation. Meanwhile, the proposed method needs to be further improved and upgraded. The current algorithm may lead to a large amount of computation for high-dimensional problems or a substantial number of splits.