An enhanced finite step length method for structural reliability analysis and reliability-based design optimization

Abstract

The finite step length (FSL) method is extensively used for structural reliability analysis due to its robustness and efficiency compared with traditional Hasofer–Lind and Rackwitz–Fiessler (HL-RF) method. However, it may generate a large computational effort when it faces some complex nonlinear limit state functions. This study explains the basic reason of inefficiency of the FSL method and proposes an enhanced finite step length (EFSL) method to improve the ability for solving complex nonlinear problems, and then apply it to reliability-based design optimization (RBDO). The tactic is to present an iterative control criterion to compensate for the deficiency of the FSL method in the oscillation amplitude criterion, which solves the problem of large computational effort caused by unchanged step length during the iterative process. Then, a comprehensive step length adjustment formula is presented, which can adaptively adjust the step length to achieve fast convergence for limit state functions with different degrees of nonlinearity. Following that, the proposed method is combined with the double loop method (DLM) to improve the efficiency and robustness for solving complex RBDO problems. The robustness and efficiency of the proposed method compared to other commonly used first-order reliability analysis methods are demonstrated by five numerical examples. In addition, four design problems are used to validate the proposed EFSL-based DLM which is effective for solving complex nonlinear RBDO problems.

1 Introduction

Uncertainties widely present in the material parameters, geometries, external loads, and other aspects, which have important implications for structural reliability (Jiang et al. 2020; Schueller and Pradlwarter 2007). To assess the impact of uncertainties on engineering structures, structural reliability analysis methods have been constantly evolving over the past decades. Generally, these methods can be classified into five categories: sampling methods (Hu and Du 2013), expansion methods (Keshavarzzadeh et al. 2016), surrogate-based methods (Yang et al. 2021), integration methods (Xu and Dang 2019), most probable point (MPP)-based methods including the first-order reliability method (FORM) (Hasofer and Lind 1974; Rackwitz and Flessler 1978) and the second-order reliability method (SORM) (Wang et al. 2020). Among them, FORM is one of the most important methods for assessing the structural reliability, which was recommended to use by the Joint Committee of Structural Safety.

When performing reliability analysis by FORM, the calculation of reliability index becomes a problem of finding the optimum solution in a constrained optimization problem. So far, the approaches for solving the constrained optimization problems are categorized as optimization scheme and iterative algorithm. The optimization scheme generally solves the problem well, but the solution process may require to use Hessian matrix or inverse matrix, which leads to a complex solution process (Gong and Yi 2011). Unlike optimization scheme, iterative algorithm has the advantage of being simple and efficient. Typically, the HL-RF method is one of the most used iterative algorithm, which was presented by Hasofer and Lind (1974) and complemented by Rackwitz and Fiessler (1978). Due to the simplicity and efficiency of the HL-RF method, it is extensively used for structural reliability analysis. For weakly nonlinear limit state functions, the HL-RF method can quickly obtain a convergent result. But, for highly nonlinear limit state functions, the HL-RF method may converge slowly or even show a phenomenon of non-convergence, such as bifurcation, chaos, and periodic oscillation (Yang 2010; Zhang et al. 2021a).

To improve the numerical stability of the HL-RF method, several methods have been developed. Through introducing merit function, iHL-RF (Liu and Kiureghian 1991) increases the robustness of the HL-RF method by using Armijo rule to select an appropriate step length. According to the chaos control principle (Keshtegar 2016), the stability transformation method (STM) (Yang 2010), the adaptive stability transformation method (ASTM) (Meng et al. 2018), and the directional stability transformation method (DSTM) (Meng et al. 2017) were developed to enhance their capability in solving nonlinear limit state functions. Yang et al. (2020) reduced the risk of periodic oscillations, bifurcations, and chaos by modifying the search direction during the iterative process and establishing a new step length adjustment formula. Gong and Yi (2011) derived a new finite step length (FSL) method using adjustment formula to accelerate the convergence process and improve the robustness of algorithm. Roudak et al. (2017) proposed to introduce two adjusting parameters in the HL-RF method to adaptively adjust step length during the iterative process, preserving the simplicity property while improving its convergence performance. Keshtegar and Meng (2017) presented a hybrid relaxed HL-RF method considering the impact of relaxed factor to accelerate the convergence process.

It is worth noting that FORM not only can be used to assess structural reliability, but can also be applied into RBDO that seeks a compromise between safety and cost (Yang et al. 2022). Usually, RBDO is categorized into three types: double loop method (DLM) (Chiralaksanakul and Mahadevan 2005; Youn and Choi 2004; Zhu et al. 2021), decoupled method (Chen et al. 2013b; Du and Chen 2004; Yu and Wang 2019), and single loop method (Biswas and Sharma 2021; Lind and Olsson 2019). Among them, DLM theoretically has better robustness, which consists of an internal reliability constraint loop and an external optimization loop. DLM includes reliability index approach-based DLM (RIA-based DLM) and performance measure approach-based DLM (PMA-based DLM) (Aoues and Chateauneuf 2010). For RIA-based DLM, the FSL method is applied in reliability constraint loop due to its simplicity and efficiency. However, DLM combined with FSL may suffer from the problem of poor convergence performance when facing complex nonlinear limit state functions.

In this study, an EFSL method is proposed to enhance the efficiency and robustness for complex limit state functions. The major contributions of the proposed method are summarized as follows. Firstly, employing a state parameter to make up for the deficiencies of the FSL method in the oscillation amplitude criterion and solving the problem of large computational effort due to the unchanged step length. Secondly, developing a comprehensive step length adjustment formula to accelerate the iterative convergence process by adaptively adjusting the step length for limit state functions with different degrees of nonlinearity. Finally, the proposed EFSL method is combined with DLM to improve the efficiency and robustness for solving complex nonlinear RBDO problems.

The rest of this paper is organized as follows. In Sect. 2, four traditional FORM iterative methods are simply introduced. In Sect. 3, the EFSL method is developed and a comprehensive step length adjustment formula is proposed. In Sect. 4, five examples are used to verify the efficiency and robustness of the proposed EFSL method. In Sect. 5, four RBDO design problems are solved using the proposed EFSL method combined with DLM. In Sect. 6, conclusions are given.

2 Review of FORM iterative algorithm

The purpose of FORM is to acquire reliability index and calculate structural failure probability (Koduru and Haukaas 2010). The reliability index can be calculated through obtaining the most probable point (MPP), which is the closest distance from origin to limit state surface in the standard normal space (U-space). According to the reliability index, the failure probability is defined as

$$P_{f} = \Phi \left( { - \beta } \right) = \Phi \left( { - \left\| {{\mathbf{U}}^{ \ast} } \right\|} \right),$$

(1)

where $P_{f}$ denotes the failure probability; $\Phi$ stands for the cumulative distribution function (CDF); $\beta$ represents the reliability index; and ${\mathbf{U}}^{\ast }$ is a vector of MPP coordinates in the U-space.

The solution of the reliability index $\beta$ can be transformed into a constrained optimization problem, which can be expressed as

$$\begin{aligned} &{\text{find }}{\mathbf{U}}^{\ast } \hfill \\ &\beta = \min \, \left\| {\mathbf{U}} \right\| \hfill \\ &{\text{s.t.G}}\left( {\mathbf{U}} \right) = 0 \end{aligned}$$

(2)

In the following, four traditional FORM iterative algorithms are briefly reviewed. For convenience of description, the limit state function can be expressed as

$$Z = G\left( {\mathbf{U}} \right) = g\left( {\mathbf{X}} \right) = g\left( {X_{1} ,X_{2} ,\ldots,X_{n} } \right),$$

(3)

where ${\mathbf{X}}$ denotes a vector comprised by random variables.

When ${\mathbf{X}}$ obeys independently normal distribution, it should satisfy ${\mathbf{X}} = {{\varvec{\upmu}}} + {\mathbf{\sigma U}}$. The vectors ${{\varvec{\upmu}}}$ and ${{\varvec{\upsigma}}}$ are the mean and standard deviation of random variable ${\mathbf{X}}$. When the correlated random variables are involved, the random variables should be transformed into independent standard normal variables by Rosenblatt or Nataf transformation (Liu and Kiureghian 1986; Rackwitz and Flessler 1978).

2.1 HL-RF iterative algorithm

The formulation of the HL-RF (Hasofer and Lind 1974; Rackwitz and Flessler 1978) method can be expressed as

$${\mathbf{U}}^{k + 1} = \frac{{\left( {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right)^{{\text{T}}} {\mathbf{U}}^{k} - g\left( {{\mathbf{U}}^{k} } \right)}}{{\left\| {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right\|}}{\mathbf{n}}^{k},$$

(4)

where k refers to the iterative number; ${\mathbf{U}}^{k}$ and ${\mathbf{U}}^{{k{ + }1}}$ are the random variable vectors at the kth and (k + 1)th iterative steps in the U-space, respectively; $g\left( {{\mathbf{U}}^{k} } \right)$ represents the value of limit state function at ${\mathbf{U}}^{k}$. $\nabla g\left( {{\mathbf{U}}^{k} } \right)$ denotes the gradient vector and ${\mathbf{n}}^{k}$ stands for the vector of normalized search direction at ${\mathbf{U}}^{k}$, which is represented as

$${\mathbf{n}}^{k} { = }\frac{{\nabla g\left( {{\mathbf{U}}^{k} } \right)}}{{\left\| {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right\|}}$$

(5)

2.2 Stability transformation method

The iterative formulation of the stability transformation method (STM) (Yang 2010) is formulated as

$${\mathbf{U}}^{k + 1} = {\mathbf{U}}^{k} + \zeta {\mathbf{C}}\left( {{\mathbf{f}}\left( {{\mathbf{U}}^{k} } \right) - {\mathbf{U}}^{k} } \right)$$

(6)

$${\mathbf{f}}\left( {{\mathbf{U}}^{k} } \right) = \frac{{\left( {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right)^{{\text{T}}} {\mathbf{U}}^{k} - g\left( {{\mathbf{U}}^{k} } \right)}}{{\left( {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right)^{{\text{T}}} \nabla g\left( {{\mathbf{U}}^{k} } \right)}}\nabla g\left( {{\mathbf{U}}^{k} } \right),$$

(7)

where $\zeta$ refers to the chaos control factor, whose value ranges from 0 to 1 (Meng et al. 2017). ${\mathbf{C}}$ denotes an involutory matrix; ${\mathbf{f}}$ represents a function vector of random variable.

2.3 Directional stability transformation method

The iterative formula of the directional stability transformation method (DSTM) (Meng et al. 2017) is defined as

$${\mathbf{U}}^{k + 1} = \beta^{k} {\mathbf{n}}^{k}$$

(8)

$$\beta^{k} = \frac{{\left( {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right)^{{\text{T}}} {\mathbf{U}}^{k} - g\left( {{\mathbf{U}}^{k} } \right)}}{{\left\| {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right\|}}$$

(9)

$${\mathbf{n}}^{k} = \frac{{{\mathbf{U}}^{k} + \zeta {\mathbf{C}}\left( {{\mathbf{f}}\left( {{\mathbf{U}}^{k} } \right) - {\mathbf{U}}^{k} } \right)}}{{\left\| {{\mathbf{U}}^{k} + \zeta {\mathbf{C}}\left( {{\mathbf{f}}\left( {{\mathbf{U}}^{k} } \right) - {\mathbf{U}}^{k} } \right)} \right\|}},$$

(10)

where ${\mathbf{n}}^{k}$ represents the current normalized search direction vector. The search direction can be divided into circumferential and radial directions, while DSTM only controls the iteration step length in circumferential direction, reducing the computational effort of STM.

2.4 Finite step length method

The basic formula of the FSL method (Gong and Yi 2011) can be expressed as

$${\mathbf{U}}^{{k{ + }1}} = {{\varvec{\upalpha}}}^{{k{ + }1}} \beta^{{k{ + }1}}$$

(11)

$${{\varvec{\upalpha}}}^{k + 1} = \frac{{{\mathbf{U}}^{k} - \lambda^{k} \nabla g\left( {{\mathbf{U}}^{k} } \right)}}{{\left\| {{\mathbf{U}}^{k} - \lambda^{k} \nabla g\left( {{\mathbf{U}}^{k} } \right)} \right\|}}$$

(12)

$$\beta^{k + 1} = - \frac{{g\left( {{\mathbf{U}}^{k} } \right) - \left( {\nabla g\left( {{\mathbf{U}}^{k} } \right)} \right)^{{\text{T}}} {\mathbf{U}}^{k} }}{{\nabla g\left( {{\mathbf{U}}^{k} } \right)^{{\text{T}}} \left( {{{\varvec{\upalpha}}}^{k + 1} } \right)}},$$

(13)

where ${{\varvec{\upalpha}}}^{k + 1}$ refers to a finite sensitivity vector at point ${\mathbf{U}}^{k}$; $\lambda$ is the step length, which should satisfy greater than 0 (Gong and Yi 2011).

When $\lambda \to \infty$, the iterative formula of the FSL method is identical to that of the HL-RF method. It implies that the HL-RF method is a particular form of the FSL method when $\lambda \to \infty$. During the iterative process, the update of step length is determined by the following criterion

$$\left\| {{\mathbf{U}}^{k + 1} - {\mathbf{U}}^{k} } \right\| \ge \left\| {{\mathbf{U}}^{k} - {\mathbf{U}}^{k - 1} } \right\|$$

(14)

When Eq. (14) is satisfied, one can set $\lambda^{k + 1} = \lambda^{k} /c$. Herein, $c$ is a step length adjusting coefficient, which is usually taken between 1.2 and 1.5 (Gong and Yi 2011).

3 The proposed method

3.1 Derivatives of the enhanced finite step length method

The robustness and effectiveness of the FSL method was verified, but it still has two problems need to be overcome. The first problem is that when facing complex nonlinear limit state functions, the oscillation amplitude in each iteration gradually decreases throughout the iterative process, and the step length updated criterion Eq. (14) does not work. The consequence is that the step length $\lambda$ does not change during the iterative process, although the oscillation exists, leading to a larger computational effort. Since the criterion in Eq. (14) is closely related to the oscillation amplitude, which is called as oscillation amplitude criterion. The second problem is that when the criterion in Eq. (14) works during the iterative process, the single step length adjustment formula of the FSL method and the unpredictable degree of nonlinear limit state functions lead to inability to adaptively adjust step length.

To solve the above-mentioned problems, a new step length updated strategy is proposed for the FSL method to enhance the capability for solving complex nonlinear problems. Herein, the proposed method is referred to as an EFSL method.

For the first problem, the purpose is to overcome the shortcomings of the oscillation amplitude criterion. Inspired by previous work in Jiang et al. (2017), a state parameter is adopted as criterion to prevent this situation, which is represented as

$$M{ = }M^{t},$$

(15)

where $M$ represents a state parameter, which is initially set to zero. $M^{t}$ is a target state parameter, which is recommended to set as 2.

During each step of the iteration, the state parameter $M$ will be added by 1 when Eq. (14) is not satisfied, and $\lambda$ does not change at this time. Conversely, the state parameter $M$ becomes 0 when Eq. (14) is satisfied. The step length $\lambda$ will be adjusted at this time and the step length adjustment formula is given subsequently. When Eq. (15) is satisfied, whether or not the criterion in Eq. (14) is satisfied at this time, the step length $\lambda$ will be adjusted. After the step length adjustment, the state parameter $M$ is changed to zero again. The reason for the recommended value of target state parameter $M^{t}$ in Eq. (15) is that when the criterion $M{ = }M^{t}$ is satisfied, the step length $\lambda$ should be updated to resolve such problem that the oscillation exists but the step length $\lambda$ keeps fixed value. Therefore, the value of $M^{t}$ should be set neither too large nor too small. If the value of $M^{t}$ takes too large or too small, it is not conducive to adjust the step length $\lambda$. According to the test experiences, taking 2 is an appropriate choice.

For the second problem, a comprehensive step length adjustment formula is developed, and the step length $\lambda$ is adaptively adjusted in the face of different degrees of nonlinearity limit state functions. The step length $\lambda$ is large for the weakly nonlinear limit state functions and the step length $\lambda$ is small for the highly nonlinear limit state functions. The proposed comprehensive compensation adjustment formula consists of two parts, whether the criterion in Eq. (14) is satisfied or not.

When the criterion in Eq. (14) is satisfied, a new step length adjustment formula is developed, which is expressed as

$$\lambda^{k + 1} = cn\left( {1 - n} \right)\lambda^{k},$$

(16)

where $n$ represents a chaotic number, which satisfies $n \in \left( {0,1} \right)$; $c$ is a control parameter, which satisfies $0 < c < 4$. The chaotic number $n$ and control parameter $c$ in Eq. (16) play an important role to adjust the step length. To reduce the step length $\lambda$, the chaotic number $n$ and control parameter $c$ should satisfy the following criterion

$$cn\left( {1 - n} \right) < 1,$$

(17)

where $n$ satisfies $n \in \left( {0,1} \right)$ and $c$ satisfies $0 < c < 4$. In theory, all the possible combinations of n and c satisfying the above criterion can be used. However, the recommended values of these two parameters are given as $n = 0.05$ and $c = 2$ according to the experience.

When the step length is updated, the state parameter $M$ becomes zero. To ensure smooth convergence, a new criterion is defined as

$$\lambda^{k + 1} \le 0.15$$

(18)

When Eq. (18) is satisfied, the adjustment formula of $\lambda$ is expressed as

$$\lambda^{k + 1} = e^{{{-}0.125\left( {k + 1} \right)}}$$

(19)

When the criterion in Eq. (14) is not satisfied, the state parameter $M$ will be added by 1. When the state parameter $M$ satisfies Eq. (15), a new step length adjustment is presented, which is defined as

$$\lambda^{k + 1} = \left\{ \begin{array}{ll} \lambda^{k} /10, & \quad \lambda^{k} > 10 \\ \lambda^{k} /1, & \quad 5 \le \lambda^{k} \le 10\\ \lambda^{k} /0.05, & \quad 0 <\lambda^{k} < 5 \end{array} \right.$$

(20)

This equation can effectively balance the adaptive adjustment of the step length $\lambda$ when facing weakly and highly nonlinear limit state functions. It should be noted that when updating the step length using Eq. (20), the state parameter $M$ will become zero again, and then move to the next iteration.

Since the nonlinear degree of limit state functions cannot be predicted in advance, the initial value of $\lambda$ should be relatively large. The initial value of $\lambda^{0}$ is shown as

$$\lambda^{0} = 2^{15}$$

(21)

3.2 Step and flowchart of the proposed EFSL method

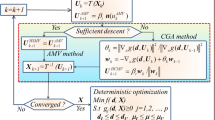
The detailed algorithm steps of the proposed EFSL method are summarized in Table 1. The flowchart of the proposed EFSL method is shown in Fig. 1.

Table 1 The detailed algorithm steps of the proposed EFSL method

Fig. 1

Flowchart of the proposed EFSL method

4 Illustrative examples of structural reliability analysis

In this section, some nonlinear numerical examples are solved with the proposed EFSL method. The reliability analysis results are compared in terms of accuracy, efficiency, and robustness to those by other methods, which include HL-RF method (Hasofer and Lind 1974; Rackwitz and Flessler 1978), STM (Yang 2010), DSTM (Meng et al. 2017), and FSL method (Gong and Yi 2011). The control factors $\zeta$ of STM and DSTM are taken as 0.10 and 0.05. The mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ and two additional different points are, respectively, selected as the initial points for different reliability analysis methods in the following examples. The involutory matrix ${\mathbf{C}}$ is considered as a unit matrix, which is applied to STM and DSTM. The convergence criterion for all these iterative algorithms is $\left\| {{\mathbf{X}}^{k + 1} - {\mathbf{X}}^{k} } \right\|/\left\| {{\mathbf{X}}^{k + 1} } \right\| < 10^{ - 6}$. The Monte Carlo simulation (MCS) method (Xiao et al. 2020) with $1 \times 10^{7}$ samples is used for calculating $\beta^{{{\text{MCS}}}}$ to validate the accuracy of the proposed method. To illustrate that the $\beta^{{{\text{MCS}}}}$ used in the examples is sufficiently accurate, the plots of the number of sampling points versus $\beta^{{{\text{MCS}}}}$ are provided to show the convergence, which are given in Figs. 2, 4, 6, 8, and 10. The number of sampling points is taken as $10^{5}$, $5 \times 10^{5}$, $10^{6}$, $5 \times 10^{6}$, $10^{7}$, $5 \times 10^{7}$ and $10^{8}$, respectively.

Fig. 2

The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in Example 1

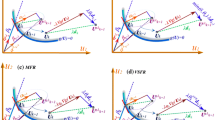
The statistical data of limit state functions for Examples 1–5 are shown in Table 2. In addition, the reliability analysis results of different methods, including calculation of MPP (${\mathbf{X}}^{\ast }$), iteration number, number of function evaluations (F-evaluations), and calculation of reliability index $\beta$ are given in Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. The number of F-evaluations is the sum of the number of performance function $g$ call and the number of gradient function $\nabla g$ call. Herein, the sensitivity analysis is evaluated by the analytical method. The iterative histories of the comparative methods are illustrated in Figs. 3, 5, 7, 9, and 11.

Table 2 The statistical data of limit state function for Examples 1–5

Table 3 Reliability analysis results of the comparative methods in Example 1

Table 4 The average number of iterations for the comparative methods in Example 1

Fig. 3

The iterative histories of the comparative methods in Example 1

Example 1

The limit state function of the first example is highly nonlinear and includes two independent random variables in normal distribution (Gong et al. 2014). As illustrated in Table 3, all the comparative methods with the exception of HL-RF method can converge. The proposed EFSL method obtains the MPP ${\mathbf{X}}^{\ast} = \left( {0.3093,4.0401} \right)$ and yields the reliability index $\beta = 4.0519$, which are approximately similar to the results in Gong et al. (2014). The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ is shown in Fig. 2. The reliability index calculated by the MCS method with $10^{7}$ samples is $\beta^{{{\text{MCS}}}} = 3.7031$. In terms of the accuracy and robustness of these methods, when the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the proposed EFSL method has similar accuracy with STM, DSTM, and FSL method for the same convergence criteria. When point (1, 1) and point (‒1, ‒1) are chosen as initial points, DSTM yields different MPPs and reliability indices compared to other methods. This reflects that the DSTM is sensitive to the choice of initial point and less robust, and inversely demonstrates the high accuracy and robustness of the proposed EFSL method.

In terms of the efficiency of these methods, the proposed EFSL method has the fewest average number of iterations and number of F-evaluations. The average convergence speed of the proposed EFSL method is approximately three times higher than that of the FSL method. The STM, FSL, and proposed EFSL method are robust, but the proposed EFSL method is more efficient. When the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the detailed iterative histories of these comparative methods are shown in Fig. 3, which can be obviously found that the proposed EFSL method has the highest efficiency compared to other methods.

Example 2

The limit state function of the second example is a nonlinear exponential function, which includes two independent random variables in normal distribution (Meng et al. 2017). As illustrated in Table 5, when the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ and two additional different points are selected as the initial points, all the comparative methods with the exception of the HL-RF method can converge and yield the reliability index $\beta = 2.8873$. These results are consistent with the results in Jiang et al. (2015). The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in this example is shown in Fig. 4. The reliability index calculated by the MCS method with $10^{7}$ samples is $\beta^{{{\text{MCS}}}} = 3.0687$. In terms of accuracy, the proposed EFSL method has similar accuracy with STM, DSTM, and FSL method for the same convergence criteria.

Table 5 Reliability analysis results of the comparative methods in Example 2

Table 6 The average number of iterations for the comparative methods in Example 2

Fig. 4

The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in Example 2

In terms of the robustness and efficiency of these methods, from the average number of iterations and number of F-evaluations shown in Tables 5 and  6, the proposed EFSL method generates the fewest iteration number and F-evaluations number. Therefore, the proposed EFSL method has the highest convergence speed compared with other methods. Similarly, the STM, DSTM, and FSL method are all robust, but the proposed EFSL method is more efficient. When the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the detailed iterative histories of these comparative methods are shown in Fig. 5 to verify the high efficiency of the proposed EFSL method.

Fig. 5

The iterative histories of the comparative methods in Example 2

Example 3

The third example is also a nonlinear problem, which includes three independent random variables in normal distribution (Gong et al. 2014). From Table 7, when the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ and two additional different points are selected as the initial points, all the comparative methods with the exception of the HL-RF method can converge successfully. The proposed EFSL method obtains the MPP ${\mathbf{X}}^{\ast} = \left( {0.8344, - 0.7324, - 3.5348} \right)$ and yields the reliability index $\beta = 3.7050$, which are consistent with the results in Yang et al. (2020). The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ is shown in Fig. 6. The reliability index calculated by the MCS method with $10^{7}$ samples is $\beta^{{{\text{MCS}}}} = 3.7236$. In terms of accuracy, the proposed EFSL method has similar accuracy with STM, DSTM, and FSL method for the same convergence criteria.

Table 7 Reliability analysis results of the comparative methods in Example 3

Table 8 The average number of iterations for the comparative methods in Example 3

Fig. 6

The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in Example 3

In terms of the efficiency and robustness of these comparative methods, the proposed EFSL method has the fewest average number of iterations and number of F-evaluations. The proposed EFSL has the highest convergence speed compared with other methods. The STM, DSTM, and FSL method are robust, but the proposed EFSL method is more efficient. When the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the detailed iterative histories of these comparative methods are shown in Fig. 7, which can be obviously found that the proposed EFSL method has the highest efficiency compared to other methods.

Fig. 7

The iterative histories of the comparative methods in Example 3

Example 4

This example is a complex limit state function including seven independent random variables with three different distributions (Gong et al. 2014). From Table 9, when the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, all the comparative methods can successfully find MPP and yield the reliability index $\beta = 2.7471$. These results are consistent with the results in Gong and Yi (2011). The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ is shown in Fig. 8. The reliability index calculated by the MCS method with $10^{7}$ samples is $\beta^{{{\text{MCS}}}} = 3.3985$. Although the reliability index changes slightly at different initial points, the same reliability index is obtained for all reliability analysis methods at the same initial point. Therefore, in terms of accuracy, all the comparative methods have similar accuracy for the same convergence criteria.

Table 9 Reliability analysis results of the comparative methods in Example 4

Fig. 8

The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in Example 4

In terms of the robustness and efficiency of these methods, from the average number of iterations and number of F-evaluations as shown in Tables 9 and 10, the HL-RF method has a high efficiency in this problem compared to STM, DSTM, and FSL method, but the proposed EFSL method has the fewest average number of iterations and number of F-evaluations. The average convergence speed of the proposed EFSL method is about eleven times higher than that of the FSL method. The proposed EFSL method has the advantage of being as simple and efficient as the HL-RF method, while ensuring the robustness. When the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the detailed iterative histories of these comparative methods are shown in Fig. 9, which can be obviously found that the proposed EFSL method has the highest convergence speed compared to other methods.

Table 10 The average number of iterations for the comparative methods in Example 4

Fig. 9

The iterative histories of the comparative methods in Example 4

Example 5

The limit state function of the final example is complex and highly nonlinear, which includes ten independent random variables in normal distribution (Roudak et al. 2017). From Table 11, when the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ and two additional different points are selected as the initial points, HL-RF method cannot converge and other methods except STM with $\zeta = 0.05$ obtain the reliability index $\beta = 3.7515$. These results are consistent with the results in Yang et al. (2020). The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ is shown in Fig. 10. It can be seen from Fig. 10 that the $\beta^{{{\text{MCS}}}}$ with $10^{5}$ samples is not converged. The reliability index calculated by the MCS method with $10^{7}$ is $\beta^{{{\text{MCS}}}} = 4.5336$. Since this limit state function is highly nonlinear, there are some errors in these comparative methods. In terms of accuracy, the proposed EFSL method has similar accuracy with DSTM, STM, and FSL method for the same convergence criteria.

Table 11 Reliability analysis results of the comparative methods in Example 5

Table 12 The average number of iterations for the comparative methods in Example 5

Fig. 10

The plot of the number of different sampling points versus $\beta^{{{\text{MCS}}}}$ in Example 5

In terms of the robustness and efficiency of these methods, the proposed EFSL method has the fewest average number of iterations and number of F-evaluations, and the average convergence speed is about six times higher than that of the FSL method. The STM, DSTM, and FSL method are robust, but the proposed EFSL method is more efficient. When the mean vector ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ is selected as the initial points, the iterative histories of these comparative methods are shown in Fig. 11, which can be obviously found that the proposed EFSL method has the highest convergence speed compared to those of other methods in this study.

Fig. 11

The iterative histories of the comparative methods in Example 5

5 The proposed method in combination with RBDO

This section introduces the typical formulation of RBDO and DLM, and then the proposed EFSL method is combined with DLM. The EFSL-based DLM is compared with the conventional optimization method through four nonlinear RBDO examples to verify the efficiency and robustness of the EFSL-based DLM. The comparison methods used in this study are chaos control (CC) method-based DLM (DLM/CC) (Yang and Yi 2009), modified chaos control (MCC) method-based DLM (DLM/MCC) (Meng et al. 2015), hybrid mean value (HMV) method-based DLM (DLM/HMV) (Du and Choi 2008), and FSL method-based DLM (DLM/FSL) (Gong and Yi 2011). The proposed EFSL-based DLM is abbreviated as DLM/EFSL.

5.1 Typical RBDO formulation

The RBDO mathematical model is defined as (Chen et al. 2013a; Yang et al. 2020)

$$\begin{aligned} &{\text{find }} {\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} \hfill \\ &\min \; f\left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right) \hfill \\ & {\text{s.t.}}\;{\text{Prob}}\left( {g_{i} \left( {{\mathbf{d}},{\mathbf{X}},{\mathbf{P}}} \right) \le 0} \right) \le P_{{f_{i} }}^{t} \, i = 1,2,\ldots,n \hfill \\ & \quad \quad \quad {\mathbf{d}}^{L} \le {\mathbf{d}} \le {\mathbf{d}}^{U} ,{{\varvec{\upmu}}}_{{\mathbf{X}}}^{L} \le {{\varvec{\upmu}}}_{{\mathbf{X}}} \le {{\varvec{\upmu}}}_{{\mathbf{X}}}^{U} \hfill \\ \end{aligned},$$

(22)

where $f\left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right)$ stands for an objective function; ${\mathbf{d}}$ refers to a vector of deterministic design variable; ${{\varvec{\upmu}}}_{{\mathbf{X}}}$ denotes the mean of random variable vector ${\mathbf{X}}$; ${{\varvec{\upmu}}}_{{\mathbf{P}}}$ indicates the mean of random parameter vector ${\mathbf{P}}$; ${\text{Prob}}\left( \cdot \right)$ is the failure probability operator; performance function $g_{i} \left( {{\mathbf{d}},{\mathbf{X}},{\mathbf{P}}} \right) \le 0$ is defined as a failure event; the probabilistic constraint is defined as failure probability less than or equal to the maximum permissible target failure probability $P_{{f_{i} }}^{t}$; ${\mathbf{d}}^{L}$ and ${\mathbf{d}}^{U}$ are the lower and upper bounds of ${\mathbf{d}}$; ${{\varvec{\upmu}}}_{{\mathbf{X}}}^{L}$ and ${{\varvec{\upmu}}}_{{\mathbf{X}}}^{U}$ are the lower and upper bounds of ${\mathbf{X}}$.

5.2 Double loop method

Due to the uncertainty of ${\mathbf{X}}$ and ${\mathbf{P}}$, the response of performance function is also uncertain. The structural failure probability can be defined as (Youn and Choi 2004)

$${\text{Prob}}\left( {g_{i} \left( {{\mathbf{d}},{\mathbf{X}},{\mathbf{P}}} \right) \le 0} \right){ = }F_{{g_{i} }} \left( 0 \right) \le \int_{{g_{i} \left( {{\mathbf{d}},{\mathbf{X}},{\mathbf{P}}} \right) \le 0}} { \cdot \cdot \cdot } \int {f_{{{\mathbf{X}},{\mathbf{P}}}} \left( {{\mathbf{X}},{\mathbf{P}}} \right)d{\mathbf{X}}d{\mathbf{P}}},$$

(23)

where $f_{{{\mathbf{X}},{\mathbf{P}}}} \left( {{\mathbf{X}},{\mathbf{P}}} \right)$ represents the joint probability density function. The multidimensional integral of Eq. (23) is computationally expensive and difficult to solve (Aoues and Chateauneuf 2010). To avoid direct integration of Eq. (23), two representative methods were developed including reliability index approach (RIA) (Zhu et al. 2021) and performance measure approach (PMA) (Hamza et al. 2020; Lee et al. 2008).

5.2.1 Reliability index approach

Reliability index approach replaces the probabilistic constraints in Eq. (22) with reliability indices as constraints, which can be transformed into the following form (Zhu et al. 2021)

$$\begin{aligned} &{\text{find }}\;{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} \hfill \\ & \min \; f\left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right) \hfill \\ & {\text{s.t}}.\;\beta_{i} \left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right) \ge \beta_{i}^{t} \, i = 1,2,\ldots,n \hfill \\ & \quad \quad \quad {\mathbf{d}}^{L} \le {\mathbf{d}} \le {\mathbf{d}}^{U} ,{{\varvec{\upmu}}}_{{\mathbf{X}}}^{L} \le {{\varvec{\upmu}}}_{{\mathbf{X}}} \le {{\varvec{\upmu}}}_{{\mathbf{X}}}^{U} \hfill \\ \end{aligned},$$

(24)

where $\beta_{i}^{t}$ denotes the target reliability index of the ith constraint.

Then, the reliability index $\beta_{i}$ can be computed by the following optimization problem

$$\begin{aligned} &{\text{find}}\;\;{\mathbf{U}}_{{^{{{\text{MPP}}}} }} \hfill \\ & \min \; \left\| {{\mathbf{U}}_{{^{{{\text{MPP}}}} }} } \;\;\right\| \hfill \\ & {\text{s.t.}}\;g_{i} \left( {{\mathbf{U}}_{{{\text{MPP}}}} } \right) = 0 \hfill \\ \end{aligned},$$

(25)

where the most probable point ${\mathbf{U}}_{{^{{{\text{MPP}}}} }}\;$ in U-space is obtained from Eq. (25), and $\beta_{i} { = }\left\| {{\mathbf{U}}_{{{\text{MPP}}}} } \right\|$.

5.2.2 Performance measure approach

Performance measure approach transforms the probabilistic constraints in Eq. (22) to performance measures as constraints (Hamza et al. 2020):

$$\begin{aligned} &{\text{find }}{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} \hfill \\ & \min \; f\left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right) \hfill \\ & {\text{s.t.}}\;g_{i} \left( {{\mathbf{d}},{\mathbf{X}}_{{{\text{MPTP}}}} ,{\mathbf{P}}_{{{\text{MPTP}}}} } \right) \ge {0 }\;\;i = 1,2,\ldots,n \hfill \\ & \qquad \quad {\mathbf{d}}^{L} \le {\mathbf{d}} \le {\mathbf{d}}^{U} ,{{\varvec{\upmu}}}_{{\mathbf{X}}}^{L} \le {{\varvec{\upmu}}}_{{\mathbf{X}}} \le {{\varvec{\upmu}}}_{{\mathbf{X}}}^{U} \hfill \\ \end{aligned},$$

(26)

where $g_{i}$ denotes the probabilistic performance measure of the ith probabilistic constraint.

The minimum performance target point ${\mathbf{U}}_{{{\text{MPTP}}}}$ can be computed by inverse reliability analysis, which can be expressed by the following formula (Hamza et al. 2020)

$$\begin{aligned} &{\text{find }} {\mathbf{U}}_{{{\text{MPTP}}}} \hfill \\ &\min \; g\left( {{\mathbf{U}}_{{{\text{MPTP}}}} } \right) \hfill \\ & {\text{s.t.}}\;\left\| {{\mathbf{U}}_{{^{{{\text{MPTP}}}} }} }\;\; \right\| = \beta^{t} \hfill \\ \end{aligned}$$

(27)

$$\left( {{\mathbf{X}}_{{{\text{MPTP}}}} ,{\mathbf{P}}_{{{\text{MPTP}}}} } \right) = T^{ - 1} \left( {{\mathbf{U}}_{{{\text{MPTP}}}} } \right)$$

(28)

The study shows that PMA is more robust compared to RIA and is not susceptible to the value of reliability index (Aoues and Chateauneuf 2010).

5.3 Integration of the EFSL method with DLM

It is verified that the proposed EFSL method has a good ability for solving nonlinear limit state functions in Sect. 4. Therefore, the proposed EFSL method is considered to be combined with DLM to improve the ability of DLM for solving complex RBDO problems. The proposed DLM/EFSL can be expressed as

$$\begin{gathered} {\text{find }}{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} \hfill \\ \min \, f\left( {{\mathbf{d}},{{\varvec{\upmu}}}_{{\mathbf{X}}} ,{{\varvec{\upmu}}}_{{\mathbf{P}}} } \right) \hfill \\ {\text{s.t.}}\beta_{{_{i} }}^{k} \ge \beta_{i}^{t} \, i = 1,2,\ldots,n \hfill \\ \, {\mathbf{d}}^{L} \le {\mathbf{d}} \le {\mathbf{d}}^{U} ,{{\varvec{\upmu}}}_{{\mathbf{X}}}^{L} \le {{\varvec{\upmu}}}_{{\mathbf{X}}} \le {{\varvec{\upmu}}}_{{\mathbf{X}}}^{U} \hfill \\ {\text{where }}\beta_{{_{i} }}^{k} { = }\left\| {{\mathbf{U}}_{i}^{k} } \right\| \hfill \\ {\mathbf{U}}_{i}^{k} = {{\varvec{\upalpha}}}_{{_{i} }}^{k} \beta_{{_{i} }}^{k} \hfill \\ \lambda^{k - 1} { = }\left\{ \begin{gathered} 2^{15} , \, k < 3 \hfill \\ \left\{ \begin{gathered} \lambda^{k - 2} /10, \, \lambda^{k - 2} > 10 \hfill \\ \lambda^{k - 2} /1, \, 5 \le \lambda^{k - 2} \le 10 \hfill \\ \lambda^{k - 2} /0.05, \, 0 < \lambda^{k - 2} < 5 \hfill \\ \end{gathered} \right.,\left\| {{\mathbf{U}}^{k - 1} - {\mathbf{U}}^{k - 2} } \right\| < \left\| {{\mathbf{U}}^{k - 2} - {\mathbf{U}}^{k - 3} } \right\|{ , }M = M^{t} , \, k \ge 3 \hfill \\ cn\left( {1 - n} \right)\lambda^{k - 2} , \, \left\| {{\mathbf{U}}^{k - 1} - {\mathbf{U}}^{k - 2} } \right\| \ge \left\| {{\mathbf{U}}^{k - 2} - {\mathbf{U}}^{k - 3} } \right\|, \, k \ge 3 \, \hfill \\ e^{{ - 0.125\left( {k - 1} \right)}} , \, \lambda^{k - 1} \le {0}{\text{.15, }}\left\| {{\mathbf{U}}^{k - 1} - {\mathbf{U}}^{k - 2} } \right\| \ge \left\| {{\mathbf{U}}^{k - 2} - {\mathbf{U}}^{k - 3} } \right\|, \, k \ge 3 \hfill \\ \end{gathered} \right. \hfill \\ {{\varvec{\upalpha}}}_{{_{i} }}^{k} = \frac{{{\mathbf{U}}_{i}^{k - 1} - \lambda^{k - 1} \nabla g\left( {{\mathbf{U}}_{i}^{k - 1} } \right)}}{{\left\| {{\mathbf{U}}_{i}^{k - 1} - \lambda^{k - 1} \nabla g\left( {{\mathbf{U}}_{i}^{k - 1} } \right)} \right\|}} \hfill \\ \beta_{{_{i} }}^{k} = - \frac{{g\left( {{\mathbf{U}}_{i}^{k - 1} } \right) - \left( {\nabla g\left( {{\mathbf{U}}_{i}^{k - 1} } \right)} \right)^{{\text{T}}} {\mathbf{U}}_{i}^{k - 1} }}{{\nabla g\left( {{\mathbf{U}}_{i}^{k - 1} } \right)^{{\text{T}}} \left( {{{\varvec{\upalpha}}}_{{_{i} }}^{k} } \right)}} \hfill \\ \end{gathered}$$

(29)

5.4 Illustrative examples of RBDO

The robustness and efficiency of the proposed DLM/EFSL method are demonstrated by four design problems including numerical and structural examples. The optimizer “fmincon” is used as a tool to perform the optimization loop. The convergence criterion is set as $\left\| {{\mathbf{X}}^{k + 1} - {\mathbf{X}}^{k} } \right\|/\left\| {{\mathbf{X}}^{k + 1} } \right\| < 10^{ - 6}$ for the inner loop, and the convergence criterion is set as $\left\| {{\mathbf{d}}^{k + 1} - {\mathbf{d}}^{k} } \right\|/\left\| {{\mathbf{d}}^{k + 1} } \right\| < 10^{ - 3}$ for the outer loop. The efficiency of the optimization method depends mainly on the number of function call, which includes the number of constraint function call and the number of objective function call. In addition, the number of constraint function call is the sum of the number of performance function call and the number of gradient function call. Since sensitivity analysis is evaluated by using the analytical method in this study, the evaluation of sensitivity is counted as one function call. Therefore, the evaluation of a constraint function and its sensitivity is counted as two function calls. The reliability index of the performance function is calculated by the MCS method at the obtained optimal design point and compared with the target reliability index to evaluate error of the proposed DLM/EFSL.

5.4.1 Design problem 1

This nonlinear benchmark example, which is extracted from Aoues and Chateauneuf (2010), includes two independent random variables $X_{1}$ and $X_{2}$ with normal distribution $X_{i} \sim N\left( {\mu_{{X_{i} }} ,0.3^{2} } \right)$ and three nonlinear performance function constraints. The target reliability indices for three constraint functions are $\beta_{i}^{t} = 3 \, \left( {i = 1,2,3} \right)$ and the initial point is set as ${\kern 1pt} {{\varvec{\upmu}}}_{{\mathbf{X}}}^{0} = \left[ {5.0,5.0} \right]^{{\text{T}}}$. The RBDO problem is formulated as

$$\begin{aligned}&{\text{find}}\;{{\varvec{\upmu}}}_{{\mathbf{X}}} = \left[ {\mu_{{X_{1} }} ,\mu_{{X_{2} }} } \right]^{{\text{T}}} \\ & \min\;f\left( {{{\varvec{\upmu}}}_{{\mathbf{X}}} } \right) = \mu_{{X_{1} }} + \mu_{{X_{2} }} \\ & {\text{s.t.}}\;P\left[ {g_{i} \left( {\mathbf{X}} \right) \ge 0} \right] \ge \Phi \left( {\beta_{i}^{t} } \right),i = 1,2,3 \\ &0 \le \mu_{{X_{1} }} \le 10,0 \le \mu_{{X_{2} }} \le 10 \\ & {{\varvec{\upmu}}}_{{\mathbf{X}}}^{0} = \left[ {5.0,5.0} \right]^{{\text{T}}} , {{\varvec{\upsigma}}}_{{\mathbf{X}}} = \left[ {0.3,0.3} \right]^{{\text{T}}} \\& {\text{where}}\;g_{1} \left( {\mathbf{X}} \right) = {{X_{1}^{2} X_{2} } \mathord{\left/ {\vphantom {{X_{1}^{2} X_{2} } {20}}} \right. \kern-\nulldelimiterspace} {20}} - 1 \\ &\quad \quad \quad g_{2} \left( {\mathbf{X}} \right) = (X_{1} + X_{2} - 5)^{2} /30 + (X_{1} - X_{2} - 12)^{2} /120 - 1 \\ & \quad \quad \quad g_{3} \left( {\mathbf{X}} \right) = 80/(X_{1}^{2} + 8X_{2} + 5) - 1 \\ & \quad \quad \quad \beta_{1}^{t} = \beta_{2}^{t} = \beta_{3}^{t} = 3 \end{aligned}$$

(30)

The optimization results of the comparative methods are summarized in Table 13, in which all the methods can successfully converge to the same optimum ${{\varvec{\upmu}}}_{{\mathbf{X}}} = \left( {3.4391,3.2866} \right)$ except for DLM/CC. These results are consistent with the results in Aoues and Chateauneuf (2010). In terms of the accuracy, the proposed DLM/EFSL is more accurate than DLM/CC. For efficiency, DLM/EFSL generates the lowest number of function calls of 978, which proves that DLM/EFSL is more efficient than the comparative methods.

Table 13 Optimization results of the comparative methods in Example 5.4.1

The reliability indices of the constraint function calculated by the MCS method at the optimal point are $\beta_{i}^{{{\text{MCS}}}}$. From Table 13, all the methods except DLM/CC have same error (− 0.0278, 0.0541,$\infty$). It means that the proposed DLM/EFSL improves the computational efficiency while retaining a high level of accuracy.

5.4.2 Design problem 2

This nonlinear mathematical problem, which is extracted from Lee and Song (2011), includes two independent random variables $X_{1}$ and $X_{2}$, which obey normal distribution $X_{i} \sim N\left( {\mu_{{X_{i} }} ,0.2^{2} } \right)$ and three highly nonlinear performance function. The target reliability indices for three probabilistic constraints are set as 2 and the initial point is ${{\varvec{\upmu}}}_{{\mathbf{X}}}^{0} = \left[ {1.0,1.0} \right]^{{\text{T}}}$. The RBDO problem is defined as

$$\begin{aligned}& {\text{find}}\;{{\varvec{\upmu}}}_{{\mathbf{X}}} = \left[ {\mu_{{X_{1} }} ,\mu_{{X_{2} }} } \right]^{{\text{T}}} \hfill \\ & \min\;f\left( {{{\varvec{\upmu}}}_{{\mathbf{X}}} } \right) = \mu_{{X_{1} }} + \mu_{{X_{2} }} \hfill \\& {\text{s.t.}}\;P\left[ {g_{i} \left( {\mathbf{X}} \right) \ge 0} \right] \ge \Phi \left( {\beta_{i}^{t} } \right),i = 1,2,3 \hfill \\ & 0.5 \le \mu_{{X_{1} }} \le 4,0.5 \le \mu_{{X_{2} }} \le 4 \hfill \\ & {{\varvec{\upmu}}}_{{\mathbf{X}}}^{0} = \left[ {1.0,1.0} \right]^{{\text{T}}} ,{{\varvec{\upsigma}}}_{{\mathbf{X}}} { = }\left[ {0.2,0.2} \right]^{{\text{T}}} \hfill \\ & {\text{where}}\;g_{1} \left( {\mathbf{X}} \right) = - 9 + 5\sin \left( {X_{1} - 1} \right)^{2} + 5X_{2} - X_{1} X_{2} \hfill \\ & \quad \quad \quad g_{2} \left( {\mathbf{X}} \right) = - 11 + 5\cos \left( { - X_{1} - 1} \right)^{2} + 5X_{2} + 1.5X_{1} X_{2} \hfill \\ & \quad \quad \quad g_{3} \left( {\mathbf{X}} \right) = 38 + 6\sin \left( {X_{1} - 1} \right)^{2} - 12X_{2} - X_{1} X_{2} \hfill \\ & \quad \quad \quad \beta_{1}^{t} = \beta_{2}^{t} = \beta_{3}^{t} = 2\end{aligned}$$

(31)

The optimization results of the comparative methods are summarized in Table 14. From Table 14, all the methods can successfully converge and these methods can obtain the same optimal solution ${{\varvec{\upmu}}}_{{\mathbf{X}}} = \left( {0.5000,2.3619} \right)$ except for DLM/CC, which is approximately similar to the result in Jiang et al. (2017). In terms of accuracy, all the comparative methods have similar accuracy for the same convergence criteria. From the number of function calls, except for the DLM/HMV, the proposed DLM/EFSL generates the lowest number of function calls of 1878. It proves that DLM/EFSL has accurate and efficient characteristics.

Table 14 Optimization results of the comparative methods in Example 5.4.2

The reliability indices of the three probabilistic constraints calculated by the MCS method at the optimal point are $\beta_{i}^{{{\text{MCS}}}}$. From Table 14, all the methods except DLM/CC have the same error (0.0567, 0.2847, 1.5113). It means that the proposed DLM/EFSL improves computational efficiency while retaining a high level of accuracy.

5.4.3 Cantilever beam design problem

This example is a vertical and lateral bending problem of cantilever beam extracted from Shan and Wang (2008), which includes two highly nonlinear performance functions, two independent design variables, and four random parameters. The tip of this beam is subjected to lateral and vertical loads of Z and Y. The random design variables are the width w and thickness t of the cross-section. The physical significance of the objective function is to minimize the weight of the cantilever beam. The length L is 100 in and the cantilever beam under lateral and vertical loads is shown in Fig. 12.

Fig. 12

Cantilever beam under lateral and vertical loads

There are two failure modes for this cantilever beam. One failure mode refers to yielding at the fixed end of the cantilever, i.e., the combined force of these two forces produces the stress M greater than the yield strength S; another is the tip displacement D exceeding the permissible value $D_{0} = 2.5^{\prime \prime }$. Two random variables and four random parameters obey normal distribution, as shown in Table 15.

Table 15 Statistical properties of random parameters in Example 5.4.3

The target reliability indices for two probabilistic constraints are set as $\beta_{i}^{t} = 3, \, i = 1,2$ and the initial point is ${\mathbf{d}}^{0} { = }\left[ {2.5,2.5} \right]^{{\text{T}}}$. The RBDO problem is described as

$$\begin{aligned} &{\text{find}}\; {\mathbf{d}} = \left[ {w,t} \right]^{{\text{T}}} \hfill \\ &\min\;f\left( {\mathbf{d}} \right) = w \cdot t \hfill \\ &{\text{s.t.}}\; P\left( {{\text{Stress }}M{: }M \le S} \right) \ge \Phi \left( {\beta_{1}^{t} } \right) \hfill \\ & P\left( {{\text{Tip displacement }}D{: }D \le D_{0} } \right) \ge \Phi \left( {\beta_{2}^{t} } \right) \hfill \\ & 0 \le w \le 5, \; 0 \le t \le 5 \hfill \\ \end{aligned},$$

(32)

where stress M and tip displacement D can be formulated as

$$M = \frac{600}{{wt^{2} }}Y + \frac{600}{{w^{2} t}}Z$$

(33)

$$D = \frac{{4L^{3} }}{Ewt}\sqrt {\left( {{Y \mathord{\left/ {\vphantom {Y {t^{2} }}} \right. \kern-\nulldelimiterspace} {t^{2} }}} \right)^{2} + \left( {{Z \mathord{\left/ {\vphantom {Z {w^{2} }}} \right. \kern-\nulldelimiterspace} {w^{2} }}} \right)^{2} }$$

(34)

The optimization results of the comparative methods are summarized in Table 16. From Table 16, all the methods with the exception of DLM/CC obtain the same objective function value 9.5202, corresponding to the same optimum point (2.4460, 3.8922). These results are consistent with the results in Yang and Gu (2004). It means that the DLM/EFSL has a high degree of accuracy. Regarding the number of function call, DLM/EFSL generates the lowest function call number of 351 and the highest convergence speed. This example indicates that DLM/EFSL performs well in terms of both convergence performance and computational efficiency.

Table 16 Optimization results of the comparative methods in Example 5.4.3

5.4.4 Vehicle side impact problem

Vehicle impacts occur frequently in traffic accidents. Because the mechanical properties of the body on both sides of the vehicle are relatively weak, improving the degree of side impact resistance of the vehicle is of great importance to the safety of passengers. Hence, the proposed DLM/EFSL is now applied to the vehicle side impact design. The finite element analysis model (Youn et al. 2004; Zhang et al. 2021b), which consists of 85,941 shell elements and 96,122 nodes, is shown in Fig. 13. In the vehicle side impact finite element simulation, the barrier impacts the side of the vehicle at a velocity of 49.89 kph. One simulation of this finite element model using the RADIOSS software on SGI Origin 2000 takes about 20 h. This study uses the European Enhanced Vehicle-Safety Committee (EEVC) side impact criteria to enable the vehicle to meet the specified internal and regulatory side impact requirements. The EEVC side impact criteria, which is shown in Table 17, include abdomen load, rib deflections, VC’s (viscous criteria), pubic symphysis force, and Head Injury Criterion (HIC). In addition, the velocity of the front door at the B-pillar and the velocity of the B-pillar at the middle point need to be considered in the side impact design.

Fig. 13

Schematic of vehicle side impact model (Zhang et al. 2021b)

Table 17 EEVC criteria for vehicle side impact

To achieve the goal of reducing weight of vehicle while ensuring the safety of personnel, an optimal model for the side impact of vehicle considering ten safety constraints is developed. The RBDO problem is formulated as

$$\begin{aligned} &\min \; {\text{Weight}}({\mathbf{\mu }}_{{\mathbf{X}}} ) \\ &{\text{s.t.}} \;P({\text{Abdomen load: F}}_{{{\text{Abd}}}} \le {\text{1}}{\text{.0kN}}) \ge P_{s} \\ & P({\text{Upper/Middle/Lower Rib deflection: Def}}_{{{\text{rib\_u}}/{\text{rib\_m}}/{\text{rib\_l}}}} \le {\text{32mm}}) \ge P_{s} \\ & P({\text{Upper/Middle/Lower VC: VC}}_{{{\text{upper/middle/lower}}}} \le 0.{\text{32m/s}}) \ge P_{s} \\ & P({\text{Pubic symphysis force: Force}}_{{{\text{public}}}} \le {\text{4}}{\text{.0kN}}) \ge P_{s} \\ & P({\text{Velocity of B - pillar at middle point: Velocity}}_{{{\text{B - pillar}}}} \le {\text{9}}{\text{.9mm/ms}}) \ge P_{s} \\ & P({\text{Velocity of front door at B - pillar: Velocity}}_{{{\text{door}}}} \le {\text{15}}{\text{.7mm/ms}}) \ge P_{s} \\ & {\mathbf{\mu }}_{{\mathbf{X}}}^{L} \le {\mathbf{\mu }}_{{\mathbf{X}}} \le {\mathbf{\mu }}_{{\mathbf{X}}}^{U} ,{\text{ }}{\mathbf{\mu }}_{{\mathbf{X}}} \in R^{{^{7} }} \\ & {\mathbf{\mu }}_{{\mathbf{X}}}^{L} {\text{ = }}\left[ {0.5,0.45,0.5,0.5,0.875,0.4,0.4} \right]^{{\text{T}}} \\ & {\mathbf{\mu }}_{{\mathbf{X}}}^{U} = \left[ {1.5,1.35,1.5,1.5,2.625,1.2,1.2} \right]^{{\text{T}}} \\ \end{aligned}$$

(35)

The optimal model includes seven random variables X₁–X₇ and four random parameters X₈–X₁₁, and their statistical characteristics are given in Table 18. They are independent and normally distributed. The mean values of $X_{8}$ and $X_{9}$ are set as 0.345. The target reliability indices for ten probabilistic constraints are set as $\beta_{{}}^{t} = 3$, corresponding to the target reliability of 99.8650%. The initial point is ${{\varvec{\upmu}}}_{{\mathbf{X}}}^{0} { = }\left[ {1.0,0.9,1.0,1.0,1.75,0.8,0.8} \right]^{{\text{T}}}$.

$$ \begin{aligned} {\text{Weight}} &= 1.98 + 4.90\mu_{X_{1} } + 6.67\mu_{{X_{2} }} + 6.98\mu_{{X_{3} }} +4.01\mu_{{X_{4} }} +1.78\mu_{X_{5} } +2.73\mu_{{X_{7} }} \hfill \\ {\text{F}}_{\text{Abd}} &= 1.16 - 0.3717X_{2} X_{4} - 0.00931X_{2} X_{10} - 0.484X_{3} X_{9} + 0.01343X_{6} X_{10} \hfill \\ {\text{Def}}_{\text{rib\_u}} &= 28.98 + 3.818X_{3} - 4.2X_{1} X_{2} + 0.0207X_{5} X_{10} + 6.63X_{6} X_{9} \hfill \\ & \quad - 7.77X_{7} X_{8} + 0.32X_{9} X_{10} \hfill \\ {\text{Def}}_{\text{rib\_m}} &= 33.86 + 2.95X_{3} + 0.1792X_{10} - 5.057X_{1} X_{2} - 11X_{2} X_{8} - 0.0215X_{5} X_{10} - 9.98X_{7} X_{8} + 22X_{8} X_{9} \hfill \\ {\text{Def}}_{\text{rib\_l}} &= 46.36 - 9.9X_{2} - 12.9X_{1} X_{8} + 0.1107X_{3} X_{10} \hfill \\ {\text{VC}}_{\text{upper}} &= 0.261 - 0.0159X_{1} X_{2} - 0.188X_{1} X_{8} - 0.019X_{2} X_{7} { + 0}{\text{.0144}}X_{3} X_{5} + 0.0008757X_{5} X_{10} + 0.08045X_{6} X_{9} + 0.00139X_{8} X_{11} + 0.00001575X_{10} X_{11} \hfill \\ {\text{VC}}_{\text{middle}} &= 0.214+0.00817X_{5} - 0.131X_{1} X_{8} - 0.0704X_{1} X_{9} { + 0}{\text{.03099}}X_{2} X_{6}- 0.018X_{2} X_{7} + 0.0208X_{3} X_{8} + 0.121X_{3} X_{9} - 0.00364X_{5} X_{6} + 0.0007715X_{5} X_{10} - 0.0005354X_{6} X_{10} + 0.00121X_{8} X_{11} \hfill \\ {\text{VC}}_{\text{lower}} &= 0.74 - 0.61X_{2} - 0.163X_{3} X_{8} + 0.001232X_{3} X_{10} - 0.166X_{7} X_{9} + 0.227X_{2}^{2} \hfill \\ {\text{Force}}_{\text{public}} &= 4.72 - 0.5X_{4} - 0.19X_{2} X_{3} - 0.0122X_{4} X_{10}+ 0.009325X_{6} X_{10} + 0.000191X_{11}^{2} \hfill \\ {\text{Velocity}}_{\text{B - Pillar}} &= 10.58 - 0.674X_{1} X_{2} - 1.95X_{2} X_{8} + 0.02054X_{3} X_{10} - 0.0198X_{4} X_{10} + 0.028X_{6} X_{10} \hfill \\ {\text{Velocity}}_{\text{door}} &= 16.45 - 0.489X_{3} X_{7} - 0.843X_{5} X_{6} + 0.0432X_{9} X_{10} - 0.0556X_{9} X_{11} - 0.000786X_{11}^{2} \hfill \\ \end{aligned} $$

(36)

Table 18 Statistical properties of random variables and parameters in Example 5.4.4

The optimization results of the comparative methods and the constraint functions at the optimal point, which are verified against the MCS method, are listed in Tables 19 and 20, respectively. From Table 19, DLM/HMV, DLM/FSL, and DLM/EFSL obtain the same objective function value 29.5578, but DLM/CC and DLM/MCC converge to objective function value 29.5567 and 29.5564. These results are approximately similar to the results in Yang and Gu (2004). It means that these comparative methods have similar degree of accuracy. In terms of efficiency, DLM/EFSL generates the lowest number of function calls compared to other comparative methods in the vehicle side impact problem, which demonstrates the superior computational efficiency of DLM/EFSL.

Table 19 Optimization results of the comparative methods in Example 5.4.4

Table 20 Calculation of constraint functions at the optimal point by MCS method in Example 5.4.4

The reliability indices of constraint functions at the optimal point are shown in Table 20. From Table 20, the DLM/HMV, DLM/FSL, and DLM/EFSL have the same error ($\infty$, 0.0017, 1.3502, 0.0001, $\infty$, $\infty$, $\infty$, − 0.5677,1.9354, 0.2029). It means that DLM/EFSL improves efficiency while retaining a high level of computational accuracy.

6 Conclusions

Although the FSL method has achieved some improvement in robustness and effectiveness compared with improved HL-RF method, it cannot compensate for the deficiency of the FSL method in the oscillation amplitude criterion and adaptively adjust the step length for limit state functions with different degrees of nonlinearity. As a result, the FSL method may result in generating larger computational effort and lower efficiency gains.

In this study, an EFSL method is proposed to overcome the shortcomings of the FSL method. The efficiency and robustness of the proposed EFSL method compared to other commonly used methods like HL-RF, STM, DSTM, and FSL method are verified by five examples. Considering that the proposed method has good capability for solving nonlinear reliability analysis problems, the proposed EFSL method is combined with the DLM to enhance the efficiency for solving complex RBDO problems. Four design problems are employed to verify the computational performance of DLM/EFSL, compared with methods, such as DLM/CC, DLM/MCC, DLM/HMV, and DLM/FSL. It is found that in design problem 2, DLM/EFSL is less computationally efficient than DLM/HMV but higher than DLM/CC, DLM/MCC, and DLM/FSL, while DLM/EFSL has the highest computational efficiency in other three design problems.

In conclusion, the proposed EFSL method improves the efficiency and robustness by adopting a new iterative control criterion and a comprehensive step length adjustment formula, which allow adaptive step length adjustment for different degrees of nonlinear limit state functions. Furthermore, DLM/EFSL is also a robust and efficient RIA-based DLM. To some extent, it has positive significance for structural reliability analysis and RBDO problems.