A new efficient hybrid approach for reliability-based design optimization problems

Abstract

The reliability-based design optimization (RBDO) is performed for mechanical design to compromise effectively between economy and safety requirements. In real mechanical applications, such RBDO problems are a highly complex task by involving computational difficulties and its resolution requires the use of appropriate optimization techniques. In this paper, a new RBDO solution approach is introduced for mechanical engineering problems. It is a combination of the reliable design space (RDS) technique with an efficient hybrid algorithm (AMDE-NM) based on the adaptive mixed differential evolution (AMDE) and Nelder–Mead local search (NM). First, the RDS strategy is used to turn the RBDO problem into a simple deterministic optimization (SDO) one, through converting the probabilistic constraints to approximate deterministic constraints, while the resolution is then carried out with the AMDE-NM algorithm. The new proposed integrated approach (RDS–AMDE-NM) is able to handle the mixed design variables with continuous, discrete, and integer types. Six mechanical problems with different features are studied to analyze the applicability and the efficiency of RDS–AMDE-NM. The obtained simulation results show the performance of the proposed approach, while new optimal solutions for two RBDO problems are presented. Furthermore, an industry case on a cylindrical spur gear is studied to investigate the reliability of the proposed method in solving real challenging mechanical RBDO problems. The obtained results reveal really that RDS–AMDE-NM is a promising RBDO approach with extensive applicability.

1 Introduction

Nowadays, decreasing cost and increasing safety of structures are of the most primary concerns in product and process design. This task requires developing and using powerful tools that provide the best balance between both considerations. Deterministic optimization approaches are usually limited and produce a high failure probability on the design constraint satisfaction. This is due to the uncertainties impact which can be related to various conditions like manufacturing process, material properties, and operating environments [1]. To assess the influence of variability factors in optimization process, reliability-based design optimization methodology is introduced as an efficient procedure for engineering design. Wherein the uncertainties are controlled closely by probability distributions using statistical models and, hence, making the best design decisions for the desired reliable level.

The general form of an RBDO problem is similar to that of a deterministic, where the lowest cost is taken as an objective and the reliability requirements are considered as probabilistic constraints. Conventionally, the key challenge in RBDO formulations is concerned with evaluating constraints probability. To deal with this task, the classical RBDO methods employ a nested double-loop procedure in which the outer deterministic optimization loop includes reliability analyses in terms of inner loops [2,3,4,5]. In reliability analysis, the failure probability of a design constraint can be estimated using simulation methods, such as the Monte Carlo simulation (MCS) [6], the importance sampling (IS) [7], and the subset simulation (SS) [8], or approximation methods which comprise the reliability index approach (RIA) [9, 10] and the performance measure approach (PMA) [11]. The RIA is defined as searching for the most probable point (MPP) employing the concept of reliability index. In contrast, the PMA is defined as finding the most probable target point (MPTP) using the concept of inverse reliability analysis. As the double-loop structure requires a high computation effort, due to the repeated constraint evaluation during the optimization, several methods have been developed to reduce the computational time. These methods can be divided into two categories: single-loop methods and decoupled methods.

The single-loop methods aim to convert the nested optimization loops into one loop by eliminating the inner reliability loops. This type of methods mainly contains two subgroups, iterative single-loop methods and complete single-loop methods. The first one employs an iterative process based on Karush–Kuhn–Tucker (KKT) conditions to avoid the reliability analysis, such as the single-loop single-vector (SLSV) [12] and the single-loop approach (SLA) [13, 14], whereas the second subgroup employs a direct process through substituting the probabilistic constraints with approximate deterministic ones in one step. Two approaches are developed in this context, the reliable design space (RDS) technique [15] and the single-loop deterministic method (SLDM) [16].

For the decoupled methods, the objective is to convert the nested optimization loops into a sequential procedure of a deterministic optimization and reliability analysis. The common approach used in this class is the sequential optimization and reliability assessment (SORA), proposed by Du and Chen [17]. There are many other approaches employed the decoupling strategy. Indeed, Cheng et al. [18] introduced the sequential approximate programming (SAP) which formulates the RBDO as a sub-programming problem where the probabilistic constraints are approximated by the Taylor expansion. Authors in [19] developed the penalty-based approach using the penalty term to decouple reliability analyses from optimization loop. Chen et al. [20] proposed the adaptive decoupling approach (ADA) based on the concept of SORA. Furthermore, Huang et al. [21] developed another efficient decoupling method, known as the incremental shifting vector (ISV), based on the shifting vector technique.

In the last few years, gradient-based optimization algorithms such as sequential quadratic programming (SQP) have been used for solving continuous RBDO problems [22, 23]. In this type of methods, derivative calculations of the objective function and constraints are required during the optimization procedure. In addition, the obtained solution is usually sensitive to the initial point, which leads to a trouble in the global optimum search, if the problem to optimize has several local optimums. In contrast to the gradient-based methods, population-based optimization algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), and differential evolution (DE) can be used efficiently in the RBDO and can solve both continuous and discrete problems. Due to their inherent advantages, based on bio-inspired mechanisms, these methods have a high capability to explore the whole search space and reach efficiently the global optimum’s neighborhood.

Tolson et al. [24] used the GA for reliability-based optimum design of water distribution systems where the reliability constraints were evaluated based on the first-order reliability method (FORM). A new approach for RBDO of structures that combines a multi-objective GA (MOGA) with finite-element reliability analysis was proposed by Mathakari et al. [25]. The authors utilized the IS method to perform the reliability analysis. Deb et al. [26] employed the GA for solving single- and multi-objective RBDO problems. In [27], the authors proposed a modified PSO algorithm to solve the discrete and non-smooth RBDO problem. In their work, the probabilistic constraints were evaluated using the SS method. Chen et al. [28] developed an approach for RBDO of composite structures by combining PSO algorithm with finite-element analysis (FEA). Li and Hu [29] provided PSO approach in conjunction with principle components analysis for many-objective RBDO of wind-excited tall buildings. In [30], the DE algorithm was coupled with single-loop reliability method based on the KKT conditions. More recently, Ho-Huu et al. [31] proposed a new hybrid approach by integrating the SORA method with improved constrained differential evolution (ICDE) algorithm to solve RBDO problems of truss structures. In [32], they developed a global single-loop deterministic approach, which is a combination of SLDM and improved differential evolution (IDE) algorithm, for solving RBDO problems of truss structures with continuous and discrete design variables.

In the majority of cases, practical RBDO problems in mechanical engineering involve several computational challenges; consider multiple conflicting objectives, include various complex conditions on geometry and mechanical resistances, as well as mixed types of design variables (integer-discrete-continuous). Therefore, this context leaves plenty of room for developing more powerful approaches in the field of RBDO using accurate optimization algorithms. The novelty of the present study is to propose an efficient optimization algorithm, hybridizing AMDE [33] with NM [34], to deal with mechanical RBDO problems.

The RDS strategy is first employed to convert the RBDO problem into a deterministic optimization problem and the hybrid AMDE-NM is then selected as an optimization tool. Six mechanical problems and real challenging application of cylindrical spur gear are used to further confirm the search performance of the new proposed approach. To the best our knowledge, the multiple-disc clutch brake and the cylindrical pressure vessel are formulated for the first time in the literature as RBDO problems.

The rest of the paper is structured as follows: Sect. 2 presents briefly the typical RBDO formulation. Section 3 introduces the proposed RDS–AMDE-NM hybrid approach. The performance of this approach is demonstrated in Sect. 4 . A real industry case is studied to examine the applicability of RDS–AMDE-NM in Sect. 5. Finally, draw some concluding remarks and point out directions for future work in Sect. 6.

2 Typical RBDO formulation

The typical RBDO problem is described as follows:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;\left\{ {d,{\mu _x}} \right\} \\ {\mathrm{min:}}\;{\mathrm{}}f\left( {d,{\mu _x},{\mu _p}} \right) \\ {\mathrm{s}}{\mathrm{.t}}{\mathrm{.:\;Prob}}{\mathrm{.}}\left( {{g_i}\left( {d,x,p} \right) \ge 0} \right) \ge {R_i}^t{\mathrm{}}i = 1,...,k\\ d^{{\varvec{L}}} \le \;d \le d^{{\varvec{U}}},\;\;\;\mu _x^{{\varvec{L}}} \le \mu _x \le \mu _x^{{\varvec{U}}} \end{array}\, \end{aligned}$$

(1)

where f(.) is the objective function, and d and x are the vectors of deterministic and random design variables, respectively. L and U are the lower and the upper bounds of the variables, respectively. p is the vector of random parameters; $\mu _x$ and $\mu _p$ denote, respectively, the mean vectors of x and p. $g_i{(.)}$ represents the ith constraint function, k is the number of constraints, Prob(.) is the probability function, and $R_i^t$ is the target reliability of the ith constraint satisfaction specified by the designer. For ease of discussion, we assume that $y = \left\{ {d,{\mu _x}} \right\} {\mathrm{\;}}$ is the vector of design decisions, and $z = \{ x,p\}$ is the random vector. Ny and Nz are the dimensions of the vectors y and z, respectively.

Obviously, the problem formulation (Eq. 1) leads to two nested optimization loops: the main design optimization (outer loop) in which the design variables y are to be determined; the second (inner loop) includes the reliability assessment, in which the reliability $R_i$ of the constraint satisfaction $g_i$ is evaluated.

- The concern in evaluating the probabilistic constraint is employing the following integral:

$$\begin{aligned} \ {\mathrm{Prob}}{\mathrm{.\;}}\left( {{g_i}\left( {d,z} \right) \ge 0} \right) = \int _{{g_i}\left( {d,z} \right) {\mathrm{}} \ge {\mathrm{0}}} {{F_z}\;\left( z \right) {\mathrm{}}dz} \, \end{aligned}$$

(2)

where $F_z$ represents the joint probability density function of the vector z. Theoretically, the exact computation of this integral is very difficult owing to the absence of analytical solvers. Simplest techniques based on simulation mechanisms such as MCS [6] and SS [7] are alternatively used and are considered as reference methods. However, the major drawback of these methods lies in the high number of function evaluations. To deal efficiently with the integral in Eq. 2, MPP-based methods such as the RIA and the PMA have been introduced. The main idea consists in transforming the constraint function $g_i$ from the original design space (Z space) to the standard normal space (U space).

If the RIA is used, the reliability index $\beta _i$ is employed to replace the probabilistic constraint ${\mathrm{Prob.}}\left( {{{\mathrm{g}}_i}\;\left( {d,\;z} \right) \ge 0} \right)$ and the reliability $R_i$ is then estimated by solving the following optimization problem:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;\left( {{u_z}} \right) \\ \min \;:{\beta _i} = \sqrt{\sum \limits _{j = 1}^{Nz} {u_{zj}^2} } \\ {\mathrm{s}}{\mathrm{.t.: }}\;{G_i}\left( {d,{u_z}} \right) = 0. \end{array}\, \end{aligned}$$

(3)

The optimal solution of the problem (Eq. 3) is the MPP in the U space. According to the FORM approximation [35], the reliability $R_i$ is given by ${R_i} = {{\varPhi }}\left( {\;{\beta _{i\;}}} \right)$.

However, if the PMA is used, the probabilistic constraint is replaced by the performance measure function, where the inverse reliability problem is stated as:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;\left( {{u_z}} \right) \\ {\mathrm{min: }}\;{G_i}\left( {d,{u_z}} \right) \\ {\mathrm{s}}{\mathrm{.t.}}{\mathrm{.}}:{\mathrm{}}\;\sqrt{\sum \limits _{j = 1}^{Nz} {u_{zj}^2} } = {\varPhi ^{ - 1}}\left( {{R_i}^t} \right) . \end{array}\ . \end{aligned}$$

(4)

The optimal solution of the problem (Eq. 4) is the MPTP in the U space. $u_z$ denotes the standard normalized vector of z, which is obtained by the following transformation [36]:

$$\begin{aligned} {u_{zj}} = {{{\varPhi }}^{ - 1}}\left( {{\mathrm{CD}}{{\mathrm{F}}_j}\left( {{z_j}} \right) } \right) , \end{aligned}$$

(5)

where $\varPhi$ and $\varPhi ^{-1}$ are, respectively, the standard normal cumulative distribution function and its inverse function. CDF$_j$ is the cumulative distribution function of $z_j$, and $G_(j)(.)$ is the ith constraint function $g_i$ in the U space.

3 Proposed hybrid approach: RDS–AMDE-NM

The proposed approach in this study involves two main stages:

• First, the RBDO problem (Eq. 1) is converted into an SDO problem (Eq. 9) by applying the RDS concept.

• Second, the formed optimization problem is solved by introducing a hybrid optimization algorithm, coupling AMDE with NM.

In the present approach, the reflection technique is employed to treat boundary constraints for the mutation process. Moreover, the simple static exterior penalty function is adopted to deal with constraints for the converted deterministic problem. The key points of the method are illustrated in the following sections.

3.1 Reliable design space technique

As mentioned above, the direct solution of RBDO problem (Eq. 1) is given by employing two nested optimization loops. The RDS technique was proposed by Shan and Wang [15] to remove the inner reliability loops and, thus, introducing an equivalent deterministic formulation. The main idea is based on the reformulation of the probabilistic constraints defined on the original design space by approximate deterministic ones in the reliable design space. Figure 1 illustrates geometrically the concept of the RDS. For an easy understanding, we assume that an optimization problem contains only one constraint with two variables $\;X = \;\left\{ {{x_1},{x_2}} \right\}$. When uncertainty is not considered, the feasible design space (FDS) is identified within the global design space by the yellow area and its boundary is determined by the deterministic constraint $(g(x_1,x_2 )=0)$. By considering the uncertainty, the RDS is separated from the deterministic FDS, as can be seen by the blue area, and its boundary is determined by the probabilistic constraint$\;\left( {{\mathrm{Prob}}.\left( {{\mathrm{g}}\left( {d,X} \right) \ge 0} \right) = {R^t}} \right)$.

Analytically, the RDS can be denoted by the region of design points whose corresponding inverse MPPs satisfy the deterministic constraints $g_i$. In other word, each design point $\mu _z$ in the RDS has its inverse MPP z within the deterministic FDS.

The inverse MPP z represents the MPP in the Z space, and its evaluation conventionally requires an iterative procedure during the optimization [12, 14]. According to Shan and Wang [15], the partial derivatives at the current design point $\mu _z$ can be employed to approximate the derivatives at its inverse MPP z. Hence, the direct calculation of z at any design point $\mu _z$ can be achieved as:

$$\begin{aligned} {\mathbf{z }}_j^i = \;{\mu _{zj}} - \;\beta _t^i \times {\sigma _{zj}} \times \alpha _j^i(\mu _z)~~~~~ i = 1,...,k\mathrm{}~~\hbox {and}~~{\mathrm{}}j = 1,...,Nz, \end{aligned}$$

(6)

where $\mu _z$ referred as the design point is the mean vector of z, $\sigma _{z}$ is the standard deviation vector of z, $\beta _t$ denotes the target reliability index vector, and $\alpha {(\mu _z)}$ is the direction cosine:

$$\begin{aligned} \ \alpha _{j}^{i}({{\mu }_{{{z}_{~}}}})=\frac{{{\sigma }_{zj}}\times \left( \frac{\partial {{g}_{i}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{zj}}} \right) }{\sqrt{\mathop {\sum }_{q=1}^{Nz}{{\left( {{\sigma }_{zq}}\frac{\partial {{g}_{i}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{zq}}} \right) }^{2}}}}\ . \end{aligned}$$

(7)

Using Eq. 6, the reliable design space of the RBDO problem is defined by approximate deterministic constraints ${\mathbf{g }_{i}}$ as:

$$\begin{aligned} \ {\mathbf{g }_{i}} (d,~{{\mu }_{{{z}_{~}}}})={{g}_{i}}(d,~{\mathbf{z }^{i}})={{g}_{i}}(d,~{{\mu }_{z}}-~\beta _{t}^{i}\times {{\sigma }_{z}}\times {{\alpha }^{i}}({{\mu }_{{{z}_{~}}}}))\ge 0\ . \end{aligned}$$

(8)

Accordingly, the RBDO problem in Eq. 1 becomes an SDO problem expressed in the following form:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}(y = \left\{ {d,{\mu _x}} \right\} )\\ \min : f(d,\mu _z)\\ \mathrm{s.t.}: \mathbf{g }_i(d,\mu _z) \ge 0 ~~~ i = 1,...,k\\ y^{{\varvec{L}}} \le \;y \le y^{{\varvec{U}}} \end{array}. \end{aligned}$$

(9)

It should be noted that the approximation presented in Eq. 6 is only valid for the normal distribution case. For other distributions, the probabilistic transformation [36] is applied to estimate the mean and the standard deviation of the equivalent normal distribution [35]. The pseudo-code of the RDS strategy is summarized in Algorithm 1.

Fig. 1

Concept of the reliable design space

3.2 Adaptive mixed differential evolution (AMDE) algorithm

The DE is a population-based evolutionary algorithm, originally developed and introduced by Storn and Price [37]. Due to its simple structure, fewer number of control parameters, and ease of implementation, the DE has been widely addressing for solving several problems in various areas of engineering during the last 2 decades. We find several studies in chemical science and engineering [38], gas oil and petroleum industry [39], defense [40], signal processing [41], image registration [42], power system transfer capability assessment [43], optimal power flow [44], mechanical precision engineering [33, 45,46,47], machining applications [48, 49], and structural design optimization [50, 51].

Recently, the AMDE algorithm has been introduced by Abderazek et al. [33] to optimize the profile geometry parameters of a spur gear pair. This technique was developed to enhance the global search ability of the basic DE. The AMDE version involves four steps including, the initialization, the mutation, the crossover, and the selection. These steps are detailed as follows.

• Initialization:

  For the AMDE, the control parameters are: the population size (NP), the maximum number of iterations (the termination criterion) ($t_{\mathrm{max}}$), the scale factors ($F_1$, $F_2$), and the crossover rate (Cr). Similar to other population-based algorithms, the AMDE algorithm starts the optimization process by a random generated ($NP\times Ny$) matrix of individuals within the boundary constraints of each decision variable. To generate the continuous variables, the following equation is used:

  $$\begin{aligned} y_{i,j}^{t = 0}& = y_i^L + \hbox {ran}{d_{i,j}}\left\{ {0,1} \right\} \nonumber \\&\times \left( {y_i^U - y_i^L} \right) {\mathrm{}}i = 1,...,Ny{\mathrm{}}~~\hbox {and}~~ j = 1,...,NP\ , \end{aligned}$$

  (10)

  where Ny as mentioned above is the dimension of the optimized problem, t is the iteration number, and rand generates a random value in the range [0, 1]. Equation 10 is only used for creating the continuous variables. To deal with discrete and integer variables, the index method is adopted (as shown in Eq. 11). This method is presented and well explained in [33]:

  $$\begin{aligned} y_{i,j}^{t = 0} = \hbox {round}\left( {y_i^L + \hbox {ran}{d_{i,j}}\left\{ {0,1} \right\} \times \left( {y_i^U - y_i^L} \right) } \right) , \end{aligned}$$

  (11)

  where round is MATLAB function that rounds the variable $y_i$ to the nearest integer. After the initialization step, the fitness of the initial solutions (individuals) is evaluated based on their fitness value, and the best individual from the initial population is selected by the elitism mechanism.

• Mutation operator:

  The mutation serves to create a new mutated vector $v_{i,j}^t$ for each individual in the current population. In this work, we chose to use the DE/rand/2/bin to generate the mutated vector. This strategy usually converges slowly but exhibits powerful exploration ability [52]:

  $$\begin{aligned} \ {v_{i,j}}^{t+1} = {y_{i,r1}}^t + {F_1} \times \left\{ {{y_{i,r2}}^t - {y_{i,r3}}^t} \right\} + {F_2} \times \left\{ {{y_{i,r4}}^t - {y_{i,r5}}^t} \right\} , \end{aligned}$$

  (12)

  where ${r_1} \ne {r_2} \ne \;{r_3} \ne {r_4} \ne {r_5} \ne j\$ are randomly chosen integer number within [1,...,NP], and $F_1$ and $F_2$ are the mutation scale factors.

• Crossover operator:

  There are various types of the crossover scheme to create the trial vector $w_{i,j}^{t + 1}$. The binomial crossover is the most used and is implemented as follows [53]:

  $$\begin{aligned} \ w_{i,j}^{t + 1} = \left\{ \begin{array}{l} v_{i,j}^{t + 1}{\mathrm{}}~\quad \hbox {if}~~\left( {\hbox {ran}{d_{i,j}}\left[ {0,1} \right] \le \hbox {Cr}} \right) \vee \left( {i = = \hbox {pr}} \right) \\ y_{i,j}^t{\mathrm{}}~\quad \hbox {otherwise}, \end{array} \right. \end{aligned}$$

  (13)

  where pr is an integer number randomly chosen within $\left\{ {1, \ldots ,Ny} \right\}$, and Cr is the crossover parameter which is usually chosen in the range [0, 1].

  To avoid the manual setting of $F_1$, $F_2$ and Cr, the self-adaptive strategy (jDE) [54] is integrated with AMDE. For more detail, the jDE procedure is presented in the follow chart given in Fig. 2.

• Selection:

  In the selection phase, the target vector is replaced by the trial vector if the objective function value of $w_{i,j}^{t + 1}$ is better than that of $y_{i,j}^t$:

  $$\begin{aligned} \ y_{i,j}^{t + 1} = \left\{ \begin{array}{l} w_{i,j}^{t + 1}{\mathrm{}}~~~~~~{\mathrm{if}}~~~~~~f\left( {w_{i,j}^{t + 1}} \right) \le {\mathrm{}}f\left( {y_{i,j}^t} \right) \\ y_{i,j}^t{\mathrm{}}~~~~~~\hbox {otherwise}. \end{array} \right. \end{aligned}$$

  (14)

Fig. 2

Flowchart of jDE technique

3.3 Nelder–Mead simplex search algorithm

The NM simplex search algorithm was originally developed by [34]. It is a derivative free method introduced for unconstrained and continuous optimization problems. Due to its simple structure and ease of implementation, the NM algorithm has been successfully combined with several meta-heuristics to solve different optimization problems in diverse fields [55,56,57,58,59,60,61,62].

In this study, the NM technique is used to enhance the local search ability of the introduced algorithm. For each generation and after the mutation and crossover operations, the NM is introduced as local search to replace the worst current solution with the best one. The pseudo-code of NM is presented in Algorithm 2. The NM contains four operations: reflection, expansion, contraction, and shrinkage. It is worth mentioning that the values of the control parameters of NM are iteratively updated according to the method proposed by Xu and Yan [61].

3.4 Constraint handling

3.4.1 Handling bound constraints

The mutation process may generate individuals where one or more components fall outside the boundary constraints of the optimization problem. In such cases, a correction procedure method is usually used to repair or substitute the infeasible individual. In this paper, the reflection method is implemented to handle with the boundary constraints [63]:

$$\begin{aligned} \ v_{i,j}^{t + 1} = \left\{ \begin{array}{l} 2 \times y_i^L - {v_{i,j}}{\mathrm{}}~~\hbox {if}~~{\mathrm{}}v_{i,j}^{t + 1} < y_i^L\\ 2 \times y_i^U - {v_{i,j}}{\mathrm{}}~~\hbox {if}~~{\mathrm{}}v_{i,j}^{t + 1} > y_i^U\\ {v_{i,j}}~~\qquad \quad \,\,\, {\mathrm{otherwise}}. \end{array} \right. \end{aligned}$$

(15)

3.4.2 Constraint functions

The most common method used in evolutionary algorithms to deal with the constraint functions is the penalty function technique. This is primarily due to its simplicity of application. The main goal of the penalty functions is to transform a constrained optimization problem to an unconstrained one. In the literature, several penalty functions have been developed and used such as static penalty, annealing penalty, adaptive co-evolutionary penalty, dynamic penalty, and death penalty [64]. In the present work, the simple static exterior penalty method is adopted to treat the converted constraints of the optimized problem. Mathematically, the method is expressed by the following equation:

$$\begin{aligned} \ F\left( y \right) = f\left( y \right) + P\left( y \right) \ , \end{aligned}$$

(16)

where F(y) is the new objective function and P(y) denotes the penalty function:

$$\begin{aligned} \ P\left( y \right) = r \times \sum \limits _{i = 1}^k {\min {{\left( {0,{\mathbf{g }_i}(y,{\mu _p})} \right) }^2}} \ , \end{aligned}$$

(17)

where r is a positive constant called penalty factor.

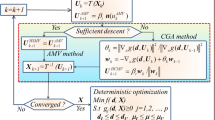
By integrating the RDS technique with the AMDE and NM algorithms, a new resolution method for RBDO mechanical problems is developed, which is addressed to handle continuous, discrete, and integer design variables. Figure 3 illustrates the flowchart of the developed RDS–AMDE-NM approach.

Fig. 3

Flowchart of RDS–AMDE-NM approach

4 Experiments and results

In this section, the performance of the RDS–AMDE-NM is shown by solving six nonlinear RBDO problems. The first four engineering problems chosen from the literature are: the cantilever beam, vehicle side impact, speed reducer, and welded beam. Furthermore, two additional problems of mechanical design are formulated in this study for first time including the multiple-disc clutch brake and the cylindrical pressure vessel.

The population size and function evolutions’ (FEs) number for each problem are given in Table 1. For the statistical analysis, all problems are independently executed 50 times. The best solution obtained among the compared algorithms is highlighted in bold face.

Table 1 NP size and FEs number of the RDS–AMDE-NM for the RBDO problems

4.1 Cantilever beam

The cantilever beam problem (Fig. 4) is widely used in the literature to test the reliability and the efficiency of RBDO methods [13, 15, 16]. The objective is to minimize the beam weight, while two probabilistic constraints are considered. The first is imposed on the stress at the fixed end, which should be less than the yield strength. The second is fixed on the tip displacement, which should be less than the allowable displacement $D_0$. The problem involves two continuous deterministic design variables: the width $d_1$ and thickness $d_2$ of the cross section. Moreover, four random parameters exist in the probabilistic constraints, supposed to be independent normally distributed where their statistical data are illustrated in Table 2. Thus, the RBDO problem is stated as follows:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;{\mathrm{}}\left( {{d_1},{d_2}} \right) \\ \min : \;{\mathrm{}}f\left( d \right) = {d_1} \times {d_2}\\ {\mathrm{s}}{\mathrm{.t.: }}\;{\mathrm{Prob}}\;\left( {{g_i}\left( {d,p} \right) \ge 0} \right) \ge R_i^t,{\mathrm{}}i = 1,2\\ {g_1} = {p_1} - \left( {\left( {\frac{{600}}{{{d_1}{d_2}^2}}} \right) \times {p_2} + \left( {\frac{{600}}{{{d_1}^2{d_2}}}} \right) \times {p_3}} \right) \\ {g_2} = {D_0} - \left( {\frac{{4{L^3}}}{{{p_4}{d_1}{d_2}}}} \right) \times \sqrt{{{\left( {\frac{{{p_2}}}{{{d_2}^2}}} \right) }^2} + {{\left( {\frac{{{p_3}}}{{{d_1}^2}}} \right) }^2}} \\ 0 \le {d_1},{d_2} \le 5\\ {R_i}^t = \varPhi \;\left( 3 \right) = 99.87\%. \end{array} \end{aligned}$$

(18)

The beam length $L = 100~in$ and the allowable displacement $D_0 = 2.5~\mathrm{in}$.

Fig. 4

Cantilever beam design problem

Fig. 5

Illustration of the deterministic FDS for the cantilever beam example

4.1.1 Formulation of the deterministic optimization problem

The feasible design space of the cantilever beam problem for the deterministic level is presented in Fig. 5. To shift the boundaries of the deterministic feasible space to the reliable space, the two probabilistic constraints in Eq. 18 are converted into approximate deterministic ones by applying the pseudo-code of the RDS strategy (Algorithm 1). Algorithm 3 presents the procedure of the RDS technique for the cantilever beam problem. Note that the same procedure is followed for the other problems studied.

After the approximate deterministic constraints have been formed, the reliable design space of the cantilever beam problem is defined, as presented in Fig. 6. Thus, the equivalent deterministic optimization problem is established as:

$$\begin{aligned} \begin{aligned}&\hbox {find}~({{d}_{1}},{{d}_{2}}) \\&\min : ~\text { }(d)={{d}_{1}}\times {{d}_{2}} \\&\mathrm{s.t.}:\text { }{\mathbf{g }_{i}}(d,{{\mu }_{{{z}_{~}}}})\ge 0,\text { }i=1,2 \\&{\mathbf{g }_{1}}=\mathbf{z} _{1}^{1}-\left( \left( \frac{600}{{{d}_{1}}{{d}_{2}}^{2}} \right) \times \mathbf{z }_{2}^{1}+\left( \frac{600}{{{d}_{1}}^{2}{{d}_{2}}} \right) \times \mathbf{z }_{3}^{1} \right) \\&{\mathbf{g }_{2}}={{D}_{0}}-\left( \frac{4{{L}^{3}}}{\mathbf{z }_{4}^{2}{{d}_{1}}{{d}_{2}}} \right) \times \sqrt{{{\left( \frac{\mathbf{z }_{2}^{2}}{{{d}_{2}}^{2}} \right) }^{2}}+{{\left( \frac{\mathbf{z }_{3}^{2}}{{{d}_{1}}^{2}} \right) }^{2}}} \\&0\le {{d}_{1}},{{d}_{2}}\le 5. \\ \end{aligned}\ . \end{aligned}$$

(19)

Fig. 6

Illustration of the RDS for the cantilever beam example

4.1.2 Results and discussion

The problem has been solved in the literature using different methods [15, 16, 65,66,67], and the optimal results of the proposed method and the compared ones are given in Table 3. From this table, it is observed that the RDS–AMDE-NM can reach the lower value of the objective function of $f({{y^*}}) = 9.520247$ with ${y^*} = \left\{ {2.445990~\mathrm{mm}, 3.892184~\mathrm{mm}} \right\}$. The RDS and SLA methods obtained the same value of the objective for this problem. The results given by both IRA-DE and PSO-4M-3M-2M are very competitive compared with those of DLA, SLDM, and Mean anchor.

Moreover, Table 4 represents the statistical results of the proposed method for 50 independent runs. It is clear from the table that RDS–AMDE-NM approach is very stable in solving this problem through achieving a small standard deviation of 8.48E–15. Moreover, the RDS–AMDE-NM needs few iterations to reach the best optimal solution ($\hbox {FEs} = 15,000$).

Table 2 Random parameters of the cantilever beam problem

Table 3 Comparison of RBDO results for the cantilever beam problem

Table 4 Statistical results of the RDS–AMDE-NM for the cantilever beam problem

4.2 Vehicle side impact

This mechanical problem has been modeled for the first time by Gu et al.[68] using the finite-element analysis (as shown in Fig. 7). The objective is to minimize the total vehicle weight, while the probabilistic constraints are related to deflections, velocities at different vehicles, and dummy locations. The problem has seven continuous random design variables and four random parameters, as presented in Table 5. All the random quantities follow the normal distribution and are statistically independent. The RBDO problem of the vehicle side impact is expressed as follows:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;\left\{ {{\mu _{x1}},{\mu _{x2}},{\mu _{x3}},{\mu _{x4}},{\mu _{x5}},{\mu _{x6}},{\mu _{x7}}} \right\} \\ \min {\mathrm{: }}\;f\left( {{\mu _x}} \right) = 1.98 + 4.90{\mu _{x1}} + 6.67{\mu _{x2}} + 6.98{\mu _{x3}} + 4.01{\mu _{x4}} + 1.78{\mu _{x5}} + 2.73{\mu _{x7}}\\ {\mathrm{s}}{\mathrm{.t}}{\mathrm{.: }}\;{\mathop {\mathrm{Prob}}\nolimits } .({g_i}(x,p) \ge 0) \ge {R_i}^t,{\mathrm{}}~~~~~~i = 1,...,10,\\ {g_1} = 1 - {F_\mathrm{AL}}\\ {g_2} = 32 - {D_\mathrm{up}}\\ {g_3} = 32 - {D_\mathrm{mid}}\\ {g_4} = 32 - {D_\mathrm{law}}\\ {g_5} = 0.32 - V{C_\mathrm{up}}\\ {g_6} = 0.32 - V{C_\mathrm{mid}}\\ {g_7} = 0.32 - V{C_\mathrm{law}}\\ {g_8} = 4 - {F_\mathrm{ps}}\\ {g_9} = 9.9 - {V_{B - \mathrm{Pillar}}}\\ {g_{10}} = 15.69 - {V_{\mathrm{door}}}\\ {\mu _{xj}}^{\mathbf{L }} \le {\mu _{xj}} \le {\mu _{xj}}^{\mathbf{U }}{\mathrm{, }}~~~~~~j = 1,...,7\\ {R_i}^t = \varPhi \;\left( 3 \right) = 99.87\% . \end{array} \end{aligned}$$

(20)

For more details, the mathematical forms of the probabilistic constraints are provided in Appendix 8.1.

Table 6 displays the best optimal values of the objective and the design variables for the vehicle side impact problem using different approaches [1, 14,15,16, 69]. Table 6 shows obviously that RDS–AMDE-NM, RDS, and RBDO-dBA methods are the most effective in solving the problem by reaching the best fitness value $f(y^*)= 28.5526$. The SLDM with the value of 28.596 is slightly better than DLA and SLA with values of 28.6528 and 28.6977, respectively. The statistical values of the proposed approach and the RBDO-dBA developed by Chakri et al. [69] are presented in Table 7.

Table 7 indicates clearly the robustness of the RDS–AMDE-NM compared with the RBDO-dBA through the small standard deviation of 9.00E–13. Moreover, the best, mean, and the worst solutions provided by the proposed approach RDS–AMDE-NM are better than those obtained with the RBDO-dBA. As mentioned in the same table, the RDS–AMDE-NM reaches the best value with the lowest FEs, which is about 65% smaller.

Fig. 7

Vehicle side impact design problem [70]

Table 5 Random design variables and random parameters of the vehicle side impact problem

Table 6 Comparison of RBDO results for the vehicle side impact problem

Table 7 Statistical results for the vehicle side impact problem

4.3 Speed reducer

The probabilistic optimization formulation of the speed reducer problem has been proposed in [71]. The problem, as described schematically in Fig. 8, contains seven continuous design variables. The teeth module $d_1$ and the number of pinion teeth $d_2$ are deterministic. The random design variables are: face width $x_1$, lengths of the shafts ($x_2$, $x_3$), and diameters of the shafts $x_4$ and $x_5$. There are also fifteen random parameters including the material properties, rotation speed, and engine power. The design problem is subjected to ten probabilistic constraints as well as one deterministic constraint. Therefore, to minimize the system weight, the probabilistic optimization problem can be formulated as follows:

$$\begin{aligned} \begin{array}{l} \mathrm{find}\;{\mathrm{}}\left\{ {{d_1},{d_2},{\mu _{x1}},{\mu _{x2}},{\mu _{x3}},{\mu _{x4}},{\mu _{x5}}} \right\} \\ \min :\;{\mathrm{}}f\left( {d,{\mu _x}} \right) = 0.7854{\mu _{x1}}{d_1}^2\left( {3.3333{d_2}^2 + 14.9334{d_2} - 43.0934} \right) - \\ 1.5079{\mu _{x1}}\left( {{\mu _{x4}}^2 + {\mu _{x5}}^2} \right) + 7.477\left( {{\mu _{x4}}^3 + {\mu _{x5}}^3} \right) {\mathrm{}} + 0.7854\left( {{\mu _{x2}}{\mu _{x4}}^2 + {\mu _{x3}}{\mu _{x5}}^2} \right) \\ \mathrm {s.t.}:\left\{ \begin{array}{l} {\mathop {\mathrm{Prob}}\nolimits } .\;\left( {{g_i}\left( {d,x,p} \right) \ge 0} \right) \ge {R_i}^t,{\mathrm{}}~~~~~~i = 1,...,10.\\ {g_{11}}(d) \ge 0, \end{array} \right. \\ {d_q}^\mathbf{{L}} \le {d_q} \le {d_q}^\mathbf{{U}},{\mathrm{}}~~~q = 1,2\\ {\mu _{xj}}^\mathbf{{L}} \le {\mu _{xj}} \le {\mu _{xj}}^\mathbf{{U}},{\mathrm{}}j = 1,...,5\\ {R_i}^t = \varPhi \;\left( {1.644} \right) = 95\% {\mathrm{}}. \end{array}\ . \end{aligned}$$

(21)

The mathematical formulas of the constraints are presented in Appendix 8.2. All the random design variables and random parameters are statistically independent with the normal distribution (Table 8).

The best optimal results of the RDS–AMDE-NM are compared with those of the RBDO-dBA [69], Enhanced SORA and DLA [71]. The comparison results are detailed in Table 9. The results show that the RDS–AMDE-NM can provide new optimal solution for the speed reducer problem, where $f(y^*)= 2856.3662$. The RBDO-dBA with best solution of 2856.547 is better than Enhanced SORA and DLA with values of 2857.25 and 2878.97, respectively.

The statistical results of the proposed approach RDS–AMDE-NM and the RBDO-dBA are collected in Table 10. The obtained results clearly show that RDS–AMDE-NM is better than RBDO-dBA in solving this problem based on the lowest values for the mean (2856.36622), the worst (2856.36622) as well as the standard deviation (9.79E–08). Moreover, the RDS–AMDE-NM can reach the best point with the lowest FEs, which is about 50% smaller.

Fig. 8

Speed reducer design problem

Table 8 Characteristics of the speed reducer problem

Table 9 Comparison of RBDO results for the speed reducer problem

Table 10 Statistical results for the speed reducer problem

4.4 Welded beam

The welded beam structure [72] (Fig. 9) must be designed for the minimum cost using four design variables: welding depth $x_1$, welding length $x_2$, beam height $x_3$, and beam thickness $x_4$. This problem involves seven parameters and five constraints associated with the geometry, the maximum permissible stress, and the tip deflection. The RBDO formulation of this example has been extensively studied in the literature [73,74,75] considering that all random design variables are continuous with the normal distribution, and the parameters are all deterministic.

In the present study, we have decided to use the modified formulation proposed by [69] where all the random design variables are considered to be discrete; all the parameters are assumed to be random; and mixed types of distribution functions are used. The modified RBDO problem of the welded beam is given by the following equation:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;{\mathrm{}}\left\{ {{\mu _{x1}},{\mu _{x2}},{\mu _{x3}},{\mu _{x4}}} \right\} \\ {\mathrm{min:\; }}f\left( {{\mu _x},{\mu _p}} \right) = {c_1}\mu _{x1}^2{\mu _{x2}} + {c_2}{\mu _{x3}}{\mu _{x4}}\left( {{\mu _{p2}} + {\mu _{x2}}} \right) \\ \mathrm{s.t.}:{~}{\mathop {\mathrm{Prob}}\nolimits } .\;\left( {{g_i}\left( {x,p} \right) \ge 0} \right) \ge {R_i}^t,{\mathrm{}}i = 1,...,5\\ {\mu _{x1}}\left( {\hbox {mm}} \right) \in \left\{ {3,4,5,....,50} \right\} \\ {\mu _{x2}},{\mu _{x3}}\left( {\hbox {mm}} \right) \in \left\{ {1,2,3,....,254} \right\} \\ {\mu _{x4}}\left( {\hbox {mm}} \right) \in \left\{ {2,3,4,5,6,7,8,10,12,14,15,16,18,20,22,25} \right\} \\ {\sigma _{x1}},\;{\sigma _{x2}} = 0.1693,{\mathrm{}}{\sigma _{x3}},\;{\sigma _{x4}} = 0.0107\\ {R_i}^t = \varPhi \;\left( 3 \right) = 99.87\% .{\mathrm{}} \end{array}\ . \end{aligned}$$

(22)

The mathematical formulas of the probabilistic constraints, for the welded beam problem, are presented in Appendix 8.3. The statistical characteristics of the system parameters are taken from [76] and listed in Table 11.

The best optimal values of the objective as well as the design variables provided by RDS–AMDE-NM and RBDO-dBA methods are presented in Table 12. It can be observed from this table that the proposed approach RDS–AMDE-NM achieves new best optimal solution for the welded beam problem, considering the case of discrete variables. Where the objective function value is $f(y^*)= 2.96502$ for $y^*= \{6.00, 210.00, 219.00, 7.00\}$.

Form the statistical results given in Table 13, the approach proposed in this study outperforms the RBDO-dBA, regarding the values of the best, the mean, and the worst solutions. In addition, the proposed approach is more robust in solving this problem with lowest value of the standard deviation of 4.54E–10. From the same table, it can be noticed that the introduced approach is capable to provide the optimized results in lesser FEs (reduction of 64%). This confirms that the proposed RDS–AMDE-NM converges faster than RBDO-dBA.

Fig. 9

Welded beam design problem

Table 11 Random parameters of the welded beam problem

Table 12 Comparison of RBDO results for the welded beam problem

Table 13 Statistical results for the welded beam problem

4.5 Multiple-disc clutch brake

The objective of this problem is to minimize the weight of the multiple-disc clutch brake, as shown in Fig. 10, while observing eight design constraints. The optimization problem has been expressed in the deterministic form by Osyczka [77] and is modified here to be a RBDO problem.

Regarding the RBDO formulation, there are five discrete design variables consisting of four random ones: the inner and the outer radiuses ($x_1, x_2$), the thickness of discs $x_3$, and the actuating force $x_4$. The deterministic variable is the number of friction surfaces $d_1$. The first three variables are assumed to follow the normal distribution with a covariant of 0.05, while the actuating force variable $x_4$ follows the log-normal distribution with a covariant of 0.10. There are also nine normally distributed random parameters and their statistical data are described in Table 14. All the random variables and random parameters are supposed to be independent. Thus, the RBDO formulation can be expressed as follows:

$$\begin{aligned} \begin{array}{l} {\mathrm{find}}\;{\mathrm{}}\left\{ {{d_1},{\mu _{x1}},{\mu _{x2}},{\mu _{x3}},{\mu _{x4}}} \right\} \\ {\mathrm{min:}}\;{\mathrm{}}f\left( {d,{\mu _x}} \right) = \pi c{\mu _{x3}}\left( {{\mu _x}_2^2 - {\mu _x}_1^2} \right) \times \left( {{d_1} + 1} \right) \\ {\mathrm{s}}{\mathrm{.t}}{\mathrm{.: }}~{\mathop {\mathrm{Prob}}\nolimits } .\;\left( {{g_i}\left( {d,x,p} \right) \ge 0} \right) \ge {R_i}^t,{\mathrm{}}~~i = 1,...,8\\ {d_1} \in \;\left\{ {2,{\mathrm{}}3,{\mathrm{}}4,{\mathrm{}}5,{\mathrm{}}6,{\mathrm{}}7,{\mathrm{}}8,{\mathrm{}}9} \right\} \\ {\mu _{x1}} \in \;\left\{ {60,{\mathrm{}}61,{\mathrm{}}62, \ldots ,80} \right\} \\ {\mu _{x2}} \in \;\left\{ {90,{\mathrm{}}91,92, \ldots ,110} \right\} \\ {\mu _{x3}} \in \;\;\left\{ {1,{\mathrm{}}1.5,{\mathrm{}}2,{\mathrm{}}2.5,{\mathrm{}}3} \right\} \\ \;{\mu _{x4}} \in \;\left\{ {600,{\mathrm{}}610,{\mathrm{}}620, \ldots ,{\mathrm{}}1000} \right\} \\ {R_i}^t = \varPhi \;\left( 3 \right) = 99.87 \%{\mathrm{}} \end{array}\ . \end{aligned}$$

(23)

The mathematical formulation of the probabilistic constraints is detailed in Appendix 8.4.

Fig. 10

Multiple-disc clutch brake design problem

To confirm the results of proposed approach for the multiple-disc clutch brake and the presser vessel RBDO problems, five additional algorithms are used: the artificial bee colony (ABC) [78], the bat algorithm (BA) [79], the particle swarm optimization (PSO) [80], the krill herd (KH) algorithm[81], and the interior search algorithm (ISA) [82]. It is worth mentioning that the used algorithms are also coupled with the RDS strategy. Concerning the specific parameters of each implemented algorithm, we keep the similar values suggested by the original authors for the two problems. For the statistical comparison, we run each algorithm 50 times.

The optimal results for the multiple-disc problem achieved by the used algorithms are given in Table 15. Table 16 details the simulated results regarding the values of the best, the mean, the worst, and the standard deviation. According to Table 15, all investigated algorithms are able to find the feasible optimal global solution, which is $f(y^*)= 0.73562276$. For the statistical analysis, Table 16 clearly shows that AMDE-NM outperforms the other implemented algorithms in terms of the mean and the worst values. Moreover, by achieving the smallest standard deviation of 7.85E–16, the AMDE-NM is the most robust to solve this problem. The mean and the worst solutions given by ABC algorithm are better than the other compared algorithms.

Figure 11 illustrates the convergence plots of the algorithms to the best results. It shows clearly that AMDE-NM can converge fast, compared to the other meta-heuristics, and took only ten iterations to find the best results. PSO and KH can reach the optimal solution at the 19th and 26th iterations, respectively. ISA and BA obtained the best solution almost in the same iteration, while ABC converges to the final value after 96 iterations.

Fig. 11

Convergence graphs for the multiple-disc clutch brake RBDO problem

The optimal solution obtained by RDS–AMDE-NM is employed to test the reliability of the constraint satisfaction for this example. Table 17 presents the constraint values in the reliable design space, the reliability index, and the failure probability of the eight constraints. The probabilistic constraints are estimated here by FORM approximation and Monte Carlo simulation using the Phimeca software. The Monte Carlo simulation is regarded as reference method with 106 samples. As it can be observed from Table 17, the calculated reliability of each constraint satisfies the imposed level, which valids the solution obtained by developed approach for this RBDO problem. For the fifth and seventh constraints, the symbol $\infty$ indicates that the reliability index has a high value, meaning that the corresponding probability of failure is very low (Fig. 12).

Table 14 Random parameters of the multiple-disc clutch brake problem

Table 15 Best simulated results obtained by the algorithms for the multiple-disc clutch brake RBDO problem

Table 16 Statistical results for the multiple-disc clutch brake RBDO problem

Table 17 Constraint value and estimated reliability of the probabilistic constraints for the multiple-disc clutch brake problem

Fig. 12

Cylindrical pressure vessel design problem

4.6 Pressure vessel

For the cylindrical pressure vessel structure presented in Fig. 13, the objective is to optimize the total fabrication cost using four mixed design variables. The thickness of the cylindrical shell $x_1$ and the thickness of the spherical head $x_2$ are discrete in multiples of 0.0625, while the inner radius $x_3$ and the length of the cylindrical segment of the vessel $x_4$ are continuous. The original design formulation was given by [83] in the deterministic term and then became widely used in the engineering field as a real-world mixed test problem. In the present work, the probabilistic optimization formulation is investigated to test the effectiveness of the proposed approach in case of mixed design variables. We assume that the four variables are random with the normal distribution and a covariant of 0.05. The RBDO problem is given as follows:

$$\begin{aligned} \begin{array}{l} {\mathrm{find}}\;{\mathrm{}}\left\{ {{\mu _{x1}},{\mu _{x2}},{\mu _{x3}},{\mu _{x4}}} \right\} \\ {\mathrm{min:\;}}f\left( {{\mu _x}} \right) = 0.6224{\mu _{x1}}{\mu _{x3}}{\mu _{x4}} + 1.7781{\mu _{x2}}{\mu _{x3}}^2 + 3.1661{\mu _{x1}}^2{\mu _{x4}} + 19.84{\mu _{x1}}^2{\mu _{x3}}\\ {\mathrm{s}}{\mathrm{.t.: }}~{\mathop {\mathrm{Prob}}\nolimits } .\;\left( {{g_i}\left( x \right) \ge 0} \right) \ge {R_i}^t,{\mathrm{}}~~i = 1,...,4\\ {g_1} = {x_1} - 0.0193{x_3}{\mathrm{}}\\ {g_2} = {x_2} - 0.00954{x_3}\\ {g_3} = \pi {x_3}^2{x_4} + \frac{{\left( {4\pi {x_3}^3} \right) }}{3} - 1296000{\mathrm{}}\\ {g_4} = 240 - {x_4}{\mathrm{}}\\ 0.0625 \le {\mu _{x1}},{\mu _{x2}} \le 6.1875,{\mathrm{}}10 \le {\mu _{x3}},{\mu _{x4}} \le 200{\mathrm{}}\\ {R_i}^t = \varPhi \;\left( {1.645} \right) = 95 \%.{\mathrm{}} \end{array} \end{aligned}$$

(24)

Tables 18 and 19 display the simulated results for the pressure vessel RBDO problem. Table 18 demonstrates clearly that only AMDE-NM, PSO, and ISA are able to get the optimal value of $f(y^*)= 8418.6674$ with ${y^*}$ = $\{$1.00 in, 0.500 in, 46.1087 in, 176.1772 in $\}$. From the statistical analysis listed in Table 19, the proposed AMDE-NM algorithm confirms that is very effective to solve this problem, comparing to the used algorithms, with lowest values of the mean, the worst, as well as the standard deviation of 6.17E–12. Both ABC and KH converge only to the near global solution. However, BA is the worst in dealing with this example with highest values of the best (12585.53), the mean (28556.45), and the worst (67892.85).

As shown in Fig.13, PSO algorithm is relatively faster than the compared algorithms to find the best fabrication cost of the presser vessel structure. The reliability analysis corresponding to the optimal solution obtained by RDS–AMDE-NM is also given in Table 20. According to this table, the desired reliability is checked for all constraint. The first and third constraints presented in bold are actives, which have the same level of required reliability.

Fig. 13

Convergence graphs for the pressure vessel RBDO problem

Table 18 Best simulated results obtained by the algorithms for the pressure vessel RBDO problem

Table 19 Statistical results for the pressure vessel RBDO problem

Table 20 Constraint value and estimated reliability of the probabilistic constraints for the pressure vessel problem

5 Industry case study

A cylindrical spur gear in a large transport machine is taken as a case study. This structure was investigated in [33, 84] in the deterministic optimization level. The problem is formulated for two objectives, regarding the maximum bending stresses and the specific sliding coefficients. The bending stress is modeled explicitly using FEA [85, 86]. In addition, several constraints related to the system performance are considered. The optimization problem is developed for three mixed design variables including two continuous (the profile shift coefficient $x_1$ and the radius of root curvature $\rho _f$ and one discrete (the pressure angle $\alpha _n$).

In this study, the RBDO for this structure is considered to explore the applicability of the proposed approach in real engineering problems. It is assumed that all the random design variables and parameters are independent with the normal distribution. According to the statistical description proposed by Zhang et al. [87], the profile shift coefficients ($x_1$, $x_2$) have a covariant of 0.033, and the radius of root curvature $\rho _f$, the pressure angle $\alpha _n$, and the normal module $m_n$ have a covariant of 0.005, while the teeth number of the pinion and the wheel $z_1$, $z_2$ are treated as deterministic. The flowchart in Fig. 14 displays the developed RBDO procedure for the problem. The mathematical RBDO model of the cylindrical spur gear is formulated as follows:

$$\begin{aligned} \ \begin{array}{l} {\mathrm{find}}\;\left\{ {{\mu _{x1}},{\mu _{\rho f}},{\mu _{\alpha n}}} \right\} \\ {\mathrm{min: }}f = {\omega _1} \times {\sigma _{F1}} + {\omega _2} \times {\gamma _{\max 1}}\\ {\mathrm{s}}{\mathrm{.t}}{\mathrm{.}}:{\mathrm{}}\left\{ \begin{array}{l} {\mathop {\mathrm{Prob}}\nolimits } .\;\left( {{g_i} \ge 0} \right) \ge {R_i}^t,{\mathrm{}}i = 1,...,5\\ {g_q} \ge 0,{\mathrm{}}q = 6,7 \end{array} \right. \\ {g_1} = {\varepsilon _\alpha } - 1.4\\ {g_2} = {s_{a1}} - 0.4{m_n}\\ {g_3} = {s_{a2}} - 0.4{m_n}\\ {g_4} = \sqrt{{r_{b2}}^2 + {{\left( {a'\sin {{\alpha '}_n}} \right) }^2}} - \frac{{{m_n}({z_2} + 2 + 2{x_2})}}{2}\\ {g_5} = \sqrt{{r_{b1}}^2 + {{\left( {a'\sin {{\alpha '}_n}} \right) }^2}} - \frac{{{m_n}({z_1} + 2 + 2{x_1})}}{2}\\ {g_6} = {10^{ - 3}} - \left| {{\sigma _{F1}} - {\sigma _{F2}}} \right| \\ {g_7} = {10^{ - 6}} - \left| {{\gamma _{\max 1}} - {\gamma _{\max 2}}} \right| \\ - 0.5 \le {\mu _{x1}} \le 0.8,{\mathrm{}}6 \le {\mu _{\rho f}} \le 8.3,{\mathrm{}}{\mu _{\alpha n}} \in \left\{ {18,{\mathrm{}}19,{\mathrm{}}20,{\mathrm{}}21,{\mathrm{}}22} \right\} \\ {R_i}^t = \varPhi \;\left( 3 \right) = 99.87\%, \end{array}\ \end{aligned}$$

(25)

where $\sigma _{F1}$ and $\sigma _{F2}$ are the maximum bending stresses, and $\gamma _{\max 1}$ and $\gamma _{\max 2}$ are the maximum specific sliding coefficients for the pinion and the wheel, respectively. $\epsilon _\alpha$ is the transverse contact ratio, $a^{'}$ is the distance of the working center, and $\alpha _n^{'}$ is pressure angle at the pitch cylinder.

Note that the last two constraints are considered to be deterministic. To provide equally strong teeth on the pinion and the wheel, their maximum bending stresses should be balanced (constraint $g_6$). Moreover, to maximize the wear resistance of the gear pair, the maximum specific sliding coefficients should be equalized at extremes of contact path (as given by the constraint $g_7$). For more details about the design problem, please refer to [33, 84].

Fig. 14

Flowchart of the RBDO procedure for the cylindrical spur gear

5.1 Simulation results

For solving this multi-objective RBDO problem, the weighted sum method is applied where the weighting factors for the objectives are chosen as: $\omega _1 = 0.9$, $\omega _2 = 0.1$, for this case study $NP= 20$ and $t_{\max } = 2500$. The best results for the cylindrical spur gear RBDO problem, after 50 runs, are given in Table 21. Results show that the proposed RDS–AMDE-NM reach the optimal solution for all runs, and provide the objective functions values of $f_1(y^*)= 692.3603$ and $f_2(y^*)= 0.9250$, with ${y^*} = \left\{ {0.382792,7.769226~\mathrm{mm},22.00^\circ } \right\}$.

Accordingly, the achieved results can provide a perfect balancing in the tooth root stresses ($\sigma _{F1}= 692.3603$ MPa, and $\sigma _{F2}= 692.3604$ MPa) and the maximum specific sliding coefficients ($\gamma _{\max 2}= \gamma _{\max 1}= 0.9250$), so that the service life of the system is significantly extended. In addition, the probabilistic constraints at the optimal solution are evaluated using Monte Carlo simulation. The results summarized in Table 22 show that the required reliability of each constraint is checked $({P_f} = \varPhi (-3)\approx 0.0013)$. This effectively demonstrates that the proposed approach is capable to solve this real RBDO problem.

Table 21 RBDO results of the cylindrical spur gear problem

Table 22 Constraint values and estimated reliability of the probabilistic constraints for the cylindrical spur gear problem

6 Conclusions

This paper presents a new solution approach, named as RDS–AMDE-NM, for mechanical RBDO problems. According to this approach, the RDS technique is used to reformulate the RBDO problem by an SDO one. After that, the optimal solution is carried out using the hybrid AMDE-NM algorithm. The MADE-NM algorithm is an efficient optimization tool using AMDE for the high exploration capability, based on the self-adaptive mechanism, and employing NM technique for the intensifying local search. In addition, the static exterior penalty method is employed in the AMDE-NM to handle the constraints and the index technique is utilized to deal with the discrete design variables.

The performance of the RDS–AMDE-NM has been confirmed by providing six mechanical RBDO problems, comprising three examples with continuous variables, two examples with discrete variables, and one with mixed variables. Commonly, the simulation results clearly demonstrated that the proposed approach performs very well in terms of efficiency and robustness. Particularly, the first two examples verified that RDS–AMDE-NM is effective for both weakly and highly dimensional RBDO problems, respectively.

By solving the speed reducer design problem, the proposed approach showed a high capability to handle a mixture of probabilistic and deterministic constraints, both random and deterministic design variables, as well as with varying variance. The last three examples demonstrated that RDS–AMDE-NM is competent for the discrete and the mixed RBDO problems. Moreover, RDS–AMDE-NM has been used to solve the RBDO problem of a real spur gear pair. The obtained results of the studied case demonstrated the efficacy and accuracy of the new method in solving mechanical problems with computational complexities. This confirmed that the RDS–AMDE-NM is a promising RBDO approach to deal with real industrial cases.

The RBDO for the multiple-disc clutch brake and pressure vessel structures have been formulated in this study for first time. For the both problems, the validity of the new obtained solutions has been checked by FORM and MCS. This will allow to use these examples as benchmarks in RBDO studies in the future.

As future research directions, it is important to notice that the presented approach has only been applied to structures with explicit behavior and the random quantities treated have only been assumed to follow Gaussian distributions. Therefore, it seems promising to extend the RDS–AMDE-NM to deal with real implicit structures involving finite-element and CAD models. In addition, the integration of RDS–AMDE-NM into probabilistic transformation methods for handling random variables with non-Gaussian distributions is also suggested to be further investigated.

Appendices

Appendix

The partial derivatives of the first function ${g_1}\left( {d,{\mu _z}}\right)$ with respect to the mean vector:

$$\begin{aligned} \frac{\partial {{g}_{1}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z1}}}= & {} 1,\frac{\partial {{g}_{1}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z2}}}=-\frac{600}{{{d}_{1}}{{d}_{2}}^{2}},\frac{\partial {{g}_{1}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z3}}}\\= & {} -\frac{600}{{{d}_{1}}^{2}{{d}_{2}}},\frac{\partial {{g}_{1}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z4}}}=0. \end{aligned}$$

The partial derivatives of the second function ${g_2}\left( {d,{\mu _z}}\right)$ with respect to the mean vector:

$$\begin{aligned} \begin{aligned}&\frac{\partial {{g}_{2}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z1}}}=0,\frac{\partial {{g}_{2}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z2}}}\\&\quad =-\frac{4{{L}^{3}}{{\mu }_{z2}}}{{{\mu }_{z4}}{{d}_{1}}{{d}_{2}}^{5}\sqrt{{{\left( \frac{{{\mu }_{z2}}}{{{d}_{2}}^{2}} \right) }^{2}}+{{\left( \frac{{{\mu }_{z3}}}{{{d}_{1}}^{2}} \right) }^{2}}}}, \\&\frac{\partial {{g}_{2}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z3}}}=-\frac{4{{L}^{3}}{{\mu }_{z3}}}{{{\mu }_{z4}}{{d}_{1}}^{5}{{d}_{2}}\sqrt{{{\left( \frac{{{\mu }_{z2}}}{{{d}_{2}}^{2}} \right) }^{2}}+{{\left( \frac{{{\mu }_{z3}}}{{{d}_{1}}^{2}} \right) }^{2}}}}, \\&\frac{\partial {{g}_{2}}(d,~{{\mu }_{{{z}_{~}}}})}{\partial ~{{\mu }_{z4}}}=\frac{4{{L}^{3}}}{{{\left( {{\mu }_{z4}} \right) }^{2}}{{d}_{1}}{{d}_{2}}}\sqrt{{{\left( \frac{{{\mu }_{z2}}}{{{d}_{2}}^{2}} \right) }^{2}}+{{\left( \frac{{{\mu }_{z3}}}{{{d}_{1}}^{2}} \right) }^{2}}}. \\ \end{aligned} \end{aligned}$$

Appendix

1.1 Vehicle side impact problem

Mathematical formulation of the probabilistic constraints of the vehicle side impact problem:

$$\begin{aligned} \begin{aligned} {{F}_{AL}}&=1.16-0.3717{{x}_{2}}{{x}_{4}}-0.00931{{x}_{2}}{{p}_{3}}\\&\quad -0.484{{x}_{3}}{{p}_{2}}+0.01343{{x}_{6}}{{p}_{4}} \\ {{D}_\mathrm{up}}&=28.98+3.818{{x}_{3}}-4.2{{x}_{1}}{{x}_{2}}+0.0207{{x}_{5}}{{p}_{3}}\\&\quad +6.63{{x}_{6}}{{p}_{2}}-7.7{{x}_{7}}{{p}_{1}}+0.32{{p}_{2}}{{p}_{3}} \\ {{D}_\mathrm{mid}}&=33.86+2.95{{x}_{3}}+0.1792{{p}_{3}}-5.057{{x}_{1}}{{x}_{2}}\\&\quad -11.0{{x}_{2}}{{p}_{1}}-0.0215{{x}_{5}}{{p}_{3}}\\&\quad -9.98{{x}_{7}}{{p}_{1}}+22.0{{p}_{1}}{{p}_{2}} \\ {{D}_\mathrm{law}}&=46.36-9.9{{x}_{2}}-12.9{{x}_{1}}{{p}_{1}}\\&\quad +0.1107{{x}_{3}}{{p}_{3}} \\ V{{C}_\mathrm{up}}&=0.261-0.0159{{x}_{1}}{{x}_{2}}-0.188{{x}_{1}}{{p}_{1}}-0.019{{x}_{2}}{{x}_{7}}\\&\quad +0.0144{{x}_{3}}{{x}_{5}}+0.0008757{{x}_{5}}{{p}_{3}}+0.08045{{x}_{6}}{{p}_{2}} \\&\quad + 0.00139{{p}_{1}}{{p}_{4}}+0.00001575{{p}_{3}}{{p}_{4}} \\ V{{C}_\mathrm{mid}}&=0.214+0.00817{{x}_{5}}-0.131{{x}_{1}}{{p}_{1}}\\&\quad -0.0704{{x}_{1}}{{p}_{2}}+0.03099{{x}_{2}}{{x}_{6}}\\&\quad -0.018{{x}_{2}}{{x}_{7}}+0.0208{{x}_{3}}{{p}_{1}}+0.121{{x}_{3}}{{p}_{2}} \\&\quad - 0.00364{{x}_{5}}{{x}_{6}}+0.0007715{{x}_{5}}{{p}_{3}}\\&\quad -0.0005354{{x}_{6}}{{p}_{3}}+0.00121{{p}_{1}}{{p}_{4}} \\ V{{C}_\mathrm{law}}&=0.74-0.61{{x}_{2}}-0.163{{x}_{3}}{{p}_{1}}\\&\quad +0.001232{{x}_{3}}{{p}_{3}}-0.166{{x}_{7}}{{p}_{2}}+0.227{{x}_{2}}^{2} \\ {{F}_\mathrm{ps}}&=4.72-0.5{{x}_{4}}-0.19{{x}_{2}}{{x}_{3}}-0.0122{{x}_{4}}{{p}_{3}}\\&\quad +0.009325{{x}_{6}}{{p}_{3}}+0.000191{{p}_{4}}^{2} \\ V{{C}_\mathrm{B-Pillar}}&=10.58-0.674{{x}_{1}}{{x}_{2}}-1.95{{x}_{2}}{{p}_{1}}\\&\quad +0.02054{{x}_{3}}{{p}_{3}}-0.0198{{x}_{4}}{{p}_{3}}+0.028{{x}_{6}}{{p}_{3}} \\ V{{C}_\mathrm{door}}&=16.45-0.489{{x}_{3}}{{x}_{7}}-0.843{{x}_{5}}{{x}_{6}}\\&\quad +0.0432{{p}_{2}}{{p}_{3}}-0.0556{{p}_{2}}{{p}_{4}}-0.000786{{p}_{4}}^{2}. \\ \end{aligned} \end{aligned}$$

1.2 Speed reducer problem

Mathematical formulas of the constraints of the speed reducer problem:

$$\begin{aligned} \begin{aligned}&{{g}_{1}}=1-\frac{{{p}_{1}}}{{{x}_{1}}{{d}_{1}}^{2}{{d}_{2}}},\text { }{{g}_{2}}=1-\frac{{{p}_{2}}}{{{x}_{1}}{{d}_{1}}^{2}{{d}_{2}}^{2}},\\&{{g}_{3}}=1-\frac{{{p}_{3}}x_{2}^{3}}{x_{4}^{4}{{d}_{1}}{{d}_{2}}},\text { }{{g}_{4}}=1-\frac{{{p}_{4}}x_{3}^{3}}{x_{5}^{4}{{d}_{1}}{{d}_{2}}}, \\&{{g}_{5}}=1-\frac{0.5\sqrt{{{\left( \frac{{{p}_{6}}{{x}_{2}}}{{{d}_{1}}{{d}_{2}}} \right) }^{2}}+{{p}_{7}}}}{{{p}_{8}}{{p}_{5}}x_{4}^{3}},\text { }{{g}_{6}}=1-\frac{0.5\sqrt{{{\left( \frac{{{p}_{6}}{{x}_{3}}}{{{d}_{1}}{{d}_{2}}} \right) }^{2}}+{{p}_{9}}}}{{{p}_{8}}{{p}_{10}}x_{5}^{3}},\\&{{g}_{7}}=1-\frac{0.5{{p}_{11}}{{d}_{1}}}{{{x}_{1}}}, \\&{{g}_{8}}=1-\frac{{{x}_{1}}}{{{p}_{12}}{{d}_{1}}},\text { }{{g}_{9}}=1-\frac{0.5({{p}_{13}}{{x}_{4}}+{{p}_{15}})}{{{x}_{2}}},\text { }\\&{{g}_{10}}=1-\frac{0.5({{p}_{14}}{{x}_{5}}+{{p}_{15}})}{{{x}_{3}}},\text { }{{g}_{11}}=1-\frac{{{d}_{1}}{{d}_{2}}}{80}.\\ \end{aligned} \end{aligned}$$

1.3 Welded beam problem

Mathematical formulas of the probabilistic constraints of the welded beam problem:

$$\begin{aligned}&{{g}_{1}}=1-\frac{\tau \left( x,p \right) }{{{p}_{6}}},\text { }{{g}_{2}}=1-\frac{\sigma \left( x,p \right) }{{{p}_{7}}},\text { }{{g}_{3}}=1-\frac{{{x}_{1}}}{{{x}_{4}}},\\&{{g}_{4}}=1-\frac{\delta \left( x,p \right) }{{{p}_{5}}},\text { }{{g}_{5}}=\frac{{{P}_{c}}\left( x,p \right) }{{{p}_{1}}}-1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\tau (x,p)=\sqrt{{{\left( {{\tau }'} \right) }^{2}}+{{\left( {{\tau }''} \right) }^{2}}+2{\tau }'{\tau }''\frac{{{x}_{2}}}{2R}},{\tau }'=\frac{{{p}_{1}}}{\sqrt{2}{{x}_{1}}{{x}_{2}}},{\tau }'=\frac{{{p}_{1}}}{\sqrt{2}{{x}_{1}}{{x}_{2}}},\\&{\tau }''=\frac{MR}{J},M={{p}_{1}}\left( {{p}_{2}}+\frac{x{}_{2}}{2} \right) , \\&R=\sqrt{\frac{x_{2}^{2}+{{\left( {{x}_{1}}+{{x}_{3}} \right) }^{2}}}{4}},J=\sqrt{2}{{x}_{1}}{{x}_{2}}\left( \frac{x_{2}^{2}}{12}+\frac{{{\left( {{x}_{1}}+{{x}_{3}} \right) }^{2}}}{4} \right) ,\\&\sigma \left( x,p \right) =\frac{6{{p}_{1}}{{p}_{2}}}{x_{3}^{2}{{x}_{4}}},\delta \left( x,p \right) =\frac{4{{p}_{1}}p_{2}^{3}}{{{p}_{3}}x_{3}^{3}{{x}_{4}}}, \\&{{P}_{c}}\left( x,p \right) =\frac{4.013{{x}_{3}}x_{4}^{3}\sqrt{{{p}_{3}}{{p}_{4}}}}{6p_{2}^{2}}\left( 1-\frac{{{x}_{3}}}{4{{p}_{2}}}\sqrt{\frac{{{p}_{3}}}{{{p}_{4}}}} \right) . \\ \end{aligned} \end{aligned}$$

1.4 Multiple-disc clutch brake problem

$$\begin{aligned} \begin{aligned}&{{g}_{1}}={{x}_{2}}-{{x}_{1}}-{{p}_{1}},\text { }{{g}_{2}}={{p}_{2}}-\left( {{d}_{1}}+1 \right) \left( {{x}_{3}}+{{p}_{3}} \right) ,\\&{{g}_{3}}={{p}_{5}}-\frac{{{x}_{4}}}{\pi \left( x_{2}^{2}-x_{1}^{2} \right) },\text { }{{g}_{4}}={{p}_{4}}{{p}_{5}}-\frac{0.005{{x}_{4}}\left( x_{2}^{3}-x_{1}^{3} \right) }{54{{\left( x_{2}^{2}-x_{1}^{2} \right) }^{2}}}, \\&{{g}_{5}}={{p}_{4}}-\frac{0.005\pi \left( x_{2}^{3}-x_{1}^{3} \right) }{54\left( x_{2}^{2}-x_{1}^{2} \right) },\text { }{{g}_{6}}=15-\frac{25\pi {{p}_{7}}}{3\left( M+{{p}_{8}} \right) },\\&{{g}_{7}}=M-1.5{{p}_{9}},\text { }{{g}_{8}}=\frac{25\pi {{p}_{7}}}{3\left( M+{{p}_{8}} \right) }\text { } \\ \end{aligned}, \end{aligned}$$

where

$$\begin{aligned} M=0.002{{p}_{6}}{{x}_{4}}{{d}_{1}}\frac{x_{2}^{3}-x_{1}^{3}}{3(x_{2}^{2}-x_{1}^{2})}. \end{aligned}$$