Kriging-based optimization of functionally graded structures

Abstract

This work presents an efficient methodology for the optimum design of functionally graded structures using a Kriging-based approach. The method combines an adaptive Kriging framework with a hybrid particle swarm optimization (PSO) algorithm to improve the computational efficiency of the optimization process. In this approach, the surrogate model is used to replace the high-fidelity structural responses obtained by a NURBS-based isogeometric analysis. In addition, the impact of key factors on surrogate modelling, as the correlation function, the infill criterion used to update the surrogate model, and the constraint handling is assessed for accuracy, efficiency, and robustness. The design variables are related to the volume fraction distribution and the thickness. Displacement, fundamental frequency, buckling load, mass, and ceramic volume fraction are used as objective functions or constraints. The effectiveness and accuracy of the proposed algorithm are illustrated through a set of numerical examples. Results show a significant reduction in the computational effort over the conventional approach.

1 Introduction

Functionally graded materials (FGM) are composites made of two or more phases with a continuous and smooth variation of the proportion of each phase. FGM were initially proposed as a means of preparing thermal barrier materials through continuous changes in its composition, microstructure, and porosity (Koizumi 1997). This feature allows FGM to eliminate delamination failure and matrix cracking due to stress concentrations between layers found in conventional laminated composites.

Thus, in addition to the optimization of geometrical features (shape, size, and topology optimization), the design of functionally graded (FG) structures can also benefit from the material tailorability. In this regard, optimization techniques are often used to obtain the volume fraction distribution that best explores the properties of the constituents.

A recent study by Nikbakht et al. (2019) found that the material distribution pattern is the most common design variable. The authors also found that the stress distribution, critical buckling load, natural frequency, and weight are among the most popular objective functions. Many researchers take advantage of the simplicity of implementation and use the Power-law index as the design variable (Na and Kim 2009; Nguyen and Lee 2017; Khorsand and Tang 2018; Moita et al. 2017; Franco et al. 2018). On a side note, the Power-law function can also be used to describe features of the structure other than the material. For example, Sun et al. (2014) employed it to describe the thickness of thin-walled structures.

It is also quite frequent the use of B-splines (Taheri et al. 2014; Kim et al. 2018; Lieu et al. 2018; Lieu and Lee2019a; Lieu and Lee 2019b; Wang et al. 2019; Do et al. 2018; Ribeiro et al. 2020) and piecewise cubic interpolation (Vel and Pelletier 2006; Ashjari and Khoshravan 2014; Asgari 2016; Nguyen and Lee 2017) to describe the volume fraction distribution. Both models allow more design flexibility than simple closed-form expressions.

Due to the complex behavior of structures made of FGM, numerical methods such as finite element analysis (FEA) and isogeometric analysis (IGA) are widely used to evaluate their structural responses. IGA has been used in association with various plate theories for composite plates analysis, such as the first-order shear deformation theory (FSDT) (Praciano et al. 2019; Auad et al. 2019; Wang et al. 2019) and higher-order shear deformation theory (HSDT) (Lieu et al. 2018; Shi et al. 2018; Do et al. 2018).

To tackle the optimization problem, population-based methods (e.g., genetic algorithms (GA) and particle swarm optimization (PSO)) are a popular choice due to their efficiency and stability (Nikbakt et al. 2018), as well as their ability to solve multimodal problems. However, these methods can quickly become time-consuming due to the high number of evaluations involved in the optimum global search.

One solution is to use parallelization techniques. Several authors have explored it and reported speed gains, as well as improved algorithm performance in composite structures optimization (Omkar and Senthilnath 2011; Rocha et al. 2014; Barroso et al. 2017). However, this approach demands high-performance computers, which is not always a feasible option.

Alternatively, the use of surrogate models offers a simple and efficient way to deal with the high-cost analyses problem by predicting the structural response at a lower computational cost if compared to that of running FEA or IGA. These models are built based on a limited number of observations of the exact response, called sampling points. The most popular surrogate models include the radial basis functions (RBF), artificial neural networks (ANN), and Kriging (Liu et al. 2017).

The basic approach in surrogate-based optimization is to work on a fixed surrogate model. In this case, a large sample is needed to produce reasonable approximations. When the sample is updated (i.e., adaptive sampling) along the optimization process, we have the so-called sequential approximate optimization (SAO) approach. For the interested reader, Liu et al. (2017) present the state-of-art of adaptive sampling in support of simulation-based complex engineering design.

Perhaps the most popular SAO algorithm is the efficient global optimization (EGO) proposed by Jones et al. (1998). This algorithm is widely used in single-objective optimization and is based on the ordinary Kriging and uses the expected improvement (EI) (Mockus et al. 1978) as the infill criterion.

Kriging was developed by the mining engineer Daniel Krige and made its way into engineering design through the work of Sacks et al. (1989) when the technique was applied to the approximation of computer experiments. As for the EI, this criterion considers the contribution of both exploration and exploitation when sampling new points. A review of the use of EI-based infill criteria for a wide range of expensive optimization problems is found in Zhan and Xing (2020).

Recent efforts have been made to reduce the computational cost of designing structures made of FGM using surrogate-based optimization. Do et al. (2018) used a deep neural network (DNN) to predict the natural frequency and the buckling load of FG plates. Despite achieving accurate predictions, the DNN still demands a significant number of high-fidelity (HF) evaluations (≈ 10,000 sampling points) for training and validating the model offline. In a correlated area, a DNN framework was also employed by Wang et al. (2020) to the design of metamaterial systems. Again, a large dataset was employed (≈ 250,000 sampling points).

On the other hand, Ribeiro et al. (2020) proposed a RBF-based algorithm where the initial sample is continuously improved using the EI and a variation of it known as weighted expected improvement (WEI) (Sóbester et al. 2005). This way, less than 1/100 of the sample used by Do et al. (2018) was necessary to achieve the same level of accuracy or higher. Both works used an IGA framework with HSDT or FSDT to assess the structural responses, but only linear eigenvalue problems were discussed.

In that light, Kriging can be a valuable tool for assisting the optimization of structures made of FGM. This is because, unlike DNN or RBF, Kriging offers manifold benefits related to the uncertainty estimation of its prediction. It also provides a natural tool to better understanding on the relevance of the design variables based on its hyperparameters. Furthermore, Kriging is very flexible in terms of correlation functions and number of hyperparameters and has great potential for reducing the computational cost when compared to other optimization approaches.

In correlated areas, Kriging has been used to assist topology optimization of metamaterials. Liu et al. (2020), for example, adopted a multi-phase sampling strategy to update the surrogate model, while Zhang et al. (2020) opted for a fixed surrogate model. Although Kriging-based approaches have been extensively applied to assist engineering design optimization problems (Cheng et al. 2014; Gan and Gu 2018; Xing et al. 2020; Chunna et al. 2020), including problems regarding laminated composite structures (Zhu et al. 2012; Passos and Luersen 2017; Keshtegar et al. 2020), to the best of the authors’ knowledge, the Kriging potential has not yet been explored for optimizing plates and shells made of FGM.

Therefore, the present work proposes an accurate and efficient Kriging-based methodology for optimum design of structures made of FGM. At each iteration, the surrogate model is updated with a single point in regions of interest according to an infill criterion. The proposed method can handle exact and approximate constraints and can also deal with the combination of exact objective function and approximate constraints. To assess the responses of the FG structures, an IGA framework was employed as the high-fidelity model (HFM).

In addition to the eigenvalue problems, the case studies section also contemplates geometric nonlinearity, an aspect overlooked in previous works dealing with SAO. The objective functions and constraints are either displacement, fundamental frequency, buckling load, mass, or ceramic volume fraction. The design variables are related to the volume fraction distribution through the thickness — ranging from simple expressions such as the Power-law function to the use of B-splines — and the thickness itself. Two homogenization schemes are considered, the Voigt and the Mori-Tanaka models.

The PSO algorithm is used to solve the optimization problems, be it in the conventional optimization or within the proposed SAO algorithm. PSO can deal with multi-modality, which is a feature observed in the functions optimized by the SAO algorithm, as will be demonstrated later in the case studies section.

Taking advantage of the Kriging flexibility, two aspects of the SAO algorithm are explored in the present work: the choice of the kernel (Gaussian or Matérn 5/2) and the infill criterion (EI and WEI). The performance of these combinations is assessed in terms of accuracy, efficiency, and robustness using a number of optimization problems of FG structures available in the literature.

The remainder of this paper is organized as follows. In Section 2, the evaluation of the effective properties and the definition of the volume fraction distribution are presented. In Section 3, the structural analysis is presented. The main aspects of the optimization of FG structures are discussed in Section 4. In Section 5, the proposed SAO approach is presented. The analysis verification is presented in Section 6, while the case studies are shown in Section 7. Finally, the conclusions are presented in Section 8.

2 Functionally graded structures

In this work, the FG structures are made by the combination of ceramic/metal. This way, the FGM can benefit from the ductility and toughness of metals and the high strength and stiffness and low thermal conductivity properties of ceramics.

Due to the inhomogeneous nature of FGM, the structural analysis of these materials depends on two main aspects: the volume fraction variation through the grading direction and the homogenization technique used to evaluate the effective properties.

The volume fraction of a given constituent represents its volume divided by the volume of all constituents (V). Thus, the total volume is given by:

$$ V_{c}(z) + V_{m}(z) = 1 $$

(1)

where the subscripts m and c refer to the metal and ceramic, respectively.

In the present work, two models are considered to describe the volume fraction variation: a Power-law function and B-splines. The Power-law function (Bao and Wang 1995) is the most popular choice in optimization problems due to its simplicity and is given by:

$$ V_{c}(z) = {\Big(\frac{2z+h}{2h}\Big)}^{N} $$

(2)

where the volume fraction at the bottom (z = −h/2) is taken as 0.0 and the top (z = +h/2) as 1.0, N is a non-homogeneity factor, and h is the total thickness of the shell, as illustrated in Fig. 1.

Fig. 1

FG plate model

The ceramic volume fraction may also be described by a B-spline curve as:

$$ V_{c}(\xi) = {\sum}_{i = 1}^{l} B_{i,p}(\xi) V_{c, i}, \quad \xi \in [0, 1] $$

(3)

where l is the number of control points, p is the degree of the basis functions, ξ is the parametric coordinate, and V_c,i(ξ) is the ceramic volume fraction of the i-th control point. This type of curve provides high-order continuity, which allows a continuous and smooth variation with designs entirely different than those limited by simple mathematical functions (Wang et al. 2019).

Based on a knot vector ${\varXi } = [\xi _{1}, \xi _{2}, \dots , \xi _{l+p+1}]$ with non-decreasing and non-negative parametric values, the B-spline basis functions are defined by the recursive Cox-de Boor formula as (Piegl and Tiller 1997):

$$ \begin{aligned} &B_{i,0}(\xi) = \begin{cases} 1, \xi_{i} \leq \xi < \xi_{i+1} \\ 0, \text{otherwise} \end{cases} \\ &B_{i,p} (\xi) = \frac{\xi - \xi_{i}}{\xi_{i+p} - \xi_{i}} B_{i,p-1}(\xi) + \frac{\xi_{i+p+1} - \xi}{\xi_{i+p+1} - \xi_{i+1}} B_{i+1,p-1}(\xi) \end{aligned} $$

(4)

where p ≥ 1.

2.1 Effective material properties

To estimate the effective material properties of FGM, a variety of homogenization schemes have been proposed. Among the most popular choices are the rule of mixture (Voigt model) and the Mori-Tanaka model. The Voigt model consists in a weighted average of the properties of the constituents, where each of them contributes with its volume fraction. This way, the effective property (P) of the material at a given point can be evaluated as (Shen 2009):

$$ P = P_{m} V_{m} + P_{c} V_{c} $$

(5)

In case of composites with spherical inclusions embedded in a matrix, the Mori-Tanaka model evaluates the effective bulk modulus (K) and effective shear modulus (G) as:

$$ \begin{array}{ll} &K = K_{m} + \frac{\displaystyle V_{c}}{\displaystyle \frac{\displaystyle 1}{\displaystyle K_{c} - K_{m}} + \frac{\displaystyle V_{m}}{\displaystyle K_{m} + \frac{\displaystyle 4G_{m}}{\displaystyle 3}}} \\ &G = G_{m} + \frac{\displaystyle V_{c}}{\displaystyle \frac{\displaystyle 1}{\displaystyle G_{c} - G_{m}} + \frac{\displaystyle V_{m}}{\displaystyle G_{m} + f_{m}}} \end{array} $$

(6)

where the parameter f_m is given by:

$$ f_{m} = \frac{G_{m} (9 K_{m} + 8 G_{m})}{6 (K_{m} + 2 G_{m})} $$

(7)

After that, the effective Young’s modulus (E) and Poisson’s ratio (ν) are computed from:

$$ E = \frac{9KG}{3K + G} \qquad \nu = \frac{3K - 2G}{2(3K + G)} $$

(8)

It is important to note that the effective density (ρ) is estimated by the Voigt model even when the Mori-Tanaka model is used to estimate other elastic properties.

2.2 Governing equations

The kinematic formulation of this work is based on the FSDT, in which segments normal to the shell midsurface remain straight but not necessarily perpendicular to the midsurface after deformation. This results in the consideration of an approximate transverse shear strain. The displacements can be written in matrix form as:

$$ \begin{bmatrix} \overline{u} \\ \overline{v} \\ \overline{w} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & z \\ 0 & 1 & 0 & -z & 0 \\ 0 & 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} u \\ v \\ w \\ \theta_{x} \\ \theta_{y} \end{bmatrix} \Rightarrow \overline{\mathbf{u}} = \mathbf{Z} \mathbf{u} $$

(9)

where u, v, and w are the midsurface displacements in the x, y, and z directions; 𝜃_x and 𝜃_y are the rotations about x and y axes, respectively; and z is the distance from a point to the midsurface.

Based on the displacement field presented in (9) and on the Marguerre theory, the in-plane strains are given by:

$$ \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} = \boldsymbol{\varepsilon}^{m} + z \boldsymbol{\kappa} $$

(10)

where m refers to the membrane strains and κ corresponds to the shell curvatures. The Marguerre theory extends the nonlinear plate theory of von Kármán for shallow shells. Due to the consideration of moderately large displacements and moderate rotations, it also allows the study on the stability of plates and shallow shells, including initial imperfections (Praciano et al.2019):

$$ \begin{aligned} \begin{bmatrix} {\varepsilon_{x}^{m}} \\ {\varepsilon_{y}^{m}} \\ \gamma_{xy}^{m} \end{bmatrix} = \begin{bmatrix} u_{,x} \\ v_{,y} \\ u_{,y} + v_{,x} \\ \end{bmatrix} +& \begin{bmatrix} w_{z,x} \ z_{0,x} \\ w_{z,y} \ z_{0,y} \\ w_{,x} \ z_{0,y} + w_{,y} \ z_{0,x} \end{bmatrix} + \begin{bmatrix} \frac{1}{2} \ {w_{,x}}^{2} \\ \frac{1}{2} \ {w_{,y}}^{2} \\ w_{,x} \ w_{, y} \end{bmatrix} \end{aligned} $$

(11)

where z₀(x,y) is the initial midsurface elevation. The deformations due to the bending are given by:

$$ \begin{bmatrix} \kappa_{x} \\ \kappa_{y} \\ \kappa_{xy} \end{bmatrix} = \begin{bmatrix} \theta_{y,x} \\ -\theta_{x,y} \\ \theta_{y,y} - \theta_{x,x} \end{bmatrix} $$

(12)

and the transverse shear strains are given by:

$$ \boldsymbol{\gamma} = \begin{bmatrix} \gamma_{xz} \\ \gamma_{yz} \end{bmatrix} = \begin{bmatrix} w_{,x} + \theta_{y} \\ w_{,y} - \theta_{x} \\ \end{bmatrix} $$

(13)

Assuming an elastic behavior, the in-plane stresses can be evaluated as:

$$ \begin{bmatrix} \sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{bmatrix} = \begin{bmatrix} Q_{11} & Q_{12} & 0 \\ Q_{12} & Q_{22} & 0 \\ 0 & 0 & Q_{66} \\ \end{bmatrix} \begin{bmatrix} \varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{bmatrix} \Rightarrow \boldsymbol{\sigma} = \mathbf{Q} \boldsymbol{\varepsilon} $$

(14)

and the transverse shear stresses as:

$$ \begin{bmatrix} \tau_{xz} \\ \tau_{yz} \end{bmatrix} = \begin{bmatrix} Q_{44} & 0 \\ 0 & Q_{55} \end{bmatrix} \begin{bmatrix} \gamma_{xz} \\ \gamma_{yz} \end{bmatrix} \Rightarrow \boldsymbol{\tau} = \mathbf{Q}_{s} \boldsymbol{\gamma} $$

(15)

where the components of the constitutive matrix Q and transverse shear constitutive matrix Q_s are given by:

$$ \begin{aligned} & \mathit{Q}_{11}= \mathit{Q}_{22} = \frac{\mathit{E}}{1-\nu^{2}} \qquad \mathit{Q}_{12}=\frac{\mathit{E} \ \nu} {1-\nu^{2}} \\ & \mathit{Q}_{44} = \mathit{Q}_{55} = \mathit{Q}_{66}=\frac{\mathit{E}}{2 \ (1+\nu)} \end{aligned} $$

(16)

The internal forces and moments can be obtained integrating the stresses through the thickness. Thus, the generalized stresses $\hat {\boldsymbol {\sigma }}$ can be written in terms of the generalized strains $\hat {\boldsymbol {\varepsilon }}$ as:

$$ \begin{bmatrix} \mathbf{N} \\ \mathbf{M} \\ \mathbf{V} \end{bmatrix} = \begin{bmatrix} \mathbf{A} & \mathbf{B} & \boldsymbol{0} \\ \mathbf{B} & \mathbf{D} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \mathbf{G} \end{bmatrix} \begin{bmatrix} \boldsymbol{\varepsilon}^{m} \\ \boldsymbol{\kappa} \\ \boldsymbol{\gamma} \end{bmatrix} \Rightarrow \hat{\boldsymbol{\sigma}} = \mathbf{C} \hat{\boldsymbol{\varepsilon}} $$

(17)

where A, B, D, and G are the extensional, membrane-bending coupling, bending, and shear stiffness matrices, respectively, whose elements are given by:

$$ \begin{aligned} &[A_{ij}, B_{ij}, D_{ij}] = {\int}_{-h/2}^{h/2} Q_{ij}(z)[1, z, z^{2}] dz \\ &G_{ij} = k_{s} {\int}_{-h/2}^{h/2} Q_{s_{ij}}(z) dz \end{aligned} $$

(18)

where k_s is known as shear correction factor and is taken as 5/6. It is also interesting noting that symmetric volume fraction distributions lead to B = 0.

3 Isogeometric analysis

In this work, the structural analyses of FG plates and shells are carried out using the IGA framework. This approach was first proposed by Hughes et al. (2005) as a way to match the exact CAD geometry by non-uniform rational B-splines (NURBS) surfaces. In this framework, the CAD basis functions are also used to approximate the solution fields. This results in the exact representation of the geometry even for coarse meshes and a much simpler mesh refinement process.

3.1 NURBS surfaces

A NURBS surface is obtained by the linear combination of basis function and a matrix of control points (p):

$$ S(\xi,\eta) = \sum\limits_{i=1}^{l} \sum\limits_{j=1}^{c} R_{ij}(\xi,\eta) \mathbf{p}_{ij} $$

(19)

where η and ξ are the parametric coordinates, and R_ij are the bivariate rational basis functions expressed by:

$$ R_{ij}(\xi,\eta) = \frac{B_{i,p}(\xi) B_{j,q}(\eta) w_{ij}}{W(\xi,\eta)} $$

(20)

where p and q are the degree order of the B-splines basis functions in the ξ and η directions, respectively, and W is the bivariate weight function, given by:

$$ W(\xi,\eta) = \sum\limits_{\hat{i}=1}^{l} \sum\limits_{\hat{j}=1}^{c} B_{\hat{i},p}(\xi) B_{\hat{j},q}(\eta) w_{\hat{i}\hat{j}} $$

(21)

3.2 Strain-displacement relations

In this work, the shell geometry is described by a bivariate NURBS:

$$ x = \sum \limits_{k=1}^{n_{cp}} R_{k} x_{k}, \quad y = \sum \limits_{k=1}^{n_{cp}} R_{k} y_{k} \quad z_{0} = \sum \limits_{k=1}^{n_{cp}} R_{k} z_{0k} $$

(22)

where n_cp is the number of control points of the surface (n_cp = l × c) and R_k are the rational basis functions.

The in-plane and transverse displacements and rotations at the midsurface are approximated from the degrees of freedom at control points as:

$$ \begin{array}{l} u = \sum \limits_{k=1}^{n_{cp}} R_{k} u_{k}, \quad v = \sum \limits_{k=1}^{n_{cp}} R_{k} v_{k}, \quad w = \sum \limits_{k=1}^{n_{cp}} R_{k} w_{k} \quad \\[.5cm] \theta_{x} = \sum \limits_{k=1}^{n_{cp}} R_{k} \theta_{xk}, \quad \theta_{y} = \sum \limits_{k=1}^{n_{cp}} R_{k} \theta_{yk} \end{array} $$

(23)

In matrix format, (23) may be written as:

$$ \mathbf{u} = \mathbf{R} \mathbf{d} $$

(24)

where d is the vector of degrees of freedom, corresponding to the displacements at control points, and R is the matrix of shape functions:

$$ \mathbf{R} = \begin{bmatrix} \mathbf{R}_{1} & \mathbf{R}_{2} & \hdots & \mathbf{R}_{n_{cp}} \end{bmatrix} $$

(25)

where:

$$ \mathbf{R}_{k} = R_{k} \mathbf{I}_{5\times5} $$

(26)

and I is the identity matrix. The generalized strains are related to the degrees of freedom as:

$$ \hat{\boldsymbol{\varepsilon}} = \begin{bmatrix} {\varepsilon_{0}^{m}} + {\varepsilon_{L}^{m}} \\ \kappa \\ \gamma \end{bmatrix} = \begin{bmatrix} \mathbf{B}_{0}^{m} \\ \mathbf{B}_{0}^{b} \\ \mathbf{B}_{0}^{s} \end{bmatrix} \mathbf{d} + \frac{1}{2} \begin{bmatrix} \mathbf{B}_{L}^{m} \\ 0 \\ 0 \end{bmatrix} \mathbf{d} $$

(27)

or

$$ \hat{\boldsymbol{\varepsilon}} = \left( \mathbf{B}_{0} + \frac{1}{2}\mathbf{B}_{L} \right) \mathbf{d} $$

(28)

Using (11)–(13) and (23)–(26), the sub-matrices are defined by:

$$ \mathbf{B}_{0}^{m} = \begin{bmatrix} R_{k,x} & 0 & Z_{x}R_{k,x} & 0 & 0 \\ 0 & R_{k,y} & Z_{y}R_{k,y} & 0 & 0 \\ R_{k,y} & R_{k,x} & Z_{x}R_{k,y} + Z_{y}R_{k,x} & 0 & 0 \end{bmatrix} $$

(29)

$$ \mathbf{B}_{0}^{b} = \begin{bmatrix} 0 & 0 & 0 & 0 & R_{k,x} \\ 0 & 0 & 0 & -R_{k,y} & 0 \\ 0 & 0 & 0 & -R_{k,x} & R_{k,y} \end{bmatrix} $$

(30)

$$ \mathbf{B}_{0}^{s} = \begin{bmatrix} 0 & 0 & R_{k,x} & 0 & R_{k} \\ 0 & 0 & R_{k,y} & -R_{k} & 0 \end{bmatrix} $$

(31)

$$ \mathbf{B}_{L}^{m} = \begin{bmatrix} 0 & 0 & W_{x}R_{k,x} & 0 & 0 \\ 0 & 0 & W_{y}R_{k,y} & 0 & 0 \\ 0 & 0 & W_{x}R_{k,y} + W_{y}R_{k,x} & 0 & 0 \end{bmatrix} $$

(32)

where:

$$ \begin{aligned} &Z_{x} = \sum \limits_{k=1}^{n_{cp}} R_{k,x} z_{0k}, \qquad &Z_{y} = \sum \limits_{k=1}^{n_{cp}} R_{k,y} z_{0k}, \\ &W_{x} = \sum \limits_{k=1}^{n_{cp}} R_{k,x} w_{k}, \quad &W_{y} = \sum \limits_{k=1}^{n_{cp}} R_{k,y} w_{k} \end{aligned} $$

(33)

3.3 Equilibrium equations

Using the D’Alembert and virtual work principles, the dynamic equilibrium equation of the model at a time t may be written as:

$$ \mathbf{M} \ddot{\mathbf{d}} + \mathbf{g}(\mathbf{d}) = \mathbf{f}(t) $$

(34)

where:

$$ \mathbf{M} = {\int}_{A} \mathbf{R}^{T} \overline{\mathbf{M}} \mathbf{R} dA $$

(35)

$$ \mathbf{f} = {\int}_{A} \mathbf{R}^{T}\mathbf{q} dA + {\int}_{S} \mathbf{R}^{T}\mathbf{f}_{s} dS $$

(36)

$$ \mathbf{g} = {\int}_{A} \overline{\mathbf{B}}^{T} \hat{\boldsymbol{\sigma}} dA $$

(37)

where M is the mass matrix and $\overline {\mathbf {B}} = \mathbf {B}_{0} + \mathbf {B}_{L}$ is the matrix that relates the variation of the generalized strains with the variation of the control points displacements ($\delta \hat {\boldsymbol {\varepsilon }} = \overline {\mathbf {B}} \delta \mathbf {d}$).

In this work, $\overline {\mathbf {M}}$ is evaluated using the Gaussian quadrature to carry out the through-the-thickness integration and is given by:

$$ \overline{\mathbf{M}} = {\int}_{-h/2}^{h/2} \rho(z) \mathbf{Z}^{T}\mathbf{Z} dz = \begin{bmatrix} I_{0} & 0 & 0 & 0 & I_{1} \\ 0 & I_{0} & 0 & -I_{1} & 0 \\ 0 & 0 & I_{0} & 0 & 0 \\ 0 & -I_{1} & 0 & I_{2} & 0 \\ I_{1} & 0 & 0 & 0 & I_{2} \end{bmatrix} $$

(38)

where

$$ [I_{0}, I_{1}, I_{2}] = {\int}_{-h/2}^{h/2} \rho(z)[1, z, z^{2}] dz $$

(39)

Finally, the tangent stiffness matrix is obtained by differentiating the internal force vector (g):

$$ \mathbf{K}_{T} = \frac{\partial\mathbf{g}}{\partial\mathbf{d}} = \mathbf{K}_{L} + \mathbf{K}_{\sigma} $$

(40)

where the material stiffness matrix K_L and the geometric stiffness matrix K_σ are given by:

$$ \mathbf{K}_{L} = {\int}_{A} \overline{\mathbf{B}}^{T} \frac{\partial{\hat{\boldsymbol{\sigma}}}}{\partial{\mathbf{d}}} dA = {\int}_{A} \overline{\mathbf{B}}^{T} \mathbf{C} \overline{\mathbf{B}} dA $$

(41)

$$ \mathbf{K}_{\sigma} = {\int}_{A} \frac{\partial{\overline{\mathbf{B}}^{T}}}{\partial{\mathbf{d}}} \boldsymbol{\sigma} dA = {\int}_{A} \mathbf{G}^{T} \mathbf{S} \mathbf{G} dA $$

(42)

where C is the constitutive matrix, defined in (17), and G and S are given by:

$$ \mathbf{G} = \begin{bmatrix} 0 & 0 & R_{k,x} & 0 & 0 \\ 0 & 0 & R_{k,y} & 0 & 0 \\ \end{bmatrix}, \quad \mathbf{S} = \begin{bmatrix} N_{x} & N_{xy} \\ N_{xy} & N_{y} \\ \end{bmatrix} $$

(43)

It is important to note that the geometric nonlinearity is addressed by the use of the Marguerre theory for nonlinear membrane strains, as shown in (10). In this case, the equilibrium of the system for displacement-independent loads is given by:

$$ \mathbf{r}(\mathbf{u}, \lambda) = \mathbf{g}(\mathbf{u}) - \lambda \mathbf{q} $$

(44)

where r is the residual vector, u is the vector of degrees of freedom, λ is the load factor which controls the load application on the structure (f = λq), and q is the vector of reference loads. This equation may be solved using a path-following method, such as the load control method, displacement control method, and the arc-length method.

3.4 Eigenvalue problems

The free vibration analysis is carried out solving the generalized eigenproblem:

$$ (\mathbf{K} - \omega^{2} \mathbf{M}) \boldsymbol{\phi} = \mathbf{0} $$

(45)

where K is the stiffness matrix of the unloaded structure, ω are the natural frequencies, and ϕ are the vibration modes.

In case of structures with negligible pre-buckling displacements, the stability analysis can be carried out in the same form as a vibration problem, but replacing the mass matrix by the geometric stiffness matrix as:

$$ (\mathbf{K} + \lambda \mathbf{K}_{\sigma}) \boldsymbol{\phi} = \mathbf{0} $$

(46)

where λ are the buckling load factors and ϕ are the buckling modes.

4 Optimization of FG structures

The general form of a constrained optimization problem can be written as (Arora 2012):

$$ \left\lbrace \begin{array}{ll} \text{Find} & \mathbf{x} \\ \text{that minimizes} & f (\mathbf{x}) \\ \text{subjected to} & g_{i}(\mathbf{x}) \leq 0 \ \ \ \ i = 1, 2, \dots, N_{ic} \\ \text{with} & \mathbf{x}_{lb} \leq \mathbf{x} \leq \mathbf{x}_{ub} \end{array} \right. $$

(47)

where x_lb and x_ub are the lower and upper bounds of the design variables x, respectively, g_i is the i-th constraint, and N_ic is the number of inequality constraints. In this framework, maximization is understood as the minimization of the negative of the objective function.

In the present work, we deal with continuous optimization problems since the design variables are the material distribution described by the ceramic volume fraction at control points of B-splines or by the Power-law index, and the thickness in two of the examples. The objective functions are either the fundamental frequency, the buckling load, or the mass, while the constraints regard the maximum ceramic volume, maximum displacement, or a specific range of fundamental frequency. The structural responses are evaluated using the methodology presented in Sections 2 and 3.

To solve the optimization problem described in (47), the PSO algorithm is used. In principle, any standard optimization technique could be used. However, PSO can offer improved performance compared to methods based on classical mathematical programming in the optimal design of FGM (Kou et al. 2012). Similar remarks were made by Ashjari and Khoshravan (2014) for the mass optimization of FG plates. Furthermore, this algorithm is well-suited for continuous optimization problems and can deal with multimodal functions with many local minima, which is often the case of the functions optimized in the SAO approach.

4.1 Particle swarm optimization

The particle swarm optimization algorithm was first proposed by Kennedy and Eberhart (1995) and is based on the behavior of animal packs, such as bird flockings and fish schoolings searching for food. The core idea is that each particle roams across the design space based on its position (x_j) and velocity (v_j) looking for the position (i.e., design) with the lowest objective function.

At the beginning, the positions and velocities are randomly generated for all particles. In the following iterations, they are updated as follows:

$$ \mathbf{x}^{i + 1}_{j} = \mathbf{x}^{i}_{j} + \mathbf{v}^{i + 1}_{j} $$

(48)

where $\mathbf {v}^{i + 1}_{j}$ is defined by:

$$ \mathbf{v}^{i + 1}_{j} = w \mathbf{v}^{i}_{j} + c_{1} r_{1} (\mathbf{x}_{p,j}^{i} - \mathbf{x}^{i}_{j}) + c_{2} r_{2} (\mathbf{x}_{g,j}^{i} - \mathbf{x}^{i}_{j}) $$

(49)

where w is the inertia weight, c₁ is the cognitive factor, c₂ is the social factor, r₁ and r₂ are uniformly distributed random numbers in the range of [0,1], $\mathbf {x}_{p,j}^{i}$ is the best position the particle j obtained until present iteration, and $\mathbf {x}_{g,j}^{i}$ is the best position the particles on the neighborhood of particle j found so far. Figure 2 illustrates each term in (49).

Fig. 2

PSO particle move

The so-called standard PSO (Bratton and Kennedy 2007) uses the ring topology to define the neighborhood of a particle. Although it does provide a robust exploratory capacity, this topology may also slow down convergence. To overcome this pitfall and avoid premature convergence, this work uses the global topology with a mutation operator (Barroso et al. 2017).

To deal with the side constraints violations, a simple procedure presented by Clerc (2012) is adopted: the variable that had its bounds violated is set to the bound and its velocity is modified by setting it to the opposite direction with half of its magnitude.

The other constraints are handled using the penalty approach proposed by Deb (2000), in which a fitness function is assigned according to the constraints violations of each design. The penalized objective function (i.e., the particle “fitness”) is evaluated as:

$$ f_{p}(\mathbf{x}) = \begin{cases} f(\mathbf{x}) & \text{if } \mathbf{x} \text{ is feasible}.\\ \displaystyle f_{\max} + {\sum}_{i = 1}^{N_{ic}} {\max} (g_{i}(\mathbf{x}), 0), & \text{otherwise}. \end{cases} $$

(50)

where $f_{\max \limits }$ is the objective function of the worst feasible solution in the neighborhood and g_i is the i-th constraint. When checking the feasibility of x, a small constraint tolerance (𝜖_tol) is considered.

The flowchart of the PSO used in this work is shown in Fig. 3. The algorithm is terminated when at least one of the following stopping criteria is satisfied: maximum number of iterations ($It_{\max \limits }$) or maximum number of successive iterations without improvement (StallGen).

Fig. 3

PSO algorithm

4.2 Mutation

Inspired by GAs, the mutation operator was introduced to maintain the swarm diversity. It is applied to the entire swarm and works by generating a random number between 0 and 1 for each variable of a given particle. If such number is less than or equal to the probability of mutation (p_mut), the velocity component is modified to a random value between the lower and upper bounds of that variable. After that, the position of the particle is updated and the side constraints are enforced.

5 Sequential approximate optimization

The SAO algorithm presented in this work is based on Kriging. In the following, the creation of the initial sample, the surrogate model formulation, the infill criteria, and metrics used to assess its performance are briefly discussed.

5.1 Design of experiments

Design of experiments (DoE) is a group of stochastic and deterministic methodologies used for formulating the sampling plan. On this matter, a uniform distribution of the sampling points is desirable, so that the capability of generalization of the surrogate model is optimized with limited resources.

Another relevant aspect is the scaling of the design variables to [0,1]^m, where m is the number of design variables. This is a standard procedure to eliminate the effect of scale discrepancy on the surrogate model performance (Forrester et al. 2008).

In this work, two methods are considered: the Hammersley sequence sampling (HSS) and the Latin hypercube sampling (LHS). The size of the initial sample is given by n = 5m.

The HSS is a low-discrepancy experimental design proposed by Kalagnanam and Diwekar (1997). It consists of a deterministic method that provides better uniformity properties than LHS in low-dimension spaces. However, it may be significantly affected as the dimensionality increases (Amouzgar and Strömberg 2017; Steponavic~e et al. 2016), particularly when m > 6 (Cho et al. 2017).

As for the LHS, this work adopts the Morris and Mitchell (1995) criterion to choose the best LHS. This criterion aims to maximize a metric known as maximin. In this case, to save computational effort, N_sp sampling plans are created and the one with the highest maximin is chosen. This approach will be referred to as LHS$_{N_{sp}}$.

5.2 Kriging

Kriging is a nonparametric interpolating model based on spatial correlation widely used in engineering to approximate complex expensive functions/experiments. The ordinary Kriging prediction is given by (Sacks et al. 1989):

$$ \hat{y}(\mathbf{x}) = \hat{\mu}+\boldsymbol{\psi}^{T} \ \boldsymbol{{\varPsi}}^{-1} (\mathbf{y}-\mathbf{1}\hat{\mu}) $$

(51)

where the first term concerns the global trend and the second term refers to the localized deviations from it that depend on ψ, the correlation vector between x and all sampling points, and Ψ, the correlation matrix (n × n) of all sampling points. These deviations are autocorrelated and are assumed to be a realization of a Gaussian stochastic process with mean zero and covariance given by (Jones et al. 1998):

$$ \text{cov}[\mathbf{Y}, \mathbf{Y}] = \sigma^{2} \ \boldsymbol{{\varPsi}} $$

(52)

where σ² is the process variance.

To build the correlation matrix, the observed responses y = {y⁽¹⁾ y⁽²⁾ ${\ {\dots } \ y^{(n)}\}}^{T}$ from the sampling plan $\mathbf {X} = \{ \mathbf {x}^{(1)} \ \mathbf {x}^{(2)} \dots$ x⁽ⁿ⁾}^T are treated as a set of normally distributed random variables Y = {Y⁽¹⁾ ${ \ Y^{(2)} \ {\dots } \ Y^{(n)}\}}^{T}$. This random vector has a mean of 1 × μ, where 1 is an n x 1 vector of ones. To model the spatial correlation between two random variables, we use the Gaussian function:

$$ \mathrm{R}[Y({\mathbf{x}}^{(i)}), Y({\mathbf{x}}^{(l)})] = \exp\left( - {\sum}_{j=1}^{m} \theta_{j} \ {d}^{p_{j}}\right) $$

(53)

and the Matérn 5/2 function:

$$ \mathrm{R}[Y({\mathbf{x}}^{(i)}), Y({\mathbf{x}}^{(l)})] = {\prod}_{j=1}^{m} \exp\left( \!-\frac{\sqrt{5} d}{\theta_{j}}\right) \left( \!1\! +\! \frac{\sqrt{5} d}{\theta_{j}} + \frac{5 {d}^{2}}{3 {\theta_{j}^{2}}} \right) $$

(54)

where $d = |x_{j}^{(i)}-x_{j}^{(l)}|$ and 𝜃_j and p_j are the surrogate hyperparameters.

Both kernels present good performance in a wide range of applications (Kianifar and Campean 2019), being the Gaussian function particularly popular in engineering design optimization. The Matérn class is still rare in this field, but it is often used in the machine learning context (Palar and Shimoyama 2018). As a result of these functions, the correlation matrix is symmetric with a diagonal of ones. And more importantly, it is also a function of the hyperparameters, which are usually estimated using the maximum likelihood estimation (MLE), discussed in the following section.

The likelihood function may be described as (Jones et al. 1998):

$$ L = -\frac{1}{{(2 \pi \sigma^{2})}^{n/2} {|\boldsymbol{{\varPsi}}|}^{1/2}} \ \exp\left( {\frac{{(\mathbf{y-1}\mu)}^{T}\boldsymbol{{\varPsi}}^{-1}(\mathbf{y-1}\mu)}{2 \sigma^{2}}}\right) $$

(55)

taking the natural logarithm, differentiating the resulting expression with respect to μ and σ and solving them for 0, the optimal estimates for the mean and the variance of the process are:

$$ \hat{\mu} = \frac{\mathbf{1^{T}} \boldsymbol{{\varPsi}^{-1}} \mathbf{y}}{\mathbf{1^{T}} \boldsymbol{{\varPsi}} \mathbf{1}} \qquad \hat{\sigma}^{2} = \frac{1}{n} \ {(\mathbf{y-1}\hat{\mu})}^{T} {\varPsi}^{-1} (\mathbf{y-1}\hat{\mu}) $$

(56)

Another interesting feature of the Gaussian theory is the ability to provide a measure of the uncertainty of the prediction $\hat {y}(\mathbf {x})$. The prediction variance is also known as mean squared error (MSE):

$$ \hat{s}^{2}(\mathbf{x}) = \hat{\sigma}^{2} \left[ 1- \boldsymbol{\psi}^{T} \boldsymbol{{\varPsi}}^{-1} \boldsymbol{\psi} + \frac{(1-\mathbf{1^{T}} \boldsymbol{{\varPsi}^{-1} \psi})^{2}}{\mathbf{1^{T}} \boldsymbol{{\varPsi}^{-1}} \mathbf{1}} \right] $$

(57)

which is always non-negative and higher in less sampled areas and reduces to 0 in sampling points since it was evaluated using a deterministic computer model (e.g., FEA or IGA). This metric is widely used to assist adaptive sampling strategies (Liu et al. 2017).

5.2.1 Estimation of the hyperparameters

After finding the closed-form expressions for the estimates of μ and σ, the likelihood function can be further simplified by substituting (56) into (55) and removing constant terms, which gives us the so-called concentrated ln-likelihood function:

$$ \ln(L) \approx -\frac{n}{2} \ \ln{(\hat{\sigma}^{2})}-\frac{1}{2}\ln{|\boldsymbol{{\varPsi}}|} $$

(58)

By maximizing this function, the values of the hyperparameters most likely to have generated the training dataset are found. Unfortunately, this function cannot be differentiated in order to obtain an analytic expression to evaluate the optimal hyperparameters. The solution of this optimization problem is not trivial.

Problems in the MLE are often related to the multi-modality of the ln-likelihood function, as well as the long ridges of nearly constant and optimal values that may lead to numerical difficulties for gradient-based problems (Martin and Simpson 2005). In this work, this is addressed by using the PSO algorithm described in Section 4.1. The MLE may also suffer from numerical issues due to ill-conditioned correlation matrices. Thus, to improve the Ψ conditioning, a small constant value (τ = 1 × 10^− 8) is added to its diagonal elements, as recommend by Bachoc (2013).

For simplicity, p_i = 2.0 is fixed and only 𝜃 needs to be trained, reducing the complexity and increasing the efficiency of the estimation process. Therefore, the estimation of the hyperparameters is described as:

$$ \left\lbrace \begin{array}{ll} \text{Find} & \boldsymbol{\theta} = \{ \theta_{i}\} \ \text{for} \ i = 1,2,\dots, m\\ \text{that maximizes} & \ln(L)(\mathbf{x}) \\ \text{with} & \theta_{lb} \leq \theta_{i} \leq \theta_{ub} \end{array} \right. $$

(59)

where 𝜃_lb and 𝜃_ub refer to the lower and upper bounds of the hyperparameter 𝜃_i, respectively. The search bounds are considered to be in logarithmic scale as there is significant change between very close values of 𝜃_i (Forrester et al. 2008; Bachoc 2013).

At last, 𝜃_i can be interpreted as a measure of how active the design variable x_i is regarding the approximated output (Forrester et al. 2008). For the Gaussian function, higher values of 𝜃_i indicate a more important design variable, while the opposite works for the Matérn 5/2 function.

5.3 Expected improvement

The expected improvement is given by (Mockus et al. 1978):

$$ \begin{array}{@{}rcl@{}} E[I(\mathbf{x})]&=&(y_{\min}-\hat{y}(\mathbf{x})) \ {\varPhi}\Big(\frac{y_{\min}-\hat{y}(\mathbf{x})}{\hat{s}(\mathbf{x})}\Big) \\ &&+\hat{s}(\mathbf{x}) \ \phi\Big(\frac{y_{\min}-\hat{y}(\mathbf{x})}{\hat{s}(\mathbf{x})}\Big) \end{array} $$

(60)

where $y_{\min \limits }$ is the current best minimum, ϕ(⋅) is the probability density function, and Φ(⋅) is the normal cumulative distribution function. The first term corresponds to the exploitation, while the second term corresponds to the exploration, which results in larger values in areas where uncertainties are high (i.e., unsampled areas). In constrained problems, $y_{\min \limits }$ is the current best feasible solution.

This criterion has been proved to find the global optimum (Locatelli 1997), but a few shortcomings are associated with it: (i) the EI equation does not allow the user to control the balance between exploitation and exploration and (ii) it may be heavily biased if the target is poorly estimated by the initial approximation.

To alleviate these shortcomings, this work uses the weighted expected improvement (Sóbester et al. 2005):

$$ \begin{array}{@{}rcl@{}} WE[I(\mathbf{x})]&=&w \ (y_{\min}-\hat{y}(\mathbf{x})) \ {\varPhi} \Big(\frac{y_{\min}-\hat{y}(\mathbf{x})}{\hat{s}(\mathbf{x})}\Big)\\ &&+(1 - w) \ \hat{s}(\mathbf{x}) \ \phi \Big(\frac{y_{\min}-\hat{y}(\mathbf{x})}{\hat{s}(\mathbf{x})}\Big) \end{array} $$

(61)

where w is the weighting factor between [0, 1]. The lower bound leads to a global extreme of the search scope range, while the upper bound exploits the current best value.

Values of w exceeding 0.5 should only be used when one is confident that the function landscape is of low modality (Sóbester et al. 2005). Thus, the present work uses the following values w = {0.2,0.35,0.50} in a cyclic search. Care should be taken to avoid division by zero in Eqs. (60) and (61) when evaluating a design that is already in the sampling plan (i.e., $\hat {s} = 0$). In this case, E[I(x)] = WE[I(x)] = 0.

The landscape of both acquisition functions (EI and WEI) is often multimodal (Jones et al. 1998; Sóbester et al.2005). To deal with this aspect, the PSO algorithm presented in Section 4 is used to the their maximization.

Finally, when the objective function is a cheap-to-evaluate function and the constraints are approximated by Kriging, the EI is directly computed as:

$$ E[I(\mathbf{x})] = \begin{cases} y_{\min} - y(\mathbf{x}), \ & y(\mathbf{x}) < y_{\min} \\ 0, & \text{otherwise} \end{cases} $$

(62)

5.4 Constraint handling

The constrained expected improvement (CEI) was proposed by Schonlau et al. (1998) to deal with problems where the constraints are also modelled by a surrogate model. The authors assumed independence between the Gaussian processes to estimate objective function. They penalized the EI as:

$$ E[I_{c}(\mathbf{x})] = E[I(\mathbf{x})] {\prod}_{i=1}^{N_{ic}} F_{i}(\mathbf{x}) $$

(63)

where F_i(x) is the probability that the i-th constraint is met. This probability is also referred as a feasibility function.

In this work, this approach is further extended to handle exact constraints and exact objective functions. Of course, the following considerations are also valid for the WEI criterion. In cases where the constraint is evaluated exactly (e.g., maximum ceramic volume fraction and mass), a small tolerance 𝜖_tol is considered when testing the feasibility of a given design. Thus, F_i(x) = 1 for feasible designs and 0 for unfeasible ones.

Based on the approach proposed by Tutum et al. (2015), the feasibility function of a constraint approximated by a surrogate model is given by:

$$ F_{i}(\mathbf{x}) = \begin{cases} 2 - \text{erf} (\overline{g}_{i}(\mathbf{x})), & \text{if} \ \overline{g}_{i}(\mathbf{x}) \geq 0 \\ 0, & \text{otherwise} \end{cases} $$

(64)

where:

$$ \overline{g}_{i}(\mathbf{x}) = \frac{g_{i,\max}-\hat{g}_{i}(\mathbf{x})}{\hat{s}_{i}(\mathbf{x})} $$

(65)

and $g_{i,\max \limits }$ is the maximum value that the constraint may assume (in this work, $g_{i,\max \limits }$ = 0). This way, if the predicted constraint is close to the threshold, the 1st condition results in a value greater than one, emphasizing near-boundary solutions, as shown in Fig. 4. As the point gets well inside the feasible region, F_i(x) approaches 1 and E[I_c(x)] = E[I(x)].

Fig. 4

Feasibility of approximate constraint

5.5 Algorithm

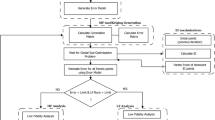
A variation of the EGO algorithm (Jones et al. 1998) is employed, as depicted in Fig. 5. Due to the computational cost involved in the maximization of the MLE, the model validation of the initial surrogate model applies the leave-one-out cross-validation (LOOCV) a bit differently than the usual procedure of re-estimating hyperparameters for each reduced sample.

Fig. 5

Kriging-based SAO algorithm

According to Jones et al. (1998), dropping a single observation has a negligible effect on the maximum likelihood estimates and the hyperparameters found considering all sampling points may be used. Thus, in practice, the maximization of the MLE is carried out considering all sampling points and only the correlation matrix Ψ and the y vector are re-computed from one sampling point removal to another. To assess the accuracy of the prediction made without the sampling point x⁽ⁱ⁾, say $\hat {y} (\mathbf {x}^{(i)})$, a metric named “standardized cross-validated residual” is calculated:

$$ SD_{CVerror} = \frac{y(\mathbf{x}^{(i)}) - \hat{y}(\mathbf{x}^{(i)})}{\hat{s}(\mathbf{x}^{(i)})} $$

(66)

where $\hat {s}(\mathbf {x}^{(i)})$ is calculated as shown in (57). This procedure is repeated for all n sampling points. In all times, the error should be roughly in the interval [-3, 3]. In case of failure of model validation, Jones et al. (1998) suggest a transformation of the dependent variable, which is the approach adopted in this work, typically, the log transformation ($\log (y)$ or $\ln (y)$). If model validation still fails, one may reconsider the kernel used or increase the sampling plan size.

The stopping criteria are the maximum number of iterations, which should be specified for each problem, and the maximum number of consecutive SAO iterations without improvement on the best solution (StallGen).

For the performance assessment of the proposed SAO algorithm, the following aspects are considered:

• 1. Efficiency: measures the computational cost to solve the optimization problem;

• 2. Accuracy: measures how close the surrogate model optimum is to the true function optimum;

• 3. Robustness: measures the ability of the model to consistently present good results in different runs.

To assess the efficiency, two metrics are considered: the speed-up and the number of HF evaluations needed to reach at least one stopping criterion. The speed-up is computed as:

$$ \text{{Speed-up}} = \frac{1}{n_{r}} \ {\sum}_{i = 1}^{n_{r}} \frac{T_{{HFM}}}{T_{SAO,i}} $$

(67)

where n_r is the number of runs, T_HFM is the average time spent in the conventional optimization, and T_SAO,i is the time spent using a SAO algorithm on the i-th run, both measured by the wall-clock time.

In this work, the average normalized root mean squared error ($\overline {{NRMSE}}$) is used to assess the accuracy of the surrogate model:

$$ \overline{{NRMSE}} = \frac{1}{n_{r}} {\sum}_{i=1}^{n_{r}} \sqrt{\frac{(y^{*}-y_{SAO,i})^{2}}{ (y^{*})^{2}}} $$

(68)

where y^∗ is the HF response at the reference solution (i.e., optimal solution) and y_SAO,i is the best response obtained by the SAO on the i-th run. Lower values of $\overline {{NRMSE}}$ indicate better performances.

Finally, to measure the SAO robustness, the standard deviation of the NRMSE is considered:

$$ SD_{{NRMSE}} = \sqrt{\frac{{\sum}_{i=1}^{n_{r}} {NRMSE}_{i}-\overline{{NRMSE}}}{n_{r}-1}} $$

(69)

Again, smaller values of $SD_{\text{NRMSE}}$ suggest a more robust SAO or to put it another way, the less variable the results are. Of course, this metric should be read in context with the accuracy metric.

6 Analysis verification

This section aims to validate the IGA formulation presented in Section 3 and to assess the accuracy of the meshes used in the case studies discussed in the following section. The first verification regards the free vibration analysis. For the validation of the structural analysis of the FG plates used for case studies 1 and 2, a mesh of 16 × 16 cubic NURBS elements for the full representation of the plate was used. Full integration was used in the element midsurface and 10 Gauss points were used for the through-thickness integration of the constitutive and mass matrices. The boundary conditions of the simply supported square plate are depicted in Fig. 6.

Fig. 6

Simply supported square plate

In the first example, the Voigt model and the Power-law function are considered. Therefore, the IGA responses for different combinations of Power-law index and thickness found in Franco et al. (2018) are reproduced. The plate is made of stainless steel (SUS3O4) and silicon nitride (Si₃N₄) and the temperature effect is considered using Toulokian’s equation (Touloukian 1967) (see Table 1). The results presented in Table 2 show excellent agreement with the reference values.

Table 1 Material properties of SUS3O4/Si₃N₄ with constant temperature (T = 300 K)

Table 2 Fundamental frequency of simply supported SUS3O4/Si₃N₄ square plate

For the second example, the homogenization technique used was the Mori-Tanaka model. The plate is also made of SUS304/Si₃N₄ (with no temperature effect) and a/h = 10. The material properties are shown in Table 3. The results for different exponents using the Power-law function are compared to those found by Do et al. (2018), as shown in Table 4. The maximum difference found is below 1%, showing that the present mesh is sufficiently accurate to model the structural responses even of thick plates.

Table 3 Material properties of SUS304/Si₃N₄

Table 4 Non-dimensional fundamental of simply supported SUS3O4/Si₃N₄ square plate

Next, for the third example, a clamped square plate with a circular hole in its center is modelled using a mesh with 8 patches, each of them with an 8 × 8 mesh of cubic NURBS elements, adding up to a total of 512 elements, as shown in Fig. 7b. The boundary and loading conditions are depicted in Fig. 7a. The geometry of the plate is given by a = 0.72 m and r = a/10.

Fig. 7

Plate with circular cutout a loading and boundary conditions b isogeometric mesh

This plate is also made of SUS3O4/Si₃N₄ (see Table 3) and the volume fraction is described by a B-spline with 9 control points symmetrically distributed through thickness. The effective properties are evaluated using the Mori-Tanaka model. The optimization problem involving this FG plate is explored by Ribeiro et al. (2020). Therefore, the optimal designs obtained by the SAO approach proposed by these authors are used to validate the present work analysis. All three optimal designs were modelled on ABAQUS considering the same mesh refinement, but with quadratic shell elements with reduced integration, known as S8R. In all cases, the difference between FEA and the present work analysis is equal to 0.01%.

For the last example, the mesh used to model the hinged cylindrical shell shown in Fig. 8 is validated based on the results of the nonlinear analysis carried out by Kim et al. (2008). The material properties are presented in Table 5. The volume fraction distribution is described by the sigmoid function (Kim et al. 2008) and the effective properties are given by the Voigt model. The load-displacement curves for two values of N are presented in Fig. 9. Very good agreement is observed between the present work analysis and the reference results.

Fig. 8

Cylindrical shell

Table 5 Material properties of the cylindrical shell

Fig. 9

Load-deflection curve of the cylindrical shell

7 Case studies

In this section, four optimization problems are solved. Two types of homogenization schemes are used (the Mori-Tanaka and the Voigt schemes) and two types of FG structures are studied (plates and a cylindrical shell). In the following case studies, KRG-G and KRG-M refer to the SAO algorithm discussed in Section 5 using the Gaussian function and the Matérn 5/2 function, respectively. In the first example, a brief study on the effect of the mutation operator shown in Section 4.1 is presented. To distinguish the results without the mutation operator (i.e., p_mut = 0.00) from the ones with it, a superscript (^∗) was added to each acronym.

If not specified in a particular example, the adopted values of the optimization parameters are presented in Table 6. For each problem, 10 independent runs (n_r) are carried out, each with a new sampling plan generated using the LHS₂₀ approach and 𝜖_tol = 1 × 10^− 5. It is worth emphasizing that the StallGen values for maximization of EI, WEI, and MLE are higher because these are cheap functions. The SAO algorithm itself stops when the best solution is not improved for 10 consecutive iterations, which is the same stopping criterion adopted for the conventional optimization using the HFM based on IGA.

Table 6 Optimization parameters

All simulations are carried out on a computer with an Intel i9-9820X @3.30 GHz processor with 10 cores and 120 GB RAM. No parallelization procedure is adopted.

7.1 Fundamental frequency maximization of FG plate with frequency constraint

The first optimization problem deals with the maximization of the fundamental frequency (ω) of a simply supported square plate studied by Franco et al. (2018). The design variables are the plate thickness and the Power-law index. The problem has two constraints on the fundamental frequency range. Therefore, an additional stopping criterion is considered: the algorithm is stopped whenever the best solution found so far is higher than 7999 rad/s, which is only 0.01% smaller than the maximum fundamental frequency allowed. This is done because the maximum objective function is known and further exploration of solutions within this tolerance may be a waste of computational effort. This problem may be expressed by:

$$ \left\lbrace \begin{array}{ll} \text{Find} & \mathbf{x} = \{h, \ N\}\\ \text{that maximizes} & \omega (\mathbf{x}) \\ \text{subjected to} \ & 3000 \leq \omega \leq 8000 \ \text{(rad/s)} \\ \text{with} & 0.005 \leq h \leq 0.060 \ \text{(m)} \\ & 0.20 \leq N \leq 10.0 \end{array} \right. $$

(70)

The constituents are silicon nitride (Si₃N₄) as the ceramic and stainless steel as metal (SUS3O4) in constant temperature at 300 K (see Table 1 for the material properties). The geometry of the plate is given by a = 0.5 m and $It_{\max \limits } = 50$. Finally, the lower and upper bounds of the hyperparameters are $\log {\theta _{lb}} = -2.0$ and $\log {\theta _{ub}} = 1.0$.

In this problem, both objective function and constraints are approximated by surrogate models. Since the constraints are actually imposed on the response surface of the objective function, the hyperparameters are calculated only once for the objective function approximation and repeated to the constraints. The performance of the SAO algorithms is described in Table 7, where the bold entries correspond to the best performance for the metric linked to each column. This convention is adopted for all case studies. Recall that the acronyms with the ^∗ superscript refer to the runs without mutation.

Table 7 Metrics for SUS3O4/Si₃N₄ FG plate with frequency constraint

In general, the EI criterion led to the best performances. Despite the significant differences in the computational cost of the Matérn 5/2 compared to the Gaussian, both correlation functions provided accurate results regarding both infill criteria.

As for the effect of the mutation, in 3 out of 4 combinations, higher accuracy was achieved when using the operator. Although the difference is not very large, which is good since it means the algorithm is capable of providing accurate results without relying on the mutation, another interesting outcome provided by the exploratory feature introduced by it consists of more robust results (smaller $SD_{\text{NRMSE}}$). Of course, due to the PSO stochastic nature, the mutation effect can be more or less pronounced depending on the complexity of the landscape being optimized.

The best designs found using both the conventional optimization and the SAO approach are compared to those obtained by Franco et al. (2018), as shown in Table 8. It is understood that the best SAO performance is the one with the highest accuracy (i.e., lowest $\overline {{NRMSE}}$). In this particular case, the best results were obtained using the EI criterion and the Gaussian function (with mutation). If the approaches had the same accuracy, then we would use the following sequence to define the best performance: highest robustness (i.e., lowest $SD_{\text{NRMSE}}$), lowest number of HF evaluations, and highest speed-up. Figure 10 illustrates the optimal ceramic volume fraction distribution through the plate thickness obtained by the SAO algorithm in Table 8.

Table 8 Optimal designs for SUS3O4/Si₃N₄ FG plate with frequency constraint

Fig. 10

Optimal volume fraction distribution for SUS3O4/Si₃N₄ FG plate problem with frequency constraint

Note that different combinations of N and h provide the highest fundamental frequency allowed of 8000 rad/s. This can be observed when the constraints are plotted on the response surface, as shown in Fig. 11b and c, where the design space is normalized [0,1]^m. Any response lying on the boundary between the approximate surface and the upper hyperplane is optimal. In addition to that, the initial ln-likelihood landscape of one of the optimizations using KRG-G/WEI is shown in Fig. 11a. It is important to note that the landscape of this function is multimodal and the optimum hyperparameters indicate that the Power-law index is more relevant than the plate thickness regarding the fundamental frequency since 𝜃₂ ≫ 𝜃₁.

Fig. 11

Surrogate model surface for SUS3O4/Si₃N₄ FG plate problem with frequency constraint a initial in-likelihood landscape b initial approximate surface c HF response surface

Figure 12 illustrates the WEI surface for the initial surrogate model shown in Fig. 11 b. Note that the PF amplifies the WEI of points near the constraint threshold and drives it to 0 where there is low likelihood of feasibility. As more points are added to the sample, the shape of the intersection between the response surface and the constraint imposed by the maximum frequency gets closer to the one observed on the HF surface.

Fig. 12

Iterations of WEI search on FG plate problem with frequency constraint using KRG-G

7.2 Fundamental frequency maximization of FG plate with volume constraint

This problem consists of the maximization of the normalized fundamental frequency of a FG square plate ($\overline {\omega }$) subjected to a constraint on the maximum volume of ceramic material (Do et al. 2018). The volume fraction is described by 13 control points symmetric about the midplane, resulting in 7 design variables. The problem may be expressed by:

$$ \left\lbrace \begin{array}{ll} \text{Find} & \mathbf{x} = \{ V_{c_{i}}\} \ \text{for i = 1, 2, \dots, 7} \\ \text{that maximizes} & \overline{\omega} (\mathbf{x}) \\ \text{subjected to} \ & \overline{V}_{c}(\mathbf{x}) \leq \overline{V}_{c,\max} \\ \text{with} & 0.0 \leq V_{c_{i}} \leq 1.0 \end{array} \right. $$

(71)

where $V_{c_{i}}$ is the volume fraction at the i-th control point, $\overline {V}_{c}$ is the percentage of ceramic material, and $\overline {V}_{c,\max \limits }$ is the maximum ceramic volume fraction. Three values of $\overline {V}_{c,\max \limits }$ were considered: 35%, 50%, and 65%. The ceramic volume fraction of a design is given by:

$$ \overline{V}_{c}(\mathbf{x}) = \frac{1}{h} {\int}_{-h/2}^{h/2} V_{c} dz $$

(72)

This integral is evaluated using Gaussian quadrature with 10 points and is exactly calculated for all designs explored by the EI (or WEI) maximization. Therefore, only the objective function is approximated by a surrogate model. The lower and upper bounds of the hyperparameters are $\log {\theta _{lb}} = -2.0$ and $\log {\theta _{ub}} = 0.0$ for the Gaussian function and $\log {\theta _{lb}} = 0.0$ and $\log {\theta _{ub}} = 2.0$ for the Matérn 5/2 function.

The constituents are the SUS3O4 as the metal and Si3N₄ as the ceramic (see Table 3). The geometry and the boundary conditions are the same as shown in Fig. 6 for a/h = 10. The performance of the SAO algorithms is described in Table 9.

Table 9 Metrics for SUS3O4/Si₃N₄ FG plate with volume constraint

Finally, the best designs for each $\overline {V}_{c,\max \limits }$ are shown in Table 10 along with the designs found by Do et al. (2018) using DNN. The authors considered 10,000 sampling points for the training and testing of the DNN. This large number of sampling points emphasizes the importance of SAO techniques in reducing the number of HF evaluations.

The SAO results in Table 10 refer to the KRG-G/WEI, KRG-G/EI, and KRG-M/WEI approaches for the $\overline {V}_{c,\max \limits } = 35\%, \ 50\%$, and 65%, respectively. The optimal volume fraction distributions are depicted in Fig. 13. As the maximum ceramic volume fraction is reduced, the distribution goes from a smooth transition to a sandwich-like composite structure with metal in its core and ceramic on the outside.

Table 10 Optimal designs for SUS3O4/Si₃N₄ FG plate with volume constraint

Fig. 13

Optimal volume fraction distributions for SUS3O₄/Si₃N₄ FG plate with volume constraint a $\overline {V}_{c,max} = 35\%$ b $\overline {V}_{c,max} = 50\%$ c $\overline {V}_{c,max} = 65\%$

7.3 Buckling load maximization of FG plate

This problem was proposed by Ribeiro et al. (2020) and deals with the maximization of the buckling load factor of a simply supported square plate. The side length measures 0.720 m and a circular hole of radius r = a/10 is placed in its center, as shown in Fig. 7. The volume fraction distribution of the FG plate is described by 9 control points symmetrically distributed, which results in 5 design variables. The effective properties are given by the Mori-Tanaka model. In addition to that, the plate thickness is also taken as variable, which increases the dimensionality of the problem. Two constraints are considered regarding the total mass of the plate and its maximum ceramic volume fraction. In short, the optimization problem may be described as:

$$ \left\lbrace \begin{array}{ll} \text{Find} & \mathbf{x} = \{h, V_{c_{i}}\} \ \text{for i = 1, 2, \dots, 5} \\ \text{that maximizes} & {\lambda_{cr}} (\mathbf{x}) \\ \text{subjected to} \ & \overline{V}_{c}(\mathbf{x}) \leq \overline{V}_{c,\max} \\ & M \leq M_{\max} \\ \text{with} & 0.0 \leq V_{c_{i}} \leq 1.0 \\ & 0.01 \leq h \leq 0.05 \ \text{(m)} \end{array} \right. $$

(73)

where λ_cr and $M_{\max \limits }$ are the critical buckling load factor and the maximum mass of the plate, respectively. Here, $\overline {V}_{c,\max \limits } = 50\%$ and $M_{\max \limits } = 100$ kg. Again, only the objective function is approximated since both constraints can be exactly evaluated without compromising the optimization. The lower and upper bounds of the hyperparameters are the same as the previous example. Finally, the performance of the SAO algorithms is described in Table 11.

Table 11 Metrics for square plate with circular hole and $\overline {V}_{c,max} = 50\%$

Fig. 14

Optimal volume fraction distribution for FG clamped plate problem

In this problem, the cost of one structural analysis is on average 3.3× more expensive (≈ 4.01 s) than the analyses carried out in previous examples (≈ 1.20 s). As a consequence, the effect of the reduced number of HF evaluations needed for convergence caused the SAO approach to reach even higher speed-ups.

Again, the SAO performance was slightly better when considering the WEI criterion. Table 12 presents the best designs found by the conventional optimization and the KRG-G WEI, as well as the best design obtained by the SAO algorithm based on RBF proposed by Ribeiro et al. (2020). The authors built an initial surrogate with the same size as in this work. However, the SAO-RBF took 20 updates to sample the optimal design and 25 iterations to reach the convergence criterion, while the present work found the optimal design after only one iteration. In both cases, a much lower computational cost is achieved since each iteration of the SAO only evaluates the HFM once, while the conventional optimization evaluates the HFM for each particle. Figure 14 illustrates the optimal ceramic volume fraction distribution through the plate thickness obtained by the SAO algorithm in Table 12.

Table 12 Optimal designs for FG plate with circular hole and $\overline {V}_{c,max} = 50\%$

7.4 Mass minimization of FG cylindrical shell

In this subsection, the cylindrical panel shown in Fig. 8 is subjected to a point load that increases in 6 increments until P₀ = 51.0 kN. The thickness and Power-law index are taken as design variables. This is a modified version of a problem proposed by Moita et al. (2017), where the following optimization formulation is considered:

$$ \left\lbrace \begin{array}{ll} \text{Find} & \mathbf{x} = \{h, \ N \}\\ \text{that minimizes} & M (\mathbf{x}) \\ \text{subjected to} \ & w_{c} \leq w_{\max} \ \text{(mm)} \\ \text{with} & 0.008 \leq h \leq 0.035 \ \text{(m)} \\ & 0.2 \leq N \leq 10.0 \end{array} \right. $$

(74)

where w_c and $w_{\max \limits }$ correspond to the displacement at the center of the shell and its maximum value, respectively, and M is the total mass of the shell. The material properties are found in Table 5 and $w_{\max \limits } = 4.0$ mm. The lower and upper bounds of the hyperparameters are $\log {\theta _{lb}} = -1.0$ and $\log {\theta _{ub}} = 2.0$. Note that, this time, the expensive-to-evaluate function is the constraint and not the objective function.

In this study, n_r = 3 for the conventional optimization using the HFM. The number of HF runs was reduced due to the time-consuming optimizations (5 to 6 h on average each). In addition, N_p = 20, Max_it = 50 and p_mut = 0.03. For the SAOs, the number of runs is kept at n_r = 10 and p_mut = 0.03. The remaining values of the optimization parameters are the same as the ones presented in Table 6.

In this particular problem, another information is reported in Table 13: the average number of iterations ($\overline {n}_{it}$), which should not be misunderstood with the number of HF evaluations that reached convergence (although until this point, $\overline {n}_{it} = \overline {n}_{p}$). This occurs because it was observed that the incremental analysis of a few designs did not reach convergence.

Table 13 Metrics for hinged-free shallow shell problem

Hence, to prevent the algorithm to continue exploring an unfeasible point in the next iteration (recall that the hyperparameters are not updated and the approximate surface is the same), a simple function to verify if a given trial design was already visited by the SAO was incorporated to the algorithm. Also as a result of that, the same initial sampling plan is used in all SAO runs. This way, there is no chance of creating a sampling plan which may end up with an analysis with no convergence, affecting the number of initial points of the surrogate model. In this particular case, the Hammersley sequence was used

Finally, the best designs found by the conventional optimization and by the KRG-M are presented in Table 14. Despite the differences in the problem formulation between the present work and Moita et al. (2017), the optimal design found by the SAO and conventional optimization are very close to the one found by Moita et al. (2017) after the two-stage optimization using HSDT. Moita et al. (2017) found that the thickness should be h = 0.0120 m and N = 0.20, which is unfeasible considering the present analysis where FSDT is used, while this work found h = 0.0123 m and N = 0.20.

Table 14 Optimal designs for cylindrical shell

It is also interesting noting that, in this case, the optimization of the Kriging hyperparameters resulted in a value of 𝜃₁ much higher than 𝜃₂, which means that the displacement is more sensitive to the thickness than to the Power-law index. Figure 15 illustrates the optimal ceramic volume fraction distribution through the shell thickness obtained by the SAO algorithm in Table 14.

Fig. 15

Optimal volume fraction distribution for cylindrical shell problem

8 Conclusion

This work presented a Kriging-based framework to assist the optimization of FG structures using adaptive sampling. The proposed methodology uses the ordinary Kriging to approximate the structural responses (e.g., displacements, buckling loads, and vibration frequencies) obtained by a NURBS-based isogeometric formulation. Two methods for the definition of the volume fraction distribution (B-splines and Power-law function) and two micromechanical models (Voigt and Mori-Tanaka) were considered.

The proposed methodology is capable of handling constrained problems, whether the constraints are approximated by Kriging or not, and can deal with problems where the objective function is exact, while the constraints are approximated. The design variables are related to the volume fraction distribution. The thickness is also considered in two of the case studies. PSO was successfully used to carry out the conventional optimization, as well as to solve the maximization problems of the infill criteria (EI or WEI) and the MLE, showing the robustness of the algorithm.

Results showed that the WEI criterion leads to a slightly better performance in terms of efficiency, but no significant difference was observed with respect to EI in terms of accuracy and robustness. In addition to that, two correlation functions (Gaussian and Matérn 5/2) were compared. In this regard, the use of the Gaussian function is clearly more efficient than that of the Matérn 5/2 function for the same number of IGA evaluations, albeit there is no significant difference in accuracy and robustness. Furthermore, in none of the cases considered in this work, the transformation of the dependent variable was needed for both correlation functions.

It should be noted that the efficiency gap between the kernels decreases as the cost of structural analyses increases. This suggests that the maximization of the likelihood function and of the infill criterion represents a smaller proportion of the computational cost, especially in the optimization of complex structures presenting nonlinear behavior.

The proposed method was up to 45× faster than the conventional optimization of FG structures. This reduction is even more expressive in terms of high-fidelity evaluations. Thousands of isogeometric analyses were replaced by a few dozen using the Kriging-based optimization. Overall, the SAO approach presented in this work can significantly reduce computational cost and greatly improve the optimization efficiency while providing an insight on the relevance of the design variables.