A hybrid PSO-GA algorithm for optimization of laminated composites

Abstract

This paper presents a new hybrid Particle Swarm Algorithm (PSO) for optimization of laminated composite structures. The method combines the standard PSO heuristics with Genetic Algorithm operators in order to improve the algorithm performance. Thus, operations that are important to the optimization of laminated composites such as mutation and layer swap are incorporated into the method. A specially designed encoding scheme is used to represent the laminate variables and the associated velocities. A study is carried-out to select the best variant of the proposed method for the optimization of laminated composites, considering different swarm topologies and genetic operators. Both strength maximization and weight minimization problems are considered. A meta-optimization procedure is used to tune the parameters of each variant in order to avoid biased results. The results showed that the proposed method led to excellent results for both traditional and dispersed laminates, representing a significant improvement over the standard PSO algorithm.

1 Introduction

Fiber reinforced composite materials have been intensively studied in last decades, since these materials have high resistance/weight and stiffness/weight ratios, corrosion and fatigue resistance, and other interesting properties for structural applications. These composites are formed from high strength fibers (e.g. carbon and glass) embedded in a polymeric matrix (resin). Typically, several layers with different fiber orientations are stacked to obtain more efficient designs, resulting in a laminated structure.

The design of laminated structures requires the determination of the number of layers and the characteristics of each layer (material, thickness and fiber orientation). Since there are large number of possibilities, the standard trial and error procedure is not appropriate, and the use of optimization techniques is attractive (Gürdal et al. 1999).

Due to the presence of discrete variables such as type of material, thickness, and orientation of fibers, the use of gradient based optimization methods (Mathematical Programming) is not suitable. Furthermore, the laminated optimization is a combinatorial optimization problem NP-hard (Suresh et al. 2007) and have many local minima (Kathiravan and Ganguli 2007).

Bio-inspired optimization methods such as Genetic Algorithms (Kogiso et al. 1994; Liu and Toropov 2013), Particle Swarm Optimization (Kovács et al. 2004; Chang et al. 2010; Ghashochi Bargh and Sadr 2012; Lakshmi and Rao 2013) and Ant Colony Optimization (Aymerich and Serra 2008; Koide et al. 2013) have been successfully applied for optimization of composite structures. Moreover, new meta-heuristics as Quantum Behaved Particle Swarm Optimization (Omkar et al. 2009; Lakshmi and Rao 2013), Artificial Bee Colony (Omkar et al. 2011; Apalak et al. 2014) and Shuffled Frog Leaping Optimization Algorithm (Fakhrabadi et al. 2013; Lakshmi and Rama Mohan Rao 2013) have also been applied to the optimization of laminated composites.

Although many new metaheuristics have been introduced recently and some of them may lead to real improvements in the optimization algorithms, this is not always the case (Weyland 2010; Sörensen 2015; Weyland 2015). Therefore, instead of proposing a new metaheuristic, this paper presents a hybrid method for optimization of composite laminates. The standard aspects of PSO are kept, as swarm neighborhood interaction and particle velocity, but a hybridization was made by considering other heuristic operators, as mutation from Genetic Algorithm and specific operators for laminate optimization, improving the search strategy of the PSO method for laminated composites.

The proposed algorithm includes a specially designed encoding scheme for position and velocity of the particles and an efficient procedure for constraint handling, ensuring that all particles positions computed along the optimization process generate valid layups, which increases the computation efficiency. The algorithm is validated using well-known benchmarks and the numerical results show that the proposed algorithm is efficient for both conventional and dispersed laminates. Since the algorithm can be used with different swarm topologies and operators, a comparative study is carried out to find the best variant for the load maximization and weight minimization problems. A calibration procedure, known as meta-optimization (Pedersen and Chipperfield 2010), is performed to guarantee that the best performance of each variant will be considered in the comparison.

The rest of the paper is organized as follows. Section 2 presents a brief review of analysis of laminated plates. Section 3 discusses the basic concepts about Particle Swarm Algorithm. The proposed hybrid algorithm is presented in Section 4. Section 5 presents the meta-optimization procedure. The numerical examples are shown in Section 6. Conclusions are discussed in Section 7.

2 Structural analysis

Laminated plates can be analyzed through the Classical Laminated Theory - CLT (Daniel and Ishai 2006). Each lamina is treated macroscopically as orthotropic material in the local axis system (x ₁,x ₂,x ₃), with the local axis x ₁ parallel to the fiber orientation, as illustrated in Fig. 1.

Fig. 1

Laminate local axis system

According to kinematic hypotheses of CLT, the strains at a point (𝜖), with relative position to laminate midplane z, can be related with the midplane strains by:

$$ \boldsymbol{\epsilon} = \boldsymbol{\epsilon}_{0} + z \, \boldsymbol{\kappa} $$

(1)

where 𝜖 ₀ corresponds to the membrane strains and κ corresponds to the laminate curvatures. This expression can be written in matrix format as:

$$ \left[\begin{array}{l} \varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \end{array}\right] = \left[\begin{array}{l} \varepsilon_{x_{0}} \\ \varepsilon_{y_{0}} \\ \gamma_{{xy}_{0}} \end{array}\right] + z \left[\begin{array}{l} \kappa_{x} \\ \kappa_{y} \\ \kappa_{xy} \end{array}\right] $$

(2)

assuming an elastic-linear behavior in each lamina, the stress (σ ₁) × strain (ε ₁) relation can be expressed in the local system by:

$$ \left[\begin{array}{l} \sigma_{1} \\ \sigma_{2} \\ \tau_{6} \end{array}\right] = \left[\begin{array}{ccc} Q_{11} & Q_{12} & 0 \\ Q_{21} & Q_{22} & 0 \\ 0 & 0 & Q_{66} \end{array}\right] \left[\begin{array}{l} \varepsilon_{1} \\ \varepsilon_{2} \\ \gamma_{6} \end{array}\right] \Rightarrow \mathbf{\sigma}_{1} = \mathbf{Q} \,\mathbf{\varepsilon}_{1} $$

(3)

the components of constitutive matrix Q are:

$$\begin{array}{@{}rcl@{}} Q_{11}&=&\frac{E_{1}}{1-\nu_{12}\nu_{21}}\\ Q_{12}&=&Q_{21}=\frac{\nu_{12} E_{2}}{1-\nu_{12}\nu_{21}}\\ Q_{22}&=&\frac{E_{2}}{1-\nu_{12}\nu_{21}}\\ Q_{66}&=&G_{12} \end{array} $$

(4)

where E ₁ and E ₂ are the Young’s modulus, G ₁₂ is the shear modulus, ν ₁₂ e ν ₂₁ are the Poisson ratios of the composite material.

In the analysis of plates and shells, it is more convenient to deal with stress resultants. These internal forces and moments can be evaluated by means of integration over the laminate thickness (t):

$$\begin{array}{@{}rcl@{}} \mathbf{N}&=& \left[ \begin{array}{l} N_{x} \\ N_{y} \\ N_{xy} \end{array} \right] = \int\limits_{-t/2}^{t/2} \left[ \begin{array}{l} \sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{array} \right] dz\\ \mathbf{M}&=& \left[ \begin{array}{l} M_{x} \\ M_{y} \\ M_{xy} \end{array} \right] = \int\limits_{-t/2}^{t/2} \left[ \begin{array}{l} \sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{array} \right] z \;dz \end{array} $$

(5)

Considering an elastic behavior, the relation between the stress resultants and the laminate strains can be written in matrix format as

$$ \left[ \begin{array}{l} \mathbf{N}\\ \mathbf{M} \end{array} \right] = \left[\begin{array}{ll} \mathbf{A}& \mathbf{B}\\ \mathbf{B}& \mathbf{D} \end{array}\right] \left[ \begin{array}{l} \pmb\epsilon_{0} \\ \boldsymbol{\kappa} \end{array} \right] $$

(6)

where A is the membrane stiffness matrix, D is the bending stiffness matrix, and B is the membrane-bending coupling matrix. The components of these matrices are given by:

$$\begin{array}{@{}rcl@{}} A_{ij} &=& \sum\limits_{k=1}^{n} \overline{Q}_{ij}^{k} (z_{k}-z_{k-1}) \\ B_{ij} &=& \sum\limits_{k=1}^{n} \frac{\overline{Q}_{ij}^{k}({z^{2}_{k}} - z^{2}_{k-1})}{2} \\ D_{ij}& =& \sum\limits_{k=1}^{n} \frac{\overline{Q}_{ij}^{k} ({z^{3}_{k}} - z^{3}_{k-1})}{3} \end{array} $$

(7)

where n is the number of plies and $\overline {Q}_{ij}$ are the elements of the material constitutive matrix in the global axis (Daniel and Ishai 2006). It is important to note that B = 0 for symmetric laminates.

3 PSO algorithm

Particle Swarm Optimization was proposed by Kennedy and Eberhart (1995) based on the behavior of animal packs, as flocks of birds or schools of fish. In the PSO algorithm, each particle searches for places with food, moving at each iteration by its velocity, which depends on its own history (cognitive aspect) and the swarm history (social aspect). In design optimization problem, the particle position denotes a design in the search space. At the beginning, the position (x) and velocity (v) of each particle is generated randomly. At each iteration, the velocity and position of each particle are updated according to:

$$ \mathbf{v}^{(i)} = w \, \mathbf{x}^{(i)} + c_{1}\, r_{1} (\mathbf{x}_{P}^{(i)} - \mathbf{x}^{(i)}) + c_{2} \, r_{2} (\mathbf{x}_{G}^{(i)} - \mathbf{x}^{(i)}) $$

(8)

$$ \mathbf{x}^{(i)} = \mathbf{x}^{(i)} + \mathbf{v}^{(i)} $$

(9)

where w is the particle inertia, c ₁ is the cognitive factor, c ₂ is the social factor, r ₁ and r ₂ are uniform random numbers between 0 and 1, x _P is related to the cognitive learning of the particle, it is considered the best position obtained by the particle during the process, and x _G is related to the social learning, it is considered the best position obtained by particle’s neighborhood.

The position considered for x _G depends on the swarm topology. In the initial version of PSO (Kennedy and Eberhart 1995), x _G was the best position obtained by all particles. This option is known in the literature as Global Topology, since the particle neighborhood is the entire swarm. This topology generally leads to a fast convergence, but makes the algorithm highly susceptible to premature convergence to non-optimal solutions. Many attempts have been made to solve the problem of premature convergence, one of them is to use other swarm topologies (Kennedy and Mendes 2002; 2006). Two topologies that present good results are the Ring Topology and the Square Topology. In the Ring Topology each particle can only be influenced by other two. The so-called standard PSO, discussed in Bratton and Kennedy (2007), use this topology. In the Square Topology, the swarm is arranged in matrix format, where each particle has a neighbor in each direction: above, below, right and left. Figure 2 illustrates the topologies discussed here for a swarm with nine particles. It is important to note that these neighborhoods are defined taking into consideration the index of the particles, thus disregarding the Euclidean distance between them.

Fig. 2

Swarm topologies

4 Hybrid PSO for laminate optimization

Genetic Algorithms (GAs) are heuristic optimization methods based in the principles of natural selection. A population of individuals (solutions) evolves along generations in order to find the best individual, meaning the best solution for an optimization problem. In each generation, a set of new individuals are generated from the old ones by the application of genetic operators, as crossover and mutation. Individuals with high fitness tend to transmit their characteristics over generations, leading to convergence to the optimum solution. GAs present good performance in combinatorial optimization problems, as Travelling Salesman Problem (Larrañaga et al. 1999) and Vehicle Routing Problem (Baker and Ayechew 2003).

GAs are well suited to discrete optimization problems, while PSO presents a good performance in continuous optimization problems. Thus, the combination of both heuristics can result in a robust optimization method for both types of problems. In the optimization of composite structures, it is expected that the hybrid algorithm perform well in the optimization of conventional laminates (𝜃∈{0^∘,±45^∘,90^∘}) and dispersed laminates (e.g. 𝜃∈{0^∘, ±5^∘, …, ±85^∘, 90^∘}).

The classical PSO algorithm was developed for the solution of unconstrained optimization problems with continuous variables. Therefore, it cannot be applied directly to the design optimization of laminated composites, since these problems involve constraints and discrete variables. Thus, this work presents an improved algorithm for laminate optimization obtained combining the classical PSO heuristics with some genetic operators. The proposed algorithm incorporating these features is discussed in the following sections.

4.1 Codification

A special encoding scheme was adopted to allow the use of PSO in the optimization of composite laminates with discrete variables. In this scheme, the particle position is represented by an integer matrix, where each row represents a variable type (thickness, orientation and material) and each column represents a laminate ply.

The decoding process is illustrated in Fig. 3. It is important to note that this process is capable of handling symmetric and balanced laminates automatically, allowing the reduction of the number of design variables. In symmetric laminates, each variable represents two symmetrical layers in relation to the laminated midplane. Thus, the number of variables is half the number of layers. When considering symmetric and balanced laminates, each variable represents two adjacent layers with the same material and thickness, but opposite orientations. Then, both layers have their correspondent symmetric pairs, resulting in 4 layers for each variable. Therefore, the number of variables are the quarter part of the number of layers. As an example, when the variables shown in the Fig. 3 are decoded as symmetric and balanced laminate, the generated layup is $[0^{(0.1,CE)}_{2}\, \pm 45^{(0.4,GE)}\, 90^{(0.2,CE)}_{2}]_{s}$.

Fig. 3

Decoding process

The particle velocity is represented by matrix of identical dimensions, but containing real numbers. Therefore, after the position update using (9), the resulting values are rounded to the closest integer.

4.2 Constraint handling

It is important to note that the position update using (9) can make some particles to leave the search space defined by the lower and upper bounds of each design variable. In many works, particles that are outside the search space are not evaluated and their cognitive learning (x _P ) are not updated until they return into the search space. Furthermore, a maximum velocity modulus v _{m a x} is considered to limit particle velocity. This approach is known in the literature as “letting the particles fly”. The influence of the maximum velocity modulus in the optimization is studied in Eberhart and Shi (2000).

In the proposed algorithm the particles are not allowed to leave the search space and the side constraints are handled by the method explored in Clerc (2012), in the variant SPSO 2011. Thus, if a particle exits the search space after application of (9), the variable that violated the side constraint assumes the bound value. The component of the particle velocity associated to the violated variable is modified, as illustrated in Fig. 4. This procedure ensures that all particles positions computed along the optimization process generate valid layups, increasing the computation efficiency.

Fig. 4

Handling side constraints

The other constraints are considered in the optimization using the adaptive penalty function proposed by Deb (2000). Although PSO algorithm can be formulated without using a penalty function by ignoring the infeasible particles in the velocity update, the use of a penalty approach allows the consideration of valuable information from slightly infeasible solutions. This aspect is important for the Ring and Square Topologies, where the neighborhoods are small, and all particles in the neighborhood may be infeasible at a given iteration. Thus, the penalized objective (f _p ) for minimization problems is defined by:

$$ f_{p}(\mathbf{x}) = \left\{\begin{array}{ll} f(\mathbf{x}), & \text{if} \;\mathbf{x}\;\text{is feasible.}\\ f_{max} + \sum\limits^{m}_{l=1} \max(c_{l}(\mathbf{x}),0), & \text{otherwise.} \end{array}\right. $$

(10)

where f _{m a x} is the objective function of the worst feasible solution, c represents the constraints, and m is the number of constraints considered in the problem. This function were chosen since it does not require user defined penalty factors.

4.3 Mutation operator

The mutation operator is used in the Genetic Algorithms to maintain the diversity of the population and avoid premature convergence to non-optimal solutions. The use of mutation in the PSO to avoid premature convergence has been addressed by some authors (Nakisa et al. 2014). Higashi and Iba (2003) combined the PSO algorithm with a Gaussian Mutation operator and studied its performance in a set of benchmarks. The modified PSO version outperformed both the standard PSO and the standard GA. Ratnaweera et al. (2004) applied the mutation operator in the particle velocity, and introduced the use of linear time-varying cognitive and social factors. The results showed significant improvement in the effectiveness of the modified PSO in multimodal benchmarks.

On the other hand, in the present work the mutation operator is applied to the particle position. The operator acts in each variable of the problem (thickness, orientation and material), having a small probability (p _{m u t} ) to trigger a mutation event. First, a random number between 0 and 1 is taken, if this number is less than or equal to p _{m u t} , then a new value is generated for the variable (an integer between the lower and upper bound of the variable). Figure 5 illustrates the application of the mutation operator.

Fig. 5

Mutation operator acting in the orientation of the second ply

4.4 Laminate operators

Special operators have been applied in the optimization of laminated structures, notably in the context of Genetic Algorithms. The motivation to use these operators is to add local search mechanisms to the optimization method. The operators used in this work are Layer Swap, Layer Addition and Layer Deletion.

The use of permutation operations may play an important role in optimization strategy for different problems. Chang et al. (2010) proposed a PSO algorithm for permutation problems (PDPSO), defining a different position update rule to handle only permutation operations. Permutation Genetic Algorithms were also explored in Liu et al. (2011, 2015) in the context of bilevel optimization of composite structures.

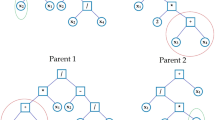
The Layer Swap operator was proposed by Le Riche and Haftka (1993) to improve the GA performance in the optimization of composite laminates. This operator was also successfully used in other works (Riche and Haftka 1995; Soremekun et al. 2001; Rocha et al. 2014). This operator is applied with a given probability (p _{s w a p} ) and swaps the positions of two plies in the layup, as shown in Fig. 6. On the other hand, the probability of a particle update corresponding exactly to a permutation of two plies is very low. It is important to note that, in the context of the Classical Laminated Theory, the swap of two plies modifies the bending stiffness (D), but does not affect the membrane stiffness (A). Therefore, this operator is important for problems with deflection, buckling, and natural frequency constraints.

Fig. 6

Swap operator

The Layer Addition and Layer Deletion operators are used in minimization problems, where the number of laminate plies is not constant. In this work, the first code related to thickness represents zero, and this value is decoded as the absence of layer, reducing the number of plies of the layup (see Fig. 7). The Layer Deletion operator has a probability p _{d e l} to set the thickness value to zero, resulting on the layer removal. The Layer Addition operator has a probability p _{a d d} to reactivate a previously removed layer. It is worth pointing out that the laminate encoding used in this work allows the position update by (9) to add and delete layers, since it can modify the layer thickness directly.

Fig. 7

Addition and deletion operators

The flowchart of the proposed Hybrid Laminate PSO algorithm is presented in the Fig. 8. Furthermore, a pseudo-code of the proposed algorithm is presented in Fig. 9. It can be noted that the mutation and laminate operators are applied after the particle position is updated using (9). The maximum number of iterations is used as termination criteria in this work. Nevertheless, other termination criteria can also be used. Furthermore, it is important to note that the proposed hybridization has a very small impact in the running time of the PSO algorithm, since the additional operations are simple and efficient in comparison with the evaluation of the structural responses.

Fig. 8

Flowchart of hybrid laminated PSO

Fig. 9

Pseudo code of the proposed algorithm

4.5 Algorithm variants

Several variants of the proposed algorithm can be obtained combining different swarm topologies and genetic operators. The performance of these variants should be properly assessed. To this end, some variants of the method are analyzed in the calibration process and numerical examples. These variants have been selected considering different operators and swarm topologies: Particle Swarm with Global Topology (PSO - G), with Ring Topology (PSO - R), with Square Topology (PSO - S) and with Global Topology and Mutation operator (PSO - GM). The method considering the Swap operator, with Global Topology and Mutation (PSO - GMS), with Ring Topology (PSO - RS) and with Square Topology (PSO - SS). The method considering the laminate operators Addition and Deletion with Global Topology and Mutation operator (PSO - GMAD), with Ring Topology (PSO - RAD) and with Square Topology (PSO - SAD). The variant MOL presented in Pedersen and Chipperfield (2010), which uses Global Topology and remove the cognitive learning behavior of the method (setting c ₁=0), is also considered. Table 1 shows each algorithm variants with its topology and genetic operators.

Table 1 Algorithm variants

5 Meta-optimization

The parameters used in an optimization method influence its performance. Unfortunately, the best parameters of an optimization method can be different for distinct problems, or even for a single problem if a different number of evaluations is considered (Pedersen 2010). Therefore, it is important to consider a set of different problems to define the default parameters of an optimization method.

Traditionally, the parameter tuning has been done by trial and error, guided by the user’s experience and recommendations found in the literature. Some works (Shi and Eberhart 1998; Trelea 2003) have tuned the parameters of the optimization algorithm using a set of benchmarks examples, including multimodal functions with many local minima. Despite being an initial reference, there is no guarantee these parameters will lead to a good effectiveness for other problems.

One way to avoid the choice of the parameters is to use adaptive parameters. Some works used PSO with linear time-varying parameters (Shi and Eberhart1999, Ratnaweera et al. 2004, Arani et al. 2013). An exploratory behavior can be obtained at the initial iterations by setting large values for inertia and cognitive factors while keeping the social factor small (e.g w=1.1, c ₁=2.0 and c ₂=0.0). Varying linearly these values during the optimization results in a exploitation behavior at the final iterations (e.g w=0.4, c ₁=0.0 and c ₂=2.0). Rao and Anandakumar (2007) proposed a PSO algorithm with self-adapted parameters during the optimization, showing improvements over some PSO variants. This self-adaptive strategy are also used in the multiobjective optimization of laminated composites in the Rao and Lakshmi (2011).

Although these studies show improvements in specific problems, the No-Free Lunch theorem (Wolpert and Macready 1997) ensure that it is not possible to these adaptive parameters lead to improvements for all problems. Therefore, in this work the problem of choosing the best parameter values for the optimization algorithm is treated as an optimization problem. This procedure is known in the literature as meta-optimization (Pedersen and Chipperfield 2010).

The meta-optimization process uses an optimization algorithm for tuning the parameters of another optimization algorithm, using a given set of problems. Normally, the objective function in the meta-optimization is the best value found by the optimizer. It is important to note that due to the non-deterministic nature of bio-inspired algorithms, many optimizations have to be processed to evaluate a single meta-optimization solution, in order to reduce the stochastic noise. For this reason, the meta-optimization process is very expensive computationally, and the use of parallel computation is highly recommended.

It is worth noting that there are few papers in this area, mainly due to the high computing power required. Grefenstette (1986) used a genetic algorithm to calibrate the parameters of another instance of GA. A similar approach was done by Meissner et al. (2006), using PSO to calibrate PSO parameters. Pedersen and Chipperfield (2010) used meta-optimization with PSO on neutral networks problems. Smit and Eiben (2009) discussed alternatives to realize meta-optimization on evolutionary algorithms.

In this paper, the optimization algorithm is calibrated for a set of laminated plate problems, considering two classes of problems: load factor maximization and weight minimization.

5.1 Swarm size and iteration number ratio

The ratio between swarm size and the number of iterations (the same as population size and number of generations in other types of evolutionary algorithms) is an important parameter that influences on the algorithm results. To describe this relation, a new parameter ρ is considered for each optimized algorithm. With the value of this parameter and the number of evaluations (N _{e v a l} ), the number of particles on the swarm (SwarmSize) can be evaluated by:

$$ \textit{SwarmSize} = \text{round}(\sqrt{\, \rho \, N_{\textit{eval}}}) $$

(11)

After obtained the SwarmSize, the number of iterations can be evaluated by:

$$ \textit{IterNum} = \text{round} \left( \frac{N_{eval}}{\textit{SwarmSize}}\right) - 1 $$

(12)

5.2 Algorithm

This work used PSO as meta-optimizer, considering the swarm topology and parameters given in Bratton and Kennedy (2007), the so-called standard PSO. The optimization parameters are treated as discrete variables. The range of each variable is presented in the Table 2.

Table 2 Meta-optimization variables range

The objective function to be maximized in the meta-optimization procedure is evaluated by the relation between the mean objective function (f _{o b j} ) obtained over N _{o p t} optimizations and the best objective function (f _{b e s t} ) of the problem:

$$ Mf_{obj} = \frac{\frac{\sum\limits_{i=1}^{N_{opt}} f_{obj}}{N_{opt}}}{f_{best}} $$

(13)

Considering a set of problems, the meta-objective function ($\overline {Mf}_{obj}$) is calculated by averaging the meta-objectives in each problem:

$$ \overline{Mf}_{obj} = \frac{\sum\limits_{i=1}^{N_{prob}} Mf_{obj}}{N_{prob}} $$

(14)

Figure 10 shows the meta-optimization process. It is important to note that (13) was written for maximization problems. In the case of minimization problems, the meta objective function is evaluated by:

$$ Mf_{obj} = \frac{f_{best}}{\frac{\sum\limits_{i=1}^{N_{opt}} f_{obj}}{N_{opt}}} $$

(15)

Fig. 10

Meta optimization process

5.3 Problem set

The meta-optimization procedure performed in this work considered a set of problems of the same class to calibrate the parameters of each variant. Two different classes of laminate optimization problems were considered: load factor maximization and weight minimization. The number of optimizations (N _{o p t} ) in each meta objective evaluation is 100. Due to the high computational cost, the meta-optimizations were performed on a SGI Cluster, with a total of 144 cores on processors AMD Opteron (TM) 6234 with 2,4 MHz frequency.

The first problem set used for parameter tuning is the load factor maximization of a simply supported laminated plate under biaxial compression (see Fig. 11). This problem was studied by others researchers (Kogiso et al. 1994; Aymerich and Serra 2008; Koide et al. 2013). The objective is to maximize the failure load, considering the Maximum Strain Criterion and buckling load factor.

Fig. 11

Laminate plate under biaxial loading

According to the Maximum Strain Criterion, the material fails when it reaches its strain limits. For thin-walled laminates subjected to compressive loads, these limit strains are ${\varepsilon ^{u}_{1}}$, ${\varepsilon ^{u}_{2}}$ and $\gamma ^{u}_{12}$. A safety factor (S _f ) is used to define an allowable limit of the material. Thus, the load factor is evaluated by the relation $\frac {{\varepsilon ^{u}_{i}}}{{\varepsilon ^{k}_{i}} S_{f}}$. These factors are computed at bottom and top of each ply and the the smallest one is taken as the laminate load factor:

$$ \lambda_{s} = \min\limits_{k} \left( \min\left( \frac{{\varepsilon^{u}_{1}}}{S_{f} |{\varepsilon^{k}_{1}}|},\frac{{\varepsilon^{u}_{2}}}{S_{f}|{\varepsilon^{k}_{2}}|} ,\frac{\gamma^{u}_{12}}{S_{f}|\gamma^{k}_{12}|}\right)\right) $$

(16)

The buckling load factor (λ _b ) of simply supported laminate plates can be evaluated by Jones (1999):

$$ \frac{\lambda_{b}}{\pi^{2}} = \frac{D_{11}\left( \frac{p}{a}\right)^{4} + E \left( \frac{p}{a}\right)^{2} \left( \frac{q}{b}\right)^{2} + D_{22} \left( \frac{q}{b}\right)^{4}} {\left( \frac{p}{a}\right)^{2} N_{x} + \left( \frac{q}{b}\right)^{2} N_{y}} $$

(17)

where E=2(D ₁₂+2D ₆₆), D _{i j} are components of the bending stiffness matrix of the composite, a and b are the dimensions of the plate, p and q are the number of half waves in x axis and y axis, respectively. This expression is evaluated for a large number of p and q values and the smallest λ _b is the buckling safety factor.

The objective function is the failure load factor:

$$ \lambda = \min (\lambda_{b}, \lambda_{s}) $$

(18)

The problem considers one constraint limiting the maximum number of contiguous plies with same angle. Therefore, the load factor maximization problem is given by:

$$\begin{array}{l} Find \; \mathbf{x}\; = \; [\theta_{1} , \theta_{2}, \ldots, \theta_{Nv}] \; that \\ \quad \quad Maximize \; \lambda \\ Subject \; to \\ \quad \quad Max \; contiguous\; plies\; \leq \; cp_{max} \end{array} $$

where x is a vector of plies orientation, N v is the number of optimization variables, c p _{m a x} is the maximum number of contiguous plies with the same angle. A set of different problems was generated considering various load cases and plate sizes. In all cases, the laminate is symmetric and balanced, the material is Graphite-Epoxy (see Table 3) with thickness of 0.127 mm. The fiber orientation is restricted to 0^∘, 45^∘ or 90^∘. Note that the Layer Addition and Layer Deletion operators are not used in this example, since the number of layers is fixed.

Table 3 Material properties for Graphite-Epoxy (GE)

In all cases the dimension a and load N _x are fixed in 508mm and 175 N/m. The values of b and N _y are defined according to b/a and N _y /N _x ratios. The following values are used for b/a: 0.25, 0.50, 0.75, 1.00, 2.00, 3.00, 4.00. For N _y /N _x : 0.25, 0.50, 0.75, 1.00. Table 4 shows the best objective function (the maximum load factor) of each case, where a total of 28 problems are defined. The buckling criterion was dominant in these results at the ratio b/a = 0.5 onwards. The Tables 5 and 6 shows the best parameters found by each method, as well the best meta-objectives reached by each one. The three methods that had higher meta-objective values are marked in bold.

Table 4 Best objectives (f _{b e s t} ) in the maximization problem set

Table 5 Parameter calibration in the maximization problem set

Table 6 Meta-objective best values in maximization problem set

The results show that the use of Layer Swap operator improves the meta-objective functions, representing an important feature of the algorithm for this kind of problems. It can be noted that Mutation operator yields improvement too. In addition, the variant PSO - GMS obtained the best results.

The second problem set considers a similar example with dispersed laminates. These laminates features angles with differences smaller than the traditional laminates, which have Δ𝜃=45^∘(𝜃∈[0^∘, ±45^∘, 90^∘]). The use of dispersed laminates enables to increase the loading capacity of fiber reinforced composite structures. Sebaey et al. (2011) studied the optimization of dispersed laminated using ACO, increasing the buckling load of composite panels subject to biaxial loading up to 8 %. It is expected that the PSO meta-heuristic presents good performance in dispersed laminates, as the small increments between allowable orientations allow these variables become almost continuous, for which PSO was originally formulated.

This meta-optimization consider a Δ𝜃=15^∘, resulting in the following orientations: 0^∘,15^∘,30^∘,45^∘,60^∘,75^∘,90^∘. The same material, dimensions and loading used in the last example are considered. A new set of best solutions was evaluated and is shown in the Table 7. Is worth emphasizing that the use of dispersed laminated allowed an increased load capacity of up to 14 %.

Table 7 Best objectives (f _{b e s t} ) in the maximization problem set considering Δ𝜃=15^∘

The best parameters and meta-objective are shown in the Tables 8 and 9. The PSO - GMS was the better variant.

Table 8 Parameter calibration in the maximization problem set for Δ𝜃=15^∘

Table 9 Meta-objective best values in the maximization problem set for Δ𝜃=15^∘

Fig. 12

Laminate plate under biaxial and shear loads

The third problem set used for parameter tuning is the minimization of simply supported laminated plate subjected to biaxial and shear loading (see Fig. 12). This problem was considered by Lopez et al. (2009). The objective is to minimize the weight of the laminate, subjected to a strength constraint evaluated using the Tsai-Wu Criterion (Tsai and Wu 1971). According to this criterion, a thin-walled lamina fails when the following condition is satisfied:

$$ F_{11} \,{\sigma_{1}^{2}} + 2 \, F_{12} \, \sigma_{1} \, \sigma_{2} + F_{22} \, {\sigma^{2}_{2}} + F_{12} \,\tau_{12}^{2} + F_{1} \, \sigma_{1} + F_{2} \, \sigma_{2} \geq 1 $$

(19)

where F _{i j} are parameters that are evaluated in function of strength properties X _T , X _C , Y _T , Y _C and S ₁₂ (Daniel and Ishai 2006). Considering a safety factor S _f that multiply the stresses so that the material point is in the failure threshold, it can be shown that:

$$ {S_{f}^{2}}\,c + S_{f}\,d - 1 = 0 $$

(20)

where $c = F_{11} \,{\sigma _{1}^{2}} + 2 \, F_{12} \, \sigma _{1} \, \sigma _{2} + F_{22} \, {\sigma ^{2}_{2}} + F_{12} \,\tau _{12}^{2}$ and d = F ₁ σ ₁ + F ₂ σ ₂. The safety factor is the positive root evaluated by the expression:

$$S_{f} = \frac{-d \pm \sqrt{d^{2}+4\,c}}{2\,c} $$

The safety factor is evaluated for all layers, the lowest of them is used in the constraint. Therefore, the weight minimization problem is defined as:

$$\begin{array}{l} Find \; \boldsymbol{x} \; = \; [ (e_{1}, \theta_{1}) , (e_{2}, \theta_{2}), \ldots, (e_{Nv} ,\theta_{Nv})] \; that \\ \quad \quad Minimize \; W \\ Subject \; to \\ \quad \quad S_{f} \geq 1 \end{array} $$

In this work, F ₁₂=0 was used in the numerical calculations.

A set of different problems was generated considering various loads. The laminate is symmetric and balanced. The length and width of the plate are 1.0 m, each ply is 0.1 mm thick. The material elastic properties are E ₁ = 116.600 MPa, E ₂ = 7673 MPa, G ₁₂ = 4173 MPa, Poisson’s ratio v ₁₂ = 0.27, and mass density 1605 kg/m ³. The strength properties are presented in the Table 10.

Table 10 Material strength properties for the minimization problem set

Nine different problems are used in the meta-optimization. Each one is related to a load case and is obtained combining biaxial load and shear load, as shown in Fig. 12 and Table 11. The obtained results for the meta-optimization are shown in Tables 12 and 13.

Table 11 Best objectives (f _{b e s t} ) in the minimization problem set

Table 12 Parameter calibration in the minimization problem set

Table 13 Meta-objective best values in the minimization problem set

The results show that the use of Layer Addition and Layer Deletion operators improves the methods for the problem set. In this case, the variant PSO - SAD presented the best results.

6 Results and discussion

The Hybrid Laminate PSO variants are explored in this section. Initially, two benchmarks will be used to validate the proposed algorithm. Next, the variants are compared in three examples, based on their reliability and mean best objective function along the number of evaluations. The number of optimizations used to trace each curve is 100. Finally, the proposed algorithm is applied to a multiobjective optimization problem.

The reliability (R e l) is defined as the ratio between the number of optimizations that found the problem best value (N _{b e s t} ) and the total number of optimizations (N _{o p t} )

$$ Rel (\%) = \frac{N_{best}}{N_{opt}} $$

(21)

The variants of the proposed algorithm will be compared with the Standard PSO (PSO - STD) algorithm presented in Bratton and Kennedy (2007), which considers a fixed number of 50 particles and the Ring Topology. Moreover, the Quantum Behaved PSO (QPSO) and Dynamically Reconfigurable Quantum PSO (DQPSO) presented in Lakshmi and Rao (2013) will also be considered. In QPSO, the particle movement is defined based in the principles of the Quantum Theory. This method only have one parameter β. The variant DQPSO improves QPSO considering groups of sub-swarms and a shuffling scheme. Here, both methods consider a fixed number of 24 particles and β varying linearly from 1.0 to 0.3 along the iterations. In the numerical examples DQPSO will use 4 groups with 6 particles each and a shuffling process when 20 %, 40 %, 60 % and 80 % of the total number of iterations is reached.

6.1 Benchmarks

Two different benchmarks will be used to assess the accuracy and efficiency of the proposed algorithm. The first one is the problem used in the maximization calibration procedure, which was optimized by Kogiso et al. (1994) using a GA. The plate dimensions are a=0.508 m and b=0.127 m. The load cases considered are N _y /N _x =0.125 and 0.250, with N _x =175 N/m. Table 14 shows the optimal layup obtained in each case, which are identical to the solutions obtained by Kogiso et al. (1994). Table 15 shows the number of generations x reliability for each method considered. The number of evaluations used in each variant is similar the values obtained by Kogiso et al. (1994). It is worth noting that for the Square Topology sometimes it is not possible to get a closer value for the number of evaluations because of the matrix format that the swarm must satisfy. The results show that the variants of the proposed algorithm obtained excellent results.

Table 14 Optimal layup found in the maximization benchmarks

Table 15 Number of generations x Reliability in maximization benchmarks

The second benchmark is the problem used in the minimization calibration procedure, which was optimized by Lopez et al. (2009) using a GA. Three load cases are considered, the load case 1 is N _x = N _y =3M N/m and N _{x y} =0.5M N/m, the load case 2 is N _x = N _y =−3M N/m and N _{x y} =0.5M N/m and the load case 3 is N _x = N _y =−3M N/m and N _{x y} =1M N/m. Table 16 shows the optimal layup obtained in each case, which present the same weights (objective function) obtained in Lopez et al. (2009). Table 17 shows the number of generations x reliability for each method considered. The number of evaluations considered in each variant is similar to the values obtained by Lopez et al. (2009). Therefore, the proposed algorithm obtained excellent results in terms of both accuracy and efficiency.

Table 16 Optimal layups found in the minimization benchmarks

Table 17 Minimization benchmarks results

6.2 Example 1

This problem consists in the optimization of a laminated plate subjected to biaxial compression and shear loads (Chang et al. 2010; Liu et al. 2000). The objective is to maximize the buckling load factor, but in this problem the shear buckling (λ _{s h} ) is also considered. The shear buckling load can be evaluated approximately by the expression obtained for a plate with infinite length (Whitney 1987), as:

$$ \lambda_{sh} = \left\{ \begin{array}{ll} \frac{4 \beta_{1}\sqrt[4]{D_{11}D^{3}_{22}}}{b^{2} N_{xy}} & \quad 1 \leq {\Gamma} \leq \infty \\ & \\ \frac{4 \beta_{1} \sqrt{D_{22}(D_{12}+2D_{66})}}{b^{2} N_{xy}} & \quad 0 \leq {\Gamma} \leq 1 \end{array} \right. $$

(22)

where the parameter Γ is computed by:

$$ {\Gamma} = \frac{D_{11}D_{22}}{D_{12}+2D{66}} $$

(23)

and the parameter β ₁ is interpolated from Table 18. The combined buckling load factor (λ _c ) can be approximated by:

$$ \frac{1}{\lambda_{c}} = \frac{1}{\lambda_{b}} + \frac{1}{\lambda_{sh}^{2}} $$

(24)

The objective function of the problem is the critical buckling factor defined as:

$$ \lambda = \min(|\lambda_{sh}|,\lambda_{c}) $$

(25)

The plate is square with edge dimension equal to 24 in. The loads are N _x =20000 lb/in, N _y =2000 lb/in and N _x y=1000 lb/in. The laminate is symmetric, balanced and has a total of 144 plies. Each ply has thickness of 0.005 in and the fiber orientation can be 0^∘, 45^∘ or 90^∘. The material properties are presented in the Table 19. The problem is defined as follows:

$$\begin{array}{l} Find \; \boldsymbol{x} \; = \; [ \theta_{1} , \theta_{2}, \ldots, \theta_{Nv}] \; that \\ \quad \quad Maximize \; \lambda \\ Subject \; to \\ \quad \quad Max \; contiguous\; plies\; \leq \; cp_{max} \end{array} $$

where c p _{m a x} is 4, the number of variables (N v) is 36, corresponding to 144 symmetric-balanced plies. The parameters used by each method are the parameters found in the first meta-optimization of maximization problem set (Δ𝜃=45^∘).

Table 18 Coefficient β ₁ for λ _{s h} (Chang et al. 2010)

Table 19 Material properties for Example 1

The optimal layup of this problem is given in Table 20. The Figs. 13 and 14 show, respectively, the reliability and mean of the best objectives obtained by each algorithm.

Fig. 13

Reliability x number of evaluations on Example 1

Fig. 14

Mean best x number of evaluations on Example 1

Table 20 Optimal layup of Example 1

According to the results, the best variants were PSO - GMS and PSO - SS. On the other hand, QPSO, DQPSO, PSO - R and PSO - GM provided poor results for this example. The use of the mutation operator alleviates the problem of convergence to non-optimal solutions, but can also slow down the convergence rate. It is also worth noting that the MOL variant performed better than standard PSO, but was inferior to most of the variants of the proposed algorithm.

The results also show that the consideration of the operator Layer Swap leads to significant improvement in all variants, especially in PSO - RS. Moreover, the square topology (PSO - S) led to excellent results, even when used without the permutation operator.

6.3 Example 2

The second example is the same one used in the minimization meta-optimization procedure discussed in the Section 5.3. The plate dimensions, material properties and problem variables are the same described previously. However, a different loading (N _x =−2 MN/m, N _y =6 MN/m and N _{x y} =0.5 MN/m) are considered here.

The problem has many optimal solutions, with the minimum weight of 144.85 N (considering g=9.81 m/s ²). It is important to note that stacking sequence does not change the laminate strength, since only the number of layers of each angle can change it. Therefore, the permutation operator (Layer Swap) will not be used in this example. Table 21 show the best layups obtained for this problem. The reliabilities and mean of the best solutions are shown in Figs. 15 and 16, respectively.

Fig. 15

Reliability x number of evaluations on Example 2

Fig. 16

Mean best x number of evaluations on Example 2

Table 21 Optimal solutions of Example 2

All variants proposed in this work obtained the optimal solution and presented a much better performance than the standard PSO. It is interesting to note that the use of Layer Add and Layer Del operators did not led to performance improvement. Thus, these operators may not be necessary, since the encoding adopted in this work (Section 4.1) allows the addition and deletion of layers to occur naturally.

6.4 Example 3

The third example is the same used in the maximization meta-optimization procedure discussed in Section 5.3, but with different data. The material properties and problem variables are the same ones described previously, but the geometry and loading are different. The plate dimensions are a=508 mm and b=203.2 mm (b/a=0.4), and the loads are N _x =175 N/m and N _y =105 N/m (N _y /N _x =0.6).

The problem was optimized considering conventional (Δ𝜃=45^∘) and dispersed laminates (Δ𝜃=15^∘ and Δ𝜃=5^∘). The optimization of conventional laminates was carried-out using the parameters calibrated with the maximization problem set for Δ𝜃=45^∘ (Table 5), while the dispersed laminates were optimized using the parameters obtained for the maximization problem set with Δ𝜃=15^∘ (Table 8).

The optimal solution using conventional orientations has λ = 3568.58, corresponding to the buckling factor. The optimization algorithms found multiple optimal solutions and some of them are shown in the Table 22. The reliabilities and mean of the best objectives are shown respectively in the Figs. 17 and 18.

Fig. 17

Reliability x number of evaluations on Example 3 (Δ𝜃=45^∘)

Fig. 18

Mean best x number of evaluations on Example 3 (Δ𝜃=45^∘)

Table 22 Optimal layup of Example 3 (Δ𝜃=45^∘)

The results show that all variants of the proposed algorithm presented better performance than the standard PSO for conventional laminates. Once again, the use of the Layer Swap operator led to significant performance improvement, specially for the Ring Topology. The variant PSO - GMS obtained the best results, but PSO - RS and PSO - SS also performed well. It is important to note that PSO - GM obtained good results, contrary to its performance in Example 2. The quantum variants also performed better in this case, but were outperformed by the variants of the proposed algorithm.

The optimal layups for dispersed laminates with Δ𝜃=15^∘ are shown in Table 23. The reliability and mean of the best objectives are presented in Figs. 19 and 20. The optimal layup found for dispersed laminates with Δ𝜃=5^∘ is presented in Table 24. The reliability and mean of the best objectives are presented in Figs. 21 and 22.

Fig. 19

Reliability x number of evaluations on Example 3 (Δ𝜃=15^∘)

Fig. 20

Mean best x number of evaluations on Example 3 (Δ𝜃=15^∘)

Fig. 21

Reliability x number of evaluations on Example 3 (Δ𝜃=5^∘)

Fig. 22

Mean best x number of evaluations on Example 3 (Δ𝜃=5^∘)

Table 23 Optimal layup of Example 3 (Δ𝜃=15^∘)

Table 24 Optimal layup of Example 3 (Δ𝜃=5^∘)

The optimization of dispersed laminates is closer to a continuous problem than the optimization of conventional laminates. However, even for dispersed laminates, the variants of the proposed algorithm presented better performance than the standard PSO, MOL and the Quantum PSO variants, specially with respect to the reliability. As in the previous examples, the results variants including the Layer Swap operator performed better than the others. The variants PSO - GMS and PSO - SS obtained the best results for dispersed laminates.

6.5 Multiobjective optimization

The last problem of this work consists in a minimization of cost and weight of a hybrid laminated plate subjected to a buckling constraint (Rao and Lakshmi 2009). Each ply has thickness equal to 0.127 mm and can be made of graphite-epoxy or glass-epoxy. The properties of these materials are shown in Table 25. The bi-objective optimization problem is defined as:

$$\begin{array}{l} Find \; \boldsymbol{x} \; = \; [ (e_{1}, \theta_{1}, m_{1}) , (e_{2}, \theta_{2},m_{2}), \ldots, (e_{Nv} ,\theta_{Nv}, m_{Nv})] \; that \\ \quad \quad Minimize \; W \; \text{and}\; C\\ Subject \; to \\ \quad \quad \lambda_{b} \leq \lambda_{lim} \end{array} $$

with λ _{l i m} =100. The laminate is symmetric and balanced, with 𝜃∈{0^∘,45^∘,90^∘}. The maximum number of layers is 200. The Pareto front of the multiobjective optimization problem can be obtained using the Weighted Compromise Programming Method (WCP) (Athan and Papalambros 1996). In this method, a single objective is defined considering weighted objectives. Here, the resultant objective function is:

$$ f_{obj} = \left[ w\,\frac{W-W_{min}}{W_{max}-W_{min}}\right]^{m} + \left[ (1-w)\, \frac{C-C_{min}}{C_{max}-C_{min}}\right]^{m} $$

(26)

where w is the weight factor of the minimization plate weight objective, W is the plate weight, C is the plate cost and m is a numerical factor. W _{m i n} , W _{m a x} , C _{m i n} and C _{m a x} are the limit values used to normalize the objectives. C _{m i n} and W _{m a x} are obtained considering only the cost minimization objective (w=0), and W _{m i n} and C _{m a x} are obtained considering only the weight minimization objective (w=1).

Table 25 Material properties for composites considered in M

Using an appropriate m the WCP method can trace convex and non-convex Pareto fronts. The optimal layups are obtained by performing single objective optimizations for different values of w. Here, m=2 and w vary from 0 to 1 in steps of 0.05. The variant PSO - SS with the parameters presented in Table 5 without considering the Layer Addition and Layer Deletion operators was used to obtain the Pareto optimal solutions presented in Table 26. The Pareto front obtained here, as well the points given in Rao and Lakshmi (2009), are shown in Fig. 23. It can be noted that there is a very good agreement between the two fronts, with the proposed hybrid algorithm presenting a slightly better solution for the cost minimization problem.

Fig. 23

Pareto front obtained in the Multi-objective optimization example

Table 26 Results obtained in the bi-objective problem

7 Conclusion

A hybrid algorithm for optimization of laminated composites using discrete variables was proposed in this paper. This algorithm uses a specially designed variable encoding and combines the PSO heuristics with GA operators. Several different variants of the proposed algorithm were generated combining different swarm topologies with different sets of genetic operators. The comparison of the variants was preceded by the calibration of the algorithm parameters via meta-optimization, ensuring that best parameters were considered for each method, avoiding biased results. The proposed algorithm presented consistently better performance than the standard PSO, the MOL and the quantum variants. Although these are good algorithms in general, their performance in the optimization of composite structures is impaired by the absence of the laminate operators.

According to the obtained results, the use of permutation operator led to significant improvements in the algorithm performance, for both traditional and dispersed laminates. The use of the Global Topology with mutation operator led to a good performance. However, the Square Topology also led to a good performance, even without using the mutation operator.

Since an optimization method with fewer input parameters is more convenient and easier to use, we suggest that the variant with Square Topology and without mutation should be considered as the standard for the proposed PSO method. In addition, this standard variant includes the permutation operator, but does not include the addition and deletion operators. Besides being simpler, the standard variant presents good performance in most of the cases. However, other variants can present better performance for specific problems.