Keywords

1 Introduction

Functionally graded materials are different from the conventional homogeneous material in which two materials are heterogeneously mixed to obtain the predefined functionally requirements. Due to its spectacular functionalities, it has wide applications in engineering science such as automobiles, marine, sports, aerospace and civil structures. Commonly, ceramic and metals are constitutes of FGM, and their volume fraction is smoothly and continuously distributed from one surface to another. Due to the continuous mixture of materials, the interface joint is absent inside the FGM structure. So that FGM can perform service in a high-temperature environment. The main lacuna of the composite structure is the delamination of laminates at the higher temperature due to the poor bonding between the interfaces of two laminates. This problem of the composite structure can be sort out by employing the functionally graded materials to maintain structural integrity. As the application and development of functionally graded materials rise dramatically, accurately modelling their mechanical properties is greatly needed.

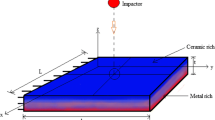
Many researchers carried out work on the material modelling and dynamic analysis of functionally graded materials. Xu and Meng [1] determined material properties of FGM beams by using the three different distribution laws, namely, power law, sigmoid law and exponential law, and performed the dynamic analysis of FGM beams by employing the analytical method. Naebe and Shirvanimoghaddam [2] presented the review paper on the material selection, fabrication and material modelling of functionally graded materials. Moita et al. [3] carried out structural and sensitivity analysis along with the material modelling and sizing optimization of FGM structures by employing the high-order shear deformation theory. The power law index and thickness are considered as design parameters, while mass, displacement, natural frequency and critical loads are taken as response parameters. Burlayenko et al. [4] applied finite element (FE) method for thermal analysis of FGM plates as well as material modelling is also carried out by using power law distribution. Kumar et al. [5] applied dynamic stiffness method for dynamic analysis of FGM rectangular plates with different boundary conditions. Classical plate theory is employed for the formulation of dynamic stiffness method. Attia and Rahman [6] carried out free vibration analysis of FGM nano-beams with considering the influence of microstructure rotation and surface energy by using the Bernoulli–Euler beam theory and found the effects of the power law index, material damping, surface elasticity, thickness and Poisson’s effects. Zur [7] employed quasi-Green's function method for the free axisymmetric and non-axisymmetric vibration of FGM plates and determined the effects of boundary conditions, gradient index and core radius. Salinic et al. [8] performed free vibration analysis of FGM structure with different geometry by using the symbolic–numeric method of initial parameters approach. Further, some researches carried out work in the past on the dynamic analysis of FGM and composite structures [9,10,11,12,13,14,15,16,17,18,19]. In the present paper, the effects power law exponent on the stochastic free vibration of FGM cantilever plate are determined. The variability in the material properties is considered as the input variables with \(\pm 10\%\) degree of stochasticity. The direct Monte Carlo simulation required large number of simulation which leads to high cost and time. To mitigate this lacuna of Monte Carlo simulation, a surrogate-based MARS model is coupled with the finite element formulation. Figure 1 illustrates the geometric view of cantilever FGM plate.

Fig. 1
figure 1

Geometric view of functionally graded material cantilever plate

Full size image

2 Mathematical Formulation

The dynamic equation of motion of the system can be expressed as [20]

$$\left[ {\tilde{M}\left( \Theta \right)} \right]\left\{ {\ddot{\delta }} \right\} + \left[ {\tilde{C}\left( \Theta \right)} \right]\left\{ {\dot{\delta }} \right\} + \left[ {\tilde{K}\left( \Theta \right)} \right]\left\{ \delta \right\} = \left[ {\overline{F}} \right],$$
(1)

where \(\left[ {\tilde{M}\left( \Theta \right)} \right]\), \(\left[ {\tilde{C}\left( \Theta \right)} \right]\), \(\left[ {\tilde{K}\left( \Theta \right)} \right]\) are the randomised mass matrix, damping matrix and stiffness matrix, respectively, while \(\left[ {\overline{F}} \right]\) is the external applied force. \(\left( \Theta \right)\) represents the degree of stochasticity. For the free vibration analysis without damping, Eq. (1) becomes

$$\left[ {\tilde{M}\left( \Theta \right)} \right]\left\{ {\ddot{\delta }} \right\} + \left[ {\tilde{K}\left( \Theta \right)} \right]\left\{ \delta \right\} = 0.$$
(2)

For free vibration displacement vector can be written as

$$\left\{ \delta \right\} = \left[ \psi \right]\sin \phi t,$$
(3)
$$\left\{ \delta \right\}^{\prime \prime } = - \phi^{2} \left[ \psi \right]\sin \phi t,$$
(4)

where \(\left[ \psi \right]\) represents the Eigen vector, \(\phi\) is the Eigen value or natural frequency. So the Eq. (2) becomes

$$- \phi^{2} \left[ {\tilde{M}\left( \Theta \right)} \right]\left\{ \psi \right\}\sin \phi t + \left[ {\tilde{K}\left( \Theta \right)} \right]\left\{ \psi \right\}\sin \phi t = 0,$$
(5)
$$\left( {\left[ {\tilde{K}\left( \Theta \right)} \right] - \phi^{2} \left[ {\tilde{M}\left( \Theta \right)} \right]} \right)\left\{ \psi \right\} = 0.$$
(6)

The material properties of constitute materials of functionally graded materials are varying continuously and smoothly throughout the depth of the plate. The local volume fraction \(\left( {f\left( z \right)} \right)\) of FGM plate which follows the power law can be expressed as [21]

$$f\left( z \right) = \left( {\frac{{h + \frac{t}{2}}}{t}} \right)^{p} ,$$
(7)

where p is the power law exponent, t is the thickness of FGM plate, h = –t/2 for top surface and h = t/2 for bottom surface. After calculation of local volume fraction, the material properties of FGM can be determined by using the rule of mixture as

$$R\left( z \right) = f\left( z \right)R_{c} + \left[ {1 - f\left( z \right)} \right]R_{m} ,$$
(8)

where R is the material properties.

3 Multivariate Adaptive Regression Splines (MARS)

Friedman pioneered to propose MARS for establishing the relationship between the set of input variables and target [22]. Similar to a machine learning model, MARS also uses iterative approach. There is no assumption considered for the functional relationship between response variable and predictor variable. MARS is the nonparametric regression statistical approach in which multiple linear regression model are created cross the range of predictor variables. In the first step of MARS model, training data sets are divided into splines (linear segments) with different slops called basic functions. Each set of training data have a separate regression model. The regression lines are connected together by using the knots. The MARS model searches the best location for the knots having the pair of basic functions [23]. The relationship between the environmental variable and responses are described by the basic functions. Each pair of basic function at the knot gives the maximum reduction in the sum-of-squares residual error. The basic functions are increased continuously until the number of basic function reached maximum level. This process causes the complicated and over fitted model. In the second step of MARS algorithm, the insignificant redundant basic function is removed [24]. The MARS model works well also for large number of input variables. Another advantage of this model is that it automatically finds the interaction between input and response variables. The MARS model \(f\left( x \right)\) with basic function and interaction can be written as [25]

$$f\left( x \right) = \gamma_{0} + \sum\limits_{n = 1}^{M} {\gamma_{n} \beta_{n}^{f} \left( {z_{i} } \right)} ,$$
(9)

where \(\beta_{n}\) is the basic function and \(\gamma\) is the constant coefficient, which is calculated by least-square method. The basic function can be written as

$$\beta_{n}^{f} \left( {z_{i} } \right) = \prod\limits_{i = 1}^{{i_{n} }} {\left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right]}_{T}^{g} ,$$

where \(i_{n}\) denotes the interaction order, \(Y_{i,n} = \pm 1\), \(z_{{j\left( {i,n} \right)}}\) represents the jth variable, \(\,\,1 \le j\left( {i,n} \right) \le m\), and \(q_{i,n}\) is the knot position of corresponding variables. ‘T’ denotes truncated power function. The basic function may be in following shapes.

$$\begin{aligned} \left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right]_{T}^{g} & = \left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right]^{g} \;{\text{for}}\,\left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right] < 0\, \\ & \left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right] = 0,\,{\text{otherwise}} \\ \end{aligned}$$
(10)

Thus, all basic function can be written as

$$A = \left\{ {\left[ {Y_{i,n} \left( {z_{{j\left( {i,n} \right)}} - q_{i,n} } \right)} \right]_{T}^{g} } \right\},\,\,\,q \in \left\{ {z_{1j} ,\,z_{2j} ,\,......z_{Mj} } \right\}.$$
(11)

In the present study, combined variation in material properties is considered as input variables, while first three natural frequencies are taken as responses. Different values of power law exponent such as p = 1, 5, 10 are considered. For each value of power law exponent, deterministic material properties of FGM plate are calculated. The degree of stochasticity in material properties is taken as \(\pm 10\%\). The stochastic input variables can be represented as

$$\Psi (p) = \Phi [p,\,\,\{ E(z)\} (\Theta ),\,\,\{ G(z)\} (\Theta ),\,\,\{ \rho (z)\} (\Theta ),\,\,\{ \mu (z)\} (\Theta )],$$

where \(\Phi\) is the Monte Carlo operator. Figure 2 represents the flowchart of stochastic free vibration analysis by using the MARS model.

Fig. 2
figure 2

Flowchart of free vibration analysis by using the MARS model

Full size image

4 Results and Discussion

The material properties of the constitutes are considered as Em = 70 Gpa, Ec = 151 Gpa, \(\upsilon_{m} = 0.25\), \(\upsilon_{c} = 0.30\), \(\rho_{m} = 2707\) Kg/m3, \(\rho_{c} = 3000\) Kg/m3 where \(E,\upsilon ,\rho\) are the elastic modulus, Poisson’s ratio and mass density, respectively. Subscript ‘c’ and ‘m’ represent the ceramic and metal. The validation of the results is carried out in two ways, namely, scatter and probability density function (PDF) plots. Figure 3 illustrates the scatter plots between the original finite element model and MARS model for first three natural frequencies with considering different sample size (n). The scatter plots reveal that sample size 2048 is well fitted with the original FE model. The accuracy of the results increased with an increase in the number of sample size. Figure 4 represents the PDF plots for first three natural frequencies of Monte Carlo simulation and the MARS model, and found that both have almost same results. The sample size 2018 is sufficient to predict the response by using MARS model. The effect of power law index on the natural frequencies are determined by using the MARS model and shown in Fig. 5. The Fig. 5 illustrates that with the increase in the power law exponent (p) all natural frequencies decreased. Because with increase in the power law exponent (p > 1), all material properties of functionally graded material suddenly decreased at the top surface (at the ceramic rich surface), ultimately reduction in the stiffness of the plate as shown in Fig. 6. The number of sample size taken for model formation is 2048 so that computational time is reduced significantly, while for the same results, the Monte Carlo simulation required 10,000 number of simulation.

Fig. 3
figure 3

Scatter plots of first three natural frequencies between original FE model and MARS model

Full size image
Fig. 4
figure 4

PDF plots of first three natural frequencies for MCS and MARS with n = 2048

Full size image
Fig. 5
figure 5

Effect of power law index (p) on the first three natural frequencies by using MARS model

Full size image
Fig. 6
figure 6

Variation in elastic modulus across the depth of plate due to change in power law index (p)

Full size image

5 Conclusions

The novelty of the present paper includes the stochastic natural frequency analysis of FGM plates by using the MARS model. The material modelling of the FGM plate is carried out by using the power law distribution. Different values of power law exponents are considered as input variables. For \(\pm 10\%\) degree of stochasticity in the material properties, it is observed that the power law exponent influences the material properties which causes to vary the natural frequencies of FGM plates. The validation of the MARS model is carried out by using the scatter plot and probability density function plot, respectively. The power law exponent and natural frequencies are found to be inversely related with each other. In future, the present model can be applied for both static and dynamic analysis of complex structures. In the present study, FGM plate is considered, but in future, this work can be extended for other structures such as sandwich structure, honeycomb structures along with the different surrogate models such as artificial neural network, polynomial neural network and radial basis function. Other boundary condition may be considered for different structures.