Modified Ambiguity Function and Wigner Distribution Associated With Quadratic-Phase Fourier Transform

Abstract

The ambiguity function (AF) and Wigner distribution (WD) play an important role not only in non-stationary signal processing but also in radar and sonar systems. In this paper, we introduce modified ambiguity function and Wigner distribution associated with quadratic-phase Fourier transform (QAF, QWD). Moreover, many various useful properties of QAF and QWD are also proposed. Marginal properties and Moyal’s formulas of these distributions have elegance and simplicity comparable to those of the AF and WD. Besides, convolutions via quadratic-phase Fourier transform are also introduced. Furthermore, convolution theorems for QAF and QWD are also derived, which seem similar to those of the classical Fourier transform (FT). In addition, applications of QAF and QWD are established such as the detection of the parameters of single-component and multi-component linear frequency-modulated (LFM) signals.

1 Introduction

The AF and WD are effective tools in signal processing as well as in many other application fields, especially in applications to the detection of LFM signals. As we all know, the conventional AF and WD of a signal $f \in L^2({\mathbb {R}})$ are defined as [7, 8]

$$\begin{aligned} \mathcal{A}\mathcal{F}_f(\tau ,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) \ f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i\omega t}\textrm{d}t, \end{aligned}$$

(1.1)

$$\begin{aligned} \mathcal{W}\mathcal{D}_f(t,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i\omega \tau }\textrm{d}\tau . \end{aligned}$$

(1.2)

Conventional convolution is one of the most extensively used concepts in mathematics with applications across diverse fields of filter designing, optics, and quantum physics. Namely, it can be used in signal and image processing. We recall that if $f, g \in L^2({\mathbb {R}}),$ then for

$$\begin{aligned} (f*g)(t) = \int _{{\mathbb {R}}}f(\tau )g(t-\tau )d\tau . \end{aligned}$$

(1.3)

Moreover, the relationships between AF (WD) and the conventional convolution can be given by [8]

$$\begin{aligned} {\mathcal {A}}_{f*g}(\tau ,\omega )= & {} \frac{1}{2\pi }\int _{\mathbb R}{\mathcal {A}}_{f}(u,\omega )\cdot {\mathcal {A}}_{g}\left( \tau -u,\omega \right) \textrm{d}u, \end{aligned}$$

(1.4)

$$\begin{aligned} {\mathcal {W}}_{f*g}(t,\omega )= & {} \frac{1}{2\pi }\int _{\mathbb R}{\mathcal {W}}_{f}(u,\omega )\cdot {\mathcal {W}}_{g}(t-u,\omega )\textrm{d}u. \end{aligned}$$

(1.5)

Let parameters $a, b, c, d, e \in {\mathbb {R}}$ (with $b\ne 0$) and $\Lambda =(a,b,c,d,e)$. With minor modifications to the definition of quadratic-phase Fourier transform (QFT) in [3], the QFT of signal $f\in L^2({\mathbb {R}})$ is defined by

$$\begin{aligned} {\mathcal {Q}}_f^{\Lambda }(\omega ):= \frac{1}{\sqrt{2\pi }} \int _{{\mathbb {R}}}\textrm{e}^{-i\left( a\omega ^{2}+b\omega t+ct^{2}+d\omega +et\right) }f(t)\textrm{d}t. \end{aligned}$$

(1.6)

As can be seen, the QFT is a generalization of FT and several other transforms. Some of the special cases of the QFT are listed in Table 1. Furthermore, some useful properties of QFT can be found in [3]. Having in mind that the QFT and convolutions associated with QFT have wide applications in both theory and applications e.g., in harmonic analysis and differential equations [3, 4] as well as in signal processing [2, 5, 11]. Since two extra parameters d, and e, then the applications of QFT are not only similar to those of the linear canonical transform (LCT) but they are also more flexible than the original LCT.

Table 1 Some of special cases of the QFT

Recently, ambiguity function and Wigner distribution associated with LCT have become novel signal detection tools, particularly the detection of LFM signals which are frequently encountered in wireless communications and other fields [1, 8, 9, 11, 13, 15,16,17,18]. Therefore, extending and generalizing the ambiguity function, and Wigner distribution associated with LCT would be meaningful and worthwhile.

This paper introduces definitions of QAF and QWD. They depend on only three parameters b, c, and e. Moreover, they seem simpler than the QWD proposed in [11] and have a wide range of potential applications. The marginal properties, Moyal’s formulas, and convolution theorems for QAF and QWD are similar to those of AF and WD. Besides, five new convolutions associated with QFT as well as their impact on QAF and QWD are also studied. In addition, as the applications, the detection of the parameters of single-component and multi-component LFM signals are also investigated.

The rest of this paper is organized as follows. Section 2 introduces the definition of QAF and QWD. Some important properties including the shifting, conjugate-symmetry, marginal, and Moyal’s formulas are also discussed in detail. Furthermore, their relationships with other time-frequency transforms such as the Short-time Fourier transform (STFT), the short-time quadratic-phase Fourier transform (STQFT), and the QFT are also given. More importantly, the convolution theorems for QAF and QWD are derived in Sect 3. In Sect. 4, the applications of the QAF and QWD for the detection and parameter estimation of LFM signals embedded in white Gaussian noise are investigated. The work ends with a conclusion in Sect. 5.

2 The Modified Ambiguity Function and Wigner Distribution Associated With QFT

2.1 Definition of QAF and QWD

Using (1.1), (1.2), and (1.3), we can express the AF and WD through the conventional convolution as follows

$$\begin{aligned} {\mathcal {A}}_f(\tau ,2\omega )= & {} [f(\tau )\textrm{e}^{-i\omega \tau }]*[f(-\tau )\textrm{e}^{-i\omega \tau }]^*, \end{aligned}$$

(2.7)

$$\begin{aligned} {\mathcal {W}}_f\left( \frac{t}{2},\omega \right)= & {} 2[f(t)\textrm{e}^{-i\omega t}]*[f(t)\textrm{e}^{-i\omega t}]^*, \end{aligned}$$

(2.8)

where the superscript “*” denotes the complex conjugation. Therefore, replacing $\textrm{e}^{-i\omega \tau }$ by $\textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}$ in (2.7) and changing variable $y=t+\dfrac{\tau }{2}$, we then have

$$\begin{aligned}&[f(\tau )\textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}]*[f(-\tau )\textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}]^*\nonumber \\&=\int _{{\mathbb {R}}}f(y)\textrm{e}^{-i(a\omega ^2+b\omega y+cy^2+d\omega +ey)}f^*(y-\tau )\textrm{e}^{i\left[ a\omega ^2+b\omega (\tau -y)+c(\tau -y)^2+d\omega +e(\tau -y)\right] }\textrm{d}y\nonumber \\&=\int _{{\mathbb {R}}}f\left( y\right) f^*\left( y-\tau \right) \textrm{e}^{-i(2b\omega +2c\tau +2e) \left( y-\frac{\tau }{2}\right) }\textrm{d}y\nonumber \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e} ^{-i(2b\omega +2c\tau +2e)t}\textrm{d}t. \end{aligned}$$

(2.9)

Similarly, replacing $\textrm{e}^{-i\omega t}$ by $\textrm{e}^{-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}$ in (2.8) and performing the change of variable $x=\dfrac{t}{2}+\dfrac{\tau }{2}$ give us

$$\begin{aligned}&2[f(t)\textrm{e}^{-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}]*[f(t)\textrm{e}^{-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}]^*\nonumber \\&\quad =2\int _{{\mathbb {R}}}f(x)\textrm{e}^{-i(a\omega ^2+b\omega x+cx^2+d\omega +ex)}\nonumber \\&\qquad \times f^*(t-x)\textrm{e}^{i\left[ a\omega ^2+b\omega (t-x)+c(t-x)^2+d\omega +e(t-x)\right] }\textrm{d}x\nonumber \\&\quad =2\int _{{\mathbb {R}}}f\left( x\right) f^*\left( t-x\right) \textrm{e}^ {-i(b\omega +ct+e)(2x-t)}\textrm{d}x\nonumber \\&\quad =\int _{{\mathbb {R}}}f\left( \frac{t}{2}+\frac{\tau }{2}\right) f^* \left( \frac{t}{2}-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +ct+e)\tau }\textrm{d}\tau . \end{aligned}$$

(2.10)

Equations (2.10) and (2.9) allow us to have the following definition:

Definition 1

For a given set of parameters $\Lambda =(a, b, c, d, e)$ (with $b\ne 0$), the QAF and QWD of a signal $f(t)\in L^2({\mathbb {R}})$ are defined as

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }(\tau ,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t, \end{aligned}$$

(2.11)

$$\begin{aligned} {\mathcal {W}}_f^{\Lambda }(t,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau . \end{aligned}$$

(2.12)

We infer directly that

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }(\tau ,2\omega )= & {} [f(\tau )\textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}]\nonumber \\{} & {} *[f^*(-\tau )\textrm{e}^{i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}], \end{aligned}$$

(2.13)

$$\begin{aligned} {\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\omega \right)= & {} 2[f(t)\textrm{e}^{-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}]\nonumber \\{} & {} *[f^*(t)\textrm{e}^{i(a\omega ^2+b\omega t+ct^2+d\omega +et)}]. \end{aligned}$$

(2.14)

As can be seen, (2.7) and (2.8) are special cases of (2.13) and (2.14), respectively.

In the first place, some of the special cases of the QAF and QWD are presented in the following remark:

Remark 1

(a)  When $\Lambda = \left( 0, 1, 0, 0, 0\right)$, ${\mathcal {Q}}_{\Lambda }$ is the well-known FT. We would like to notice that the QAF and QWD are simply the conventional AF and WD, respectively.

$$\begin{aligned}&{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )={\mathcal {A}}_f(\tau ,\omega ),\,\,\, {\mathcal {W}}_f^{\Lambda }(t,\omega )={\mathcal {W}}_f(t,\omega ). \end{aligned}$$

(b)  Let $\Lambda = \left( \frac{\cot \theta }{2}, \csc \theta , \frac{\cot \theta }{2}, 0, 0\right)$. The QAF and QWD become the ambiguity function and Wigner distribution associated with the FRFT

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }(\tau ,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i\left( \omega \csc \theta +\tau \cot \theta \right) \tau }\textrm{d}t, \\ {\mathcal {W}}_f^{\Lambda }(t,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i\left( \omega \csc \theta +t\cot \theta \right) \tau }\textrm{d}\tau . \end{aligned}$$

(c)  Let $\Lambda = \left( a, b, c , 0, 0\right)$. In such a particular case, ${\mathcal {Q}}_{\Lambda }$ is the LCT. Equations (2.11), and (2.12) take the form

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }(\tau ,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2c\tau )t}\textrm{d}t, \\ {\mathcal {W}}_f^{\Lambda }(t,\omega )= & {} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct)\tau }\textrm{d}\tau , \end{aligned}$$

which are therefore ambiguity function and Wigner distribution associated with the LCT [16].

Secondly, we will investigate the relationships between the QAF (QWD) with AF (WD). Assume $f_c(t)=f(t)\textrm{e}^{ict^2}$, then the QAF and QWD of $f_c(t)$, respectively, can be expressed by the AF and WD of f(t) as follows

$$\begin{aligned} {\mathcal {A}}_{f_c}^{\Lambda }\left( \tau ,\omega \right)&=\int _{{\mathbb {R}}}f_c \left( t+\frac{\tau }{2}\right) f_c^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) \textrm{e}^{ic \left( t+\frac{\tau }{2}\right) ^2}f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-ic\left( t-\frac{\tau }{2}\right) ^2} \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t- \frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2e)t}\textrm{d}t\\&={\mathcal {A}}_{f}\left( \tau ,b\omega +2e\right) , \end{aligned}$$

and

$$\begin{aligned} {\mathcal {W}}_{f_c}^{\Lambda }\left( t,\omega \right)&=\int _{{\mathbb {R}}}f_c \left( t+\frac{\tau }{2}\right) f_c^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) \textrm{e}^{ic \left( t+\frac{\tau }{2}\right) ^2}f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-ic\left( t-\frac{\tau }{2}\right) ^2}\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +e)\tau } \textrm{d}\tau ={\mathcal {W}}_{f}\left( t,b\omega +e\right) . \end{aligned}$$

Therefore, the relationships between the QAF and AF as well as the QWD and WD are given by

$$\begin{aligned} {\mathcal {A}}_{f_c}^{\Lambda }\left( \tau ,\omega \right) ={\mathcal {A}}_{f}\left( \tau ,b\omega +2e\right) , \,\,{\mathcal {W}}_{f_c}^{\Lambda }\left( t,\omega \right) ={\mathcal {W}}_{f}\left( t,b\omega +e\right) . \end{aligned}$$

At the end of this section, we use a rectangular function $rect_{\alpha }(t)$ (with $\alpha >0$), having a duration of $2\alpha$ and centered at the origin as a test case

$$\begin{aligned} rect_{\alpha }(t) = {\left\{ \begin{array}{ll} 1, &{} \text { if } |t|\le \alpha \\ 0, &{} \text { if } |t|> \alpha . \end{array}\right. } \end{aligned}$$

The closed-form expressions for QAF and QWD of $rect_{\alpha }(t)$, respectively, can be derived as follows:

$$\begin{aligned} {\mathcal {A}}_{rect_{ \alpha }}^{\Lambda }(\tau ,\omega )= & {} \frac{2\sin \left[ (b\omega +2c\tau +2e) \left( \alpha -\frac{\vert \tau \vert }{2}\right) \right] }{b\omega +2c\tau +2e},\,\,\quad \vert \tau \vert \le \alpha , \\ {\mathcal {W}}_{rect_{ \alpha }}^{\Lambda }(t,\omega )= & {} \frac{2\sin \left[ (b\omega +2ct+e)(2\alpha -2\vert t\vert )\right] }{b\omega +2ct+e},\,\,\quad \vert t \vert \le \alpha . \end{aligned}$$

The magnitude of the continuous time QAF and QWD of the rectangular function $rect_{\frac{1}{2}}(t)$ with $\Lambda =(a,1,1,d,1)$ are displayed in Fig. 1.

Fig. 1

Magnitude of the continuous-time QAF and QWD of a rectangle function

2.2 Properties of the QAF and QWD

Properties of the QAF and QWD will be obtained in this subsection. For this purpose, using the function ${{\,\textrm{sinc}\,}}t:=\dfrac{\sin t}{t}$, we recall the next lemma

Lemma 1

(cf., e.g., Theorem 12, [12]) The formula

$$\begin{aligned} \frac{1}{2}\left[ f(t+0)+f(t-0)\right] = \lim _{\lambda \rightarrow \infty }\frac{\lambda }{\pi }\int _{{\mathbb {R}}}f(\tau ) {{\,\textrm{sinc}\,}}{\left[ \lambda (t-\tau )\right] }\textrm{d}\tau \end{aligned}$$

holds true if   $\dfrac{f(t)}{1+|t|}$  belongs to $L^2({\mathbb {R}}).$

From (2.11) and (2.12), the relationship between the QAF and QWD is established as follows:

$$\begin{aligned} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,v)\textrm{e}^ {i[(b(vt-\omega \tau )+e(2t-\tau )]}\textrm{d}v\textrm{d} \tau =\frac{2\pi }{b}{\mathcal {W}}_f^{\Lambda }(t,\omega ). \end{aligned}$$

(2.15)

Proof

By applying Lemma 1, we obtain

$$\begin{aligned}&\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,v)\textrm{e}^ {i[(b(vt-\omega \tau )+e(2t-\tau )]}\textrm{d}v\textrm{d}\tau \\&\quad =\int _{{\mathbb {R}}^3}f\left( x+\frac{\tau }{2}\right) f^*\left( x-\frac{\tau }{2}\right) \textrm{e}^{-i(bv+2c\tau +2e)x}\textrm{e}^{i[(b(vt-\omega \tau )+e(2t-\tau )]}\textrm{d}x\textrm{d}v\textrm{d}\tau \\&\quad =\int _{{\mathbb {R}}^2}f\left( x+\frac{\tau }{2}\right) f^*\left( x-\frac{\tau }{2}\right) \textrm{e}^{-i[b\omega \tau +2c\tau x+(2x-2t+\tau )e]}\\&\qquad \times \left( \lim _{\lambda \rightarrow \infty }\int _{ - \lambda }^\lambda \textrm{e}^{ibv(t-x)} \textrm{d}v\right) \textrm{d}\tau \textrm{d}x\\&\quad =\frac{2\pi }{b}\int _{{\mathbb {R}}}\lim _{\lambda \rightarrow \infty }\frac{b\lambda }{\pi } \int _{{\mathbb {R}}}f\left( x+\frac{\tau }{2}\right) f^*\left( x-\frac{\tau }{2}\right) \\&\qquad \times \textrm{e}^{-i[b\omega \tau +2c\tau x+(2x-2t+\tau )e]} {{\,\textrm{sinc}\,}}{\left[ b\lambda (t-x)\right] }\textrm{d}x\textrm{d}\tau \\&\quad =\frac{2\pi }{b}\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) )\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&\quad =\frac{2\pi }{b}{\mathcal {W}}_f^{\Lambda }(t,\omega ). \end{aligned}$$

Thus, the proof of (2.15) is completed. $\square$

• (1) Shifting Properties

  • (i) Time- shift Property: The QAF and QWD of ${\bar{f}}(t)=f(t-t_0)$ can be presented by

    $$\begin{aligned} {\mathcal {A}}_{{\bar{f}}}^{\Lambda }(\tau ,\omega )=\textrm{e}^{i(b\omega +2c\tau +2e)t_0} {\mathcal {A}}_f^{\Lambda }\left( \tau ,\omega \right) ,\,\, {\mathcal {W}}_{{\bar{f}}}^{\Lambda }(t,\omega )={\mathcal {W}}_f^ {\Lambda }\left( t-t_0,\omega +\frac{2ct_0}{b}\right) . \end{aligned}$$

  • (ii) Frequency Shifting Property: Let ${\hat{f}}(t)=f(t)\textrm{e}^{iu_0t}$ then

    $$\begin{aligned} {\mathcal {A}}_{{\hat{f}}}^{\Lambda }(\tau ,\omega )=\textrm{e}^{iu_0\tau } {\mathcal {A}}_f^{\Lambda }\left( \tau ,\omega \right) ,\,\, {\mathcal {W}}_{{\hat{f}}}^{\Lambda }(t,\omega )={\mathcal {W}}_f^{\Lambda } \left( t,\omega -\frac{u_0}{b}\right) . \end{aligned}$$

  • (iii) Joint Time-Frequency Shifting Property: The QAF and QWD of $f'(t)=f(t-t_0)\textrm{e}^{iu_0t}$ can be expressed as

    $$\begin{aligned}&{\mathcal {A}}_{f'}^{\Lambda }(\tau ,\omega )=\textrm{e}^{iu_0\tau }\textrm{e}^{i(b\omega +2c\tau +2e)t_0} {\mathcal {A}}_f^{\Lambda }\left( \tau ,\omega \right) ,\\&{\mathcal {W}}_{f'}^{\Lambda }(t,\omega )={\mathcal {W}}_f^{\Lambda } \left( t-t_0,\omega -\frac{u_0}{b}+\frac{2ct_0}{b}\right) . \end{aligned}$$

Proof

We prove properties (i) and (ii), since the proof of property (iii) is straightforward.

• (i) Due to the formulas (2.11) and (2.12), it is easy to see that

  $$\begin{aligned}&{\mathcal {A}}_{{\bar{f}}}^{\Lambda }(\tau ,\omega )=\int _{{\mathbb {R}}}{\bar{f}}\left( t+\frac{\tau }{2}\right) \left[ {\bar{f}}\left( t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&\quad =\int _{{\mathbb {R}}}f\left( t-t_0+\frac{\tau }{2}\right) f^*\left( t-t_0-\frac{\tau }{2}\right) \textrm{e} ^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&\quad =\textrm{e}^{-i(b\omega +2c\tau +2e)t_0}\int _{{\mathbb {R}}}f\left( t-t_0+\frac{\tau }{2}\right) f^* \left( t-t_0-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2c\tau +2e)(t-t_0)}\textrm{d}t\\&\quad =\textrm{e}^{-i(b\omega +2c\tau +2e)t_0}{\mathcal {A}}_{f}^{\Lambda }\left( \tau ,\omega \right) , \end{aligned}$$

  and

  $$\begin{aligned} {\mathcal {W}}_{{\bar{f}}}^{\Lambda }(t,\omega )&=\int _{{\mathbb {R}}}{\bar{f}}\left( t+\frac{\tau }{2}\right) \left[ {\bar{f}}\left( t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t-t_0+\frac{\tau }{2}\right) f^*\left( t-t_0-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t-t_0+\frac{\tau }{2}\right) f^*\left( t-t_0-\frac{\tau }{2}\right) \textrm{e}^{-i\left[ b\left( \omega +\frac{2ct_0}{b}\right) +2c(t-t_0)+e\right] \tau }\textrm{d}\tau \\&={\mathcal {W}}_{f}^{\Lambda }\left( t-t_0,\omega +\frac{2ct_0}{b}\right) . \end{aligned}$$

• (ii) By simple computations, we have

  $$\begin{aligned} {\mathcal {A}}_{{\hat{f}}}^{\Lambda }(\tau ,\omega )&=\int _{{\mathbb {R}}}{\hat{f}}\left( t+\frac{\tau }{2}\right) \left[ {\hat{f}}\left( t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) \textrm{e}^{iu_0\left( t+\frac{\tau }{2}\right) }f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-iu_0\left( t-\frac{\tau }{2}\right) } \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\textrm{e}^{iu_0\tau }\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^* \left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct+2e)t}\textrm{d}t\\&=\textrm{e}^{iu_0\tau }{\mathcal {A}}_{f}^{\Lambda }\tau ,\omega ). \end{aligned}$$

  In addition

  $$\begin{aligned} {\mathcal {W}}_{{\hat{f}}}^{\Lambda }(t,\omega )&=\int _{{\mathbb {R}}}{\hat{f}} \left( t+\frac{\tau }{2}\right) \left[ {\hat{f}}\left( t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) \textrm{e}^{iu_0 \left( t+\frac{\tau }{2}\right) }f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-iu_0\left( t-\frac{\tau }{2}\right) }\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t -\frac{\tau }{2}\right) \textrm{e}^{-i\left[ b\left( \omega -\frac{u_0}{b}\right) +2ct+e\right] \tau }\textrm{d}\tau \\&={\mathcal {W}}_{f}^{\Lambda }\left( t,\omega -\frac{u_0}{b}\right) . \end{aligned}$$

$\square$

Symplectic covariance is the fundamental property of the WD and AF [6, 14]. We will consider some special cases of these properties for QAF and QWD in what follows

• (2) Conjugation properties

• (i) Conjugation-Covarriance Property:

  $$\begin{aligned} \left[ {\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )\right] ^*={\mathcal {A}}_{f}^{\Lambda _1} (-\tau ,-\omega ),\,\,\left[ {\mathcal {W}}_{f}^{\Lambda }(t,\omega )\right] ^* ={\mathcal {W}}_f^{\Lambda }\left( t,\omega \right) , \end{aligned}$$

  where $\Lambda _1=(a,b,c,d,-e).$

• (ii) Symmetry-Conjugation Property: The QAF and QWD of $\breve{f}(t)=f(-t)$ have the forms

  $$\begin{aligned} {\mathcal {A}}_{\breve{f}}^{\Lambda }(\tau ,\omega )={\mathcal {A}}_{f}^{\Lambda _2}(\tau ,\omega ),\,\, {\mathcal {W}}_{\breve{f}}^{\Lambda }(t,\omega )={\mathcal {W}}_{f}^{\Lambda _3}\left( -t,\omega \right) , \end{aligned}$$

  where $\Lambda _2=(a,-b,-c,d,-e),\,\Lambda _3=(a,b,-c,d,e).$ Moreover

  $$\begin{aligned} {\mathcal {A}}_{f^*}^{\Lambda }(\tau ,\omega )={\mathcal {A}}_{f}^{\Lambda _3}(-\tau ,\omega ),\,\, {\mathcal {W}}_{f^*}^{\Lambda }(t,\omega )={\mathcal {W}}_{f}^{\Lambda _2}\left( t,\omega \right) . \end{aligned}$$

Proof

We prove (i). From (2.11), we derive

$$\begin{aligned} \left[ {\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )\right] ^*&=\int _{{\mathbb {R}}}f^* \left( t+\frac{\tau }{2}\right) f\left( t-\frac{\tau }{2}\right) \textrm{e}^{i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\int _{{\mathbb {R}}}f\left( t+\frac{-\tau }{2}\right) f^*\left( t-\frac{-\tau }{2}\right) \textrm{e}^{-i\left[ b(-\omega )+2c(-\tau )+2(-e)\right] t}\textrm{d}t\\&={\mathcal {A}}_{f}^{\Lambda _1}(-\tau ,-\omega ), \end{aligned}$$

where $\Lambda _1=(a,b,c,d,-e).$

Furthermore, based on (2.12), we can write

$$\begin{aligned}&\left[ {\mathcal {W}}_{f}^{\Lambda }(t,\omega )\right] ^*=\int _{{\mathbb {R}}}f^* \left( t+\frac{\tau }{2}\right) f\left( t-\frac{\tau }{2}\right) \textrm{e}^{i(b\omega +2ct+e)\tau }\textrm{d}\tau . \end{aligned}$$

Let $-\tau =x$, the desired relation can be achieved as follows

$$\begin{aligned} \left[ {\mathcal {W}}_{f}^{\Lambda }(t,\omega )\right] ^*&=\int _{{\mathbb {R}}}f \left( t+\frac{x}{2}\right) f^*\left( t-\frac{x}{2}\right) \textrm{e}^{-i(b\omega +2ct+e)x}dx\\&={\mathcal {W}}_f^{\Lambda }\left( t,\omega \right) . \end{aligned}$$

Moreover, QAF and QWD of $\breve{f}(t)$ can be presented as

$$\begin{aligned}&{\mathcal {A}}_{\breve{f}}^{\Lambda }(\tau ,\omega )=\int _{{\mathbb {R}}}f \left( -t+\frac{\tau }{2}\right) \left[ f\left( -t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t \end{aligned}$$

$$\begin{aligned}&=\int _{{\mathbb {R}}}f\left( -t+\frac{\tau }{2}\right) f^*\left( -t-\frac{\tau }{2}\right) \textrm{e}^{-i\left[ (-b)\omega +2(-c)\tau +2(-e)\right] (-t)}\textrm{d}t\\&={\mathcal {A}}_{f}^{\Lambda _2}(\tau ,\omega ), \end{aligned}$$

and

$$\begin{aligned} {\mathcal {W}}_{\breve{f}}^{\Lambda }(t,\omega )&=\int _{{\mathbb {R}}}f \left( -t-\frac{\tau }{2}\right) \left[ f\left( -t+\frac{\tau }{2}\right) \right] ^* \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\int _{{\mathbb {R}}}f\left( -t-\frac{\tau }{2}\right) f^*\left( -t+\frac{\tau }{2}\right) \textrm{e}^{-i\left[ b\omega +2(-c)(-t)+e\right] \tau }\textrm{d}\tau \\&={\mathcal {W}}_{f}^{\Lambda _3}\left( -t,\omega \right) , \end{aligned}$$

where $\Lambda _2=(a,-b,-c,d,-e), \Lambda _3=(a,b,-c,d,e).$ Hence, (ii) is proved. The QAF and QWD of $f^*(t)$ can be obtained in a similar way. The proof is completed. $\square$

Furthermore, the marginal properties of QAF and QWD are elegance and similar to those of the AF and WD, which will be obtained in properties (3) and (4) as follows

• (3) Time and time delay marginal properties

For any $f,g\in L^2({{\mathbb {R}}})$, we have

$$\begin{aligned} \int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )d\omega&=\frac{2\pi }{b}f \left( \frac{\tau }{2}\right) f^*\left( -\frac{\tau }{2}\right) , \end{aligned}$$

(2.16)

$$\begin{aligned} \int _{{\mathbb {R}}}{\mathcal {W}}_f^{\Lambda }(t,\omega )d\omega&=\frac{2\pi }{b} \vert f(t)\vert ^2. \end{aligned}$$

(2.17)

Proof

We prove (2.16). Invoking (2.11) and Lemma 1, we can compute the left-hand side of (2.16) as

$$\begin{aligned} \int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )d\omega&=\int _{{\mathbb {R}}} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t \textrm{d}\omega \\&=\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(2c\tau +2e)t}\left( \lim _{\lambda \rightarrow \infty }\int _{ - \lambda }^\lambda \textrm{e}^{-ib\omega t}\textrm{d}\omega \right) \textrm{d}t\\&=\frac{2\pi }{b}\lim _{\lambda \rightarrow \infty }\frac{b\lambda }{\pi }\int _{{\mathbb {R}}}f \left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^ {-i(2c\tau +2e)t}{{\,\textrm{sinc}\,}}{\left( b\lambda t\right) }\textrm{d}t\\&=\frac{2\pi }{b} f\left( \frac{\tau }{2}\right) f^*\left( -\frac{\tau }{2}\right) . \end{aligned}$$

We ignore the proof of (2.17) because it is very similar to the proof of (2.16). $\square$

• (4) QFT marginal properties

The time and frequency marginal properties of the QAF and QWD can be presented by

$$\begin{aligned} \int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )d\tau&=2\pi {\mathcal {Q}}_{f}^ {\Lambda }\left( \frac{\omega }{2}\right) \left[ {\mathcal {Q}}_{\breve{f}}^{\Lambda } \left( \frac{\omega }{2}\right) \right] ^*, \end{aligned}$$

(2.18)

$$\begin{aligned} \int _{{\mathbb {R}}}{\mathcal {W}}_f^{\Lambda }(t,\omega )dt&=2\pi \left| {\mathcal {Q}}_f^{\Lambda }(\omega )\right| ^2. \end{aligned}$$

(2.19)

where $\breve{f}(t)=f(-t).$

Proof

It is straightforward to get

$$\begin{aligned}&\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )\textrm{d}\tau =\int _{{\mathbb {R}}} \int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^ {-i(b\omega +2c\tau +2e)t}\textrm{d}t \textrm{d}\tau ,\\&\quad \int _{{\mathbb {R}}}{\mathcal {W}}_f^{\Lambda }(t,\omega )dt=\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f\left( t+\frac{\tau }{2}\right) f^*\left( t-\frac{\tau }{2}\right) \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \textrm{d}t. \end{aligned}$$

Let $x=t+\dfrac{\tau }{2}, y= t-\dfrac{\tau }{2},$ we then have

$$\begin{aligned}&\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )\textrm{d}\tau =\int _{{\mathbb {R}}} \int _{{\mathbb {R}}}f\left( x\right) f^*\left( y\right) \textrm{e}^ {-i[b\omega +2c(x-y)+2e]\frac{(x+y)}{2}}\textrm{d}x\textrm{d}y\\&\quad =\left( \int _{{\mathbb {R}}}f(x)\textrm{e}^{-i\left[ a\left( \frac{\omega }{2}\right) ^2+b\left( \frac{\omega }{2}\right) x+cx^2+d\left( \frac{\omega }{2}\right) +ex\right] }\textrm{d}x\right) \\&\qquad \times \left( \int _{{\mathbb {R}}}f^*(y)\textrm{e}^{i\left[ a\left( \frac{\omega }{2}\right) ^2+b\left( \frac{\omega }{2}\right) (-y)+c(-y)^2+d\left( \frac{\omega }{2}\right) +e(-y)\right] }\textrm{d}y\right) \\&\quad =2\pi {\mathcal {Q}}_{f}^{\Lambda }\left( \frac{\omega }{2}\right) \left[ {\mathcal {Q}}_{\breve{f}}^{\Lambda }\left( \frac{\omega }{2}\right) \right] ^*, \end{aligned}$$

where $\breve{f}(t)=f(-t).$ In addition

$$\begin{aligned}&\int _{{\mathbb {R}}}{\mathcal {W}}_f^{\Lambda }(t,\omega )\textrm{d}t= \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f\left( x\right) f^*\left( y\right) \textrm{e}^{-i[b\omega +c(x+y)+e](x-y)}\textrm{d}x\textrm{d}y\\&\quad =\left( \int _{{\mathbb {R}}}f(x)\textrm{e}^{-i(a\omega ^2+b\omega x +cx^2+d\omega +ex)}dx\right) \cdot \left( \int _{{\mathbb {R}}}f^*(y)\textrm{e}^ {i(a\omega ^2+b\omega y+cy^2+d\omega +ey)}\textrm{d}y\right) \\&\quad =2\pi {\mathcal {Q}}_f^{\Lambda }(\omega )\left[ {\mathcal {Q}}_f^{\Lambda }(\omega )\right] ^*=2\pi \left| {\mathcal {Q}}_f^{\Lambda }(\omega )\right| ^2. \end{aligned}$$

Thus, we obtain (2.18) and (2.19). The proof is completed. $\square$

• (5) Moyal formula

Assume that $f, g\in L^2({\mathbb {R}})$, the Moyal formula of the QAF and QWD can be represented as

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega ) [{\mathcal {A}}_g^{\Lambda }(\tau ,\omega )]^*\textrm{d}\tau \textrm{d}\omega =\frac{2\pi }{b}\vert \langle f, g\rangle \vert ^2, \end{aligned}$$

(2.20)

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {W}}_f^{\Lambda }(t,\omega )[{\mathcal {W}}_g^{\Lambda } (t,\omega )]^*\textrm{d}t\textrm{d}\omega =\frac{2\pi }{b}\vert \langle f, g\rangle \vert ^2, \end{aligned}$$

(2.21)

where $\langle .,.\rangle$ denotes the usual inner product in $L^2({\mathbb {R}})$ given by $\langle f, g\rangle =\int _{{\mathbb {R}}}f(t)g^*(t)\textrm{d}t.$

Proof

We will just prove (2.20). For (2.21), we proceed in a similar way. By virtue of Lemma 1, we derive that

$$\begin{aligned}{} & {} \int _\mathbb {R} {\int _\mathbb {R} {\mathcal {A}_f^\Lambda } } (\tau ,\omega ){[\mathcal {A}_g^\Lambda (\tau ,\omega )]^*}{\text {d}}\tau {\text {d}}\omega \\{} & {} \qquad = \int _{{\mathbb {R}^4}} f \left( {t + \frac{\tau }{2}} \right) {f^*}\left( {t - \frac{\tau }{2}} \right) {{\text {e}}^{ - i(b\omega + 2c\tau + 2e)t}}\\{} & {} \qquad \quad {g^*}\left( {x + \frac{\tau }{2}} \right) g\left( {x - \frac{\tau }{2}} \right) {{\text {e}}^{i(b\omega + 2c\tau + 2e)x}}{\text {d}}t{\text {d}}x{\text {d}}\tau {\text {d}}\omega \\{} & {} \qquad = \int _{{\mathbb {R}^3}} f \left( {t + \frac{\tau }{2}} \right) {f^*}\left( {t - \frac{\tau }{2}} \right) {g^*}\left( {x + \frac{\tau }{2}} \right) g\left( {x - \frac{\tau }{2}} \right) {{\text {e}}^{ - i(2c\tau + 2e)t}}{{\text {e}}^{i(2c\tau + 2e)x}}\\{} & {} \qquad \quad \times \left( {\mathop {\lim }\limits _{\lambda \rightarrow \infty } \int _{ - \lambda }^\lambda {{{\text {e}}^{ib\omega (x - t)}}} d\omega } \right) {\text {d}}\tau {\text {d}}x{\text {d}}t \\{} & {} \qquad = \frac{{2\pi }}{b}\int _\mathbb {R} {\int _\mathbb {R} {{g^*}} } \left( {x + \frac{\tau }{2}} \right) g\left( {x - \frac{\tau }{2}} \right) {{\text {e}}^{i(2c\tau + 2e)x}}\\{} & {} \qquad \quad \times \left\{ {\mathop {\lim }\limits _{\lambda \rightarrow \infty } \frac{{b\lambda }}{\pi }\int _\mathbb {R} f \left( {t + \frac{\tau }{2}} \right) {f^*}\left( {t - \frac{\tau }{2}} \right) ){{\text {e}}^{ - i(2c\tau + 2e)t}}\left[ {b\lambda (x - t)} \right] {\text {d}}t} \right\} {\text {d}}x{\text {d}}\tau \\{} & {} \qquad = \frac{{2\pi }}{b}\int _\mathbb {R} {\int _\mathbb {R} {{g^*}} } \left( {x + \frac{\tau }{2}} \right) g\left( {x - \frac{\tau }{2}} \right) f\left( {x + \frac{\tau }{2}} \right) {f^*}\left( {x - \frac{\tau }{2}} \right) {\text {d}}x{\text {d}}\tau . \end{aligned}$$

By making the change of variables $y=x+\dfrac{\tau }{2}, z= x-\dfrac{\tau }{2},$ we obtain

$$\begin{aligned} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )[{\mathcal {A}}_g^ {\Lambda }(\tau ,\omega )]^*d\tau d\omega&=\frac{2\pi }{b}\int _{{\mathbb {R}}} \int _{{\mathbb {R}}}g^*\left( y\right) g\left( z\right) f\left( y\right) f^* \left( z\right) \textrm{d}y\textrm{d}z\\&=\frac{2\pi }{b}\left[ \int _{{\mathbb {R}}}f(y)g^*\left( y\right) \textrm{d}y\right] \cdot \left[ \int _{{\mathbb {R}}}f\left( z\right) g^*\left( z\right) dz\right] ^*\\&=\frac{2\pi }{b}\left| \langle f, g\rangle \right| ^2, \end{aligned}$$

which is the desired result. $\square$

• (6) Relationship with the STFT

The STFT of a signal f(t) is defined as [18]

$$\begin{aligned} {\mathcal {S}}_f(t,\omega )=\int _{{\mathbb {R}}}f(\tau )g^*(\tau -t)\textrm{e}^{-i\omega \tau }\textrm{d}\tau , \end{aligned}$$

where g(t) is the window function.

The relationships between the QAF (QWD) and the STFT can be presented by

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }\left( \tau ,\frac{\omega -2c\tau -2e}{b}\right)&=\textrm{e}^{i\frac{\omega \tau }{2}}{\mathcal {S}}_f(\tau ,\omega ),\\ {\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\frac{\omega -2ct-2e}{2b}\right)&=2\textrm{e}^{i\frac{\omega t}{2}}{\mathcal {S}}_f(t,\omega ). \end{aligned}$$

Proof

By changing variable $x=t+\dfrac{\tau }{2},$ we then have

$$\begin{aligned}&{\mathcal {A}}_f^{\Lambda }(\tau ,\omega )=\int _{{\mathbb {R}}}f\left( x\right) f^*\left( x-\tau \right) \textrm{e}^{-i(b\omega +2c\tau +2e)\left( x-\frac{\tau }{2}\right) }\textrm{d}x, \nonumber \\&{\mathcal {W}}_f^{\Lambda }(t,\omega )=2\int _{{\mathbb {R}}}f\left( x\right) f^*\left( 2t-x\right) \textrm{e}^{-2i(b\omega +2ct+e)\left( x-t\right) }\textrm{d}x. \end{aligned}$$

(2.22)

Therefore, by substituting $\omega$ with $\dfrac{\omega -2c\tau -2e}{b}$ and $g(t)=f(t),$ we get

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }\left( \tau ,\frac{\omega -2c\tau -2e}{b}\right)&=\textrm{e}^{i\frac{\omega \tau }{2}}\int _{{\mathbb {R}}}f\left( x\right) f^*\left( x-\tau \right) \textrm{e}^{-i\omega x}\textrm{d}x=\textrm{e}^{i\frac{\omega \tau }{2}}{\mathcal {S}}_f(\tau ,\omega ). \end{aligned}$$

Likewise, if $g(t)=\breve{f}(t)=f(-t)$, we then have

$$\begin{aligned} {\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\frac{\omega -2ct-2e}{2b}\right)&=2\textrm{e}^{i\frac{\omega t}{2}}\int _{{\mathbb {R}}}f\left( x\right) f^*\left( t-x\right) e^{-i\omega x}\textrm{d}x\\&=2\textrm{e}^{i\frac{\omega t}{2}}\int _{{\mathbb {R}}}f\left( x\right) \breve{f}^*\left( x-t\right) \textrm{e}^{-i\omega x}\textrm{d}x=2\textrm{e}^{i\frac{\omega t}{2}}{\mathcal {S}}_f(t,\omega ), \end{aligned}$$

which yields the desired result. $\square$

• (7) Relationship with the STQFT

The STQFT of a signal f(t) with the window function g(t) is defined as

$$\begin{aligned} {\mathcal {S}}^{\Lambda }_f(t,\omega )=\int _{{\mathbb {R}}}f(\tau )g^*(\tau -t)\textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}\textrm{d}\tau . \end{aligned}$$

The relationships between the QAF (QWD) and STQFT can be given by

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }(\tau ,\omega )&=\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega \tau +d\omega )}{\mathcal {S}}^{\Lambda }_f(\tau ,\omega ), \\ {\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\frac{\omega }{2}\right)&=2\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega t+d\omega )}{\mathcal {S}}^{\Lambda }_f(t,\omega ). \end{aligned}$$

Proof

With the aid of (2.22), we can write

$$\begin{aligned} {\mathcal {A}}_f^{\Lambda }\left( \tau ,\omega \right)&=\int _{{\mathbb {R}}}f(t)f^* \left( t-\tau \right) \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{e}^ {i(b\omega +2c\tau +2e)\frac{\tau }{2}}\textrm{d}t\\&=\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega \tau +d\omega )}\int _ {{\mathbb {R}}}f\left( t\right) \left( f^*\left( t-\tau \right) \textrm{e}^ {i\left[ c(t-\tau )^2-e(t-\tau )\right] }\right) \\&\qquad \times \textrm{e}^{-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}\textrm{d}t\\&=\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega \tau +d\omega )}\int _ {{\mathbb {R}}}f\left( t\right) g^*\left( t-\tau \right) \textrm{e}^ {-i(a\omega ^2+b\omega t+ct^2+d\omega +et)}\textrm{d}t\\&=\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega \tau +d\omega )}{\mathcal {S}}^{\Lambda }_f(\tau ,\omega ), \end{aligned}$$

where the window function $g(t)=f(t)\textrm{e}^{-i\left( ct^2-et\right) }$.

Similarly, if the window function is chosen as $g(t)=f(-t)\textrm{e}^{-i\left( ct^2-et\right) }$, we then have

$$\begin{aligned}&{\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\frac{\omega }{2}\right) =2\int _{{\mathbb {R}}}f \left( \tau \right) f^*\left( t-\tau \right) \textrm{e}^{-i(b\omega +2ct+2e)\tau } \textrm{e}^{-i(b\omega +2ct+2e)\frac{t}{2}}\textrm{d}\tau \\&=2\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega t+d\omega )}\int _{{\mathbb {R}}}f \left( \tau \right) \left( f^*\left( t-\tau \right) \textrm{e}^{i\left[ c(t-\tau )^2+e(t-\tau )\right] }\right) \\&\qquad \times \textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}\textrm{d}\tau \\&=2\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega t+d\omega )}\int _{{\mathbb {R}}}f \left( \tau \right) g^*\left( \tau -t\right) \textrm{e}^{-i(a\omega ^2+b\omega \tau +c\tau ^2+d\omega +e\tau )}\textrm{d}\tau \\&=2\textrm{e}^{i(a\omega ^2+\frac{1}{2}b\omega t+d\omega )}{\mathcal {S}}^{\Lambda }_f(t,\omega ). \end{aligned}$$

This indicates that ${\mathcal {W}}_f^{\Lambda }\left( \frac{t}{2},\frac{\omega }{2}\right) =2\textrm{e}^ {i(a\omega ^2+\frac{1}{2}b\omega t+d\omega )}{\mathcal {S}}^{\Lambda }_f(t,\omega ).$ $\square$

Table 2 Some useful properties of QAF

Table 3 Some useful properties of QWD

• (8) Relationship with the QFT

For any $f, g\in L^2({\mathbb {R}})$, we have

$$\begin{aligned} {\mathcal {A}}_{Q_f^{\Lambda }}^{\Lambda }(\tau ,\omega )&=\frac{\textrm{e}^ {-i(d\tau +el)}}{b}{\mathcal {A}}_f^{\Lambda }\left( -\frac{2(a+c)\tau }{b} -\frac{2e}{b}-\omega ,\tau -\frac{2e}{b}\right) , \end{aligned}$$

(2.23)

$$\begin{aligned} {\mathcal {W}}_{Q_f^{\Lambda }}^{\Lambda }(t,\omega )&=\frac{2}{b}{\mathcal {W}}_ f^{\Lambda }\left( -\frac{2(a+c)}{b}t-\frac{d+e}{b}-\omega ,t\right) , \end{aligned}$$

(2.24)

where $l=-\dfrac{2(a+c)\tau }{b}-\dfrac{2e}{b}-\omega$.

Proof

Let $f_e(t)=\textrm{e}^{-i(ct^2+et)}$, we may observe that

$$\begin{aligned} {\mathcal {Q}}_f^{\Lambda }(\omega ) = \frac{1}{\sqrt{2\pi }} \int _{{\mathbb {R}}}\textrm{e}^{-i\left( a\omega ^{2}+b\omega t+d\omega \right) }f_e(t)\textrm{d}t. \end{aligned}$$

The equation above, Lemma 1, and equation (2.11) allow us to recognize that

$$\begin{aligned} {\mathcal {A}}_{Q_f^{\Lambda }}^{\Lambda }(\tau ,\omega )&=\int _{{\mathbb {R}}}Q_f^{\Lambda } \left( t+\frac{\tau }{2}\right) \left[ Q_f^{\Lambda }\left( t-\frac{\tau }{2}\right) \right] ^ *\textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\frac{1}{2\pi }\int _{{\mathbb {R}}^3}\textrm{e}^{-i\left[ a\left( t+\frac{\tau }{2}\right) ^ {2}+b\left( t+\frac{\tau }{2}\right) u +d\left( t+\frac{\tau }{2}\right) \right] }\textrm{e}^ {i\left[ a\left( t-\frac{\tau }{2}\right) ^{2}+b\left( t-\frac{\tau }{2}\right) v+d\left( t-\frac{\tau }{2}\right) \right] }\\&\qquad \times f_e(u)f_e^*(v)\textrm{e}^{-i(b\omega +2c\tau +2e)t} \textrm{d}u\textrm{d}v\textrm{d}t\\&=\frac{1}{2\pi }\int _{{\mathbb {R}}^3}f_e(u)f_e^*(v)\textrm{e}^{-i \left[ \frac{b}{2}(u+v)+d\right] \tau }\textrm{e}^{-i\left[ 2(a+c) \tau +2e+b\omega +b(u-v)\right] t}\textrm{d}u\textrm{d}v\textrm{d}t\\&=\frac{1}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f_e(u)f_e^*(v) \textrm{e}^{-i\left[ \frac{b}{2}(u+v)+d\right] \tau }\\&\qquad \times \left( \lim _{\lambda \rightarrow \infty }\int _{ - \lambda }^\lambda \textrm{e}^{-i\left[ 2(a+c)\tau +2e+b\omega +b(u-v)\right] t}\textrm{d}t\right) \textrm{d}u\textrm{d}v\\&=\frac{1}{b}\int _{{\mathbb {R}}}\textrm{e}^{-i\left[ \frac{b}{2}u+d\right] \tau }f_e(u)\\&\qquad \times \left\{ \lim _{\lambda \rightarrow \infty }\frac{b \lambda }{\pi } \int _{{\mathbb {R}}}\textrm{e}^{-\frac{ibv\tau }{2}}f_e^*(v) {{\,\textrm{sinc}\,}}{\left\{ \lambda \left[ 2(a+c)\tau +2e+b\omega +b(u-v)\right] \right\} } \textrm{d}v\right\} \textrm{d}u\\&=\frac{1}{b}\int _{{\mathbb {R}}}f_e(u)\left[ f_e\left( \frac{2(a+c)\tau }{b} +\frac{2e}{b}+\omega +u\right) \right] ^*\textrm{e}^{-ib\tau \left[ \frac{(a+c) \tau }{b}+\frac{e}{b}+\frac{\omega }{2}+\frac{d}{b}+u\right] }\textrm{d}u. \end{aligned}$$

Then, by talking $u=x-\dfrac{(a+c)\tau }{b}-\dfrac{e}{b}-\dfrac{\omega }{2},$ we derive

$$\begin{aligned}&{\mathcal {A}}_{Q_f^{\Lambda }}^{\Lambda }(\tau ,\omega )=\int _{{\mathbb {R}}}f_e \left( x-\frac{(a+c)\tau }{b}-\frac{e}{b}-\frac{\omega }{2}\right) \times \\&\quad \left[ f_e\left( x+\frac{(a+c)\tau }{b}+\frac{e}{b}+\frac{\omega }{2}\right) \right] ^*\textrm{e}^{-ib\tau \left( x+\frac{d}{b}\right) }\textrm{d}x. \end{aligned}$$

Furthermore, considering $l=-\dfrac{2(a+c)\tau }{b}-\dfrac{2e}{b}-\omega ,$ the above relation can be rewritten as

$$\begin{aligned} {\mathcal {A}}_{Q_f^{\Lambda }}^{\Lambda }(t,\omega )&=\frac{1}{b}\int _ {{\mathbb {R}}}f_e\left( x+\dfrac{l}{2}\right) \left[ f_e\left( x-\dfrac{l}{2}\right) \right] ^* \textrm{e}^{-ib\tau \left( x+\frac{d}{b}\right) }\textrm{d}x\\&=\frac{1}{b}\int _{{\mathbb {R}}}f\left( x+\dfrac{l}{2}\right) \left[ f\left( x-\dfrac{l}{2}\right) \right] ^*\textrm{e}^{-i(2cx+e)l} \textrm{e}^{-ib\tau \left( x+\frac{d}{b}\right) }\textrm{d}x\\&=\frac{\textrm{e}^{-i(d\tau +el)}}{b}\int _{{\mathbb {R}}}f \left( x+\dfrac{l}{2}\right) \left[ f\left( x-\dfrac{l}{2}\right) \right] ^* \textrm{e}^{-i\left[ b\left( \tau -\frac{2e}{b}\right) +2cl+2e\right] x}\textrm{d}x\\&=\frac{\textrm{e}^{-i(d\tau +el)}}{b}{\mathcal {A}}_f^{\Lambda }\left( l,\tau -\frac{2e}{b}\right) \\&=\frac{\textrm{e}^{-i(d\tau +el)}}{b}{\mathcal {A}}_f^{\Lambda } \left( -\frac{2(a+c)\tau }{b}-\frac{2e}{b}-\omega ,\tau -\frac{2e}{b}\right) , \end{aligned}$$

which yields (2.23).

Now, for proving (2.24), making use of the definition of the QWD, we start by interpreting the left-hand side of it:

$$\begin{aligned}&{\mathcal {W}}_{Q_f^{\Lambda }}^{\Lambda }(t,\omega )=\int _{{\mathbb {R}}}Q_f^{\Lambda } \left( t+\frac{\tau }{2}\right) \left[ Q_f^{\Lambda }\left( t-\frac{\tau }{2}\right) \right] ^* \textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}\tau \\&=\frac{1}{2\pi }\int _{{\mathbb {R}}^3}\textrm{e}^{-i\left[ a\left( t+\frac{\tau }{2}\right) ^ {2}+b\left( t+\frac{\tau }{2}\right) u +d\left( t+\frac{\tau }{2}\right) \right] }\textrm{e}^ {i\left[ a\left( t-\frac{\tau }{2}\right) ^{2}+b\left( t-\frac{\tau }{2}\right) v+d\left( t-\frac{\tau }{2}\right) \right] }\\&\qquad \times f_e(u)f_e^*(v)\textrm{e}^{-i(b\omega +2ct+e)\tau }\textrm{d}u\textrm{d}v\textrm{d}\tau \\&=\frac{1}{2\pi }\int _{{\mathbb {R}}^3}f_e(u)f_e^*(v)\textrm{e}^{ibt(v-u)}\textrm{e}^ {-i\left[ 2t(a+c)+d+e+b\omega +\frac{b}{2}(u+v)\right] \tau }\textrm{d}u\textrm{d}v\textrm{d}\tau \\&=\frac{1}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f_e(u)f_e^*(v)\textrm{e}^{ibt(v-u)} \left( \lim _{\lambda \rightarrow \infty }\int _{ - \lambda }^\lambda \textrm{e}^{-i \left[ 2t(a+c)+d+e+b\omega +\frac{b}{2}(u+v)\right] \tau }d\tau \right) \textrm{d}u\textrm{d}v\\&=\frac{2}{b}\int _{{\mathbb {R}}}\textrm{e}^{-ibtu}f_e(u)\times \\&\quad \left\{ \lim _{\lambda \rightarrow \infty }\frac{b\lambda }{2\pi }\int _{{\mathbb {R}}} \textrm{e}^{ibtv}f_e^*(v){{\,\textrm{sinc}\,}}{\left\{ \lambda \left[ 2t(a+c)+d+e+b\omega +\frac{b}{2}(u+v) \right] \right\} }\textrm{d}v\right\} \textrm{d}u\\&=\frac{2}{b}\int _{{\mathbb {R}}}f_e(u)\left[ f_e\left( -\frac{4(a+c)t}{b} -\frac{2(d+e)}{b}-2\omega -u\right) \right] ^*\times \\&\quad \textrm{e}^{-ibt\left[ \frac{4(a+c)t}{b}+\frac{2(d+e)}{b}+2\omega +2u\right] }\textrm{d}u. \end{aligned}$$

Again, talking $u=-\dfrac{2(a+c)t}{b}-\dfrac{(d+e)}{b}-\omega +\dfrac{x}{2},$ the equation above can be recast as

$$\begin{aligned} {\mathcal {W}}_{Q_f^{\Lambda }}^{\Lambda }(t,\omega )&=\frac{2}{b}\int _{{\mathbb {R}}}f_e \left( -\frac{2(a+c)t}{b}-\frac{(d+e)}{b}-\omega +\frac{x}{2}\right) \\&\quad \times \left[ f_e\left( -\frac{2(a+c)t}{b}-\frac{(d+e)}{b} -\omega -\frac{x}{2}\right) \right] ^*\textrm{e}^{-ibtx}\textrm{d}x. \end{aligned}$$

Next, considering $k=-\dfrac{2(a+c)t}{b}-\dfrac{(d+e)}{b}-\omega ,$ it follows that

$$\begin{aligned} {\mathcal {W}}_{Q_f^{\Lambda }}^{\Lambda }(t,\omega )&=\frac{2}{b}\int _{{\mathbb {R}}} f_e\left( k+\dfrac{x}{2}\right) \left[ f_e\left( k-\dfrac{x}{2}\right) \right] ^*\textrm{e}^{-ibtx}\textrm{d}x\\&=\frac{2}{b}\int _{{\mathbb {R}}}f\left( k+\dfrac{x}{2}\right) \left[ f\left( k-\dfrac{x}{2}\right) \right] ^*\textrm{e}^{-i(2ck+e)x}\textrm{e}^{-ibtx}\textrm{d}x\\&=\frac{2}{b}\int _{{\mathbb {R}}}f\left( k+\dfrac{x}{2}\right) \left[ f\left( k-\dfrac{x}{2}\right) \right] ^*\textrm{e}^{-i(bt+2ck+e)x}\textrm{d}x\\&=\frac{2}{b}{\mathcal {W}}_f^{\Lambda }\left( k,t\right) \\&=\frac{2}{b}{\mathcal {W}}_f^{\Lambda }\left( -\frac{2(a+c)t}{b}-\frac{(d+e)}{b}-\omega ,t\right) , \end{aligned}$$

which is the desired result. $\square$

3 Convolution Theorems for the QAF and QWD

Convolutions are used in the modeling of a great diversity of applied problems such as signal and image processing, optics as well as filter designing [2, 5]. In this section, two convolutions associated with the QFT and their convolution theorems will be introduced. Moreover, the relationships between proposed convolutions and QAF as well as QWD will be given, which are different from those in [11, 13], in the sense that they are simpler, more elegant, and similar to (1.5) and (1.4). Furthermore, convolution theorems for the QAF and QWD of three convolutions proposed in [3] will be also presented in the rest of this section.

Definition 2

For any functions $f, g \in L^2({\mathbb {R}})$, we define two new convolution operators $f\underset{i}{\star }g\,\,(i\in \{1,2\})$ via the QFT as follows:

$$\begin{aligned} (f\underset{1}{\star }g)(t)&=\frac{1}{\sqrt{2\pi }} \int _{{\mathbb {R}}}f(\tau )g\left( t-\tau -\frac{d}{b}\right) \textrm{e}^{-i\left[ c\tau ^2-ct^2+c\left( t-\tau -\frac{d}{b}\right) ^2-\frac{ed}{b}\right] }\textrm{d}\tau ,\nonumber \\ (f\underset{2}{\star }g)(t)&=\frac{1}{\sqrt{2\pi }}\int _{{\mathbb {R}}}f(\tau )g(t-\tau ) \textrm{e}^{2ic\tau (t-\tau )}\textrm{d}\tau . \end{aligned}$$

(3.25)

After simple computation, we recognize that the proposed convolutions have the following properties. Namely, for any $f,g,h\in L^2({\mathbb {R}})$ and $i\in \{1,2\}$, we have

• (i) Commutativity: $f\underset{i}{\star }\ g=g \underset{i}{\star }f.$

• (ii) Associativity: $(f\underset{i}{\star } g)\underset{i}{\star }h= f\underset{i}{\star }(g\underset{i}{\star }h).$

• (iii) Distributivity: $f\underset{i}{\star }(g+ h)=f\underset{i}{\star }g+f\underset{i}{\star }h.$

Theorem 2

For any pair of square integrable functions $f, g\in L^2({\mathbb {R}})$, the following identities are satisfied

$$\begin{aligned} {\mathcal {Q}}_{f\underset{1}{\star }g}^{\Lambda }(\omega )&= \textrm{e}^{ai\omega ^{2}}\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega ), \end{aligned}$$

(3.26)

$$\begin{aligned} {\mathcal {A}}_{f\underset{1}{\star }g}^{\Lambda }(\tau ,\omega )&=\frac{\textrm{e}^{-\frac{id}{b}(b\omega +2e)}}{2\pi }\int _{\mathbb R}{\mathcal {A}}_{f}^{\Lambda }(\gamma ,\omega )\cdot {\mathcal {A}}_{g}^{\Lambda }\left( \tau -\gamma ,\omega \right) \textrm{d}\gamma , \end{aligned}$$

(3.27)

$$\begin{aligned} {\mathcal {W}}_{f\underset{1}{\star }g}^{\Lambda }(t,\omega )&=\frac{1}{2\pi }\int _{\mathbb R}{\mathcal {W}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {W}}_{g}^{\Lambda }\left( t-u-\frac{d}{b},\omega \right) \textrm{d}u. \end{aligned}$$

(3.28)

Proof

First, we prove factorization identity (3.26). Due to the formula (1.6), we have

$$\begin{aligned}&\textrm{e}^{ai\omega ^{2}}\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega )\\&\quad =\frac{1}{2\pi }\textrm{e}^{ai\omega ^{2}}\int _{\mathbb R}\int _{{\mathbb {R}}}f(u)g(v)\textrm{e}^{-i(a\omega ^2+b\omega u+cu^2+d\omega +eu)}\textrm{e}^{-i(a\omega ^2+b\omega v+cv^2+d\omega +ev)}\textrm{d}u\textrm{d}v\\&\quad =\frac{1}{2\pi }\int _{{\mathbb {R}}}\int _{\mathbb R}f(u)g(v)\textrm{e}^{-i\left[ a\omega ^2+b\omega \left( u+v+\frac{d}{b}\right) +cu^2+cv^2+d\omega +e \left( u+v+\frac{d}{b}\right) -\frac{ed}{b}\right] }\textrm{d}u\textrm{d}v. \end{aligned}$$

Setting $s=u+v+\dfrac{d}{b}$, it is easy to see that

$$\begin{aligned}&\textrm{e}^{ai\omega ^{2}}\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^ {\Lambda }(\omega )=\frac{1}{\sqrt{2\pi }}\int _{\mathbb R}\textrm{e}^{-i(a\omega ^2+b\omega s+cs^2+d\omega +es)}\\&\qquad \times \left\{ \frac{1}{\sqrt{2\pi }}\int _{\mathbb R}f(u)g\left( s-u-\frac{d}{b}\right) \textrm{e}^{-i \left[ cu^2-cs^2+c\left( s-u-\frac{d}{b}\right) ^2-\frac{ed}{b}\right] }\textrm{d}u \right\} \textrm{d}s\\&\quad =\frac{1}{\sqrt{2\pi }}\int _{{\mathbb {R}}}\textrm{e}^{-i(a\omega ^2+b\omega s+cs^2 +d\omega +es)}(f\underset{1}{\star }g)(s)\textrm{d}s. \end{aligned}$$

Now, owing to (2.11) and (3.25), we obtain

$$\begin{aligned} {\mathcal {A}}_{f\underset{1}{\star }g}^{\Lambda }(\tau ,\omega )&=\int _{{\mathbb {R}}}(f\underset{1}{\star }g)\left( \eta +\frac{\tau }{2}\right) \cdot \left[ (f\underset{1}{\star }g) \left( \eta -\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i\big (b\omega +2c\tau +2e\big )\eta }\textrm{d}\eta \\&=\int _{{\mathbb {R}}}\left\{ \frac{1}{\sqrt{2\pi }}\int _{{\mathbb {R}}}f(x)g\left( \eta +\frac{\tau }{2}-\frac{d}{b}-x\right) \textrm{e}^{-i\left[ cx^2-c\left( \eta +\frac{\tau }{2}\right) ^2+c\left( \eta +\frac{\tau }{2}-x-\frac{d}{b}\right) ^2 -\frac{ed}{b}\right] }\textrm{d}x \right\} \\&\quad \times \left\{ \frac{1}{\sqrt{2\pi }}\int _{{\mathbb {R}}}f^*(y)g^*\left( \eta -\frac{\tau }{2}-\frac{d}{b}-y\right) \textrm{e}^{i\left[ cy^2-c\left( \eta -\frac{\tau }{2}\right) ^2+c\left( \eta -\frac{\tau }{2}-\frac{d}{b}-y\right) ^2-\frac{ed}{b}\right] }\textrm{d}y \right\} \\&\quad \times \textrm{e}^{-i\big (b\omega +2c\tau +2e\big )\eta }\textrm{d}\eta . \end{aligned}$$

Setting $x=p+\dfrac{\gamma }{2}$ and $y=p-\dfrac{\gamma }{2}$, the above equation becomes

$$\begin{aligned}&{\mathcal {A}}_{f\underset{1}{\star }g}^{\Lambda }(\tau ,\omega ) =\frac{1}{2\pi }\int _{{\mathbb {R}}}\textrm{e}^{-i\big (b\omega +2c\tau +2e\big )\eta }\\&\times \int _{{\mathbb {R}}}f\left( p+\dfrac{\gamma }{2}\right) g\left( \eta +\frac{\tau }{2}-\frac{d}{b}-p-\frac{\gamma }{2}\right) \textrm{e}^{-i\left[ c\left( p+\frac{\gamma }{2}\right) ^2-c\left( \eta +\frac{\tau }{2}\right) ^2+c\left( \eta +\frac{\tau }{2}-p-\frac{\gamma }{2} -\frac{d}{b}\right) ^2\right] }\textrm{d}p\\&\times \int _{{\mathbb {R}}}f^*\left( p-\dfrac{\gamma }{2}\right) g^*\left( \eta -\frac{\tau }{2}-\frac{d}{b}-p+\frac{\gamma }{2}\right) \textrm{e}^ {i\left[ c\left( p-\frac{\gamma }{2}\right) ^2-c\left( \eta -\frac{\tau }{2}\right) ^2+c\left( \eta -\frac{\tau }{2}-p+\frac{\gamma }{2}-\frac{d}{b}\right) ^2\right] } \textrm{d}\gamma \textrm{d}\eta . \end{aligned}$$

By talking $\eta =p+q+\dfrac{d}{b}$ such that $\textrm{d}\eta =\textrm{d}q$. It is easy to verify that the above expression has the following form

$$\begin{aligned} {\mathcal {A}}_{f\underset{1}{\star }g}^{\Lambda }(\tau ,\omega )&=\frac{\textrm{e}^{-\frac{id}{b}(b\omega +2e)}}{2\pi }\int _{\mathbb R}\left\{ \int _{\mathbb R}f\left( p+\dfrac{\gamma }{2}\right) f^*\left( p-\dfrac{\gamma }{2}\right) \textrm{e}^{-i\big (b\omega +2c\gamma +2e\big )p} \textrm{d}p\right\} \\&\qquad \times \left\{ \int _{{\mathbb {R}}}g\left( q+\frac{\tau -\gamma }{2}\right) g^* \left( q-\frac{\tau -\gamma }{2}\right) \textrm{e}^{-i\left[ b\omega +2c\left( \tau -\gamma \right) +2e\right] q}\textrm{d}q\right\} \textrm{d}\gamma \\&=\frac{\textrm{e}^{-\frac{id}{b}(b\omega +2e)}}{2\pi }\int _ {{\mathbb {R}}}{\mathcal {A}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {A}}_ {g}^{\Lambda }\left( \tau -\gamma ,\omega \right) \textrm{d}\gamma , \end{aligned}$$

which is (3.27).

Next, we turn to the proof of (3.28). It follows from (2.11) that

$$\begin{aligned}{} & {} {\mathcal {W}}_{f\underset{1}{\star }g}^{\Lambda }(t,\omega )=\int _{\mathbb R}(f\underset{1}{\star }g)\left( t+\frac{\eta }{2}\right) \cdot \left[ (f\underset{1}{\star }g) \left( t-\frac{\eta }{2}\right) \right] ^*\textrm{e}^{-i\big (b\omega +2ct+e\big )\eta }\textrm{d}\eta \\= & {} \int _{{\mathbb {R}}}\left\{ \frac{1}{\sqrt{2\pi }}\int _{\mathbb R}f(\tau )g\left( t+\frac{\eta }{2}-\frac{d}{b}-\tau \right) \textrm{e}^{-i\left[ c\tau ^2-c \left( t+\frac{\eta }{2}\right) ^2+c\left( t+\frac{\eta }{2}-\tau -\frac{d}{b}\right) ^2-\frac{ed}{b}\right] }\textrm{d}\tau \right\} \\{} & {} \quad \times \left\{ \frac{1}{\sqrt{2\pi }}\int _{\mathbb R}f^*(\gamma )g^*\left( t-\frac{\eta }{2}-\frac{d}{b}-\gamma \right) \textrm{e}^{i \left[ c\gamma ^2-c\left( t-\frac{\eta }{2}\right) ^2+c\left( t-\frac{\eta }{2}-\gamma -\frac{d}{b} \right) ^2-\frac{ed}{b}\right] }\textrm{d}\gamma \right\} \\{} & {} \qquad \times \textrm{e}^{-i\big (b\omega +2ct+e\big )\eta }\textrm{d}\eta . \end{aligned}$$

Performing the change of variables $\tau =u+\dfrac{p}{2}$ and $\gamma =u-\dfrac{p}{2}$, we achieve

$$\begin{aligned} {\mathcal {W}}_{f\underset{1}{\star }g}^{\Lambda }(t,\omega )= & {} ]imu\frac{1}{2\pi }\int _{\mathbb R}\textrm{e}^{-i\big (b\omega +2ct+e\big )\eta } \int _{{\mathbb {R}}}f\left( u+\frac{p}{2}\right) g\left( t+\frac{\eta }{2}-\frac{d}{b}-u-\frac{p}{2}\right) \\{} & {} \textrm{e}^{-i\left[ c\left( u+\frac{p}{2}\right) ^2-c\left( t+\frac{\eta }{2}\right) ^2+c\left( t+\frac{\eta }{2}-u-\frac{p}{2} -\frac{d}{b}\right) ^2\right] }\textrm{d}p\times \\{} & {} \int _{\mathbb R}f^*\left( u-\frac{p}{2}\right) g^*\left( t-\frac{\eta }{2}-\frac{d}{b}-u+\frac{p}{2} \right) \\{} & {} \textrm{e}^{i\left[ c\left( u-\frac{p}{2}\right) ^2-c\left( t-\frac{\eta }{2}\right) ^2+c\left( t-\frac{\eta }{2}-u+\frac{p}{2}-\frac{d}{b}\right) ^2\right] }\textrm{d}u\textrm{d}\eta . \end{aligned}$$

By talking $\eta =p+q$ such that $\textrm{d}\eta =\textrm{d}q$, the above equation turns into

$$\begin{aligned} {\mathcal {W}}_{f\underset{1}{\star }g}^{\Lambda }(t,\omega )= & {} \frac{1}{2\pi } \int _{{\mathbb {R}}}\left\{ \int _{{\mathbb {R}}}f\left( u+\frac{p}{2}\right) f^* \left( u-\frac{p}{2}\right) \textrm{e}^{-i\big (b\omega +2cu+e\big )p} \textrm{d}p\right\} \\{} & {} \qquad \times \left\{ \int _{{\mathbb {R}}}g\left( t-u-\frac{d}{b}+\frac{q}{2}\right) g^* \left( t-u-\frac{d}{b}-\frac{q}{2}\right) \textrm{e}^{-i\left[ b\omega +2c \left( t-u-\frac{d}{b}\right) +e\right] q}\textrm{d}q\right\} \textrm{d}u\\= & {} \frac{1}{2\pi }\int _{{\mathbb {R}}}{\mathcal {W}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {W}}_{h}^{\Lambda }\left( t-u-\frac{d}{b},\omega \right) \textrm{d}u, \end{aligned}$$

which proves (3.28). The proof is concluded. $\square$

The following theorem can be derived in the same way as Theorem 2, and so we omit its proof.

Theorem 3

Assume that $f, g\in L^2({\mathbb {R}})$, two following identities hold

$$\begin{aligned} {\mathcal {Q}}_{f\underset{2}{\star }g}^{\Lambda }(\omega )= & {} \textrm{e}^{ai\omega ^{2}+id\omega }\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega ), \nonumber \\ {\mathcal {A}}_{f\underset{2}{\star }g}^{\Lambda }(\tau ,\omega )= & {} \frac{1}{2\pi }\int _{\mathbb R}{\mathcal {A}}_{f}^{\Lambda }(\gamma ,\omega )\cdot {\mathcal {A}}_{g}^{\Lambda }\left( \tau -\gamma ,\omega \right) \textrm{d}\gamma , \end{aligned}$$

(3.29)

and

$$\begin{aligned} {\mathcal {W}}_{f\underset{2}{\star }g}^{\Lambda }(t,\omega )=\frac{1}{2\pi }\int _{\mathbb R}{\mathcal {W}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {W}}_{g}^{\Lambda }(t-u,\omega )\textrm{d}u. \end{aligned}$$

(3.30)

As can be seen, the identities (1.5) and (1.4) can be deduced from the identities (3.29) and (3.30) when $\Lambda = \left( 0,1,0, 0, 0\right)$. We now recall some of the convolutions which can be found in [3].

Definition 3

If $f, g\in L^2({{\mathbb {R}}})$ then the new elements $f\underset{i}{\star }g,\,(i\in \{3,4,5\})$ below introduced define convolutions followed by their factorization identities:

$$\begin{aligned} (f\underset{3}{\star }g)(t)&=\frac{b}{2\pi }\int _{{\mathbb {R}}^2}f(u)g(v) \textrm{e}^{-i(cu^2+cv^2-ct^2+eu+ev-et)-\frac{(bt-bu-bv-d)^2}{2}}\textrm{d}u\textrm{d}v,\\ {\mathcal {Q}}_{f\underset{3}{\star }g}^{\Lambda }(\omega )&= \textrm{e}^{-\frac{1}{2}\omega ^{2}+ai\omega ^{2}}\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega ),\\ (f\underset{4}{\star }g)(t)&=\frac{b}{2\pi }\int _{{\mathbb {R}}^2}f(u)g(v) \textrm{e}^{-i(cu^2+cv^2-ct^2+eu+ev-et)-\frac{(bt-bu-bv)^2}{2}}\textrm{d}u\textrm{d}v,\\ {\mathcal {Q}}_{f\underset{4}{\star }g}^{\Lambda }(\omega )&= \textrm{e}^{-\frac{1}{2}\omega ^{2}+ai\omega ^{2}+id\omega }\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega ),\\ (f\underset{5}{\star }g)(t)&=\frac{b}{\sqrt{2} \, \pi }\int _{\mathbb R^2} \textrm{e}^{-i(cu^{2}+cv^{2}-c\frac{t^2}{2}+eu+ev-\frac{et}{\sqrt{2}})-\frac{(bt-bu-bv-2d+d\sqrt{2})^2}{2}} f(u)g(v)\textrm{d}u\textrm{d}v,\\ {\mathcal {Q}}_{f\underset{5}{\star }g}^{\Lambda }(\omega )&= \textrm{e}^{-\frac{1}{2}\omega ^{2}}\, {\mathcal {Q}}_{f}^{\Lambda }(\omega )\cdot {\mathcal {Q}}_{g}^{\Lambda }(\omega ). \end{aligned}$$

The next theorems introduce the relationships between the three convolutions above and QAF (QWD).

Theorem 4

Given a pair of square integrable functions $f,g\in L^2({\mathbb R})$, the following results hold

$$\begin{aligned} {\mathcal {A}}_{f\underset{3}{\star }g}^{\Lambda }(\tau ,\omega )&= \frac{b\textrm{e}^{-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2}\textrm{e}^{-i \left( \omega +\frac{2e}{b}\right) d}\textrm{e}^{ie\tau }}{4\pi \sqrt{\pi }}\int _{\mathbb R}\int _{{\mathbb {R}}}\, {\mathcal {A}}_{f}^{\Lambda }\left( p,\omega \right) \cdot {\mathcal {A}}_{g}^{\Lambda } \left( q,\omega \right) \times \nonumber \\&\quad \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\textrm{e}^{-ie(p+q)}\textrm{d}p\textrm{d}q, \end{aligned}$$

(3.31)

$$\begin{aligned} {\mathcal {W}}_{f\underset{3}{\star }g}^{\Lambda }(t,\omega )&= \frac{b\textrm{e}^{-\omega ^{2}}}{2\pi \sqrt{\pi }}\int _{\mathbb R}\int _{{\mathbb {R}}}\, {\mathcal {W}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {W}}_{g}^ {\Lambda }(v,\omega )\textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{d}u\textrm{d}v. \end{aligned}$$

(3.32)

Proof

In order to prove (3.31), we proceed as

$$\begin{aligned} {\mathcal {A}}_{f\underset{3}{\star }g}^{\Lambda }(\tau ,\omega )&= \int _{{\mathbb {R}}}(f\underset{3}{\star }g)\left( t+\frac{\tau }{2}\right) \left[ (f\underset{3}{\star }g)\left( t-\frac{\tau }{2}\right) \right] ^* \textrm{e}^{-i(b\omega +2c\tau +2e)t}\textrm{d}t\\&=\frac{b^2}{4\pi ^2}\int _{{\mathbb {R}}^5}f(\tau _1)g(\tau _2)f^*(\gamma _1) g^*(\gamma _2)\textrm{e}^{-i(b\omega +2c\tau +2e)t}\\&\quad \times \textrm{e}^{-i\left[ c\tau _1^2+c\tau _2^2-c\left( t+\frac{\tau }{2}\right) ^2+e\tau _1+e\tau _2-e\left( t+\frac{\tau }{2}\right) \right] -\frac{\left[ b\left( t +\frac{\tau }{2}\right) -b\tau _1-b\tau _2-d\right] ^2}{2}}\\&\quad \times \textrm{e}^{i\left[ c\gamma _1^2+c\gamma _2^2-c\left( t-\frac{\tau }{2}\right) ^2+e\gamma _1+e\gamma _2-e\left( t-\frac{\tau }{2}\right) \right] -\frac{\left[ b\left( t-\frac{\tau }{2}\right) -b\gamma _1 -b\gamma _2-d\right] ^2}{2}}\textrm{d}\tau _1\textrm{d} \tau _2\textrm{d}\gamma _1\textrm{d}\gamma _2\textrm{d}t. \end{aligned}$$

By changing variables $\tau _1=u+\dfrac{p}{2},\,\gamma _1=u-\dfrac{p}{2}, \,\tau _2=v+\dfrac{q}{2},\,\gamma _2=v-\dfrac{q}{2},$ we realize

$$\begin{aligned} {\mathcal {A}}_{f\underset{3}{\star }g}^{\Lambda }(\tau ,\omega )&=\frac{b^2}{4\pi ^2}\int _{{\mathbb {R}}^5}f\left( u+\frac{p}{2}\right) f^* \left( u-\frac{p}{2}\right) g\left( v+\frac{q}{2}\right) g^*\left( v-\frac{q}{2}\right) \\&\quad \times \textrm{e}^{-i(2cup+2cvq+ep+eq-e\tau )}\\&\quad \times \textrm{e}^{-i(b \omega +2e)t}\textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{e}^{-\frac{b^2}{4} (\tau -p-q)^2}\textrm{d}u\textrm{d}v\textrm{d}p\textrm{d}q\textrm{d}t\\&=\frac{b^2}{4\pi ^2}\int _{{\mathbb {R}}^4}f\left( u+\frac{p}{2}\right) f^* \left( u-\frac{p}{2}\right) g\left( v+\frac{q}{2}\right) g^*\left( v -\frac{q}{2}\right) \\ {}&\quad \times \textrm{e}^{-i(2cup+2cvq+ep+eq-e\tau )}\\&\quad \times \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\left( \int _ {{\mathbb {R}}}\textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{e}^{-i\left( b\omega +2e\right) t} dt\right) \textrm{d}u\textrm{d}v\textrm{d}p\textrm{d}q. \end{aligned}$$

Having now in mind the following well-known identity (see [10, 12]),

$$\begin{aligned} \dfrac{1}{\sqrt{2\pi }}\int _{{\mathbb {R}}}\textrm{e}^{\pm ixt}\textrm{e}^{-kt^2} \textrm{d}t=\dfrac{1}{\sqrt{2k}}\textrm{e}^{-\frac{1}{4k}x^2}\quad (k>0, \,x\in {\mathbb {R}}), \end{aligned}$$

(3.33)

it follows that

$$\begin{aligned} \int _{{\mathbb {R}}}\textrm{e}^{-\left[ bt-b(u+v) -d\right] ^2}\textrm{e}^{-i\left( b\omega +2e\right) t}\textrm{d}t= \frac{\sqrt{\pi }}{b} \textrm{e}^{-i(b\omega +2e)\left( u+v+\frac{d}{b}\right) } \textrm{e}^{-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2} \end{aligned}$$

holds true. Then

$$\begin{aligned} {\mathcal {A}}_{f\underset{3}{\star }g}^{\Lambda }(\tau ,\omega )&=\frac{b\textrm{e}^ {-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2}}{4\pi \sqrt{\pi }}\int _ {{\mathbb {R}}^4}f\left( u+\frac{p}{2}\right) f^*\left( u-\frac{p}{2}\right) g\left( v+\frac{q}{2}\right) g^*\left( v-\frac{q}{2}\right) \\&\quad \times \textrm{e}^{-i(2cup+2cvq+ep+eq-e\tau )}\textrm{e}^{-i(b\omega +2e) \left( u+v+\frac{d}{b}\right) }\\&\quad \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\textrm{d}u\textrm{d}v\textrm{d}p\textrm{d}q\\&=\frac{b\textrm{e}^{-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2}\textrm{e}^ {-i\left( \omega +\frac{2e}{b}\right) d}e^{ie\tau }}{4\pi \sqrt{\pi }}\int _ {{\mathbb {R}}^2}\int _{{\mathbb {R}}}f\left( u+\frac{p}{2}\right) f^*\left( u-\frac{p}{2}\right) \textrm{e}^{-i\left[ b\omega +2cp+2e\right] u}\textrm{d}u\\&\quad \times \left( \int _{{\mathbb {R}}}g\left( v+\frac{q}{2}\right) g^*\left( v-\frac{q}{2}\right) \right. \\&\quad \left. \textrm{e}^{-i\left[ b\omega +2cq+2e\right] v}\textrm{d}v\right) \textrm{e}^{-\frac{b^2}{4} (\tau -p-q)^2}\textrm{e}^{-ie(p+q)}\textrm{d}p\textrm{d}q\\&=\frac{b\textrm{e}^{-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2}\textrm{e}^{-i\left( \omega +\frac{2e}{b}\right) d}e^{ie\tau }}{4\pi \sqrt{\pi }}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}} \, {\mathcal {A}}_{f}^{\Lambda }\left( p,\omega \right) \cdot {\mathcal {A}}_{g}^{\Lambda }\left( q,\omega \right) \\&\quad \times \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\textrm{e}^{-ie(p+q)}\textrm{d}p\textrm{d}q. \end{aligned}$$

Therefore, we obtain (3.31). To verify (3.32), we proceed as

$$\begin{aligned} {\mathcal {W}}_{f\underset{3}{\star }g}^{\Lambda }(t,\omega )&=\int _{{\mathbb {R}}}(f\underset{3}{\star }g)\left( t+\frac{\eta }{2}\right) \left[ (f\underset{3}{\star }g)\left( t-\frac{\eta }{2}\right) \right] ^* \textrm{e}^{-i(b\omega +2ct+e)\eta }\textrm{d}\eta \\&=\frac{b^2}{4\pi ^2}\int _{{\mathbb {R}}^5}f(\tau _1)g(\tau _2)f^*(\gamma _1)g^* (\gamma _2)\textrm{e}^{-i(b\omega +2ct+e)\eta }\times \\&\quad \textrm{e}^{-i\left[ c\tau _1^2+c\tau _2^2-c\left( t+\frac{\eta }{2}\right) ^2 +e\tau _1+e\tau _2-e\left( t+\frac{\eta }{2}\right) \right] -\frac{\left[ b\left( t+\frac{\eta }{2}\right) -b\tau _1-b\tau _2-d\right] ^2}{2}}\times \\&\quad \textrm{e}^{i\left[ c\gamma _1^2+c\gamma _2^2-c\left( t-\frac{\eta }{2}\right) ^2+e\gamma _1 +e\gamma _2-e\left( t-\frac{\eta }{2}\right) \right] -\frac{\left[ b\left( t-\frac{\eta }{2}\right) -b\gamma _1-b\gamma _2-d\right] ^2}{2}}\textrm{d}\tau _1\textrm{d} \tau _2\textrm{d}\gamma _1\textrm{d}\gamma _2\textrm{d}\eta . \end{aligned}$$

Then, considering $\tau _1=u+\dfrac{p}{2},\,\gamma _1=u-\dfrac{p}{2},\,\tau _2=v+\dfrac{q}{2},\,\gamma _2=v-\dfrac{q}{2},$ the above relation can be expressed as

$$\begin{aligned} {\mathcal {W}}_{f\underset{3}{\star }g}^{\Lambda }(t,\omega )&=\frac{b^2}{4\pi ^2} \int _{{\mathbb {R}}^5}f\left( u+\frac{p}{2}\right) f^*\left( u-\frac{p}{2}\right) g \left( v+\frac{q}{2}\right) g^*\left( v-\frac{q}{2}\right) \\&\qquad \times \textrm{e}^{-i(2cup+2cvq+ep+eq)}\textrm{e}^{-ib\omega \eta } \textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{e}^{-\frac{b^2}{4}(\eta -p-q)^2} \textrm{d}u\textrm{d}v\textrm{d}p\textrm{d}q\textrm{d}\eta \\&=\frac{b^2}{4\pi ^2}\int _{{\mathbb {R}}^4}f\left( u+\frac{p}{2}\right) f^* \left( u-\frac{p}{2}\right) g\left( v+\frac{q}{2}\right) g^*\left( v -\frac{q}{2}\right) \\&\quad \textrm{e}^{-i(2cup+2cvq+ep+eq)}\times \textrm{e}^{-[bt-b(u+v)-d]^2}\left( \int _{{\mathbb {R}}}\textrm{e}^ {-\frac{b^2}{4}(\eta -p-q)^2}\textrm{e}^{-ib\omega \eta }\textrm{d}\eta \right) \textrm{d}u\textrm{d}v\textrm{d}p\textrm{d}q. \end{aligned}$$

Thanks to formula

$$\begin{aligned} \int _{{\mathbb {R}}}\textrm{e}^{-\frac{b^2}{4}(\eta -p-q)^2} \textrm{e}^{-ib\omega \eta }\textrm{d}\eta =\frac{2\sqrt{\pi }}{b} \textrm{e}^{-ib\omega (p+q)}\textrm{e}^{-\omega ^2}, \end{aligned}$$

the relation

$$\begin{aligned}&{\mathcal {W}}_{f\underset{3}{\star }g}^{\Lambda }(t,\omega )=\frac{b\textrm{e}^ {-\omega ^2}}{2\pi \sqrt{\pi }}\int _{{\mathbb {R}}^4}f\left( u+\frac{p}{2}\right) f^*\left( u-\frac{p}{2}\right) g\left( v+\frac{q}{2}\right) g^*\left( v-\frac{q}{2}\right) \\&\qquad \times \textrm{e}^{-i(2cup+2cvq+ep+eq)}\textrm{e}^{-[bt-b(u+v)-d]^2} \textrm{e}^{-ib\omega (p+q)}\textrm{d}u\textrm{d}v\textrm{d}p\\&=\frac{b\textrm{e}^{-\omega ^2}}{2\pi \sqrt{\pi }}\int _{{\mathbb {R}}^2} \left( \int _{{\mathbb {R}}}f\left( u+\frac{p}{2}\right) f^*\left( u-\frac{p}{2}\right) \textrm{e}^{-i(b\omega +2cu+e)p}\textrm{d}p\right) \\&\qquad \times \left( \int _{{\mathbb {R}}}g\left( v+\frac{q}{2}\right) g^* \left( v-\frac{q}{2}\right) \textrm{e}^{-i(b\omega +2cu+e)q}\textrm{d}q\right) \textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{d}u\textrm{d}v\\&= \frac{b\textrm{e}^{-\omega ^{2}}}{2\pi \sqrt{\pi }}\int _{{\mathbb {R}}}\int _ {{\mathbb {R}}}\, {\mathcal {W}}_{f}^{\Lambda }(u,\omega )\cdot {\mathcal {W}}_{g}^{\Lambda } (v,\omega )\textrm{e}^{-[bt-b(u+v)-d]^2}\textrm{d}u\textrm{d}v \end{aligned}$$

holds. Thus, we deduce (3.32). The proof is completed. $\square$

The two following theorems will be omitted because their proofs are very similar to the proof of Theorem 4.

Theorem 5

If $f,g\in L^2({{\mathbb {R}}})$, then the following holds

$$\begin{aligned} {\mathcal {A}}_{f\underset{4}{\star }g}^{\Lambda }(\tau ,\omega )&= \frac{b\textrm{e}^{-\frac{1}{4}\left( \omega +\frac{2e}{b}\right) ^2} \textrm{e}^{ie\tau }}{4\pi \sqrt{\pi }}\int _{\mathbb R}\int _{{\mathbb {R}}}\, {\mathcal {A}}_{f}^{\Lambda }\left( p,\omega \right) \cdot {\mathcal {A}}_{g}^ {\Lambda }\left( q,\omega \right) \\&\quad \times \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\textrm{e}^{-ie(p+q)}\textrm{d}p\textrm{d}q,\\ {\mathcal {W}}_{f\underset{4}{\star }g}^{\Lambda }(t,\omega )&= \frac{b\textrm{e}^ {-\omega ^{2}}}{2\pi \sqrt{\pi }}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\, {\mathcal {W}}_{f}^ {\Lambda }(u,\omega )\cdot {\mathcal {W}}_{g}^{\Lambda }(v,\omega )\textrm{e}^{-b^2(t-u-v)^2}\textrm{d}u\textrm{d}v. \end{aligned}$$

Theorem 6

For any pair of functions $f,g\in L^2({{\mathbb {R}}})$, we have

$$\begin{aligned} {\mathcal {A}}_{f\underset{5}{\star }g}^{\Lambda }(\tau ,\omega )&=\frac{b\textrm{e}^ {-\frac{1}{b^2}\left[ b\omega +c\tau +2e \right] ^2}\textrm{e}^{-i\left[ b\omega +c\tau +2e\right] \frac{d(2-\sqrt{2})}{b}}e^{\frac{ie\sqrt{2}\tau }{2}}}{4\pi \sqrt{\pi }}\\&\quad \times \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\, {\mathcal {A}}_{f}^{\Lambda } \left( p,\omega +\frac{c\tau }{b} \right) {\mathcal {A}}_{g}^{\Lambda }\left( q,\omega +\frac{c\tau }{b}\right) \textrm{e}^{-\frac{b^2}{4}(\tau -p-q)^2}\textrm{e}^{-ie(p+q)} \textrm{d}p\textrm{d}q,\\ {\mathcal {W}}_{f\underset{5}{\star }g}^{\Lambda }(t,\omega )&= \frac{b\textrm{e}^ {-\frac{1}{b^2}\left[ b\omega +ct+\frac{(2-\sqrt{2})}{2}e\right] ^2}}{2\pi \sqrt{\pi }} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\, {\mathcal {W}}_{f}^{\Lambda }\left( u,\omega +\frac{2ct+(2-\sqrt{2})e}{2b}\right) \\&\quad \times {\mathcal {W}}_{g}^{\Lambda }\left( v,\omega +\frac{2ct+(2-\sqrt{2})e}{2b} \right) \textrm{e}^{-[bt-b(u+v)-2d+d\sqrt{2}]^2}\textrm{d}u\textrm{d}v. \end{aligned}$$

4 Applications

The LFM signals are frequently encountered in applications such as radar and sonar [7].

In this section, the applications of QAF and QWD in the detection of single-component and multi-component LFM signals will be investigated. Besides, simulations are given to verify the proposed methods.

4.1 Single-Component LFM Signal

Let us consider the single-component LFM signal with the amplitude $A_0$, initial frequency $\omega _0$, and frequency rate $m_0$ as follows

$$\begin{aligned} f(t)=A_0\textrm{e}^{i(\omega _0t+m_0t^2)},\,\,\quad -\frac{T}{2}\le t \le \frac{T}{2}. \end{aligned}$$

The QAF of f(t) is computed as

$$\begin{aligned} {\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )&=\int _{-\frac{T}{2}}^{\frac{T}{2}}A_0 \textrm{e}^{i\left[ \omega _0\left( t+\frac{\tau }{2}\right) +m_0\left( t+\frac{\tau }{2}\right) ^2\right] }\nonumber \\&\quad \times A_0^*\textrm{e}^{-i\left[ \omega _0\left( t-\frac{\tau }{2}\right) +m_0 \left( t-\frac{\tau }{2}\right) ^2\right] }\textrm{e}^{-i\big (b\omega +2c\tau +2e\big )t} \textrm{d}t\nonumber \\&=\vert A_0\vert ^2\textrm{e}^{i\omega _0 \tau }\int _{-\frac{T}{2}}^{\frac{T}{2}} \textrm{e}^{i(2m_0\tau -b\omega -2c\tau -2e)t}\textrm{d}t\nonumber \\&=2\vert A_0\vert ^2\textrm{e}^{i\omega _0 \tau } \frac{\sin \left\{ \frac{T}{2} \left( 2m_0\tau -b\omega -2c\tau -2e\right) \right\} }{2m_0 \tau -b\omega -2c\tau -2e}\nonumber \\&=\vert A_0\vert ^2T \textrm{e}^{i\omega _0 \tau }{{\,\textrm{sinc}\,}}\left\{ \frac{T}{2} \left( 2m_0\tau -b\omega -2c\tau -2e\right) \right\} . \end{aligned}$$

(4.34)

Similarly, the QWD of f(t) can be given by

$$\begin{aligned} {\mathcal {W}}_{f}^{\Lambda }(t,\omega )&=\int _{-\frac{T}{2}}^{\frac{T}{2}}A_0 \textrm{e}^{i\left[ \omega _0\left( t+\frac{\tau }{2}\right) +m_0 \left( t+\frac{\tau }{2}\right) ^2\right] }\times \nonumber \\&\quad A_0^*\textrm{e}^{-i\left[ \omega _0\left( t-\frac{\tau }{2}\right) +m_0\left( t-\frac{\tau }{2}\right) ^2\right] }\textrm{e}^{-i\big (b\omega +2ct +e\big )\tau } \textrm{d}\tau \nonumber \\&=\vert A_0\vert ^2T{{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left( \omega _0+2m_0t -b\omega -2ct-e\right) \right\} , \end{aligned}$$

(4.35)

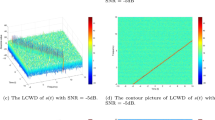
which is only dependent on parameters b, c,  and e. Since the QAF and QWD of a single-component LFM signal f(t) generates impulses at a straight line $2m_0\tau -b\omega -2c\tau -2e=0$ in the $(\tau ,\omega )$-plane and $\omega _0+2m_0t-b\omega -2ct-e=0$ in the $(t,\omega )$-plane, respectively, then the QAF and QWD can be used to detect a single-component LFM signal by suitably choosing the parameters b, c,  and e in (4.34) and (4.35). For instance, the detection and estimation for single-component LFM signal $r(t)=\textrm{e}^{i(0.5t+0.6t^2)}\,\,(|t|\le 10)$ with SNR = -5dB by QAF and QWD for $\Lambda =(a,-0.5,-0.125,d,1)$ are displayed in Fig. 2. Moreover, Fig.  3 shows the QWD of LFM signal $v(t)=\textrm{e}^{i(0.2t+0.3t^2)}\,\,(|t|\le 5)$ with SNR = 10dB at different values of $\Lambda =(1,-1,-1,1,e)$, $e=-3, e=1,$ and $e=5$.

Fig. 2

The detection and parameters estimation for r(t) with SNR = -5dB by QAF and QWD

Fig. 3

The detection and parameters estimation for v(t) with SNR = 10dB at different values of $\Lambda =(1,-1,-1,1,e)$

Fig. 4

The detection and parameters estimation for bi-component LFM signal s(t) with SNR = 10 dB

4.2 Multi-component LFM signal

We now consider the general form of multi-component LFM signal, which is given by

$$\begin{aligned} f(t)=\sum _{k=1}^{n}f_k(t),\,\,\frac{T}{2} \le t \le \frac{T}{2}, \end{aligned}$$

where $f_k(t)=A_k \textrm{e}^{i(\omega _kt+m_kt^2)},\,k=\{1,\ldots n\}\, (n\in {\mathbb {N}}).$

It is easily proven that

$$\begin{aligned}&{\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )=\sum _{k=1}^{n}{\mathcal {A}}_{f_k}^{\Lambda }(\tau ,\omega )+\sum _{k_1\ne k_2=1}^{n}{\mathcal {A}}_{f_{k_1},f_{k_2}}^{\Lambda }(\tau ,\omega ). \end{aligned}$$

Meanwhile, the QAF of cross-term ${\mathcal {A}}_{f_{k_1},f_{k_2}}^{\Lambda }(\tau ,\omega )$ can be calculated as

$$\begin{aligned} {\mathcal {A}}_{f_{k_1},f_{k_2}}^{\Lambda }(\tau ,\omega )&=\int _{{\mathbb {R}}}f_{k_1} \left( t+\frac{\tau }{2}\right) \left[ f_{k_2}\left( t-\frac{\tau }{2}\right) \right] ^*\textrm{e}^{-i\big (b\omega +2c\tau +2e\big )t} \textrm{d}t\\&=\int _{-\frac{T}{2}}^{\frac{T}{2}}A_{k_1}\textrm{e}^{i\left[ \omega _{k_1} \left( t+\frac{\tau }{2}\right) +m_{k_1}\left( t+\frac{\tau }{2}\right) ^2\right] }A_{k_2}^ *\textrm{e}^{-i\left[ \omega _{k_2}\left( t-\frac{\tau }{2}\right) +m_{k_2}\left( t -\frac{\tau }{2}\right) ^2\right] }\nonumber \\&\quad \times \textrm{e}^{-i\big (b\omega +2c\tau +2e\big )t} \textrm{d}t\\&=A_{k_1}A_{k_2}^*\textrm{e}^{i\left[ \frac{(m_{k_1}-m_{k_2})}{4}\tau ^2+ \frac{(\omega _{k_1}+\omega _{k_2})}{2}\tau \right] }\nonumber \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\textrm{e}^{i \left[ (m_{k_1}-m_{k_2})t^2+(\omega _{k_1}-\omega _{k_2}+m_{k_1}\tau +m_{k_2} \tau -b\omega -2c\tau -2e)t\right] }\textrm{d}t. \end{aligned}$$

Therefore, the QAF of $f(t)=\sum _{k=1}^{n}f_k(t)$ has the form

$$\begin{aligned} {\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )&=\sum _{k=1}^{n}\vert A_k\vert ^2T \textrm{e}^{i\omega _k \tau } {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left( 2m_k\tau -b \omega -2c\tau -2e\right) \right\} \nonumber \\&\quad +\sum _{{k_1\ne k_2=1}}^{n}A_{k_1}A_{k_2}^*\textrm{e}^{i \left[ \frac{(m_{k_1}-m_{k_2})}{4}\tau ^2+\frac{(\omega _{k_1} +\omega _{k_2})}{2}\tau \right] }\nonumber \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\textrm{e}^{i \left[ (m_{k_1}-m_{k_2})t^2+(\omega _{k_1}-\omega _{k_2}+m_{k_1}\tau +m_{k_2}\tau -b\omega -2c\tau -2e)t\right] }\textrm{d}t. \end{aligned}$$

(4.36)

Despite the fact that the existence of cross-terms can not generate the impulse in $(\tau ,\omega )$-plane but they still have an influence on the detection performance. Therefore, the relation (4.36) indicates that the QAF is an effective tool for detecting multi-component LFM signals. When $m_1=m_2=\ldots =m_n=m$, we obtain

$$\begin{aligned} {\mathcal {A}}_{f}^{\Lambda }(\tau ,\omega )&=\left[ \sum _{k=1}^{n}\vert A_k\vert ^2 \textrm{e}^{i\omega _k \tau }\right] \cdot T{{\,\textrm{sinc}\,}}\left\{ \frac{T}{2} \left( 2m\tau -b\omega -2c\tau -2e\right) \right\} \\&\quad +\sum _{{k_1\ne k_2=1}}^{n}A_{k_1}A_{k_2}^*T\textrm{e}^{i \frac{(\omega _{k_1}+\omega _{k_2})}{2}\tau } \\&\quad {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2} \left( \omega _{k_1}-\omega _{k_2}+2m\tau -b\omega -2c\tau -2e\right) \right\} . \end{aligned}$$

In the same way, the QWD of $f(t)=\sum _{k=1}^{n}f_k(t)$ has the form

$$\begin{aligned} {\mathcal {W}}_{f}^{\Lambda }(t,\omega )&=\sum _{k=1}^{n}\vert A_{k} \vert ^2T {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left( \omega _k+2m_kt-b\omega -2ct-e\right) \right\} \\&\quad +\sum _{{k_1\ne k_2=1}}^{n}A_{k_1}A_{k_2}^*\textrm{e}^ {i\left[ (\omega _{k_1}-\omega _{k_2})t+(m_{k_1}-m_{k_2})t^2\right] }\times \\&\quad \int _{-\frac{T}{2}}^{\frac{T}{2}}\textrm{e}^ {i\frac{(m_{k_1}-m_{k_2})}{4}\tau ^2}\textrm{e}^{i \left[ (m_{k_1}+m_{k_2}-2c)t+\frac{\omega _{k_1}+\omega _ {k_2}}{2}-b\omega -e\right] \tau }\textrm{d}\tau , \end{aligned}$$

When $m_1=m_2=\ldots =m_n=m$, the QWD of multi-component LFM signal f(t) can be given by

$$\begin{aligned} {\mathcal {W}}_{f}^{\Lambda }(t,\omega )&=\sum _{k=1}^{n}\vert A_k\vert ^2 T{{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left( \omega _k+2mt-b\omega -2ct-e\right) \right\} \\&\quad +\sum _{{k_1\ne k_2=1}}^{n}A_{k_1}A_{k_2}^*T\textrm{e}^{i(\omega _{k_1}-\omega _{k_2})t} {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left( 2(m-c)t+\frac{\omega _{k_1}+\omega _{k_2}}{2}-b\omega -e\right) \right\} , \end{aligned}$$

For the purpose of illustration, considering a bi-component LFM signal

$$\begin{aligned} s(t)=\textrm{e}^{i(0.2t+0.3t^2)}+\textrm{e}^{i(0.4t+0.3t^2)}, \,\,(|t|\le 5). \end{aligned}$$

For the choices $\Lambda =(a,1,1,d,1)$ and SNR =10 dB, the graphical representation of ${\mathcal {A}}_{s}^{\Lambda }(\tau ,\omega )$ and ${\mathcal {W}}_{s}^{\Lambda }(t,\omega )$ are plotted in Fig. 4.

5 Conclusion

In the present study, the modified ambiguity function and Wigner distribution associated with the quadratic-phase Fourier transform are defined. Some useful properties of them are studied. The convolutions associated with QFT as well as convolution theorems for QAF and QWD are presented, which are so simple and similar to the FT case. As the main application, the detection and parameter estimation of one-component and multi-component LFM signals are investigated by using the QAF and QWD. Some simulations are illustrated to verify the derived results.