1 Introduction

Without a doubt, one of the most important tools for examining the time–frequency of stationary signals is the Fourier transform. Over the years, the FT has had a significant impact on the mathematical, biological, chemical, and engineering sectors due to its successful stories. However, the FT is unable to analyze non-stationary signals since it cannot give any meaningful information about the localization properties of the spectrum contents. With the FT, we are only able to study signals in the frequency and time domains separately. In [1,2,3,4], Castro et al. introduced the quadratic-phase Fourier transform (QPFT), a superlative generalized version of the Fourier transform (FT) that offers a unified treatment of both transient and non-transient signals in a clear and insightful manner. For a given set of parameters \(\Omega =(a,b,c,d,e), b\ne 0\) the QPFT of any signal \(f\in L^2({\mathbb {R}})\) is defined by

$$\begin{aligned} {\mathcal {Q}}_{a,b,c}^{d,e}[f](u)=\int _{{\mathbb {R}}}f(t){\mathcal {K}}_{a,b,c}^{d,e}(t,u)dt, \end{aligned}$$
(1.1)

where the quadratic-phase Fourier kernel \({\mathcal {K}}_{a,b,c}^{d,e}(t,u)\) is given by

$$\begin{aligned} {\mathcal {K}}_{a,b,c}^{d,e}(t,u)=\sqrt{\frac{|b|}{2\pi }}e^{i(at^2+btu+cu^2+dt+eu)},\quad a,b,c,d,e\in {\mathbb {R}}. \end{aligned}$$
(1.2)

Numerous studies on the quadratic-phase Fourier transform have been conducted (see to [5, 6]). Because the QPFT is controlled by a set of free parameters, it has shown to be a dependable tool for the effective representation of signals requiring multiple controllable parameters, that arise in various scientific and engineering fields, such as filter design, harmonic analysis, sampling, image processing, signal processing-particularly for the detection of linear-frequency-modulating (LFM) signals-and sampling theory [9,10,11, 22].

On the other hand, of all the time–frequency distributions, the most basic parametric time–frequency analysis tools are the classical WD and the classical AF, which are primarily used to analyze the time–frequency features of non-stationary signals, especially in applications to detect LFM signals [7, 8, 12,13,14,15,16,17,18,19,20,21]. For any finite energy signal f(t) the WD and the AF are defined in terms of tensor products as [26,27,28,29,30]

$$\begin{aligned} {\mathcal {W}}_f(t,u)= & {} \int _{{\mathbb {R}}} \left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-iu\varphi }d\varphi ,\quad (t,u)\in {\mathbb {R}}^2, \end{aligned}$$
(1.3)
$$\begin{aligned} {\mathcal {A}}_f(\varphi ,u)= & {} \int _{{\mathbb {R}}} \left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-iut}dt,\quad (\varphi ,u)\in {\mathbb {R}}^2, \end{aligned}$$
(1.4)

where superscript \(*\) denotes complex conjugate and \(\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t) =f\left( t+\frac{\varphi }{2}\right) f^*\left( t-\frac{\varphi }{2}\right) \) is the fractional instantaneous auto-correlation function. Following the classical definition of WD and AF, authors in [22, 23] firstly investigate the WD associated with the QPFT. Recently, Bhat And Dar [24] introduced a version of WD and AF associated with QPFT and defined it as: For a finte energy signal f(t),  the WD and AF associated with QPFT, defined for \(f\in L^2({\mathbb {R}})\) as [22,23,24]

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b,c}^{d,e}}_f(t,u)= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{d,e}(\varphi ,u)d\varphi , \end{aligned}$$
(1.5)
$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b,c}^{d,e}}_f(\varphi ,u)= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{d,e}(t,u)dt, \end{aligned}$$
(1.6)

where \({\mathcal {K}}_{a,b,c}^{d,e}(t,u)\) is given in (1.2). They investigate the properties and the applications of the WD and AF associated with the QPFT to the detection of non-stationary signals. In contrast to [22,23,24], this article presents a different definition for WD and AF related to QPFT, which is based on the flexibility of the Fourier kernel.

The contributions of this paper are mentioned below:

  • To introduce a new WD and AF in the quadratic phase Fourier domain.

  • To study the fundamental properties of the NQPWD and NQPAF, including the conjugate symmetry, non-linearity, shifting, scaling, frequency marginal and Moyal formula.

  • To derive the relationship of NQPWD and NQPAF with the short-time Fourier Transform.

  • To study the convolution and correlation properties of the NQPWD.

  • With the help of simulations, we offer applications of the suggested distributions in the detection of single-component and multi-component LFM signals to demonstrate the benefits of the theory.

1.1 Paper outlines

The paper is organized as follows: in Sect. 2, the definition and the essential properties of the NQPWD and NQPAF are introduced. In Sect. 3, the applications of the proposed NQPWD and NQPAF to the detection of single-component and multi-component LMF signals is provided. Finally, a conclusion is drawn in Sect. 4.

2 New quadratic-phase Wigner distribution and ambuigty function

In this section, we shall introduce the notion of the new quadratic phase Wigner Distribution(NQPWD) and new quadratic phase ambiguity function followed by some of its properties.

2.1 Definition of the NQPWD and NQPAF

We can modify the expressions of classical WD and AF as

$$\begin{aligned} {\mathcal {W}}_f(t,u)= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-iu\varphi }d\varphi \nonumber \\= & {} \int _{{\mathbb {R}}}e^{-i{u}\left( t+\frac{\varphi }{2}\right) }\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i{u}\left( t-\frac{\varphi }{2}\right) }d\varphi \nonumber \\= & {} \int _{{\mathbb {R}}}\left( f_u\underset{\frac{\varphi }{2}}{\otimes }f_u^*\right) (t)d\varphi , \end{aligned}$$
(2.1)

where

$$\begin{aligned} f_u(t)=f(t)e^{-i{u}t}. \end{aligned}$$
(2.2)

On substituting the Fourier kernels \(e^{-iut}\) with QPFT kernels \({\mathcal {K}}_{a,b,c}^{d,e}(t,u)\) in (2.3), we obtain

$$\begin{aligned} f_{u,a,b,c}^{d,e}(t)=f(t){\mathcal {K}}_{a,b,c}^{d,e}(t,u). \end{aligned}$$
(2.3)

Now, by replacing \(f_u(t)\) with \(f_{u,a,b,c}^{d,e}(t)\) in (2.1) and then using (2.3), we obtain NQPWD as

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)= & {} \int _{{\mathbb {R}}}\left( f_{u,a,b,c}^{d,e}\underset{\frac{\varphi }{2}}{\otimes }f_{u,a,b,c}^{*d,e}\right) (t)d\varphi \nonumber \\= & {} \int _{{\mathbb {R}}}{\mathcal {K}}_{a,b,c}^{d,e}\left( {t}+\frac{\varphi }{2},u\right) \left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{*d,e}\left( {t}-\frac{\varphi }{2},u\right) d\varphi \nonumber \\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{d,e}\left( {t}+\frac{\varphi }{2},u\right) {\mathcal {K}}_{a,b,c}^{*d,e}\left( {t}-\frac{\varphi }{2},u\right) d\varphi \nonumber \\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \end{aligned}$$
(2.4)

where \({\mathcal {K}}_{a,b}^{d}(\varphi ,u)=\dfrac{|b|}{2\pi }e^{i(2at\varphi +bu\varphi +d\varphi )}.\)

$$\begin{aligned} {\mathcal {A}}_f(\varphi ,u)= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-iut}dt \nonumber \\= & {} \int _{{\mathbb {R}}}e^{-i\frac{u}{2}\left( t+\frac{\varphi }{2}\right) }\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-i\frac{u}{2}\left( t-\frac{\varphi }{2}\right) }dt\nonumber \\= & {} \int _{{\mathbb {R}}}\left( {{\bar{f}}}_u\underset{\frac{\varphi }{2}}{\otimes }{{\hat{f}}^*}_u\right) (t)dt, \end{aligned}$$
(2.5)

where

$$\begin{aligned} {{\bar{f}}}_u(t)=f(t)e^{-i\frac{u}{2}t}\quad \text{ and }\quad {{\hat{f}}}_u(t)=f(t)e^{i\frac{u}{2}t}. \end{aligned}$$
(2.6)

by substituting the Fourier kernels with the QPFT kernels, (2.6) gives

$$\begin{aligned} {{\bar{f}}}_{u,a,b,c}^{d,e}(t)=f(t){\mathcal {K}}_{a,b,c}^{d,e}\left( t,\frac{u}{2}\right) \quad \text{ and }\quad {{\hat{f}}}_{u,a,b,c}^{d,e}(t)=f(t){\mathcal {K}}_{a,b,c}^{d,e}\left( t,-\frac{u}{2}\right) . \end{aligned}$$
(2.7)

Now by replacing \({{\bar{f}}}_u(t)\) with \({{\bar{f}}}_{u,a,b,c}^{d,e}(t)\) and \({{\hat{f}}}_u(t)\) with \( {{\hat{f}}}_{u,a,b,c}^{d,e}(t)\) in (2.5) and then using (2.7), we obtain NQPAF as

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(\varphi ,u)= & {} \int _{{\mathbb {R}}}\left( {{\bar{f}}}_{u,a,b,c}^{d,e}\underset{\frac{\varphi }{2}}{\otimes }{{\hat{f}}}_{u,a,b,c}^{*d,e}\right) (t)dt\nonumber \\= & {} \int _{{\mathbb {R}}}{\mathcal {K}}_{a,b,c}^{d,e}\left( {t}+\frac{\varphi }{2},\frac{u}{2}\right) \left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{*d,e}\left( \frac{\varphi }{2}-t,\frac{u}{2}\right) dt\nonumber \\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b,c}^{d,e}\left( {t}+\frac{\varphi }{2},\frac{u}{2}\right) {\mathcal {K}}_{a,b,c}^{*d,e}\left( \frac{\varphi }{2}-t,\frac{u}{2}\right) dt\nonumber \\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt \end{aligned}$$
(2.8)

where \({\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)=\dfrac{|b|}{2\pi }e^{i(2at\varphi +but+d\varphi +eu)}.\)

With the virtue of above equations (2.4) and (2.8), we have following definition

Definition 2.1

The new quadratic-phase Wigner distribution and ambiguity function of any signal f in \( L^2({\mathbb {R}})\) is defined as

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)=\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi . \end{aligned}$$
(2.9)

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(\varphi ,u)=\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt. \end{aligned}$$
(2.10)

where \({\mathcal {K}}_{a,b}^{d}(\varphi ,u)=\dfrac{|b|}{2\pi }e^{i(2at\varphi +bu\varphi +d\varphi )}\) and \({\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)=\dfrac{|b|}{2\pi }e^{i(2at\varphi +but+d\varphi +eu)}\).

It can easily be seen that, the NQPWD and NQPAF have following relationship with the corresponding classical WD and AF

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)=|b|{\mathcal {W}}_f\left( t,-bu-d-2at\right) . \end{aligned}$$
(2.11)

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(\varphi ,u)=|b|e^{i(d\varphi +eu)}{\mathcal {A}}_f\left( \varphi ,-bu-2a\varphi \right) . \end{aligned}$$
(2.12)

Therefore the proposed transforms (2.9) and (2.10) inherit the vital advantages of the classical WD and the classical AF and also preserve the features of the QPFT.

Additionally, the prolificacy of the NQPWD and NQPAF given in Definition 2.1 can be ascertained from the following important deductions:

  1. (i)

    The new quadratic-phase cross-Wigner distribution and ambiguity function of the finite energy signals f and g are given by

    $$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f,g}(t,u)=\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }g^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi . \end{aligned}$$
    (2.13)

    And

    $$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f,g}(t,u)=\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }g^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt. \end{aligned}$$
    (2.14)
  2. (ii)

    Taking \(a=a/2b,\quad b=-1/b,\quad c=c/2b,\quad d=0,\quad e=0\,\) the NQPWD the NQPWD and NQPAF defined in (2.9) and (2.10) respectively, yield to the well known WD and AF associated to the linear canonical transform defined by Zhang in [25]:

    $$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)=\frac{1}{2\pi |b|}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(\frac{a}{b}\varphi -\frac{u}{b})t}dt. \end{aligned}$$
    (2.15)

    And

    $$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(t,u)=\frac{1}{2\pi |b|}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(\frac{a}{b}t-\frac{u}{b})\varphi }d\varphi . \end{aligned}$$
    (2.16)
  3. (iii)

    When we choose \(a=\cot \theta /2,\quad b=-\csc \theta ,\quad c=\cot \theta ,\quad d=0,\quad e=0,\) the NQPWD and NQPAF defined in (2.9) and (2.10) respectively, give the new fractional Fourier Wigner distribution and new fractional Fourier ambiguity function:

    $$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)=\frac{1}{-2\pi \sin \theta }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(t\cot \theta -u\csc \theta )\varphi }d\varphi . \end{aligned}$$
    (2.17)

    And

    $$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(t,u)=\frac{1}{-2\pi \sin \theta }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(\varphi \cot \theta -u\csc \theta )t}dt. \end{aligned}$$
    (2.18)
  4. (iv)

    When \(a=0,\quad b=-1,\quad c=0,\quad d=0,\quad e=0,\) is chosen, the NQPWD (2.4) and NQPAF (2.10) reduce to the classical Wigner distribution and ambiguity function given in (1.3) (1.4).

Thus it is clear from above discussions that the NQPWD (2.4) and NQPAF (2.10) are more flexible than the existing classes of WD and AF due to the presence of five free parameters a, b, c, d and e.

2.2 Properties of NQPWD and NQPAF

All the properties of the NQPWD and NQPAF’s are examined in this subsection along with thorough proofs.

Theorem 2.1

(Symmetry-conjugation property) For \(f\in L^2({\mathbb {R}}),\) we have

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f^*}(t,u)=-{\mathcal {W}}^{{\mathcal {Q}}_{-a,b}^{-d}}_{f}(t,-u),\quad {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f^*}(\varphi ,u)={\mathcal {A}}^{{\mathcal {Q}}_{-a,-b}^{-d,-e}}_{f}(-\varphi ,-u) \end{aligned}$$
(2.19)

And

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{Pf}(t,u)=-{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{-d}}_{f}(-t,-u), \quad {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{Pf}(\varphi ,u)=-{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{-d,-e}}_{f}(-\varphi ,-u), \end{aligned}$$
(2.20)

where \(Pf(t)=f(-t)\).

Proof

We have from Definition 2.1

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f^*}(t,u)= & {} \int _{{\mathbb {R}}}\left( f^*\underset{\frac{\varphi }{2}}{\otimes }f\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \\= & {} \frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f^*\underset{\frac{\varphi }{2}}{\otimes }f\right) (t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \\{} & {} \buildrel \varphi =-\psi \over =-\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f^*\underset{\frac{-\psi }{2}}{\otimes }f\right) (t)e^{i[2at(-\psi )+bu(-\psi )+d(-\psi )]}d\psi \\= & {} -\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\psi }{2}}{\otimes }f^*\right) (t)e^{i[2(-a)t\psi +b(-u)\psi +(-d)\psi ]}d\psi \\= & {} -\int _{{\mathbb {R}}}\left( f\underset{\frac{\psi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{-a,b}^{-d}(\psi ,-u)d\psi \\= & {} -{\mathcal {W}}^{{\mathcal {Q}}_{-a,b}^{-d}}_{f}(t,-u). \end{aligned}$$

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f^*}(\varphi ,u)= & {} \int _{{\mathbb {R}}}\left( f^*\underset{\frac{\varphi }{2}}{\otimes }f\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\= & {} \dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f^*\underset{\frac{\varphi }{2}}{\otimes }f\right) (t)e^{i(2at\varphi +but+d\varphi +eu)}dt\\= & {} \dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{-\varphi }{2}}{\otimes }f^*\right) (t)e^{i(2at\varphi +but+d\varphi +eu)}dt\\= & {} \dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{-\varphi }{2}}{\otimes }f^*\right) (t)e^{i[2(-a)t(-\varphi )+(-b)(-u)t+(-d)(-\varphi )+(-e)(-u)]}dt\\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{-\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{-a,-b}^{-d,-e}(-\varphi ,-u)dt\\= & {} {\mathcal {A}}^{{\mathcal {Q}}_{-a,-b}^{-d,-e}}_{f}(-\varphi ,-u) \end{aligned}$$

Now,

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{Pf}(t,u)= & {} \int _{{\mathbb {R}}}\left( Pf\underset{\frac{\varphi }{2}}{\otimes }Pf^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \\= & {} \frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{-\varphi }{2}}{\otimes }f^*\right) (-t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \\&\buildrel -\varphi =\psi \over =&-\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\psi }{2}}{\otimes }f^*\right) (-t)e^{-i(2at\psi +bu\psi +d\psi )}d\psi \\= & {} -\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\psi }{2}}{\otimes }f^*\right) (-t)e^{i[2a(-t)\psi +b(-u)\psi +(-d)\psi ]}d\psi \\= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\psi }{2}}{\otimes }f^*\right) (-t){\mathcal {K}}_{a,b}^{-d}(\psi ,-u)d\psi \\= & {} -{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{-d}}_{f}(-t,-u). \end{aligned}$$

Similarly we can prove that \( {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{Pf}(\varphi ,u)=-{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{-d,-e}}_{f}(-\varphi ,-u).\)

Hence completes the proof. \(\square \)

Theorem 2.2

(Non-linearity) Let \(f(t)=f_1(t)+f_2(t)\) be in \(L^2({\mathbb {R}}),\) then we have

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f}(t,u)={\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_1}(t,u)+{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_2}(t,u)+{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_1,f_2}(t,u)+{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_2,f_1}(t,u). \nonumber \\ \end{aligned}$$
(2.21)

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f}(t,u)={\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f_1}(t,u)+{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f_2}(t,u)+{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f_1,f_2}(t,u)+{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f_2,f_1}(t,u). \end{aligned}$$
(2.22)

Proof

For the sake of brevity, we omit proof. \(\square \)

Theorem 2.3

(Time shift) Let \(f\in L^2({\mathbb {R}}),\) then for every \(t_1\in {\mathbb {R}} \), the NQPWD and NQPAF of the signal \(f(t-t_1)\) can be expressed as:

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f(t-t_1)}(t,u)={\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( t-t_1,u+2t_1\frac{a}{b}\right) ,\nonumber \\{} & {} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t-t_1)}(\varphi ,u)=e^{i(2a\varphi +bu)t_1}{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t)}(\varphi ,u). \end{aligned}$$
(2.23)

Proof

From the definitions of NQPWD and NQPAF, we have:

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f(t-t_1)}(t,u)\\{} & {} =\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1)e^{i[2a(t-t_1)\varphi +2at_1\varphi +bu\varphi +d\varphi ]}d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1)e^{i\left[ 2a(t-t_1)\varphi +b\left( u+2\frac{a}{b}t_1\right) \varphi +d\varphi \right] }d\varphi \\{} & {} =\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1){\mathcal {K}}_{a,b}^{d}\left( \varphi ,u+2t_1\frac{a}{b}\right) d\varphi \\{} & {} ={\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( t-t_1,u+2t_1\frac{a}{b}\right) . \end{aligned}$$

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t-t_1)}(\varphi ,u)= & {} \int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\= & {} \dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t-t_1)e^{i(2at\varphi +but+d\varphi +eu)}dt\\&\buildrel t-t_1=t_0 \over =&\dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t_0)e^{i[2a(t_0+t_1)\varphi +bu(t_0+t_1)+d\varphi +eu)}dt_0\\= & {} e^{i(2a\varphi +bu)t_1}\dfrac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t_0)e^{i[2at_0\varphi +but_0+d\varphi +eu)}dt_0\\= & {} e^{i(2a\varphi +bu)t_1}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t_0){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt_0\\= & {} e^{i(2a\varphi +bu)t_1}{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f}(\varphi ,u). \end{aligned}$$

Which completes the proof. \(\square \)

Theorem 2.4

(Frequency shift) Let \(f\in L^2({\mathbb {R}}),\) then for every \(u_1\in {\mathbb {R}} \), the NQPWD and NQPAF of the signal \({\tilde{f}}(t)=f(t)e^{iu_1t}\) can be expressed as:

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{{\tilde{f}}}(t,u)={\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( t,u+\frac{k}{B}u_1\right) ,\quad {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{{\tilde{f}}}(\varphi ,u)=e^{iu_1\varphi }{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{ f}(\varphi ,u).\nonumber \\ \end{aligned}$$
(2.24)

Proof

Using Definition 2.1, we have

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{{\tilde{f}}(t)}(t,u)\\{} & {} =\int _{{\mathbb {R}}}\left( {\tilde{f}}\underset{\frac{\varphi }{2}}{\otimes }{\tilde{f}}^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}e^{iu_1\left( t+\frac{\varphi }{2}\right) }\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{-iu_1\left( t-\frac{\varphi }{2}\right) }e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i[u_1\varphi +(2at\varphi +bu\varphi +d\varphi )]}d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i\left[ 2at\varphi +b\left( u+\frac{u_1}{b}\right) \varphi +d\varphi \right] }d\varphi \\{} & {} =\int _{{\mathbb {R}}} \left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d}\left( \varphi ,u+\frac{u_1}{b}\right) d\varphi \\{} & {} ={\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( t,u+\frac{u_1}{b}\right) . \end{aligned}$$

And

$$\begin{aligned}{} & {} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{{\tilde{f}}(t)}(\varphi ,u)\\{} & {} =\int _{{\mathbb {R}}}\left( {\tilde{f}}\underset{\frac{\varphi }{2}}{\otimes }{\tilde{f}}^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}e^{iu_1\left( t+\frac{\varphi }{2}\right) }\left( f\underset{\frac{\varphi }{2}}{\otimes } f^*\right) (t)e^{-iu_1\left( t-\frac{\varphi }{2}\right) }e^{i(2at\varphi +but+d\varphi +eu)}dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(u_1\varphi +2at\varphi +but+d\varphi +eu)}dt\\{} & {} =e^{iu_1\varphi }\frac{|b|}{2\pi }\int _{{\mathbb {R}}} \left( f\underset{\frac{\varphi }{2}}{\otimes } f^*\right) (t)e^{i(2at\varphi +but+d\varphi +eu)}dt\\{} & {} =e^{iu_1\varphi }\int _{{\mathbb {R}}} \left( f\underset{\frac{\varphi }{2}}{\otimes } f^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\{} & {} =e^{iu_1\varphi }{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{ f}(\varphi ,u), \end{aligned}$$

which completes the proof \(\square \)

Theorem 2.5

(Scaling property) Let \(f\in L^2({\mathbb {R}}),\) then for every \(\lambda >0\), the NQPWD and NQPAF of the signal \({\hat{f}}(t)=\sqrt{\lambda } f(\lambda t)\) can be expressed as:

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{{\hat{f}}}(t,u)={\mathcal {W}}^{{\mathcal {Q}}_{{a}/{\lambda ^2},b}^{{d}/{\lambda }}}_ f\left( \lambda t,\frac{u}{\lambda }\right) ,\quad {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{{\hat{f}}}(\varphi ,u)={\mathcal {A}}^{{\mathcal {Q}}_{a/\lambda ^2,b}^{d/\lambda ,e\lambda }}_{ f}\left( \lambda \varphi ,\frac{u}{\lambda }\right) . \end{aligned}$$
(2.25)

Proof

From the definition of NQPWD, we have

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{{\hat{f}}}(t,u)\\{} & {} =\int _{{\mathbb {R}}}\left( {\hat{f}}\underset{\frac{\varphi }{2}}{\otimes }{\hat{f}}^*\right) ( t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi \\{} & {} =\frac{\lambda |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\lambda t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \\{} & {} \buildrel \lambda \varphi =\beta \over =\frac{\lambda |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\beta }{2}}{\otimes } f^*\right) (\lambda t)e^{i\left( 2at\frac{\beta }{\lambda }+bu\frac{\beta }{\lambda }+d\frac{\beta }{\lambda }\right) }\frac{d\beta }{\lambda }\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\beta }{2}}{\otimes } f^*\right) (\lambda t)e^{i[2(a/\lambda )t\beta +b(u/\lambda )\beta +(d/\lambda )\beta ]}d\beta \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\beta }{2}}{\otimes } f^*\right) (\lambda t)e^{i\left[ 2({a}/{\lambda ^2})(\lambda t)\beta + b({u}/{\lambda })\beta +({d}/{\lambda })\beta \right] }d\beta \\{} & {} =\int _{{\mathbb {R}}}\left( f\underset{\frac{\beta }{2}}{\otimes } f^*\right) (\lambda t){\mathcal {K}}_{a/\lambda ^2,b}^{d/\lambda }\left( \beta ,\frac{u}{\lambda }\right) d\beta \\{} & {} ={\mathcal {W}}^{{\mathcal {Q}}_{{a}/{\lambda ^2},b}^{{d}/{\lambda }}}_ f\left( \lambda t,\frac{u}{\lambda }\right) . \end{aligned}$$

And

$$\begin{aligned}{} & {} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{{\hat{f}}(t)}(\varphi ,u)\\{} & {} =\lambda \int _{{\mathbb {R}}} \left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\lambda t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\{} & {} =\frac{\lambda |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\lambda t)e^{i(2at\varphi +but+d\varphi +eu)}dt\\{} & {} \buildrel {\varvec{\lambda t=\eta }} \over =\frac{\lambda |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\eta )e^{i[2a\frac{\eta }{\lambda }\varphi +bu\frac{\eta }{\lambda }+d\varphi +eu]}.\frac{d\eta }{\lambda }\\{} & {} =\frac{\lambda |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\eta )e^{i[2\frac{a}{\lambda ^2}a{\eta }(\lambda \varphi )+b\frac{u}{\lambda }{\eta }+d\varphi +eu]}.\frac{d\eta }{\lambda }\\{} & {} =\frac{ |b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\eta )e^{i[2\frac{a}{\lambda ^2}{\eta }(\lambda \varphi )+b(\frac{u}{\lambda }){\eta }+\frac{d}{\lambda }(\lambda \varphi )+\lambda e(\frac{u}{\lambda })]}.{d\eta }\\{} & {} =\int _{{\mathbb {R}}} \left( f\underset{\frac{\lambda \varphi }{2}}{\otimes } f^*\right) (\eta ){\mathcal {K}}_{a/\lambda ^2,b}^{d/\lambda ,e\lambda }\left( \lambda \varphi ,\frac{u}{\lambda }\right) d\eta \\{} & {} ={\mathcal {A}}^{{\mathcal {Q}}_{a/\lambda ^2,b}^{d/\lambda ,e\lambda }}_{ f}\left( \lambda \varphi ,\frac{u}{\lambda }\right) . \end{aligned}$$

Hence completes the proof. \(\square \)

Theorem 2.6

(Frequency marginal property) The frequency marginal property of NQPWD and NQPAF is given by

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)dt=\left| {\mathcal {Q}}_{a,b,c}^{d,e}[f(t)]\left( u\right) \right| ^2, \end{aligned}$$
(2.26)
$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t)}(\varphi ,u)d\varphi = {\mathcal {Q}}_{a,b,c}^{d,e}[f]\left( \frac{u}{2}\right) {\mathcal {Q}}_{a,b,c}^{*d,e}[f]\left( \frac{-u}{2}\right) \end{aligned}$$
(2.27)

Proof

From Definition 2.1, we have

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)dt\\{} & {} =\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d}(\varphi ,u)d\varphi dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi dt\\{} & {} \buildrel \varvec{\frac{\varphi }{2}=x-t} \over =\frac{|b|}{\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{x-t}{\otimes }f^*\right) (t)e^{i[2at{2(x-t)}+bu{2(x-t)}+d{2(x-t)}]}dx dt.\\{} & {} =\frac{|b|}{\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(x)f^*\left( 2t-x\right) e^{i[2at{2(x-t)}+bu{2(x-t)}+d{2(x-t)}]}dx dt.\\{} & {} \buildrel \varvec{2t=x+y}\over =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(x)f^*\left( y\right) e^{i\left[ 2a\left( \frac{x+y}{2}\right) 2\left( {x-\frac{x+y}{2}}\right) +bu2\left( {x-\frac{x+y}{2}}\right) +d2\left( {x-\frac{x+y}{2}}\right) \right] }dx dy\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(x)f^*\left( y\right) e^{i\left[ a(x^2-y^2)+b(x-y)u+d(x-y)\right] }dx dy\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}f(x)e^{i\left[ ax^2+bxu+dx\right] }dx\\{} & {} \qquad \qquad \times \int _{{\mathbb {R}}}f^*\left( y\right) e^{i\left[ a(-y^2)+b(-y)u+d(-y)\right] } dy\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}f(x)e^{i\left[ ax^2+bxu+dx\right] }dx\\{} & {} \qquad \qquad \times \int _{{\mathbb {R}}}f^*(y)e^{-i\left[ ay^2+byu+dy\right] } dy\\{} & {} =\sqrt{\frac{b}{2\pi i}}\int _{{\mathbb {R}}}f(x)e^{i\left( ax^2+bxu+cu^2+dx+eu\right) }dx\\{} & {} \qquad \qquad \times \left[ \sqrt{\frac{b}{2\pi i}}\int _{{\mathbb {R}}}f(y) e^{i\left( ay^2+byu+cu^2+dy+eu\right) }dy\right] ^*\\{} & {} =\int _{{\mathbb {R}}}f(x) {\mathcal {K}}_{a,b,c}^{d,e}\left( x,u\right) dx\left[ \int _{{\mathbb {R}}}f(y){\mathcal {K}}_{a,b,c}^{d,e}\left( y,u\right) dy\right] ^*\\{} & {} =\left| {\mathcal {Q}}_{a,b,c}^{d,e}[f(t)]\left( u\right) \right| ^2. \end{aligned}$$

And

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t)}(\varphi ,u)d\varphi \\{} & {} =\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dtd\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(2at\varphi +but+d\varphi +eu)}dtd\varphi \\{} & {} \buildrel \varvec{\frac{\varphi }{2}=s-t}\over =\frac{|b|}{2\pi }\int _{{\mathbb {R}}^2}\left( f\underset{s-t}{\otimes }f^*\right) (t)e^{i[4a(s-t)t+but+2d(s-t)+eu]}ds dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}^2}f(s)f^*\left( 2t-s\right) e^{i[4a(s-t)t+but+2d(s-t)+eu]}ds dt\\{} & {} \buildrel {2\textbf{t}=\mathbf{s+v}}\over =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(s)f^*\left( v\right) e^{i\left[ 4a\left( s-\frac{s+v}{2}\right) \left( \frac{s+v}{2}\right) -bu\left( \frac{s+v}{2}\right) +2d\left( s-\frac{s+v}{2}\right) +eu\right] }ds dv\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(s)f^*\left( v\right) e^{{i}\left[ 2a\left( s-v\right) \left( \frac{s+v}{2}\right) +bu\left( \frac{s+v}{2}\right) \left( \frac{s+v}{2}\right) +d\left( s-v\right) +eu\right] }ds dv\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}^2}f(s)f^*\left( v\right) e^{i\left[ a\left( s^2-v^2\right) +bu\left( \frac{s+v}{2}\right) +d(s-v)+eu\right] }ds dv\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}f(s)e^{{i}\left[ as^2+bs\left( \frac{u}{2}\right) +c(\frac{u}{2})^2+ds+e(\frac{u}{2})\right] }ds\\{} & {} \quad \times \int _{{\mathbb {R}}}f^*\left( v\right) e^{{-i}\left[ av^2+bv\left( \frac{-u}{2}\right) +c(\frac{-u}{2})^2+dv+e(\frac{-u}{2})\right] } dv\\{} & {} =\int _{{\mathbb {R}}}f(s){\mathcal {K}}_{a,b,c}^{d,e}\left( s,\frac{u}{2}\right) ds \left[ \int _{{\mathbb {R}}}f\left( v\right) {\mathcal {K}}_{a,b,c}^{d,e}\left( v,\frac{-u}{2}\right) dv\right] ^*\\{} & {} ={\mathcal {Q}}_{a,b,c}^{d,e}[f]\left( \frac{u}{2}\right) {\mathcal {Q}}_{a,b,c}^{*d,e}[f]\left( \frac{-u}{2}\right) , \end{aligned}$$

which completes the proof. \(\square \)

It is clear from above theorem that the marginal properties of the NQPWD and NQPAF have elegance and simplicity comparable to those of the WD and AF defined in [22,23,24].

Theorem 2.7

(Moyal formula) Let \(f\in L^2({\mathbb {R}}),\) then the Moyal formula for the NQPWD and NQPAF can be expressed as:

$$\begin{aligned} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ f(t,u)\left[ {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ g(t,u)\right] ^*dtdu= & {} \frac{|b|}{2\pi }\left| \langle f,g\rangle \right| ^2. \end{aligned}$$
(2.28)
$$\begin{aligned} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_ {f}(\varphi ,u)\left[ {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_ {g}(\varphi ,u)\right] ^*d\varphi du= & {} \frac{|b|}{2\pi }\left| \langle f,g\rangle \right| ^2. \end{aligned}$$
(2.29)

Proof

From definition 2.1, we have

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ f(t,u)\left[ {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ g(t,u)\right] ^*dtdu\\{} & {} {=}\left( \frac{|b|}{2{\pi }}\right) ^2\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t) {\mathcal {K}}_{a,b}^{d}(\varphi ,u){\mathcal {K}}_{a,b}^{*d}(\gamma ,u)d\varphi d\gamma dtdu\\{} & {} =\left( \frac{|b|}{2\pi }\right) ^2\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t)\\{} & {} \qquad \qquad \qquad \qquad \times e^{i(2at\varphi +bu\varphi +d\varphi )}e^{-i(2at\gamma +bu\gamma +d\gamma )}d\varphi d\gamma dtdu\\{} & {} =\left( \frac{|b|}{2\pi }\right) ^2\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t)\\{} & {} \qquad \qquad \qquad \qquad \times e^{i(\varphi -\gamma )(2at+d)}e^{i(\varphi -\gamma )bu}d\varphi d\gamma dtdu\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t)\\{} & {} \qquad \qquad \qquad \qquad \times e^{i(\varphi -\gamma )(2at+d)} \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}}e^{i(\varphi -\gamma )bu}du\right) d\varphi d\gamma dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t)\\{} & {} \qquad \qquad \qquad \qquad \times e^{i(\varphi -\gamma )(2at+d)} \delta (\varphi -\gamma )d\varphi d\gamma dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{\frac{\gamma }{2}}{\otimes }f^*\right) (t)\left( g^*\underset{\frac{\gamma }{2}}{\otimes }g\right) (t)d\gamma dt \end{aligned}$$

By making the change of variable \(\frac{\gamma }{2}=x-t,\) we have

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ f(t,u)\left[ {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ g(t,u)\right] ^*dtdw\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\left( f\underset{x-t}{\otimes }f^*\right) (t)\left( g^*\underset{x-t}{\otimes }g\right) (t)d\gamma dt\\{} & {} =\frac{|b|}{\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(x)f^*(2t-x)g^*(x)g(2t-x)dxdt \end{aligned}$$

Now taking \(2t-x=y,\) we obtain

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ f(t,u)\left[ {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ g(t,u)\right] ^*dtdw\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(x)f^*(y)g^*(x)g(y)dxdy\\{} & {} =\frac{|b|}{2\pi }\left( \int _{{\mathbb {R}}}f(x)g^*(x)dx\right) \left( \int _{{\mathbb {R}}}f^*(y)g(y)dy\right) \\{} & {} =\frac{|b|}{2\pi }\left| \langle f,g\rangle \right| ^2. \end{aligned}$$

Similarly, using the same variable substitutions we can obtain (2.29). Which completes the proof. \(\square \)

2.3 Relationship with STFT

In this subsection we shall obtain the relationship of the NQPWD and NQPAF with the STFT.

The short-time Fourier transform of a signal f(t) is defined as

$$\begin{aligned} {\mathcal {V}}_g(t,u)=\int _{{\mathbb {R}}}=f(x)g^*(x-t)e^{-ixu}dx. \end{aligned}$$
(2.30)

Then the following theorem reflects the relationship between the NQPWD and NQPAF with the STFT of a signal f(t),

Theorem 2.8

The NQPWD and NQPAF of a signal f(t) with parameters a, b, c, d, e can be expressed in terms of the STFT as

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( \frac{t}{2},\frac{u}{2}\right) {=}\frac{|b|}{\pi }e^{{-}it\left( at{+}b\frac{u}{2}{+}d\right) }{\mathcal {V}}_g(t,-2at-bu-2d),\quad \text{ where }\quad g(t){=} f(-t).\nonumber \\ \end{aligned}$$
(2.31)

And

$$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f}(\varphi ,u)=\frac{|b|}{2\pi }e^{i\left( eu+d\varphi -\frac{b}{2}u\varphi -a\varphi ^2\right) }{\mathcal {V}}_f(\varphi ,-2a\varphi -bu) \end{aligned}$$
(2.32)

Proof

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f\left( \frac{t}{2},\frac{u}{2}\right) \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) \left( \frac{t}{2}\right) e^{i\left( a{t}\varphi +b\frac{u}{2}\varphi +d\varphi \right) }d\varphi \\{} & {} =\frac{|b|}{\pi }\int _{{\mathbb {R}}}f\left( x\right) f^*\left( t-x\right) e^{i\left( a{t}(2x-t)+b\frac{u}{2}(2x-t)+d(2x-t)\right) }dx \\{} & {} =\frac{|b|}{\pi }e^{-it\left( at+b\frac{u}{2}+d\right) }\int _{{\mathbb {R}}}f\left( x\right) f^*\left( -(x-t)\right) e^{ix\left( 2at+bu+2d\right) }dx \\{} & {} =\frac{|b|}{\pi }e^{-it\left( at+b\frac{u}{2}+d\right) }\int _{{\mathbb {R}}}f\left( x\right) f^*\left( -(x-t)\right) e^{-ix\left( -2at-bu-2d\right) }dx \\{} & {} =\frac{|b|}{\pi }e^{-it\left( at+b\frac{u}{2}+d\right) }{\mathcal {V}}_g(t,-2at-bu-2d), \end{aligned}$$

where \({\mathcal {V}}_g(t,-2at-bu-2d) \) denotes the classical short-time Fourier transform with respect to the window function \(g(t)=f(-t).\)

$$\begin{aligned}{} & {} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f}(\varphi ,u)\\{} & {} =\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t){\mathcal {K}}_{a,b}^{d,e}(\varphi ,u)dt\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(2at\varphi +but+d\varphi +eu)}dt \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}f\left( x\right) f^*\left( x-{\varphi }\right) e^{i\left[ 2a\left( x-\frac{\varphi }{2}\right) \varphi +bu\left( x-\frac{\varphi }{2}\right) +d\varphi +eu\right] }dx \\{} & {} =\frac{|b|}{2\pi }e^{i\left( eu+d\varphi -\frac{b}{2}u\varphi -a\varphi ^2\right) }\int _{{\mathbb {R}}}f\left( x\right) f^*\left( x-{\varphi }\right) e^{-ix\left( -2a{\varphi }-bu\right) }dx \\{} & {} =\frac{|b|}{2\pi }e^{i\left( eu+d\varphi -\frac{b}{2}u\varphi -a\varphi ^2\right) }{\mathcal {V}}_f(\varphi ,-2a\varphi -bu), \end{aligned}$$

where \({\mathcal {V}}_f(\varphi ,-2a\varphi -bu) \) denotes the classical short-time Fourier transform with respect to the window function f(t). \(\square \)

Fig. 1
figure 1

Absolute value of the NQPWD and NQPAF of a mono-component signal \(f(t)=e^{i(0.3t+0.4t^2)}\) for \((1,-\sqrt{2},0,0,0)\) with with SNR = − 5 dB

Full size image
Fig. 2
figure 2

Absolute value of the NQPWD and NQPAF of a mono-component signal \(f(t)=e^{i(0.3t+0.4t^2)}\) for \((1,-\sqrt{2},0,0,0)\) with SNR = 10 dB

Full size image
Fig. 3
figure 3

Absolute value of the NQPWD of a mono-component signal \(f(t)=e^{i(0.3t+0.4t^2)}\) corresponding to particular choices of parameters with SNR = 10 dB

Full size image
Fig. 4
figure 4

Absolute value of the NQPAF of a mono-component signal \(f(t)=e^{i(0.3t+0.4t^2)}\) corresponding to particular choices of parameters with SNR = 10 dB

Full size image
Fig. 5
figure 5

Absolute value of the NQPWD of a bi-component signal \(f(t)=e^{i(0.3t+0.4t^2)}+e^{i(0.2t+0.4t^2)}\) corresponding to particular choices of parameters with SNR = 10 dB

Full size image
Fig. 6
figure 6

Absolute value of the NQPWD of a bi-component signal \(f(t)=e^{i(0.3t+0.4t^2)}+e^{i(0.2t+0.4t^2)}\) corresponding to particular choices of parameters with SNR = 10 dB

Full size image

2.4 Correlation and correlation for the NQPWD

Theorem 2.9

(Convolution) For \(f,g\in L^2({\mathbb {R}})\), the NQPWD holds the following result

$$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f*g}(t,u){=}\frac{\pi }{|b|}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f}\left( w,u{-}\frac{2a}{b}(w-t)\right) {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {g}\left( t-w,u{+}\frac{2a}{b}w\right) dw,\nonumber \\ \end{aligned}$$
(2.33)

where \(f*g(t)=\int _{{\mathbb {R}}}f(\varphi )g(t-\varphi )d\varphi \) represents classical convolution of f and g.

Proof

From Definition 2.1, we have

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f*g}(t,u)\\{} & {} =\int _{{\mathbb {R}}}\left( (f*g)\underset{\frac{\zeta }{2}}{\otimes }(f*g)^*\right) (t){\mathcal {K}}_{a,b}^{d}(\zeta ,{u})d\zeta \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( (f*g)\underset{\frac{\zeta }{2}}{\otimes }(f*g)^*\right) (t)e^{i(2a\zeta t+bu\zeta +d\zeta )}d\zeta \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f(\varphi )g\left( t{+} \frac{\zeta }{2}{-}\varphi \right) d\varphi \int _{{\mathbb {R}}}f^*(\eta )g^*\left( t{-} \frac{\zeta }{2}{-}\eta \right) d\eta e^{i(2a\zeta t+bu\zeta +d\zeta )}d\zeta .\\ \end{aligned}$$

Setting \(\varphi =w+\frac{p}{2}\) and \(\eta =w-\frac{p}{2},\) so that \(d\varphi =\frac{dp}{2}\) and \(d\eta = dw,\) above yields

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f*g}(t,u)\\{} & {} =\frac{|b|}{4\pi }\int _{{\mathbb {R}}}\left[ \int _{{\mathbb {R}}}f\left( w+\frac{p}{2}\right) g\left( t+ \frac{\zeta }{2}-w-\frac{p}{2}\right) dp\right. \\{} & {} \qquad \quad \times \left. \int _{{\mathbb {R}}}f^*\left( w-\frac{p}{2}\right) g^*\left( t- \frac{\zeta }{2}-w+\frac{p}{2}\right) dw\right] e^{i(2at\zeta +bu\zeta +d\zeta )}d\zeta . \end{aligned}$$

Now taking \(\zeta =p+q,\) so that \(d\zeta =dq,\) we obtain

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f*g}(t,u)\\{} & {} =\frac{|b|}{4\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f\left( w+\frac{p}{2}\right) g\left( t+ \frac{p+q}{2}-w-\frac{p}{2}\right) f^*\left( w-\frac{p}{2}\right) \\{} & {} \qquad \qquad \qquad \times g^*\left( t- \frac{p+q}{2}-w+\frac{p}{2}\right) e^{i[2at(p+q)+bu(p+q)+d(p+q)]}dpdqdw\\{} & {} =\frac{|b|}{4\pi }\int _{{\mathbb {R}}}\left[ \left( \int _{{\mathbb {R}}}f\left( w+\frac{p}{2}\right) f^*\left( w-\frac{p}{2}\right) e^{i(2atp+bup+dp)}dp\right) \right. \\{} & {} \qquad \times \left. \left( \int _{{\mathbb {R}}} g\left( (t-w)+ \frac{q}{2}\right) g^*\left( (t-w)- \frac{q}{2}\right) e^{i(2atq+buq+dq)}dq\right) \right] dw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}\left[ \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}}f\left( w{+}\frac{p}{2}\right) f^*\left( w{-}\frac{p}{2}\right) e^{i\left[ 2awp+b\left( u-\frac{2a}{b}(w{-}t)\right) p{+}dp\right] }dp\right) \right. \\{} & {} \qquad {\times }\left. \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}} g\left( (t{-}w){+} \frac{q}{2}\right) g^*\left( (t{-}w){-} \frac{q}{2}\right) e^{i\left[ 2a(t{-}w)q{+}b\left( u{+}\frac{2a}{b}w \right) q{+}dq\right] }dq\right) \right] dw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}\left[ \int _{{\mathbb {R}}}f\left( w+\frac{p}{2}\right) f^*\left( w-\frac{p}{2}\right) {\mathcal {K}}_{a,b}^{d}\left( p,(u-2\frac{a}{b}(w-t))\right) dp\right. \\{} & {} \qquad \times \left. \int _{{\mathbb {R}}} g\left( (t-w)+ \frac{q}{2}\right) g^*\left( (t-w)- \frac{q}{2}\right) {\mathcal {K}}_{a,b}^{d}\left( q,u+2\frac{a}{b}w\right) dq\right] dw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f}\left( w,u+\frac{2a}{b}(w-t)\right) {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {g}\left( t-w,u+\frac{2a}{b}w\right) dw. \end{aligned}$$

Which completes the proof. \(\square \)

Theorem 2.10

(Correlation) For \(f,g\in L^2({\mathbb {R}})\), the following result holds for the NQPWD:

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f\circ g}(t,u)\nonumber \\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{-a,b}^{-d}}_ {f^*}\left( w,-(u-2\frac{a}{b}(w-t))\right) {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {g}\left( t+w,u-2\frac{a}{b}w\right) dw,\nonumber \\ \end{aligned}$$
(2.34)

where \(f\circ g=\int _{{\mathbb {R}}}f^*(\varphi )g(t+\varphi )d\varphi \) represents classical correlation of f and g.

Proof

From Definition 2.1, we have

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f\circ g}(t,u)\\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\left( (f\circ g)\underset{\frac{\zeta }{2}}{\otimes }(f\circ g)^*\right) (t){\mathcal {K}}_{a,b}^{d}(\zeta ,{u})d\varphi \\{} & {} =\frac{|b|}{2\pi }\int _{{\mathbb {R}}}(f\circ g)\left( t+ \frac{\zeta }{2}\right) (f\circ g)^*\left( t-\frac{\zeta }{2}\right) e^{i(2a\zeta t+bu\zeta +d\zeta )}d\zeta \\{} & {} {=}\frac{|b|}{2\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f^*(\varphi )g\left( t{+} \frac{\zeta }{2}{+}\varphi \right) d\varphi \int _{{\mathbb {R}}}f(\eta )g^*\left( t- \frac{\zeta }{2}{+}\eta \right) d\eta e^{i(2a\zeta t+bu\zeta +d\zeta )}d\zeta . \end{aligned}$$

Setting \(\varphi =w+\frac{p}{2}\) and \(\eta =w-\frac{p}{2},\) so that \(d\varphi =\frac{dp}{2}\) and \(d\eta = dw,\) above yields

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f\circ g}(t,u)\\{} & {} =\frac{|b|}{4\pi }\int _{{\mathbb {R}}}\left[ \int _{{\mathbb {R}}}f^*\left( w+\frac{p}{2}\right) g\left( t+ \frac{\zeta }{2}+w+\frac{p}{2}\right) dp\right. \\{} & {} \qquad \quad \times \left. \int _{{\mathbb {R}}}f\left( w-\frac{p}{2}\right) g^*\left( t- \frac{\zeta }{2}+w-\frac{p}{2}\right) dw\right] e^{i(2a\zeta t+bu\zeta +d\zeta )}d\zeta . \end{aligned}$$

Now taking \(\zeta =q-p,\) so that \(d\zeta =dq,\) we obtain

$$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {f\circ g}(t,u)\\{} & {} =\frac{|b|}{4\pi }\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}f^*\left( w+\frac{p}{2}\right) g\left( t+ k\frac{q-p}{2}+w+\frac{p}{2}\right) f\left( w-\frac{p}{2}\right) \\{} & {} \qquad \qquad \qquad \times g^*\left( t- k\frac{q-p}{2}+w-\frac{p}{2}\right) e^{i[2a(q-p)t+b(q-p)u+d(q-p)]}dpdqdw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}\left[ \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}}f^*\left( w+\frac{p}{2}\right) f\left( w-\frac{p}{2}\right) e^{-i(2atp+bup+dp)}dp\right) \right. \\{} & {} \qquad \times \left. \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}} g\left( t+ \frac{q}{2}+w\right) g^*\left( t- \frac{q}{2}+w\right) e^{i(2atq+buq+dq)}dq\right) \right] dw\\{} & {} {=}\frac{\pi }{|b|}\int _{{\mathbb {R}}}\left[ \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}}f^*\left( w{+}\frac{p}{2}\right) f\left( w{-}\frac{p}{2}\right) e^{i\left[ 2({-}a)wp+b\left( -(u-2\frac{a}{b}(w-t))\right) p{+}({-}d)p\right] }dp\right) \right. \\{} & {} \qquad \times \left. \left( \frac{|b|}{2\pi }\int _{{\mathbb {R}}} g\left( (t{+}w){+} \frac{q}{2}\right) g^*\left( (t+w){-} \frac{q}{2}\right) e^{i[2a(t+w)q{+}b\left( u-2\frac{a}{b}w\right) q+dq]}dq\right) \right] dw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}\left[ \int _{{\mathbb {R}}}f^*\left( w+\frac{p}{2}\right) f\left( w{-}\frac{p}{2}\right) {\mathcal {K}}_{{-}a,b}^{-d}\left( p,{-}(u-2\frac{a}{b}(w{-}t))\right) dp\right. \\{} & {} \qquad \times \left. \int _{{\mathbb {R}}} g\left( (t+w)+ \frac{q}{2}\right) g^*\left( (t+w)- \frac{q}{2}\right) {\mathcal {K}}_{a,b}^{d}\left( q,u-2\frac{a}{b}w\right) dq\right] dw\\{} & {} =\frac{\pi }{|b|}\int _{{\mathbb {R}}}{\mathcal {W}}^{{\mathcal {Q}}_{-a,b}^{-d}}_ {f^*}\left( w,-(u-2\frac{a}{b}(w-t))\right) {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_ {g}\left( t+w,u-2\frac{a}{b}w\right) dw. \end{aligned}$$

Which completes the proof. \(\square \)

Remark 2.11

It is pertinent to mention that for the choices \(\Omega =(a/2b,-1/b,c/2b, 0,0)\) and \(\Omega =(\cot \theta ,-\csc \theta ,cot\theta ,0,0)\), Theorems 2.9 and 2.10 give the corresponding convolution and correlation theorems associated with the novel linear canonical Wigner distribution [25] and the novel fractional Wigner distribution, respectively.

3 Applications of the NQPWD and NQPAF in detection of LFM signals

The LFM or "chirp" signals are a type of non-stationary signals that are widely used in information and optical systems, sonar, radar, and communications, among other applications. Here, with the help of simulations, the one-component and multi-component LFM signals are detected, respectively, using the recently defined NQPWD and NQPAF.

  • One component LFM signal: consider a one-component LFM signal as

    $$\begin{aligned} f(t)=A_0e^{i(\lambda _1t+\lambda _2t^2)}, \quad -\frac{T}{2}\le t\le \frac{T}{2}. \end{aligned}$$
    (3.1)

    where \(A_0,\) \(\lambda _1\)and \(\lambda _2\) represent the amplitude, initial frequency and frequency rate of f(t), respectively. Now by Definition 2.1, we have

    $$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)\nonumber \\{} & {} =\frac{|b|}{2\pi }\int _{-\frac{T}{2}}^{\frac{T}{2}}\left( f\underset{\frac{\varphi }{2}}{\otimes }f^*\right) (t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \nonumber \\{} & {} =\frac{|b|}{2\pi }\int _{-\frac{T}{2}}^{\frac{T}{2}}A_0e^{i\left[ \lambda _1\left( t+\frac{\varphi }{2}\right) +\lambda _2\left( t+\frac{\varphi }{2}\right) ^2\right] }A^*_0e^{-i\left[ \lambda _1\left( t-\frac{\varphi }{2}\right) +\lambda _2\left( t-\frac{\varphi }{2}\right) ^2\right] }e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \nonumber \\{} & {} =\frac{|A_0|^2|b|}{2\pi }\nonumber \\{} & {} \int _{-\frac{T}{2}}^{\frac{T}{2}}e^{i\left[ \lambda _1t+\lambda _1\frac{\varphi }{2}+\lambda _2t^2+\lambda _2t\varphi +\lambda _2\frac{\varphi ^2}{4}\right] }e^{-i\left[ \lambda _1t-\lambda _1 \frac{\varphi }{2}+\lambda _2t^2-\lambda _2t\varphi +\lambda _2\frac{\varphi ^2}{4}\right] }e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \nonumber \\{} & {} {=}\frac{|A_0|^2|b|}{2\pi }\int _{{-}\frac{T}{2}}^{\frac{T}{2}}e^{i[\lambda _1\varphi {+}2\lambda _2t\varphi {+}\varphi (2at+bu+d)]}d\varphi \nonumber \\{} & {} {=}\frac{|A_0|^2|b|}{2\pi }\int _{{-}\frac{T}{2}}^{\frac{T}{2}}e^{i\left[ \lambda _1{+}d{+}(2\lambda _2 {+}2a)t{+}bu\right] \varphi }d\varphi \nonumber \\{} & {} =\frac{|A_0|^2T|b|}{2\pi }sinc\left\{ \frac{T}{2}\left[ (2\lambda _2 +2a)t+bu+(\lambda _1+d)\right] \right\} . \end{aligned}$$
    (3.2)

    Using same procedure the NQPAF of one-component LFM signal f(t) given by (3.1) can be presented as

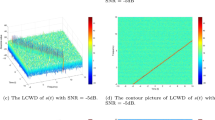
    $$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_{f(t)}(\varphi ,u)=\frac{|A_0|^2T|b|}{2\pi }e^{i[(\lambda _1+d)\varphi +eu]}sinc\left\{ \frac{T}{2}[\left( 2\lambda _2+2a\right) \varphi +bu]\right\} . \nonumber \\ \end{aligned}$$
    (3.3)

    From (3.2) and (3.3), we observe that the NQPWD and NQPAF of a single component signal f(t) given in (3.1) is able to generate impulses in (t, u) plane at a straight line \(\left( bu+(2\lambda _2 +2a)t+(\lambda _1+d)\right) =0,\) and in \((\varphi , u)\) plane at a straight line \([\left( 2\lambda _2+2a\right) \varphi +bu]=0\) respectively, both are dependent on the parameters (a, b, c, d, e). Ttherefore, the NQPWD and NQPAF can be applied to the detection of single-component LFM signals and it is very useful and effective since there is a choice of selecting the parameters from (a, b, c, d, e). For instance, the detection and estimation for a single-component signal \(f(t)=e^{i(0.3t+0.4t^2)}\) at \(T=10\) with SNR = -5dB using NQPWD and NQPAF at \((1,-\sqrt{2},0,0,0)\) are displayed in Fig. 1. Figure 2 shows the NQPWD and NQPAF of single-component LFM signal f(t) with SNR = 10dB. Furthermore, Figs. 3 and 4 shows the detection and estimation for the single-component LFM signal f(t) with SNR = 10 db by NQPWD and NQPAF for different values of parameters, viz: \((0,-1,1,0,0)\) and \((0,-1,2,2,0)\), respectively.

  • Multi-component LFM signal: consider the following multi-component LFM signal

    $$\begin{aligned} f(t)=\sum _{j=1}^{n}f_j(t), \quad f_j(t)=A_je^{i(\alpha _jt+\beta _jt^2)}, \quad -\frac{T}{2}\le t\le \frac{T}{2}. \end{aligned}$$
    (3.4)

    The NQPWD of multi-component LFM signal can be written as

    $$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u) \\{} & {} =\sum _{j=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_j}(t,u)+\sum _{j_1\ne j_2=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_{j_1},f_{j_2}}(t,u) \end{aligned}$$

    The first sum in last equation stands for the auto-terms of one-component signals, whereas the second represent the cross terms that are given by

    $$\begin{aligned}{} & {} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_{j_1},f_{j_2}}(t,u)\nonumber \\{} & {} =\frac{|b|}{2\pi }\int _{-\frac{T}{2}}^{\frac{T}{2}}\left( f_{j_1}\underset{\frac{\zeta }{2}}{\otimes }f^*_{j_2}\right) (t)e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \nonumber \\{} & {} =A_{j_1}A^*_{j_2}\frac{|b|}{2\pi }\nonumber \\{} & {} \int _{-\frac{T}{2}}^{\frac{T}{2}}e^{i\left[ \alpha _{j_1}\left( t+\frac{\varphi }{2}\right) +\beta _{j_1}\left( t+\frac{\varphi }{2}\right) ^2\right] }e^{-i\left[ \alpha _{j_2}\left( t-\frac{\varphi }{2}\right) +\beta _{j_2}\left( t-\frac{\varphi }{2}\right) ^2\right] }e^{i(2at\varphi +bu\varphi +d\varphi )}d\varphi \nonumber \\{} & {} =A_{j_1}A^*_{j_2}\frac{|b|}{2\pi }e^{i[(\alpha _{j_1}-\alpha _{j_2})t+(\beta _{j_1}-\beta _{j_2})t^2]}\nonumber \\{} & {} \quad \int _{-\frac{T}{2}}^{\frac{T}{2}}e^{i\left( \frac{\beta _{j_1}-\beta _{j_2}}{4}\right) \varphi ^2}e^{i\left[ bu+(\beta _{j_1}+\beta _{j_2}+2a)t+\frac{\varphi }{2}(\alpha _{j_1}+\alpha _{j_2}+2d)\right] }d\varphi . \end{aligned}$$
    (3.5)

    Hence the NQPWD of a multi-component signal \(f(t)=\sum _{j=1}^{n}f_j(t)\) is given by

    $$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)= & {} \sum _{j=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_j}(t,u)+\sum _{j_1\ne j_2=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_{j_1},f_{j_2}}(t,u)\\= & {} \sum _{j=1}^{n}\frac{|A_j|^2T|b|}{2\pi }sinc\left\{ \frac{T}{2}\left[ (2\beta _j +2a)t+bu+(\alpha _j+d)\right] \right\} \\{} & {} +\sum _{j_1\ne j_2=1}^{n}A_{j_1}A^*_{j_2}\frac{|b|}{2\pi }e^{i[(\alpha _{j_1}-\alpha _{j_2})t+(\beta _{j_1}-\beta _{j_2})t^2]}\\ \qquad \qquad \qquad{} & {} \times \int _{-\frac{T}{2}}^{\frac{T}{2}}e^{i\left( \frac{\beta _{j_1}-\beta _{j_2}}{4}\right) \varphi ^2}e^{i\left[ bu+(\beta _{j_1}+\beta _{j_2}+2a)t+\frac{\varphi }{2}(\alpha _{j_1}+\alpha _{j_2}+2d)\right] }d\varphi \end{aligned}$$

    Because the auto-terms \({\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_j}\) can produce impulses that the cross-terms \({\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_{j_1},f_{j_2}},\) cannot, the multi-component LFM signal can still be detected even though the presence of cross-terms affects detection performance. This indicates that the NQPWD is also useful and powerful for detecting multi-component LFM signals. For the special case \(\beta _1=\beta _2=....=\beta _n=\beta ,\) we have

    $$\begin{aligned} {\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_f(t,u)= & {} \sum _{j=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_j}(t,u)+\sum _{j_1\ne j_2=1}^{n}{\mathcal {W}}^{{\mathcal {Q}}_{a,b}^{d}}_{f_{j_1},f_{j_2}}(t,u)\\= & {} \sum _{j=1}^{n}\frac{|A_j|^2T|b|}{2\pi }sinc\left\{ \frac{T}{2}\left[ (2\beta +2a)t+bu+(\alpha _j+d)\right] \right\} \\{} & {} +\sum _{j_1\ne j_2=1}^{n}A_{j_1}A^*_{j_2}T\frac{|b|}{2\pi }e^{i[(\alpha _{j_1}-\alpha _{j_2})t]}\\{} & {} \qquad \qquad \qquad \qquad \times sinc\left\{ \frac{T}{2}\left[ (2\beta +2a)t+bu+\frac{\alpha _{j_1}+\alpha _{j_2}}{2}+d \right] \right\} . \end{aligned}$$

    Again for \(\beta _1=\beta _2=....=\beta _n=\beta ,\) and using the same procedure, the NQPAF of the multi-component signal \(f(t)=\sum _{j=1}^{n}f_j(t)\) can be expressed as

    $$\begin{aligned} {\mathcal {A}}^{{\mathcal {Q}}_{a,b}^{d,e}}_f(t,u)= & {} \sum _{j=1}^{n}\frac{|A_j|^2T|b|}{2\pi }e^{i[(\alpha _j+d)\varphi +eu]}sinc\left\{ \frac{T}{2}[\left( 2\beta +2a\right) \varphi +bu]\right\} \\{} & {} +\sum _{j_1\ne j_2=1}^{n}A_{j_1}A^*_{j_2}T\frac{|b|}{2\pi }e^{i\left[ \left( \frac{\alpha _{j_1}+\alpha _{j_2}}{2}+d\right) \varphi +eu\right] }\\{} & {} \qquad \qquad \qquad \qquad \times sinc\left\{ \frac{T}{2}\left[ (2\beta +2a)\varphi +bu+\frac{\alpha _{j_1}+\alpha _{j_2}}{2} \right] \right\} . \end{aligned}$$

    For instance the detection and estimation for the bi-component LFM signal \(f(t)=e^{i(0.3t+0.4t^2)}+e^{i(0.2t+0.4t^2)}\) at \(T=10\) with SNR=10dB using NQPWD and NQPAF for different values of parameters are displayed in Figs. 5 and 6, respectively. Thus t is clear from Figs. 5 and 6 that the NQPWD and NQPAF are useful in detection of bi-component LFM signals.

4 Conclusion

The three main goals of the work have been achieved: first, two novel distributions have been introduced in the context of time–frequency analysis: the new quadratic phase Wigner distribution and the new quadratic phase ambiguity function. Second, we used operator theory tools to establish the fundamental features of the suggested transforms, such as the marginal, conjugate-symmetry, shifting, scaling and Moyal’s equations. Furthermore, with the help of classical convolution and correlation, we derive the convolution and correlation for the NQPWD. Third, to demonstrate the benefit of the theory, the newly defined NQPWD and NQPAF are also applied for the detection of single-component and multi-component LFM signals.