1 Introduction

The 2D-NS-LCT (also known as two-dimensional free metaplectic transformations) has found many applications in digital signal processing, optical system modeling, and many other areas (Ding and Pei, 2011; Ding et al., 2012; Dong and Galatsanos, 2002; Koç et al., 2010; Liu et al., 2010; Pei and Ding, 2001; Pei and Ding, 2009; Ravi et al., 2018; Rodrigo et al., 2007b; Zhang, 2023; Zhao et al., 2014). The 2D-NS-LCT is also known as generalized of some well-known transforms such as the gyrator transform, the coupling transform, and the homogenous coordinate/affine transform (Pei and Ding, 2001; Rodrigo et al., 2007a), in which the two dimensions are coupled to each other by four additional cross-parameters. With six constraints and ten independent parameters, 2D-NS-LCT is more flexible in applications in optics, and signal processing, especially in image processing (Koç et al., 2010; Pei and Ding, 2001; Ravi et al., 2018). It can be considered to solve some problems that typical one-dimensional transform cannot deal with. The 2D-NS-LCT of a signal f with real parameters \(\mathcal {M}=(A,B,C,D) \left( \textrm{det}(B)\ne 0\right) \) is defined as Koç et al. (2010)

$$\begin{aligned} F_{\mathcal {M}}(u,v) =&\mathbb {L}_{\mathcal {M}}\{f(x,y)\}(u,v) := \int _{\mathbb {R}^2} {f(x,y)\mathcal {K}_{\mathcal {M}}(x,y,u,v) \textrm{d}x\textrm{d}y}, \end{aligned}$$
(1.1)

where

$$\begin{aligned} \mathcal {K}_{\mathcal {M}}(x,y,u,v):=&\frac{1}{2\pi \sqrt{-\textrm{det}(B)}}\textrm{e}^{i\frac{k_1u^2 +k_2uv+k_3v^2}{2\textrm{det}(B)}}\\&\quad \times \textrm{e}^{i\frac{(-b_{22}u+b_{12}v)x +(b_{21}u-b_{11}v)y}{\textrm{det}(B)}} \textrm{e}^{i\frac{p_1x^2+p_2xy+p_3y^2}{2\textrm{det}(B)}}, \end{aligned}$$

and the values of \(k_1, k_2, k_3, p_1, p_2,\) and \(p_3\) are given by

$$\begin{aligned} \left\{ \begin{array}{llllll} k_1=b_{22}d_{11}-b_{21}d_{12}, \\ k_2=2(b_{11}d_{12}-b_{12}d_{11})\\ k_3=b_{11}d_{22}-b_{12}d_{21}\\ p_1=a_{11}b_{22}-a_{21}b_{12}\\ p_2=2(a_{12}b_{22}-a_{22}b_{12})\\ p_3=a_{22}b_{11}-a_{12}b_{21}. \end{array} \right. \end{aligned}$$
(1.2)

The parameter matrix A, B, C and D are all \(2\times 2\) submatrices and B is invertible:

\(A= \begin{pmatrix} a_{11}&{}a_{12}\\ a_{21}&{}a_{22} \end{pmatrix},\) \( B= \begin{pmatrix} b_{11}&{}b_{12}\\ b_{21}&{}b_{22} \end{pmatrix},\) \( C= \begin{pmatrix} c_{11}&{}c_{12}\\ c_{21}&{}c_{22} \end{pmatrix},\) \( D= \begin{pmatrix} d_{11}&{}d_{12}\\ d_{21}&{}d_{22} \end{pmatrix}. \) In this case the transformation matrix \(\mathcal {M}=(A,B,C,D)\) of the system is defined as

$$\begin{aligned} \mathcal {M}= \begin{pmatrix} a_{11}&{}a_{12}&{}b_{11}&{}b_{12}\\ a_{21}&{}a_{22}&{}b_{21}&{}b_{22}\\ c_{11}&{}c_{12}&{}d_{11}&{}d_{12}\\ c_{21}&{}c_{22}&{}d_{21}&{}d_{22} \end{pmatrix}. \end{aligned}$$

The corresponding parameter matrices must satisfy the constraints

$$\begin{aligned} AB^{T}=BA^{T},\,CD^{T}=DC^{T},\,AD^{T}-BC^{T}=I, \end{aligned}$$
(1.3)

or

$$\begin{aligned} A^{T}C=C^{T}A,\,B^{T}D=D^{T}B,\,A^{T}D-C^{T}B=I, \end{aligned}$$
(1.4)

where I is a \(2\times 2\) identity matrix. As can be seen, the constraints of (1.3) and (1.4) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{llllll} a_{11}b_{21}+a_{12}b_{22}=a_{21}b_{11}+a_{22}b_{12}\\ c_{11}d_{21}+c_{12}d_{22}=c_{21}d_{11}+c_{22}d_{12}\\ a_{11}d_{11}+a_{12}d_{12}-(b_{11}c_{11}+b_{12}c_{12})=1\\ a_{21}d_{21}+a_{22}d_{22}-(b_{21}c_{21}+b_{22}c_{22})=1\\ a_{11}d_{21}+a_{12}d_{22}=b_{11}c_{21}+b_{12}c_{22}\\ a_{21}d_{11}+a_{22}d_{12}=b_{21}c_{11}+b_{22}c_{12}, \end{array} \right. \end{aligned}$$
(1.5)

and

$$\begin{aligned} \left\{ \begin{array}{llllll} &{}a_{11}c_{12}+a_{21}c_{22}=a_{12}c_{11}+a_{22}c_{21}\\ &{}b_{11}d_{12}+b_{21}d_{22}=b_{12}d_{11}+b_{22}d_{21}\\ &{}a_{11}d_{11}+a_{21}d_{21}-(b_{11}c_{11}+b_{21}c_{21})=1\\ &{}a_{12}d_{12}+a_{22}d_{22}-(b_{12}c_{12}+c_{22}d_{22})=1\\ &{}a_{11}d_{12}+a_{21}d_{22}=b_{12}c_{11}+b_{22}c_{21}\\ &{}a_{12}d_{11}+a_{22}d_{21}=b_{11}c_{12}+b_{21}c_{22}, \end{array} \right. \end{aligned}$$
(1.6)

respectively.

Let \(k:=(k_1,k_2,k_3), \,p:=(p_1,p_2,p_3),\,k-p:=(k_1-p_1,k_2-p_2,k_3-p_3)\) and

$$\begin{aligned} \mathcal {C}_k(x,y):=\textrm{e}^{\frac{i}{2\textrm{det}(B)} \left[ k_1x^2+k_2xy+k_3y^2\right] },\, f_k(x,y):=f(x,y)\mathcal {C}_k(x,y). \end{aligned}$$
(1.7)

Thus, equation (1.1) becomes

$$\begin{aligned} \mathbb {L}_{\mathcal {M}}\{f(x,y)\}(u,v)= \frac{\mathcal {C}_{k}(u,v)}{2\pi \sqrt{-\textrm{det}(B)}}\int _{\mathbb {R}^2} {f_p(x,y)\textrm{e}^{i\frac{(-b_{22}u+b_{12}v)x +(b_{21}u-b_{11}v)y}{\textrm{det}(B)}}\textrm{d}x\textrm{d}y}. \end{aligned}$$

Using (1.3), and (1.7) the reversibility of 2D-NS-LCT can be expressed as follows

$$\begin{aligned} f(x,y)=\frac{\mathcal {C}_{-p}(x,y)}{2\pi \sqrt{-\textrm{det}(B)}} \int _{\mathbb {R}^2} {F_{\mathcal {M}}(u,v)\mathcal {C}_{-k}(u,v) \textrm{e}^{-i\frac{(-b_{22}x+b_{21}y)u+(b_{12}x-b_{11}y)v}{\textrm{det}(B)}}\textrm{d}u\textrm{d}v}. \end{aligned}$$

In the sequel, let \(\mathcal {M}^{-1}=\left( D^{T},-B^{T},-C^{T},A^{T}\right) \), we call

$$\begin{aligned} \mathbb {L}_{\mathcal {M}^{-1}}\{f(x,y)\}(u,v)&=\frac{\mathcal {C}_{-p} (u,v)}{2\pi \sqrt{-\textrm{det}(B)}}\int _{\mathbb {R}^2}f_{-k}(x,y) \\&\quad \times \textrm{e}^{-i\frac{(-b_{22}u+b_{21}v)x+(b_{12}u-b_{11}v)y}{\textrm{det}(B)}}\textrm{d}x\textrm{d}y \end{aligned}$$

the inverse transform of \(\mathbb {L}\).

The classical one-dimensional Wigner distribution and ambiguity function (1D-WD, 1D-AF), as well as the one-dimensional Wigner distribution, and ambiguity function associated with the linear canonical transform (1D-WD-LCT, 1D-AF-LCT), are very crucial in optics, signal processing nonstationary signals and the detection of chirp signals. Their properties and diverse applications can be found in several recent publications (Bai et al., 2012; Che et al., 2012; Johnston, 1989; Minh, 2023; Pei and Ding, 2010; Pei and Ding, 2010; Shah and Teali, 2023; Zhang and Lou, 2015; Zhang, 2016; Zhang et al., 2021). The classical 2D-WD and 2D-AF are very conducive to two-dimensional signal processing. Namely, they are used to estimate and detect 2D-linear frequency-modulated (2D-LFM) and can be defined as Pei and Ding (2010)

$$\begin{aligned} {2D}{\mathcal {W}}{\mathcal {D}}_f(x,y,u,v)= & {} \int _{\mathbb {R}^2}f\left( x+\frac{\tau }{2}, y+\frac{\eta }{2}\right) f^*\left( x-\frac{\tau }{2}, y-\frac{\eta }{2}\right) \textrm{e}^{-i(u\tau +v\eta )}\textrm{d}\tau \textrm{d}\eta ,\nonumber \\ \end{aligned}$$
(1.8)
$$\begin{aligned} {2D}\mathcal{A}\mathcal{F}_f(\tau ,\eta ,u,v)= & {} \int _{\mathbb {R}^2}f\left( x+\frac{\tau }{2}, y+\frac{\eta }{2}\right) f^*\left( x-\frac{\tau }{2}, y-\frac{\eta }{2}\right) \textrm{e}^{-i(ux+vy)}\textrm{d}x\textrm{d}y,\nonumber \\ \end{aligned}$$
(1.9)

where the superscript “*” denotes the complex conjugation. In addition, the combinations of 2D-NS-LCT and 2D-WD (2D-AF) can inherit the advantages of 2D-NS-LCT and the excellent characteristics of 2D-WD (2D-AF), which can be found in some recent publications (Teali et al., 2023; Wei and Shen, 2022; Zhang et al., 2023; Zayed, 2019). Naturally, the 2D-WD in the 2D-NS-LCT domain (2D-WDNL) and 2D-AF in the 2D-NS-LCT domain (2D-AFNL) can be deduced directly by substituting the kernels of the two-dimensional Fourier transform by the kernels of 2D-NS-LCT, respectively. They can be defined as follows (Zhang et al., 2023)

$$\begin{aligned} {2DWL}_f(x,y,u,v)&=\int _{\mathbb {R}^2}f\left( x+\frac{\tau }{2}, y+\frac{\eta }{2}\right) f^*\left( x-\frac{\tau }{2}, y-\frac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {K}_{\mathcal {M}}(\tau ,\eta ,u,v)\textrm{d}\tau \textrm{d}\eta , \end{aligned}$$
(1.10)
$$\begin{aligned} {2DAL}_f(\tau ,\eta ,u,v)&=\int _{\mathbb {R}^2}f\left( x+\frac{\tau }{2}, y+ \frac{\eta }{2}\right) f^*\left( x-\frac{\tau }{2}, y-\frac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {K}_{\mathcal {M}}(x,y,u,v)\textrm{d}x\textrm{d}y. \end{aligned}$$
(1.11)

Nevertheless, the complete theoretical system and extensions of the 2D-WD (2D-AF) associated 2D-NS-LCT remain unknown, so additional knowledge on them is very welcome. The main contributions of the paper is summarized below:

  • To formulate the novel definition of 2D-NLCWD and 2D-NLCAF. Furthermore, the classical 2D-WD and 2D-AF exist as special cases of the proposed distributions. Therefore, our new distributions fully inherit the advantages of both 2D-NS-LCT and 2D-WD and 2D-AF. More specifically, we also obtain the 2D-WD and 2D-AF associated with the gyrator transform, which promises to have interesting potential applications.

  • To explore the fundamental properties of the proposed distributions, including the shift properties, the conjugation symmetry property, the marginal properties, the Moyal formula, and the relationship with the 2D-STFT.

  • To execute certain graphical simulations for the detection of the single-component and multi-component 2D-LFM signals by using the proposed distributions. More importantly, the 2D-NLCWD and 2D-NLCAF are flexible than 2D-WDNL and 2D-AFNL in detecting 2D-LFM signals since there are three extra parameters.

The rest of the article is organized as follows: Section 2 gives the definition of 2D-NLCWD and 2D-NLCAF. Moreover, a brief review of proposed distributions and some of their special cases are also presented. Section 3 gives some important properties of the proposed distributions such as the shift properties, the conjugation symmetry properties, the marginal properties, the Moyal formula, and the relationship with the 2D-STFT. In Sect. 4, we apply the proposed transform to detect and estimate the single-component and multi-component 2D-LFM signals. Finally, the conclusion is given in Sect. 5.

2 The 2D-NLCWD and 2D-NLCAF

As can be seen, the relationships between 2D-WD, 2D-AF and the 2D-classical convolution can be presented by

$$\begin{aligned} {2D}\mathcal{W}\mathcal{D}_f\left( \frac{x}{2},\frac{y}{2},u,v\right)= & {} 4[f(x,y)\textrm{e}^{-i(ux+vy)}]*[f^*(x,y)\textrm{e}^{i(ux+vy)}], \end{aligned}$$
(2.1)
$$\begin{aligned} {2D}\mathcal{A}\mathcal{F}_f(\tau ,\eta ,2u,2v)= & {} [f(\tau ,\eta ) \textrm{e}^{-i(u\tau +v\eta )}]*[f^*(-\tau ,-\eta )\textrm{e}^{i(u\tau +v \eta )}], \end{aligned}$$
(2.2)

where \(*\) is defined as

$$\begin{aligned} (f*g)(x,y) := \int _{\mathbb {R}^2}f(\tau ,\eta )g(x-\tau ,y-\eta )\textrm{d}\tau \textrm{d}\eta , \end{aligned}$$
(2.3)

where \(f, g \in L^2(\mathbb {R}^2).\)

Therefore, this allows us to define the new kind 2D-NLCWD and 2D-NLCAF as

Definition 1

For given set of parameters \(\mathcal {M}=(A,B,C,D)\) the new 2D-NLCWD and 2D-NLCAF of a signal \(f\in L^2(\mathbb {R})\) are defined as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( \frac{x}{2},\frac{y}{2},u,v\right) =4 \left[ f(x,y)\mathcal {K}_{\mathcal {M}}(x,y,u,v)\right] *\left[ f(x,y) \mathcal {K}_{\mathcal {M}}(u,v,x,y)\right] ^*, \end{aligned}$$
(2.4)
$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,2u,2v)=\left[ f(\tau ,\eta ) \mathcal {K}_{\mathcal {M}}(\tau ,\eta ,u,v)\right] *\left[ f(-\tau ,-\eta ) \mathcal {K}_{\mathcal {M}}(u,v,\tau ,\eta )\right] ^*. \end{aligned}$$
(2.5)

By using (2.3), (2.4), (2.5) and performing the change of variables, we obtain

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) =\int _{\mathbb {R}^2}f \left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {K}_{\mathcal {M}}\left( x+\dfrac{\tau }{2},y+\dfrac{\eta }{2},u,v\right) \mathcal {K}_{\mathcal {M}}^*\left( u,v,x-\dfrac{\tau }{2},y-\dfrac{\eta }{2}\right) \textrm{d}\tau \textrm{d}\eta , \end{aligned}$$
(2.6)
$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,u,v)=\int _{\mathbb {R}^2}f \left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {K}_{\mathcal {M}}\left( x+\dfrac{\tau }{2},y+\dfrac{\eta }{2}, \dfrac{u}{2},\dfrac{v}{2}\right) \mathcal {K}_{\mathcal {M}}^*\left( \dfrac{u}{2}, \dfrac{v}{2},\dfrac{\tau }{2}-x,\dfrac{\eta }{2}-y\right) \textrm{d}x\textrm{d}y. \end{aligned}$$
(2.7)

Due to the notations (1.7), the kernel of 2D-NS-LCT can be rewritten as

$$\begin{aligned} \mathcal {K}_{\mathcal {M}}(x,y,u,v):=&\frac{1}{2\pi \sqrt{-\textrm{det}(B)}} \mathcal {C}_{k}(u,v)\mathcal {C}_{p}(x,y)\textrm{e}^{i\frac{(-b_{22}u +b_{12}v)x+(b_{21}u-b_{11}v)y}{\textrm{det}(B)}}. \end{aligned}$$

Therefore, by simple computations, equations (2.6) and (2.7) become

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) =\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2 \vert \textrm{det}(B)\vert }\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)} \nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^* \left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\tau +b_{11}v\eta ) -(b_{12}+b_{21})(u\eta +v\tau )\right] }\textrm{d}\tau \textrm{d}\eta , \end{aligned}$$
(2.8)
$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,u,v)=\frac{\mathcal {C}_{k-p}^{\frac{1}{4}} (u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{4\textrm{det}(B)}(b_{12}-b_{21})(v\tau -u\eta )} \nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}ux+b_{11}vy) -(b_{12}+b_{21})(uy+vx)\right] }\textrm{d}x\textrm{d}y, \end{aligned}$$
(2.9)

where \(\mathcal {C}_{k-p}^{\frac{1}{4}}(u,v)=\left[ \mathcal {C}_{k-p}(u,v)\right] ^{\frac{1}{4}}.\)

It is easy to see that the 2D-NLCWD and 2D-NLCAF can not deduced from 2D-WDNL and 2D-AFNL. Moreover, they are modulated and scaling versions of cross-term 2D-WD and cross-term 2D-AF in time and frequency variables, respectively

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) =\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert }\textrm{e}^{\frac{i}{\textrm{det}(B)} (b_{12}-b_{21})(vx-uy)} \\&\quad \times {2D}\mathcal{W}\mathcal{D}_{f_{p}, f_{k}}\left( x,y,\frac{2b_{22}u-(b_{12}+b_{21})v}{2\textrm{det}(B)},\frac{2b_{11} v-(b_{12}+b_{21})u}{2\textrm{det}(B)}\right) , \end{aligned}$$

and

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) = \frac{\mathcal {C}_{k-p}^{\frac{1}{4}}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{4\textrm{det}(B)}(b_{12}-b_{21})(v\tau -u\eta )} \\&\quad \times {2D}\mathcal{A}\mathcal{F}_{f_{p}, f_{k}}\left( \tau ,\eta ,\frac{2b_{22}u-(b_{12}+b_{21})v}{2\textrm{det}(B)}, \frac{2b_{11}v-(b_{12}+b_{21})u}{2\textrm{det}(B)}\right) . \end{aligned}$$

We now consider some special cases of (2.8) and (2.9) as follows

  • By choosing

    $$\begin{aligned} \mathcal {M}= \begin{pmatrix} a_{11}&{}0&{}b_{11}&{}0\\ 0&{}a_{22}&{}0&{}b_{22}\\ c_{11}&{}0&{}d_{11}&{}0\\ 0&{}c_{22}&{}0&{}d_{22} \end{pmatrix}, \end{aligned}$$

    the 2D-NS-LCT reduces to the 2D-separable linear canonical transform (2D-S-LCT). We can mention some well-known of its special cases including the 2D- Fourier transform, the 2D-Fresnel transform, the 2D- fractional Fourier transform, the 2D-chirp transform and the 2D-scaling transform (Pei and Ding, 2001). We thus obtain novel distributions corresponding to 2D-S-LCT.

  • In the case \(k_i=p_i\,(i\in \{1,2,3\}),\, b_{12}=b_{21}\), the 2D-NLCWD and 2D-NLCAF can be considered as special cases of distributions introduced in Wei and Shen (2022), which are given by

    $$\begin{aligned} {2D}&\mathcal {W}_f^{\mathcal {M}}\left( x,y,u,v\right) \\&=\frac{1}{4\pi ^2\vert \textrm{det}(B)\vert }\int _{\mathbb {R}^2}f\left( x+\dfrac{\tau }{2}, y +\dfrac{\eta }{2}\right) f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\textrm{e}^{\frac{i}{\textrm{det}(B)}\left[ (-b_{22}u+b_{12}v)\tau +(b_{21}u-b_{11}v) \eta \right] }\textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2p_1x\tau +p_2(x\eta +y\tau )+2p_3y \eta \right] }\textrm{d}\tau \textrm{d}\eta ,\\ {2D}\mathcal {L}_f^{\mathcal {M}}&(\tau ,\eta ,u,v)\\&=\frac{1}{4\pi ^2\vert \textrm{det}(B)\vert }\int _{\mathbb {R}^2}f\left( x+\dfrac{\tau }{2}, y +\dfrac{\eta }{2}\right) f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\textrm{e}^{\frac{i}{\textrm{det}(B)}\left[ (-b_{22}u+b_{12}v)x+(b_{21}u-b_{11}v)y\right] } \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2p_1x\tau +p_2(x\eta +y\tau )+2p_3y\eta \right] }\textrm{d}x\textrm{d}y. \end{aligned}$$

  • By choosing

    $$\begin{aligned} \mathcal {M}_{\theta }= \begin{pmatrix} \cos \theta &{}0&{}0&{}\sin \theta \\ 0&{}\cos \theta &{}\sin \theta &{}0\\ 0&{}-\sin \theta &{}\cos \theta &{}0\\ -\sin \theta &{}0&{}0&{}\cos \theta \end{pmatrix}. \end{aligned}$$

    In such a particular case, 2D-NS-LCT is the gyrator transform, which promises to be a useful tool in holography, image processing, beam characterization, mode transformation, and quantum information (Dong and Galatsanos, 2002; Liu et al., 2010; Pei and Ding, 2009; Rodrigo et al., 2007b). Then, equations (2.8), and (2.9) take the form

    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}_{\theta }}\left( x,y,u,v\right) = \frac{1}{4\pi ^2\sin ^2\theta }\int _{\mathbb {R}^2}f\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) \nonumber \\&\quad \times f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \textrm{e}^{i(x\eta +y\tau )\cot \theta } \textrm{e}^{-i(u\eta +v\tau )\csc \theta }\textrm{d}\tau \textrm{d}\eta , \end{aligned}$$
    (2.10)
    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}_{\theta }}(\tau ,\eta ,u,v)= \frac{1}{4\pi ^2\sin ^2\theta }\int _{\mathbb {R}^2}f\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) \nonumber \\&\quad \times f^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \textrm{e}^{i(x\eta +y\tau )\cot \theta } \textrm{e}^{-i(uy+vx)\csc \theta }\textrm{d}x\textrm{d}y, \end{aligned}$$
    (2.11)

    which are therefore 2D-WD and 2D-AF associated with the gyrator transform. When \(\theta =\dfrac{\pi }{2}\), (2.10) and (2.11) turn to the well- known 2D-WD and 2D-AF (cf. (1.8), (1.9)), respectively.

3 Properties of the 2D-NLCWD and 2D-NLCAF

Properties of the 2D-NLCWD and 2D-NLCAF will be obtained in this section.

  • (1) Conjugation properties

  1. (i)

    Conjugation-Covarriance Property:

    $$\begin{aligned} \left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*&={2D}\mathcal{L}\mathcal{W}_f^{\overline{\mathcal {M}}}\left( x,y,u,v\right) ,\\ \left[ {2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,u,v)\right] ^*&={2D}\mathcal{L}\mathcal{A}_f^{\overline{\mathcal {M}}}(-\tau ,-\eta ,-u,-v), \end{aligned}$$

    where matrix parameter \(\overline{\mathcal {M}}=(D^T,B^T,C^T,A^T).\)

  2. (ii)

    Symmetry-Conjugation Property: The 2D-NLCWD and 2D-NLCAF of \(\breve{f}(x,y)=f(-x,-y)\) can be expressed as the forms

    $$\begin{aligned} {2D}\mathcal{L}\mathcal{W}_{\breve{f}}^{\mathcal {M}}\left( x,y,u,v\right) ={2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( -x,-y,-u,-v\right) , \\ {2D}\mathcal{L}\mathcal{A}_{\breve{f}}^{\mathcal {M}}(\tau ,\eta ,u,v)={2D} \mathcal{L}\mathcal{A}_{f}^{\mathcal {M}}(-\tau ,-\eta ,-u,-v). \end{aligned}$$

Proof

We prove \((\textrm{i})\). Using (2.8), we may observe that

$$\begin{aligned}&\left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*= \frac{\mathcal {C}_{p-k}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{21}-b_{12})(vx-uy)} \nonumber \\&\quad \times \int _{\mathbb {R}^2}f_k\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) f_p^*\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\tau +b_{11}v\eta ) -(b_{12}+b_{21})(u\eta +v\tau )\right] }\textrm{d}\tau \textrm{d}\eta . \end{aligned}$$

Changing the variables \(-\tau =\tau _1, -\eta =\eta _1\) allow us to realize that

$$\begin{aligned}&\left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^* =\frac{\mathcal {C}_{p-k}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{21}-b_{12})(vx-uy)} \nonumber \\&\quad \times \int _{\mathbb {R}^2}f_k\left( x+\dfrac{\tau _1}{2}, y+\dfrac{\eta _1}{2}\right) f_p^*\left( x-\dfrac{\tau _1}{2}, y-\dfrac{\eta _1}{2}\right) \nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\tau _1+b_{11}v\eta _1) -(b_{12}+b_{21})(u\eta _1+v\tau _1)\right] }\textrm{d}\tau _1\textrm{d}\eta _1. \end{aligned}$$

Let \(\overline{\mathcal {M}}=(D^T,B^T,C^T,A^T)\), which is defined as

$$\begin{aligned} \overline{\mathcal {M}}= \begin{pmatrix} d_{11}&{}d_{21}&{}b_{11}&{}b_{21}\\ d_{12}&{}d_{22}&{}b_{12}&{}b_{22}\\ c_{11}&{}c_{21}&{}a_{11}&{}a_{21}\\ c_{12}&{}c_{22}&{}a_{12}&{}a_{22} \end{pmatrix}. \end{aligned}$$

It is easy to see that \(\overline{\mathcal {M}}\) satisfies the relation (1.3). In addition, based on (1.2), (1.5) and (1.6), we obtain

$$\begin{aligned} \left\{ \begin{array}{llllll} \overline{k_1}=a_{11}b_{22}-a_{21}b_{12}, \\ \overline{k_2}=2(a_{21}b_{11}-a_{11}b_{21})=2(a_{12}b_{22}-a_{22}b_{12})\\ \overline{k_3}=a_{22}b_{11}-a_{12}b_{21}\\ \overline{p_1}=b_{22}d_{11}-b_{21}d_{12}\\ \overline{p_2}=2(b_{22}d_{21}-b_{21}d_{22})=2(b_{11}d_{12}-b_{12}d_{11})\\ \overline{p_3}=b_{11}d_{22}-b_{12}d_{21}. \end{array} \right. \end{aligned}$$

Therefore

$$\begin{aligned} \left\{ \begin{array}{ll} \overline{k}=(\overline{k_1},\overline{k_2},\overline{k_3})=(p_1,p_2,p_3)=p\\ \overline{p}=(\overline{p_1},\overline{p_2},\overline{p_3})=(k_1,k_2,k_3)=k. \end{array} \right. \end{aligned}$$
(3.1)

Thus, we can achieve the desired relation as follows

$$\begin{aligned}&\left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*= \frac{\mathcal {C}_{\overline{k}-\overline{p}}(u,v)}{4\pi ^2\vert \textrm{det}(B^T)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B^T)}(b_{21}-b_{12})(vx-uy)}\\&\quad \times \int _{\mathbb {R}^2}f_{\overline{p}}\left( x+\dfrac{\tau _1}{2}, y +\dfrac{\eta _1}{2}\right) f_{\overline{k}}^*\left( x-\dfrac{\tau _1}{2}, y-\dfrac{\eta _1}{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B^T)}\left[ 2(b_{22}u\tau _1+b_{11} v\eta _1)-(b_{12}+b_{21})(u\eta _1+v\tau _1)\right] }\textrm{d}\tau _1\textrm{d}\eta _1={2D} \mathcal{L}\mathcal{W}_f^{\overline{\mathcal {M}}}\left( x,y,u,v\right) . \end{aligned}$$

Furthermore, from (2.9) and (3.1), we derive

$$\begin{aligned}&\left[ {2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,u,v)\right] ^*= \frac{\mathcal {C}^{\frac{1}{4}}_{p-k}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{4\textrm{det}(B)}(b_{21}-b_{12})(v\tau -u\eta )} \\&\quad \times \int _{\mathbb {R}^2}f_k\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) f_p^*\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}ux+b_{11}vy) -(b_{12}+b_{21})(uy+vx)\right] }\textrm{d}x\textrm{d}y\\&=\frac{\mathcal {C}^{\frac{1}{4}}_{\overline{k}-\overline{p}}(u,v)}{4\pi ^2 \vert \textrm{det}(B^T)\vert }\textrm{e}^{\frac{i}{4\textrm{det} (B^T)}(b_{21}-b_{12})(v\tau -u\eta )}\nonumber \\&\quad \times \int _{\mathbb {R}^2}f_{\overline{p}}\left( x+\dfrac{-\tau }{2}, y +\dfrac{-\eta }{2}\right) f_{\overline{k}}^* \left( x-\dfrac{-\tau }{2}, y-\dfrac{-\eta }{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ 2[b_{22}(-u) x+b_{11}(-v)y]-(b_{12}+b_{21})[(-u)y+(-v)x]\right\} }\textrm{d}x\textrm{d}y\\&={2D}\mathcal{L}\mathcal{A}_f^{\overline{\mathcal {M}}}(-\tau ,-\eta ,-u,-v). \end{aligned}$$

The proof is completed. \(\square \)

  • (2) 2D-NS-LCT marginal property

The 2D-NS-LCT marginal property of the 2D-NLCWD and 2D-NLCAF can be given as follows

$$\begin{aligned}&\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}} \left( x,y,u,v\right) \textrm{d}x\textrm{d}y\nonumber \\&\hspace{99.58464pt}=\mathbb {L}_{\mathcal {M}}\{f(x,y)\}(u,v) \cdot \mathbb {L}_{\mathcal {M}^{-1}}\{f^*(x,y)\}(u,v), \end{aligned}$$
(3.2)
$$\begin{aligned}&\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}(\tau ,\eta ,u,v) \textrm{d}\tau \textrm{d}\eta \nonumber \\&\hspace{56.9055pt}=\mathbb {L}_{\mathcal {M}}\{f(x,y)\}\left( \frac{u}{2}, \frac{v}{2}\right) \cdot \mathbb {L}_{\mathcal {M}^{-1}}\{f^*(x,y)\} \left( -\frac{u}{2}, -\frac{v}{2}\right) . \end{aligned}$$
(3.3)

Proof

We will just prove (3.2). For (3.3), we proceed in a similar way. With the aid of (2.8), we obtain

$$\begin{aligned}&\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \textrm{d}x\textrm{d}y=\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert }\\&\quad \times \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y +\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)}\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\tau +b_{11}v\eta ) -(b_{12}+b_{21})(u\eta +v\tau )\right] }\textrm{d}\tau \textrm{d}\eta \textrm{d}x\textrm{d}y. \end{aligned}$$

Next, considering \(x_1=x+\dfrac{\tau }{2}, y_1=y+\dfrac{\eta }{2},x_2= x-\dfrac{\tau }{2},y_2= y-\dfrac{\eta }{2},\) we get

$$\begin{aligned}&\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \textrm{d}x\textrm{d}y\\&=\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert }\int _{\mathbb {R}^2} \int _{\mathbb {R}^2}f_p\left( x_1, y_1\right) f_k^*\left( x_2, y_2\right) \textrm{e}^{\frac{i}{2\textrm{det}(B)}(b_{12}-b_{21})(vx_1-uy_1)}\\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}(b_{12}-b_{21})(vx_2-uy_2)} \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}ux_1+b_{11}vy_1) -(b_{12}+b_{21})(uy_1+vx_1)\right] }\\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}ux_2+b_{11}vy_2) -(b_{12}+b_{21})(uy_2+vx_2)\right] }\textrm{d}x_1\textrm{d}y_1\textrm{d}x_2\textrm{d}y_2 \end{aligned}$$
$$\begin{aligned}&=\Bigg [ \frac{\mathcal {C}_{k}(u,v)}{2\pi \sqrt{-\textrm{det}(B)}}\int _{\mathbb {R}^2} {f(x_1,y_1)\textrm{e}^{i\frac{(-b_{22}u+b_{12}v)x_1+(b_{21}u-b_{11}v)y_1}{\textrm{det}(B)}}\mathcal {C}_{p}(x_1,y_1)\textrm{d}x_1\textrm{d}y_1}\Bigg ]\\&\quad \times \Bigg [ \frac{\mathcal {C}_{-p}(u,v)}{2\pi \sqrt{-\textrm{det}(B)}}\int _{\mathbb {R}^2} {f^*(x_2,y_2)\textrm{e}^{-i\frac{(-b_{22}u+b_{21}v)x_2+(b_{12}u-b_{11}v)y_2}{\textrm{det}(B)}}\mathcal {C}_{-k}(x_2,y_2)\textrm{d}x_2\textrm{d}y_2}\Bigg ]\\&=\mathbb {L}_{\mathcal {M}}\{f(x,y)\}(u,v) \cdot \mathbb {L}_{\mathcal {M}^{-1}}\{f^*(x,y)\}(u,v), \end{aligned}$$

which yields (3.2). The proof is concluded. \(\square \)

The Moyal formulas of 2D-NLCWD and 2D-NLCAF will be obtained in (3) as follows.

  • (3) Moyal formula

Assume \(b_{11}^2+(b_{12}+b_{21})^2> 0\) and \(b_{22}^2+(b_{12}+b_{21})^2>0\). The Moyal formula of the 2D-NLCWD and 2D-NLCAF of \(f, g\in L^2(\mathbb {R}^2)\) can be presented by

$$\begin{aligned}&\int _{\mathbb {R}^4}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^* \textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v=\frac{1}{\pi ^2}\vert \langle f, g\rangle \vert ^2, \end{aligned}$$
(3.4)
$$\begin{aligned}&\int _{\mathbb {R}^4}{2D}\mathcal{A}\mathcal{F}_f^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) \left[ {2D}\mathcal{A}\mathcal{F}_f^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) \right] ^* \textrm{d}\tau \textrm{d}\eta \textrm{d}u\textrm{d}v=\frac{1}{\pi ^2}\vert \langle f, g\rangle \vert ^2, \end{aligned}$$
(3.5)

where the usual inner product in \( L^2(\mathbb {R}^2)\) as \(\langle .,.\rangle \), which is given by

$$\begin{aligned} \langle f, g\rangle =\int _{\mathbb {R}^2}f\left( x_1, y_1\right) g^*\left( x_1, y_1\right) \textrm{d}x_1\textrm{d}y_1. \end{aligned}$$

Proof

In order to prove (3.4), we start by interpreting the left-hand side of it.

$$\begin{aligned}&\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*\textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v\\&=\left( \frac{1}{4\pi ^2\vert \textrm{det}(B)\vert }\right) ^2\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} \int _{\mathbb {R}^2}\int _{\mathbb {R}^2} f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k\left( x-\dfrac{\varepsilon }{2}, y -\dfrac{\sigma }{2}\right) \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u \tau +b_{11}v\eta )-(b_{12}+b_{21})(u\eta +v\tau )\right] } \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\varepsilon +b_{11} v\sigma )-(b_{12}+b_{21})(u\sigma +v\varepsilon )\right] }\textrm{d}\tau \textrm{d}\eta \textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v\\&=\left( \frac{1}{4\pi ^2\vert \textrm{det}(B)\vert }\right) ^2\int _{\mathbb {R}^2} \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k \left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left\{ 2[b_{22}u(\varepsilon -\tau ) +b_{11}v(\sigma -\eta )]-(b_{12}+b_{21})[u(\sigma -\eta )+v(\varepsilon -\tau )]\right\} } \textrm{d}\tau \textrm{d}\eta \textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v\\&=\left( \frac{1}{4\pi ^2\vert \textrm{det}(B)\vert }\right) ^2\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k \left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \left[ \int _{\mathbb {R}}\textrm{e}^{\frac{i}{2\textrm{det}(B)}[2b_{22}(\varepsilon -\tau ) -(b_{12}+b_{21})(\sigma -\eta )]u}\textrm{d}u\right] \\&\quad \times \left[ \int _{\mathbb {R}}\textrm{e}^{\frac{i}{2\textrm{det}(B)}[2b_{11} (\sigma -\eta )]-(b_{12}+b_{21})(\varepsilon -\tau )]v}\textrm{d}v\right] \textrm{d}\tau \textrm{d}\eta \textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y\\&=\frac{1}{\pi ^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2} f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k \left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \delta \left[ 2b_{22}(\varepsilon -\tau )-(b_{12}+b_{21})(\sigma -\eta )\right] \\&\quad \times \delta \left[ 2b_{11}(\sigma -\eta )]-(b_{12}+b_{21})(\varepsilon -\tau )\right] \textrm{d}\tau \textrm{d}\eta \textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y, \end{aligned}$$

where \(\delta \) denotes the Dirac delta function. Since \(b_{11}^2+(b_{12}+b_{21})^2> 0\) and \(b_{22}^2+(b_{12}+b_{21})^2>0\) then

$$\begin{aligned}&\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*\textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v\\&=\frac{1}{\pi ^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k\left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \\&\quad \times \Bigg [\int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^* \left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \delta \left[ 2b_{22}(\varepsilon -\tau )-(b_{12}+b_{21})(\sigma -\eta )\right] \\&\hspace{14.22636pt}\delta \left[ 2b_{11}(\sigma -\eta )]-(b_{12}+b_{21})(\varepsilon -\tau )\right] \textrm{d}\tau \textrm{d}\eta \Bigg ]\textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y\\&=\frac{1}{\pi ^2}\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}f_p\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) f_k^*\left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \\&\quad \times g_p^*\left( x+\dfrac{\varepsilon }{2}, y+\dfrac{\sigma }{2}\right) g_k\left( x-\dfrac{\varepsilon }{2}, y-\dfrac{\sigma }{2}\right) \textrm{d}\varepsilon \textrm{d}\sigma \textrm{d}x\textrm{d}y. \end{aligned}$$

Making the substitution \(x_1=x+\dfrac{\varepsilon }{2}, y_1= y+\dfrac{\sigma }{2}, x_2=x-\dfrac{\varepsilon }{2}, y_2= y-\dfrac{\sigma }{2}\) implies that

$$\begin{aligned}&\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \left[ {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) \right] ^*\textrm{d}x\textrm{d}y\textrm{d}u\textrm{d}v\\&=\frac{1}{\pi ^2}\left[ \int _{\mathbb {R}^2}f\left( x_1, y_1\right) g^*\left( x_1, y_1\right) \textrm{d}x_1\textrm{d}y_1\right] \left[ \int _{\mathbb {R}^2}f\left( x_2, y_2\right) g^* \left( x_2, y_2\right) \textrm{d}x_2\textrm{d}y_2\right] ^*\\&=\frac{1}{\pi ^2}\vert \langle f, g\rangle \vert ^2, \end{aligned}$$

which is the desired result.

The proof of (3.5) will be omitted because its proof is very similar to the proof of (3.4). \(\square \)

For convenience in proving the time-shift property, we denote

$$\begin{aligned} \left\{ \begin{array}{llllll} \tilde{b}_{11}=\dfrac{2b_{11}}{4b_{11}b_{22}-(b_{12}+b_{21})^2}\\ \tilde{b}_{12}=\dfrac{b_{12}+b_{21}}{4b_{11}b_{22}-(b_{12}+b_{21})^2}\\ \tilde{b}_{22}=\dfrac{2b_{22}}{4b_{11}b_{22}-(b_{12}+b_{21})^2}. \end{array} \right. \end{aligned}$$

  • (4) Time- shift Property

  1. (i)

    The 2D-NLCWD of \(\overline{f}(x,y)=f(x-x_0,y-y_0)\) is

    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\overline{f}}^{\mathcal {M}}\left( x,y,u,v\right) \\&\hspace{56.9055pt}=\Omega _1(x,y,u,v)\cdot {2D}\mathcal{L}\mathcal{W}_{f}^{\mathcal {M}} \left( x-x_0,y-y_0,u+\delta _1,v+\delta _2\right) , \end{aligned}$$

    where

    $$\begin{aligned} \left\{ \begin{array}{ll} \delta _1=-\tilde{b}_{11}\left[ (p_1+k_1)x_0+\frac{(p_2+k_2)y_0}{2}\right] -\tilde{b}_{12}\left[ \frac{(p_2+k_2)x_0}{2}+(p_3+k_3)y_0\right] \\ \delta _2=-\tilde{b}_{12}\left[ (p_1+k_1)x_0+\frac{(p_2+k_2)y_0}{2}\right] -\tilde{b}_{22}\left[ \frac{(p_2+k_2)x_0}{2}+(p_3+k_3)y_0\right] , \end{array} \right. \end{aligned}$$

    and

    $$\begin{aligned}&\Omega _1(x,y,u,v)=\mathcal {C}_{k-p}(x_0,y_0)\mathcal {C}_{p-k}(\delta _1,\delta _2)\nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2(k_1-p_1)\delta _1 +(k_2-p_2)\delta _2]u+[(k_2-p_2)\delta _1+2(k_3-p_3)\delta _2]v\right\} }\nonumber \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(p_1-k_1)x_0x+(p_2-k_2) (xy_0+x_0y)+2(p_3-k_3)yy_0\right] } \nonumber \\&\quad \times \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21}) (x_0\delta _2-\delta _1y_0+vx_0-uy_0-\delta _2x+\delta _1y)}. \end{aligned}$$
    (3.6)
  2. (ii)

    The 2D-NLCAF of \(\overline{f}(x,y)=f(x-x_0,y-y_0)\) is given by

    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\overline{f}}^{\mathcal {M}}(\tau ,\eta ,u,v)=\Omega _2 (\tau ,\eta ,u,v)\cdot {2D}\mathcal{L}\mathcal{A}_{f}^{\mathcal {M}}(\tau ,\eta ,u+\zeta _1,v+\zeta _2), \end{aligned}$$

    where

    $$\begin{aligned} \left\{ \begin{array}{ll} \zeta _1=-\tilde{b}_{11}\left[ 2(p_1-k_1)x_0+(p_2-k_2)y_0\right] \\ \hspace{5cm}-\tilde{b}_{12}\left[ (p_2-k_2)x_0+2(p_3-k_3)y_0\right] \\ \zeta _2=-\tilde{b}_{12}\left[ 2(p_1-k_1)x_0+(p_2-k_2)y_0\right] \\ \hspace{5cm}-\tilde{b}_{22}\left[ (p_2-k_2)x_0+2(p_3-k_3)y_0\right] , \end{array} \right. \end{aligned}$$

    and

    $$\begin{aligned}&\Omega _2(\tau ,\eta ,u,v)=\mathcal {C}_{k-p}(x_0,y_0)\mathcal {C}_{p-k}^{\frac{1}{4}} (\zeta _1,\zeta _2)\textrm{e}^{\frac{i}{4\textrm{det}(B)}(b_{12}-b_{21}) (\zeta _1\eta -\zeta _2\tau )}\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ 2b_{22} (u+\zeta _1)-(b_{12}+b_{21})(v+\zeta _2)\right] x_0+\left[ 2b_{11}(v+\zeta _2) -(b_{12}+b_{21})(u+\zeta _1)\right] y_0\right\} }\nonumber \\&\quad \times \textrm{e}^{-\frac{i}{8\textrm{det}(B)}\left\{ [2(k_1-p_1)\zeta _1 +(k_2-p_2)\zeta _2]u+[(k_2-p_2)\zeta _1+2(k_3-p_3)\zeta _2]v\right\} }\\&\quad \times \textrm{e}^{\frac{i}{4\textrm{det}(B)} \left\{ 2(p_1+k_1)x_0\tau +(p_2+k_2)(x_0\eta +y_0\tau )+2(p_3+k_3)y_0\eta \right\} }. \end{aligned}$$

Proof

We prove (i). Due to the notation (1.7), it is easy to verify that

$$\begin{aligned} \mathcal {C}_{k}(u,v)&=\mathcal {C}_{k}(u+\delta _1,v+\delta _2) \mathcal {C}_{-k}(\delta _1,\delta _2)\nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)} \left[ (2k_1\delta _1+k_2\delta _2)u+(k_2\delta _1+2k_3\delta _2)v\right] }. \end{aligned}$$
(3.7)

With the help of (3.7), we deduce

$$\begin{aligned}&f\left( x-x_0+\frac{\tau }{2},y-y_0+\frac{\eta }{2}\right) f^* \left( x-x_0-\frac{\tau }{2},y-y_0-\frac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {C}_{p}\left( x+\frac{\tau }{2},y+\frac{\eta }{2}\right) \mathcal {C}_{k}^*\left( x-\frac{\tau }{2},y-\frac{\eta }{2}\right) \nonumber \\&=f_k\left( x-x_0+\frac{\tau }{2},y-y_0+\frac{\eta }{2}\right) f_k^* \left( x-x_0-\frac{\tau }{2},y-y_0-\frac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(p_1-k_1)x_0x +(p_2-k_2)(xy_0+x_0y)+2(p_3-k_3)yy_0\right] }\nonumber \\&\quad \times \mathcal {C}_{k-p}(x_0,y_0) \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left( \omega _1\tau +\omega _2\eta \right) }, \end{aligned}$$
(3.8)

where

$$\begin{aligned} \left\{ \begin{array}{ll} (p_1+k_1)x_0+\dfrac{(p_2+k_2)}{2}y_0=\omega _1\\ \dfrac{(p_2+k_2)}{2}x_0+(p_3+k_3)y_0=\omega _2. \end{array} \right. \end{aligned}$$

Finding \(\delta _1,\delta _2\) satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} 2b_{22}\delta _1-(b_{12}+b_{21})\delta _2=-\omega _1\\ -(b_{12}+b_{21})\delta _1+2b_{11}\delta _2=-\omega _2, \end{array} \right. \end{aligned}$$

which gives us

$$\begin{aligned} \left\{ \begin{array}{ll} \delta _1=-\tilde{b}_{11}\omega _1-\tilde{b}_{12}\omega _2\\ \delta _2=-\tilde{b}_{12}\omega _1-\tilde{b}_{22}\omega _2. \end{array} \right. \end{aligned}$$

Due to the formulas (2.8),(3.7) and (3.8), we can be recast as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\overline{f}}^{\mathcal {M}}\left( x,y,u,v\right) = \frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)}\\&\quad \times \int _{\mathbb {R}^2}f\left( x-x_0+\dfrac{\tau }{2}, y-y_0+\dfrac{\eta }{2}\right) f^*\left( x-x_0-\dfrac{\tau }{2}, y-y_0-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \mathcal {C}_{p}\left( x+\frac{\tau }{2},v+\frac{\eta }{2}\right) \mathcal {C}_{k}\left( x-\frac{\tau }{2},v-\frac{\eta }{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22}u\tau +b_{11}v\eta )-(b_{12}+b_{21})(u\eta +v\tau )\right] }\textrm{d}\tau \textrm{d}\eta \\&=\mathcal {C}_{k-p}(x_0,y_0)\mathcal {C}_{p-k}(\delta _1,\delta _2)\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2(k_1-p_1)\delta _1 +(k_2-p_2)\delta _2]u+[(k_2-p_2)\delta _1+2(k_3-p_3)\delta _2]v\right\} }\\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left[ 2(p_1-k_1)x_0x+(p_2-k_2) (xy_0+x_0y)+2(p_3-k_3)yy_0\right] }\\&\quad \times \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(x_0\delta _2- \delta _1y_0+vx_0-uy_0-\delta _2x+\delta _1y)}\\&\quad \times \Bigg [\frac{\mathcal {C}_{k-p}(u+\delta _1,v+\delta _2)}{4\pi ^2\vert \textrm{det}(B)\vert }\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21}) \left[ (v+\delta _2)(x-x_0)-(u+\delta _1)(y-y_0)\right] }\nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x-x_0+\dfrac{\tau }{2}, y-y_0+ \dfrac{\eta }{2}\right) f_k^*\left( x-x_0-\dfrac{\tau }{2}, y-y_0-\dfrac{\eta }{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ 2b_{22}(u+\delta _1) -(b_{12}+b_{21})(v+\delta _2)\right] \tau +\left[ 2b_{11}(v+\delta _2)-(b_{12}+b_{21})(u+\delta _1)\right] \eta \right\} }\textrm{d}\tau \textrm{d}\eta \Bigg ]\\&=\Omega _1(x,y,u,v)\cdot \mathcal{L}\mathcal{W}_{f}^{\mathcal {M}}\left( x-x_0,y-y_0,u+\delta _1,v+\delta _2\right) , \end{aligned}$$

where \(\Omega _1(x,y,u,v)\) is given by (3.6). The proof is completed. \(\square \)

  • (5) Frequency Shifting Property

  1. (i)

    The 2D-NLCWD of \(\widehat{f}(x,y)=f(x,y)\textrm{e}^{i(u_0x+v_0y)}\) has the form

    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\widehat{f}}^{\mathcal {M}}(x,y,u,v)=\mathcal {C}_{p-k} (t_1,t_2)\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(t_1y-t_2x)}\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2(k_1-p_1) t_1+(k_2-p_2)t_2]u+[(k_2-p_2)t_1+2(k_3-p_3)t_2]v\right\} }\\&\quad \times {2D}\mathcal{L}\mathcal{W}_{f}^{\mathcal {M}}(x,y,u+t_1,v+t_2). \end{aligned}$$

    where

    $$\begin{aligned} \left\{ \begin{array}{ll} t_1=-2\tilde{b}_{11}u_0\textrm{det}(B)-\tilde{b}_{12}v_0\textrm{det}(B)\\ t_2=-\tilde{b}_{12}u_0\textrm{det}(B)-2\tilde{b}_{22}v_0\textrm{det}(B). \end{array} \right. \end{aligned}$$
  2. (ii)

    The 2D-NLCAF of \(\widehat{f}(x,y)=f(x,y) \textrm{e}^{i(u_0x+v_0y)}\) can be expressed as

    $$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\widehat{f}}^{\mathcal {M}}(\tau ,\eta ,u,v)= \textrm{e}^{i(u_0\tau +v_0\eta )}{2D}\mathcal{L}\mathcal{A}_{f}^{\mathcal {M}}(\tau ,\eta ,u,v). \end{aligned}$$

Proof

We prove \((\textrm{i})\) since the proof of property \((\textrm{ii})\) is straightforward. By simple computations, we proceed as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\widehat{f}}^{\mathcal {M}}(x,y,u,v)=\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2 \vert \textrm{det}(B)\vert }\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)} \nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^* \left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \textrm{e}^{i\left[ u_0\left( x+\frac{\tau }{2}\right) +v_0\left( y+\frac{\eta }{2}\right) \right] }\nonumber \\&\quad \times \textrm{e}^{-i\left[ u_0\left( x-\frac{\tau }{2}\right) +v_0 \left( y-\frac{\eta }{2}\right) \right] }\textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left[ 2(b_{22} u\tau +b_{11}v\eta )-(b_{12}+b_{21})(u\eta +v\tau )\right] }\textrm{d}\tau \textrm{d}\eta \nonumber \\&=\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^*\left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \nonumber \\&\quad \times \textrm{e}^{i[u_0\tau +v_0\eta ]}\textrm{e}^{-\frac{i}{2\textrm{det}(B)} \left\{ [2b_{22}\tau -(b_{12}+b_{21})\eta ]u+[2b_{11}\eta -(b_{12}+b_{21})\tau ]v\right\} } \textrm{d}\tau \textrm{d}\eta . \end{aligned}$$
(3.9)

We now find parametters \(t_1,t_2\), which satisfy

$$\begin{aligned}&u_0\tau +v_0\eta \nonumber \\&\hspace{0.0pt}=-\frac{1}{2\textrm{det}(B)}\Bigg \{[2b_{22} \tau -(b_{12}+b_{21})\eta ]t_1+[2b_{11}\eta -(b_{12}+b_{21})\tau ]t_2\Bigg \}. \end{aligned}$$
(3.10)

By simple computations, we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} 2b_{22}t_1-(b_{12}+b_{21})t_2=-2u_0\textrm{det}(B)\\ -(b_{12}+b_{21})t_1+2b_{11}t_2=-2v_0\textrm{det}(B). \end{array} \right. \end{aligned}$$

Therefore, the above equations turn into

$$\begin{aligned} \left\{ \begin{array}{ll} t_1=-2\tilde{b}_{11}u_0\textrm{det}(B)-2\tilde{b}_{12}v_0\textrm{det}(B)\\ t_2=-2\tilde{b}_{12}u_0\textrm{det}(B)-2\tilde{b}_{22}v_0\textrm{det}(B). \end{array} \right. \end{aligned}$$

Using (3.7) and (3.10), the relation (3.9) turns to

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\widehat{f}}^{\mathcal {M}}(x,y,u,v)=\frac{\mathcal {C}_{k-p}(u,v)}{4\pi ^2\vert \textrm{det}(B)\vert }\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)}\\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^* \left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2b_{22}\tau -(b_{12}+b_{21})\eta ](u+t_1) +[2b_{11}\eta -(b_{12}+b_{21})\tau ](v+t_2)\right\} }\textrm{d}\tau \textrm{d}\eta \\&=\mathcal {C}_{p-k}(t_1,t_2)\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(t_1y-t_2x)}\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2(k_1-p_1)t_1+(k_2-p_2)t_2] u+[(k_2-p_2)t_1+2(k_3-p_3)t_2]v\right\} }\\&\quad \times \Bigg [\frac{\mathcal {C}_{k-p}(u+t_1,v+t_2)}{4\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})[(v+t_2)x-(u+t_1)y]}\\&\quad \times \int _{\mathbb {R}^2}f_p\left( x+\dfrac{\tau }{2}, y+\dfrac{\eta }{2}\right) f_k^* \left( x-\dfrac{\tau }{2}, y-\dfrac{\eta }{2}\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ [2b_{22} \tau -(b_{12}+b_{21})\eta ](u+t_1)+[2b_{11}\eta -(b_{12}+b_{21})\tau ] (v+t_2)\right\} }\textrm{d}\tau \textrm{d}\eta \Bigg ]\\&=\mathcal {C}_{p-k}(t_1,t_2)\textrm{e}^{-\frac{i}{2\textrm{det}(B)} \left\{ [2(k_1-p_1)t_1+(k_2-p_2)t_2]u+[(k_2-p_2)t_1+2(k_3-p_3)t_2]v\right\} }\times \\&\hspace{85.35826pt}\textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21}) (t_1y-t_2x)}{2D}\mathcal{L}\mathcal{W}_{f}^{\mathcal {M}}(x,y,u+t_1,v+t_2), \end{aligned}$$

which completes the proof. \(\square \)

  • (6) Relationship with the 2D-STFT

The STFT of a signal f(x, y) is defined as

$$\begin{aligned} \mathcal {S}_{f,g}(x,y,u,v)= \int _{\mathbb {R}^2}f (\tau ,\eta )g(\tau -x,\eta -y)\textrm{e}^{-i(u\tau +v\eta )} \textrm{d}\tau \textrm{d}\eta , \end{aligned}$$

where g(x, y) is the window function.

The relationships between the 2D-NLCWD and the 2D-STFT can be given by

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( \frac{x}{2},\frac{y}{2},2 \tilde{b}_{11}u\textrm{det}(B)+2\tilde{b}_{12}v\textrm{det}(B),2 \tilde{b}_{12}u\textrm{det}(B)+2\tilde{b}_{22}v\textrm{det}(B)\right) \nonumber \\&\quad =\Omega _3(x,y,u,v)\cdot \mathcal {S}_{f,g}\left( x,y,u,v\right) , \end{aligned}$$
(3.11)

where

$$\begin{aligned}&g(x_1,y_1)=f_k^*\left( -x_1, -y_1\right) \mathcal {C}_{p}(x_1,y_1) \textrm{e}^{-\frac{i}{\textrm{det}(B)}\left[ (2p_1x+p_2y)x_1+(p_2x+2p_3y)y_1\right] }\\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left\{ \left[ 2b_{22}u-(b_{12} +b_{21})v\right] x_1+\left[ 2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }, \end{aligned}$$

and

$$\begin{aligned}&\Omega _3(x,y,u,v)=\frac{\mathcal {C}_{p}(x,y)}{\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{i(b_{12}-b_{21})\left[ (\tilde{b}_{12}u-\tilde{b}_{22}v)x -(\tilde{b}_{11}u_1+\tilde{b}_{12}v)y\right] }\\&\quad \times \mathcal {C}_{k-p}\left( 2\tilde{b}_{11}u\textrm{det}(B)+2\tilde{b}_{12} v\textrm{det}(B),2\tilde{b}_{12}u\textrm{det}(B)+2\tilde{b}_{22}v\textrm{det}(B)\right) . \end{aligned}$$

In addition, the relationships between the 2D-NLCAF and the 2D-STFT can be presented by

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_f^{\mathcal {M}}\left( \tau ,\eta ,4\tilde{b}_{11}u \textrm{det}(B)+4\tilde{b}_{12}v\textrm{det}(B),4\tilde{b}_{12}u \textrm{det}(B)+4\tilde{b}_{22}v\textrm{det}(B)\right) \nonumber \\&\hspace{156.49014pt}=\Omega _4(\tau ,\eta ,u,v)\cdot \mathcal {S}_{f,h}\left( \tau ,\eta ,u,v\right) , \end{aligned}$$
(3.12)

where

$$\begin{aligned}&h(x_1,y_1)=f_k^*\left( x_1, y_1\right) \mathcal {C}_{p}(x_1,y_1) \textrm{e}^{\frac{i}{\textrm{det}(B)}\left[ (2p_1\tau +p_2\eta )x_1 +(p_2\tau +2p_3\eta )y_1\right] }\\&\quad \times \textrm{e}^{-\frac{i}{4\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21}) v\right] x_1+\left[ (2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }, \end{aligned}$$
$$\begin{aligned}&\Omega _4(\tau ,\eta ,u,v)=\frac{\mathcal {C}_p(\tau ,\eta )}{4\pi ^2 \vert \textrm{det}(B)\vert }\textrm{e}^{i(b_{12}-b_{21})\left[ (\tilde{b}_{11}u+ \tilde{b}_{12}v)\tau -(\tilde{b}_{12}u+\tilde{b}_{22}v)\eta \right] }\\&\quad \times \mathcal {C}^{\frac{1}{4}}_{k-p}\left( 4\tilde{b}_{11}u \textrm{det}(B)+4\tilde{b}_{12}v\textrm{det}(B),4\tilde{b}_{12}u\textrm{det} (B)+4\tilde{b}_{22}v\textrm{det}(B)\right) . \end{aligned}$$

Proof

Performing the change of variables \(x_1=x+\dfrac{\tau }{2}, y_1=y+\dfrac{\eta }{2}\), the relations (2.8) becomes

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( x,y,u,v\right) = \frac{\mathcal {C}_{k-p}(u,v)}{\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times \int _{\mathbb {R}^2}f_p\left( x_1, y_1\right) f_k^* \left( 2x-x_1, 2y-y_1\right) \nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)} \left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] (2x_1-2x)+\left[ (2b_{11}v-(b_{12}+b_{21})u \right] (2y_1-2y)\right\} }\textrm{d}x_1\textrm{d}y_1. \end{aligned}$$
(3.13)

By virtue of (3.7), and (3.13), we proceed as

$$\begin{aligned} {2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}&\left( x,y,u,v\right) \mathcal {C}_{p-k}(u,v) \textrm{e}^{\frac{i}{\textrm{det}(B)}(b_{21}-b_{12})(vx-uy)}\\&=\frac{1}{\pi ^2\vert \textrm{det}(B)\vert }\textrm{e}^{\frac{2i}{\textrm{det}(B)} \left[ (2p_1x+p_2y)x+(p_2x+2p_3y)y\right] }\mathcal {C}_{-p}(2x,2y)\\&\quad \times \int _{\mathbb {R}^2}f\left( x_1, y_1\right) f_k^*\left( 2x-x_1, 2y-y_1\right) \mathcal {C}_{p}(x_1-2x,y_1-2y)\\&\quad \times \textrm{e}^{\frac{i}{\textrm{det}(B)}\left[ (2p_1x+p_2y)(x_1-2x)+(p_2x+2p_3y)(y_1-2y)\right] }\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] (x_1-2x)+\left[ (2b_{11}v-(b_{12}+b_{21})u\right] (y_1-2y)\right\} }\\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] x_1 +\left[ (2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }\textrm{d}x_1\textrm{d}y_1\\&=\frac{1}{\pi ^2\vert \textrm{det}(B)\vert }\mathcal {C}_{p}^2(2x,2y)\mathcal {C}_{-p}(2x,2y)\\&\quad \times \int _{\mathbb {R}^2}f\left( x_1, y_1\right) g\left( x_1-2x, y_1-2y\right) \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] x_1+\left[ (2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }\textrm{d}x_1\textrm{d}y_1, \end{aligned}$$

where

$$\begin{aligned}&g(x_1,y_1)=f_k^*\left( -x_1, -y_1\right) \mathcal {C}_{p}(x_1,y_1)\textrm{e}^{-\frac{i}{\textrm{det}(B)} \left[ (2p_1x+p_2y)x_1+(p_2x+2p_3y)y_1\right] }\\&\quad \times \textrm{e}^{\frac{i}{2\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] x_1+\left[ (2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }. \end{aligned}$$

This allow us to recognize that

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( \frac{x}{2},\frac{y}{2},u,v\right) \mathcal {C}_{p-k}(u,v) \textrm{e}^{\frac{i}{2\textrm{det}(B)}(b_{21}-b_{12})(vx-uy)}\nonumber \\&=\frac{\mathcal {C}_{p}(x,y)}{\pi ^2\vert \textrm{det}(B)\vert }\int _{\mathbb {R}^2}f\left( x_1, y_1\right) g\left( x_1-x, y_1-y\right) \nonumber \\&\quad \times \textrm{e}^{-\frac{i}{2\textrm{det}(B)}\left\{ \left[ (2b_{22}u-(b_{12}+b_{21})v\right] x_1+ \left[ (2b_{11}v-(b_{12}+b_{21})u\right] y_1\right\} }\textrm{d}x_1\textrm{d}y_1\nonumber \\&=\frac{\mathcal {C}_{p}(x,y)}{\pi ^2\vert \textrm{det}(B)\vert }\mathcal {S}_{f,g} \left( x,y,\frac{2b_{22}u-(b_{12}+b_{21})v}{2\textrm{det}(B)},\frac{2b_{11} v-(b_{12}+b_{21})u}{2\textrm{det}(B)}\right) . \end{aligned}$$
(3.14)

Next, let us consider

$$\begin{aligned} \left\{ \begin{array}{ll} 2b_{22}u-(b_{12}+b_{21})v=2u_1\textrm{det}(B)\\ -(b_{12}+b_{21})u+2b_{11}v=2v_1\textrm{det}(B). \end{array} \right. \end{aligned}$$

It is easy to verify that the above expression has the following form

$$\begin{aligned} \left\{ \begin{array}{ll} u=2\tilde{b}_{11}u_1\textrm{det}(B)+2\tilde{b}_{12}v_1\textrm{det}(B)\\ v=2\tilde{b}_{12}u_1\textrm{det}(B)+2\tilde{b}_{22}v_1\textrm{det}(B). \end{array} \right. \end{aligned}$$

Invoking equation above, the relation (3.14) can be rewritten as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_f^{\mathcal {M}}\left( \frac{x}{2},\frac{y}{2},2\tilde{b}_{11}u \textrm{det}(B)+2\tilde{b}_{12}v\textrm{det}(B),2\tilde{b}_{12}u\textrm{det}(B)+2 \tilde{b}_{22}v\textrm{det}(B)\right) \\&=\mathcal {C}_{k-p}\left( 2\tilde{b}_{11}u\textrm{det}(B)+2\tilde{b}_{12}v \textrm{det}(B),2\tilde{b}_{12}u\textrm{det}(B)+2\tilde{b}_{22}v\textrm{det}(B)\right) \\&\quad \times \frac{\mathcal {C}_{p}(x,y)}{\pi ^2\vert \textrm{det}(B)\vert } \textrm{e}^{i(b_{12}-b_{21})\left( [\tilde{b}_{12}u+\tilde{b}_{22}v]x-[\tilde{b}_{11} u+\tilde{b}_{12}v]y\right) }\mathcal {S}_{f,g}\left( x,y,u,v\right) , \end{aligned}$$

which yields (3.11). We ignore the proof of (3.12) since it can be deduced in the similar way. \(\square \)

4 Applications

In this section, the 2D-NLCWD and 2D-NLCAF will be used for the detection of single-component and multi-component 2D-LFM signals as effective. Without loss of generality, we assume that \(\textrm{det}(B)=1.\)

4.1 Single-component 2D- LFM signal

Suppose that the single-component 2D-LFM signal is modeled as follows

$$\begin{aligned} \mathcal {S}(x,y)=A_0\textrm{e}^{i\left[ (m_0x+n_0x^2)+(r_0y+s_0y^2)\right] } \,\,(n_0\cdot s_0 \ne 0),\quad -\frac{T}{2}\le x, \,y \le \frac{T}{2}, \end{aligned}$$
(4.1)

where the amplitude \(A_0\), initial frequency \(m_0,r_0\), and frequency rate \(n_0,s_0\).

It is observed that

$$\begin{aligned}&\mathcal {S}_p\left( x+\frac{\tau }{2}, y+\frac{\eta }{2}\right) \mathcal {S}_k^*\left( x-\frac{\tau }{2}, y-\frac{\eta }{2}\right) \\&\hspace{56.9055pt}=\vert A_0\vert ^2\mathcal {C}_{p-k}(x,y)\mathcal {C}_{p-k}^{\frac{1}{4}} (\tau ,\eta )\textrm{e}^{i\left[ (m_0\tau +r_0\eta )+2(n_0x\tau +s_0y\eta )\right] }\\&\quad \times \textrm{e}^{\frac{i}{2}\left[ (p_1+k_1)x\tau +(p_2+k_2) \frac{x\eta +y\tau }{2}+(p_3+k_3)y\eta \right] }. \end{aligned}$$

By applying (2.4), the 2D-NLCWD of \(\mathcal {S}(x,y)\) can be derived as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}}^{\mathcal {M}}\left( x,y,u,v\right) \\&=\frac{\vert A_0\vert ^2\mathcal {C}_{k-p}(u,v)\mathcal {C}_{p-k}(x,y)}{4\pi ^2} \textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\int _{-\frac{T}{2}}^{\frac{T}{2}} \int _{-\frac{T}{2}}^{\frac{T}{2}}\mathcal {C}_{p-k}^{\frac{1}{4}}(\tau ,\eta ) \\&\quad \times \textrm{e}^{i\left[ \frac{(p_1+k_1)}{2}x+\frac{(p_2+k_2)}{4}y+m_0 +2n_0x-b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \tau } \\&\quad \times \textrm{e}^{i\left[ \frac{(p_2+k_2)}{4}x+\frac{(p_3+k_3)}{2}y+r_0 +2s_0y-b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \eta }\textrm{d}\tau \textrm{d}\eta . \end{aligned}$$

When \(p=k\), which means \(p_1=k_1, p_2=k_2,p_3=k_3,\) we infer directly that

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}}^{\mathcal {M}}\left( x,y,u,v\right) = \frac{\vert A_0\vert ^2}{4\pi ^2}\textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\textrm{e}^{i\left[ p_1x+ \frac{p_2}{2}y+m_0+2n_0x-b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \tau } \textrm{d}\tau \nonumber \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\textrm{e}^{i\left[ \frac{p_2}{2} x+p_3y+r_0+2s_0y-b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \eta }\textrm{d}\eta \nonumber \\&=\frac{\vert A_0\vert ^2T^2}{4\pi ^2}\textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ p_1x+\frac{p_2}{2}y+m_0+2n_0x-b_{22} u+\frac{(b_{12}+b_{21})}{2}v\right] \right\} \nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ \frac{p_2}{2}x+p_3y+r_0+2s_0y-b_{11} v+\frac{(b_{12}+b_{21})}{2}u\right] \right\} . \end{aligned}$$
(4.2)

Similarly, by simple computations and owing to (2.5), the 2D-NLCAF of \(\mathcal {S}(x,y)\) can given by

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) \\&=\frac{\vert A_0\vert ^2\mathcal {C}_{k-p}^{\frac{1}{4}}(u,v)\mathcal {C}_{p-k}^{\frac{1}{4}} (\tau ,\eta )}{4\pi ^2}\textrm{e}^{\frac{i}{4}(b_{12}-b_{21})(v\tau -u\eta )} \textrm{e}^{i(m_0\tau +r_0\eta )} \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\int _{-\frac{T}{2}}^{\frac{T}{2}}\mathcal {C}_{p-k} (x,y)\textrm{e}^{i\left[ 2n_0\tau +\frac{(p_1+k_1)}{2}\tau +\frac{(p_2+k_2)}{4}\eta -b_{22} u+\frac{(b_{12}+b_{21})}{2}v\right] x} \\&\quad \times \textrm{e}^{i\left[ 2s_0\eta +\frac{(p_3+k_3)}{2}\eta +\frac{(p_2+k_2)}{4}\tau -b_{11} v+\frac{(b_{12}+b_{21})}{2}u\right] y}\textrm{d}x\textrm{d}y. \end{aligned}$$

When \(p=k\), equation above becomes

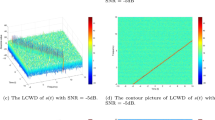
$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) = \frac{\vert A_0\vert ^2T^2}{4\pi ^2}\textrm{e}^{\frac{i}{4}(b_{12}-b_{21}) (v\tau -u\eta )}\textrm{e}^{i(m_0\tau +r_0\eta )}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2n_0\tau +p_1\tau +\frac{p_2}{2} \eta -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \right\} \nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2s_0\eta +p_3\eta +\frac{p_2}{2} \tau -b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \right\} . \end{aligned}$$
(4.3)

Equations (4.2) and (4.3) show that if we choose a suitable parameter \(\mathcal {M}\), the 2D-NLCWD and 2D-NLCAF of the single-component 2D-LFM signal \(\mathcal {S}(x,y)\) can produce pulse signals. This indicates that the 2D-NLCWD and 2D-NLCAF are useful and effective for detecting single-component 2D-LFM signals. For example, we consider the single-component 2D-LFM signal:

$$\begin{aligned} \mathcal {S}_0(x,y)=2\textrm{e}^{i\left[ (2x+2x^2)+(2y+2y^2)\right] },\,\,T=40. \end{aligned}$$

and the parameter

$$\begin{aligned} \mathcal {M}_0= \begin{pmatrix} 1&{}0&{}1&{}1\\ 0&{}1&{}1&{}2\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1 \end{pmatrix}. \end{aligned}$$

The 2D-NLCWD and 2D-NLCAF of \(\mathcal {S}_0(x,y)\) in some special value of (x, y) and \((\tau ,\eta )\) are shown in Fig. 1 and Fig. 2.

Fig. 1
figure 1

The absolute part of 2D-NLCWD of single-component 2D-LFM signal \(\mathcal {S}_0(x,y)\)

Full size image
Fig. 2
figure 2

The absolute part of 2D-NSLCAF of of single-component 2D-LFM signal \(\mathcal {S}_0(x,y)\)

Full size image

Furthermore, using (1.10) and (1.11), the 2D-WDNL and 2D-AFNL can be given by

$$\begin{aligned} {2DWL}_{\mathcal {S}}^{\mathcal {M}}\left( x,y,u,v\right)&=\frac{\vert A_0\vert ^2\mathcal {C}_{k}(u,v)}{2\pi i}\int _{-\frac{T}{2}}^{\frac{T}{2}}\int _{-\frac{T}{2}}^{\frac{T}{2}} \mathcal {C}_{p}(\tau ,\eta )\\&\quad \times \textrm{e}^{i\left[ m_0+2n_0x-b_{22}u+b_{12}v\right] \tau } \textrm{e}^{i\left[ r_0+2s_0y+b_{21}u-b_{11}v\right] \eta }\textrm{d}\tau \textrm{d}\eta ,\\ {2DAL}_{\mathcal {S}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right)&=\frac{\vert A_0\vert ^2\mathcal {C}_{k}(u,v)}{2\pi i}\textrm{e}^{i(m_0\tau +r_0\eta )}\int _{-\frac{T}{2}}^{\frac{T}{2}} \int _{-\frac{T}{2}}^{\frac{T}{2}}\mathcal {C}_{p}(x,y)\\&\quad \times \textrm{e}^{i\left[ 2n_0\tau -b_{22}u+b_{12}v\right] x} \textrm{e}^{i\left[ 2s_0\eta +b_{21}u-b_{11}v\right] y}\textrm{d}x\textrm{d}y, \end{aligned}$$

and when \(p=0\), we have

$$\begin{aligned}&{2DWL}_{\mathcal {S}}^{\mathcal {M}}\left( x,y,u,v\right) =\frac{\vert A_0\vert ^2T^2 \mathcal {C}_{k}(u,v)}{2\pi i}{{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ m_0+2n_0x-b_{22}u+b_{12}v\right] \right\} \nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ r_0+2s_0y+b_{21}u-b_{11}v\right] \right\} , \end{aligned}$$
(4.4)
$$\begin{aligned}&{2DAL}_{\mathcal {S}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) =\frac{\vert A_0\vert ^2 T^2\mathcal {C}_{k}(u,v)}{2\pi i}\textrm{e}^{i(m_0\tau +r_0\eta )}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2n_0\tau -b_{22}u+b_{12}v\right] \right\} {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2s_0\eta +b_{21}u-b_{11}v\right] \right\} . \end{aligned}$$
(4.5)

Comparing (4.2) with (4.4) and (4.3) with (4.5), we realize that the 2D-NLCWD and 2D- NLCAF are more flexible than 2D-WDNL and 2D-AFNL in detecting a single-component LFM since extra parameters \(p_1,p_2,p_3\).

Fig. 3
figure 3

The 2D-NLCWD of tri-component 2D-LFM signal \(\mathcal {V}_0(x,y)\) with \(T=40\)

Full size image

4.2 Multi-component 2D-LFM signal

The general of multi-component 2D-LFM signal has the form

$$\begin{aligned} \mathcal {V}(x,y)=\sum _{j=1}^{n}\mathcal {S}_j(x,y),\,\,\ -\frac{T}{2} \le x,y \le \frac{T}{2},\,n\in \mathbb {N}, \end{aligned}$$

where \(\mathcal {S}_j(x,y)=A_j\textrm{e}^{i\left[ (m_jx+n_jx^2)+(r_jy+s_jy^2)\right] }, \,(n_j,s_j \ne 0, \,\forall j\in \{1,...n\}).\)

It follows from (2.4) that

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {V}}^{\mathcal {M}}\left( x,y,u,v\right) \\&\hspace{56.9055pt}=\sum _{j=1}^{n}{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}_j}^{\mathcal {M}}\left( x,y,u,v\right) +\sum _{j_1\ne j_2=1}^{n}{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}_{j_1},\mathcal {S}_{j_2}}^{\mathcal {M}}\left( x,y,u,v\right) , \end{aligned}$$

where

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}_j}^{\mathcal {M}}\left( x,y,u,v\right) \\&=\frac{\vert A_j\vert ^2\mathcal {C}_{k-p}(u,v)\mathcal {C}_{p-k}(x,y)}{4\pi ^2} \textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\int _{-\frac{T}{2}}^{\frac{T}{2}} \int _{-\frac{T}{2}}^{\frac{T}{2}}\mathcal {C}_{p-k}^{\frac{1}{4}}(\tau ,\eta )\\&\quad \times \textrm{e}^{i\left[ \frac{(p_1+k_1)}{2}x+\frac{(p_2+k_2)}{4} y+m_j+2n_jx-b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \tau }\\&\quad \times \textrm{e}^{i\left[ \frac{(p_2+k_2)}{4}x+\frac{(p_3+k_3)}{2} y+r_j+2s_jy-b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \eta }\textrm{d}\tau \textrm{d}\eta , \end{aligned}$$

and the 2D-NLCWD of cross-term \({2D}\mathcal{L}\mathcal{W}_{\mathcal {S}_{j_1},\mathcal {S}_{j_2}}^{\mathcal {M}}\left( x,y,u,v\right) \)

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {S}_{j_1},\mathcal {S}_{j_2}}^{\mathcal {M}} \left( x,y,u,v\right) =\frac{A_{j_1}A_{j_2}^*\mathcal {C}_{k-p}(u,v) \mathcal {C}_{p-k}(x,y)}{4\pi ^2}\textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times \textrm{e}^{i\left[ (n_{j_1}-n_{j_2})x^2+(s_{j_1}-s_{j_2}) y^2+(m_{j_1}-m_{j_2})x+(r_{j_1}-r_{j_2})y\right] }\nonumber \\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\int _{-\frac{T}{2}}^{\frac{T}{2}} \mathcal {C}_{p-k}^{\frac{1}{4}}(\tau ,\eta )\textrm{e}^{i\left[ \frac{(n_{j_1} -n_{j_2})}{4}\tau ^2+\frac{(s_{j_1}-s_{j_2})}{4}\eta ^2\right] }\nonumber \\&\quad \times \textrm{e}^{i\left[ \frac{(p_1+k_1)}{2}x+\frac{(p_2+k_2)}{4}y+ \frac{m_{j_1}+m_{j_2}}{2}+(n_{j_1}+n_{j_2})x-b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \tau }\nonumber \\&\quad \times \textrm{e}^{i\left[ \frac{(p_2+k_2)}{4}x+\frac{(p_3+k_3)}{2}y+ \frac{r_{j_1}+r_{j_2}}{2}+(s_{j_1}+s_{j_2})y-b_{11}v+\frac{(b_{12}+b_{21})}{2} u\right] \eta }\textrm{d}\tau \textrm{d}\eta . \end{aligned}$$
(4.6)

When \(p=k, n_{j_1}=n_{j_2}=n_0\,,\,s_{j_1}=s_{j_2}=s_0, \forall j_1\ne j_2\), we obtain

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{W}_{\mathcal {V}}^{\mathcal {M}}\left( x,y,u,v\right) = \sum _{j=1}^{n}\frac{\vert A_j\vert ^2T^2}{4\pi ^2}\textrm{e}^{i(b_{12}-b_{21})(vx-uy)}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ p_1x+\frac{p_2}{2}y+m_j+2n_0x -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \right\} \nonumber \\&\quad {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ \frac{p_2}{2}x+p_3y+r_j+2s_0y -b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \right\} \nonumber \\&\quad +\sum _{j_1\ne j_2=1}^{n}\frac{A_{j_1}A_{j_2}^*T^2}{4\pi ^2}\textrm{e}^{i(b_{12}-b_{21})(vx-uy)} \textrm{e}^{i\left[ (m_{j_1}-m_{j_2})x+(r_{j_1}-r_{j_2})y\right] }\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\Bigg \{\frac{T}{2}\Big [p_1x+\frac{p_2}{2}y+\frac{m_{j_1}+m_{j_2}}{2} +2n_0x-b_{22}u+\frac{(b_{12}+b_{21})}{2}v\Big ]\Bigg \}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\Bigg \{\frac{T}{2}\Big [\frac{p_2}{2}x+p_3y+\frac{r_{j_1}+r_{j_2}}{2} +2s_0y-b_{11}v+\frac{(b_{12}+b_{21})}{2}u\Big ]\Bigg \}. \end{aligned}$$
(4.7)

Simlilary, the 2D-NLCAF of \(\mathcal {V}(x,y)\) can be expressed as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {V}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) \\&\hspace{56.9055pt}=\sum _{j=1}^{n}{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}_j}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) +\sum _{j_1\ne j_2=1}^{n}{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}_{j_1},\mathcal {S}_{j_2}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) , \end{aligned}$$

where

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}_j}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) = \frac{\vert A_j\vert ^2\mathcal {C}_{k-p}^{\frac{1}{4}}(u,v)\mathcal {C}_{p-k}^{\frac{1}{4}} (\tau ,\eta )}{4\pi ^2}\textrm{e}^{\frac{i}{4}(b_{12}-b_{21})(v\tau -u\eta )}\textrm{e}^{i(m_j\tau +r_j\eta )}\\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\int _{-\frac{T}{2}}^{\frac{T}{2}} \mathcal {C}_{p-k}(x,y)\textrm{e}^{i\left[ 2n_j\tau +\frac{(p_1+k_1)}{2}\tau + \frac{(p_2+k_2)}{4}\eta -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] x} \\&\quad \times \textrm{e}^{i\left[ 2s_j\eta +\frac{(p_3+k_3)}{2}\eta +\frac{(p_2+k_2)}{4} \tau -b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] y}\textrm{d}x\textrm{d}y, \end{aligned}$$

and

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {S}_{j_1},\mathcal {S}_{j_2}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) =\frac{A_{j_1}A_{j_2}^*\mathcal {C}_{k-p}^{\frac{1}{4}}(u,v)\mathcal {C}_{p-k}^{\frac{1}{4}} (\tau ,\eta )}{4\pi ^2}\textrm{e}^{\frac{i}{4}(b_{12}-b_{21})(v\tau -u\eta )}\\&\quad \times \textrm{e}^{i\left[ \frac{(n_{j_1}-n_{j_2})}{4}\tau ^2+\frac{(s_{j_1}-s_{j_2})}{4} \eta ^2+\frac{(m_{j_1}+m_{j_2})}{2}\tau +\frac{(r_{j_1}+r_{j_2})}{2}\eta \right] }\\&\quad \times \int _{-\frac{T}{2}}^{\frac{T}{2}}\int _{-\frac{T}{2}}^{\frac{T}{2}}\mathcal {C}_{p-k} (x,y)\textrm{e}^{i\left[ (n_{j_1}-n_{j_2})x^2+(s_{j_1}-s_{j_2})y^2\right] }\\&\quad \times \textrm{e}^{i\left[ (m_{j_1}-m_{j_2})+(n_{j_1}+n_{j_2})\tau +\frac{(p_1+k_1)}{2} \tau +\frac{(p_2+k_2)}{4}\eta -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] x} \\&\quad \times \textrm{e}^{i\left[ (r_{j_1}-r_{j_2})+(s_{j_1}+s_{j_2})\eta +\frac{(p_3+k_3)}{2} \eta +\frac{(p_2+k_2)}{4}\tau -b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] y}\textrm{d}x\textrm{d}y. \end{aligned}$$

When \(p=k, n_{j_1}=n_{j_2}=n_0\,, \,s_{j_1}=s_{j_2}=s_0, \forall j_1\ne j_2\), the 2D-NLCAF of \(\mathcal {V}(x,y)\) can be presented as

$$\begin{aligned}&{2D}\mathcal{L}\mathcal{A}_{\mathcal {V}}^{\mathcal {M}}\left( \tau ,\eta ,u,v\right) = \sum _{j=1}^{n}\frac{\vert A_j\vert ^2T^2}{4\pi ^2}\textrm{e}^{\frac{i}{4}(b_{12}-b_{21}) (v\tau -u\eta )}\textrm{e}^{i(m_j\tau +r_j\eta )}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2n_0\tau +p_1\tau +\frac{p_2}{2} \eta -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\right] \right\} \nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\left\{ \frac{T}{2}\left[ 2s_0\eta +p_3\eta +\frac{p_2}{2} \tau -b_{11}v+\frac{(b_{12}+b_{21})}{2}u\right] \right\} \nonumber \\&\quad +\sum _{j_1\ne j_2=1}^{n}\frac{A_{j_1}A_{j_2}^*T^2}{4\pi ^2}\textrm{e}^{\frac{i}{4} (b_{12}-b_{21})(v\tau -u\eta )}\textrm{e}^{i\left[ \frac{(m_{j_1}+m_{j_2})}{2}\tau +\frac{(r_{j_1}+r_{j_2})}{2}\eta \right] }\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\Bigg \{\frac{T}{2}\Big [(m_{j_1}-m_{j_2})+2n_0\tau +p_1\tau +\frac{p_2}{2}\eta -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\Big ]\Bigg \}\nonumber \\&\quad \times {{\,\textrm{sinc}\,}}\Bigg \{\frac{T}{2}\Big [(r_{j_1}-r_{j_2})+2s_0\eta +p_3\eta +\frac{p_2}{2}\tau -b_{22}u+\frac{(b_{12}+b_{21})}{2}v\Big ]\Bigg \}. \end{aligned}$$
(4.8)

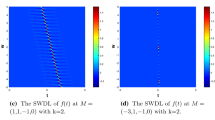
From (4.7) and (4.8), we conclude that 2D-NLCWD and 2D-NLCAF are very useful in detecting of multi-component 2D-LFM signals. Therefore, the algorithms of 2D-NLCWD and 2D-NLCAF for multi-component 2D-LFM signals detection can also be easily deduced as well. The 2D-NLCWD of tri-component 2D chirp signal

$$\begin{aligned} \mathcal {V}_0(x,y)&=\textrm{e}^{i\left[ (0.1x+0.3x^2)+(0.1y+0.3y^2)\right] }\\&\quad +\textrm{e}^{i\left[ (0.5x+0.6x^2)+(0.5y+0.6y^2)\right] } +\textrm{e}^{i\left[ (0.7x+0.9x^2)+(0.7y+0.9y^2)\right] }, \end{aligned}$$

with the parameter \(\mathcal {M}_0 \) in some special value of (x, y) are shown in Fig. 3.

5 Conclution

We have introduced two new distributions associated with 2D-NS-LCT. Then, we have proved some important properties of the proposed 2D integral transforms in great detail such as the shift properties, the conjugation symmetry properties, the marginal properties, the Moyal formula, and the relationship with the 2D-STFT. As a main consequence and application, the detection of single-component and multi-component 2D-LFM signals is also demonstrated by using the proposed transforms. Furthermore the proposed new distributions are more flexible than 2D-WDNL and 2D-AFNL in detecting 2D-LFM signals.