1 Introduction

Singular systems, also referred to as descriptor systems, implicit systems, or differential–algebraic systems, have been recognized to describe the behavior of many practical systems [3, 9], since they can embody the intrinsic nature of the dynamics and static modes, simultaneously. In the past decades, a lot of efforts concerning the systems have been successfully made upon the premise of standard system theory [22, 27, 35, 38, 41, 42]. Besides, time-delay phenomenon is generally known as a key source of the instability and poor performance in control systems. Thus, various types of singular systems with time delay have been studied by many researchers, including continuous-time systems and discrete-time ones. Control design and stability analysis which is of great significance for singular time-delay systems (STS) have been reported, e.g., stability and stabilization [2, 11, 37], \(H_{\infty }\) control and filter [25, 26, 40], and observer design [4, 12, 13].

Sliding mode control (SMC) has been known as an effective robust control strategy due to its various attractive features such as rapid response and good transient performance, particularly strong robustness against the uncertainty through the control channel (i.e., the matched uncertainty [5, 32]), and it has found to be widely applied to many technical problems [30, 43, 44] and various complex systems [1, 7, 19, 23, 33]. As for the STS, the passivity analysis has been studied via SMC in [36], where an integral-type sliding surface scheme has been provided in this excellent work. Furthermore, based on a novel integral sliding surface design, dissipativity issue for a class of T–S fuzzy singular systems with nonlinear perturbation and time-varying delay has been considered by [8]. However, as mentioned, most of the reports are obtained upon the premise that all the system states are completely accessible.

On another research front, it has been approved that the state may not be totally obtained or even not easy to be evaluated through the output measurement in many practical systems. Up to now, by incorporating the merits of the observer into the SMC effectively, observer-based SMC approach, also called sliding mode observer (SMO) strategy [29], has been developed to solve the state estimation problems for a variety of complex systems and engineering plants successfully, see [6, 10, 14,15,16,17,18, 20, 21, 24, 28, 34, 39] and the references therein. To name a few, in [28], a class of Markovian jump systems with quantization and actuator faults have been investigated by the SMO, and state estimation for a type of uncertain Markovian jump singular systems has been concerned via SMC in [34]. It is observed that, compared to the mature SMC theory of singular systems on the basis of the full states measurement, the research on SMO for singular systems has received less attention, which may be in its infancy. This is the first motivation of the study.

It should be pointed out that the SMO design for a class of Markovian jump singular systems with unmeasured states has been reported in [34]. Recently, the observer-based \(H_{\infty }\) SMC for a class of uncertain stochastic STS has been considered in [6]. Nevertheless, the uncertainties may often appear through the control channel, which is an intricate issue, but little research effort has been made for such systems. This is the second motivation of the paper. As such, the observer-based control problem of the STS may remain challenging and open, which finally makes us proceed to the present study.

In this paper, the \(H_{\infty }\) performance and admissibility for a class of uncertain STS is investigated via a novel SMO scheme. The main contribution can be fourfold as follows:

  • A newly technical route of the system’s analysis is put forward. Generally, the main thoughts for majority of the observer-based control systems are that: Stability analysis is addressed through the original system and its observer such that the error system can converge to the equilibrium state. However, the present route is that: If the stability of the original system and the error system is first guaranteed, then the observer states can tend to be stable therewith.

  • A peculiar observer is introduced to estimate the unmeasured states, by which a novel integral sliding surface is designed in such a way the resultant dynamics during the sliding mode, i.e., sliding mode dynamics (SMDs), are well shown, and the entire control scheme could be further boosted.

  • A newly strict LMI criterion is provided, which leads to that the SMDs are admissible with certain prescribed \(H_{\infty }\) disturbance attenuation level.

  • A novel adaptive controller is synthesized to suppress the unknown perturbation through the control channel and guarantee the finite-time reachability of the sliding surface since the initial moment, which keeps the desirable performance of the closed-loop systems.

The rest of this paper is organized as follows. Some preliminaries are given in Sect. 2. In Sect. 3, the main results of the observer-based SMC design are addressed. A specific example is provided to support the effectiveness and superiority of the method in Sect. 4. Conclusions are given in Sect. 5.

Notations: The notations used in this paper are standard. \(P>0\) means that matrix P is positive definite; \(\lambda _{M}(P)\) denotes the maximum eigenvalue of P; the symmetric elements of a symmetric matrix is denoted by “ * ”; “ T ” represents the transpose of a vector or a matrix. sym\(\{P\}\) is denoted as \(P+P^{\mathrm{{T}}}\). \(\Vert \cdot \Vert \) denotes the Euclidean norm of a vector or spectral norm of a matrix, diag\(\{Q\}\) represents a block-diagonal matrix Q, and \(\Vert \psi (t)\Vert _{d} =sup _{-d\le t\le 0}\Vert \psi (t)\Vert \) stands for the norm of a function \(\psi (t)\). \(L_{2}[0, \infty )\) is the space of integral vectors over \([0, \infty )\).

2 Problem Formulation

Consider the following uncertain STS described by

$$\begin{aligned} \left\{ \begin{array}{l} E\dot{x}(t)= (A+ \Delta A(t))x(t)+(A_{d}+\Delta A_{d}(t))x(t-d(t))\\ \qquad \qquad \quad +\,B(u(t)+f(t,x))+Dv(t), \\ y(t)= Cx(t),\\ x(\theta )=\psi (\theta ),\quad \theta \in [-d,~0] \end{array} \right. \end{aligned}$$
(1)

where \(x(t)\in {\mathscr {R}}^{n}\) is the system state, \(u(t)\in {\mathscr {R}}^{m}\) is the control input signal, \(y(t)\in {\mathscr {R}}^{p}\) is the measured output signal, and \(v(t)\in {\mathscr {R}}^{l}\) represents a set of exogenous disturbance which belongs to \(L_{2}[0, \infty )\). \(\psi (\theta )\) is a compatible vector-valued initial function. \(A, A_{d}, B, C\), and D are known real matrices, B is of full column rank. \(E \in {\mathscr {R}}^{n\times n}\) may be singular, i.e., rank\((E)=r\le n\). d(t) is a time-varying function satisfying \(0<d(t)\le d\), and \({\dot{d}}\le \mu <1\).

Assumption 1

The structural uncertainties \(\Delta A(t)\) and \(\Delta A_{d}(t)\) are norm bounded, i.e.,

$$\begin{aligned}{}[\Delta A(t)~~\Delta A_{d}(t)]=MF(t)[N~~N_{d}], \end{aligned}$$

where M, N and \(N_{d}\) are known constant matrices, and F(t) is an unknown matrix function satisfying \(F^{\mathrm{T}}(t)F(t)\le I\).

Assumption 2

The function f(t, x) represents the lumped perturbation of a physical plant through the control channel, and it satisfies \(\Vert f(t,x)\Vert \le \alpha \Vert y(t)\Vert \) [10], where \(\alpha >0\) is unknown, i.e., f(t, x) may be bounded, and the exact information is generally not available in practice.

Before proceeding, we give a definition concerning the following system (2) and some lemmas:

$$\begin{aligned} E\dot{x}(t)=Ax(t)+A_{d}x(t-d(t)). \end{aligned}$$
(2)

Definition 1

[36] The system (2) is said to be

  1. (a)

    regular if \(det (sE-A)\) is not identically zero;

  2. (b)

    impulse free if deg(det\((sE-A))=rank (E)\);

  3. (c)

    stable if, for any \(\varepsilon >0\), there exist a scalar \(\delta (\varepsilon )>0\) such that, for any compatible initial condition \(\psi (t)\) satisfying \(\Vert \psi (t)\Vert _{d}\le \delta (\varepsilon )\), the solution x(t) of (2) satisfies \(\Vert x(t)\Vert <\varepsilon \) for \(t\ge 0\), and further, \(x(t)\rightarrow 0\) as \(t\rightarrow \infty \);

  4. (d)

    asymptotically stable if the system (2) is stable, and furthermore, there is a scalar \(\alpha >0\) such that, for any compatible initial condition \(\psi (t)\) satisfying \(\Vert \psi (t)\Vert _{d}<\alpha \), the solution \(x(t)\rightarrow 0\) as \(t\rightarrow \infty \);

  5. (e)

    admissible, if it is regular, impulse free, and stable.

Lemma 1

[40] Suppose that piecewise continuous real square matrices \(Z(t), X, Q>0\) satisfy that \(Z^{\mathrm{{T}}}(t)X+X^{\mathrm{{T}}}Z(t)+Q<0\) for all t. Then, the following hold:

  1. (1)

    Z(t) and X are invertible;

  2. (2)

    \(\Vert Z^{-1}(t)\Vert \ge \delta \) for some \(\delta >0\).

Lemma 2

[31] Let \(P\in {\mathscr {R}}^{n\times n}\) be symmetric such that \(E_{L}^{\mathrm{T}}PE_{L}>0\) and \(Q\in {\mathscr {R}}^{(n-r)\times (n-r)}\) is non-singular. Then, \(PE+R^{\mathrm{T}}QS^{\mathrm{T}}\) is non-singular and its inverse is expressed as: \((PE+R^{\mathrm{T}}QS^\mathrm{T})^{-1}={\mathscr {P}}E^{\mathrm{T}}+S{\mathscr {Q}}R\), where \({\mathscr {P}}\in {\mathscr {R}}^{n\times n}\) is a symmetric matrix and \({\mathscr {Q}}\in {\mathscr {R}}^{(n-r)\times (n-r)}\) is a non-singular matrix with

$$\begin{aligned} {\mathscr {Q}}=(S^{\mathrm{T}}S)^{-1}Q^{-1}(RR^{\mathrm{T}})^{-1}, ~~E_{R}^{\mathrm{T}}{\mathscr {P}}E_{R}=(E_{L}^{\mathrm{T}}PE_{L})^{-1} \end{aligned}$$

where \(R^{\mathrm{T}}, S\in {\mathscr {R}}^{n\times (n-r)}\) are any matrices with full column rank and satisfy \({\textit{RE}}=0\) and \({\textit{ES}}=0\). E is decomposed as \(E=E_{L}E_{R}^{\mathrm{T}}\) with \(E_{L}, E_{R}\in {\mathscr {R}}^{n\times r}\) are of full column rank.

3 Main Results

In this section, a novel sliding mode observer (SMO) scheme is developed for the STS (1), which includes the design of particular non-fragile observer and novel integral-type sliding surface as well as the adaptive sliding mode controller.

3.1 Non-fragile Observer Design

The following state observer is designed to estimate the unmeasured system states

$$\begin{aligned} \left\{ \begin{array}{l} E\dot{{\hat{x}}}(t)=A\hat{x}(t)+A_{d}\hat{x}(t-d(t))+(L+\Delta L(t))[y(t)-C\hat{x}(t)], \\ \hat{y}(t)= C\hat{x}(t),\\ \hat{x}(\theta )=\hat{\psi } (\theta ), \theta \in [-d,~0] \end{array} \right. \end{aligned}$$
(3)

where \(\hat{x}(t) \in {\mathscr {R}}^{n}\) represents the estimation of \(x(t), L\in {\mathscr {R}}^{n\times p}\) is the observer gain to be designed later, and \(\Delta L(t)\) is an additive gain variation satisfying \(\Vert \Delta L(t)\Vert \le \delta \), where \(\delta >0\) is a constant, namely the observer may be affected by some factors [6, 12].

Let the estimation error be \(e(t)=x(t)-\hat{x}(t)\). Then, the error system can be expressed by subtracting (3) from (1) as

$$\begin{aligned} \left\{ \begin{array}{l} E\dot{e}(t)= (A-{\textit{LC}}- \Delta L(t)C)e(t)+A_{d}e(t-d(t))\\ \qquad \qquad \quad +\,\Delta A(t)x(t)+\Delta A_{d}(t)x(t-d(t))\\ \qquad \qquad \quad +\,B(u(t)+f(t,x))+Dv(t), \\ y_{e}(t)= Ce(t)\\ \end{array} \right. \end{aligned}$$
(4)

where \(y_{e}(t)\) denotes the output of the error system.

Remark 1

It is noted that the control input is generally utilized for conventional observer designs (e.g., see [4, 6, 10, 12, 17, 18, 21, 24, 28, 34, 39]). To the best of the authors’ knowledge, the existing SMO is developed with the so-called composite controller in general, i.e., controller itself and its compensator (or called the discontinuous output error injection term) are both required to satisfy the main goal. In this article, the composite controller will be no longer needed for the SMO, and the convenience is that: Control signal is only performed on the original system, and the actions of the error system and the observer respond automatically. Thus, this simplifies the observer design in some meaningful sense.

3.2 Novel Integral Sliding Surface Design

Now, a novel integral sliding surface function is introduced as follows:

$$\begin{aligned} s(t)= & {} G[Ee(t)-Ee(0)]+G[E\hat{x}(t)-E\hat{x}(0)]\nonumber \\&-\,\int _0^{t}G(A+{\textit{BK}})\hat{x}(\theta )\mathrm {d}\theta , \end{aligned}$$
(5)

where matrix K is to be determined, and \(G\in {\mathscr {R}}^{m\times n}\) is a known matrix satisfying \({\textit{GB}}\) is non-singular, and it is assumed that G satisfies \({\textit{GE}}={\textit{HC}}\) with H given thereafter. In fact, one type of the rank restrictions could be configured as \(rank \left[ \begin{array}{cc}{\textit{GE}}\\ C \end{array}\right] =rank (C)\), from which matrix H can be found to satisfy the equality constraint. Besides, a general method for calculating the equality constraint will be given in Remark 5. In accordance with the condition, it follows that the sliding surface function (5) becomes

$$\begin{aligned} \begin{aligned} s(t)&=H[y(t)-\hat{y}(t)]-H[y(0)-\hat{y}(0)]+G[E\hat{x}(t)-E\hat{x}(0)]\\&\quad -\,\int _0^{t}G(A+{\textit{BK}})\hat{x}(\theta )\mathrm {d}\theta . \end{aligned} \end{aligned}$$

Then, it is observed that the integral sliding surface will be available for the design.

In order to achieve the sliding motion, the equivalent controller will be developed via the SMC theory [32], i.e., \(s(t)=0\) and \({\dot{s}}(t)=0\) hold, simultaneously. So, it follows from \({\dot{s}}(t)=0\), i.e.,

$$\begin{aligned} {\dot{s}}(t)= & {} {\textit{GAe}}(t)+{\textit{GA}}_{d}x(t-d(t))+G[\Delta A(t)x(t)+\Delta A_{d}(t)\\&\cdot x(t-d(t))]+{\textit{GB}}[u(t)+f(t,x)]+GDv(t)-{\textit{GBK}}\hat{x}(t)\\= & {} 0; \end{aligned}$$

thus, the equivalent controller can be obtained by

$$\begin{aligned} u_{eq}(t)= & {} K\hat{x}(t)-f(t,x)-({\textit{GB}})^{-1}G[Ae(t)+\Delta A(t)x(t)\nonumber \\&+\,(A_{d}+\Delta A_{d}(t))x(t-d(t))+Dv(t)]. \end{aligned}$$
(6)

Then, substituting (6) into (1) results in the dynamical equation of the system (1) during the sliding mode as

$$\begin{aligned} E\dot{x}(t)= & {} (A+ {\textit{BK}}+B_{G}\Delta A(t))x(t)+B_{G}(A_{d}+\Delta A_{d}(t))\nonumber \\&\cdot x(t-d(t))-({\textit{BK}}+B_{A})e(t)+D_{B}v(t) \end{aligned}$$
(7)

where \(B_{G}=I-B({\textit{GB}})^{-1}G, B_{A}=B({\textit{GB}})^{-1}{\textit{GA}}\) and \(D_{B}=B_{G}D\).

Similarly, based on (6) and (4), one can further get the associated dynamical equation of the error system (4) during the sliding mode given by

$$\begin{aligned} E\dot{e}(t)= & {} (A_{G}-{\textit{LC}}-{\textit{BK}}- \Delta L(t)C)e(t)+A_{d}e(t-d(t))\nonumber \\&\quad +\,({\textit{BK}}+B_{G}\Delta A(t))x(t)+(B_{G}\Delta A_{d}(t)-B_{d})\nonumber \\&\cdot x(t-d(t))+D_{B}v(t) \end{aligned}$$
(8)

where \(A_{G}=A-B_{A}, B_{d}=B({\textit{GB}})^{-1}{\textit{GA}}_{d}\).

Then, the sliding mode dynamics (SMDs) of the closed-loop systems can be shown as

$$\begin{aligned} \left\{ \begin{array}{l} E\dot{x}(t)=A_{K}(t)x(t)+A_{d}(t)x(t-d(t))-({\textit{BK}}+B_{A})e(t)+D_{B}v(t),\\ E\dot{e}(t)=A_{L}(t)e(t)+A_{d}e(t-d(t))+({\textit{BK}}+B_{G}\Delta A(t)) x(t)\\ \qquad \qquad +\,(B_{G}\Delta A_{d}(t)-B_{d})x(t-d(t))+D_{B}v(t) \end{array} \right. \end{aligned}$$
(9)

where \(A_{K}(t)=A+ {\textit{BK}}+B_{G}\Delta A(t), A_{d}(t)=B_{G}(A_{d}+\Delta A_{d}(t)), A_{L}(t)=A_{G}-{\textit{LC}}-{\textit{BK}}- \Delta L(t)C\).

Remark 2

The main feature of the sliding surface which is worth mentioning is that: Different from the existing forms such as [6, 8, 34, 36], the error term Ee(t) is introduced, which performs to avoid the difficulties caused by the perturbation (i.e., f(t, x)), as is seen from the derivative of the SMDs. The design could also be of benefit to demonstrate one highlight of the SMC that the sliding motion may be insensitive to all matched uncertainties.

Remark 3

As seen in chapter 3.1, the controller u(t) appears in the error system (4). Via the developed SMC in the sequel, the expected performance of the closed-loop systems composed of (1), (3), and (4) will be shown by the SMDs (9), so as to achieve the main goal. The analytical route of the stability differs from the existing SMO scheme, please see the Introduction and correlated results, e.g., [6, 10, 17, 18, 21, 24, 28, 34, 39] for more details.

Definition 2

The SMDs (9) are said to be admissible with \(H_{\infty }\) disturbance attenuation level \(\gamma \), if the following two targets are satisfied:

T1. :

The SMDs are admissible with \(v(t)=0\);

T2. :

Under zero initial conditions, the \(H_{\infty }\) performance measure below is held with nonzero external disturbance \(v(t)\in L_{2}[0, \infty )\) and the prescribed disturbance attenuation level \(\gamma >0 \):

$$\begin{aligned} \int _0^{\infty }y_{e}^{\mathrm{{T}}}(t)y_{e}(t)\mathrm{d}t\le \gamma ^{2}\int _0^{\infty }v^{\mathrm{{T}}}(t)v(t)\mathrm{d}t. \end{aligned}$$
(10)

3.3 Performance Analysis of the Sliding Motion

In this part, sufficient conditions for the admissibility of the SMDs with \(H_{\infty }\) disturbance attenuation level are addressed.

Theorem 1

Consider the sliding surface function defined in (5) and the SMDs in (9). Given a scalar \(\gamma >0\), if positive definite matrices \(P, Q_{1}\) and \(Q_{2}\), matrix \({{\tilde{P}}}\), positive scalars \(\varepsilon _{1}\) and \(\varepsilon _{2}\) can be found to satisfy the following matrix inequalities:

$$\begin{aligned} {\tilde{P}}^{\mathrm{T}}E= & {} E^{\mathrm{T}}{\tilde{P}}\ge 0, \end{aligned}$$
(11)
$$\begin{aligned} \varTheta= & {} \left[ \begin{array}{ccccccc} \varTheta _{1}&{} \quad \varTheta _{2}&{} \quad \varTheta _{4}&{} \quad 0&{} \quad {\tilde{P}}^{\mathrm{T}}D_{B}&{} \quad {\tilde{P}}^{\mathrm{T}}B_{G}M&{} \quad 0\\ *&{} \quad \varTheta _{3}&{} \quad -{\tilde{P}}^{\mathrm{T}}B_{d}&{} \quad {\tilde{P}}^{\mathrm{T}}A_{d}&{} \quad {\tilde{P}}^{\mathrm{T}}D_{B}&{} \quad 0&{} \quad {\tilde{P}}^{\mathrm{T}}B_{G}M\\ *&{} \quad *&{} \quad \varTheta _{5}&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -(1-\mu )Q_{2}&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\gamma ^{2}I&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\varepsilon _{1}I&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\varepsilon _{2}I \end{array}\right] <0,\nonumber \\ \end{aligned}$$
(12)

where \(\varTheta _{1}=sym \{{\tilde{P}}^\mathrm{T}(A+{\textit{BK}})\}+Q_{1}+(\varepsilon _{1}+\varepsilon _{2})N^{\mathrm{T}}N, \varTheta _{2}=-{\tilde{P}}^{\mathrm{T}}({\textit{BK}}+B_{A})+({\tilde{P}}^\mathrm{T}{\textit{BK}})^{\mathrm{T}}, \varTheta _{3}=sym \{{\tilde{P}}^\mathrm{T}(A_{G}-{\textit{LC}}-{\textit{BK}})\}+Q_{2}+{\tilde{P}}^{\mathrm{T}}{\tilde{P}}+(\delta ^{2}+1)C^{\mathrm{T}}C, \varTheta _{4}={\tilde{P}}^\mathrm{T}B_{G}A_{d}+(\varepsilon _{1}+\varepsilon _{2})N^{\mathrm{T}}N_{d}, \varTheta _{5}=-(1-\mu )Q_{1}+(\varepsilon _{1}+\varepsilon _{2})N_{d}^{\mathrm{T}}N_{d}, {\tilde{P}}^{\mathrm{T}}=E^{\mathrm{T}}P+{\textit{SQ}}^\mathrm{T}R\), and \(R^{\mathrm{T}}, S\in {\mathscr {R}}^{n\times (n-r)}\) are any matrices with full column rank such that \({\textit{RE}}=0\) and \({\textit{ES}}=0\), then the SMDs (9) are admissible with the \(H_{\infty }\) disturbance attenuation level \(\gamma \), which implies the closed-loop systems are admissible with the \(H_{\infty }\) disturbance attenuation level \(\gamma \) under the developed scheme.

Proof

Step 1: \(H_{\infty }\) performance analysis. Choose the following Lyapunov function

$$\begin{aligned} V(t)= & {} x^{\mathrm{T}}(t)E^{\mathrm{T}}PEx(t)+\int _{t-d(t)}^{t}x^\mathrm{T}(\theta )Q_{1}x(\theta )\mathrm{d}\theta \\&+\,e^{\mathrm{T}}(t)E^\mathrm{T}PEe(t)+\int _{t-d(t)}^{t}e^{\mathrm{T}}(\theta )Q_{2}e(\theta )\mathrm{d}\theta . \end{aligned}$$

By taking the derivative of V(t) by t, one has

$$\begin{aligned} {\dot{V}}(t)= & {} x^{\mathrm{T}}(t)[E^{\mathrm{T}}PA_{K}(t)+A_{K}^{\mathrm{T}}(t)PE+Q_{1}]x(t)+2x^{\mathrm{T}}(t)E^{\mathrm{T}}PA_{d}(t)x(t-d(t))\nonumber \\&-\,2x^{\mathrm{T}}(t)E^{\mathrm{T}}P({\textit{BK}}+B_{A})e(t)+2x^{\mathrm{T}}(t)E^{\mathrm{T}}PD_{B} v(t)-(1-{\dot{d}}(t))\nonumber \\&\cdot x^{\mathrm{T}}(t-d(t))Q_{1}x(t-d(t))+e^{\mathrm{T}}(t)[E^{\mathrm{T}}P A_{L}(t)+A_{L}^{\mathrm{T}}(t)PE+Q_{2}]e(t)\nonumber \\&+\,2e^{\mathrm{T}}(t)E^{\mathrm{T}}PA_{d}e(t-d(t))+2e^{\mathrm{T}}(t) E^{\mathrm{T}}P[{\textit{BK}}+B_{G}\Delta A(t)]x(t)\nonumber \\&+\,2e^{\mathrm{T}}(t)E^{\mathrm{T}}P[B_{G}\Delta A_{d}(t)-B_{d}] x(t-d(t)))+2e^{\mathrm{T}}(t)E^{\mathrm{T}}PD_{B}v(t)\nonumber \\&-\,(1-{\dot{d}}(t))e^{\mathrm{T}}(t-d(t)) Q_{2}e(t-d(t)). \end{aligned}$$
(13)

Note that \({\textit{RE}}=0\), it follows that

$$\begin{aligned}&\left\{ \begin{array}{l} 0=2x^{\mathrm{T}}(t){\textit{SQ}}^{\mathrm{T}}{\textit{RE}}{\dot{x}}(t)\\ \quad =2x^{\mathrm{T}}(t){\textit{SQ}}^{\mathrm{T}}R[A_{K}(t)x(t)+A_{d}(t)x(t-d(t))-({\textit{BK}}+B_{A})e(t)+D_{B}v(t)],\\ 0=2e^{\mathrm{T}}(t){\textit{SQ}}^{\mathrm{T}}{\textit{RE}}{\dot{e}}(t)\\ \quad =2e^{\mathrm{T}}(t){\textit{SQ}}^{\mathrm{T}}R\{A_{L}(t)e(t)+A_{d}e(t-d(t))+({\textit{BK}}+B_{G}\Delta A(t))x(t)\\ \qquad +(B_{G}\Delta A_{d}(t)-B_{d})x(t-d(t))+D_{B}v(t)\}. \end{array} \right. \end{aligned}$$
(14)

By combining (13) and (14) and denoting the matrix \({\tilde{P}}^\mathrm{T}=E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R\), we get

$$\begin{aligned}&y_{e}^{\mathrm{T}}(t)y_{e}(t)-\gamma ^{2}v^{\mathrm{T}}(t)v(t)+{\dot{V}} (t)\nonumber \\&\quad =x^{\mathrm{T}}(t)[{\tilde{P}}^{\mathrm{T}}A_{K}(t)+A_{K}^{\mathrm{T}}(t){\tilde{P}}+Q_{1}]x(t)+2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}A_{d}(t)x(t-d(t))\nonumber \\&\qquad -2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}({\textit{BK}}+B_{A})e(t)+2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}D_{B}v(t)-(1-{\dot{d}}(t))\nonumber \\&\qquad \cdot x^{\mathrm{T}}(t-d(t))Q_{1}x(t-d(t))+e^{\mathrm{T}}(t)[{\tilde{P}}^{\mathrm{T}}A_{L}(t)+A_{L}^{\mathrm{T}}(t){\tilde{P}}+Q_{2}\nonumber \\&\qquad +C^{\mathrm{T}}C] e(t)+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}A_{d}e(t-d(t))+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}[{\textit{BK}}+B_{G}\nonumber \\&\qquad \cdot \Delta A(t)]x(t)+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}[B_{G}\Delta A_{d}(t)-B_{d}]x(t-d(t)))+2e^{\mathrm{T}}(t)\nonumber \\&\qquad \cdot {\tilde{P}}^{\mathrm{T}}D_{B} v(t)-(1-{\dot{d}}(t))e^\mathrm{T}(t-d(t))Q_{2}e(t-d(t))-\gamma ^{2}v^{\mathrm{T}}(t)v(t). \end{aligned}$$
(15)

Then, consider the following performance index

$$\begin{aligned} J=\int _0^{\infty }[y_{e}^{\mathrm{{T}}}(t)y_{e}(t)- \gamma ^{2}v^{\mathrm{{T}}}(t)v(t)]\mathrm{d}t. \end{aligned}$$

To facilitate the result, (15) is renewed below

$$\begin{aligned}&y_{e}^{\mathrm{T}}(t)y_{e}(t)-\gamma ^{2}v^{\mathrm{T}}(t)v(t)+{\dot{V}} (t)\nonumber \\&\quad =x^{\mathrm{T}}(t)[sym \{{\tilde{P}}^{\mathrm{T}}(A+{\textit{BK}})\}+Q_{1}]x(t)+2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}A_{d}x(t-d(t))\nonumber \\&\qquad -2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}({\textit{BK}}+B_{A})e(t)+2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}D_{B}v(t)+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}A_{d}e(t-d(t))\nonumber \\&\qquad +e^{\mathrm{T}}(t)[sym \{{\tilde{P}}^{\mathrm{T}}(A_{G}-{\textit{LC}}-{\textit{BK}})\}+Q_{2}+C^{\mathrm{T}}C]e(t)+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}{\textit{BK}}x(t)\nonumber \\&\qquad -2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{d}x(t-d(t))+2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}D_{B}v(t)-\gamma ^{2}v^{\mathrm{{T}}}(t)v(t)-(1-{\dot{d}}(t))\nonumber \\&\qquad \cdot x^{\mathrm{T}}(t-d(t))Q_{1}x(t-d(t))-(1-{\dot{d}}(t)) e^{\mathrm{T}}(t-d(t))Q_{2}e(t-d(t))\nonumber \\&\qquad +2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}\Delta A(t)x(t)+2x^{\mathrm{T}}(t) {\tilde{P}}^{\mathrm{T}}B_{G}\Delta A_{d}(t)x(t-d(t))\nonumber \\&\qquad -2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}\Delta L(t)Ce(t)+2e^\mathrm{T}(t){\tilde{P}}^{\mathrm{T}}B_{G}\Delta A(t)x(t)\nonumber \\&\qquad +2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}\Delta A_{d}(t)x(t-d(t)). \end{aligned}$$
(16)

Moreover, the following inequalities are obtained

$$\begin{aligned}&2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}[\Delta A(t)x(t)+\Delta A_{d}(t)x(t-d(t))]\nonumber \\&\quad =2x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}MF(t)[Nx(t)+N_{d}x(t-d(t))]\nonumber \\&\quad \le \varepsilon _{1}^{-1}x^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}MM^{\mathrm{T}}B_{G}^{\mathrm{T}}{\tilde{P}}x(t)+\varepsilon _{1}[Nx(t)+N_{d}x(t-d(t))]^{\mathrm{T}}\nonumber \\&\quad \cdot [Nx(t)+N_{d}x(t-d(t))], \end{aligned}$$
(17)
$$\begin{aligned}&2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}[\Delta A(t)x(t)+\Delta A_{d}(t)x(t-d(t))]\nonumber \\&\quad =2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}MF(t)[Nx(t)+N_{d}x(t-d(t))]\nonumber \\&\quad \le \varepsilon _{2}^{-1}e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}B_{G}MM^{\mathrm{T}}B_{G}^{\mathrm{T}}{\tilde{P}}e(t)+\varepsilon _{2}[Nx(t)+N_{d}x(t-d(t))]^{\mathrm{T}}\nonumber \\&\quad \cdot [Nx(t)+N_{d}x(t-d(t))]. \end{aligned}$$
(18)

and

$$\begin{aligned}&-\,2e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}\Delta L(t)Ce(t)\le 2\delta \Vert e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}\Vert \Vert Ce(t)\Vert \nonumber \\&\quad \le e^{\mathrm{T}}(t){\tilde{P}}^{\mathrm{T}}{\tilde{P}}e(t)+\delta ^{2}e^\mathrm{T}(t)C^{\mathrm{T}}Ce(t). \end{aligned}$$
(19)

Thus, with the combination of (16)–(19), one has the following quadratic form

$$\begin{aligned} y_{e}^{\mathrm{T}}(t)y_{e}(t)-\gamma ^{2}v^{\mathrm{T}}(t)v(t)+\dot{V}(t)\le \xi ^{\mathrm{T}}(t){\varXi }\xi (t) \end{aligned}$$
(20)

where

$$\begin{aligned} \xi ^{\mathrm{T}}(t)= & {} [x^{\mathrm{T}}(t)~e^{\mathrm{T}}(t)~x^{\mathrm{T}}(t-d(t))~e^{\mathrm{T}}(t-d(t))~v^{\mathrm{T}}(t)],\\ {\varXi }= & {} \left[ \begin{array}{ccccc} {\varTheta _{1}}&{} \quad {\varTheta _{2}}&{} \quad {\tilde{P}}^{\mathrm{T}}B_{G}A_{d}&{} \quad 0&{} \quad {\tilde{P}}^{\mathrm{T}}D_{B}\\ *&{} \quad {\varTheta _{3}}&{} \quad -{\tilde{P}}^{\mathrm{T}}B_{d}&{} \quad {\tilde{P}}^{\mathrm{T}}A_{d}&{} \quad {\tilde{P}}^{\mathrm{T}}D_{B}\\ *&{} \quad *&{} \quad -(1-\mu )Q_{1}&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -(1-\mu )Q_{2}&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\gamma ^{2}I\\ \end{array}\right] \\&+\,(\varepsilon _{1}+\varepsilon _{2})\left[ \begin{array}{ccccc}N^{\mathrm{T}}\\ 0\\ N_{d}^{\mathrm{T}}\\ 0\\ 0 \end{array}\right] [N~~0 ~~N_{d}~~0 ~~0 ]. \end{aligned}$$

By the Schur complement, (12) is equivalent to the inequality \({\varXi }<0\). Thus, for all \(\xi (t)\ne 0\), it follows

$$\begin{aligned} y_{e}^{\mathrm{T}}(t)y_{e}(t)-\gamma ^{2}v^\mathrm{T}(t)v(t)+{\dot{V}}(t)<0. \end{aligned}$$
(21)

Hence, under the zero initial conditions, i.e., \(V(0)=0\), and consider that \(V(\infty )\ge 0\), the following can be given by integrating (21) with respect to t from 0 to \(\infty \):

$$\begin{aligned} J= & {} \int _{0}^{\infty }[y_{e}^{\mathrm{{T}}}(t)y_{e}(t)-\gamma ^{2}v^{\mathrm{{T}}}(t)v(t)+{\dot{V}}(t)]\mathrm{d}t+V(0)-V(\infty )\\\le & {} \int _{0}^{\infty }[y_{e}^{\mathrm{{T}}}(t)y_{e}(t)-\gamma ^{2}v^{\mathrm{{T}}}(t)v(t)+{\dot{V}}(t)]\mathrm{d}t\\= & {} \int _{0}^{\infty }\xi ^{\mathrm{T}}(t){\varXi }\xi (t)\mathrm{d}t\le -\lambda _{v}\int _{0 }^{\infty }\Vert v(t)\Vert ^{2}\mathrm{d}t \end{aligned}$$

where \(\lambda _{v}=\lambda _{M}(-{\varXi })>0 \), which ensures T2.

Step 2: Admissibility analysis. When \(v(t)=0\), we show the SMDs are regular and impulse free. It is worth mentioning that the regularity and non-impulsiveness of the SMDs could be proved if both the pair \((E, A_{K}(t))\) and \((E, A_{L}(t))\) are regular and impulse free. Then, recalling (15), it follows that

$$\begin{aligned} \qquad ~~\xi ^{\mathrm{T}}(t){\varOmega }\xi (t)\le \xi ^{\mathrm{T}}(t){\varXi }\xi (t)<0 , for all ~\xi (t)\ne 0 \end{aligned}$$

where \({\varOmega }=\left[ \begin{array}{ccccc} {\varOmega }_{1}&{}{\varOmega }_{2}&{}{\tilde{P}}^{\mathrm{T}}A_{d}(t)&{}0&{}{\tilde{P}}^{\mathrm{T}}D_{B}\\ *&{}{\varOmega }_{3}&{}{\tilde{P}}^{\mathrm{T}}(B_{G}\Delta A_{d}(t)-B_{d})&{}{\tilde{P}}^{\mathrm{T}}A_{d}&{}{\tilde{P}}^{\mathrm{T}}D_{B}\\ *&{}*&{}-(1-\mu )Q_{1}&{}0&{}0\\ *&{}*&{}*&{}-(1-\mu )Q_{2}&{}0\\ *&{}*&{}*&{}*&{}-\gamma ^{2}I \end{array}\right] \) with \({\varOmega }_{1}=sym \{{\tilde{P}}^\mathrm{T}A_{K}(t)\}+Q_{1}, {\varOmega }_{2}=-{\tilde{P}}^{\mathrm{T}} ({\textit{BK}}+B_{A})+({\tilde{P}}^{\mathrm{T}}{\textit{BK}}+{\tilde{P}}^{\mathrm{T}}B_{G}\Delta A(t))^{\mathrm{T}}, {\varOmega }_{3}=sym \{{\tilde{P}}^\mathrm{T}A_{L}(t)\}+Q_{2}+C^{\mathrm{T}}C\), which implies \({\varOmega }<0\). Since rank\((E)=r\), there exist non-singular matrices U and \(V\in {\mathscr {R}}^{n\times n}\) such that \(UEV=\left[ \begin{array}{cc} I_{r}&{}0\\ 0&{}0 \end{array}\right] \). Thus, it follows \(RU^{-1}=R_{1}[0 ~~I_{n-r}]\), where \(R_{1}\in {\mathscr {R}}^{(n-r)\times (n-r)}\) is any non-singular matrix. In like manner, one can define some matrix decomposition as follows:

$$\begin{aligned} UA_{K}(t)V= & {} \left[ \begin{array}{cc} A_{K1}(t)&{} \quad A_{K2}(t)\\ A_{K3}(t)&{} \quad A_{K4}(t) \end{array}\right] ,~U^{-\mathrm T}PU^{\mathrm{T}}=\left[ \begin{array}{cc} P_{1}&{} \quad P_{2}\\ P_{2}^{\mathrm{T}}&{} \quad P_{3} \end{array}\right] ,\\ UA_{L}(t)V= & {} \left[ \begin{array}{cc} A_{L1}(t)&{} \quad A_{L2}(t)\\ A_{L3}(t)&{} \quad A_{L4}(t) \end{array}\right] ,\\ V^{\mathrm{T}}S= & {} \left[ \begin{array}{cc} S_{1}\\ S_{2} \end{array}\right] ,\\ V^{T}Q_{1}V= & {} \left[ \begin{array}{cc} Q_{11}&{} \quad Q_{12}\\ Q_{12}^{\mathrm{T}}&{} \quad Q_{22} \end{array}\right] ,\\ V^{\mathrm{T}}Q_{2}V= & {} \left[ \begin{array}{cc} Q_{V11}&{} \quad Q_{V12}\\ Q_{V12}^{\mathrm{T}}&{} \quad Q_{V22} \end{array}\right] . \end{aligned}$$

Due to \({\varOmega }<0\), it is obtained that

$$\begin{aligned} \left[ \begin{array}{cc} sym \{{\tilde{P}}^{\mathrm{T}}A_{K}(t)\}+Q_{1}&{} \quad {\varOmega }_{2}\\ *&{} \quad sym \{{\tilde{P}}^{\mathrm{T}}A_{L}(t)\}+Q_{2} \end{array}\right] <0. \end{aligned}$$
(22)

Then, pre- and post-multiplying (22) by \( diag \{V^\mathrm{T},~V^{\mathrm{T}}\}\) and \( diag \{V,~V\}\) yields

$$\begin{aligned} \left[ \begin{array}{cccc} \star &{} \quad \star &{} \quad \star &{} \quad \star \\ \star &{} \quad \varLambda _{1}&{} \quad \star &{} \quad \star \\ \star &{} \quad \star &{} \quad \star &{} \quad \star \\ \star &{} \quad \star &{} \quad \star &{} \quad \varLambda _{2} \end{array}\right] <0 \end{aligned}$$
(23)

where \(\varLambda _{1}=sym \{S_{2}Q^\mathrm{T}R_{1}A_{K4}(t)\}+Q_{22}, \varLambda _{2}=sym \{S_{2}\cdot Q^{\mathrm{T}}R_{1}A_{L4}(t)\}+Q_{V22}, ``\star ''\) represents the term that is irrelevant to the subsequent proof. In view of (23) and Lemma 1, it follows that both \(A_{K4}(t)\) and \(A_{L4}(t)\) are non-singular, thereby completing the proof of the regularity and non-impulsiveness of the SMDs. Also, it follows that Q is non-singular. In the end, the asymptotic stability will be tested by virtue of the Lyapunov stability theory. By invoking (20) with \(v(t)=0\), one can have \({\dot{V}} (t)\le \eta ^{\mathrm{T}}(t){\varSigma }\eta (t)\), where \(\eta ^{\mathrm{T}}(t)=[x^{\mathrm{T}}(t)~e^{\mathrm{T}}(t)~x^{\mathrm{T}}(t-d(t))~e^{\mathrm{T}}(t-d(t))]\), and \({\varSigma }=\left[ \begin{array}{cccc} {\varSigma }_{1}&{} \quad {\varSigma }_{2}&{} \quad {\tilde{P}}^{\mathrm{T}}B_{G}A_{d}&{} \quad 0\\ *&{} \quad {\varSigma }_{3}&{} \quad -{\tilde{P}}^{\mathrm{T}}B_{d}&{} \quad {\tilde{P}}^{\mathrm{T}}A_{d}\\ *&{} \quad *&{} \quad -(1-\mu )Q_{1}&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -(1-\mu )Q_{2} \end{array}\right] +(\varepsilon _{1}+\varepsilon _{2})\left[ \begin{array}{cccc}N^{\mathrm{T}}\\ 0\\ N_{d}^{\mathrm{T}}\\ 0 \end{array}\right] [N~~0 ~~N_{d}~~0 ]\)  with

\({\varSigma }_{1}=sym \{{\tilde{P}}^\mathrm{T}(A+{\textit{BK}})\}+Q_{1}+\varepsilon _{1}^{-1}{\tilde{P}}^{\mathrm{T}}B_{G}MM^\mathrm{T}B_{G}^{\mathrm{T}}{\tilde{P}}, {\varSigma }_{2}=-{\tilde{P}}^{\mathrm{T}}({\textit{BK}}+B_{A})+({\tilde{P}}^{\mathrm{T}}{\textit{BK}})^{\mathrm{T}}, {\varSigma }_{3}=sym \{{\tilde{P}}^{\mathrm{T}}(A_{G}-{\textit{LC}}-{\textit{BK}})\}+Q_{2}+\varepsilon _{2}^{-1}{\tilde{P}}^{\mathrm{T}}B_{G}MM^{\mathrm{T}}B_{G}^{\mathrm{T}}{\tilde{P}}+{\tilde{P}}^{\mathrm{T}}{\tilde{P}}+\delta ^{2}C^{\mathrm{T}}C\).

Notice that (12) also results in \({\varSigma }<0\), and \({\dot{V}}(t)<0 \) (for all \(\eta (t)\ne 0\)), which indicates the SMDs are asymptotically stable by Definition 1. Thus, T 1 is satisfied, thereby completing the proof.\(\square \)

Remark 4

The admissible criterion of the SMDs is provided by Theorem 1; however, the formulation is not a linear program. It contains the matrix equality constraint in (11), which may be a trouble in numerical computation. And the matrix P is not explicitly expressed in Theorem 1, which may also result in some difficulty for the selection of V(t) due to the unsolved P. Further, it may even lead to the resultant parameters such as the gains K and L to be inaccurate. To this end, the following is focused on solving the feasibility of the problem in terms of a strict LMI.

Theorem 2

Given a scalar \(\gamma >0\), the SMDs (9) are admissible with \(H_{\infty }\) disturbance attenuation level \(\gamma \), if there exist positive definite matrices \(P, Q_{1}, Q_{2}\), a non-singular matrix Q, matrices X, Y, U and V, and scalars \(\varepsilon _{i}\) (\(i=1, 2\)) such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{cccccccc} {\varPi }_{1}&{} \quad {\varPi }_{2}&{} \quad {\varPi }_{4}&{} \quad 0&{} \quad {\varPi }_{8}&{} \quad {\varPi }_{10}&{} \quad 0&{} \quad 0\\ *&{} \quad {\varPi }_{3}&{} \quad {\varPi }_{5}&{} \quad {\varPi }_{7}&{} \quad {\varPi }_{9}&{} \quad 0&{} \quad {\varPi }_{11}&{} \quad {\varPi }_{12}\\ *&{} \quad *&{} \quad {\varPi }_{6}&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -(1-\mu )Q_{2}&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\gamma ^{2}I&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\varepsilon _{1}I&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\varepsilon _{2}I&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad **&{} \quad -I \end{array}\right] <0, \end{aligned}$$
(24)

where \({\varPi }_{1}=sym \{(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)A+E^\mathrm{T}X+SY\}+Q_{1}+(\varepsilon _{1}+\varepsilon _{2})N^{\mathrm{T}}N, {\varPi }_{2}=-(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)B_{A}-(E^{\mathrm{T}}X+SY)+(E^\mathrm{T}X+SY)^{\mathrm{T}}, {\varPi }_{3}=sym \{(E^{\mathrm{T}}P+{\textit{SQ}}^\mathrm{T}R)A_{G}-(E^{\mathrm{T}}U+{\textit{SV}})C-(E^\mathrm{T}X+SY)\}+Q_{2}+(\delta ^{2}+1)C^{\mathrm{T}}C, {\varPi }_{4}=(E^\mathrm{T}P+{\textit{SQ}}^{\mathrm{T}}R)B_{G}A_{d}+(\varepsilon _{1}+\varepsilon _{2})N^\mathrm{T}N_{d}, {\varPi }_{5}=-(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)B_{d}, {\varPi }_{6}=-(1-\mu )Q_{2}+(\varepsilon _{1}+\varepsilon _{2})N_{d}^\mathrm{T}N_{d}, {\varPi }_{7}=(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)A_{d}, {\varPi }_{8}=(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)D_{B}, {\varPi }_{9}=(E^\mathrm{T}P+{\textit{SQ}}^{\mathrm{T}}R)D_{B}, {\varPi }_{10}=(E^{\mathrm{T}}P+{\textit{SQ}}^\mathrm{T}R)B_{G}M, {\varPi }_{11}=(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)B_{G}M, {\varPi }_{12}=E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R\) and \(R^{\mathrm{T}}, S\in {\mathscr {R}}^{n\times (n-r)}\) are any matrices with full column rank satisfying \({\textit{RE}}=0, {\textit{ES}}=0\). Moreover, the gain matrices L and K can be given by \(L=(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)^{-1}(E^{\mathrm{T}}U+{\textit{SV}})\) and \(K=B^{+}(E^{\mathrm{T}}P+{\textit{SQ}}^{\mathrm{T}}R)^{-1}(E^{\mathrm{T}}X+SY)\), respectively.

Proof

In view of Theorem 1, it follows \(\tilde{P}=PE+R^{\mathrm{T}}QS^{\mathrm{T}}\). Thus, (11) is obviously true. In other words, if there exist positive definite matrices \(P, Q_{1}\) and \(Q_{2}\), a non-singular matrix Q, scalars \(\varepsilon _{i}\) (\(i=1, 2\)) such that (12) can be satisfied, the SMDs will be admissible with \(H_{\infty }\) disturbance attenuation level \(\gamma \). Decompose E as \(E=E_{L}E_{R}^{\mathrm{T}}\) where \(E_{L}, E_{R}\in {\mathscr {R}}^{n\times r}\) are of full column rank. From another perspective, by Lemma 2, it follows that \(PE+R^{\mathrm{T}}QS^{\mathrm{T}}\) is non-singular, and its inverse can be represented by the form: \((PE+R^{\mathrm{T}}QS^{\mathrm{T}})^{-1}={\mathscr {P}}E^{\mathrm{T}}+S{\mathscr {Q}}R\) where \({\mathscr {P}}\in {\mathscr {R}}^{n\times n}\) is a symmetric matrix and \({\mathscr {Q}}\in {\mathscr {R}}^{(n-r)\times (n-r)}\) is a non-singular matrix. Define \(U=PL, V=Q^{\mathrm{T}}RL, X=P{\textit{BK}}\), and \(Y=Q^\mathrm{T}{\textit{RBK}}\), then by the Schur complement, (12) becomes (24), which is recognized as a strict LMI and can be solved by the MATLAB software. The proof is completed.\(\square \)

Remark 5

Now, a general algorithm which aims to solve the LMI (24) subject to the equality constraint \({\textit{GE}}={\textit{HC}}\) is presented. In brief, similar to the algorithm in [10], the following minimization problem is outlined to solve the undetermined parameters in Theorem 2 and the matrix H:

$$\begin{aligned} min ~ \sigma , ~~subject~to ~~\left[ \begin{array}{cc} -\sigma I&{} \quad ({\textit{GE}}-{\textit{HC}})^{\mathrm{T}}\\ *&{} \quad -I \end{array}\right] <0 ~~and ~~(24). \end{aligned}$$

It is seen that the design is converted into a minimization problem involving an LMI and linear objective which may be solved by applying the MATLAB software. If \(\sigma \) is equal to or tends to zero sufficiently small, the equality condition \({\textit{GE}}={\textit{HC}}\) can be ensured. The verbatim argument is omitted here for brevity.

3.4 Adaptive Reaching Motion Controller Synthesis

In this section, the synthesis of an adaptive SMC law is considered, by which the finite-time reachability of the sliding mode can be ensured.

Assumption 3

[33] Unknown scalar \(q>0\) can be found to satisfy the inequality:

$$\begin{aligned} \Vert x(t-d(t))\Vert \le q\Vert x(t)\Vert . \end{aligned}$$
(25)

Since the system states x(t) are not completely measurable, the estimation error e(t) may not be computable either, which is often the case in practical systems. However, with the relationships among x(t), y(t), e(t), and \(\hat{y}(t)\), we assume that there exist unknown scalars \(\upsilon _{i}>0 ~(i=1, 2, 3)\) satisfying \(\Vert x(t)\Vert \le \upsilon _{1}\Vert y(t)\Vert \) and \(\Vert e(t)\Vert \le \upsilon _{2}\Vert y(t)\Vert +\upsilon _{3}\Vert \hat{y}(t)\Vert \). At this point, unknown scalars \(l_{i}>0\) (\(i=1, 2\)) can be found such that the following estimation is satisfied based on the above discussions:

$$\begin{aligned} {\mathscr {S}}= & {} \Vert {\textit{GA}}\Vert \Vert e(t)\Vert +\Vert {\textit{GA}}_{d}\Vert \Vert x(t-d(t))\Vert +\Vert G\Delta A(t)\Vert \Vert x(t)\Vert \nonumber \\&+\,\Vert G\Delta A_{d}(t)\Vert \Vert x(t-d(t))\Vert +\Vert {\textit{GB}}\Vert \Vert f(t,x)\Vert \nonumber \\\le & {} l_{1}\Vert y(t)\Vert +l_{2}\Vert \hat{y}(t)\Vert , ~t\ge 0 \end{aligned}$$
(26)

where \(l_{1}\) and \(l_{2}\) are unknown positive constants to be estimated.

Notice that the estimation bounds \(l_{1}\) and \(l_{2}\) are not accessible in practical design. Let \(\hat{l}_{i}(t)\) be the estimates of \(l_{i}\) with the errors being \(\tilde{l}_{i}(t)=\hat{l}_{i}(t)-l_{i}\) (\(i=1, 2\)). In the position, an adaptive sliding mode controller is constructed as

$$\begin{aligned} \begin{aligned} u(t)=&K\hat{x}(t)-({\textit{GB}})^{-1}[\hat{l}_{1}(t)\Vert y(t)\Vert +\hat{l}_{2}(t)\Vert \hat{y}(t)\Vert \\ {}&+\Vert GD\Vert \Vert v(t)\Vert +\rho ]sgn(s(t))\end{aligned} \end{aligned}$$
(27)

with the associated updating laws designed by

$$\begin{aligned} \dot{\hat{l}}_{1}(t)=c_{1}\Vert y(t)\Vert \Vert s(t)\Vert ~~ and ~~~\dot{\hat{l}}_{2}(t)=c_{2}\Vert \hat{y}(t)\Vert \Vert s(t)\Vert , \end{aligned}$$

where \(c_{i}>0~(i=1,2)\) are constants as the adaptive gains chosen by the designer, and \(\rho >0\) is a small scalar.

Theorem 3

With the gain matrix K obtained in Theorem 2 and the integral sliding surface function designed by (5), the finite-time reachability of the expected sliding mode can be guaranteed, if the controller (27) is applied.

Proof

Select a Lyapunov function

$$\begin{aligned} \hat{V}(t)=0.5\left[ s^{\mathrm{T}}(t)s(t)+c_{1}^{-1}\tilde{l}_{1}^{2}(t)+c_{2}^{-1}{\tilde{l}}_{2}^{2}(t)\right] . \end{aligned}$$
(28)

Differentiating \(\hat{V}(t)\) with respect to t yields

$$\begin{aligned} \dot{\hat{V}}(t)= & {} s^{\mathrm{T}}(t){\dot{s}}(t)+c_{1}^{-1}{\tilde{l}}_{1}(t)\dot{{\tilde{l}}}_{1}(t)+c_{2}^{-1}{\tilde{l}}_{2}(t)\dot{{\tilde{l}}}_{2}(t)\nonumber \\= & {} s^{\mathrm{T}}(t)\{{\textit{GAe}}(t)+{\textit{GA}}_{d}x(t-d(t))+G[\Delta A(t)x(t)\nonumber \\&+\,\Delta A_{d}(t)x(t-d(t))]+{\textit{GB}}[u(t)+f(t,x)]+GDv(t)\nonumber \\&-\,{\textit{GBK}}\hat{x}(t)\}+c_{1}^{-1}{\tilde{l}}_{1}(t)\dot{\tilde{l}}_{1}(t)+c_{2}^{-1}{\tilde{l}}_{2}(t)\dot{{\tilde{l}}}_{2}(t). \end{aligned}$$
(29)

Taking (26) and (27) into consideration, (29) becomes

$$\begin{aligned} \dot{\hat{V}}(t)= & {} s^{\mathrm{T}}(t)\{{\textit{GAe}}(t)+{\textit{GA}}_{d}x(t-d(t))+G[\Delta A(t)x(t)\nonumber \\&+\,\Delta A_{d}(t) x(t- d(t))+Dv(t)]-[\hat{l}_{1}(t)\Vert y(t)\Vert \nonumber \\&+\,\hat{l}_{2}(t)\Vert \hat{y}(t)\Vert +\Vert GD\Vert \Vert v(t)\Vert +\rho ]sgn(s(t))\nonumber \\&+\,{\textit{GBf}}(t,x)\}+c_{1}^{-1}{\tilde{l}}_{1}(t)\dot{{\tilde{l}}}_{1}(t)+c_{2}^{-1}{\tilde{l}}_{2}(t)\dot{{\tilde{l}}}_{2}(t)\nonumber \\\le & {} \Vert s(t)\Vert \{\Vert {\textit{GA}}\Vert \Vert e(t)\Vert +\Vert {\textit{GA}}_{d}\Vert \Vert x(t-d(t))\Vert \nonumber \\&+\,\Vert G\Delta A(t)\Vert \Vert x(t)\Vert +\Vert G\Delta A_{d}(t)\Vert \Vert x(t-d(t))\Vert \nonumber \\&+\,\Vert GD\Vert \Vert v(t)\Vert +\Vert {\textit{GB}}\Vert \Vert f(t,x)\Vert \}-[\hat{l}_{1}(t)\Vert y(t)\Vert \nonumber \\&+\,\hat{l}_{2}(t)\Vert \hat{y}(t)\Vert +\Vert GD\Vert \Vert v(t)\Vert +\rho ]s^{\mathrm{T}}(t)sgn(s(t))\nonumber \\&+\,c_{1}^{-1}{\tilde{l}}_{1}(t)\dot{{\tilde{l}}}_{1}(t)+c_{2}^{-1}{\tilde{l}}_{2}(t)\dot{{\tilde{l}}}_{2}(t)\\\le & {} \Vert s(t)\Vert [l_{1}\Vert y(t)\Vert +l_{2}\Vert \hat{y}(t)\Vert ]-\Vert s(t)\Vert [\hat{l}_{1}(t)\Vert y(t)\Vert \nonumber \\&+\,\hat{l}_{2}(t)\Vert \hat{y}(t)\Vert +\rho ]+c_{1}^{-1}\tilde{l}_{1}(t)\dot{{\tilde{l}}}_{1}(t)+c_{2}^{-1}\tilde{l}_{2}(t)\dot{{\tilde{l}}}_{2}(t). \end{aligned}$$

Substituting the designed adaptive laws results in

$$\begin{aligned} \dot{\hat{V}}(t)\le -\rho \Vert s(t)\Vert <0,~~~{if} ~~s(t)\ne 0. \end{aligned}$$

Notice that \(\dot{\hat{l}}_{i}(t)=\dot{{\tilde{l}}}_{i}(t)>0\), it indicates that there exist an instant \(T^{*}\) such that \(\tilde{l}_{i}(t)>0\) for \(t>T^{*}\). Thus, one has \(c_{i}^{-1}\tilde{l}_{i}(t)\dot{{\tilde{l}}}_{i}(t)>0\) for \(t>T^{*}\). It follows that \(s^{\mathrm{T}}(t){\dot{s}}(t)<0\) for \(t>T^{*}\). Hence, the reaching condition of the sliding mode can be satisfied. Furthermore, with the fact \(s(0)=0\), it follows the closed-loop systems can be kept on the predesigned sliding surface in finite-time since the initial moment, thereby completing the proof.\(\square \)

Remark 6

It should be mentioned that the external disturbance v(t) may be unknown and bounded by \(\Vert v(t)\Vert \le \kappa \), where \(\kappa >0\) is unknown. Then, the following steps are provided to deal with such case.

  1. (i)

    The estimation as follows can be ensured for unknown scalars \(l_{i}>0\) (\(i=1, 2, 3\)) that

    $$\begin{aligned} {\mathscr {X}}= & {} \Vert {\textit{GA}}\Vert \Vert e(t)\Vert +\Vert {\textit{GA}}_{d}\Vert \Vert x(t-d(t))\Vert +\Vert G\Delta A(t)\Vert \Vert x(t)\Vert \nonumber \\&+\,\Vert G\Delta A_{d}(t)\Vert \Vert x(t-d(t))\Vert +\Vert GD\Vert \Vert v(t)\Vert +\Vert {\textit{GB}}\Vert \Vert f(t,x)\Vert \nonumber \\\le & {} l_{1}\Vert y(t)\Vert +l_{2}\Vert \hat{y}(t)\Vert +l_{3}, ~t\ge 0 \end{aligned}$$

    with the estimation \(\hat{l}_{3}(t)\) of \(l_{3}\) and its error being \({\tilde{l}}_{3}(t)=\hat{l}_{3}(t)-l_{3}\), and the updating law is designed as \(\hat{l}_{3}(t)=c_{3}\Vert s(t)\Vert \);

  2. (ii)

    The adaptive controller can be synthesized as the following form

    $$\begin{aligned}\qquad u(t)= & {} K\hat{x}(t)-({\textit{GB}})^{-1}[\hat{l}_{1}(t)\Vert y(t)\Vert +\hat{l}_{2}(t)\Vert \hat{y}(t)\Vert \\&+\,\hat{l}_{3}(t)+\rho ]sgn(s(t)). \end{aligned}$$

    The concern is similar with the earlier discussion.

Remark 7

A novel adaptive controller is presented for the STS, which does not depend on the information of the delayed states, while the design in [6] is absolutely a memory controller. And the unknown bounds \(l_{i}\) \((i=1,2,3)\) could be well tracked, respectively, which further ensures the desirable performance.

Remark 8

It is worth noting that the SMO strategy has been widely applied into many practical aspects, e.g., power converters [14, 16] and PEM fuel cell air-feed system [15]. In this work, a novel SMO design scheme is presented for the STS, which may be regarded as a meaningful expansion of the SMO approach for singular systems. To this end, the design can be easily extended onto normal state-space systems (or with time delay) as well. As such, the proposed approach may be anticipated and challenging in future applications.

4 Illustrative Example

In this section, a numerical example is presented to demonstrate the potential and superiority of the developed scheme with comparisons.

Example 1

Let us consider the STS given by [12] with the data as follows:

$$\begin{aligned} E= & {} \left[ \begin{array}{cc} 1&{}\quad 0\\ 0&{}\quad 0 \end{array}\right] , A=\left[ \begin{array}{cc} 0.5&{}\quad 1\\ 0&{}\quad -1 \end{array}\right] , A_{d}=\left[ \begin{array}{cc} 0.5&{}\quad 0\\ -1&{}\quad 0.5 \end{array}\right] , B=\left[ \begin{array}{cc} 1\\ 1 \end{array}\right] , \\ D= & {} \left[ \begin{array}{cc} 0.2\\ 0.3 \end{array}\right] , \Delta L(t)=\left[ \begin{array}{cc} 0.1\\ 0.1 \end{array}\right] sint\cdot 0.1, M=N=N_{d}=0, \end{aligned}$$

Select \(C=[1~0], S=[0~1]^{\mathrm{T}}, R=S^{\mathrm{T}}, v(t)=e^{-0.1t}sin(2t/3), \delta =0.025\) , and \(G=[1~1]\) so that H is easily obtained as \(H=1\). As is pointed out in [12], given scalar \(\gamma =1.0\) and the derivative of the time-varying delay \(\mu =0.3\), by solving the LMI (24), the associated gain matrices are computed by

$$\begin{aligned} L=\left[ \begin{array}{cc} 10.9951&0.2588 \end{array}\right] ^{\mathrm{T}}, K=\left[ \begin{array}{cc} -2.6730&0.1964 \end{array}\right] .\end{aligned}$$

Also, as discussed in [12], when considering the system with a constant time delay \(d=0.36\) (i.e., \(\mu =0\)), in like manner, one can get

$$\begin{aligned} L=\left[ 7.6855\,0.5731 \right] ^{\mathrm{T}}, K=\left[ -1.7329 \,0.0382 \right] .\end{aligned}$$

Therefore, the developed sliding surface function and adaptive SMC law are given by

$$\begin{aligned} s(t)= & {} y(t)-\hat{y}(t)-[y(0)-\hat{y}(0)]+\left[ 1\quad 0 \right] [\hat{x}(t)-\hat{x}(0)]\\&-\,\int _{0}^{t}\left[ -2.9659\,0.0765 \right] \hat{x}(\theta )\mathrm{d}\theta . \end{aligned}$$

and

$$\begin{aligned} u(t)= & {} \left[ -1.7329\quad 0.0382\right] {\hat{x}}(t) -0.5[{\hat{l}}_{1}(t)\Vert y(t)\Vert +{\hat{l}}_{2}(t)\Vert {\hat{y}}(t)\Vert \\&+\,0.5\Vert v(t)\Vert +1.6]sgn(s(t)), \end{aligned}$$

with the estimation \(\hat{l}_{1}(t)\) and \(\hat{l}_{2}(t)\) designed by the updating laws given below:

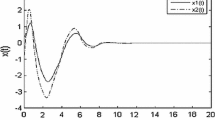
$$\begin{aligned} \dot{\hat{l}}_{1}(t)=2.5\Vert s(t)\Vert \Vert y(t)\Vert , ~\dot{\hat{l}}_{2}(t)=2.0\Vert s(t)\Vert \Vert \hat{y}(t)\Vert . \end{aligned}$$

Simulation results are provided in Figs. 1 and 2 under the initial conditions \(x(\theta )=[2.5~~2.6871]^{\mathrm{T}}\) and \(\hat{x}(\theta )=[-1.5~~2.2924]^{\mathrm{T}}, \theta \in [-0.36,~0]\). From the simulation, it can be seen that the state responses are faster than that of [12], see Figure 1 in [12] for detail, which also indicates the fast response of the SMO approach well.

Fig. 1
figure 1

Response of the system state without f(t, x)

Full size image
Fig. 2
figure 2

Response of the observer

Full size image
Fig. 3
figure 3

Response of the system state with f(t, x)

Full size image
Fig. 4
figure 4

Response of the observer

Full size image
Fig. 5
figure 5

Sliding variable

Full size image
Fig. 6
figure 6

Control input

Full size image
Fig. 7
figure 7

Adaptive estimations

Full size image
Fig. 8
figure 8

Response of the system state with f(t, x) in [13]

Full size image
Fig. 9
figure 9

Response of the observer state in [13]

Full size image

Furthermore, if the perturbation appears through the control channel, e.g., \(f(t,x)=[sin^{2}t+1.5 ~~ -cost-2]x(t)\), the correlated simulation results are shown in Figs. 3, 4, 5, 6, and 7 based on the proposed method; however, the result in [12] may be unable to cope with the complex case, which may further imply the superiority of our design. Among them, Figs. 3 and 4 show the responses of system state and the observer; the sliding surface function and adaptive controller are plotted in Figs. 5 and 6; Fig. 7 depicts the adaptive estimations.

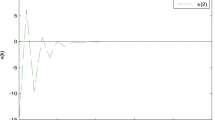
Besides the above discussions, we further make another comparison upon the basis of the stability analysis of the system between the method of Ref. [13] and our’s. By the stability result of the Theorem 3 in [13], we get matrix \({\tilde{K}}=\left[ 1.8488 \, 1.1736\right] \); thus, the controller gain matrix is obtained as \(K=\left[ 8.7287 \, 1.2312\right] \). In this way, the matrix \({\tilde{L}}\) in [13] can be given as \({\tilde{L}}=\left[ 85.2378\quad 24.2038 \right] ^{\mathrm{T}}\) so that the observer gain matrix is computed as \({L}=\left[ 1.6062\quad 0.7978 \right] ^{\mathrm{T}}\). However, it should be pointed out that the estimated state variable by [13] cannot be stabilized due to the perturbation f(t, x) through the control channel, and the system states diverge rapidly, so we reduce the simulation time to 5 s, rather than 15 s, see Figs. 8 and 9. Further, as is seen from Figs. 3 and 4, the evolutions of the system states can be desirable, despite the matched uncertainty, time delay, and external disturbance. Therefore, the SMO scheme performs better than the method by [13] under some complicated conditions in this paper.

5 Conclusions

The robust \(H_{\infty }\) control problem for a class of uncertain STS with unmeasured states has been investigated by a novel SMO scheme in this paper. A simple observer has been designed to estimate the unmeasured states, and a novel integral-type sliding surface has been developed. Moreover, the resultant SMDs to be admissible with \(H_{\infty }\) performance index have been ensured via a new LMI framework. Then, the sliding mode phase has been satisfied by utilizing a novel adaptive SMC law from the initial time. The validity and superiority of the proposed method have been verified via an illustrative example. This may provide a selectable method to study the singular systems in future research directions.