Observer-Based $H_\infty$ Sliding Mode Controller Design for Uncertain Stochastic Singular Time-Delay Systems

Abstract

The paper is concerned with the observer-based $H_\infty$ sliding mode controller design for a class of uncertain stochastic singular time-delay systems subjected to input nonlinearity. Using the sliding mode control, a robust law is established to guarantee the reachability of the sliding surface in a finite time interval, and the sufficient condition for asymptotic stability of the error system and sliding mode dynamics with disturbance attenuation level is presented in terms of linear matrix inequalities. Finally, an example illustrates the proposed method.

1 Introduction

Singular systems, also referred to as descriptor systems, generalized state-space systems, differential-algebraic systems or semi-state systems, are popular in describing the behaviors of some practical systems, such as economic systems, chemical process, circuit systems, electric systems, power systems, robotic systems, networked control systems, space navigation systems and biological systems [1, 4, 27, 30]. Wu et al. considered stochastic stability analysis for discrete-time singular Markov jump systems with time-varying delay and piecewise-constant transition probabilities [28]. Liu [13] solved the exponential robust stability and stabilization problems for uncertain time-varying delay singular systems. Kao et al. [8] have recently considered stabilization of singular Markovian jump systems with generally uncertain transition rates. Sliding mode control (SMC), due to its attractive features such as fast response and good transient response, insensitivity to variations in system parameters and external disturbances, has become an effective robust control approach for a wide variety of practical engineering systems such as robot manipulators, aircraft, underwater vehicles, spacecraft, flexible space structures, electrical motors, power systems and automotive engines [3, 20, 32]. Many results have been reported on sliding mode control for different kinds of control systems, including stochastic systems [2, 16–18], uncertain systems [10, 21, 23, 26, 29], time-delay systems [15, 17, 23, 25, 26, 31], Markovian jump systems [2, 9, 11, 16, 17, 24, 25] and singular systems [5–7, 12, 14, 22–25, 31]. Wu and Ho D.W.C [22] studied SMC of singular stochastic hybrid systems. Wu et al. [25] probed SMC with bounded $H_2$ gain performance of Markovian jump singular time-delay systems. Liu et al. [14] investigated dynamic soft variable structure control of singular systems.

As is known, input nonlinearity is often found in practice systems and can cause a serious degradation of the system performance. Then the effects of input nonlinearity must be taken into account when analyzing and implementing a SMC scheme [5, 10, 26, 31]. Yang et al. [31] considered SMC for Markovian switching singular systems with time-varying delays and nonlinear perturbations. Ding et al. [5] dealt with exponential stabilization using SMC for singular systems with time-varying delays and nonlinear perturbations. In practice, the state of the system is expensive to measure or even not available due to the factors of cost, technique, etc. State observation is an important problem for control systems. Moreover, time delays usually happen due to inevitable effects of control equipment, signal transmission and so on, which can degrade the performance of control systems designed and even destabilize the systems without considering the delays.

To the authors’ knowledge, the observer-based sliding mode control problem has attracted more and more attention (see [9, 10, 17, 19, 24, 26] and references therein). But there are few investigations on the observer-based $H_{\infty }$ sliding mode control for stochastic singular systems, especially with uncertainties and time delays. Wu et al. [26] investigated the observer-based sliding mode control problem for uncertain nonlinear neutral delay systems. The $H_{\infty }$ non-fragile observer-based sliding mode control for uncertain time-delay systems and It $\hat{o}$ stochastic systems with Markovian switching were considered in [9] and [10], respectively. But the above approaches proposed in the above papers are not workable for singular systems. On the other hand, the sliding mode control problem for singular time-delay systems were considered to guarantee the robust exponential stability and generalized quadratical stability in [5] and [23], respectively. Wu et al. [24] presented some good results about state estimation and sliding mode control of Markovian jump singular systems. And the sliding mode controllers were designed for Markovian jumping singular systems [31]. However, to the best of our knowledge, there is no report on observer-based $H_\infty$ sliding mode controller design for uncertain stochastic singular time-delay systems subjected to input nonlinearity, which is still challenging and of importance.

Motivated by the aforementioned reasons, the purpose of this paper lies in the development of observer-based $H_\infty$ sliding mode controller for uncertain stochastic singular time-delay systems with input nonlinearity. Our work is not a simple extension of [9] and [21]; the main difficulties come from the establishment of a novel switching function, which has a nonlinear differentiable sub-function and takes the singular matrix $E$ into account. And the control input is designed to guarantee that the estimated state can be driven to the sliding surface when the input nonlinearity is presented. Hence, we propose a more simple and convenient method to design the observer and controller gain matrix compared with the methods in [9, 10, 17, 26]. In Sect. 2, system description and definitions are presented. In Sect. 3, based on an $H_\infty$ non-fragile observer, a sliding mode control law is established to guarantee the reachability of the sliding surface in a finite time interval. The sufficient condition for the asymptotic stability of the overall closed-loop system with a disturbance attenuation level is derived via LMI. In Sect. 4, an example is provided to illustrate the validity of the proposed method. Section 5 is conclusion.

Notation In this paper, $L_{\mathbb {F}_{0}}^{P}([-\tau , 0];{\mathbf {R}}^{n})$ is the family of all $\mathbb {F}_{0}$-measurable $C([-\tau , 0];{\mathbf {R}}^{n})$-valued random variables $\xi =\{\xi (\theta ):-\tau \le \theta \le 0\}$ such that $\sup _{-\tau \le \theta \le 0}{\mathbb {E}}\{\Vert \xi (\theta )\Vert _{2}^{2}\}<\infty$, where ${\mathbb {E}}\{\cdot \}$ stands for the mathematical expectation operator with respect to the given probability measure $\mathbb {P}. {\mathbf {R}}^{n}$ and ${\mathbf {R}}^{n\times m}$ denote $n-$dimensional Euclidean space and the set of all $n\times m$ real matrices, respectively; $A^{T}$ denotes the transpose of matrix $A;I$ and $0$ represent the identity matrix and a zero matrix in appropriate dimension, respectively. $P>0 (P\ge 0)$ means that the matrix $P$ is a real symmetric and positive definite (semi-positive definite) matrix. $\Vert \cdot \Vert$ denotes the standard Euclidean norm of a vector or the induced norm of a matrix. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.

2 System Description and Definitions

Consider a class of uncertain time-delay systems subjected to input nonlinearity described by:

$$\begin{aligned} \left\{ \begin{aligned}&E{\mathrm {d}}x(t)=\,[(A+\varDelta \ A(t))x(t)+(A_{1}+\varDelta \ A_{1}(t))x(t-\tau )+B\phi (u) \\&\qquad \quad +f(x)+Gv(t)]{\mathrm {d}}t+g(x(t), t){\mathrm {d}}\beta (t), \\&y(t)=\,Cx(t)+Dx(t-\tau ), \\&x(t)=\,\phi (t), t\in [-\tau , 0], \\ \end{aligned} \right. \end{aligned}$$

(1)

where $x(t)\in {\mathbf {R}}^{n}$ is the state vector; $\phi (u)\in {\mathbf {R}}^{m}$ is the control input; $f(x)$ is the nonlinear disturbance input, $v(t)$ is the exogenous noise; $g(x(t), t)$ is the stochastic perturbations. $\beta (t)$ is the one-dimensional Brownian motion satisfying ${\mathbb {E}}\{{\mathrm {d}}\beta (t)\}=0$ and ${\mathbb {E}}\{{\mathrm {d}}\beta ^{2}(t)\}={\mathrm {d}}t. \phi (t)\in L_{\mathbb {F}_{0}}^{P}([-\tau ,0];~{\mathbf {R}}^{n})$ is a compatible vector-valued continuous function. $\tau$ denotes the time delay. Here, $E, A, A_{1}, B, G, C$ and $D$ are real constant matrices of appropriate dimensions. The ${\mathrm {rank}}E=r<n, \varDelta A(t)$ and $\varDelta A_{1}(t)$ are the uncertainties which are assumed to be the form of

$$\begin{aligned}{}[\varDelta \ A(t)), \varDelta \ A_{1}(t))]=MF(t)[S, S_{1}] \end{aligned}$$

(2)

where $M, S$ and $S_{1}$ are the real constant matrices and $F(t): {\mathbf {R}}\longmapsto {\mathbf {R}}^{k\times l}$ is the unknown time-varying matrix function satisfying

$$\begin{aligned} F^{T}(t)F(t)\le I. \end{aligned}$$

(3)

The following assumptions and lemmas are necessary for the sake of convenience. We will assume the followings to be valid.

Assumption 1

The nonlinear input $\phi (u)$ applied to the system satisfies the following property:

$$\begin{aligned} u^{T}\phi (u)\ge \alpha u^{T}u. \end{aligned}$$

(4)

where $\alpha$ is a nonzero positive constant, and $\phi (0)=0$.

Assumption 2

For $\forall x_{1}, x_{2}, f(x)$ satisfies

$$\begin{aligned} \parallel f(x_{1})-f(x_{2})\parallel \le \rho \parallel x_{1}-x_{2}\parallel . \end{aligned}$$

(5)

where $\rho$ is a positive constant.

Assumption 3

For $g(x(t), t)$ there is a constant matrix $H$ such that

$$\begin{aligned} {\mathrm {trace}}\left[ g^{T}(x(t), t)PEg(x(t), t)\right] \le \Vert Hx(t)\Vert ^{2} \end{aligned}$$

(6)

for all $t\ge 0$.

Assumption 4

The singular system (1) is regular and impulse-free.

Lemma 1

Let $Q=Q^{T}, S, R=R^{T}$ be matrices of appropriate dimensions, then $R<0, Q-SR^{-1}S^{T}<0$ is equivalent to

$$\begin{aligned} \left[ \begin{array}{cc} Q &{} S\\ S^{T} &{} R\\ \end{array}\right] <0 \end{aligned}$$

(7)

Lemma 2

Let $D, E$ and $F(t)$ be real matrices of appropriate dimensions with $F(t)$ satisfying $F^{T}(t)F(t)\le I$ and scalar $\varepsilon >0$, the following inequality

$$\begin{aligned} DF(t)E+E^{T}F^{T}(t)D^{T}\le \varepsilon DD^{T}+\frac{1}{\varepsilon }E^{T}E \end{aligned}$$

(8)

is always satisfied.

3 Sliding Mode Control

3.1 $H_\infty$ Non-Fragile Observer Design

First, the following non-fragile state observer is utilized to estimate the state of uncertain time-delay systems (1)

$$\begin{aligned} E\dot{\hat{x}}(t)=A\hat{x}(t)+A_{1}\hat{x}(t-\tau )+B\phi (u)+f(\hat{x})+(L+\varDelta L(t))(y(t)-C\hat{x}(t)), \end{aligned}$$

(9)

where $L\in {\mathbf {R}}^{n\times q}$ is the observer gain to be designed later and $\varDelta L(t)$ is a nonlinear function matrix satisfying $\parallel \varDelta L(t)\parallel \le \delta$, where $\delta$ is a positive constant.

Define the error $e(t)=x(t)-\hat{x}(t)$, then it follows from systems (1) and (12) that

$$\begin{aligned} \left\{ \begin{aligned} E{\mathrm {d}}e(t)=\,&\{[(A+\varDelta A(t))-(L+\varDelta L(t))C]e(t)+[(A_{1}+\varDelta A_{1}(t)) \\&-(L+\varDelta L(t))D]e(t-\tau )+\varDelta A(t)\hat{x}(t)+[\varDelta A_{1}(t) \\&-(L+\varDelta L(t))D]\hat{x}(t-\tau )+f(x)-f(\hat{x})+Gv(t)\}{\mathrm {d}}t \\&+g(x(t), t){\mathrm {d}}\beta (t), \\ y_{e}(t)=\,&Ce(t)+De(t-\tau )+D\hat{x}(t-\tau ). \\ \end{aligned}\right. \end{aligned}$$

(10)

Then, we introduce $H_{\infty }$ performance measure as follows:

$$\begin{aligned} J={\mathbb {E}}\left\{ \int _{0}^{\infty }[y_{e}^{T}(s)y_{e}(s)-\gamma ^{2}v^{T}(s)v(s)]{\mathrm {d}}t\right\} , \end{aligned}$$

Therefore, the problem is to determine the error $e(t)$ within the upper bound, i.e.,

$$\begin{aligned} {\mathbb {E}}\left\{ {\mathrm {sup}}_{v(t)\in L_{2}}\frac{\parallel y_{e}(t)\parallel _{2}}{\parallel v(t)\parallel _{2}}\right\} <\gamma . \end{aligned}$$

3.2 Switching Surface and Control Scheme Design

A novel switching function is chosen as

$$\begin{aligned} s(t)=\sigma (t)+B^{T}E\hat{x}(t), \end{aligned}$$

(11)

with

$$\begin{aligned} \dot{\sigma }(t)=B^{T}BK\hat{x}(t)-B^{T}A_{1}\hat{x}(t-\tau )-B^{T}f(\hat{x}), \end{aligned}$$

where the matrix $K$ is to be chosen later, obviously, $B^{T}B$ is non-singularity.

Remark 1

Notice that the switching surface function is designed with the singular matrix $E$, and the matrix $A_{1}$ and the nonlinear disturbance $f(x)$ are taken into account, which enable to avoid some difficulties caused by time delays and disturbances when deriving the following sliding mode dynamics.

Control input $\phi (u)$ in system (1) should be appropriately designed such that the estimated state in system (10) can be driven onto the sliding surface even when the input nonlinearity presented. The SMC law is derived as follows:

$$\begin{aligned} u(t)=-\frac{\varPsi (\hat{x})}{\alpha \Vert s(t)\Vert }s(t), \end{aligned}$$

(12)

where $\varPsi (\hat{x})=\beta +\Vert K\hat{x}(t)\Vert +\Vert (B^{T}B)^{-1}B^{T}A\hat{x}(t)\Vert +\Vert (B^{T}B)^{-1}B^{T}L(y-C\hat{x}(t))\Vert +\delta \Vert (B^{T}B)^{-1}B^{T}\Vert \cdot \Vert y-C\hat{x}(t)\Vert >0$, and $\beta$ is an arbitrarily positive scalar.

3.3 Reachability Analysis

This proposed control scheme above will drive the estimate state to approach the sliding mode surface $s(t)=0$ in a finite time interval, and it is stated in the following theorem.

Theorem 1

If the control input $u(t)$ is designed as (12), then the trajectories of the observer system (9) converges to the sliding surface $s(t)=0$ in a finite time interval.

Proof

From system (9) and Eq. (11), we have

$$\begin{aligned} \dot{s}(t)=B^{T}(BK+A)\hat{x}(t)+B^{T}B\phi (u)+B^{T}(L+\varDelta L(t))(y-C\hat{x}(t)). \end{aligned}$$

(13)

Let $V_{1}(t)=\frac{1}{2}s^{T}(t)(B^{T}B)^{-1}s(t)$, It follow from Eq. (13) that

$$\begin{aligned} \dot{V}_{1}(t)= & {} \,s^{T}(t)(B^{T}B)^{-1}\left[ B^{T}(BK+A)\hat{x}(t)+B^{T}B\phi (u)+B^{T}(L\right. \nonumber \\&\left. +\varDelta L(t))(y-C\hat{x}(t))\right] \nonumber \\= & {} \,s^{T}(t)\phi (u)+s^{T}(t)\left[ K\hat{x}(t)+(B^{T}B)^{-1}B^{T}A\hat{x}(t)+(B^{T}B)^{-1}B^{T}L(y \right. \nonumber \\&\left. -\,\, C\hat{x}(t))+(B^{T}B)^{-1}B^{T}\varDelta L(t)(y-C\hat{x}(t))\right] \nonumber \\\le & {} \, s^{T}(t)\phi (u)+\parallel s(t)\parallel (\parallel K\hat{x}(t)\parallel +\parallel (B^{T}B)^{-1}B^{T}A\hat{x}(t)\parallel \nonumber \\&+\parallel (B^{T}B)^{-1}B^{T}L(y-C\hat{x}(t))\parallel \nonumber \\&+\delta \parallel (B^{T}B)^{-1}B^{T}\parallel \cdot \parallel y-C\hat{x}(t) \parallel ). \end{aligned}$$

(14)

Using Eq. (12) and Assumption 1, we have $u^{T}\phi (u)=-\frac{\varPsi (\hat{x})}{\alpha \Vert s(t)\Vert }s^{T}(t)\phi (u)\ge \alpha u^{T}u$, then

$$\begin{aligned} s^{T}(t)\phi (u)\le -\varPsi (\hat{x})\Vert s(t)\Vert . \end{aligned}$$

(15)

Substituting (15) into (14) yields

$$\begin{aligned} \dot{V}_{1}(t)\le -\beta \parallel s(t)\parallel <0, \quad for \parallel s(t)\parallel \ne 0. \end{aligned}$$

(16)

From (16), we prove the trajectory of the observer system (9) can converge to the surface $s(t)=0$ in a finite time interval. The proof is completed. $\square$

From $\dot{s}(t)=0$, the following equivalent control law can be obtained as

$$\begin{aligned} \begin{aligned} \phi _{eq}(u)=&-K\hat{x}(t)-(B^{T}B)^{-1}B^{T}A\hat{x}(t)-(B^{T}B)^{-1}B^{T}(L \\&~+\varDelta L(t))(y-C\hat{x}(t)). \end{aligned} \end{aligned}$$

(17)

Substituting (17) into the observer system (9) and noting $\bar{B}=\,I-B(B^{T}B)^{-1}B^{T}$, the sliding mode dynamics in the state estimation space can be obtained as follows

$$\begin{aligned} \begin{aligned} E\dot{\hat{x}}(t)=\,&(\bar{B}A-BK)\hat{x}(t)+A_{1}\hat{x}(t-\tau )+\bar{B}(L+\varDelta L(t))[Ce(t) \\&+De(t-\tau )+D\hat{x}(t-\tau )]+f(\hat{x}). \end{aligned} \end{aligned}$$

(18)

Hence, the stability of the overall closed-loop system with (1) and (4) will be analyzed through the error system (10) and the sliding mode dynamics (18).

3.4 Analysis of Asymptotic Stability

In the following theorem, the sufficient condition for the asymptotic stability of the overall closed-loop system with a disturbance attenuation level is given via LMI.

Theorem 2

Consider that the systems (1) with (10) and (18). Given a scalar $\gamma >0$, the switching function is chosen as (11), and the SMC law is chosen as (12). If there exist matrices $L, K$, invertible matrices $P_{0}, Q_{0}$, symmetric positive definite matrices $Q_{1}>0, Q_{2}>0$, and scalars $\alpha >0, \beta >0, \varepsilon _{i}>0~(i=1,2), \delta >0$, such that the following conditions hold

$$\begin{aligned} \left\{ \begin{aligned}&Q_{0}EP_{0}=\mathrm {diag}\{I_{r},0\}, \\ \\&\varGamma = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varGamma _{11} &{} \varGamma _{12} &{}\; \frac{1}{2}H^{T}H+C^{T}L^{T}\bar{B}^{T}P^{T} &{} -PLD+C^{T}D &{} PG &{} N_{1}\\ *&{} \varGamma _{22} &{} D^{T}L^{T}\bar{B}^{T}P^{T} &{} D^{T}D &{} 0 &{} 0\\ *&{} *&{} \varGamma _{33} &{} \varGamma _{34} &{} 0 &{} N_{2}\\ *&{} *&{} *&{} \varGamma _{44} &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\gamma ^{2}I &{} 0\\ *&{} *&{} *&{} *&{} *&{} N_{3}\\ \end{array}\right] <0, \\ \end{aligned} \right. \end{aligned}$$

(19)

where

$$\begin{aligned} P= & {} P_{0}Q_{0},\\ \varGamma _{11}= & {} \, P(A-LC)+(A-LC)^{T}P^{T}+\frac{1}{\varepsilon _{1}}S^{T}S+(4\delta ^{2}+1)C^{T}C \\&+\,\rho ^{2}I+Q_{1}+\frac{1}{2}H^{T}H, \\ \varGamma _{12}= & {} \, \frac{1}{\varepsilon _{1}}S^{T}S_{1}+P(A_{1}-LD)+C^{T}D, \\ \varGamma _{22}= & {} \, \frac{1}{\varepsilon _{1}}S_{1}^{T}S_{1}+(2\delta ^{2}+1)D^{T}D-Q_{1}, \\ \varGamma _{33}= & {} \, P(\bar{B}A-BK)+(\bar{B}A-BK)^{T}P^{T}+\frac{1}{\varepsilon _{2}}S^{T}S+\frac{1}{2}H^{T}H+\rho ^{2}I+Q_{2}, \\ \varGamma _{34}= & {} \, \frac{1}{\varepsilon _{2}}S^{T}S_{1}+PA_{1}+P\bar{B}LD, \\ \varGamma _{44}= & {} \, \frac{1}{\varepsilon _{2}}S^{T}_{1}S_{1}+(2\delta ^{2}+1)D^{T}D-Q_{2}, \\ N_{1}= & {} \, [PM, ~~P, ~~0, ~~0], ~~~N_{2}=[0, ~~0, ~~P\bar{B}, ~~P], \\ N_{3}= & {} \, {\mathrm {diag}}\left\{ -\frac{1}{\varepsilon _{1}+\varepsilon _{2}}I,~-\frac{1}{4}I,~-\frac{1}{3}I,~-I\right\} .\\ \end{aligned}$$

the overall closed-loop system with (9) and (12) is asymptotically stable with disturbance attenuation level $\gamma$.

Proof

It is easy to know that there must exist two invertible matrices $P_{0}$ and $Q_{0}$ such that

$$\begin{aligned} Q_{0}EP_{0}={\mathrm {diag}}\{I_{r}, 0\}. \end{aligned}$$

Assume that $P=P_{0}Q_{0}$ satisfying $PE=P_{0}{\mathrm {diag}}[I_{r}, 0]P_{0}^{-1}\ge 0$. Thus, we could choose the following Lyapunov function candidate:

$$\begin{aligned} \begin{aligned} V_{2}(t)=\,&e^{T}(t)PEe(t)+\int _{t-\tau }^{t}e^{T}(s)Q_{1}e(s)ds+\hat{x}^{T}(t)PE\hat{x}(t) \\&+\int _{t-\tau }^{t}\hat{x}^{T}(s)Q_{2}\hat{x}(s)ds. \end{aligned} \end{aligned}$$

(20)

First, we consider the overall closed-loop system with $v(t)=0$, we have

$$\begin{aligned} {\mathcal {L}}V_{2}(t)= & {} \, 2e^{T}(t)P\{[(A+\varDelta A(t))-(L+\varDelta L(t))C]e(t)+[(A_{1}+\varDelta A_{1}(t)) \nonumber \\&-\,(L+\varDelta L(t))D]e(t-\tau )+\varDelta A(t)\hat{x}(t)+[\varDelta A_{1}(t)-(L\nonumber \\&+\,\varDelta L(t))D]\hat{x}(t-\tau )+f(x)-f(\hat{x})\}+e^{T}(t)Q_{1}e(t)\nonumber \\&-\,e^{T}(t-\tau )Q_{1}e(t-\tau )+\frac{1}{2}\mathrm {trace}\left\{ g^{T}(x(t), t)PEg(x(t), t)\right\} \nonumber \\&+\,2\hat{x}^{T}(t)P\{(\bar{B}A-BK)\hat{x}(t)+A_{1}\hat{x}(t-\tau ) +\bar{B}(L+\varDelta L(t))[Ce(t) \nonumber \\&+\,De(t-\tau )+D\hat{x}(t-\tau )]+f(\hat{x})\}+\hat{x}^{T}(t)Q_{2}\hat{x}(t) \nonumber \\&-\,\hat{x}^{T}(t-\tau )Q_{2}\hat{x}(t-\tau )\nonumber \\= & {} \, e^{T}(t)\left[ P(A-LC)+(A-LC)^{T}P^{T}\right] e(t)+2e^{T}(t)P(\varDelta A(t)e(t) \nonumber \\&+\,\varDelta A_{1}(t)e(t-\tau ))-2e^{T}(t)P\varDelta L(t)Ce(t)+2e^{T}(t)P(A_{1} \nonumber \\&-\,LD)e(t-\tau )-2e^{T}(t)P\varDelta L(t)De(t-\tau ) \nonumber \\&+\,2e^{T}(t)P(\varDelta A(t)\hat{x}(t)+\varDelta A_{1}(t)\hat{x}(t-\tau ))-2e^{T}(t)PLD\hat{x}(t-\tau )\nonumber \\&-\,2e^{T}(t)P\varDelta L(t)D\hat{x}(t-\tau )+2e^{T}(t)P(f(x)-f(\hat{x}))+e^{T}(t)Q_{1}e(t) \nonumber \\&-\,e^{T}(t-\tau )Q_{1}e(t-\tau )+\frac{1}{2}\mathrm {trace}\left\{ g^{T}(x(t), t)PEg(x(t), t)\right\} \nonumber \\&+\,\hat{x}^{T}(t)\left[ P(\bar{B}A-BK)+(\bar{B}A-BK)^{T}P^{T}\right] \hat{x}(t) \nonumber \\&+\,2\hat{x}^{T}(t)PA_{1}\hat{x}(t-\tau )+2\hat{x}^{T}(t)P\bar{B}L[Ce(t)+De(t-\tau ) \nonumber \\&+\,D\hat{x}(t-\tau )]+2\hat{x}^{T}(t)P\bar{B}\varDelta L(t)[Ce(t)+De(t-\tau )+D\hat{x}(t-\tau )] \nonumber \\&+\,2\hat{x}^{T}(t)Pf(\hat{x})+\hat{x}^{T}(t)Q_{2}\hat{x}(t) -\hat{x}^{T}(t-\tau )Q_{2}\hat{x}(t-\tau ). \end{aligned}$$

(21)

Using Assumption 2 and Lemmas  2–3, we have

$$\begin{aligned}&2e^{T}(t)P[\varDelta Ae(t)+\varDelta A_{1}e(t-\tau )]\le \varepsilon _{1}e^{T}(t)PMM^{T}P^{T}e(t)\nonumber \\&\quad +\frac{1}{\varepsilon _{1}}\left[ Se(t)+S_{1}e(t-\tau )\right] ^{T}[Se(t)+S_{1}e(t-\tau )], \end{aligned}$$

(22)

$$\begin{aligned}&-\!2e^{T}(t)P\varDelta L(t)Ce(t)\le 2\delta \parallel P^{T}e(t)\parallel \cdot \parallel Ce(t)\parallel \nonumber \\&\quad \le e^{T}(t)PP^{T}e(t)+\delta ^{2}e^{T}(t)C^{T}Ce(t),\end{aligned}$$

(23)

$$\begin{aligned}&-2e^{T}(t)P\varDelta L(t)De(t-\tau )\le e^{T}(t)PP^{T}e(t)+\delta ^{2}e^{T}(t-\tau )D^{T}De(t-\tau ),\end{aligned}$$

(24)

$$\begin{aligned}&2e^{T}(t)P(\varDelta A\hat{x}(t)+\varDelta A_{1}\hat{x}(t-\tau ))\le \varepsilon _{2}e^{T}(t)PMM^{T}P^{T}e(t)\nonumber \\&\quad +\frac{1}{\varepsilon _{2}}[S\hat{x}(t)+S_{1}\hat{x}(t-\tau )]^{T}[S\hat{x}(t)+S_{1}\hat{x}(t-\tau )], \end{aligned}$$

(25)

$$\begin{aligned}&-2e^{T}(t)P\varDelta L(t)D\hat{x}(t-\tau )\le e^{T}(t)PP^{T}e(t)+\delta ^{2}\hat{x}^{T}(t-\tau )D^{T}D\hat{x}(t-\tau ),\end{aligned}$$

(26)

$$\begin{aligned}&2e^{T}(t)P(f(x)-f(\hat{x}))\le 2\rho \Vert e^{T}(t)P\Vert \cdot \Vert e(t)\Vert \le e^{T}(t)PP^{T}e(t)+\rho ^{2}e^{T}(t)e(t),\end{aligned}$$

(27)

$$\begin{aligned}&2\hat{x}^{T}(t)P\bar{B} \varDelta L(t)Ce(t)\le \hat{x}^{T}(t)P\bar{B}\bar{B}^{T}P^{T}\hat{x}(t)+ \delta ^{2}e^{T}(t)C^{T}Ce(t),\end{aligned}$$

(28)

$$\begin{aligned}&2\hat{x}^{T}(t)P\bar{B}\varDelta L(t)De(t-\tau ) \le \hat{x}^{T}(t)P\bar{B}\bar{B}^{T}P^{T}\hat{x}(t)+\delta ^{2}e^{T}(t-\tau )D^{T}De(t-\tau ), \end{aligned}$$

(29)

$$\begin{aligned}&2\hat{x}^{T}(t)P\bar{B}\varDelta L(t)D\hat{x}(t-\tau ) \le \hat{x}^{T}(t)P\bar{B}\bar{B}^{T}P^{T}\hat{x}(t)+\delta ^{2}\hat{x}^{T}(t-\tau )D^{T}D\hat{x}(t-\tau ), \end{aligned}$$

(30)

$$\begin{aligned}&2\hat{x}^{T}(t)Pf(\hat{x})\le 2\rho \Vert \hat{x}^{T}(t)P\Vert \cdot \Vert \hat{x}(t)\Vert \le \hat{x}^{T}(t)PP^{T}\hat{x}(t)+\rho ^{2}\hat{x}^{T}(t)\hat{x}(t). \end{aligned}$$

(31)

In light of Assumption 3, it holds

$$\begin{aligned} \begin{aligned}&{\mathrm {trace}}\left[ g^{T}(x(t), t)PEg(x(t), t)\right] \le \Vert Hx(t)\Vert ^{2}=[e(t)+\hat{x}(t)]^{T}H^{T}H[e(t)+\hat{x}(t)].\\ \end{aligned} \end{aligned}$$

(32)

Now substituting (22)–(32) into (21), we result in

$$\begin{aligned} {\mathcal {L}}V_{2}(t)\le \omega ^{T}(t)\varXi \omega (t), \end{aligned}$$

where $\omega ^{T}(t)=[e^{T}(t), e^{T}(t-\tau ),\hat{x}^{T}(t),\hat{x}^{T}(t-\tau )]$, and

$$\begin{aligned} \begin{aligned} \varXi =\begin{bmatrix} {\begin{matrix} \varXi _{1} &{}\quad \frac{1}{\varepsilon _{1}}S^{T}S_{1}+P(A_{1}-LD) &{}\quad \frac{1}{2}H^{T}H+C^{T}L^{T}\bar{B}^{T}P^{T} &{}\quad -PLD\\ *&{}\quad \varXi _{2} &{}\quad D^{T}L^{T}\bar{B}^{T}P^{T} &{}\quad 0 \\ *&{}\quad *&{}\quad \varXi _{3} &{}\quad \frac{1}{\varepsilon _{2}}S^{T}S_{1}+PA_{1}+P\bar{B}LD\\ *&{}\quad *&{}\quad *&{}\quad \varXi _{4}\\ \end{matrix}} \end{bmatrix} \end{aligned} \end{aligned}$$

(33)

with

$$\begin{aligned} \begin{aligned} \varXi _{1}=&P(A-LC)+(A-LC)^{T}P^{T}+(\varepsilon _{1}+\varepsilon _{2})PMM^{T}P^{T} +\frac{1}{\varepsilon _{1}}S^{T}S \\&+4PP^{T}+2\delta ^{2}C^{T}C+\rho ^{2}I+Q_{1}+\frac{1}{2}H^{T}H, \\ \varXi _{2}=&\frac{1}{\varepsilon _{1}}S^{T}_{1}S_{1}+2\delta ^{2}D^{T}D-Q_{1}, \\ \varXi _{3}=&P(\bar{B}A-BK)+(\bar{B}A-BK)^{T}P^{T}+\frac{1}{\varepsilon _{2}}S^{T}S+\frac{1}{2}H^{T}H \\&+3P\bar{B}\bar{B}^{T}P^{T}+PP^{T} +\rho ^{2}I+Q_{2}, \\ \varXi _{4}=&\frac{1}{\varepsilon _{2}}S_{1}^{T}S_{1}+2\delta ^{2}D^{T}D-Q_{2}.\\ \end{aligned} \end{aligned}$$

It can be shown that if LMI (19) is satisfied, $\varXi <0$ holds by Lemma 1. Thus

$$\begin{aligned} {\mathcal {L}}V_{2}(t)\le \omega ^{T}(t)\varXi \omega (t)<0,\qquad \forall \quad \omega (t)\ne 0, \end{aligned}$$

which shows that the closed-loop system is asymptotically stable.

Then consider the following performance index

$$\begin{aligned} \begin{aligned} J(t)&=\int _{0}^{\infty }[y_{e}^{T}(s)y_{e}(s)-\gamma ^{2}v^{T}(s)v(s)]ds, \\&\le \int _{0}^{\infty }[y_{e}^{T}(s)y_{e}(s)-\gamma ^{2}v^{T}(s)v(s)+{\mathcal {L}}V_{2}(s)]ds\\&=\int _{0}^{\infty }q^{T}(s)\Pi q(s)ds\\ \end{aligned} \end{aligned}$$

(34)

where $q^{T}(t)=[e^{T}(t), e^{T}(t-\tau ), \hat{x}^{T}(t), \hat{x}^{T}(t-\tau ), v(t)]$, and

$$\begin{aligned} \begin{array}{cccc} \Pi =\left[ \begin{array}{cccc} \varXi _{1}+C^{T}C &{}\quad \frac{1}{\varepsilon _{1}}S^{T}S_{1}+P(A_{1}-LD)+C^{T}D &{}\quad \frac{1}{2}H^{T}H+C^{T}L^{T}\bar{B}^{T}P^{T} \\ *&{}\quad \varXi _{2}+D^{T}D &{}\quad D^{T}L^{T}\bar{B}^{T}P^{T} \\ *&{}\quad *&{}\quad \varXi _{3} \\ *&{}\quad *&{}\quad *\\ *&{}\quad *&{}\quad *\end{array} \right. \\ \\ \left. \begin{array}{cccc} -PLD+C^{T}D &{}\quad PG \\ D^{T}D &{}\quad 0 \\ \frac{1}{\varepsilon _{2}}S^{T}S_{1}+PA_{1}+P\bar{B}LD &{}\quad 0 \\ \varXi _{4}+D^{T}D &{}\quad 0 \\ *&{}\quad -\gamma ^{2}I \end{array} \right] \end{array} \end{aligned}$$

(35)

By utilizing Lemma 1, it is obvious that $\Pi <0$ is equivalent to (19). This means that $J(t)<0~(\mathrm {for} ~\omega (t)\ne 0)$. And then it results in

$$\begin{aligned} {\mathbb {E}}\left\{ \sup \limits _{v(t)\in L_{2}}\frac{\Vert y_{e}(t)\Vert ^{2}}{\Vert v(t)\Vert ^{2}}\right\} <\gamma . \end{aligned}$$

So the overall closed-loop system (18) is asymptotically stable with disturbance attenuation $\gamma$. Then the proof is obtained. $\square$

Remark 2

Our results can be applied to the uncertain stochastic systems with time delays, when all the matrix $E$ in Theorem 1 and Theorem 2 are assumed to be the identity matrix $I$.

Remark 3

According to the above proposed approach, we derive that $P=P_{0}Q_{0}$ such that $Q_{0}EP_{0}={\mathrm {diag}}\{I_{r},0\}$, and then $\varGamma <0$ in (19) is a linear matrix inequality with the matrix variables $L, K, Q_{1}>0$ and $Q_{2}>0$, which could be solved by MATLAB Toolbox. Therefore, when solving the LMI (19), we could also give the design of the observer gain matrix $L$ and the controller gain matrix $K$, which is more simple and convenient than the methods in [9, 10, 17, 26]. From Theorem 1, we conclude that our proposed method is more convenient and less conservative.

4 Numerical Examples

In this section, a numerical example demonstrates the effectiveness of the method mentioned above. Consider the system in the form of (1) with parameters as follows:

$$\begin{aligned} \begin{aligned}&E=\begin{bmatrix}-0.18&\quad 0.36&\quad 0.6\\ -0.06&\quad 0&\quad 0.2\\ 0.09&\quad -0.18&\quad -0.3\end{bmatrix}, ~ A=\begin{bmatrix}-12.5&\quad -3.2&\quad 2.1\\ 9&\quad 1&\quad -1.5\\ 0.5&\quad -9&\quad 16\end{bmatrix}, \\&A1=\begin{bmatrix}-2.4&\quad 1&\quad 0\\ 0&\quad 1.2&\quad -1\\ -0.56&\quad -3&\quad 6\end{bmatrix}, ~ B=\begin{bmatrix}21 \\ 3 \\ 25\end{bmatrix}, ~ G=\begin{bmatrix}10 \\ 2 \\ 16\end{bmatrix}, \\&C=\begin{bmatrix}2&\quad -1&\quad 0\\ -1&\quad 5&\quad 0.75\end{bmatrix}, ~ D=\begin{bmatrix}-4&\quad -3&\quad 0 \\ -5&\quad 9&\quad -1\end{bmatrix}. \\ \end{aligned} \end{aligned}$$

Let the initial value be $x(t)=\phi (t)=[-1.5,1,0.5]^{T}$ for any $t\in [-0.8,0]$ and the exogenous noise be $v(t)=1/(e^{t}+50)$. Assume the uncertain parameter matrix function $F(t)=0.5\, e^{-t}$ and the constant matrices:

$$\begin{aligned} \begin{aligned}&M=\begin{bmatrix}5&\quad -2&\quad 1\\ 1&\quad 0.5&\quad 0\\ 1&\quad -2&\quad 0.6\end{bmatrix}, ~ S=\begin{bmatrix}0&\quad 0&\quad 0.1 \\ 0&\quad 0.5&\quad 0.5 \\ 1&\quad 1&\quad 1\end{bmatrix}, ~ S1=\begin{bmatrix}-1&\quad 0.2&\quad 0 \\ 0&\quad 2&\quad 0.1 \\ 0.5&\quad 0&\quad 5\end{bmatrix}. \end{aligned} \end{aligned}$$

And $f(x)=0.75\, \mathrm {sin}(x(t)), ~\rho =0.75$ in Assumption 2 and $H=\begin{bmatrix}1.5&\quad 0&\quad 1.2\\ -3&\quad 1.6&\quad -1.8\end{bmatrix}$ in Assumption 3.

Firstly, we know there exist two invertible matrices $Q_{0}=\begin{bmatrix}\frac{25}{9}&\quad -\frac{25}{3}&\quad 0 \\ 0&\quad -\frac{50}{3}&\quad 0 \\ \frac{1}{2}&\quad 0&\quad 1\end{bmatrix}$ and $P_{0}=\begin{bmatrix}0&\quad 1&\quad \frac{10}{3} \\ 1&\quad 0&\quad 0 \\ 0&\quad 0&\quad 1\end{bmatrix}$ such that $Q_{0}EP_{0}=\begin{bmatrix}1&\quad 0&\quad 0 \\ 0&\quad 1&\quad 0 \\ 0&\quad 0&\quad 0\end{bmatrix}$. So we can take

$$\begin{aligned} P=P_{0}Q_{0}=\begin{bmatrix}1.6667&\quad -16.6667&\quad 3.3333 \\ 2.7778&\quad -8.3333&\quad 0 \\ 0.5000&\quad 0&\quad 1.0000\end{bmatrix}. \end{aligned}$$

Then, we set the scalars $\alpha =2, \beta =5, \gamma =0.24, \varepsilon _{1}=0.15, \varepsilon _{2}=0.2, \delta =0.36$ and $\varDelta L(t)=\begin{bmatrix}0.6&\quad 0 \\ 0&\quad 0.6 \\ 0&\quad 0\end{bmatrix}$. Now we can obtain the matrices by LMI (19) in the Theorem 2 and MATLAB as follows:

$$\begin{aligned} \begin{aligned}&L=\begin{bmatrix}-2.6405&\quad 0.6929\\ -0.6626&\quad -0.0290\\ 2.9673&\quad -0.2930\end{bmatrix}, ~ K=10^{5}\times \begin{bmatrix} 1.2877&0.6281&0.6690 \end{bmatrix}, \\&Q_{1}=\begin{bmatrix}296.9642&\quad 77.5053&\quad -52.9202 \\ 77.5053&\quad 129.0531&\quad -35.2497 \\ -52.9202&\quad -35.2497&\quad 89.4454\end{bmatrix}, ~ Q_{2}=10^{6}\times \begin{bmatrix}7.1513&\quad 3.4884&\quad 3.7151 \\ 3.4884&\quad 1.7018&\quad 1.8123 \\ 3.7151&\quad 1.8123&\quad 1.9302\end{bmatrix}. \end{aligned} \end{aligned}$$

Therefore, we can design the non-fragile state observer as (9) and the overall closed-loop system with (9) and (12) is asymptotically stable with disturbance attenuation level $\gamma =0.24$, where the switching function as (11) is

$$\begin{aligned} \begin{aligned} s(t)=&\begin{bmatrix}-1.7100&3.0600&5.700\end{bmatrix}\hat{x}(t)-\int _{0}^{t}\begin{bmatrix}21&3&25\end{bmatrix}f(\hat{x}){\mathrm {d}}t\\&+\int _{0}^{t}10^{8}\times \begin{bmatrix}1.3843&6.7521&7.1918\end{bmatrix}\hat{x}(s) \\&-\begin{bmatrix}-64.4000&-50.4000&147.0000\end{bmatrix}\hat{x}(s-\tau ){\mathrm {d}}s, \end{aligned} \end{aligned}$$

and the SMC law as (12) is $u(t)=-\frac{\varPsi (\hat{x})}{2\Vert s(t)\Vert }s(t)$ and

$$\begin{aligned} \begin{aligned} \varPsi (\hat{x})=\,&5+\Vert 10^{5}\times \begin{bmatrix} 1.2877&0.6281&0.6690 \end{bmatrix}\hat{x}(t)\Vert \\&+\Vert \begin{bmatrix}-0.2074&-0.2690&0.4089\end{bmatrix}\hat{x}(t)\Vert \\&+\Vert \begin{bmatrix}0.0156&0.0066\end{bmatrix}\left( y-\begin{bmatrix}2&-1&0\\ -1&5&0.75\end{bmatrix}\hat{x}(t)\right) \Vert \\&+0.36\Vert \begin{bmatrix}0.0195&0.0028&0.0233\end{bmatrix}\Vert \cdot \Vert y-\begin{bmatrix}2&-1&0\\ -1&5&0.75\end{bmatrix}\hat{x}(t)\Vert . \end{aligned} \end{aligned}$$

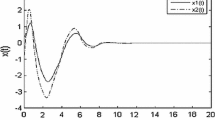
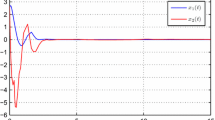
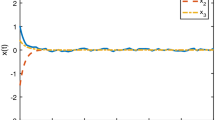
Figures 1, 2, 3 and 4 illustrate the simulation results. Figure 1 shows the trajectories of the system states $x_{1}, x_{2}, x_{3}$ and the estimated states $\hat{x}_{1}, \hat{x}_{2}, \hat{x}_{3}$. The responses of the error states $e_{1}, e_{2}, e_{3}$ are shown if Fig. 2. And the sliding mode switching function $s(t)$ is shown in Fig. 3 with the nonlinear control input $\phi (u)$ shown in Fig. 4.

Fig. 1

State trajectories of $x_{1}, \hat{x}_{1};x_{2}, \hat{x}_{2};x_{3}, \hat{x}_{3}$

Fig. 2

Trajectories of error states $e_{1}, e_{2}, e_{3}$

Fig. 3

Sliding mode switching function $s(t)$

Fig. 4

Nonlinear control input $\phi (u)$

5 Conclusions

The problem of non-fragile observer-based $H_\infty$ sliding mode control for singular system with time-varying delay and nonlinear perturbations has been addressed. Based on the sliding mode control strategy and LMI technique, some criteria on asymptotic stability of the error system and sliding mode dynamics with disturbance attenuation level are derived in terms of LMIs. Finally, a numerical example demonstrates the effectiveness of the method mentioned above. Moreover, we will consider the relate topics, such as stochastic singular time-varying delay systems, network-based framework, in the current and future work to achieve more industrial oriented results. Motivated by [3, 32], we also will utilize our simple and convenient approach to the practical models.