Mean-Square Exponential Stability and Stabilisation of Stochastic Singular Systems with Multiple Time-Varying Delays

Abstract

The stability and stabilisation problems for a series of continuous stochastic singular systems with multiple time-varying delays are studied in this paper. First, a useful lemma is proposed and a delay-distribution-dependent Lyapunov functional is constructed. Then, a novel delay-distribution-dependent condition is given to ensure the unforced stochastic singular systems to be regular and impulse-free. The mean-square exponential stability of the whole system is guaranteed under the proposed lemma. As a result, a suitable feedback controller is designed via strict linear matrix inequality such that the system’s stabilisation problem is guaranteed. Finally, numerical examples are illustrated to show the proposed result are less conservative than the existing ones and the potential of such technology.

1 Introduction

Singular systems, which are known as descriptor systems, implicit systems, differential algebraic systems or generalised state-space systems, have extensive applications in electrical circuits, power systems, economics and other areas [1, 5, 13]. In recent decades, many results have been reported on the control of singular systems, for example, the problem of state feedback $H_{\infty }$ control for discrete singular systems was investigated in [33] and it is not necessary to assume the system to be regular. Considering the relationship between slow and fast subsystems of the singular system, a novel bounded real lemma (BRL) was provided in [10], and robust $H_{\infty }$ performance was obtained on the basis of BRL. Furthermore, for discrete-time singular Markov jump systems with actuator saturation, the regularity, causality and bounded state stability of such systems was investigated in [19], and the $H_{\infty }$ controller was designed with singular value decomposition approach. A necessary and sufficient condition was proposed in [26] to ensure the sliding mode dynamics to be stochastic admissible. For nonlinear singular Itô stochastic systems with Markovian switching parameters, the sliding mode controller designing approach was introduced in [25].

On the other hand, time-delay frequently occurs in various practical systems such as chemical processes, biological systems and networked control system [3, 8, 17, 38]. The existence of time-delay may induce instability and poor performance. Therefore, many results have been established for singular systems with time-delay which can be classified into two types, delay-independent condition and delay-dependent condition (see [2, 6, 7, 12, 14–16, 18–20, 23, 24, 27, 30, 31, 34–37, 39, 40] and the references therein). Most of the research results have focused on delay-dependent conditions for the less conservatism. Such as, in [7], a delay-range-dependent condition for unforced singular systems with multiple time-varying delays was given to ensure the system to be regular, impulse-free and $\alpha$-stable, then, a method to estimate the system’s convergence rate was proposed. For time-delay singular system, a kind of delay-dependent BRL was established in [34], and the regularity, impulse-freeness and stability of the singular system with a prescribed $H_{\infty }$ performance was guaranteed. A kind of passivity-based sliding mode control approach was studied in [24] for a class of uncertain nonlinear singular time-delay systems. Based on the delay partitioning technique, a delay-dependent stochastic stability condition was derived in [30] for discrete-time singular Markov jump systems with time-varying delay and piecewise-constant transition probabilities. Reference [40] has considered the exponential $H_{\infty }$ filtering problem for discrete-time switched singular systems with time-varying delay. For stochastic system with multiple delay, [32] has dealt with the problem of robust exponential stability for a class of uncertain stochastic neural networks with multiple delays via multiple-difference-dependent Lyapunov–Krasovskii functional and free-weighting matrices method. Besides, in terms of Linear matrix inequality (LMI), the stability analysis of stochastic neural networks with multiple time-delays is given in [9].

To the author’s knowledge, the research on the stochastic singular system with multiple time-varying delays is rather limited, because the study of singular system with multiple time-varying delays is much more complicated than the singular system with single time-delay or without time-delay, it is due to the difficulty of guaranteeing the stability of the fast subsystem [11, 21, 37]. Therefore, the main purpose of this research is: (1) to propose a useful lemma which is used to guarantee the mean-square exponential stability of stochastic singular system; (2) to use the statistical distribution of each time-delays, so that a less conservative delay-distribution-dependent condition is given, which result in that the stochastic singular system is regular, impulse-free and mean-square exponential stable; (3) not to use free-weighting matrix to deal with cross-product term, and hence the produced method includes much fewer matrix variables than the existing one; (4) that the corresponding controller design approach is given to ensure the mean-square exponential stability of the closed-loop system. These four aspects form the novelty of the work given in this paper. Finally, three numerical examples are given to show the effectiveness of the proposed methods.

Notation: $\mathbb {R}^{n}$ and $\mathbb {R}^{m\times n}$ denote the $n$-dimensional Euclidean space and the set of all $m\times n$ real matrices, respectively. The notation $X>Y(X\geqslant Y)$ means that $X$ and $Y$ are symmetric matrices and $X-Y$ is positive definition (positive semi-definition). $I$ and $0$ represent the identical matrix and the zero matrix, respectively. The superscript “T” represents the transpose, and $\mathrm{diag}\{\ldots \}$ means the block-diagonal matrix. For an arbitrary matrix $B$ and two symmetric matrices $A$ and $C$

$$\begin{aligned} \left[ \begin{array}{ll}A &{}\quad B\\ * &{}\quad C\end{array}\right] \end{aligned}$$

denotes a symmetric matrix, where $*$ denotes the entries implied by symmetry. $\Vert \phi \Vert _{c}=\sup _{-\tau \leqslant t\leqslant 0}\Vert \phi (t)\Vert$.

2 Problem Formulation

Consider a class of continuous-time linear singular systems with multiple time-varying delays, which can be described as

$$\begin{aligned} \left\{ \begin{array}{l}E\dot{x}(t)=Ax(t)+\sum _{k=1}^{p}A_{k}x(t-d_{k}(t))+Bu(t) \\ x(t)=\phi (t),\quad -\max (\bar{d}_{k})\leqslant t \leqslant 0\end{array},\right. \end{aligned}$$

(1)

where $x(t)\in \mathbb {R}^{n}$ is the state vector, $u(t)\in \mathbb {R}^{m}$ is the control input, the matrix $E\in \mathbb {R}^{n\times n}$ may be singular and satisfying $\mathrm{rank}(E)=r\leqslant n$, $A$, $A_{k}$ and $B$ are known constant matrices, $\phi (t)\in C_{\tau }^{\upsilon }$ is a compatible vector valued continuous function which denotes the initial condition of $x(t)$, and $d_{k}(t),k=1,2,\ldots ,p$ is the time-varying delay satisfying

$$\begin{aligned} 0<\underline{d}_{k}\leqslant d_{k}(t) \leqslant \bar{d}_{k}, \quad \dot{d}_{k}(t)\leqslant \mu <1 , \end{aligned}$$

(2)

where $\mu$ is a given scalar, $\underline{d}_{k}$ and $\bar{d}_{k}$ are scalars representing the lower and the upper bound of the time-varying delay $d_{k}(t)$. The unforced system ($u(t)=0$) of (1) can be written as

$$\begin{aligned} E\dot{x}(t)=Ax(t)+\sum _{k=1}^{p}A_{k}x(t-d_{k}(t)). \end{aligned}$$

(3)

There exist scalars $\tau _{k}$ satisfying $\underline{d}_{k}\leqslant \tau _{k}\leqslant \bar{d}_{k}$, and denoting a series of variables $\delta _{k}(t)$ as

$$\begin{aligned} \delta _{k}(t)=\left\{ \begin{array}{ll} 1, &{}\quad d_{k}(t)\in [\underline{d}_{k},\tau _{k}]\\ 0, &{}\quad d_{k}(t)\in (\tau _{k},\bar{d}_{k}] \end{array}.\right. \end{aligned}$$

(4)

Define $\hat{d}_{k}(t)=\delta _{k}(t)d_{k}(t)$ and $\tilde{d}_{k}(t)=(1-\delta _{k})d_{k}(t)$, the unforced system (3) can be rewritten as the following stochastic unforced singular system with multiple time-varying delays:

$$\begin{aligned} E\dot{x}(t)=Ax(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)A_{k}x(t-\hat{d}_{k}(t))+(1-\delta _{k}(t))A_{k}x(t-\tilde{d}_{k}(t))\right] . \end{aligned}$$

(5)

Remark 1

In [4, 7], the derived stability criteria are dependent on the varying range of the time-varying delay. However, if some values of the delay are changed largely whereas the probabilities of the delay in such large range are very small, thus, the obtained results are much conservative in [4, 7] where only the information of delay variation range is considered. In this study, by employing the information of delay distributions [22], the corresponding result can be improved.

Throughout the paper, the following definition and lemma are made.

Definition 1

[7, 27]

• 1. System (5) is said to be regular if $\mathrm{det}(sE-A)$ is not identically zero.

• 2. System (5) is said to be impulse-free if $\mathrm{deg}(\mathrm{det}(sE-A))=\mathrm{rank}(E)$.

• 3. The stochastic singular system (5) is said to be mean-square exponentially stable, if there exist scalars $\alpha >0$ and $\beta >0$ such that, for any compatible initial condition $\phi (t), \, \mathbb {E}\{\Vert x(t)\Vert ^{2}\}\leqslant \beta \mathrm{e}^{-\alpha t}\Vert \phi \Vert _{c}^{2}, t>0$.

• 4. System (5) is said to be mean-square exponentially admissible if it is regular, impulse-free and mean-square exponentially stable.

Lemma 1

[29] For any given symmetric positive definite matrix $V\in \mathbb {R}^{n\times n}$, and scalars $\alpha >0$, $0\leqslant h_{1}<h_{2}$, if there exists a vector function $\dot{e}(\theta ):[-h_{2},0]\rightarrow \mathbb {R}^{n}$ such that the following integration is well defined, then

$$\begin{aligned} \gamma (t)&=-\int _{-h_{2}}^{-h_{1}}\dot{e}(t+\theta )^\mathrm{T}\mathrm{e}^{\alpha \theta }V\dot{e}(t+\theta )\mathrm{d}\theta \nonumber \\&\leqslant \frac{\alpha }{\mathrm{e}^{\alpha h_{1}}-\mathrm{e}^{\alpha h_{2}}}\left[ \begin{array}{cc} e(t-h_{1}) \\ e(t-h_{2})\end{array}\right] ^\mathrm{T}\left[ \begin{array}{cc} V &{} -V\\ -V &{} V \end{array}\right] \left[ \begin{array}{cc} e(t-h_{1})\\ e(t-h_{2})\end{array}\right] \end{aligned}$$

Remark 2

Lemma 1 is used to deal with cross-product terms, thus, the number of decision variables is less than the one with free-weight matrix technology to deal with cross-product terms.

3 Main Results

In this section, a useful lemma is first proposed and a novel delay-distribution-dependent condition to ensure the stochastic singular system (5) to be regular, impulse-free and mean-square exponentially stable is derived from this lemma.

Lemma 2

Suppose that a series of positive continuous functions $f_{k}(t),k=1,2,\ldots ,p$ satisfy

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\{f_{k}(t)\}&\leqslant \zeta _{1}\sum _{k=1}^{p}\left\{ \sup _{t-\bar{d}_{k}\leqslant s \leqslant t-\tau _{k}}f_{k}(s)\right\} \nonumber \\&+\,\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{t-\tau _{k}\leqslant s \leqslant t-\underline{d}_{k}} f_{k}(s)\right\} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\alpha t} \end{aligned}$$

where $\alpha >0, 0<2\zeta _{1}<1, \zeta _{2}>0, \beta >1, 0<2\zeta _{1}\mathrm{e}^{\delta \max \{\bar{d}_{k}\}}<1, 0<\delta <\min \{\alpha ,\min (\bar{d}_{k}^{-1})\ln {\tilde{\eta }}\}, \tilde{\eta }>1, \bar{d}_{k}>0$, then

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\{f_{k}(t)\} \leqslant \beta \mathrm{e}^{-\delta t}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s \leqslant 0}f_{k}(s)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta t}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}},\quad t\geqslant 0 . \end{aligned}$$

Proof

Similarly as Lemma 2 of [36], for $t\geqslant 0$, we have

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\{f_{k}(t)\}&\leqslant \zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{t-\bar{d}_{k}\leqslant s \leqslant t-\tau _{k}}f_{k}(s)\right\} \nonumber \\&+\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{t-\tau _{k}\leqslant s \leqslant t-\underline{d}_{k}}f_{k}(s)\right\} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\delta t}\nonumber \\&\leqslant 2\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{t-\bar{d}_{k}\leqslant s \leqslant t}f_{k}(s)\right\} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\delta t} \end{aligned}$$

(6)

If the following inequality holds,

$$\begin{aligned}&2\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{t-\bar{d}_{k}\leqslant s \leqslant t}f_{k}(s)\right\} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\delta t}\\&\quad \leqslant \beta \mathrm{e}^{-\delta t}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s \leqslant 0}f_{k}(s)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta t}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}} \end{aligned}$$

then, Lemma 2 can be obtained, and we will proof it by contradiction approach.

If the second inequality of Lemma 2 is true, there exists a scalar $\varepsilon _{0}>0$

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(t)\right\} <\beta \mathrm{e}^{-\delta t}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta t}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0}. \end{aligned}$$

(7)

Note that

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(0)\right\}&\leqslant 2\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(0)\right\} +\sum _{k=1}^{p}\zeta _{2}\nonumber \\&< \beta \sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(0)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0}. \end{aligned}$$

(8)

By using contradiction method, if Eq. (7) is not true, thus, there exists $\bar{t}$ such that

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(\bar{t})\right\} =\beta \mathrm{e}^{-\delta \bar{t}}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta \bar{t}}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0} \end{aligned}$$

(9)

and

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(t)\right\} <\beta \mathrm{e}^{-\delta t}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} +\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta t}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0}, \quad t<\bar{t}.\nonumber \\ \end{aligned}$$

(10)

For $t\in \left[ -\bar{d}_{k},0\right]$, we have the following results:

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(t)\right\}&\leqslant \sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s \leqslant 0}f_{k}(s)\right\} \nonumber \\&< \sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} \beta \mathrm{e}^{-\delta t}+\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta t}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0}.\quad \end{aligned}$$

(11)

Therefore, (10) holds for any $t\in \left[ -\bar{d}_{k},\bar{t}\right)$. However, from (6), (9), and (11), we can see that

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(\bar{t})\right\}&\leqslant 2\zeta _{1}\sum _{k=1}^{p}\left\{ \sup _{\bar{t}-\bar{d}_{k}\leqslant s \leqslant \bar{t}}f_{k}(s)\right\} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\delta \bar{t}}\nonumber \\&< 2\zeta _{1}\sum _{k=1}^{p}\mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} \beta \mathrm{e}^{-\delta \bar{t}}\nonumber \\&+\sum _{k=1}^{p}\frac{2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}\zeta _{2}\mathrm{e}^{-\delta \bar{t}}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+2\zeta _{1}\varepsilon _{0} +\sum _{k=1}^{p}\zeta _{2}\mathrm{e}^{-\delta \bar{t}}\nonumber \\&< \mathbb {E}\left\{ \sup _{-\bar{d}_{k}\leqslant s\leqslant 0}f_{k}(s)\right\} \beta \mathrm{e}^{-\delta \bar{t}}+\sum _{k=1}^{p}\frac{\zeta _{2}\mathrm{e}^{-\delta \bar{t}}}{1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}}+\varepsilon _{0}. \end{aligned}$$

(12)

Obviously, (12) contradicts (9) and Lemma 2 can be obtained with $\varepsilon _{0}\rightarrow 0$. The proof is completed.$\square$

Remark 3

Due to $\beta >1$, $0<2\zeta _{1}<1$ and $0<1-2\zeta _{1}\mathrm{e}^{\delta \max \{\bar{d}_{k}\}}<1$, it is not difficult to conclude that Eq. (8) always holds.

Remark 4

Equation (11) holds for $\beta >1$, $\mathrm{e}^{-\delta t}>1$, $\varepsilon _{0}>0$, $\zeta _{2}\mathrm{e}^{-\delta t}>0$ and $1-2\zeta _{1}\mathrm{e}^{\delta \bar{d}_{k}}>0$.

Next, we will considering the admissibility of system (5).

Theorem 1

Denoting $\mathbb {E}\{\delta _{k}(t)=1\}=\tilde{\delta }_{k}$, given positive scalars $\bar{d}_{k}$, $\underline{d}_{k}$ and $\tilde{\delta }_{k}$, $k=1,\ldots ,p$, $0\leqslant \mu <1$ and $\alpha >0$. System (5) is mean-square exponentially admissible if there exist a nonsingular matrix $P$, positive definite matrices $Q_{kv}$, $Z_{kw}$, $k=1,\ldots ,p$, $v=1,2,3,4,5$, $w=1,2,3,4$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varPi &{} \phi _{1,2} &{} \phi _{1,3} &{} \phi _{1,4} &{} \phi _{1,5}\\ * &{} \phi _{2,2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} \phi _{3,3} &{} 0 &{} 0\\ * &{} * &{} * &{} \phi _{4,4} &{} 0\\ * &{} * &{} * &{} * &{} \phi _{5,5}\end{array}\right] <0 \end{aligned}$$

(13)

with the constraint

$$\begin{aligned} E^\mathrm{T}P=P^\mathrm{T}E\geqslant 0, \end{aligned}$$

(14)

where

$$\begin{aligned} \varPi =&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varPi _{1} &{} P^\mathrm{T}\tilde{A}_{1} &{} P^\mathrm{T}\tilde{A}_{2} &{} 0 &{} \varXi _{1} &{} \varXi _{2}\\ * &{} U_{1} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} U_{2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} U_{3} &{} 0 &{} \varXi _{3}\\ * &{} * &{} * &{} * &{} U_{4} &{} \varXi _{4}\\ * &{} * &{} * &{} * &{} * &{} U_{5}\end{array}\right] \\ \end{aligned}$$

with elements defined as

$$\begin{aligned} \varPi _{1}&= A^\mathrm{T}P+P^\mathrm{T}A+\alpha E^\mathrm{T}P+\sum _{k=1}^{p}\left( Q_{k1}+Q_{k2}+Q_{k3}+\tilde{\delta }_{k}Q_{k4}+(1-\tilde{\delta }_{k})Q_{k5}\right. \\&\qquad \qquad \quad \qquad \qquad \qquad \qquad \qquad \qquad \left. +\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}E^\mathrm{T}Z_{k1}E+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}E^\mathrm{T}Z_{k2}E\right) \\ \tilde{A}_{1}&= \left[ \tilde{\delta }_{1}A_{1} \quad \tilde{\delta }_{2}A_{2} \quad \ldots \quad \tilde{\delta }_{p}A_{p}\right] ,\\ \tilde{A}_{2}&= \left[ (1-\tilde{\delta }_{1})A_{1} \quad (1-\tilde{\delta }_{2})A_{2} \quad \ldots \quad (1-\tilde{\delta }_{p})A_{p}\right] \\ \varXi _{1}&= \left[ -\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{1}}}E^\mathrm{T}Z_{11}E \quad \ldots \quad -\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{p}}}E^\mathrm{T}Z_{p1}E\right] ,\\ \varXi _{2}&= \left[ -\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{1}}}E^\mathrm{T}Z_{12}E \quad \ldots \quad -\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{p}}}E^\mathrm{T}Z_{p2}E\right] \\ \varXi _{3}&= \mathrm{diag}\left\{ -\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{1}}-\mathrm{e}^{\alpha \tau _{1}}}E^\mathrm{T}Z_{13}E,\ldots , -\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{p}}-\mathrm{e}^{\alpha \tau _{p}}}E^\mathrm{T}Z_{p3}E\right\} ,\\ \varXi _{4}&= \mathrm{diag}\left\{ -\frac{\alpha }{\mathrm{e}^{\alpha \tau _{1}}-\mathrm{e}^{\alpha \bar{d}_{1}}}E^\mathrm{T}Z_{14}E, \ldots , -\frac{\alpha }{\mathrm{e}^{\alpha \tau _{p}}-\mathrm{e}^{\alpha \bar{d}_{p}}}E^\mathrm{T}Z_{p4}E\right\} ,\\ U_{1}&= \mathrm{diag}\left\{ -\tilde{\delta }_{1}(1-\mu )\mathrm{e}^{-\alpha \tau _{1}}Q_{14},\ldots ,-\tilde{\delta }_{p}(1-\mu )\mathrm{e}^{-\alpha \tau _{p}}Q_{p4}\right\} ,\\ U_{2}&= \mathrm{diag}\left\{ -(1-\tilde{\delta }_{1})(1-\mu )\mathrm{e}^{-\alpha \bar{d}_{1}}Q_{15},\ldots ,-(1-\tilde{\delta }_{p})(1-\mu )\mathrm{e}^{-\alpha \bar{d}_{p}}Q_{p5}\right\} ,\\ U_{3}&= \mathrm{diag}\left\{ -\mathrm{e}^{-\alpha \underline{d}_{1}}Q_{11}+\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{1}}-\mathrm{e}^{\alpha \tau _{1}}}E^\mathrm{T}Z_{13}E, \ldots ,\right. \\&\left. -\mathrm{e}^{-\alpha \underline{d}_{p}}Q_{p1}+\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{p}}-\mathrm{e}^{\alpha \tau _{p}}}E^\mathrm{T}Z_{p3}E\right\} \\ U_{4}&= \mathrm{diag}\{-\mathrm{e}^{-\alpha \bar{d}_{1}}Q_{12}+\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{1}}}E^\mathrm{T}Z_{11}E+\frac{\alpha }{\mathrm{e}^{\alpha \tau _{1}}-\mathrm{e}^{\alpha \bar{d}_{1}}}E^\mathrm{T}Z_{14}E,\\&\quad \ldots , -\mathrm{e}^{-\alpha \bar{d}_{p}}Q_{p2}+\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{p}}}E^\mathrm{T}Z_{p1}E+\frac{\alpha }{\mathrm{e}^{\alpha \tau _{p}}-\mathrm{e}^{\alpha \bar{d}_{p}}}E^\mathrm{T}Z_{p4}E\}\\ U_{5}&= \mathrm{diag}\{-\mathrm{e}^{-\alpha \tau _{1}}Q_{13}+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{1}}}E^\mathrm{T}Z_{12}E+\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{1}}-\mathrm{e}^{\alpha \tau _{1}}}E^\mathrm{T}Z_{13}E\\&+\frac{\alpha }{\mathrm{e}^{\alpha \tau _{1}}-\mathrm{e}^{\alpha \bar{d}_{1}}}E^\mathrm{T}Z_{14}E,\ldots ,-\mathrm{e}^{-\alpha \tau _{p}}Q_{p3}+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{p}}}E^\mathrm{T}Z_{p2}E\\&+\frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{p}}-\mathrm{e}^{\alpha \tau _{p}}}E^\mathrm{T}Z_{p3}E +\frac{\alpha }{\mathrm{e}^{\alpha \tau _{p}}-\mathrm{e}^{\alpha \bar{d}_{p}}}E^\mathrm{T}Z_{p4}E\}\\ \phi _{1,2}&= \left[ \sqrt{\bar{d}_{1}}V_{11}^\mathrm{T}Z_{11} \quad \sqrt{\bar{d}_{2}}V_{11}^\mathrm{T}Z_{21} \quad \ldots \quad \sqrt{\bar{d}_{p}}V_{11}^\mathrm{T}Z_{p1}\right] ,\\ \phi _{1,3}&= \left[ \sqrt{\tau _{1}}V_{11}^\mathrm{T}Z_{12} \quad \sqrt{\tau _{2}}V_{11}^\mathrm{T}Z_{22} \quad \ldots \quad \sqrt{\tau _{p}}V_{11}^\mathrm{T}Z_{p2}\right] ,\\ \phi _{1,4}&= \left[ \sqrt{\tau _{1}-\underline{d}_{1}}V_{12}^\mathrm{T}Z_{13} \quad \sqrt{\tau _{2}-\underline{d}_{2}}V_{12}^\mathrm{T}Z_{23} \quad \ldots \quad \sqrt{\tau _{p}-\underline{d}_{p}}V_{12}^\mathrm{T}Z_{p3}\right] ,\\ \phi _{1,5}&= \left[ \sqrt{\bar{d}_{1}-\tau _{1}}V_{13}^\mathrm{T}Z_{14} \quad \sqrt{\bar{d}_{2}-\tau _{2}}V_{13}^\mathrm{T}Z_{24} \quad \ldots \quad \sqrt{\bar{d}_{p}-\tau _{p}}V_{13}^\mathrm{T}Z_{p4}\right] ,\\ V_{11}&= \left[ A \quad \tilde{A}_{11} \quad \tilde{A}_{21} \quad \mathbf 0 _{1\times 3p}\right] , \tilde{A}_{11}=\left[ \tilde{\delta }_{1}A_{1} \quad \tilde{\delta }_{2}A_{2} \quad \ldots \quad \tilde{\delta }_{p}A_{p}\right] ,\\ \tilde{A}_{21}&= \left[ (1-\tilde{\delta }_{1})A_{1} \quad (1-\tilde{\delta }_{2})A_{2} \quad \ldots \quad (1-\tilde{\delta }_{p})A_{p}\right] ,\\ V_{12}&= \left[ A \quad \tilde{A}_{12} \quad \mathbf 0 _{1\times 4p}\right] , V_{13}=\left[ A \quad \mathbf 0 _{1\times p} \quad \tilde{A}_{12}\quad \mathbf 0 _{1\times 3p}\right] ,\\ \tilde{A}_{12}&= \left[ A_{1} \quad A_{2} \quad \ldots \quad A_{p}\right] ,\\ \phi _{2,2}&= \mathrm{diag}\{-Z_{11},-Z_{21},\ldots ,-Z_{p1}\}, \phi _{3,3}=\mathrm{diag}\{-Z_{12},-Z_{22},\ldots ,-Z_{p2}\}\\ \phi _{4,4}&= \mathrm{diag}\{-Z_{13},-Z_{23},\ldots ,-Z_{p3}\}, \phi _{5,5}=\mathrm{diag}\{-Z_{14},-Z_{24},\ldots ,-Z_{p4}\} \end{aligned}$$

Proof

First, the regularity and impulse-freeness of the system (5) is shown as follows. Since $\mathrm{rank}(E)=r\leqslant n$, there exist two nonsingular matrices $R$ and $L$ such that

$$\begin{aligned} REL=\left[ \begin{array}{c@{\quad }c} I_{r} &{} 0\\ 0 &{} 0 \end{array}\right] , \quad RAL=\left[ \begin{array}{c@{\quad }c} A_{11} &{} A_{12} \\ A_{21} &{} A_{22}\end{array}\right] , \quad R^{-\mathrm{T}}PL=\left[ \begin{array}{c@{\quad }c} \hat{P}_{11} &{} \hat{P}_{12} \\ \hat{P}_{21} &{} \hat{P}_{22} \end{array}\right] . \end{aligned}$$

(15)

Substitute (15) into (13) and (14), it is straight forward to obtain $A_{22}^\mathrm{T}\hat{P}_{22}+\hat{P}_{22}^\mathrm{T}A_{22}<0$ and we can conclude that $A_{22}$ is nonsingular, from Definition 1, it implies that system (5) is regular and impulse-free. Next, we will show the mean-square exponential stability of the system (5). Choose the following Lyapunov functionals:

$$\begin{aligned} V(x(t))=\sum _{i=1}^{3}V_{i}(x(t)), \end{aligned}$$

(16)

where

$$\begin{aligned} V_{1}(x(t))&= x^\mathrm{T}(t)E^\mathrm{T}Px(t)\\ V_{2}(x(t))&= \sum _{k=1}^{p}\left\{ \int _{t-\underline{d}_{k}}^{t}\mathrm{e}^{\alpha (s-t)}x^\mathrm{T}(s)Q_{k1}x(s)\mathrm{d}s+ \int _{t-\bar{d}_{k}}^{t}\mathrm{e}^{\alpha (s-t)}x^\mathrm{T}(s)Q_{k2}x(s)\right. \\&\qquad \quad \left. +\int _{t-\tau _{k}}^{t}\mathrm{e}^{\alpha (s-t)}x^\mathrm{T}(s)Q_{k3}x(s)+\delta _{k}(t)\int _{t-\hat{d}_{k}(t)}^{t}\mathrm{e}^{\alpha (s-t)}x^\mathrm{T}(s)Q_{k4}x(s)\right. \\&\qquad \quad \left. +(1-\delta _{k}(t))\int _{t-\tilde{d}_{k}(t)}^{t}\mathrm{e}^{\alpha (s-t)}x^\mathrm{T}(s)Q_{k5}x(s)\mathrm{d}s\right\} \\ V_{3}(x(t))&= \sum _{k=1}^{p}\left\{ \int _{-\bar{d}_{k}}^{0}\int _{t+\theta }^{t}\mathrm{e}^{\alpha (s-t)}(E\dot{x}(s))^\mathrm{T}Z_{k1}(E\dot{x}(s))\mathrm{d}s\mathrm{d}\theta \right. \\&\qquad \quad \left. +\int _{-\tau _{k}}^{0}\int _{t+\theta }^{t}\mathrm{e}^{\alpha (s-t)}(E\dot{x}(s))^\mathrm{T}Z_{k2}(E\dot{x}(s))\mathrm{d}s\mathrm{d}\theta \right. \\&\qquad \quad \left. +\int _{-\tau _{k}}^{-\underline{d}_{k}}\int _{t+\theta }^{t}\mathrm{e}^{\alpha (s-t)}(E\dot{x}(s))^\mathrm{T}Z_{k3}(E\dot{x}(s))\mathrm{d}s\mathrm{d}\theta \right. \\&\qquad \quad \left. +\int _{-\bar{d}_{k}}^{-\tau _{k}}\int _{t+\theta }^{t}\mathrm{e}^{\alpha (s-t)}(E\dot{x}(s))^\mathrm{T}Z_{k4}(E\dot{x}(s))\mathrm{d}s\mathrm{d}\theta \right\} .\\ \end{aligned}$$

Denoting $\mathbb {E}\{\delta _{k}(t)=1\}=\tilde{\delta }_{k}$, then, the time-derivative of $V(x(t))$ along with the solution of (5) is given by

$$\begin{aligned} \mathbb {E}\{\dot{V}(x(t))\}=\sum _{k=1}^{3}\mathbb {E}\{\dot{V}_{k}(x(t))\}, \end{aligned}$$

(17)

where

$$\begin{aligned} \mathbb {E}\{\dot{V}_{1}(x(t))\}&= \mathbb {E}\{2x^\mathrm{T}(t)P^\mathrm{T}E\dot{x}(t)\}\\ \mathbb {E}\{\dot{V}_{2}(x(t))\}&= \sum _{k=1}^{p}\left\{ \sum _{i=1}^{3}(x^\mathrm{T}(t)Q_{ki}x(t))-\mathrm{e}^{-\alpha \underline{d}_{k}}x^\mathrm{T}(t-\underline{d}_{k})Q_{k1}x(t-\underline{d}_{k})\right. \\&\left. -\mathrm{e}^{-\alpha \bar{d}_{k}}x^\mathrm{T}(t-\bar{d}_{k})Q_{k2}x(t-\bar{d}_{k})-\mathrm{e}^{-\alpha \tau _{k}}x^\mathrm{T}(t-\tau _{k})Q_{k3}x(t-\tau _{k})\right. \\&\left. +\,\tilde{\delta }_{k}x^\mathrm{T}(t)Q_{k4}x(t)+(1- \tilde{\delta }_{k})x^\mathrm{T}(t)Q_{k5}x(t)-\tilde{\delta }_{k}(1-\dot{\hat{d}}_{k}(t))\mathrm{e}^{-\alpha \hat{d}_{k}(t)}\right. \\&\left. \times x^\mathrm{T}(t-\hat{d}_{k}(t))Q_{k4}x(t-\hat{d}_{k}(t))-(1-\tilde{\delta }_{k})(1-\dot{\tilde{d}}_{k}(t))\mathrm{e}^{-\alpha \tilde{d}_{k}(t)}\right. \\&\left. \times x^\mathrm{T}(t-\tilde{d}_{k}(t))Q_{k5}x(t-\tilde{d}_{k}(t))-\alpha V_{2}(x(t))\right\} \\ \mathbb {E}\{\dot{V}_{3}(x(t))\}&= \mathbb {E}\left\{ \sum _{k=1}^{p}\left\{ \bar{d}_{k}(E\dot{x}(t))^\mathrm{T}Z_{k1}(E\dot{x}(t))\right. \right. \\&\left. -\int _{-\bar{d}_{k}}^{0}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k1}(E\dot{x}(t+\theta ))\mathrm{d}\theta \right. \\&\left. \left. +\tau _{k}(E\dot{x}(t))^\mathrm{T}Z_{k2}(E\dot{x}(t))-\int _{-\tau _{k}}^{0}\mathrm{e}^{\alpha \theta }(E\dot{x}(t\!+\!\theta ))^\mathrm{T}Z_{k2}(E\dot{x}(t\!+\!\theta ))\mathrm{d}\theta \right. \right. \\&+(\tau _{k}-\underline{d}_{k})(E\dot{x}(t))^\mathrm{T}Z_{k3}(E\dot{x}(t))\\&\left. \left. -\int _{-\tau _{k}}^{-\underline{d}_{k}}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k3}(E\dot{x}(t+\theta ))\mathrm{d}\theta \right. \right. \\&+(\bar{d}_{k}-\tau _{k})(E\dot{x}(t))^\mathrm{T}Z_{k4}(E\dot{x}(t))\\&\left. \left. -\int _{-\bar{d}_{k}}^{-\tau _{k}}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k4}(E\dot{x}(t+\theta ))\mathrm{d}\theta -\alpha V_{3}(x(t))\right\} \right\} . \end{aligned}$$

According to Lemma 1, we have

$$\begin{aligned}&-\int _{-\bar{d}_{k}}^{0}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k1}(E\dot{x}(t+\theta ))\mathrm{d}\theta \nonumber \\&\quad \leqslant \frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}\left[ \begin{array}{cc} x(t)\\ x(t-\bar{d}_{k})\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} E^\mathrm{T}Z_{k1}E &{} -E^\mathrm{T}Z_{k1}E\\ -E^\mathrm{T}Z_{k1}E &{} E^\mathrm{T}Z_{k1}E\end{array}\right] \left[ \begin{array}{cc} x(t)\\ x(t-\bar{d}_{k})\end{array}\right] \end{aligned}$$

(18)

Similarly, the following results can be obtained:

$$\begin{aligned}&-\int _{-\tau _{k}}^{0}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k2}(E\dot{x}(t+\theta ))\mathrm{d}\theta \nonumber \\&\quad \leqslant \frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}\left[ \begin{array}{cc} x(t)\\ x(t-\tau _{k})\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} E^\mathrm{T}Z_{k2}E &{} -E^\mathrm{T}Z_{k2}E\\ -E^\mathrm{T}Z_{k2}E &{} E^\mathrm{T}Z_{k2}E\end{array}\right] \left[ \begin{array}{cc} x(t)\\ x(t-\tau _{k})\end{array}\right] \nonumber \\&-\int _{-\tau _{k}}^{-\underline{d}_{k}}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k3}(E\dot{x}(t+\theta ))\mathrm{d}\theta \nonumber \\&\quad \leqslant \frac{\alpha }{\mathrm{e}^{\alpha \underline{d}_{k}}-\mathrm{e}^{\alpha \tau _{k}}}\left[ \begin{array}{cc} x(t-\underline{d}_{k})\\ x(t-\tau _{k})\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} E^\mathrm{T}Z_{k3}E &{} -E^\mathrm{T}Z_{k3}E\\ -E^\mathrm{T}Z_{k3}E &{} E^\mathrm{T}Z_{k3}E\end{array}\right] \left[ \begin{array}{cc} x(t-\underline{d}_{k})\\ x(t-\tau _{k})\end{array}\right] \nonumber \\&-\int _{-\bar{d}_{k}}^{-\tau _{k}}\mathrm{e}^{\alpha \theta }(E\dot{x}(t+\theta ))^\mathrm{T}Z_{k4}(E\dot{x}(t+\theta ))\mathrm{d}\theta \nonumber \\&\quad \leqslant \frac{\alpha }{\mathrm{e}^{\alpha \tau _{k}}-\mathrm{e}^{\alpha \bar{d}_{k}}}\left[ \begin{array}{cc} x(t-\tau _{k})\\ x(t-\bar{d}_{k})\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} E^\mathrm{T}Z_{k4}E &{} -E^\mathrm{T}Z_{k4}E\\ -E^\mathrm{T}Z_{k4}E &{} E^\mathrm{T}Z_{k4}E\end{array}\right] \left[ \begin{array}{cc} x(t-\tau _{k})\\ x(t-\bar{d}_{k})\end{array}\right] \quad \quad \end{aligned}$$

(19)

Denoting

$$\begin{aligned} \eta ^\mathrm{T}(t)=\left[ x^\mathrm{T}(t) \quad \omega _{1}^\mathrm{T}(t) \quad \omega _{2}^\mathrm{T}(t) \quad \omega _{3}^\mathrm{T}(t) \quad \omega _{4}^\mathrm{T}(t) \quad \omega _{5}^\mathrm{T}(t)\right] , \end{aligned}$$

where

$$\begin{aligned} \omega _{1}^\mathrm{T}(t)=&\left[ x^\mathrm{T}(t-\hat{d}_{1}(t)) \quad x^\mathrm{T}(t-\hat{d}_{2}(t)) \quad \ldots \quad x^\mathrm{T}(t-\hat{d}_{p}(t))\right] \\ \omega _{2}^\mathrm{T}(t)=&\left[ x^\mathrm{T}(t-\tilde{d}_{1}(t)) \quad x^\mathrm{T}(t-\tilde{d}_{2}(t)) \quad \ldots \quad x^\mathrm{T}(t-\tilde{d}_{p}(t))\right] \\ \omega _{3}^\mathrm{T}(t)=&\left[ x^\mathrm{T}(t-\underline{d}_{1}) \quad x^\mathrm{T}(t-\underline{d}_{2}) \quad \ldots \quad x^\mathrm{T}(t-\underline{d}_{p})\right] \\ \omega _{4}^\mathrm{T}(t)=&\left[ x^\mathrm{T}(t-\bar{d}_{1}) \quad x^\mathrm{T}(t-\bar{d}_{2}) \quad \ldots \quad x^\mathrm{T}(t-\bar{d}_{p})\right] \\ \omega _{5}^\mathrm{T}(t)=&\left[ x^\mathrm{T}(t-\tau _{1}) \quad x^\mathrm{T}(t-\tau _{2}) \quad \ldots \quad x^\mathrm{T}(t-\tau _{p})\right] . \end{aligned}$$

Substitute (18), (19) into (17), we have the following result via augmented technology:

$$\begin{aligned}&\mathbb {E}\{\dot{V}(x(t))+\alpha V(x(t))\}\\&\quad \leqslant \eta ^\mathrm{T}(t)\left[ \varPi +\phi _{1,2}\phi _{2,2}\phi _{1,2}^\mathrm{T} +\phi _{1,3}\phi _{3,3}\phi _{1,3}^\mathrm{T}+\phi _{1,4}\phi _{4,4}\phi _{1,4}^\mathrm{T}+\phi _{1,5}\phi _{5,5}\phi _{1,5}^\mathrm{T}\right] \eta (t). \end{aligned}$$

According to Schur complement, (13) can be derived from

$$\begin{aligned} \mathbb {E}\{\dot{V}(x(t))+\alpha V(x(t))\}<0. \end{aligned}$$

Next, we will derive the mean-square exponential stability of the system (5), define

$$\begin{aligned} \zeta (t)=L^{-1}x(t)=\left[ \begin{array}{cc} \zeta _{1}(t)\\ \zeta _{2}(t)\end{array}\right] . \end{aligned}$$

Since system (5) is regular, there exist two nonsingular matrices $\hat{R}$ and $L$ such that

$$\begin{aligned} \hat{R}=\left[ \begin{array}{c@{\quad }c} I_{r} &{} -A_{12}A_{22}^{-1} \\ 0 &{} A_{22}^{-1} \end{array}\right] R \end{aligned}$$

and

$$\begin{aligned} \hat{R}EL=&\left[ \begin{array}{c@{\quad }c} I_{r} &{} 0\\ 0 &{} 0\end{array}\right] , \quad \hat{R}AL=\left[ \begin{array}{c@{\quad }c} \hat{A}_{11} &{} 0\\ \hat{A}_{21} &{} I\end{array}\right] , \quad \hat{R}A_{k}L=\left[ \begin{array}{c@{\quad }c} A_{k11} &{} A_{k12}\\ A_{k21} &{} A_{k22}\end{array}\right] ,\nonumber \\ \hat{R}^{-T}PL=&\left[ \begin{array}{c@{\quad }c} P_{11} &{} P_{12} \\ P_{21} &{} P_{22} \end{array}\right] , \quad L^\mathrm{T}Q_{ki}L=\left[ \begin{array}{c@{\quad }c} Q_{ki11} &{} Q_{ki12}\\ Q_{ki21} &{} Q_{ki22}\end{array}\right] , \end{aligned}$$

(20)

where $\hat{A}_{11}=A_{11}-A_{12}A_{22}^{-1}A_{21}$, $\hat{A}_{21}=A_{22}^{-1}A_{21}$, $R$ and $L$ are defined in Eq. (15), then, the system (5) can be rewritten as

$$\begin{aligned} \dot{\zeta }_{1}(t)=&\hat{A}_{11}\zeta _{1}(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)\left( A_{k11}\zeta _{1}(t-\hat{d}_{k}(t))+A_{k12}\zeta _{2}(t-\hat{d}_{k}(t))\right) \right. \nonumber \\&\qquad \qquad \qquad \qquad \left. +(1-\delta _{k}(t))\left( A_{k11}\zeta _{1}(t-\tilde{d}_{k}(t))+A_{k12}\zeta _{2}(t-\tilde{d}_{k}(t))\right) \right] \nonumber \\ -\zeta _{2}(t)=&\hat{A}_{21}\zeta _{1}(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)\left( A_{k21}\zeta _{1}(t-\hat{d}_{k}(t))+A_{k22}\zeta _{2}(t-\hat{d}_{k}(t))\right) \right. \nonumber \\&\qquad \qquad \qquad \qquad \left. +(1-\delta _{k}(t))\left( A_{k21}\zeta _{1}(t-\tilde{d}_{k}(t))+A_{k22}\zeta _{2}(t-\tilde{d}_{k}(t))\right) \right] . \end{aligned}$$

(21)

From the constructed Lyapunov functional in (16), it is not difficult to conclude that

$$\begin{aligned} \lambda _{\min }(P_{11})\mathbb {E}\{\Vert \zeta _{1}(t)\Vert ^{2}\}\leqslant \mathbb {E}\{x^\mathrm{T}(t)E^\mathrm{T}Px(t)\} \leqslant \mathbb {E}\{V(x(t))\}, \end{aligned}$$

(22)

where $\lambda _{\min }(P_{11})$ denotes the minimum eigenvalue of $P_{11}$. Considering $\mathbb {E}\{\dot{V}(x(t))+\alpha V(x(t))\}\leqslant 0$, and there exists a sufficient large $k>0$, the following result is obtained:

$$\begin{aligned} \mathbb {E}\{V(x(t))\}\leqslant \mathrm{e}^{-\alpha t}V(\phi (t))\leqslant k \mathrm{e}^{-\alpha t}\Vert \phi _{c}\Vert ^{2}. \end{aligned}$$

Combined (22) together, we have

$$\begin{aligned} \mathbb {E}\{\Vert \zeta _{1}(t)\Vert ^{2}\}\leqslant \frac{k\mathrm{e}^{-\alpha t}}{\lambda _{\min }(P_{11})}\Vert \phi _{c}\Vert ^{2}. \end{aligned}$$

(23)

The mean-square exponential stability condition of fast subsystem $\zeta _{1}(t)$ is guaranteed. Next, in order to get the mean-square exponential stability condition of slow subsystem $\zeta _{2}(t)$, the following functional is constructed as:

$$\begin{aligned} \chi (t)=&\sum _{k=1}^{p}\left[ \zeta _{2}^\mathrm{T}(t)Q_{k422}\zeta _{2}(t)-\frac{1}{4}\zeta _{2}^\mathrm{T}(t-\hat{d}_{k}(t))Q_{k422}\zeta _{2}(t-\hat{d}_{k}(t))\right. \nonumber \\&\left. +\zeta _{2}^\mathrm{T}(t)Q_{k522}\zeta _{2}(t)-\frac{1}{4}\zeta _{2}^\mathrm{T}(t-\tilde{d}_{k}(t))Q_{k522}\zeta _{2}(t-\tilde{d}_{k}(t))\right] . \end{aligned}$$

(24)

Pre-multiplying the second equation of (21) with $\zeta _{2}^\mathrm{T}(t)P_{22}$, we have

$$\begin{aligned} 0=&\zeta ^\mathrm{T}_{2}(t)P_{22}\zeta _{2}(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)\zeta _{2}^\mathrm{T}(t)P_{22}A_{k22}\zeta _{2}(t-\hat{d}_{k}(t))\right] \nonumber \\&+\sum _{k=1}^{p}\left[ (1-\delta _{k}(t))\zeta _{2}^\mathrm{T}(t)P_{22}A_{k22}\zeta _{2}(t-\tilde{d}_{k}(t))\right] +\zeta _{2}^\mathrm{T}(t)P_{22}\omega (t), \end{aligned}$$

(25)

where

$$\begin{aligned} \omega (t)=\hat{A}_{21}\zeta _{1}(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)A_{k21}\zeta _{1}(t-\hat{d}_{k}(t))+(1-\delta _{k}(t))A_{k21}\zeta _{1}(t-\tilde{d}_{k}(t))\right] \end{aligned}$$

Summing (24) and (25) yields to

$$\begin{aligned} \chi (t)&= \zeta _{2}^\mathrm{T}(t)\left[ P_{22}+P_{22}^\mathrm{T}+\sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] \zeta _{2}(t)\nonumber \\&+\sum _{k=1}^{p}\left[ 2\delta _{k}(t)\zeta _{2}^\mathrm{T}(t)P_{22}A_{k22}\zeta _{2}(t-\hat{d}_{k}(t))\right. \nonumber \\&\left. +2(1-\delta _{k}(t))\zeta _{2}^\mathrm{T}(t)P_{22}A_{k22}\zeta _{2}(t-\tilde{d}_{k}(t))\right] \nonumber \\&+\sum _{k=1}^{p}\left[ -\zeta _{2}^\mathrm{T}(t-\hat{d}_{k}(t))\frac{Q_{k422}}{4}\zeta _{2}(t-\hat{d}_{k}(t))\right. \nonumber \\&\left. -\zeta _{2}^\mathrm{T}(t-\tilde{d}_{k}(t))\frac{Q_{k522}}{4}\zeta _{2}(t-\tilde{d}_{k}(t))\right] +2\zeta _{2}^\mathrm{T}(t)P_{22}\omega (t)\nonumber \\&\leqslant \left[ \begin{array}{ccccccc} \zeta _{2}(t)\\ \zeta _{2}(t-\hat{d}_{1}(t))\\ \vdots \\ \zeta _{2}(t-\hat{d}_{p}(t))\\ \zeta _{2}(t-\tilde{d}_{1}(t))\\ \vdots \\ \zeta _{2}(t-\tilde{d}_{p}(t))\end{array}\right] ^\mathrm{T}\varPsi \left[ \begin{array}{ccccccc} \zeta _{2}(t)\\ \zeta _{2}(t-\hat{d}_{1}(t))\\ \vdots \\ \zeta _{2}(t-\hat{d}_{p}(t))\\ \zeta _{2}(t-\tilde{d}_{1}(t))\\ \vdots \\ \zeta _{2}(t-\tilde{d}_{p}(t))\end{array}\right] \nonumber \\&+\tilde{\theta }\zeta _{2}^\mathrm{T}(t)\zeta _{2}(t)+\tilde{\theta }^{-1}\omega ^\mathrm{T}(t)P_{22}^\mathrm{T}P_{22}\omega (t), \end{aligned}$$

(26)

where

$$\begin{aligned} \varPsi =\left[ \begin{array}{ccccccc} \varPsi _{1} &{} \delta _{1}(t)P_{22}A_{122} &{} \ldots &{} \delta _{p}(t)P_{22}A_{p22} &{} \eta _{1}(t)P_{22}A_{122} &{} \ldots &{} \eta _{p}(t)P_{22}A_{p22}\\ * &{} -\frac{1}{4}Q_{1422} &{} \ldots &{} 0 &{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ * &{} * &{} \ldots &{} -\frac{1}{4}Q_{p422} &{} 0 &{} \ldots &{} 0\\ * &{} * &{} \ldots &{} * &{} -\frac{1}{4}Q_{1522} &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ * &{} * &{} \ldots &{} * &{} * &{} \ldots &{} -\frac{1}{4}Q_{p522}\end{array}\right] \end{aligned}$$

$\varPsi _{1}=P_{22}+P_{22}^\mathrm{T}+\sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right)$, $\eta _{i}(t)=1-\delta _{i}(t),i=1,\ldots ,p$, $\tilde{\theta }$ is any positive scalar. From inequality (13), we can conclude that there exists a sufficient small $\hat{\eta }>0$ and satisfying $\hat{\eta }-\tilde{\theta }>0$ such that

$$\begin{aligned} \varPsi \leqslant -\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \hat{\eta }I &{} 0 &{} \ldots &{} 0\\ 0 &{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 0\end{array}\right] . \end{aligned}$$

(27)

Since $\tilde{\theta }$ can be chosen arbitrary and $\hat{\eta }-\tilde{\theta }>0$, thus we can always find a scalar $\tilde{\eta }>1$, such that

$$\begin{aligned} \sum _{k=1}^{p}\left[ Q_{k422}+Q_{k522}\right] +(\hat{\eta }-\tilde{\theta })I\geqslant \tilde{\eta }\sum _{k=1}^{p}(Q_{k422}+Q_{k522}). \end{aligned}$$

(28)

Using (24), (26), (27) and (28), we have the following result:

$$\begin{aligned}&\mathbb {E}\left\{ \zeta _{2}^\mathrm{T}(t)\left[ \sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] \zeta _{2}(t)\right\} \nonumber \\&\quad \leqslant \frac{\tilde{\eta }^{-1}}{4}\mathbb {E}\left\{ \zeta _{2}^\mathrm{T}(t-\hat{d}_{k}(t))\left[ \sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] \zeta _{2}(t-\hat{d}_{k}(t))\right\} \nonumber \\&\qquad +\frac{\tilde{\eta }^{-1}}{4}\mathbb {E}\left\{ \zeta _{2}^\mathrm{T}(t-\tilde{d}_{k}(t))\left[ \sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] \zeta _{2}(t-\tilde{d}_{k}(t))\right\} \nonumber \\&\qquad +(\tilde{\eta }\tilde{\theta })^{-1}\mathbb {E}\left\{ \omega ^\mathrm{T}(t)P_{22}^\mathrm{T}P_{22}\omega (t)\right\} \end{aligned}$$

(29)

which infers to

$$\begin{aligned} \sum _{k=1}^{p}\mathbb {E}\left\{ f_{k}(t)\right\}&\leqslant \tilde{\eta }_{1}^{-1}\sum _{k=1}^{p}\left\{ \sup _{t-\bar{d}_{k}\leqslant s \leqslant t-\tau _{k}}f_{k}(s)\right\} \\&+\tilde{\eta }_{1}^{-1}\left\{ \sup _{t-\tau _{k}\leqslant s \leqslant t-\underline{d}_{k}}f_{k}(s)\right\} +\sum _{k=1}^{p}\xi \mathrm{e}^{-\delta t}, \end{aligned}$$

where $0<\delta <\min \{\alpha , \min (\bar{d}_{k}^{-1})\ln \tilde{\eta }\}$, $f_{k}(t)=\zeta _{2}^\mathrm{T}(t)(Q_{k422}+Q_{k522})\zeta _{2}(t)$, $\tilde{\eta }_{1}^{-1}=\frac{\tilde{\eta }^{-1}}{4}$ and $\xi =(\tilde{\eta }\tilde{\theta })^{-1}\lambda _{\max }(P_{22}^\mathrm{T}P_{22})m\Vert \phi _{c}\Vert ^{2}$ and $m$ is sufficient large. Applying to Lemma 2 to the above inequality yields to

$$\begin{aligned} \mathbb {E}\{\Vert \zeta _{2}(s)\Vert ^{2}\}&\leqslant \lambda _{\min }^{-1}\left[ \sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] p\beta \mathrm{e}^{-\delta t}\max \left( \Vert \zeta _{2}(s)\Vert _{\bar{d}_{k}}^{2}\right) \nonumber \\&+ \frac{p\lambda _{\min }^{-1}\left[ \sum _{k=1}^{p}\left( Q_{k422}+Q_{k522}\right) \right] \xi \mathrm{e}^{-\delta t}}{1-2\tilde{\eta }_{1}^{-1}\mathrm{e}^{\delta \min (\bar{d}_{k})}} \end{aligned}$$

(30)

Combining (23) and (30) together with Definition 1, the system (5) is mean-square exponentially stable. The proof is completed. $\square$

Remark 5

Without using free-weight matrix technology, Lemma 1 is used to deal with the cross-term, thus, the number of variables in our research is less than the one in the method of [7].

Remark 6

Notice $\tilde{\eta }>1$, $\eta _{1}^{-1}=\frac{\tilde{\eta }^{-1}}{4}$ thus $0<\tilde{\eta }_{1}^{-1}<\frac{1}{4}$ and $0<2\tilde{\eta }_{1}^{-1}<\frac{1}{2}<1$, which satisfies the condition of Lemma 1.

However, in Theorem 1, the equality constraints are involved in (6), and some numerical problems will arisen with it. Using the similar method of [28], choosing $G\in \mathbb {R}^{n\times n}$ satisfying $E^\mathrm{T}G=0$ and $\mathrm{rank}(G)=r$. Denote $P=P_{1}E+GW^\mathrm{T}$, where $P_{1}>0$ and $W\in \mathbb {R}^{n\times (n-r)}$, then, we have the following corollary.

Corollary 1

Denoting $\mathbb {E}\{\delta _{k}(t)=1\}=\tilde{\delta }_{k}$, given positive scalars $\bar{d}_{k}$, $\underline{d}_{k}$ and $\tilde{\delta }_{k}$, $k=1,\ldots ,p$, $0\leqslant \mu <1$ and $\alpha >0$. System (5) is mean-square exponentially admissible if there exist positive definition matrices $P_{1}$, $Q_{kv}$, $Z_{kw}$, $k=1,\ldots ,p$, $v=1,2,3,4,5$, $w=1,2,3,4$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \hat{\varPi } &{} \phi _{1,2} &{} \phi _{1,3} &{} \phi _{1,4} &{} \phi _{1,5}\\ * &{} \phi _{2,2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} \phi _{3,3} &{} 0 &{} 0\\ * &{} * &{} * &{} \phi _{4,4} &{} 0\\ * &{} * &{} * &{} * &{} \phi _{5,5}\end{array}\right] <0 , \end{aligned}$$

(31)

where

$$\begin{aligned} \hat{\varPi }&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \hat{\varPi }_{1} &{} (E^\mathrm{T}P_{1}+WG^\mathrm{T})\tilde{A}_{1} &{} (E^\mathrm{T}P_{1}+WG^\mathrm{T})\tilde{A}_{2} &{} 0 &{} \varXi _{1} &{} \varXi _{2}\\ * &{} U_{1} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} U_{2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} U_{3} &{} 0 &{} \varXi _{3}\\ * &{} * &{} * &{} * &{} U_{4} &{} \varXi _{4}\\ * &{} * &{} * &{} * &{} * &{} U_{5}\end{array}\right] \\ \hat{\varPi }_{1}&= A^\mathrm{T}P_{1}E+E^\mathrm{T}P_{1}A+A^\mathrm{T}GW^\mathrm{T}+WG^\mathrm{T}A+\alpha E^\mathrm{T}P_{1}E\\&+\sum _{k=1}^{p}\left( Q_{k1}+Q_{k2}+Q_{k3}+\tilde{\delta }_{k}Q_{k4}+(1-\tilde{\delta }_{k})Q_{k5}\right. \\&\quad \qquad \quad \left. +\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}E^\mathrm{T}Z_{k1}E+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}E^\mathrm{T}Z_{k2}E\right) \end{aligned}$$

the rest parameters are the same as those in Theorem 1.

Proof

Substitute $P=P_{1}E+GW^\mathrm{T}$ in (13) and (31) can be obtained directly.

Next, the stabilisation problem of system (1) will be considered as follows. Similar to unforced system (3) with $\delta _{k}(t)$, the system (1) can be rewritten as

$$\begin{aligned} E\dot{x}(t)=Ax(t)+\sum _{k=1}^{p}\left[ \delta _{k}(t)A_{k}x(t-\hat{d}_{k})+(1-\delta _{k}(t))A_{k}x(t-\tilde{d}_{k})\right] +Bu(k).\nonumber \\ \end{aligned}$$

(32)

Theorem 2

Given positive scalars $\bar{d}_{k}$, $\underline{d}_{k}$ and $\tilde{\delta }_{k}$, $k=1,\ldots ,p$, $0\leqslant \mu <1$ and $\alpha >0$. System (32) is mean-square exponentially admissible if there exists a nonsingular matrix $X$, positive definition matrices $\hat{Q}_{kv}$, $\hat{Z}_{kw}$, $k=1,\ldots ,p$, $v=1,2,3,4,5$, $w=1,2,3,4$ and matrix $Y$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varPsi &{} \hat{\phi }_{1,2} &{} \hat{\phi }_{1,3} &{} \hat{\phi }_{1,4} &{} \hat{\phi }_{1,5}\\ * &{} \hat{\phi }_{2,2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} \hat{\phi }_{3,3} &{} 0 &{} 0\\ * &{} * &{} * &{} \hat{\phi }_{4,4} &{} 0\\ * &{} * &{} * &{} * &{} \hat{\phi }_{5,5}\end{array}\right] <0 \end{aligned}$$

(33)

with the following constraint

$$\begin{aligned} X^\mathrm{T}E^\mathrm{T}=EX\geqslant 0, \end{aligned}$$

(34)

where

$$\begin{aligned} \varPsi&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c}\varPsi _{1} &{} \tilde{A}_{1}X &{} \tilde{A}_{2}X &{} 0 &{} \hat{\varXi }_{1} &{} \hat{\varXi }_{2}\\ * &{} \hat{U}_{1} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} \hat{U}_{2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} \hat{U}_{3} &{} 0 &{} \hat{\varXi }_{3}\\ * &{} * &{} * &{} * &{} \hat{U}_{4} &{} \hat{\varXi }_{4}\\ * &{} * &{} * &{} * &{} * &{} \hat{U}_{5}\end{array}\right] \\ \varPsi _{1}&= X^\mathrm{T}A^\mathrm{T}+AX+Y^\mathrm{T}B^\mathrm{T}+BY+\alpha X^\mathrm{T}E^\mathrm{T}\\&+\sum _{k=1}^{p}\left( \hat{Q}_{k1}+\hat{Q}_{k2}+\hat{Q}_{k3}+\tilde{\delta }_{k}Q_{k4}+(1-\delta _{k})Q_{k5}\right. \\&\left. +\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}E^\mathrm{T}\hat{Z}_{k1}E+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}E^\mathrm{T}\hat{Z}_{k2}E\right) \\ \end{aligned}$$

$$\begin{aligned} \hat{U}_{i}&= \mathrm{diag}\{X^\mathrm{T},\ldots ,X^\mathrm{T}\}U_{i}\mathrm{diag}\{X,\ldots ,X\},\quad i=1,2,3,4,5\\ \hat{\varXi }_{i_{1}}&= \mathrm{diag}\{X^\mathrm{T},\ldots ,X^\mathrm{T}\}\varXi _{i_{1}}\mathrm{diag}\{X,\ldots , X\},\quad i_{1}=1,2,3,4\\ \hat{\phi }_{1,j_{1}}&= \mathrm{diag}\{X^\mathrm{T},\ldots ,X^\mathrm{T}\}\phi _{1,j_{1}}\mathrm{diag}\{X,\ldots , X\}, \quad j_{1}=2,3,4,5\\ \hat{\phi }_{j_{2},j_{2}}&= \mathrm{diag}\{X^\mathrm{T},\ldots ,X^\mathrm{T}\}\phi _{j_{2},j_{2}}\mathrm{diag}\{X,\ldots , X\}, \quad j_{2}=2,3,4,5. \end{aligned}$$

Proof

Design the feedback controller as $u(t)=Kx(t)=YX^{-1}x(t)$, where $X=P^{-1}$. In (13), $A$ is replaced by $A+BK$, then, the inequality can be written as

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c}\tilde{\varPi } &{} \phi _{1,2} &{} \phi _{1,3} &{} \phi _{1,4} &{} \phi _{1,5}\\ * &{} \phi _{2,2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} \phi _{3,3} &{} 0 &{} 0\\ * &{} * &{} * &{} \phi _{4,4} &{} 0\\ * &{} * &{} * &{} * &{} \phi _{5,5}\end{array}\right] <0, \end{aligned}$$

(35)

where

$$\begin{aligned} \tilde{\varPi }&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \tilde{\varPi }_{1} &{} P^\mathrm{T}\tilde{A}_{1} &{} P^\mathrm{T}\tilde{A}_{2} &{} 0 &{} \varXi _{1} &{} \varXi _{2}\\ * &{} U_{1} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} U_{2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} U_{3} &{} 0 &{} \varXi _{3}\\ * &{} * &{} * &{} * &{} U_{4} &{} \varXi _{4}\\ * &{} * &{} * &{} * &{} * &{}U_{5}\end{array}\right] \\ \tilde{\varPi }&= A^\mathrm{T}P+P^\mathrm{T}A+Y^\mathrm{T}B^\mathrm{T}PX+X^\mathrm{T}P^\mathrm{T}BY+\alpha E^\mathrm{T}P\\&+\sum _{k=1}^{p}\left( Q_{k1}+Q_{k2}+Q_{k3}+\delta _{k}Q_{k4}+(1-\delta _{k})Q_{k5}\right. \\&\left. +\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}E^\mathrm{T}Z_{k1}E+ \frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}E^\mathrm{T}Z_{k2}E\right) . \end{aligned}$$

Pre- and post-multiplying (35) and (14) by $\mathrm{diag}\{X^\mathrm{T},\ldots ,X^\mathrm{T}\}$ and $\mathrm{diag}\{X,\ldots ,X\}$, respectively. Define $\hat{Q}_{k\upsilon }=X^\mathrm{T}Q_{k\upsilon }X$ and $\hat{Z}_{k\omega }=X^\mathrm{T}Z_{k\omega }X$, $k=1,\ldots ,p$, $\upsilon =1,2,3,4,5$, $\omega =1,2,3,4$. Then, (33) and (34) are obtained directly. This concludes the proof. $\square$

In Theorem 2, the corresponding result is not a strict LMI. Similar to Corollary 1, define $X=X_{1}E^\mathrm{T}+G_{1}^\mathrm{T}W_{1}^\mathrm{T}$, where $X$ is positive definition and $EG_{1}^\mathrm{T}=0$. Then, we have the following corollary.

Corollary 2

Given positive scalars $\bar{d}_{k}$, $\underline{d}_{k}$ and $\tilde{\delta }_{k}$, $k=1,\ldots ,p$, $0\leqslant \mu <1$ and $\alpha >0$. System (32) is mean-square exponentially admissible if there exist positive definition matrices $X_{1}$, $\hat{Q}_{kv}$, $\hat{Z}_{kw}$, $k=1,\ldots ,p$, $v=1,2,3,4,5$, $w=1,2,3,4$ and a matrix $Y$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \hat{\varPsi } &{} \hat{\phi }_{1,2} &{} \hat{\phi }_{1,3} &{} \hat{\phi }_{1,4} &{} \hat{\phi }_{1,5}\\ * &{} \hat{\phi }_{2,2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} \hat{\phi }_{3,3} &{} 0 &{} 0\\ * &{} * &{} * &{} \hat{\phi }_{4,4} &{} 0\\ * &{} * &{} * &{} * &{} \hat{\phi }_{5,5}\end{array}\right] <0, \end{aligned}$$

(36)

where

$$\begin{aligned} \hat{\varPsi }&=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c}\varPsi _{1} &{} \tilde{A}_{1}(X_{1}E^\mathrm{T}+G_{1}^\mathrm{T}W_{1}^\mathrm{T}) &{} \tilde{A}_{2}(X_{1}E^\mathrm{T}+G_{1}^\mathrm{T}W_{1}^\mathrm{T}) &{} 0 &{} \hat{\varXi }_{1} &{} \hat{\varXi }_{2}\\ * &{} \hat{U}_{1} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} \hat{U}_{2} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} \hat{U}_{3} &{} 0 &{} \hat{\varXi }_{3}\\ * &{} * &{} * &{} * &{} \hat{U}_{4} &{} \hat{\varXi }_{4}\\ * &{} * &{} * &{} * &{} * &{} \hat{U}_{5}\end{array}\right] \\ \varPsi _{1}&= EX_{1}^\mathrm{T}A^\mathrm{T}+AX_{1}E+W_{1}G_{1}A^\mathrm{T}+AG_{1}^\mathrm{T}W_{1}^\mathrm{T}+Y^\mathrm{T}B^\mathrm{T}+BY+\alpha EX_{1}^\mathrm{T}E^\mathrm{T}\\&\quad +\sum _{k=1}^{p}\left( \hat{Q}_{k1}+\hat{Q}_{k2}+\hat{Q}_{k3}+\tilde{\delta }_{k}Q_{k4}+(1-\delta _{k})Q_{k5}\right. \\&\left. +\frac{\alpha }{1-\mathrm{e}^{\alpha \bar{d}_{k}}}E^\mathrm{T}\hat{Z}_{k1}E+\frac{\alpha }{1-\mathrm{e}^{\alpha \tau _{k}}}E^\mathrm{T}\hat{Z}_{k2}E\right) .\\ \end{aligned}$$

Proof

The proof is similar to Corollary 1, and it is omitted here.

4 Numerical Examples

In this section, three numerical examples are provided to show the effectiveness of the proposed methods.

4.1 Example 1

Consider the following unforced singular time-delay system in [7]:

$$\begin{aligned} E\!=\!\left[ \begin{array}{c@{\quad }c} -1 &{} 2\\ -2 &{} 4 \end{array}\right] \!, \quad A\!=\!\left[ \begin{array}{c@{\quad }c} -4.7 &{} 0.4\\ -4.9 &{} 0.8 \end{array}\right] \!, \quad A_{1}\!=\!\left[ \begin{array}{c@{\quad }c} 0.7 &{} -0.95\\ 1.1 &{} -1.75 \end{array}\right] \!, \quad A_{2}\!=\!\left[ \begin{array}{c@{\quad }c} 1 &{} -0.8\\ 1.4 &{} -1.3 \end{array}\right] \!. \end{aligned}$$

As in [7], let $\underline{d}_{1}=0.1$, $\bar{d}_{1}=0.5$, $\underline{d}_{2}=0.2$ and $\mu =0.3$. Given various $\alpha$, compared with [7], using Corollary 2, the maximum allowable $\bar{d}_{2}$ to ensure the mean-square exponentially stable of the unforced system are listed in Table 1. For simplicity, we choose $\tau _{1}=\frac{\bar{d}_{1}+\underline{d}_{1}}{2}$, $\tilde{\delta }_{1}=0.5$, $\tau _{2}=\tau _{1}$, $\tilde{\delta }_{2}=\frac{\tau _{2}-\underline{d}_{2}}{\bar{d}_{2}-\underline{d}_{2}}$. From Table 1, it can be found that our results are less conservative than the results of [4, 7].

Table 1 Maximum allowable $\bar{d}_{2}$ for different $\alpha$

Remark 7

In our research, the information of statistical distribution of each time-delays is fully considered. Thus, the main advantage of our method is that it uses the full information of time-varying delays. That’s the reasons that our research result is less conservative than the results in [4, 7].

Remark 8

Without using free-weight matrix, the number of decision variables in our paper is 20 and less the those in [7] (the number of decision variables is 24) and [4] (the number of decision variables is 22).

4.2 Example 2

Consider the singular system (1) with the following parameters as:

$$\begin{aligned}&E=\left[ \begin{array}{l@{\quad }l} 1 &{} 0\\ 0 &{} 0\end{array}\right] , \quad A=\left[ \begin{array}{l@{\quad }l} -1.5 &{} -1\\ 0 &{} -1 \end{array}\right] ,\quad A_{1}=\left[ \begin{array}{l@{\quad }l} -1 &{} 0\\ -1 &{} -2 \end{array}\right] ,\\&\quad A_{2}=\left[ \begin{array}{l@{\quad }l} 0.3 &{} 0\\ 0.2 &{} 1 \end{array}\right] ,\quad B=\left[ \begin{array}{l} -0.2\\ -1 \end{array}\right] . \end{aligned}$$

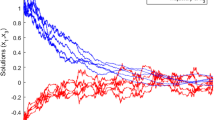
The state response of open-loop system ($u(t)=0$) is shown in Fig. 1, $d_{1}(t)=0.3+0.1\sin (2t)$, $d_{2}(t)=0.4+0.2\cos (t)$. From Fig. 1, it can be found that the open-loop system is unstable.

Fig. 1

State response of the open-loop system (Example 2)

Next, we will consider the state response of closed-loop system, set $\underline{d}_{1}=0.2$, $\bar{d}_{1}=0.4$, $\underline{d}_{2}=0.2$, $\bar{d}_{2}=0.6$, $\mu =0.3$, $\alpha =0.4$, $\tau _{1}=\tau _{2}=0.3$, $\tilde{\delta }_{1}=0.5$, $\tilde{\delta }_{2}=0.2500$, and $G_{1}=\left[ \begin{array}{cc}0 &{} 1\\ 0 &{} 1\end{array}\right]$. Using Corollary 2, we have the following results:

$$\begin{aligned}&X_{1}=\left[ \begin{array}{c@{\quad }c} 26.3315 &{} 9.1780\\ 9.1780 &{} 7.7079\end{array}\right] , \quad Y=[71.7662 \; 158.1402], \\&\quad \hat{Q}_{11}=\left[ \begin{array}{c@{\quad }c} 2.4889 &{} 2.3311\\ 2.3311 &{} 13.8269\end{array}\right] ,\quad \hat{Q}_{21}=\left[ \begin{array}{c@{\quad }c} 2.4965 &{} 2.3310\\ 2.3310 &{} 13.8270\end{array}\right] ,\\&\quad \hat{Q}_{12}=\left[ \begin{array}{c@{\quad }c} 4.0194 &{} 2.5028\\ 2.5028 &{} 14.5967\end{array}\right] ,\quad \hat{Q}_{22}=\left[ \begin{array}{c@{\quad }c} 4.0268 &{} 2.6569\\ 2.6569 &{} 15.3583\end{array}\right] ,\\&\quad \hat{Q}_{13}=\left[ \begin{array}{c@{\quad }c} 2.6622 &{} 2.4302\\ 2.4302 &{} 14.2117\end{array}\right] , \quad \hat{Q}_{23}=\left[ \begin{array}{c@{\quad }c} 2.6694 &{} 2.4280\\ 2.4280 &{} 14.2120\end{array}\right] , \\ {}&\quad \hat{Q}_{14}=\left[ \begin{array}{c@{\quad }c} 43.8057 &{} 29.3595\\ 29.3595 &{} 51.5046\end{array}\right] ,\quad \hat{Q}_{24}=\left[ \begin{array}{c@{\quad }c} 15.1616 &{} 11.1710\\ 11.1710 &{} 38.5489\end{array}\right] , \\ {}&\quad \hat{Q}_{15}=\left[ \begin{array}{c@{\quad }c} 45.3688 &{} 31.3683\\ 31.3683 &{} 55.6711\end{array}\right] , \quad \hat{Q}_{25}=\left[ \begin{array}{c@{\quad }c} 14.9742 &{} 13.7472\\ 13.7472 &{} 36.9889\end{array}\right] ,\\&\quad \hat{Z}_{11}=\left[ \begin{array}{c@{\quad }c} 3.3246 &{} 0.0913\\ 0.0913 &{} 1.5380\end{array}\right] , \quad \hat{Z}_{21}=\left[ \begin{array}{c@{\quad }c} 3.1185 &{} 0.0887\\ 0.0887 &{} 1.0583\end{array}\right] ,\\ {}&\quad \hat{Z}_{12}=\left[ \begin{array}{c@{\quad }c} 3.7660 &{} 0.0998\\ 0.0998 &{} 1.9805\end{array}\right] , \hat{Z}_{22}=\left[ \begin{array}{c@{\quad }c} 3.7945 &{} 0.0999\\ 0.0999 &{} 1.9806\end{array}\right] , \\ {}&\quad \hat{Z}_{13}=\left[ \begin{array}{c@{\quad }c} 1.9850 &{} 0.0682\\ 0.0682 &{} 4.0113\end{array}\right] , \quad \hat{Z}_{23}=\left[ \begin{array}{c@{\quad }c} 1.9846 &{} 0.0685\\ 0.0685 &{} 4.0125\end{array}\right] ,\\&\quad \hat{Z}_{14}=\left[ \begin{array}{c@{\quad }c} 0.1842 &{} 0.0030\\ 0.0030 &{} 4.3874\end{array}\right] , \quad \hat{Z}_{24}=\left[ \begin{array}{c@{\quad }c} 0.5002 &{} 0.0114\\ 0.0114 &{} 1.8596\end{array}\right] .\\ \end{aligned}$$

Then, $K$ is computed as $K=\left[ -7.5659 \quad 29.5257\right]$. The state response of the closed-loop system is as shown in Fig. 2, as expected, the system state convergences to the equilibrium point quickly.

Fig. 2

State response of the closed-loop system (Example 2)

4.3 Example 3

In this example, the system (1) with the following parameters is considered as:

$$\begin{aligned} E&= \left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array}\right] , \quad A=\left[ \begin{array}{cc} -2 &{} 0\\ 0 &{} -0.9 \end{array}\right] , \quad A_{1}=\left[ \begin{array}{cc} -1 &{} 0.6\\ -0.4 &{}-1 \end{array}\right] ,\\ A_{2}&= \left[ \begin{array}{cc} 0 &{} -0.6\\ -0.6 &{} 0 \end{array}\right] , \quad B=\left[ \begin{array}{c} 0.1\\ -0.5 \end{array}\right] . \end{aligned}$$

Let $d_{1}(t)=0.3+0.1\sin (2t)$, $d_{2}(t)=0.4+0.2\cos (t)$. Then, we have $\underline{d}_{1}=0.2$, $\underline{d}_{2}=0.2$, $\bar{d}_{1}=0.4$, $\bar{d}_{2}=0.6$, $\mu =0.3$. Figure 3 shows the state response of the open-loop system (1) ($u(t)=0$), and the results present that the open-loop system is unstable. Then, considering the feedback controller, with Corollary 2, and considering $\alpha =0.3$, we have the controller gain as $K=\left[ -5.0680 \; 54.3055\right]$, and the state response of closed-loop system is shown as Fig. 4, it is clearly that the closed-loop system is stable.

Fig. 3

State response of the open-loop system (Example 3)

Fig. 4

State response of the closed-loop system (Example 3)

5 Conclusion

The problem of delay-distribution-dependent mean-square exponential stability has been considered for continuous-time stochastic singular systems with multiple time-varying delays in this paper. Using the statistical information of time-delays, a delay-distribution-dependent condition is given, which is less conservative than the existing ones. Without using the free-weighting matrix technology, the number of decision variables in our research are much fewer than the method in [4, 7]. Besides, a useful lemma is proposed to ensure the mean-square exponential stability of the stochastic singular systems. Furthermore, a suitable feedback controller is derived from the basis of such delay-distribution-dependent conditions. Finally, numerical examples have been provided to illustrate the less conservatism and the effectiveness of the proposed approach.