1 Introduction

The sine signal is a single frequency wave and is used widely in the communication technology, signal processing and filtering [25] and system identification [2, 37]. Many period signals under certain conditions can be decomposed into the sine combinations with different frequencies, amplitudes and phases. The signal modeling is estimating the characteristic parameters of the signals from the measured data. The sine-wave parameter estimation problems have been received much attentions. For example, Belega et al. [3] studied the accuracy of the sine-wave parameter estimation by means of the windowed three-parameter sine-fitting algorithm; Chen et al. [5] studied the multi-harmonic fitting algorithm based on four parameters sine fitting to improve the global convergence; Li et al. [19] derived a gradient-based iterative identification algorithm for estimating parameters of the signal model with known and unknown frequencies. Some of these methods are based on the statistic analysis. This paper considers the optimization algorithm for estimating the signal parameters.

The mathematical model is the basics of controller design [36, 39]. Many identification algorithms can estimate system parameters and system models [15, 26]. In general, the identification algorithm is derived by defining and minimizing a cost function [27–32, 35]. The parameters to be estimated are defined as the parameter vector. Then, the parameter estimates can be obtained by means of optimization algorithms. The identification algorithms have been used widely in industrial robot, signal processing and network communication [8, 41]; Guo et al. [14] investigated the recursive identification method for finite impulse response systems with binary-valued outputs and communication channels; Janot et al. [16] addressed a revised Durbin–Wu–Hausman test for the industrial robot identification; Zhao et al. [43] studied the multi-frequency identification algorithm to identify the amplitude and phase of a multi-frequency signal. This paper studies the application of the identification algorithm to the signal modeling.

In system identification, some identification algorithms focus on reducing the computation load and enhancing the accuracy [40]. Since the gradient optimization method only needs computing the first-order derivation, the gradient identification algorithm has low computation load [10]. However, the gradient algorithm has low computation accuracy. Many improved gradient algorithms have been proposed for enhancing the computation accuracy. Andrei [1] illustrated an adaptive conjugate gradient algorithm for large-scale unconstrained optimization by minimizing the quadratic approximation of the objective function at the current point; Deng et al. [7] developed a three-term conjugate gradient algorithm for solving large-scale unconstrained optimization problems by rectifying the steepest descent direction with the difference between the current iterative points and the gradients; Necoara et al. [24] devised a fully distributed dual gradient method based on a weighted step size and analyzed the convergence rate. Although these improved algorithms can polish up the convergence rate and the estimation accuracy, the computation load is heavy.

The innovation is the useful information that can improve the parameter estimation accuracy. It can promote the convergence of the algorithms during the recursive process. In order to enhance the estimation accuracy by using more innovation, the multi-innovation theory is used widely in the system identification. Mao et al. [23] studied a data filtering-based multi-innovation stochastic gradient algorithm for Hammerstein nonlinear systems; Zhang et al. [42] considered a multi-innovation auto-constructed least squares identification method for 4 freedom ship maneuvering identification modeling; in this paper, the multi-innovation method is expanded into the signal modeling for the sine-wave or periodic signals.

In general, the identification methods are divided into the online identification and the off-line identification. The iterative identification methods are used to the off-line identification [12, 38]. In view of the online identification, Li et al. [22] studied a parallel adaptive self-tuning recursive least squares algorithm for the time-varying system; Ding et al. [11] developed a recursive least squares parameter identification algorithms for nonlinear systems; Ding et al. [13] studied a recursive least squares parameter estimation method for a class of output nonlinear systems based on the model decomposition; Ding et al. [9] presented a least squares algorithm for a dual-rate state space system with time delay. Considering the advantages of the least squares algorithm, a recursive least squares parameter estimation algorithm is derived to estimate the parameters of a periodic signal.

The major contributions of the work in this paper are listed in the following.

  • This paper studies the problem of the parameter estimation. The proposed methods can be used not only for the sine combination signals but also for other periodic signals. These parameter estimation methods can be used in signal processing and signal modeling.

  • On the basis of the gradient searching, a stochastic gradient (SG) parameter estimation algorithm is presented. In order to improve the estimation accuracy and the convergence rate, a multi-innovation stochastic gradient (MISG) parameter estimation algorithm is presented by means of expanding the scalar innovation into the innovation vector.

  • For the purpose of enhancing the algorithm stabilization and the parameter estimation accuracy, a recursive least squares (RLS) algorithm is derived using the trigonometric function expansion. This technique transforms the nonlinear optimization into the linear optimization. Therefore, the algorithm stabilization is improved significantly.

The rest of this paper is organized in the following. Section 2 derives the SG method. Section 3 deduces the MISG algorithm. Section 4 gives the RLS parameter estimation algorithm. Section 5 provides some examples to illustrate and compare the effectiveness of the proposed parameter estimation methods. Section 6 draws some concluding remarks.

2 Stochastic Gradient Method

Let us introduce some notation.

Symbol

Meaning

\({\varvec{X}}^{\tiny \text{ T }}\)

The transpose of the vector or matrix X

\(\hat{{\varvec{\theta }}}(k)\)

The estimate of \({\varvec{\theta }}\) at recursion k

\(A:=X\)

I.e., \(X:=A\), X is defined by A

\(\text {tr}[{\varvec{X}}]\)

The trace of the square matrix \({\varvec{X}}\)

\(\Vert {\varvec{X}}\Vert \)

\(\Vert {\varvec{X}}\Vert ^2:=\text {tr}[{\varvec{X}}{\varvec{X}}^{\tiny \text{ T }}]\)

e(k)

The innovation scalar at recursion k

\({\varvec{E}}(p,k)\)

The innovation vector, i.e., the multi-innovation at recursion k

\({\varvec{\varphi }}(k)\)

The information vector at recursion k

\({\varvec{\varPhi }}(p,k)\)

The information matrix at recursion k

Consider the combination sine signals with different frequencies, phases and amplitudes:

$$\begin{aligned} y(t)=a_1\sin (\omega _1t+\phi _1)+a_2\sin (\omega _2t+\phi _2)+\cdots +a_n\sin (\omega _nt+\phi _n), \end{aligned}$$
(1)

where \(a_1\), \(a_2\), \(\ldots \), \(a_n\) are the amplitudes, \(\omega _1\), \(\omega _2\), \(\ldots \), \(\omega _n\) are the frequencies and \(\phi _1\), \(\phi _2\), \(\ldots \), \(\phi _n\) are the phases. These parameters are the characteristic parameters of the combination sine signals. The goal is to estimate these parameters by means of presenting new identification methods.

Suppose that the frequencies of the combination sine signals are known, then the phases and amplitudes are to be identified. Define the parameter vector

$$\begin{aligned} {\varvec{\theta }}:=[a_1,a_2,\ldots ,a_n,\phi _1,\phi _2,\ldots , \phi _n]^{\tiny \text{ T }}\in {\mathbb R}^{2n}. \end{aligned}$$

In the identification test, assume that the sampling period is h and the sampling time is \(t_k:=kh\). The measured data are represented as \(\{t_k,y(t_k)\}\). Let \(y(k):=y(t_k)\) for simplification. Define the difference between the observation output and the model output:

$$\begin{aligned} \varepsilon (k):=y(k)-\sum _{i=1}^na_i\sin (\omega _ikh+\phi _i). \end{aligned}$$

Then, define the cost function

$$\begin{aligned} J({\varvec{\theta }}):=\frac{1}{2}\varepsilon ^2(k). \end{aligned}$$

Taking the first-order derivative of \(J({\varvec{\theta }})\) with respect to \({\varvec{\theta }}\) gives

$$\begin{aligned} \mathrm{grad}[J({\varvec{\theta }})]:= & {} \frac{\partial J({\varvec{\theta }})}{\partial {\varvec{\theta }}}\\= & {} \left[ \frac{\partial J({\varvec{\theta }})}{\partial a_1},\frac{\partial J({\varvec{\theta }})}{\partial a_2}, \ldots ,\frac{\partial J({\varvec{\theta }})}{\partial a_n},\frac{\partial J({\varvec{\theta }})}{\partial \phi _1}, \frac{\partial J({\varvec{\theta }})}{\partial \phi _2},\ldots ,\frac{\partial J({\varvec{\theta }})}{\partial \phi _n}\right] ^{\tiny \text{ T }}\in {\mathbb R}^{2n},\\ \frac{\partial J({\varvec{\theta }})}{\partial a_i}= & {} -\sin (\omega _ikh+\phi _i) \varepsilon (k),\\ \frac{\partial J({\varvec{\theta }})}{\partial \phi _i}= & {} -a_i\cos (\omega _ikh+\phi _i) \varepsilon (k), \quad i=1,2,\ldots ,n. \end{aligned}$$

Define the information vector

$$\begin{aligned} {\varvec{\varphi }}(k):= & {} [\sin (\omega _1kh+\phi _1),\ldots ,\sin (\omega _nkh+\phi _n), a_1\cos (\omega _1kh+\phi _1),\\&\ldots ,a_n\cos (\omega _nkh+\phi _n)]^{\tiny \text{ T }}\in {\mathbb R}^{2n}. \end{aligned}$$

Let \(k=1,2,\ldots \) be a recursive variable and let \(\hat{{\varvec{\theta }}}(k)\) be the estimate of \({\varvec{\theta }}\) at recursion k. Utilizing the gradient search and minimizing the cost function \(J({\varvec{\theta }})\), we have the SG parameter estimation algorithm:

$$\begin{aligned} \hat{{\varvec{\theta }}}(k+1)= & {} \hat{{\varvec{\theta }}}(k)+\frac{\hat{{\varvec{\varphi }}}(k)}{r(k+1)}e(k), \end{aligned}$$
(2)
$$\begin{aligned} e(k)= & {} y(k)-\sum _{i=1}^n\hat{a}_i(k)\sin (\omega _ikh+\hat{\phi }_i(k)), \end{aligned}$$
(3)
$$\begin{aligned} \hat{{\varvec{\varphi }}}(k)= & {} [\sin (kh\omega _1+\hat{\phi }_1(k)), \ldots ,\sin (kh\omega _n+\,\hat{\phi }_n(k)),\nonumber \\&\hat{a}_1(k)\cos (\omega _1kh+\hat{\phi }_1(k)),\ldots , \hat{a}_n(k)\cos (\omega _nkh+\hat{\phi }_n(k))]^{\tiny \text{ T }},\end{aligned}$$
(4)
$$\begin{aligned} r(k+1)= & {} r(k)+\Vert \hat{{\varvec{\varphi }}}(k)\Vert ^2,\quad r(0)=1. \end{aligned}$$
(5)

The steps of computing the parameter estimate \(\hat{{\varvec{\theta }}}(k+1)\) using the SG method are as follows.

  1. 1.

    To initiate: let \(k=0\), preset the recursive length L and let \(\hat{{\varvec{\theta }}}(0)\) be an arbitrary small real vector.

  2. 2.

    Collect the measured data y(k).

  3. 3.

    Compute \(\hat{{\varvec{\varphi }}}(k)\) using (4) and compute \(r(k+1)\) using (5).

  4. 4.

    Compute e(k) using (3).

  5. 5.

    Update \(\hat{{\varvec{\theta }}}(k+1)\) using (2), if \(k=L\), then terminate the recursive procedure; otherwise, \(k:=k+1\), go to Step 2.

3 The Multi-innovation Stochastic Gradient Algorithm

For the SG algorithm, the SG algorithm has low computation accuracy. In order to enhance the computation precision, more measurement data are utilized to the algorithm at each recursion. The dynamical window data scheme is adopted to derive the MISG algorithm. The dynamical window data are a batch data, and the data length is p. In the SG algorithm, e(k) is called the scalar innovation. This innovation can promote the algorithm estimation accuracy.

Consider that the dynamical window data with length p are \(y(k), y(k-1), \ldots , y(k-p+1)\). Expand the scalar innovation e(k) into the innovation vector

$$\begin{aligned} {\varvec{E}}(p,k):=\left[ \begin{array}{l} y(k)-\sum _{i=1}^n\hat{a}_i(k)\sin (\omega _ikh+\hat{\phi }_i(k)) \\ y(k-1)-\sum _{i=1}^n\hat{a}_i(k)\sin ((kh-h)\omega _i+\hat{\phi }_i(k)) \\ \vdots \\ y(k-p+1)-\sum _{i=1}^n\hat{a}_i(k)\sin ((kh-ph+h)\omega _i+\hat{\phi }_i(k)) \end{array}\right] \in {\mathbb R}^{p}, \end{aligned}$$

where \(\hat{a}_i(k)\) denotes the estimate of \(a_i\) and \(\hat{\phi }_i(k)\) denotes the estimate of \(\phi _i\) at time \(t=kh\). Expand the information vector into the information matrix

$$\begin{aligned} {\varvec{\varPhi }}(p,k):=[{\varvec{\varphi }}(k),{\varvec{\varphi }}(k-1),\ldots ,{\varvec{\varphi }}(k-p+1)]\in {\mathbb R}^{2n\times p}. \end{aligned}$$

According to the gradient searching, the MISG parameter estimation algorithm is listed in the following:

$$\begin{aligned} \hat{{\varvec{\theta }}}(k+1)= & {} \hat{{\varvec{\theta }}}(k)-\frac{\hat{{\varvec{\varPhi }}}(p,k)}{r(k+1)}{\varvec{E}}(p,k), \end{aligned}$$
(6)
$$\begin{aligned} {\varvec{E}}(p,k)= & {} [e(k),e(k-1),\ldots ,e(k-p+1)]^{\tiny \text{ T }}, \end{aligned}$$
(7)
$$\begin{aligned} e(k-i)= & {} y(k-i)-\sum _{j=1}^n\hat{a}_j(k)\sin ((k-i)h\omega _j+\hat{\phi }_j(k)), \quad i=0,1,\ldots ,p-1,\nonumber \\ \end{aligned}$$
(8)
$$\begin{aligned} {\varvec{\varPhi }}(p,k)= & {} [\hat{{\varvec{\varphi }}}(k),\hat{{\varvec{\varphi }}}(k-1),\ldots ,\hat{{\varvec{\varphi }}}(k-p+1)], \end{aligned}$$
(9)
$$\begin{aligned} \hat{{\varvec{\varphi }}}(k-i)= & {} [-\sin ((k-i)h\omega _1+\hat{\phi }_1(k)), \ldots ,-\sin ((k-i)h\omega _n+\hat{\phi }_n(k)),\nonumber \\&-\hat{a}_1(k)\cos ((k-i)h\omega _1+\hat{\phi }_1(k)), \ldots , -\hat{a}_n(k)\cos ((k-i)h\omega _n\nonumber \\&+\hat{\phi }_n(k))]^{\tiny \text{ T }},\quad i=0,1,\ldots ,p-1, \end{aligned}$$
(10)
$$\begin{aligned} r(k+1)= & {} r(k)+\Vert {\varvec{\varPhi }}(p,k)\Vert ^2, \quad r(0)=1. \end{aligned}$$
(11)

The steps of computing the parameter estimate \(\hat{{\varvec{\theta }}}(k+1)\) using the MISG method are as follows.

  1. 1.

    To initiate: preset the recursive length L and the innovation length p; let \(\hat{{\varvec{\theta }}}(0)\) be an arbitrary small real vector.

  2. 2.

    Collect measured data y(k); compute \(\hat{{\varvec{\varphi }}}(k-i)\) using (10); form \({\varvec{\varPhi }}(p,k)\) using (9).

  3. 3.

    Compute \(e(k-i)\) using (8) and form \({\varvec{E}}(p,k)\) using (7).

  4. 4.

    Compute \(r(k+1)\) using (11).

  5. 5.

    Update the parameter estimate \(\hat{{\varvec{\theta }}}(k+1)\) using (6), if \(k=L\), then terminate the recursive procedure; otherwise \(k:=k+1\), go to Step 2.

4 The Recursive Least Squares Algorithm

The least squares optimization method is widely used in system identification. This paper expands this method to the signal modeling. It is obvious that the sine combination signal is a nonlinear function with respect to the parameters to be estimated. In order to derive the recursive least squares algorithm to estimate the parameters of the combination sine signal, rewriting the sine combination signal in (1) gives

$$\begin{aligned} y(t)= & {} a_1\cos \phi _1\sin \omega _1t+a_1\sin \phi _1\cos \omega _1t +a_2\cos \phi _2\sin \omega _2t\nonumber \\&+a_2\sin \phi _2\cos \omega _2t +\cdots +a_n\cos \phi _n\sin \omega _nt +a_n\sin \phi _n\cos \omega _nt. \end{aligned}$$
(12)

Let \(c_i:=a_i\cos \phi _i\), \(d_i:=a_i\sin \phi _i\), thus y(t) can be expressed as

$$\begin{aligned} y(t)=\sum _{i=1}^nc_i\sin \omega _it+d_i\cos \omega _it. \end{aligned}$$

Define the parameter vector

$$\begin{aligned} {\varvec{\theta }}:=[c_1,d_1,c_2,d_2,\ldots ,c_n,d_n]^{\tiny \text{ T }}\in {\mathbb R}^{2n}. \end{aligned}$$

In the identification test, the sampling time is \(t_k:=kh\) and the measured data length is L. The observation output data are \(y(k):=y(kh)\), \(k=1,2,\ldots \).

Define the information vector

$$\begin{aligned} {\varvec{\varphi }}(k):=[\sin \omega _1kh,\cos \omega _1kh,\sin \omega _2kh,\cos \omega _2kh, \ldots ,\sin \omega _nkh,\cos \omega _nkh]^{\tiny \text{ T }}\in {\mathbb R}^{2n}. \end{aligned}$$

Define the criterion function

$$\begin{aligned} J({\varvec{\theta }}):=\frac{1}{2}\sum _{j=1}^ke^2(j), \end{aligned}$$

where \(e(j):=y(j)-{\varvec{\varphi }}^{\tiny \text{ T }}(j){\varvec{\theta }}\).

Define the stack output vector \({\varvec{Y}}_k\) and the stack information vector \({\varvec{\varPhi }}_k\), respectively,

$$\begin{aligned} {\varvec{Y}}_k:=\left[ \begin{array}{l} y(1) \\ y(2) \\ \vdots \\ y(k) \end{array}\right] \in {\mathbb R}^k, \quad {\varvec{\varPhi }}_k:=\left[ \begin{array}{l} {\varvec{\varphi }}^{\tiny \text{ T }}(1) \\ {\varvec{\varphi }}^{\tiny \text{ T }}(2) \\ \vdots \\ {\varvec{\varphi }}^{\tiny \text{ T }}(k) \end{array}\right] \in {\mathbb R}^{k\times 2n}. \end{aligned}$$

Then, the criterion function can be rewritten as

$$\begin{aligned} J({\varvec{\theta }})=\frac{1}{2}\Vert {\varvec{Y}}_k-{\varvec{\varPhi }}_k{\varvec{\theta }}\Vert ^2. \end{aligned}$$

Minimizing the criterion function \(J({\varvec{\theta }})\) gives the least squares parameter estimate

$$\begin{aligned} \hat{{\varvec{\theta }}}(k)=({\varvec{\varPhi }}_k^{\tiny \text{ T }}{\varvec{\varPhi }}_k)^{-1}{\varvec{\varPhi }}_k^{\tiny \text{ T }}{\varvec{Y}}_k. \end{aligned}$$
(13)

Obviously, the least squares estimate \(\hat{\varvec{\theta }}(k)\) involves computing the inverse matrix \(({\varvec{\varPhi }}_k^{\tiny \text{ T }}{\varvec{\varPhi }}_k)^{-1}\). In order to avoid computing the inverse matrix, this paper develops a RLS algorithm to estimate the parameters of the combination sine signal for the online estimation. Define a matrix

$$\begin{aligned} {\varvec{P}}^{-1}(k):={\varvec{\varPhi }}_k^{\tiny \text{ T }}{\varvec{\varPhi }}_k=\sum _{j=1}^k{\varvec{\varphi }}(j){\varvec{\varphi }}^{\tiny \text{ T }}(j). \end{aligned}$$
(14)

Rewriting (14), we have

$$\begin{aligned} {\varvec{P}}^{-1}(k)=\sum _{j=1}^{k-1}{\varvec{\varphi }}(j){\varvec{\varphi }}^{\tiny \text{ T }}(j)+{\varvec{\varphi }}(k){\varvec{\varphi }}^{\tiny \text{ T }}(k). \end{aligned}$$
(15)

Ulteriorly, Eq. (15) can be represented as

$$\begin{aligned} {\varvec{P}}^{-1}(k)={\varvec{P}}^{-1}(k-1) +{\varvec{\varphi }}(k){\varvec{\varphi }}^{\tiny \text{ T }}(k)={\varvec{P}}^{-1}(0) +\sum _{j=1}^k{\varvec{\varphi }}(j){\varvec{\varphi }}^{\tiny \text{ T }}(j), \end{aligned}$$

where \({\varvec{P}}^{-1}(0)=p_0{\varvec{I}}>0\),    \(p_0=10^6\).

Because \({\varvec{Y}}_k:=\left[ \begin{array}{l} {\varvec{Y}}_{k-1} \\ y(k) \end{array} \right] \in {\mathbb R}^{k}\),    \({\varvec{\varPhi }}_k:=\left[ \begin{array}{l} {\varvec{\varPhi }}_{k-1} \\ {\varvec{\varphi }}^{\tiny \text{ T }}(k) \end{array} \right] \in {\mathbb R}^{k\times {2n}}\), Eq. (13) can be represented as

$$\begin{aligned} \hat{{\varvec{\theta }}}(k)= & {} {\varvec{P}}(k){\varvec{\varPhi }}_k^{\tiny \text{ T }}{\varvec{Y}}_k \\= & {} {\varvec{P}}(k)\left[ \begin{array}{l} {\varvec{\varPhi }}_{k-1} \\ {\varvec{\varphi }}^{\tiny \text{ T }}(k) \end{array} \right] ^{\tiny \text{ T }}\left[ \begin{array}{l} {\varvec{Y}}_{k-1} \\ y(k) \end{array} \right] \\= & {} {\varvec{P}}(k)[{\varvec{\varPhi }}_{k-1}{\varvec{Y}}_{k-1}+{\varvec{\varphi }}(k)y(k)]\\= & {} {\varvec{P}}(k)[{\varvec{P}}^{-1}(k-1){\varvec{P}}(k-1){\varvec{\varPhi }}_{k-1}{\varvec{Y}}_{k-1}+{\varvec{\varphi }}(k)y(k)]\\= & {} {\varvec{P}}(k)[{\varvec{P}}^{-1}(k-1)\hat{{\varvec{\theta }}}(k-1)+{\varvec{\varphi }}(k)y(k)]\\= & {} {\varvec{P}}(k)[{\varvec{P}}^{-1}(k)-{\varvec{\varphi }}(k){\varvec{\varphi }}^{\tiny \text{ T }}(k)]\hat{{\varvec{\theta }}}(k-1)+{\varvec{P}}(k){\varvec{\varphi }}(k)y(k)\\= & {} \hat{{\varvec{\theta }}}(k-1)+{\varvec{P}}(k){\varvec{\varphi }}(k)[y(k)-{\varvec{\varphi }}^{\tiny \text{ T }}(k)\hat{{\varvec{\theta }}}(k-1)]. \end{aligned}$$

In order to avoid computing the inverse matrix \({\varvec{P}}^{-1}(k)\), we use the matrix inverse forum \(({\varvec{A}}+{\varvec{B}}{\varvec{C}})^{-1}={\varvec{A}}^{-1}{\varvec{B}}({\varvec{I}}+{\varvec{C}}{\varvec{A}}^{-1}{\varvec{B}})^{-1}{\varvec{C}}{\varvec{A}}^{-1}\) to \({\varvec{P}}^{-1}(k)={\varvec{P}}^{-1}(k-1)+{\varvec{\varphi }}(k){\varvec{\varphi }}^{\tiny \text{ T }}(k)\), and have

$$\begin{aligned} {\varvec{P}}(k)={\varvec{P}}(k-1)-\frac{{\varvec{P}}(k-1){\varvec{\varphi }}(k){\varvec{\varphi }}^{-1}(k){\varvec{P}}(k-1)}{1+{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}. \end{aligned}$$
(16)

Introducing the gain vector \({\varvec{L}}(k):={\varvec{P}}(k){\varvec{\varphi }}(k)\) and multiplying by \({\varvec{\varphi }}(k)\) both side of (16), we have

$$\begin{aligned} {\varvec{P}}(k){\varvec{\varphi }}(k)= & {} \left[ {\varvec{P}}(k-1)-\frac{{\varvec{P}}(k-1){\varvec{\varphi }}(k){\varvec{\varphi }}^{-1}(k){\varvec{P}}(k-1)}{1+{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}\right] {\varvec{\varphi }}(k)\\= & {} {\varvec{P}}(k-1){\varvec{\varphi }}(k)\left[ 1-\frac{{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}{1+{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}\right] . \end{aligned}$$

From the above analysis, we obtain the following equation

$$\begin{aligned} {\varvec{L}}(k)={\varvec{P}}(k-1){\varvec{\varphi }}(k)\left[ 1-\frac{{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}{1+{\varvec{\varphi }}(k){\varvec{P}}(k-1){\varvec{\varphi }}(k)}\right] . \end{aligned}$$

However, the parameters in the parameter vector \({\varvec{\theta }}\) are not the characteristic parameters of the combination sine signal. According to the previous definition \(c_i:=a_i\cos \phi _i\), \(d_i:=a_i\sin \phi _i\), the estimates of the characteristic parameters \(a_i\) and \(\phi _i\) are computed by

$$\begin{aligned} \hat{a}_i(k)=\sqrt{\hat{c}^2_i(k)+\hat{d}^2_i(k)}, \quad \hat{\phi }_i(k)=\arctan {\frac{\hat{d}_i(k)}{\hat{c}_i(k)}}. \end{aligned}$$

Let \(\hat{{\varvec{\theta }}}_r(k):=[\hat{a}_1(k),\ldots ,\hat{a}_n(k),\hat{\phi }_1(k),\ldots ,\hat{\phi }_n(k)]^{\tiny \text{ T }}\in {\mathbb R}^{2n}\) denote the estimates of the characteristic parameters of the combination sine signal.

Finally, we obtain the RLS algorithm:

$$\begin{aligned} \hat{{\varvec{\theta }}}(k)= & {} \hat{{\varvec{\theta }}}(k-1)+{\varvec{L}}(k)[y(k)-{\varvec{\varphi }}(k)\hat{{\varvec{\theta }}}(k-1)], \end{aligned}$$
(17)
$$\begin{aligned} {\varvec{L}}(k)= & {} \frac{{\varvec{P}}(k-1){\varvec{\varphi }}(k)}{1+{\varvec{\varphi }}^{\tiny \text{ T }}(k)[{\varvec{P}}(k-1){\varvec{\varphi }}(k)]}, \end{aligned}$$
(18)
$$\begin{aligned} {\varvec{P}}(k)= & {} {\varvec{P}}(k-1)-{\varvec{L}}(k)[{\varvec{P}}(k-1){\varvec{\varphi }}(k)]^{\tiny \text{ T }}, \quad {\varvec{P}}(0)=p_0{\varvec{I}}, \end{aligned}$$
(19)
$$\begin{aligned} {\varvec{\varphi }}(k)= & {} [\sin \omega _1kh,\cos \omega _1kh,\sin \omega _2kh,\cos \omega _2kh, \ldots ,\sin \omega _nkh,\cos \omega _nkh]^{\tiny \text{ T }}, \quad \end{aligned}$$
(20)
$$\begin{aligned} \hat{a}_i(k)= & {} \sqrt{\hat{c}^2_i(k)+\hat{d}^2_i(k)}, \quad \hat{\phi }_i(k)=\arctan {\frac{\hat{d}_i(k)}{\hat{c}_i(k)}}, \quad i=1,2,\ldots ,n, \end{aligned}$$
(21)
$$\begin{aligned} \hat{{\varvec{\theta }}}_r(k)= & {} [\hat{a}_1(k),\hat{\phi }_1(k),\ldots ,\hat{a}_n(k),\hat{\phi }_n(k)]^{\tiny \text{ T }}. \end{aligned}$$
(22)

The steps of computing the characteristic parameter estimate are as follows.

  1. 1.

    To initialize: let \(k=0\) and preset recursive length L; let \(\hat{{\varvec{\theta }}}(0)\) be an arbitrary small vector; let \(p_0=10^6\).

  2. 2.

    Collect the measured data y(k).

  3. 3.

    Compute \({\varvec{\varphi }}(k)\) using (20); compute \({\varvec{P}}(k)\) using (19).

  4. 4.

    Compute \({\varvec{L}}(k)\) using (18).

  5. 5.

    Update the parameter estimate \(\hat{{\varvec{\theta }}}(k)\) using (17) and obtain the characteristic parameter estimate \(\hat{{\varvec{\theta }}}_r(k)\) using (21)–(22), if \(k=L\), terminate the recursive procedure and obtain the parameter estimate \(\hat{{\varvec{\theta }}}_r(k)\); otherwise, go to Step 2.

5 Illustrative Examples

Example 1

Consider the combination sine signals with four different frequencies,

$$\begin{aligned} y(t)= & {} 1.8\sin {(0.07t+0.95)}+2.9\sin {(0.5t+0.8)}+4\sin {(2t+0.76)}\\&+2.5\sin {(1.6t+1.1)}, \end{aligned}$$

where \(a_1=1.8\), \(a_2=2.9\), \(a_3=4\), \(a_4=2.5\), \(\phi _1=0.95\), \(\phi _2=0.8\), \(\phi _3=0.76\), \(\phi _4=1.1\) are the true values of the parameters to be estimated and \(\omega _1=0.07\) rad/s, \(\omega _2=0.5\) rad/s, \(\omega _3=2\) rad/s, \(\omega _4=1.6\) rad/s are the known angular frequency.

Case 1

The MISG method simulation.

Use the proposed MISG algorithm to estimate the characteristic parameters of the combination sine signals in this example. In the simulation, the white noise sequence with zero mean and variance \(\sigma ^2=0.20^2\) is added to the signal. The sampling period is \(h=0.2\) s, and the data length is \(L=2000\). In order to test the performance of the MISG algorithm, three different innovation length data with \(p=1\), \(p=4\) and \(p=6\) are adopted. The parameter estimates and their estimation errors \(\delta :=\Vert \hat{{\varvec{\theta }}}(k)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \) are listed in Table 1. The parameter estimation errors \(\delta :=\Vert \hat{{\varvec{\theta }}}(k)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \) versus k are shown in Fig. 1. In addition, the estimated signal and the actual signal are compared for testing the estimation accuracy. The comparison results are shown in Fig. 2, where the dot-line denotes the estimated signal and the solid-line denotes the actual signal.

Table 1 The MISG parameter estimates and their estimation errors
Full size table

Case 2

The RLS method simulation.

Next, the proposed RLS algorithm is used to estimate the characteristic parameters. In the simulation, the white noise sequence with zero mean and variance \(\sigma ^2=0.10^2\), \(\sigma ^2=0.50^2\) are added, respectively, to the combination sine signal. In the simulation, the sampling period is \(h=1\) s and the data length is \(L=2000\). The parameter estimates and their estimation errors \(\delta :=\Vert \hat{{\varvec{\theta }}}(k)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \) are shown in Table 2. The parameter estimation errors versus k are shown in Fig. 3.

Fig. 1
figure 1

The MISG estimation error \(\delta \) versus k

Full size image
Fig. 2
figure 2

The MISG fitting curves

Full size image

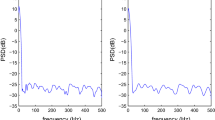
For the purpose of testing the performance of the proposed RLS method, the estimated combination sine signal obtained by the RLS method and the actual combination sine signal are shown in Fig. 4.

Example 2

In this example, a period signal is provided to test the proposed parameter estimation method. Consider a period square wave with the following description,

$$\begin{aligned} f(t)={\left\{ \begin{array}{ll} A, &{} -\frac{T}{2}\le t <0,\\ -A, &{} 0\le t\le \frac{T}{2}, \end{array}\right. } \end{aligned}$$

where \(T=\frac{2\pi }{3}\) s, \(A=2\). The period square wave is shown in Fig. 5.

Using the Fourier expansion, this square wave can be expanded into the sum of odd harmonics. According to the Fourier expansion formula, the coefficients are, respectively

Table 2 The RLS parameter estimates and their estimation errors
Full size table
$$\begin{aligned} a_i= & {} \frac{2}{T}\int _{-\frac{T}{2}}^{0}-A\cos {i\omega _0t\mathrm{d}t} +\frac{2}{T}\int _{0}^{\frac{T}{2}}A\cos {i\omega _0t\mathrm{d}t} \\= & {} \frac{-2A}{Ti\omega _0}\sin {i\omega _0t}\bigg |_{-\frac{T}{2}}^0 +\frac{2A}{Ti\omega _0}\sin {i\omega _0t}\bigg |_0^{\frac{T}{2}}=0, \\ b_i= & {} \frac{2}{T}\int _{-\frac{T}{2}}^{0}-A\sin {i\omega _0t\mathrm{d}t} +\frac{2}{T}\int _{0}^{\frac{T}{2}}A\sin {i\omega _0t\mathrm{d}t} \\= & {} \frac{2A}{Ti\omega _0}\cos {i\omega _0t}\bigg |_{-\frac{T}{2}}^0 +\frac{-2A}{Ti\omega _0}\cos {i\omega _0t}\bigg |_0^{\frac{T}{2}} =\frac{A}{\pi i}(2-2\cos {i\pi }). \end{aligned}$$
Fig. 3
figure 3

The RLS estimation error \(\delta \) versus k of Example 1

Full size image
Fig. 4
figure 4

The RLS fitting curves

Full size image

As a result, when i is even number, \(b_i=0\); when i is odd number, \(b_i=\frac{4A}{\pi i}\). Therefore, the Fourier expansion is given by

$$\begin{aligned} f(t)=\frac{4A}{\pi }\left( \sin \omega _0t+ \frac{1}{3}\sin 3\omega _0t+\frac{1}{5}\sin 5\omega _0t+\cdots +\frac{1}{n}\sin n\omega _0t+\cdots \right) . \end{aligned}$$

where \(\omega _0\) is the fundamental harmonic frequency and \(\omega _0=2\pi /T\). The fundamental harmonic frequency equals the frequency of the square wave.

Taking the 1, 3, 5, 7 harmonics, we have

$$\begin{aligned} f(t)=\frac{4A}{\pi }\left( \sin \omega _0t+ \frac{1}{3}\sin 3\omega _0t+\frac{1}{5}\sin 5\omega _0t+\frac{1}{7}\sin 7\omega _0t\right) . \end{aligned}$$

Let \(a_1:=\frac{4A}{\pi }\), \(a_2:=\frac{4A}{3\pi }\), \(a_3:=\frac{4A}{5\pi }\) and \(a_4:=\frac{4A}{7\pi }\), f(t) becomes

$$\begin{aligned} f(t)=a_1\sin \omega _0t+a_2\sin 3\omega _0t+a_3\sin 5\omega _0t+a_4\sin 7\omega _0t. \end{aligned}$$

In the above equation, the amplitudes are unknown, while the phases are zero. Using the proposed RLS parameter estimation method to estimate parameters \(a_1\), \(a_2\), \(a_3\) and \(a_4\), the parameter estimates and their estimation errors \(\delta :=\Vert \hat{{\varvec{\theta }}}(k)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \) are displayed in Table 3. The parameter estimation errors versus k are shown in Fig. 6.

Choosing the estimated parameters with \(k=2000\) and \(\sigma ^2=0.20^2\), we obtain the following function

$$\begin{aligned} f(t)=2.54441\sin 3t+0.84968\sin 9t+0.51463\sin 15t+0.36396\sin 21t. \end{aligned}$$

The estimated square wave and the original square wave are shown in Fig. 7.

Fig. 5
figure 5

The square signal wave

Full size image
Table 3 The RLS parameter estimates and the estimation errors for the square wave
Full size table
Fig. 6
figure 6

The RLS estimation error \(\delta \) versus k of Example 2

Full size image
Fig. 7
figure 7

The RLS square wave fitting curves of Example 2

Full size image

From the simulation results, we can draw the following conclusions.

  1. 1.

    Table 1 and Fig. 1 show that the parameter estimates obtained by the MISG method become more accurate with the increasing in the innovation length p.

  2. 2.

    When \(p=1\), the MISG method degenerates into the SG method. From the last column in Table 1, it can be seen that the MISG method has higher accuracy than the SG method.

  3. 3.

    The parameter estimation errors given by the RLS algorithm become smaller with the increasing in k—see Figs. 3 and 6. The parameter estimation accuracy is related to the noise variance. The larger the noise variance is, the lower the parameter estimation accuracy is.

  4. 4.

    The fitting curve given by the RLS method is more closed to the actual signal curve than the fitting curve given by the MISG method—see Figs. 3 and 4. This means that the RLS algorithm has more effectiveness than the MISG method.

6 Conclusion

This paper considers the parameter estimation problems of the periodic signals based on the combination sine signals. According to the gradient searching, the SG parameter estimation algorithm for the combination sine signal is derived. On the basis of the SG algorithm, the MISG parameter estimation method is proposed for improving the estimation accuracy. Furthermore, the RLS parameter estimation algorithm is derived for enhancing the estimation accuracy by the function expansion. The simulation results show that the MISG algorithm and the RLS method can estimate the signal parameters. Because the RLS algorithm is derived by means of the linear optimization while the MISG method is deduced by means of the nonlinear optimization principle, the RLS algorithm has higher accuracy and stabilization than the MISG method. The method used in this paper can be extended to analyze the convergence of the identification algorithms for linear or nonlinear control systems [6, 20, 21] and applied to hybrid switching-impulsive dynamical networks [18] and uncertain chaotic delayed nonlinear systems [17] or applied to other fields [4, 33, 34].