Recursive Least Squares Parameter Estimation for a Class of Output Nonlinear Systems Based on the Model Decomposition

Abstract

In this paper, we study the parameter estimation problem of a class of output nonlinear systems and propose a recursive least squares (RLS) algorithm for estimating the parameters of the nonlinear systems based on the model decomposition. The proposed algorithm has lower computational cost than the existing over-parameterization model-based RLS algorithm. The simulation results indicate that the proposed algorithm can effectively estimate the parameters of the nonlinear systems.

1 Introduction

Iterative methods and recursive methods have widely been used in system identification [7, 8, 15], system control [31, 33], signal processing [30] and multivariate pseudo-linear regressive analysis [37] and for solving matrix equations [6]. The parameter estimation methods have received much attention in system identification [28, 38, 39]. For example, Wang [35] gave a least squares-based recursive estimation algorithm and an iterative estimation algorithm for output error moving average systems using the data filtering technique. Dehghan et al. [5] studied the fourth-order variants of the Newton’s method without the second-order derivatives for solving nonlinear equations. Shi et al. [32] studied the output feedback stabilization of networked control systems with random delays modeled by the Markov chains. Li [25] developed a maximum likelihood estimation algorithm for Hammerstein CARARMA systems based on the Newton iteration. Wang and Zhang [43] proposed an improved least squares identification algorithm for multivariable Hammerstein systems.

The typical nonlinear systems include the Wiener systems [14], the Hammerstein systems [18], the Hammerstein–Wiener systems [3] and feedback nonlinear systems [1, 20]. A Wiener nonlinear model is composed of a linear dynamic block followed by a static nonlinear function and a Hammerstein model puts a nonlinear function before a linear dynamic block [2, 44]. Vörös [34] proposed the key term separation technique for identifying Hammerstein systems with multi-segment piecewise-linear characteristics. Recently, a decomposition-based Newton iterative identification method was proposed for a Hammerstein nonlinear FIR system with ARMA noise [12].

This paper considers the parameter identification problem of a special class of output nonlinear systems, whose output is the nonlinear function of the past outputs [7, 8]. For this class of nonlinear systems with colored noise, Wang et al. [36] gave a least squares-based and a gradient-based iterative identification algorithms; Hu et al. [21] proposed a recursive extended least squares parameter estimation algorithm using the over-parameterization model and a multi-innovation generalized extended stochastic gradient algorithm for nonlinear autoregressive moving average systems [22]; Bai presented an optimal two-stage identification algorithm for Hammerstein–Wiener nonlinear systems [4]. The least squares algorithms play a key role in the parameter estimation of linear systems [17, 19, 29]. This paper derives a new recursive least squares algorithm for output nonlinear systems using the hierarchical identification principle. The proposed method has less computational load and can be extended to study parameter estimation of dual-rate/multi-rate sampled systems [9, 10, 26].

This paper is organized as follows: Section 2 gives the representation of a class of nonlinear systems. Sections 3 and 4 derive a least squares algorithm and a model decomposition-based recursive least squares algorithm. Section 5 gives the computational efficiency of the proposed algorithm and the recursive extended least squares algorithm. Section 6 provides a numerical example to show the effectiveness of the proposed algorithm. Finally, some concluding remarks are offered in Sect. 7.

2 The System Description and its Identification Model

Let us define some notation. “$A=:X$”or “$X:=A$” stands for “A is defined as X”; $\mathbf{1}_n$ denotes an n-dimensional column vector whose elements are all 1; ${\varvec{I}}$ (${\varvec{I}}_n$) represents an identity matrix of appropriate sizes ($n\times n$); z denotes a unit forward shift operator with $zx(t)=x(t+1)$ and $z^{-1}x(t)=x(t-1)$. Define the polynomials in the unit backward shift operator $z^{-1}$:

$$\begin{aligned} A'(z):= & {} a'_1z^{-1}+a'_2z^{-2}+\cdots +a'_{n_a}z^{-n_a},\\ A(z):= & {} a_1z^{-1}+a_2z^{-2}+\cdots +a_{n_a}z^{-n_a},\\ B(z):= & {} b_1z^{-1}+b_2z^{-2}+\cdots +b_{n_b}z^{-n_b},\\ D(z):= & {} 1+d_1z^{-1}+d_2z^{-2}+\cdots +d_{n_d}z^{-n_d}, \end{aligned}$$

and the parameter vectors:

$$\begin{aligned} {\varvec{a}}:= & {} [a_1, a_2, \ldots , a_{n_a}]^{\tiny \text{ T }}\in {\mathbb R}^{n_a},\\ {\varvec{b}}:= & {} [b_1, b_2, \ldots , b_{n_b}]^{\tiny \text{ T }}\in {\mathbb R}^{n_b},\\ {\varvec{c}}:= & {} [c_1, c_2, \ldots , c_{n_c}]^{\tiny \text{ T }}\in {\mathbb R}^{n_c},\\ {\varvec{d}}:= & {} [d_1, d_2, \ldots , d_{n_d}]^{\tiny \text{ T }}\in {\mathbb R}^{n_d}. \end{aligned}$$

A Hammerstein system (i.e., an input nonlinear system) can be expressed as [11]

$$\begin{aligned} y(t)=A'(z)y(t)+B(z)f(u(t))+D(z)v(t), \end{aligned}$$

by extending the input nonlinearity to the output nonlinearity, we can obtain a special class of nonlinear systems [21, 36]:

$$\begin{aligned} y(t)=A(z)f(y(t))+B(z)u(t)+D(z)v(t), \end{aligned}$$

(1)

where u(t) and y(t) are the input and output of the system, respectively, and v(t) is white noise with zero mean and variance $\sigma ^2$.

For simplicity, assume that the nonlinear part is a linear combination of a known basis ${\varvec{f}}:=(f_1, f_2, \ldots , f_{n_c})$ with coefficients $(c_1, c_2, \ldots , c_{n_c})$:

$$\begin{aligned} \bar{y}(t):=f(y(t))=c_1f_1(y(t))+c_2f_2(y(t))+\cdots +c_{n_c}f_{n_c}(y(t))={\varvec{f}}(y(t)){\varvec{c}}. \end{aligned}$$

For the parameter identifiability, we must fix one of the coefficients $c_i$’s, or $\Vert {\varvec{c}}\Vert =1$ with $c_1>0$ [11].

Equation (1) can be rewritten as

$$\begin{aligned} y(t)= & {} \sum \limits _{i=1}^{n_a}{a_i}z^{-i}{f(y(t))} +\sum \limits _{i=1}^{n_b}{b_i}z^{-i}{u(t)}+\sum \limits _{i=1}^{n_d}d_iz^{-i}v(t)+v(t)\nonumber \\= & {} a_1f(y(t-1))+a_2f(y(t-2))+\cdots +a_{n_a}f(y(t-n_a))\nonumber \\&+\,b_1u(t-1)+b_2u(t-2)+\cdots +b_{n_b}u(t-n_b)\nonumber \\&+\,d_1v(t-1)+d_2v(t-2)+\cdots +d_{n_d}v(t-{n_d})+v(t). \end{aligned}$$

(2)

Define the information matrix ${\varvec{F}}(t)$, the input information vector ${\varvec{\varphi }}(t)$ and the noise information vector ${\varvec{\psi }}(t)$ as

$$\begin{aligned} {\varvec{F}}(t):= & {} \left[ \begin{array}{cccc}f_1(y(t-1)) &{} f_2(y(t-1)) &{} \ldots &{} f_{n_c}(y(t-1))\\ f_1(y(t-2)) &{} f_2(y(t-2)) &{} \ldots &{} f_{n_c}(y(t-2))\\ \vdots &{} \vdots &{} &{} \vdots \\ f_1(y(t-n_a)) &{} f_2(y(t-n_a)) &{} \ldots &{} f_{n_c}(y(t-n_a))\\ \end{array}\right] \in {\mathbb R}^{n_a\times n_c}, \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{\varphi }}(t):= & {} [u(t-1), u(t-2), \ldots , u(t-n_b)]^{\tiny \text{ T }}\in {\mathbb R}^{n_b}, \end{aligned}$$

(4)

$$\begin{aligned} {\varvec{\psi }}(t):= & {} [v(t-1), v(t-2), \ldots , v(t-n_d)]^{\tiny \text{ T }}\in {\mathbb R}^{n_d}. \end{aligned}$$

(5)

Then, Eq. (2) can be written as

$$\begin{aligned} y(t)={\varvec{a}}^{\tiny \text{ T }}{\varvec{F}}(t){\varvec{c}}+{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}+{\varvec{\psi }}^{\tiny \text{ T }}(t){\varvec{d}}+v(t). \end{aligned}$$

(6)

The objective of identification is to present new methods for estimating the unknown parameter vector ${\varvec{c}}$ for the nonlinear part and the unknown parameter vectors ${\varvec{a}}$, ${\varvec{b}}$ and ${\varvec{d}}$ for the linear subsystems from the measurement data $\{u(t), y(t):\ t=1, 2, 3,\ldots \}$.

3 The Least Squares Algorithm Based on the Model Decomposition

Let $\hat{{\varvec{\theta }}}(t):=\left[ \begin{array}{c} \hat{{\varvec{a}}}(t) \\ \hat{{\varvec{d}}}(t) \end{array} \right]$ and $\hat{{\varvec{\vartheta }}}(t):=\left[ \begin{array}{c} \hat{{\varvec{b}}}(t) \\ \hat{{\varvec{c}}}(t) \end{array} \right]$ denote the estimates of ${\varvec{\theta }}:=\left[ \begin{array}{c} {\varvec{a}} \\ {\varvec{d}} \end{array} \right]$ and ${\varvec{\vartheta }}:=\left[ \begin{array}{c} {\varvec{b}} \\ {\varvec{c}} \end{array} \right]$ at time t, respectively, and ${\varvec{\varTheta }}:=\left[ \begin{array}{c} {\varvec{\theta }} \\ {\varvec{\vartheta }} \end{array} \right]$. For the identification model in (6), using the hierarchical identification principle (the decomposition technique), define the quadratic cost functions:

$$\begin{aligned} J_1({\varvec{\theta }}):= & {} J({\varvec{a}}, \hat{{\varvec{b}}}(t-1), \hat{{\varvec{c}}}(t-1), {\varvec{d}})\\= & {} \sum \limits _{j=1}^t\left[ \begin{array}{c}y(j)-{\varvec{\varphi }}^{\tiny \text{ T }}(j) \hat{{\varvec{b}}}(t-1)-[\hat{{\varvec{c}}}^{\tiny \text{ T }}(t-1){\varvec{F}}^{\tiny \text{ T }}(j), {\varvec{\psi }}^{\tiny \text{ T }}(j)] {\varvec{\theta }}\end{array}\right] ^2,\\ J_2({\varvec{\vartheta }}):= & {} J(\hat{{\varvec{a}}}(t), {\varvec{b}}, {\varvec{c}}, \hat{{\varvec{d}}}(t))\\= & {} \sum \limits _{j=1}^t\left[ \begin{array}{c}y(j)-{\varvec{\psi }}^{\tiny \text{ T }}(j) \hat{{\varvec{d}}}(t)-[{\varvec{\varphi }}^{\tiny \text{ T }}(j), \hat{{\varvec{a}}}^{\tiny \text{ T }}(t){\varvec{F}}(j)] {\varvec{\vartheta }}\end{array}\right] ^2. \end{aligned}$$

Define the output vector ${\varvec{Y}}_t$ and the information matrices ${\varvec{\varPhi }}_t$, ${\varvec{\varPsi }}_t$, ${\varvec{\varOmega }}_t$ and ${\varvec{\varXi }}_t$ as

$$\begin{aligned} {\varvec{Y}}_t:= & {} [y(1), y(2), \ldots , y(t)]^{\tiny \text{ T }}\in {\mathbb R}^t, \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{\varPhi }}_t:= & {} [{\varvec{\varphi }}(1),{\varvec{\varphi }}(2), \ldots , {\varvec{\varphi }}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{t\times {n_b}}, \end{aligned}$$

(8)

$$\begin{aligned} {\varvec{\varPsi }}_t:= & {} [{\varvec{\psi }}(1), {\varvec{\psi }}(2), \ldots , {\varvec{\psi }}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{t\times {n_d}}, \end{aligned}$$

(9)

$$\begin{aligned} \hat{{\varvec{\varOmega }}}_t:= & {} \left[ \begin{array}{cccc}{\varvec{F}}(1)\hat{{\varvec{c}}}(t-1) &{} {\varvec{F}}(2)\hat{{\varvec{c}}}(t-1) &{} \ldots &{} {\varvec{F}}(t)\hat{{\varvec{c}}}(t-1)\\ \hat{{\varvec{\psi }}}(1) &{} \hat{{\varvec{\psi }}}(2) &{} \ldots &{}\hat{{\varvec{\psi }}}(t)\\ \end{array}\right] ^{\tiny \text{ T }}\in {\mathbb R}^{t\times (n_a+n_d)}, \end{aligned}$$

(10)

$$\begin{aligned} \hat{{\varvec{\varXi }}}_t:= & {} \left[ \begin{array}{cccc}{\varvec{\varphi }}(1) &{} {\varvec{\varphi }}(2) &{} \ldots &{} {\varvec{\varphi }}(t)\\ {\varvec{F}}^{\tiny \text{ T }}(1)\hat{{\varvec{a}}}(t) &{} {\varvec{F}}^{\tiny \text{ T }}(2)\hat{{\varvec{a}}}(t) &{} \ldots &{} {\varvec{F}}^{\tiny \text{ T }}(t)\hat{{\varvec{a}}}(t)\\ \end{array}\right] ^{\tiny \text{ T }}\in {\mathbb R}^{t\times (n_b+n_c)}. \ \end{aligned}$$

(11)

Then, $J_1({\varvec{\theta }})$ and $J_2({\varvec{\vartheta }})$ can be equivalently written as

$$\begin{aligned} J_1({\varvec{\theta }})= & {} \Vert {\varvec{Y}}_t-{\varvec{\varPhi }}_t\hat{{\varvec{b}}}(t-1)-\hat{{\varvec{\varOmega }}}_t{\varvec{\theta }}\Vert ^2,\\ J_2({\varvec{\vartheta }})= & {} \Vert {\varvec{Y}}_t-{\varvec{\varPsi }}_t\hat{{\varvec{d}}}(t)-\hat{{\varvec{\varXi }}}_t{\varvec{\vartheta }}\Vert ^2. \end{aligned}$$

For the two optimization problems, letting the partial derivatives of $J_1({\varvec{\theta }})$ and $J_2({\varvec{\vartheta }})$ with respect to ${\varvec{\theta }}$ and ${\varvec{\vartheta }}$ be zero gives

$$\begin{aligned} \left. \frac{\partial J_1({\varvec{\theta }})}{\partial {\varvec{\theta }}}\right| _{{{\varvec{\theta }}}=\hat{{\varvec{\theta }}}(t)}= & {} -2\hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t[{\varvec{Y}}_t-{\varvec{\varPhi }}_t\hat{{\varvec{b}}}(t-1)-\hat{{\varvec{\varOmega }}}_t\hat{{\varvec{\theta }}}(t)] =\mathbf{0}, \end{aligned}$$

(12)

$$\begin{aligned} \left. \frac{\partial J_2({\varvec{\vartheta }})}{\partial {\varvec{\vartheta }}}\right| _{{{\varvec{\vartheta }}}=\hat{{\varvec{\vartheta }}}(t)}= & {} -2\hat{{\varvec{\varXi }}}^{\tiny \text{ T }}_t[{\varvec{Y}}_t-{\varvec{\varPsi }}_t\hat{{\varvec{d}}}(t)-\hat{{\varvec{\varXi }}}_t\hat{{\varvec{\vartheta }}}(t)] =\mathbf{0}. \end{aligned}$$

(13)

or

$$\begin{aligned} \hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t\hat{{\varvec{\varOmega }}}_t\hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t[{\varvec{Y}}_t-{\varvec{\varPhi }}_t\hat{{\varvec{b}}}(t-1)],\\ \hat{{\varvec{\varXi }}}_t^{\tiny \text{ T }}\hat{{\varvec{\varXi }}}_t\hat{{\varvec{\vartheta }}}(t)= & {} \hat{{\varvec{\varXi }}}^{\tiny \text{ T }}_t[{\varvec{Y}}_t-{\varvec{\varPsi }}_t\hat{{\varvec{d}}}(t)]. \end{aligned}$$

In order to ensure that the inverses of the matrices $\hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t\hat{{\varvec{\varOmega }}}_t$ and $\hat{{\varvec{\varXi }}}_t^{\tiny \text{ T }}\hat{{\varvec{\varXi }}}_t$ exist, we suppose that the information matrices $\hat{{\varvec{\varOmega }}}_t$ and $\hat{{\varvec{\varXi }}}_t$ are persistently exciting. Let $\hat{{\varvec{\varPsi }}}_t$, $\hat{{\varvec{\psi }}}(t)$ $\hat{v}(t)$ be the estimates of ${\varvec{\varPsi }}_t$, ${\varvec{\psi }}(t)$ and v(t) at time t.

Replacing the unknown ${\varvec{\varPsi }}_t$ in (12)–(13) with $\hat{{\varvec{\varPsi }}}_t$, we have the following least squares algorithm for estimating the parameter vectors ${\varvec{\theta }}$ and ${\varvec{\vartheta }}$:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} [\hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t\hat{{\varvec{\varOmega }}}_t]^{-1}\hat{{\varvec{\varOmega }}}^{\tiny \text{ T }}_t[{\varvec{Y}}_t-{\varvec{\varPhi }}_t\hat{{\varvec{b}}}(t-1)], \end{aligned}$$

(14)

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} [\hat{{\varvec{\varXi }}}_t^{\tiny \text{ T }}\hat{{\varvec{\varXi }}}_t]^{-1}\hat{{\varvec{\varXi }}}_t[{\varvec{Y}}_t-\hat{{\varvec{\varPsi }}}_t\hat{{\varvec{d}}}(t)], \end{aligned}$$

(15)

$$\begin{aligned} \hat{{\varvec{\varPsi }}}_t= & {} [\hat{{\varvec{\psi }}}(1), \hat{{\varvec{\psi }}}(2), \ldots , \hat{{\varvec{\psi }}}(t)]^{\tiny \text{ T }}, \end{aligned}$$

(16)

$$\begin{aligned} \hat{{\varvec{\psi }}}(t)= & {} [\hat{v}(t-1), \hat{v}(t-2), \ldots , \hat{v}(t-n_d)]^{\tiny \text{ T }}, \end{aligned}$$

(17)

$$\begin{aligned} \hat{v}(t)= & {} y(t)-\hat{{\varvec{a}}}^{\tiny \text{ T }}(t){\varvec{F}}(t)\hat{{\varvec{c}}}(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t)-\hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{d}}}(t). \end{aligned}$$

(18)

The procedures of computing the parameter estimates $\hat{{\varvec{\theta }}}(t)$ and $\hat{{\varvec{\vartheta }}}(t)$ are listed in the following.

• 1. To initialize: let $t=p$, collect the input–output data $\{u(i),y(i): i=0, 1, 2, \ldots , p-1\}$ ($p\gg n_a+n_b+n_c+n_d$) and set the initial values $\hat{{\varvec{b}}}(p-1)=\mathbf{1}_{n_b}/{p_0}$, $\hat{{\varvec{c}}}(p-1)=$ a random vector with $\Vert \hat{{\varvec{c}}}(p-1)\Vert =1$, $\hat{v}(i)=$ a random number. $p_0$ is normally a large positive number (e.g., $p_0=10^6$), give the basis function $f_j(*)$.

• 2. Collect the input–output data u(t) and y(t), form ${\varvec{Y}}_t$ using (7), ${\varvec{F}}(t)$ using (3), ${\varvec{\varphi }}(t)$ using (4), ${\varvec{\varPhi }}_t$ using (8) and $\hat{{\varvec{\psi }}}(t)$ using (17).

• 3. Compute $\hat{{\varvec{\varOmega }}}_t$ using (10).

• 4. Update the parameter estimate $\hat{{\varvec{\theta }}}(t)$ using (14) and read $\hat{{\varvec{a}}}(t)$ and $\hat{{\varvec{d}}}(t)$ from $\hat{{\varvec{\theta }}}(t)=\left[ \begin{array}{c} \hat{{\varvec{a}}}(t) \\ \hat{{\varvec{d}}}(t) \end{array} \right]$.

• 5. Compute $\hat{{\varvec{\varXi }}}_t$ using (11) and form $\hat{{\varvec{\varPsi }}}_t$ using (16).

• 6. Update the parameter estimate $\hat{{\varvec{\vartheta }}}(t)$ using (15), read $\hat{{\varvec{b}}}(t)$ from $\hat{{\varvec{\vartheta }}}(t)=\left[ \begin{array}{c} \hat{{\varvec{b}}}(t) \\ \hat{{\varvec{c}}}(t) \end{array} \right]$ and normalize $\hat{{\varvec{c}}}(t)$ using

  $$\begin{aligned} \hat{{\varvec{c}}}(t)=\mathrm{sgn}\{[\hat{{\varvec{\vartheta }}}(t)](n_b+1)\}\frac{[\hat{{\varvec{\vartheta }}}(t)](n_b+1:n_b+n_c)}{\Vert [\hat{{\varvec{\vartheta }}}(t)](n_b+1:n_b+n_c)\Vert }. \end{aligned}$$

• 7. Compute $\hat{v}(t)$ using (18).

• 8. Increase t by 1, go to Step 2 and continue calculation.

4 The Recursive Least Squares Algorithm Based on the Model Decomposition

For the identification model in (6), define the quadratic cost functions:

$$\begin{aligned} J_3({\varvec{\theta }}):= & {} \sum \limits _{j=1}^t\left[ \begin{array}{c}y(j)-{\varvec{\varphi }}^{\tiny \text{ T }}(j){\varvec{b}}-[{\varvec{c}}^{\tiny \text{ T }}{\varvec{F}}^{\tiny \text{ T }}(j), {\varvec{\psi }}^{\tiny \text{ T }}(j)]{\varvec{\theta }}\end{array}\right] ^2,\\ J_4({\varvec{\vartheta }}):= & {} \sum \limits _{j=1}^t\left[ \begin{array}{c}y(j)-{\varvec{\psi }}^{\tiny \text{ T }}(j){\varvec{d}}-[{\varvec{\varphi }}^{\tiny \text{ T }}(j), {\varvec{a}}^{\tiny \text{ T }}{\varvec{F}}(j)]{\varvec{\vartheta }}\end{array}\right] ^2. \end{aligned}$$

Define the information matrices ${\varvec{\varphi }}_1(t)$, ${\varvec{\varOmega }}_t$ and ${\varvec{\varXi }}_t$ as

$$\begin{aligned} {\varvec{\varphi }}_1(t):= & {} [{\varvec{c}}^{\tiny \text{ T }}{\varvec{F}}^{\tiny \text{ T }}(t), {\varvec{\psi }}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{n_a+n_d}, \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{\varOmega }}_t:= & {} \left[ \begin{array}{cccc}{\varvec{F}}(1){\varvec{c}}&{} {\varvec{F}}(2){\varvec{c}}&{} \ldots &{} {\varvec{F}}(t){\varvec{c}}\\ {\varvec{\psi }}(1) &{} {\varvec{\psi }}(2) &{} \ldots &{} {\varvec{\psi }}(t)\\ \end{array}\right] ^{\tiny \text{ T }}\in {\mathbb R}^{t\times (n_a+n_d)}, \end{aligned}$$

(20)

$$\begin{aligned} {\varvec{\varXi }}_t:= & {} \left[ \begin{array}{cccc}{\varvec{\varphi }}(1) &{} {\varvec{\varphi }}(2) &{} \ldots &{} {\varvec{\varphi }}(t)\\ {\varvec{F}}^{\tiny \text{ T }}(1){\varvec{a}}&{} {\varvec{F}}^{\tiny \text{ T }}(2){\varvec{a}}&{} \ldots &{} {\varvec{F}}^{\tiny \text{ T }}(t){\varvec{a}}\\ \end{array}\right] ^{\tiny \text{ T }}\in {\mathbb R}^{t\times (n_b+n_c)}. \ \end{aligned}$$

(21)

Then, $J_3({\varvec{\theta }})$ and $J_4({\varvec{\vartheta }})$ can be equivalently rewritten as

$$\begin{aligned} J_3({\varvec{\theta }})= & {} \Vert {\varvec{Y}}_t-{\varvec{\varPhi }}_t{\varvec{b}}-{\varvec{\varOmega }}_t{\varvec{\theta }}\Vert ^2,\\ J_4({\varvec{\vartheta }})= & {} \Vert {\varvec{Y}}_t-{\varvec{\varPsi }}_t{\varvec{d}}-{\varvec{\varXi }}_t{\varvec{\vartheta }}\Vert ^2. \end{aligned}$$

Similarly, minimizing $J_3({\varvec{\theta }})$ and $J_4({\varvec{\vartheta }})$, we can obtain the least squares estimates:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} [{\varvec{\varOmega }}_t^{\tiny \text{ T }}{\varvec{\varOmega }}_t]^{-1}{\varvec{\varOmega }}_t^{\tiny \text{ T }}[{\varvec{Y}}_t-{\varvec{\varPhi }}_t{\varvec{b}}], \end{aligned}$$

(22)

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} [{\varvec{\varXi }}_t^{\tiny \text{ T }}{\varvec{\varXi }}_t]^{-1}{\varvec{\varXi }}_t^{\tiny \text{ T }}[{\varvec{Y}}_t-{\varvec{\varPsi }}_t{\varvec{d}}]. \end{aligned}$$

(23)

Define the covariance matrix,

$$\begin{aligned} {\varvec{P}}_1^{-1}(t):= & {} {\varvec{\varOmega }}_t^{\tiny \text{ T }}{\varvec{\varOmega }}_t=\sum \limits _{j=1}^t{\varvec{\varphi }}_1(j){\varvec{\varphi }}_1^{\tiny \text{ T }}(j)\nonumber \\= & {} {\varvec{P}}_1^{-1}(t-1)+{\varvec{\varphi }}_1(t){\varvec{\varphi }}_1^{\tiny \text{ T }}(t)\in {\mathbb R}^{(n_a+n_d)\times (n_a+n_d)},\quad {\varvec{P}}(0)={\varvec{I}}_{n_a+n_d}.\qquad \quad \end{aligned}$$

(24)

Hence, Eq. (22) can be rewritten as

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} {\varvec{P}}_1(t){\varvec{\varOmega }}_t^{\tiny \text{ T }}[{\varvec{Y}}_t-{\varvec{\varPhi }}_t{\varvec{b}}]\nonumber \\= & {} {\varvec{P}}_1(t)[{\varvec{\varOmega }}_{t-1}^{\tiny \text{ T }}, {\varvec{\varphi }}_1(t)]\left[ \begin{array}{c}{\varvec{Y}}_{t-1}-{\varvec{\varPhi }}_{t-1}{\varvec{b}}\\ y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}\end{array}\right] \nonumber \\= & {} {\varvec{P}}_1(t){\varvec{P}}^{-1}_1(t-1){\varvec{P}}_1(t-1)\left\{ {\varvec{\varOmega }}_{t-1}^{\tiny \text{ T }}[{\varvec{Y}}_{t-1}-{\varvec{\varPhi }}_{t-1}{\varvec{b}}]+{\varvec{\varphi }}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}]\right\} \nonumber \\= & {} {\varvec{P}}_1(t){\varvec{P}}^{-1}_1(t-1)\hat{{\varvec{\theta }}}(t-1)+{\varvec{P}}_1(t){\varvec{\varphi }}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}]. \end{aligned}$$

(25)

Applying the matrix inversion lemma [7, 27]

$$\begin{aligned} ({\varvec{A}}+{\varvec{B}}{\varvec{C}})^{-1}={\varvec{A}}^{-1}-{\varvec{A}}^{-1}{\varvec{B}}({\varvec{I}}+{\varvec{C}}{\varvec{A}}^{-1}{\varvec{B}})^{-1}{\varvec{C}}{\varvec{A}}^{-1}. \end{aligned}$$

to (24) gives

$$\begin{aligned} {\varvec{P}}_1(t)={\varvec{P}}_1(t-1)-\frac{{\varvec{P}}_1(t-1){\varvec{\varphi }}_1(t){\varvec{\varphi }}_1^{\tiny \text{ T }}(t){\varvec{P}}_1(t-1)}{1+{\varvec{\varphi }}_1^{\tiny \text{ T }}(t){\varvec{P}}_1(t-1){\varvec{\varphi }}_1(t)}. \end{aligned}$$

(26)

Pre-multiplying both sides of (24) by ${\varvec{P}}_1(t)$ gives

$$\begin{aligned} {\varvec{I}}={\varvec{P}}_1(t){\varvec{P}}_1^{-1}(t-1)+{\varvec{P}}_1(t){\varvec{\varphi }}_1(t){\varvec{\varphi }}^{\tiny \text{ T }}_1(t). \end{aligned}$$

(27)

Substituting (27) into (25) gives the recursive estimate of the parameter vector ${\varvec{\theta }}$:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} [{\varvec{I}}-{\varvec{P}}_1(t){\varvec{\varphi }}_1(t){\varvec{\varphi }}^{\tiny \text{ T }}_1(t)]\hat{{\varvec{\theta }}}(t-1)+{\varvec{P}}_1(t){\varvec{\varphi }}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}]\nonumber \\= & {} \hat{{\varvec{\theta }}}(t-1)+{\varvec{P}}_1(t){\varvec{\varphi }}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t){\varvec{b}}-{\varvec{\varphi }}^{\tiny \text{ T }}_1(t)\hat{{\varvec{\theta }}}(t-1)]. \end{aligned}$$

(28)

Define the gain vector ${\varvec{L}}_1(t):={\varvec{P}}_1(t){\varvec{\varphi }}_1(t)\in {\mathbb R}^{n_a+n_d}$. Using (26), it follows that

$$\begin{aligned} {\varvec{L}}_1(t)=\frac{{\varvec{P}}_1(t-1){\varvec{\varphi }}_1(t)}{1+{\varvec{\varphi }}_1^{\tiny \text{ T }}(t) {\varvec{P}}_1(t-1){\varvec{\varphi }}_1(t)}. \end{aligned}$$

(29)

Using (29), Eq. (26) can be rewritten as

$$\begin{aligned} {\varvec{P}}_1(t)={\varvec{P}}_1(t-1)-{\varvec{L}}_1(t){\varvec{\varphi }}_1^{\tiny \text{ T }}(t){\varvec{P}}_1(t-1)=[{\varvec{I}}-{\varvec{L}}_1(t){\varvec{\varphi }}_1^{\tiny \text{ T }}(t)]{\varvec{P}}_1(t-1),\ {\varvec{P}}_1(0)=p_0{\varvec{I}}. \end{aligned}$$

(30)

Here, we can see that the right-hand sides of (19) and (28) contain the unknown parameter vectors ${\varvec{c}}$ and ${\varvec{b}}$, respectively. The solution is to replace the unknown ${\varvec{b}}$ and ${\varvec{\varphi }}_1(t)$ in (28) and (30) with their corresponding estimates $\hat{{\varvec{b}}}(t-1)$ and $\hat{{\varvec{\varphi }}}_1(t)=[\hat{{\varvec{c}}}^{\tiny \text{ T }}(t-1){\varvec{F}}^{\tiny \text{ T }}(t), \hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}$, we have

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+{\varvec{P}}_1(t){\varvec{\varphi }}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t-1)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_1(t)\hat{{\varvec{\theta }}}(t-1)],\nonumber \\ {\varvec{P}}_1(t)= & {} [{\varvec{I}}_{n_a+n_d}-{\varvec{L}}_1(t)\hat{{\varvec{\varphi }}}_1^{\tiny \text{ T }}(t)]{\varvec{P}}_1(t-1),\ {\varvec{P}}_1(0)=p_0{\varvec{I}}_{n_a+n_d}, \end{aligned}$$

(31)

$$\begin{aligned} \hat{{\varvec{\psi }}}(t)= & {} [\hat{v}(t-1), \hat{v}(t-2), \ldots , \hat{v}(t-n_d)]^{\tiny \text{ T }}\in {\mathbb R}^{n_d}. \end{aligned}$$

(32)

Define the information vector ${\varvec{\varphi }}_2(t):=[{\varvec{\varphi }}^{\tiny \text{ T }}(t), {\varvec{a}}^{\tiny \text{ T }}{\varvec{F}}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{n_b+n_c}$ and the covariance matrix ${\varvec{P}}_2^{-1}(t):={\varvec{\varXi }}_t^{\tiny \text{ T }}{\varvec{\varXi }}_t\in {\mathbb R}^{(n_b+n_c)\times (n_b+n_c)}$ and the gain vector ${\varvec{L}}_2(t):={\varvec{P}}_2(t){\varvec{\varphi }}_2(t)\in {\mathbb R}^{n_b+n_c}$. Similarly, some unknown terms are replaced with their estimates; we can obtain the recursive estimate of the parameter vector ${\varvec{\vartheta }}$:

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} \hat{{\varvec{\vartheta }}}(t-1)+{\varvec{P}}_2(t)\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_2(t)[y(t)-\hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{d}}}(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_2(t)\hat{{\varvec{\vartheta }}}(t-1)], \end{aligned}$$

(33)

$$\begin{aligned} \hat{{\varvec{\varphi }}}_2(t)= & {} [{\varvec{\varphi }}^{\tiny \text{ T }}(t), \hat{{\varvec{a}}}^{\tiny \text{ T }}(t){\varvec{F}}(t)]\in {\mathbb R}^{n_b+n_c}. \end{aligned}$$

(34)

Thus, we can summarize the recursive least squares algorithm for estimating the parameter vectors ${\varvec{\theta }}$ and ${\varvec{\vartheta }}$ of the nonlinear systems based on the model decomposition (the ON-RLS algorithm for short) as follows:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+{\varvec{L}}_1(t)[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t-1)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_1(t)\hat{{\varvec{\theta }}}(t-1)], \end{aligned}$$

(35)

$$\begin{aligned} {\varvec{L}}_1(t)= & {} {\varvec{P}}_1(t-1)\hat{{\varvec{\varphi }}}_1(t)[1+\hat{{\varvec{\varphi }}}_1^{\tiny \text{ T }}(t){\varvec{P}}_1(t-1)\hat{{\varvec{\varphi }}}_1(t)]^{-1}, \end{aligned}$$

(36)

$$\begin{aligned} {\varvec{P}}_1(t)= & {} [{\varvec{I}}_{n_a+n_d}-{\varvec{L}}_1(t)\hat{{\varvec{\varphi }}}_1^{\tiny \text{ T }}(t)]{\varvec{P}}_1(t-1),\ {\varvec{P}}_1(0)=p_0{\varvec{I}}_{n_a+n_d}, \end{aligned}$$

(37)

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} \hat{{\varvec{\vartheta }}}(t-1)+{\varvec{L}}_2(t)[y(t)-\hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{d}}}(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_2(t)\hat{{\varvec{\vartheta }}}(t-1)], \end{aligned}$$

(38)

$$\begin{aligned} {\varvec{L}}_2(t)= & {} {\varvec{P}}_2(t-1)\hat{{\varvec{\varphi }}}_2(t)[1+\hat{{\varvec{\varphi }}}_2^{\tiny \text{ T }}(t){\varvec{P}}_2(t-1)\hat{{\varvec{\varphi }}}_2(t)]^{-1}, \end{aligned}$$

(39)

$$\begin{aligned} {\varvec{P}}_2(t)= & {} [{\varvec{I}}_{n_b+n_c}-{\varvec{L}}_2(t)\hat{{\varvec{\varphi }}}_2^{\tiny \text{ T }}(t)]{\varvec{P}}_2(t-1),\ {\varvec{P}}_2(0)=p_0{\varvec{I}}_{n_b+n_c}, \end{aligned}$$

(40)

$$\begin{aligned} \hat{{\varvec{\varphi }}}_1(t)= & {} [\hat{{\varvec{c}}}^{\tiny \text{ T }}(t-1){\varvec{F}}^{\tiny \text{ T }}(t), {\varvec{\psi }}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}, \end{aligned}$$

(41)

$$\begin{aligned} \hat{{\varvec{\varphi }}}_2(t)= & {} [{\varvec{\varphi }}^{\tiny \text{ T }}(t), \hat{{\varvec{a}}}^{\tiny \text{ T }}(t){\varvec{F}}(t)]^{\tiny \text{ T }}, \end{aligned}$$

(42)

$$\begin{aligned} {\varvec{\varphi }}(t)= & {} [u(t-1), u(t-2), \ldots , u(t-n_b)]^{\tiny \text{ T }}, \end{aligned}$$

(43)

$$\begin{aligned} \hat{{\varvec{\psi }}}(t)= & {} [\hat{v}(t-1), \hat{v}(t-2), \ldots , \hat{v}(t-n_d)]^{\tiny \text{ T }}, \end{aligned}$$

(44)

$$\begin{aligned} \hat{v}(t)= & {} y(t)-\hat{{\varvec{a}}}^{\tiny \text{ T }}(t){\varvec{F}}(t)\hat{{\varvec{c}}}(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t)-\hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{d}}}(t), \end{aligned}$$

(45)

$$\begin{aligned} {\varvec{F}}(t)= & {} \left[ \begin{array}{cccc}f_1(y(t-1)) &{} f_2(y(t-1)) &{} \ldots &{} f_{n_c}(y(t-1))\\ f_1(y(t-2)) &{} f_2(y(t-2)) &{} \ldots &{} f_{n_c}(y(t-2))\\ \vdots &{} \vdots &{} \quad &{} \vdots \\ f_1(y(t-n_a)) &{} f_2(y(t-n_a)) &{} \ldots &{} f_{n_c}(y(t-n_a))\\ \end{array}\right] , \end{aligned}$$

(46)

$$\begin{aligned} \hat{{\varvec{\varTheta }}}(t)= & {} \left[ \begin{array}{cc} \hat{{\varvec{\theta }}}(t)\\ \hat{{\varvec{\vartheta }}}(t) \end{array}\right] . \end{aligned}$$

(47)

The procedures of computing the parameter estimation vectors $\hat{{\varvec{\theta }}}(t)$ and $\hat{{\varvec{\vartheta }}}(t)$ in (35)–(47) are listed in the following.

• 1. To initialize: let $t=1$, and set the initial values ${\varvec{P}}_1(0)=p_0{\varvec{I}}_{n_a+n_d}$, $\hat{{\varvec{\theta }}}(0)=\mathbf{1}_{n_a+n_d}/p_0$, $\hat{{\varvec{b}}}(0)=\mathbf{1}_{n_b}/{p_0}$, ${\varvec{P}}_2(0)=p_0{\varvec{I}}_{n_b+n_c}$, $p_0=10^6$, $\Vert \hat{{\varvec{c}}}(0)\Vert =1$, give the basis function $f_j(*)$.

• 2. Collect the input–output data u(t) and y(t), form ${\varvec{F}}(t)$ using (46), ${\varvec{\varphi }}(t)$ using (43), $\hat{{\varvec{\psi }}}(t)$ using (44) and compute $\hat{{\varvec{\varphi }}}_1(t)$ in (41).

• 3. Compute ${\varvec{L}}_1(t)$ using (36) and ${\varvec{P}}_1(t)$ using (37).

• 4. Update the parameter estimate $\hat{{\varvec{\theta }}}(t)$ using (35) and read $\hat{{\varvec{a}}}(t)$ and $\hat{{\varvec{d}}}(t)$ from $\hat{{\varvec{\theta }}}(t)=\left[ \begin{array}{c} \hat{{\varvec{a}}}(t) \\ \hat{{\varvec{d}}}(t) \end{array} \right]$.

• 5. Form $\hat{{\varvec{\varphi }}}_2(t)$ in (42) and compute ${\varvec{L}}_2(t)$ using (39) and ${\varvec{P}}_2(t)$ using (40).

• 6. Update the parameter estimate $\hat{{\varvec{\vartheta }}}(t)$ using (38) and read $\hat{{\varvec{b}}}(t)$ from $\hat{{\varvec{\vartheta }}}(t)=\left[ \begin{array}{c} \hat{{\varvec{b}}}(t) \\ \hat{{\varvec{c}}}(t) \end{array} \right]$ and normalize $\hat{{\varvec{c}}}(t)$ using

  $$\begin{aligned} \hat{{\varvec{c}}}(t)=\mathrm{sgn}\{[\hat{{\varvec{\vartheta }}}(t)\}(n_b+1)\}\frac{[\hat{{\varvec{\vartheta }}}(t)](n_b+1:n_b+n_c)}{\Vert [\hat{{\varvec{\vartheta }}}(t)](n_b+1:n_b+n_c)\Vert }, \end{aligned}$$

  (48)

  and let $\hat{{\varvec{\vartheta }}}(t)=\left[ \begin{array}{c} \hat{{\varvec{b}}}(t) \\ \hat{{\varvec{c}}}(t) \end{array} \right]$.

• 7. Compute $\hat{v}(t)$ using (45).

• 8. Increase t by 1, go to Step 2 and continue the recursive calculation.

The flowchart for computing the estimates $\hat{{\varvec{\theta }}}(t)$ and $\hat{{\varvec{\vartheta }}}(t)$ in (35)–(47) is shown in Fig. 1.

Fig. 1

The flowchart of computing the parameter estimates $\hat{{\varvec{\theta }}}(t)$ and $\hat{{\varvec{\vartheta }}}(t)$

To show the advantages of the proposed ON-RLS algorithm, the following gives the stochastic gradient algorithm with a forgetting factor $\lambda$ for estimating the parameter vectors ${\varvec{\theta }}$ and ${\varvec{\vartheta }}$ of the nonlinear systems (the ON-SG algorithm for short) [11]:

$$\begin{aligned} \hat{{\varvec{\theta }}}(t)= & {} \hat{{\varvec{\theta }}}(t-1)+\frac{\hat{{\varvec{\varphi }}}_1(t)}{r_1(t)}[y(t)-{\varvec{\varphi }}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t-1)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_1(t)\hat{{\varvec{\theta }}}(t-1)], \end{aligned}$$

(49)

$$\begin{aligned} r_1(t)= & {} \lambda r_1(t)+\Vert \hat{{\varvec{\varphi }}}_1(t)\Vert ^2,\ 0\leqslant \lambda \leqslant 1,\ r_1(0)=1, \end{aligned}$$

(50)

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} \hat{{\varvec{\vartheta }}}(t-1)+\frac{\hat{{\varvec{\varphi }}}_2(t)}{r_2(t)}[y(t)-\hat{{\varvec{\psi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{d}}}(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}_2(t)\hat{{\varvec{\vartheta }}}(t-1)], \end{aligned}$$

(51)

$$\begin{aligned} r_2(t)= & {} \lambda r_2(t)+\Vert \hat{{\varvec{\varphi }}}_2(t)\Vert ^2,\ r_2(0)=1. \end{aligned}$$

(52)

Remark 1

The ON-RLS algorithm in (35)–(47) has faster convergence rates than the ON-SG algorithm in (49)–(52)—see the last columns in Tables 3 and 4.

5 The Comparison of the Computational Efficiency

In order to show the advantage of the ON-RLS algorithm, the following gives simply recursive extended least squares algorithm in [21] for comparison.

Define the parameter vectors,

$$\begin{aligned} {\varvec{\vartheta }}:=\left[ \begin{array}{c} {\varvec{a}}\otimes {\varvec{c}} \\ {\varvec{b}} \\ {\varvec{d}} \end{array}\right] \in {\mathbb R}^n, \quad n:=n_an_c+n_b+n_d. \end{aligned}$$

Then, we have the following recursive extended least squares (RELS) algorithm [21]:

$$\begin{aligned} \hat{{\varvec{\vartheta }}}(t)= & {} \hat{{\varvec{\vartheta }}}(t-1)+{\varvec{L}}(t)[y(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{\vartheta }}}(t-1)],\ \hat{{\varvec{\vartheta }}}(0)=\mathbf{1}_n/{p_0},\\ {\varvec{L}}(t)= & {} {\varvec{P}}(t-1)\hat{{\varvec{\varphi }}}(t)[1+\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t){\varvec{P}}(t-1)\hat{{\varvec{\varphi }}}(t)]^{-1},\\ {\varvec{P}}(t)= & {} [{\varvec{I}}_n-{\varvec{L}}(t)\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t)]{\varvec{P}}(t-1),\ {\varvec{P}}(0)=p_0{\varvec{I}}_n,\\ \hat{{\varvec{\varphi }}}(t)= & {} [{\varvec{h}}^{\tiny \text{ T }}(y(t-1)),\ldots , {\varvec{h}}^{\tiny \text{ T }}(y(t-n_a)), \\&\quad u(t-1), \ldots , u(t-n_b), \hat{v}(t-1),\ldots , \hat{v}(t-n_d)]^{\tiny \text{ T }},\\ {\varvec{h}}(t)= & {} [h_1(y(t)), h_2(y(t)), \ldots , h_{n_c}(y(t))]^{\tiny \text{ T }}\in {\mathbb R}^{n_c},\\ \hat{v}(t)= & {} y(t)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(t)\hat{{\varvec{\vartheta }}}(t). \end{aligned}$$

Table 1 The computational efficiency of the ON-RLS algorithm

Table 2 The computational efficiency of the RELS algorithm

Remark 2

Compared with the recursive extended least squares algorithm, which involves the covariance matrix ${\varvec{P}}(t)$ of large size $(n_an_c+n_b+n_d)\times (n_an_c+n_b+n_d)$, the ON-RLS algorithm has less computational load because it involves two covariance matrices ${\varvec{P}}_1(t)$ and ${\varvec{P}}_2(t)$ of small sizes $(n_a+n_d)\times (n_a+n_d)$ and $(n_b+n_c)\times (n_b+n_c)$—see the details in Tables 1 and 2. From the simulation example (omitted in the paper), we can see that the parameter estimation errors given by the ON-RLS algorithm are very close to those given by the RELS algorithm.

It has been just pointed out by Golub and Van Loan [16] that the flop (floating point operation) counting is a necessarily crude approach to the measuring of program efficiency since it ignores subscripting, memory traffic, and the countless other overheads associated with program execution, the flop counting is just a “quick and dirty” accounting method that captures only one of the several dimensions of the efficiency issue although multiplication/division and addition/subtraction with different lengths are different. The flop numbers of the ON-RLS and RELS algorithms at each recursion are given in Tables 1 and 2. Their total flops are, respectively, given by

$$\begin{aligned} N_1:= & {} 4(n_a+n_d)^2+4(n_b+n_c)^2+4n_an_c+5n_a+10n_b+7n_c+10n_d,\\ N_2:= & {} 4(n_an_c+n_b+n_d)^2+6(n_an_c+n_b+n_d). \end{aligned}$$

In order to compare the computational efficiency of these two algorithms, we count the difference between the amount of calculation of these two algorithms. When $n_a>2$ and $n_b>2$, $n_an_b>n_a+n_b$, $N_2>4(n_a+n_b+n_c+n_d)^2+6(n_a+n_b+n_c+n_d)$. Then, we have

$$\begin{aligned} N_2-N_1> & {} 4(n_a+n_c+n_b+n_d)^2+6(n_a+n_c+n_b+n_d)-4(n_a+n_d)^2\\&-\,4(n_b+n_c)^2-4n_an_c-5n_a-10n_b-7n_c-10n_d\\= & {} 10n_an_c+(8n_b-5)n_a+(8n_c-4)n_b+(8n_b-4)n_d>0. \end{aligned}$$

It is clear that the ON-RLS algorithm requires less computational load than the RELS algorithm. For example, when $n_a=n_b=n_c=n_d=5$, we have $N_2-N_1=5110-1060=4050$ flops.

6 Example

Consider the following nonlinear system:

$$\begin{aligned} y(t)= & {} A(z)f(y(t))+B(z)u(t)+D(z)v(t),\\ A(z)= & {} a_1z^{-1}+a_2z^{-2}=-0.75z^{-1}-0.61z^{-2},\\ B(z)= & {} b_1z^{-1}=0.96z^{-1},\\ D(z)= & {} 1+d_1z^{-1}=1+0.4z^{-1},\\ f(y(t))= & {} c_1y(t)+c_2{\sin }(y(t))=0.61y(t)+0.79{\sin }(y(t)),\\ {\varvec{\theta }}= & {} [a_1, a_2, d_1]^{\tiny \text{ T }}\\= & {} [-0.75, -0.61, 0.4]^{\tiny \text{ T }},\\ {\varvec{\vartheta }}= & {} [b_1, c_1, c_2]^{\tiny \text{ T }}=[0.96, 0.61, 0.79]^{\tiny \text{ T }},\\ {\varvec{\varTheta }}= & {} [a_1, a_2, d_1, b_1, c_1, c_2]^{\tiny \text{ T }}=[-0.75, -0.61, 0.4, 0.96, 0.61, 0.79]^{\tiny \text{ T }}. \end{aligned}$$

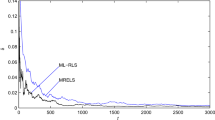
In simulation, the input $\{u(t)\}$ is taken as a persistent excitation signal sequence with zero mean and unit variance, and $\{v(t)\}$ as a white noise sequence with zero mean and variance $\sigma ^2=0.50^2$. Applying the ON-RLS algorithm and the ON-SG algorithm with $\lambda =0.99$ to estimate the parameters of this system, the parameter estimates and errors are given in Tables 3 and 4, and the parameter estimation errors $\delta :=\Vert \hat{{\varvec{\varTheta }}}(t)-{\varvec{\varTheta }}\Vert /\Vert {\varvec{\varTheta }}\Vert$ versus t are shown in Figs. 2 and 3.

Table 3 The ON-RLS parameter estimates and errors

Table 4 The ON-SG parameter estimates and errors

Fig. 2

The ON-RLS estimation errors versus t ($\sigma ^2=0.50^2$)

From Tables 3, 4 and Figs. 2, 3, we can draw the following conclusions.

• It is clear that the parameter estimation errors given by two algorithms become smaller with the data length increasing.

• The parameter estimation accuracy of the ON-RLS algorithm is higher than that of the ON-SG algorithm.

• The parameter estimates given by the ON-RLS algorithm converge faster to their true values compared with the ON-SG algorithm for appropriate forgetting factors.

Fig. 3

The ON-SG estimation errors versus t ($\sigma ^2=0.50^2$)

7 Conclusions

Using the hierarchical identification principle, a recursive least squares algorithm is derived for a special class of output nonlinear systems by transforming a nonlinear system into two identification models. The proposed algorithm can give a satisfactory identification accuracy and has higher computational efficiencies compared with the recursive extended least squares parameter estimation algorithm in [21]. The proposed algorithm can be extended to study identification problems of multivariable systems [13], linear-in-parameters systems [41, 42] and impulsive dynamical systems [23, 24] and applied to other fields [45–47].