1 Introduction

Complex networks exist widely in the internet, food webs, electrical power grids, image processing, social networks, and so on [1–3, 36]. The modeling of complex networks is the basics of analysis, control, and synchronization, and the modeling methods may use the least squares [12–15] and other parameter estimation approaches [16, 17, 27, 38, 39]. A complex network is a large set of interconnected nodes, in which a node is a fundamental unit with specific contents. Among the various behaviors of networks, the synchronization in complex networks has been extensively investigated [43, 47, 48]. Synchronization can be found to be important in many areas of applications, from the brain function and epilepsy to the emergence of coherent behaviors.

In recent years, many synchronization criteria have been obtained, including the master stability function-based criteria, the matrix measure analysis-based criteria, and the Lyapunov function-based criteria. The first one computes the maximum Lyapunov exponent of the variational equations [30], which provides a numerical condition for synchronization of complex networks. The second one, proposed by Chen in [6, 7], has been successful in treating local synchronization with complex network topologies. The last one uses the Lyapunov function method to obtain analytical conditions for network synchronization [8, 24, 26], in which the complex networks consist of many different special features, such as switching behaviors [32], time-varying coupling [25, 35], nonlinearities [18, 19, 40, 41] etc. As we know, the dynamical behaviors of network’s node are often subject to instantaneous perturbations caused by abrupt jumps at certain instants during the evolutionary process of some realistic systems. That is, this kind of systems exhibits impulsive phenomena. To characterize the impulsive effects on complex systems, some results about the stability and synchronization criteria have been obtained in [37, 46, 49]. However, an impulsive system consists of nonlinear subsystems, and there exist some switching phenomena, (i.e., the system may switch from the \(k-1\)-th subsystem to the \(k\)-th subsystem according to some certain switching law).It is also worth noting that in the practical cases, the time delays in couplings and in dynamical nodes often appear, which may cause instability of dynamical systems [21]. All these effects of impulse, switching, and multiple delays can be characterized by a unified hybrid switching-impulsive dynamical networks with multiple delays. Since the existence of impulse, switching events, and delays will cause oscillations and instability, leading to poor performances, it is necessary to consider these effects on network synchronization.

Recently, the unified stability criteria of impulsive dynamical systems have attracted increasing attention. Some new and pioneering results on unified stability and synchronization conditions have been proposed [9, 29]. Chen et al. investigated the problems of the robust stability for uncertain impulsive systems with time-delay [9]. By using the Lyapunov function and Razumikhin-type method, a unified sufficient condition has been obtained in the form of linear matrix inequalities. Lu et al. [29] studied the synchronization of impulsive dynamical networks, in which two types of impulses have been considered: synchronization impulse and desynchronization impulse. On the basis of the work in [23], this paper focuses on the unified synchronization of hybrid switching-impulsive dynamical networks with multiple delays.

The rest of this paper is organized as follows. In Sect. 2, the conceptions of the contraction theory and the partial contraction principle are briefly reviewed. The hybrid switching-impulsive dynamical network with multiple delays is described in Sect. 3. In Sect. 4, some unified synchronization criteria of the hybrid network are established. A numerical example is given to illustrate the effectiveness of the results in Sect. 5. Finally, conclusion is drawn in Sect. 6.

2 Basic Conception

Before giving the main results of this paper, we briefly give an introduction to the basic definitions and main results of the contraction and partial contraction theory, which can be found in [31, 34, 42].

Consider a nonlinear system

$$\begin{aligned} \dot{x}=f(x,t), \end{aligned}$$
(1)

where \(x\in {\mathbb R}^n\) is the state vector and \(f\) is considered to be continuously differentiable map. Then, we have

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t}(\delta x^{\mathrm{T}}\delta x)=2\delta x^{\mathrm{T}}\delta \dot{x}=2\delta x^{\mathrm{T}}\frac{\partial f}{\partial x}\delta x\le 2\lambda _{\max }\delta x^{\mathrm{T}}\delta x, \end{aligned}$$

where \(\delta x\in {\mathbb R}^n\) is a virtual displacement between neighboring solution trajectories of system (1). The Jacobian matrix is defined as \(J=\frac{\partial f}{\partial x}\), and the largest eigenvalue of symmetric part of Jacobian is represented by \(\lambda _{\max }(x,t)\). If \(\lambda _{\max }\) is strictly uniformly negative, any infinitesimal length \(\Vert \delta x\Vert \) converges exponentially to zero. The nonlinear system (1) of the contraction theory is presented in the following. A nonlinear system (1) is contracting if and only if the largest eigenvalue of the Jacobian matrix is uniformly negative. If this condition holds, all trajectories will converge exponentially to a single particular trajectory independent of initial conditions.

Next, we summarize the concept of the partial contraction theory, which is based on the contraction theory and derived from a very simple general result [31]. Consider a nonlinear systems of the form

$$\begin{aligned} \dot{x}=f(x,x,t) \end{aligned}$$
(2)

and assume that the auxiliary system

$$\begin{aligned} \dot{y}=f(y,x,t) \end{aligned}$$
(3)

is contracting with respect to \(y\). If a particular solution of the auxiliary \(y\)-system verifies a specific smooth property, all trajectories of the original \(x\)-system verify this property exponentially. Based on this condition, the original system is said to be partial contracting.

Definition 1

[33] The average impulsive dwell-time of the impulsive sequence \(\zeta =\{t_1,t_2,\dots \}\) is denoted as a positive scalar function \(T^*\) if there exist positive integer \(N_0\) and positive function \(T(t)\), such that

$$\begin{aligned} \frac{1}{T^*}\sum _{j=1}^{N_{\zeta }(t)}\Delta _j-N_0\le N_{\zeta }(t)\le \frac{1}{T^*}\sum _{j=1}^{N_{\zeta }(t)}\Delta _j+N_0, \end{aligned}$$

where \(N_{\zeta }(t)\) is the number of impulsive times for a given impulsive sequence \(\zeta \), and \(\Delta _j\) denotes the period between the impulses following the \(j\)-th impulse.

Remark 1

[29]. The concept of “average impulsive interval” is introduced by referring to the concept of average dwell-time to characterize how often or how seldom impulses occur. This new concept will be utilized to derive a unified criterion for the synchronization analysis of impulsive dynamical networks, which is simultaneously applicable for CDN’s with desynchronizing impulses or synchronizing impulses. Further it is applicable to impulsive signals with a wider range of impulsive interval.

Definition 2

[50] The matrix measure of matrix \(A=(a_{ij})\in {\mathbb R}^{n\times n}\) is defined as

$$\begin{aligned} \mu _{.}(A)=\lim _{\varepsilon \rightarrow 0^+}\frac{\Vert I_n+\varepsilon A\Vert -1}{\varepsilon }, \end{aligned}$$

where \(\Vert \cdot \Vert \) is the matrix norm, and \(I_n\) denotes the identity matrix. Then, the matrix measures

$$\begin{aligned} \mu _{1}(A)&= \max \limits _j\bigg \{a_{jj}+\sum \limits _{i=1,i\ne j}^n|a_{ij}|\bigg \},\\ \mu _{2}(A)&= \frac{1}{2}\lambda _{\max }(A^{\mathrm{T}}+A),\\ \mu _{\infty }(A)&= \max \limits _i\bigg \{a_{ii}+\sum \limits _{j=1,j\ne i}^n|a_{ij}|\bigg \}, \end{aligned}$$

where \(\lambda _{\max }(\cdot )\) is the maximum eigenvalue.

Lemma 1

[22] For matrix \(A\in {\mathbb R}^{n\times n}\), \(B\in {\mathbb R}^{n\times n}\), the following inequality holds:

$$\begin{aligned} \Vert \exp [(A+zB)t]\Vert \le \exp [\mu (A+zB)t]\le \exp [(\mu (A)+\Vert B\Vert )t], \quad |z|=1, \end{aligned}$$

where \(\mu (A)\) is the matrix measure of matrix \(A\).

3 Problem Formulation and Preliminaries

In this section, we consider a hybrid switching-impulsive dynamical network with multiple delays consisting of \(N\) coupled nodes, with each node being an \(n\)-dimensional dynamical system. The proposed network can be described by

$$\begin{aligned} \dot{x}_i(t)&= f_{\sigma (k)}(x_i(t))+g_{\sigma (k)}(x_i(t-\tau (t)))\nonumber \\&+\sum \limits _{l=1}^{m}\sum \limits _{j=1}^N\varepsilon _l^{\sigma (k)}c_{ijl}^{\sigma (k)}(t)\Gamma _l^{\sigma (k)}(t)x_j(t-\tau _l(t)), \quad t\ne t_k,\end{aligned}$$
(4)
$$\begin{aligned} \Delta x_i(t)&= B_{ik}x_i(t),\quad t=t_k,\end{aligned}$$
(5)
$$\begin{aligned} x_i(\theta )&= \varphi _i(\theta ), \quad \theta \in [-\bar{\tau },0], \end{aligned}$$
(6)

where \(t\in {\mathbb R}^+\) is the set of positive integers, and \(x_i(t)\in {\mathbb R}^n\) is the state variable of node \(i\), \(i=1,2,\dots ,N\). \(\sigma :{\mathbb R}^+\rightarrow I=\{1,2,\dots ,r\}\), which is represented by \(\sigma (k)\) according to \([t_{k-1},t_k)\rightarrow I\), is a piecewise constant function of time, \(\varepsilon _l^{\sigma (k)}\) called a switch signal. \(f_{\sigma (k)}\) and \(g_{\sigma (k)}\) are continuously differentiable maps, and time delays \(\tau (t)\) and \(\tau _l(t)\) are bounded time-varying with

$$\begin{aligned} 0\le \tau (t)\le \tau ,\ 0\le \tau _l(t)\le \tau _l\ (l=1,2,\ldots ,m),\ \bar{\tau }=\max \{\tau ,\tau _1,\tau _2,\ldots ,\tau _m\}, \end{aligned}$$

\(\varphi _i(\theta )\) is a vector-valued initial continuous function defined on the interval \([-\bar{\tau },0]\), \(\Gamma _{\sigma (k)}(t)=(r_{ij}^{\sigma (k)}(t))_{n\times n}\) is the inner-coupling matrix, and \(C_l^{\sigma (k)}(t)=(c_{ijl}^{\sigma (k)}(t))_{N\times N}\) represents the outer-coupling configurations. Assume that \(c_{iil}^{\sigma (k)}(t)=-\sum _{j=1,j\ne i}^Nc_{ijl}^{\sigma (k)}(t)\) (\(i=1,2,\dots ,N\)). The impulsive instant sequence \(\{t_k\}\) satisfies

$$\begin{aligned} 0\le t_0\le t_1\le \dots \le t_k\le \ldots , \Delta x_i(t_k)=x_i(t_k^+)-x_i(t_k^-), \end{aligned}$$

where \(x(t_k^-)=\lim \limits _{t\rightarrow t_k^-}x(t)\) denotes the state jumps at the switching instants \(t_k\), \(t_k^-\rightarrow +\infty \), and \(B_{ik}\in R^{n\times n}\) are impulsive constant matrices.

Before the main results are derived, a definition of synchronization for network (4–6) is needed.

Definition 3

The \(N\) nodes of the hybrid switching-impulsive network (4–6) are said to achieve synchronization if

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert x_i(t)-x_j(t)\Vert =0, \quad i,j=1,2,\dots ,N. \end{aligned}$$

Remark 2

The hybrid network (4–6) includes many existing network models.

(a1) When

$$\begin{aligned}&f_{\sigma (k)}(x_i(t))=f(x_i(t)),g_{\sigma (k)}(x_i(t-\tau (t)))=0,c_{ijl}^{\sigma (k)}(t)=c_{ij}^{\sigma (k)},\tau _l(t)=d(t), \\&\varepsilon _l^{\sigma (k)}=1,\Gamma _l^{\sigma (k)}=\Gamma _{\sigma (k)},B_k=0, \end{aligned}$$

there exists no impulsive effect. For this case, the networks (4–6) are equivalent to the system in [28] as

$$\begin{aligned} \dot{x}_i(t)=f(x_i(t))+\sum \limits _{j=1}^Nc_{ij}^{\sigma (t)}\Gamma _{\sigma (t)}x_j(t-d(t)). \end{aligned}$$
(7)

(a2) When

$$\begin{aligned}&f_{\sigma (k)}(x_i(t))=Ax_i(t)+f(x_i(t)), g_{\sigma (k)}x_i(t-\tau (t))=0,\\&c_{ijl}^{\sigma (k)}(t)=G_{ij},\tau _l(t)=\tau (t),\varepsilon _l^{\sigma (k)}=1,\Gamma _l^{\sigma (k)}=\Gamma , \end{aligned}$$

there exists no switching. For this case, the network (4–6) becomes the network in [11] as

$$\begin{aligned} \dot{x}_i(t)&= Ax_i(t)+f(x_i(t))+\sum \limits _{j=1}^NG_{ij}\Gamma x_j(t-\tau (t)),\quad t\ne t_k,\end{aligned}$$
(8)
$$\begin{aligned} \Delta x_{i}(t)&= D_{ik}x_i(t),\quad t=t_k,\\ x_i(\theta )&= \varphi _i(\theta ), \quad \theta \in [-\bar{\tau },0].\nonumber \end{aligned}$$
(9)

(a3) When

$$\begin{aligned}&f_{\sigma (k)}(x_i(t))=Cx_i(t)+Bf(x_i(t)),g_{\sigma (k)}(x_i(t-\tau (t)))=0,\\&c_{ijl}^{\sigma (k)}(t)=a_{ij},\varepsilon _l^{\sigma (k)}=1,\Gamma _l^{\sigma (k)}(t)=\Gamma ,x_j(t-\tau _l(t))=x_j, \end{aligned}$$

the network (4–6) without switches becomes the system in [29] as

$$\begin{aligned} \dot{x}_i(t)&= Cx_i(t)+Bf(x_i(t))+c\sum \limits _{j=1}^NG_{ij}\Gamma x_j(t-\tau (t)),t\ne t_k,\\ x_j(t)-x_i(t)&= \mu (x_j(t)-x_i(t)),t=t_k,\\ x_i(\theta )&= \varphi _i(\theta ), \theta \in [-\bar{\tau },0]. \end{aligned}$$

Based on the partial contraction theory, construct an auxiliary system of system (4–6) as

$$\begin{aligned} \dot{y}_i(t)&= f_{\sigma (k)}(y_i(t))+g_{\sigma (k)}(y_i(t-\tau (t)))\nonumber \\&+\sum \limits _{l=1}^m\sum \limits _{j=1}^N\varepsilon _l^{\sigma (k)}c_{ijl}^{\sigma (k)}(t)\Gamma _l^{\sigma (k)}(t)y_j(t-\tau _l(t))\nonumber \\&-\,\alpha \sum \limits _{j=1}^Ny_j(t)+\alpha \sum \limits _{j=1}^{N}x_j(t), \quad t\ne t_k,\end{aligned}$$
(10)
$$\begin{aligned} \Delta y_i(t)&= B_{k}y_i(t), \quad t=t_k,\end{aligned}$$
(11)
$$\begin{aligned} y_i(\theta )&= \varphi _i(\theta ), \quad \theta \in [-\bar{\tau },0], \end{aligned}$$
(12)

which has a particular solution \(y_1=y_2=\dots =y_N\), where constant \(\alpha \) is determined.

According to the partial contraction theory, if the auxiliary system in (10–12) is contracting with respect to \(y\), all system trajectories of system in (4–6) will verify the independent property \(x_1=x_2=\dots =x_N\) exponentially.

Let \(\delta y_i(t)\) denote the virtual displacement of the state variable of node \(i\) of system in (10–12); one has

$$\begin{aligned}&\delta \dot{y}_{_i}(t)=\frac{\partial f_{\sigma (k)}(y_{_i}(t))}{\partial y_{_i}(t)}\delta y_{_i}(t) +\frac{\partial g_{\sigma (k)}(y_{_i}(t-\tau (t)))}{\partial y_{_i}(t-\tau (t))}\delta y_{_i}(t-\tau (t))\end{aligned}$$
(13)
$$\begin{aligned}&\quad +\sum \limits _{l=1}^{m}\sum \limits _{j=1}^N\varepsilon _l^{\sigma (k)}c_{ijl}^{\sigma (k)}(t)\Gamma _l^{\sigma (k)}(t)\delta y_{_j}(t-\tau _l(t))-\alpha \sum \limits _{j=1}^{N}\delta y_{_j}(t), \quad t\ne t_k,\end{aligned}$$
(14)
$$\begin{aligned}&\Delta \delta y_{_i}(t)=B_k\delta y_{_i}(t), \quad t=t_k. \end{aligned}$$
(15)

Then, the virtual system in (13–15) can be rewritten in the following Kronecker-product form:

$$\begin{aligned} \delta \dot{y}(t)&= A_{\sigma (k)}\delta y(t)+B_{\sigma (k)}\delta y(t-\tau (t)) +\sum \limits _{l=1}^{m}D_l^{\sigma (k)}(t)\delta y(t-\tau _{l}(t))\nonumber \\&-L\delta y(t), \quad t\ne t_k,\end{aligned}$$
(16)
$$\begin{aligned} \Delta \delta y(t_{})&= E_{k}\delta y(t), \quad t=t_k, \end{aligned}$$
(17)

where \(A_{\sigma (k)}=(I_{N}\otimes F_{\sigma (k)})\), \(B_{\sigma (k)}=(I_N\otimes G_{\sigma (k)})\), \(D_l^{\sigma (k)}(t)=\varepsilon _l^{\sigma (k)}(C_l^{\sigma (k)}(t)\otimes \Gamma _l^{\sigma (k)}(t))\), and \(E_k=(I_N\otimes B_k))\) with \(L=\alpha _N\),

$$\begin{aligned} F_{\sigma (k)}&= \mathrm{diag}\left[ \frac{\partial f_{\sigma (k)}}{\partial y_{_1}(t)}, \frac{\partial f_{\sigma (k)}}{\partial y_{_2}(t)}, \ldots ,\frac{\partial f_{\sigma (k)}}{\partial y_{_N}(t)} \right] \!,\\ G_{\sigma (k)}&= \mathrm{diag}\left[ \frac{\partial g_{\sigma (k)}}{\partial y_{_1}(t-\tau (t))}, \frac{\partial g_{\sigma (k)}}{\partial y_{_2}(t-\tau (t))}, \ldots ,\frac{\partial g_{\sigma (k)}}{\partial y_{_N}(t-\tau (t))}\right] \!. \end{aligned}$$

Remark 3

In this paper, the contraction and partial contraction theory are used to study the synchronization of hybrid networks if initial conditions or temporary disturbances are forgotten exponentially fast. Unlike most existing results based on the Lyapunov stability method, the contraction theory does not require explicit knowledge of specific attractors. The system description in terms of differential equations is used to carry out stability analysis using the virtual displacements. Moreover, some assumptions on the nonlinear function \(f(x_i(t))\) and \(g(x_j(t-\tau (t)))\) in network (4–6) are released via contraction analysis, such as

$$\begin{aligned} \Vert f(x(t))-f(y(t))\Vert \le L\Vert x(t)-y(t)\Vert , f_{\sigma }^{\mathrm{T}}(x_i)P_{\sigma }x_i\le \varphi _{\sigma } x_i^{\mathrm{T}}P_{\sigma }x_i, \end{aligned}$$
$$\begin{aligned} \Vert g(x(t-\tau ))-g(y(x(t-\tau )))\Vert \le K\Vert x(t-\tau )-y(t-\tau )\Vert , \Vert x_{i}(t-\tau )\Vert \le \rho _ix_i(t), \end{aligned}$$

where \(L\), \(K\) and \(\rho _i\) are nonnegative constants, \(\varphi _\sigma \) are continuous functions, which are used to obtain the synchronization criteria of dynamical networks [11] based on the Lyapunov stability theorem. Also Jacobi matrix of the nonlinear function is used for the study of synchronization, which means that the obtained criteria are local.

To facilitate our analysis, some other helpful lemmas should be given subsequently.

Lemma 2

The virtual system in (16–17) is contracting if

$$\begin{aligned} \delta \dot{y}(t)=\bigg (A_{\sigma (k)}+z_{_0}B_{\sigma (k)}+\sum _{l=1}^mz_{_l}D_{_l}^{\sigma (k)}-L+K\bigg )\delta y(t), \quad \forall |z_i|=1, \end{aligned}$$
(18)

where

$$\begin{aligned} z_{_i}=\exp (j\omega _{_i}),\omega _{_i}\in [0,2\pi ](i=0,1,2,\dots ,m),j=\sqrt{-1}, \end{aligned}$$

and

$$\begin{aligned} K=\left\{ \begin{array}{ll} 0, &{}t\in [t_{k-1},t_{_k}),\\ E_{k}, &{}t=t_{_k}. \end{array} \right. \end{aligned}$$

is exponentially stable.

Proof

The proof can be obtained by using the method in [4]. Lemma 2 can handle the delay effect.

4 Main Results

In this section, we will present a simple dwell-time-based unified condition for the globally exponential converge of a hybrid switching-impulsive dynamical network with stable (contracting) discrete dynamics or unstable (noncontracting) discrete dynamics (that is, the synchronizing impulses or desynchronizing impulses) to a synchronization manifold \(x_1=x_2=\dots =x_N\) by using the partial contraction theory.

Theorem 1

The hybrid switching-impulsive dynamical network (4–6) synchronizes in the sense that \(x_1=x_2=\dots =x_N\), if there exists a constant \(\eta <0\) such that one of the following two conditions hold,

(A1):

\(\varrho _{_{i+1}}+\frac{\ln \beta }{\Delta _{i+1}}\le \eta \),    \(i\in [0,N_{\zeta }(t)]\),

(A2):

\(\varrho _{_{i+1}}+\frac{\ln \beta }{T^*}\le \eta \),    \(i\in [0,N_{\zeta }(t)]\), if \(T^*\) exists,

where \(\varrho _{_{i+1}}(t)=\mu (A_{\sigma (i+1)}-L)+\Vert B_{\sigma (i+1)}\Vert +\sum \limits _{l=1}^m\Vert D_l^{\sigma (i+1)}(t)\Vert \), and \(\beta =\max \limits _j(\beta _j)\) with \(\beta _j=\Vert I+E_j\Vert \), \(j=1,2,\ldots ,N_{\zeta }(t)\).

Proof

From the hybrid network in (18), if \(t\in [t_0,t_1)\), we get

$$\begin{aligned} \delta y(t)=\exp \bigg \{\int _{t_0}^t[A_{\sigma (1)}-L+z_0B_{\sigma (1)}+\sum _{l=1}^{m}z_lD_l^{\sigma (1)}(s)]\mathrm{d}s\bigg \}\delta y(t_0). \end{aligned}$$
(19)

\(\square \)

Taking the norm on both sides of (19) and using Lemma 1, we can obtain

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \Vert \exp \bigg \{\int _{t_0}^t[A_{\sigma (1)}\!-\!L\!+\!z_0B_{\sigma (1)}\!+\!\sum _{l=1}^mz_lD_l^{\sigma (1)}(s)]ds\bigg \}\Vert \cdot \Vert \delta y(t_0)\Vert \nonumber \\&\le \exp \bigg \{\int _{t_0}^t[\mu (A_{\sigma (1)}\!-\!L)\!+\!\Vert B_{\sigma (1)}\Vert \!+\!\sum _{l=1}^m\Vert D_l^{\sigma (1)}(s)\Vert ]\mathrm{d}s\bigg \}\Vert \delta y(t_0)\Vert .\nonumber \\ \end{aligned}$$
(20)

Thus, for \(t=t_1\), we have

$$\begin{aligned} \delta y(t_1^+)=(I+E_1)\delta y(t_1), \end{aligned}$$
(21)

so

$$\begin{aligned} \Vert \delta y(t_1^+)\Vert&\le \Vert I+E_1\Vert \cdot \Vert \delta y(t_1)\Vert \nonumber \\&\le \beta _1\Vert \delta y(t_0)\Vert \exp \bigg \{\!\int _{t_0}^{t_1}\bigg [\mu (A_{\sigma (1)}-L) +\Vert B_{\sigma (1)}\Vert +\sum _{l=1}^m\Vert D_l^{\sigma (1)}(s)\Vert \bigg ]\mathrm{d}s\bigg \}.\nonumber \\ \end{aligned}$$
(22)

For \(t\in [t_1,t_2)\), it follows from (18) that

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \Vert \exp \bigg \{\int _{t_1}^t[A_{\sigma (2)}-L +z_1B_{\sigma (2)}+\sum _{l=1}^mz_lD_l^{\sigma (2)}(s)]\mathrm{d}s\bigg \}\Vert \cdot \Vert \delta y(t_{1})\Vert \nonumber \\&\le \beta _1\Vert \delta y(t_0)\Vert \exp \bigg \{\int _{t_1}^t[\mu (A_{\sigma (2)}-L) +\Vert B_{\sigma (2)}\Vert +\sum _{l=1}^{m}\Vert D_l^{\sigma (2)}(s)\Vert ]\mathrm{d}s\nonumber \\&+\int _{t_{0}}^{t}[\mu (A_{\sigma (1)}-L)+\Vert B_{\sigma (1)}\Vert +\sum _{l=1}^m\Vert D_{l}^{\sigma (1)}(s)\Vert ]\mathrm{d}s\bigg \}. \end{aligned}$$
(23)

Similarly, for \(t\in [t_k,t_{k+1})\),

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \beta _1\beta _2\ldots \beta _k\Vert \delta y(t_0)\Vert \exp \bigg \{\int _{t_k}^t\varrho _{_{k+1}}(s)\mathrm{d}s+\ldots +\int _{t_1}^{t_2}\varrho _{_2}(s)\mathrm{d}s\nonumber \\&\qquad \qquad \qquad +\int _{t_0}^{t_1}\varrho _{_1}(s)\mathrm{d}s\bigg \}, \end{aligned}$$
(24)

where

$$\begin{aligned} \varrho _{_{i+1}}(t)=\mu (A_{\sigma (i+1)}-L)+\Vert B_{\sigma (i+1)}\Vert +\sum \limits _{l=1}^m\Vert D_l^{\sigma (i+1)}(t)\Vert . \end{aligned}$$

Letting \(\beta =\max \limits _j(\beta _{j})\), it follows ( 24), and we have

$$\begin{aligned} \Vert \delta y(t)\Vert \le \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{k+1}\exp \bigg (\sum \limits _{j=0}^{N_{\zeta }(t)}\varrho _{_{j+1}}\Delta _{j+1}\bigg ). \end{aligned}$$
(25)

Next, we firstly consider that the average impulsive dwell-time \(T^*\) does not exist. That is to say that the impulsive set (\(t_k, E_k\)) is not countable. Therefore, we have

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \Vert \delta y(t_0)\Vert \beta ^{-1}\prod \limits _{j=0}^{N_{\zeta }(t)}\exp (\ln \beta +\varrho _{_{j+1}}\Delta _{j+1})\nonumber \\&\le \Vert \delta y(t_{0})\Vert \beta ^{-1}\exp \bigg [\sum \limits _{j=0}^{N_{\zeta }(t)}(\ln \beta +\varrho _{_{j+1}}\Delta _{j+1})\bigg ]\nonumber \\&\le \Vert \delta y(t_{0})\Vert \beta ^{-1}\exp \bigg [\sum \limits _{j=0}^{N_{\zeta }(t)}(\frac{\ln \beta }{\Delta _{j+1}}+\varrho _{_{j+1}})\Delta _{j+1}\bigg ],\nonumber \\&\le \Vert \delta y(t_{0})\Vert \beta ^{-1}\exp [\eta (t-t_0)], \end{aligned}$$
(26)

where \(\eta =\max \limits _j(\frac{\ln \beta }{\Delta _j}+\varrho _{_{j}})\).

Secondly, we take into account that the average dwell-time \(T^*\) exists. To obtain the unified synchronization criterion, consider two cases \(\beta \ge 1\) and \(\beta <1\) based on Definition 1.

Case 1. \(\beta \ge 1\).

In this case, the discrete dynamics is unstable (that is, the desynchronizing impulses). Then, from (25), we get

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \Vert \delta y(t_{0})\Vert \beta ^{-1}\beta ^{\bigg (\frac{\sum _{j=0}^{N_{_\zeta }(t)}\Delta _{j+1}}{T^{*}} +N_0\bigg )}\exp \bigg (\sum \limits _{j=0}^{N_{\zeta }(t)}\varrho _{_{j+1}}\Delta _{j+1}\bigg )\nonumber \\&= \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{N_0}\exp \bigg (\sum \limits _{j=0}^{N_{\zeta }(t)}\varrho _{_{j+1}}\Delta _{j+1} +\frac{\sum _{j=0}^{N_{_\zeta }(t)}\Delta _{j+1}}{T^{*}}\ln \beta \bigg )\nonumber \\&= \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{N_0}\exp \bigg (\sum \limits _{j=0}^{N_{\zeta }(t)}[\varrho _{_{j+1}} +\frac{\ln \beta }{T^*}]\Delta _{j+1}\bigg )\nonumber \\&\le \Vert \delta y(t_0)\Vert \beta ^{N_{0}-1}\exp \bigg (\eta \sum \limits _{j=0}^{N_{\zeta }(t)}\Delta _{j+1}\bigg )\nonumber \\&= \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{N_0}\exp [\eta (t-t_0)], \end{aligned}$$
(27)

where \(\eta =\max \limits _i(\varrho _{_{i+1}}+\frac{\ln \beta }{T^*})\).

Case 2. \(\beta <1\).

In this case, the discrete dynamics is stable (that is, the synchronizing impulses). Then, from (25), we get

$$\begin{aligned} \Vert \delta y(t)\Vert&\le \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{\bigg (\frac{\sum _{j=0}^{N_{_\zeta }(t)}\Delta _{j+1}}{T^{*}}-N_0\bigg )} \exp \bigg (\sum \limits _{j=0}^{N_{\zeta }(t)}\varrho _{_{j+1}}\Delta _{j+1}\bigg )\nonumber \\&\le \Vert \delta y(t_0)\Vert \beta ^{-1}\beta ^{-N_0}\exp \bigg (\eta (t-t_0)\bigg ). \end{aligned}$$
(28)

Therefore, from ( 27) and ( 28), we get

$$\begin{aligned} \Vert \delta y(t)\Vert \le \max \big \{\beta ^{-N_0},\beta ^{N_0}\big \}\Vert \delta y(t_0)\Vert \beta ^{-1}\exp \bigg (\eta (t-t_{0})\bigg ). \end{aligned}$$
(29)

Since we can always choose \(\alpha \) such that \(\varrho _{i+1}+\frac{\ln \beta }{\Delta _{i+1}}<0\) (or \(\varrho _{i+1}+\frac{\ln \beta }{\Delta _{i+1}}<\eta \), if \(T^*\) exists). Then, there exists \(\eta <0\) such that one of the two conditions in Theorem 1 is satisfied. So it implies that system (18) is globally exponentially stable. From Lemma 2, it is easy to see that the hybrid network in (16–17) is contracting. Using the parting contraction theory, we know that all trajectories of the system in (4–6) globally exponentially converge to the synchronization manifold \(x_1=x_2=\dots =x_N\). The proof is completed. \(\Box \)

Remark 4

From Theorem 1, a general criterion for guaranteeing the globally exponential synchronization of network (4–6) is established. We consider both the impulsive \(\frac{\ln \beta }{\Delta _i}\) (or \(\frac{\ln \beta }{T^*}\)) and switching effects \(\varrho _i\) in the aggregated form. No additional limitation is imposed on \(\frac{\ln \beta }{\Delta _i}\) (or \(\frac{\ln \beta }{T^*}\)) and \(\varrho _i\). Furthermore, unlike the conditions based on the Lyapunov stability theorem, there is no sign requirement on the derivative of Lyapunov function \(V(t)\) in the interval \([t_{k-1},t_k)\), which is required to obtain the stability conditions of hybrid switching-impulsive systems [44, 45] (that is, the continuous subsystems in interval \([t_{k-1},t_k)\) must be required to be asymptotical stable). Then, Theorem 1 is less conservative than the results in [44, 45].

Remark 5

Theorem 1 gives the conditions based on the average impulsive dwell-time. It is noted that when \(\beta >1\) (noncontracting or unstable discrete-systems dynamics), the impulses may desynchronize the systems, and then the impulses are required not to happen so frequently. Meanwhile, an upper bound on the average impulsive dwell-time is obtained. When \(\beta \le 1\) (contracting or stable discrete-systems dynamics), the impulses can synchronize the systems, and then the impulses are required to happen so frequently. A lower bound on the average impulsive dwell-time is obtained. Although a recent similar result was obtained in [29], the Lyapunov function has been used for synchronization of impulsive dynamical networks, compared to Theorem 1. Theorem 1 gives an alternative unified condition if average impulsive dwell-time does not exist. Moreover, the network in (4–6) includes both the impulse and switching effects, which is more general than the systems proposed in [10, 29].

Remark 6

The criterion in Theorem 1 considers only the complete synchronization of hybrid networks. In fact, we can extend this unified criterion based on the average impulsive dwell-time and contraction theory to study other kinds of synchronization, such as the generalized synchronization, which have been investigated in [9].

Corollary 1

For network (16–17), if there exists a constant \(\eta <0\) such that the following conditions hold

$$\begin{aligned} \varrho _{_{i+1}}+\frac{\ln \beta }{\inf \limits _i\{t_{i+1}-t_{i}\}}\le \eta ,\quad i\in [0,N_{\zeta }(t)],\beta >1, \end{aligned}$$
(30)

then the network in (4–6) synchronizes in the sense that \(x_{1}=x_{2}=\ldots =x_{N}\), where \(\beta \) and \(\varrho _{i}\) are given in Theorem 1 and

$$\begin{aligned} \varrho _{_{i+1}}+\frac{\ln \beta }{\sup \limits _i\{t_{i+1}-t_{i}\}}\le \eta ,\quad i\in [0,N_{\zeta }(t)],\beta \le 1. \end{aligned}$$
(31)

then the network (4–6) synchronizes in the sense that \(x_1=x_2=\ldots =x_N\), where \(\beta \) and \(\varrho _i\) are given in Theorem 1.

Proof

For \(\beta >1\), the impulses should not happen frequently. Then, the average impulsive dwell-time \(T^*\) in condition (1) of Theorem 1 can be replaced with \(\inf \limits _k\{t_{k+1}-t_k\}\). Therefore, the criteria on (30) can be easily obtained. For \(\beta \le 1\), the proof is similar and omitted. \(\square \)

Remark 7

From conditions (30) and (31), we know that the average impulsive dwell-time \(T^{*}\) satisfies \(\inf \limits _k\{t_{k+1}-t_k\}<T^*<\sup \limits _k\{t_{k+1}-t_k\}\). For \(\beta >1\), we get \(\ln \beta >0\), and then the condition (a1) of Theorem 1 based on the average impulsive dwell-time is less conservative than condition (a1) of Corollary 1. For \(\beta \le 1\), we get \(\ln \beta \le 0\), and then condition (1) of Theorem 1 based on the average impulsive dwell-time is less conservative than condition (a1) of Corollary 1. Moreover, it is noted that the synchronization criterion in Theorem 1 based on the average impulsive dwell-time is less than the results in [9] based on conditions of Corollary 1.

5 Illustrative Example

In this section, an example will be given to illustrate the main results proposed in this paper for both contracting and noncontracting discrete dynamics (that is, \(\beta <1\) and \(\beta \le 1\)).

Example

Consider the classical Lorenz chaotic system,

$$\begin{aligned} \dot{x}_{i1}&= 10(x_{i2}-x_{i1}),\end{aligned}$$
(32)
$$\begin{aligned} \dot{x}_{i2}&= 28x_{i1}-x_{i2}-x_{i1}x_{i3},\end{aligned}$$
(33)
$$\begin{aligned} \dot{x}_{i3}&= x_{i1}x_{i2}-\frac{8}{3}x_{i3}, \end{aligned}$$
(34)

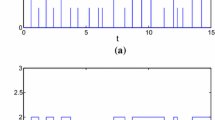
where \(x_i=(x_{i1},x_{i2},x_{i3})^{\mathrm{T}}\in {\mathbb R}^3\) is the state vector of node \(i\). Then, the system in (32–34) exhibits chaotic behavior with the initial conditions \(x_{i1}=0.4, x_{i2}=0.6\), and \(x_{i3}=0.5\), which is shown in Fig. 1.

Fig. 1
figure 1

The chaotic attractor of system (32–34)

Full size image

In this example, we consider two cases of the synchronization of a hybrid network without switching effects.

Case 1. Let us firstly consider the hybrid dynamical network of system (32–34) with five nodes, under which the discrete dynamics is contracting (\(\beta <1\)):

$$\begin{aligned} \dot{x}_i(t)&= Ax_i(t)+f(x_i(t))+\sum \limits _{l=1}^4\sum \limits _{j=1}^5\varepsilon _lc_{ijl}(t)\Gamma (t)x_j(t-\tau _l(t)), \quad t\ne t_k\end{aligned}$$
(35)
$$\begin{aligned} \Delta x_i(t)&= B_kx_{i}(t),\quad t=t_k, \end{aligned}$$
(36)

where

$$\begin{aligned} A=\left[ \begin{array}{l@{\quad }l@{\quad }l} -10&{}10&{} 0\\ 28&{} -1&{} 0\\ 0&{} 0&{} -\frac{8}{3} \end{array}\right] \!,\quad f(x_i)=\left[ \begin{array}{l} 0\\ -x_{i1}x_{i3}\\ x_{i1}x_{i2} \end{array}\right] \!. \end{aligned}$$

The coupling delays are \(\tau _1(t)=0\), \(\tau _2(t)=0.1+0.05 \sin (t)\), \(\tau _3(t)=0.2+0.1\sin (t)\), and \(\tau _4(t)=0.3+0.2\sin (t)\), the inner-coupling matrix \(\Gamma (t)=\Gamma =\mathrm{diag}[1,1,1]\), the outer-coupling matrices

$$\begin{aligned} C_1(t)&= \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -2&{} 1&{} 0&{} 0&{} 1\\ 1&{} -2&{} 1&{} 0&{} 0\\ 0&{} 1&{} -2&{} 1&{} 0\\ 0&{} 0&{} 1&{} -2&{} 1\\ 1&{} 0&{} 0&{} 1&{} -2 \end{array}\right] ,\quad C_2(t)=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -3&{} 2&{} 1&{} 0&{} 0\\ 0&{} -2&{} 1&{} 1&{} 0\\ 0&{} 0&{} -1&{} 1&{} 0\\ 1&{} 0&{} 0&{} -3&{} 2\\ 1&{} 1&{} 0&{} 0&{} -2 \end{array}\right] ,\\ C_3(t)&= \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -1&{} 1&{} 0&{} 0&{} 0\\ 0&{} -1&{} 1&{} 0&{} 0\\ 0&{} 0&{} -1&{} 1&{} 0\\ 0&{} 0&{} 0&{} -1&{} 1\\ 1&{} 0&{} 0&{} 0&{} -1 \end{array}\right] ,\quad C_4(t)=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -2&{} 1&{} 1&{} 0&{} 0\\ 0&{} -2&{} 1&{} 0&{} 1\\ 1&{} 0&{} -2&{} 1&{} 0\\ 0&{} 1&{} 0&{} -2&{} 1\\ 1&{} 1&{} 0&{} 0&{} -2 \end{array}\right] . \end{aligned}$$

If we select the coupling strength \(\varepsilon =1\) in the auxiliary system (10–12), we can get

$$\begin{aligned} \varrho =\mu (I_N\otimes A+I_N\otimes J_1-L+C_1\otimes \Gamma )+\sum \limits _{l=2}^4\Vert C_l\otimes \Gamma \Vert =30.9312, \end{aligned}$$

where

$$\begin{aligned} J_1=\frac{\partial f(x_i(t))}{\partial x_i(t)}= \left[ \begin{array}{lll} 0&{}0&{} 0 \\ -x_{i3}&{} 0&{}-x_{i1}\\ x_{i2}&{} x_{i1}&{}0 \end{array}\right] . \end{aligned}$$

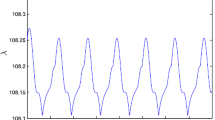
In this case, we consider the contracting discrete dynamics \(\beta \le 1\) (that is, synchronizing impulses). Taking the impulsive control matrix \(B_k=\mathrm{diag}[-0.8,-0.8,-0.8]\), which implies that \(\beta =0.04\), the average impulsive dwell-time \(T^*=0.1\), and the impulsive sequence is depicted in Fig. 2. From condition (2a) in Theorem 1, we have \(\varrho +\frac{\ln \beta }{T^*}=-10.2443<0\). Then, the dynamical network (35–36) can achieve synchronization under the effect of the contracting discrete dynamics, which are shown in Fig. 3. However, from the impulsive sequence of Fig. 2, it is easy to see that the maximum impulsive interval \(\Delta _{\max }=\sup \{t_k-t_{k-1}\}=0.25\). If we use the conception of \(\sup \{t_k-t_{k-1}\}\) to take place of the average impulsive dwell-time \(T^*\) in Corollary 1, then we have \(\varrho +\frac{\ln \beta }{\sup \{t_{k}-t_{k-1}\}}=9.0690>0\), and Corollary 1 cannot ensure the synchronization since they require that \(\varrho +\frac{\ln \beta }{\sup \{t_k-t_{k-1}\}}<0\) for all \(t\ge t_0\). Therefore, the conditions in Theorem 1 based on the average impulsive dwell-time are less conservative than the results in [5, 20].

Fig. 2
figure 2

The contracting discrete dynamics \(\beta =0.04\)

Full size image

Case 2. Next, we consider the hybrid dynamical network of system in (32–34) under the effect of noncontracting discrete dynamics (\(\beta >1\)),

$$\begin{aligned}&\dot{x}_i(t)=Ax_i(t)\!\!+\!\!f(x_i(t))\!+\!\!\sum \limits _{l=1}^4\sum \limits _{j=1}^5\varepsilon _lh_{jl}(t)(x_j(t\!-\!\tau _l(t))\!-\!x_i(t-\tau _l(t))), \quad t\!\ne \!t_k\end{aligned}$$
(37)
$$\begin{aligned}&\Delta x_i(t)=B_kx_i(t),\quad t=t_k, \end{aligned}$$
(38)

where \(A\), \(f(x_i)\), and the coupling delays \(\tau _l\) \((l=1,2,3,4)\) are still the same as Case 1. The nonlinear function is

$$\begin{aligned} \sum \limits _{j=1}^5h_{j1}=(I_N\otimes \Gamma _1)x_i, h_{j2}=C_k\Gamma x_j(t-\tau _k(t)), (k=2,3,4), \end{aligned}$$

where \(\Gamma =I_3\), \(C_2, C_3\), and \(C_4\) are the same as Case 1, and \(\Gamma _1=[0, 0, 0; -40, 0, 0; 0, 0, 0,]\).

If we select \(\varepsilon _i=0.05\) \((i=2,3,4)\) in the auxiliary system (10–12), we can get \(\varrho =-0.4128<0\). In this case, we consider the noncontracting discrete dynamics \(\beta >1\) (that is, desynchronizing impulses). Taking the impulsive control matrix \(B_k=\mathrm{diag}[0.1, 0.1, 0.1]\), which implies that \(\beta =1.21>1\), the average impulsive dwell-time \(T^*=0.5\), and the impulsive sequence is depicted in Fig. 4. From condition (2) in Theorem 1, we have \(\varrho +\frac{\ln \beta }{T^*}=-0.0316<0\). Then, the dynamical network in (37–38) can achieve synchronization under the effect of the noncontracting discrete dynamics, which is shown in Fig. 5. However, from the impulsive sequence of Fig. 4, it is easy to see that the minimum impulsive interval \(\Delta _{\min }=\inf \{t_k-t_{k-1}\}=0.1\). If we use the conception of \(\inf \{t_{k}-t_{k-1}\}\) to take place of the average impulsive dwell-time \(T^*\) in Corollary 1, then we have \(\varrho +\frac{\ln \beta }{\inf \{t_k-t_{k-1}\}}=1.4934>0\), and the Corollary 1 cannot ensure synchronization since they require that \(\varrho +\frac{\ln \beta }{\inf \{t_k-t_{k-1}\}}<0\) for all \(t\ge t_0\). Therefore, the conditions in Theorem 1 based on the average impulsive dwell-time are less conservative than the results in [5, 20].

Fig. 3
figure 3

Synchronization errors of the dynamical network (35–36) under the contracting discrete dynamics

Full size image
Fig. 4
figure 4

The noncontracting discrete dynamics \(\beta =1.21\)

Full size image
Fig. 5
figure 5

The synchronization errors of the dynamical network in (37–38) under the noncontracting discrete dynamics

Full size image

6 Conclusion

Based on the contraction theory and the conception of average impulsive dwell-time, several unified criteria for globally exponential synchronization of the hybrid switching-impulsive network have been presented. Two cases have been considered: contracting discrete dynamics and noncontracting discrete dynamics. According to the theoretical analysis, these conditions generalize and relax most existing results on synchronization of the hybrid network.