1 Introduction

With the development of industrial technology, the requirements of system reliability have increased. To improve the reliability of a system, fault detection and isolation and fault-tolerant control have been studied widely, and many outstanding results have been achieved, such as those reported in [5, 8, 10, 13, 17, 38, 43, 44, 51] and the references therein. It should be noted that more accurate information on the fault, such as the size and shape of the fault, can be obtained by fault estimation, which is more challenging than fault detection and isolation. Recently, outstanding results relating to fault estimation have been achieved [16, 18, 30, 45, 49, 52, 53].

It is well known that many practical systems are nonlinear, and challenges remain in the fault estimation and fault accommodation of a nonlinear system. Takagi–Sugeno (T–S) fuzzy models are a useful tool for the description of a nonlinear system and have thus attracted considerable attention in recent decades [9, 22–24, 28, 35, 36, 39–42, 46–48].

Employing T–S fuzzy systems, excellent results relating to fault estimation and fault accommodation have been achieved [1–4, 6, 7, 14, 15, 19, 20, 26, 33, 34, 37]. The existing methods require restrictive assumptions, such as those of rank constraints of \(C_iB_i\) [19], stable system matrices [14], the same measurement output matrices [1–4, 6, 7, 15, 20, 26] and a single faulty actuator or sensor [33, 37].

Note that both sensor faults and actuator faults may exist in practical engineering. The problems of fault estimation and fault accommodation for T–S fuzzy systems with simultaneous sensor and actuator faults are receiving increasing research attention. Employing an ingenious transformation, a new descriptor fuzzy sliding-mode observer has been designed to estimate the system state and sensor and actuator faults simultaneously, and an observer-based fault-tolerant control scheme has been developed to stabilize a closed-loop system [27]. Additionally, two observers have been designed to estimate sensor and actuator faults, separately [32]. For fuzzy systems with the same or proportional control matrices \(B_i\), a fuzzy proportional integral observer has been designed to estimate sensor and actuator faults [21].

It should be noted that modern industrial systems are becoming much more complex, which is increasing the number of fuzzy rules. Thus, the stability analysis, controller design and fault estimation for such T–S fuzzy systems have become much more difficult [29, 37]. To resolve this problem, T–S fuzzy systems with nonlinear local models have been proposed, and excellent results have been achieved [11, 12, 29, 31, 37].

To the best of the authors’ knowledge, the problems of fault estimation and fault accommodation for fuzzy systems, which have local nonlinear models and sensor and actuator faults, simultaneously, have not been fully investigated and developing their solutions remains an important challenge. This background provides the motivation for the present study.

For T–S fuzzy systems with local nonlinear models, this paper proposes a fuzzy fault estimation observer that can be used in the estimation of the system state and sensor and actuator faults simultaneously. Furthermore, an observer-based fault-tolerant controller is designed to compensate for the effect of faults and to stabilize the closed-loop system. The main contributions of this paper are summarized as follows. (1) For T–S fuzzy systems with local nonlinear models having sensor and actuator faults, simultaneously, the problems of fault estimation and fault accommodation are addressed for the first time. (2) Compared with previous results, the proposed observer not only is robust against the disturbance but also has a wider application range and more freedom for design. (3) The observer and controller are designed separately, which avoids their coupling and reduces the computation complexity.

This paper is organized as follows. The system description and definitions are presented in Sect. 2. In Sects. 3 and 4, the fuzzy fault estimation observer and the observer-based fault-tolerant controller are designed, respectively. Simulation is provided in Sect. 5. Finally, Conclusions are given in Sect. 6.

Throughout this paper, I and O denote an identity matrix and a zero matrix of appropriate dimensions, respectively. The symbol \(*\) in a matrix denotes the transposed element in the symmetric position. \(\Vert a\Vert \) denotes the Euclidean norm of a vector a; i.e., \(\Vert a\Vert =(a^Ta)^{1/2}\). For an arbitrary matrix A, \(A^T\), \(A^-\) and \(A^{-1}\) denote the transposed matrix, left-inverse matrix and inverse matrix of A, respectively.

2 System Description and Definitions

In this paper, we consider continuous-time T–S fuzzy systems with local nonlinear models and additive sensor and actuator faults. The ith rule of T–S fuzzy systems can be written as follows.

Plant Rule i:

IF \(\xi _1(t)\) is \(\pi _{i1}\) and \(\cdots \) \(\xi _k(t)\) is \(\pi _{ik}\),

THEN

$$\begin{aligned}&\dot{x}(t)=A_ix(t)+N_ig_{i}(x(t))+B_i(u(t)+f_a(t))+E_id(t) \end{aligned}$$
(1)
$$\begin{aligned}&y(t)=C_ix(t)+Ff_s(t) \end{aligned}$$
(2)
$$\begin{aligned}&y_L(t)=C_{Li}x(t) \end{aligned}$$
(3)

where \(x(t)\in R^n\), \(u(t)\in R^{p_1}\), \(y(t)\in R^q\), \(y_L(t)\in R^{q_1}\), \(f_a(t)\in R^{p_1}\) and \(f_s(t)\in R^{m}\) are the state vector, input vector, measurement output vector, controlled output vector, additive actuator fault vector and sensor fault vector, respectively. \(d(t)\in R^{p_2}\) represents the exogenous disturbance vector which is assumed to belong to \(L_2[0,\infty )\). \(g_{i}(x(t))\in R^{p_3}\) represents the nonlinear part of the ith local model. \(\xi _j(t)\) and \(\pi _{ij}~(i=1,2,\ldots ,r; j=1,2,\ldots ,k)\) are the premise variables and fuzzy sets, where k and r are the number of premise variables and IF–THEN rules, respectively. \(A_i,N_i,B_i,E_i,C_i,F,C_{Li}\) are constant real matrices.

The fuzzy systems can be written as follows:

$$\begin{aligned}&\dot{x}(t)=\sum _{i=1}^r\mu _i[A_ix(t)+N_ig_{i}(x(t))+B_i(u(t)+f_a(t))+E_id(t)] \end{aligned}$$
(4)
$$\begin{aligned}&y(t)=\sum _{i=1}^r\mu _i[C_ix(t)+Ff_s(t)] \end{aligned}$$
(5)
$$\begin{aligned}&y_L(t)=\sum _{i=1}^r\mu _iC_{Li}x(t) \end{aligned}$$
(6)

where \(\xi (t)=[\xi _1(t),\xi _2(t),\ldots ,\xi _k(t)]\). For each \(i=1,2,\ldots ,r\), \(\mu _i\) is the abbreviation of \(\mu _i(\xi (t))\), where \(\mu _i(\xi (t))=\sigma _i(\xi (t))/\sum \nolimits _{i=1}^r\sigma _i(\xi (t))\), \(\sigma _i(\xi (t))=\prod \limits _{j=1}^k\pi _{ij}(\xi _j(t))\), and \(\pi _{ij}(\xi _j(t))\) is the grade of membership of \(\xi _j(t)\) in \(\pi _{ij}\). It is obvious that \(\mu _i(\xi (t))\ge 0\), and \(\sum \limits _{i=1}^r\mu _i(\xi (t))=1\).

In this paper, the following assumptions are needed.

Assumption 1

In fuzzy systems (4)–(6), \((A_i,B_i)\) are controllable, \((A_i,C_i)\) are observable, and \(q\ge p_1+m\).

Assumption 2

It is supposed that F is of full column rank, and \(C_i\) are of full row rank.

Assumption 3

The nonlinear functions \(g_{i}(x(t))\) are Lipschitz with respect to the state x(t); that is, there exist constants \(c_i\) such that

$$\begin{aligned} \Vert g_{i}(x(t_1))-g_{i}(x(t_2))\Vert \le c_i \Vert x(t_1)-x(t_2)\Vert \end{aligned}$$
(7)

where \(x(t_1), x(t_2)\in R^n\) and \(c_i\) are Lipschitz constants of \(g_{i}(x(t))\).

In Assumption 2, if \(F\in R^{q\times m}\) is not of full column rank i.e., \(rank(F)=m_1<m\), then a matrix decomposition method previously proposed in [8] can be used. Specifically, F can be rewritten as \(F=F_1F_2\), where \(F_1 \in R^{q\times m_1}\) and \(rank(F_1)= m_1\). We can thus treat \(F_2f_s(t)\) as a sensor fault vector and design an observer to estimate it.

Remark 1

In fuzzy systems (4)–(6), we use the nonlinear functions \(g_{i}(x(t))\) to represent the nonlinear parts of local models. The nonlinear consequences represent important nonlinear properties of the original nonlinear system. Additionally, the number of fuzzy rules can be reduced using the local nonlinear models, which implies that the computational burden is reduced [12, 29, 37].

Remark 2

It should be noted that the measurement noise is not considered in (5). Without loss of generality, let the measurement noise \(d_1(t)\in R^{q_1}\), and the distribution matrix of \(d_1(t)\) be \(\bar{F}\in R^{q\times q_1}\). We assume that \(q>q_1\). It is not difficult to find a coordinate transformation matrix T such that \(T\bar{F}=0\). According to this transformation, we can choose Ty(t) as the new measurement output. Thus, the effect of the measurement noise can be removed.

The objective of this paper is to design a robust observer for fuzzy systems (4)–(6) to estimate x(t), \(f_a(t)\), \(f_s(t)\), simultaneously, and design an observer-based fault-tolerant controller to compensate for the faults and guarantee system stability.

The following definition and lemmas are useful in obtaining our main results.

Definition 1

For an arbitrary matrix \(A\in R^{n\times m}\), if \(A^-\in R^{m\times n}\) satisfies \(A^-A=I_m\), we say that \(A^-\) is a left-inverse matrix of A.

Lemma 1

[50]. For an arbitrary matrix \(A\in R^{n\times m}\), \(rank(A)=m\), then we have

  1. 1.

    \(A^-=(A^TA)^{-1}A^T\) is a left-inverse matrix of A.

  2. 2.

    If \(A^{-*}\) is a left-inverse matrix of A, the general form of left-inverse matrix of A can be obtained as

    $$\begin{aligned} A^-=A^{-*}+X-XAA^{-*} \end{aligned}$$
    (8)

    where \(X\in R^{m\times n}\) is an arbitrary matrix with appropriate dimension.

Lemma 2

[50]. For the solvable matrix equation \(AX=B\), \(X=GB\) is a solution of the equation, if and only if the matrix G satisfies \(AGA=A\). Specifically, if A is of full column rank, \(X=A^-B\) is a solution of the equation \(AX=B\).

Lemma 3

[29]. For matrices (or vectors) A and B with appropriate dimensions, the following condition holds,

$$\begin{aligned} A^TB+B^TA \le \varepsilon A^TA+\varepsilon ^{-1}B^TB \end{aligned}$$
(9)

where \(\varepsilon \) is an arbitrary positive scalar.

Lemma 4

[9]. If the following conditions hold

$$\begin{aligned}&S_{ii}<0,~~~~1 \le i\le r \end{aligned}$$
(10)
$$\begin{aligned}&\frac{2}{r-1}S_{ii}+S_{ij}+S_{ji}< 0,~~~~1 \le i \ne j \le r \end{aligned}$$
(11)

we have

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _jS_{ij}<0. \end{aligned}$$
(12)

3 Fault Estimation

Let \(\bar{x}(t)=[x^T(t),f_s^T(t)]^T\), then the T–S fuzzy systems (4)–(5) can be rewritten as

$$\begin{aligned} G\dot{{\bar{x}}}(t)= & {} \sum _{i=1}^r\mu _i[A_{1i}\bar{x}(t)+N_{1i}g_{i}(x)+B_{1i}(u(t)+f_a(t))\nonumber \\&+\,F_{1}f_s(t)+E_{1i}d(t)] \end{aligned}$$
(13)
$$\begin{aligned} y(t)= & {} \sum _{i=1}^r\mu _i[C_{1i}\bar{x}(t)]\nonumber \\= & {} \sum _{i=1}^r\mu _i[C_{0i}\bar{x}(t)+Ff_s(t)] \end{aligned}$$
(14)

where \(G=\left[ \begin{array}{ccc} I_n&{} O \\ O &{} O_{q\times m}\\ \end{array} \right] \), \(A_{1i}=\left[ \begin{array}{ccc} A_i&{} O \\ O &{} -F\\ \end{array} \right] \), \(N_{1i}=\left[ \begin{array}{ccc} N_i \\ O_{q\times p_3}\\ \end{array} \right] \), \(B_{1i}=\left[ \begin{array}{ccc} B_i \\ O_{q\times p_1}\\ \end{array} \right] \), \(F_{1}=\left[ \begin{array}{ccc} O_{n\times m} \\ F\\ \end{array} \right] \), \(E_{1i}=\left[ \begin{array}{ccc} E_i \\ O_{q\times p_2}\\ \end{array} \right] \), \(C_{1i}=[C_i~~F]\), \(C_{0i}=[C_i~~O_{q\times m}]\), and \(g_i(x)\) represent \(g_i(x(t))\).

Since F is of full column rank, according to Lemmas 1, 2 and (14), we have

$$\begin{aligned} f_s(t)=F^-(y(t)-\sum _{i=1}^r\mu _i[C_{0i}\bar{x}(t)]) \end{aligned}$$
(15)

where \(F^-\) is a left-inverse matrix of F. Substituting (15) in (13), we have

$$\begin{aligned} G\dot{{\bar{x}}}(t)= & {} \sum _{i=1}^r\mu _i[A_{1i}\bar{x}(t)+N_{1i}g_{i}(x)+B_{1i}(u(t)+f_a(t))\nonumber \\&+\,F_{1}(F^-(y(t)-C_{0i}\bar{x}(t))+E_{1i}d(t)]\nonumber \\= & {} \sum _{i=1}^r\mu _i[(A_{1i}-F_1F^-C_{0i})\bar{x}(t)+N_{1i}g_{i}(x)\nonumber \\&+\,B_{1i}(u(t)+f_a(t))+F_{1}F^-y(t)+E_{1i}d(t)] \end{aligned}$$
(16)

Obviously, the ith local model of the T–S fuzzy systems (16) can be written as

$$\begin{aligned} G\dot{\bar{x}}(t)= & {} (A_{1i}-F_1F^-C_{0i})\bar{x}(t)+N_{1i}g_{i}(x)\nonumber \\&+\,B_{1i}(u(t)+f_a(t))+F_{1}F^-y(t)+E_{1i}d(t) \end{aligned}$$
(17)

Adding \(K_{1i}C_{1i}\dot{\bar{x}}(t)\) to both sides of (17), we have

$$\begin{aligned} G_{1i}\dot{\bar{x}}(t)= & {} (A_{1i}-F_{1}F^-C_{0i})\bar{x}(t)+N_{1i}g_{i}(x)+B_{1i}(u(t)+f_a(t))\nonumber \\&+\,F_{1}F^-y(t)+E_{1i}d(t)+K_{1i}C_{1i}\dot{\bar{x}}(t) \end{aligned}$$
(18)

where \(G_{1i}=G+K_{1i}C_{1i}\), and \(K_{1i}=[K_{11i}^T~~K_{12i}^T]^T\in R^{(n+q)\times q}\) is the gain matrices to be determined.

It is not difficult to obtain \(G_{1i}=\left[ \begin{array}{ccc} I+K_{11i}C_{i}&{} K_{11i}F \\ K_{12i}C_{i}&{} K_{12i}F \\ \end{array} \right] \). Our purpose is to choose suitable matrices \(K_{11i}\), \(K_{12i}\) such that \(G_{1i}\) is of full column rank, which means that there exists a left-inverse matrix of \(G_{1i}\). Let \(K_{11i}=O_{n\times q}\), \(K_{12i}=\mathrm{diag}\{\lambda _{i1}, \lambda _{i2},\ldots ,\lambda _{iq}\}\), where \(\lambda _{ij}\) denotes arbitrary nonzero constants, \(j=1,2,\ldots ,q\); then \(G_{1i}=\left[ \begin{array}{ccc} I&{} O \\ K_{12i}C_{i}&{} K_{12i}F \\ \end{array} \right] \). Note that F is of full column rank. It is then not difficult to find that \(G_{1i}\) is of full column rank. According to Lemma 1, there exist left-inverse matrices of \(G_{1i}\). One of the left-inverse matrices of \(G_{1i}\) can be written as

$$\begin{aligned} G_{1i}^{-*}=\left[ \begin{array}{ccc} I&{} O \\ -F^-C_i&{} F^-K_{12i}^{-1} \\ \end{array} \right] \end{aligned}$$
(19)

According to Lemma 2 and (18), we have

$$\begin{aligned} \dot{\bar{x}}(t)= & {} A_{2i}\bar{x}(t)+N_{2i}g_{i}(x)+B_{2i}(u(t)+f_a(t))+F_{2i}y(t)\nonumber \\&+\,E_{2i}d(t)+G_{1i}^{-*}K_{1i}C_{1i}\dot{\bar{x}}(t) \end{aligned}$$
(20)

where \(A_{2i}=G_{1i}^{-*}(A_{1i}-F_{1}F^-C_{0i})\), \(N_{2i}=G_{1i}^{-*}N_{1i}\), \(B_{2i}=G_{1i}^{-*}B_{1i}\), \(F_{2i}=G_{1i}^{-*}F_{1}F^-\), \(E_{2i}=G_{1i}^{-*}E_{1i}\).

Note that \(G_{1i}^{-*}K_{1i}=\left[ \begin{array}{ccc} O \\ F^- \\ \end{array} \right] \) is independent of i. Let \(H=G_{1i}^{-*}K_{1i}\). From (14), we have

$$\begin{aligned} \sum _{i=1}^r\mu _iG_{1i}^{-*}K_{1i}C_{1i}\dot{\bar{x}}(t)=H\sum _{i=1}^r\mu _iC_{1i}\dot{\bar{x}}(t)=H\dot{y}(t) \end{aligned}$$
(21)

The overall fuzzy systems can be rewritten as

$$\begin{aligned} \dot{\bar{x}}(t)= & {} \sum _{i=1}^r\mu _i[A_{2i}\bar{x}(t)+N_{2i}g_{i}(x)+B_{2i}(u(t)+f_a(t))+F_{2i}y(t)\nonumber \\&~~~~~~~~+E_{2i}d(t)+H\dot{y}(t)] \end{aligned}$$
(22)
$$\begin{aligned} y(t)= & {} \sum _{i=1}^r\mu _i[C_{1i}\bar{x}(t)]=\sum _{i=1}^r\mu _i[C_{0i}\bar{x}(t)+Ff_s(t)] \end{aligned}$$
(23)

Remark 3

To estimate the sensor fault, the descriptor observer method is applied widely, and excellent results have been obtained [6, 14]. Employing this method, pioneering results, including fault estimation for fuzzy systems with unmeasurable premise variables [1, 2, 4, 15] and the design of robust fault detection observers [1, 4], have been achieved. In the cited papers, the system output matrices of the fuzzy systems must be the same. Our method can be used in the case that the fuzzy systems have different output matrices. Additionally, in this paper, for every local model, an augmented descriptor local model is constructed by treating the senor fault as a virtual state. We can obtain new fuzzy systems by choosing a gain matrix for each local model, and the gain matrices may be different from each other. Compared with previously obtained results [1, 2, 4, 6, 14, 15], for which the gain matrices must be the same, in this paper, there is more freedom of design.

Remark 4

In this paper, we choose the left-inverse matrix rather than the Moore–Penrose generalized inverse matrix. It is worth pointing out that the Moore–Penrose generalized inverse matrices of F and \(G_{1i}\) are unique, while the left-inverse matrices of F and \(G_{1i}\) are not unique. The general forms of the left-inverse matrices of F and \(G_{1i}\) are \(F^-=(F^TF)^{-1}F^T+X-XF(F^TF)^{-1}F^T\) and \(G_{1i}^-=G_{1i}^{-*}+Y-YG_{1i}G_{1i}^{-*}\), respectively, where X, Y are arbitrary real matrices with appropriate dimensions. We can therefore get different left-inverse matrices by choosing different X and Y, which provides more freedom of design.

On the basis of the above discussion, we construct a fuzzy fault estimation observer for fuzzy systems (22) and (23):

$$\begin{aligned} \dot{z}(t)= & {} \sum _{i=1}^r\mu _i[A_{2i}z(t)+N_{2i}g_{i}(\hat{x})+B_{2i}(u(t)+\hat{f}_a(t))\nonumber \\&+\,(F_{2i}+A_{2i}H)y(t)+K_{2i}(y(t)-\hat{y}(t))] \end{aligned}$$
(24)
$$\begin{aligned} \dot{\hat{f}}_a(t)= & {} \sum _{i=1}^r\mu _i[K_{3i}(y(t)-\hat{y}(t))] \end{aligned}$$
(25)
$$\begin{aligned} \hat{\bar{x}}(t)= & {} z(t)+Hy(t) \end{aligned}$$
(26)
$$\begin{aligned} \hat{y}(t)= & {} \sum _{i=1}^r\mu _i[C_{1i}\hat{\bar{x}}(t)] \end{aligned}$$
(27)

where z(t) is the observer state. \(\hat{\bar{x}}(t)\) and \(\hat{f}_a(t)\) are the estimations of \(\bar{x}(t)\) and \(f_a(t)\), respectively, and \(g_{i}(\hat{x})\) represents \(g_i(\hat{x}(t))\). \(K_{2i}\) and \(K_{3i}\) are the observer gain matrices to be designed.

Theorem 1

Given the \(H_\infty \) performance level \(\gamma _1\), the fuzzy fault estimation observer (24)–(27) can asymptotically estimate the system state and faults with the \(H_\infty \) performance level \(\gamma _1\), that is

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty } e(t)=0,~~if~~\omega (t)=0; \end{aligned}$$
(28)
$$\begin{aligned}&\,\int _0^te^T(s)e(s)ds\le \gamma _1^2\int _0^t\omega ^T(s)\omega (s)ds,~~~if~~\omega (t)\ne 0, \end{aligned}$$
(29)

if there exist a symmetric positive-definite matrix P, matrices \(Q_j\), and positive scalars \(\delta _1\), \(\delta _2\), ..., \(\delta _r\), for \(i,j=1,2,\ldots ,r\), such that the following linear matrix inequalities hold true.

$$\begin{aligned}&\varOmega _{ii}<0,~~~~1 \le i\le r \end{aligned}$$
(30)
$$\begin{aligned}&\frac{2}{r-1}\varOmega _{ii}+\varOmega _{ij}+\varOmega _{ji}< 0,~~~~1 \le i \ne j \le r \end{aligned}$$
(31)

where

$$\begin{aligned} \varOmega _{ij}=\left[ \begin{array}{cccc} \varXi _{ij}+\delta _ic_i^2I+I &{}~ PE_{3i} &{}~ PN_{3i} \\ {*} &{}~ -\rho _1I&{}~ O \\ {*} &{}~ {*} &{}~ -\delta _iI\\ \end{array}\right] , \end{aligned}$$
(32)

\(e(t)=[(\bar{x}(t)-\hat{\bar{x}}(t))^T, (f_a(t)-\hat{f}_a(t))^T]^T\), \(\omega (t)=[d^T(t), \dot{f}_a^T(t)]^T\), \(c_i\) are the Lipschitz constants of \(g_i(x)\), \(\rho _1=\gamma _1^2\), and \(\varXi _{ij}\), \(N_{3i}\), \(E_{3i}\) will be specified later. The gain matrices of the observer can be obtained by \(K_{4i}=\left[ \begin{array}{ccc} K_{2i} \\ K_{3i} \\ \end{array}\right] =P^{-1}Q_j\).

Proof

Let \(\tilde{\bar{x}}(t)=\bar{x}(t)-\hat{\bar{x}}(t)\), \(\tilde{f}_a(t)=f_a(t)-\hat{f}_a(t)\), \(\tilde{g}_i=g_i(x)-g_i(\hat{x})\). From (22)–(24), (26)–(27), we have

$$\begin{aligned} \dot{\tilde{\bar{x}}}(t)= & {} \dot{\bar{x}}(t)-\dot{\hat{\bar{x}}}(t)\nonumber \\= & {} \dot{\bar{x}}(t)-\dot{z}(t)-H\dot{y}(t)\nonumber \\= & {} \sum _{i=1}^r\mu _i[A_{2i}\bar{x}(t)-A_{2i}z(t)+N_{2i}\tilde{g}_{i}+B_{2i}\tilde{f}_a(t)\nonumber \\&+\,E_{2i}d(t)-A_{2i}H y(t)-K_{2i}(y(t)-\hat{y}(t))]\nonumber \\= & {} \sum _{i=1}^r\mu _i[A_{2i}\bar{x}(t)-A_{2i}(\hat{\bar{x}}(t)-Hy(t))+N_{2i}\tilde{g}_{i}+B_{2i}\tilde{f}_a(t)\nonumber \\&+\,E_{2i}d(t)-A_{2i}H y(t)-K_{2i}(y(t)-\hat{y}(t))]\nonumber \\= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[(A_{2i}-K_{2i}C_{1j})\tilde{\bar{x}}(t)+N_{2i}\tilde{g}_{i}\nonumber \\&+\,B_{2i}\tilde{f}_a(t)+E_{2i}d(t)] \end{aligned}$$
(33)

From (23), (25), (27), we have

$$\begin{aligned} \dot{\tilde{f}}_a(t)=\sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[-K_{3i}C_{1j}\tilde{\bar{x}}(t)+\dot{f}_a(t)] \end{aligned}$$
(34)

The error dynamic is represented as

$$\begin{aligned} \dot{e}=\sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[(A_{3i}-K_{4i}C_{3j})e(t)+N_{3i}\tilde{g}_i+E_{3i}\omega (t)] \end{aligned}$$
(35)

where \(e(t)=\left[ \begin{array}{ccc} \tilde{\bar{x}}(t) \\ \tilde{f}_a(t)\\ \end{array}\right] \), \(A_{3i}=\left[ \begin{array}{ccc} A_{2i}&{}&{}B_{2i} \\ O&{}&{}O \\ \end{array}\right] \), \(K_{4i}=\left[ \begin{array}{ccc} K_{2i} \\ K_{3i} \\ \end{array}\right] \), \(C_{3j}=[C_{1j}~~O]\), \(N_{3i}=\left[ \begin{array}{ccc} N_{2i} \\ O \\ \end{array}\right] \), \(E_{3i}=\left[ \begin{array}{ccc} E_{2i}&{}&{}O \\ O&{}&{}I \\ \end{array}\right] \), \(\omega (t)=\left[ \begin{array}{ccc} d(t) \\ \dot{f}_a(t)\\ \end{array}\right] \).

Choose the Lyapunov function \(V(t)=e^T(t)Pe(t)\), where P is a symmetric positive-definite matrix. The differential of V(t) along the error dynamic (35) is

$$\begin{aligned} \dot{V}(t)= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[e^T(t)((A_{3i}-K_{4i}C_{3j})^TP+P(A_{3i}-K_{4i}C_{3j}))e(t)\nonumber \\&~~~~~~~~~~~~~~~~+2e^T(t)PN_{3i}\tilde{g}_i+2e^T(t)PE_{3i}\omega (t)] \end{aligned}$$
(36)

According to Lemma 3, for \(i=1,2,\ldots ,r\), we have

$$\begin{aligned} 2e^T(t)PN_{3i}\tilde{g}_i\le \frac{1}{\delta _i}e^T(t)PN_{3i}N_{3i}^TPe(t)+ \delta _i\tilde{g}_i^T\tilde{g}_i \end{aligned}$$
(37)

where \(\delta _1,~\delta _2,\ldots ,\delta _r\) are positive scalars.

Since \(g_{i}(x)\) are Lipschitz with respect to the state x(t), and \(e(t)=[\tilde{\bar{x}}^T(t), f_a^T(t)]^T\), we have

$$\begin{aligned} \tilde{g}_i^T\tilde{g}_i= & {} \Vert g_i(x)-g_i(\hat{x})\Vert ^2\nonumber \\\le & {} c_i^2~ \Vert x(t)-\hat{x}(t)\Vert ^2\nonumber \\\le & {} c_i^2~ \Vert \bar{x}(t)-\hat{\bar{x}}(t)\Vert ^2\nonumber \\\le & {} c_i^2~e^T(t)e(t) \end{aligned}$$
(38)

where \(c_i\) are the Lipschitz constants of \(g_i(x)\).

From (36)–(38), we have

$$\begin{aligned} \dot{V}(t)\le & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[e^T(t) ((A_{3i}-K_{4i}C_{3j})^TP+P(A_{3i}-K_{4i}C_{3j})\nonumber \\&+\,\frac{1}{\delta _i}PN_{3i}N_{3i}^TP+\delta _ic_i^2I)e(t)+ 2e^T(t)PE_{3i}\omega (t)] \end{aligned}$$
(39)

Let

$$\begin{aligned} J_1(t)=\dot{V}(t)+e^T(t)e(t)-\gamma _1^2\omega ^T(t)\omega (t) \end{aligned}$$
(40)

It is not difficult to find that (28) and (29) are satisfied if \(J_1(t)<0\). Specifically, if \(\omega (t)=0\), (40) can be written as \(J_1(t)=\dot{V}(t)+e^T(t)e(t)\); i.e., \(J_1(t)<0\) implies \(\dot{V}(t)<-e^T(t)e(t)\le 0\). From Lyapunov theory, we obtain \(\lim \limits _{t\rightarrow \infty } e(t)=0\). Meanwhile, if \(\omega (t)\ne 0\), under the zero initial condition, (40) can be rewritten as

$$\begin{aligned} \int _0^tJ_1(s)ds=V(t)+\int _0^te^T(s)e(s)ds-\gamma _1^2\int _0^t \omega ^T(s)\omega (s)ds \end{aligned}$$
(41)

Since \(V(t)>0\), thus \(J_1(t)<0\) means \(\int _0^te^T(s)e(s)ds\le \gamma _1^2\int _0^t\omega ^T(s)\omega (s)ds\).

From (39) and (40), we can obtain

$$\begin{aligned} J_1(t)= & {} \dot{V}(t)+e^T(t)e(t)-\gamma _1^2\omega ^T(t)\omega (t)\nonumber \\\le & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[e^T(t)((A_{3i}-K_{4i}C_{3j})^TP+P(A_{3i}-K_{4i}C_{3j})\nonumber \\&+\,\frac{1}{\delta _i}PN_{3i}N_{3i}^TP+\delta _ic_i^2I)e(t)+2e^T(t)PE_{3i}\omega (t)\nonumber \\&+\,e^T(t)e(t)-\gamma _1^2\omega ^T(t)\omega (t)]\nonumber \\= & {} \zeta ^T(t)\varLambda \zeta (t) \end{aligned}$$
(42)

where

$$\begin{aligned} \varLambda =\sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\left[ \begin{array}{ccc} \varXi _{ij}+\frac{1}{\delta _i}PN_{3i}N_{3i}^TP+\delta _ic_i^2I+I &{}~ PE_{3i} \\ {*} &{}~-\gamma _1^2I\\ \end{array}\right] , \end{aligned}$$

\(\zeta (t)=[e^T(t), \omega ^T(t)]^T\), \(\varXi _{ij}=(A_{3i}-K_{4i}C_{3j})^TP+P(A_{3i}-K_{4i}C_{3j})\).

Obviously, \(\varLambda <0\) implies \(J_1(t)<0\). According to the Schur complement, \(\varLambda <0\), if and only if

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\varOmega _{ij}<0 \end{aligned}$$
(43)

where \(\varOmega _{ij}\) are the same as that in (32).

From Lemma 4, if (30) and (31) are satisfied, then (43) holds, which means that \(J_1(t)<0\); i.e., the fault estimation observer (24)–(27) can asymptotically estimate the state and the faults with the \(H_\infty \) performance level \(\gamma _1\).

The proof is completed. \(\square \)

Remark 5

Compared with previous results [9, 27], it is worth pointing out that the derivative of the measurement output is not used in the observer (24)–(27). Thus, our method has a wider range of application.

Remark 6

From the observer (24)–(27), it is not difficult to find that the estimations of the system state and sensor fault can be obtained as

$$\begin{aligned} \hat{x}(t)= & {} [I_{n}~O_{n\times m}]~\hat{\bar{x}}(t) \end{aligned}$$
(44)
$$\begin{aligned} \hat{f}_s(t)= & {} [O_{m \times n}~I_{m}]~\hat{\bar{x}}(t) \end{aligned}$$
(45)

where \(\hat{x}(t)\) and \(\hat{f}_s(t)\) are the estimations of x(t) and \(f_s(t)\), respectively. Furthermore, according to (25), the estimation of the actuator fault can be obtained.

Remark 7

Note that the minimum \(H_\infty \) attenuation value of the observer (24)–(27) (i.e., \(\gamma _1\)) can be obtained from linear matrix inequalities:

$$\begin{aligned}&min~~~\gamma _1\\&s.t.~~~(30),~(31) \end{aligned}$$

Remark 8

In the last few years, various types of fault estimation observers have been proposed, and excellent results have been achieved. However, most of the studies focused on systems subject only to an actuator fault or sensor fault, and some restrictive assumptions were necessary; e.g., the rank constraints of \(C_iB_i\), stable system matrices, the same measurement output matrices, and a single faulty actuator or sensor. Our observer can not only estimate the system state and actuator and sensor faults simultaneously but also be applied to systems without these assumptions. An example will be given in Section 5 to illustrate this point.

4 Fault Accommodation

This section presents the design of an observer-based fault-tolerant controller, which can compensate the effect of the faults and stabilize the fuzzy systems. Figure 1 is the structural diagram of the closed-loop system.

Fig. 1
figure 1

Structure diagram of the closed-loop system

Full size image

In addition to (7), the following assumption about \(g_i(x)\) is needed.

Assumption 4

The nonlinear functions \(g_i(x)\) satisfy \(g_i(0) = 0\).

Note that \(g_i(x)\) are Lipschitz functions; i.e., Assumption 4 implies the inequation

$$\begin{aligned} \Vert g_i(x)\Vert \le c_i \Vert x(t)\Vert \end{aligned}$$
(46)

where \(c_i\) are the Lipschitz constants.

Employing the technique of parallel distribution compensation, the observer-based fault-tolerant controller can be constructed as

$$\begin{aligned} u(t)=\sum _{i=1}^r\mu _i[-\bar{K}_{i}\hat{x}(t)-\hat{f}_a(t)] \end{aligned}$$
(47)

where \(\bar{K}_{i}\) are the controller gain matrices to be designed.

Substituting (47) in (4), we have

$$\begin{aligned} \dot{x}(t)= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[A_ix(t)+N_ig_i(x)+B_i(-\bar{K}_{j}\hat{x}(t)-\hat{f}_a(t)+f_a(t))+E_id(t)]\nonumber \\= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[A_ix(t)-B_i\bar{K}_{j}\hat{x}(t)+N_ig_{i}(x)+B_i\tilde{f}_a(t)+E_id(t)]\nonumber \\= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[(A_i-B_i\bar{K}_{j})x(t)+N_ig_{i}(x)+B_i\bar{K}_{j}\tilde{x}(t)\nonumber \\&~~~~~~~~~~~~~~~~+B_i\tilde{f}_a(t)+E_id(t)] \end{aligned}$$
(48)

where \(\tilde{x}(t)=x(t)-\hat{x}(t)\), \(\tilde{f}_a(t)=f_a(t)-\hat{f_a}(t)\)

The closed-loop system can be described as

$$\begin{aligned}&\dot{x}(t)=\sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[(A_i-B_i\bar{K}_{j})x(t)+N_ig_{i}(x)+\bar{B}_{ij}\varphi (t)] \end{aligned}$$
(49)
$$\begin{aligned}&y_L(t)=\sum _{i=1}^r\mu _iC_{Li}x(t) \end{aligned}$$
(50)

where \(\bar{B}_{ij}=[B_i\bar{K}_{j}~~B_i~~E_i]\), \(\varphi (t)=[\tilde{x}^T(t)~~\tilde{f}_a^T(t)~~d^T(t)]^T\).

Theorem 2

Given the \(H_\infty \) performance level \(\gamma _2\), the closed-loop system (49)–(50) is robust stable with the \(H_\infty \) performance level \(\gamma _2\), that is

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty } x(t)=0,~~if~~\varphi (t)=0 \end{aligned}$$
(51)
$$\begin{aligned}&\int _0^ty_{L}^T(s)y_{L}(s)ds\le \gamma _2^2\int _0^t\varphi ^T(s)\varphi (s)ds,~~if~~\varphi (t)\ne 0, \end{aligned}$$
(52)

if there exist a symmetric positive-definite matrix \(\bar{P}\), matrices \(Q_j\), and positive scalars \(\epsilon _1\), \(\epsilon _2\), ..., \(\epsilon _r\), for \(i,j=1,2,\ldots ,r\), such that the following linear matrix inequalities hold true:

$$\begin{aligned}&\varPhi _{ii}<0,~~~~1 \le i\le r \end{aligned}$$
(53)
$$\begin{aligned}&\frac{2}{r-1}\varPhi _{ii}+\varPhi _{ij}+\varPhi _{ji}< 0,~~~~1 \le i \ne j \le r \end{aligned}$$
(54)

where

$$\begin{aligned} \varPhi _{ij}=\left[ \begin{array}{ccccccc} \varPsi _{ij} &{} B_iQ_j&{} B_i&{} E_i &{} \bar{P}C_{Li}^T &{} \epsilon _iN_i &{} c_i\bar{P} \\ {*} &{} -2\rho _2\bar{P}+\rho _2I_n &{} O &{} O &{} O &{} O &{} O \\ {*} &{} {*}&{} -\rho _2I_{p_1} &{} O &{} O &{} O &{} O \\ {*} &{} {*}&{} {*} &{} -\rho _2I_{p_2} &{} O &{} O &{} O \\ {*} &{} {*}&{} {*} &{} {*} &{} -I_{q_1} &{} O &{} O \\ {*} &{} {*}&{} {*} &{} {*} &{} {*} &{} \epsilon _iI_{p_3} &{} O\\ {*} &{} {*}&{} {*} &{} {*} &{} {*} &{} {*} &{} \epsilon _iI_n\\ \end{array} \right] \end{aligned}$$
(55)

\(\varPsi _{ij}=A_i\bar{P}+\bar{P}A_i^T-B_iQ_j-Q_j^TB_i^T\), \(\rho _2=\gamma _2^2\). The gain matrices of the controller can be obtained by \(\bar{K}_{j}=Q_j\bar{P}^{-1}\).

Proof

Choose the Lyapunov function \(V(t)=x^T(t)Px(t)\), where \(P=\bar{P}^{-1}\) is a symmetric positive-definite matrix. The differential of V(t) along (49) can be obtained as

$$\begin{aligned} \dot{V}(t)= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[x^T(t)((A_i-B_i\bar{K}_{j})^TP+P(A_i-B_i\bar{K}_{j}))x(t)\nonumber \\&+\,2x^T(t)PN_ig_{i}(x)+2x^T(t)P\bar{B}_{ij}\varphi (t)] \end{aligned}$$
(56)

According to Lemma 3 and (46), for \(i=1,2,\ldots ,r\), we have

$$\begin{aligned} 2x^T(t)PN_ig_{i}(x)\le & {} \epsilon _ix^T(t)PN_iN_i^TPx(t)+\frac{1}{\epsilon _i}g_{i}(x)^Tg_{i}(x)\nonumber \\\le & {} x^T(t)\left( \epsilon _iPN_iN_i^TP+\frac{1}{\epsilon _i}c_i^2I\right) x(t) \end{aligned}$$
(57)

where \(\epsilon _1,~\epsilon _2,\ldots ,~\epsilon _r\) are positive scalars.

Let

$$\begin{aligned} J_2(t)=\dot{V}(t)+y_L^T(t)y_L(t)-\gamma _2^2\varphi ^T(t)\varphi (t) \end{aligned}$$
(58)

It follows from the Proof of Theorem 1 that (51)–(52) are satisfied if \(J_2(t)<0\).

From (50) and (56)–(58), we have

$$\begin{aligned} J_2(t)= & {} \dot{V}(t)+\sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[x^T(t)C_{Li}^TC_{Lj}x(t)]-\gamma _2^2\varphi ^T(t)\varphi (t)\nonumber \\= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[x^T(t)((A_i-B_i\bar{K}_{j})^TP+P(A_i-B_i\bar{K}_{j})+C_{Li}^TC_{Lj})x(t)\nonumber \\&+\,2x^T(t)PN_ig_{i}(x)+2x^T(t)P\bar{B}_{ij}\varphi (t)-\gamma _2^2\varphi ^T(t)\varphi (t)]\nonumber \\\le & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j[x^T(t)((A_i-B_i\bar{K}_{j})^TP+P(A_i-B_i\bar{K}_{j})+C_{Li}^TC_{Lj}\nonumber \\&+\,\epsilon _iPN_iN_i^TP+\frac{1}{\epsilon _i}c_i^2I)x(t)+2x^T(t)P\bar{B}_{ij}\varphi (t)-\gamma _2^2\varphi ^T(t)\varphi (t)]\nonumber \\= & {} \sum _{i=1}^r\sum _{j=1}^r\mu _i\mu _j\left[ \begin{array}{ccc} x(t)\\ \varphi (t)\\ \end{array} \right] ^T\left[ \begin{array}{ccc} \varUpsilon _{ij} &{} P\bar{B}_{ij}\\ {*} &{} -\gamma _2^2I\\ \end{array} \right] \left[ \begin{array}{ccc} x(t)\\ \varphi (t)\\ \end{array} \right] \end{aligned}$$
(59)

where

$$\begin{aligned} \varUpsilon _{ij}=(A_i-B_i\bar{K}_{j})^TP+P(A_i-B_i\bar{K}_{j})+C_{Li}^TC_{Lj}+\epsilon _iPN_iN_i^TP+\frac{1}{\epsilon _i}c_i^2I \end{aligned}$$

Thus, \(J_2(t)<0\), if

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\left[ \begin{array}{ccc} \varUpsilon _{ij} &{} P\bar{B}_{ij}\\ {*} &{} -\gamma _2^2I\\ \end{array} \right] <0 \end{aligned}$$
(60)

According to the Schur complement, (60) can be written as

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\left[ \begin{array}{ccccccc} \bar{\varUpsilon }_{ij} &{} PB_i\bar{K}_{j}&{} PB_i &{} PE_i &{} C_{Li}^T &{} \epsilon _iPN_i &{} c_iI\\ {*} &{} -\gamma _2^2I &{} O &{} O &{} O &{} O &{} O\\ {*} &{} {*} &{} -\gamma _2^2I &{} O &{} O &{} O &{} O\\ {*} &{} {*} &{} {*}&{} -\gamma _2^2I &{} O &{} O &{} O\\ {*} &{} {*} &{} {*} &{} {*} &{} -I &{} O &{} O\\ {*} &{} {*} &{} {*} &{} {*} &{} {*} &{} -\epsilon _iI &{} O\\ {*} &{} {*} &{} {*} &{} {*} &{} {*} &{} {*} &{} -\epsilon _iI\\ \end{array} \right] <0 \end{aligned}$$
(61)

where \(\bar{\varUpsilon }_{ij}=(A_i-B_i\bar{K}_{j})^TP+P(A_i-B_i\bar{K}_{j})\).

Let \(X=diag\{P^{-1},P^{-1},I_{p_1},I_{p_2},I_{q_1},I_{p_3},I_n\}\). Pre- and post-multiplying by X and its transpose in (61), then we have

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\left[ \begin{array}{ccccccc} \varPsi _{ij} &{} B_iQ_j&{} B_i&{} E_i &{} \bar{P}C_{Li}^T &{} \epsilon _iN_i &{} c_i\bar{P} \\ {*} &{} -\gamma _2^2\bar{P}\bar{P} &{} O &{} O &{} O &{} O &{} O \\ {*} &{} {*}&{} -\gamma _2^2I &{} O &{} O &{} O &{} O \\ {*} &{} {*}&{} {*} &{} -\gamma _2^2I &{} O &{} O &{} O \\ {*} &{} {*}&{} {*} &{} {*} &{} -I &{} O &{} O \\ {*} &{} {*}&{} {*} &{} {*} &{} {*} &{} -\epsilon _iI &{} O\\ {*} &{} {*}&{} {*} &{} {*} &{} {*} &{} {*} &{} -\epsilon _iI\\ \end{array} \right] <0 \end{aligned}$$
(62)

where \(\varPsi _{ij}=A_i\bar{P}+\bar{P}A_i^T-B_iQ_j-Q_j^TB_i^T\), \(\bar{P}=P^{-1}\), \(Q_j=\bar{K}_jP^{-1}\).

According to Lemma 3, it is easy to obtain that

$$\begin{aligned} \bar{P}+\bar{P}\le \bar{P}\bar{P}+I \end{aligned}$$
(63)

Obviously, (63) is equivalent to

$$\begin{aligned} -\gamma _2^2\bar{P}\bar{P} \le -2\gamma _2^2\bar{P}+\gamma _2^2I \end{aligned}$$
(64)

Thus, (62) holds, if

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{j=1}^r\mu _i\mu _j\varPhi _{ij}\le 0 \end{aligned}$$
(65)

where \(\varPhi _{ij}\) are the same forms as that in (55).

According to Lemma 4, if (53)–(54) are satisfied, then (65) holds, which implies that \(J_2(t)<0\); i.e., the closed-loop system (49)–(50) is robust stable with the \(H_\infty \) performance level \(\gamma _2\).

The proof is completed. \(\square \)

Remark 9

In this section, a robust fault-tolerant controller is designed for fuzzy systems with local nonlinear models and having sensor and actuator faults, simultaneously. It is worth pointing out that the observer and controller are designed separately. Compared with previous excellent results of fault estimation and fault accommodation, such as those reported in [2, 3, 7], the separate design can avoid coupling between the design of the observer and the design of the controller and reduce computation complexity.

Remark 10

From the observer and controller design processes, we find that, if \(d(t)=0\) and the actuator fault is constant, the error dynamic (35) is asymptotically stable; i.e., we can obtain accurate estimations of the system state and faults. Additionally, the closed-loop system (49)–(50) is asymptotically stable.

Remark 11

The main purpose of this paper is to develop a general framework of fault estimation and fault accommodation for a class of T–S fuzzy systems with local nonlinear models. In this paper, the parameterized linear matrix inequality techniques are used to reduce conservatism. It is worth pointing out that a fuzzy Lyapunov functional can be chosen to be less conservative. However, the computational complexity will increase, and interested readers can refer to the literature [2, 4, 6].

5 Simulation Results

In this section, an example is presented to illustrate the effectiveness of the proposed approach.

Consider fuzzy systems with local nonlinear models and having sensor and actuator faults, simultaneously, which are described in forms of (4)–(6), where

$$\begin{aligned} A_1= & {} \left[ \begin{array}{ccc} -1&{}0&{}0\\ 0&{}-2&{}0\\ 1&{}0&{}1\\ \end{array} \right] ,\quad A_2=\left[ \begin{array}{ccc} 1&{}-2&{}2\\ 2&{}-1&{}0\\ 1&{}3&{}-3\\ \end{array} \right] ,\quad ~B_1=\left[ \begin{array}{ccc} -2&{}-2\\ 2&{}-2\\ -2&{}0\\ \end{array} \right] ,\quad ~B_2=\left[ \begin{array}{ccc} 0&{}-2\\ -2&{}0\\ -2&{}0\\ \end{array} \right] \\ N_1= & {} \left[ \begin{array}{ccc} 0\\ 0\\ 1\\ \end{array} \right] ,\quad ~N_2=\left[ \begin{array}{ccc} 0\\ 1\\ 0\\ \end{array} \right] ,\quad ~E_1=\left[ \begin{array}{ccc} 0\\ 0.2\\ 0.2\\ \end{array} \right] ,\quad ~E_2=\left[ \begin{array}{ccc} 0.1\\ 0.1\\ 0\\ \end{array} \right] ,\quad ~C_1=\left[ \begin{array}{ccc} 1&{}2&{}-1\\ -1&{}0&{}0\\ 1&{}1&{}2\\ \end{array} \right] \\ C_2= & {} \left[ \begin{array}{ccc} 1&{}1&{}-5\\ -1&{}1&{}0\\ 1&{}0&{}1\\ \end{array}\right] ,\quad ~F=\left[ \begin{array}{ccc} 1\\ 2\\ -1\\ \end{array} \right] ,\quad ~C_{L1}=\left[ \begin{array}{ccc} 1&{}0&{}1\\ \end{array} \right] ,\quad ~C_{L2}=\left[ \begin{array}{ccc} 1&{}1&{}0\\ \end{array} \right] , \end{aligned}$$

\(g_1(x)=sin(x_1(t))\), \(g_2(x)=cos(x_1(t))-\frac{1}{2}\), and \(d(t)\in [-2,~2]\) is a random disturbance, \(f_a(t)=\left[ \begin{array}{ccc} f_{a1}(t)\\ f_{a2}(t)\\ \end{array} \right] \) and \(f_s(t)\) are actuator and sensor faults, respectively. It is assumed that

$$\begin{aligned} f_{a1}(t)= & {} \left\{ \begin{aligned}&0&~~~~ {t<10}\\&2\left( 1-e^{-3(t-10)}\right)&~~~~{t\ge 10} \end{aligned} \right. \\ f_{a2}(t)= & {} \left\{ \begin{aligned}&0&{t<10}\\&\frac{0.5}{1+2^{-t+20}}&~~{t\ge 10} \end{aligned} \right. \\ f_{s}(t)= & {} \left\{ \begin{aligned}&0&~~~~~ {t<10}\\&2\sin (2(t-10))&~~~{t\ge 10} \end{aligned} \right. \end{aligned}$$
Fig. 2
figure 2

The state \(x_1(t)\) and its estimation

Full size image
Fig. 3
figure 3

The state \(x_2(t)\) and its estimation

Full size image
Fig. 4
figure 4

The state \(x_3(t)\) and its estimation

Full size image
Fig. 5
figure 5

The actuator fault \(f_{a1}(t)\) and its estimation

Full size image
Fig. 6
figure 6

The actuator fault \(f_{a2}(t)\) and its estimation

Full size image
Fig. 7
figure 7

The sensor fault \(f_s(t)\) and its estimation

Full size image
Fig. 8
figure 8

The controlled output \(y_L(t)\)

Full size image
Fig. 9
figure 9

The estimation error of system state when \(d(t)=0\)

Full size image
Fig. 10
figure 10

The estimation error of faults when \(d(t)=0\)

Full size image
Fig. 11
figure 11

The controlled output \(y_L(t)\) when \(d(t)=0\)

Full size image
Fig. 12
figure 12

The estimation error of \(x_1(t)\)

Full size image
Fig. 13
figure 13

The estimation error of \(x_2(t)\)

Full size image
Fig. 14
figure 14

The estimation error of \(x_3(t)\)

Full size image
Fig. 15
figure 15

The estimation error of sensor fault \(f_s(t)\)

Full size image
Fig. 16
figure 16

The controlled output \(y_L(t)\)

Full size image

The membership functions are chosen as \(\mu _1(y_1(t))=e^{-y_1^2(t)}\) and \(\mu _2(y_1(t))=1-e^{-y_1^2(t)}\).

We choose \(K_{111}=K_{112}=O_{3\times 3}\), \(K_{121}=diag\{1,2,3\}\), \(K_{122}=diag\{3,3,5\}\) and \(F^-=[0.1667,~0.3333,~-0.1667]\). According to the design procedure in this paper, let the \(H_\infty \) performance levels of the observer and the controller are \(\gamma _1=1.414\), \(\gamma _2=2.646\), respectively. From the LMIs (30)–(31) and (53)–(54), we can obtain the gain matrices of the observer and the controller as follows :

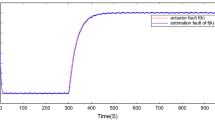
$$\begin{aligned} K_{21}= & {} \left[ \begin{array}{cccc} 29.4506 &{} 13.6322 &{} 4.5079\\ -4.6073 &{} -9.3340 &{} -9.1684\\ 15.2131 &{} 14.5619 &{} 10.1461\\ 14.0316 &{} 11.3855 &{} 7.1741\\ \end{array} \right] ,\quad ~K_{22}=\left[ \begin{array}{ccc} 15.7310&{} 9.6833&{} 45.0395\\ -3.6626&{} 1.6692&{} -15.3778\\ 6.0072&{} 2.7857&{} 34.3002\\ 6.3029&{} 3.7716&{} 29.1411\\ \end{array} \right] \\ K_{31}= & {} \left[ \begin{array}{ccc} -25.924&{} -28.008&{} -17.129\\ -30.071&{} 2.9043&{} 11.270\\ \end{array} \right] ,\quad K_{32}=\left[ \begin{array}{ccc} -8.4368&{} -12.313&{} -68.520\\ -15.654&{} -17.347&{} -11.626\\ \end{array} \right] \\ \bar{K}_{1}= & {} \left[ \begin{array}{ccc} -1.2725&{} 0.5348&{} -3.5126\\ -2.2522&{} -1.0509&{} -0.1390\\ \end{array} \right] ,\quad ~\bar{K}_{2}=\left[ \begin{array}{ccc} -1.3197&{} -1.9193&{} -0.0632\\ -4.4444&{} -1.5458&{} -1.4911\\ \end{array} \right] \end{aligned}$$

The simulation results of this example are provided in Figs. 2, 3 ,4, 5, 6, 7 and 8. Figures 2, 3 ,4, 5, 6 and 7 clearly show that the proposed observer can estimate the system state and sensor and actuator faults, simultaneously. Additionally, Fig. 8 illustrates that the proposed controller can compensate for the faults and stabilize the closed-loop system. Furthermore, according to Remark 7, it is not difficult to obtain a minimum \(H_\infty \) attenuation value of the observer of 0.2163.

Furthermore, for the case that there is no external disturbance, the simulation results are provided in Figs. 9, 10 and 11.

We carry out a simulation to compare the performance of our method with that of a previously proposed method [2]. Since the actuator fault was not considered in the latter, we assume that \(f_a(t)=0\). Additionally, we assume that the second local model has the same measurement output matrix as the first one. The comparison results are provided in Figs. 12, 13, 14, 15 and 16. Our method clearly provides similar or better results. Compared with the previously proposed method [2], our method can be used for fuzzy systems with an actuator fault and different measurement output matrices; i.e., our method has a wider application range.

6 Conclusions

This paper investigated the problems of fault estimation and fault accommodation for T–S fuzzy systems with local nonlinear models and having sensor and actuator faults, simultaneously. In the design of the observer, to avoid the sensor fault being amplified by observer gain matrices, the sensor fault is treated as a virtual state, and we then design a fuzzy fault estimation observer for the new fuzzy systems. Using the estimation information, an observer-based fault-tolerant controller is designed to guarantee the robust stability of the closed-loop system. Finally, simulation results show the effectiveness of the proposed method. It is worth pointing out that the issues of fuzzy systems with unmeasurable premise variables [1–4, 26] and type-2 T–S fuzzy systems [22–25] are interesting and practical and will be considered in our future works.