1 Introduction

Over the recent decades, the system reliability requirements have increased in the practical applications of safely-critical systems, especially flight control systems. To improve the reliability and safety of such systems, the model-based on fault diagnosis (FD) in dynamic systems has attracted considerable attention from many researchers. Among the various FD methods, the observer-based FD technique is the one that has been widely and most extensively considered; see survey articles: [1–6]. The basic idea of the observer-based FD is to estimate the states and/or the faults of the system from measurements using some types of observers, and define a residual evaluation function to compare the residual evaluation value with a predefined threshold.

In almost all of the above referenced articles, the study on observer-based FD is mainly concentrated on linear systems. Since almost all realistic physical processes exhibit nonlinear dynamics, FD for nonlinear systems has received a great deal of attention recently; for examples, see [7–9]. In particular, an important approach to nonlinear system FD is to model the considered nonlinear systems as Takagi and Sugeno (T–S) fuzzy systems [10], which have been proven to be a good universal approximator to nonlinear behaviors [11]. The prominent feature of T–S fuzzy models is that they are represented by some locally linear time-invariant submodels in the form of IF-THEN rules. In recent years, we have witnessed rapidly growing interest in FD observers’ design for T–S fuzzy models [12–18].

In some cases, fault accommodation strategies are needed, i.e., the control algorithm must be adapted based on fault detection for controlling the faulty system. Aircraft flight control systems [19] are good examples for applications of fault accommodation/active reliable control. In such cases, it is important to carry out fault estimation (FE) in addition to detection. In the last decade, there have been fruitful results on adaptive or robust FE, which can be found in [20–26]. In [24], the authors studied the problem of robust FE observer design for discrete-time T–S fuzzy systems via piecewise Lyapunov functions. In [25], the authors have designed a bank of sliding mode observers to detect and isolate the fault, and proposed a novel adaptive FE observer to estimate actuator faults.

It should be pointed out that the membership functions in all the above mentioned studies on fuzzy systems are required to be known. If the membership functions are unknown, for example, they may contain immeasurable premise variables or uncertain parameters, then the existing parallel distributed compensator (PDC) strategy based on fault-detection and/or FE results in the above studies cannot be used. In [27], a linear fault-detection filter with fixed gains was proposed for the T–S fuzzy It\(\widehat{o}\) stochastic system. It is noted that the linear fault-detection filter design may be conservative to some degree because it does not use any membership function information, especially for highly nonlinear complex systems. In [28], a switching-type fault-detection filter was used to detect the fault, which had a promising feature by means of which the membership function information can be employed to construct. Although the comparison results have illustrated the merits of the proposed switching-type fault-detection filter in [28], the computational burdens are heavy, especially for the multiple faults. To the best of the authors’ knowledge, up to now, the FD problem for fuzzy systems with uncertain grades of membership has not been fully investigated and remains as important and challenging one, which has motivated the current study.

The main objective of this article is to investigate the FD problem of uncertain nonlinear systems against actuator faults. The considered nonlinear systems are described by T–S fuzzy models with local nonlinear parts and uncertain grades of membership. The type of actuator faults under consideration contains bias faults and gain faults. First, by introducing a switching technique, a fault-detection observer is constructed to detect the fault. Furthermore, an adaptive FE observer design method combined with the proposed switching technique is developed. It is noted that the proposed FD scheme utilizes the lower and upper bounds information of the unknown membership functions, external disturbances, faults, and their coupling, and the obtained fault errors converge exponentially to zero. Finally, an example of NSV reentry dynamic model is given to illustrate the effectiveness and merits of the proposed method.

The structure of this article is as follows: following the introduction, the system description and the problem under consideration are given in Sect. 2. In Sect. 3, the FD problem is addressed. An example is given in Sect. 4 to show the superiority and effectiveness of proposed method. Finally, conclusions are drawn in Sect. 5.

2 System description and problem statement

2.1 System description

The following continuous-time T–S fuzzy dynamic model with local nonlinear parts can be used to represent a class of complex nonlinear systems subject to parameter uncertainties, in the form described as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}(t)=&{}\sum \limits _{i=1}^{N}\alpha _{i}(\theta (t))(A_{i}x(t)+B_{i}u(t)+N_{i}\phi (x(t))\\ &{}+G_{i}w(t))\\ y(t)=&{}\sum \limits _{i=1}^{N}\alpha _{i}(\theta (t))(C_{i}x(t)+N_{i1}\phi (x(t))), \end{array} \right. \nonumber \\ \end{aligned}$$
(1)

where \(N\) is the number of inference rules; \(x(t)\in R^{n}\) is the system state vector, and assumed to be measurable; \(u(t)\in R^{m}\) is the control input vector; \(y(t)\in R^{s}\) is the output vector; \(w(t)=\left[ w_{1}(t) \cdots w_{k}(t) \cdots w_{p}(t) \right] ^{T} \in R^{p}\) is the disturbance input; \(\theta (t)\) is the premise variable that contains the system states and unknown parameters; and \(A_{i},\ B_{i},\ G_{i},\ C_{i}\), \(N_{i}\), and \(N_{i1}\) are the known constant matrices with appropriate dimensions. As discussed in [29], \(\phi (x(t))\) is a known nonlinear function and reserved as the nonlinear part of local models. The membership functions \(\alpha _{i}(\theta (t))\) \((i=1, \ldots , N)\) are uncertain due to the existence of the parameter uncertainties and satisfy the following properties:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}0\le \underline{\alpha }_{i}\le \alpha _{i}(\theta (t))\le \overline{\alpha }_{i}\le 1,\ \mathrm {for}\ i=1,\ ...,\ N\\ &{}\sum \limits _{i=1}^{N}\alpha _{i}(\theta (t))=1, \end{array} \right. \end{aligned}$$
(2)

where \(\underline{\alpha }_{i}\), \(\overline{\alpha }_{i}\) \((i=1, \ldots , N)\) are the known constants.

To formulate the FD problem of this article, the fault model must be established first. Here, the types of actuator faults under consideration are bias faults and gain faults, which commonly occur in practice. Let \(u_{i}^{f}(t)\) represent the signal from the \(i\)th actuator that has failed, in this article, the following actuator faults are considered:

$$\begin{aligned} u_{i}^{f}(t)=(1-\rho _{i})u_{i}(t)+f_{i},\ i=1,\ 2, \ldots m \end{aligned}$$
(3)

where \(\rho _{i}, f_{i} (i=1,\ 2,\ ...\ m)\) are the unknown constants. Note that when \(\rho _{i}\ne 0, f_{i}=0\), there is an actuator gain fault for the \(i\)th actuator \(u_{i}(t)\); when \(\rho _{i}=0, f_{i}\ne 0\), there is an actuator bias fault for the \(i\)th actuator \(u_{i}(t)\); and when \(\rho _{i}=0\), \(f_{i}=0\), there is no fault for the \(i\)th actuator \(u_{i}(t)\).

Denote

$$\begin{aligned} \rho =diag\{\rho _{1},\ \ldots ,\ \rho _{m}\},\ F=[f_{1},\ \ldots ,\ f_{m}]^{T} \end{aligned}$$

Then, we have

$$\begin{aligned} u^{f}(t)=(I-\rho )u(t)+F \end{aligned}$$

Note that when \(\rho =0_{m\times m}\), \(F=0_{m\times 1}\), there is no fault for the system (1). The dynamics under normal case and faulty cases are described as

$$\begin{aligned}&\left\{ \begin{array}{ll} \dot{x}(t)=&{}\sum \limits _{i=1}^{N}\alpha _{i}(\theta (t))(A_{i}x(t)+B_{i}u^{f}(t)+N_{i}\phi (x(t))\\ &{}+G_{i}w(t))\\ y(t)=&{}\sum \limits _{i=1}^{N}\alpha _{i}(\theta (t))(C_{i}x(t)+N_{i1}\phi (x(t))) \end{array} \right. \end{aligned}$$
(4)

Remark 1

It is noted that, when a nonlinear system has complex nonlinearities, the constructed T–S fuzzy model with local linear parts must consist of a number of fuzzy rules. Then, the detector/estimator design for such a T–S fuzzy model becomes very difficult. In this article, a class of T–S fuzzy models with local nonlinear parts discussed in [29] are exploited to describe the considered nonlinear systems, which need fewer fuzzy rules and less computational burden.

We shall make the following assumptions throughout:

Assumption 1

It is assumed that only one single actuator fails at one time, and there exist known constants \(\overline{\rho }_{i}\), \(\underline{\rho }_{i}\), \(\overline{f}_{i}\), \(\underline{f}_{i}\) such that

$$\begin{aligned} \underline{\rho }_{i}\le \rho _{i}\le \overline{\rho }_{i},\ \underline{f}_{i}\le f_{i}\le \overline{f}_{i},\ \mathrm {for}\ i=1,\ 2,\ldots , m\nonumber \\ \end{aligned}$$
(5)

Assumption 2

For disturbance input component \(w_{k}(t)\), there exist two known constants \(\underline{w}_{k}\), \(\overline{w}_{k}\) such that

$$\begin{aligned} \underline{w}_{k}\le w_{k}(t)\le \overline{w}_{k},\ \mathrm {for}\ k=1,\ 2,\ \ldots ,\ p \end{aligned}$$
(6)

Assumption 3

In this article, we assume that the nonlinear function \(\phi (x(t))\) satisfies the following:

$$\begin{aligned}&||\phi (x(t))-\phi (\widehat{x}(t))||\le \vartheta ||R(x(t)-\widehat{x}(t))|| \end{aligned}$$
(7)
$$\begin{aligned}&-\phi (x(t))(Ex(t)-\phi (x(t)))\le 0, \end{aligned}$$
(8)

where \(\vartheta \) is a constant; and \(E\), \(R\) are constant matrices with proper dimensions.

Remark 2

It is well known that Assumptions 1, 2 are quite natural and common in the robust fault-tolerant control literature, which physically means that the boundaries of disturbance and fault signals are known. Assumption 3 implies that \(\phi (x(t))\) is a sector-bounded Lipschitz function, which has also been given in [29].

2.2 State-feedback controller design

To investigate the FD problem for closed-loop fuzzy systems, the state-feedback controller under fault-free (normal) case and faulty cases must be designed first. In order to ensure that the output \(y(t)\) tracks a given reference-input vector \(y_{r}(t)\) without steady-state error, we define \(e(t)=y_{r}(t)-Sy(t)\), where \(S\in R^{l\times s}\) is a known matrix used to form the output required to track the reference signal, and introduce an augmented state-space \(\xi (t)=[ (\int _{0}^{t}e(\tau )d\tau )^{T} x^{T}(t) ]^{T} \), the augmented system can be changed into

$$\begin{aligned} \dot{\xi }(t)&= \sum _{i=1}^{N}\alpha _{i}(\theta (t))(\overline{A}_{i}\xi (t)+\overline{B}_{i}u^{f}(t)\nonumber \\&+\,\overline{G}_{i}w(t)+B_{r}y_{r}(t)\nonumber \\&+\,\overline{N}_{i}\phi (x(t))), \end{aligned}$$
(9)

where

$$\begin{aligned}&\overline{A}_{i}=\left[ \begin{array}{cc} 0 &{} -SC_{i} \\ 0 &{} A_{i}\\ \end{array} \right] \overline{B}_{i}=\left[ \begin{array}{c} 0 \\ B_{i}\\ \end{array} \right] \overline{G}_{i}=\left[ \begin{array}{c} 0 \\ G_{i}\\ \end{array} \right] \\&\quad \overline{B}_{r}=\left[ \begin{array}{c} I \\ 0\\ \end{array} \right] \\&\overline{N}_{i}=\left[ \begin{array}{c} -SN_{i1} \\ N_{i}\\ \end{array} \right] \end{aligned}$$

In order to obtain a tracking controller with state-feedback plus tracking error integral, a state-feedback controller is designed such that the following control objectives are satisfied:

  1. (1)

    The closed-loop system in normal case is stable with a good disturbance attenuation performance.

  2. (2)

    The closed-loop system in faulty cases is stable with an acceptable disturbance attenuation performance.

Consider the following state-feedback controller:

$$\begin{aligned} u(t)=K_{a}(t)\xi (t)+K_{b}(t)\phi (x(t)), \end{aligned}$$
(10)

where \(K_{a}(t)\), and \(K_{b}(t)\) are the gains required to be determined. Then, the augmented closed-loop system can be obtained as

$$\begin{aligned} \dot{\xi }(t)&= \sum _{i=1}^{N}\alpha _{i}(\theta (t))((\overline{A}_{i}+\overline{B}_{i}(I-\rho )K_{a}(t))\xi (t)\nonumber \\&\quad +(\overline{N}_{i}+\overline{B}_{i}(I-\rho )K_{b}(t))\phi (x(t))\nonumber \\&\quad +\,\overline{B}_{i}F+\overline{G}_{i}w(t)\nonumber \\&\quad +B_{r}y_{r}(t)). \end{aligned}$$
(11)

Since the membership functions are unknown, the existing PDC controller design methods cannot be used here. In Appendix, we will present a non-PDC controller design method.

2.3 Problem statement

With the property of \(\sum _{i=1}^{N}\alpha _{i}(\theta (t))=1\), the closed-loop system (11) can be rewritten as

$$\begin{aligned} \dot{\xi }(t)&= \left[ (\overline{A}_{l}+\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{A}_{il})\right. \nonumber \\&\quad \left. +(\overline{B}_{l}+\,\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{B}_{il})(I-\rho )K_{a}(t)\right] \xi (t)\nonumber \\&\quad +\,\left[ (\overline{N}_{l}+\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{N}_{il})\right. \nonumber \\&\quad \left. +\,(\overline{B}_{l}+\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{B}_{il}) (I-\rho )K_{b}(t)\right] \nonumber \\&\quad \times \phi (x(t))\nonumber \\&\quad +\,(\overline{G}_{l}+\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{G}_{il})w(t)\nonumber \\&\quad +\,(\overline{B}_{l}+\sum _{i=1}^{N}\alpha _{i}(\theta (t))\overline{B}_{il})F +B_{r}y_{r}(t) \end{aligned}$$
(12)

with \(\overline{A}_{il}=\overline{A}_{i}-\overline{A}_{l}\), \(\overline{B}_{il}=\overline{B}_{i}-\overline{B}_{l}\), \(\overline{G}_{il}=\overline{G}_{i}-\overline{G}_{l}\), \(\overline{N}_{il}=\overline{N}_{i}-\overline{N}_{l}\), and \((\overline{A}_{l},\ \overline{B}_{l},\ \overline{N}_{l},\ \overline{G}_{l})\) is the deterministic part of the subsystem containing the equilibrium point of the original system. For brevity, in the sequel, we choose \(\overline{A}_{l}=\overline{A}_{1}, \overline{B}_{l}=\overline{B}_{1}, \overline{G}_{l}=\overline{G}_{1}, \overline{N}_{l}=\overline{N}_{1}\).

The problem considered in this article is to present a novel FD approach of actuators for the closed-loop fuzzy system (12). Meanwhile, the proposed approach can utilize the information of the uncertain grades of membership, external disturbances, local nonlinear parts, faults, and their coupling to construct the FD observers in a less conservative way.

3 Fault diagnosis

3.1 fault-detection observer design

Consider the closed-loop system (12) in fault-free case described by

$$\begin{aligned} \dot{\xi }(t)&= \left[ (\overline{A}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{A}_{i1})\right. \nonumber \\&\quad \left. +\,(\overline{B}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1})K_{a}(t)\right] \xi (t)\nonumber \\&\quad +\,\left[ (\overline{N}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{N}_{i1})+(\overline{B}_{1}\right. \nonumber \\&\quad \left. +\,\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1})K_{b}(t)\right] \phi (x(t))\nonumber \\&\quad +\,B_{r}y_{r}(t)+(\overline{G}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{G}_{i1})w(t)\nonumber \\ \end{aligned}$$
(13)

Define \(\alpha _{i}(\theta (t))w(t)=d_{i}(t)\), and \(\alpha _{i}(\theta (t))w_{k}(t)=d_{ik}(t)\), then we have

$$\begin{aligned} d_{i}(t)=\left[ \begin{array}{ccccc} d_{i1}(t) &{} \cdots &{} d_{ik}(t) &{} \cdots &{} d_{ip}(t) \\ \end{array} \right] ^{T} \end{aligned}$$
(14)

Because of \(0\le \underline{\alpha }_{i}\le \alpha _{i}(\theta (t))\le \overline{\alpha }_{i}\le 1\) and \(\underline{w}_{k}\le w_{k}(t)\le \overline{w}_{k}\), which implies

$$\begin{aligned} \underline{d}_{ik}\le d_{ik}(t)\le \overline{d}_{ik}, \end{aligned}$$
(15)

where \(\underline{d}_{ik}\) and \(\overline{d}_{ik}\) can be determined by the known constants \(\underline{\alpha }_{i}\), \(\overline{\alpha }_{i}\), \(\underline{w}_{k}\) and \(\overline{w}_{k}\). Then, the system (13) is rewritten as

$$\begin{aligned} \dot{\xi }(t)&= \left[ \overline{A}_{1}+\overline{B}_{1}K_{a}(t)+\sum _{i=2}^{N}\alpha _{i}(\theta (t))(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\right] \nonumber \\&\quad \times \,\xi (t)+[\overline{N}_{1}+\overline{B}_{1}K_{b}(t)+\sum _{i=2}^{N}\alpha _{i}(\theta (t))(\overline{N}_{i1}\nonumber \\&\quad +\,\overline{B}_{i1}K_{b}(t))]\phi (x(t))+\overline{G}_{1}w(t)\nonumber \\&\quad +\sum _{i=2}^{N}\overline{G}_{i1}d_{i}(t)+B_{r}y_{r}(t) \end{aligned}$$
(16)

The fault-detection observer is designed as

$$\begin{aligned} {\dot{\widehat{\xi }^{0}}}(t)&= (\overline{A}_{1}+\overline{B}_{1}K_{a}(t))\widehat{\xi }^{0}(t) +(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))\phi (\widehat{x}(t))\nonumber \\&\quad +\sum _{i=2}^{N}\widehat{\alpha }_{i}^{0}(t)(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)+\overline{G}_{1}\widehat{w}^{0}(t)\nonumber \\&\quad +\sum _{i=2}^{N}\overline{G}_{i1}\widehat{d}_{i}^{0}(t) +\sum _{i=2}^{N}\widehat{\alpha }_{i1}^{0}(t)(\overline{N}_{i1}+\overline{B}_{i1}K_{b}(t))\nonumber \\&\quad \times \phi (x(t))+B_{r}y_{r}(t), \end{aligned}$$
(17)

where \(\widehat{\xi }^{0}(t)\) is the estimation of \(\xi (t)\), \(\widehat{x}(t)\) is the estimation of \(x(t)\), and \(\widehat{\alpha }_{i}^{0}(t)\), \(\widehat{\alpha }_{i1}^{0}(t)\), \(\widehat{w}^{0}(t)\), \(\widehat{d}_{i}^{0}(t)\) are the switching signals, which are determined according to some switching laws to be defined later.

Define the error vector as \(e_{0}(t)=\xi (t)-\widehat{\xi }^{0}(t)\); combining (16) with (16), the observer error system can be obtained as

$$\begin{aligned} \dot{e_{0}}(t)&= (\overline{A}_{1}+\overline{B}_{1}K_{a}(t))e_{0}(t)\nonumber \\&\quad +\sum _{i=2}^{N}(\alpha _{i}(\theta (t))-\widehat{\alpha }_{i}^{0}(t))(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)\nonumber \\&\quad +\,\overline{G}_{1}(w(t)-\widehat{w}^{0}(t))\nonumber \\&\quad +\,\sum _{i=2}^{N}\overline{G}_{i1}(d_{i}(t)-\widehat{d}_{i}^{0}(t))+(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))\nonumber \\&\quad \times \, (\phi (x(t))-\phi (\widehat{x}(t)))+\sum _{i=2}^{N}(\alpha _{i}(\theta (t))\nonumber \\&\quad -\,\widehat{\alpha }_{i1}^{0}(t))(\overline{N}_{i1}+\overline{B}_{i1} K_{b}(t))\phi (x(t)). \end{aligned}$$
(18)

By applying the switching technique, we propose a novel observer which is particularly designed for fault-detection purpose. The following theorem establishes the convergence of the proposed observer.

Theorem 1

The observer error \(e_{0}(t)\) in (18) converges exponentially to zero if there exists a positive-definite matrix \(P=P^{T}\), and a positive number \(\epsilon \), such that the following matrix inequalities are feasible:

$$\begin{aligned}&P(\overline{A}_{1}+\overline{B}_{1}K_{a}(t))+(\overline{A}_{1}+\overline{B}_{1}K_{a}(t))^{T}P+\epsilon P<0 \end{aligned}$$
(19)
$$\begin{aligned}&\vartheta P(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))R\Theta +\vartheta (R\Theta )^{T}(\overline{N}_{1}\nonumber \\&\quad +\overline{B}_{1}K_{b}(t))^{T}P -\epsilon P<0 \end{aligned}$$
(20)

and the switching signals \(\widehat{\alpha }_{i}^{0}(t)\), \(\widehat{\alpha }_{i1}^{0}(t)\), \(\widehat{w}^{0}(t)\) and \(\widehat{d}_{i}^{0}(t)\) are designed according to the following switching laws:

$$\begin{aligned} \widehat{\alpha }_{i}^{0}(t)&= \underline{\alpha }_{i}+(\overline{\alpha }_{i}-\underline{\alpha }_{i})D(e_{0}^{T}(t)P(\overline{A}_{i1}\nonumber \\&+\,\overline{B}_{i1}K_{a}(t))\xi (t))\end{aligned}$$
(21)
$$\begin{aligned} \widehat{\alpha }_{i1}^{0}(t)&= \underline{\alpha }_{i}+(\overline{\alpha }_{i}-\underline{\alpha }_{i})D(e_{0}^{T}(t)P(\overline{N}_{i1}+\overline{B}_{i1}K_{b}(t))\nonumber \\&\quad \times \phi (x(t))) \end{aligned}$$
(22)
$$\begin{aligned} \widehat{w}_{k}^{0}(t)&= \underline{w}_{k}+(\overline{w}_{k}-\underline{w}_{k})D(e_{0}^{T}(t)[P\overline{G}_{1}]_{k}) \end{aligned}$$
(23)
$$\begin{aligned} \widehat{d}_{ik}^{0}(t)&= \underline{d}_{ik}+(\overline{d}_{ik}-\underline{d}_{ik})D(e_{0}^{T}(t)[P\overline{G}_{i1}]_{k}) \end{aligned}$$
(24)

for \(i=2,\ldots , N\), where the function \(D(z)\) is defined by

$$\begin{aligned} D(z)=\left\{ \begin{array}{ll} 1,&{} \mathrm {if}\ z \ge 0,\\ 0,&{} \mathrm {else}. \end{array}\right. \end{aligned}$$

Proof

Choose the Lyapunov function as

$$\begin{aligned} V(t)=e_{0}^{T}(t)Pe_{0}(t) \end{aligned}$$

The proof is similar to a few of the proofs of Theorem 2, and we will present it later. \(\square \)

Remark 3

If the membership functions are unknown, then a linear fault-detection filter design with fixed gains has been considered in [27]. However, the results in [27] may be conservative to some degree because the linear fault-detection filter design does not use any membership function information. To reduce the conservatism, a switching mechanism which depends on the lower and upper bounds of the unknown membership functions has been introduced in [28] to design a fault-detection filter with varying gains. It is noted that, to get convex filter design conditions, the authors imposed restrictions on the Lyapunov matrix, and the involved number of LMIs is \(2^{2N-1}+2\). Compared with [28], by introducing the switching technique, the proposed fault-detection method in Theorem 1 only needs two LMIs. As we know, larger number of conditions in the above computations may result in numerical problems (slow progress) with the LMI solver.

3.2 Fault estimation observer design

In this section, we will present an FE approach. Assume that the \(j\)th actuator is faulty, then the closed-loop system (12) is described as

$$\begin{aligned} \dot{\xi }(t)&= \left[ (\overline{A}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{A}_{i1})\right. \nonumber \\&\quad \left. +\,(\overline{B}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1}) K_{a}(t)\right] \xi (t)\nonumber \\&\quad +\left[ (\overline{N}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{N}_{i1})+(\overline{B}_{1}\right. \nonumber \\&\quad +\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1})K_{b}(t)]\phi (x(t))\nonumber \\&\quad \left. +\,(\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{G}_{i1}+\overline{G}_{1})w(t)-\overline{b}_{1,j}[\rho _{j}u_{j}(t)-f_{j}\right] \nonumber \\&\quad -\sum _{i=2}^{N}\overline{b}_{i1,j}[\rho _{i}^{j}(t)u_{j}(t)-f_{i}^{j}(t)]+B_{r}y_{r}(t), \end{aligned}$$
(25)

where \(\overline{b}_{i1,j}=\overline{b}_{i,j}-\overline{b}_{1,j},\ (i=2,\ldots , N)\).

Define \(\alpha _{i}(\theta (t))w(t)=d_{i}(t)\), and \(\alpha _{i}(\theta (t))w_{k}(t)=d_{ik}(t)\), then the closed-loop system (25) is rewritten as

$$\begin{aligned} \dot{\xi }(t)&= [(\overline{A}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{A}_{i1})+(\overline{B}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1})\nonumber \\&\quad \times K_{a}(t)]\xi (t) +[(\overline{N}_{1}+\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{N}_{i1})+(\overline{B}_{1}\nonumber \\&\quad +\sum _{i=2}^{N}\alpha _{i}(\theta (t))\overline{B}_{i1})K_{b}(t)]\phi (x(t))+\overline{G}_{1}w(t)\nonumber \\&\quad +\sum _{i=2}^{N}\overline{G}_{i1}d_{i}(t)-\overline{b}_{1,j}[\rho _{j}u_{j}(t)-f_{j}]-\sum _{i=2}^{N}\overline{b}_{i1,j}\nonumber \\&\quad \times [\rho _{i}^{j}(t)u_{j}(t) -f_{i}^{j}(t)]+B_{r}y_{r}(t). \end{aligned}$$
(26)

The observer for the \(j\)th fault is designed as

$$\begin{aligned} \dot{\widehat{\xi }^{j}}(t)&= (\overline{A}_{1}+\overline{B}_{1}K_{a}(t))\widehat{\xi }^{j}(t) +(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))\phi (\widehat{x}(t))\nonumber \\&\quad +\sum _{i=2}^{N}\widehat{\alpha }_{i}^{j}(t)(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)+\overline{G}_{1}\widehat{w}^{j}(t)\nonumber \\&\quad +\sum _{i=2}^{N}\overline{G}_{i1}\widehat{d}_{i}^{j}(t)+\sum _{i=2}^{N}\widehat{\alpha }_{i1}^{j}(t)(\overline{N}_{i1}+\overline{B}_{i1}K_{b}(t))\nonumber \\&\quad \times \,\phi (x(t))-\overline{b}_{1,j}[\widehat{\rho }_{j}(t)u_{j}(t)-\widehat{f}_{j}(t)]\nonumber \\&\quad -\sum _{i=2}^{N}\widehat{\rho }_{i1}^{j}(t)\overline{b}_{i1,j}u_{j}(t)+\sum _{i=2}^{N}\widehat{f}_{i1}^{j}(t)\overline{b}_{i1,j}+B_{r}y_{r}(t),\nonumber \\ \end{aligned}$$
(27)

where \(\widehat{\xi }^{j}(t)\) is the estimation of \(\xi (t)\), \(\widehat{x}(t)\) is the estimation of \(x(t)\), and \(\widehat{\alpha }_{i}^{j}(t), \widehat{\alpha }_{i1}^{j}(t), \widehat{w}^{j}(t), \widehat{d}_{i}^{j}(t), \widehat{f}_{i1}^{j}(t), \widehat{\rho }_{i1}^{j}(t)\) are the switching signals, which are determined according to some switching laws to be defined later, \(\widehat{\rho }_{j}(t)\) is the estimation of \(\rho _{j}\), and \(\widehat{f}_{j}(t)\) is the estimation of \(f_{j}\). Define the error vectors \(e_{j}(t)=\xi (t)-\widehat{\xi }^{j}(t), \widetilde{\rho }_{j}(t)=\rho _{j}-\widehat{\rho }_{j}(t), \widetilde{f}_{j}(t)=f_{j}-\widehat{f}_{j}(t)\), combine (26) with (27), the observer error system can be obtained as

$$\begin{aligned} \dot{e}_{j}(t)&= (\overline{A}_{1}+\overline{B}_{1}K_{a}(t))e_{j}(t)+\sum _{i=2}^{N}(\alpha _{i}(\theta (t))-\widehat{\alpha }_{i}^{j}(t)) \nonumber \\&\times (\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)+\overline{G}_{1}(w(t)-\widehat{w}^{j}(t))\nonumber \\&+\sum _{i=2}^{N}\overline{G}_{i1}(d_{i}(t)-\widehat{d}_{i}^{j}(t))+(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))\nonumber \\&\times (\phi (x(t))-\phi (\widehat{x}(t)))+\sum _{i=2}^{N}(\alpha _{i}(\theta (t))-\widehat{\alpha }_{i1}^{j}(t))\nonumber \\&\times (\overline{N}_{i1}+\overline{B}_{i1} K_{b}(t))\phi (x(t))-\overline{b}_{1,j}\widetilde{\rho }_{j}(t)u_{j}(t) \nonumber \\&+\,\overline{b}_{1,j}\widetilde{f}_{j}(t)-\sum _{i=2}^{N}(\rho _{i}^{j}(t)-\widehat{\rho }_{i1}^{j}(t))\overline{b}_{i1,j}u_{j}(t)\nonumber \\&+\sum _{i=2}^{N}(f_{i}^{j}(t)-\widehat{f}_{i1}^{j}(t))\overline{b}_{i1,j} \end{aligned}$$
(28)

Theorem 2

The observer error \(e_{j}(t)\) in (28) converges asymptotically to zero if there exists a positive-definite matrix \(P=P^{T}\) satisfying (19), (20), and the switching signals \(\widehat{\alpha }_{i}^{j}(t)\), \(\widehat{\alpha }_{i1}^{j}(t)\), \(\widehat{w}^{j}(t)\), \(\widehat{d}_{i}^{j}(t)\), \(\widehat{f}_{i1}^{j}(t)\), \(\widehat{\rho }_{i1}^{j}(t)\) are designed by the following switching laws

$$\begin{aligned} \widehat{\alpha }_{i}^{j}(t)&= \underline{\alpha }_{i}+(\overline{\alpha }_{i}-\underline{\alpha }_{i})D(e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)) \end{aligned}$$
(29)
$$\begin{aligned} \widehat{\alpha }_{i1}^{j}(t)&= \underline{\alpha }_{i}+(\overline{\alpha }_{i}-\underline{\alpha }_{i})D(e_{j}^{T}(t)P(\overline{N}_{i1}+\overline{B}_{i1}K_{b}(t)) \nonumber \\&\times \phi (x(t))) \end{aligned}$$
(30)
$$\begin{aligned} \widehat{w}_{k}^{j}(t)&= \underline{w}_{k}+(\overline{w}_{k}-\underline{w}_{k})D(e_{j}^{T}(t)[P\overline{G}_{1}^{j}]_{k}) \end{aligned}$$
(31)
$$\begin{aligned} \widehat{d}_{ik}^{j}(t)&= \underline{d}_{ik}+(\overline{d}_{ik}-\underline{d}_{ik})D(e_{j}^{T}(t)[P\overline{G}_{i1}^{j}]_{k}) \end{aligned}$$
(32)
$$\begin{aligned} \widehat{\rho }_{i1}^{j}(t)&= -\underline{\rho }_{i}^{j}-(\overline{\rho }_{i}^{j}-\underline{\rho }_{i}^{j})D(e_{j}^{T}(t)[P\overline{b}_{i1,j}]u_{j}(t)) \end{aligned}$$
(33)
$$\begin{aligned} \widehat{f}_{i1}^{j}(t)&= \underline{f}_{i}^{j}+(\overline{f}_{i}^{j}-\underline{f}_{i}^{j})D(e_{j}^{T}(t)[P\overline{b}_{i1,j}]) \end{aligned}$$
(34)

for \(i=2,\ldots , N\); and \(\widehat{\rho }_{j}(t)\), \(\widehat{f}_{j}(t)\) are determined according to the following adaptive laws

$$\begin{aligned} \dot{\widehat{\rho }}_{j}(t)&= -2\eta _{1}e_{j}^{T}(t)P\overline{b}_{1,j}u_{j}(t) \end{aligned}$$
(35)
$$\begin{aligned} \dot{\widehat{f}}_{j}(t)&= 2\eta _{2}e_{j}^{T}(t)P\overline{b}_{1,j}, \end{aligned}$$
(36)

where \(\eta _{1}\), \(\eta _{2}\) are prespecified positive scalars which define the learning rates for (35) and (36). Moreover, the fault errors \(\widetilde{\rho }_{j}(t)\), \(\widetilde{f}_{j}(t)\) converge exponentially to zero under a persistently exciting.

Proof

Choose the Lyapunov function as

$$\begin{aligned} V(t)=V_{1}(t)+V_{2}(t)+V_{3}(t) \end{aligned}$$
(37)

where

$$\begin{aligned} V_{1}(t)&= e_{j}^{T}(t)Pe_{j}(t)\\ V_{2}(t)&= \frac{1}{2\eta _{1}}\widetilde{\rho }_{j}^{2}(t)\\ V_{3}(t)&= \frac{1}{2\eta _{2}}\widetilde{f}_{j}^{2}(t) \end{aligned}$$

Taking the time-derivative of \(V_{i}(t)\) along the solution of (28), we have

$$\begin{aligned} \dot{V}_{1}(t)&= e_{j}^{T}(t)(P(\overline{A}_{1}+\overline{B}_{1}K_{a}(t))+(\overline{A}_{1}+\overline{B}_{1}K_{a}(t))^{T}P)\nonumber \\&\times \, e_{j}(t)+e_{j}^{T}(t)P(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))(\phi (x(t))\nonumber \\&-\,\phi (\widehat{x}(t)))+(\phi (x(t))-\phi (\widehat{x}(t)))^{T}(\overline{N}_{1}+\overline{B}_{1}\nonumber \\&\times \, K_{b}(t))^{T}Pe_{j}(t)+2e_{j}^{T}(t)P(\sum _{i=2}^{N}(\alpha _{i}(\theta (t))\nonumber \\&-\,\widehat{\alpha }_{i}^{j}(t))(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)+\sum _{i=2}^{N}(\alpha _{i}(\theta (t))\nonumber \\&-\,\widehat{\alpha }_{i1}^{j}(t))(\overline{N}_{i1}+\overline{B}_{i1} K_{b}(t))\phi (x(t))+\overline{G}_{1}(w(t)\nonumber \\&-\,\widehat{w}^{j}(t))+\sum _{i=2}^{N}\overline{G}_{i1}(d_{i}^{j}(t)-\widehat{d}_{i}^{j}(t))-\overline{b}_{1,j}\widetilde{\rho }_{j}(t)\nonumber \\&\times \, u_{j}(t)+\overline{b}_{1,j}\widetilde{f}_{j}(t)-\sum _{i=2}^{N}(\rho _{i}^{j}(t)-\widehat{\rho }_{i1}^{j}(t))\overline{b}_{i1,j}\nonumber \\&\times \, u_{j}(t)+\sum _{i=2}^{N}(f_{i}^{j}(t)-\widehat{f}_{i1}^{j}(t))\overline{b}_{i1,j})\\ \dot{V}_{2}(t)&= \frac{1}{\eta _{1}}\widetilde{\rho }_{j}(t)\,\dot{\widetilde{\rho }}_{j}(t)=\frac{1}{\eta _{1}}\widetilde{\rho }_{j}(t)(\dot{\rho }_{j}-\dot{\widehat{\rho }}_{j}(t))\\ \dot{V}_{3}(t)&= \frac{1}{\eta _{2}}\widetilde{f}_{j}(t)\dot{\widetilde{f}}_{j}(t)=\frac{1}{\eta _{2}}\widetilde{f}_{j}(t)(\dot{f}_{j}-\dot{\widehat{f}}_{j}(t)) \end{aligned}$$

From the switching laws given in (29), we have

$$\begin{aligned}&e_{j}^{T}(t)P(\sum _{i=2}^{N}(\alpha _{i}(\theta (t))-\widehat{\alpha }_{i}^{j}(t))(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)\nonumber \\&\quad =\sum _{i=2}^{N}(\alpha _{i}(\theta (t))-\underline{\alpha }_{i}-(\overline{\alpha }_{i}-\underline{\alpha }_{i})D(e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}\nonumber \\&\quad \times K_{a}(t))\xi (t))e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t) \end{aligned}$$
$$\begin{aligned} =\left\{ \begin{array}{l} \sum \limits _{i=2}^{N}(\alpha _{i}(\theta (t))-\overline{\alpha }_{i})e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)),\\ \mathrm {if}\ e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)) \ge 0,\\ \sum \limits _{i=2}^{N}(\alpha _{i}(\theta (t))-\underline{\alpha }_{i})e_{j}^{T}(t)P(\overline{A}_{i1}+\overline{B}_{i1}K_{a}(t))\xi (t)),\\ \mathrm {else}. \end{array} \right. \end{aligned}$$

\(\le 0\)

Since \(\rho _{j}\), \(f_{j}\) are constants, then \(\dot{\rho }_{j}=0\), \(\dot{f}_{j}=0\). Combine (19) and (29)-(34), it is obviously obtained that

$$\begin{aligned}&\dot{V}(t)\le -\epsilon e_{j}^{T}(t)Pe_{j}(t)+e_{j}^{T}(t)P(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))\nonumber \\&\quad \times (\phi (x(t))-\phi (\widehat{x}(t)))+(\phi (x(t))-\phi (\widehat{x}(t)))^{T}(\overline{N}_{1}\nonumber \\&\quad +\overline{B}_{1}K_{b}(t))^{T}Pe_{j}(t)-\widetilde{\rho }_{j}(t)(2e_{j}^{T}(t)P\overline{b}_{1,j}u_{j}(t)\nonumber \\&\quad +\frac{1}{\eta _{1}}\dot{\widehat{\rho }}_{j}(t))+\widetilde{f}_{j}(t)(2e_{j}^{T}(t)P\overline{b}_{1,j}-\frac{1}{\eta _{2}}\dot{\widehat{f}}_{j}(t)) \end{aligned}$$
(38)

Combine with (35) and (36), we have

$$\begin{aligned}&\dot{V}(t)\le -\epsilon e_{j}^{T}(t)Pe_{j}(t)\!+\!e_{j}^{T}(t)P(\overline{N}_{1}\!+\!\overline{B}_{1}K_{b}(t))(\phi (x(t))\nonumber \\&\quad -\,\phi (\widehat{x}(t)))+(\phi (x(t))-\phi (\widehat{x}(t)))^{T}(\overline{N}_{1}+\overline{B}_{1}\nonumber \\&\quad \times \, K_{b}(t))^{T} Pe_{j}(t) \end{aligned}$$
(39)

Note that

$$\begin{aligned} x(t)-\widehat{x}(t)=\varTheta e_{0}(t),\ \varTheta :=\left[ \begin{array}{cc} 0_{n\times 1} &{} I_{n\times n} \\ \end{array} \right] \end{aligned}$$

This together with (7), (19) and (20) leads to

$$\begin{aligned} \dot{V}(t)<-m||e_{j}(t)||^{2}\le 0 \end{aligned}$$

with \(m=\epsilon ||P||-2\vartheta ||P(\overline{N}_{1}+\overline{B}_{1}K_{b}(t))R\Theta ||\). On the other hand, let \(\widetilde{e}_{j}(t)=[ e_{j}^{T}(t) \widetilde{\rho }_{j}^{T}(t) \widetilde{f}_{j}^{T}(t) ]\), by (37), there exists a positive constant \(\delta \) such that

$$\begin{aligned} 0\le \delta ||\widetilde{e}_{j}(t)||\le V(t) \end{aligned}$$
(40)

Then

$$\begin{aligned}&0\le \delta ||\widetilde{e}_{j}(t)||\le V(t)\le V(0)+\int \limits _{0}^{t}\dot{V}(\tau )d\tau \le V(0)\nonumber \\&\quad -\int \limits _{0}^{t}m||e_{j}(\tau )||^{2}d\tau \le V(0) \end{aligned}$$
(41)

which means that the solution of the system described by (28) is uniformly bounded. Also, (41) implies that

$$\begin{aligned} lim_{t\rightarrow \infty }\int \limits _{0}^{t}m||e_{j}(\tau )||^{2}d\tau \le V(0) \end{aligned}$$
(42)

Since \(\widetilde{e}_{j}(t)\) is uniformly bounded, it follows that \(e_{j}(t)\), \(\widetilde{\rho }_{j}(t)\) and \(\widetilde{f}_{j}(t)\) are uniformly bounded, which implies \(e_{j}(t)\) is uniformly continuous. Therefore, \(\epsilon ||e_{j}(\tau )||^{2}\) is also uniformly continuous. Applying Barbalat’s Lemma to (42) yields \(lim_{t\rightarrow \infty }m||e_{j}(t)||^{2}=0\), i.e.,

$$\begin{aligned} lim_{t\rightarrow \infty }e_{j}(t)=0 \end{aligned}$$
(43)

Furthermore, by Lemma 1 in [4] and the following persistently exciting, that is, there exist \(\mu \) and \(T> 0\) such that,

$$\begin{aligned} \mu I\le \int \limits _{t}^{t+T}u_{j}^{T}(\tau )\overline{b}_{1,j}^{T}\overline{b}_{1,j}u_{j}(\tau )d\tau \quad \forall t\ge 0 \end{aligned}$$
(44)
$$\begin{aligned} \mu I\le \int \limits _{t}^{t+T}\overline{b}_{1,j}^{T}\overline{b}_{1,j}d\tau \forall t\ge 0 \end{aligned}$$
(45)

the fault errors \(\widetilde{\rho }_{j}(t), \widetilde{f}_{j}(t)\) converge exponentially to zero. \(\square \)

Remark 4

For linear time-invariant systems, by applying the adaptive technique, the authors in [4] investigated the actuator FD problem under the multiple-model structure for locked actuators and loss of actuator effectiveness, and proposed an adaptive UIO design approach for FD under some equality constraints. However, for nonlinear systems subject to parameter uncertainties, the above method is hard to work. For fuzzy systems, as the parameter uncertainties introduce uncertain grades of membership to the fuzzy systems, the favorable property offered by sharing the same premises in the fuzzy plant and fuzzy detectors/estimators in [24–26] cannot be applied in this article. In Theorem 2, combining the switching and adaptive techniques, the presented FE scheme utilizes the information of the lower and upper bounds of unknown membership functions, external disturbances, faults to construct the FE observer with varying gains, which can guarantee that the fault errors \(\widetilde{\rho }_{j}(t)\), \(\widetilde{f}_{j}(t)\) converge exponentially to zero.

3.3 fault-detection threshold design

The following assumption is required for the purpose of fault-detection decision:

Assumption 4

The steady-state values of the closed-loop, (13) and (26), are different from each other for \(\forall j\in {1,\ldots , m}\).

To address the fault-detection problem, the following model–match index in [30] is proposed to describe the dynamic behavior of the current system:

$$\begin{aligned} J_{0}^{\sigma }(t)&= c_{1}||e_{0}^{\sigma }(t)||^{2}\nonumber \\&+\,c_{2}\int _{0}^{t}exp(-\mu (t-s))||e_{0}^{\sigma }(s)||^{2}ds \end{aligned}$$
(46)

where \(e_{0}^{\sigma }(t)\) is the \(\sigma \)th component of \(e_{0}(t), c_{1}>0\) is the weight for the instantaneous residual signal, \(c_{2}>0\) is the weight for the past residual signals, and \(\mu >0\) is a forgetting factor that determines the memory of the index., Then we have

Fault-detection decision scheme If there exists an index \(\sigma \in \{1,\ 2,\ldots n+s\}\), a sufficient small positive scalar \(\varepsilon _{0}\), and a constant \(T_{d}\) such that

$$\begin{aligned} J_{0}^{\sigma }(t)\ge \varepsilon _{0},\ \mathrm {for}\ t\ge T_{d}, \end{aligned}$$
(47)

then a fault is detected at \(t=T_{d}\).

Remark 5

By Theorem 1, it is easy to see from (46) that \(J_{0}(t)\) will converge to zero in the fault-free case. Once a fault occurs, by Assumption 4, at least one of the components of \(J_{0}(t)\) will not approach zero, and thus the fault can be detected according to the proposed fault-detection decision scheme. Furthermore, if the \(j\)th actuator fault occurs, from Theorem 2 and Assumption 4, it is known that \(e_{j}(t)\) will converge asymptotically to zero, and such convergence does not hold for other errors.

4 Simulation example

In this section, a NSV attitude dynamics in a reentry phase is given as

$$\begin{aligned}&J\dot{\omega }=-\Omega J\omega +\delta \nonumber \\&\quad \dot{\gamma }=R(\cdot )\omega \end{aligned}$$
(48)

where \(\omega =[p\ q\ r]^{T}=[x_{1}(t)\ x_{2}(t)\ x_{3}(t)]^{T}\) is the angular rate (roll, pitch, and yaw rate, respectively); and \(\gamma =[\mu \ \beta \ \alpha ]^{T}=[x_{4}(t)\ x_{5}(t)\ x_{6}(t)]^{T}\) are the attitude angles (bank, sideslip, and angle of attack, respectively); The parameter matrices are given as

$$\begin{aligned}&\Omega =\left[ \begin{array}{c@{\quad }c@{\quad }c} 0 &{} -x_{3}(t) &{} x_{2}(t) \\ x_{3}(t) &{} 0 &{} -x_{1}(t) \\ x_{2}(t) &{} x_{1}(t) &{} 0 \\ \end{array} \right] \\&R(\cdot )=\left[ \begin{array}{c@{\quad }c@{\quad }c} cos(x_{6}(t)) &{} 0 &{} sin(x_{6}(t)) \\ sin(x_{6}(t)) &{} 0 &{} -cos(x_{6}(t)) \\ 0 &{} 1 &{} 0 \\ \end{array} \right] \end{aligned}$$

To demonstrate the validity and applicability of the suggested FD method, we consider the reentry phase of (48) with the altitude of \(H\) = 40 km and speed of \(V\) = 2500 m/s as the initial states, the inertia \(J\) is borrowed from [31]. As stated in [32], the nonlinearity of NSV reentry attitude dynamics mainly comes from the attack angle \(\alpha \) and the attitude angular velocity \(\omega \). During the phase of reentry \(\alpha \in [0,\ \pi /4]\), \(\omega \in [-0.5,\ 0.5]\), we choose six operating points: \([\alpha ,\ \omega ]\in \{[0,\ -0.5],\ [0,\ 0],\ [0,\ 0.5],\) \([\pi /4,\ -0.5],\) \([\pi /4,\ 0],\ [\pi /4,\ 0.5]\}\). Under the membership functions and the six operating points, the fuzzy system is described by

$$\begin{aligned} \dot{x}(t)&= \sum _{i=1}^{6}\alpha _{i}(x(t))(A_{i}x(t)+B_{i}u(t)+N_{i}\phi (x(t))\nonumber \\&+\,G_{i}w(t))\nonumber \\ y(t)&= \sum _{i=1}^{6}\alpha _{i}(x(t))C_{i}x(t) \end{aligned}$$
(49)

the parameter matrices \(A_{i}\), \(B_{i}\), \(C_{i}\) are given in [32], and

$$\begin{aligned} G_{1}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1&0.01&0.01&0&0&0 \end{array} \right] ^{T}\\ G_{2}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1&0.01&0&0&0.01&0 \end{array} \right] ^{T}\\ G_{3}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.15&0.01&0.01&0.01&0&0 \end{array} \right] \\ G_{4}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.01&0.02&0.01&0&0&0 \end{array} \right] \\ G_{5}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1&0.01&0.01&0&0&0 \end{array} \right] \\ G_{6}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1&0.03&0.01&0&0&0.05 \end{array} \right] \\ N_{1}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&0.03&0.15&0&0&0 \end{array} \right] \\ N_{2}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.015&0.03&0&0.1&0&0 \end{array} \right] \\ N_{3}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.005&0.03&0.1&0&0&0 \end{array} \right] \\ N_{4}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.015&0.03&0&0&0.1&0 \end{array} \right] \\ N_{5}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.015&0&0&0&0.03&0 \end{array} \right] \\ N_{6}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.015&0.03&0&0&0&0.1 \end{array} \right] \end{aligned}$$

the local nonlinear part is assumed to be \(\phi (x(t))=(1-cos(x_{1}(t)))sin(x_{1}(t))\), and \(\phi (x(t))\in co\{0,\ \frac{2}{\pi }x_{1}(t)\}\). By virtue of the Canchy mean value theorem, it follows that \(||\phi (x(t))-\phi (\widehat{x}(t))||\le \vartheta ||R(x(t)-\widehat{x}(t))||\), where \(\vartheta =2.1\) and \(R=[1 0 0 0 0 0]\).

In order to ensure that the attitude angle \([x_{4}(t)\ x_{5}(t)\) \(x_{6}(t)]^{T}\) tracks a reference input \(y_{r}(t)\), let \(S=I_{3\times 3}\) and \(y_{r}(t)=[5^{o}\ 0^{o}\ 5^{o}]^{T}\).

As the nonlinear plant suffers parameter uncertainties [32], the membership functions \(\alpha _{i}(x(t))\) are assumed to be uncertain and belong to [0 1]. It is noted that, the FD approaches given in [24–26] cannot be applied for this class of systems. In this simulation, a common state-feedback controller is designed, The external disturbance is \(w(t)=0.1e^{-t}sin(5t)\). By Lemma 1, the state-feedback controllers are obtained with gains as:

$$\begin{aligned} K_{a}&= 10^{7}\left[ \begin{array}{ccccc} 0.1985 &{} 0.0678 &{} 0.0045 &{} -0.8634 &{} -0.0145 \\ -0.0141 &{} -0.0149 &{} 0.2621 &{} 0.0375 &{} -0.3519\\ 0.1477 &{} -0.1966 &{} -0.0006 &{} -0.3300 &{} -0.0193\\ \end{array}\right. \\&\left. \begin{array}{cccc} -0.0991 &{} -3.7358 &{} -0.2892 &{} -0.0206\\ -0.0209 &{} 0.2338 &{} 0.0487 &{} -1.2152\\ -0.8740 &{} -2.7018 &{} 0.8260 &{} -0.0499\\ \end{array} \right] \end{aligned}$$
$$\begin{aligned} K_{b}=10^{5}\left[ \begin{array}{c} -4.8655 \\ 0.2575 \\ -1.1380 \\ \end{array} \right] \end{aligned}$$

It is assumed that the system operates without faults at the beginning. From \(t=50s\), the fault occurs in the first actuator (\(j=1\)), and the second and third actuators are fault free; the faulty actuator is set up as

$$\begin{aligned} u_{1}^{f}(t)=\rho _{1} u_{1}(t)+f_{1}, \end{aligned}$$

where

$$\begin{aligned} \rho _{1}&= \left\{ \begin{array}{ll} 0,\ &{} 0\le t\le 50,\\ 0.8,&{} t>50. \end{array} \right. \\ f_{1}&= \left\{ \begin{array}{ll} 0,\ &{} 0\le t\le 50,\\ 6\times &{}10^{5},\ t>50. \end{array} \right. \end{aligned}$$

The objective is to design FD observers in the form of (17) and (27) to detect and estimate the occurred fault. By solving the LMIs (19) and (20), we get the Lyapunov matrices \(P\) as follows:

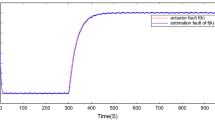
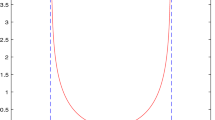
$$\begin{aligned} P=10^{4}\left[ \begin{array}{ccccc} 0.2230 &{} -0.0497 &{} 0.0119 &{} -0.0009 &{} 0.0027 \\ -0.0497&{} 0.0282 &{} 0.0016&{} 0.0001 &{} -0.0002 \\ 0.0119 &{} 0.0016 &{} 0.5695 &{} -0.0029 &{}-0.0366 \\ -0.0009&{} 0.0001 &{} -0.0029 &{} 0.0221 &{} 0.0036 \\ 0.0027 &{} -0.0002 &{}-0.0366 &{} 0.0036 &{}0.0628 \\ -0.0080&{} 0.0038 &{} -0.0040 &{} 0.0003 &{}-0.0003 \\ -0.0981&{} -0.0117 &{} -0.1679 &{} 0.0009 &{}-0.0686 \\ 0.0342 &{} -0.0130 &{} 0.0330 &{} 0.0001 &{} 0.0003 \\ 0.0137 &{} -0.0031&{} -0.2015 &{} 0.0016 &{} 0.0362 \\ \end{array} \right. \end{aligned}$$
$$\begin{aligned} \left. \begin{array}{cccc} -0.0080&{} -0.0981&{} 0.0342 &{} 0.0137 \\ 0.0038 &{} -0.0117 &{} -0.0130 &{} -0.0031\\ -0.0040&{} -0.1679 &{} 0.0330 &{} -0.2015\\ 0.0003 &{} 0.0009 &{} 0.0001 &{} 0.0016\\ -0.0003&{} -0.0686&{} 0.0003 &{} 0.0362\\ 0.0066 &{} 0.0016 &{} -0.0058 &{} 0.0005\\ 0.0016 &{} 1.6427&{} -0.0378 &{} -0.1041\\ -0.0058&{} -0.0378 &{} 0.0704 &{} -0.0225\\ 0.0005 &{} -0.1041 &{} -0.0225 &{} 0.6558\\ \end{array} \right] \end{aligned}$$

Figures 1, 2, 3 show the simulation results of the model–match indexes with \(c_{1}=c_{2}=\mu =1\) in (46). Setting \(\varepsilon _{0}=0.05\), the function \(J_{0}(t)\) generated by the fault-detection observer is shown in Fig. 1. It is shown that the fault is detected at \(t\) = 50.66 s. Figures 2 and 3, respectively, present the estimation results of the considered bias fault and the gain fault given by the corresponding adaptive observer. From Figs. 2 and 3, it can be seen that both bias fault and gain fault can be estimated accurately and promptly.

Fig. 1
figure 1

\(J_{0}(t)\) generated by fault-detection observer corresponding to the fault in the first actuator

Full size image
Fig. 2
figure 2

Bias fault \(f_{1}=6\times 10^{5}\) and its estimation \(\widehat{f}_{1}(t)\)

Full size image
Fig. 3
figure 3

Gain fault \(\rho _{1}=0.8\) and its estimation \(\widehat{\rho }_{1}(t)\)

Full size image

The state estimation error \(e_{1}(t)\) generated by the FE observer has been given in Fig. 4. From Fig. 4, it can be seen that although this FE observer can track the faulty system state, the introduced switching laws lead to the chatter phenomenon close to the equilibrium.

Fig. 4
figure 4

State estimation error \(e_{1}(t)\) generated by the FE observer corresponding to the fault in the first actuator

Full size image

5 Conclusion

This article investigates the FD problem for T–S fuzzy models with local nonlinear parts and uncertain grades of membership. The system states are chosen as the inputs of the FD observers. By introducing the switching and adaptive techniques, the presented FD scheme utilizes information about the lower and upper bounds of the unknown membership functions, external disturbances, faults, and their coupling to construct a bank of FD observers. It is noted that the obtained fault errors converge exponentially to zero. Finally, an example is given to illustrate the effectiveness and merits of the new results. For the future research, the studies on fault-tolerant control for fuzzy systems with uncertain grades of membership are under investigation.